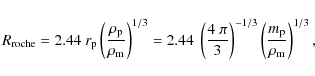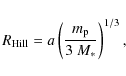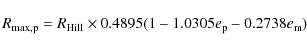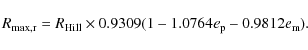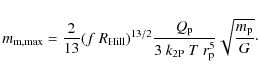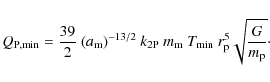EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 521 (October 2010) A&A, 521 (2010) A76 Full HTML
Free Access
Issue
A&A
Volume 521, October 2010
Article Number A76
Number of page(s) 6
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201014955
Published online 22 October 2010
A&A 521, A76 (2010)


 

Limits on the orbits and masses of moons around currently-known transiting exoplanets

C. Weidner - K. Horne

Scottish Universities Physics Alliance (SUPA), School of Physics and Astronomy, University of St. Andrews, North Haugh, St. Andrews, Fife KY16 9SS, UK

Received 7 May 2010 / Accepted 20 July 2010

Abstract
Aims. Current and upcoming space missions may be able to detect moons of transiting extra-solar planets. In this context it is important to understand if exomoons are expected to exist and what their possible properties are.
Methods. Using estimates for the stability of exomoon orbits from numerical studies, a list of 87 known transiting exoplanets is tested for the potential to host large exomoons.
Results. For 92% of the sample, moons larger than Luna can be excluded on prograde orbits, unless the parent exoplanet's internal structure is very different from the gas-giants of the solar system. Only WASP-24b, OGLE2-TR-L9, CoRoT-3b and CoRoT-9b could have moons above 0.4 $m_\oplus$, which is within the likely detection capabilities of current observational facilities. Additionally, the range of possible orbital radii of exomoons of the known transiting exoplanets, with two exceptions, is below 8 Jupiter-radii and therefore rather small.

Key words: astrobiology - planets and satellites: detection - planets and satellites: dynamical evolution and stability - planets and satellites: formation

1 Introduction

Currently more than 460 exoplanets[*] have been detected through various methods. With improving instrument precision smaller and less massive objects are or will be soon accessible observationally. With current instruments like Kepler it should even be possible to detect moons of exoplanets (Simon et al. 2009,2007; Kipping et al. 2009; Sartoretti & Schneider 1999; Kipping 2009). But as most planets are found by methods most sensitive to massive planets with a small semi-major axis (``Hot-Jupiters'') the question arises not only if it is possible to detect exomoons but also how likely it is for them to form and survive in the first place. Several studies (Domingos et al. 2006; Barnes & O'Brien 2002) explore the stability of orbits around gas giants.

In this contribution we apply to a sample of observed exoplanets the results of Domingos et al. (2006) on the stability of moons around gas giants. Our sample (Table 1) includes all published transiting exoplanets for which the mass and radius of the planet and the host star, and the orbital parameters are all reasonably well known.

2 Stability domains for exomoons

The region of orbital stability around a close-in gas-giant planet is set by two radii. We assume that the smallest orbit is set by the Roche-radius. Any moon larger than a few km within the Roche-limit of its planet would be torn apart by the tidal forces between the planet and the moon. The Roche-radius, $R_{\rm roche}$, depends mainly on the density of the two interacting objects and can be written for fluid-like objects as (Binney & Tremaine 1987):

\begin{displaymath} R_{\rm roche} = 2.44~r_{\rm p} \left(\frac{\rho_{\rm p}}{\rh... ...ght)^{-1/3} \left(\frac{m_{\rm p}}{\rho_{\rm m}}\right)^{1/3}, \end{displaymath} (1)

where $r_{\rm p}$ is the radius of the planet, $\rho_{\rm p}$and $\rho_{\rm m}$ are the mean densities of the planet and the moon, and $m_{\rm p}$ the mass of the planet. Of course the Roche criterion also limits the minimal semi-major axis, a, of the planet's orbit around its star. The second part of Eq. (1) shows that $R_{\rm roche}$ is independent of $r_{\rm p}$.

The outer limit for stable orbits of a moon around an exoplanet is the so-called Hill-radius, which defines the sphere in which the gravitational pull of the planet on the moon is larger than that of the star. The Hill-radius is given as (Burns 1986):

\begin{displaymath} R_{\rm Hill} = a \left(\frac{m_{\rm p}}{3~M_{\rm\ast}}\right)^{1/3}, \end{displaymath} (2)

where $M_{\rm\ast}$ is the mass of the star.

By using numerical integrations of the equations of motion, recent studies (e.g. Barnes & O'Brien 2002) found that the Hill-radius over estimates the maximum stable orbital radius by a factor f. Domingos et al. (2006) studied this question in detail and derived two equations for the maximal stable orbital radii, one for prograde motion of the moon and the other one for retrograde motion. Both depend on the eccentricities, $e_{\rm p}$, for the planet's orbit and $e_{\rm m}$ for the moon's. For a prograde satellite Domingos et al. (2006) give:

\begin{displaymath} R_{\rm max, p} = R_{\rm Hill} \times 0.4895 (1 - 1.0305e_{\rm p} - 0.2738e_{\rm m}) \end{displaymath} (3)

and for retrograde ones:

\begin{displaymath} R_{\rm max, r} = R_{\rm Hill} \times 0.9309 (1 - 1.0764e_{\rm p} - 0.9812e_{\rm m}). \end{displaymath} (4)

Table 1:   Properties of the 87 transiting exoplanets.

Barnes & O'Brien (2002) also studied the possible lifetime of a moon due to orbital decay as a result of tidal dissipation of angular momentum. Based on this result Domingos et al. (2006) also derived an equation for the maximum mass a moon can have for a given distance to the planet:

\begin{displaymath} m_{\rm m, max} = \frac{2}{13} (f~R_{\rm Hill})^{13/2} \frac{... ...3~k_{\rm 2P}~T~r_{\rm p}^{5}} \sqrt{\frac{m_{\rm p}}{G}}\cdot \end{displaymath} (5)

$Q_{\rm p}$ is the dimensionless tidal dissipation factor, $k_{\rm 2P}$ the tidal Love number, T the moon's lifetime and $f~R_{\rm Hill}$ either the pro- or the retrograde Hill radius. $Q_{\rm p}$ is very poorly constrained even for the planets of the solar system and even more uncertain for exoplanets. Following Barnes & O'Brien (2002) we chose $Q_{\rm p}$ = 105and $k_{\rm 2P}$ = 0.51. For the satellite lifetime, T, we adopt the minimum age of the parental star if given. For stars lacking age determinations, a minimum age of 1 Gyr is used. We consider moon/planet mass ratios $q \le$ 0.1, though, the tidal effects on the planetary rotation by moons with q > 0.01 might already modify the result (Barnes & O'Brien 2002). Such cases are marked with a ``d'' in Table 1.

The largest uncertainty in Eq. (5) lies in $Q_{\rm p}$. While a $Q_{\rm p} \sim 10^5$ is commonly used, Cassidy et al. (2009) suggested values as high as 1013 for exoplanets. A recent study (Lainey et al. 2009) derived $Q_{\rm p} = 3.6 \times10^4$ for Jupiter through astrometric observations of the planet and its moon Io. In this context it is interesting to note (Barnes & O'Brien 2002) that the actual detection of exomoons will give some important constrains on $Q_{\rm p}$, as Eq. (5) can be written the following way:

\begin{displaymath} Q_{\rm P,min} = \frac{39}{2}~(a_{\rm m})^{-13/2}~ k_{\rm 2P}... ... m}~T_{\rm min}~r_{\rm p}^{5} \sqrt{\frac{G}{m_{\rm p}}}\cdot \end{displaymath} (6)

Here only a minimal value for $Q_{\rm p}$ can be achieved as an observed exomoon need not necessarily be the most-massive moon possible for that planet.

3 Results

A list of currently known transiting exoplanets is shown in Table 1. In addition to the observed parameters of these planets, the table gives the Roche-radii, maximal pro- and retrograde Hill-radii and the maximal pro- and retrograde moon masses (Eqs. (1), (3)-(5)) for these systems. We used $Q_{\rm p}$ of 105 and $\rho_{\rm m}$ of 3 g cm-3 for the calculations.

In Fig. 1 the maximal stable prograde orbital radii, $R_{\rm max, p}$, for moons are shown for the known transiting exoplanets from Table 1. Plotted as a shaded region are the Roche limits for moons with densities between 1 and 6 g cm-3. For the majority of the known exoplanets stable moons on prograde orbits are possible. Depending on the density of the moon the percentage is between 63% ( $\rho _{\rm m} = 1$ g cm-3), 85% ( $\rho_{\rm m} = 3$ g cm-3) and 93% ( $\rho _{\rm m} = 6$ g cm-3).

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14955fg1.ps}\vspace*{-1mm} \vspace*{-2.5mm} \end{figure} Figure 1:

Open circles: largest stable prograde orbital radii for moons of the known transiting exoplanets as shown in Table 1. The minimal stable orbits for any substantial moon is given by the Roche-radii for moons with $\rho _{\rm m} = 1$ g cm-3 and $\rho _{\rm m} = 6$ g cm-3 (shaded region). All moons are assumed to reside on circular orbits ( $e_{\rm m} = 0$).

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14955fg2.ps}\vspace*{-1mm} \vspace*{-3.5mm} \end{figure} Figure 2:

Solid lines: Maximal stable prograde orbital radii vs. planet mass for different semi-major axis of the planets for a 1.0 $M_\odot $ star. The dashed-shaded region is minimal stable orbit given by the Roche-radii for moons with a density of $\rho _{\rm m} = 1$ to 6 g cm-3. For both the planet and the moon zero eccentricity is assumed. Open circles are known exoplanets orbiting a 1.0 $\pm $ 0.1 $M_\odot $ stars.

Open with DEXTER

It should be noted here, that the majority of the Hill-radii derived through Eq. (3) agree within better than 10% with the ones derived by Donnison (2010) for the 43 exoplanets of their sample which coincide with our sample. Though, Donnison (2010) does not investigate the possible masses of the exomoons and does not consider the Roche radii as an inner limits of the orbits of the moons.

The limiting $R_{\rm max, p}$, calculated from Eq. (3) are shown as solid lines in Fig. 2 for exoplanets with planetary masses between 0.01 and 40  $M_{\rm Jupiter}$ around a 1.0 $M_\odot $ star for ten different orbital separations, a, from 0.01 to 0.1 AU. The dashed-shaded region marks the Roche-radii of the planet in respect to moons with densities between 1 and 6 g cm-3. The eccentricity for both the planet and the moon is set to zero as non-zero eccentricities would only reduce the Hill-radii. Moons around planets on orbits of 0.02 AU and less are excluded, while only high-density ( $\rho_{\rm m} > 3$ g cm-3) moons can survive for planets on the 0.03 AU orbit. Also plotted in the Fig. 2 are the exoplanets from Table 1 for which the host stars are within 0.1 $M_\odot $ of 1.0 $M_\odot $. 11 out of 27 of these exoplanets have $R_{\rm max, p}$ within their Roche-radii, depending on the density of the moon. Therefore, a detection of a moon around one of these exoplanets would give strong constrains on the density of the moon.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14955fg3.ps}\vspace*{-2mm} \end{figure} Figure 3:

Open circles: Maximal possible moon mass for prograde moons of the known transiting exoplanets from Table 1. Shown as horizontal dotted lines are the mass of the Earth, of Ganymede and Titan, the largest moons in the solar system, and of the Earth's moon. For the error bars only the minimal and maximal ages of the stars are considered. All moons are assumed to reside on circular orbits ( $e_{\rm m} = 0$). The dashed lines are the maximal possible moon masses for theoretical mass-radius relations for gaseous exoplanets from Fortney et al. (2007) around a 1 $M_\odot $ star. The top-most dashed line corresponds to 300 Myr old exoplanets on a 0.1 AU orbit and with a core mass, $m_{\rm core}$, of 25 $M_\oplus $. The parameters for the exoplanets on the dashed line in the middle are age = 1 Gyr, a = 0.045 AU and $m_{\rm core} = 50~M_\oplus$. The lower dashed line plots 4.5 Gyr old exoplanets with a = 0.02 AU and without a solid core.

Open with DEXTER

The maximal possible masses for moons on prograde orbits around the known transiting exoplanets (Eq. (5)) are shown in Fig. 3. As is visible only very few exoplanets (7 of 87, 8%) have the potential for moons as massive as the Earth's moon or larger, independent of the density of the moons. But as Eq. (5) scales linearly with $Q_{\rm p}$ of the planet, larger moons would be possible for exoplanets with very different internal structures than our solar system Gas Giants. Also shown as dashed lines in Fig. 3 are maximal moon masses for theoretical mass-radius relations from Fortney et al. (2007) for different ages of the exoplanets, different orbital separations and different solid core fractions of the exoplanets. The top-most dashed lines corresponds to 300 Myr old exoplanets with 25 $M_\oplus $ solid cores, orbiting at 0.1 AU around a 1 $M_\odot $ star. The middle dashed line shows explanets with 50 $M_\oplus $ core mass, which are 1 Gyr old and at a distance of 0.045 AU to the host star. And finally the lowest dashed line are 4.5 Gyr old exoplanets with a = 0.02 AU and without a solid core. In all three cases a host star mass of 1 $M_\odot $ is assumed in order to calculate the Hill radii (Eq. (2)) needed for Eq. (5).

Relatively small changes of the exoplanetary radii due to contraction with time translate into a large changes of the maximal moon mass as Eq. (5) depends to the one over 5th power on the exoplanet radius.

The dependence of the fraction of exoplanets with possible major moons on the tidal dissipation factor ($Q_{\rm p}$) is quantified in Fig. 4. The fraction rises quite steeply for $Q_{\rm p}$ values from 104 to 109 and then saturates at the fraction of exoplanets which can have moons at all. This fraction is set by the density of the moon through the Roche limit of the orbit.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14955fg4.ps}\vspace*{-2mm} \end{figure} Figure 4:

Dependence of the fraction of exoplanets from Table 1 with possible major moons ( $m_{\rm exom} \ge m_{\rm Luna}$) on the tidal dissipation factor, $Q_{\rm p}$, of the planet. The solid line refers to moon with a density of 1 g cm-3, the dotted line to 3 g cm-3 and the dashed line to 6 g cm-3, as also indicated within the plot. The final percentages reached are the fractions of planets which can have any moon at all at a given density, which is independent of $Q_{\rm p}$.

Open with DEXTER

4 Discussion and conclusions

With the use of the results of Domingos et al. (2006) on stable orbits around gas giants the maximal and minimal orbital radii for hypothetical exomoons around the known transiting exoplanets are calculated.

Due to their much larger Hill-radii (for zero eccentricity of the planet and the moon) retrograde moons have larger maximal possible orbital radii and larger maximal masses than prograde moons.

Only WASP-24b (Street et al. 2010), OGLE2-TR-L9 (Snellen et al. 2009; Lendl et al. 2010), CoRoT-3b (Deleuil et al. 2008) and CoRoT-9b (Deeg et al. 2010) can have a large earth-sized (0.39, 0.51, 1.7 and 27 $M_\oplus $, respectively) prograde moons, for a $Q_{\rm p}$ of 105. In the case of WASP-24b and OGLE2-TR-L9 this is due to young minimum age of the stars, for CoRoT-3b the large mass of the planet (brown dwarf) of about 22 $M_{\rm Jup}$ enables massive moons, and in the case of CoRoT-9b the rather large distance of the planet to its parental star allows for large Hill-radii and therefore large moons. Therefore, these four exoplanets might be considered the best current candidates to search for exomoons.

Additionally, SWEEPS-04 (Sahu et al. 2006), CoRoT-6b (Fridlund et al. 2010) and CoRoT-13b (Cabrera et al. 2010) have the potential for moons of the size of the Earth's moon ( $m_{\rm Luna} \approx$ 1.2 $\times10^{-2}$ $M_\oplus $). When considering also retrograde moons several exoplanets could have Earth-sized or even larger moons. But the formation of large retrograde moons seems to be unlikely at least from the point of view of the Solar System moons. Therefore, 92% of the here studied exoplanets probably can have only very small prograde moons.

For WASP-19b (Hebb et al. 2010), CoRoT-7b (Queloz et al. 2009), WASP-18b (Southworth et al. 2009; Hellier et al. 2009), WASP-12b (Hebb et al. 2009), OGLE-TR-56b (Udalski et al. 2002; Southworth 2010), WASP-33b (Collier Cameron et al. 2010), TrES-3 (O'Donovan et al. 2007; Southworth 2010), WASP-4b (Wilson et al. 2008; Southworth 2010), OGLE-TR-113b (Southworth 2010; Bouchy et al. 2004), CoRoT-1b (Pont et al. 2010; Barge et al. 2008), CoRoT-14b (Tingley et al. 2010) and GJ 1214b (Charbonneau et al. 2009) prograde moons larger than a few kilometers radius are excluded. This translates into 15% of the total sample. Even when considering moons of a high density of 6 g cm-3 and an extreme $Q_{\rm p}$ of 1013, WASP-19b, CoRoT-7b, WASP-18b and WASP-12b are excluded to have large moons. In the case of HD 80606b (Hidas et al. 2010; Hebrard et al. 2010; Naef et al. 2001) both retro- and prograde moons are excluded due to the large eccentricity of the planets orbit. For this planet, only for a moon with a density larger than 31 g cm-3 would be the Roche-radius smaller than the prograde Hill-radius.

Therefore it is reasonable to conclude that for the vast majority of transiting exoplanets the existence of exomoons as large as the Earth moon or larger is rather unlikely, unless the tidal dissipation factor $Q_{\rm p}$ is considerably larger than 105 for these planets. The actual detection of exomoons would give considerable insight into the internal structure of the host planet and possibly the moon itself due to the relatively limited parameters space of possible orbits around the known transiting exoplanets.

As the ``habitable zone'' of M dwarfs is very close to the star, the rotational period of a planet becomes tidally locked to its orbital period (Peale 1977b) or the planet could be in a spin-orbit resonance, like Mercury in the Solar System. Several studies (Joshi et al. 1997; Heath et al. 1999; Merlis & Schneider 2010) argue that despite tidal-locking such planets might still bear life, though the odds for Earth-like life would seem rather low. Exomoons around tidally-locked gas giants may circumvent the problem of tidal-locking (Kaltenegger 2010). If close-in exoplanets or the exomoons of Hot-Jupiters could be habitable (for Earth-like life) is controversially discussed in the literature (Kiang et al. 2007; Segura et al. 2010; Peale 1977a; Cuntz et al. 2010; Khodachenko et al. 2007; Kaltenegger 2010; Scalo et al. 2007; Jones & Sleep 2010; Heath et al. 1999; Tarter et al. 2007; Williams et al. 1997; Lammer 2007), but of great interest as M dwarfs are the most common stars in the Galaxy.

The lowest-mass star in the current sample of transiting exoplanets is the M4.5 dwarf GJ 1214, with a mass of $M_{\rm GJ 1214} \approx$ 0.16 $M_\odot $. A hypothetical Jupiter-sized gas giant in the habitable zone of this star ( $R_{\rm habit} \approx $0.057 AU)[*] could host a prograde moon no larger than the Earth moon, unless the $Q_{\rm p}$ of the planet is significantly larger than 105 and any such moon would be very close to the planet ( $R_{\rm max,pro}$$\approx$ 8 $R_{\rm Jupiter}$).

It should also be noted here that 95% of the exoplanets included here have maximal possible prograde orbital radii less than 4 $\times10^5$ km ($\approx$5.7  $R_{\rm Jupiter}$), independent of the density of the moon and the $Q_{\rm p}$ of the planet. In our Solar System only two moons with masses similar to that of Earth's moon are so close to their planets: Jupiter's moon Io ( $m_{\rm Io} \approx 1.2$  $m_{\rm Luna}$, $a_{\rm Io}$$\approx$ 6 $R_{\rm Jupiter}$) and the Earth moon itself ( $a_{\rm Luna} \approx 5.5~R_{\rm Jupiter}$). The formation of very massive moons within the Hill-sphere of close-in exoplanets might therefore be considered very difficult (Namouni 2010) - at least on the basis of our current knowledge of the Solar System. Even if the formation of close-in massive exomoons is possible, the contraction of its host planet with time (Fortney et al. 2007) will lead to the orbital decay and eventual destruction of less and less massive exomoons over time due to the strong dependence of the maximal possible moon mass (Eq. (5)) on the radius of the planet.

Acknowledgements
We like to thank the referee Jason Barnes for helpful suggestions. C.W. is happy to thank Christine Liebig, Moira Jardine, and Andrew Collier Cameron for helpful discussions. The authors also gratefully acknowledge the use of the Extrasolar Planets Encyclopedia (http://exoplanet.eu/).

References

  1. Barge, P., Baglin, A., Auvergne, M., et al. 2008, A&A, 482, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Barnes, J. W., & O'Brien, D. P. 2002, ApJ, 575, 1087 [NASA ADS] [CrossRef] [Google Scholar]
  3. Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton, NJ: Princeton University Press), 747 [Google Scholar]
  4. Bouchy, F., Pont, F., Santos, N. C., et al. 2004, A&A, 421, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Burns, J. A. 1986, in Some Background about Satellites, ed. J. A. Burns, & M. S. Matthews (Tucson, AZ: University of Arizona Press), IAU Colloq., 77, 117 [Google Scholar]
  6. Cabrera, J., Bruntt, H., Ollivier, M., et al. 2010, A&A, in press [arXiv:1007.5481] [Google Scholar]
  7. Cassidy, T. A., Mendez, R., Arras, P., Johnson, R. E., & Skrutskie, M. F. 2009, ApJ, 704, 1341 [NASA ADS] [CrossRef] [Google Scholar]
  8. Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Collier Cameron, A., Guenther, E., Smalley, B., et al. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cuntz, M., Guinan, E. F., & Kurucz, R. L. 2010, in Solar and Stellar Variability: Impact on Earth and Planets, ed. A. G. Kosovichev, A. H. Andrei, & J.-P. Roelot, IAU Symp., 264, 419 [Google Scholar]
  11. Deeg, H. J., Moutou, C., Erikson, A., et al. 2010, Nature, 464, 384 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  12. Deleuil, M., Deeg, H. J., Alonso, R., et al. 2008, A&A, 491, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Domingos, R. C., Winter, O. C., & Yokoyama, T. 2006, MNRAS, 373, 1227 [NASA ADS] [CrossRef] [Google Scholar]
  14. Donnison, J. R. 2010, MNRAS, 406, 1918 [NASA ADS] [Google Scholar]
  15. Enoch, B., Collier Cameron, A., Parley, N. R., & Hebb, L. 2010, A&A, 516, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fridlund, M., Hébrard, G., Alonso, R., et al. 2010, A&A, 512, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Heath, M. J., Doyle, L. R., Joshi, M. M., & Haberle, R. M. 1999, Origins of Life and Evolution of the Biosphere, 29, 405 [Google Scholar]
  19. Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hebb, L., Collier-Cameron, A., Triaud, A. H. M. J., et al. 2010, ApJ, 708, 224 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hebrard, G., Desert, J., Diaz, R. F., et al. 2010, A&A, 516, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Hellier, C., Anderson, D. R., Cameron, A. C., et al. 2009, Nature, 460, 1098 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hidas, M. G., Tsapras, Y., Mislis, D., et al. 2010, MNRAS, 406, 1146 [NASA ADS] [Google Scholar]
  24. Jones, B. W., & Sleep, P. 2010, MNRAS, 407, 1259 [Google Scholar]
  25. Joshi, M. M., Haberle, R. M., & Reynolds, R. T. 1997, Icarus, 129, 450 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kaltenegger, L. 2010, ApJ, 712, L125 [NASA ADS] [CrossRef] [Google Scholar]
  27. Khodachenko, M. L., Ribas, I., Lammer, H., et al. 2007, Astrobiol., 7, 167 [Google Scholar]
  28. Kiang, N. Y., Segura, A., Tinetti, G., et al. 2007, Astrobiol., 7, 252 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kipping, D. M. 2009, MNRAS, 392, 181 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kipping, D. M., Fossey, S. J., & Campanella, G. 2009, MNRAS, 400, 398 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lainey, V., Arlot, J., Karatekin, Ö., & van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Lammer, H. 2007, Astrobiol., 7, 27 [Google Scholar]
  33. Lendl, M., Afonso, C., Koppenhoefer, J., et al. 2010, A&A, in press [arXiv:1007.0589] [Google Scholar]
  34. Merlis, T. M., & Schneider, T. 2010, J. Adv. Model. Earth Systems, submitted [arXiv:1001.5117] [Google Scholar]
  35. Naef, D., Latham, D. W., Mayor, M., et al. 2001, A&A, 375, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Namouni, F. 2010, ApJ, 719, L145 [NASA ADS] [CrossRef] [Google Scholar]
  37. O'Donovan, F. T., Charbonneau, D., Bakos, G. Á., et al. 2007, ApJ, 663, L37 [NASA ADS] [CrossRef] [Google Scholar]
  38. Peale, S. J. 1977a, Ann. Geophys., 33, 23 [Google Scholar]
  39. Peale, S. J. 1977b, in Planetary Satellites, ed. J. A. Burns (Tucson, AZ: University of Arizona Press), IAU Colloq., 28, 87 [Google Scholar]
  40. Pont, F., Endl, M., Cochran, W. D., et al. 2010, MNRAS, 402, L1 [NASA ADS] [CrossRef] [Google Scholar]
  41. Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Sahu, K. C., Casertano, S., Bond, H. E., et al. 2006, Nature, 443, 534 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  43. Sartoretti, P., & Schneider, J. 1999, A&AS, 134, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Scalo, J., Kaltenegger, L., Segura, A. G., et al. 2007, Astrobiol., 7, 85 [Google Scholar]
  45. Segura, A., Walkowicz, L. M., Meadows, V., Kasting, J. F., & Hawley, S. L. 2010, Astrobiol., in press [arXiv:1006.0022] [Google Scholar]
  46. Simon, A. E., Szatmáry, K., & Szabó, G. M. 2007, A&A, 470, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Simon, A. E., Szabó, G. M., & Szatmáry, K. 2009, Earth Moon Planets, 105, 385 [Google Scholar]
  48. Snellen, I. A. G., Koppenhoefer, J., van der Burg, R. F. J., et al. 2009, A&A, 497, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Southworth, J. 2010, MNRAS, in press [arXiv:1006.4443] [Google Scholar]
  50. Southworth, J., Hinse, T. C., Dominik, M., et al. 2009, ApJ, 707, 167 [NASA ADS] [CrossRef] [Google Scholar]
  51. Street, R. A., Simpson, E. K., Barros, S. C. C., et al. 2010, ApJ, submitted [Google Scholar]
  52. Tarter, J. C., Backus, P. R., Mancinelli, R. L., et al. 2007, Astrobiol., 7, 30 [NASA ADS] [CrossRef] [Google Scholar]
  53. Tingley, B., Endl, M., Gazzano, J.-C., et al. 2010, A&A, submitted [Google Scholar]
  54. Udalski, A., Zebrun, K., Szymanski, M., et al. 2002, Acta Astron., 52, 115 [Google Scholar]
  55. Williams, D. M., Kasting, J. F., & Wade, R. A. 1997, Nature, 385, 234 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  56. Wilson, D. M., Gillon, M., Hellier, C., et al. 2008, ApJ, 675, L113 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... 460 exoplanets[*]
For an up-to-date list see http://exoplanet.eu/
... AU)[*]
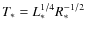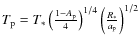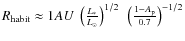Since from $T_\ast = L_\ast^{1/4}R_\ast^{-1/2}$ (in solar units) and $T_{\rm p} = T_\ast \left(\frac{1-A_{\rm p}}{4}\right)^{1/4} \left(\frac{R_{\rm\ast}}{a_{\rm p}}\right)^{1/2}$, follows $R_{\rm habit} \approx 1 AU~\left(\frac{L_\ast}{L_\odot}\right)^{1/2}~ \left(\frac{1-A_{\rm p}}{0.7}\right)^{-1/2}$.

All Tables

Table 1:   Properties of the 87 transiting exoplanets.

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14955fg1.ps}\vspace*{-1mm} \vspace*{-2.5mm} \end{figure} Figure 1:

Open circles: largest stable prograde orbital radii for moons of the known transiting exoplanets as shown in Table 1. The minimal stable orbits for any substantial moon is given by the Roche-radii for moons with $\rho _{\rm m} = 1$ g cm-3 and $\rho _{\rm m} = 6$ g cm-3 (shaded region). All moons are assumed to reside on circular orbits ( $e_{\rm m} = 0$).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14955fg2.ps}\vspace*{-1mm} \vspace*{-3.5mm} \end{figure} Figure 2:

Solid lines: Maximal stable prograde orbital radii vs. planet mass for different semi-major axis of the planets for a 1.0 $M_\odot $ star. The dashed-shaded region is minimal stable orbit given by the Roche-radii for moons with a density of $\rho _{\rm m} = 1$ to 6 g cm-3. For both the planet and the moon zero eccentricity is assumed. Open circles are known exoplanets orbiting a 1.0 $\pm $ 0.1 $M_\odot $ stars.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14955fg3.ps}\vspace*{-2mm} \end{figure} Figure 3:

Open circles: Maximal possible moon mass for prograde moons of the known transiting exoplanets from Table 1. Shown as horizontal dotted lines are the mass of the Earth, of Ganymede and Titan, the largest moons in the solar system, and of the Earth's moon. For the error bars only the minimal and maximal ages of the stars are considered. All moons are assumed to reside on circular orbits ( $e_{\rm m} = 0$). The dashed lines are the maximal possible moon masses for theoretical mass-radius relations for gaseous exoplanets from Fortney et al. (2007) around a 1 $M_\odot $ star. The top-most dashed line corresponds to 300 Myr old exoplanets on a 0.1 AU orbit and with a core mass, $m_{\rm core}$, of 25 $M_\oplus $. The parameters for the exoplanets on the dashed line in the middle are age = 1 Gyr, a = 0.045 AU and $m_{\rm core} = 50~M_\oplus$. The lower dashed line plots 4.5 Gyr old exoplanets with a = 0.02 AU and without a solid core.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14955fg4.ps}\vspace*{-2mm} \end{figure} Figure 4:

Dependence of the fraction of exoplanets from Table 1 with possible major moons ( $m_{\rm exom} \ge m_{\rm Luna}$) on the tidal dissipation factor, $Q_{\rm p}$, of the planet. The solid line refers to moon with a density of 1 g cm-3, the dotted line to 3 g cm-3 and the dashed line to 6 g cm-3, as also indicated within the plot. The final percentages reached are the fractions of planets which can have any moon at all at a given density, which is independent of $Q_{\rm p}$.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.