EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 521 (October 2010) A&A, 521 (2010) A24 Full HTML
Free Access
Issue
A&A
Volume 521, October 2010
Article Number A24
Number of page(s) 4
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201014853
Published online 15 October 2010
A&A 521, A24 (2010)

Improved radial velocity orbit of the young binary brown dwarf candidate Cha H 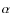${\sf\alpha}$ 8[*]

V. Joergens1,2 - A. Müller1,3 - S. Reffert4

1 - Max-Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
2 - Zentrum für Astronomie Heidelberg, Institut für Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
3 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
4 - Zentrum für Astronomie Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany

Received 23 April 2010 / Accepted 9 June 2010

Abstract
The very young brown dwarf candidate Cha H$\alpha $ 8 was recently discovered to have a close ($\sim$1 AU) companion by means of radial velocity monitoring. We present additional radial velocity data obtained with UVES/VLT between 2007 and 2010, which significantly improve the orbit determination of the system. The combined data set spans ten years of radial velocity monitoring for Cha H$\alpha $ 8. A Kepler fit to the data yields an orbital period of 5.2 years, an eccentricity of e = 0.59, and a radial velocity semi-amplitude of 2.4 km s-1. A companion mass $M_2\sin i$ (which is a lower limit due to the unknown orbital inclination i) of $25 \pm 7$  $M_{\rm Jup}$ and of $31 \pm 8$  $M_{\rm Jup}$ is derived when using model-dependent mass estimates for the primary of 0.07 $M_{\odot}$ and 0.10 $M_{\odot}$, respectively. Assuming random orientation of orbits in space, we find a very high probability that the companion of Cha H$\alpha $ 8 is of substellar nature: With a greater than 50% probability ($i \geq$ 60$^{\circ}$), the companion mass is between 30 and 35  $M_{\rm Jup}$and the mass ratio M2/M1 smaller than 0.4; with a greater than 87% probability ($i \geq$ 30$^{\circ}$) the companion mass is between 30 and 69  $M_{\rm Jup}$ and the mass ratio smaller than 0.7. The absence of any evidence of the companion in the cross-correlation function together with the size of the radial velocity amplitude also indicate a mass ratio of at most 0.7, and likely smaller. Furthermore, the new data exclude the possibility that the companion has a mass in the planetary regime ($\leq$13  $M_{\rm Jup}$). We show that the companion contributes significantly to the total luminosity of the system: model-dependent estimates provide a minimum for the luminosity ratio L2/L1 of 0.2. Cha H$\alpha $ 8 is the fourth known spectroscopic brown dwarf or very low-mass stellar binary with determined orbital parameters, and the second known very young one. With an age of only about 3 Myr, it is of particular interest to very low-mass formation and evolution theories. In contrast to most other spectroscopic binaries, it has a relatively long orbital period and it might be possible to determine the astrometric orbit of the primary and, thus, the orbital inclination.

Key words: techniques: radial velocities - binaries: spectroscopic - stars: individual: Cha H$\alpha $ 8 - stars: pre-main sequence - stars: low-mass - planets and satellites: detection

1 Introduction

Brown dwarf (BD) and very low-mass stellar (VLMS, $M \leq 0.1~M_{\odot}$) binaries are key objects to understand formation and evolution in the low-mass regime, in particular when they are very young. Roughly a hundred BD/VLMS binaries have been detected in recent years, predominantly by direct (adaptive optics or Hubble Space Telescope) imaging (e.g., http://www.vlmbinaries.org). For several of these visual BD/VLM binaries, it was possible to directly monitor the orbital motion and derive constraints on the orbital parameters and mass (e.g., Bouy et al. 2004; Dupuy et al. 2009; Konopacky et al. 2010; Stumpf et al. 2010). High-resolution spectroscopic monitoring for radial velocity (RV) variations led to the detection of a few very close ($\lesssim$1 AU) spectroscopic BD/VLM binaries. For four of them, RV orbital parameters were determined: PPl 15, a double-lined spectroscopic binary (SB2) in the Pleiades (Basri & Martín 1999); 2MASS J05352184-0546085 (hereafter 2M0535-05), a very young eclipsing SB2 system in Orion (Stassun et al. 2006); Cha H$\alpha $ 8, a very young spectroscopic binary in Chamaeleon I (Joergens & Müller 2007); and 2MASS J03202839-0446358, an SB1 at the M/L transition (Blake et al. 2008). Furthermore, for a few close visual BD/VLM binaries follow-up RV measurements permitted additional constraints of their orbits, e.g., GJ 569B (Zapatero Osorio et al. 2004; Simon et al. 2006; Konopacky et al. 2010); and 2MASS J07464256+2000321 (Konopacky et al. 2010). When combined with angular distance measurements or eclipse detections, spectroscopic binaries allow valuable dynamical mass determinations. Either the astrometric orbit or the eclipse light curve can provide the inclination i of the orbital plane, which is the missing parameter in the spectroscopic mass $M_2\sin i$. The mass is the most important input parameter for evolutionary models, which at ages <10 Myr and masses $\leq$0.3  $M_{\rm\odot}$ rely on only three measurements, the two components of the young eclipsing BD binary 2M0535-05 (Stassun et al. 2006; Mathieu et al. 2007) and the low-mass component of the pre-main sequence star UZ Tau E ( $0.294 \pm 0.027~M_{\rm\odot}$, Prato et al. 2002).

After 2M0535-05, Cha H$\alpha $ 8[*] is the second known very young ($\sim$3 Myr) BD/VLM spectroscopic binary and, therefore, of particular interest in the context of BD/VLM evolution and formation. Cha H$\alpha $ 8 is a very low-mass member (M5.75-M6.5, Comerón et al. 2000; Luhman 2004, 2007) of the nearby ($\sim$160 pc) Cha I star-forming region. An estimate of its mass based on evolutionary model tracks (Baraffe et al. 1998) yields 0.07 $M_{\odot}$ when using the values for effective temperature and bolometric luminosity by Comerón et al. (2000) and 0.10 $M_{\odot}$ when using those by Luhman (2007), respectively. Thus, Cha H$\alpha $ 8 is either a BD or a VLMS. A more detailed description of Cha H$\alpha $ 8 and its properties can be found in Joergens & Müller (2007).

RV data obtained until 2007 (Joergens & Müller 2007) showed that Cha H$\alpha $ 8 has a companion in a few years orbit with a potentially very low mass close to or in the planetary mass regime. This made Cha H$\alpha $ 8 a candidate for being the first BD/VLMS with an RV planet. We present here new RV measurements for Cha H$\alpha $ 8 which significantly improve the RV orbit for the system.

Table 1:   RV measurements of Cha H$\alpha $ 8.

2 Radial velocities and orbital solution

\begin{figure} \par\includegraphics[width=9cm,clip]{14853fg1.ps} \end{figure} Figure 1:

RV measurements of Cha H$\alpha $ 8 between 2000 and 2010 based on UVES/VLT spectra. New RV data measured between Jun 2007 and Mar 2010 are marked with black-filled points, previously obtained RV data with grey-filled points. Overplotted is the best-fit Keplerian orbit, which has a semi-amplitude of 2.4 km s-1, a period of 5.2 years and an eccentricity of e = 0.59.

Open with DEXTER

Spectroscopic observations of Cha H$\alpha $ 8 were carried out between 2000 and 2010 with the Ultraviolet and Visual Echelle Spectrograph (UVES, Dekker et al. 2000) attached to the VLT 8.2 m KUEYEN telescope at a spectral resolution $\lambda$/ $\Delta \lambda$ of 40 000 in the red optical wavelength regime. RVs were measured from these spectra based on a cross-correlation technique employing telluric lines for the wavelength calibration. Details of the data analysis can be found in Joergens (2006, 2008).

RV measurements for spectra taken between 2000 and 2002 provided already evidence of an RV companion to Cha H$\alpha $ 8 (Joergens 2006). Follow-up RV monitoring between 2005 and March 2007 allowed the determination of a first spectroscopic orbital solution for Cha H$\alpha $ 8 (Joergens & Müller 2007). Here, we present new RV data based on UVES spectra taken between June 2007 and March 2010. Table 1 lists the new RV measurements of Cha H$\alpha $ 8 and previous RV data. The latter were reprocessed for this work by using a slightly refined wavelength range for the cross-correlation to exclude a region that had been found to be contaminated by telluric lines and imperfectly corrected CCD cosmetic blemishes and that introduced additional scatter. The given errors $\sigma_{\rm RV}$ are in most cases the sample standard deviation of two consecutive individual measurements taking into account an additional minimum error of 150 m s-1. This minimum error accounts for both RV noise due to activity and fluctuations in the standard deviation for a small number of measurements. It is derived from an estimate of the RV noise based on the night-to-night rms scatter in the data.

The combined data set spans 9.9 years of RV monitoring for Cha H$\alpha $ 8 between 2000 and 2010. We calculate an improved orbital solution based on these data by fitting the six free parameters period, periastron time, eccentricity, longitude of periastron, RV semi-amplitude, and system velocity. The fitting procedure uses a global optimization method that is based on the genetic algorithm PIKAIA (Charbonneau 2002), as in the previous work. The reduced $\chi^2$ of the orbital fit is 1.45.

The fitted Kepler orbit is that of a companion revolving Cha H$\alpha $ 8 with a period of 1895 d (5.2 yr) on an eccentric (e=0.59) orbit and causing an RV semi-amplitude of 2.4 km s-1. The derived lower limit to the semi-major axis of the primary $a_1 \sin i$ is 0.34 AU. Figure 1 shows the RV measurements and the RV curve of the best-fit Kepler model. The complete list of determined orbital elements is given in Table 2.

The minimum mass of the companion $M_2\sin i$ in the case of a single-lined RV orbit depends on the primary mass, which is not very precisely determined for Cha H$\alpha $ 8, as is common in this mass and age regime. Using the two available estimates for the primary mass (0.07 and 0.10 $M_{\odot}$, cf. Sect. 1), the mass $M_2\sin i$ of the companion is determined to be 25 and 31 $M_{\rm Jup}$, respectively. The given errors in $M_2\sin i$ (cf. Table 2) are based on the fit and do not take into account additional possible errors in the primary mass, such as those introduced by the evolutionary models used to estimate the primary mass. The semi-major axis of the companion, which also depends on the primary mass estimate, is of the order of 1 AU.

The new orbit solution for Cha H$\alpha $ 8 is based on more epochs of RV measurements that cover a significantly larger portion of the orbital phase than the one derived by Joergens & Müller (2007). As illustrated in Fig. 1, previous data covered only about half of the total orbit, while the new measurements monitor the system at orbital phases that were so far completely unconstrained. Thus, the constraints on the orbit are now much stronger than in 2007 (one should not be misled by the apparently superior goodness of the fit of the previous orbit, which is in fact a result of undersampling). Because of this much larger phase coverage, the refinement of the RV data, and the introduction of a minimum error, an orbital solution is derived that has a significantly longer orbital period, and a slightly larger RV semi-amplitude and eccentricity than previously anticipated. The newly derived companion mass is consequently higher but being within 1$\sigma$ still consistent with that found previously ($16 \pm 4$  $M_{\rm Jup}$ and $20 \pm 5$  $M_{\rm Jup}$; note that the error ranges for $M_2\sin i$ are quoted incorrectly in Joergens & Müller 2007).

It has already been demonstrated in detail (Joergens & Müller 2007) that the detected RV variations cannot be caused by activity. The main arguments are summarized in the following: (i) The timescale of the RV variations is much too long to be explained by any phenomena that causes rotational modulation (the rotation rate of Cha H$\alpha $ 8 is of the order of a few days; Joergens & Guenther 2001; Joergens et al. 2003); (ii) accretion can also be excluded as source of RV noise because neither mid-IR (Persi et al. 2000; Comerón et al. 2000) nor L-band observations (Jayawardhana et al. 2003; Luhman et al. 2008) indicate the presence of disk material surrounding Cha H$\alpha $ 8. H$\alpha $ measurements also provide no evidence of accretion (e.g. Mohanty et al. 2005).

Table 2:   Orbital and physical parameters derived for the best-fit Keplerian model of Cha H$\alpha $ 8.

3 Discussion and conclusions

Following up on the discovery of an RV companion orbiting the BD candidate Cha H$\alpha $ 8 (Joergens & Müller 2007), we have monitored the system between 2007 and 2010 with high-resolution spectroscopy with UVES at the VLT. The combined data set spans 9.9 years of RV monitoring of Cha H$\alpha $ 8 and constitutes the longest RV monitoring program of a BD or VLMS. We have presented a significantly improved RV orbit solution of the system. The best-fit Kepler orbit of Cha H$\alpha $ 8 has a 5.2 yr period, an RV semi-amplitude of 2.4 km s-1, and an eccentricity of 0.59. We determined the spectroscopic minimum mass $M_2\sin i$ for the companion to be $25 \pm 7$  $M_{\rm Jup}$ and $31 \pm 8$  $M_{\rm Jup}$ for the two available model-dependent mass estimates for the primary of 0.07 $M_{\odot}$ and 0.10 $M_{\odot}$, respectively.

Based on the new RV data and orbit solution, we have been able to exclude that the companion of Cha H$\alpha $ 8 has a mass in the planetary mass regime ($\leq$ $13~M_{\rm Jup}$). New RV measurements (black-filled points in Fig. 1) significantly improve the phase coverage compared to previously available data (grey-filled points in Fig. 1) and show that the RV amplitude is larger than previously anticipated and that the orbit is inconsistent with a planetary mass of the companion.

The companion of Cha H$\alpha $ 8 is with high probability of substellar nature. This follows based on statistical considerations, as described in this paragraph, and it follows also independently based on the absence of companion lines, as described later. While RV orbits permit only the determination of lower mass limits $M_2\sin i$ due to the unknown inclination i, for orbits oriented randomly in space, there is a high probability that the true mass lies not too far from this limit. In the following, we calculate the absolute companion mass M2 for different inclinations. For this purpose, M2 is derived directly from the mass function rather than using the value of $M_2\sin i$ given in Table 2, which is for non-negligible companion masses valid only for large inclinations. Furthermore, it is taken into account that the companion contributes increasingly to the total luminosity when considering increasingly smaller inclinations (see paragraph after next) and, therefore, that the primary mass becomes increasingly low compared to the value derived for the unresolved luminosity. Here, the luminosity determined by Luhman (2007) for the unresolved system is used, which corresponds to a mass of the unresolved source of 0.10 $M_{\odot}$. We find that with a probability of greater than 50% (inclination greater than 60$^{\circ}$), the companion of Cha H$\alpha $ 8 has a mass between 30 and 35  $M_{\rm Jup}$. With a probability higher than 87% ( $i \geq 30^{\circ}$), it has a mass between 30 and 69  $M_{\rm Jup}$.

The mass ratio $q\equiv M_2/M_1$ of Cha H$\alpha $ 8 seems to be on the small side compared to other known BD/VLM binaries: it is at minimum 0.3, with more than 50% probability smaller than 0.4, and with more than 87% probability smaller than 0.7. This is smaller than the mass ratio of the majority of BD/VLMS detected through direct imaging, where 68% have $q \geq 0.8$ (value derived for binaries with a total mass <0.2 $~M_{\odot}$ as listed in the VLM binary archive as of July 2009 and applying small updates; cf. also Burgasser et al. 2007).

The companion of Cha H$\alpha $ 8 contributes significantly to the total luminosity of the system. The luminosity ratio L2 / L1 is estimated for different inclinations by employing low-mass evolutionary model tracks (Baraffe et al. 1998) and assuming the coevality of the binary components. For the luminosity of the unresolved system and its effective temperature, the values determined by Luhman (2007; $L_{\rm {tot}} =0.037$ $L_{\odot}$, $T_{\rm {eff}} = 3024$ K) are used, which correspond to a mass of the unresolved source of 0.10 $M_{\odot}$. At minimum, i.e. for $i =90^{\circ}$, the luminosity ratio L2 / L1 of the Cha H$\alpha $ 8 system is found to be 0.2. For larger inclinations, it becomes increasingly large, e.g., L2 / L1 =0.3 for $i =60^{\circ}$ and L2 / L1=0.7 for $i =30^{\circ}$, respectively. The limiting case is to consider a companion that is as luminous as the primary (i.e., $L_1= L_2 =L_{\rm {tot}}/2$). Comparison with evolutionary tracks shows that in this case the system would be slightly older (almost 5 Myr) and both components would have a mass of $M_1 = M_2\approx 0.085~M_{\odot}$. This constitutes the model-dependent minimum mass of the primary when using the parameters by Luhman (2007). Furthermore, it implies a minimum orbital inclination of 24$^{\circ}$. However, we show in the next paragraph that the components cannot have equal luminosities and masses but that L2/L1 and q are instead significantly smaller than 1.

There is no evidence of spectral lines of the companion in the spectra: neither exhibits the cross-correlation function a second peak, nor does its width or shape (bisector velocity span) correlate with RV. This implies that the companion is either too faint to be directly detected and/or that its signal is engulfed completely by the rotational broadening of the line profile ( $v \sin i =16 \pm 3$ km s-1; Joergens & Guenther 2001). In the latter case, blending effects can cause the net RV signal to be weaker than the true RV amplitude. To determine the maximum mass and luminosity ratio that is consistent with the absence of secondary lines and at the same time with the measured RV variation, we simulate rotationally broadened Gaussian functions representing the two components of a hypothetical binary using the eccentricity and period as determined here, the primary mass of Cha H$\alpha $ 8, allowing RV amplitudes of $\geq$2.4 km s-1, inclinations of 24-90$^{\circ}$, and involving again evolutionary models to estimate the luminosity ratio. The case in which both components have equal masses, and, therefore, equal luminosities, can be excluded immediately because the net RV signal would then be zero. More generally, we find that the mass ratio cannot be too high because the simulated RV curves would be of too small net amplitude due to blending. We derive a conservative upper limit to both[*] the mass and luminosity ratio of about 0.7.

Because of its very young age ($\sim$3 Myr) and the small number of known BD/VLMS spectroscopic binaries with determined orbital parameters, the very low-mass binary system Cha H$\alpha $ 8 is potentially of great interest for understanding formation and evolution close to and below the substellar borderline. Cha H$\alpha $ 8 has a relatively long orbit for a spectroscopic system and might therefore become one of the few spectroscopic binaries for which the relative astrometric orbit of the primary can be determined and for which absolute dynamical masses can be measured. Therefore, an astrometric monitoring program of this object is ongoing.

Acknowledgements
We acknowledge the excellent work of the ESO staff at Paranal, who took the data presented here in service mode. Furthermore, we are grateful to ESO for the possibility of immediate observations in 2010, which allowed us to sample the RV minimum of Cha H$\alpha $ 8. We would also like to thank an anonymous referee for very helpful comments. Part of this work was funded by the ESF. This publication has made use of the Very-Low-Mass Binaries Archive housed at http://www.vlmbinaries.org and maintained by Nick Siegler, Chris Gelino, and Adam Burgasser.

References

  1. Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A 337, 403 [Google Scholar]
  2. Basri, G., & Martín, E. L. 1999, ApJ, 118, 2460 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blake, C. H., Charbonneau, D., White, R. J., et al., ApJ, 678, L125 [Google Scholar]
  4. Bouy, H., Duchéne, G., Köhler, R., et al. 2004, A&A 423, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Burgasser, A. J., Reid, I. N., & Siegler, N. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 427 [Google Scholar]
  6. Charbonneau, P. 2002, Release Notes for PIKAIA 1.2, NCAR Technical Note 451+STR (Boulder: National Center for Atmospheric Research) [Google Scholar]
  7. Comerón, F., Neuhäuser, R., & Kaas, A. A. 2000, A&A, 359, 269 [NASA ADS] [Google Scholar]
  8. Dekker, H., D'Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in SPIE 4008, ed. M. Iye, & A. Moorwood, 534 [Google Scholar]
  9. Dupuy, T. J., Liu, M. C., Bowler, B. P., et al. 2009, ApJ, 706, 328 [NASA ADS] [CrossRef] [Google Scholar]
  10. Jayawardhana, R., Ardila, D. R., Stelzer, B., & Haisch, Jr. K. E. 2003, AJ, 126, 1515 [NASA ADS] [CrossRef] [Google Scholar]
  11. Joergens, V. 2006, A&A, 446, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Joergens, V. 2008, A&A, 492, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Joergens, V., & Guenther, E. 2001, A&A, 379, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Joergens, V., & Müller, A. 2007, ApJ, 666, L113 [NASA ADS] [CrossRef] [Google Scholar]
  15. Joergens, V., Fernández, M., Carpenter, J. M., & Neuhäuser, R. 2003, ApJ, 594, 971 [NASA ADS] [CrossRef] [Google Scholar]
  16. Konopacky, Q. M., Ghez, A. M., Barman, T. S., et al. 2010, ApJ, 711, 1087 [NASA ADS] [CrossRef] [Google Scholar]
  17. Luhman, K. L. 2004, ApJ, 614, 398 [Google Scholar]
  18. Luhman, K. L. 2007, ApJS 173, 104 [NASA ADS] [CrossRef] [Google Scholar]
  19. Luhman, K. L., Allen, L. E., Allen, P. R. et al. 2008, ApJ, 675, 1375 [NASA ADS] [CrossRef] [Google Scholar]
  20. Mathieu, R. D., Baraffe, I., Simon, M., Stassun, K. G., & White, R. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 411 [Google Scholar]
  21. Mohanty, S., Jayawardhana, R., & Basri, G. 2005, ApJ, 626, 498 [NASA ADS] [CrossRef] [Google Scholar]
  22. Prato, L., Simon, M., Mazeh, T., et al. 2002, ApJ, 579, L99 [NASA ADS] [CrossRef] [Google Scholar]
  23. Persi, P., Marenzi, A. R., Olofsson, G., et al. 2000, A&A, 357, 219 [NASA ADS] [Google Scholar]
  24. Simon, M., Bender, C., & Prato, L. 2006, ApJ, 644, 1183 [NASA ADS] [CrossRef] [Google Scholar]
  25. Stassun, K. G., Mathieu, R. D., & Valenti, J. A. 2006, Nature, 440, 311 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  26. Stumpf, M. B., Brandner, W., Henning, Th., et al. 2010, [arXiv:0811.0556] [Google Scholar]
  27. Zapatero Osorio, M. R., Lane, B. F., Pavlenko, Ya., et al. 2004, ApJ, 615, 958 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... 8[*]
Based on observations obtained at the Very Large Telescope of the European Southern Observatory at Paranal, Chile in program 279.C-5018(A), 380.C-0619(A), 082.C-0023(A+B), 385.C-0510(A).
...$\alpha $ 8[*]
Simbad name: [NC98] Cha HA 8.
... both[*]
Note that for young BDs, the mass-luminosity relation according to the applied evolutionary tracks is much less steep than for old field BDs, leading to constraints on the mass ratio that are of similar order as the luminosity ratio.

All Tables

Table 1:   RV measurements of Cha H$\alpha $ 8.

Table 2:   Orbital and physical parameters derived for the best-fit Keplerian model of Cha H$\alpha $ 8.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{14853fg1.ps} \end{figure} Figure 1:

RV measurements of Cha H$\alpha $ 8 between 2000 and 2010 based on UVES/VLT spectra. New RV data measured between Jun 2007 and Mar 2010 are marked with black-filled points, previously obtained RV data with grey-filled points. Overplotted is the best-fit Keplerian orbit, which has a semi-amplitude of 2.4 km s-1, a period of 5.2 years and an eccentricity of e = 0.59.

Open with DEXTER
In the text
Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.