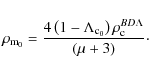| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 4 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201014602 | |
| Published online | 20 October 2010 | |
Brans-Dicke model constrained from the Big Bang nucleosynthesis and magnitude redshift relations of supernovae
(Research Note)
E. P. B. A. Thushari1 - R. Nakamura1 - M. Hashimoto1 - K. Arai2
1 - Department of Physics, Kyushu University, Fukuoka, 812-8581, Japan
2 -
Department of Physics, Kumamoto University, Kumamoto, 860-8555, Japan
Received 31 March 2010 / Accepted 12 July 2010
Abstract
We investigated the Brans-Dicke model with a variable cosmological term (![]() )
with the coupling constant
)
with the coupling constant
![]() .
We constrained the parameters inherent in this model from a comparison
between the Big Bang nucleosynthesis and the observed abundances.
Furthermore, we studied the magnitude redshift (m-z) relations for the
.
We constrained the parameters inherent in this model from a comparison
between the Big Bang nucleosynthesis and the observed abundances.
Furthermore, we studied the magnitude redshift (m-z) relations for the ![]() with and without another constant cosmological term in a flat universe.
Observational data of type Ia supernovae (SNIa) are used in the
redshift range of 0.01<z<2.
We found that our model with an energy density of the constant
cosmological term of 0.7 can explain the SNIa observations, though
the model parameters are insensitive to the m-z relation.
with and without another constant cosmological term in a flat universe.
Observational data of type Ia supernovae (SNIa) are used in the
redshift range of 0.01<z<2.
We found that our model with an energy density of the constant
cosmological term of 0.7 can explain the SNIa observations, though
the model parameters are insensitive to the m-z relation.
Key words: primordial nucleosynthesis - dark energy - early Universe - cosmology: observations - dark matter - cosmology: theory
1 Introduction
Astronomical observations indicate that the cosmological constant in the very early universe exceeds the present value by some 120 orders of magnitude, which is estimated in modern theories of elementary particles (Weinberg 1989). This is one of the fine-tuning problems in cosmology called the ``cosmological constant problem''. To explain the puzzle in cosmology, new modified theories are needed beyond the standard model. The behavior of the cosmological term has motivated various functional forms of the cosmological term. The mechanism of the dynamical reduction of the cosmological term is formulated as a time dependent function (Silviera & Waga 1997) and in terms of a scalar field (Weinberg 1989; Huterer & Turner 1999). On the other hand, generalized scalar tensor theories have been investigated (Wagoner 1970; Endo & Fukui 1977; Fukui et al. 2001).
One of them the Brans-Dicke (BD) theory with a variable cosmological term (![]() )
as a function of scalar field (
)
as a function of scalar field (![]() )
(Endo & Fukui 1977).
This model has been investigated for the early universe and constrained
from the Big Bang nucleosynthesis (BBN) (Arai et al. 1987; Etoh et al. 1997; Nakamura et al. 2006) for the coupling constant
)
(Endo & Fukui 1977).
This model has been investigated for the early universe and constrained
from the Big Bang nucleosynthesis (BBN) (Arai et al. 1987; Etoh et al. 1997; Nakamura et al. 2006) for the coupling constant
![]() .
Present observations suggest that the value of
.
Present observations suggest that the value of ![]() exceeds 40 000 (Berti et al. 2003; Bertotti et al. 2005). Therefore it is worthwhile to reconstrain the parameters in the Brans-Dicke model with a variable cosmological term (
exceeds 40 000 (Berti et al. 2003; Bertotti et al. 2005). Therefore it is worthwhile to reconstrain the parameters in the Brans-Dicke model with a variable cosmological term (![]() )
for a new value of
)
for a new value of ![]() .
The
.
The ![]() has played a very important role in explaining the characteristics of the early universe (Arai et al. 1987; Etoh et al. 1997; Nakamura et al. 2006). However, we still need an answer to the question ``How does this model work at the present epoch?''.
Therefore we adopt the magnitude redshift (m-z) relations
of type Ia supernova (SNIa) observations. This is because the
cosmological term significantly affects the cosmic expansion rate of
the universe at the low redshifts. The SNIa observations imply that the
universe is accelerating at the present epoch (Perlmutter et al. 1999; Riess et al. 1998, 1999).
has played a very important role in explaining the characteristics of the early universe (Arai et al. 1987; Etoh et al. 1997; Nakamura et al. 2006). However, we still need an answer to the question ``How does this model work at the present epoch?''.
Therefore we adopt the magnitude redshift (m-z) relations
of type Ia supernova (SNIa) observations. This is because the
cosmological term significantly affects the cosmic expansion rate of
the universe at the low redshifts. The SNIa observations imply that the
universe is accelerating at the present epoch (Perlmutter et al. 1999; Riess et al. 1998, 1999).
In Sect. 2 the formulation of the ![]() is reviewed. Parameters inherent in this model are constrained in Sect. 3 from the Big Bang nucleosynthesis for
is reviewed. Parameters inherent in this model are constrained in Sect. 3 from the Big Bang nucleosynthesis for
![]() .
In Sect. 4 the m-z relation is investigated for the
.
In Sect. 4 the m-z relation is investigated for the ![]() with including another constant cosmological term in a flat universe. Recent SNIa observational data (Astier et al. 2006; Riess et al. 2007; Kessler et al. 2009) are adopted to constrain the models. Concluding remarks are given in Sect. 5.
with including another constant cosmological term in a flat universe. Recent SNIa observational data (Astier et al. 2006; Riess et al. 2007; Kessler et al. 2009) are adopted to constrain the models. Concluding remarks are given in Sect. 5.
2 Brans-Dicke model with a variable cosmological term
The field equations for the ![]() are written as follows (Arai et al. 1987):
are written as follows (Arai et al. 1987):
where
where a(t) is the scale factor and k is the curvature constant. Here we adopt c=1. The expansion is described by the following equation derived from the (0,0) component of Eq. (1):
where
We adopt the simplest case of the coupling between the scalar, and the matter field is
where
where p is the pressure.
A particular solution of Eq. (2) is obtained from Eqs. (1) and (5):
where
The gravitational ``constant'' G is expressed as
The density
where the energy density of matter varies as
Then, Eq. (6) is integrated to give
where B is an integral constant, and here we use the normalized value of B:
![\begin{figure}
\par\includegraphics[height=7.8cm,width=7.4cm,angle=-90,clip]{14602fg1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14602-10/Timg39.png)
|
Figure 1:
Time evolutions of the scale factor in the |
| Open with DEXTER | |
The original Brans-Dicke theory is deduced for ![]() and is reduced to the Friedmann model when
and is reduced to the Friedmann model when ![]() = const. and
= const. and
![]() .
Physical parameters have been used to solve Eqs. (4), (7), and (11):
G0 = 6.6726
.
Physical parameters have been used to solve Eqs. (4), (7), and (11):
G0 = 6.6726 ![]()
![]() ,
,
![]() (Spergel et al. 2003), and
(Spergel et al. 2003), and
![]() (Berti et al. 2003; Bertotti et al. 2005). Figure 1 shows the evolution of the scale factor in the
(Berti et al. 2003; Bertotti et al. 2005). Figure 1 shows the evolution of the scale factor in the ![]() for the several values of B*. We identify considerable deviations in the
for the several values of B*. We identify considerable deviations in the ![]() from the Friedmann model at t<100 s, which depends on the specific parameters. Therefore the
from the Friedmann model at t<100 s, which depends on the specific parameters. Therefore the ![]() should be constrained from the BBN (Arai et al. 1987; Etoh et al. 1997; Nakamura et al. 2006).
should be constrained from the BBN (Arai et al. 1987; Etoh et al. 1997; Nakamura et al. 2006).
3 Parameters constrained from the Big Bang nucleosynthesis
The Big Bang nucleosynthesis provides powerful constraints on possible
deviation from the standard cosmology (Malaney & Mathews. 1993). As shown in Fig. 1, the expansion rates of the ![]() differ significantly from those of the standard Friedmann model.
differ significantly from those of the standard Friedmann model.
The abundance of light elements in the ![]() has already been investigated (Arai et al. 1987; Etoh et al. 1997; Nakamura et al. 2006). In the previous studies, the parameters inherent in the
has already been investigated (Arai et al. 1987; Etoh et al. 1997; Nakamura et al. 2006). In the previous studies, the parameters inherent in the ![]() have been constrained for
have been constrained for
![]() .
But we consider the case
.
But we consider the case
![]() for convenience, because the Cassini measurements of the Shapiro time delay indicate
for convenience, because the Cassini measurements of the Shapiro time delay indicate
![]()
![]() 104 (Berti et al. 2003; Bertotti et al. 2005). The detailed method of nucleosynthesis is described in Nakamura et al. 2006.
104 (Berti et al. 2003; Bertotti et al. 2005). The detailed method of nucleosynthesis is described in Nakamura et al. 2006.
Figure 2 shows the calculated abundances of
![]() ,
,
![]() ,
and
,
and
![]() for B*=2 and
for B*=2 and ![]() .
The
.
The
![]() uncertainties
in nuclear reaction rates are indicated by the dashed lines. The
horizontal dotted lines indicate the observational values of
uncertainties
in nuclear reaction rates are indicated by the dashed lines. The
horizontal dotted lines indicate the observational values of
![]() ,
,
![]() ,
and
,
and
![]() as follows:
Yp = 0.2516
as follows:
Yp = 0.2516 ![]() 0.0080 (Fukugita & Kawasaki 2006; Carr et al. 2010),
Yp= 0.326
0.0080 (Fukugita & Kawasaki 2006; Carr et al. 2010),
Yp= 0.326 ![]() 0.075 (Komatsu et al. 2010),
0.075 (Komatsu et al. 2010),
![]()
![]() 10-5 (Pettini et al. 2008),
10-5 (Pettini et al. 2008),
![]()
![]() 10-10 (Melendez & Ramirez 2004). Here two observational values of
10-10 (Melendez & Ramirez 2004). Here two observational values of
![]() are used. The solid vertical lines indicate the WMAP constraint of the baryon-to-photon ratio,
are used. The solid vertical lines indicate the WMAP constraint of the baryon-to-photon ratio,
![]()
![]() 10-10 (Komatsu et al. 2010).
10-10 (Komatsu et al. 2010).
The intersection range of the two observational values of
![]() is used to constrain the parameters. We found that the values of
is used to constrain the parameters. We found that the values of ![]() derived from
derived from
![]() and
and ![]() are tightly consistent with the value by the WMAP, though the lower limit of
are tightly consistent with the value by the WMAP, though the lower limit of
![]() is barely consistent. These agreements lead us to obtain the parameter ranges of
is barely consistent. These agreements lead us to obtain the parameter ranges of
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[height=9cm,width=8cm,angle=-360,clip]{14602fg2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14602-10/Timg55.png)
|
Figure 2:
Light element abundances of
|
| Open with DEXTER | |
4 m - z relation in the BD
 with and without a constant cosmological term
with and without a constant cosmological term
The distance modulus
![]() of the source at the redshift z is
of the source at the redshift z is
where m and M, are the apparent and absolute magnitudes respectively, and rl stands for the radial distance in units of Mpc.
We adopt the SNIa (Astier et al. 2006; Riess et al. 2007; Kessler et al. 2009) for which ![]() is defined by
is defined by
where
For the homogeneous and isotropic universe, the relation between the
radial distance and the redshift is derived from the Robertson-Walker
metric as (Weinberg 2008)
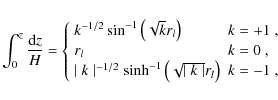
where
We conclude from the WMAP results that we live in a closely geometrically flat universe (Dunckley et al. 2009). The present matter density
where the
Using the analogy with the Lemaître model, Eq. (15) is transformed as
Here, the energy density parameters are defined as
The value
![\begin{figure}
\par\includegraphics[height=7.4cm,width=8.4cm,angle=360,clip]{14602fg3.eps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/13/aa14602-10/Timg73.png)
|
Figure 3:
Distance modulus vs. redshift for the flat universe in the Friedmann model and the |
| Open with DEXTER | |
Figure 3 shows the m-z relation in the ![]() for the SNIa observations. Matter is dominant in this model. The energy
density of the cosmological term is always less than
for the SNIa observations. Matter is dominant in this model. The energy
density of the cosmological term is always less than ![]() in the best-fit parameter region predicted in Sect. 3. The energy
density of the cosmological term always takes negative values in the
obtained parameter region. The parameter B* is not effective to change the values of
in the best-fit parameter region predicted in Sect. 3. The energy
density of the cosmological term always takes negative values in the
obtained parameter region. The parameter B* is not effective to change the values of
![]() and
and
![]() .
Because this model is matter dominant, it cannot be constrained by the SNIa observations.
.
Because this model is matter dominant, it cannot be constrained by the SNIa observations.
The Friedmann model with the energy density parameters of
![]() is merged into the
is merged into the ![]() model with the reduced
model with the reduced
![]() (where
(where
![]() and N is
defined as degrees of freedom). This is inconsistent with the present
accelerating universe, which should contain a sufficient amount of dark
energy to accelerate the universe. To explain the present
accelerating universe, we need some modification of the
cosmological term.
and N is
defined as degrees of freedom). This is inconsistent with the present
accelerating universe, which should contain a sufficient amount of dark
energy to accelerate the universe. To explain the present
accelerating universe, we need some modification of the
cosmological term.
As the next approach, the ![]() is modified by adding another constant cosmological term
is modified by adding another constant cosmological term
![]() .
The expansion rate in this model is written by
.
The expansion rate in this model is written by
The present matter density is
Here the energy density parameter of the constant cosmological term is fixed to be 0.7.
We find that this model is consistent with the SNIa observations as seen in Fig. 3. The total cosmological term becomes large in this model and consistent with the present accelerating universe with reduced
![]() (where
(where
![]() ). For
). For ![]() ,
the
,
the ![]() with
with
![]() predicts
predicts
![]()
![]() 10-2 and
10-2 and
![]() .
.
![]() always gets negative values in the parameter region of
always gets negative values in the parameter region of ![]() predicted in Sect. 3. If we consider the total value of energy densities, the contribution from
predicted in Sect. 3. If we consider the total value of energy densities, the contribution from
![]() to the total energy density is always between
to the total energy density is always between ![]() .
Therefore the cosmological term is dominant in the present epoch and
can be constrained from the present SNIa observations. We conclude that
the
.
Therefore the cosmological term is dominant in the present epoch and
can be constrained from the present SNIa observations. We conclude that
the ![]() with
with
![]() has nearly the same energy density parameters as the Friedmann model with
has nearly the same energy density parameters as the Friedmann model with
![]() .
Although the cosmological term is not important at the early epoch,
it plays a very important role at the present era. All the
parameters inherent in the
.
Although the cosmological term is not important at the early epoch,
it plays a very important role at the present era. All the
parameters inherent in the ![]() become insufficient as far as the m-z relation is concerned.
become insufficient as far as the m-z relation is concerned.
5 Concluding remarks
Previous BBN calculations restricted the parameter range as -
![]() and -
and -
![]() for
for
![]() (Nakamura et al. 2006). On the other hand, our high value of
(Nakamura et al. 2006). On the other hand, our high value of
![]() leads to reduces the parameter range of B* (-
leads to reduces the parameter range of B* (-
![]() )
and
)
and ![]() (
(
![]() ). The models parameters are inefficient in the m-z relations of the SNIa.
). The models parameters are inefficient in the m-z relations of the SNIa.
In Sect. 4, the value of
![]() is found to be much smaller compared with the other terms in Eq. (17). Even though
is found to be much smaller compared with the other terms in Eq. (17). Even though ![]() is increased until 104, the contribution from
is increased until 104, the contribution from
![]() to Eq. (17) is always less than
to Eq. (17) is always less than ![]() in that particular parameter range. There is no considerably negative
effect from the assumption we made in Sect. 4 to neglect the value
of
in that particular parameter range. There is no considerably negative
effect from the assumption we made in Sect. 4 to neglect the value
of
![]() .
In the parameter range
.
In the parameter range
![]() ,
,
![]() has taken negative values according to Eq. (17).
This may not conflict with theories, because the pressure of dark
energy must be negative to reproduce the present accelerated expansion
(Carroll 1992).
has taken negative values according to Eq. (17).
This may not conflict with theories, because the pressure of dark
energy must be negative to reproduce the present accelerated expansion
(Carroll 1992).
Note that from Eq. (7), ![]()
![]()
![]() and at the present epoch,
and at the present epoch,
![]() is directly connected with
is directly connected with
![]() .
Dark energy is written in terms of dark matter. However, dark energy
and dark matter should be distinguishable to give rise to an
accelerated expansion, because the evolution of the scale factor
criticallydepends on the composition of each energy density of the
universe. Therefore, the
.
Dark energy is written in terms of dark matter. However, dark energy
and dark matter should be distinguishable to give rise to an
accelerated expansion, because the evolution of the scale factor
criticallydepends on the composition of each energy density of the
universe. Therefore, the ![]() without a constant cosmological term is indistinguishable from the matter-dominant Friedmann model with the parameters of
without a constant cosmological term is indistinguishable from the matter-dominant Friedmann model with the parameters of
![]() .
Note that the variable
.
Note that the variable ![]() term in the
term in the ![]() plays a minor role to accelerate the universe at the present epoch. Because of this, we modified
plays a minor role to accelerate the universe at the present epoch. Because of this, we modified ![]() by adding a constant cosmological term. It has no relation to the
expansion rate of the universe at the early epoch. However, the energy
stored in the constant cosmological term played a major role in
accelerating the universe at the present epoch as seen in Fig. 3.
Since this model contains enough dark energy to accelerate the
universe, it is constrained by the SNIa observations. In the
present research, we investigated the
by adding a constant cosmological term. It has no relation to the
expansion rate of the universe at the early epoch. However, the energy
stored in the constant cosmological term played a major role in
accelerating the universe at the present epoch as seen in Fig. 3.
Since this model contains enough dark energy to accelerate the
universe, it is constrained by the SNIa observations. In the
present research, we investigated the ![]() at the early epoch to determine the intrinsic parameters and introduce new parameters at the present epoch for the m-z relation.
Because we demonstrated a possibility of a non-standard model which is
compatible with the observations, it is worthwhile to examine more
generally the functional form of the cosmological term (e.g. Fukui
et al. 2001).
at the early epoch to determine the intrinsic parameters and introduce new parameters at the present epoch for the m-z relation.
Because we demonstrated a possibility of a non-standard model which is
compatible with the observations, it is worthwhile to examine more
generally the functional form of the cosmological term (e.g. Fukui
et al. 2001).
References
- Arai, K., Hashimoto, M., & Fukui, T. 1987, A&A, 179, 17 [NASA ADS] [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berti, E., Buonanno, A., & Will, C. M. 2005, Phys. Rev. D, 71, 084025 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bertotti, B., Iess, L., & Tortora, P. 2003, Nature, 425, 374 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carr, B. J., Kohri, K., Sendouda, Y., & Yokoyama, J., et al. 2010, Phys. Rev. D, 81, 104109 [Google Scholar]
- Carroll, S. M., & Press, W. H. 1992, ARA&A, 30, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Dunckley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Endo, M., & Fukui, T. 1977, Gen. Rel. Grav., 8, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Etoh, T., Hashimoto, M., Arai, K., & Fujimoto, S. 1997, A&A, 325, 893 [NASA ADS] [Google Scholar]
- Fukugita, M., & Kawasaki, M. 2006, ApJ, 646, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Fukui, T., Arai, K., & Hashimoto, M. 2001, Class. Quant. Grav., 18, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- Huterer, D., & Turner, M. S. 1999, Phys. Rev. D, 60, 081301 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Becker, A. C., Cinabro, D., et al. 2009, ApJS, 185, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2010, ApJS, submitted [arXiv:1001.4538v2] [Google Scholar]
- Malaney, R. A., & Mathews, G. J. 1993, Phys. Rep., 229, 145 [Google Scholar]
- Melendez, J., & Ramirez, I. 2004, ApJ, 615, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, R., Hashimoto, M., Gamow, S., & Arai, K. 2006, A&A, 448, 23 [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Zych, B. J., Murphy, M. T., Lewis, A., & Steidel, C. C. 2008, MNRAS, 391, 1499 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Kirshner, R. P., Schmidt, B. P., et al. 1999, AJ, 117, 707 [Google Scholar]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Silviera, V., & Waga, I. 1997, Phys. Rev. D, 56, 4625 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 1972, Gravitation and Cosmology (New York: John Wiley) [Google Scholar]
- Weinberg, S. 1989, Rev. Mod. Phys., 61, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Weinberg, S. 2008, Cosmology (New York: Oxford Unversity Press) [Google Scholar]
- Wagoner, R. V. 1970, Phys. Rev. D, 1, 3209 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[height=7.8cm,width=7.4cm,angle=-90,clip]{14602fg1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14602-10/Timg39.png)
|
Figure 1:
Time evolutions of the scale factor in the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=9cm,width=8cm,angle=-360,clip]{14602fg2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14602-10/Timg55.png)
|
Figure 2:
Light element abundances of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=7.4cm,width=8.4cm,angle=360,clip]{14602fg3.eps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/13/aa14602-10/Timg73.png)
|
Figure 3:
Distance modulus vs. redshift for the flat universe in the Friedmann model and the |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



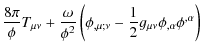
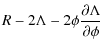
![\begin{displaymath}%
{\rm d}s^{2}=-{\rm d}t^{2}+a\left(t\right)^{2}\left[{\frac{...
...{\rm d}\theta^{2}+r^{2}\sin^{2}\theta {\rm d}\phi^{2}}\right],
\end{displaymath}](/articles/aa/full_html/2010/13/aa14602-10/img20.png)
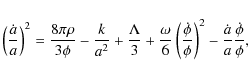


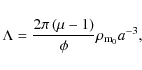

![\begin{displaymath}%
\dot{\phi}=\frac{1}{a^{3}}\left[\frac{8\pi\mu}{2\omega +3}\rho_{{\rm m}_{0}}t+B \right],
\end{displaymath}](/articles/aa/full_html/2010/13/aa14602-10/img37.png)
![\begin{displaymath}%
\mu_{\rm th}=m-M=5 \log _{10}\left[\left(1+z\right)r_{l}\right] +25,
\end{displaymath}](/articles/aa/full_html/2010/13/aa14602-10/img57.png)
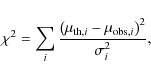
![\begin{displaymath}%
H=\left[\frac{1}{4}\left(\frac{\dot{\phi}}{\phi}\right)^{2}...
...}\right]^{\frac{1}{2}}-\frac{1}{2}\frac{\dot{\phi}}{\phi}\cdot
\end{displaymath}](/articles/aa/full_html/2010/13/aa14602-10/img65.png)
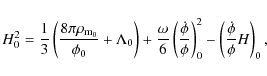
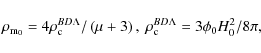
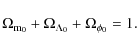
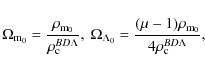
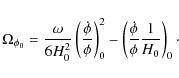
![\begin{displaymath}%
H=\left[\frac{1}{4}\left(\frac{\dot{\phi}}{\phi}\right)^{2}...
...}\right]^{\frac{1}{2}}-\frac{1}{2}\frac{\dot{\phi}}{\phi}\cdot
\end{displaymath}](/articles/aa/full_html/2010/13/aa14602-10/img81.png)