EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 521 (October 2010) A&A, 521 (2010) A75 Full HTML
Highlight
Free Access
Issue
A&A
Volume 521, October 2010
Article Number A75
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201014521
Published online 22 October 2010
A&A 521, A75 (2010)

The chemically peculiar double-lined spectroscopic binary HD 90264[*]

C. Quiroga - A. F. Torres - L. S. Cidale

Departamento de Espectroscopía, Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque S/N, B1900FWA La Plata, Buenos Aires, Argentina Instituto de Astrofísica de La Plata (CCT La Plata - CONICET, UNLP), Paseo del Bosque S/N, B1900FWA La Plata, Buenos Aires, Argentina

Received 27 March 2010 / Accepted 21 July 2010

Abstract
Context. HD 90264 is a chemically peculiar (CP) double-lined spectroscopic binary system of the type He-weak. Double-lined binaries are unique sources of data for stellar masses, physical properties, and evolutionary aspects of stars. Therefore, the determination of orbital elements is of great importance to study how the physical characteristics of CP stars are affected by a companion.
Aims. We carried out a detailed spectral and polarimetric study of the spectroscopic binary system HD 90264 to characterize its orbit, determine the stellar masses, and investigate the spectral variability and possible polarization of the binary components.
Methods. We employed medium-resolution échelle spectra and polarimetric data obtained at the 2.15-m telescope at CASLEO Observatory, Argentina. We measured radial velocities and line equivalent widths with IRAF packages. The radial velocity curves of both binary components were obtained combining radial velocity data derived from the single line of Hg II $\lambda $3984 $\AA$ and the double lines of Mg II $\lambda $4481 $\AA$. Polarimetric data were studied by means of the statistical method of Clarke & Stewart and the Welch test.
Results. We found that both components of the binary system are chemically peculiar stars, deficient in helium, where the primary is a He variable and the secondary is a Hg-Mn star. We derived for the first time the orbital parameters of the binary system. We found that the system has a quasi-circular orbit (e $\sim$ 0.04) with an orbital period of 15.727 days. Taking into account the circular orbit solution, we derived a mass ratio of $q = M_{{\rm He-w}} / M_{{\rm Hg-Mn}}$ = 1.22. We also found a rotational period of around 15-16 days, suggesting a spin-orbit synchronization. Possible signs of intrinsic polarization have also been detected.
Conclusions. HD 90264 is the first known binary system comprised of a He variable star as the primary component and a Hg-Mn star as the secondary one.

Key words: binaries: spectroscopic - stars: chemically peculiar - stars: individual: HD 90264

1 Introduction

Among the upper-main-sequence chemically peculiar (CP) stars are the generally so-called Ap and Bp stars. These stars show slow rotation and abnormal abundance enhancements of some chemical species in their atmospheres as compared to ``normal'' A and B dwarfs of the same effective temperature (Jascheck & Jascheck 1987). According to their chemical peculiarity the stars are classified in the following subgroups (Preston 1974): CP1 (metallic line stars, earlier designation Am, with overabundance of metals), CP2 (overabundance of Si, Cr, and Sr-Cr-Eu, earlier known as Ap stars), CP3 (overabundance of Hg and/or Mn) and CP4 (He-weak, B-type objects with abnormally weak lines of He I). In addition, Preston (1974) clearly distinguished two main groups: a non-magnetic sequence of Am and Hg-Mn stars and a magnetic sequence of Ap and some He-weak stars. On the other hand, a large fraction of these stars are known to be binaries: the CP1 subgroup has 32.5% binaries and the CP2 group has 66% binaries with large magnetic fields (Seggewiss 1993), while more than 67.7% of the CP3 stars are members of binary systems (or of systems of higher multiplicity) (Hubrig & Mathys 1996,1995). Based on the information of 45 binary systems with known orbital periods, Gerbaldi et al. (1985) found a deficiency of binaries for the He-weak stars, Si stars, Si-Cr, and Si-Sr stars and also confirmed a predominance of double-lined binaries (SB2) among Hg-Mn stars and a total absence of SB2 systems among the Si ones. This study also revealed a great deficiency among low-eccentricity systems for all peculiar stars except for the Hg-Mn ones, which was confirmed by Leone & Catanzaro (1999).

The slow rotational velocity is generally accepted as a more direct reason for the CP phenomenon, but the origin of the braking mechanism is not clearly established. The most attractive theories are magnetic braking and orbital synchronization. Evidence in favor or against both hypotheses were widely discussed by Abt (1979,1965) and Wolff (1983).

The occurrence of CP stars in spectroscopic binaries might provide intriguing information about a possible connection between rotation, magnetism, and abundance anomalies (Hubrig et al. 2006a; Budaj 1999; Noels et al. 2004). The interaction of the companions not only influences the evolution of the system and changes the chemical composition of their atmospheres but also determines the internal rotation properties of the stars. In particular, double-lined binaries are unique sources of data for stellar masses, physical properties, and evolutionary aspects of stars. Furthermore, the determination of orbital elements is of great importance to study how the physical characteristics of CP stars are affected by a companion.

The aim of this research is to study HD 90264 in detail, which seems to be the only He-weak star ever reported to belong to a SB2 system (Pedersen & Thomsen 1977). We here present spectroscopic data that allowed us for the first time to derive the orbital parameters, the stellar masses, and the spectral variability. Polarimetric data are also reported.

1.1 The star

The source HD 90264 (=HR 4089 = CPD -66 1243; $\alpha_{2000}$ = 10$^{\rm h}$22$^{\rm m}$58$^{\rm s}$, $\delta_{2000}$ = $-66^{\circ}$54 ${\hbox{$^\prime$ }}$05 ${\hbox{$^{\prime\prime}$ }}$) is a bright (mV = 4.95) B9 V star, member of the Sco-Cen Complex in the region of the Lower Centaurus Crux association (de Zeeuw et al. 1999). Jaschek et al. (1969) classified it as a chemically peculiar star belonging to the He-weak group due to a disagreement between the observed spectral type (B9) and the one inferred from the UBV photometry (B6). Pedersen & Thomsen (1977) found it to be a spectroscopic binary showing two spectra and identified it as a possible He variable. They determined three periods, P = 0.9445, 1.0565, 17.7 days, which reproduced the variation in the photometric R-index equally well. The star exhibits an IR excess of 28% (Groote & Kaufmann 1981) and a moderate enhancement of the photoelectric parameter $\Delta a$-index (Maitzen 1981), which measures the strength of the $\lambda $5200 Å flux depression.

Hubrig & Mathys (1996) reported that HD 90264 showed a strong feature of Hg II $\lambda $3984 Å in one of the binary components and proposed that the star might rather belong to the group of the P-Ga He-weak stars, hotter analogs of the nonmagnetic Hg-Mn stars (Borra et al. 1983), than be related to the magnetic Si stars.

Circularly polarized spectra measurements of HD 90264, obtained with the focal reducer and low-dispersion spectrograph (FORS1) at the Very Large Telescope (VLT) of the European Southern Observatory (ESO) revealed a weak mean longitudinal magnetic field  $\langle B_{1} \rangle$ of 114 $\pm$ 108 G (Hubrig et al. 2006b).

Fundamental parameters of this star such as absolute magnitude ($M_{\rm V}$ = -0.403), distance from the sun (d = 117.5 pc), effective temperature ( $T_{\rm eff}$ = 15 300 K) and age (t  = 18 $\times$ 106 years) were published by Westin (1985), who included HD 90264 in a study of the distribution and kinematics of early-type stars. On the other hand, Gomez et al. (1998) reported $M_{\rm V}$ = -0.8 and d = 134 pc. In addition, Hunger & Groote (1999) estimated for this star a  $T_{\rm eff}$ = 14 600 K, a surface gravity $\log ~g$ = 4.04, an age of 76 $\times$ 106 years, and a mass M* = 4.3 $M_{\odot}$, when studying the H/He abundance anomalies in B-type stars as a consequence of the existence of fractionated stellar winds.

Based on line profile fitting of Fe II lines, Dolk et al. (2003) estimated a projected rotational velocity $V \sin~i$ = 7 km s-1, which is one order of magnitude lower than the 79 km s-1 given in the Bright Star Catalogue.

2 Observations

High-resolution spectroscopic observations were carried out with the 2.15-m Jorge Sahade telescope at Complejo Astronómico el Leoncito (CASLEO), San Juan, Argentina, during six observing runs between 2005 and 2008. We used a REOSC échelle spectrograph in cross-dispersion mode with a Tek 1024 $\times$ 1024 pixel CCD as detector. A grating of 400 lines mm-1 was used except for the observing run in May 2008, where we chose a grating of 316 lines mm-1. The covered wavelength ranges were $\lambda\lambda$3500-6000 Å and $\lambda\lambda$3900-7100 Å, respectively. The signal-to-noise ratio (S/N) of the spectra was higher than 100 and the selected instrumental configuration yielded a resolving power, R, of 13 000 in the blue region of the spectrum. A Th-Ar lamp was used as a comparison source, with a reference exposure taken immediately after each stellar target at the same telescope position. Spectral CCD images were reduced with IRAF[*] packages, CCDRED and ECHELLE, and all spectra were measured with the SPLOT task. Table 1, Cols. 1 and 2, shows the log of observations.

Polarimetric data were also obtained in April and June, 2007, with the photopolarimeter of Turin Observatory attached at the 2.15-m telescope of CASLEO. The instrument can take simultaneous measurements in five channels with color bands close to those of the standard UBVRI system, based on the design principles of Piirola (1973,1988). The final response of the five photomultipliers corresponds to equivalent wavelengths of 0.36, 0.43, 0.53, 0.65 and 0.86 $\mu$m. During each observing run a set of zero and highly polarized standard stars were observed to determine the instrumental polarization and the coordinate transformation of the polarization position angle into the equatorial system, respectively. We subtracted the instrumental polarization from all data, which is typically of $\sim$0.01%.

\begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{14521fg1.eps} \end{figure} Figure 1:

Sample of the variation of the line profiles of Hg II $\lambda $3984 Å (left), He I $\lambda $4471 Å and Mg II $\lambda $4481 Å (center-left), H$\beta $ (center-right) and Mn II $\lambda $5302 Å (right) with the orbital phase.

Open with DEXTER

2.1 The line spectrum

The star HD 90264 displays a rich absorption sharp-lined spectrum. In addition to the typical lines of H I and He I, it is possible to distinguish lines of single-ionized elements such as Mg II, Mn II, Hg II, Si II, P II, and Fe II.

The double-lined nature of the star is clearly seen in most of the lines, while the transition at $\lambda $3984 Å appears as a single-lined feature (see Fig. 1, left). We identified this transition as caused by Hg II and not Mn II, because the Mn II lines show double-lined features. Therefore, one of the binary components is a chemically peculiar star of Hg-Mn and hereafter we will use the line of Hg II $\lambda $3984 Å to identify this star. We were not able to find either Hg I $\lambda $4358 Å or Pt II $\lambda $4046.45 Å (the latter is closely blended with the Hg I $\lambda $4046.56 Å, which is also not observed). We also searched for Hg II $\lambda $6149 Å, but were not able to find it probably due to a blend with Fe II lines. Numerous lines of P II were found, but not Ga II. While Sr II $\lambda $4077 Å is absent, Sr II $\lambda $4215 Å might be among other very weak lines. The Si II $\lambda $$\lambda $3853, 3856, 3862, 4128, and 4130 Å are well identified, but they are not enhanced.

The radial velocity (RV) values were obtained by a Gaussian fit of line profiles, except for the H I lines, for which we measured the barycentric wavelength of the profiles. Owing to the double component nature and numerous absorption lines, it was hard to perform a confident line-identification. Therefore, to avoid ambiguous or wrong identification of chemical elements, we first calculated the spectroscopic orbit of the Hg-Mn star (see details in Sect. 3), traced by the single line of Hg II $\lambda $3984 Å and then checked if the measured RV of other individual lines agreed with the RV curve computed previously. In Table 1 we quote the orbital phase and report our measurements of RVs for Hg II $\lambda $3984 Å and Mg II $\lambda $4481 Å derived from our spectroscopic observations and spectra taken from the ESO Science Archive Catalog (http://vizier.u-strasbg.fr) and Nitschelm (2004).

Table 1 also lists our measurements of the equivalent width (EW) of the Hg II $\lambda $3984 Å line and the EWs derived from some lines observed in the spectra of both stars: H$\beta $, He I $\lambda $4471 Å, Mg II $\lambda $4481 Å, Si II $\lambda $4130 Å, and Mn II $\lambda $5302 Å. All these lines are observed in absorption. A sample of the variation of the line profiles (Hg II $\lambda $3984 Å, He I $\lambda $4471 Å, Mg II $\lambda $4481 Å, H$\beta $ and Mn II $\lambda $5302 Å) with the orbital phase is displayed in Fig. 1. Except for the He I and H I lines, all absorption lines could be easily deconvolved into their stellar components. The line intensity of both stars is almost the same, pointing at a similar spectral type, although the lines of Mn II are more intense in the Hg-Mn star. The measured EWs of He I lines of both stars are smaller than expected for a B8 V star (Didelon 1982), indicating that they present a deficiency in helium. We also noted that the EW of He I $\lambda $4471 Å line, which is not related to the Hg-Mn star, is variable (see Table 1, Col. 10), thus confirming the helium variable nature of this object (Pedersen & Thomsen 1977). We will identify this star as the He-w star.

We estimated an error of 10% in our measurements for the EW and of 5 km s-1 for the RV. The accuracy in our measurements is mainly limited by the instrumental resolution, the S/N ratio of our spectra, and the continuum determination.

3 The spectroscopic orbits

Although HD 90264 is a bright double-lined spectroscopic binary, its orbital parameters were not computed until now.

Table 1:   Log of observations with their corresponding orbital phase; measurements of radial velocities (RVs) and line equivalent widths (EWs).

Table 2:   Orbital solutions for HD 90264.

In order to obtain the orbital parameters, we minimized the weighted sum $\sum_{i=1}^{N} w_{i}({\rm O{-}C})_{i}^2$, where O and C are the observed and computed RV values, respectively, w are the corresponding weights and N is the number of data points. Because all data have the same quality, we took the same weight for all of them. The best circular orbital solution obtained from the RVs of Hg II $\lambda $3984 Å gives a period of P = 15.7260 $\pm$ 0.0015 days. Later, we computed a new orbital solution combining the RVs of Hg II $\lambda $3984 Å with those of Mg II $\lambda $4481 Å to obtain the RV curves of both stars. In this case, a slightly different period of P = 15.7275 $\pm$ 0.0008 days was found. We calculated both circular and eccentric orbits. Table 2 lists the obtained orbital solutions. The notation has the usual meaning: $\gamma$ is the barycentric velocity, K is the orbital semi-amplitude, e is the eccentricity, $\omega$ is the longitude of the periastron, T0 is the time of maximum velocity for circular orbits and the time of periastron passage for eccentric orbits. The elliptical orbit gives a slightly better solution than the circular one and, according to the Lucy & Sweeney (1971) test, the value found for the eccentricity is significant. In Fig. 2 we show the obtained orbital solutions for circular and eccentric orbits. However, as the obtained eccentricity e = 0.044 $\pm$ 0.014 is very low, the orbit is almost circular.

Thus, considering the orbital solution derived from a circular orbit, we obtained the semi-major axis sizes, which are $a_{{\rm He-w}}$ $\sin~ i$ = 0.089 $\pm$ 0.002 AU and $a_{{\rm Hg-Mn}}~ \sin~ i~$ = 0.109 $\pm$ 0.002 AU for the primary and secondary binary components, respectively. In addition, combining the semi-amplitudes of both stars (Table 2), we derived a mass ratio $q = M_{{\rm He-w}} / M_{{\rm Hg-Mn}}$ = 1.22 $\pm$ 0.05, which implies stellar masses of $M_{{\rm He-w}}$ $\sin^3~ i$ = 2.3 $\pm$ 0.1 $M_{\odot}$ for the primary component and $M_{{\rm Hg-Mn}}~ \sin^3~ i~$ = 1.9 $\pm$ 0.1 $M_{\odot}$ for the secondary. Then, assuming that the primary star has a stellar mass of 4.3 $M_{\odot}$ (Hunger & Groote 1999), we determined a stellar mass for the companion of $M_{{\rm Hg-Mn}}$ $\sim$ 3.5 $M_{\odot}$, which is close to the expected value for late B-type dwarves, namely 3.8 $M_{\odot}$ for a B8-type star (Cox 2000). We also obtained an inclination angle for the orbital plane of the binary system of i $\sim$ 54$^\circ$. This value is consistent with the photometric observations obtained by the Hipparcos satellite ($H_{\rm p}$ = 4.9278 $\pm$ 0.0004, Adelman 2001), which present no evidence of eclipses.

\begin{figure} \par\includegraphics[angle=90,width=8.3cm,clip]{14521fg2.eps} \end{figure} Figure 2:

Radial velocity data and orbital solutions for HD 90264. Open circles and filled triangles represent data from CASLEO (Mg II and Hg II, respectively). Star symbols correspond to data from Nitschelm (2004) and ESO/UVES Science Archive Catalog (Vizier). The solid and dotted lines trace the circular and eccentric orbits, respectively.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{14521fg3.eps} \end{figure} Figure 3:

Variation of the equivalent widths (EWs) of H$\beta $ and Mg II, Hg II and Mn II lines with the orbital phase. Semifilled squares ( top-left) represent the sum of the equivalent widths of the H$\beta $ line of both stars, open circles represent data related to the Hg-Mn star, and filled triangles correspond to the He-w star. Error bars are omitted when they are less than the symbol size.

Open with DEXTER

4 Spectral variability

In Figs. 3 and 4 we show the variability of the EWs of some absorption lines with the orbital period, and below we describe the behavior of each line transition.

1.
H (Fig. 3, top-left): because it was not possible to separate the line profile of each star, we present the variation of the total EW with the orbital phase. We observed that the EW increases by a factor of 1.5 from phases around 0 to 0.5. We were not able to find confident periods shorter than the orbital one, instead we obtained two possible periods of 36.0 and 25.0 days. We might attribute these large periods to the effect of line intensity variations in both stars.

2.
Hg II 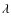$\lambda $3984 Å (Fig. 3, bottom-left): this line is only observed in the Hg-Mn star. It shows slight intensity variations with the orbital period with a minimum at around phase 0.5. The best period found for the EW data is 15.2 days, which is very close to the orbital one.

3.
Mg II 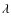$\lambda $4481 Å (Fig. 3, top-right): both line components remain constant with the orbital period. The intensity of the Mg line of the He-w star is slightly stronger than that of the Hg-Mn one.

4.
Mn II 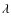$\lambda $5302 Å (Fig. 3, bottom-right): none of the line components shows line-EW variations with the orbital period. The strongest line is seen in the Hg-Mn star. We did not find emission features in the Mn II line profiles as for the He-weak star 3 Cen A and other Hg-Mn stars (Wahlgren & Hubrig 2004).

5.
Si II 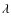$\lambda $4130 Å (Fig. 4, top): this line is clearly seen in both stars, and is strongest in the He-w star. The line displays small intensity variations with the orbital period in the Hg-Mn star with a maximum at phase 0. The best period that fits these data is 16.2 days, which is close to the orbital period. No variations are observed in the He-w star. The sum of the line-EWs of both stars phased with the orbital period are illustrated in the third plot to highlight the found variation.

6.
He I 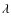$\lambda $4471 Å (Fig. 4, bottom): the He I line of the Hg-Mn star is weaker than that of the He-w star. In addition, the line-EW of the Hg-Mn star remains almost constant, while the He-w star shows line intensity variations by a factor of up to 3 between the maximum and minimum. Two maxima of different values are observed around phases 0 and 0.5. The sum of the line-EWs of both stars phased with the orbital period are depicted in the third plot to emphasize the found variation. We determined a periodic variability of 15.8 days, this value is also close to the orbital period (see Table 2).

5 Polarimetry

Table 3 lists for each night the observed polarimetric data in the UBVRI bands in terms of the weighted mean values of the Stokes parameters PX and PY (in percent terms), the corresponding degree of linear polarization P($\%$), the position angle PA (in degrees), and their corresponding mean errors ME. The number of observations N is also indicated. To obtain the averaged values of P($\%$) and PA for each night, we used weights determined from the inverse square of the estimated error for each observation. The estimated error is taken either from the least-square fit of the double cosine curves to the eight integrations acquired at the different positions of the $\lambda/2$ plate or from the photon statistics, whichever is greater (Piirola 1973,1988).

The standard criterion to evaluate if a measurement is polarized to some degree, either from intrinsic or interstellar effects, involves a comparison of a determined value with an estimate of its uncertainty. However, the degree of the linear polarization is a biased estimator of the true polarization; partly due to the noise on the signal (photon noise or intensity scintillation), which introduces a partial coherence between the measurements of the Stokes parameters, and partly to the conversion to the equatorial frame, which carries errors of the axis transformation that may be systematically different at each wavelength. This introduces difficulties in the analysis of the data of low polarization or low signal-to-noise level. Because UBVRI polarization of HD 90264 is too low to claim from its mean errors that the binary system is polarized, we used the statistical method of Clarke & Stewart (1986) to gain a confident detection. According to this method, we detected polarization at 99% confidence level in the U, V, and R bands in April 2007. In June 2007, we found polarization at 95% confidence level only in the B band. However, in none of the observing runs statistical polarization was detected in the I band. Unfortunately, most of the nights did not have good polarimetric conditions.

In addition, we looked for polarimetric variability by means of the Welch test, because ``Welch procedures may result in a polarimetric difference being detected between sets of points when none of the individual points is polarized, because the Welch test weights observations with respect to mean values and standard mean errors'' (Clarke & Stewart 1986). From our data we only detected a night-to-night variability in the position angle of the V band in June 2007 with a confidence level of 99%. At this point, we should recall that our data are in the same orbital phase, thus no large variations are expected between both observing runs.

\begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{14521fg4.eps} \end{figure} Figure 4:

Variation of the equivalent widths (EWs) of Si II and He I lines with the orbital phase: plots on the left and center illustrate the variation corresponding to each star, the plots on the right indicate the total contribution of both stars to the EW. Absence of error bars indicates that the magnitude of error is less than the symbol size.

Open with DEXTER

Table 3:   Polarimetric data of HD 90264.

Figure 5 shows the behavior of the average of all polarimetric data (P($\%$), PA, PX, and PY) with the wavelength for all observing nights. The fit of our data with the Serkowski's law (Serkowski et al. 1975) for interstellar polarization is shown in a dashed line. Taking into account that a) Serkowski's law does not seem to fit our data well, although if the error bars were only slightly larger, the dashed line would be a reasonable fit; b) based on the stellar polarization data of the Heiles (2000) catalogs, the stars in the field of HD 90264 do not show a tendency to present interstellar polarization; c) there is a difference of 30$^\circ$ in the position angle in the B band in relation to the PA of the other bands; and d) there is a confident statistical detection of low polarization, we can conclude that HD 90264 might present a variable intrinsic polarization.

\begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{14521fg5.eps} \end{figure} Figure 5:

Average of polarimetric data of HD 90264 with wavelength: a) polarization degree P($\%$), b) position angle PA, c) and  d) Stokes parameters PX and PY, respectively. The dashed line in plot  a) shows the fit of our data with the Serkowski's law for interstellar polarization.

Open with DEXTER

6 Discussion and conclusions

We made a study of the chemically peculiar star HD 90264 based on spectral and polarimetric data. This object displays a clear SB2 spectrum with both stars deficient in helium. The system consists of a He variable star and a Hg-Mn companion star in a quasi-circular orbit. Assuming a circular orbit solution, we derived for the first time the orbital parameters of HD 90264 and found an orbital period of 15.727 $\pm$ 0.001 days. The found orbital solution agrees with the statistical work of Gerbaldi et al. (1985) and Budaj (1999). In addition, we derived a mass ratio of q = 1.22 $\pm$ 0.05, which indicates that for the primary star $M_{{\rm He-w}}~ \sin^3~ i$ = 2.3 $\pm$ $0.1~M_\odot$ and for the secondary $M_{{\rm Hg-Mn}}~ \sin^3~ i$ = 1.9 $\pm$  $0.1~M_\odot$.

The He variable star displays variations in the He I $\lambda $4471 Å line with a period of 15.8 days, reaching two maxima around phases 0 and 0.5, which suggests the presence of two opposed enhanced helium abundance patches. Instead, the Hg-Mn star shows variations in the Hg and Si lines with a period of about 15.2 and 16.2 days, respectively, and does not show variation in the He I $\lambda $4471 line. The periods of the line variations observed in both stars are close to the orbital period. Variations in the H$\beta $ line were also detected.

In the framework of the oblique rotator models, the variations of the observed line spectrum is related to the rotational period, and the observed spectral changes are explained as a consequence of a non-homogeneous emitting surface due to a non-uniform distribution of elements over the stellar surface. The periods found in the variations of the line equivalent widths of both stars are very close to the determined orbital period (15.727 days). This result suggests a spin-orbit synchronization in a quasi-circular orbit. Thus, assuming a 15.727 days variation in line intensity due to rotation, we found that the equatorial rotational velocity of the star is 11.6 km s-1. This value is consistent with the measurement of $V \sin~i$ = 7 km s-1 determined by Dolk et al. (2003), if we consider an inclination angle of  ${\sim}37^{\circ}$, a lower value than the one derived from the mass ratio.

We could also test the spin-orbit synchronization of HD 90264 with the Kitamura and Kondo test (Kitamura & Kondo 1978). From the relation

\begin{eqnarray*}V \sin~i = 50.6 \frac{R_{\rm sync} \sin~i}{P}, \end{eqnarray*}


where $V \sin~i$ is in km s-1, P is the orbital period in days, and $R_{\rm sync}$ is the stellar radius, when synchronism has been reached, in solar radii, we obtained for $i = 54^{\circ}$, $R_{\rm sync} \sim 2.7~R_{\odot}$, and for $i = 37^{\circ}$, $R_{\rm sync} \sim 3.6~R_{\odot}$. Because an expected value for the radius of a B6-type star is $R_{*} = 3.6~R_{\odot}$ (see Cox 2000), the necessary condition for synchronism, $R_{*} \ge R_{\rm sync}$, is fulfilled in both cases.

In addition, we could estimate the spin-orbit synchronization time-scale of the system according to the two competing theories developed to explain the spin-orbit synchronization observed in detached closed binaries: the tidal theory of Zahn (1975,1977) and the hydrodynamical theory of Tassoul (1988,1987). We computed the characteristic synchronization time, in Zahn's case,

\begin{eqnarray*}t_{{\rm sync}}\propto~q^{2}\left(1+\frac{1}{q}\right)^{-5/6}(R_{*}/a)^{-17/2}\sim~2.77\times 10^{9}~{\rm years}, \end{eqnarray*}


and in Tassoul's case,

\begin{eqnarray*}t_{{\rm sync}}\propto~q\left(1+\frac{1}{q}\right)^{-3/8}(R_{*}/a)^{-33/8}\sim~3.89\times 10^{5}~{\rm years}, \end{eqnarray*}


where q = M1 / M2 is the mass ratio of the system, M1 and M2 are the masses of the primary and secondary stars, respectively, R* is the radius of the primary star, and a is the true mean separation of the binary components. For these calculations we also assumed the primary radius to be 3.6 $R_{\odot}$, and computed the orbital separation $a\sim 52.66~R_{\odot}$ for $i = 54^{\circ}$. The comparison between the obtained time-scales for the synchronization of the system with the estimated age of HD 90264, which is ${\le}7.6$ $\times$ 107 years, would agree with the spin-orbit synchronization in the context of Tassoul's theory, which is based on the dissipation of the energy of large-scale meridional flows. If the inclination angle is smaller, the result is the same.

Concerning the polarimetric data, we found that HD 90264 might present a low level of intrinsic polarization. However, further observations are needed to confirm this result and the possible polarimetric variations with the orbital period of the binary system.

Acknowledgements
We thank our anonymous referee for the many comments and suggestions that helped to improve this manuscript. This research has made use of the VizieR catalogue access tool, CDS, Strasburg, France. L.C. acknowledges financial support from the Agencia de Promoción Científica y Tecnológica (Préstamo BID, PICT 111) and the Programa de Incentivos G11/089 of the Universidad Nacional de La Plata, Argentina.

References

  1. Abt, H. A. 1965, ApJS, 11, 429 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abt, H. A. 1979, AJ, 84, 1591 [NASA ADS] [CrossRef] [Google Scholar]
  3. Adelman, S. J. 2001, A&A, 367, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Borra, E. F., Landstreet, J. D., & Thompson, I. 1983, ApJS, 53, 151 [NASA ADS] [CrossRef] [Google Scholar]
  5. Budaj, J. 1999, MNRAS, 310, 419 [NASA ADS] [CrossRef] [Google Scholar]
  6. Clarke, D., & Stewart, B. G. 1986, Vistas Astron., 29, 27 [Google Scholar]
  7. Cox, A. N. 2000, Allen's Astrophysical Quantities (New York: Springer-Verlag New York, Inc.) [Google Scholar]
  8. de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
  9. Didelon, P. 1982, A&AS, 50, 199 [NASA ADS] [Google Scholar]
  10. Dolk, L., Wahlgren, G. M., & Hubrig, S. 2003, A&A, 402, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Gerbaldi, M., Floquet, M., & Hauck, B. 1985, A&A, 146, 341 [NASA ADS] [Google Scholar]
  12. Gomez, A. E., Luri, X., Grenier, S., et al. 1998, A&A, 336, 953 [NASA ADS] [Google Scholar]
  13. Groote, D., & Kaufmann, J. P. 1981, A&A, 94, L23 [NASA ADS] [Google Scholar]
  14. Heiles, C. 2000, AJ, 119, 923 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hubrig, S., & Mathys, G. 1995, Comments Astrophys., 18, 167 [Google Scholar]
  16. Hubrig, S., & Mathys, G. 1996, A&AS, 120, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Hubrig, S., González, J. F., Savanov, I., et al. 2006a, MNRAS, 371, 1953 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hubrig, S., North, P., Schöller, M., & Mathys, G. 2006b, Astron. Nachr., 327, 289 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hunger, K., & Groote, D. 1999, A&A, 351, 554 [NASA ADS] [Google Scholar]
  20. Jascheck, C., & Jascheck, M. 1987, The Classification of Stars (Cambridge: Cambridge University Press) [Google Scholar]
  21. Jaschek, M., Jaschek, C., & Arnal, M. 1969, PASP, 81, 650 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kitamura, M., & Kondo, M. 1978, Ap&SS, 56, 341 [NASA ADS] [CrossRef] [Google Scholar]
  23. Leone, F., & Catanzaro, G. 1999, A&A, 343, 273 [NASA ADS] [Google Scholar]
  24. Lucy, L. B., & Sweeney, M. A. 1971, AJ, 76, 544 [NASA ADS] [CrossRef] [Google Scholar]
  25. Maitzen, H. M. 1981, A&A, 95, 213 [NASA ADS] [Google Scholar]
  26. Nitschelm, C. 2004, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, ed. R. W. Hilditch, H. Hensberge, & K. Pavlovski (San Francisco: ASP), ASP Conf. Ser., 318, 291 [Google Scholar]
  27. Noels, A., Montalbán, J., & Maceroni, C. 2004, in The A-Star Puzzle, ed. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss (Cambridge: Cambridge University Press), IAU Symp., 224, 47 [Google Scholar]
  28. Pedersen, H., & Thomsen, B. 1977, A&AS, 30, 11 [Google Scholar]
  29. Piirola, V. 1973, A&A, 27, 383 [NASA ADS] [Google Scholar]
  30. Piirola, V. 1988, in Polarized Radiation of Circumstellar Origin, ed. G. V. Coyne, A. M. Magalhaes, A. F. Moffat, R. E. Schulte-Ladbeck, & S. Tapia (Vatican City: Vatican Press), 735 [Google Scholar]
  31. Preston, G. W. 1974, ARA&A, 12, 257 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  32. Seggewiss, W. 1993, in IAU Colloq., 138, Peculiar versus Normal Phenomena in A-type and Related Stars, ed. M. M. Dworetsky, F. Castelli, & R. Faraggiana (San Francisco: ASP), ASP Conf. Ser., 44, 137 [Google Scholar]
  33. Serkowski, K., Mathewson, D. S., & Ford, V. L. 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] [Google Scholar]
  34. Tassoul, J. 1987, ApJ, 322, 856 [NASA ADS] [CrossRef] [Google Scholar]
  35. Tassoul, J. 1988, ApJ, 324, L71 [NASA ADS] [CrossRef] [Google Scholar]
  36. Wahlgren, G. M., & Hubrig, S. 2004, A&A, 418, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Westin, T. N. G. 1985, A&AS, 60, 99 [Google Scholar]
  38. Wolff, S. C. 1983, The A-stars: Problems and perspectives. Monograph series on nonthermal phenomena in stellar atmospheres (Washington, D.C.: NASA), SP-463 [Google Scholar]
  39. Zahn, J. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
  40. Zahn, J. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]

Footnotes

... 90264[*]
Based on observations taken at Complejo Astronómico El Leoncito (CASLEO), operated under an agreement between the Consejo Nacional de Investigaciones Científicas y Técnicas de la República Argentina, the Secretaría de Ciencia y Tecnología de la Nación and the National Universities of La Plata, Córdoba and San Juan.
... IRAF[*]
IRAF is distributed by the National Optical Astronomy Observatories, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation.

All Tables

Table 1:   Log of observations with their corresponding orbital phase; measurements of radial velocities (RVs) and line equivalent widths (EWs).

Table 2:   Orbital solutions for HD 90264.

Table 3:   Polarimetric data of HD 90264.

All Figures

  \begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{14521fg1.eps} \end{figure} Figure 1:

Sample of the variation of the line profiles of Hg II $\lambda $3984 Å (left), He I $\lambda $4471 Å and Mg II $\lambda $4481 Å (center-left), H$\beta $ (center-right) and Mn II $\lambda $5302 Å (right) with the orbital phase.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.3cm,clip]{14521fg2.eps} \end{figure} Figure 2:

Radial velocity data and orbital solutions for HD 90264. Open circles and filled triangles represent data from CASLEO (Mg II and Hg II, respectively). Star symbols correspond to data from Nitschelm (2004) and ESO/UVES Science Archive Catalog (Vizier). The solid and dotted lines trace the circular and eccentric orbits, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{14521fg3.eps} \end{figure} Figure 3:

Variation of the equivalent widths (EWs) of H$\beta $ and Mg II, Hg II and Mn II lines with the orbital phase. Semifilled squares ( top-left) represent the sum of the equivalent widths of the H$\beta $ line of both stars, open circles represent data related to the Hg-Mn star, and filled triangles correspond to the He-w star. Error bars are omitted when they are less than the symbol size.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=14cm,clip]{14521fg4.eps} \end{figure} Figure 4:

Variation of the equivalent widths (EWs) of Si II and He I lines with the orbital phase: plots on the left and center illustrate the variation corresponding to each star, the plots on the right indicate the total contribution of both stars to the EW. Absence of error bars indicates that the magnitude of error is less than the symbol size.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{14521fg5.eps} \end{figure} Figure 5:

Average of polarimetric data of HD 90264 with wavelength: a) polarization degree P($\%$), b) position angle PA, c) and  d) Stokes parameters PX and PY, respectively. The dashed line in plot  a) shows the fit of our data with the Serkowski's law for interstellar polarization.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.