EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 521 (October 2010) A&A, 521 (2010) A27 Full HTML
Highlight
Free Access
Issue
A&A
Volume 521, October 2010
Article Number A27
Number of page(s) 14
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201014244
Published online 15 October 2010
A&A 521, A27 (2010)

Evolution of the infrared Tully-Fisher relation up to z = 1.4

M. Fernández Lorenzo1,2 - J. Cepa1,2 - A. Bongiovanni1,2 - A. M. Pérez García1,2 - M. A. Lara-López1,2 - M. Povic1,2 - M. Sánchez-Portal3

1 - Instituto de Astrofísica de Canarias (IAC), C/ Vía Láctea S/N, 38200 La Laguna, Spain
2 - Departamento de Astrofísica, Universidad de La Laguna, Spain
3 - Herschel Science Centre, INSA/ESAC, Madrid, Spain

Received 11 February 2010 / Accepted 8 May 2010

Abstract
Context. The Tully-Fisher relation represents a connection between fundamental galaxy parameters, such as its total mass and the mass locked in stars. Therefore, the study of the evolution of this relation in the optical and infrared bands can provide valuable information about the evolution of the individual galaxies through the changes found in each band.
Aims. This work aims to study the Tully-Fisher relation at high redshift in the B, V, R, I, and $K_{\rm S}$-bands by comparison with the local relations derived from a large sample of galaxies in the redshift range 0.1<z<0.3, processed in the same way, and with the same instrumental constraints that the high-redshift sample.
Methods. Using the large amount of photometric information available in the AEGIS database, we determined the optimal procedure for obtaining reliable k-corrections. Instrumental magnitudes were then k- and extinction corrected and the absolute magnitudes derived, using the concordance cosmological model. The rotational velocities were inferred from the widths of optical lines in DEEP2 spectra. At high redshift, this method is found to provide more accurate results than using the rotation curve, because of spatial resolution limitations. Morphology was determined by visual classification of the HST images. From the above information, the Tully-Fisher relations in B, V, R, I, and $K_{\rm S}$-bands are derived for the local and high-redshift sample.
Results. We detect evolution in the B, V, and R-bands in the sense that galaxies were brighter in the past at the same rotation velocity. The change in luminosity is more noticeable in the bluer bands. This colour evolution, unnoticed in our previous work, is detected thanks to the more reliable k-corrections carried out in this paper, which included photometry from B to IRAC bands. The change in the ( $V-K_{\rm S}$) and (R-I) colours (for a fixed velocity) could be interpreted as an ageing of the stellar populations as consequence of the star formation decrease since z=1.25. In addition, we conclude that spiral galaxies may have doubled their stellar masses in the past 8.6 Gyr.

Key words: galaxies: evolution - galaxies: fundamental parameters - galaxies: spiral - galaxies: kinematics and dynamics

1 Introduction

The relation between the luminosity and maximum rotational velocity of spiral galaxies (Tully & Fisher 1977) is an important distance estimator, which has been used for measuring the Hubble constant H0 (e.g., Tully & Pierce 2000). The study of this relation at different cosmic times can probe evolution in galaxy properties such as its total mass, or the relation between dark and luminous matter (Zwaan et al. 1995). Any consistent model of galaxy formation and evolution should be able to reproduce the evolution of the Tully-Fisher relation (hereafter TFR). Its study therefore has important implications for determining fundamental cosmological parameters, the study of structure formation, and the evolution of disc galaxies (Navarro & Steinmetz 2000).

Traditionally, the internal kinematics of nearby galaxies has been measured using 21 cm line widths, but the limited sensitivity of radio telescopes prevents the effective use of this method at high redshift. Optical lines become important in evolutionary studies of TFR, and some authors have studied the relation between both velocity indicators. For example, Mathewson et al. (1992) compared the projected rotation velocity measured from H ${\rm\alpha}$ rotation curves, with the velocity measured from integrated HI profiles at the 50% of the maximun flux level. They obtained a difference of 10 km s-1, which they attributed to the HI widths measuring not only the rotational velocity but the internal galaxy turbulence as well. This turbulence is important mainly in the most external regions of the galaxy, where the gravity is lower. However, the optical emission does not extent so far. The contribution of turbulence to the rotational velocity is negligible when using these lines. Vogt et al. (1997,1996) modelled rotation curves using optical long-slit observations, and found a modest luminosity evolution in the B-band TFR ( $\Delta M_B$(high z-local) $\leq$ -0.4 at $\langle z\rangle=0.5$). However, Rix et al. (1997) and Simard & Pritcher (1998) found a stronger evolution ( $\Delta M_B\approx-1.5$ at z=0.4), modelling the kinematics of disc galaxies in a similar way. Subsequent works have measured the evolution of the TFR, again finding different and even conflicting results. Ziegler et al. (2002), and Böhm et al. (2004), found a relation at high redshift (z=1) shallower than that measured in local samples, and evidence of a luminosity evolution with lookback time of ${\Delta}M_B \approx -1$ mag at redshift z=1. In contrast to previous findings, these authors claimed that less massive galaxies were brighter in the past (at fixed rotational velocity), while the most massive follow the local relation. However, other groups, such as Bamford et al. (2006), have detected luminosity evolution but no slope change. Moreover, these authors found differences in luminosity evolution ranging from -0.2 to -2 mag.

To cope with contributions to line widths other than those produced by rotational velocity, Weiner et al. (2006a) measured kinematic line widths ( $\sigma_{\rm 1D}$), and spatially resolved rotation and dispersion profiles. They combined line-of-sight rotation and dispersion ( $S^2_{0.5}=0.5V^2_{\rm rot}+\sigma^2_{\rm 2D}$), and found that this combination correlates well with the integrated line width, demostrating that $\sigma_{\rm 1D}$is a robust velocity indicator, that allows constructing scaling relations with velocity for a population of diverse kinematic properties (dispersion and rotation-dominated galaxies). In another paper, Weiner et al. (2006b) used $\sigma_{\rm 1D}$ to study the evolution in the B and J-band TFRs, finding a slope evolution in both bands, and a larger intercept evolution in the B-band (-1.5 mag versus -0.5 mag in the J-band up to z=1.2). This slope change, which implies a large evolution for the most massive galaxies, is in the opposite sense to that found by Ziegler et al. (2002) and Böhm et al. (2004). Although the B-band TFR derived by Weiner et al. (2006b) using resolved rotation velocities also implies that the intercept has evolved, the sample is too small and noisy to measure slope evolution. In addition, Kassin et al. (2007) demonstrated that the scatter in the stellar-mass TFR is lower when using S0.5 instead of $V_{\rm rot}$. In Fernández Lorenzo et al. (2009), we analysed the optical line widths to study the evolution of the TFR in B, R, and I-bands, demostrating that all optical emision lines can be used to determine galaxy kinematics. We also constructed our local TFRs from data derived in a similar way to the sample of high redshift galaxies, and found evidence of luminosity evolution in all three bands for the greatest redshift range of our sample, 1.1<z<1.3.

In contrast to the variety of results found in the optical bands, there seemed to be a consensus about the absence of evolution in the K-band TFR (Conselice et al. 2005; Flores et al. 2006). However, Puech et al. (2008) find K-band evolution in the sense that galaxies had been fainter in the past, a result opposite to what is found in the optical bands (for example, Bamford et al. 2006). The disagreement between this work and that of Flores et al. (2006) (both use 3D spectroscopy for deriving velocities) is produced by the method for correcting the rotation velocity and, above all, the local relation used as a reference. Several works have studied the local TFR in the K-band finding different results, with a slope ranging from -6.88 (Hammer et al. 2007) to -11.3 (Verheijen 2001). Identifying the reason for these disagreements is crucial for obtaining reliable conclusions about the evolution of the infrared TFR by fixing the local relation. Masters et al. (2008) presented a universal calibration of the TFR in the 2MASS J, H, and K-bands. In all three bands, they showed that the relation is steeper for later-type spirals, and obtained a slope of -10.017 in the K-band correcting all galaxies to Sc type.

In this era of precision cosmology, increasingly large, deep and accurate galaxy surveys are required for the study of galaxy evolution. Within these surveys, the DEEP2 project (Davis et al. 2007,2003) provides the galaxy spectra with a highest resolution. Furthermore, the large amount of photometry information available in the Extended Groth Strip (EGS) allows an additional step in the study of the TFR: its colour evolution. Models of disc galaxy formation predict different colour evolution depending on whether the evolution is mainly due to collapse or accretion (see, for example, Westera et al. 2002). In our previous work (Fernández Lorenzo et al. 2009), we studied for first time the (R-I) TFR evolution up to z<1.3, but the large scatter of this relation prevented us from distinguishing between one galaxy model and another.

In the present work, we extend our previous sample to include all the galaxies in the Extended Groth Strip (EGS) with DEEP2 spectra available, in the redshift range 1.1<z<1.4, with the aim of confirming or not the prima facie evidence of evolution found previously (Fernández Lorenzo et al. 2009). We also extend our study to the V and $K_{\rm S}$-bands, in addition to the B, R, and I-bands, to study the most probable galaxy formation model, since the Westera et al. (2002) models predict larger colour differences in these bands. The local sample (0.1<z<0.3) is also extended to the whole EGS. Using this new local sample, we expect to set a more reliable TFR slope at z=0 to compare with our high-redshift sample.

This paper is organised as follows. In Sect. 2, a description of the data and the sample selection criteria are provided. The study of k-corrections and derivation of the absolute magnitudes and rotation velocities are described in Sect. 3. The results are presented in Sect. 4, and our last two sections provide the discussion of the results and conclusions. Throughout this article, the concordance cosmology with ${\Omega}_{\rm\Lambda0}=0.7$, ${\Omega}_{\rm m0}=0.3$, and $H_0=70 \rm\ km \rm\ s^{-1} \rm\ Mpc^{-1}$ is assumed. All magnitudes are in the AB zeropoint system.

2 Data and sample selection

The sample consists of galaxies in the Groth Strip Survey (GSS) sky region. The baseline for spectroscopy target pre-selection were the galaxies for which DEEP2 spectra (Data Release 3, DR3) in this field were available in the redshift ranges 0.1<z<0.3 and 1.1<z<1.4. The DEEP2 project (Davis et al. 2007,2003) is a survey using the DEIMOS multi-object spectrograph (Faber et al. 2003) in the Keck telescopes, to study the distant Universe. The grating used was the 1200 l/mm one, covering a spectral range of 6500-9100 Å with a dispersion of 0.33 Å/px, equivalent to a resolution $R=\rm\lambda/\rm\Delta\lambda=4000$. Despite both 1D and 2D spectra being available, in this work we use only the integrated spectra provided by DR3 (Horne 1986), because of the limited spatial resolution at high redshift. These spectra were extracted along the locus of constant lambda from the 2D spectra, using the routine do_extract.pro. Therefore, the 1D spectra provided by the DEEP2 team are corrected for the effects of tilted slits.

The photometric data used here are part of the AEGIS survey (Davis et al. 2007), for which B, R, and I-band photometry were taken with the CFH12K mosaic camera (Cuillandre et al. 2001), installed on the 3.6-m Canada-France-Hawaii Telescope (CFHT). These magnitudes are included in the DEEP2 photometric catalogue (Data Release 1, DR1, Coil et al. 2004) and the magnitude errors from sky noise and redshift are also available. The data in the V-band (F606W) were taken from the HST catalogue. As IR photometry, we used the $K_{\rm S}$-band, which was taken with Palomar WIRC (Bundy et al. 2006). Finally, for high-z galaxies, we used data taken with the Infrared Array Camera (IRAC), on the Spitzer Space Telescope (Barmby et al. 2008) in the IRAC1 ( $\rm 3.6 \ \mu m$) and IRAC2 ( $\rm 4.5 \ \mu m$) bands. In Table 1, we present the limited magnitude and PSF (Point Spread Function) of each measurement. B, R, and I-band magnitudes already being corrected for Galactic reddening based on Schlegel et al. (1998) dust maps. The V-band was corrected following the same work. The Galactic reddening for the $K_{\rm S}$ and IRAC-bands is lower (<0.005 mag) than the error in these magnitudes, so was not been considered.

Table 1:   Depth and average image quality of each measurement.

Since in the present work, we study the TFR in V and $K_{\rm S}$-bands, we limited the sample to galaxies with these photometric bands, further selected by restricting the sample to galaxies with emission lines in their spectra, necessary for obtaining the rotation velocity. In addition, for the high-redshift sample, we only selected galaxies for which with IRAC1 and IRAC2-bands photometry available, since they roughly correspond to NIR photometry in the rest-frame and can provide a more reliable k-correction in the $K_{\rm S}$-band.

The inclination angle (i) must also be included as a selection criteria, since no correlation between magnitude and rotation velocity can be observed for inclinations lower than 25$^{\circ}$ (Fernández Lorenzo et al. 2009). The inclination angle was calculated from the major to minor axis ratio as found in the HST catalogue, while the inclination errors were obtained by comparing with the inclination derived using SExtractor (Bertin & Arnouts 1996) in the combined V+I HST images. In this way, we estimated the mean error to be ${\pm}$2.5$^{\circ}$ for the local sample, and ${\pm}$6$^{\circ}$ for the high-redshift sample. Galaxies almost edge-on are more affected by extinction, but in our sample all galaxies have inclinations lower than 80$^{\circ}$. Therefore, the inclination of the final sample ranges between 25$^{\circ}$ and 80$^{\circ}$.

The second selection criteria was the morphology. Full details of the morphology classification were given in Fernández Lorenzo et al. (2009) to which the interested reader is referred. To select spiral galaxies, we performed a visual classification of every galaxy using HST images. The objects were divided into five groups: elliptical/S0 (1%), spirals (66%), irregulars (5%), interacting (5%), and unknown (23%). To classify our visually unknown objects, GIM2D (Simard 1998) was used. The objects with a Sérsic index lower than 2.5 were considered as spirals. The objects visually classified as unknown that could not be fitted with GIM2D (5% of ``unknown'' objects), were discarded. Finally, after applying all these criteria, we were left with 128 galaxies in the local sample, and 113 in the high redshift (1.1<z<1.4) sample.

3 Data analysis

The luminosity and rotation velocity of disc galaxies are the parameters involved in the TFR. At high redshift, several, not obvious, corrections are necessary to reliably obtain these parameters. Moreover, some corrections can dramatically change the results emulating evolution. Apart from Galactic extinction, which affects the observed magnitudes of local and high redshift galaxies in an identical way, the corrections required to obtain the absolute magnitudes in each band are the k-correction and the intrinsic extinction. We now try to determine the most effective way of calculating the absolute magnitudes and kinematics of spiral galaxies.

3.1 Rest-frame magnitudes

To calculate the k-correction in the B, V, R, I, and $K_{\rm S}$-bands, we need to know the spectral energy distribution (SED) of the galaxy. Since the SED is generally unknown, or at least not known with the required photometric accuracy, it is necessary to use an appropiate set of templates to reproduce the SED of each galaxy. In addition, the errors in the photometric information used to fit the template and its spectral coverage can strongly affect the best-fit template and thus the k-corrections. In the present work, we use the photometry included in the AEGIS catalogues. Since different instruments were used to obtain the magnitudes at different wavelengths, the same aperture might not enclose a similar fraction of the light in each band, due to the PSF, the seeing or the pixel scale, that act more or less spreading the object image. Then, we choose the photometry as close to the total magnitudes as possible, to fit the SEDs. For the B, R, and I-bands, Coil et al. (2004) measured the total R magnitudes from an aperture that systematically contains the whole galaxy flux, whereas the B and I magnitudes were corrected to total ones using the colours (B-R)1'' and (R-I)1'', respectively. For the V-band, we chose the MAG_BEST in the catalogue, which provides a nearby to total magnitude of the object. For the $K_{\rm S}$-band, we used MAG_AUTO because it is available for a larger number of objects than the aperture magnitudes, and we confirmed that there is no significant difference between aperture and MAG_AUTO photometry because of the larger errors in this band. Finally, for the IRAC-bands, we used the MAG_APER photometry in an aperture of 1.5'' (only for the high redshift sample) because aperture corrections derived from average mosaic PSFs were applied to the aperture magnitudes but not to MAG_AUTO, so we did not use MAG_AUTO in this case. We checked that there is a good correlation between the photometry in 1.5'' and 2.14'' apertures, and that the whole galaxy could be enclosed inside the aperture of 1.5''.

Since the photometric bands available in this work do not match the rest-frame optical magnitudes, and the $K_{\rm S}$-band photometry is very noisy, we performed a careful and systematic study to determine the most reliable way of performing a k-correction on our data using various sets of templates and methods (see Appendix A). We found that the best result is obtained by performing a nonnegative linear combination of five templates based on the Bruzual & Charlot (2003) stellar evolution synthesis codes using kcorrect. However, when a noisier band is present in the data, the k-corrections calculated by this code are unsuitable, because the photometric error in the observed quantity propagates to the rest-frame magnitude (Appendix A). In this case, we found that the optimal k-correction is achieved using photometric information that roughly matches the rest-frame band for which we wish to calculate the k-correction. The rest-frame magnitude in the noisy band is then more accurately calculated directly from the best-fit template instead of k-correcting the observed data. This is the case for our $K_{\rm S}$-band data that is roughly matched at rest-frame by the IRAC2-band. On the other hand, the k-correction in our optical bands can only be determined by interpolation, a procedure that requires available information at larger and shorter wavelengths than the band that we wish to correct. Finally, we calculated the rest-frame magnitudes used in this work by convolving the rest-frame best-fit kcorrect template with the filter response in each band.

\begin{figure} \par\mbox{\includegraphics[scale=0.41]{14244fg1a.eps}\includegrap... ...1c.eps}\includegraphics[scale=0.41]{14244fg1d.eps} } \vspace*{-2mm} \end{figure} Figure 1:

Example spectra (not flux-calibrated) of the high-z galaxies in our sample. The x-axis represents the rest-frame wavelengths in $\AA$. The green line is the fit to the [OII] $\lambda \lambda $3727 $\AA$ double line obtained with dipso, imposing that both lines had the same width.

Open with DEXTER

3.2 Intrinsic extinction

The absolute magnitudes were inferred from the luminosity distance corresponding to the measured redshifts, by assuming a concordance cosmology. Finally, the absolute magnitudes were corrected for intrinsic extinction. This correction is basically based on inclination. In this work, we adopted the Tully et al. (1998) procedure, which is valid for local galaxies. Since the dust content of the galaxies may have evolved with redshift, our extinction correction may be either under or overestimated, so we consider both possibilities below. According to this method, the extinction $A_{\lambda}$ as a function of inclination i in the $\lambda$-band, is defined to be

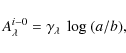
\begin{displaymath}A_{\lambda}^{i-0}={\gamma}_{\lambda} \ \log \ (a/b), \end{displaymath} (1)

where

\begin{displaymath}{\gamma}_B=-0.35 (15.31+M_B) \end{displaymath} (2)

\begin{displaymath}{\gamma}_R=-0.24 (15.91+M_R) \end{displaymath} (3)

\begin{displaymath}{\gamma}_I=-0.20 (16.61+M_I) \end{displaymath} (4)

\begin{displaymath}{\gamma}_K=-0.045 (18.01+M_K), \end{displaymath} (5)

and a/b is the galaxy major-to-minor axis ratio. These equations are valid for the magnitudes in the Vega zeropoint system, so our magnitudes were converted into the Vega-system to perform the extinction correction. For the V-band extinction, we used the Calzetti's law (Calzetti et al. 2000) obtaining AVi-0 = 0.8  ABi-0.

3.3 Kinematic line widths

Most local velocities have been derived historically from radio measurements, usually from 21 cm line widths at 50 per cent of the peak intensity (for example, Giovanelli et al. 1997). As already known (Bosma 1981), the rotation curves are not perfectly flat at large radii. Since the observed HI and H ${\rm\alpha}$ gas emission do not span the same radii, the velocities measured from both lines can provide different results. In addition, turbulent motions broaden the HI profile and affect both the optical versus radio velocity width determinations (Mathewson et al. 1992). Moreover, the existence of three types of rotation curves, depending on the relation between the maximum velocity and the velocity of the flat region (Verheijen 2001), can complicate the comparison. Mathewson et al. (1992) compared the rotation velocity measured from H ${\rm\alpha}$ rotation curves with the velocity measured from integrated HI profiles at the 50% level. They measured a ratio of $2V_{\rm c}$(H ${\rm\alpha}$)/W50i(HI) $\sim$ 0.94, which they attributed to the contribution of the turbulence to the measured HI velocity, thus overestimating the rotational velocity obtained using this line, as already mentioned. This contribution is more important in the most external regions of the galaxy where the gravity is lower, while the optical emission does not spread to this region. Applying diverse corrections, Rix et al. (1997) found a factor of $0.86~\pm~0.04$ between $2V_{\rm c}$(H ${\rm\alpha}$) and W20i(HI), which must be considered when comparing our results with those obtained for other local samples using 21 cm.

\begin{figure} \par\includegraphics[scale=0.43]{14244fg2a.eps}\includegraphics[s... ...44fg2c.eps}\includegraphics[scale=0.43]{14244fg2d.eps}\vspace*{2mm} \end{figure} Figure 2:

Comparison between local TFRs obtained from DEEP2 data (0.1<z<0.3) in B, R, I, and $K_{\rm S}$-bands, and Verheijen (2001) local TFRs (dashed lines). The solid line represents the linear fit to the DEEP2 data. The parameters of the fit are shown in Table 2.

Open with DEXTER

In the DEEP2 survey, the long axis of every individual slitlet is orientated along the major axis of each galaxy, with sufficient accuracy to derive rotation velocities. Masks in each field are generally oriented at 2 different mask PAs, which are $-49^{\circ}$ and 41$^{\circ}$ in EGS. In a given mask, each slitlet can be oriented across the range ${\pm}$30$^{\circ}$ with respect to the long axis of the slitmask. By combining the mask and slit PAs, the maximum slit misalignments ($\delta$) are either 11$^{\circ}$ or 19$^{\circ}$. We checked this for a subsample of galaxies, in the ACS images, and found good agreement between the slit and the major axis, differences always being lower than 20$^{\circ}$. This slit misalignment causes a negligible error in the velocity as already pointed out by Giovanelli et al. (1997) for PA offsets smaller than 15$^{\circ}$. Weiner et al. (2006a) concluded that the spatially resolved kinematics (2D) depends strongly on slit position angle alignment with galaxy major axis, but that integrated line width does not. For example, applying the standard cos-1($\delta$) correction, the difference in log( $V_{\rm max}$) for a $\delta=20^{\circ}$ would be $\sim$0.012 for a galaxy similar to the Milky Way at z=0.2, which is lower than the error in log( $V_{\rm max}$) for our local sample. We therefore chose not to apply the slit misalignment correction.

The optical line used in this work to derive the rotation velocity is not the same for each sample of galaxies because of the limited DEEP2 spectral range. We measured the H ${\rm\alpha}$ line for the local sample, and the [OII] $\lambda \lambda $3727 $\AA$ double line for the high-redshift sample. In Fernández Lorenzo et al. (2009), we demonstrated that both optical emission lines can be used to determine disc-rotation velocities with the aim of comparing different redshift samples. To calculate the rotation velocity, we used

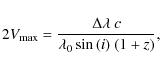
\begin{displaymath}2V_{\rm max} = \frac{{\Delta}{\lambda} \ c}{\lambda_{0}\sin{(i)} \ (1+z)}, \end{displaymath} (6)

where i is the inclination angle, ${\lambda}_0$ the line central wavelength at z=0, and ${\Delta}{\lambda}$ the line width at 20% of peak intensity. Equation (6) is derived from the Doppler effect, applying the corrections related to cosmology and inclination. We determined ${\Delta}{\lambda}$ with the Gaussian fitting routines in the Starlink package dipso (Howarth et al. 1996), which calculate the full-width half-maximum (FWHM). The spectral range and resolution of the DEEP2 spectra were designed to resolve the [OII] doublet, and all our spectra fulfill this aim. In Fig. 1, we represent four cases with different S/N and line blending. To measure the [OII] $\lambda \lambda $3727 $\AA$ double line, we assumed that both lines have the same width. We corrected for the instrumental width as in Fernández Lorenzo et al. (2009). Where the profile is Gaussian, the line width at 20% of the peak intensity can be compared with other velocity width measurements such as the FWHM and velocity dispersion, $\sigma $, using

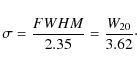
\begin{displaymath}{\sigma} = \frac{FWHM}{2.35} = \frac{W_{20}}{3.62} \cdot \end{displaymath} (7)

Since our objects have been classified visually as spiral galaxies (see Sect. 2), we assume that all galaxies rotate. However, we cannot verify the accuracy of this assumption with the existing data for the high redshift sample.

Table 2:   Parameters of the Tully-Fisher relations obtained by fitting DEEP2 data in the redshift range 0.1<z<0.3 used as local reference.

4 Results

4.1 Local relations

In Fernández Lorenzo et al. (2009), we derived the local TFRs by fitting the DEEP2 data points in the redshift range 0.1<z<0.3. In this work, we extend the local sample to the entire Groth field with ACS data available, to determine a more reliable TFR slope at z=0 for comparison with our high-redshift sample. Although the bands that we wish to study are V and $K_{\rm S}$, we derived the local TFRs in B, R, and I-bands as well, to compare with our previous results.

We performed an error-weighted least squares fitting to the DEEP2 data points in the redshift range 0.1<z<0.3, to estimate the slope a, and the intercept b of the local TFR in each band. A more detailed explanation of the fitting procedure can be found in Fernández Lorenzo et al. (2009). We adopted $\log(2V_{\rm max})$ as the dependent variable in the fit. This is the so-called inverse TFR, which is less sensitive to luminosity incompleteness bias (Schechter 1980; Willick 1994). The results obtained for each band are given in Table 2. In addition, we show the values calculated by Verheijen (2001) for the local ``RC/FD sample (without NGC 3992)'' case, by fitting $V_{\rm max}$ (the same sample used for comparison in our previous work). In Fig. 2, we represented both relations in the B, R, I, and $K_{\rm S}$-bands. As in our previous work, the slope of the TFR in each band is very similar to that found locally by Verheijen (2001), even for the $K_{\rm S}$-band, and consistent within his errors. Moreover, our $K_{\rm S}$-band TFR slope is consistent with that derived by Masters et al. (2008) after correcting for incompleteness, morphology, and luminosity dependence. Unlike the slope, we obtained a zeropoint of the relations lower than those of Verheijen (2001). However, this difference is very similar in all bands, so it may be related to the true rotation velocity versus observed line width relation. Rix et al. (1997) simulated observations of disc velocity fields with true circular velocity $V_{\rm c}$, and found that $\langle\sigma\rangle/V_{\rm c} = 0.6$, where the observed $\langle\sigma\rangle$ represents an average over all inclination angles. This result implies that $2V_{\rm c} = 0.92~W_{20}$. In our case, a ratio of $\langle\sigma\rangle/V_{\rm c} \sim 0.4$, which implies that $2V_{\rm c} = 1.38~W_{20}$, would be necessary to explain the difference found in our local TFRs. Rix et al. (1997) found that factors as line profile asymmetries, fiber size, or inclination effects work towards reducing $\langle\sigma\rangle/V_{\rm c}$. The spectra that we use were not acquired using fibers, but may be affected by e.g. slit misalignment, which also reduces $\langle\sigma\rangle/V_{\rm c}$. Since we wish to compare our high redshift sample with a sample of local galaxies observed with the same instrumentation and analysed following the same procedures, both samples are expected to be affected in a similar way by these factors. Consequently, the possible differences found in the TFR should be meaningful.

\begin{figure} \par\includegraphics[scale=0.42]{14244fg3a.eps}\includegraphics[s... ...pace*{4cm}\includegraphics[scale=0.42]{14244fg3e.eps}\hspace*{4cm}\end{figure} Figure 3:

Tully-Fisher relation in B, V, R, I, and $K_{\rm S}$-bands for the redshift range 1.1<z<1.4. Black diamonds are galaxies with inclination $45^{\circ }<i<80^{\circ }$, and grey points are galaxies with $25^{\circ }<i<45^{\circ }$. Thin and dashed lines represent the local TFR and its 2$\sigma $uncertainty in the offset. The thick line is the weighted least squares fit to all points. The fit was performed by fixing the slope to the local one in each case.

Open with DEXTER

4.2 High-redshift sample

In Fig. 3, we present B, V, R, I, and $K_{\rm S}$-band TFRs, for the redshift range 1.1<z<1.4, to test the evidence of evolution found in our previous work but with a larger sample of galaxies. To examine the intercept evolution, we fixed the slope to have the same value as for the local TFR in each band. The large scatter in the high-z relation is noticeably smaller when we limit the sample to galaxies with inclination $i>45^{\circ}$ (see Fig. 3), which is the lowest value used in some works (for example, Nakamura et al. 2006). When we fitted the TFR separately for objects with $i<45^{\circ}$, we found a smaller amount of evolution than for all objects together. For galaxies with $i>45^{\circ}$, the opposite result was found, i.e. we measured greater evolution in the zeropoint. For galaxies with low inclination, an error in the inclination angle yields larger velocity errors than for more inclined galaxies. Nevertheless, the error in the extinction will be more noticeable for galaxies with high inclination. If the error in the extinction were the reason for the differences found for both inclination ranges, then for the $K_{\rm S}$-band there would be no difference in the evolution found for galaxies with low and high inclination, because the extinction is negligible in this band. However, when both inclination ranges were fitted independently for the $K_{\rm S}$-band, we found that the difference was identical to those for the other bands. Therefore, a velocity error caused by an inclination error seems to be the reason for the disagreement between both inclination ranges. Although in terms of the velocity, the results are more reliable for galaxies with $i>45^{\circ}$, the evolution in the zeropoint of the TFRs does not change significantly if the whole sample is used. Therefore, we fitted all galaxies together to increase, into the bargain, the statistical significance of the result. Measuring the scatter in the TFR and its evolution are important to constraining models of galaxy formation. Masters et al. (2008) observed that the scatter in the local K-band TFR increases with decreasing rotation velocity. In our local sample, the scatter is 1.21 mag in the $K_{\rm S}$-band, but reduces to 0.9 mag when we consider objects with $\log(2V_{\rm max})>2.2$. For $\log(2V_{\rm max})=2.2$, the scatter in the K-band TFR obtained from Masters et al. (2008) is $\sim$0.9 mag. However, the scatter in our high-redshift sample (1.23 mag) is larger than the scatter of $\sim$0.5 mag obtained in Masters et al. (2008) for $\log(2V_{\rm max})=2.5$, that is the average velocity of our high redshift sample. Although the scatter does not differ significantly from those of our local relations (in agreement with the result found by Conselice et al. 2005, for their samples at z<0.7 and z>0.7), it is two to three times higher than those of the local relations of Verheijen (2001), Masters et al. (2008), or Hammer et al. (2007). This is probably due to the measurement errors being larger than for z=0 galaxies.

Table 3:   Magnitude evolution found in each band assuming a constant slope.

As we assumed that the slope does not change with the redshift, we were able to infer the evolution in the magnitude for each band, from the difference between the high-redshift and local TFRs for a fixed velocity. The results are shown in Table 3. For the B-band, we found a change in magnitude of $\Delta M_{\rm B}=-1.13$ at z=1.25, which is larger than 2$\sigma $, and consistent with our previous work (Fernández Lorenzo et al. 2009), and the results of other authors (e.g., Böhm et al. 2004; Bamford et al. 2006). However, for both R and I-band, we found weaker evidence of evolution, which can probably be attributed to the more reliable k-corrections carried out in this work. The most interesting result is a smaller difference in the intercept as the band wavelenght increases, the change in the zeropoint for I and $K_{\rm S}$-bands being smaller than 1$\sigma $. The difference in magnitude found for the $K_{\rm S}$-band is compatible with no evolution, and agrees with the results of Conselice et al. (2005) and Flores et al. (2006). Nevertheless, Puech et al. (2008) found evolution in the $K_{\rm S}$-band TFR, in the sense that galaxies were fainter in the past. They attributed their disagreement with Flores et al. (2006) to both the local relation slope used as reference and the more accurate measurement of the rotation velocities of Puech et al. (2008). However, if the Puech et al. (2008) data are compared with the Verheijen (2001) local relation (the same used by Flores et al. 2006), no evolution is found. Therefore, the local TFR slope plays a fundamental role in the evolution of the $K_{\rm S}$-band TFR, and is studied separately in the next section.

5 Discussion

Several authors have studied the infrared TFR in both the K and $K_{\rm S}$-bands. To compare with these works, we need to know the relation between both bands. From Grocholski & Sarajedini (2002), a Bessell K-band is related to the 2MASS $K_{\rm S}$-band as $K=K_{\rm S}-(-0.044\pm0.003)-(0.000\pm0.005)(J-K)$. Assuming that the 2MASS and Palomar $K_{\rm S}$-bands are equivalent, the difference between the K and $K_{\rm S}$-bands is within the errors in our $K_{\rm S}$-band absolute magnitudes, and therefore we can compare our results with those obtained in other works.

5.1 The slope in the local K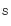$_{\sf S}$-band TFR

\begin{figure} \par\includegraphics[scale=0.48]{14244fg4a.eps}\includegraphics[scale=0.48]{14244fg4b.eps}\vspace*{3mm} \end{figure} Figure 4:

Local Tully-Fisher relation in the $K_{\rm S}$-band for the Millenium mock galaxies. The grey points are the objects with $M_{\rm bulge} < 0.15$  $M_{\rm star}$ and MK< -16. The dashed line is the relation obtained with our local sample and the dot-dash line is the local relation obtained by Hammer et al. (2007) for a sample of SDSS galaxies with $\log(V_{\rm flat})\geq2.2$. The solid line is the fit to the data for MK<-18 (left) and MK<-21 (right).

Open with DEXTER

To study the discrepancies found by the authors in the slope of the local $K_{\rm S}$-band TFR, we used the Millenium simulation database (Springel et al. 2005) produced by the Virgo consortium. From this simulation, the catalogue that we used, contained in the millimil database, is the table DeLucia2006a, from which we took the data corresponding to maximum rotational velocity ( $v_{\rm max}$), Johnson B, V, R, I, and K absolute rest-frame magnitudes (dust extinction included), redshift, mass of bulge ( $M_{\rm bulge}$), and the total mass in stars ( $M_{\rm star}$) (Croton et al. 2006; De Lucia & Blaizot 2007). Using the upper value of bulge-to-total (B/T) mass ratio for late-type galaxies from Laurikainen et al. (2007), we selected the objects with $M_{\rm bulge} < 0.15 ~M_{\rm star}$ as being representative of spiral galaxies. In Fig. 4, we present the data for MK< -16. The K-band magnitudes were converted into the AB system using MK(AB) = MK(Vega)+1.9 (Hewett et al. 2006). The slope of the local TFR obtained using simulated galaxies seems to depend on the magnitude range considered. For instance, when we fit galaxies with MK< -18, we obtain a slope very close to our sample of local galaxies. However, for MK<-21, the slope is closer to the K-band TFR found by Hammer et al. (2007), who restricted their sample to SDSS galaxies with log( $V_{\rm flat})\geq 2.2$ (the local TFR used by Puech et al. 2008). For the other bands, we found the same variations in the slope as found for the K-band.

If we assume that the slopes of the TFRs depend on the magnitude range considered, then our local relations cannot be compared with our high redshift sample, which consists of galaxies brighter than MK = -20.5. To be able to compare our high redshift data with a local relation derived for the same magnitude range, we used the Millenium data. We calculated the difference in the zeropoint between our local sample and Millenium data by setting the same slope across the same magnitude range as for our local one. As happened when comparing with Verheijen (2001) local relations, we obtained a similar difference in the intercept of the relation for all bands, whose value corresponds to the ratio of rotation velocity to line width. Nevertheless, the difference in the zeropoint was found to be lower, the zeropoint of the Verheijen (2001) relations being greater than the Millenium local zeropoints. We then calculated the Millenium local TFR relations for the brightest galaxies and we applied the shift to the zeropoint required to compare with our high redshift sample. Finally, we fit the data of the high redshift sample by setting the slope to the new local one determined using Millenium data. We found a greater change in luminosity for all bands, but for the I-band, the difference in the zeropoint of the high redshift relation with respect to the Millenium local one was still found to be within 2$\sigma $ (where $\sigma $ is the uncertainty in the local offset), and for the $K_{\rm S}$-band the difference is within $\sim$$1\sigma$. Therefore, we found smaller luminosity evolution as passing from blue to redder bands, consistent with the results obtained in the present work. This result supports our measurement of no evolution of the TFR for the $K_{\rm S}$-band.

5.2 The colour evolution of disc galaxies

The colours of galaxies provide information about their stellar content and, by using evolutionary models, the history of star formation. Studying the colour evolution versus rotational velocity thus allows us to study the change in the stellar content of a galaxy relative to its total mass. In Fig. 5, we present the colours ( $V-K_{\rm S}$) and (R-I) versus rotational velocity for local and high-redshift galaxies. For ( $V-K_{\rm S}$), we have a larger dispersion, and the evolution of $\sim$0.35 mag found by setting the slope to the theoretical local ( $V-K_{\rm S}$) relation, is within the dispersion (smaller than 1$\sigma $). However, there is a clear change of $\sim$0.33 mag with redshift, in the (R-I) colour at fixed velocity (>$2{\sigma}$). The galaxies are therefore redder today, which may represent an ageing of the stellar population caused by a star formation decrease in the past 8.6 Gyr. As in the case of the evolution in R and I-band TFRs, we found a different result from that found in Fernández Lorenzo et al. (2009), because of the more reliable k-corrections carried out in the present work, where we used additional photometric information.

\begin{figure} \par\includegraphics[width=9cm,clip]{14244fg5.eps}\vspace*{2mm} \end{figure} Figure 5:

Colour ( $V-K_{\rm S}$) vs. rotation velocity (up) and colour (R-I) vs. rotation velocity (down). Black diamonds represent the galaxies in the redshift range 1.1<z<1.4, while open squares are the galaxies in the redshift range 0.1<z<0.3. Difference between the local ( $V-K_{\rm S}$) TFRs (up) and (R-I) TFRs (down) (thin lines) and its 2$\sigma $ uncertainty (dashed lines) are shown. Thick lines are the fit to the high redshift data when setting the slope to the local relation in each case.

Open with DEXTER

The colour evolution of simulated disc galaxies with redshift has been investigated by other studies. In Fernández Lorenzo et al. (2009), we compared the results with Westera et al. (2002), who studied the colour evolution of disc galaxies in two models of galaxy formation called the accretion and collapse models. Using these models, the change in colours observed here can be more accurately reproduced by the accretion model, but the predicted evolution in the (V-K) colour would be twice that found here, and the change in magnitude is in the opposite sense to that predicted by the simulations. In a subsequent paper, Westera et al. (2007) investigated the effect of the initial mass function (IMF) on the colour evolution of disc galaxies by considering two different IMFs: Salpeter and Kroupa. The evolution in the (g-K) colour derived from their work (for the Kroupa IMF without absorption) would again be larger than the result found here, assuming $(g-K)\approx(V-K_{\rm S})$, mainly because of the change in the K-band of $\sim$1 mag predicted by the simulations. However, this change in K would lead, according to their inferred evolution of the $M_{\ast}/L_{K}$, to a growth of a factor $\sim$6 in the stellar mass since z=1.25. Nevertheless, according to the $M_{\ast}/L_{r}$ and $M_{\ast}/L_{i}$ determined in the same work, this change in stellar mass would produce an evolution of $\Delta M_r=0.36$ and $\Delta M_i=0.26$ from z=1.25 to z=0, which would imply that galaxies were fainter in the past. This result is the opposite of that found here, and that found by van Starkenburg et al. (2006) for the R-band. Our results are therefore inconsistent with the simulations of Westera et al. (2002,2007).

5.3 Comparison with other works

As we discuss in Fernández Lorenzo et al. (2009), the evolution found in the optical bands is more likely due to a change in luminosity than in velocity. Conselice et al. (2005) and Flores et al. (2006) obtained the same result as this work, i.e. no evolution in the K-band TFR, whereas Puech et al. (2008) detected a change in the K-band TFR zeropoint, which they attributed to an average brightening of galaxies since $z\sim0.6$ by $0.66~\pm~0.14$ mag. They explain this brightening as a growth in stellar mass by a factor of $\sim$2.5 since z=0.6, as evaluated from the evolution in $\log(M_{\rm stellar}/L_K$) found by Drory et al. (2004). They claim that the result is consistent with the gaseous O/H phase abundance of $z~\sim~0.6$ emission-line galaxies, which is half of that found in present-day spirals (Rodrigues et al. 2008).

However, assuming a change in $\log(M_{\rm stellar}/L_K$) with redshift in the way described by Drory et al. (2004), but no evolution in the K-band TFR as found in the present work, we conclude that the spiral intermediate-mass galaxies have doubled their stellar masses since z=1.25, which agrees rather well with expectations from stellar mass density studies (Drory et al. 2004). From the mass-to-light ratios in u, r, i, and K-bands of Westera et al. (2007, who found a similar result for the K-band to that of Drory et al. 2004, in the past 9 Gyr#, but considering our growth in stellar mass by a factor of 2, the evolution in the optical bands would be $\Delta M_u=-1.3$; $\Delta M_r=-0.79$; $\Delta M_i=-0.67$ (for a Salpeter IMF without absorption), which are consistent with the result found in the present work. Assuming at least the same evolution in the K-band magnitude at z=1.25 as that found by Puech et al. (2008) at z=0.6, the stellar mass should have grown at least by a factor of 3.5 when applying the evolution in $\log(M_{\rm stellar}/L_K)$ found by Drory et al. (2004). However, the stellar mass should have grown by a factor of 2.6 since z=1.25, if the change in the gaseous O/H abundance were attributed to all gas being transformed into stars (Rodrigues et al. 2008). Given the short lives of the most massive stars responsible for the enrichment of the ISM (interstellar medium), and the time required for cooling the gas to form new stars, the change in O/H in the past 8.6 Gyr will not only be due to a rise in O, but also a drop in H. The change in stellar mass inferred from the metallicity evolution is therefore probably an upper limit.

The stellar mass can also increase by means of galaxy merger processes or the accretion of small galaxies. In the first case, the galaxy disc would be destroyed if the mass of the merger were larger than $\sim$15$\%$ of the parent galaxy mass. The accretion of small galaxies, although a probable contribution to increasing the stellar mass, is not enough to explain a growth of a factor 3.5. Hence, our result of a doubling in stellar mass since z=1.25 seems more plausible and consistent. The increase in stellar mass is probably caused by gas being transformed into stars, which would be consistent with there being a higher SFR density at $z\sim1$-2 than today (Bouwens et al. 2009). This gas could be present either in the disc, the halo, or both. Tacconi et al. (2010) found empirical evidence that the higher star formation rates at $z\sim1$-2 are the consequence of large molecular gas reservoirs (both due to continuous gas inflow from the halos, and minor but not major mergers) and not of a higher star formation efficiency than that at $z\sim0$. Nevertheless, doubling the amount of gas at z=1.25, to account for a doubling of the stellar mass at z=0, would result in higher extinctions in the optical bands than those derived from the Tully et al. (1998) equations used in this work, because they have been obtained using local galaxy samples. Were this the case, the evolution found in the optical bands would be larger than the evolution observed in this work.

6 Conclusions

We have studied the evolution of the TFR in B, V, R, I, and $K_{\rm S}$-bands, using two sample of galaxies selected from the GSS, one in the redshift range 0.1<z<0.3, which is representative of local galaxies, and a high redshift sample in the redshift range 1.1<z<1.4. The rotation velocity of all 241 spiral galaxies were measured from optical lines widths, using DEEP2 spectra. Morphology was determined from HST images, and the absolute magnitudes were derived from a carefully study of the k-correction made with a large set of photometric information. The results of this study can be summarized as follows.

We analysed four sets of templates and concluded that the SED of a spiral galaxy is more accurately reproduced by the nonnegative linear combination of five templates based on the Bruzual & Charlot (2003) stellar evolution synthesis codes obtained by kcorrect. However, when the data include a noisy band, the k-corrections calculated by this code are unsuitable. We also found that the most reliable k-correction is obtained from information in a observed band that roughly match the rest-frame band. In this case, the rest-frame magnitude in the noisy band is more accurate when calculated directly from the best-fit template.

When the observed photometry does not match the rest-frame bands, it is possible to calculate the rest-frame magnitudes via an interpolation method, as long as enough information at longer and shorter wavelengths is available. However, an extrapolation method is not reliable for galaxies at $z\sim 1.25$ since the results can vary by more than one magnitude mainly because of the poorer fit of the template.

New local TFRs were constructed by increasing the sample of our previous work (Fernández Lorenzo et al. 2009) in the redshift range 0.1<z<0.3. We inferred a similar difference in the zeropoint of the TFR for all bands when we compared with the Verheijen (2001) local relations, which we assumed to equal the ratio of rotation velocity to line width.

We derived the high redshift 1.1<z<1.4 TFRs by fixing the slope to the local one in each band, to study the evolution of the zeropoints. We confirmed the evolution in the B-band TFR found in our previous work (Fernández Lorenzo et al. 2009), in the sense that galaxies were brighter in the past, and no evolution in the $K_{\rm S}$-band TFR. Furthermore, for the other bands we detected a gradual evolution, with a change in luminosity becoming more noticiable as the band became bluer.

We studied the slope of the local $K_{\rm S}$-band TFR by comparing with Millenium simulated data. We found that the slope varies depending on the luminosity range used in the fit. Considering this effect, we calculated new local $K_{\rm S}$-band TFR from the Millenium data in the same luminosity range as our high redshift sample, confirming again that there is no evolution in the $K_{\rm S}$-band TFR.

Assuming the change in the stellar mass-to-light ratio M/LK found by Westera et al. (2007), which is consistent with that of Drory et al. (2004), but no evolution in the $K_{\rm S}$-band, we have found that galaxies have probably doubled their stellar mass in the past 8.6 Gyr. This growth is probably mainly due to gas being transformed into stars, as supported by the change in the gaseous O/H abundance found by Rodrigues et al. (2008). From the mass-to-light ratios derived by Westera et al. (2007) for the optical bands (IMF of Salpeter), and assuming this change in stellar mass, we inferred an evolution in the optical luminosity similar to that found in the present work. However, the luminosity and colour evolution simulated by Westera et al. (2007) is not consistent with that found here and would imply a growth of $\sim$6 in the stellar mass from z=1.25 to z=0.

Therefore, the galaxies, despite having doubled their stellar mass in the past 8.6 Gyr, are nowadays fainter and redder in the optical bands, which may reflect an ageing of the stellar populations caused by the star formation density decrease observed in the past 8.6 Gyr. This is supported by the change found in the $(V-K_{\rm S})$ and (R-I) colours (for a fixed velocity), in the sense that galaxies were bluer in the past.

Acknowledgements
This work was supported by the Spanish Plan Nacional de Astronomía y Astrofísica under grant AYA2008-06311-C02-01. We thank the DEEP2 group for making their catalogues and data publicly available. Funding for the DEEP2 survey has been provided by NSF grants AST95-09298, AST-0071048, AST-0071198, AST-0507428, and AST-0507483, as well as NASA LTSA grant NNG04GC89G. The work is based on observations obtained at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council of Canada, the Institut National des Sciences de l'Univers of the Centre National de la Recherche Scientifique of France, and the University of Hawaii. This study makes use of data from AEGIS, a multiwavelength sky survey conducted with the Chandra, GALEX, Hubble, Keck, CFHT, MMT, Subaru, Palomar, Spitzer, VLA, and other telescopes and supported in part by the NSF, NASA, and the STFC. The Millenium Simulation database used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory. We thank the SAO/NASA Astrophysics Data System (ADS) that is always so useful.

Appendix A: Deriving the k-corrections

\begin{figure} \par\mbox{\includegraphics[scale=0.44]{14244fga1a.eps}\includegra... ...1c.eps}\includegraphics[scale=0.44]{14244fga1d.eps} } \vspace*{5mm} \end{figure} Figure A.1:

Differences between the B, V, R, I, $K_{\rm S}$, IRAC1, and IRAC2-band magnitudes derived from the best-fit template normalized to the observed V-band magnitude ( $m_{\rm temp}$), and the corresponding observed magnitudes ( $m_{\rm obs}$), for our high-redshift sample. a) Templates of SWIRE. b) Templates of Poggianti. c) Templates of BC03. d) Templates provided by kcorrect.

Open with DEXTER

We present a systematic study using various sets of templates and methods to establish the most reliable k-correction for our data.

We performed the following tests:

(i)
We compared the results obtained by fitting different sets of spiral templates to the data, to establish the set of templates that more closely fits our high redshift sample (see Sect. A.1).

(ii)
We estimated the accuracy of the rest-frame photometry reproduced by the templates, since our photometry does not match the rest-frame optical magnitudes, and the 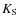$K_{\rm S}$-band errors are large. We calculated the best-fit template of z=1.25 galaxies with a known SED (i.e.: templates of local galaxies redshifted to z=1.25) from the photometric information in the same bands and using the same weights that we evaluated for our real sample. We then determined the differences between the rest-frame optical magnitudes calculated from the original rest-frame SED, and those from the best-fit template (see Sect. A.2).

(iii)
We compared the accuracy of the k-corrections derived using this interpolation method with those obtained using an observed band that roughly match the rest-frame magnitude (see Sect. A.3).

A.1 Optimal set of templates

To evaluate the templates that more closely describe each of our galaxies, we used the code bpz, which implements the Bayesian photometric redshift method described in Benítez (2000). We restricted the code redshift range to 0.95-1.4, where all the galaxies of our sample are located. This code was applied using four different sets of spiral galaxy templates:

(i)
The templates of SWIRE, formed by 7 spirals ranging from early to late types (S0-Sdm), and generated with the GRASIL code (Silva et al. 1998).

(ii)
The templates of Poggianti (1997), that consist of models of Sa and Sc spirals computed for various redshifts from 0 to 3.

(iii)
The Bruzual & Charlot (2003, hereafter BC03) collection of galaxy templates used by Tremonti et al. (2003) in the analysis of SDSS (Sloan Digital Sky Survey) galaxy spectra. The library includes 39 templates, obtained from 13 models and three metallicities Z=0.008, 0.02, and 0.05 (see Table A.1 for the description of the 13 models).

(iv)
The templates produced by the routine kcorrect (Blanton & Roweis 2007), which are a nonnegative linear combination of five templates based on the BC03 stellar evolution synthesis code.

For each galaxy, we calculated the redshifted best-fit template to be

\begin{displaymath}{\lambda} = {\lambda_{0}} \ (1+z) \end{displaymath} (A.1)

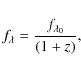
\begin{displaymath}f_{\lambda} = \frac{f_{\lambda_{0}}}{(1+z)}, \end{displaymath} (A.2)

where ${\lambda}_0$ is the wavelength and $f_{\lambda_{0}}$ is the flux density in $\rm erg \ s^{-1} \ cm ^{-2} \ \AA^{-1}$ of the template at z=0. We then normalized to the V-band to obtain the SED of each galaxy. As this template is the closest representation of the photometry observed, we can infer which set of templates reproduces our data the most accurately by calculating the difference between the observed magnitude $m_{\rm obs}$ and the magnitude $m_{\rm temp}$ obtained from the redshifted template, in each band. To calculate $m_{\rm temp}$, we projected the template into the filter Q, using the expresion

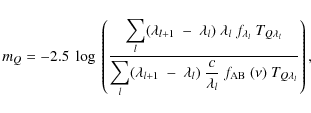
\begin{displaymath}m_Q = -2.5 \ \log \ \left(\frac {\displaystyle\sum_l (\lambda... ...lambda_l}} \ f_{\rm AB} \ (\nu) \ T_{Q \lambda_{l} }}\right), \end{displaymath} (A.3)

where $T_{Q \lambda_{\rm l} }$ is the filter transmission in the Q-band at the wavelength $\lambda_{\rm l}$, $f_{\rm AB} \ (\nu) = 3.631 \times 10^{-20}$ erg s-1 cm-2 Hz-1 is the flux density of the AB standard source, and c is the speed of light.

Table A.1:   Description of the templates from BC03 and number of galaxies ($N_{\rm G}$) in our sample that were fitted to each one by bpz.

In Fig. A.1, we present the result for all galaxies in each set of templates. For our objects, with a median redshift of $\langle z\rangle =1.25$, B, V, R, and I-bands correspond to UV rest-frame wavelengths, while $K_{\rm S}$, IRAC1, and IRAC2-bands correspond to NIR rest-frame wavelenghts. For all sets of templates, the larger difference found in the $K_{\rm S}$-band is caused by the photometric errors in this magnitude (the fits of bpz and kcorrect are weighted by the photometric errors). However, there is a clear difference between UV and NIR in the comparison with the SWIRE templates (Fig. A.1a). For this set, the galaxies are bluer than the templates. In contrast, for the templates of Poggianti (1997) (Fig. A.1b), the opposite happens, i.e. the galaxies are redder than the templates. However, with the set of BC03 (Fig. A.1c), the agreement between observed-frame bands and the magnitudes obtained from the templates, is better. The combination of the templates of BC03 achieved using kcorrect (Fig. A.1d) provides a similar result, but with smaller dispersions. In this case, the template supplied by the code does not need to be normalized to V-band. In addition to the best-fit template, kcorrect evaluates the k-correction for each band used in the fit. This k-correction is the difference between the redshifted and rest-frame band, both calculated from the best-fit template. Our rest-frame magnitudes would then be obtained by subtracting these k-corrections from the observed magnitudes. However, the photometric errors in the observed quantities propagate into the rest-frame magnitudes obtained in this way. This has a strong effect on colour evolution studies if one of the observed bands have substantially larger errors than the others. This is the case for our $K_{\rm S}$-band data, so we used another approach to derive the rest-frame $K_{\rm S}$ magnitudes. Since the observed IRAC2-band roughly matched the rest-frame $K_{\rm S}$-band, and the fit of the template is quite good in the wavelength range corresponding to IRAC2 (see Fig. A.1d), we directly used the magnitudes obtained in this band from the rest-frame best-fit template instead of k-correcting the data. For the optical bands, the rest-frame magnitudes calculated from the best-fit template or using the k-corrections of kcorrect are equivalent in terms of the TFR, because the average difference between both methods is almost null (see Fig. A.1d). As in $K_{\rm S}$-band, the best-fit templates determined by kcorrect were then used, but not the k-corrections provided by this software.



A.2 The reliability of the photometry

\begin{figure} \par\includegraphics[width=7.7cm,clip]{14244fga2.eps}\vspace*{1.5mm} \end{figure} Figure A.2:

Difference between the magnitudes calculated from each rest-frame template of BC03 and from the best-fit template (at z=0) calculated by kcorrect from the photometry of the redshifted template at z=1.25. See Table A.1 for the description of the templates from BC03. The grey zones represent the templates that were fitted by bpz for some of our galaxies.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14244fga3.eps} % \end{figure} Figure A.3:

Rest-frame $K_{\rm S}$-band magnitude calculated from each of the templates from BC03 normalized to an IRAC2 magnitude of 21.5 in the redshifts z=1.1, 1.25, and 1.4. The description of the templates is the same as in Fig. A.2.

Open with DEXTER

Since our photometry does not match the rest-frame optical magnitudes, we need to know how reliably kcorrect can reproduce the optical SED of a galaxy at 1.1<z<1.4 from the photometric information available. To determine this, we redshifted the templates from BC03 to our median redshift, z=1.25, and we calculated the magnitudes in $B, V, R, I, K_{\rm S}$, IRAC1, and IRAC2-bands. We then introduced this photometry in kcorrect to obtain the best-fit template. We assumed the average magnitude error in our data to be the standard deviation used by the code in every band. In this way, the bands were weighted as the real data. We then calculated the difference in magnitude between the non-redshifted templates from BC03 and the template produced by kcorrect for the rest-frame B, V, R, I, and $K_{\rm S}$-bands. These differences are represented in Fig. A.2 and provide a first order estimation of the accuracy of the rest-frame magnitudes obtained in the previous section. Because we did not include photometric information for the optical rest-frame wavelength range, the kcorrect template provides interpolated magnitudes for these bands. The general trend found for the B-band is that kcorrect provides a fainter rest-frame magnitude that the template from BC03 does, while the $K_{\rm S}$-band rest-frame magnitudes are brighter. However, the average difference for V, R, and I-bands is $\sim$0 when considering the full set of templates. For the constant star formation model (first 3 templates) and the two exponential models (last 6 templates), the error in the SED reconstructed by kcorrect is $\sim$0.1, whereas the poorest fit corresponds to a simple stellar population. In general, the fitting of more recent bursts infers optical rest-frame magnitudes that are brighter than the real magnitudes of the templates from BC03, while the optical information about the oldest burst reconstructed by kcorrect tends to imply that it is fainter than reality. For the simple stellar populations that reproduce the data for some of our galaxies, the errors in some cases are $\sim$0.4. A recalculation of the k-corrections in our previous work (Fernández Lorenzo et al. 2009), by adding the $K_{\rm S}$-band photometry to the B, R, and I-bands used in this work, shows that our previous rest-frame magnitudes were overestimated, especially in the I-band. Moreover, the best-fit template of BC03 provided by bpz is different if we use only the information in the B, R and I-bands, or if we introduce also the infrared information. We repeated the procedure used in the Fig. A.2, but introducing only the optical bands (B, V, R, and I) in the kcorrect fit, so that the rest-frame magnitudes are extrapolated rather than interpolated. The error in the k-corrected magnitudes was found to be between 0.5 and 1.5 mag for most of the templates. The extrapolation method is therefore unsuitable for high redshift galaxies.

A.3 Comparison of methods

We studied the k-corrections obtained using an observed band that roughly matches the rest-frame magnitude. In our redshift range, IRAC2 provides information about the SED region corresponding to rest-frame $K_{\rm S}$-band. Hence, if we normalize the redshifted best-fit template to the IRAC2-band, and calculate the $K_{\rm S}$ magnitude from this template at z=0, we can achieve a higher accuracy in the rest-frame $K_{\rm S}$-band magnitudes. The main difficulty in using this procedure is the error in the choice of the template. To quantify this error, we compared the k-corrected $K_{\rm S}$-band magnitude obtained from all templates of BC03 redshifted to z=1.1, 1.25, and 1.4, and normalized to the same IRAC2 magnitude. In Fig. A.3, we present our results. The greatest difference between two templates is $\sim$0.1 mag at z=1.4. We repeated the same procedure with the SWIRE templates, obtaining a similar result. Using photometry that roughly matches the rest-frame $K_{\rm S}$-band, the k-correction is quite independent of the template, mainly due to the smaller difference in the infrared SEDs between early and late-types spirals (see, for example, Mannucci et al. 2001). However, for optical B, V, R, and I-bands, this does not hold. Some of the galaxies have J-band photometry from Palomar data, which corresponds to the rest-frame V-band magnitude at z=1.25. Following the same procedure as used with the $K_{\rm S}$-band data (Fig. A.3), but normalizing the templates to mJ=22.5, we found that the maximum difference between the rest-frame V-band of two different templates was $\sim$0.3. Since the errors in the J-band are larger than the IRAC2 errors, this method is not as effective for the V-band as for the $K_{\rm S}$-band k-correction.

\begin{figure} \par\includegraphics[width=8cm,clip]{14244fga4a.eps}\par\includegraphics[width=8cm,clip]{14244fga4b.eps} \end{figure} Figure A.4:

Comparison between the k-corrected magnitude obtained from kcorrect best-fit template and from the best-fit template of BC03. For $K_{\rm S}$-band ( up), the normalization of the template from BC03 was done to the observed IRAC2-band. For V-band ( down), the template of BC03 was normalized to the observed V-band. The solid line shows the least-square fits with slope 1.

Open with DEXTER

Finally, we applied both methods to our sample of galaxies instead of redshifted templates. In Fig. A.4, we present the rest-frame magnitudes calculated from the best-fit template of BC03 normalized to the IRAC2-band, versus the rest-frame magnitudes calculated from the best-fit template of kcorrect. In addition, we present the result for the V-band, but the template from BC03 being normalized to the observed-frame V-band rather than the J-band. For the $K_{\rm S}$-band, the difference between both methods is negligible, but we found a larger scatter between the values of rest-frame V-band. Even so, both values provide us the same mean result because the averaged differences are almost zero.

\begin{figure} \par\mbox{\includegraphics[scale=0.44]{14244fga5a.eps}\includegraphics[scale=0.44]{14244fga5b.eps} }\end{figure} Figure A.5:

Comparison between the rest-frame B-band ( left) and $K_{\rm S}$-band ( right) magnitudes calculated from the best-fit template obtained using the $g, r, i, z, K_{\rm S}$, IRAC1, and IRAC2-bands aperture magnitudes in 1.5'' aperture, and those obtained using the $B, V, R, I, K_{\rm S}$, IRAC1, and IRAC2 total magnitudes. The solid lines represent the one to one relations.

Open with DEXTER

A.4 Aperture effects

All the photometry used in this work is part of the AEGIS project and has already been corrected for aperture and PSF effects. However, the magnitudes derived at the same aperture for all bands are not available. We therefore decided to compare the results obtained in this work with those obtained using other optical photometry. We used the aperture photometry in the g, r, i, and z-bands, which are provided with the CFHTLS data and are also part of AEGIS. The aperture used by this team is 1.5'', enough to cover the whole galaxies in the high redshift sample. We then calculated the best-fit template using the aperture photometry in the $g, r, i, z, K_{\rm S}$, IRAC1, and IRAC2 bands, with an aperture of 1.5'' (for the noisy $K_{\rm S}$-band we used mag_AUTO). In Fig. A.5, we present the rest-frame B and $K_{\rm S}$-bands calculated this way, using the total magnitudes in the $B, V, R, I, K_{\rm S}$, IRAC1, and IRAC2-bands determined as described in Sect. 3.1 of this paper. The dispersion obtained in the rest-frame B-band is mainly due to the interpolation, as we found previously (Fig. A.2). For the rest-frame $K_{\rm S}$-band, we obtain very good agreement between the magnitudes derived from aperture and total photometry, since these k-corrections are basically dependent on the IRAC2-band, which roughly corresponds to the rest-frame $K_{\rm S}$-band. In this case, the k-correction is not too dependent on the template, as we explained in Sect. A.3 (and Fig. A.3).

References

  1. Bamford, S. P., Aragón-Salamanca, A., & Milvang-Jensen, B. 2006, MNRAS, 366, 308 [NASA ADS] [CrossRef] [Google Scholar]
  2. Barmby, P., Huang, J.-S., Ashby, M. L. N., et al. 2008, ApJS, 177, 431 [NASA ADS] [CrossRef] [Google Scholar]
  3. Benítez, N. 2000, ApJ, 536, 571 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
  6. Böhm, A., Ziegler, B. L., Saglia, R. P., et al. 2004, A&A, 420, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bosma, A. 1981, AJ, 86, 1825 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 (BC03) [NASA ADS] [CrossRef] [Google Scholar]
  10. Bundy, K., Ellis, R. S., Conselice, C. J., et al. 2006, ApJ, 651, 120 [NASA ADS] [CrossRef] [Google Scholar]
  11. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  12. Coil, A. L., Newman, J. A., Kaiser, N., et al. 2004, ApJ, 617, 765 [NASA ADS] [CrossRef] [Google Scholar]
  13. Conselice, C. J., Bundy, K., Ellis, R. S., et al. 2005, ApJ, 628, 160 [NASA ADS] [CrossRef] [Google Scholar]
  14. Croton, D. J., Springel, V., White, S., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cuillandre, J.-C., Starr, B., Isani, S., McDonald, J. S., & Luppino, G. 2001, ASPC, 232, 398 [NASA ADS] [Google Scholar]
  16. Davis, M., Faber, S. M., Newman, J., et al. 2003, SPIE, 4834, 161 [Google Scholar]
  17. Davis, M., Guhathakurta, P., Konidaris, N., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
  18. De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
  19. Drory, N., Bender, R., Feulner, G., et al. 2004, ApJ, 608, 742 [NASA ADS] [CrossRef] [Google Scholar]
  20. Faber, S. M., Phillips, A. C., Kibrick, R. I., et al. 2003, SPIE, 4841, 1657 [Google Scholar]
  21. Fernández Lorenzo, M., Cepa, J., Bongiovanni, A., et al. 2009, A&A, 496, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Flores, H., Hammer, F., Puech, M., Amram, P., & Balkowski, C. 2006, A&A, 455, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Giovanelli, R., Haynes, M. P., Herter, T., et al. 1997, AJ, 113, 22 [NASA ADS] [CrossRef] [Google Scholar]
  24. Grocholski, A. J., & Sarajedini, A. 2002, AJ, 123, 1603 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hammer, F., Puech, M., Chemin, L., Flores, H., & Lehnert, M. D. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hewett P. C., Warren S. J., Leggett S. K., & Hodgkin S. T. 2006, MNRAS, 367, 454 [NASA ADS] [CrossRef] [Google Scholar]
  27. Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Howarth, I. D., Murray, J., Mills, D., & Berry, D. S. 1996, Starlink User Note 50.21 [Google Scholar]
  29. Kassin, S. A., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L35 [NASA ADS] [CrossRef] [Google Scholar]
  30. Laurikainen, E., Salo, H., Buta, R., et al. 2007, IAU Symp., 235, 36 [NASA ADS] [Google Scholar]
  31. Mannucci, F., Basile, F., Poggianti, B. M., et al. 2001, MNRAS, 326, 745 [NASA ADS] [CrossRef] [Google Scholar]
  32. Masters, K. L., Springob, C. M., & Huchra, J. P. 2008, AJ, 135, 1738 [NASA ADS] [CrossRef] [Google Scholar]
  33. Mathewson, D. S., Ford, V. L., & Buchhorn, M. 1992, ApJS, 81, 413 [NASA ADS] [CrossRef] [Google Scholar]
  34. Nakamura, O., Aragón-Salamanca, A., Milvang-Jensen, B., et al. 2006, MNRAS, 366, 144 [NASA ADS] [CrossRef] [Google Scholar]
  35. Navarro, J. F., & Steinmetz, M. 2000, ApJ, 538, 477 [NASA ADS] [CrossRef] [Google Scholar]
  36. Poggianti, B. M. 1997, A&AS, 122, 399 [Google Scholar]
  37. Puech, M., Flores, H., Hammer, F., et al. 2008, A&A, 484, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Rix, H.-W., Guhathakurta, P., Colless, M., & Ing, K. 1997, MNRAS, 285, 779 [NASA ADS] [CrossRef] [Google Scholar]
  39. Rodrigues, M., Hammer, F., Flores, H., et al. 2008, A&A, 492, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  41. Schechter, P. L. 1980, AJ, 85, 801 [NASA ADS] [CrossRef] [Google Scholar]
  42. Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] [Google Scholar]
  43. Simard, L. 1998, Astronomical Data Analysis Software and Systems VII, 145, 108 [NASA ADS] [Google Scholar]
  44. Simard, L., & Pritcher, C. 1998, ApJ, 505, 96 [NASA ADS] [CrossRef] [Google Scholar]
  45. Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  46. Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
  47. Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2003, A&AS, 35, 770 [Google Scholar]
  48. Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
  49. Tully, R. B., & Pierce, M. J., 2000, ApJ, 533, 744 [NASA ADS] [CrossRef] [Google Scholar]
  50. Tully, R. B., Pierce, M. J., Huang, J.-S., et al. 1998, AJ, 115, 2264 [NASA ADS] [CrossRef] [Google Scholar]
  51. van Starkenburg, L., van der Werf, P. P., Yan, L., & Moorwood, A. F. M. 2006, A&A, 450, 25 [Google Scholar]
  52. Verheijen, M. A. W. 2001, ApJ, 563, 694 [NASA ADS] [CrossRef] [Google Scholar]
  53. Vogt, N. P., Forbes, D. A., Phillips, A. C., et al. 1996, ApJ, 465, 15 [Google Scholar]
  54. Vogt, N. P., Phillips, A. C., Faber, S. M., et al. 1997, ApJ, 479, 121 [Google Scholar]
  55. Weiner, B. J., Willmer, C. N. A., Faber, S. M., et al., 2006a, ApJ, 653, 1027 [NASA ADS] [CrossRef] [Google Scholar]
  56. Weiner, B. J., Willmer, C. N. A., Faber, S. M., et al., 2006b, ApJ, 653, 1049 [NASA ADS] [CrossRef] [Google Scholar]
  57. Westera, P., Samland, M., Buser, R., & Gerhard, O. E. 2002, A&A, 389, 761 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Westera, P., Samland, M., Kautsch, S. J., Buser, R., & Ammon, K. 2007, A&A, 465, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Willick, J. A. 1994, ApJS, 92, 1 [NASA ADS] [CrossRef] [Google Scholar]
  60. Ziegler, B. L., Böhm, A., Fricke, K. J., et al. 2002, ApJ, 564, L69 [NASA ADS] [CrossRef] [Google Scholar]
  61. Zwaan, M. A., van der Hulst, J. M., de Blok, W. J. G., & McGaugh, S. S. 1995, MNRAS, 273, L35 [NASA ADS] [Google Scholar]

All Tables

Table 1:   Depth and average image quality of each measurement.

Table 2:   Parameters of the Tully-Fisher relations obtained by fitting DEEP2 data in the redshift range 0.1<z<0.3 used as local reference.

Table 3:   Magnitude evolution found in each band assuming a constant slope.

Table A.1:   Description of the templates from BC03 and number of galaxies ($N_{\rm G}$) in our sample that were fitted to each one by bpz.

All Figures

  \begin{figure} \par\mbox{\includegraphics[scale=0.41]{14244fg1a.eps}\includegrap... ...1c.eps}\includegraphics[scale=0.41]{14244fg1d.eps} } \vspace*{-2mm} \end{figure} Figure 1:

Example spectra (not flux-calibrated) of the high-z galaxies in our sample. The x-axis represents the rest-frame wavelengths in $\AA$. The green line is the fit to the [OII] $\lambda \lambda $3727 $\AA$ double line obtained with dipso, imposing that both lines had the same width.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[scale=0.43]{14244fg2a.eps}\includegraphics[s... ...44fg2c.eps}\includegraphics[scale=0.43]{14244fg2d.eps}\vspace*{2mm} \end{figure} Figure 2:

Comparison between local TFRs obtained from DEEP2 data (0.1<z<0.3) in B, R, I, and $K_{\rm S}$-bands, and Verheijen (2001) local TFRs (dashed lines). The solid line represents the linear fit to the DEEP2 data. The parameters of the fit are shown in Table 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[scale=0.42]{14244fg3a.eps}\includegraphics[s... ...pace*{4cm}\includegraphics[scale=0.42]{14244fg3e.eps}\hspace*{4cm}\end{figure} Figure 3:

Tully-Fisher relation in B, V, R, I, and $K_{\rm S}$-bands for the redshift range 1.1<z<1.4. Black diamonds are galaxies with inclination $45^{\circ }<i<80^{\circ }$, and grey points are galaxies with $25^{\circ }<i<45^{\circ }$. Thin and dashed lines represent the local TFR and its 2$\sigma $uncertainty in the offset. The thick line is the weighted least squares fit to all points. The fit was performed by fixing the slope to the local one in each case.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[scale=0.48]{14244fg4a.eps}\includegraphics[scale=0.48]{14244fg4b.eps}\vspace*{3mm} \end{figure} Figure 4:

Local Tully-Fisher relation in the $K_{\rm S}$-band for the Millenium mock galaxies. The grey points are the objects with $M_{\rm bulge} < 0.15$  $M_{\rm star}$ and MK< -16. The dashed line is the relation obtained with our local sample and the dot-dash line is the local relation obtained by Hammer et al. (2007) for a sample of SDSS galaxies with $\log(V_{\rm flat})\geq2.2$. The solid line is the fit to the data for MK<-18 (left) and MK<-21 (right).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{14244fg5.eps}\vspace*{2mm} \end{figure} Figure 5:

Colour ( $V-K_{\rm S}$) vs. rotation velocity (up) and colour (R-I) vs. rotation velocity (down). Black diamonds represent the galaxies in the redshift range 1.1<z<1.4, while open squares are the galaxies in the redshift range 0.1<z<0.3. Difference between the local ( $V-K_{\rm S}$) TFRs (up) and (R-I) TFRs (down) (thin lines) and its 2$\sigma $ uncertainty (dashed lines) are shown. Thick lines are the fit to the high redshift data when setting the slope to the local relation in each case.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[scale=0.44]{14244fga1a.eps}\includegra... ...1c.eps}\includegraphics[scale=0.44]{14244fga1d.eps} } \vspace*{5mm} \end{figure} Figure A.1:

Differences between the B, V, R, I, $K_{\rm S}$, IRAC1, and IRAC2-band magnitudes derived from the best-fit template normalized to the observed V-band magnitude ( $m_{\rm temp}$), and the corresponding observed magnitudes ( $m_{\rm obs}$), for our high-redshift sample. a) Templates of SWIRE. b) Templates of Poggianti. c) Templates of BC03. d) Templates provided by kcorrect.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.7cm,clip]{14244fga2.eps}\vspace*{1.5mm} \end{figure} Figure A.2:

Difference between the magnitudes calculated from each rest-frame template of BC03 and from the best-fit template (at z=0) calculated by kcorrect from the photometry of the redshifted template at z=1.25. See Table A.1 for the description of the templates from BC03. The grey zones represent the templates that were fitted by bpz for some of our galaxies.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14244fga3.eps} % \end{figure} Figure A.3:

Rest-frame $K_{\rm S}$-band magnitude calculated from each of the templates from BC03 normalized to an IRAC2 magnitude of 21.5 in the redshifts z=1.1, 1.25, and 1.4. The description of the templates is the same as in Fig. A.2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{14244fga4a.eps}\par\includegraphics[width=8cm,clip]{14244fga4b.eps} \end{figure} Figure A.4:

Comparison between the k-corrected magnitude obtained from kcorrect best-fit template and from the best-fit template of BC03. For $K_{\rm S}$-band ( up), the normalization of the template from BC03 was done to the observed IRAC2-band. For V-band ( down), the template of BC03 was normalized to the observed V-band. The solid line shows the least-square fits with slope 1.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[scale=0.44]{14244fga5a.eps}\includegraphics[scale=0.44]{14244fga5b.eps} }\end{figure} Figure A.5:

Comparison between the rest-frame B-band ( left) and $K_{\rm S}$-band ( right) magnitudes calculated from the best-fit template obtained using the $g, r, i, z, K_{\rm S}$, IRAC1, and IRAC2-bands aperture magnitudes in 1.5'' aperture, and those obtained using the $B, V, R, I, K_{\rm S}$, IRAC1, and IRAC2 total magnitudes. The solid lines represent the one to one relations.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.