| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913513 | |
| Published online | 19 October 2010 | |
Young stellar clusters and associations in M 33
M. Grossi1,2 - E. Corbelli2 - C. Giovanardi2 - L. Magrini2
1 - CAAUL, Observatório Astronómico de Lisboa, Universidade de Lisboa, Tapada de Ajuda, 1349-018, Lisboa, Portugal
2 - INAF - Osservatorio Astrofisico di Arcetri, L.go E. Fermi 5, 50125 Firenze, Italy
Received 20 October 2009 / Accepted 4 June 2010
Abstract
Aims. We analyse multi-wavelength observations of 32 young star clusters and associations in M 33 with known oxygen abundance (
![]() (O/H) < 8.7). The data set includes ultraviolet (UV), optical, mid-infrared (MIR), CO (1-0) and 21-cm line (H I) observations.
We derive the spectral energy distribution (SED) of these systems
and the properties of their gaseous environment to investigate the
process of star formation and the interplay with the interstellar
medium (ISM).
(O/H) < 8.7). The data set includes ultraviolet (UV), optical, mid-infrared (MIR), CO (1-0) and 21-cm line (H I) observations.
We derive the spectral energy distribution (SED) of these systems
and the properties of their gaseous environment to investigate the
process of star formation and the interplay with the interstellar
medium (ISM).
Methods. We determine age, bolometric luminosities, masses, and
the extinction by comparing the multi-band integrated photometry to
single-age stellar population models. The best-fit solutions have been
obtained using the Large Magellanic Cloud (LMC) extinction curves.
Results. The stellar system ages range between 2 and 15 Myr, masses are between
![]() and
and
![]()
![]() ,
and the intrinsic extinction, AV,
varies from 0.3 to 1 mag. We find a correlation between age and
extinction (young clusters being more reddened than older ones), and
between the cluster mass and size. From the MIR emission we infer the
presence of a dust component around the clusters whose fractional
luminosity at 24
,
and the intrinsic extinction, AV,
varies from 0.3 to 1 mag. We find a correlation between age and
extinction (young clusters being more reddened than older ones), and
between the cluster mass and size. From the MIR emission we infer the
presence of a dust component around the clusters whose fractional
luminosity at 24 ![]() m, L24/
m, L24/
![]() ,
decreases with the galactocentric distance. However, the total infrared luminosity inferred from L24 is smaller than what we derive from the extinction corrections. We also find that the H
,
decreases with the galactocentric distance. However, the total infrared luminosity inferred from L24 is smaller than what we derive from the extinction corrections. We also find that the H![]() luminosity predicted by population synthesis models is higher than the observed one, especially for low-mass systems (M < 104
luminosity predicted by population synthesis models is higher than the observed one, especially for low-mass systems (M < 104 ![]() ).
This difference is reduced, but not erased, when the incomplete
sampling of the initial mass function (IMF) at the high-mass end
is taken into account.
).
This difference is reduced, but not erased, when the incomplete
sampling of the initial mass function (IMF) at the high-mass end
is taken into account.
Conclusions. Our results suggest that a non-negligible fraction
of UV ionising and non-ionising radiation is leaking into the ISM
outside the H II regions. This agrees with the large UV and H![]() diffuse fractions observed in M 33, but it implies that stellar
systems younger than 3 Myr retain, on average, only 30% of
their Lyman-continuum photons. However, the uncertainties in cluster
ages and the stochastic fluctuations of the IMF do not allow us to
accurately quantify this issue. We also consider the possibility that
this discrepancy is the consequence of a suppressed or delayed
formation of the most massive stars, given that it mainly affects the
young and less massive clusters. We do not find any clear correlation
between the cluster mass and the gas surface density or metallicity.
diffuse fractions observed in M 33, but it implies that stellar
systems younger than 3 Myr retain, on average, only 30% of
their Lyman-continuum photons. However, the uncertainties in cluster
ages and the stochastic fluctuations of the IMF do not allow us to
accurately quantify this issue. We also consider the possibility that
this discrepancy is the consequence of a suppressed or delayed
formation of the most massive stars, given that it mainly affects the
young and less massive clusters. We do not find any clear correlation
between the cluster mass and the gas surface density or metallicity.
Key words: galaxies: individuals: M 33 - stars: formation - galaxies: star clusters - galaxies: ISM
1 Introduction
M 33 is the nearest late-type spiral, its properties being in
between earlier-type spirals like the Milky Way and M 31 and the
star-forming dwarf galaxies in the Local Group. With a relatively high
star-formation rate per unit area (
![]()
![]() yr-1 kpc-2), seven times higher than M 31 (Kennicutt 1998)
and a low inclination, M 33 is an ideal environment to study the
properties of young stellar systems and star-forming regions.
yr-1 kpc-2), seven times higher than M 31 (Kennicutt 1998)
and a low inclination, M 33 is an ideal environment to study the
properties of young stellar systems and star-forming regions.
Young star clusters and associations are important for studying the ongoing star-formation activity and the chemical evolution of their parent galaxy. The study of young stellar populations enables us to analyse the initial phase of the cluster evolution, which is mainly driven by hot massive stars. Despite their short lifetime, these stars play an important role in galaxy evolution, because they are the main source of ionisation, heating, and the chemical enrichment of the interstellar medium (ISM). Massive stars trace the current star-formation activity, they power the infrared (IR) radiation of dust and, at the end of their lives, they eventually trigger further star-formation events via supernova explosions. Moreover, from the properties of the gas and dust distribution of the cluster environment one can better understand the mutual relation between star formation and the ISM.
A number of studies have analysed the cluster population of M 33 both from space (Chandar et al. 1999,2001) and from the ground (Ma et al. 2004,2001,2002),
although they have mainly concentrated on rather evolved stellar
systems with ages between a few tens of Myr and few Gyrs.
Nonetheless, the population of young stellar systems (
![]() 10 Myr) in
M 33 has not been thoroughly investigated, and only a few studies have been dedicated to such young star-forming systems.
10 Myr) in
M 33 has not been thoroughly investigated, and only a few studies have been dedicated to such young star-forming systems.
A recent multi-wavelength analysis of radio-selected sources in
M 33 led to the identification of 11 young, optically-visible
stellar clusters without finding any highly obscured systems (Buckalew et al. 2006). Extinction seems generally lower in M 33 than in the Milky Way, and the absence of large molecular complexes (Rosolowsky et al. 2007) may imply that even in an early star-formation phase stellar clusters may not be highly extincted.
Corbelli et al. (2009) examined the properties of young stellar clusters in M 33 selected at 24 ![]() m with H
m with H![]() counterparts and stressed the importance of combining multiple
wavelength observations (from the UV to MIR) to study star-forming
sites and to improve the understanding of massive star formation. Verley et al. (2009,2007)
showed that MIR images of M 33 obtained with the Spitzer telescope allow us to identify H II regions with 24
counterparts and stressed the importance of combining multiple
wavelength observations (from the UV to MIR) to study star-forming
sites and to improve the understanding of massive star formation. Verley et al. (2009,2007)
showed that MIR images of M 33 obtained with the Spitzer telescope allow us to identify H II regions with 24 ![]() m luminosities as low as
m luminosities as low as
![]() erg s-1 and to study the star-formation properties of the M 33 disc.
erg s-1 and to study the star-formation properties of the M 33 disc.
Here we present a multi-wavelength analysis of a sample of
32 young clusters and associations in M 33 selected from the
catalogues of emission-line objects of Magrini et al. (2007b) and Rosolowsky & Simon (2008).
Our aim was to define a list of young stellar systems selected on the basis of their H![]() emission, for which a measure of their metal abundance was available. In addition, our objects have a 24
emission, for which a measure of their metal abundance was available. In addition, our objects have a 24 ![]() m counterpart in the catalogue of Verley et al. (2007).
The final sample includes well known giant H II
regions such as NGC 588 and IC132, located in the outskirts of the
galaxy, large OB associations such as C400 and B0222, and more compact
H II regions such as B0670 or LGCHII11 with sizes smaller than 10 pc.
m counterpart in the catalogue of Verley et al. (2007).
The final sample includes well known giant H II
regions such as NGC 588 and IC132, located in the outskirts of the
galaxy, large OB associations such as C400 and B0222, and more compact
H II regions such as B0670 or LGCHII11 with sizes smaller than 10 pc.
We use UV (GALEX), UBVRI (Local Group Survey), MIR (Spitzer IRAC and MIPS) observations to constrain ages, masses, extinction, and dust properties of the sample from the comparison to model spectral energy distributions (SEDs). We search for possible correlations among the derived parameters, we compare the properties of these stellar systems to their metallicity, we look for radial gradients in the observed emissions at different wavelengths, and finally, we use archival CO and H I observations to relate the total stellar masses to the local gas content.
The data are presented in Sect. 2, and in Sect. 3 we discuss the sample selection. The method to derive the photometric measurements in the different bands is described in Sect. 4, while an overview of the SED-fitting technique is given in Sect. 5. The results are discussed topic by topic in Sect. 6. The issue of the ionising photon deficiency within the clusters is analysed in Sect. 7. The properties of the gaseous environment of the sample are presented in Sects. 8, 9 we summarise our results and conclusions.
![\begin{figure}
\par\includegraphics[width=12cm]{13513fg01.eps} \vspace{6mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg27.png)
|
Figure 1: Location of the 32 clusters selected in this study, overlayed on the GALEX (FUV and NUV) images of M 33. |
| Open with DEXTER | |
2 The data set: archival UV, optical and IR images
Table 1: Sample of young clusters in M 33 selected in this work.
2.1 Galex images
We used Galaxy Evolution Explorer (GALEX; Martin et al. 2005) observations of M 33
in the far-UV (FUV,
![]() Å) and near-UV (NUV,
Å) and near-UV (NUV,
![]() Å), distributed by Gil de Paz et al. (2007). The angular resolution (FWHM) is
Å), distributed by Gil de Paz et al. (2007). The angular resolution (FWHM) is ![]() 4
4
![]() in the FUV and
in the FUV and ![]() 5
5
![]() 5
in the NUV images, corresponding to approximately 20 pc at
the M 33 distance. The exposure time was 3400 s in both
filters. A more detailed description of GALEX observations of M 33
and of the data reduction and calibration procedures can be found in Thilker et al. (2005).
5
in the NUV images, corresponding to approximately 20 pc at
the M 33 distance. The exposure time was 3400 s in both
filters. A more detailed description of GALEX observations of M 33
and of the data reduction and calibration procedures can be found in Thilker et al. (2005).
2.2 Ground-based optical data: the Local Group Survey
UBVRI images of M 33 have been taken from the Local Group Survey (LGS) of galaxies currently forming stars (Massey et al. 2006).
M 33 observations have been performed
with the Kitt Peak National Observatory 4-m telescope using the
wide-field Mosaic cameras. Narrowband images through the filters
centred on [O III] ![]() 5007, H
5007, H![]() and [S II]
and [S II] ![]() 6731 are also provided (Massey et al. 2007). The data are resampled to a scale of 0.27 arcsec/pixel. The FWHM of the point spread function in the V band is 1
6731 are also provided (Massey et al. 2007). The data are resampled to a scale of 0.27 arcsec/pixel. The FWHM of the point spread function in the V band is 1
![]() 1, corresponding to
1, corresponding to ![]() 4 pc. More details about the
observations and data reduction can be found in these papers.
4 pc. More details about the
observations and data reduction can be found in these papers.
We also made use of an optical narrowband H![]() image of M 33
obtained with the 0.6 m Burrell-Schmidt
telescope at Kitt Peak National Observatory (Hoopes & Walterbos 2000).
The
image of M 33
obtained with the 0.6 m Burrell-Schmidt
telescope at Kitt Peak National Observatory (Hoopes & Walterbos 2000).
The
![]() pixel CCD provides a field of view of
pixel CCD provides a field of view of
![]() square degrees, with a scale of 2.03 arcsec/pixel. The final mosaic covers an area of about
square degrees, with a scale of 2.03 arcsec/pixel. The final mosaic covers an area of about
![]() square degrees.
More details on the observations and reduction procedure can be found in
Hoopes & Walterbos (2000).
square degrees.
More details on the observations and reduction procedure can be found in
Hoopes & Walterbos (2000).
2.3 Spitzer images
Spitzer IRAC and MIPS images of M 33 were obtained under
the Guaranteed Time Observer (GTO) programme PID 5 (PI
R. Gehrz). We used the IRAC (3.6-8 ![]() m) and MIPS (24
m) and MIPS (24 ![]() m) maps of M 33 produced by Verley et al. (2007). The spatial resolution of the IRAC maps is between 1
m) maps of M 33 produced by Verley et al. (2007). The spatial resolution of the IRAC maps is between 1
![]() 7 and 2
7 and 2
![]() (
(![]() 7 pc), while at 24
7 pc), while at 24 ![]() m it is 6
m it is 6
![]() (24 pc). The map scale is 1.2 arcsec/pixel in both IRAC and MIPS images.
(24 pc). The map scale is 1.2 arcsec/pixel in both IRAC and MIPS images.
2.4 CO and HI maps
We used the 3-mm CO map of M 33 (J=1-0 rotational line) obtained from the combination of the
Berkeley Illinois Maryland Association (BIMA) array
(Engargiola et al. 2003; Rosolowsky et al. 2007)
and the Five College Radio Astronomy Observatory (FCRAO) single dish (Heyer et al. 2004). The final resolution of the merged map is 13
![]() .
The median noise level of the channel maps is 240 mK, corresponding to a mass sensitivity of
.
The median noise level of the channel maps is 240 mK, corresponding to a mass sensitivity of
![]()
![]() (4
(4![]() detection in two adjacent channels; see Rosolowsky et al. (2007)
using a conversion factor
detection in two adjacent channels; see Rosolowsky et al. (2007)
using a conversion factor
![]() cm-2 (K km s-1)-1.
cm-2 (K km s-1)-1.
The 21-cm observations of M 33 have been taken at the Westerbork
Radio Synthesis Telescope (WRST) array (Deul & van der Hulst 1987), with a spatial resolution of 24
![]()
![]() 48
48
![]() .
.
Table 2: UV and optical photometric measurements. The last column displays the aperture radius used for the photometry.
3 Sample selection
The sample was selected from the catalogues of emission line
objects of Magrini et al. (2007b) and of Rosolowsky & Simon (2008).
The two catalogues contains 72 and 61 H II regions respectively.
The oxygen abundances were obtained using the temperature-sensitive emission line [O III] ![]() 4363,
with a direct measurement of the electron temperature. The condition of
a measured and not assumed electron temperature is essential, because
the determination of the ionic and total chemical abundances
exponentially depends on it.
4363,
with a direct measurement of the electron temperature. The condition of
a measured and not assumed electron temperature is essential, because
the determination of the ionic and total chemical abundances
exponentially depends on it.
The 32 H II regions of the sample were selected
on the basis of their shape and their position, preferentially round
and/or located in regions of the galaxy not too crowded in the H![]() map. Then we searched for a 24
map. Then we searched for a 24 ![]() m counterpart in the Spitzer/MIPS map of Verley et al. (2007), and by cross-correlating the two lists of objects we ended up with 25 sources with metal abundances within the range
m counterpart in the Spitzer/MIPS map of Verley et al. (2007), and by cross-correlating the two lists of objects we ended up with 25 sources with metal abundances within the range
![]() (O/H) <
8.7. We then added seven more regions at large galactocentric radii,
which have a clear detection in the 24
(O/H) <
8.7. We then added seven more regions at large galactocentric radii,
which have a clear detection in the 24 ![]() m map even though they are not included in the Verley et al. (2007)
catalogue. The final sample includes well known giant H II
regions such as NGC 588 and IC132, which are located in the
outskirts of the galaxy, large OB association as C400 and B0222,
and more compact H II regions such as B0670 or LGCHII11 with sizes smaller than 10 pc. Figure 1
shows
the position of the selected clusters and associations overlayed on the
GALEX (FUV) image. In the rest of the paper we will refer to these
young stellar systems by using the term ``clusters'' even though, in
many cases, their size is larger than that of typical bound clusters.
m map even though they are not included in the Verley et al. (2007)
catalogue. The final sample includes well known giant H II
regions such as NGC 588 and IC132, which are located in the
outskirts of the galaxy, large OB association as C400 and B0222,
and more compact H II regions such as B0670 or LGCHII11 with sizes smaller than 10 pc. Figure 1
shows
the position of the selected clusters and associations overlayed on the
GALEX (FUV) image. In the rest of the paper we will refer to these
young stellar systems by using the term ``clusters'' even though, in
many cases, their size is larger than that of typical bound clusters.
Table 3:
H![]() and Spitzer IRAC/MIPS photometry of the sample. Flux units are in erg s-1 cm-2.
and Spitzer IRAC/MIPS photometry of the sample. Flux units are in erg s-1 cm-2.
![\begin{figure}
\par\mbox{\includegraphics[width=4.5cm,bb=25 30 430 230]{13513fg0...
...[width=4.5cm,bb=25 30 430 230]{13513fg025.ps} }
\vspace*{-3.45mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg82.png)
|
Figure 2: Output best-fit SEDs in units of AB magnitudes, overlayed on the measured integrated magnitudes from 1000 to 10 000 Å. Vertical bars indicate the uncertainty on the photometry, while the horizontal ones show the approximate width of each filter. The numbers at the top-left corners of the plots correspond to the cluster ID given in Table 1. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.7cm,bb=20 30 410 230]{13513fg0...
...cs[width=4.4cm,bb=45 30 410 230]{13513fg035.ps} }
\vspace*{2.2mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg83.png)
|
Figure 3:
Model SED for each cluster in flux units ( |
| Open with DEXTER | |
4 Multi-wavelength photometry
We performed aperture photometry within circular regions choosing different apertures for each object. The aperture radius was defined on the basis of the extent of the V radial profiles, given the better resolution of the LGS images. The same position and aperture radius was applied to extract the photometry in the different bandpasses. The measurements were obtained using the IDL routine APER. Background subtraction was not straightforward because the clusters are found in different local environments. The contamination of nearby bright stars depends mainly on the object location in the galaxy and on the age of the background stellar population, and this is particulary critical in the R, I bands where the contamination by older stars is higher. The annuli for the background determination were selected individually for each cluster in regions where the contamination of bright nearby objects was minimal.
Table 2 displays the UV and optical photometry of the cluster sample and the corresponding uncertainties, which include the errors from the object count rate, the sky variance, and the zero point calibration.
4.1 UV photometry
The flux density in the FUV and NUV filters was measured within circular apertures given in Table 2,
and the median background flux was estimated in annuli of 5 pixel
width, chosen in a way to reduce the contamination of nearby sources.
Conversion from count rates to the AB photometric system (Oke 1990) was obtained using the zero-points ZP
![]() and ZP
and ZP
![]() (Morrissey et al. 2005). UV magnitudes were corrected for foreground Galactic extinction following Schlegel et al. (1998) before starting the analysis of the cluster SEDs.
(Morrissey et al. 2005). UV magnitudes were corrected for foreground Galactic extinction following Schlegel et al. (1998) before starting the analysis of the cluster SEDs.
4.2 UBVRI and H
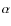 photometry
photometry
UBVRI instrumental magnitudes were converted to the standard Johnson and Cousin system using stars from the Massey et al. (2006) catalogue. The colour term in the UVBRI transformation (described in Massey et al. 2006) was ignored, as it is smaller than the errors we report. The contribution of the Galactic foreground extinction was also subtracted from the optical magnitudes according to Schlegel et al. (1998).
The continuum emission in the H![]() image was removed by subtracting the R-band
image scaled by a factor 0.40, which was determined from the
aperture photometry of 20 field stars in both filters. The calibration
factor of
image was removed by subtracting the R-band
image scaled by a factor 0.40, which was determined from the
aperture photometry of 20 field stars in both filters. The calibration
factor of
![]() erg s-1 cm-2 given in Massey et al. (2007) was applied to the count rates measured within apertures that included the total H
erg s-1 cm-2 given in Massey et al. (2007) was applied to the count rates measured within apertures that included the total H![]() emission around the cluster.
The fluxes are displayed in Table 3. As a further check, H
emission around the cluster.
The fluxes are displayed in Table 3. As a further check, H![]() fluxes were determined for the same apertures on the map of Hoopes & Walterbos (2000), adopting a calibration factor of
fluxes were determined for the same apertures on the map of Hoopes & Walterbos (2000), adopting a calibration factor of
![]() erg s-1 cm-2. The resulting measurements agreed with the LGS map within 5% (1
erg s-1 cm-2. The resulting measurements agreed with the LGS map within 5% (1![]() ).
).
H![]() and oxygen emission lines may significantly contribute to the total flux in the R, V and U bands.
We estimated the contamination from [O III]
and oxygen emission lines may significantly contribute to the total flux in the R, V and U bands.
We estimated the contamination from [O III] ![]() 5007 and H
5007 and H![]() lines to the photometry in the V and R
filters, using the narrowband images provided by LGS. The
correction was obtained by subtracting the flux measured in the
narrowband image within the same aperture used for the optical
photometry (last column in Table 2). We used the calibration factor of
lines to the photometry in the V and R
filters, using the narrowband images provided by LGS. The
correction was obtained by subtracting the flux measured in the
narrowband image within the same aperture used for the optical
photometry (last column in Table 2). We used the calibration factor of
![]() and
and
![]() erg s-1 cm-2 Å-1 for the H
erg s-1 cm-2 Å-1 for the H![]() and [O III] images respectively, as given in Massey et al. (2007).
The U photometry is affected by the contamination from the [O II]
and [O III] images respectively, as given in Massey et al. (2007).
The U photometry is affected by the contamination from the [O II] ![]() 3727 line, but the LGS does not provide a narrowband image centred on this wavelength.
Thus we multiplied the [O III] narrowband fluxes for the [O II] /[O III] line ratio derived for the clusters in the Rosolowsky & Simon (2008) catalogue. For those without a direct measurement of this ratio, we applied an average value of [O II] /[O III] = 1. In some cases this correction was not sufficient to reduce the excess in the U-band photometry.
3727 line, but the LGS does not provide a narrowband image centred on this wavelength.
Thus we multiplied the [O III] narrowband fluxes for the [O II] /[O III] line ratio derived for the clusters in the Rosolowsky & Simon (2008) catalogue. For those without a direct measurement of this ratio, we applied an average value of [O II] /[O III] = 1. In some cases this correction was not sufficient to reduce the excess in the U-band photometry.
4.3 IRAC and MIPS (24 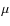 m) photometry
m) photometry
Photometry at 3.6, 4.5, and 5.8 ![]() m was derived through the same apertures used for the UV-optical bands, while the larger apertures chosen for the H
m was derived through the same apertures used for the UV-optical bands, while the larger apertures chosen for the H![]() photometry were adopted to measure 8 and 24
photometry were adopted to measure 8 and 24 ![]() m
fluxes.
Uncertainties include Poisson noise photon flux, background
fluctuations and a 10% flux calibration uncertainty for both the IRAC (Reach et al. 2005; Fazio et al. 2004) and MIPS bands (Engelbracht et al. 2007). Table 3 displays the fluxes at 3.6, 4.5, 5.8, 8.0, and 24
m
fluxes.
Uncertainties include Poisson noise photon flux, background
fluctuations and a 10% flux calibration uncertainty for both the IRAC (Reach et al. 2005; Fazio et al. 2004) and MIPS bands (Engelbracht et al. 2007). Table 3 displays the fluxes at 3.6, 4.5, 5.8, 8.0, and 24 ![]() m for the sample.
m for the sample.
Table 4: Results from the SED-fitting technique.
![\begin{figure}
\par\mbox{\includegraphics[width=7.4cm,bb=45 15 435 405]{13513fg0...
...aphics[width=7.4cm,bb=45 15 435 405]{13513fg04d.ps} }
\vspace{2mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg93.png)
|
Figure 4:
Top-left: cluster ages and masses determined from the SED fitting. Top-right:
mass versus radius relation: the solid line with a slope of
1.5 provides the best linear fits to the data points. The
dotted-line shows the minimum size corresponding to the resolution of
the V-band image. Bottom-left: bolometric luminosity distribution of the sample. Bottom-right: (B-V)0 colour distribution as a function of age. The symbols correspond to three different age bins: |
| Open with DEXTER | |
5 SED fitting with CHORIZOS
CHi-square cOde for parameteRized modelling and characterIZation of phOtometry and Spectrophotometry (CHORIZOS) is a ![]() minimization code that enables one to fit an arbitrary family of spectral energy distributions to a set of photometric and
spectrophotometric data (Maíz-Apellániz 2004).
It compares an observed set of magnitudes to a grid of model SEDs and calculates the
probability for a given model to be consistent with the observed photometry.
It allows one to constrain both intrinsic parameters (such as age and metallicity) and extrinsic ones such as
extinction law and colour excess.
The user selects the SED family and chooses the behaviour of each parameter to be fixed,
constrained within a certain range, or to be kept free.
The code uses the monochromatic equivalents of E(B-V) and RV, E(4405-5495) and
R5495, where 4405 and 5495 are the assumed central wavelengths in Angstrom of the Band V filters. It allows one to choose between the galactic extinction law of Cardelli et al. (1989), the average LMC and LMC2 laws of Misselt et al. (1999) and the Small Magellanic Curve (SMC) extinction law of Gordon & Clayton (1998). Then a
minimization code that enables one to fit an arbitrary family of spectral energy distributions to a set of photometric and
spectrophotometric data (Maíz-Apellániz 2004).
It compares an observed set of magnitudes to a grid of model SEDs and calculates the
probability for a given model to be consistent with the observed photometry.
It allows one to constrain both intrinsic parameters (such as age and metallicity) and extrinsic ones such as
extinction law and colour excess.
The user selects the SED family and chooses the behaviour of each parameter to be fixed,
constrained within a certain range, or to be kept free.
The code uses the monochromatic equivalents of E(B-V) and RV, E(4405-5495) and
R5495, where 4405 and 5495 are the assumed central wavelengths in Angstrom of the Band V filters. It allows one to choose between the galactic extinction law of Cardelli et al. (1989), the average LMC and LMC2 laws of Misselt et al. (1999) and the Small Magellanic Curve (SMC) extinction law of Gordon & Clayton (1998). Then a ![]() analysis is performed to assign a likelihood to each SED as a function of the range of parameters.
analysis is performed to assign a likelihood to each SED as a function of the range of parameters.
The code includes a set of STARBURST99 (Leitherer et al. 1999) instantaneous burst models for a range of ages and metallicities, produced using a Salpeter (1955) stellar initial mass function
(IMF) with masses within the range 0.1-100 ![]() .
The metallicity of the cluster models was chosen at Z
= 0.004, 0.008 and 0.02, while the age varied between 1 and
100 Myr. We extinguished the theoretical SEDs with all the
available extinction laws using a routine provided with the code.
.
The metallicity of the cluster models was chosen at Z
= 0.004, 0.008 and 0.02, while the age varied between 1 and
100 Myr. We extinguished the theoretical SEDs with all the
available extinction laws using a routine provided with the code.
We ran CHORIZOS for all the objects in our sample using seven magnitudes (from FUV to I bands). We did not include the 3.6 and 4.5 ![]() m IRAC bands in the fitting because the contribution of hot dust emission starts at
m IRAC bands in the fitting because the contribution of hot dust emission starts at
![]() m (Kennicutt et al. 2003; Carico et al. 1988) and the STARBURST99 models become inapplicable above that wavelength (Leitherer et al. 1999).
A more detailed analysis of the MIR region of the cluster SEDs will be
presented elsewhere (Giovanardi et al. 2010, in prep.).
m (Kennicutt et al. 2003; Carico et al. 1988) and the STARBURST99 models become inapplicable above that wavelength (Leitherer et al. 1999).
A more detailed analysis of the MIR region of the cluster SEDs will be
presented elsewhere (Giovanardi et al. 2010, in prep.).
We performed the fitting procedure by setting the metallicity at the values displayed in Table 1,
leaving the other parameters (i.e. age and intrinsic extinction in
M 33) unconstrained. Then we reran the code a second time, with a
higher resolution grid, to refine the estimate of the parameters. The
errors on the age and the extinction are estimated by the procedure. To
assess the goodness of the fit, we relied on the value of ![]() provided by CHORIZOS; on
average clusters with
provided by CHORIZOS; on
average clusters with
![]() were considered as good fits.
were considered as good fits.
Figures 2 and 3 show our SED-fitting results.
For each cluster we display the output best-fit SED in units of AB magnitudes from 1000 to 10 000 Å overlaid on our measurements to show the quality of the fitting (Fig. 2), and the model
SED in flux units (![]() F
F
![]() ,
erg s-1 cm-2) from 1000 to
,
erg s-1 cm-2) from 1000 to
![]() Å to compare the UV, optical and IR emission of the clusters (Fig. 3). The numbers at the
top-left and bottom-right corners of the plots correspond to the cluster ID given in Table 1. The best-fit SEDs overlaid on the observed magnitudes (Fig. 2) show that in some cases the U photometry disagrees with the model, despite our attempt to take into account the effects of [O II] line contamination, causing an increase in the value of
Å to compare the UV, optical and IR emission of the clusters (Fig. 3). The numbers at the
top-left and bottom-right corners of the plots correspond to the cluster ID given in Table 1. The best-fit SEDs overlaid on the observed magnitudes (Fig. 2) show that in some cases the U photometry disagrees with the model, despite our attempt to take into account the effects of [O II] line contamination, causing an increase in the value of ![]() .
Comparison between the best-fit model SEDs and the MIR photometry (Fig. 3) shows an excess emission at 3.6
.
Comparison between the best-fit model SEDs and the MIR photometry (Fig. 3) shows an excess emission at 3.6 ![]() m and 4.5
m and 4.5 ![]() m bands, suggesting that this non-stellar emission may be due to a hot dust component.
m bands, suggesting that this non-stellar emission may be due to a hot dust component.
6 Results: comparison of cluster properties
6.1 Ages, masses, sizes, and colours
The SED fittings confirm the young age of the clusters, being younger than ![]() 15 Myr. The results of the fitting procedure are displayed in Table 4. Uncertainties in age are given in Table 4
and are less than 0.2 (in log years). Variations in the IMF slope
from the standard Salpeter value, or stochastic effects in the IMF
when sampling small mass clusters, may increase the quoted
uncertainties (Cerviño & Luridiana 2004; Corbelli et al. 2009). We will discuss the issue of stochastic fluctuations in Sect. 7.1.
15 Myr. The results of the fitting procedure are displayed in Table 4. Uncertainties in age are given in Table 4
and are less than 0.2 (in log years). Variations in the IMF slope
from the standard Salpeter value, or stochastic effects in the IMF
when sampling small mass clusters, may increase the quoted
uncertainties (Cerviño & Luridiana 2004; Corbelli et al. 2009). We will discuss the issue of stochastic fluctuations in Sect. 7.1.
CHORIZOS also determines the bolometric correction to the V magnitude
for each best-fit model. Knowing the age, metallicity, and the
bolometric luminosity, we inferred the stellar mass using the
STARBURST99 evolutionary synthesis models. Figure 4 (top-left
panel) displays the distribution in age and mass of the clusters. It
shows that most of the clusters in our sample are found in a very
narrow range of ages, while the mass distribution encompasses two
orders of magnitude, between ![]()
![]() and
and ![]() 4
4 ![]() 104
104 ![]() .
In this and in the following figures we used different symbols (and
colours) for clusters within different age bins: filled (blue) dots
correspond to ages younger than 3 Myr, (green) squares to clusters
with ages in the range 3-8 Myr, while the oldest ones
(>8 Myr) are indicated with (red) triangles.
.
In this and in the following figures we used different symbols (and
colours) for clusters within different age bins: filled (blue) dots
correspond to ages younger than 3 Myr, (green) squares to clusters
with ages in the range 3-8 Myr, while the oldest ones
(>8 Myr) are indicated with (red) triangles.
Observations of Giant Molecular Clouds (GMCs) in different environments indicate that they follow a mass-radius relation
![]() (Harris & Pudritz 1994; Wilson & Scoville 1990; Larson 1981).
Thus, once we derived the masses, we checked whether the stellar
systems under study follow a similar mass-radius relation or not. As an
estimate of the size of the cluster we used the half-light radius
measured in the V band. As we show in the upper-right panel of Fig. 4,
we find a correlation between the half-light radii of the clusters and
the mass obtained from the SED fitting, with a slope of
(Harris & Pudritz 1994; Wilson & Scoville 1990; Larson 1981).
Thus, once we derived the masses, we checked whether the stellar
systems under study follow a similar mass-radius relation or not. As an
estimate of the size of the cluster we used the half-light radius
measured in the V band. As we show in the upper-right panel of Fig. 4,
we find a correlation between the half-light radii of the clusters and
the mass obtained from the SED fitting, with a slope of
![]() .
The correlation is stronger for clusters with sizes smaller than
10 pc, while the others show a larger scatter around the best-fit
line.
.
The correlation is stronger for clusters with sizes smaller than
10 pc, while the others show a larger scatter around the best-fit
line.
Compact star clusters (R < 10 pc) with ages between few tens and few hundreds of Myr show a poor correlation between mass and radius (Larsen 2004; Zepf et al. 1999), implying that the GMC mass-radius relation must be broken at a certain stage during the cluster evolution. Larsen (2004) find
![]() in a sample of relatively young compact clusters (age <1 Gyr and R
< 10 pc) in nearby spiral galaxies. On the other hand, cluster
complexes with a range of ages more similar to our sample (
in a sample of relatively young compact clusters (age <1 Gyr and R
< 10 pc) in nearby spiral galaxies. On the other hand, cluster
complexes with a range of ages more similar to our sample (
![]() 10 Myr) but larger sizes (R > 85 pc) follow a similar mass-radius relation to GMCs,
10 Myr) but larger sizes (R > 85 pc) follow a similar mass-radius relation to GMCs,
![]() (Bastian et al. 2005).
Our results seem to indicate that even at scales smaller than those of
stellar complexes young stellar systems still display a similar trend
to the GMCs, and that the observed stellar densities are representative
of the proto-cluster cloud environment.
(Bastian et al. 2005).
Our results seem to indicate that even at scales smaller than those of
stellar complexes young stellar systems still display a similar trend
to the GMCs, and that the observed stellar densities are representative
of the proto-cluster cloud environment.
The bottom-left panel of Fig. 4 shows the bolometric luminosity distribution of the clusters, obtained from the SED fitting. The plot of the dereddened (B-V)0 colour as a function of age (bottom-right panel) gives an overview of the colour range of the sample. Given their young age, the clusters are characterised by very blue colours and, as expected, ``older'' clusters are redder than the younger ones.
6.2 Metallicity
The metallicity gradient in M 33, from 1 to![\begin{figure}
\par\includegraphics[width=8cm,bb=65 365 490 780]{13513fg05.ps}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg102.png)
|
Figure 5: Cluster oxygen abundance versus galactocentric distance, mass, and age. The solid line in the top panel shows the metallicity radial gradient relation found by Rosolowsky & Simon (2008). |
| Open with DEXTER | |
The central panel of Fig. 5 shows that this correlation is lacking in our sample, indicating that the metal abundance is related to the local environmental properties of the clusters rather than being influenced by the cluster mass. Neither do we find a clear trend between the metallicity and age (lower panel); the Spearman correlation coefficient is -0.32, indicating a poor degree of correlation between these two parameters.
6.3 Extinction
Massey & Hutchings (1983) first concluded from the analysis of the IUE spectra of M 33 H II regions that its extinction curve is different from the galactic one, and that it is characterised by a weak 2175 Å hump similar to that of the LMC. Dodorico & Benvenuti (1983) find a similar result after a study of the H II region IC132. For the brightest H II region of M 33, NGC 604, a reddening parameter E(B-V) = 0.12 has been obtained assuming a LMC curve (González Delgado & Pérez 2000).
The E(B-V) values we derive for the M 33 clusters range between 0.1 and 0.5 mag, corresponding to a visual extinction AV between 0.3 and 1 mag. Chandar et al. (1999) obtained E(B-V) values between 0.06 and 0.33 mag, with the majority of the clusters being found around 0.1 mag. Park & Lee (2007) derived reddening values between 0.05 and 0.20 mag. Yet both samples are different from ours because they have a large range of ages as mentioned in Sect. 1. The LMC average and LMC2 curves of Misselt et al. (1999) were the ones providing the best fits in the majority of the cases, even though the SMC extinction curve was adopted for one cluster (C400). Additional evidence supporting the choice of either the LMC average or the LMC2 extinction curve comes from the UV colours. The SMC extinction law predicts larger variations in the FUV-NUV colour than what was observed in our sample.
Figure 6 shows that there is a correlation between the cluster age and AV (top-left).
Younger clusters are more reddened, because they are still partially
embedded in the parent molecular cloud where they formed.
AV does not appear to clearly correlate with the metallicity (top-centre), and neither does it correlate with the 8 ![]() m (top-right) nor the 24
m (top-right) nor the 24 ![]() m luminosities (bottom-left) normalised to the bolometric one. A trend between the extinction
and the total hydrogen column density is also lacking (H2+H I +H II ; see also Sect. 8), as displayed in the bottom-right panel.
m luminosities (bottom-left) normalised to the bolometric one. A trend between the extinction
and the total hydrogen column density is also lacking (H2+H I +H II ; see also Sect. 8), as displayed in the bottom-right panel.
6.4 Radial gradients
We searched for possible variations of the cluster properties with
the galactocentric radius, especially with regard to their UV, H![]() or MIR emissions (see Fig. 7).
or MIR emissions (see Fig. 7).
Neither AV (top-left) nor the
![]()
![]() ratio (not displayed) show a clear trend with the galactocentric distance. A radial change in AV would imply a decreasing dust attenuation, as it is found for example in M 51 (Calzetti et al. 2005). In this galaxy the UV colour, AV,
and the age of the clusters do vary with the distance, with the
clusters becoming younger and less extinct as one moves to the outer
regions of the galaxy. Extinction is related to the dust-to-gas ratio,
which depends on the metallicity of a galaxy. Because steep metallicity
gradients are observed in many galaxies, one would expect that the
attenuation properties would also change with the galactocentric
distance. The shallow metallicity gradient in M 33 (Rosolowsky & Simon 2008; Magrini et al. 2007b) might explain the lack of a clear correlation between AV, or
ratio (not displayed) show a clear trend with the galactocentric distance. A radial change in AV would imply a decreasing dust attenuation, as it is found for example in M 51 (Calzetti et al. 2005). In this galaxy the UV colour, AV,
and the age of the clusters do vary with the distance, with the
clusters becoming younger and less extinct as one moves to the outer
regions of the galaxy. Extinction is related to the dust-to-gas ratio,
which depends on the metallicity of a galaxy. Because steep metallicity
gradients are observed in many galaxies, one would expect that the
attenuation properties would also change with the galactocentric
distance. The shallow metallicity gradient in M 33 (Rosolowsky & Simon 2008; Magrini et al. 2007b) might explain the lack of a clear correlation between AV, or
![]()
![]() ,
and the galactocentric radius.
,
and the galactocentric radius.
The
![]() /
/
![]() ratio (top-centre, H
ratio (top-centre, H![]() corrected
for extinction) decreases with galactocentric distance for the youngest
clusters (filled dots). However, since the youngest age bin includes
several low-mass clusters, this might be due to a selection effect:
most of the selected low-mass clusters are at large galactocentric
radii in regions that are not too crowded in the H
corrected
for extinction) decreases with galactocentric distance for the youngest
clusters (filled dots). However, since the youngest age bin includes
several low-mass clusters, this might be due to a selection effect:
most of the selected low-mass clusters are at large galactocentric
radii in regions that are not too crowded in the H![]() map (see the last panel in the figure). We will discuss this in more detail in Sect. 7.
Note that the H
map (see the last panel in the figure). We will discuss this in more detail in Sect. 7.
Note that the H![]() luminosity of the clusters with ages around 10 Myr is more than
one order of magnitude higher than what STARBURST99 predicts, implying
that subsequent star-formation episodes must have occurred in order to
explain the observed H
luminosity of the clusters with ages around 10 Myr is more than
one order of magnitude higher than what STARBURST99 predicts, implying
that subsequent star-formation episodes must have occurred in order to
explain the observed H![]() emission.
emission.
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,bb=45 15 420 405]{13513fg06a...
...,bb=45 15 420 405]{13513fg06e.ps} }\hspace*{3cm}\vspace*{-3.5mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg104.png)
|
Figure 6:
Visual extinction (AV) versus age (top-left),
the measured oxygen abundance (top-centre), the ratio of the the 8 |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,bb=28 10 400 400]{13513fg07a...
...6cm,bb=28 10 400 400]{13513fg07e.ps} }\hspace*{3cm}\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg105.png)
|
Figure 7:
Cluster galactocentric distance versus AV (top-left), the
|
| Open with DEXTER | |
We see a well defined radial trend for the MIR fractional
luminosities. Both the L24/
![]() (top-right) and the L8/
(top-right) and the L8/
![]() ratios (bottom-left) decrease by at least one order of magnitude at large galactocentric radii, at the edge of the star-forming disc.
The MIR emission at 24
ratios (bottom-left) decrease by at least one order of magnitude at large galactocentric radii, at the edge of the star-forming disc.
The MIR emission at 24 ![]() m is mainly due to very small grains with effective radii between 15 and 40 Å (Draine & Li 2007).
Variations in the abundance of small grains with respect to big ones at
larger radii, or, more generally, a radial gradient in the dust-to gas
ratio or in the dust temperature, may also contribute to the decrease
of the 24
m is mainly due to very small grains with effective radii between 15 and 40 Å (Draine & Li 2007).
Variations in the abundance of small grains with respect to big ones at
larger radii, or, more generally, a radial gradient in the dust-to gas
ratio or in the dust temperature, may also contribute to the decrease
of the 24 ![]() m emission (Habart et al. 2001; Abergel et al. 2002; Calzetti et al. 2005).
The luminosity at 8
m emission (Habart et al. 2001; Abergel et al. 2002; Calzetti et al. 2005).
The luminosity at 8 ![]() m
is likely dominated by Polyciclic Aromatic Hydrocarbons (PAH) features
around star-forming regions excited by the cluster UV radiation, and we
find a good correlation between 8
m
is likely dominated by Polyciclic Aromatic Hydrocarbons (PAH) features
around star-forming regions excited by the cluster UV radiation, and we
find a good correlation between 8 ![]() m and the FUV luminosities of the clusters (Fig. 8).
The PAH emission is reduced in low-metallicity objects, but over the
small range of metal abundances in our sample there is no clear
dependence of the L8/
m and the FUV luminosities of the clusters (Fig. 8).
The PAH emission is reduced in low-metallicity objects, but over the
small range of metal abundances in our sample there is no clear
dependence of the L8/
![]() ratio on the metallicity. At larger radii the volume density of the ISM
decreases, therefore one would expect that dust and PAHs may be more
efficiently removed from star-forming sites in the outer regions of the
disc (Roussel et al. 2005).
ratio on the metallicity. At larger radii the volume density of the ISM
decreases, therefore one would expect that dust and PAHs may be more
efficiently removed from star-forming sites in the outer regions of the
disc (Roussel et al. 2005).
The total stellar mass does not seem to be clearly related to the cluster position within the galaxy as shown in the bottom-right panel of Fig. 7, even though the smallest mass clusters of the sample (
![]() )
are mainly located at large galactocentric distances.
)
are mainly located at large galactocentric distances.
6.5 Bolometric luminosity
The SED-fitting method provides the value of the bolometric luminosity
for each cluster,
![]() (see Table 5). We compared this parameter with the bolometric
luminosities estimated from observations of the total IR and UV
emission, i.e.
(see Table 5). We compared this parameter with the bolometric
luminosities estimated from observations of the total IR and UV
emission, i.e.
![]() ,
where
,
where
![]() is the albedo for a standard dust composition and grain size distribution (Weingartner & Draine 2001).
is the albedo for a standard dust composition and grain size distribution (Weingartner & Draine 2001).
The sum of the FUV and NUV luminosities provides a measure
of the cluster emission below 3000 Å, which is close to the bolometric luminosity
if the cluster is young and unobscured by dust (Bell et al. 2005; Thilker et al. 2007). If extinction corrections are unknown, one can use
![]() to estimate the
fraction of the UV emission absorbed by the dust. Therefore
to estimate the
fraction of the UV emission absorbed by the dust. Therefore
![]() is considered to provide a good approximation of the bolometric luminosities of young
clusters (see Corbelli et al. 2009; Thilker et al. 2007).
Verley et al. (2009)
have shown that the total IR luminosity in M 33 can be estimated from the 24
is considered to provide a good approximation of the bolometric luminosities of young
clusters (see Corbelli et al. 2009; Thilker et al. 2007).
Verley et al. (2009)
have shown that the total IR luminosity in M 33 can be estimated from the 24 ![]() m emission and it is approximately
m emission and it is approximately
![]() (see Eq. (4) in Verley et al. 2009).
(see Eq. (4) in Verley et al. 2009).
Figure 9 shows that the
model bolometric luminosities are higher than the observed ones for
![]() erg s-1.
This difference could be due to two main reasons: a) the
assumption of a complete IMF may be incorrect when we consider clusters
with bolometric luminosity (and mass) below a certain threshold,
leading to an overestimate of the total cluster luminosity; b) the
estimated total IR emission of the clusters is lower than the amount of
energy missing in the non-ionising UV region of the spectrum, implying
that there is a deficit of non-ionising radiation in young clusters
with bolometric luminosities lower than
erg s-1.
This difference could be due to two main reasons: a) the
assumption of a complete IMF may be incorrect when we consider clusters
with bolometric luminosity (and mass) below a certain threshold,
leading to an overestimate of the total cluster luminosity; b) the
estimated total IR emission of the clusters is lower than the amount of
energy missing in the non-ionising UV region of the spectrum, implying
that there is a deficit of non-ionising radiation in young clusters
with bolometric luminosities lower than
![]() erg s-1. We will discuss these issues in more detail in the next section.
erg s-1. We will discuss these issues in more detail in the next section.
7 The deficit of ionising radiation
In the previous section we pointed out
that the total IR emission of the clusters with
![]() )
< 39.5is lower than the amount of energy missing in the non-ionising
UV region of the spectrum. Here we want to compare the observed H
)
< 39.5is lower than the amount of energy missing in the non-ionising
UV region of the spectrum. Here we want to compare the observed H![]() luminosity
with that predicted by an instantaneous burst model to check whether
there is a deficit of UV-ionising radiation in the sample of clusters
under study.
luminosity
with that predicted by an instantaneous burst model to check whether
there is a deficit of UV-ionising radiation in the sample of clusters
under study.
We ran STARBUST99 to obtain the expected H![]() luminosity of each
cluster at the age, metallicity, and mass we determined, and we plot
in Fig. 10 the ratio of the extinction-corrected observed H
luminosity of each
cluster at the age, metallicity, and mass we determined, and we plot
in Fig. 10 the ratio of the extinction-corrected observed H![]() luminosity to the model one -
luminosity to the model one -
![]()
![]() - versus the age (left-panel) and the mass (central-panel) of the clusters. The figures show that this ratio
decreases with age and mass, while the right-panel shows a shallow radial trend with the galactocentric radius for the youngest clusters.
There is a significant discrepancy between the observed and model H
- versus the age (left-panel) and the mass (central-panel) of the clusters. The figures show that this ratio
decreases with age and mass, while the right-panel shows a shallow radial trend with the galactocentric radius for the youngest clusters.
There is a significant discrepancy between the observed and model H![]() emission especially in young (t < 3 Myr) and low-mass (
emission especially in young (t < 3 Myr) and low-mass (![]() (
(
![]() )
systems, for which
)
systems, for which
![]() is
less than 0.5, or -0.3
in logarithmic units. This would imply that more than 50% of the
ionising flux is missing from these clusters, a higher percentage than
what was found in other studies (see Sect. 7.3).
is
less than 0.5, or -0.3
in logarithmic units. This would imply that more than 50% of the
ionising flux is missing from these clusters, a higher percentage than
what was found in other studies (see Sect. 7.3).
The error bars in Fig. 10 show how the ratio of H![]() luminosities varies if one takes into account the uncertainties of the best-fit ages (Table 4). The upper errors bars are larger for clusters older than 2.5-3 Myr, because the model H
luminosities varies if one takes into account the uncertainties of the best-fit ages (Table 4). The upper errors bars are larger for clusters older than 2.5-3 Myr, because the model H![]() emission rapidly decreases after this epoch. For the youngest clusters (t < 3 Myr), the mean
emission rapidly decreases after this epoch. For the youngest clusters (t < 3 Myr), the mean
![]()
![]() ratio is 0.19
+0.17-0.002, while for those with an age between 3 and 8 Myr the mean is
ratio is 0.19
+0.17-0.002, while for those with an age between 3 and 8 Myr the mean is
![]() .
On the other hand, clusters older than 8 Myr (triangles in Fig. 10)
are very luminous at H
.
On the other hand, clusters older than 8 Myr (triangles in Fig. 10)
are very luminous at H![]() wavelengths for their age, because
wavelengths for their age, because
![]() is
more than 10 times higher than the prediction of simple stellar
population models.
It is likely that in these cases the assumption of an instantaneous
burst is incorrect and an extended star-formation activity is required
to explain the observed H
is
more than 10 times higher than the prediction of simple stellar
population models.
It is likely that in these cases the assumption of an instantaneous
burst is incorrect and an extended star-formation activity is required
to explain the observed H![]() emission.
emission.
Hence, even taking into account the uncertainties of the cluster ages, the missing fraction of ionising radiation is rather large in young clusters, and we examine four different hypotheses to explain this issue.
First we discuss how the incomplete sampling of the IMF and
statistical fluctuations can affect the prediction of cluster
luminosities. Then we consider the effects related to the cluster
environment such as dust absorption and photon-leakage (i.e. a large
fraction of UV radiation escapes the H II region). Finally we briefly discuss whether
the delayed formation of the most massive stars
or a truncated IMF can offer alternative explanations for the low H![]() luminosity observed in very young clusters.
luminosity observed in very young clusters.
7.1 The consequence of sampling effects in the IMF
The library of models that we used for the SED fitting assumes a standard
Salpeter IMF, fully populated up to a high-mass end of 100 ![]() .
It is possible that the
difference between the expected and observed H
.
It is possible that the
difference between the expected and observed H![]() luminosities in the
youngest clusters is because we are overestimating the number of massive stars
owing to the incompleteness of the IMF at the high-mass end.
luminosities in the
youngest clusters is because we are overestimating the number of massive stars
owing to the incompleteness of the IMF at the high-mass end.
Incomplete sampling is often neglected, and it is assumed that the mass
spectrum of stellar clusters can be represented by a continuous function
given by the underlying IMF. On the other hand, numerical simulations
of synthetic clusters by a stochastic generation of stars show that this assumption is correct for massive systems (M > 104 ![]() ), whereas large deviations at the high-mass end occur for small clusters (Corbelli et al. 2009). The critical mass below which
statistical fluctuations become relevant depends on the cluster age and metallicity, and on the spectral range under study (Cerviño et al. 2002,2003).
For example, according to Fatuzzo & Adams (2008), sampling
effects dominate in the FUV range when extinction corrected FUV fluxes are below 1039 erg s-1.
Most of our selected objects lie above this threshold, but the
situation might change if we are interested in the UV ionising
radiation, because it has a steeper dependence on the stellar mass than
the non-ionising continuum. Hence, to estimate the H
), whereas large deviations at the high-mass end occur for small clusters (Corbelli et al. 2009). The critical mass below which
statistical fluctuations become relevant depends on the cluster age and metallicity, and on the spectral range under study (Cerviño et al. 2002,2003).
For example, according to Fatuzzo & Adams (2008), sampling
effects dominate in the FUV range when extinction corrected FUV fluxes are below 1039 erg s-1.
Most of our selected objects lie above this threshold, but the
situation might change if we are interested in the UV ionising
radiation, because it has a steeper dependence on the stellar mass than
the non-ionising continuum. Hence, to estimate the H![]() luminosities of the smallest clusters in our sample, sampling effects need to be considered.
luminosities of the smallest clusters in our sample, sampling effects need to be considered.
In Fig. 11 we show how the median bolometric (diamonds) and H![]() (stars) luminosities of a cluster depend on its mass. The simulation was carried out as described in Corbelli et al. (2009),
but here we assumed a maximum stellar mass of 100
(stars) luminosities of a cluster depend on its mass. The simulation was carried out as described in Corbelli et al. (2009),
but here we assumed a maximum stellar mass of 100 ![]() to be consistent with the fitting procedure used in this paper. The luminosities are computed for zero-age main-sequence stars.
to be consistent with the fitting procedure used in this paper. The luminosities are computed for zero-age main-sequence stars.
Low-mass clusters have a larger dispersion around the median H![]() luminosity than around the bolometric luminosity. Moreover,
luminosity than around the bolometric luminosity. Moreover,
![]() deviates considerably from a simple linear relation (solid line) at masses lower than 1450
deviates considerably from a simple linear relation (solid line) at masses lower than 1450 ![]() .
Below this limit the IMF is not fully populated at its high-end, and the stronger dependence of
.
Below this limit the IMF is not fully populated at its high-end, and the stronger dependence of
![]() on the stellar mass implies that the mean value of
on the stellar mass implies that the mean value of
![]() /
/
![]() increases, despite the occasional presence of outliers.
increases, despite the occasional presence of outliers.
![\begin{figure}
\par\includegraphics[width=8cm,bb=50 20 414 400]{13513fg08.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg120.png)
|
Figure 8:
FUV luminosity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,bb=110 365 470 765]{13513fg09.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg121.png)
|
Figure 9:
Comparison between the cluster bolometric luminosity determined from the SED spectral fitting (y-axis)
and the observed bolometric luminosity derived by adding the measured
FUV, NUV, and the total IR luminosity estimated following Verley et al. (2009)
as
|
| Open with DEXTER | |
The IMF statistical fluctuations introduce a large dispersion in the observable properties of the low-mass clusters (M < 1450 ![]() ), when the linear relation between cluster mass and
), when the linear relation between cluster mass and
![]() breaks down.
Thus, to account for the incomplete sampling of the IMF in these clusters, we will use the H
breaks down.
Thus, to account for the incomplete sampling of the IMF in these clusters, we will use the H![]() luminosity and the dispersions derived with our simulation (see Fig. 11). Note that all clusters with M < 1450
luminosity and the dispersions derived with our simulation (see Fig. 11). Note that all clusters with M < 1450 ![]() in our sample are quite young, hence their expected H
in our sample are quite young, hence their expected H![]() emission is well represented by the simulated data in Fig. 11.
For older and massive clusters we shall use the luminosities obtained
for a complete IMF (STARBURST99) with the dispersion given by our
simulation. Cerviño et al. (2003)
have shown that the minimum mass below which we expect stochastic
effects, as well as the dispersion around the mean or median value,
have a very weak dependence on the cluster age during the first
10 Myr.
emission is well represented by the simulated data in Fig. 11.
For older and massive clusters we shall use the luminosities obtained
for a complete IMF (STARBURST99) with the dispersion given by our
simulation. Cerviño et al. (2003)
have shown that the minimum mass below which we expect stochastic
effects, as well as the dispersion around the mean or median value,
have a very weak dependence on the cluster age during the first
10 Myr.
The expected H![]() luminosities of low-mass clusters are lower when stochastic effects are considered, as shown in Fig. 12. The error bars in the figure include both the dispersion of the model H
luminosities of low-mass clusters are lower when stochastic effects are considered, as shown in Fig. 12. The error bars in the figure include both the dispersion of the model H![]() luminosity and the uncertainty due to the error on the age of the clusters. The mean
luminosity and the uncertainty due to the error on the age of the clusters. The mean
![]()
![]() ratio
ratio![]() for the youngest clusters (t < 3 yr) is 0.30
+0.8-0.07.
Therefore, taking into account the stochastic effects reduces the
discrepancy between the expected and observed values, but the large
uncertainties prevent us to draw any firm conclusions on how the
missing H
for the youngest clusters (t < 3 yr) is 0.30
+0.8-0.07.
Therefore, taking into account the stochastic effects reduces the
discrepancy between the expected and observed values, but the large
uncertainties prevent us to draw any firm conclusions on how the
missing H![]() flux depends on the cluster mass, age, or galactocentric radius, as we show in Fig. 12.
flux depends on the cluster mass, age, or galactocentric radius, as we show in Fig. 12.
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,bb=70 360 450 770]{13513fg10...
...hics[width=6cm,bb=60 360 440 770]{13513fg10c.ps} }
\vspace*{3mm} \end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg123.png)
|
Figure 10:
Ratio of the observed (extinction corrected) to the
model H |
| Open with DEXTER | |
7.2 Dust absorption
Dust within or around the cluster can absorb the UV photons emitted by
the hot massive stars, reducing the amount of ionising radiation, and
contributing to the lack of observed H![]() photons.
photons.
The good spatial correlation between 24 ![]() m and H
m and H![]() emissions
shows that the dust is predominantly heated by OB stars within the H II regions. The Spitzer resolution at 70 and 160
emissions
shows that the dust is predominantly heated by OB stars within the H II regions. The Spitzer resolution at 70 and 160 ![]() m is not sufficient to resolve our sources, and we estimated the total IR luminosity from the 24
m is not sufficient to resolve our sources, and we estimated the total IR luminosity from the 24 ![]() m emission following Verley et al. (2009).
This agrees with what other studies found when the IR luminosity is dominated by emission at wavelengths longer than 24
m emission following Verley et al. (2009).
This agrees with what other studies found when the IR luminosity is dominated by emission at wavelengths longer than 24 ![]() m.
Nevertheless, the total IR luminosities are lower than what is required by the modest extinctions obtained
from the SED-fitting procedure. Some additional contribution to
m.
Nevertheless, the total IR luminosities are lower than what is required by the modest extinctions obtained
from the SED-fitting procedure. Some additional contribution to
![]() might come from a hot dust component heated
by young stars in these sources. The SED indicates an excess above the expected stellar emission at 3.6 and 4.5
might come from a hot dust component heated
by young stars in these sources. The SED indicates an excess above the expected stellar emission at 3.6 and 4.5 ![]() m.
However, given the limited MIR emission detected around the clusters
and, more generally, the low dust content of M 33, it is difficult
to explain the missing ionising radiation as an effect of dust
absorption only (see Sects. 6.4 and 6.5), even though this
mechanism would explain the observed trend with cluster age.
m.
However, given the limited MIR emission detected around the clusters
and, more generally, the low dust content of M 33, it is difficult
to explain the missing ionising radiation as an effect of dust
absorption only (see Sects. 6.4 and 6.5), even though this
mechanism would explain the observed trend with cluster age.
On the other hand, the way dust is distributed within or around the H II regions may produce different attenuation of the emitted light, and the usual assumption of a homogeneous dust screen may lead to an underestimation of the effects of dust extinction (Petersen & Gammelgaard 1997). For example, a clumpy dust distribution would explain the missing fraction of ionising radiation (40%) observed in the super star clusters of SBS 0335-052 (Reines et al. 2008). A more detailed analysis of the dust properties for these clusters, taking into account more complex dust distributions, will be addressed elsewhere (Giovanardi et al. 2010, in prep.).
7.3 Leakage of UV photons
UV photons not absorbed by dust grains can escape from the star-forming region and explain the origin of the extended diffuse UV emission observed by GALEX in the M 33 disc (Thilker et al. 2005).
The importance of taking into account the leakage of ionising photons from
H II regions has been increasingly discussed in recent years, especially
after the discovery of the diffuse ionised gas (DIG) in the
ISM of the Milky Way (Reynolds et al. 1974), and in the discs of other spiral galaxies (Greenawalt et al. 1998).
The DIG components of galaxies such as M 31 (Walterbos & Braun 1996), the LMC (Oey & Kennicutt 1998,1997), the SMC (Relaño et al. 2002),
amount to the 30% and 50% of the total H![]() luminosity.
Studies of field OB stars in M 33 (Hoopes & Walterbos 2003,2000) have given evidence that at least 20%-30% Lyman continuum photons must be able to escape from the H II regions in this galaxy.
Nonetheless, there is still a debate about whether the energy budget of photons leaking out of H II regions is sufficient to ionise the DIG or if additional mechanisms should be considered (Voges et al. 2008).
luminosity.
Studies of field OB stars in M 33 (Hoopes & Walterbos 2003,2000) have given evidence that at least 20%-30% Lyman continuum photons must be able to escape from the H II regions in this galaxy.
Nonetheless, there is still a debate about whether the energy budget of photons leaking out of H II regions is sufficient to ionise the DIG or if additional mechanisms should be considered (Voges et al. 2008).
Theoretical models have shown that the amount of leakage is regulated by the structure and clumpiness of the ISM (Miller & Cox 1993; Wood & Mathis 2004). Inhomogeneities in the medium favour the leakage of radiation because the presence of low-density regions may increase the mean free path of the photons (Reines et al. 2008; Voges et al. 2008). The leakage also depends on the spectrum of the ionising radiation, and on the evolutionary stage of the cluster, with the fraction of escaping photons being larger when stars experience a hard Wolf-Rayet phase, which occurs, depending on the mass and metallicity of a star, between 3 and 6 Myr (Castellanos et al. 2002).
Relating the leakage of ionising photons to the beginning of the W-R phase (Castellanos et al. 2002) may explain the age-dependence of the
![]()
![]() ratio for clusters older than 3 Myr, but the issue would still remain open for the youngest systems.
ratio for clusters older than 3 Myr, but the issue would still remain open for the youngest systems.
7.4 Deficiency or delayed formation of massive stars
The previous considerations cast some doubts on leakage and dust absorption as the only processes causing the deficiency of ionising radiation.
If the star-formation process is not instantaneous, clusters might reach their expected H![]() luminosity only after all stars have formed, especially the most massive ones, which determine the cluster H
luminosity only after all stars have formed, especially the most massive ones, which determine the cluster H![]() luminosity
rather than the total mass. Massive stars might form later during the
cluster evolution either because they need particular physical
conditions and processes to take place (Palla 2005) or because the time-scale for the gas to collapse is longer in a low-density environment such as the disc of M 33 (Elmegreen 1999).
Therefore, the delayed formation of the most massive stars appears as
an interesting and promising way to explain why only very young
clusters are underluminous in H
luminosity
rather than the total mass. Massive stars might form later during the
cluster evolution either because they need particular physical
conditions and processes to take place (Palla 2005) or because the time-scale for the gas to collapse is longer in a low-density environment such as the disc of M 33 (Elmegreen 1999).
Therefore, the delayed formation of the most massive stars appears as
an interesting and promising way to explain why only very young
clusters are underluminous in H![]() ,
and this should be investigated in detail in future work. Particularly, it would be interesting to know whether the excess of H
,
and this should be investigated in detail in future work. Particularly, it would be interesting to know whether the excess of H![]() emission in the oldest clusters could also be explained by this scenario without the assumption of multiple burst events.
emission in the oldest clusters could also be explained by this scenario without the assumption of multiple burst events.
![\begin{figure}
\par\includegraphics[width=8cm,bb=85 365 475 775]{13513fg11.ps}
\vspace*{3mm}\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg124.png)
|
Figure 11:
Expected median bolometric (diamonds) and H |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,bb=70 360 450 770]{13513fg12...
...ps} \includegraphics[width=6cm,bb=60 360 440 770]{13513fg12c.ps} }\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg125.png)
|
Figure 12:
Ratio of the observed (extinction corrected) to the model H |
| Open with DEXTER | |
A strong deficiency of massive stars compared to what is predicted by a stochastically sampled IMF should also be considered. For example, truncated models of the stellar IMF (Meurer et al. 2009; Pflamm-Altenburg et al. 2009, and references therein) predict lower cluster luminosities than stochastically sampled models (Corbelli et al. 2009). This is because truncated models link the cluster mass to the most massive stars that can form in a cluster, without considering the occasional presence of outliers. The IMF over the whole galaxy in this case would deviate from the power law assumed in each cluster, and it will be steeper. Assessing the details of the IMF in M 33 and its variance requires the availability of deep colour-magnitude diagrams for the stellar members of each cluster. This is difficult to attain in compact young clusters and is clearly beyond the scope of this study.
8 The gaseous environments of young clusters
Finally, we investigated whether the mass of young clusters is related to the surface density of the different phases of the surrounding ISM (ionised, atomic, molecular gas).
As described in Sect. 2.4, the spatial resolution of the CO and H I maps is 13
![]() and 24
and 24
![]()
![]() 48
48
![]() respectively. Thus, the size of the clusters (see Table 2)
is smaller than the resolution of the CO images for roughly half of the
objects in our sample, while none of the clusters can be resolved with
the beam size of the 21-cm map.
For this reason we limit our analysis to areas of the ISM that are
larger than the clusters. Using an aperture equal to the lowest
resolution gas map (H I,
i.e. 24 arcsec), centred on the optical position of each object,
we measured the gas surface densities associated with it.
respectively. Thus, the size of the clusters (see Table 2)
is smaller than the resolution of the CO images for roughly half of the
objects in our sample, while none of the clusters can be resolved with
the beam size of the 21-cm map.
For this reason we limit our analysis to areas of the ISM that are
larger than the clusters. Using an aperture equal to the lowest
resolution gas map (H I,
i.e. 24 arcsec), centred on the optical position of each object,
we measured the gas surface densities associated with it.
Figure 13 shows the
measured surface density of the different gaseous components as well as
the total gas surface density compared to the cluster stellar mass.
There is no trend with cluster age, the surface density of the
surrounding ISM is not affected by the early stages of cluster
evolution. The ionised gas seems to better correlate with the cluster
mass (as expected, since the most massive clusters have a higher number
of ionising photons). Concerning the H I gas, one can only infer from the figure that the majority of the clusters are found in a narrow regions of surface density (
![]() cm-2), which is no big surprise given the rather flat H I distribution in the M 33 disc. Clusters are born in correspondence to H I filaments, but there is no clear connection between the stellar mass and the gas surface density (Verley et al. 2010).
cm-2), which is no big surprise given the rather flat H I distribution in the M 33 disc. Clusters are born in correspondence to H I filaments, but there is no clear connection between the stellar mass and the gas surface density (Verley et al. 2010).
![\begin{figure}
\par\includegraphics[width=10cm,bb=53 345 630 840]{13513fg13.ps}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg127.png)
|
Figure 13: Surface density of ionised ( top-left), atomic ( top-right), molecular ( bottom-left), and total ( bottom-right) hydrogen as a function of the stellar mass of the cluster. Symbols and colour codes are the same as for Fig. 4. |
| Open with DEXTER | |
The bottom-right panel of Fig. 13 shows the sum of all gaseous components (ionised, atomic, molecular) versus the stellar mass. It shows that the gaseous environment of these clusters is dominated by the atomic component. For a change of two orders of magnitude in cluster mass there is only half an order of magnitude change in the total gas column density. Because the scatter of this correlation is large, as Verley et al. (2009) have already pointed out, the gas surface density is not the only parameter which determines the star-formation rate and the mass of the newly born clusters.
9 Summary and conclusions
We analysed multi-wavelength observations of a sample of young star clusters and associations in M 33 combining UV (GALEX), optical (UBVRI), MIR (Spitzer/IRAC-MIPS), 3-mm (BIMA-FCRAO) and 21-cm (WSRT) observations. The UV and optical data sets were used to derive their age and mass, and the line-of-sight extinction by fitting the measured SEDs to a set of single-burst stellar population models. The model SEDs were reddened using various extinction laws (Milky Way, LMC, SMC), and the best-fit solutions were obtained with the LMC laws.
We find ages between 2 and 15 Myr and stellar masses between
![]() and
and
![]()
![]() .
The extinction towards these stellar systems, AV varies between 0.3 and 1 mag, indicating that they are not highly obscured even in an early evolutionary phase.
As expected, older clusters are less extinct than younger ones.
We also find a correlation between mass and radius with
.
The extinction towards these stellar systems, AV varies between 0.3 and 1 mag, indicating that they are not highly obscured even in an early evolutionary phase.
As expected, older clusters are less extinct than younger ones.
We also find a correlation between mass and radius with
![]() .
There is no clear trend between extinction and other parameters such as
metallicity or total gas surface density.
The fractional luminosities at 8
.
There is no clear trend between extinction and other parameters such as
metallicity or total gas surface density.
The fractional luminosities at 8 ![]() m and 24
m and 24 ![]() m
decrease with the galactocentric distance, suggesting a lower PAHs and
small-grain abundance in the outer regions of the galaxy. A comparison
between the model SEDs and the Spitzer/IRAC fluxes shows an excess emission at 3.6
m
decrease with the galactocentric distance, suggesting a lower PAHs and
small-grain abundance in the outer regions of the galaxy. A comparison
between the model SEDs and the Spitzer/IRAC fluxes shows an excess emission at 3.6 ![]() m and 4.5
m and 4.5 ![]() m, which may be due to a hot dust component, heated by the ionising radiation of the cluster massive stars.
m, which may be due to a hot dust component, heated by the ionising radiation of the cluster massive stars.
We find a discrepancy between the observed H![]() luminosity and that expected from population synthesis models, especially in young (<3 Myr) and low-mass (
luminosity and that expected from population synthesis models, especially in young (<3 Myr) and low-mass (
![]()
![]() )
clusters. The ratio of the observed-to-model H
)
clusters. The ratio of the observed-to-model H![]() luminosity increases with cluster age and ranges between 20% and 90%.
We showed that this difference can be reduced but not removed if one
takes into account the uncertainties of the age from the SED-fitting
procedure and the stochasticity of the IMF at the high mass-end.
Similarly, the gap between the best-fit bolometric luminosity (derived
assuming a fully sampled IMF) and the total observed luminosity (UV and
IR) cannot be fully explained if only a stochastically sampled IMF is
considered. We then discussed other possible scenarios:
luminosity increases with cluster age and ranges between 20% and 90%.
We showed that this difference can be reduced but not removed if one
takes into account the uncertainties of the age from the SED-fitting
procedure and the stochasticity of the IMF at the high mass-end.
Similarly, the gap between the best-fit bolometric luminosity (derived
assuming a fully sampled IMF) and the total observed luminosity (UV and
IR) cannot be fully explained if only a stochastically sampled IMF is
considered. We then discussed other possible scenarios:
- 1.
- Absorption of Lyman continuum photons by dust
in H II regions cannot fully explain this discrepancy because
the IR emissions inferred from the 24
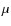 m
luminosity is generally lower
than expected from the derived extinction. This suggests that UV
continuum photons are missing, but not because of dust absorption only.
m
luminosity is generally lower
than expected from the derived extinction. This suggests that UV
continuum photons are missing, but not because of dust absorption only.
- 2.
- The escape of UV ionising and non-ionising photons from the H II region because of a clumpy and porous ISM is a likely scenario that would be supported by the large UV and H
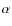 diffuse fractions observed in this galaxy.
diffuse fractions observed in this galaxy.
- 3.
- Finally we discussed the possibility of a delayed formation of
the most massive stars in these clusters as a consequence of the
increase in the observed-to-expected H
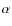 luminosity ratio with age and mass.
Because the oldest clusters in our sample are also the most massive
ones, a stronger suppression of massive star formation in low-mass
systems than what is predicted by a stochastically sampled IMF would
also alleviate the problem.
luminosity ratio with age and mass.
Because the oldest clusters in our sample are also the most massive
ones, a stronger suppression of massive star formation in low-mass
systems than what is predicted by a stochastically sampled IMF would
also alleviate the problem.
We thank the anonymous referee for the comments and suggestions that contributed to improve the paper. This work is based on observations made with the NASA Galaxy Evolution Explorer and with the Spitzer Space Telescope. GALEX is operated for NASA by the California Institute of Technology under NASA contract NAS5-98034. The Spitzer Space Telescope is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This research draws upon data provided by The Resolved Stellar Content of Local Group Galaxies Currently Forming Stars, PI: Dr. Philip Massey, as distributed by the NOAO Science Archive. NOAO is operated by the Association of Universities for Research in Astronomy (AURA), Inc. under a cooperative agreement with the National Science Foundation.
References
- Abergel, A., Bernard, J. P., Boulanger, F., et al. 2002, A&A, 389, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bastian, N., Gieles, M., Efremov, Y. N., & Lamers, H. J. G. L. M. 2005, A&A, 443, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., Papovich, C., Wolf, C., et al. 2005, ApJ, 625, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Boulesteix, J., Courtes, G., Laval, A., Monnet, G., & Petit, H. 1974, A&A, 37, 33 [NASA ADS] [Google Scholar]
- Buckalew, B. A., Kobulnicky, H. A., Darnel, J. M., et al. 2006, ApJS, 162, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, Jr., R. C., Bianchi, L., et al. 2005, ApJ, 633, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carico, D. P., Sanders, D. B., Soifer, B. T., et al. 1988, AJ, 95, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Castellanos, M., Díaz, Á. I., & Tenorio-Tagle, G. 2002, ApJ, 565, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Cerviño, M., & Luridiana, V. 2004, A&A, 413, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerviño, M., Valls-Gabaud, D., Luridiana, V., & Mas-Hesse, J. M. 2002, A&A, 381, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerviño, M., Luridiana, V., Pérez, E., Vílchez, J. M., & Valls-Gabaud, D. 2003, A&A, 407, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandar, R., Bianchi, L., & Ford, H. C. 1999, ApJS, 122, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Chandar, R., Bianchi, L., & Ford, H. C. 2001, A&A, 366, 498 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbelli, E., Verley, S., Elmegreen, B. G., & Giovanardi, C. 2009, A&A, 495, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courtes, G., Petit, H., Petit, M., Sivan, J.-P., & Dodonov, S. 1987, A&A, 174, 28 [NASA ADS] [Google Scholar]
- Deul, E. R., & van der Hulst, J. M. 1987, A&AS, 67, 509 [NASA ADS] [Google Scholar]
- Dodorico, S., & Benvenuti, P. 1983, MNRAS, 203, 157 [NASA ADS] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. 1999, in The Evolution of Galaxies on Cosmological Timescales, ed. J. E. Beckman, & T. J. Mahoney, ASP Conf. Ser., 187, 145 [Google Scholar]
- Engargiola, G., Plambeck, R. L., Rosolowsky, E., & Blitz, L. 2003, ApJS, 149, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Blaylock, M., Su, K. Y. L., et al. 2007, PASP, 119, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Fatuzzo, M., & Adams, F. C. 2008, ApJ, 675, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Boissier, S., Madore, B. F., et al. 2007, ApJS, 173, 185 [NASA ADS] [CrossRef] [Google Scholar]
- González Delgado, R. M., & Pérez, E. 2000, MNRAS, 317, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., & Clayton, G. C. 1998, ApJ, 500, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, S. M., Duric, N., Kirshner, R. P., Goss, W. M., & Viallefond, F. 1999, ApJS, 120, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Greenawalt, B., Walterbos, R. A. M., Thilker, D., & Hoopes, C. G. 1998, ApJ, 506, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Habart, E., Verstraete, L., Boulanger, F., et al. 2001, A&A, 373, 702 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E., & Pudritz, R. E. 1994, ApJ, 429, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M. H., Corbelli, E., Schneider, S. E., & Young, J. S. 2004, ApJ, 602, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Hodge, P. W., Skelton, B. P., & Ashizawa, J. 2002, Astrophys. Space Sci. Library, 221, An Atlas of Local Group Galaxies [Google Scholar]
- Hoopes, C. G., & Walterbos, R. A. M. 2000, ApJ, 541, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Hoopes, C. G., & Walterbos, R. A. M. 2003, ApJ, 586, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, S. S. 2004, in The Formation and Evolution of Massive Young Star Clusters, ed. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota, ASP Conf. Ser., 322, 19 [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, J., Zhou, X., Kong, X., et al. 2001, AJ, 122, 1796 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, J., Zhou, X., Chen, J., et al. 2002, AJ, 123, 3141 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, J., Zhou, X., & Chen, J.-S. 2004, Chin. J. A&A, 4, 125 [NASA ADS] [Google Scholar]
- Magrini, L., Corradi, R. L. M., Mampaso, A., & Perinotto, M. 2000, A&A, 355, 713 [NASA ADS] [Google Scholar]
- Magrini, L., Corbelli, E., & Galli, D. 2007a, A&A, 470, 843 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magrini, L., Vílchez, J. M., Mampaso, A., Corradi, R. L. M., & Leisy, P. 2007b, A&A, 470, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz-Apellániz, J. 2004, PASP, 116, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Massey, P., & Hutchings, J. B. 1983, ApJ, 275, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., Olsen, K. A. G., Hodge, P. W., et al. 2006, AJ, 131, 2478 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., McNeill, R. T., Olsen, K. A. G., et al. 2007, AJ, 134, 2474 [NASA ADS] [CrossRef] [Google Scholar]
- Mayall, N. U., & Aller, L. H. 1942, ApJ, 95, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Meurer, G. R., Wong, O. I., Kim, J. H., et al. 2009, ApJ, 695, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, W. W. I., & Cox, D. P. 1993, ApJ, 417, 579 [Google Scholar]
- Misselt, K. A., Clayton, G. C., & Gordon, K. D. 1999, ApJ, 515, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Morrissey, P., Schiminovich, D., Barlow, T. A., et al. 2005, ApJ, 619, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., & Kennicutt, Jr., R. C. 1997, MNRAS, 291, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., & Kennicutt, Jr., R. C. 1998, Publ. Astron. Soc. Aust., 15, 141 [Google Scholar]
- Oke, J. B. 1990, AJ, 99, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F. 2005, in Massive Star Birth: A Crossroads of Astrophysics, ed. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 196 [Google Scholar]
- Park, W.-K., & Lee, M. G. 2007, AJ, 134, 2168 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, L., & Gammelgaard, P. 1997, A&A, 323, 697 [NASA ADS] [Google Scholar]
- Pflamm-Altenburg, J., Weidner, C., & Kroupa, P. 2009, MNRAS, 395, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Reach, W. T., Megeath, S. T., Cohen, M., et al. 2005, PASP, 117, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Reines, A. E., Johnson, K. E., & Hunt, L. K. 2008, AJ, 136, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Relaño, M., Peimbert, M., & Beckman, J. 2002, ApJ, 564, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, R. J., Roesler, F. L., & Scherb, F. 1974, ApJ, 192, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., & Simon, J. D. 2008, ApJ, 675, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., Keto, E., Matsushita, S., & Willner, S. P. 2007, ApJ, 661, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H., Gil de Paz, A., Seibert, M., et al. 2005, ApJ, 632, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Searle, L. 1971, ApJ, 168, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Hoopes, C. G., Bianchi, L., et al. 2005, ApJ, 619, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Boissier, S., Bianchi, L., et al. 2007, ApJS, 173, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Verley, S., Hunt, L. K., Corbelli, E., & Giovanardi, C. 2007, A&A, 476, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verley, S., Corbelli, E., Giovanardi, C., & Hunt, L. K. 2009, A&A, 493, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verley, S., Corbelli, E., Giovanardi, C., & Hunt, L. K. 2010, A&A, 510, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viallefond, F., Goss, W. M., van der Hulst, J. M., & Crane, P. C. 1986, A&AS, 64, 237 [Google Scholar]
- Vilchez, J. M., Pagel, B. E. J., Diaz, A. I., Terlevich, E., & Edmunds, M. G. 1988, MNRAS, 235, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, E. S., Oey, M. S., Walterbos, R. A. M., & Wilkinson, T. M. 2008, AJ, 135, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Walterbos, R. A. M., & Braun, R. 1996, in The Minnesota Lectures on Extragalactic Neutral Hydrogen, ed. E. D. Skillman, ASP Conf. Ser., 106, 1 [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. D., & Scoville, N. 1990, ApJ, 363, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, K., & Mathis, J. S. 2004, MNRAS, 353, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Zepf, S. E., Ashman, K. M., English, J., Freeman, K. C., & Sharples, R. M. 1999, AJ, 118, 752 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... ratio
![[*]](/icons/foot_motif.png)
- Note that to derive the mean ratio we discarded the two lowest mass clusters with the largest error bars.
All Tables
Table 1: Sample of young clusters in M 33 selected in this work.
Table 2: UV and optical photometric measurements. The last column displays the aperture radius used for the photometry.
Table 3:
H![]() and Spitzer IRAC/MIPS photometry of the sample. Flux units are in erg s-1 cm-2.
and Spitzer IRAC/MIPS photometry of the sample. Flux units are in erg s-1 cm-2.
Table 4: Results from the SED-fitting technique.
All Figures
![\begin{figure}
\par\includegraphics[width=12cm]{13513fg01.eps} \vspace{6mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg27.png)
|
Figure 1: Location of the 32 clusters selected in this study, overlayed on the GALEX (FUV and NUV) images of M 33. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.5cm,bb=25 30 430 230]{13513fg0...
...[width=4.5cm,bb=25 30 430 230]{13513fg025.ps} }
\vspace*{-3.45mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg82.png)
|
Figure 2: Output best-fit SEDs in units of AB magnitudes, overlayed on the measured integrated magnitudes from 1000 to 10 000 Å. Vertical bars indicate the uncertainty on the photometry, while the horizontal ones show the approximate width of each filter. The numbers at the top-left corners of the plots correspond to the cluster ID given in Table 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=4.7cm,bb=20 30 410 230]{13513fg0...
...cs[width=4.4cm,bb=45 30 410 230]{13513fg035.ps} }
\vspace*{2.2mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg83.png)
|
Figure 3:
Model SED for each cluster in flux units ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=7.4cm,bb=45 15 435 405]{13513fg0...
...aphics[width=7.4cm,bb=45 15 435 405]{13513fg04d.ps} }
\vspace{2mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg93.png)
|
Figure 4:
Top-left: cluster ages and masses determined from the SED fitting. Top-right:
mass versus radius relation: the solid line with a slope of
1.5 provides the best linear fits to the data points. The
dotted-line shows the minimum size corresponding to the resolution of
the V-band image. Bottom-left: bolometric luminosity distribution of the sample. Bottom-right: (B-V)0 colour distribution as a function of age. The symbols correspond to three different age bins: |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,bb=65 365 490 780]{13513fg05.ps}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg102.png)
|
Figure 5: Cluster oxygen abundance versus galactocentric distance, mass, and age. The solid line in the top panel shows the metallicity radial gradient relation found by Rosolowsky & Simon (2008). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,bb=45 15 420 405]{13513fg06a...
...,bb=45 15 420 405]{13513fg06e.ps} }\hspace*{3cm}\vspace*{-3.5mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg104.png)
|
Figure 6:
Visual extinction (AV) versus age (top-left),
the measured oxygen abundance (top-centre), the ratio of the the 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,bb=28 10 400 400]{13513fg07a...
...6cm,bb=28 10 400 400]{13513fg07e.ps} }\hspace*{3cm}\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg105.png)
|
Figure 7:
Cluster galactocentric distance versus AV (top-left), the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,bb=50 20 414 400]{13513fg08.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg120.png)
|
Figure 8:
FUV luminosity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,bb=110 365 470 765]{13513fg09.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg121.png)
|
Figure 9:
Comparison between the cluster bolometric luminosity determined from the SED spectral fitting (y-axis)
and the observed bolometric luminosity derived by adding the measured
FUV, NUV, and the total IR luminosity estimated following Verley et al. (2009)
as
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,bb=70 360 450 770]{13513fg10...
...hics[width=6cm,bb=60 360 440 770]{13513fg10c.ps} }
\vspace*{3mm} \end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg123.png)
|
Figure 10:
Ratio of the observed (extinction corrected) to the
model H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,bb=85 365 475 775]{13513fg11.ps}
\vspace*{3mm}\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg124.png)
|
Figure 11:
Expected median bolometric (diamonds) and H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,bb=70 360 450 770]{13513fg12...
...ps} \includegraphics[width=6cm,bb=60 360 440 770]{13513fg12c.ps} }\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg125.png)
|
Figure 12:
Ratio of the observed (extinction corrected) to the model H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=10cm,bb=53 345 630 840]{13513fg13.ps}
\end{figure}](/articles/aa/full_html/2010/13/aa13513-09/Timg127.png)
|
Figure 13: Surface density of ionised ( top-left), atomic ( top-right), molecular ( bottom-left), and total ( bottom-right) hydrogen as a function of the stellar mass of the cluster. Symbols and colour codes are the same as for Fig. 4. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


