EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) L6 Full HTML
Free Access
Issue
A&A
Volume 520, September-October 2010
Article Number L6
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201015442
Published online 28 September 2010
A&A 520, L6 (2010)

LETTER TO THE EDITOR

Evidence for a sharp structure variation inside a red-giant star

A. Miglio1,[*] - J. Montalbán1 - F. Carrier 2 - J. De Ridder2 - B. Mosser3 - P. Eggenberger4 - R. Scuflaire1 - P. Ventura5 - F. D'Antona5 - A. Noels1 - A. Baglin3

1 - Institut d'Astrophysique et de Géophysique de l'Université de Liège, 17 Allée du 6 Août, 4000 Liège, Belgium
2 - Instituut voor Sterrenkunde, K.U. Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
3 - LESIA, UMR8109, Université Pierre et Marie Curie, Université Denis Diderot, Observatoire de Paris, 92195 Meudon, France
4 - Observatoire de Genève, Université de Genève, 51 chemin des Maillettes, 1290 Sauverny, Switzerland
5 - INAF - Osservatorio di Roma, via Frascati, 33 Monteporzio Catone, RM, Italy

Received 21 July 2010 / Accepted 3 September 2010

Abstract
Context. The availability of precisely determined frequencies of radial and non-radial oscillation modes in red giants is finally paving the way for detailed studies of the internal structure of these stars.
Aims. We look for the seismic signature of regions of sharp structure variation in the internal structure of the CoRoT target HR 7349.
Methods. We analyse the frequency dependence of the large frequency separation and second frequency differences, as well as the behaviour of the large frequency separation obtained with the envelope auto-correlation function.
Results. We find evidence for a periodic component in the oscillation frequencies, i.e. the seismic signature of a sharp structure variation in HR 7349. In a comparison with stellar models we interpret this feature as caused by a local depression of the sound speed that occurs in the helium second-ionization region. Using solely seismic constraints this allows us to estimate the mass ( M=1.2+0.6-0.4 $M_\odot $) and radius ( R=12.2+2.1-1.8 $R_\odot $) of HR 7349, which agrees with the location of the star in an HR diagram.

Key words: asteroseismology - stars: interiors - stars: oscillations - stars: fundamental parameters - stars: individual: HR 7349

1 Introduction

Red giant stars are cool, highly luminous stars. They play a predominant role in stellar, galactic, and extragalactic astrophysics because they serve as distance and age indicators for globular clusters and nearby galaxies (see e.g. Lee et al. 1993; Girardi & Salaris 2001). Moreover their observed chemical composition is a fundamental ingredient in the study of the chemical evolution of their host galaxy (see e.g. Catelan 2009, and references therein).

All red giants have an extended and diluted convective envelope surrounding a dense core, which makes their structure and therefore their pulsation properties very different from that of our Sun. As in solar-like stars however, their convective envelope can stochastically excite acoustic oscillation modes. While stochastic oscillations have been firmly detected in a few bright G and K giants since Frandsen et al. (2002), a major breakthrough was achieved thanks to the photometric space-based observations with the CoRoT[*] satellite (Baglin et al. 2006), leading to the unambiguous detection of radial and non-radial oscillation modes in thousands of red giants (De Ridder et al. 2009; Mosser et al. 2010; Hekker et al. 2009; Carrier et al. 2010). Moreover, the Kepler space-telescope has also started monitoring red giants for photometric variations and has already detected radial and non-radial oscillation modes in a large number of field giants as well as cluster members (Stello et al. 2010; Bedding et al. 2010a). As the precise detection of oscillation modes in the Sun fostered helioseismic inferences in the 1990s, we now have the chance to start probing the internal structure of these cool evolved stars thanks to the recent advances in observational stellar seismology.

Stellar global acoustic oscillation modes show up in the frequency spectrum as discrete peaks. While the average spacing between the frequencies $\nu$ of modes of the same spherical degree (large frequency separation, $\Delta \nu $) represents an estimate of the mean density of the star (Tassoul 1980; Vandakurov 1967), periodic deviations from a constant $\Delta \nu $ are signatures of so-called acoustic glitches, i.e. regions of sharp-structure variation in the stellar interior. Any localised region of sharp variation of the sound speed c induces in the frequencies an oscillatory component with a periodicity related to the sound-travel time measured from that region to the surface of the star (Vorontsov 1988; Gough 1990). Its amplitude depends on the sharpness of the glitch and decays with $\nu$, because as the frequency increases, the wavelength of the mode becomes comparable with or less than the extent of the glitch. These sharp variations are found in zones of rapidly changing chemical composition, in ionization zones of major chemical elements, or in regions where the energy transport switches from radiative to convective.

In the Sun, the detection and interpretation of a large number of acoustic oscillation modes led to the determination of the depth of both the solar convective envelope and of the helium second-ionization zone, and allowed us to estimate the helium abundance in the envelope, otherwise inaccessible by other means (see Christensen-Dalsgaard 2002, for a review).

The possibility and relevance of detecting sharp structure variations in other main-sequence stars, as well as first attempts to look for these signatures, have been addressed in several papers in the literature (see e.g. Théado et al. 2005; Monteiro et al. 2000; Monteiro & Thompson 1998; Mazumdar & Antia 2001; Houdek & Gough 2007; Miglio et al. 2003; Mazumdar 2005; Bedding et al. 2010b; Basu et al. 2004; Roxburgh & Vorontsov 1998; Ballot et al. 2004; Perez Hernandez & Christensen-Dalsgaard 1998; Verner et al. 2006).

Here we report on the detection of a sharp-structure variation in the red giant CoRoT target HR 7349 (HD181907), a star with a physical structure very different from the Sun, yet showing global oscillations modes that allow us to probe its internal structure.

2 Evidence for an oscillatory component in the frequency spacings

Carrier et al. (2010) have determined the eigenfrequencies of HR 7349. They have shown that the first frequency differences $\Delta\nu_{n,\ell}\equiv\nu_{n,\ell}-\nu_{n-1,\ell}$ are modulated. In order to investigate this modulation, we have analysed these first frequency differences and compared them to the function $\Delta\nu(\nu)$ derived from the method developed by Mosser & Appourchaux (2009). This envelope autocorrelation function (EACF) is obtained from the auto-correlation of the times series, performed as the Fourier spectrum of the windowed Fourier spectrum; the windows are Hanning filters covering the frequency range where significant excess power is observed. Because the modulation is rapid, we had to use narrow filters, with a FWHM varying between 1 and 2 times the mean value of the large separation. An EACF computed with a narrow filter benefits from the low filtering, but suffers from larger error bars.

Figure 1 shows the large separations for $\ell =0,1$, and 2 superimposed on the function $\Delta\nu(\nu)$ obtained with a filter width equal to 1.4 times the mean value of the large separation, which represents an acceptable compromise between the filtering of the signal and the noise level. We remark that both values and error bars of $\Delta\nu(\nu)$ and $\Delta \nu _{n,\ell }$ closely agree. The modulation seen in the function $\Delta\nu(\nu)$ is present in all autocorrelations performed with a filter that is narrow enough to respect the Shannon criterion.

We have detrended the low-frequency gradient of $\Delta\nu(\nu)$in order to emphasize the modulation, which is of the order of $7~\mu$Hz (a period of about $\mathcal{T}_0 = 0.14$ Ms).

That the modulation is seen with two independent methods, is present over more than 2.5 periods, and remains detectable even if a significant level of noise is added to the spectrum makes us confident that the oscillation found in the frequency differences is genuine.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{figure/15442fg1.eps} \end{figure} Figure 1:

Large separations $\Delta \nu _{n,\ell }$ computed by Carrier et al. (2010) ($\ell =0$: black squares; 1: stars; 2: triangles) are superimposed on the $\Delta \nu _{n,\ell }$ function given by the autocorrelation of the time series (solid thick line). The $\pm $1-$\sigma $ error bars are given by the two adjacent curves; they agree with the error bars of $\Delta \nu _{n,\ell }$. Both $\Delta \nu _{n,\ell }$ and $\Delta \nu _{n,\ell }$ show a periodic modulation with a period of the order of 0.14 Ms. The zebra regions indicate 1-$\Delta \nu $wide frequency ranges. The inset shows the filter used for performing the envelope autocorrelation function, with a full-width at half-maximum $\delta \nu _{{\rm H}}$ equal to 1.4 times the mean value of the large separation.

Open with DEXTER

The uncertainty of the period $\mathcal{T}_0$ of the oscillatory component was estimated with a Monte Carlo simulation. We assumed that the frequencies are independent and are Gaussian-distributed around their observed value with a standard deviation equal to their 1-$\sigma $ error bar as listed by Carrier et al. (2010). We then generated 5000 realizations of the frequencies, computed the frequency differences, and applied a non-linear regression procedure. Each time a cost function S, defined as

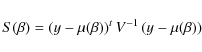
\begin{displaymath}S(\beta)=\left(y-\mu(\beta)\right)^t V^{-1}\left(y-\mu(\beta)\right) \end{displaymath} (1)

was minimized, where y is the matrix of observed frequency differences, V is the covariance matrix of the observed frequency differences, and $\mu(\beta)$ is the matrix containing the non-linear model

\begin{displaymath}\mu(\beta; \nu) = a + b \nu + A \sin(2\pi~ \mathcal{T}_0 \nu) + B \cos(2\pi~ \mathcal{T}_0 \nu) \end{displaymath} (2)

with $\beta \equiv (a,b,A,B,\mathcal{T}_0)$ the fit parameters, and $\nu$ the covariates. The uncertainty of $\mathcal{T}_0$ was then derived as the standard deviation of the sample of $\mathcal{T}_0$ values. As a result, we obtain a period $\mathcal{T}_0=0.13 \pm 0.02$ Ms from the component detected in $\Delta \nu $ and $\mathcal{T}_0=0.14 \pm 0.03$ Ms when fitting the behaviour of the second frequency differences $\Delta_2 \nu$ (as defined in Gough 1990).

3 Interpretation of the oscillatory component

As recalled in Sect. 1, the periodicity of the component allows us to infer the location of the glitch in terms of its acoustic depth or in terms of its relative acoustic radius (as suggested by Ballot et al. 2004). For HR 7349 we find: $t_0/T = 0.55 \pm 0.07$, where t is the sound travel time from the centre to the glitch, and T is the acoustic radius of the star ( $T=(2\langle \Delta\nu\rangle)^{-1}$).

To interpret this observational evidence, we consider in Fig. 2 the location of acoustic glitches in the structure of red-giant models computed with the code ATON (Ventura et al. 2008). We find that at about half the acoustic radius the sound speed has a sharp variation owing to a local depression of the first adiabatic exponent[*] $\gamma _1$ in the helium second-ionization zone. We therefore interpret the periodic component detected in the frequencies of HR 7349 as the signature of helium second ionization. This interpretation is further supported by a direct comparison between observed and numerically computed pulsation frequencies in models of red giants (see Sect. 4).

\begin{figure} \par\includegraphics[width=8.8cm,clip]{figure/15442fg2.eps} \end{figure} Figure 2:

a) Behaviour of $\gamma _1$ as a function of t/T in a 1.2 $M_\odot $, 12 $R_\odot $ model: the region where helium undergoes its second ionization induces a local minimum in $\gamma _1$. In the same model the base of the convective envelope is located at $t/T = 2\times 10^{-2}$. b) Location of acoustic glitches in a model of the Sun.

Open with DEXTER

We notice that while in the Sun and solar-like stars the base of the convective envelope is located at about half the stellar acoustic radius (see Fig. 2), in red giants it is located at a small relative acoustic radius (typically less than 10-1 for the models considered, depending on the mass and evolutionary state).

Furthermore, we find that in the models the relative acoustic radius of the He second-ionization region ( $t_{\rm HeII}/T$) and the average $\Delta \nu $ determine the mass and radius of the star (see Fig. 3). We ascribe this dependence to the the fact that the temperature stratification in the envelope of red-giant stars depends mostly on M and R (see e.g. Kippenhahn & Weigert 1990); a thorough discussion on this topic will be reported in detail in a forthcoming paper.

On the basis of seismic constraints only, we can thus derive from Fig. 3 the mass of HR 7349 ( M= 1.2+0.6-0.4 $M_\odot $) and, through the scaling of $\Delta \nu $ with the mean stellar density, its radius ( R= 12.2+2.1-1.8 $R_\odot $).

Because the parallax of this nearby red giant is known, an independent radius estimate of HR 7349 can be obtained via the precise absolute luminosity and effective temperature (Carrier et al. 2010), leading to $R = 12.2 \pm 1.1$ $R_\odot $, in agreement with the seismically inferred radius. We also notice that the mass and radius estimates are also compatible to those obtained by the combination of the frequency corresponding to the maximum oscillation power ( $\nu_{\rm max}$), $\langle\Delta\nu\rangle$, and $T_{\rm eff}$ (Carrier et al. 2010).

\begin{figure} \par\includegraphics[width=8.8cm,clip]{figure/15442fg3.eps} \par\end{figure} Figure 3:

Behaviour of the relative acoustic radius of the second helium ionization region ( $t_{\rm HeII}/T$) as a function of the average large frequency separation in stellar models with different mass (0.7 to 3 $M_\odot $), initial chemical composition (helium mass fraction Y=0.25, 0.278, heavier-elements mass fraction Z=0.02, 0.01), and convection-efficiency parameter ( $\alpha _{\rm MLT}=1.6, 1.9$). The position of HR 7349 in this diagram is represented by the black dot with error bars.

Open with DEXTER

4 Direct comparison with numerically computed oscillation frequencies

We consider a red giant model of 1.2 $M_\odot $ and 12 $R_\odot $ computed with the stellar evolutionary code ATON (Ventura et al. 2008). The model has an initial helium mass fraction Y=0.278 and a heavier-elements mass fraction Z=0.02. For this model we computed adiabatic oscillation frequencies of spherical degree $\ell =0,1$ and 2 in the domain 15-40 $\mu$Hz with an Eulerian version of the code LOSC (Scuflaire et al. 2008).

In a red giant model, differently from the Sun, non-radial oscillation modes in the frequency domain of solar-like oscillations (Kjeldsen & Bedding 1995) are expected to have a mixed pressure and gravity nature. In the model we considered (see Fig. 3) the spectrum of $\ell = 1$ and 2 modes is mostly populated by modes with a dominant gravity-like behaviour. These modes exhibit a high inertia compared to radial modes, and therefore show surface amplitudes significantly smaller than the purely acoustic radial modes (Eggenberger et al. 2010; Dupret et al. 2009; Christensen-Dalsgaard 2004; Dziembowski et al. 2001). Nonetheless, among this large number of non-radial oscillation modes, few modes are efficiently trapped in the acoustic cavity of the star and have inertias similar to those of radial modes (see Fig. 4).

We then compute $\Delta\nu(\nu)$ and $\Delta_2\nu(\nu)$ by selecting radial modes and the $\ell = 1$ modes corresponding to local minima in the inertia, hence strongly trapped in the acoustic cavity. We find an average value of the large frequency separation of 3.4 $\mu$Hz and clear periodic components in $\Delta\nu(\nu)$ (open squares in Fig. 5) and  $\Delta_2\nu(\nu)$.

The comparison between the model and observed frequency separations clearly supports the interpretation that the periodic component is caused by the local depression in the sound speed in the second helium ionization zone. This feature is well represented by current models that have a mass and radius determined from the periodicity of the component and the average value of the large frequency separation (see Fig. 3).

\begin{figure} \par\includegraphics[width=9cm]{figure/15442fg4.eps} \end{figure} Figure 4:

Mode inertias of radial modes (full dots), $\ell = 1$ modes (asterisks) and $\ell =2$ modes (open triangles) for a 1.2 $M_\odot $ red-giant model.

Open with DEXTER

We notice that the periodic component related to the He second-ionization zone is expected to have an amplitude decaying with frequency, as shown in numerically computed frequencies (open squares in Fig. 5) and in analytical approximations (Monteiro & Thompson 1998; Houdek & Gough 2007). Although current error bars are too large to draw a firm statement, the amplitude of the observed component computed with $\ell =0$ and 1 modes seems to show the expected behaviour, while we notice that the observed $\ell =2$ modes show a larger scatter.

5 Conclusions

In summary, we have shown that the acoustic pulsation modes detected by CoRoT in the red giant star HR 7349 bear the signature of a sharp-structure variation inside the star. Comparison with stellar models allows us to interpret this feature as caused by a local depression of the sound speed occurring in the helium second-ionization region.

\begin{figure} \par\includegraphics[width=9cm]{figure/15442fg5.eps} \par\end{figure} Figure 5:

Open squares represent $\Delta \nu _{n,\ell }$ computed from $\ell =0,1,2$ adiabatic frequencies in a 1.2 $M_\odot $ red giant model. The solid line shows a sinusoidal component with amplitude decreasing with frequency (see Monteiro & Thompson 1998; Houdek & Gough 2007) fitted to the $\ell =0,1$ large separation determined by Carrier et al. (2010) (dots with error bars).

Open with DEXTER

Besides representing the first seismic inference of a local feature in the internal structure of an evolved low-mass star, this detection allows a mass ( M=1.2+0.6-0.4 $M_\odot $) and radius ( R=12.2+2.1-1.8 $R_\odot $) estimate based solely on seismic constraints. Moreover, for this nearby star, we could also check that our radius estimate is compatible with the one based on luminosity and effective temperature ( $R = 12.2 \pm 1.1$ $R_\odot $). This additional test reinforces the proposed interpretation and approach, which could be applied to the thousands of pulsating giants of unknown distance that are currently being observed with the space satellites CoRoT (see Hekker et al. 2009 and; in particular, Fig. 6 in Mosser et al. 2010) and Kepler (Bedding et al. 2010a; Borucki et al. 2010; Gilliland et al. 2010). A reliable seismic estimate of the mass and radius of these stars would represent an essential ingredient for stellar population studies (Miglio et al. 2009) and for characterizing planets orbiting around these evolved distant stars (see e.g. Hatzes & Zechmeister 2007).

We finally recall that the detectability of the signature of He ionization can potentially lead us to a seismic estimate of the envelope helium abundance in old stars. Indeed, as shown for the Sun and solar-like stars, the amplitude of the periodic component depends on the envelope helium abundance (see e.g. Basu et al. 2004; Houdek & Gough 2007, and references therein). While CoRoT and Kepler observations will provide other targets and further reduce the uncertainty on the oscillation frequencies, a thorough study on the required precision in terms of seismic and non-seismic observational constraints, as well as and in terms of models, should be undertaken to aim for reliable seismic estimate of the envelope helium abundance in giants.

Acknowledgements
J.M. acknowledges the Belgian Prodex-ESA for support (contract C90310). F.C. is a postdoctoral fellow of the Funds for Scientific Research, Flanders (FWO).

References

  1. Baglin, A., Michel, E., Auvergne, M., et al. 2006, in Proceedings of SOHO 18/GONG 2006/HELAS I, Beyond the spherical Sun, ESA SP, 624 [Google Scholar]
  2. Ballot, J., Turck-Chièze, S., & García, R. A. 2004, A&A, 423, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Basu, S., Mazumdar, A., Antia, H. M., & Demarque, P. 2004, MNRAS, 350, 277 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bedding, T. R., Huber, D., Stello, D., et al. 2010a, ApJ, 713, L176 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bedding, T. R., Kjeldsen, H., Campante, T. L., et al. 2010b, ApJ, 713, 935 [NASA ADS] [CrossRef] [Google Scholar]
  6. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Carrier, F., De Ridder, J., Baudin, F., et al. 2010, A&A, 509, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Catelan, M. 2009, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]
  9. Christensen-Dalsgaard, J. 2002, Rev. Mod. Phys., 74, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  10. Christensen-Dalsgaard, J. 2004, Sol. Phys., 220, 137 [NASA ADS] [CrossRef] [Google Scholar]
  11. De Ridder, J., Barban, C., Baudin, F., et al. 2009, Nature, 459, 398 [Google Scholar]
  12. Dupret, M., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Dziembowski, W. A., Gough, D. O., Houdek, G., & Sienkiewicz, R. 2001, MNRAS, 328, 601 [NASA ADS] [CrossRef] [Google Scholar]
  14. Eggenberger, P., Miglio, A., Montalban, J., et al. 2010, A&A, 509, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Frandsen, S., Carrier, F., Aerts, C., et al. 2002, A&A, 394, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [NASA ADS] [CrossRef] [Google Scholar]
  17. Girardi, L., & Salaris, M. 2001, MNRAS, 323, 109 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gough, D. O. 1990, Lecture Notes in Physics (Berlin: Springer Verlag), 367, 283 [Google Scholar]
  19. Hatzes, A. P., & Zechmeister, M. 2007, ApJ, 670, L37 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hekker, S., Kallinger, T., Baudin, F., et al. 2009, A&A, 506, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Houdek, G., & Gough, D. O. 2007, MNRAS, 375, 861 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Springer-Verlag) [Google Scholar]
  23. Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
  24. Lee, M. G., Freedman, W. L., & Madore, B. F. 1993, ApJ, 417, 553 [Google Scholar]
  25. Mazumdar, A. 2005, A&A, 441, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Mazumdar, A., & Antia, H. M. 2001, A&A, 377, 192 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Miglio, A., Christensen-Dalsgaard, J., di Mauro, M. P., Monteiro, M. J. P. F. G., & Thompson, M. J. 2003, in Asteroseismology Across the HR Diagram, ed. M. J. Thompson, M. S. Cunha, & M. J. P. F. G. Monteiro, 537 [Google Scholar]
  28. Miglio, A., Montalbán, J., Baudin, F., et al. 2009, A&A, 503, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  29. Monteiro, M. J. P. F. G., & Thompson, M. J. 1998, in New Eyes to See Inside the Sun and Stars, ed. F.-L. Deubner, J. Christensen-Dalsgaard, & D. Kurtz, IAU Symp., 185, 317 [Google Scholar]
  30. Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., & Thompson, M. J. 2000, MNRAS, 316, 165 [NASA ADS] [CrossRef] [Google Scholar]
  31. Mosser, B., & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Mosser, B., Belkacem, K., Goupil, M.-J., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Perez Hernandez, F., & Christensen-Dalsgaard, J. 1998, MNRAS, 295, 344 [NASA ADS] [CrossRef] [Google Scholar]
  34. Roxburgh, I. W., & Vorontsov, S. V. 1998, in New Eyes to See Inside the Sun and Stars, ed. F.-L. Deubner, J. Christensen-Dalsgaard, & D. Kurtz, IAU Symp., 185, 391 [Google Scholar]
  35. Scuflaire, R., Montalbán, J., Théado, S., et al. 2008, Ap&SS, 316, 149 [NASA ADS] [CrossRef] [Google Scholar]
  36. Stello, D., Basu, S., Bruntt, H., et al. 2010, ApJ, 713, L182 [NASA ADS] [CrossRef] [Google Scholar]
  37. Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef] [Google Scholar]
  38. Théado, S., Vauclair, S., Castro, M., Charpinet, S., & Dolez, N. 2005, A&A, 437, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Vandakurov, Y. V. 1967, AZh, 44, 786 [NASA ADS] [Google Scholar]
  40. Ventura, P., D'Antona, F., & Mazzitelli, I. 2008, Ap&SS, 316, 93 [NASA ADS] [CrossRef] [Google Scholar]
  41. Verner, G. A., Chaplin, W. J., & Elsworth, Y. 2006, ApJ, 640, L95 [NASA ADS] [CrossRef] [Google Scholar]
  42. Vorontsov, S. V. 1988, in Advances in Helio- and Asteroseismology, ed. J. Christensen-Dalsgaard, & S. Frandsen, IAU Symp., 123, 151 [Google Scholar]

Footnotes

...[*]
Postdoctoral Researcher, Fonds de la Recherche Scientifique - FNRS, Belgium.
... CoRoT[*]
The CoRoT space mission, launched on December 27th 2006, has been developed and is operated by CNES, with the contribution of Austria, Belgium, Brazil, ESA (RSSD and Science Programme), Germany and Spain.
... exponent[*]
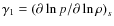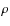$\gamma_1=\left(\partial \ln{p}/\partial \ln{\rho}\right)_s$, where p, $\rho$, and s denote pressure, density, and specific entropy.

All Figures

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figure/15442fg1.eps} \end{figure} Figure 1:

Large separations $\Delta \nu _{n,\ell }$ computed by Carrier et al. (2010) ($\ell =0$: black squares; 1: stars; 2: triangles) are superimposed on the $\Delta \nu _{n,\ell }$ function given by the autocorrelation of the time series (solid thick line). The $\pm $1-$\sigma $ error bars are given by the two adjacent curves; they agree with the error bars of $\Delta \nu _{n,\ell }$. Both $\Delta \nu _{n,\ell }$ and $\Delta \nu _{n,\ell }$ show a periodic modulation with a period of the order of 0.14 Ms. The zebra regions indicate 1-$\Delta \nu $wide frequency ranges. The inset shows the filter used for performing the envelope autocorrelation function, with a full-width at half-maximum $\delta \nu _{{\rm H}}$ equal to 1.4 times the mean value of the large separation.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figure/15442fg2.eps} \end{figure} Figure 2:

a) Behaviour of $\gamma _1$ as a function of t/T in a 1.2 $M_\odot $, 12 $R_\odot $ model: the region where helium undergoes its second ionization induces a local minimum in $\gamma _1$. In the same model the base of the convective envelope is located at $t/T = 2\times 10^{-2}$. b) Location of acoustic glitches in a model of the Sun.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figure/15442fg3.eps} \par\end{figure} Figure 3:

Behaviour of the relative acoustic radius of the second helium ionization region ( $t_{\rm HeII}/T$) as a function of the average large frequency separation in stellar models with different mass (0.7 to 3 $M_\odot $), initial chemical composition (helium mass fraction Y=0.25, 0.278, heavier-elements mass fraction Z=0.02, 0.01), and convection-efficiency parameter ( $\alpha _{\rm MLT}=1.6, 1.9$). The position of HR 7349 in this diagram is represented by the black dot with error bars.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{figure/15442fg4.eps} \end{figure} Figure 4:

Mode inertias of radial modes (full dots), $\ell = 1$ modes (asterisks) and $\ell =2$ modes (open triangles) for a 1.2 $M_\odot $ red-giant model.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{figure/15442fg5.eps} \par\end{figure} Figure 5:

Open squares represent $\Delta \nu _{n,\ell }$ computed from $\ell =0,1,2$ adiabatic frequencies in a 1.2 $M_\odot $ red giant model. The solid line shows a sinusoidal component with amplitude decreasing with frequency (see Monteiro & Thompson 1998; Houdek & Gough 2007) fitted to the $\ell =0,1$ large separation determined by Carrier et al. (2010) (dots with error bars).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.