EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) L8 Full HTML
Free Access
Issue
A&A
Volume 520, September-October 2010
Article Number L8
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201015301
Published online 30 September 2010
A&A 520, L8 (2010)

LETTER TO THE EDITOR

Variations of the spectral index of dust emissivity from Hi-GAL observations of the Galactic plane[*]

D. Paradis1 - M. Veneziani1,2 - A. Noriega-Crespo1 - R. Paladini1 - F. Piacentini2 - J. P. Bernard3,4 - P. de Bernardis2 - L. Calzoletti 5 - F. Faustini5 - P. Martin6 - S. Masi2 - L. Montier3,4 - P. Natoli7 - I. Ristorcelli3,4 - M. A. Thompson8 - A. Traficante7 - S. Molinari9

1 - Spitzer Science Center, California Institute of Technology, Pasadena, CA 91125, USA
2 - Dipartimento di Fisica, Universita di Roma 1 La Sapienza, 00185 Roma, Italy
3 - Université de Toulouse, UPS, CESR, 9 avenue du Colonel Roche, 31028 Toulouse Cedex 4, France
4 - CNRS, UMR 5187, 31028 Toulouse, France
5 - ASI Science Data Center, 00044 Frascati (Rome), Italy
6 - Canadian Institute for Theoretical Astrophysics, University of Toronto, 60 St. George Street, Toronto, ON M5S 3H8, Canada
7 - Dipartimento di Fisica, Universita di Roma Tor Vergata, Rome, Italy
8 - Centre for Astrophysics Research, Science & Technology Institute, University of Hertfordshire, Hatfield, AL10 9AB, UK
9 - INAF - IFSI - via Fosso del Cavaliere 100, Rome, Italy

Received 30 June 2010 / Accepted 13 September 2010

Abstract
Context. Variations in the dust emissivity are critical for gas mass determinations derived from far-infrared observations, but also for separating dust foreground emission from the Cosmic Microwave Background (CMB). Hi-GAL observations allow us for the first time to study the dust emissivity variations in the inner regions of the Galactic plane at resolution below 1$^\circ$.
Aims. We present maps of the emissivity spectral index derived from the combined Herschel PACS 160 $\mu $m, SPIRE 250 $\mu $m, 350 $\mu $m, and 500 $\mu $m data, and the IRIS 100 $\mu $m data, and we analyze the spatial variations of the spectral index as a function of dust temperature and wavelength in the two science demonstration phase Hi-GAL fields, centered at $l=30^\circ $ and $l=59^\circ $.
Methods. Applying two different methods, we determine both dust temperature and emissivity spectral index between 100 and 500 $\mu $m, at an angular resolution ($\theta$) of 4$^{\prime}$.
Results. Combining both fields, the results show variations of the emissivity spectral index in the range 1.8-2.6 for temperatures between 14 and 23 K. The median values of the spectral index are similar in both fields, i.e. 2.3 in the range 100-500 $\mu $m, while the median dust temperatures are equal to 19.1 K and 16.0 K in the $l=30^\circ $ and $l=59^\circ $ field, respectively. Statistically, we do not see any significant deviations in the spectra from a power law emissivity between 100 and 500 $\mu $m. We confirm the existence of an inverse correlation between the emissivity spectral index and dust temperature, found in previous analyses.

Key words: dust, extinction - infrared: ISM

1 Introduction

The large dust grains (big grain component as defined in Désert et al. 1990) dominate the total dust mass, as well as the observed emission in the far-infrared (FIR) domain (Draine & Li 2007). They radiate in thermal equilibrium with the interstellar radiation field, and their emission spectrum, assuming a fixed dust abundance and a single grain size, is well approximated by

\begin{displaymath}I_{\nu}(\lambda) \propto \epsilon_0 \left (\frac{\lambda}{\lambda_0} \right ) ^{-\beta} B_{\nu}(\lambda,T_{\rm d}), \end{displaymath} (1)

where $\rm I_{\nu}(\lambda)$ is the specific intensity or brightness, $B_{\nu}$ is the Planck function, $T_{\rm d}$ is the dust temperature, $\epsilon_0$ is the emissivity at wavelength $\lambda_0$, and $\beta $ is the emissivity spectral index.

Previous observations in the submillimeter (submm), at arcminute resolution, such as those by the balloon-borne experiments PRONAOS (Dupac et al. 2003) and ARCHEOPS (Désert et al. 2008) found evidence of an inverse relationship between $T\rm _d$ and $\beta $ in various environments of the interstellar medium (ISM). In PRONAOS data, variations of the spectral index were observed in the range 2.4 to 0.8 for dust temperatures between 11 and 80 K, whereas ARCHEOPS data showed a more pronounced inverse relationship with $\beta $ values going from 4 to 1 between 7 and 27 K. Recently Veneziani et al. (2010) highlighted a similar trend analyzing $T\rm _d$ and $\beta $ for eight high Galactic latitude clouds, by combining IRAS, DIRBE, and WMAP data with BOOMERanG observations. The $\beta $ values vary from 5 to 1 in the temperature range 7-20 K, with a behavior similar to that derived from ARCHEOPS data. These variations of $\beta $ with dust temperature could be owing to intrinsic properties of amorphous dust grains, as proposed by Mény et al. (2007), but the impact of the noise and the temperature mixing along the line of sight (LOS) must be carefully taken into consideration, before a physical interpretation can be made.Variations of the apparent spectral index in a sample of cores in the Galactic plane have been observed (Hill et al. 2006) using SCUBA and SIMBA. However, because of the restricted wavelength range of their observations, these authors could not attribute them to temperature variations. Moreover, none of the previous analyses allowed the study of the $T_{\rm d} -\beta$ correlation at arcminute scales in the inner regions of the Galactic plane. Thanks to the Herschel Hi-GAL data ( $\theta=37^{\prime \prime}$, 2 $^\circ \times 2 ^\circ$ maps, centered in the Galactic plane at $l=30^\circ $ and $l=59^\circ $, see Molinari et al. 2010a, b), we can now extend for the first time this type of analysis to the inner Galactic plane, and on continuous fields of diffuse emission. An overview of the Herschel instruments is given in Pilbratt et al. (2010). In this paper we analyze emissivity variations between 100 and 500 $\mu $m. We then derive both the dust temperature and spectral index from Eq. (1), assuming a single temperature along the LOS. This assumption is relatively correct for the $l=59^\circ $ field, where there is less contamination along the LOS in comparison with the $l=30^\circ $ field. Indeed, the LOS toward the inner $l=30^\circ $ field crosses several regions with a presumably wider range of temperatures. An accurate temperature determination requires sampling both sides of the emission peak. The 70 $\mu $m brightness is generally contaminated by out-of-equilibrium emission from very small grains (VSGs) and cannot be used to derive thermal dust temperature without an accurate subtraction of this component. This contribution has been investigated by Compiegne et al. (2010). Therefore we include the IRAS data at 100 $\mu $m in our analysis, for which we estimate an average VSG contamination of less than 10%. This implies degrading the original resolution of the Hi-GAL data by adopting the IRAS angular resolution of 4$^{\prime}$. We note, as a consequence, an averaging effect within the resolution element, which also needs to be taken into account in the interpretation of the results of the present analysis.

\begin{figure} \par\includegraphics[width=14.7cm]{fig_new/15301fig1.eps} \end{figure} Figure 1:

Left: spectral index in the 100 to 500 $\mu $m range, versus dust temperature for each SDP field, combining IRIS 100 $\mu $m with PACS 160 and SPIRE 250, 350 and 500 $\mu $m data, using the least-square fit method in red and the MCMC method in blue. Middle and right: spatial distribution of the emissivity spectral index and reduced $\chi ^2$, respectively, derived from the least-square fit method, for each SDP field.

Open with DEXTER

One of the key aspects in the analysis of CMB is the ability to separate its emission from the other astrophysical foregrounds (including thermal dust) through multifrequency observations. While it is not easy to achieve successful component separation over the Galactic plane, determining the dust spectral index variations across the sky can efficiently help in reducing the number of unknowns in the problem (Ricciardi et al. 2010).

2 Data

We use the ROMAGAL Herschel PACS and SPIRE maps described in Traficante et al. (in prep.), combined with the IRIS (Improved Reprocessing of the IRAS Survey, see Miville-Deschênes & Lagache 2005) 100 $\mu $m data. Multiplicative factors (0.78,1.02, 1.05 and 0.94 at 160, 250, 350 and 500 $\mu $m, respectively) have been applied to the data (Swinyard et al. 2010; Griffin et al. 2010; Poglitsch et al. 2010). An absolute calibration accuracy of 20% and 15% for PACS and SPIRE has been adopted. We applied the offsets given in Bernard et al. (2010)[*]. All maps have been convolved with a Gaussian kernel, with a FWHM of 4$^{\prime}$, i.e. equal to the IRIS 100 $\mu $m angular resolution. In addition, the maps have been rebinned on a uniform grid with a pixel size of 1.65$^{\prime}$. The IRIS 100 $\mu $m calibration uncertainty is taken to be 13.5% (see Miville-Deschênes & Lagache 2005).

\begin{figure} \par\includegraphics[width=13.cm]{fig_new/15301fig2.eps} \end{figure} Figure 2:

Representative SEDs combining IRIS 100 $\mu $m with PACS 160 $\mu $m and SPIRE 250, 350 and 500 $\mu $m, modeled by the gray-body law with $T\rm _d$ and $\beta $ derived from the least-square fit method between 100 and 500 $\mu $m ( left and central panels), and between 100 and 350 $\mu $m ( right panel).

Open with DEXTER

3 Variations of the emissivity spectral index with temperature

We use two different methods for the simultaneous derivation of the dust temperature and the emissivity spectral index. Both allow us to fit the data with a modified blackbody function (see Eq. (1)). In the first method we perform an $\chi ^2$ minimization, applying the same code as described in Dupac et al. (2001), using the IDL least-square fit curvefit function to deduce the $T\rm _d$ and $\beta $ parameters, as well as their 1$\sigma$ uncertainties. The second method estimates the best-fit parameters by looking for the maximum likelihood, using a Monte Carlo Markov Chain (MCMC) algorithm (Lewis & Bridle 2002) and represents a bayesian approach to parameter estimation. The posterior distribution for the parameters is sampled by using the Metropolis-Hastings algorithm, and a maximum likelihood estimate is derived jointly for $\beta $ and $T_{\rm d}$. We chose a wide flat a priori probablity density of the parameters, i.e. 0 K $ < T_{\rm d} < 60$ K and - $1 < \beta < 5$, in order not to constrain the fit results. A benefit of this method is that it also recovers the joint posterior distribution of the two estimated parameters. We make use of this feature to explore the $T_{\rm d}$-$\beta $ correlation as explained below.

We fit the spectral energy distribution (SED) between 100 and 500 $\mu $m for each pixel of the maps, using both methods. The color correction is computed iteratively in all channels. Results of the $T_{\rm d}$-$\beta $ determination for each field are shown in Fig. 1. Only pixels with a surface brightness at 500 $\mu $m higher than 105 MJy/sr and 50 MJy/sr for the $l=30^\circ $ and $l=59^\circ $ fields, respectively, have been considered. Both methods show a clear anti-correlation $T_{\rm d}$-$\beta $ in each field. These two independent methods also highlight a good agreement. The $\beta $ values range from $\simeq $2.6 to $\simeq $1.9 for temperatures between 17.5-23 K for the $l=30^\circ $ field, and from $\simeq $2.7 to $\simeq $1.8, between 14 and 21 K, for the $l=59^\circ $ field. The assumption made of a single temperature along the LOS may hold in the $l=59^\circ $ field, but is certainly too simplistic for the $l=30^\circ $ field, since temperature variations along the LOS are larger in the inner field (see Bernard et al. 2010). The analysis of the $l=30^\circ $field would certainly require an accurate combination of temperatures and column densities. However, our methods do not allow the simultaneous fitting of a complex mixture of spectra. Even if the $l=30^\circ $ field is potentially characterized by several grain temperatures along the LOS (associated to Sagittarius, Scuttum-Crux and Perseus, as described in Bernard et al. 2010), and therefore could induce a spurious $T_{\rm d}$-$\beta $ inverse correlation (Masi et al. 1995; Shetty et al. 2009), the $l=59^\circ $ field, less contaminated by various dust mixing effects, still highlights a pronounced behavior in the $T_{\rm d}$-$\beta $ parameter space. Both fields, with a different mixture of temperatures, present a $T_{\rm d}$-$\beta $ anti-correlation. We therefore interpret this as an indication that the mixture of temperatures is probably not the dominant responsible effect for the observed anti-correlation.

The spatial distribution of $\beta $ is shown in Fig. 1. Warmer regions, which most often correspond to bright regions, show lower beta values. However, the $l=59^\circ $ field presents a gradient along the East-West direction, which is not observed in the PACS or SPIRE surface brightness maps. The stripes visible in the maps are associated to low-level residual stripes in the IRIS data. In the $l=59^\circ $ field, $\beta $ values higher than 2.6 located at $l=57^\circ$48$^{\prime}$, $b=-0^\circ$20$^{\prime}$ correspond to one of the less active star-forming regions, although the PACS 160 data show an artifact at this location, disclosed by a high $\chi ^2$(see Fig. 1). In the same field, the lowest $\beta $ values ($\leq$1.8) are found for an HII region, with a bright source nearby at $l=59^\circ $38$^{\prime}$, $b=+0^\circ$38$^{\prime}$. Representative examples of SEDs with a gray-body fit are presented in Fig. 2, illustrating the agreement between the data and the model.

The two parameters $T_{\rm d}$-$\beta $ are degenerate in the parameter space, creating a spurious inverse relation (Shetty et al. 2009) that has to be considered while investigating if an intrinsic physical correlation indeed exists. In order to properly estimate the relationship between $T_{\rm d}$ and $\beta $, we have to take into account the correlation that is shown by the spectral shape in Eq. (1) and caused by calibration uncertainties. One way to include the effect of the degeneracy is to estimate this effect not only for the $T_{\rm d}$-$\beta $ best-fit values but for points included in the 68% contours of the two-dimensional posterior probability obtained with the MCMC method. Within the 68% contours the points are not uniformly distributed, but their density is higher close to the maximum of the probability, increasing their weight, and lower close to the boundaries. Assuming the model $\beta = A(T_{\rm d}/20~{\rm K})^{-\alpha}$, between 100 and 500 $\mu $m in both fields, the fit is then performed on all the $T_{\rm d}$-$\beta $ couples inside a posteriori probability contour of each pixel, chosen randomly, one for each pixel and weighted as described. We then take a point within the contour for each pixel of the map and fit the trend to estimate the A and $\alpha$ parameters. We repeat this procedure until we obtain a good sampling of the shape of the distribution of posterior probabilities. This method has been successfully tested on BOOMERanG data (Veneziani et al. 2010) and allows us to include the effects of degeneracy in the error bars. The resulting A and $\alpha$ ditributions are well approximated by Gaussian functions, even if a slight asymmetry is present. The center of the Gaussian is the more likely value, while the error is estimated by marginalizing over the other parameter. The best-fit values so obtained are

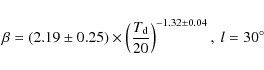
\begin{displaymath}\beta=(2.19 \pm 0.25) \times \left(\frac{T_{\rm d}}{20} \right) ^{-1.32 \pm 0.04}, ~l =30^\circ \end{displaymath} (2)

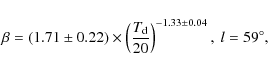
\begin{displaymath}\beta=(1.71\pm0.22) \times \left( \frac{T_{\rm d}}{20} \right) ^{-1.33\pm0.04}, ~ l =59^\circ, \end{displaymath} (3)

Figure 3 shows the results of the fitting method over the probability 68% contours with only a few pixels out of $\sim$3500 contours for clarity. The best-fit Hi-GAL $T_{\rm d}$-$\beta $ relation is plotted, as well as the ARCHEOPS, BOOMERanG, and PRONAOS ones for comparison.
\begin{figure} \par\includegraphics[width=6.2cm]{fig_new/15301fig3.eps} \vspace*{2.5mm} \end{figure} Figure 3:

$T_{\rm d}$-$\beta $ two-dimensional 68% contour posterior probabilities derived from the MCMC method, shown for $\simeq $15-25 pixels for the two SDP fields. The overplotted lines correspond to Hi-GAL (solid red and blue lines for the $l=30^\circ $ and $l=59^\circ $ fields, respectively), ARCHEOPS (dashed line), BOOMERanG (line with circles) and PRONAOS (line with squares) best-fits, respectively. The $T_{\rm d}$-$\beta $ relationship is estimated over all points within the contours. The gray points correspond to the $T_{\rm d}$-$\beta $ data points derived from the MCMC method (see Fig. 1, left panels).

Open with DEXTER
Our results highlight a steeper $T_{\rm d}$-$\beta $ law in the inner Galactic plane in both fields than in external regions and high latitude clouds observed with ARCHEOPS and BOOMEranG. Whereas the wavelength range covered by PRONAOS is almost the same as that of Herschel, the $T_{\rm d}$-$\beta $ relation ( $\beta=1/(\delta+\omega T_{\rm d})$) is flatter, with $\beta $values going from 2.0 to 1.7, in the range 13-26 K. These results could indicate different dust properties in the inner Galactic plane, as compared to the outer galaxy observed with ARCHEOPS, the solar neighborhood observed with PRONAOS, and high latitude clouds observed with BOOMEranG. We therefore think that these different $T_{\rm d}$-$\beta $ relations could be caused by changes in dust properties with the environments.

4 Variations of the emissivity spectral index with wavelength

In the previous section we have found evidence of spectral index variations with temperature. As predicted by Mény et al. (2007), a flattening of the emissivity spectrum (and so a lower $\beta $) is expected for wavelengths longer than 500 $\mu $m as a consequence of the internal structure of the grains. Recently, Gordon et al. (2010) highlighted an emission excess at 500 $\mu $m in the Large Magellanic Cloud that could be of the same origin. However, this excess is of about 10%, which is lower than the SPIRE calibration uncertainties of 15%. The Herschel data do not allow us to study emissivity variations at longer wavelengths than 500 $\mu $m.

Although the SEDs in each field (left and central panel of Fig. 2) do not provide evidence for any departures from a power law, we analyze the possibility of an emissivity excess at 500 $\mu $m. To properly perform this study, the temperature estimates need to be done independently of the 500 $\mu $m data. Therefore we have redone the $T_{\rm d}$ and $\beta $ determination with the least-square fit method using only data between 100 and 350 $\mu $m, and we compare the emission at 500 $\mu $m with the value predicted by extrapolating the emissivity power law between 100 and 350 $\mu $m. The predicted values are systematically lower than the data at 500 $\mu $m in both fields, by 16% in $l=30^\circ $ and 13% in $l=59^\circ $, which could favor the hypothesis of an emissivity excess at this wavelength. These values are not significant compared to the uncertainties on the SPIRE data. Moreover, we suspect that the PACS 160 $\mu $m data suffer from calibration issues, as discussed in Bernard et al. (2010). The calibration uncertainty at 160 $\mu $m does not impact the results of the global analysis described above, but here the limitation of the wavelength range (100-350 $\mu $m) removes some constraints on the fit, resulting in an overestimate with respect to the data at 250 $\mu $m, and an underestimate at 500 $\mu $m (see Fig. 2, right panel). However, if we slightly shift down the 160 $\mu $m data points, the apparent underestimate at 500 $\mu $m would disappear. For this reason, we do not claim that this excess is real and we think instead that the emissivity spectra are relatively constantbetween 100 and 500 $\mu $m with similar median $\beta $ values in both fields, i.e. 2.3, even if the median temperature is statistically lower in the $l=59^\circ $ field ( $T_{\rm d} \simeq 19.1$ K for $l=30^\circ $ and $T_{\rm d} \simeq 16.0$ K for $l=59^\circ $).

5 Conclusions

We investigated variations in the spectral index of the dust emissivity, with temperature and wavelength, in the inner Galactic plane, using the new Herschel observations in two Hi-GAL fields, centered at $l=30^\circ $ and $l=59^\circ $, acquired during the Herschel Science Demonstration phase, combined with the IRIS 100 $\mu $m data. We fitted the SEDs for each pixel of the two fields with two independent methods, deriving simultaneously the emissivity spectral index and the dust temperature by adjusting a modified blackbody function to the data. The results are similar with both methods. Using a Monte Carlo Markov Chain algorithm method we computed the 68% likelihood contours for each point. We find a $T_{\rm d}$-$\beta $ inverse correlation, with the local variation going from 1.8 to 2.6 for temperatures between 14 and 23 K, shown for the first time in the inner Galactic plane. Moreover, our results indicate a different trend with respect to previous investigations based on BOOMERanG, ARCHEOPS, and PRONOAS data, probably because of different dust properties in the inner Galactic plane compared to other environments. An extensive follow-up analysis will be required to take into consideration the mixture of temperatures along the line of sight. The median value of $\beta $ is similar in both fields, equal to 2.3, slightly higher than the usual reference value of 2. We do not favor the hypothesis of an emissivity excess at 500 $\mu $m, as suggested for the Large Magellanic Cloud. A complementary forthcoming study will combine Planck with Herschel data to investigate possible changes in the dust emissivity spectrum at wavelengths larger than 500 $\mu $m, as reported in previous studies of dust emission in our Galaxy.

Acknowledgements
Data processing and maps production have been possible thanks to ASI generous support via contract I/038/080/0. M.V. is grateful to Davide Pietrobon for software support.

References

  1. Bernard, J.-P., Paradis, D., Marshall, D., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Compiegne, M., Flagey, N., Noriega-Crespo, et al. 2010, ApJ, submitted [Google Scholar]
  3. Désert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
  4. Désert, F.-X., Macías-Pérez, J. F., Mayet, F., et al. 2008, A&A, 481, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
  6. Dupac, X., Giard, M., Bernard, J.-Ph., et al. 2001, ApJ, 553, 604 [Google Scholar]
  7. Dupac, X., Bernard, J.-Ph., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Gordon, K., Galliano, F., Hony, S., et al. 2010, A&A, 518, 89 [Google Scholar]
  9. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
  10. Hill, T., Thompson, M. A., Burton, M. G., et al. 2006, MNRAS, 368, 1223 [NASA ADS] [CrossRef] [Google Scholar]
  11. Lewis, A., & Bridle, S. 2002, Phys. Rev., 66, 103511 [Google Scholar]
  12. Masi, S., Aquilini, E., Boscaleri, A., et al. 1995, ApJ, 452, 253 [NASA ADS] [CrossRef] [Google Scholar]
  13. Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
  14. Mény, C., Gromov, V., Boudet, N., et al. 2007, A&A, 468, 171 [Google Scholar]
  15. Miville-Deschênes, M. A., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
  16. Molinari, S., Swinyard, B., Bally, J., et al. 2010a, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
  17. Molinari, S, Swinyard, B., Bally, J., et al. 2010b, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  19. Poglitsch, A., Waelkens, A., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Ricciardi, S., Bonaldi, A., Natoli, P. et al. 2010, MNRAS, 406, 1644 [NASA ADS] [Google Scholar]
  21. Shetty, R., Kauffmann, J., Schnee, S., et al. 2009, ApJ, 696, 2234 [NASA ADS] [CrossRef] [Google Scholar]
  22. Stepnik, B., Abergel, A., Bernard, J. P., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Swinyard, B. M., Ade, P., Baluteau, J. P., et al. 2010, A&A, 518, L4 [Google Scholar]
  24. Veneziani, M., Ade, P. A. R., Bock, J. J., et al. ApJ, 2010, 713, 959 [Google Scholar]

Footnotes

... plane[*]
Herschel is an ESA space observatory with science instruments provided by European-led Principal investigator consortia and with important participation from NASA.
...Bernard et al. (2010)[*]
See their Table 1

All Figures

  \begin{figure} \par\includegraphics[width=14.7cm]{fig_new/15301fig1.eps} \end{figure} Figure 1:

Left: spectral index in the 100 to 500 $\mu $m range, versus dust temperature for each SDP field, combining IRIS 100 $\mu $m with PACS 160 and SPIRE 250, 350 and 500 $\mu $m data, using the least-square fit method in red and the MCMC method in blue. Middle and right: spatial distribution of the emissivity spectral index and reduced $\chi ^2$, respectively, derived from the least-square fit method, for each SDP field.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=13.cm]{fig_new/15301fig2.eps} \end{figure} Figure 2:

Representative SEDs combining IRIS 100 $\mu $m with PACS 160 $\mu $m and SPIRE 250, 350 and 500 $\mu $m, modeled by the gray-body law with $T\rm _d$ and $\beta $ derived from the least-square fit method between 100 and 500 $\mu $m ( left and central panels), and between 100 and 350 $\mu $m ( right panel).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.2cm]{fig_new/15301fig3.eps} \vspace*{2.5mm} \end{figure} Figure 3:

$T_{\rm d}$-$\beta $ two-dimensional 68% contour posterior probabilities derived from the MCMC method, shown for $\simeq $15-25 pixels for the two SDP fields. The overplotted lines correspond to Hi-GAL (solid red and blue lines for the $l=30^\circ $ and $l=59^\circ $ fields, respectively), ARCHEOPS (dashed line), BOOMERanG (line with circles) and PRONAOS (line with squares) best-fits, respectively. The $T_{\rm d}$-$\beta $ relationship is estimated over all points within the contours. The gray points correspond to the $T_{\rm d}$-$\beta $ data points derived from the MCMC method (see Fig. 1, left panels).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.