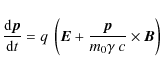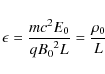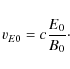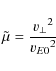EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) A105 Full HTML
Free Access
Issue
A&A
Volume 520, September-October 2010
Article Number A105
Number of page(s) 8
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201014964
Published online 11 October 2010
A&A 520, A105 (2010)

Scaling of particle acceleration in 3D reconnection at null points

P. K. Browning1 - S. Dalla1,2 - D. Peters1 - J. Smith1

1 - Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, Manchester M13 9PL, UK
2 - Jeremiah Horrocks Institute, University of Central Lancashire, Preston PR1 2HE, UK

Received 10 May 2010 / Accepted 9 July 2010

Abstract
Context. The strong electric fields associated with magnetic reconnection are likely to be responsible for the presence of high energy protons and electrons observed in solar flares. There is much evidence for 3D reconnection in the solar corona, and we discuss particle acceleration at 3D reconnection sites. The simplest configuration for 3D reconnection is at a 3D null point, where reconnection can take place in spine and fan modes.
Aims. The aim is to understand the properties of accelerated particles generated by 3D magnetic reconnection, using a test particle approach, and thus contribute to understanding the origin of high energy protons and electrons in solar flares. We analyse the properties of electrons in the magnetic configuration we previously used to study protons. In addition, we discuss the dependence of the particle properties on the parameters of the reconnection, such as strengths of electric and magnetic fields.
Methods. A theoretical framework is presented which can be used to interpret particle acceleration at 3D null points, and which shows how strong acceleration can arise. We also use a test particle approach to calculate particle trajectories in simple model 3D reconnecting nulls. A modified guiding-centre approach is used for electrons, whilst the full equation of motion is solved for protons.
Results. Most particle acceleration takes place when particles closely approach the spine or fan, and we have derived scalings for the sizes of the localised regions in which strong acceleration occurs. The energy spectra of protons and electrons are compared, and it is shown that the spatial distribution of accelerated electrons differs from protons. A significant number of trapped, high-energy particles can be generated, which may be observed as coronal HXR sources. The effectiveness of acceleration increases with the electric-field magnitude, and decreases with magnetic-field magnitude.
Conclusions. Both protons and electrons can be effectively accelerated at 3D reconnecting null points. The particle properties depend on the geometry and field parameters, so that, in principle, the field configuration may be inferred from observed properties of particles.

Key words: Sun: particle emission - Sun: X-rays, gamma rays - magnetic reconnection - Sun: flares - Sun: corona

1 Introduction

The role of electric fields associated with magnetic reconnection as accelerators of charged particles is a subject of growing interest. The basic idea is that the strong super-Dreicer electric fields, intrinsic to magnetic reconnection, can directly accelerate charged particles. A major motivation for such studies is to provide an explanation for the large numbers of high energy charged particles inferred from observations of solar flares, particularly in the light of recent observations from RHESSI (e.g. Lin et al. 2003). The presence and properties of accelerated charged particles are also important as a diagnostic of reconnection, since it is virtually impossible to observe the process of reconnection of magnetic field lines in the solar corona directly. Furthermore, magnetic reconnection has been proposed as a particle accelerator in many other contexts: including fusion plasmas (Helander et al. 2002), the Earth's magnetosphere, the heliopause (Lazarian & Opher 2009), microquasars (De Gouevia Dal Pino & Lazarian 2005), pulsars (De Gouevia Dal Pino & Lazarian 2000) and jets in AGNs (Birk et al. 2001). The acceleration of charged particles at magnetic reconnection sites has been widely studied, especially in 2D configurations such as magnetic X points, with and without a ``guide field'', and current sheets (e.g.: Litvinenko 1996; Zharkova & Gordovksyy 2005; Deeg et al. 1991; Vekstein & Browning 1997; Browning & Vekstein 2001; Hannah & Fletcher 2006; Wood & Neukirch 2005). Clearly, such 2D models are highly idealised and 3D configurations are more representative of nature; 3D reconnection is a subject of growing interest, and it is clear that there are distinct qualitative differences between 2D and 3D reconnection (e.g. Birn & Priest 2007).

A natural first step to understanding particle acceleration in the latter is to consider the (arguably) simplest 3D reconnection geometry: a 3D magnetic null point. This is also the most obvious generalisation of the widely-studied 2D X-point. It is becoming clear that 3D null points should be quite ubiquitous in the solar corona; for example, significant numbers of magnetic nulls have been calculated to exist in Quiet Sun fields extrapolated from magnetograms (Longcope & Parnell 2009) and simulations of emerging flux predict a surprisingly large number of null points (Maclean et al. 2009). Several observations of solar flares are suggestive of the presence of reconnection at 3D nulls (Filippov 1999; Aulanier et al. 2000; Fletcher et al. 2001; Des Jardins et al. 2009) and there is also evidence of reconnecting 3D nulls in the Earth's magnetosphere (Xiao et al. 2006). The topology of a 3D null has a spine curve and a fan plane (Lau & Finn 1990), corresponding to the separatrix lines of a 2D X-point. Reconnection may occur in two modes, known as spine or fan reconnection, involving strong current concentrations at the spine or fan, respectively (Priest & Titov 1996).

Particle acceleration in reconnecting fields may be very usefully studied using the test particle approach, in which the equation of motion

\begin{displaymath} \frac{{\rm d} \vec{p}}{{\rm d}t} =q~ \left( \vec{E} + \frac{ \vec{p}}{m_0 \gamma ~ c} \times \vec{B}\right) \end{displaymath} (1)

(or its non-relativistic limit) is solved in given background electromagnetic fields $\vec{E}$ and $\vec{B}$; here, $\vec{p}$ is the particle momentum, m0 the rest mass, q the charge, $\gamma$ the Lorentz factor and c the speed of light. This approach has been extensively used for 2D fields (see references cited above). Previously, we analysed trajectories of single particles (Dalla & Browning 2005, hereafter referred to as Paper I) and of a population of protons (Dalla & Browning 2006, Paper II) in the fields characteristic of spine reconnection at a 3D null point, and have more recently considered also fan reconnection (Dalla & Browning 2008, Paper III).

The magnetic field at a simple current-free null is given by

              Bx = B0   x/L (2)
By = B0 L   y/L (3)
Bz = - 2   B0   z/L (4)

where L is the global field length scale and B0 is the magnetic field strength near the boundary of the reconnection site (see Fig. 1). The model electric fields investigated, for both spine and fan reconnection are given by Priest & Titov (1996) (see also Papers I-III for expressions for $\vec{E}$). Note that the model electromagnetic fields apply only to the outer ``ideal'' reconnection region, and actually diverge as the spine line or fan plane (according to the mode of reconnection) is approached; we remove these divergences by applying a cut-off close to the spine/fan (see Papers I and III). More realistically, the electromagnetic fields in these localised regions should be calculated invoking resistivity or other non-ideal effects; in these regions, particles may also be accelerated directly by parallel electric fields. Nevertheless, the volume of these ``dissipation'' regions is very small, and the proportion of particles reaching them is thus very low: hence, the energy spectra obtained should be unaffected by their neglect, except for a few particles in the high energy tail.

\begin{figure} \par\includegraphics[width=9cm,clip]{14964fg1.eps} \end{figure} Figure 1:

The configuration at the 3D null point showing typical fieldlines, the null point, the spine (coinciding with the z axis in the coordinate system used here) and the fan (coinciding with the xy plane).

Open with DEXTER

The global electromagnetic fields are quantified by the strength of the magnetic fields and electric fields at the global scale (the edge of the reconnection region), B0 and E0 respectively, and the typical global length-scale L. Clearly particle behaviour will also depend on the species charge q and mass m; usually, we consider protons or electrons, so q = e. Hitherto, we have presented results for particle acceleration mainly for a single set of parameters for the reconnecting electromagnetic fields, representative of the solar corona. The aim of this paper is to gain an overview of the previous results and to determine the effect of varying the electromagnetic fields, as well as considering different particle species. In previous work, we analysed only protons, but here we will also consider electrons, and investigate the extent to which the efficacy of acceleration is species-dependent.

In Sect. 3 of this paper, we thus consider a population of electrons and calculate their trajectories for the same electromagnetic fields previously used for protons. Numerical integration of electron trajectories is much more demanding than that for protons. This is because the time-scale characterising the electron gyromotion, the electron gyroperiod, is 1837 times smaller than for protons, requiring a much smaller integration time-step than in the proton case. The full orbit approach that we adopted previously, in order to be able correctly to describe particle motion in the dissipation region, becomes prohibitively time-consuming in the case of electrons. For this reason, gyro-averaged equations for particle motion were derived and electron trajectories obtained by integrating them everywhere except in a small region in which the adiabatic description for electrons fails, and the full Lorentz equations are solved.

The purpose of the present paper is to analyse fully how acceleration at a reconnecting 3D null point varies with particle species and with the magnitudes of the governing electromagnetic fields. Although we specifically use the idealised model fields of Priest & Titov (1996), the results should be quite generic. We focus mainly on spine reconnection; however, the scalings will apply equally to fan reconnection, and the differences between spine and fan modes have already been discussed in Paper III. Essentially, this paper completes our study of particle acceleration in the Priest and Titov electromagnetic fields, and provides a very useful framework for undertaking and interpreting test particle studies in more realistic field configurations. In Sect. 2, we consider all the governing variables and relevant dimensionless parameters, and analyse how these are expected to affect the acceleration process. This sets up a theoretical framework for interpretation of our numerical results on particle acceleration at 3D nulls, which is also applicable to more complex and realistic 3D null point model fields. Section 3 considers electron acceleration, and compares this with our previous studies of protons. Numerical results demonstrating the scaling of the particle acceleration process with the parameters of the external fields are presented in Sect. 4. Conclusions are presented in Sect. 5.

2 Parameters and scalings

In order to interpret numerical results on particle orbits, it is very useful first to consider the relevant dimensionless parameters and how these affect the particle behaviour. Following Burkhart et al. (1990), Vekstein & Priest (1995) and Vekstein & Browning (1997), who considered particle acceleration in 2D reconnecting fields, we can identify two basic parameters which are equally relevant to 3D configurations. Firstly, the degree of magnetisation at the global scale is quantified by

\begin{displaymath} \epsilon= \frac{m c^2 E_0} {q {B_0}^2 L} = \frac{\rho_0}{L} \end{displaymath} (5)

where $\rho_0$ is the Larmor radius of a particle with perpendicular velocity equal to the global electric drift speed vE0, given by:

\begin{displaymath}v_{E0} = c \frac{E_0}{B_0}\cdot \end{displaymath} (6)

If $\epsilon \ll 1$, which is always the case for any parameters representing the solar corona on global length-scales, the particles are strongly magnetised and can be well modelled by a guiding-centre approach. However, as seen below, even if particles are strongly-magnetised globally, non-adiabatic behaviour may develop on local scales.

Secondly, the strength of the driving electric field is quantified by the parameter

\begin{displaymath} \tilde{\mu} = \frac{{v_{\perp}}^2}{{v_{E0}}^2} \end{displaymath} (7)

where $v_{\perp}$ is the perpendicular speed associated with the gyro-motion, which for a distribution of particles may be equated to the thermal speed of the plasma. The nomenclature indicates that this can also be expressed as the dimensionless magnetic moment when speeds are normalised to the global drift speed (vE0):

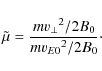
\begin{displaymath}\tilde{\mu} = \frac{m {v_{\perp}}^2/2B_0}{m {v_{E0}}^2/2B_0}\cdot \end{displaymath} (8)

If the electric drift at global length scales is strong compared with the thermal gyro-motion ( $\tilde{\mu} \ll 1$), we are in the strong-drift regime, corresponding to fast reconnection; in practice, this regime is reached when $\tilde{\mu} \approx 1$ (Vekstein & Browning 1997). In this case, particles may undergo strong acceleration due to the electric drift and there is significant motion across the field (see Papers I-III). In the converse case ( $\tilde{\mu} > 1$), particles mainly follow fieldlines with a weak cross-field drift (the more familiar text-book case).

Expressing $v_{E0} = M_i v_{\rm A}$, where Mi is the magnetic Mach number of the reconnection inflow and $v_{\rm A}$ is the Alfven speed at global scales, we can also write

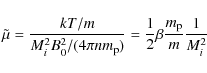
\begin{displaymath}\tilde{\mu} = \frac{k T/m}{M_i^2 B_0^2/(4 \pi n m_{\rm p})} = \frac{1}{2} \beta \frac{m_{\rm p}}{m} \frac{1}{M_i^2} \end{displaymath} (9)

where n is density, T is temperature and $\beta = 2n k T/B_0^2$ is the usual plasma beta. While Mi is always less than 1, $\beta$ is also small in the solar corona; it can be seen that the strong-drift regime requires $M_i > \beta^{-1/2}$ for protons, with a stronger condition, $M_i > \frac{m_{p}}{m_{e}}\beta^{-1/2}$, for electrons. Similarly (see Browning & Vekstein 2001), we can express

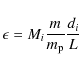
\begin{displaymath}\epsilon = M_i \frac{m}{m_{\rm p}} \frac{d_i}{L} \end{displaymath} (10)

where $d_i =c/\omega_{p,i}$ is the ion skin depth. Note that both $\epsilon$and $\tilde{\mu}$ are species dependent.

In the case of 2D magnetic null points, it has been shown (e.g. Vekstein & Priest 1995; Burkhart et al. 1990) that the condition of strong magnetisation breaks down in the vicinity of the X-point, in a region of size $r* \approx \epsilon^{1/3} L$. This defines the size of the unmagnetised region, which arises since the Larmor radius becomes increasingly large as the magnetic field approaches zero. This limiting length-scale can be derived either by equating the local gyro-frequency of the particles ( $\omega_{\rm L}(r*)$) to the local electric drift time ( vE0(r*)/r*), or by equating the inertial term in the equation of motion to the electric field acceleration. Within the unmagnetised region, particles are directly accelerated by the electric field. This may also be intepreted in terms of the magnitude of the electric field: even the strong-electric-field guiding-centre theory presented by Northrop (1963) is valid only if the perpendicular electric field is zeroth-order or less (with reference to the relevant small parameter, which is the dimensionless Larmor radius), and hence breaks down if $E_{\perp}$ becomes of larger magnitude.

What is the equivalent condition for reconnection at 3D nulls? Whilst particles can become unmagnetised near the null, as at 2D X-points, due to the reducing magnetic field strength, they can also become unmagnetised near the spine curve or fan plane, due to the increasing drift speed. The spine and fan regimes must be considered separately. In each case, we define $\delta$ (corresponding to r* of the 2D case) to be the length-scale of the unmagnetised region; this is found from the condition

\begin{displaymath} \delta \omega_{\rm L}(\delta) \approx v_{E}(\delta), \end{displaymath} (11)

where $\omega_{\rm L} = e\ B/c\ m$ is the local Larmor frequency and $v_E(\delta)$ is the local electric drift speed. Near a 3D null, we have

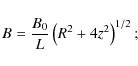
\begin{displaymath}B = \frac{B_0}{L} \left(R^2 + 4z^2\right)^{1/2}; \end{displaymath} (12)

here, R is a cylindrical radial coordinate.

For spine reconnection, consider first particles which are approaching the spine (the z axis) but are still far from the null ( $z = {\rm O}(1)$). Thus $B \approx B_0 = {\rm O}(1)$ while $E \sim E_0 L/R$; hence $v_E \sim cE_0 L/B_0 R$. The condition (11) becomes

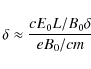
\begin{displaymath}\delta \approx \frac{c E_0 L/B_0 \delta}{e B_0/c m} \end{displaymath} (13)

\begin{displaymath}\Rightarrow \delta \sim L \epsilon^{1/2}. \end{displaymath} (14)

However, if particles approach the null itself (so $z \sim R$), then $B \sim B_0 r/L$, where now the spherical radius (or distance from the null) $r \sim z \sim R$tends to zero. In this case,

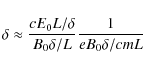
\begin{displaymath}\delta \approx \frac{c E_0 L/ \delta}{B_0 \delta/L } \frac{1}{e B_0 \delta/c m L} \end{displaymath} (15)

\begin{displaymath}\Rightarrow \delta \sim L \epsilon^{1/4}. \end{displaymath} (16)

Hence the unmagnetised region is a narrow cylindrical region around the spine, given by $R \le \delta \approx L \epsilon^{1/2}$, bulging out into a larger sphere near the null, $r \le \delta \approx L \epsilon^{1/4}$.

For the fan reconnection regime, the scaling of the electric drift speed is

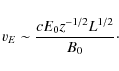
\begin{displaymath}v_E \sim \frac{c E_0 z^{-1/2} L^{1/2}}{B_0}\cdot \end{displaymath} (17)

Following similar arguments to above, it can be shown that the particles become unmagnetised if they approach the fan plane within a distance

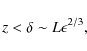
\begin{displaymath}z < \delta \sim L \epsilon^{2/3}, \end{displaymath} (18)

or within a spherical region around the null, so that the distance from the null is

\begin{displaymath}r < \delta \sim L \epsilon^{2/7}. \end{displaymath} (19)

Particle acceleration can thus happen in two ways. Firstly, as discussed by Vekstein & Browning (1997), the streamline curvature and non-uniformity of the $\vec{E} \times \vec{B}$ drift can lead to particle acceleration and gains in parallel velocity, even in the guiding-centre regime. Also, the curvature and gradient drifts can allow particles to move parallel to the electric field and hence gain energy (Guo et al. 2010). This happens to some extent in our trajectories. The natural velocity-scale for this is the electric-drift speed vE0 = cE0/B0, and we would thus expect velocity gained to scale with this, while the kinetic energy gain should scale as $K \sim m E_0^2/B_0$. It should be noted, however, that the actual speed acquired by individual particles may exceed vE by a large factor. Secondly, when particles reach the unmagnetised regions (near the spine or fan), as described above, they are directly accelerated by the electric field until the weak magnetic field causes them to be ejected from this region. The strong increase in electric field in 3D null reconnection, as the spine line or fan plane are approached, means this effect can be very significant. This is illustrated in Fig. 2, which analyses a typical particle trajectory for spine reconnection (taken from Paper I) in order to show the origins of the acceleration. Note that as the particle approaches the spine, the Larmor radius ($\rho $) becomes large, associated with strong increases in electric field and electric drift-speed. The kinetic energy rises gradually during the approach, in which the particle is moving adiabatically, but rises sharply in the vicinity of the spine, as the electric field directly accelerates the particle there. Consideration of the magnetic moment ($\mu $) shows that the motion is approximately adiabatic except near the spine, where there is a jump in magnetic moment.

\begin{figure} \par\includegraphics[width=9cm,clip]{14964fg2.ps} \end{figure} Figure 2:

An analysis of the quantities involved in the acceleration of a typical particle in spine reconnection. The standard field parameters of Papers I and II are used. From top to bottom panels, the quantities displayed are: distance from the null (r); electric field magnitude (E); Larmor radius ($\rho $); magnetic moment ($\mu $); relative Larmor radius ($\rho /r$); kinetic energy ( $E_{\rm kin}$); parallel speed ( $v_{\parallel }$); electric drift-speed (vE).

Open with DEXTER

It should be noted that the simple Priest and Titov fields have unphysical singularities; these would be resolved in more realistic models which include resistive (or other) dissipative effects near the spine/fan. However, in a highly conducting plasma the dissipative region will have a very small size, and the electric fields will still become very large in the outer ideal region before dropping to zero within the dissipation layer. Consider, for example, the analytical model fields of Craig & Fabling (1996), which include self-consistently the resistive term in Ohm's law. The electric field is described by a function which grows to large values as the radius approaches zero (in spine reconnection), but which then drops smoothly to zero in a region which scales as $r \sim \eta^{-1/2}$, where $\eta$ is the resistivity. Particles which arrive close to the spine or fan (according to the mode of reconnection) may thus be strongly accelerated, and the overall effectiveness of acceleration is thus determined mainly by the proportion of particles which reach these strong field regions.

We can interpret the particle trajectories as follows. In the case of spine reconnection, consider a particle entering in the inflow region in z >0. Initially, the particle is well modelled by a guiding-centre approach, and it is carried towards the spine by the electric drift which is in a constant-$\phi$ plane (here $\phi$ is the azimuthal angle) while experiencing weak azimuthal drifts; thus the dominant velocity components are vr < 0and vz<0. Near the spine, the azimuthal electric field produces a strong increase in $v_{\phi}$, causing the particle to rotate about the spine (gaining kinetic energy as its potential energy changes - note that, as pointed out in Paper I, potential energy is proportional to $\cos \phi$). However, the increasing azimuthal speed builds up a centrifugal radial acceleration term $v_{\phi}^2/r$, so that vr becomes positive and the particle is ejected from the vicinity of the spine. Note that in this case, the energy gain should scale as $K \sim e E_0 L$.

The analytical results in this section will be used to interpret the numerical results presented in Sect. 4. First, however, we need to produce particle trajectories for electrons (as well as ions, as has been done previously), and this is discussed in the next section.

3 Electron acceleration

Previous test particle results for 3D nulls (Papers I-III) have considered only protons. In principle, the same code used to calculate proton orbits could also be used to study electrons; but it is extremely inefficient to solve the full equation of motion for electrons across the bulk of the region, due to their very small Larmor radius. In fact, whilst individual trajectories can be calculated in this way, the computer time required to develop a full spectrum is prohibitively large. A further difference between electrons and ions is that the former, due to their much smaller rest mass, often acquire relativistic speeds, whereas the latter can be well-modelled by the non-relativistic equation of motion. It is thus natural to use a relativistic guiding-centre approach in order to calculate electron trajectories: the rapid gyromotion is averaged out, appearing only through the magnetic moment $\mu $, which is an adiabatic invariant. It is then required to calculate the parallel and perpendicular (drift) velocities of the guiding centre. It must be recalled that this approach is valid in the case of small Larmor radius and large gyro-frequency: $\rho \ll l$ and $\omega_{\rm L} \gg T^{-1}$ where l and Tare the length-scales and time-scale of the background fields (which must be defined locally, so that l, for example, is not necessarily the same as L).

In the case of fast magnetic reconnection, the motion is dominated by the strong electric drift (see Sect. 2). We thus use the guiding-centre equations given by Northrop (1963), which incorporate the strong-electric-drift terms, as previously used to study particle acceleration in 2D reconnecting fields (Vekstein & Browning 1997; Browning & Vekstein 2001; Wood & Neukirch 2005). As mentioned above, we must extend the approach used by these authors by using the full relativistic guiding-centre equations.

However, whilst the guiding-centre approximation is very good on global scales, we know, as discussed above, that the Larmor radius becomes large as particles approach the spine; thus the guiding-centre approximation breaks down and the full equation of motion (1) must be solved. We have therefore developed a code which switches between the guiding-centre and full equation of motion as appropriate. The switching condition depends on the comparison of the Larmor radius and local length-scale, hence on the local value of $\epsilon_l \equiv mv_{\perp} /eBl$. By comparing single particle trajectories for guiding-centre and full-trajectory codes, we find that, in practice, accurate trajectories are obtained from the guiding-centre code only if $\epsilon_l$ is very small. The switching is then determined geometrically, transitioning to a full-trajectory calculation when the particle approaches either within a certain small distance from the spine or a larger distance from the null: this is as predicted in Sect. 2 above, but the exact length-scales for switching are determined empirically. When a full trajectory switches to a guiding-centre, we determine the starting $v_{\perp}$ value - and hence $\mu $ - by averaging over several gyro-orbits and subtracting the calculated drift components. The initial guiding-centre location is obtained also by averaging. Switching back to a full trajectory code, we use the known values of $v_{\perp}$, $v_{\Vert}$and v $_{\rm drift}$, along with a randomly-assigned gyro-phase, to specify the initial cartesian components of $\bf v$; the initial position is determined by the guiding-centre position with a correction for the known gyro-radius and randomly assigned gyro-phase. The results have been tested against full-trajectory simulations, and give very good accuracy but greatly improved computational time.

Using this approach, we determine the energy spectrum for a population of electrons injected randomly in the inflow region of a spherical surface r = L for the spine reconnection regime. We consider exactly the same electromagnetic fields used for protons in Paper II, regarded here as the standard condition set: these are B0 =100 Gauss, E0 = 1.5 kV/m = 0.05 statvolt/cm and scale-length L = 10 km. Other parameters are also the same as for the proton simulations: thus, we consider a population of 10 000 electrons with initial velocities randomly distributed according to a Maxwellian with temperature 1 million K (=86 eV). The results, showing how a steady-state spectrum develops in time, are shown in Fig. 3. This must be compared with the proton spectrum (Fig. 2 of Paper II, also reproduced in Fig. 5 below, left panel) for the same conditions. The spatial distribution of electrons accelerated to different energies is shown in Fig. 4, which again should be compared with the equivalent proton results (Fig. 3 of Paper II). Note that in this diagram the spine corresponds to latitudes of $\pm$ $90^{\circ}$ (and any longitude value) while the fan plane corresponds to zero latitude. The colour-coding is according to the final energies of the particles; this shows how the energy gain of a particle depends on its injection position. However, the dependence of energy gain on initial position is much less clear for electrons than for protons (see Papers I and II); this is because electrons are much more strongly affected by their initial velocity, as discussed below.

An important conclusion is that the 3D reconnection does indeed accelerate electrons quite efficiently. For our chosen field parameters, electrons with energies of up to almost 100 keV are produced, which compares favourably with flare observations. The electrons are less strongly accelerated than the protons - in the sense that the proportion of electrons accelerated is less - but electrons have an overall harder spectrum. The electron energy spectrum shows a fairly distinctive broken-power law shape, with a flatter slope at high energies. This is also consistent with observations.

The times shown in Fig. 3 are normalised with respect to the electron gyro-period. It may be seen that, in these normalised units, it takes much longer for electrons to establish a steady-state energy spectrum than protons (around $2 \times10^{7}$ gyro-periods). However, the electron gyro-period is of course much shorter than that for protons: for our chosen standard conditions, the electron gyro-period is $t_{\rm g,e} = 4 \times10^{-9}$ s whereas the proton gyro-period is $t_{\rm g,p} = 7 \times 10^{-6}$ s. Thus, electrons reach a steady-state in a time of about 80 ms, which is very similar to the value for protons, 70 ms (see Paper II).

It may also be noted from Fig. 4 that the spatial distribution of the accelerated electrons differs from that of protons. This means that emission from high energy protons and electrons may be spatially separated, as also predicted in the case of 2D reconnection with a guide field by Browning & Vekstein (2001) and Zharkova & Gordovksyy (2005). This is consistent with RHESSI observations (as noted by Zharkova & Gordovksyy 2005). The reasons for the difference here is associated with the parameter $\tilde{\mu}$ given by Eq. (7). The drift speed is the same for protons and electrons, but (for the same thermal energy) $v_{\perp}$ is different. Hence, for our chosen parameters, the electrons are actually in the weak-drift regime whereas protons are in the strong-drift regime, leading to quite different behaviour. The electron spatial distribution seems much less structured, since the trajectories are far more sensitive to the initial velocity.

\begin{figure} \par\includegraphics[width=9cm,clip]{14964fg3.ps} \end{figure} Figure 3:

Time evolution of the energy spectra for electrons in standard conditions.

Open with DEXTER

\begin{figure} \par\includegraphics[width=12cm,clip]{14964fg4.ps} \end{figure} Figure 4:

Initial and final positions of electrons, colour-coded according to their final energy.

Open with DEXTER

\begin{figure} \par\includegraphics[width=17cm,clip]{14964fg5.ps} \end{figure} Figure 5:

Time evolution of proton spectrum for B=100 Gauss (standard conditions, left) and B=20 Gauss ( right).

Open with DEXTER

4 The effect of changes in the field magnitudes: numerical results

We now analyse how the parameters of the accelerated population of energetic particles scale if we vary the magnitudes of the electric and magnetic field in our spine reconnection configuration.

In each case, we inject a population of 10 000 protons on random positions in the inflow regions at a distance of L = 10 km from the null, with initial velocities distributed according to a Maxwellian with temperature 106 K; these are followed until a steady-state energy spectrum is achieved.

The first thing to point out is that the acceleration time ( $t_{\rm acc}$), or the time for the energy spectrum to reach a steady-state, depends on the field magnitudes. The acceleration time is dominated by the time for the particles to reach the spine due to the electric drift (when they are near the spine, they gain energy much more rapidly, as seen in Fig. 2). This scales as

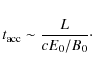
\begin{displaymath}t_{\rm acc} \sim \frac{L}{cE_{0}/B_{0}}\cdot \end{displaymath} (20)

However, in our simulations, time is non-dimensionalised with respect to the gyro-period $\tau_{\rm g}$; hence in order to reach a steady-state spectrum, the particles must be followed for a dimensionless time which scales as $t_{\rm final} \sim \frac{L}{v_{E0} \tau_{\rm g}} \propto \frac{B_0^2}{E_0}$. Notice that doubling the magnetic field thus requires increasing the simulation time by a factor of 4, which makes it impractical to run for large magnetic field strengths. This is illustrated in Fig. 5 which compares the time variation of the energy spectra for B0=100 Gauss (left) and B0=20 Gauss (right). The plot for B0=100 Gauss is the same as Paper II. Here we can see that a smaller value of the magnetic field results in stronger and faster particle acceleration.

Now we consider steady-state energy spectra with varying field magnitudes. As discussed above, these require following particles for correspondingly varying times $t_{\rm acc}$. Three condition sets are considered: standard conditions (see above); a factor of 5 decrease in magnetic field (B = 20 Gauss); a factor of 5 increase in electric field (E = 0.025 statvolt/cm).

The scaling with magnitude of the magnetic field can be partly understood by considering the electric drift-speed which is $v_{E0}=\frac{c E_0 }{B_0}$. Decreasing the magnitude of the magnetic field results in a more efficient drift of particles towards the region of strong electric field, and consequently more particles being accelerated. Conversely, increasing the electric field enhances the acceleration. It can be seen from Fig. 6 that either increasing electric field or reducing magnetic field increases, overall, the number of non-thermal particles (this can be best seen by looking at the reduction in the number of low energy, thermal particles). However, note that with a simple dependence purely on drift-speed, we would expect that increasing the electric field by a factor of 5 would have the same effect as reducing the magnetic field by the same factor. It can be seen from Fig. 6 that the situation is more complex than this, and the shape of the spectra is quite different. This is probably due to the fact that the non-adiabatic behaviour, as discussed in Sect. 2, plays a very significant role, and this is not dependent on the drift-speed. At stronger electric fields, the energy spectrum has a similar slope, but generally a larger number of accelerated particles; notably, the spectrum extends to higher energies, with a fraction of particles attaining energies of almost 100 MeV. Reducing the magnetic field leads to a spectrum which departs significantly from a simple power law form. The acceleration is enhanced, especially in the intermediate energy range.

The effect of varying field magnitudes on the spatial distribution of accelerated particles can be seen in Fig. 7, which shows the injection and final positions of particles, colour-coded according to their final energies. The case shown has reduced electric field magnitude (by a factor of 1/5) compared with standard conditions. This should be compared with Fig. 3 of Paper II. It can be seen clearly that there are no particles in the highest energy range (>10 MeV). Furthermore, the dependence of particle energy gain on injection poistion is weaker for the reduced electric field, since the initial velocity has relatively more effect. However, it is still the case that those particles whose injection position allows them to approach closest to the spine gain the most energy. The escaping high-energy particles are concentrated, as before, in jets along the spine (corresponding to latitudes of close to  $90^{\circ}$). A considerable population of high-energy particles is also found in the outflow region at a broad range of latitudes. These form a trapped high-energy population, with particles bouncing in the fieldlines and only weakly drifting across the field.

\begin{figure} \par\includegraphics[width=9cm]{14964fg6.ps} \end{figure} Figure 6:

The effects of varying electric and magnetic field magnitudes on the steady-state energy spectra.

Open with DEXTER

\begin{figure} \par\includegraphics[width=12cm,clip]{14964fg7.ps} \end{figure} Figure 7:

Particle injection (top) and final (bottom) positions plot for an electric field strength 1/5 of standard ( $t_{\rm final}=50~000$).

Open with DEXTER

5 Summary and conclusions

We have considered acceleration of charged particles at reconnecting 3D magnetic null points, for spine reconnection, focusing on understanding the acceleration process and how it depends on particle species and on the magnitudes of the underlying electromagnetic fields. Both protons and electrons have been considered, with the development of a new code which switches from guiding-centre to full equation of motion in order to model the latter.

As well as completing the analysis of charged particle acceleration in the idealised model fields of Priest & Titov (1996), we have provided a theoretical framework for interpretation of other studies of particle acceleration at 3D nulls. Acceleration can take place both adiabatically, away from the spine and fan, and non-adiabatically, when the particles can become unmagnetised. In our configuration, the latter process dominates, and we have identified the scalings for the sizes of the regions in which direct electric field acceleration takes place.

We found that electrons are generally less efficiently accelerated than protons, because they are more likely to be in the weak-electric-drift regime. Thus, the fraction of electrons accelerated is lower, and their spectra are harder than those for protons. However, the maximum energies that can be attained are similar. For our standard parameter set, electrons can be accelerated to energies of up to 10 MeV, which compares favourably with observed electron energies in flares. The acceleration time (the time it takes for most particles in the population to reach their final energies) is very similar for electrons and protons, and is of the order of tens of microseconds. The spatial distribution of accelerated electrons is different, with less concentration into beams. Electron trajectories are more dependent on the initial velocity because their drift towards the region of strong electric fields is less efficient than for protons. Similarly, higher Z ion species will be accelerated more effectively than protons. Note that recent simulations of test particles near 3D nulls in fields from MHD simulations are broadly in line with our results: it is demonstrated that protons can be accelerated significantly by convective electric fields, whereas electrons are not efficiently accelerated (Guo et al. 2010).

Since electron trajectories differ from protons, currents and charge seperation will be generated which could affect the governing electromagnetic fields. This could reduce the acceleration. A similar situation arises in most 2D test particle models, at least in the presence of a guide field (Zharkova & Gordovksyy 2005). However, this effect should be insignificant so long as the number of high-energy particles is sufficiently small compared with the background population; indeed, in our model, only a small fraction of particles are accelerated. Furthermore, the generation of electromagnetic fields by the high-energy particles may be mitigated by adjustments of the background, thermal particles (sometimes known as a ``return current''). Nevertheless, the development of more self-consistent models is an important subject for future work.

The number of particles accelerated increases as the electric field strength increases, and decreases with increasing magnetic field strength. The maximum energy attainable increases as the electric field strength is increased. However, the dependence of the shape of the energy spectrum on the electric and magnetic fields is quite complex, and the spectra cannot be simply defined by a single power law index.

Finally, we discuss two predictions of our work in the light of recent observations. Firstly, the results on spine reconnection (reported previously in Paper II) indicate that jets of escaping high energy particles will emerge along the spine line. Recently, a strong correlation has been observed in 3 flares between footpoint positions and the locations of the spine lines (Des Jardins et al. 2009). This is consistent with our predictions, since the footpoint positions are located where the energetic particles escaping along the spine impact on the chromosphere.

Secondly, we predict the appearance of a significant population of trapped high energy particles; indeed; the highest energy particles tend to be trapped rather than escaping. This may be interpreted in terms of the parameter $\tilde{\mu}$ discussed in Sect. 2, as follows. When particles pass near the spine and are accelerated, their perpendicular velocity is greatly increased, hence they are likely to be in the large $\tilde{\mu}$ (weak electric drift) regime (see Fig. 2). In this regime, particles tend to bounce along the fieldlines while the relatively weak electric drift causes only a slow cross field drift (see Paper I and Vekstein & Browning 1997); hence, the particles are trapped. This might well provide an explanation for the coronal HXR sources observed in some flares which are inconsistent with the standard thin-target interpretation (Krucker et al. 2008). The reconnection could produce a population of high energy electrons which remain trapped for a long time in the corona, which emit weakly in HXR as they collide with background thermal plasma, as well as the escaping beams which propagate to the chromosphere.

Acknowledgements
The authors are grateful to the UK STFC for financial support.

References

  1. Aulanier, G., DeLuca, E. E., Antiochos, S. K., McMullen, R. A., & Golub, L. 2000, ApJ, 540, 1126 [NASA ADS] [CrossRef] [Google Scholar]
  2. Birk, G. T., Crusius-Watzel, A. R., & Lesch, H. 2001, ApJ, 559, 96 [NASA ADS] [CrossRef] [Google Scholar]
  3. Birn, J., & Priest, E. R. 2007, Reconnection of Magnetic Fields, C.U.P. [Google Scholar]
  4. Browning, P. K., & Vekstein, G. E. 2001, J. Geophys. Res., 106, A9 [Google Scholar]
  5. Burkhart, G. E., Drake, J. F., & Chen, J. 1990, J. Geophys. Res. A, 95, 18822 [Google Scholar]
  6. Craig, I. J. D., & Fabling, R. B. 1996, ApJ, 462, 969 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dalla, S., & Browning, P. K. 2005, A&A, 436, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Dalla, S., & Browning, P. K. 2006, ApJ, 640, L99 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dalla, S., & Browning, P. K. 2008, A&A, 491, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Deeg, H. J., Borovsky, J. E., & Duric, N. 1991, Phys. Fluids B, 3, 2660 [NASA ADS] [CrossRef] [Google Scholar]
  11. De Gouevia Dal Pino, E. M., & Lazarian, A. 2000, ApJ, L31, 536 [Google Scholar]
  12. De Gouevia Dal Pino, E. M., & Lazarian, A. 2005, A&A, 441, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Des Jardins, A., Canfield, R., Longcope, D., Fordyce, C., & Waitukaitis, W. 2009, ApJ, 696, 1628 [NASA ADS] [CrossRef] [Google Scholar]
  14. Egedal, J., Fox, W., Katz, N., et al. 2008, J. Geophys. Res. Space Phys., 113, A12207 [NASA ADS] [CrossRef] [Google Scholar]
  15. Filippov, B. 1999, Sol. Phys., 185, 297 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fletcher, L., Metcalf, T. R., Alexander, D., Brown, D. S., & Ryder, L. A. 2001, ApJ, 554, 451 [NASA ADS] [CrossRef] [Google Scholar]
  17. Guo, J.-N., Buchner, J., Otto, A., et al. 2010, A&A, 513, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Hannah, I. G., & Fletcher, L. 2006, Sol. Phys., 236, 59 [NASA ADS] [CrossRef] [Google Scholar]
  19. Helander, P., Eirksson, L. G., Akers, R. J., et al. 2002, Phys. Rev. Lett. 89, 235002 [NASA ADS] [CrossRef] [Google Scholar]
  20. Krucker, S., Battaglia, M., Cargill, P. J., et al. 2008, A&ARv, 16, 155 [Google Scholar]
  21. Lau, Y.-T., & Finn, J. M. 1990, ApJ, 350, 672 [NASA ADS] [CrossRef] [Google Scholar]
  22. Lazarian, A., & Opher, M. 2009, ApJ, 703, 8 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lin, R. P., Krucker, S., Hurford, G. J., et al. 2003, ApJ, 595, L66 [Google Scholar]
  24. Litvinenko, Y. E. 1996, ApJ, 462, 997 [NASA ADS] [CrossRef] [Google Scholar]
  25. Litvinenko, Y. E. 2006, A&A, 452, 1069 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Longcope, D. W., & Parnell, C. E. 2009, Sol. Phys., 254, 51 [NASA ADS] [CrossRef] [Google Scholar]
  27. Maclean, R. C., Parnell, C. E., & Galsgaard, K. 2009, Sol. Phys., 260, 299 [NASA ADS] [CrossRef] [Google Scholar]
  28. Northrop, T. 1963, The adiabatic motion of charged particles (Interscience) [Google Scholar]
  29. Priest, E. R., & Titov, V. S. 1996, Phil. Trans. R. Soc. Lond. A, 354, 2951 [Google Scholar]
  30. Vekstein, G. E., & Priest, E. R. 1995, Phys. Plasma, 2, 3169 [Google Scholar]
  31. Vekstein, G. E., & Browning, P. K. 1997, Phy. Plasma, 4, 2261 [Google Scholar]
  32. Wood, P., & Neukirch, T. 2005, Sol. Phys., 227, 73 [NASA ADS] [CrossRef] [Google Scholar]
  33. Xiao, C. J., Wang, X. G., Pu, Z. Y., et al. 2006, Nature Phys., 2, 478 [Google Scholar]
  34. Zharkova, V., & Gordovskyy, M. 2005, MNRAS, 356, 1107 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{14964fg1.eps} \end{figure} Figure 1:

The configuration at the 3D null point showing typical fieldlines, the null point, the spine (coinciding with the z axis in the coordinate system used here) and the fan (coinciding with the xy plane).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{14964fg2.ps} \end{figure} Figure 2:

An analysis of the quantities involved in the acceleration of a typical particle in spine reconnection. The standard field parameters of Papers I and II are used. From top to bottom panels, the quantities displayed are: distance from the null (r); electric field magnitude (E); Larmor radius ($\rho $); magnetic moment ($\mu $); relative Larmor radius ($\rho /r$); kinetic energy ( $E_{\rm kin}$); parallel speed ( $v_{\parallel }$); electric drift-speed (vE).

Open with DEXTER
In the text

   \begin{figure} \par\includegraphics[width=9cm,clip]{14964fg3.ps} \end{figure} Figure 3:

Time evolution of the energy spectra for electrons in standard conditions.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{14964fg4.ps} \end{figure} Figure 4:

Initial and final positions of electrons, colour-coded according to their final energy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{14964fg5.ps} \end{figure} Figure 5:

Time evolution of proton spectrum for B=100 Gauss (standard conditions, left) and B=20 Gauss ( right).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{14964fg6.ps} \end{figure} Figure 6:

The effects of varying electric and magnetic field magnitudes on the steady-state energy spectra.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{14964fg7.ps} \end{figure} Figure 7:

Particle injection (top) and final (bottom) positions plot for an electric field strength 1/5 of standard ( $t_{\rm final}=50~000$).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.