| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014924 | |
| Published online | 08 October 2010 | |
Detailed abundances of a large sample of giant stars in M 54 and in the
Sagittarius nucleus![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
E. Carretta1 - A. Bragaglia1 - R. G. Gratton2 - S. Lucatello2,3 - M. Bellazzini1 - G. Catanzaro4 - F. Leone5 - Y. Momany2,6 - G. Piotto7 - V. D'Orazi2
1 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
2 -
INAF - Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122 Padova, Italy
3 -
Excellence Cluster Universe, Technische Universität München, Boltzmannstr. 2, 85748 Garching, Germany
4 -
INAF - Osservatorio Astrofisico di Catania, via S.Sofia 78, 95123 Catania, Italy
5 -
Dipartimento di Fisica e Astronomia, Università di Catania, via S.Sofia 78, 95123 Catania, Italy
6 -
European Southern Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile
7 -
Dipartimento di Astronomia, Università di Padova, Vicolo dell'Osservatorio 2, 35122 Padova, Italy
Received 4 May 2010 / Accepted 21 June 2010
Abstract
Homogeneous abundances of light elements, ![]() -elements,
and Fe-group elements from high-resolution FLAMES spectra are presented
for 76 red giant stars in NGC 6715 (M 54),
a massive globular cluster (GC) lying in the nucleus of the
Sagittarius dwarf galaxy. We also derived detailed abundances for
27 red giants belonging to the Sgr nucleus. Our abundances measure
the intrinsic metallicity dispersion (
-elements,
and Fe-group elements from high-resolution FLAMES spectra are presented
for 76 red giant stars in NGC 6715 (M 54),
a massive globular cluster (GC) lying in the nucleus of the
Sagittarius dwarf galaxy. We also derived detailed abundances for
27 red giants belonging to the Sgr nucleus. Our abundances measure
the intrinsic metallicity dispersion (
![]() dex, rms scatter) of M 54, with the bulk of stars peaking at [Fe/H]
dex, rms scatter) of M 54, with the bulk of stars peaking at [Fe/H] ![]() -1.6 and a long tail extending to higher metallicities, similar to
-1.6 and a long tail extending to higher metallicities, similar to ![]() Cen.
The spread in these probable nuclear star clusters exceeds those of
most GCs: these massive clusters are located in a region intermediate
between normal GCs and dwarf galaxies. The GC M 54 exibits a
Na-O anticorrelation, a typical signature of GCs, which is instead
absent for the Sgr nucleus. The light elements (Mg, Al, Si)
participating in the high temperature Mg-Al cycle show that the
entire pattern of (anti)correlations produced by proton-capture
reactions in H-burning is clearly different between the most metal-rich
and most metal-poor components in the two most massive GCs in the
Galaxy, confirming early results based on the
Na-O anticorrelation. As in
Cen.
The spread in these probable nuclear star clusters exceeds those of
most GCs: these massive clusters are located in a region intermediate
between normal GCs and dwarf galaxies. The GC M 54 exibits a
Na-O anticorrelation, a typical signature of GCs, which is instead
absent for the Sgr nucleus. The light elements (Mg, Al, Si)
participating in the high temperature Mg-Al cycle show that the
entire pattern of (anti)correlations produced by proton-capture
reactions in H-burning is clearly different between the most metal-rich
and most metal-poor components in the two most massive GCs in the
Galaxy, confirming early results based on the
Na-O anticorrelation. As in ![]() Cen,
stars affected by most extreme processing, i.e. showing the
signature of more massive polluters, are those of the metal-rich
component. These observations can be understood if the burst of star
formation giving birth to the metal-rich component was delayed by as
much as 10-30 Myr with respect to the metal-poor one. The
evolution of these massive GCs can be easily reconciled in the general
scenario for the formation of GCs sketched previously by ourselves,
taking into account that
Cen,
stars affected by most extreme processing, i.e. showing the
signature of more massive polluters, are those of the metal-rich
component. These observations can be understood if the burst of star
formation giving birth to the metal-rich component was delayed by as
much as 10-30 Myr with respect to the metal-poor one. The
evolution of these massive GCs can be easily reconciled in the general
scenario for the formation of GCs sketched previously by ourselves,
taking into account that ![]() Cen
may have already incorporated the surrounding nucleus of its progenitor
and lost the
remainder of the hosting galaxy while the two are still observable as
distinct components in M 54 and the surrounding field.
Cen
may have already incorporated the surrounding nucleus of its progenitor
and lost the
remainder of the hosting galaxy while the two are still observable as
distinct components in M 54 and the surrounding field.
Key words: stars: abundances - stars: atmospheres - stars:
Population II - globular clusters: individual: NGC 6715
(M 54) - globular clusters: individual: NGC 5139 (![]() Cen) - globular clusters: general
Cen) - globular clusters: general
1 Introduction
NGC 6715 (M 54) is a massive globular cluster (GC) immersed
in the nucleus of the Sgr (SgrN), a dwarf galaxy currently
disrupting within our Galaxy (see Ibata et al. 1994; Bellazzini et al. 2008,
from now B08, and references therein). Therefore, in this Chinese box
game, it is at the same time the nearest bona fide cluster of
extragalactic origin and the second most massive GC in the
Milky Way, ![]() Cen being the most massive (see Harris 1996).
Cen being the most massive (see Harris 1996).
The complexity of the nature of GCs has been extensively investigated (see Gratton et al. 2004; Charbonnel 2005, for comprehensive reviews): their stars do not satisfy the very definition of a simple stellar population (SSP). In contrast, all the evidence suggests that GCs had a significant and very peculiar chemical evolution including self-enrichment of metals from ejecta of massive stars early in their lifetime. In turn, this is most likely related to their formation mechanisms (e.g. Carretta 2006) and the environment in which they formed (Carretta et al. 2010a).
In addition to earlier studies (see Kraft 1994, for references), our completed survey of 19 GCs (Carretta et al. 2009a,b) confirmed star-to-star variations in light elements (O, Na, Mg, Al, Si as well as F and lighter elements Li, C, N, see Smith & Martell 2003; Smith et al. 2005) in all studied clusters. The GCs targeted have masses spanning the typical range of Galactic GCs, from the small (mainly disk) objects such as M 4 and M 71 to the more massive (mainly inner halo) clusters such as NGC 7078 (M 15) and NGC 2808. This universality of the chemical pattern is the result of the superposition of at least two stellar generations; these are slightly spaced in time, and distinct in terms of the signature of early pollution by the ejecta that only more massive stars, now extinct, may have been able to produce (Gratton et al. 2001) in proton-capture reactions of H-burning at high temperature (Denisenkov & Denisenkova 1989; Langer et al. 1993).
However, for most of the GCs studied, these observed variations in
light elements are not accompanied by a dispersion in the abundances of
heavier elements mostly produced in supernovae explosions. As far
as Fe is concerned, most GCs can still be considered mono-metallic. The
upper limit to the scatter in [Fe/H]![]() is smaller than 0.05 dex, meaning that the degree of homogeneity
is better than 12% in most cases (Carretta et al. 2009c).
is smaller than 0.05 dex, meaning that the degree of homogeneity
is better than 12% in most cases (Carretta et al. 2009c).
On the other hand, an intrinsic spread in
Fe abundances has been known for a long time to exist in some GCs,
the most noticeable examples being M 54 and ![]() Cen (see e.g. the references in Carretta et al. 2010b).
For inference, these observations call for quite large and
repeated bursts of star formation, involving all the available range in
masses, due to the nucleosynthetic origin of heavy elements in
explosive burning. Possibly also some delay between individual bursts
is required, to allow the replenishing of a gas pool up to some
critical threshold.
Cen (see e.g. the references in Carretta et al. 2010b).
For inference, these observations call for quite large and
repeated bursts of star formation, involving all the available range in
masses, due to the nucleosynthetic origin of heavy elements in
explosive burning. Possibly also some delay between individual bursts
is required, to allow the replenishing of a gas pool up to some
critical threshold.
Multiple (even relatively recent) episodes of star formation in
these objects carry a strong resemblance to what is found for dwarf
galaxies in the local universe (e.g. Tolstoy et al. 2009). In some cases (e.g. ![]() Cen, Bekki & Freeman 2003), it has been explicitly suggested that the GCs were the nuclei of currently disrupted dwarf galaxies (see Boker 2008, and references therein).
Cen, Bekki & Freeman 2003), it has been explicitly suggested that the GCs were the nuclei of currently disrupted dwarf galaxies (see Boker 2008, and references therein).
The nearby, extragalactic cluster M 54 is a key object, being the most massive of the four GCs associated with the merging Sgr dwarf spheroidal (dSph) galaxy and the second most massive of all MW GCs, as shown in Fig. 1. The GC M 54 is old and metal-poor (e.g. Layden & Sarajedini 1997 found [Fe/H = -1.79 and the same age as GCs of similar metallicity). By obtaining and studying the full extent of the Na-O anticorrelation, the most striking signal of early pollution in GCs, we can answer the following key questions about the still obscure formation process of these old stellar aggregates: (i) did GCs form through the same path in every galactic environment? (ii) Is the occurrence of multiple stellar generations, as indicated by different degrees of O-depletion/Na-enhancement, unavoidable in the formation and first evolution of GCs in all galaxies?
While some studies of the chemical composition of red giant branch (RGB) stars in this GC exist in the literature (Brown et al. 1999, hereinafter BWG99), they are limited to just a few stars, hence useful only to provide some interesting average values. What is still lacking is an extensive survey, and adequate analysis and sampling of the chief signature of early chemical evolution in GCs. With a collection of high resolution spectra for a large sample of cluster stars, we can shed light on the complex scene where this initial evolution occurred, possibly in the core of giant clouds/associations or even, in the case of the most massive clusters such as M 54, of dwarf galaxies (Bekki et al. 2007).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg1.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg11.png)
|
Figure 1:
The distribution of the total visual absolute magnitudes (a proxy for
total mass) for all globular clusters in the Harris (1996)
catalogue. Red lines indicate the location of the GCs already analysed
in our project ``Na-O anticorrelation and HB''. Blue lines
show the additional clusters under scrutiny and the black arrow
indicates the position of NGC 6715 (M 54) in this
distribution. The most massive cluster (not indicated) is |
| Open with DEXTER | |
In Carretta et al. (2010b), we pointed out how the similarities found in the chemistry for the two most massive clusters in the Galaxy, M 54 and ![]() Cen,
can be simply explained assuming that they are essentially similar
objects (namely, nuclear star clusters at the centre of dwarf
galaxies). Their differences are indeed accounted for if these GCs are
observed at different
stages of their evolution.
Cen,
can be simply explained assuming that they are essentially similar
objects (namely, nuclear star clusters at the centre of dwarf
galaxies). Their differences are indeed accounted for if these GCs are
observed at different
stages of their evolution.
In this paper, we present the full analysis of the data and the detailed chemical composition of a large sample of stars in M 54 and SgrN, providing further support of the above scenario previously sketched in Carretta et al. (2010a).
The paper is organised as follows. Section 2 describes the target
selection criteria and observations. Section 3 outlines the
analysis procedure, illustrating also the derivation of the adopted
atmospheric parameters and their uncertainties. Section 4 deals
with the Fe distribution, while in Sects. 5 and 6 the
Na-O and Mg-Al anticorrelations are discussed, respectively. The ![]() and Fe-peak element abundances in the program stars are described in
Sect. 7. Section 8 examines our current understanding of
GC formation scenario and, finally, a summary and conclusions
are given in Sect. 9.
and Fe-peak element abundances in the program stars are described in
Sect. 7. Section 8 examines our current understanding of
GC formation scenario and, finally, a summary and conclusions
are given in Sect. 9.
2 Target selection, observations, and input data
Photometric data (V,I magnitudes) were taken from Monaco et al. (2002), in addition to unpublished B magnitudes provided by one of the authors (MB).
2.1 Selection of targets and observations
This step is not trivial in the complex M 54+Sgr field, where the cluster and nuclear components are intermingled (see e.g. Siegel et al. 2007, B08; Giuffrida et al. 2010). Moreover, since the RGB of M 54 shows a colour dispersion, particular care is needed to select genuine first-ascent red giants and not asymptotic giant branch (AGB) stars.
For this task, we relied on a pre-release of the ACS HST catalogue (later presented in Siegel et al. 2007). The majority of the selected sample of RGB stars in M 54 is concentrated in the inner
![]() ,
and the M 54 RGB is almost unrecognisable at
,
and the M 54 RGB is almost unrecognisable at
![]() from the cluster center. Nevertheless, the final M 54 RGB sample included 167 stars within
from the cluster center. Nevertheless, the final M 54 RGB sample included 167 stars within
![]() ,
having
,
having
![]() .
On the other hand, the SgrN RGB sample included 60 stars within
.
On the other hand, the SgrN RGB sample included 60 stars within
![]() and in the same V range.
and in the same V range.
Afterward, both samples were ``cleaned'' from stars having any close neighbour within
![]() and magnitudes brighter than V+1.0, where V
is the target magnitude. Thus, the final selection included about
190 RGB stars in M 54 and Sgr; from this sample, we
selected the stars that had been assigned to FLAMES fibres and observed
in our pointings, as shown in Fig. 2.
and magnitudes brighter than V+1.0, where V
is the target magnitude. Thus, the final selection included about
190 RGB stars in M 54 and Sgr; from this sample, we
selected the stars that had been assigned to FLAMES fibres and observed
in our pointings, as shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg17.png)
|
Figure 2: The colour-magnitude diagram of M 54 and Sgr nucleus showing our final selection of targets for FLAMES observations. Green circles enclose 52 candidate RGB stars of Sgr and blue circles enclose 82 candidate red giant branch targets of M 54. All targets lie within a radial distance of 9 arcmin from the cluster center and satisfy the selection criteria described in the text. |
| Open with DEXTER | |
The spectroscopic data were collected in service mode using the ESO
high resolution multifibre spectrograph FLAMES (Pasquini et al. 2002)
mounted on the VLT UT2. Observations were performed with two
GIRAFFE setups: the high-resolution gratings HR11 (centred on
5728 Å) and HR13 (centered on
6273 Å), chosen to enable us to measure the Na doublets at
5682-5688 Å and 6154-6160 Å, the [O I] forbidden lines at 6300 and 6363 Å, and several lines of Fe-peak and ![]() -elements. The spectral resolutions are R = 24 200 (HR11) and R = 22 500 (HR13) at the centre of the spectra.
-elements. The spectral resolutions are R = 24 200 (HR11) and R = 22 500 (HR13) at the centre of the spectra.
We performed two pointings: the first one (HR13 only) was devoted to observations of the metal-rich sequence of the Sgr nucleus; in this case, metal abundances are high enough to safely derive Na from the weak doublet at 6154-6160 Å. The second pointing (both HR11 and HR13) was used on the metal-poor sequence, which is mostly composed of M 54 stars. Spare fibres left in the first pointing were also positioned on faint metal-poor stars, doubling in some case the exposure time in HR13 for these objects.
At the end, only 2 exposures (out of the 8 planned) were
executed for the first pointing, whereas 10 exposures with HR11
and 9 with HR13 were completed for the second one. This is not a
source of concern since target stars of the SgrN are all quite cool and
metal-rich objects, with strong lines which can be reliably measured.
Simultaneous FLAMES-UVES observations, with resolution
![]() and covering the spectral range from 4800 to 6800 Å, were
obtained in each pointing. The log of observations is summarised in
Table 1.
and covering the spectral range from 4800 to 6800 Å, were
obtained in each pointing. The log of observations is summarised in
Table 1.
Table 1: Log of FLAMES observations.
2.2 Radial velocities and membership
We used the one-dimesional (1D), wavelength-calibrated spectra provided
by the dedicated ESO Giraffe pipeline. Radial velocities (RVs) were
measured using the IRAF![]() task FXCORR with appropriate templates and are shown in Table 2 (only available online at CDS).
task FXCORR with appropriate templates and are shown in Table 2 (only available online at CDS).
Obvious interlopers in M 54 and the nucleus of Sgr were identified
on the basis of their RVs and disregarded from further analysis if the
measured RV differed by more than 3![]() from the average of the cluster/nucleus stars. The mean values of RV that we derived are 143.7 (
from the average of the cluster/nucleus stars. The mean values of RV that we derived are 143.7 (
![]() )
and 142.4 (
)
and 142.4 (
![]() ) km s-1
from the 76 stars in M 54 and the 27 in SgrN,
respectively, used in the analysis. As extensively discussed in
B08, the RV alone is not enough to discriminate between M 54 and
SgrN members.
) km s-1
from the 76 stars in M 54 and the 27 in SgrN,
respectively, used in the analysis. As extensively discussed in
B08, the RV alone is not enough to discriminate between M 54 and
SgrN members.
In total, we observed 76 RGB stars belonging to M 54, 7 with UVES spectra and 69 with GIRAFFE spectra (18 with only HR11, and 51 with both HR11 and HR13). We also obtained spectra for 74 stars in the nucleus of Sgr, although not all stars were found to be suitable for a reliable abundance analysis (see below).
2.3 Near-infrared photometry from 2MASS
Our V band photometry was complemented with K magnitudes to obtain atmospheric parameters as described in the next section. K band magnitudes were obtained by cross-correlating our photometric catalogue with the Point Source Catalogue of 2MASS (Skrutskie et al. 2006). These K magnitudes were transformed to the TCS photometric system, as used in Alonso et al. (1999). However, because of the quite severe crowding in the field and its distance, reliable near-infrared magnitude could not be derived for all target stars (see Table 2, only available online at CDS).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg21.png)
|
Figure 3: The I,V-I CMD of program stars, showing the adopted separation between the globular cluster M 54 (blue filled circles) and the stars of the Sgr nucleus (green squares). Filled square symbols are stars in the nucleus retained for further analysis, whereas open squares are stars heavily affected by TiO bands and disregarded. |
| Open with DEXTER | |
We used the I, V-I CMD shown in Fig. 3 to separate by eye inspection the sequence of M 54 from the stars in SgrN. Spectra of the coolest stars (see Fig. 3) in the latter component are heavily affected by titanium oxide (TiO) bands, which severely depress the continuum, in particular in the HR13 spectral range. They were omitted from further analysis.
After the first abundance analysis, we found that three stars, attributed by us to the SgrN on the basis of magnitudes, appear to have achieved a better ionisation equilibrium if analysed with the same relation between effective temperature and K magnitude used for the cluster M 54 (see below). They are all very close to the cluster centre (within 2.5 arcmin), hence it is probable that their magnitudes are somewhat uncertain. Hereinafter, we assume that these stars belong to M 54.
A list of all the target stars retained in our final sample (76 RGB stars in M 54, and 27 giant stars in Sgr nucleus) is provided in Table 2, together with coordinates, magnitudes, and heliocentric radial velocities (the table is available only in electronic form at CDS).
3 Atmospheric parameters and analysis
Our abundance analysis traces as closely as possible the homogeneous procedures adopted in Carretta et al. (2006, 2007a-c, 2009a,b) and Gratton et al. (2006, 2007) for measuring equivalent widths (EWs) and deriving atmospheric parameters. The same set of atomic parameters and model atmospheres were used. Therefore, only a few points of the analysis will be summarised here.
3.1 Atmospheric parameters
Adopted atmospheric parameters and iron abundances are listed in Table 3 (available only in electronic form at CDS) for all the 76+27 program stars analysed in the present work.
We derived first estimates of
![]() and
bolometric corrections for all our stars, regardless of whether or not
they are labelled as belonging to M 54 or SgrN, on the basis of
their V-K colours. For M 54 stars without K magnitudes, these estimates were obtained using a relation defined to be a function of I magnitudes for stars with both filters. For the stars of
the SgrN, we derived the missing K magnitudes using V-K as a function of V-I. We adopted a reddening of
E(B-V)=0.14
and
bolometric corrections for all our stars, regardless of whether or not
they are labelled as belonging to M 54 or SgrN, on the basis of
their V-K colours. For M 54 stars without K magnitudes, these estimates were obtained using a relation defined to be a function of I magnitudes for stars with both filters. For the stars of
the SgrN, we derived the missing K magnitudes using V-K as a function of V-I. We adopted a reddening of
E(B-V)=0.14![]() , a true distance modulus of
(m-M)0=17.10 from Monaco et al. (2004), and the relations
E(V-K) = 2.75 E(B-V),
AV = 3.1 E(B-V),
and
AK = 0.353 E(B-V) from Cardelli et al. (1989).
, a true distance modulus of
(m-M)0=17.10 from Monaco et al. (2004), and the relations
E(V-K) = 2.75 E(B-V),
AV = 3.1 E(B-V),
and
AK = 0.353 E(B-V) from Cardelli et al. (1989).
We refined the
![]() estimates for the M 54 stars using a relation between
estimates for the M 54 stars using a relation between
![]() (from V-K and the Alonso et al. calibration) and K magnitudes. This approach yields much smaller internal errors than using colours directly (see Carretta et al. 2007a
and other papers of this project), but it cannot be applied to the
stars of SgrN because it assumes that cluster stars define one single
sequence in the colour-magnitude diagram.
(from V-K and the Alonso et al. calibration) and K magnitudes. This approach yields much smaller internal errors than using colours directly (see Carretta et al. 2007a
and other papers of this project), but it cannot be applied to the
stars of SgrN because it assumes that cluster stars define one single
sequence in the colour-magnitude diagram.
Concerning the potential contamination by AGB stars, the
good agreement we obtain, on average, between abundances based on
neutral and singly ionised species (e.g. iron) supports the
atmospheric parameters we used, including surface gravities ![]() .
These were obtained from the apparent magnitudes, effective
temperatures, distance moduli, and bolometric corrections from Alonso
et al. (1999), assuming a mass of 0.85
.
These were obtained from the apparent magnitudes, effective
temperatures, distance moduli, and bolometric corrections from Alonso
et al. (1999), assuming a mass of 0.85 ![]()
![]() , and
, and
![]() as the bolometric magnitude for the Sun.
as the bolometric magnitude for the Sun.
We derived values of the microturbulent velocities vt by eliminating trends in the relation between abundances from Fe neutral lines and expected line strength (see Magain 1984).
Finally, we interpolated models with the proper atmospheric parameters, whose abundances matched those derived from Fe I lines within the Kurucz (1993) grid of model atmospheres (with the option for overshooting being selected).
3.2 Errors in the atmospheric parameters
The procedure for error estimations was tuned and described in previous papers of this project (see Carretta et al. 2007c, 2009a,b) and the description is not repeated here. We only point out two main differences in the error estimates with respect to the other analysed GCs, both tailored to deal with an object having an intrinsic metallicity dispersion.
To determine the impact of errors in the adopted model metallicities on the final abundances, we usually considered that these errors coincide with the rms scatter in [Fe/H] over all stars of a GC. These estimates assume that the observed dispersion is an artifact caused by errors. Since we suspected a real dispersion for M 54, we used the following approach. We first derived a relation expressing the spread in [Fe/H] for the other 19 GCs in our database (assumed to be homogeneous in Fe) as a bivariate function of the median values of signal-to-noise ratio (S/N) and the effective temperature of stars. We then entered the values appropriate for M 54 in this relation, and obtained 0.046 dex and 0.058 dex as the values of the typical errors in [A/H] (for GIRAFFE and UVES spectra, respectively). These values may be compared with the intrinsic scatter of iron abundances in M 54, which is 4 times larger (see next section).
As in the other papers of this series, we then considered the contribution of uncertainties in EW to the errors in abundances as the quadratic sum of two terms: the first one is characteristic of each line (but constant from star to star) and can be attributed to problems in continuum tracing or blends; the second one is characteristic of each EW measure and can be attributed to random noise. The second term contributes to internal (i.e. star-to-star) errors in the abundances, while the first one is important when considering systematic abundance-scale errors. To estimate correctly these terms for M 54, we need to consider the true star-to-star dispersion in abundances. Hence, we computed the offsets of the abundances from individual Fe I lines with respect to the mean value for each star; for each line, we then averaged these offsets over all stars, which is turn provided estimates of the term characteristic of each line; and finally subtracted the average offsets from the abundances from individual Fe I lines. The quadratic average in the dispersions of these corrected abundances for each star represents an estimate of the random noise term. Applying this procedure, we derived values of 0.077 dex and 0.060 dex (for GIRAFFE and UVES, respectively). These values should be divided by the square root of the mean number of lines used in the analysis for each atomic species.
Tables of sensitivities of abundance ratios to variations in the atmospheric parameters, star-to-star (internal) errors and systematic errors being given in the Appendix.
4 Iron abundances and metallicity dispersion in M 54
Homogeneity is crucial to detecting subtle effects when comparing different clusters. Thus, adopted line lists, atomic parameters and reference solar abundances (from Gratton et al. 2003) are strictly homogeneous for all stars analysed in the present program. Equivalent widths (EWs) were measured with the same semi-automatic procedure described in detail in Bragaglia et al. (2001), with a careful definition of the local continuum around each line, a crucial step at the limited resolution of our GIRAFFE spectra.
The correction of EW from GIRAFFE spectra to the system defined by UVES spectra (see Carretta et al. 2009a) was deemed not necessary here, because we found that on average the difference was negligible: EW(GIRAFFE)-EW(UVES) = +0.91 ![]() 0.8 mÅ,
rms = 10.9 mÅ from 209 lines in 4 stars observed
with both UVES and GIRAFFE instruments. We could then safely merge the
results obtained with UVES and GIRAFFE.
0.8 mÅ,
rms = 10.9 mÅ from 209 lines in 4 stars observed
with both UVES and GIRAFFE instruments. We could then safely merge the
results obtained with UVES and GIRAFFE.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg4.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg27.png)
|
Figure 4: Derived metallicity distribution of stars in M 54 ( left panels: abundances from Fe I lines (top), from Fe II lines (middle) and their difference (bottom)) and in the nucleus of Sgr (right panels) as a function of the effective temperature. Filled red circles are stars with both HR11 and HR13 GIRAFFE spectra, green cross stars with GIRAFFE HR13 only, and blue filled squares are stars with UVES spectra. |
| Open with DEXTER | |
We plot the abundances of Fe as a function of effective temperature for the stars belonging to M 54 and SgrN in the left and right panels of Fig. 4, respectively. The lower panels in these figures show good agreement between iron abundances from neutral and singly ionised lines over the whole range in temperature. This represents a good sanity check, since the ionisation equilibrium for Fe is quite sensitive to any possible problem in the abundance analysis.
The average metallicity is [Fe/H] = -1.559 ![]() 0.021 dex (
0.021 dex (
![]() dex, 76 stars) for M 54 and =-0.622
dex, 76 stars) for M 54 and =-0.622 ![]() 0.068 dex (
0.068 dex (
![]() dex, 27 stars) for SgrN, using neutral Fe lines. The average differences Fe II - Fe I are +0.041 dex (
dex, 27 stars) for SgrN, using neutral Fe lines. The average differences Fe II - Fe I are +0.041 dex (
![]() ,
76 stars) and +0.011 dex (
,
76 stars) and +0.011 dex (
![]() ,
20 stars), respectively. Since the internal errors in [Fe/H] are
of the order of 0.02 dex (average of internal errors from UVES and
GIRAFFE spectra, see
Appendix A), our first result is that the intrinsic metallicity dispersion in M 54 is confirmed by high resolution spectroscopy at more than 8
,
20 stars), respectively. Since the internal errors in [Fe/H] are
of the order of 0.02 dex (average of internal errors from UVES and
GIRAFFE spectra, see
Appendix A), our first result is that the intrinsic metallicity dispersion in M 54 is confirmed by high resolution spectroscopy at more than 8![]() (see also Carretta et al. 2010b).
(see also Carretta et al. 2010b).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg5.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg32.png)
|
Figure 5: V,B-V CMD for stars in M 54. Stars with metallicity above (red filled squares) and below (blue filled circles) the cluster average ratio [Fe/H] = -1.56 dex are marked. |
| Open with DEXTER | |
To show that this is not an artifact of the analysis, we indicated with different colours stars of M 54 with [Fe/H] ratios below or above the cluster average in the V,B-V CMD of Fig. 5. Stars with higher [Fe/H] values are typically redder than those with lower [Fe/H]'s along the RGB. This agrees with a real metallicity difference, but not with expectations from analysis errors (stars analysed with a temperature too low should appear as more metal-poor). Furthermore, we can exclude any impact of He variations: in He-rich stars, the [Fe/H] ratio is expected to be slightly higher because of the corresponding decrease in H content. However, stars with higher He content should also be bluer than He-normal stars (see Bragaglia et al. 2010), at odds with what is observed for M 54.
4.1 Comparison with previous results: B08
Sixty-four stars in common with the B08 sample allow us to cross-check
the reliability and the accuracy of the adopted radial velocity and
metallicity scales. It turns out that both scales display
differences in the zero point at a level smaller than ![]() ,
giving no reason for concern. On the other hand, the overall agreement is very good.
,
giving no reason for concern. On the other hand, the overall agreement is very good.
The upper panel of Fig. 6 shows that there is only a small difference in the RV zero points of the two sets (
![]() ,
on average) and, most importantly, the
,
on average) and, most importantly, the ![]() scatter is
scatter is
![]() ,
thus confirming the results of the tests performed by B08. We note
that the difference between the two independent estimates are smaller
than
,
thus confirming the results of the tests performed by B08. We note
that the difference between the two independent estimates are smaller
than
![]() in 78% of the cases, hence the distribution of the scatter has a peak that is
significantly narrower than a Gaussian distribution.
in 78% of the cases, hence the distribution of the scatter has a peak that is
significantly narrower than a Gaussian distribution.
A moderate difference in zeropoint is also evident when
comparing the two metallicity scales: B08 metallicities from
calcium triplet are on average 0.15 dex higher than those derived
here. The lower panel of Fig. 6
shows that once this difference is corrected for, the agreement between
the two independent sets of metallicity estimates is satisfactory over
the whole 2 dex
range of metallicity considered. The ![]() scatter (0.14 dex) is comparable to the internal accuracy of B08 measurements alone (0.11 dex).
scatter (0.14 dex) is comparable to the internal accuracy of B08 measurements alone (0.11 dex).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14924fg6.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg37.png)
|
Figure 6:
Comparison with the RV and [Fe/H] estimates by B08. Upper panel:
differences in the radial velocity; the continuous line marks the mean difference, the dotted lines enclose the
|
| Open with DEXTER | |
4.2 Comparison with other samples: Smecker-Hane & McWilliam (2009)
There are no stars in common between our study and the samples of BWG99 (M 54 giants) and Sbordone et al. (2007, hereinafter S07; 5 stars in Terzan 7 and 15 stars of the Sgr dSph). On the other hand, five of our stars are included in the sample of 14 stars analysed by Smecker-Hane & McWilliam (2009, hereinafter SHM09). Their program stars were selected to span the full range of colours (metallicities) of RGB stars. SHM09 excluded all stars within 2 arcmin of the centre of M 54, and considered all their objects as belonging to the Sgr galaxy. The only possible exception was the star I-73, for which they found evidence of significant processing by proton-capture reactions (see also McWilliam & Smecker-Hane 2005a). However, only two of the common stars are assigned to the SgrN according to our classification: star 38003327 is SHM09 I-150 and star 38004527 is SHM09 II-44, with radial distances from the centre of M 54 of 4.7 and 9 arcmin, respectively. We assigned the other three stars, all with metallicity [Fe/H] < -1.4 dex, to M 54, using the criteria described in Sect. 2. They are star 38000597 (=SHM09 I-41) (at 3.5 arcmin from the centre of M 54), star 38000877 (=SHM09 I-73), and star 38001507 (=SHM09 I-87) (both at 2.3 arcmin). In our analysis (see below), star 38000877 (=SHM09 I-73) unequivocally shows the signature of matter processed in H-burning at high temperature (large O-depletion, and Na-enhancement) typical of GC stars. On the other hand, the most metal-poor star in the sample by SHM09, 38000597 (=SHM09 I-41), was also originally assigned by ourselves to the SgrN component, on the basis of its colour. Only after the first abundance analysis was it re-classified as an M 54 star, since this provided a much better ionisation equilibrium.
We note that almost all these stars are well within the the tidal radius of M 54 (7.47 arcmin, Harris 1996). We concede that (i) it is not easy to distinguish cluster and nuclear components with very similar RVs and colours and (ii) a metal-poor component is certainly present among the field stars of the Sgr dSph (e.g. McWilliam & Smecker-Hane 2005a; Bonifacio et al. 2006, priv. comm.). We then caution that a clearcut separation between M 54 and SgrN is difficult in the low metallicity regime, although it may be more probable to find a higher fraction of M 54 stars within its tidal radius.
On average, we derive [Fe/H] values that are lower by
0.19 dex than those found by SHM09. This difference is caused
by the average difference in the temperatures used in the analysis
![]() K
(rms = 104 K). SHM09 adopted temperatures derived
from excitation equilibrium; they also derived photometric
temperatures, which agree very well with our own (average offset of
6 K, with an rms of 58 K)
K
(rms = 104 K). SHM09 adopted temperatures derived
from excitation equilibrium; they also derived photometric
temperatures, which agree very well with our own (average offset of
6 K, with an rms of 58 K)![]() .
.
4.3 Comparison with the metallicity distribution of other GCs
The ideal touchstone to be compared with M 54 is obviously the most massive GC in the Milky Way: ![]() Cen.
We compare these clusters for a number of reasons, in addition to
these 2 GCs representing the high-mass tail of the GC mass
distribution:
Cen.
We compare these clusters for a number of reasons, in addition to
these 2 GCs representing the high-mass tail of the GC mass
distribution:
- both systems exhibit an intrinsic dispersion in metallicity;
- both are associated with (M 54) or suspected to be born in a dwarf galaxy (
 Cen, see Bekki & Freeman 2003);
Cen, see Bekki & Freeman 2003);
- both lie in the intermediate region (in the MV versus half mass radius) between Ultra Compact Dwarfs (UCDs) and GCs, very close to the low-mass limit of the UCDs (see Fig. 1 in Tolstoy et al. 2009);
- they have similar total mass.
In Carretta et al. (2010b), we compared the metallicity distributions in M 54+SgrN (our data) and ![]() Cen.
Although the metallicity distribution functions (MDFs) are different,
there are some similarities in the global appearance. Briefly:
Cen.
Although the metallicity distribution functions (MDFs) are different,
there are some similarities in the global appearance. Briefly:
- in both cases, the MDF is skewed toward metal-poor stars, with the bulk at [Fe/H] = -1.6, -1.5 dex;
- this peak is followed by a gradual decrease toward higher metallicity, up to [Fe/H] = -1.0 with more or less obvious secondary peaks;
- finally, a long tail up to solar metallicities is observed in both systems, provided that stars in SgrN and in the RGB-a are included (see Carretta et al. 2010b).
A generic expectation is that stellar systems closer to the
Galactic centre will be more dynamically evolved, as tidal shocks
accelerate their dynamical evolution. ![]() Cen is
more than five times closer to the centre of our Galaxy than the system
consisting of M 54+SgrN: dynamical evolution might have been much
faster for the former.
Cen is
more than five times closer to the centre of our Galaxy than the system
consisting of M 54+SgrN: dynamical evolution might have been much
faster for the former.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg7.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg40.png)
|
Figure 7:
Rms scatter in Fe I as a function of the absolute total visual
magnitudes for the 19 GCs in Carretta et al. (2009c; red circles), for M 54 (present work, blue square) and for M 22, NGC 2419 and |
| Open with DEXTER | |
A comparison with other Galactic GCs is provided in Fig. 7, where we show the run of the rms scatter in Fe I as a function of the cluster luminosity (a proxy for the cluster mass). Red filled circles are the 19 GCs previously analysed by ourselves (Carretta et al. 2009c), which can be assumed to be mono-metallic, as far as the iron abundance is concerned. We found that the (small) intrinsic scatter in these GCs correlates with cluster mass, a result that can be explained if GCs originating in more massive precursors are more able to retain any inhomogeneities established in the previous phase of rapid enrichment (see Carretta et al. 2009c, 2010a).
In Fig. 7, we also
plot the spread in iron derived for a few other clusters where the
analysis of individual stars was possible from high/intermediate
dispersion spectroscopy. For M 22, a line connects the values
derived by Da Costa et al. (2009, based on a calibration of the EWs of the Ca infrared triplet) and those of Marino et al. (2009,
from direct high resolution spectroscopy, more similar in concept to
our approach). The other GCs considered are M 54 (this study), ![]() Cen (NDC95; the derived spread, 0.32 dex, is exactly the same value obtained by Johnson et al. 2009, hereinafter CJ09), and the distant halo cluster NGC 2419 (Cohen 2009).
It is not easy to assess whether the three most massive clusters
in our Galaxy define a separate sequence as a function of the total
mass (luminosity). Taken together, all clusters shown in this figure
seem to trace a relation between intrinsic spread in iron and MV with high statistical significance, with a steep increase at the high mass end.
Cen (NDC95; the derived spread, 0.32 dex, is exactly the same value obtained by Johnson et al. 2009, hereinafter CJ09), and the distant halo cluster NGC 2419 (Cohen 2009).
It is not easy to assess whether the three most massive clusters
in our Galaxy define a separate sequence as a function of the total
mass (luminosity). Taken together, all clusters shown in this figure
seem to trace a relation between intrinsic spread in iron and MV with high statistical significance, with a steep increase at the high mass end.
Adding in this figure also the metallicity spreads derived for three
dwarf galaxies in the Local Group (WLM, Sculptor and Fornax)![]() ,
we note that the metallicity dispersions are not order of magnitudes
larger, in these galaxies. The intrinsic spreads observed in likely
nuclear star clusters such as M 54 and
,
we note that the metallicity dispersions are not order of magnitudes
larger, in these galaxies. The intrinsic spreads observed in likely
nuclear star clusters such as M 54 and ![]() Cen
are comparable to those measured in small galaxies. The latter seem to
continue to higher masses the trend defined by GCs, whose most
massive representatives are located in a
region intermediate between those of ``normal'' GCs and dwarf
galaxies. It would be interesting to also add to this plane UCDs (MV from -10 to about -14.5, see Tolstoy et al. 2009);
unfortunately, a simple estimate of the metallicity spread from
spectroscopic observations of individual stars is not yet available.
Cen
are comparable to those measured in small galaxies. The latter seem to
continue to higher masses the trend defined by GCs, whose most
massive representatives are located in a
region intermediate between those of ``normal'' GCs and dwarf
galaxies. It would be interesting to also add to this plane UCDs (MV from -10 to about -14.5, see Tolstoy et al. 2009);
unfortunately, a simple estimate of the metallicity spread from
spectroscopic observations of individual stars is not yet available.
Finally, while the number of stars observed in NGC 2419 is
still too small, we note that the MDF of M 22 seems to differ from
that of the two most massive clusters. In particular, Fig. 8
shows that in M 22 the MDF is approximately bell-shaped, with a
moderate spread around a metal-poor value, totally lacking the minor
multiple peaks at higher metallicity observed in both M 54 and ![]() Cen (Carretta et al. 2010b).
Moreover, the long tail at almost solar metallicities is completely
absent. In the scenario described in Carretta et al. (2010a),
this tail simply corresponds to the residual component of the ancestral
dwarf galaxy still (partly) visible around the clusters. This is not
surprising, because M 22 lies even closer to the central regions
of the Galaxy than
Cen (Carretta et al. 2010b).
Moreover, the long tail at almost solar metallicities is completely
absent. In the scenario described in Carretta et al. (2010a),
this tail simply corresponds to the residual component of the ancestral
dwarf galaxy still (partly) visible around the clusters. This is not
surprising, because M 22 lies even closer to the central regions
of the Galaxy than ![]() Cen,
and it is possible that in this case the envelope of the progenitor
galaxy was completely stripped by tidal interaction with the densest
Galactic regions before the formation of more metal-rich objects.
Cen,
and it is possible that in this case the envelope of the progenitor
galaxy was completely stripped by tidal interaction with the densest
Galactic regions before the formation of more metal-rich objects.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg41.png)
|
Figure 8: MDF of our total sample (M 54+SgrN) as compared to M 22 from a sample of 31 giant stars by Marino et al. (2009). Both distributions are normalised to the total number of objects in each sample. |
| Open with DEXTER | |
5 The Na-O anticorrelation in M 54
As in previous papers (e.g. Carretta et al. 2009a, and references therein), we used the EWs of the forbidden [O I] lines at 6300.3 and 6363.8 Å to derive oxygen abundances. Abundances of Na are from EWs of the two doublets of Na I at 5682-88 and 6154-60 Å. They were corrected for the effect of departures from LTE as in Gratton et al. (1999).
The Na-O anticorrelation obtained for M 54 is shown in Fig. 9.
Despite the scatter in [Fe/H] values, metal-poor and metal-rich
stars are intermingled well along almost the full length of the
anticorrelation. Apart from the case of ![]() Cen (see below), this is the
most pronounced known example of O-depletions anticorrelated with Na-enhancements among RGB stars in a GC.
Cen (see below), this is the
most pronounced known example of O-depletions anticorrelated with Na-enhancements among RGB stars in a GC.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg9.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg42.png)
|
Figure 9: Na-O anticorrelation in M 54 from UVES and GIRAFFE spectra; blue and red circles indicate stars that are respectively more metal-poor and more metal-rich than the cluster average [Fe/H] = -1.56. Upper limits to [O/Fe] are indicated by arrows. The typical star-to-star error bars are also shown. |
| Open with DEXTER | |
The interquartile range of the distribution of [O/Na] ratios,
IQR[O/Na], can be assumed to be a quantitative measure of the extension
of the anticorrelation (see Carretta 2006);
from the global sample of 76 RGB stars in M 54, we found
that IQR[O/Na] = 1.169, a record high for our sample
of GCs. This is second in value only to the extension we found in ![]() Cen (IQR[O/Na] = 1.310) using data from NDC95.
Cen (IQR[O/Na] = 1.310) using data from NDC95.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg43.png)
|
Figure 10: Fraction of stars in the P, I, and E components in the 19 clusters analysed by Carretta et al. (2009a, red filled circles) and in M 54 (large black circles). |
| Open with DEXTER | |
In Carretta et al. (2009a), we separated the stars observed in each of the 19 GCs into three distinct populations, according to their abundance ratios [O/Fe] and [Na/Fe]. We identified (see e.g. Fig. 13 below) a primordial component P sharing the same Na, O abundances as field stars of similar metallicity, and two components of second generation stars, defining the O-poor part of the Na-O anticorrelation. These last two components consist of objects with either intermediate (I) ([O/Na] > -0.9 dex) and extremely modified composition (E) ([O/Na] < -0.9 dex), with respect to the first generation P stars.
For M 54, we found that the P fraction of first generation stars is
![]() = 26
= 26 ![]()
![]() ,
where the error is simply due to the statistics. This value is very similar (see Fig. 10) to the P fraction observed in other GCs by Carretta et al. (2009a: on average
,
where the error is simply due to the statistics. This value is very similar (see Fig. 10) to the P fraction observed in other GCs by Carretta et al. (2009a: on average ![]() with
rms = 7%), regardless of their mass, metallicity, and global
parameters. The constant fraction of first generation stars is an
important constraint in models of formation of GCs.
with
rms = 7%), regardless of their mass, metallicity, and global
parameters. The constant fraction of first generation stars is an
important constraint in models of formation of GCs.
The observed fraction of intermediate stars found in M 54 is
![]() = 46
= 46 ![]()
![]() and
it does not look peculiar. However, M 54 has the highest fraction
of second generation stars with extreme composition found to date in
our sample of 20 GCs, exceeding the previous record achieved for
NGC 2808 (Carretta et al. 2009a), of
and
it does not look peculiar. However, M 54 has the highest fraction
of second generation stars with extreme composition found to date in
our sample of 20 GCs, exceeding the previous record achieved for
NGC 2808 (Carretta et al. 2009a), of
![]() = 28
= 28 ![]()
![]() (see Fig. 10).
(see Fig. 10).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg11.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg50.png)
|
Figure 11: Cumulative distributions of the distances from the cluster centre relative to stars in M 54 belonging to the P, I, and E stellar components. |
| Open with DEXTER | |
The cumulative distributions of radial distances from the centre of M 54 for the three P, I, and E stellar components are shown in Fig. 11. First generation stars are less concentrated than the I stars, with a quite high level of confidence. No conclusion can be drawn with high statistical significance about the radial distribution of the E component.
To summarise, both M 54 and ![]() Cen (see Fig. 12)
extend to the most massive GCs in the Galaxy, the correlation between
the extension of the Na-O anticorrelation and the total cluster mass
(using the total visual absolute magnitude as proxy). This
supports the definition of GC given in Carretta et al. (2010a) as those clusters exhibiting the Na-O anticorrelation.
Cen (see Fig. 12)
extend to the most massive GCs in the Galaxy, the correlation between
the extension of the Na-O anticorrelation and the total cluster mass
(using the total visual absolute magnitude as proxy). This
supports the definition of GC given in Carretta et al. (2010a) as those clusters exhibiting the Na-O anticorrelation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg12.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg51.png)
|
Figure 12:
Relation between the total absolute magnitude of clusters and the IQR[O/Na]. M 54 (circle) and |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg13.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg52.png)
|
Figure 13:
Na-O anticorrelation in M 54 for the stars of the metal-rich ( upper left panel) and the metal-poor ( upper right panel) components analysed here. The corresponding lower panels show the same in |
| Open with DEXTER | |
However, as anticipated in Carretta et al. (2010b),
our most striking finding is that this feature has a clearly different
extent if we consider separately the metal-poor and metal-rich
components in M 54, as shown in the upper panels of Fig. 13.
The average metallicity [Fe/H] = -1.56 dex is adopted as the
separation limit in metallicity. The minimum value [Na/Fe]
![]() is the same for both the metal-rich and metal-poor population (so that the P fractions are similar, within the errors:
is the same for both the metal-rich and metal-poor population (so that the P fractions are similar, within the errors:
![]()
![]()
![]() and
and
![]()
![]()
![]() ). However, the E fractions differ dramatically such taht
). However, the E fractions differ dramatically such taht
![]()
![]()
![]()
![]()
![]()
![]() .
As a consequence, the extension of the Na-O anticorrelation,
which is driven by the E component, is much longer for the
metal-rich component: IQR[O/Na]
.
As a consequence, the extension of the Na-O anticorrelation,
which is driven by the E component, is much longer for the
metal-rich component: IQR[O/Na]
![]() ,
compared to a modest IQR[O/Na]
,
compared to a modest IQR[O/Na]
![]() of the metal-poor component. The corresponding distributions of the [O/Na] ratio, shown in Fig. 14, appear to be unequivocally different.
of the metal-poor component. The corresponding distributions of the [O/Na] ratio, shown in Fig. 14, appear to be unequivocally different.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{14924fg14.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg63.png)
|
Figure 14: Distribution of the [O/Na] ratios in the metal-rich ( lower panel) and metal-poor ( upper panel) components in M 54. |
| Open with DEXTER | |
Even more interestingly, we also found the same phenomenon in ![]() Cen, as shown in Fig. 13 (lower panels; see also Carretta et al. 2010b)! This
feature, observed in the data since the work of NDC95, seems to have been almost overlooked up to now
Cen, as shown in Fig. 13 (lower panels; see also Carretta et al. 2010b)! This
feature, observed in the data since the work of NDC95, seems to have been almost overlooked up to now![]() . In truth, NDC95 already (p. 695, left column) noted an apparent dependence
of the operation of the ON cycle on [Fe/H], confirming early findings by Cohen & Bell (1986) and Paltoglou & Norris (1989). NDC95 stated that they were unable to offer any explanation of this result for the
. In truth, NDC95 already (p. 695, left column) noted an apparent dependence
of the operation of the ON cycle on [Fe/H], confirming early findings by Cohen & Bell (1986) and Paltoglou & Norris (1989). NDC95 stated that they were unable to offer any explanation of this result for the ![]() Cen stars.
However, at the time, changes in abundances resulting in the
Na-O anticorrelation were mostly interpreted as internal changes
due to evolutionary mixing in the observed stars. Only a few years
later, Gratton et al. (2001) discovered the Na-O anticorrelation among unevolved cluster stars, changing forever the interpretative framework.
Cen stars.
However, at the time, changes in abundances resulting in the
Na-O anticorrelation were mostly interpreted as internal changes
due to evolutionary mixing in the observed stars. Only a few years
later, Gratton et al. (2001) discovered the Na-O anticorrelation among unevolved cluster stars, changing forever the interpretative framework.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{14924fg15.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg64.png)
|
Figure 15: Abundance ratios [O/Fe] ( upper panel) and [Na/Fe] ( lower panel) for stars in M 54+Sgr in the present work and in the literature. Blue open circles and blue filled squares are our stars in M 54 with GIRAFFE and UVES spectra, respectively. Green open circles and filled squares are our stars in Sgr with GIRAFFE and UVES spectra, respectively. Open black star symbols are 5 giants in M 54 from Brown et al. (1999), black crosses are 5 giants in Terzan 7, and filled triangles giants in Sgr from S07. Black open ``star explosion'' symbols are Sgr giants from Smecker-Hane & McWilliam (2009, submitted). Finally, small grey symbols are samples of Galactic field stars (Fulbright 2000; Gratton et al. 2003; Reddy et al. 2003; Venn et al. 2004). |
| Open with DEXTER | |
Thus, we find that a common feature of the two most massive GCs in
the Galaxy, both with a large metallicity spread, is to show a
different extension of the Na-O anticorrelation in their
metal-poor and metal-rich components, with the latter reaching higher
degrees of processing by proton-capture reaction in H-burning at high
temperature![]() .
.
What about the stars in the Sgr nucleus? In Fig. 15,
the run of [O/Fe] and [Na/Fe] ratios as a function of
metallicity is shown for both M 54 and SgrN from this work, and
compared to literature samples: BWG99 for M 54, S07 for
Terzan 7, another GC associated with Sgr, and again S07 and SHM09
for Sgr (main body)![]() .
.
In the following, when comparing abundances in M 54 with those in
the SgrN, we consider the metal-poor and the metal-rich cluster
components (shown as blue open circles) together; the SgrN data from
our study are plotted as green open circles. For figures referring to a
single cluster (either M 54 or ![]() Cen), stars in the metal-rich and metal-poor components are indicated
with filled red and blue symbols, respectively, when relevant to the discussion.
Cen), stars in the metal-rich and metal-poor components are indicated
with filled red and blue symbols, respectively, when relevant to the discussion.
The large spread in O and Na abundances (anticorrelated with each other) is confined only to stars in M 54. Those in SgrN represent a run of these elements as a function of the metallicity typical of Galactic field stars, apart from the well-known offsets already observed for stars in Sgr (S07, SHM09 and references therein). The [O/Fe] ratios are clearly below the mean locus of Galactic stars and Na is also quite deficient in Sgr stars with respect to disk stars in the solar neighbourhood. The scatter we found in O abundances for SgrN stars is larger than in the results by S07, based on higher dispersion UVES spectra. We propose that part of our scatter can be explained by our use of intermediate resolution GIRAFFE spectra, in particular at these high metallicities, where the effect of unrecognised blends might be more severe. However, part of the observed scatter may also be genuine, intrinsic to the Sgr stellar population, as shown in the bottom panel of Fig. 15, where the dispersion in Na for our data is roughly comparable to the results of SHM09, obtained with HIRES at the Keck telescope (open ``star explosion'' symbols).
A couple of stars, attributed to SgrN on purely photometric criteria,
instead exhibited abundances (Fe, O, Na) similar to those of
stars in M 54. The same pattern was found by SHM09 in their
star I-73: its composition ([O/Fe] = -0.91,
as quoted in McWilliam & Smecker-Hane 2005a; [Al/Fe] = +1.40, [Na/Fe] = +0.38, [Fe/H] = -1.13, SHM09, with our solar
abundances) makes its membership of M 54 very likely![]() .
Anyway, even including these few stars in the M 54 sample would
not change our
results; in contrast, they would be strengthened, since these
stars are on the metal-rich side of the metallicity distribution in
the cluster.
.
Anyway, even including these few stars in the M 54 sample would
not change our
results; in contrast, they would be strengthened, since these
stars are on the metal-rich side of the metallicity distribution in
the cluster.
In summary, the GC M 54 shows a well developed, very extended Na-O anticorrelation that is not observed in the surrounding nucleus of the Sgr dSph. We note that the same occurrence seems to hold for another dwarf galaxy, Fornax, where evidence of stars participating in a Na-O anticorrelation are found among its GCs (Letarte et al. 2006), but not among field stars in the galaxy itself (Shetrone et al. 2003). The Na-O anticorrelation is thus a distinctive signature of some event only occurring in the formation and early evolution of GCs. We return later to this point.
6 The high temperature Mg-Al cycle
The proton-capture reactions involving Mg, Al (and Si, see Yong et al. 2005; Carretta et al. 2009b) require a much higher temperature regime and consequently allow us to probe the contribution from polluters of, on average, higher mass.
Al abundances were derived from the subordinate doublet at 6696-98 Å, only for stars observed with UVES. The Mg abundances are typically obtained from two to three high excitation lines, while abundances of Si (partly produced in proton-capture reactions if the temperature is high enough) are estimated from several transitions (see Carretta et al. 2009b for details; and Gratton et al. 2003 for the atomic parameters).
A summary of the correlations and anticorrelations among elements involved in the Mg-Al cycle of H burning at high temperatures is given in Fig. 16 for stars analysed in this work as well as in previous studies, for both M 54 and the Sgr dwarf galaxy.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg16.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg65.png)
|
Figure 16: Summary of the (anti)correlations involved in the Mg-Al cycle for stars of SgrN and of M 54 analysed in the present work and in previous literature studies. Symbols are as in Fig. 15. |
| Open with DEXTER | |
A clear, strong correlation between abundances of Na and Al is seen in
M 54 from our data, which is clearly supported by the five stars
analysed by BWG99. Considering all samples together, stars in SgrN seem
to have a roughly constant Na level. Star SHM09=I-73 has a
very high Al abundance, comparable to some of the M 54 stars:
this supports its membership of the cluster and not of
SgrN. In this respect, the ratio [Na/Al] can be used as a
useful diagnostic. As discussed e.g. by CJ09 in the case of ![]() Cen, a constant ratio [Na/Al]
Cen, a constant ratio [Na/Al] ![]() -0.2 dex is expected if only SNe contributed to the metal
enrichment, because Na and Al production have a similar dependence on
metallicity (Arnett 1971; Woosley & Weaver 1995).
On the other hand, in the dense environment of GCs, other
polluters may raise the Na and Al abundances over the level
possible to SNe alone. However, these enhancements might be (and
usually are) not scaled in lockstep, due e.g. to the different
temperature thresholds required to trigger the Ne-Na and Mg-Al cycles.
Hence,
we may regard any large deviation of the ratio [Na/Al] from the
value of -0.2 dex as probably being caused by proton-capture
reactions polluting cluster stars. This ratio is -1.02 dex for the
suspected cluster star I-73 in SHM09, but -0.51 dex
for the most metal-poor star ([Fe/H] = -1.62 dex) in
their sample, again casting some doubts on the unambiguous
classification of the most metal-poor objects as genuine example of the
Sgr nuclear component. We
note that two other stars (I-242 and I-38) have [Na/Al]
-0.2 dex is expected if only SNe contributed to the metal
enrichment, because Na and Al production have a similar dependence on
metallicity (Arnett 1971; Woosley & Weaver 1995).
On the other hand, in the dense environment of GCs, other
polluters may raise the Na and Al abundances over the level
possible to SNe alone. However, these enhancements might be (and
usually are) not scaled in lockstep, due e.g. to the different
temperature thresholds required to trigger the Ne-Na and Mg-Al cycles.
Hence,
we may regard any large deviation of the ratio [Na/Al] from the
value of -0.2 dex as probably being caused by proton-capture
reactions polluting cluster stars. This ratio is -1.02 dex for the
suspected cluster star I-73 in SHM09, but -0.51 dex
for the most metal-poor star ([Fe/H] = -1.62 dex) in
their sample, again casting some doubts on the unambiguous
classification of the most metal-poor objects as genuine example of the
Sgr nuclear component. We
note that two other stars (I-242 and I-38) have [Na/Al] ![]() -0.5 dex, which is quite different from the value expected from SNe. However, their high metallicity ([Fe/H]
-0.5 dex, which is quite different from the value expected from SNe. However, their high metallicity ([Fe/H] ![]() -0.46) makes it very difficult to misclassify them as stars in M 54.
-0.46) makes it very difficult to misclassify them as stars in M 54.
A quite good anticorrelation is observed between Mg and Al for M 54 (upper right panel in Fig. 16), with moderate Mg depletions associated with large enhancements in Al abundances, in both our sample and BWG99. This behaviour is evidently not present in the Sgr field stars, where, in contrast, Mg and Al abundances are possibly positively correlated with each other.
The large enhancements in Al abundances are a signature of very high temperatures achieved during H-burning. At this high temperature, we expect leakage from the Mg-Al chain (Yong et al. 2005; Carretta et al. 2009b) producing some fresh Si. This is exactly what is observed in M 54 (Fig. 16, bottom-left panel). There seems to be a small offset in the [Si/Fe] ratio with respect to BWG99, even after correcting for different solar abundances. Apart from this, a good correlation is again observed only for cluster stars. We also note in this panel that the two metal-poor stars in the Sgr sample of SHM09 (the above mentioned O-depleted star I-73 and the most metal-poor object in their sample, star I-41, with [Fe/H] = -1.62 dex) are well mixed with the stars of M 54, as also seen for the Al-Na correlation, strengthening the conclusions reached above concerning their possible membership to M 54.
Most stars in M 54 show a correlation between the ![]() -elements Mg and Si. However, although more confused than expected, a Mg-Si anticorrelation is rather evident in the bottom-right panel of Fig. 16: the most Mg-poor stars in M 54 (reaching respectable depletions of [Mg/Fe]
-elements Mg and Si. However, although more confused than expected, a Mg-Si anticorrelation is rather evident in the bottom-right panel of Fig. 16: the most Mg-poor stars in M 54 (reaching respectable depletions of [Mg/Fe] ![]() -0.5 dex)
are also Si-rich. In contrast, the field stars of SgrN
exhibit the normal correlation expected between two elements from
-0.5 dex)
are also Si-rich. In contrast, the field stars of SgrN
exhibit the normal correlation expected between two elements from ![]() -capture processes.
-capture processes.
The observed variations in Al are quite large in M 54; this GC does not resemble clusters such as M 4, being more NGC 2808-like. This is not unexpected since we found (Carretta et al. 2009b) that the production of Al is a tight function of a bi-linear combination of MV and [Fe/H], with aluminium being enhanced mostly in metal-poor and/or massive GCs. M 54 obviously exhibits both these characteristics, thereby its stars show the signatures of the very high temperatures reached by proton-capture reactions in H-burning (>65 MK, as suggested by the production of 28Si, see Arnould et al. 1999).
Unfortunately, we have only a handful of stars (the 7+2 with
UVES spectra) where the main outcome of the Mg-Al cycle (Al) is
measurable. On the other hand, if the similarities between M 54
and ![]() Cen
are not merely a fortuitous coincidence, we should see the signature of
polluters with on average a high mass (temperature) also in
Cen
are not merely a fortuitous coincidence, we should see the signature of
polluters with on average a high mass (temperature) also in ![]() Cen. This is exactly what is shown in Figs. 17 and 18 using data from high resolution spectra by NDC95 and from intermediate resolution spectroscopy of a large sample of giants in
Cen. This is exactly what is shown in Figs. 17 and 18 using data from high resolution spectra by NDC95 and from intermediate resolution spectroscopy of a large sample of giants in ![]() Cen with Na and Al abundances derived by CJ09. In both panels of Fig. 17,
the Na-Al correlation has more or less the same extent as the one
we found in M 54; moreover, because of to the much larger sample,
the appearance of a clear bimodality (already hinted at by our limited
sample) is striking: apart from a few outliers, stars in
Cen with Na and Al abundances derived by CJ09. In both panels of Fig. 17,
the Na-Al correlation has more or less the same extent as the one
we found in M 54; moreover, because of to the much larger sample,
the appearance of a clear bimodality (already hinted at by our limited
sample) is striking: apart from a few outliers, stars in ![]() Cen seem to be tightly clustered into two distinct groups, at high-Na/high-Al and low-Na/low-Al, respectively.
Cen seem to be tightly clustered into two distinct groups, at high-Na/high-Al and low-Na/low-Al, respectively.
| Figure 17:
Na-Al correlation for giants in |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg18.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg68.png)
|
Figure 18:
Mg-Al anticorrelation for giants in |
| Open with DEXTER | |
More importantly, in these extensive sets of abundances we retrieve, for elements involved in the Mg-Al chain, the same phenomenon seen for elements participating in the ON and NeNa cycles: the Na-Al correlation (as well as the Mg-Al anticorrelation) is preferentially far more extended among the cluster stars of the metal-rich component than in more metal-poor ones. The same effect is also visible in our smaller sample of stars in M 54. A metallicity dependence of the distributions of Na and Al was already noted by CJ09: by exploiting their large sample, combined with that of Johnson et al. (2008), CJ09 were able to trace in the Al distribution the equivalent of the primordial, intermediate, and extreme populations we have defined from the Na-O anticorrelation. Moreover, they found that in the [Al/Fe] distribution the components of metal-rich and metal-poor stars differed at the 94% level of confidence (using [Fe/H] = -1.2 as a separating metallicity).
Finally, the same sort of segregation in metallicity can be recognised also for the Si-Al correlation in Fig. 19, although less clearly; we recall that 28Si production is the result of only a secondary leakage in the main Mg-Al cycle.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg19.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg69.png)
|
Figure 19:
Si-Al correlation for giants in |
| Open with DEXTER | |
While some hints of a metallicity-dependence for light elements involved in proton-capture reactions were previously found for ![]() Cen,
this is the first time they are reliably assessed for M 54.
Moreover, the novelty of our findings is to consider that the entire pattern of anticorrelations and correlations established for these elements is clearly different between the
most metal-rich and most metal-poor stellar components in the two most massive clusters in the Galaxy.
We assume that this cannot be ruled out as a mere chance coincidence
and must be incorporated as a constraint in any formation model about
these objects.
Cen,
this is the first time they are reliably assessed for M 54.
Moreover, the novelty of our findings is to consider that the entire pattern of anticorrelations and correlations established for these elements is clearly different between the
most metal-rich and most metal-poor stellar components in the two most massive clusters in the Galaxy.
We assume that this cannot be ruled out as a mere chance coincidence
and must be incorporated as a constraint in any formation model about
these objects.
7 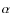 -elements and Fe-group elements
-elements and Fe-group elements
We measured a number of lines due to several ![]() -
(Mg, Si, Ca and Ti) and Fe-peak elements (Sc, V, Cr, Mn, Co,
Ni, Cu, beside obviously Fe) in our UVES and GIRAFFE spectra of
stars of M 54 and SgrN. Mean abundances are listed in Table 4,
where we provide the number of stars where lines were measured and the
rms scatter of the mean. Hyperfine structure was taken into
account for Sc, Mn, and Co following Gratton et al. (2003) and for Cu from Sobeck (priv. comm.).
-
(Mg, Si, Ca and Ti) and Fe-peak elements (Sc, V, Cr, Mn, Co,
Ni, Cu, beside obviously Fe) in our UVES and GIRAFFE spectra of
stars of M 54 and SgrN. Mean abundances are listed in Table 4,
where we provide the number of stars where lines were measured and the
rms scatter of the mean. Hyperfine structure was taken into
account for Sc, Mn, and Co following Gratton et al. (2003) and for Cu from Sobeck (priv. comm.).
Table 4: Mean abundances from UVES and GIRAFFE spectra for stars in the GC M 54 and Sgr nucleus.
Abundances of all species in the individual stars are given in Tables 5-7, only available at CDS.
7.1 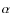 -elements
-elements
For Ti, lines of both neutral and singly ionised species were available in the spectral range of the UVES spectra; the good ionisation equilibrium that we found for both Fe and Ti (see Table 4) supports the reliability of the adopted parameters, also for stars of the SgrN.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg20.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg70.png)
|
Figure 20:
Run of abundance ratios for the |
| Open with DEXTER | |
The run of the ![]() -elements Mg, Si, Ca, and Ti I as a function of metallicity are shown in Figs. 20 and 21.
We recall that some stars in M 54 appear to be quite Mg-poor,
showing signatures of extensive processing by H-burning at high
temperature. For the Sgr galaxy, on the other hand, a rather tight
relation between [Mg/Fe] and [Fe/H] is visible
in the upper panel of Fig. 20,
with maybe a hint of a residual offset between our values and those
of S07. No Mg-poor stars appear in this component at any
metallicity, confirming that the stars in SgrN are not formed from gas
enriched by light elements as in the case of cluster stars. Stars in
M 54 observed by BWG99 and the few giants in Ter 7 studied by
S07 have properties that are very well mixed with our M 54 sample
and with the stars in the Sgr nucleus, respectively.
-elements Mg, Si, Ca, and Ti I as a function of metallicity are shown in Figs. 20 and 21.
We recall that some stars in M 54 appear to be quite Mg-poor,
showing signatures of extensive processing by H-burning at high
temperature. For the Sgr galaxy, on the other hand, a rather tight
relation between [Mg/Fe] and [Fe/H] is visible
in the upper panel of Fig. 20,
with maybe a hint of a residual offset between our values and those
of S07. No Mg-poor stars appear in this component at any
metallicity, confirming that the stars in SgrN are not formed from gas
enriched by light elements as in the case of cluster stars. Stars in
M 54 observed by BWG99 and the few giants in Ter 7 studied by
S07 have properties that are very well mixed with our M 54 sample
and with the stars in the Sgr nucleus, respectively.
The [Si/Fe] ratios follow an almost flat distribution as a function of the metallicity in the whole M 54 sample; an offset again seems to be present in the average [Si/Fe] ratio for M 54 between ourselves and BWG99 (lower panel in Fig. 20).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg21.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg71.png)
|
Figure 21:
Run of abundance ratios for the |
| Open with DEXTER | |
We found a larger scatter in our [Ca/Fe] ratios among our SgrN stars with respect to literature sample and, viz,
a smaller scatter concerning Ti; in particular,
[Ti/Fe] ratios derived by S07 seem to be very low compared to
abundances from our study and from SHM09. We note that adding stars
from Monaco et al. (2005)
would not alleviate the discrepancy, since they would fall half
way between S07 values and ours+SHM09. In M 54, we found that
[Ca/Fe] slightly increases as [Fe/H] increases; this same feature is
also present in the next-of-kin cluster ![]() Cen, which is clearly evident in the NDC95 data, and in the analysis by CJ09.
Cen, which is clearly evident in the NDC95 data, and in the analysis by CJ09.
In all plots of ![]() -elements, we can identify similar features. The metal-poor component, represented by M 54 stars, has high levels of
-elements, we can identify similar features. The metal-poor component, represented by M 54 stars, has high levels of ![]() -elements
that are typical of the Galactic metal-poor (halo) component.
At higher metallicities, there is a smooth, steady decline in all
abundance ratios of the Sgr field component. This pattern, offset
in the high [Fe/H] regime at lower [
-elements
that are typical of the Galactic metal-poor (halo) component.
At higher metallicities, there is a smooth, steady decline in all
abundance ratios of the Sgr field component. This pattern, offset
in the high [Fe/H] regime at lower [![]() /Fe] ratios
with respect to the Galactic disk population, is present in both our
data and those of Sgr field stars by SHM09. This is a well known
feature of Sgr since the first large samples of stars in this
disrupting galaxy were gathered for abundance analysis (see
Smecker-Hane & McWilliam 2002, 2009; S07, and references therein).
/Fe] ratios
with respect to the Galactic disk population, is present in both our
data and those of Sgr field stars by SHM09. This is a well known
feature of Sgr since the first large samples of stars in this
disrupting galaxy were gathered for abundance analysis (see
Smecker-Hane & McWilliam 2002, 2009; S07, and references therein).
Elements derived by ![]() -capture
processes are produced almost exclusively in massive, fast evolving
stars that end their life as core-collapse SNe (e.g. Wheeler
et al. 1989, and references therein). The elemental ratio [
-capture
processes are produced almost exclusively in massive, fast evolving
stars that end their life as core-collapse SNe (e.g. Wheeler
et al. 1989, and references therein). The elemental ratio [![]() /Fe], and in particular the knee point as a function of metallicity, is driven by the clock
of stellar evolution, since the major producers of
iron (and iron-peak elements) are the smaller mass stars exploding as
type Ia SNe after a time delay of about 0.5-3 Gyr with
respect to the original episode of star formation (Tinsley 1979; Matteucci & François 1989). The high and almost constant level of
/Fe], and in particular the knee point as a function of metallicity, is driven by the clock
of stellar evolution, since the major producers of
iron (and iron-peak elements) are the smaller mass stars exploding as
type Ia SNe after a time delay of about 0.5-3 Gyr with
respect to the original episode of star formation (Tinsley 1979; Matteucci & François 1989). The high and almost constant level of ![]() -elements in M 54 shows that stars in this cluster formed before the typical e-folding time for SN Ia contributing their
ejecta to the gas pool. The complete lack of stars more metal poor than [Fe/H]
-elements in M 54 shows that stars in this cluster formed before the typical e-folding time for SN Ia contributing their
ejecta to the gas pool. The complete lack of stars more metal poor than [Fe/H] ![]() -2
also suggests that the burst of star formation originating M 54
probably occurred in a system already enriched by the ejecta of massive
stars.
-2
also suggests that the burst of star formation originating M 54
probably occurred in a system already enriched by the ejecta of massive
stars.
From what it is observed in the Sgr galaxy (Figs. 20 and 21)
it is not easy to detect a turn down point in every plot. However,
if we consider M 54 itself as a representative sample of the
metal-poor component of the Sgr complex![]() we can conclude that a knee can be confidently located at metallicities in the range [Fe/H] =
we can conclude that a knee can be confidently located at metallicities in the range [Fe/H] =
![]() .
By averaging Si, Ca, and Ti - silicon being only
slightly involved in proton-capture reactions - the position of
the knee seems to be confirmed at [Fe/H]
.
By averaging Si, Ca, and Ti - silicon being only
slightly involved in proton-capture reactions - the position of
the knee seems to be confirmed at [Fe/H] ![]() -1.3 dex. This feature confirms once more that Sgr was most likely
subject to a lower star-formation rate in its evolution than the Milky
Way, whose knee occurs at a metallicity of
-1.3 dex. This feature confirms once more that Sgr was most likely
subject to a lower star-formation rate in its evolution than the Milky
Way, whose knee occurs at a metallicity of ![]() .
.
7.2 Fe-peak elements
Abundances of Sc II, V I, Cr I, and Ni I are displayed as a function of the metallicity in Figs. 22 and 23 for stars analysed in M 54 and SgrN.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg22.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg74.png)
|
Figure 22: Run of abundance ratios for Sc II and V I. Symbols are as in Fig. 15. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg23.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg75.png)
|
Figure 23: Run of abundance ratios for Cr I and Ni I. |
| Open with DEXTER | |
These elements on average (see Table 4) closely track Fe in M 54, with a flat distribution around a solar [El/Fe] ratio for both the metal-rich and metal-poor components (maybe apart from V I). On the other hand, all elements belonging to the Fe-group exhibit a small deficiency with respect to the solar ratio in stars of SgrN (again, with the exception of V). The offsets observed in the run of Fe-group elements with respect to previous analysis are easily accounted for by the different scales of adopted atmospheric and atomic parameters.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg24.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg76.png)
|
Figure 24: [Mn/Fe] as a function of
metallicity for field stars (tiny squares)
from several studies (see text); the average values for M 54 (this
study, large blue filled circle) and 19 GCs of this project
(Gratton et al. 2006; Carretta et al. 2007b, Carretta et al., in prep.) are indicated by red filled circles, with 1 |
| Open with DEXTER | |
The run of [Mn/Fe] as a function of the metallicity (Fig. 24) is important because Mn production is related to the available neutron excess (see Arnett 1971). By comparing Mn abundances in environments with different metallicity, McWilliam et al. (2003) concluded that Mn yields were metallicity-dependent in both type Ia SNe and core-collapse SNe. As a consequence, the deficiency of Mn observed in metal-rich stars of Sgr can be interpreted as evidence of a significant contribution from metal-poor SNe Ia, even at high metallicities. Therefore, the yields from these metal-poor SNe, incorporated in the gas from where the metal-rich Sgr component formed, could explain the underabundance in [Mn/Fe] observed in Sgr stars at high metal abundance, when compared with Galactic field stars at the same metallicity.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg25.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg77.png)
|
Figure 25: The ratio [Cu/Fe] as a function of metallicity for field stars (tiny squares) of the Galactic halo and disk from Mishenina et al. (2002) and for the stars of M 54 and SgrN with UVES spectra (blue and green large filled squares, respectively) from the present study. |
| Open with DEXTER | |
The same conclusion is obtained from the abundance ratios [Cu/Fe] (see McWilliam & Smecker-Hane 2005b). The large deficiency in Cu for metal-rich Sgr stars, is also visible in our data (albeit quite sparse, see Fig. 25). This underabundance, with respect to field stars in the Galaxy, can be explained as being due to a substantial contribution from metal-poor SN Ia, since Cu is almost entirely produced by SN II, whose Cu yields are metallicity dependent (Woosley & Weaver 1995). At the high metallicity regime sampled by the SgrN component, the only way to reproduce this deficiency is then to invoke an extra contribution from metal-poor type Ia SNe to the gas pool from which these stars formed. Here we only note that our stars in M 54 are well mixed with those attributed by McWilliam & Smecker-Hane (2005b, their Fig. 1) to the metal-poor component of the Sgr nucleus, stressing once again the difficulty of disentangling cluster and nucleus at these low metallicities.
The analysis of elements produced by neutron-capture processes in stars of M 54 and SgrN will be presented in a separate paper.
8 Testing the scenario for GC formation
8.1 General considerations
In Carretta et al. (2010a), we noted that the definition of globular cluster commonly used is not entirely unambiguous. There are old open clusters whose masses and sometime ages may exceed those of populous stellar clusters in the Magellanic Clouds and that lie on the extension of the locus populated by Galactic GCs in the MV versus age plane. To draw an objective distinction, we then dubbed as bona fide globular clusters those where a Na-O anticorrelation is found. Carretta (2006) speculated that this feature is so universal among GCs that it should be related to their origin. We subsequently expanded this view to a comprehensive, albeit still qualitative, scenario for the formation of GCs as distinct from other systems of similar mass (such as dwarf spheroidal galaxies, see Carretta et al. 2010a), for which the Na-O anticorrelation is not observed. Whenever data are indeed available for both GCs and field stars in the same galaxy (Fornax - Letarte et al. 2006; Shetrone et al. 2003, Sgr - this study), only stars in clusters do actually contribute to the Na-O anticorrelation.
The main differences between GCs and dwarf dSphs are quite evident when
comparing the two massive clusters examined in this paper with typical
low mass dSphs: the two GCs lie at least 3 times (M 54,
and much more ![]() Cen)
closer to the central potential well of the Milky Way than any of
the dSphs, except for Sgr itself. This obvious observation spurred us
to outline in Carretta et al. (2010a)
a model where the ancestors of both dSphs and GCs started as
cosmological fragments, but those that ultimately evolved into
currently observed GCs started their evolution much closer to the
central region of our Galaxy.
Cen)
closer to the central potential well of the Milky Way than any of
the dSphs, except for Sgr itself. This obvious observation spurred us
to outline in Carretta et al. (2010a)
a model where the ancestors of both dSphs and GCs started as
cosmological fragments, but those that ultimately evolved into
currently observed GCs started their evolution much closer to the
central region of our Galaxy.
Very briefly, the model sketched predicts that strong interactions with the main Galaxy trigger the transformation of some gas into stars in the first phases. This event forms a precursor whose core-collapse SNe enrich the system in metals, triggering a burst of star formation. At the end, an expanding association free of the primordial gas, swept away by energetic winds by SN II and massive stars, remains. After a while, the low velocity winds from evolving fast-rotating massive stars or intermediate-mass AGB stars replenish (or a cooling flow re-collects into) the central regions a new gas reservoir. It is only in this phase that a second generation of stars can be born as a very compact central cluster, which is what we currently observe as a GC, together with the primordial stars.
The advantage of this scenario is to include a coherent picture of the different stellar generations in GCs (Gratton et al. 2001; Carretta et al. 2009a) within a global view of the Galaxy formation. This approach is not new, but started with the work of Searle & Zinn (1978). Several pieces of support can be found in the scientific literature: dynamical interactions are known to be a strong trigger of star formation in galactic satellites, as suggested by both observations (Zaritsky & Harris 2004) and theoretical cosmological simulations (e.g. Kravtsov et al. 2004).
Moreover, we provided in Carretta et al. (2010a)
several arguments suggesting that the present GCs started their
evolution as objects whose baryonic masses were at least 20 times
higher than the currently observed masses, and successively lost a
large fraction of their primordial mass (as also found by
theoretical modelling, see e.g. Baumgardt et al. 2008; D'Ercole et al. 2008).
These arguments (including metallicity, chemistry, kinematic, and
density distribution) will not be repeated; here we highlight two other
convincing pieces of evidence that are appropriate when discussing
cases such as M 54 and ![]() Cen, at the very high mass end of the mass distribution of GCs.
Cen, at the very high mass end of the mass distribution of GCs.
The first piece of evidence comes from the comparison between nuclear
star clusters, residing at the centre of dwarf galaxies, and GCs with
extended hot HBs made by Georgiev et al. (2009). In their Fig. 4b, they show that in the mass-size plane (as represented by MV versus half mass radius ![]() )
massive Galactic GCs occupy the same region populated by nuclear star clusters, but GCs such as M 54 and
)
massive Galactic GCs occupy the same region populated by nuclear star clusters, but GCs such as M 54 and ![]() Cen
are offset toward larger sizes. They propose that this finding can be
explained by the expansion of the tidal radius, as well as of
the
Cen
are offset toward larger sizes. They propose that this finding can be
explained by the expansion of the tidal radius, as well as of
the ![]() ,
that follows the accretion of the fragments into the halo of a much
more massive galaxy. This evidence is quite appealing, since it fits in
several ways with our outlined scenario, where all GCs originate in
much larger fragments: M 54 and
,
that follows the accretion of the fragments into the halo of a much
more massive galaxy. This evidence is quite appealing, since it fits in
several ways with our outlined scenario, where all GCs originate in
much larger fragments: M 54 and ![]() Cen illustrate in two snapshots the likely mechanism of loss of the surrounding host galaxy, already completed for
Cen illustrate in two snapshots the likely mechanism of loss of the surrounding host galaxy, already completed for ![]() Cen and still ongoing in the case of M 54.
Cen and still ongoing in the case of M 54.
The second piece of evidence can be illustrated by repeating for
M 54 an argument originally made by Suntzeff & Kraft (1996) for a closed box chemical evolution model of ![]() Cen. From studies in the solar neighbourhood, we know that the yield per stellar generation is about 0.01 (Tinsley 1979);
this means that some 1% of the available gas is transformed into
metals in a single stellar generation. On the other hand, we found that
metallicities for stars in M 54 range from [Fe/H] = -1.6 to
[Fe/H] = -1.3 dex, i.e. from
Cen. From studies in the solar neighbourhood, we know that the yield per stellar generation is about 0.01 (Tinsley 1979);
this means that some 1% of the available gas is transformed into
metals in a single stellar generation. On the other hand, we found that
metallicities for stars in M 54 range from [Fe/H] = -1.6 to
[Fe/H] = -1.3 dex, i.e. from
![]() to
to
![]() ,
with a change of
,
with a change of ![]() =
0.0005. This is 1/20 of the yield of a stellar generation. We are
then left with
only two options: (i) to selectively lose the metal-rich gas
component (lowering the effective yield per stellar generation)
or (ii) to lose 95% of the gas before transforming into metals. In
the second case, and considering the narrow mass range of the polluters
required to produce the O-Na anticorrelation, we conclude that the
precursors had a baryonic mass some 200 times higher than
M 54 and
=
0.0005. This is 1/20 of the yield of a stellar generation. We are
then left with
only two options: (i) to selectively lose the metal-rich gas
component (lowering the effective yield per stellar generation)
or (ii) to lose 95% of the gas before transforming into metals. In
the second case, and considering the narrow mass range of the polluters
required to produce the O-Na anticorrelation, we conclude that the
precursors had a baryonic mass some 200 times higher than
M 54 and ![]() Cen. This is comparable to the current baryonic mass of the Sgr dwarf galaxy (Majewski et al. 2003; Niederste-Ostholt et al. 2010).
Cen. This is comparable to the current baryonic mass of the Sgr dwarf galaxy (Majewski et al. 2003; Niederste-Ostholt et al. 2010).
8.2 Extension of the model to the high mass range
As sketched in Carretta et al. (2010b), the results we obtained for M 54 (and by extension for ![]() Cen)
might be explained by a very simple extension of the scenario for
cluster formation we considered insofar (Carretta et al. 2010a).
The main modification is to switch from a single cooling flow to
multiple, nearly simultaneous cooling flows, or episodes of gas
gathering. We assume this not to be unlikely in the most massive
objects.
Cen)
might be explained by a very simple extension of the scenario for
cluster formation we considered insofar (Carretta et al. 2010a).
The main modification is to switch from a single cooling flow to
multiple, nearly simultaneous cooling flows, or episodes of gas
gathering. We assume this not to be unlikely in the most massive
objects.
To clarify our conclusions, we first recall our main observational findings:
- 1.
- M 54 has a range in metal abundances of a few tenths of a dex.
- 2.
- The Na-O anticorrelation can be observed at all metallicities.
- 3.
- However, the anticorrelation is more extended at higher metallicities, where we observe a large incidence of extremely O-poor, which are most likely very He-rich stars (that is, the very He-rich population is more metal-rich than the average of the He-normal population).
In our interpretative scenario, the explanation of finding 3
requires appropriate timing. We expect the extension of the
anticorrelation to be determined by the mass of the polluters.
In the case of intermediate-mass AGB stars, large mass
polluters (6-8 ![]() ,
lifetimes
,
lifetimes
![]() Myr, using the isochrones by Marigo et al. 2008)
produce an extended anticorrelation, with very low O abundances,
and large production of He. Smaller mass polluters (5-6
Myr, using the isochrones by Marigo et al. 2008)
produce an extended anticorrelation, with very low O abundances,
and large production of He. Smaller mass polluters (5-6 ![]() ,
lifetime
,
lifetime
![]() Myr)
produce a much less extended anticorrelation, with minimal effects
on He. Hence, to explain the observations we propose that the
metal-poor second generation is formed by the
ejecta of intermediate mass AGB stars, while the metal-rich one is
formed (only)
by the ejecta of the very massive ones. The easiest way to avoid
contribution by massive polluters is to delay the cooling flow
(or gas replenishing): so we need to delay the flowing of the
gas for the metal-poor
component by about 10-30 Myr. This can easily be obtained if we
assume that the metal-rich primordial component formed
Myr)
produce a much less extended anticorrelation, with minimal effects
on He. Hence, to explain the observations we propose that the
metal-poor second generation is formed by the
ejecta of intermediate mass AGB stars, while the metal-rich one is
formed (only)
by the ejecta of the very massive ones. The easiest way to avoid
contribution by massive polluters is to delay the cooling flow
(or gas replenishing): so we need to delay the flowing of the
gas for the metal-poor
component by about 10-30 Myr. This can easily be obtained if we
assume that the metal-rich primordial component formed
![]() Myr later than the metal-poor primordial component. In this case, while the 6-8
Myr later than the metal-poor primordial component. In this case, while the 6-8 ![]() stars of the metal-poor component are in their AGB phase, massive
stars of the metal-rich component continue to explode as
core-collapse SNe. This might
cause a considerable input of energy in the system, preventing the
formation of the cooling flow, and certainly gas collection, until the
rate of SN explosions becomes low enough. A quiet phase then
follows, lasting some tens Myr. In this phase, cooling flow
formation is possible for both the metal-poor component (with AGB
polluters of 5-6
stars of the metal-poor component are in their AGB phase, massive
stars of the metal-rich component continue to explode as
core-collapse SNe. This might
cause a considerable input of energy in the system, preventing the
formation of the cooling flow, and certainly gas collection, until the
rate of SN explosions becomes low enough. A quiet phase then
follows, lasting some tens Myr. In this phase, cooling flow
formation is possible for both the metal-poor component (with AGB
polluters of 5-6 ![]() ), and the metal-rich one (with AGB polluters of 6-8
), and the metal-rich one (with AGB polluters of 6-8 ![]() ).
The second generation stars form nearly simultaneously in the
metal-poor and metal-rich cooling flows: finally, the SN explosion
of stars formed in these cooling flows (or the onset of
type Ia SNe) stops this later phase of star formation.
).
The second generation stars form nearly simultaneously in the
metal-poor and metal-rich cooling flows: finally, the SN explosion
of stars formed in these cooling flows (or the onset of
type Ia SNe) stops this later phase of star formation.
This scenario is actually very similar to what we had already considered for the formation of small clusters (in groups, see Carretta et al. 2010a). The only basic difference is that here we assume that the adjacent star-forming regions also produce a cooling flow. Hence, the main difference is that in this working hypothesis the star formation continues at a high rate for a prolonged period (although shifting toward other regions of the global star-forming area), while in the case of the small mass clusters the star formation declines earlier, though not so rapidly as the residual star formation, and then late SNe do not have an impact on the formation of the cooling flow.
Hidden in this scenario is the hypothesis that metallicity increases with time within the star forming region, i.e., that areas where star formation occurred later are also more metal-rich, which is reasonable but not entirely obvious.
This scenario of course needs verifications (e.g. for what concerns the neutron-capture elements) and it is for the moment quite speculative. However, we conclude that it is on the whole a reasonable extension to higher masses of what we have considered insofar for more typical GCs.
To understand the mechanism we put forward more clearly,
it is necessary to have a deeper look at what is known about star
formation, which is still far from being properly understood. However,
various authors (see the review by McKee & Ostriker 2007,
and references therein) suggest that star formation within a Giant
Molecular Cloud (GMC) occurs on timescales comparable to a few
times (1-3) the crossing time, which is roughly
![]() Myr, where M6 is the mass of the cloud in units of 10
Myr, where M6 is the mass of the cloud in units of 10
![]() .
Using this relation, we find the crossing time to be:
.
Using this relation, we find the crossing time to be:
- 5.6 Myr for 10
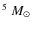 ;
;
- 10 Myr for 10
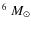 ;
;
- 18 Myr for 10
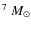 ;
;
- 32 Myr for 10
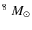 .
.
On the other hand, Galactic GMCs seem to have an upper limit to their mass, of a few 106 ![]() ;
higher masses are usually called a giant molecular association, because
they fragment into smaller pieces. It is not clear if this depends
on either metallicity or environment. This is most ikely the reason why
GCs do not form anymore in the Milky Way, given the low efficiency
with which GMCs can be transformed in clusters. Fragmentation of the
larger molecular
clouds may also lead to more complicated geometries, and then to lower
efficiencies in the cloud-to-cluster transformation.
;
higher masses are usually called a giant molecular association, because
they fragment into smaller pieces. It is not clear if this depends
on either metallicity or environment. This is most ikely the reason why
GCs do not form anymore in the Milky Way, given the low efficiency
with which GMCs can be transformed in clusters. Fragmentation of the
larger molecular
clouds may also lead to more complicated geometries, and then to lower
efficiencies in the cloud-to-cluster transformation.
While these arguments are purely qualitative, they do not appear inconsistent with the scenario we propose. Of course, fine tuning is required to properly match observations, but at least the order of magnitudes for the relevant quantities seem to be correct.
9 Summary
In this paper, we have presented the most extensive survey,
to date, of the chemical composition of red giant stars in
the GC M 54, which lies in the nucleus of the Sgr dwarf
galaxy. We have derived accurate abundances of elements involved in
proton-capture reactions of H-burning at high
temperature (O, Na, Mg, Al, Si), of ![]() -elements,
and of Fe-peak elements for 76 RGB stars in M 54 from
FLAMES spectra. The abundances of the same species are also
homogeneously obtained for a sample of 27 stars within the nuclear
component of Sgr.
-elements,
and of Fe-peak elements for 76 RGB stars in M 54 from
FLAMES spectra. The abundances of the same species are also
homogeneously obtained for a sample of 27 stars within the nuclear
component of Sgr.
For the first time, the metallicity spread within this cluster
is obtained and well constrained by high resolution spectra. The iron
spread found is intermediate in value between those observed in
smaller, normal Galactic GCs and the dispersion in metallicity
associated with the few dwarf galaxies investigated so far. This
finding supports the idea that both M 54 and ![]() Cen
can be identified as nuclear star clusters, once (or still,
in the first case) in the nucleus of dwarf galaxies. In Carretta
et al. (2010b), we already
demonstrated that the most metal-rich tail of the metallicity
distribution is given by SgrN stars in the case of M 54 and
restricted to stars on the anomalous RGB in the case of
Cen
can be identified as nuclear star clusters, once (or still,
in the first case) in the nucleus of dwarf galaxies. In Carretta
et al. (2010b), we already
demonstrated that the most metal-rich tail of the metallicity
distribution is given by SgrN stars in the case of M 54 and
restricted to stars on the anomalous RGB in the case of ![]() Cen.
Cen.
Comparing our results to literature data for ![]() Cen,
we find that these two massive clusters are similar in several
characteristics, the most notable being the presence of multiple
populations, clearly evident from both spectroscopy and photometry.
In particular, the Na-O and the Mg-Al anticorrelations among
proton-capture elements is present for both the metal-poor and the
metal-rich stellar component in each cluster, being more extended for
the second one.
Cen,
we find that these two massive clusters are similar in several
characteristics, the most notable being the presence of multiple
populations, clearly evident from both spectroscopy and photometry.
In particular, the Na-O and the Mg-Al anticorrelations among
proton-capture elements is present for both the metal-poor and the
metal-rich stellar component in each cluster, being more extended for
the second one.
We know that the Na-O anticorrelation is present in all GCs, which is
related to the existence of multiple stellar generations such that it
can be considered the main signature of a bona fide globular
cluster, as distinct from the star formation in other environments
(Carretta et al. 2010a).
As a consequence, the absence of the anticorrelation in the very
metal-rich component at near solar metallicities in both M 54 and ![]() Cen
has led us to conclude that this population was formed by means of
different channels, probably involving the host galaxy (still
observable in the case of M 54).
Cen
has led us to conclude that this population was formed by means of
different channels, probably involving the host galaxy (still
observable in the case of M 54).
The presence and different extension of the Na-O anticorrelation (also supported by the Mg-Al data) for the metal-poor and moderately metal-rich cluster components suggest a simple extension of the scenario for the formation of GCs illustrated in Carretta et al. (2010a). We would require (i) that the primordial population of the metal-rich component be enriched in metals with respect to the metal-poor component; and (ii) that the mass range of the polluters acting to form the second generation be different for the two components (with more massive polluters at work for the metal-rich one, where the anticorrelations are more extended).
We have shown that the simplest way to explain the observed features in M 54 (and by analogy in ![]() Cen)
is to assume that the primordial population of the moderately
metal-rich component formed with a small delay (as much as
10-30 Myr) after the corresponding population of the metal-poor
component, whereas the second generation was formed more or less
simultaneously in both
components.
Cen)
is to assume that the primordial population of the moderately
metal-rich component formed with a small delay (as much as
10-30 Myr) after the corresponding population of the metal-poor
component, whereas the second generation was formed more or less
simultaneously in both
components.
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. We warmly thank Andy McWilliam for sending us his manuscript and data on Sgr in advance of publication. We thank Jennifer Sobeck for sharing the Cu linelist in advance of publication. This work was partially funded by the Italian MIUR under PRIN 2003, 2007 and by the grant INAF 2005 ``Experimenting nucleosynthesis in clean environments''. S.L. is grateful to the DFG cluster of excellence ``Origin and Structure of the Universe'' for partial support. M.B. acknowledges the financial support of INAF through the PRIN-2007 grant CRA 1.06.10.04. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France and of NASA's Astrophysical Data System.
References
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnett, W. D. 1971, ApJ, 166, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Arnould, M., Goriely, S., & Jorissen, A. 1999, A&A, 347, 572 [NASA ADS] [Google Scholar]
- Battaglia, G., Tolstoy, E., Helmi, A., et al. 2006, A&A, 459, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baumgardt, H., Kroupa, P., & Parmentier, G. 2008, MNRAS, 384, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., & Freeman, K. C. 2003, MNRAS, 346, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., Campbell, S. W., Lattanzio, J. C., & Norris, J. E. 2007, MNRAS, 377, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Ibata, R. A., Chapman, S. C., et al. 2008, AJ, 136, 1147 (B08) [NASA ADS] [CrossRef] [Google Scholar]
- Boker, T. 2008, ApJ, 672, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Carretta, E., Gratton, R. G., et al. 2001, AJ, 121, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Carretta, E., Gratton, R. G., et al. 2010, A&A, 519, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. A., Wallerstein, G., & Gonzalez, G. 1999, AJ, 118, 1245 (BWG99) [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2006, AJ, 131, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2008, Mem.SAIt., 79, 508 [NASA ADS] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., Lucatello, S., & Momany, Y. 2007a, A&A, 464, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007b, A&A, 464, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007c, A&A, 464, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009b, A&A, 505, 139 (Paper VIII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., D'Orazi, V., & Lucatello, S. 2009c, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010a, A&A, 516, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010b, ApJ, 714, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonnel, C. 2005, in IAU Symp., 228, 347 [Google Scholar]
- Charbonnel, C. 2006, EAS, Publ. Ser., 19, 125 [Google Scholar]
- Cohen, J. G. 2009, poster presented at the meeting, The Milky Way and the Local Group - Now and in the Gaia Era, August-September, Heidelberg [Google Scholar]
- Cohen, J. G., & Bell, R. A. 1986, ApJ, 305, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Da Costa, G. S., Held, E. V., Saviane, I., & Gullieuszik, M. 2009, ApJ, 705, 1481 [NASA ADS] [CrossRef] [Google Scholar]
- Denisenkov, P. A., & Denisenkova, S. N. 1989, A. Tsir., 1538, 11 [NASA ADS] [Google Scholar]
- D'Ercole, A., Vesperini, E., D'Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Georgiev, I. Y., Hilker, M., Puzia, T. H., Goudfrooij, P., & Baumgardt, H. 2009, MNRAS, 396, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Giuffrida, G., Sbordone, L., Zaggia, S., et al. 2010, A&A, 513, 62 [Google Scholar]
- Gratton, R. G., Carretta, E., Eriksson, K., & Gustafsson, B. 1999, A&A, 350, 955 [NASA ADS] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Carretta, E., Claudi, R., Lucatello, S., & Barbieri, M. 2003, A&A, 404, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2006, A&A, 455, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2007, A&A, 464, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Irwin, M. J., & Gilmore, G. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Pilachowski, C. A., Rich, M. R., & Fulbright, J. P. 2009, ApJ, 698, 2048 (CJ09) [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P. 1994, PASP, 106, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Gnedin, O. Y., & Klypin, A. A. 2004, ApJ, 609, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, CD-ROM 13, Smithsonian Astrophysical [Google Scholar]
- Langer, G. E., Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Layden, A. C., & Sarajedini, A. 1997, ApJ, 486, L107 [CrossRef] [Google Scholar]
- Leaman, R., Cole, A. A., Venn, K. A., et al. 2009, ApJ, 699, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Letarte, B., Hill, V., Jablonka, P., et al. 2006, A&A, 453, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 483, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, A. F., Milone, A. P., Piotto, G., et al. 2009, A&A, 505, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, A. F., Piotto, G., Gratton, R., et al. 2010, in Light elements in the Universe, ed. C. Charbonnel, M. Tosi, F. Primas, & C. Chiappini (Cambridge Univ. Press), IAU Symp., 268, 183 [Google Scholar]
- Matteucci, F., & Franois, P. 1989, MNRAS, 239, 885 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Smecker-Hane, T. A. 2005a, in Cosmic abundances as records of stellar evolution and nucleosynthesis in honor of D.L. Lambert, ed. T. G. Banrnes III, & F. N. Bash (San Francisco: ASP), ASP Conf. Ser., 336, 221 [Google Scholar]
- McWilliam, A., & Smecker-Hane, T. A. 2005b, ApJ, 622, L29 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Rich, M. R., & Smecker-Hane, T. A. 2003, ApJ, 592, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Monaco, L., Ferraro, F. R., Bellazzini, M., & Pancino, E. 2002, ApJ, 578, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Monaco, L., Bellazzini, M., Ferraro, F. R., & Pancino, E. 2004, MNRAS, 353, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Monaco, L., Bellazzini, M., Bonifacio, P., et al. 2005, A&A, 441, 141 (M05) [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Monaco, L., Bellazzini, M., Bonifacio, P., et al. 2007, A&A, 464, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niederste-Ostholt, M., Belokurov, V., Evans, N. W., & Penarrubia, J. 2010, ApJ, 712, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., & Da Costa, G. S. 1995, ApJ, 447, 680 (NDC95) [NASA ADS] [CrossRef] [Google Scholar]
- Paltoglou, G., & Norris, J. E. 1989, ApJ, 336, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Reddy, B. E., Tomkin, J., Lambert, D. L., & Allende prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L., Bonifacio, P., Buonanno, R., et al. 2007, A&A, 465, 815 (S07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M., Venn, K. A., Tolstoy, E., et al. 2003, AJ, 125, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, M. H., Dotter, A., Majewski, S. R., et al. 2007, ApJ, 667, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smecker-Hane, T. A., & McWilliam, A. 2002, unpublished[arXiv:astro-ph/0205411] [Google Scholar]
- Smecker-Hane, T. A., & McWilliam, A. 2009, submitted (SHM09) [Google Scholar]
- Smith, G. H., & Martell, S. L. 2003, PASP, 115, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., Cunha, K., Ivans, I. I., Lattanzio, J. C., & Campbell, S. 2005, ApJ, 633, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Suntzeff, N. B., & Kraft, R. P. 1996, AJ, 111, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1979, ApJ, 229, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstoy, E., Irwin, M. J., Helmi, A., et al. 2004, ApJ, 617, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Venn, K. A., Irwin, M., Shetrone, M. D., et al. 2004, AJ, 128, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, J. C., Sneden, C., & Truran, J. W. 1989, ARA&A, 27, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Grundahl, F., Nissen, P. E., Jensen, H. R., & Lambert, D. L. 2005, A&A, 438, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaritsky, D., & Harris, J. 2004, ApJ, 604, 167 [Google Scholar]
Online Material
Appendix A: Error estimates
Table A.1: Sensitivities of abundance ratios to variations in the atmospheric parameters and to errors in the equivalent widths, and errors in abundances for stars in M 54 observed with UVES.
Table A.2: Sensitivities of abundance ratios to variations in the atmospheric parameters and to errors in the equivalent widths, and errors in abundances for stars in M 54 observed with GIRAFFE.
Table A.3: Sensitivities of abundance ratios to variations in the atmospheric parameters and to errors in the equivalent widths, and errors in abundances for stars in SgrN observed with GIRAFFE.
We refer the reader to the analogous Appendices in Carretta et al. (2009a,b) for a detailed discussion of the procedure adopted for error estimates. In the following, we provide only the main tables of sensitivities of abundance ratios to the adopted errors in the atmospheric parameters and EWs and the final estimates of internal and systematic errors for all species analysed using UVES and GIRAFFE spectra of stars in M 54 and in SgrN.
Sensitivities of abundance ratios to atmospheric parameters.
The sensitivities of derived abundances to the adopted atmospheric parameters were obtained by repeating our abundance analysis by changing only one atmospheric parameter each time for all stars in M 54 and in the nucleus of Sgr, separately, and taking the average value of the slope change versus abundance. This exercise was repeated for both UVES and GIRAFFE spectra.The amount of the variations in the atmospheric parameters is shown in the first line of the headers in Tables A.1-A.3, whereas the resulting response in abundance changes of all elements (the sensitivities) are shown in Cols. 3 to 6 of these tables, for abundances in M 54 from UVES and GIRAFFE spectra and for stars in the Sgr nucleus from GIRAFFE, respectively.
Errors in atmospheric parameters.
A detailed discussion of how they can be estimated is given in Carretta et al. (2007c); in Sect. 4 of the present paper, we describe the changes in the estimates required to take into account the intrinsic spread in iron observed in M 54.The other difference is that for the Sgr field (nucleus) stars,
errors in temperature were derived directly from the calibration by
Alonso et al. (1999), since we used the relation between
![]() and the K magnitudes only for the cluster M 54.
and the K magnitudes only for the cluster M 54.
Adopted errors in atmospheric parameters are listed in the second (internal errors) and third line (systematic errors) of the headers in Tables A.1-A.3. These errors, multiplied by the sensitivities of abundances to variations in the individual parameters, and summed in quadrature, provide the total internal and systematic errors listed in the last two columns of these tables.
Footnotes
- ... nucleus
![[*]](/icons/foot_motif.png)
- Based on observations collected at ESO telescopes under programme 081.D-286.
- ...
![[*]](/icons/foot_motif.png)
- Appendix is only available in electronic form at http://www.aanda.org
- ...
![[*]](/icons/foot_motif.png)
- Tables 2, 3, and 5-7 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/viz-bin/qcat?J/A+A/520/A95
- ... [Fe/H]
![[*]](/icons/foot_motif.png)
- We adopt the usual spectroscopic notation,
i.e. for any
given species X [X] =
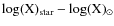 and
and 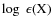 =
=
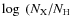 ) +
12.0 for absolute number density abundances.
) +
12.0 for absolute number density abundances.
- ... IRAF
![[*]](/icons/foot_motif.png)
- IRAF is distributed by the National Optical Astronomical Observatory, which are operated by the Association of Universities for Research in Astronomy, under contract with the National Science Foundation.
- ...)=0.14
![[*]](/icons/foot_motif.png)
- Monaco et al. (2005) concluded that no differential reddening affects the field from which our sample was selected.
- ...
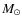
![[*]](/icons/foot_motif.png)
- Derived values of surface gravity are not very sensitive to the exact value of the adopted mass.
- ...
of 58 K)
![[*]](/icons/foot_motif.png)
- In our survey, we prefer not to rely on temperatures derived from the excitation equilibrium, since our sample also includes metal-poor GCs and rather warm stars, where the limited spectral coverage of GIRAFFE HR11 and HR13 may not allow a large enough number of Fe lines to be reliably measured. Our photometric approach was devised to secure more homogeneous parameters for all analysed GCs, including the present one.
- ... Fornax)
![[*]](/icons/foot_motif.png)
- The dispersion in [Fe/H] for WLM is directly given by
Leaman et al. (2009).
For Sculptor and Fornax, we obtained the
 rms scatter
from the FWHM of the histograms of metallicities presented by Tolstoy
et al. (2004)
and Battaglia et al. (2006),
respectively.
rms scatter
from the FWHM of the histograms of metallicities presented by Tolstoy
et al. (2004)
and Battaglia et al. (2006),
respectively.
- ... now
![[*]](/icons/foot_motif.png)
- Another piece of evidence in
 Cen is the observed
anticorrelation of C and N abundances (NDC95), where the most
C-poor, N-enhanced stars all belong to the metal-rich component.
However, since C and N are also affected by standard
evolutionary mixing and extra-mixing episodes (see e.g. Charbonnel 2006; Carretta 2008, and reference
therein), this is somewhat less clear evidence.
Cen is the observed
anticorrelation of C and N abundances (NDC95), where the most
C-poor, N-enhanced stars all belong to the metal-rich component.
However, since C and N are also affected by standard
evolutionary mixing and extra-mixing episodes (see e.g. Charbonnel 2006; Carretta 2008, and reference
therein), this is somewhat less clear evidence.
- ... temperature
![[*]](/icons/foot_motif.png)
- This same result also has been confirmed also by Marino
et al. (2010)
in their ongoing analysis of a large sample of stars in
 Cen.
Cen.
- ... body)
![[*]](/icons/foot_motif.png)
- We do not use data from M05 in this and other
comparisons because these authors derived only three
 -elements
(Mg, Ca, Ti) for 15 bright giants in the
Sgr main body. Their abundances are intermingled for these
elements with those of Sbordone et al. (2007), who studied
many more atomic species.
-elements
(Mg, Ca, Ti) for 15 bright giants in the
Sgr main body. Their abundances are intermingled for these
elements with those of Sbordone et al. (2007), who studied
many more atomic species.
- ... likely
![[*]](/icons/foot_motif.png)
- In 2005, a metallicity dispersion in M 54
had still not been very fully assessed, although we now know of stars
as metal-rich as [Fe/H]
 -1.2 dex in our M 54 sample, not very different from
the [Fe/H] = -1.13 dex of star I-73.
-1.2 dex in our M 54 sample, not very different from
the [Fe/H] = -1.13 dex of star I-73.
- ... Sgr complex
![[*]](/icons/foot_motif.png)
- An extensive study by Chou et al. (2009) also reports that farther along the Sgr stream an increasing number of metal-poor stars is observed to show abundances typical of Galactic halo stars and similar to those of the metal-poor cluster M 54 (see also Monaco et al. 2007).
All Tables
Table 1: Log of FLAMES observations.
Table 4: Mean abundances from UVES and GIRAFFE spectra for stars in the GC M 54 and Sgr nucleus.
Table A.1: Sensitivities of abundance ratios to variations in the atmospheric parameters and to errors in the equivalent widths, and errors in abundances for stars in M 54 observed with UVES.
Table A.2: Sensitivities of abundance ratios to variations in the atmospheric parameters and to errors in the equivalent widths, and errors in abundances for stars in M 54 observed with GIRAFFE.
Table A.3: Sensitivities of abundance ratios to variations in the atmospheric parameters and to errors in the equivalent widths, and errors in abundances for stars in SgrN observed with GIRAFFE.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg1.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg11.png)
|
Figure 1:
The distribution of the total visual absolute magnitudes (a proxy for
total mass) for all globular clusters in the Harris (1996)
catalogue. Red lines indicate the location of the GCs already analysed
in our project ``Na-O anticorrelation and HB''. Blue lines
show the additional clusters under scrutiny and the black arrow
indicates the position of NGC 6715 (M 54) in this
distribution. The most massive cluster (not indicated) is |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg17.png)
|
Figure 2: The colour-magnitude diagram of M 54 and Sgr nucleus showing our final selection of targets for FLAMES observations. Green circles enclose 52 candidate RGB stars of Sgr and blue circles enclose 82 candidate red giant branch targets of M 54. All targets lie within a radial distance of 9 arcmin from the cluster center and satisfy the selection criteria described in the text. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg21.png)
|
Figure 3: The I,V-I CMD of program stars, showing the adopted separation between the globular cluster M 54 (blue filled circles) and the stars of the Sgr nucleus (green squares). Filled square symbols are stars in the nucleus retained for further analysis, whereas open squares are stars heavily affected by TiO bands and disregarded. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg4.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg27.png)
|
Figure 4: Derived metallicity distribution of stars in M 54 ( left panels: abundances from Fe I lines (top), from Fe II lines (middle) and their difference (bottom)) and in the nucleus of Sgr (right panels) as a function of the effective temperature. Filled red circles are stars with both HR11 and HR13 GIRAFFE spectra, green cross stars with GIRAFFE HR13 only, and blue filled squares are stars with UVES spectra. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg5.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg32.png)
|
Figure 5: V,B-V CMD for stars in M 54. Stars with metallicity above (red filled squares) and below (blue filled circles) the cluster average ratio [Fe/H] = -1.56 dex are marked. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14924fg6.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg37.png)
|
Figure 6:
Comparison with the RV and [Fe/H] estimates by B08. Upper panel:
differences in the radial velocity; the continuous line marks the mean difference, the dotted lines enclose the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg7.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg40.png)
|
Figure 7:
Rms scatter in Fe I as a function of the absolute total visual
magnitudes for the 19 GCs in Carretta et al. (2009c; red circles), for M 54 (present work, blue square) and for M 22, NGC 2419 and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg41.png)
|
Figure 8: MDF of our total sample (M 54+SgrN) as compared to M 22 from a sample of 31 giant stars by Marino et al. (2009). Both distributions are normalised to the total number of objects in each sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg9.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg42.png)
|
Figure 9: Na-O anticorrelation in M 54 from UVES and GIRAFFE spectra; blue and red circles indicate stars that are respectively more metal-poor and more metal-rich than the cluster average [Fe/H] = -1.56. Upper limits to [O/Fe] are indicated by arrows. The typical star-to-star error bars are also shown. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg43.png)
|
Figure 10: Fraction of stars in the P, I, and E components in the 19 clusters analysed by Carretta et al. (2009a, red filled circles) and in M 54 (large black circles). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg11.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg50.png)
|
Figure 11: Cumulative distributions of the distances from the cluster centre relative to stars in M 54 belonging to the P, I, and E stellar components. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg12.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg51.png)
|
Figure 12:
Relation between the total absolute magnitude of clusters and the IQR[O/Na]. M 54 (circle) and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg13.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg52.png)
|
Figure 13:
Na-O anticorrelation in M 54 for the stars of the metal-rich ( upper left panel) and the metal-poor ( upper right panel) components analysed here. The corresponding lower panels show the same in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{14924fg14.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg63.png)
|
Figure 14: Distribution of the [O/Na] ratios in the metal-rich ( lower panel) and metal-poor ( upper panel) components in M 54. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{14924fg15.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg64.png)
|
Figure 15: Abundance ratios [O/Fe] ( upper panel) and [Na/Fe] ( lower panel) for stars in M 54+Sgr in the present work and in the literature. Blue open circles and blue filled squares are our stars in M 54 with GIRAFFE and UVES spectra, respectively. Green open circles and filled squares are our stars in Sgr with GIRAFFE and UVES spectra, respectively. Open black star symbols are 5 giants in M 54 from Brown et al. (1999), black crosses are 5 giants in Terzan 7, and filled triangles giants in Sgr from S07. Black open ``star explosion'' symbols are Sgr giants from Smecker-Hane & McWilliam (2009, submitted). Finally, small grey symbols are samples of Galactic field stars (Fulbright 2000; Gratton et al. 2003; Reddy et al. 2003; Venn et al. 2004). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg16.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg65.png)
|
Figure 16: Summary of the (anti)correlations involved in the Mg-Al cycle for stars of SgrN and of M 54 analysed in the present work and in previous literature studies. Symbols are as in Fig. 15. |
| Open with DEXTER | |
| In the text | |
| |
Figure 17:
Na-Al correlation for giants in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg18.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg68.png)
|
Figure 18:
Mg-Al anticorrelation for giants in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg19.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg69.png)
|
Figure 19:
Si-Al correlation for giants in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg20.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg70.png)
|
Figure 20:
Run of abundance ratios for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg21.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg71.png)
|
Figure 21:
Run of abundance ratios for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg22.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg74.png)
|
Figure 22: Run of abundance ratios for Sc II and V I. Symbols are as in Fig. 15. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14924fg23.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg75.png)
|
Figure 23: Run of abundance ratios for Cr I and Ni I. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg24.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg76.png)
|
Figure 24: [Mn/Fe] as a function of
metallicity for field stars (tiny squares)
from several studies (see text); the average values for M 54 (this
study, large blue filled circle) and 19 GCs of this project
(Gratton et al. 2006; Carretta et al. 2007b, Carretta et al., in prep.) are indicated by red filled circles, with 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14924fg25.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa14924-10/Timg77.png)
|
Figure 25: The ratio [Cu/Fe] as a function of metallicity for field stars (tiny squares) of the Galactic halo and disk from Mishenina et al. (2002) and for the stars of M 54 and SgrN with UVES spectra (blue and green large filled squares, respectively) from the present study. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


