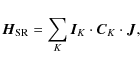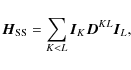EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) A64 Full HTML
Free Access
Issue
A&A
Volume 520, September-October 2010
Article Number A64
Number of page(s) 6
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201014787
Published online 04 October 2010
A&A 520, A64 (2010)

Hyperfine structure in the rotational spectra of trans-formic acid: Lamb-dip measurements and quantum-chemical calculations[*]

G. Cazzoli1 - C. Puzzarini1 - S. Stopkowicz2 - J. Gauss2

1 - Dipartimento di Chimica ``G. Ciamician'', Università di Bologna, via Selmi 2, 40126 Bologna, Italy
2 - Institut für Physikalische Chemie, Universität Mainz, 55099 Mainz, Germany

Received 14 April 2010 / Accepted 3 June 2010

Abstract
Context. Formic acid, HCOOH, is the simplest organic acid and the first that has been identified in the interstellar medium. Its astrophysical relevance has motivated this spectroscopic study.
Aims. The aim of this investigation is to provide very accurate rest frequencies for the trans isomer of HCOOH as well as to improve the spectroscopic and hyperfine parameters available in the literature for this molecule.
Methods. The Lamb-dip technique has been exploited in order to record the rotational spectrum of trans-HCOOH at sub-Doppler resolution in the millimeter- and submillimeter-wave frequency ranges and, when possible, to resolve the hyperfine structure due to the hydrogen nuclei. THz measurements have been carried out as well. The experimental investigation has been supported by high-level quantum-chemical calculations.
Results. As a consequence, we report here the most accurate ground-state rotational parameters known so far for the main isotopic species of trans-HCOOH as well as an accurate and reliable set of hyperfine parameters.
Conclusions. The improvement in the accuracy of the ground-state rotational and hyperfine parameters as well as of the rest frequencies of rotational transitions might therefore be useful for future radioastronomical observations.

Key words: methods: laboratory - techniques: spectroscopic - ISM: molecules - submillimeter: ISM - radio lines: ISM - molecular data

1 Introduction

Formic acid (HCOOH) exists in two rotameric forms, defined by whether the two hydrogen atoms are cis or trans to each other. Both rotamers are near prolate asymmetric tops with a planar structure and $C_{\rm s}$ symmetry (Winnewisser et al. 2002). The cis-rotamer lies approximately 1365(30) cm-1 (Hocking 1976) higher in energy than the trans form; therefore, the latter is about 800 times more abundant at room temperature. The trans-HCOOH isomer is the subject of the present study, and we refer to this form along the text, if not otherwise specified. To the best of our knowledge, all radioastronomical observations reported in the literature refer to the trans-rotamer of the main isotopologue.

The astrophysical relevance of formic acid stems from the fact that it is the simplest organic acid and the first observed in the interstellar medium (Zuckerman et al. 1971). It has been observed in various star-forming regions, in dense molecular clouds, etc.; we refer interested readers to Lattanzi et al. (2008) and references therein for an exhaustive list. We only point out that, as it is a species of intermediate complexity that shares common structural elements with biologically important species such as glycine, it represents a transition step between simpler species that are formed in the gas phase and complex hydrogenated species that are formed on grain surfaces (Turner et al. 1999).

As is well-known, astrophysical investigations require knowledge of accurate rest frequencies and/or accurate predictions for them. These are provided by laboratory measurements, and in this respect, sub-Doppler techniques such as the Lamb-dip method, whenever applicable, are the most suitable. In particular, the launch of the Herschel space observatory and the near-future operating international interferometer ALMA require knowledge of the transition frequencies of the molecules of astrophysical relevance in submillimeter-wave and THz regions with accuracies preferably better than 100 kHz (see, for example, Lattanzi et al. 2007, 2008). For these reasons, we report the investigation of the rotational spectrum of HCOOH in the 80-600 GHz frequency range recorded by means of the Lamb-dip technique, thus providing transition frequencies with an accuracy of 1 kHz, hence accurate spectroscopic parameters, as well as THz measurements performed with an accuracy of about 50-70 kHz. The Lamb-dip technique also allowed us to resolve the hyperfine structure of the spectrum due to the spin-rotation and spin-spin interactions of the two hydrogens.

The microwave and millimeter-wave rotational spectrum of formic acid has been studied since the 50s, but only quite recently Winnewisser et al. (2002) have reported measurements in the 835-993 GHz frequency range with an accuracy of 50-100 kHz and in the 1-2.9 THz frequency region with an uncertainty of 5 MHz. We also refer the reader to Winnewisser et al. (2002) for an exhaustive description of previous laboratory measurements. There is only one study of the hyperfine structure of the rotational spectrum reporting radio-frequencies measured with a molecular-beam spectrometer with an accuracy of 0.15 kHz (Chardon et al. 1976). Their analysis led to all the diagonal terms of the spin-rotation tensor for the two hydrogens, but only the two Caa constants were actually determined to a good accuracy. As explained later in the text, the spin-rotation constants of Chardon et al. (1976) provide erroneous predictions for the hyperfine structure in the millimeter-wave frequency range. More precisely, according to the values by Chardon et al. (1976), symmetric splittings of tens of kHz were expected in the millimeter-wave region, while smaller asymmetric splittings have actually been observed. To clarify this point, state-of-the-art quantum-chemical calculations of the hyperfine parameters involved have been carried out. As is made clearer later in the text, these computations allowed proper analysis and assignment of the spectra recorded.

2 Hyperfine structure of the rotational spectrum

The Hamiltonian describing the hyperfine structure of the rotational spectrum of HCOOH can be given in terms of different contributions:

\begin{displaymath}% {\vec H} = {\vec H}_{\rm ROT} + {\vec H}_{\rm SR} + {\vec H}_{\rm SS}, \end{displaymath} (1)

where ${\vec H}_{\rm ROT}$ is the rotational part of the Hamiltonian operator (Gordy & Cook 1984), ${\vec H}_{\rm SR}$ is the Hamiltonian describing the spin-rotation interactions (Townes & Schawlow 1955; Flygare 1974), and ${\vec H}_{\rm SS}$ is the spin-spin Hamiltonian (Townes & Schawlow 1955; Flygare 1974) describing the direct dipolar spin-spin interactions. While  ${\vec H}_{\rm ROT}$ is briefly addressed in the spectra-analysis section, but for all details we refer the reader to Winnewisser et al. (2002), the description of the other two Hamiltonians is provided below.

The spin-rotation Hamiltonian,

\begin{displaymath}% {\vec H}_{\rm SR} = \sum_K {{\vec I}_K} \cdot {{\vec C}_K} \cdot {\vec J}, \end{displaymath} (2)

with K running over all nuclei with a non-zero nuclear spin  ${\vec I}_K$ (hydrogens in the present case), describes the interaction between the considered nuclear magnetic moment and the effective magnetic field of a rotating molecule through the spin-rotation tensor  ${\vec C}_K$ (Townes & Schawlow 1955; Flygare 1974).

The dipolar spin-spin (Townes & Schawlow 1955; Flygare 1974) Hamiltonian,

\begin{displaymath}% {\vec H}_{\rm SS} = \sum_{K<L} {\vec I}_K {\vec D}^{KL} {\vec I}_L, \end{displaymath} (3)

describes the dipolar interaction between two nuclear magnetic moments, namely  ${\vec I}_K$ and  ${\vec I}_L$ (the two hydrogens in the present case), through the dipolar spin-spin coupling tensor  ${\vec D}^{KL}$.

The various hyperfine components result from the $\Delta F_1$, $\Delta F$ = 0, $\pm$1 selection rules, where F1 and F are the hyperfine quantum numbers originating from the coupling schemes F1=J+IH1 and F=F1+IH2.

3 Computational details

The experimental investigation was supported by quantum-chemical calculations of the hyperfine parameters involved, namely, of the spin-rotation and spin-spin interaction tensors. To ensure high accuracy, all quantum-chemical calculations were performed using state-of-the-art coupled-cluster (CC) techniques (Bartlett & Musia\l 2007), together with large atomic-orbital basis sets. More precisely, equilibrium-value calculations were carried out using the CC singles and doubles (CCSD) approach (Purvis & Bartlett 1982) augmented by a perturbative treatment of triple excitations (CCSD(T); Raghavachari et al. 1989) in conjunction with the large cc-pCVnZ (n = Q,5) basis sets (Dunning 1989; Woon & Dunning 1995). All electrons have been included in the electron-correlation treatment, and the semi-experimental equilibrium geometry (Demaison et al. 2007) was used as reference structure. Vibrational corrections have also been considered as discussed in the following. They were computed at the CCSD(T)/cc-pCVTZ level of theory. The CFOUR program package (2009) was used for all calculations reported in the present work.

Let us start by considering the spin-rotation interaction, which requires computing the second-rank tensor  ${\vec C}_K$. Each element of the spin-rotation tensor has both an electronic and a nuclear contribution. The electronic contribution can be evaluated as the second derivative of the electronic energy with respect to the rotational angular momentum ${\vec J}$ and the nuclear spin  ${\vec I}_K$ (Flygare 1974). This is efficiently done using analytic second-derivative techniques (Stanton & Gauss 2000; Gauss & Stanton 1996,1997) in conjunction with perturbation-dependent basis functions (Gauss et al. 1996); the latter are often referred to as rotational London atomic orbitals and were employed to improve basis-set convergence. On the other hand, the nuclear contribution only depends on the geometrical structure of the molecule.

The expression for the components of the dipolar spin-spin coupling tensor  ${\vec D}^{KL}$ can be found, for instance, in Gordy & Cook (1984), and Abragam (1961). It is easily seen that the dipolar-coupling tensor  ${\vec D}^{KL}$is completely determined once the molecular geometry is known, thus not requiring any knowledge of the electronic structure of the molecule. However, this strictly applies only to the case of a rigid, non-vibrating molecule.

Vibrational corrections to both spin-rotation and spin-spin tensors were evaluated with second-order vibrational perturbation theory (VPT2) (Mills 1972). The VPT2 approach has been described in detail in Auer et al. (2003) and already used to compute vibrational corrections for hyperfine parameters (see, for example, Cazzoli et al. 2009; Puzzarini et al. 2009; van der Tak et al. 2009). Within the VPT2 scheme, vibrational corrections are obtained by expanding the expectation value of the considered property over the vibrational wavefunction in a Taylor series around the equilibrium value with respect to normal-coordinate displacements. The required harmonic force field has been computed in a fully analytic manner (Gauss & Stanton 1997), while both the cubic force field and the corresponding derivatives of the considered property were obtained using finite-difference techniques as described in Stanton & Gauss (2000) and Stanton et al. (1998). The vibrational corrections, defined as the difference between the vibrationally averaged and equilibrium values determined at the same computational level, were then added to the best equilibrium results to derive theoretical best estimates for the ground-state data. The latter can be directly compared to the experimental values.

\begin{figure} \par\includegraphics[width=12cm,clip]{14787-fig1.eps} \end{figure} Figure 1:

The hyperfine structure of the J = 182,16  $\leftarrow $ 182,17 rotational transition of trans-HCOOH. The recorded spectrum (top: P=0.6 mTorr, mod. depth = 7 kHz; bottom: P=0.3 mTorr, mod. depth = 5 kHz) is compared to the predicted ones obtained, from the bottom, using the data from Chardon et al. (1976, in green), only the computed spin-rotation constants (in blue), computed spin-rotation and spin-spin constants (in red).

Open with DEXTER

4 Experimental details

For Lamb-dip measurements, a frequency-modulated, computer-controlled spectrometer in conjunction with a conventional free space cell, as shown in Cazzoli & Dore (1990a), was employed. To increase the sensitivity of the spectrometer as well as the Lamb-dip effect, the radiation path is doubled (Dore et al. 1999). A detailed description of the spectrometer is given in Cazzoli & Dore (1990b), whereas our experimental set up for performing sub-Doppler resolution spectroscopy has been described in some previous papers (see, for example, Cazzoli et al. 2002a,b, 2003). Therefore, here, we only report the main details relevant to the present investigation. The millimeter and submillimeter-wave sources employed are either frequency multipliers driven by Gunn diode oscillators or Gunn diodes themselves, covering, on the whole, the 80-600 GHz frequency range. The frequency modulation is obtained by sine-wave modulating the 73 MHz local oscillator of the synchronization loop at 1.666 kHz. A liquid He-cooled InSb detector was used, and its output was processed by means of a Lock-in amplifier tuned at twice the modulation frequency, so that the second derivative of the natural line profile was recorded. Those transitions that ended up too weak for observing the Lamb-dip effect were recorded at a Doppler-limited resolution.

In addition, Doppler-limited measurements were also carried out in the 1.0-1.6 THz frequency range. In particular, the THz frequency source is actually a tripler followed by another tripler (RPG GmbH), and the overall radiation power is 10 to 40 $\mu$W (with also the twelfth harmonic detectable). As for the millimeter-/submillimeter-wave spectrometer, the frequency-modulation technique was employed, and the 80 MHz local oscillator of the synchronization loop is sine-wave modulated at either 333 Hz or 10 Hz, depending on the detector used. These are a liquid He-cooled Ge bolometer and a Golay detector, and their output was processed by means of a Lock-in amplifier tuned at twice the modulation frequency (i.e., 666 Hz for the former, 20 Hz for the latter). Another difference (with respect to the millimeter-submillimeter-wave spectrometer) concerns the radiation path. In fact, in the THz region, parabolic mirrors need to be used for collimating and focalizing the radiation instead of high density polyethylene lenses.

For both Lamb-dip and THz measurements, the frequency sources are phase-locked to a rubidium frequency standard. The Lamb-dip measurements were always carried out at pressures lower than 0.5 mTorr. Such low values of working pressure have been chosen to minimize the dip widths as much as possible in view of improving the resolution, as well as to avoid pressure frequency shift. In addition, the source power was adequately reduced to have narrow and undistorted dips. The modulation depth used was adjusted in the range 5 to 15 kHz according to the experimental conditions and the transitions under consideration. Concerning Doppler-limited measurements, higher values of pressure (i.e., 20-30 mTorr and up to 50-90 mTorr in the THz region) and modulation depth (i.e., 300-400 kHz in the mm-/submm-wave region and 2.25-3 MHz in the THz frequency range) were employed. All measurements have been carried out at room temperature, using a commercial sample of trans-formic acid without any further purifications.

Going into more detail, about one hundred rotational transitions were recorded with an accuracy of about 1 kHz, and for most of them the hyperfine structure was resolved, while a total of about 150 rotational transitions were measured at Doppler-limited resolution in the submillimeter-wave and THz frequency regions. All transition frequencies are collected in Table S1 of the supplementary material.

\begin{figure} \par\includegraphics[width=11.5cm,clip]{14787-fig2.eps} \vspace*{4mm} \end{figure} Figure 2:

Line profile analysis of the hyperfine structure of the J = 221,21  $\leftarrow $ 220,22 rotational transition of trans-HCOOH: recorded spectrum in black, calculated spectrum in red and residual (observed - calculated) in green.

Open with DEXTER

5 Spectra analysis

The first step toward recording and analyzing the hyperfine structure of the rotational spectrum of HCOOH was its prediction employing the values for the spin-rotation constants available in the literature. An example is provided by the bottom spectrum of Fig. 1 for the J = 182,16  $\leftarrow $ 182,17 transition. The corresponding spectrum recorded by means of the Lamb-dip technique is also depicted in Fig. 1, which is the first from the top. At first sight, it is clear that the two hyperfine structures differ significantly, with the former characterized by a quartet with splittings as large as $\sim$60-70 kHz and the latter by a narrow triplet with two features not completely resolved. As this was systematically observed for other transitions as well, we resorted to quantum-chemical predictions for the hyperfine parameters involved. Computed spin-rotation constants led to the second spectrum from the bottom of Fig. 1. While the extent of the hyperfine splittings is well reproduced, their asymmetry is not. Only by accounting for the dipolar spin-spin coupling (second spectrum of Fig. 1 from the top), the recorded hyperfine structure is correctly predicted. Therefore, after these first analyses, predictions of the hyperfine structure for the other considered transitions were carried out based on the computed spin-rotation and spin-spin interaction constants.

Once the spectra were recorded, the transition frequencies were determined either by fitting the experimental data points to a parabolic function or by a line profile analysis (see Cazzoli & Dore 1990a), with the latter used in the analysis of hyperfine structure involving partially blended features and/or distorted dips. A graphical example of the line profile analysis is provided by Fig. 2. In all cases the reported frequencies were obtained as averages of a set of measurements, which have been found to be very reproducible. In fact, in the case of Lamb-dip measurements, the frequency differences for a given set are well within 1 kHz. Therefore, the latter can be considered a conservative estimate of experimental uncertainties. For Doppler-limited measurements, the frequencies were obtained only by fitting the experimental data points to a parabolic function, and 20 kHz and 50 kHz (75 kHz in the case of detection with Golay) can be considered conservative estimates for the experimental uncertainties in the 500-600 GHz and THz frequency regions, respectively. Figure 3 presents an example of THz measurements: a portion of the b Q band, with Ka = 9  $\leftarrow $ 8, is depicted. The good signal-to-noise ratio is also evident.

\begin{figure} \par\includegraphics[width=15.5cm,clip]{14787-fig3.eps} \end{figure} Figure 3:

Portion of the b Q band, with Ka = 9  $\leftarrow $ 8, recorded in the THz region (P = 90 mTorr, mod. depth = 2.25 MHz).

Open with DEXTER

Table 1:   Rotational and hyperfine parameters of trans-HCOOH.

The analysis of the frequencies obtained in this work, as well as those taken from the literature, were performed with an A-reduced Watson Hamiltonian in the Ir representation (nearly prolate asymmetric top molecules ($\kappa$ = -0.95)).

6 Results and discussion

The retrieved frequency values are included in least-squares fits in which each line frequency has been weighted proportionally to the inverse square of its experimental uncertainty. Two different fits were carried out: the first one including our measurements together with the radio-frequencies (rf) recorded by means of a molecular-beam spectrometer by Chardon et al. (1976), and the second one also including the submillimeter-wave and THz measurements from Winnewisser et al. (2002). Both fits have been carried out with Pickett's SPCAT/SPFIT suite of programs (Pickett 1991). The results are reported in Table 1, where the present spectroscopic parameters are compared with those available in the literature as well as with our computed values.

Concerning the rotational parameters, the comparison of interest uses the data reported by Winnewisser et al. (2002). From Table 1, it is evident that, while the results of the two fits carried out in the present work agree within the standard uncertainties, discrepancies greater than the error bars are observed with respect to those from Winnewisser et al. (2002). Due to the accuracy of the Lamb-dip measurements carried out in the millimeter- and submillimeter-wave regions and thanks to the improved THz measurements (i.e., the uncertainties have been reduced from from 5 MHz to 50-75 kHz), we consider our rotational parameters (in particular, the rotational constants) more reliable.

It is evident from the results for hyperfine parameters reported in Table 1 why the results from Chardon et al. (1976) predict such overly large hyperfine structures, as seen in Fig. 1. In fact, even if incorrectly determined, i.e., with uncertainties of about 50% or more, the Cbb and Ccc constants are too large by about one order of magnitude, and they also have the wrong sign in the case of the hydrogen linked to the carbon atom. There are two comments that should be added. The first is that, for each hydrogen, the sum of Cbb and Ccc constants given by Chardon et al. (1976) is reasonably good, thus suggesting that the information they had at hand is not sufficient for a proper determination of all the diagonal terms. In this respect, it is noted that in the fit we had to fix the ratio between the two Ccc constants to the theoretical value, as they cannot be simultaneously determined. The second remark is that the rf values by Chardon et al. (1976) are reproduced very well by our fit (i.e., within the given uncertainties[*]; see Table S1 in supplementary material), hence by our hyperfine parameters. Our comparison shows very good agreement between our experimental results and the computed values, which explains why the calculated parameters are able to predict the hyperfine structure of the rotational spectrum, as shown in Fig. 1. Quantum-chemical calculations provide the full spin-rotation and spin-spin tensors, including the off-diagonal elements. The latter have no relevance in predicting spectra as they cannot be determined experimentally.

Finally, a comment on our calculated values is deserved. From our previous work (see, for example, Cazzoli et al. 2009; Puzzarini et al. 2009; Cazzoli et al. 2010), we already know that the CCSD(T) method employed in conjunction with a core-valence basis set of at least quadruple-zeta quality is suitable for obtaining equilibrium values for quantitative predictions, while a triple-zeta quality basis is usually sufficient to provide accurate vibrational corrections. Including vibrational corrections is mandatory for obtaining quantitative agreement with experiment. In fact, for both spin-rotation and spin-spin constants, vibrational corrections range from 0.06 kHz to 0.5 kHz, where the lower values apply to the smaller constants. The full set of computed data are collected in the supplementary material (see Table S2).

7 Conclusion

On the whole, we present the most accurate ground-state rotational parameters of HCOOH known so far. Since this molecule has a strong astrophysical relevance, we are convinced that the improved ground-state rotational parameters and rest frequencies obtained in the present investigation could be very useful for future observational purposes.

In the present investigation it is shown that, by employing the Lamb-dip technique, the hyperfine structure of rotational spectra can be recorded with high resolution, allowing determination of hyperfine parameters with good accuracy. Furthermore, the comparison between theory and experiment demonstrates that quantum-chemical computations can provide reliable reference values and, therefore if required, they can support, guide or even replace experimental determinations.

Acknowledgements
This work has been supported in Bologna by ``PRIN 2007'' funds (project ``Trasferimenti di energia, carica e molecole in sistemi complessi'') and by the University of Bologna (RFO funds), and in Mainz by the Deutsche Forschungsgemeinschaft and the Fonds der Chemischen Industrie.


References

  1. Abragam, A. 1961, Principles of Nuclear Magnetism (New York: Oxford University Press) [Google Scholar]
  2. Auer, A. A., Gauss, J., & Stanton, J. F. 2003, J. Chem. Phys., 118, 10407 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bartlett, R. J., & Musia▯, M. 2007, Rev. Mod. Phys., 79, 291 [NASA ADS] [CrossRef] [Google Scholar]
  4. Cazzoli, G., & Dore, L. 1990a, J. Mol. Spectrosc., 143, 231 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cazzoli, G., & Dore, L. 1990b, J. Mol. Spectrosc., 141, 49 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cazzoli, G., Dore, L., Cludi, L., Puzzarini, C., & Beninati, S. 2002a, J. Mol. Spectrosc., 215, 160 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cazzoli, G., Dore, L., Puzzarini, C., & Beninati, S. 2002b, Phys. Chem. Chem. Phys., 4, 3575 [CrossRef] [Google Scholar]
  8. Cazzoli, G., Puzzarini, C., & Lapinov, A. V. 2003, ApJ, 592, L95 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cazzoli, G., Puzzarini, C., Harding, M. E., & Gauss, J. 2009, Chem. Phys. Lett., 473, 21 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cazzoli, G., Dore, L., Puzzarini, C., & Gauss, J. 2010, Mol. Phys., in press, [DOI: 10.1080/00268976.2010.484395] [Google Scholar]
  11. CF OUR A quantum chemical program package written by J. F. Stanton, J. Gauss, M. E. Harding, & P. G. Szalay, with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, M. Heckert, O. Heun, C. Huber, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. Matthews, T. Metzroth, D. P. O'Neill, D. R. Price, E. Prochnow, K. Ruud, F. Schiffmann, S. Stopkowicz, M. E. Varner, J. Vázquez, F. Wang, & J. D. Watts, and the integral packages MOLECULE, J. Almlöf, P. R. Taylor, PROPS, P. R. Taylor, ABACUS, T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, & J. Olsen, and ECP routines by A. V. Mitin, & C. van Wüllen, For the current version, see http://www.cfour.de [Google Scholar]
  12. Chardon, J.-C., Genty, C., Guichon, D., & Theobald, J.-G. 1976, J. Chem. Phys., 64, 1434 [NASA ADS] [CrossRef] [Google Scholar]
  13. Demaison, J., Herman, M., & Liévin, J. 2007, J. Chem. Phys., 126, 164305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Dore, L., Degli Esposti, C., Mazzavillani, A., & Cazzoli, G. 1999, Chem. Phys. Lett., 300, 489 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dunning, T. H., Jr. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  16. Flygare, W. H. 1974, Chem. Rev., 74, 653 [CrossRef] [Google Scholar]
  17. Gauss, J., & Stanton, J. F. 1996, J. Chem. Phys., 104, 2574 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gauss, J., & Stanton, J. F. 1997, Chem. Phys. Lett., 276, 70 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gauss, J., Ruud, K., & Helgaker, T. 1996, J. Chem. Phys., 105, 2804 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gordy, W., & Cook, R. L. 1984, Microwave Molecular Spectra, ed. A. Weissberger (New York: Wiley), 3rd edition [Google Scholar]
  21. Hocking, W. M. 1976, Z. Naturforsch., 31A, 1113 [Google Scholar]
  22. Lattanzi, V., Walters, A., Drouin, B. J., & Pearson, J. C. 2007, ApJ, 662, 771 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lattanzi, V., Walters, A., Drouin, B. J., & Pearson, J. C. 2008, ApJS, 176, 536 [NASA ADS] [CrossRef] [Google Scholar]
  24. Mills, I. A. 1972, in Modern Spectroscopy: Modern Research, ed. K. N. Rao, & C. W. Matthews (New York: Academic) [Google Scholar]
  25. Pickett, H. M. 1991, J. Mol. Spectrosc., 148, 371 [Google Scholar]
  26. Purvis, G. D., III, & Bartlett, R. J. 1982, J. Chem. Phys., 76, 1910 [NASA ADS] [CrossRef] [Google Scholar]
  27. Puzzarini, C., Cazzoli, G., Harding, M. E., Vázquez, J., & Gauss, J. 2009, J. Chem. Phys., 131, 234304 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  28. Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
  29. Stanton, J. F., & Gauss, J. 2000, Int. Rev. Phys. Chem., 19, 61 [CrossRef] [Google Scholar]
  30. Stanton, J. F., Lopreore, C. L., & Gauss, J. 1998, J. Chem. Phys., 108, 7190 [NASA ADS] [CrossRef] [Google Scholar]
  31. Townes, C. H., & Schawlow, A. L. 1955, Microwave Spectroscopy (New York: McGraw-Hill) [Google Scholar]
  32. Turner, B. E., Terzieva, R., & Herbst, E. 1999, ApJ, 518, 699 [NASA ADS] [CrossRef] [Google Scholar]
  33. van der Tak, F. F. S., Müller, H. S. P., Harding, M. E., & Gauss, J. 2009, A&A, 507, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Winnewisser, M., Winnewisser, P. B., Stein, M., et al. 2002, J. Mol. Spectrosc., 216, 259 [NASA ADS] [CrossRef] [Google Scholar]
  35. Woon, D. E., & Dunning, T. H., Jr. 1995, J. Chem. Phys., 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]
  36. Zuckerman, B., Ball, J. A., & Gottlieb, C. A. 1971, ApJ, 163, L41 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... calculations[*]
Tables S1 and S2 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/520/A64
... uncertainties[*]
Only the hyperfine components of the J = 94,5  $\leftarrow $ 94,6 rotational transition have been discarded as the corresponding residuals are about 25 times greater than the given uncertainties. A possible explanation is a typographical error in Chardon et al. (1976).
Copyright ESO 2010

All Tables

Table 1:   Rotational and hyperfine parameters of trans-HCOOH.

All Figures

  \begin{figure} \par\includegraphics[width=12cm,clip]{14787-fig1.eps} \end{figure} Figure 1:

The hyperfine structure of the J = 182,16  $\leftarrow $ 182,17 rotational transition of trans-HCOOH. The recorded spectrum (top: P=0.6 mTorr, mod. depth = 7 kHz; bottom: P=0.3 mTorr, mod. depth = 5 kHz) is compared to the predicted ones obtained, from the bottom, using the data from Chardon et al. (1976, in green), only the computed spin-rotation constants (in blue), computed spin-rotation and spin-spin constants (in red).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=11.5cm,clip]{14787-fig2.eps} \vspace*{4mm} \end{figure} Figure 2:

Line profile analysis of the hyperfine structure of the J = 221,21  $\leftarrow $ 220,22 rotational transition of trans-HCOOH: recorded spectrum in black, calculated spectrum in red and residual (observed - calculated) in green.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.5cm,clip]{14787-fig3.eps} \end{figure} Figure 3:

Portion of the b Q band, with Ka = 9  $\leftarrow $ 8, recorded in the THz region (P = 90 mTorr, mod. depth = 2.25 MHz).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.