EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) A81 Full HTML
Free Access
Issue
A&A
Volume 520, September-October 2010
Article Number A81
Number of page(s) 13
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913952
Published online 06 October 2010
A&A 520, A81 (2010)

Evidence of heavy-element ashes in thermonuclear X-ray bursts with photospheric superexpansion

J. J. M. in 't Zand1 - N. N. Weinberg2

1 - SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
2 - Astronomy Department and Theoretical Astrophysics Center, University of California, Berkeley, 601 Campbell Hall, Berkeley, CA 94720, USA

Received 23 December 2009 / Accepted 28 April 2010

Abstract
A small subset of thermonuclear X-ray bursts on neutron stars exhibit such a strong photospheric expansion that for a few seconds the photosphere is located at a radius $r_{\rm ph} \ga 10^3~$km. Such ``superexpansions'' imply a large and rapid energy release, a feature characteristic of pure He burst models. Previous calculations have shown that during a pure He burst, the freshly synthesized heavy-element ashes of burning can be ejected in a strong radiative wind and produce significant spectral absorption features. We search the burst data catalogs and literature and find 32 superexpansion bursts, 24 of which were detected with BeppoSAX and three with RXTE at high time resolution. We find that these bursts exhibit the following interesting features: (1) At least 31 are from (candidate) ultracompact X-ray binaries in which the neutron star accretes hydrogen-deficient fuel, suggesting that these bursts indeed ignite in a helium-rich layer. (2) In two of the RXTE bursts we detect strong absorption edges during the expansion phase. The edge energies and depths are consistent with the H-like or He-like edge of iron-peak elements with abundances $\ga$100 times solar, suggesting that we are seeing the exposed ashes of nuclear burning. (3) The superexpansion phase is always followed by a moderate expansion phase during which $r_{\rm ph} \sim 30$ km and the luminosity is near the Eddington limit. (4) The decay time of the bursts, $\tau _{{\rm decay}}$, ranges from short ($\approx$10 s) to intermediate ($\ga$103 s). However, despite the large range of $\tau _{{\rm decay}}$, the duration of the superexpansion is always a few seconds, independent of $\tau _{{\rm decay}}$. By contrast, the duration of the moderate expansion is always of order $\tau _{{\rm decay}}$. (5) The photospheric radii $r_{\rm ph}$ during the moderate expansion phase are much smaller than steady state wind models predict. We show that this may be further indication that the wind contains highly non-solar abundances of heavy elements.

Key words: X-rays: binaries - nuclear reactions, nucleosynthesis, abundances - stars: neutron - radiative transfer - X-rays: general

1 Introduction

X-ray bursts are thermonuclear shell flashes that result from the unstable burning of fuel accreted on the surface of a neutron star (NS) from a Roche-lobe filling companion star (Lamb & Lamb 1978; Woosley & Taam 1976; Maraschi & Cavaliere 1977; Grindlay et al. 1976; for reviews, see Strohmayer & Bildsten 2006; Lewin et al. 1995). Approximately $20 \%$ of all bursts exhibit some degree of photospheric radius expansion (PRE; see, e.g., Galloway et al. 2008a) due to a flux exceeding the Eddington limit, resulting in a radiatively driven expansion of the photosphere (Tawara et al. 1984a,b; Ebisuzaki et al. 1983; Lewin et al. 1984). During the expansion, the emission area increases while the bolometric luminosity remains nearly constant (near the Eddington limit). As a result, the photosphere cools and the detected X-ray flux decreases. Eventually the bolometric luminosity decreases, the photosphere returns to the NS surface, and the X-ray flux rises again, signifying the start of the main burst.

In a small fraction of bursts (we estimate no more than a few tenths of a percent), the PRE is so extreme that for a few seconds the detected X-ray flux decreases to less than 1% of its peak value. Such extreme PREs create the illusion of a precursor to the main burst, as first reported by Hoffman et al. (1978). Given that the peak temperature of a burst is typically 2.5 keV, close to the soft end of a typical X-ray device's bandpass, such a dip implies that the effective temperature decreases to less than $0.2~{\rm ~keV}$ (assuming pure black body radiation at a constant bolometric flux and a hydrogen column density of $10^{22}~{\rm H{-}atoms~cm}^{-2}$, typical for an X-ray burst source). This corresponds to a radius expansion factor of 100 or more, implying that the photosphere moves out to radii $r_{\rm ph} \ga 10^3~{\rm km}$. We call such an extreme PRE a superexpansion to distinguish it from the much more common moderate PRE with an expansion factor of a few.

In X-ray burst models, bursts that ignite in helium-rich layers have high peak luminosities that often exceed the Eddington limit and drive strong radiative winds (Woosley et al. 2004; Hanawa & Sugimoto 1982; Fujimoto et al. 1987; Paczynski 1983). Superexpansion bursts are the most luminous of all X-ray bursts and may be the result of nearly pure helium ignition; as such they serve as a useful test bed for helium burst models. In addition, calculations show that heavy-element ashes of nuclear burning can be ejected in the winds of PRE bursts and produce strong spectral absorption features (Weinberg et al. 2006b). The brightness and powerful, long-lasting winds of superexpansion bursts makes them ideal candidates for detecting spectral evidence of heavy-element ash ejection.

Helium bursts can be of either short or long duration depending on the properties of the accretion (Bildsten 1998; Fujimoto et al. 1981). If the NS accretes a H/He mixture, the bursts tend to be short (seconds). If, however, the system is an ultracompact X-ray binary (UCXB) and the NS accretes hydrogen deficient material, the bursts tend to be much longer (several tens of minutes, i.e., the ``intermediate-duration bursts''; Cumming et al. 2006; in 't Zand et al. 2005). This is because in UCXBs, unlike in mixed H/He accretors, there is no stable CNO burning to keep the freshly accreted envelope hot. As a result, the helium fuel ignites at a greater depth, where the thermal time is longer. As we will show, the superexpansion bursts that we find are all associated with (candidate) UCXBs.

The volume of data on superexpansion has increased substantially since the last detailed publication on extreme PREs (van Paradijs et al. 1990). At that time only 4 superexpansion bursts were known. It therefore makes sense to revisit the subject. In Sect. 2 we report on an additional 28 superexpansion bursts, most of them found in archival BeppoSAX and RXTE data. In Sect. 3 we examine the spectroscopic features of the best-covered superexpansion bursts. We find evidence for a variable absorption edge that may be due to exposed heavy-element ashes of nuclear burning. In Sect. 4 we describe the spectroscopic features of the other superexpansion bursts. We find that in all 32 bursts the superexpansion phase is followed by a moderate expansion phase. In Sect. 5 we show that the duration of the two phases are uncorrelated. We place these results in the context of models of helium-rich X-ray bursts and radiation-driven NS winds in Sect. 6 and conclude in Sect. 7.

2 Search for superexpansion bursts

Table 1:   Measurements of 32 bursts with superexpansion.

We searched for bursts with precursors in the literature (Galloway et al. 2008a; Kuulkers et al. 2003 and other relevant literature; see Table 1) and data of the Proportional Counter Array (PCA; operational since January 1996) on RXTE up to and including 2008 and in all data of the two Wide Field Cameras (WFCs; operational between June 1996 and April 2002) on BeppoSAX. Both instrument packages consist of proportional counters with similar efficiency curves and spectral resolution (20% full-width at half maximum), and bandpasses that start at 2 keV. The PCA (Jahoda et al. 2006) consists of 5 proportional counter units (PCUs) that each have a propane-filled and a xenon-filled gas layer. The xenon layer is the main detector and is read out at high time and energy resolution between 2 and 60 keV. The propane layer is used for anti-coincidence. It has only 0.125 s time resolution and no energy resolution. However, since it has additional sensitivity between 1.5 and 2 keV, it is useful for studying the soft phases of X-ray bursts. The net collecting area of the xenon layers combined is about 8000 cm2, the field of view 2$^\circ$ (full-width to zero response) and there is no angular resolution. The time resolution can be set to 1 $\rm\mu s$ at best. The two WFCs (Jager et al. 1997) each had a net collecting area of 140 cm2, a field of view of 40$^\circ$, an angular resolution of 5$^\prime$ in a bandpass of 2 to 28 keV. The time resolution was 0.5 ms. The observation program of the PCA is in large part dedicated to bursting NSs, yielding large exposure times (of order megaseconds; Galloway et al. 2008a) despite the small field of view. Thanks to the wide field of view of the WFCs, long exposure times were acquired on the majority of bursting NSs, resulting in an unprecedented ability to detect rare and unexpected events such as superexpansion bursts.

\begin{figure} \par\includegraphics[width=8.4cm,clip]{13952f1.ps} \end{figure} Figure 1:

Time profiles of the 2-30 keV photon flux of 24 X-ray bursts detected from 4U 1722-30 with BeppoSAX WFC (this includes 21 bursts with precursor, see Table 1, and three without at MJD 50521.804, 50527.181 and 50532.411). The photon flux is scaled between -1 and 4 phot s-1 cm-2. The horizontal dotted lines indicate a flux level of 0 phot s-1 cm-2. The MJD indicated in each panel refers to t=0 s. The profiles have been aligned to the start time of the precursor.

Open with DEXTER

Our search through $\approx$3400 bursts and the literature turned up 32 superexpansion bursts from 8 different systems, see Table 1. All the bursts that have been unambiguously identified with an object (7 out of 8 systems) are from (candidate) UCXBs as listed by in 't Zand et al. (2007). The UCXB candidacy of the only transient, XB 1715-321, has been put forward in Jonker et al. (2007). The one burst not unambiguously identified with an object is from 4U 1708-23. Of the 32 bursts listed, 22 are from 4U 1722-30 (in the globular cluster Terzan 2), 21 of which were detected with BeppoSAX-WFC (see Fig. 1 and Kuulkers et al. 2003). Almost all bursts from 4U 1722-30 have a precursor; for a burster with precursors, it has relatively frequent bursts (once every few days). The superexpansion burst from 4U 1820-30 is a superburst (Strohmayer & Brown 2002, hereafter SB02).

3 Spectral analysis of the 3 PCA bursts

The data for the three PCA superexpansion bursts are of higher quality than the WFC burst data due to the PCA's large photon collecting area. The quality is especially good because at least three PCUs were employed during these observations (this is generally true of only $\approx$5% of the PCA's observation time). Nonetheless, the spectroscopic resolution of the PCA is modest (17% FWHM at 6 keV) and only relatively broad spectral features can be resolved.

High-time-resolution spectrally-resolved data are available for the first 30 s of the burst from 4U 0614+091. Such data are available for much of the 4U 1722-30 burst, except between 3 and 8 s after burst onset. The superburst from 4U 1820-30 had good spectral coverage throughout but only at a modest time resolution of 16 s (the ``Standard-2'' data collecting mode). We describe the spectral data and analysis method in more detail in Appendix A.

\begin{figure} \par\mbox{\includegraphics[height=0.675\columnwidth,angle=270]{13... ...includegraphics[height=0.615\columnwidth,angle=270]{13952f2f.ps} }\end{figure} Figure 2:

Spectral fits to the PCA bursts from 4U 0614+09 and 4U 1722-30 during time intervals when the absorbed black body plus reflection model fails to fit the data (see Fig. B.1 for example time intervals when the black body plus reflection model provides a good fit to these bursts). Left plots: the 4U 0614+09 spectrum between 1.65 and 1.78 s after burst onset (this is the second data point after the superexpansion phase in Fig. 3). Middle plots: the 4U 0614+09 spectrum between 2.53 and 2.65 s after burst onset (ninth data point). Right plots: the 4U 1722-30 spectrum for the 7 s long interval indicated by the grey bar in Fig. 3. The upper panels show the observed photon flux (crosses) and the fitted black body plus reflection model (histogram). The middle panels show the fractional deviation of the data points from the black body plus reflection model. The lower panels show the deviations after an absorption edge is included in the model.

Open with DEXTER

\begin{figure} \par\includegraphics[width=6.3cm,angle=0]{13952f3a.ps}\includegra... ...gle=0]{13952f3b.ps}\includegraphics[width=6cm,angle=0]{13952f3c.ps} \end{figure} Figure 3:

Time profiles of various spectral parameters for 3 superexpansion bursts detected with RXTE-PCA from 4U 0614+09 ( left; see also Kuulkers et al. 2010), 4U 1722-30 ( center; see also Molkov et al. 2000) and 4U 1820-30 (right; see also Ballantyne & Strohmayer 2004; Strohmayer & Brown 2002). Time is in seconds since burst onset (see Table A.1). Top panels: total PCA countrate for the xenon layers (solid line, in units of 104 s-1) and propane layer (dot-dashed grey line, in units of 1250 s-1), after subtracting the pre-burst levels. The horizontal dashed lines mark a count rate of zero. Second panels: bolometric flux of the fitted black body if no reflection component is included, corrected for detector dead time and for absorption. The errors were not determined, but they become large when kT<1 keV. Third panels: black body temperature in keV. Fourth panels: black body radius assuming isotropic emission. Assumed distances: 3.2 kpc (4U 0614+09; Kuulkers et al. 2010), 9.5 kpc (4U 1722-30; Kuulkers et al. 2003) and 7.6 kpc (4U 1820-30; Kuulkers et al. 2003); Fifth and sixth panels: absorption edge energy $E_{\rm edge}$ in keV and optical depth $\tau _{\rm opt}$. Bottom panels: reduced $\chi ^2$ value for each fit to the black body + reflection + edge model. We left out the data for 4U 1820-30 between 2000 and 2500 s, because these are not understood (see Ballantyne & Strohmayer 2004). The grey vertical bars for 4U 0614+09 and 4U 1722-30 delimit the time intervals for the spectra shown in Fig. 2. $N_{\rm H}$ was fixed for 4U 0614+09 and 4U 1820-30 and free for 4U 1722-30 because a fixed value did not yield good fits.

Open with DEXTER

Typically burst spectra are well fit by an absorbed black body model (Hoffman et al. 1977; Swank et al. 1977; Strohmayer & Bildsten 2006). Deviations from this model have been reported for the superexpansion burst from M15 X-2 (van Paradijs et al. 1990) and the PCA superexpansion superburst from 4U 1820-30 (SB02). In the latter case, SB02 detected a broad emission line between 5.8 and 6.4 keV and an absorption edge at 8-9 keV at times >100 s after burst onset (at earlier times the blackbody temperature was evolving too quickly for the Standard-2 accumulations to resolve). To model these features, SB02 included a Gaussian emission line and an absorption edge in their spectral model. With these components, they found acceptable fits with reduced $\chi^2\sim1$; both the line and edge were strongly required to adequately model the data. SB02 further noted that features of the Gaussian line - its finite width and an energy centroid that is often significantly less than 6.4 keV - suggested that the line was produced by reflection from a relativistic accretion disk. Indeed, excellent fits to the data were obtained by modeling the line as an Fe fluorescence feature from an accretion disk and accounting for smearing of the absorption edge due to disk motions (Ballantyne & Strohmayer 2004; and Ballantyne 2004).

3.1 Absorption edges

As shown in Appendix B (see top row of Fig. B.1), the bursts from 4U 0614+091 and 4U 1722-30 also show significant deviation from an absorbed black body. The deviations are similar to those seen in the 4U 1820-30 superburst: a broad emission line at 6 to 7 keV and an edge at $\approx$10 keV that varies with time.

Motivated by the success of Ballantyne & Strohmayer (2004) at fitting the deviations in 4U 1820-30 with a model that includes a reflection component, we attempted to fit the spectra of the 4U 0614+091 and 4U 1722-30 bursts using the same black body plus reflection model as Ballantyne & Strohmayer (provided to us by D. Ballantyne, see Appendix B). Although, as shown in Fig. B.1, the model fits some of the spectra, it fails to fit all the spectra, particularly spectra just after the end of the superexpansion phase. Examples of when the black body plus reflection model fail are shown in the top row of Fig. 2. These include two spectra of 4U 0614+091 within a few seconds after the superexpansion and one spectrum of 4U 1722-30 during the first 7 s after the superexpansion (as indicated by the grey bar in Fig. 3). In these three examples, the edges are deeper or at lower energies than the reflection model can accommodate.

It is worth noting that during the superexpansion, the flux of both bursts drops below the pre-burst level (see top panel of Fig. 3). This may be because the expanding shell and super-Eddington flux disrupt the disk and temporarily stop the accretion. Alternatively, the disk is not disrupted and we just do not see the accretion flux because the expanding shell surrounds and obscures the inner disk. Whatever the cause, it is perhaps not surprising that the disk reflection model fails at times immediately following the superexpansion. Furthermore, even when the reflection model does fit the data, it often yields unreasonable results; for instance, it requires that the majority of the flux be in the reflection component rather than the direct black body component. This results in unreasonable values for the black body luminosity and radius.

The failure of the reflection model to fit some of the spectral data from 4U 0614+091 and 4U 1722-30 prompted us to add another component to the spectral model: an absorption edge stemming from the primary (non-reflected) spherically symmetric burst emission. Weinberg et al. (2006b) have suggested that such a signature should appear in the spectra of radius expansion bursts due to the presence of heavy ashes of nuclear burning in the photosphere (see Sect. 6.2). To model such an edge, we multiply the spectral energy distribution by $M(E)={\rm exp}[-\tau_{\rm opt}\;(E/E_{\rm edge})^{-3}]$for photon energies $E>E_{\rm edge}$ and M(E)=1 otherwise[*]. The fit parameters are the optical depth of the line $\tau _{\rm opt}$ and the edge energy $E_{\rm edge}$. Our full spectral model thus accounts for three features: an absorbed black body, the reflection of the burst flux from an inner accretion disk, and an absorption edge formed in the photosphere.

We find that including such an edge significantly improves the fits[*], as illustrated in the lower row of plots in Fig. 2. The evolution of the absorption edge parameters $\tau _{\rm opt}$and $E_{\rm edge}$ is shown in Fig. 3 for the three PCA bursts. The absorption edge from 4U 0614+091 exhibits a peculiar increase in $E_{\rm edge}$ from  $4.63\pm0.05$ keV just after the superexpansion to $8.5\pm0.1$ keV less than 2 s later (see also left and middle panels of Fig. 2). For the next 2 s, $E_{\rm edge}$remains nearly constant at 8.5 keV, after which no significant edge is detected. While $E_{\rm edge}$ is increasing, $\tau _{\rm opt}$is large (between 2 and 3), after which it becomes substantially less than 1.

The fit to the first spectral data point from 4U 1722-30 (8 s after burst onset) yields an absorption edge with $E_{\rm edge}\simeq11$ keV and $\tau_{\rm opt}\simeq1$. The parameters remain near these values until the temperature peaks at 23 s after onset, after which the parameters quickly change to $E_{\rm edge}\simeq 6{-}7$ keV and $\tau_{\rm opt}\simeq0.5$. Since there is no spectral data immediately following the superexpansion (from 3 to 8 s), we do not know if the increase in $E_{\rm edge}$ seen in the spectra from 4U 0614+091 occurs in the case of 4U 1722-30.

The absorption edge from 4U 1820-30 is shallow, but still detected with significance thanks to the high quality signal provided by the long duration of the burst. This is particularly clear when co-adding all the data accumulated over a long time span (e.g., all data between 5000 and 10 000 s).

Although we obtain reasonable fits to the data once we include an edge in the model, the limited spectral resolution of the PCA precludes an unambiguous identification of these features as absorption edges. Higher spectral resolution observations of superexpansion bursts, for instance with XMM-Newton or Chandra, would be extremely useful.

3.2 Other spectral features of the 3 PCA bursts

The evolution of some of the other spectral parameters is shown in Fig. 3. We do not show the results for the reflection parameters as these are not of immediate interest. The top panel shows the light curve for both the xenon and propane detector layers. The most conspicuous feature is the significant dip in the light curve during the superexpansion phase; the flux drops below the pre-burst level signifying that the large burst flux temporarily disrupts or obscures the accretion on to the NS. The propane layer is most sensitive at 1.5 to 2 keV and the signal from this layer is strongest when the black body temperature $kT\approx1$ keV immediately following the superexpansion. The light curve from 4U 1722-30 has a 2 s long spike near the end of the superexpansion phase that is especially pronounced in the propane layer. It may be due to a brief contraction and re-expansion of the photosphere, although interpreting the spike is difficult because there is no spectral data available during this time interval. There are indications of similar spikes in the 4U 1722-30 bursts detected with the WFC (Fig. 1). A similar feature has been reported in a burst from M15 X-2 (van Paradijs et al. 1990).

The 3 PCA bursts show a phase of moderate expansion after the superexpansion. During the moderate expansion phase, the black body temperature increases and the radius decreases. We define the end of the moderate expansion phase to be the time at which the temperature peaks, which is attributed to the photosphere ``touching-down'' on the NS surface (e.g., Galloway et al. 2008b,a; Kuulkers et al. 2003; Lewin et al. 1993). This is nicely illustrated in Fig. 3 in the bursts from 4U 1722-30 and 4U 1820-30, where touch down occurs 23 and 1400 s after burst onset, respectively. The moment of touch down in 4U 0614+09 was not covered by the PCA, but was observed with FREGATE on HETE-II to be at 90 s (Kuulkers et al. 2010).

In the bursts from 4U 0614+09 and 4U 1722-30, we find that at the start of the superexpansion phase, when the X-ray flux begins to drop, the photosphere is apparently moving out at velocities $v_{\rm ph} \approx 3\times10^4~{\rm km~s}^{-1}$ and $v_{\rm ph} \approx 10^3~{\rm km~s}^{-1}$, respectively (left and middle panels of Fig. 3; this estimate is simply the change in apparent radius divided by the time over which that change occurred). It is difficult to determine whether these measurements reflect the true velocities of the photosphere due to uncertainties, e.g., in the black body color correction (Pavlov et al. 1991; London et al. 1986). Calculations by Madej et al. (2004) show that the observed color temperature of a black body fit may differ by a factor of 1.3 to 1.4 from the effective temperature for a 1 keV black body and about 1.6 for a 3 keV black body. Consequently, inferred radii would need to be corrected by a factor of 1.7 to 2.6. In addition, the PCA calibrated data do not cover photon energies below 3 keV and, thus, the peak of the thermal spectrum when the expansion is large. We nonetheless consider the expansion velocities to be reliable to within a factor of a few.

The radii during the moderate expansion phase of the 4U 1820-30 superburst are unreasonably small (i.e., < $10~{\rm km}$). It cannot be attributed to an underestimated value of the distance as this is well measured both optically (Heasley et al. 2000) and from comparing the burst peak flux to the Eddington limit of a hydrogen-poor photosphere (e.g., Galloway et al. 2008a; Zdziarski et al. 2007). A color correction would, however, increase the measured radii to acceptable values (see also Strohmayer & Brown 2002). The superburst also behaves somewhat unusual between 2000 and 2500 s after burst onset. The behavior is unexplained and the data in this time frame is excluded in both our analysis and that of Ballantyne & Strohmayer (2004).

4 Spectroscopic features of the other bursts

When there is sufficient sensitivity, other superexpansion bursts show some or all of the features seen in the 3 PCA bursts. The edge is difficult to detect in bursts measured with instruments other than the PCA, although the burst from M15 X-2 measured with Ginga showed indications of edges in the spectrum (see Fig. 6 in van Paradijs et al. 1990). The one feature that is always seen is a phase of moderate expansion following the superexpansion. The spike in low-energy flux a few seconds after superexpansion is not always seen (e.g., it is not seen in the PCA bursts from 4U 0614+09 and 4U 1820-30).

The burst from 4U 0614+09 has a very fast rise and the precursor is merely 0.05 s long (Fig. 3). For such short durations, smaller detectors might fail to catch the precursor and instead first see the burst during the end of the superexpansion phase, when the photospheric radius is decreasing. An example of this might be the long burst detected from 2S 0918-549 with the BeppoSAX WFCs (in 't Zand et al. 2005). This burst lacks a precursor and yet spectroscopic analysis of the rising phase reveals a black body radius that is rapidly decreasing, as if the burst was preceded by a superexpansion phase. The very long burst from SLX 1737-282 ( $\tau_{\rm decay}=659\pm32$ s, see also Falanga et al. 2008; in 't Zand et al. 2002) also lacks a precursor despite having a radius that decreases during the rise, although the decrease is not as extreme as in 2S 0918-549.

There are a few bursts that also show two expansion phases, but whose expansion factor in the first phase is too small (between 5 and 10) to qualify as a superexpansion. Their X-ray signal is not completely lost, but their light curve still shows a deep dip. This is true of all ordinary X-ray bursts detected from 4U 1820-30 with the PCA (Galloway et al. 2008a), a second PCA burst from 4U 1722-30 detected at MJD 54526.679 (Galloway, priv. comm.), a burst from M15 X-2 (Smale 2001), and a few bursts from the non-UCXBs 4U 1705-44, KS 1731-260, SAX J1747.0-2853, and SAX J1808.4-3658.

5 Measurement of expansion durations

\begin{figure} \par\includegraphics[width=7.5cm,clip]{13952f4.ps} \end{figure} Figure 4:

Duration of radius expansion phases versus decay time $\tau _{{\rm decay}}$ for each superexpansion burst. For data, see Table 1. Crosses mark the duration of a burst's superexpansion phase ( $t_{\rm se}$) and asterisks mark the duration of its moderate expansion phase ( $t_{\rm me}$). The dashed line marks the relationships $t_{\rm se},t_{\rm me}=\tau _{\rm decay}$.

Open with DEXTER

We define the duration of the superexpansion phase, $t_{\rm se}$, as the time between the end of the precursor and the start of the main burst. In practice (allowing for statistical uncertainties), this is the time over which the flux is less than about $10\%$ of its peak value. We define the duration of the moderate expansion phase, $t_{\rm me}$, as the time between the end of the superexpansion and the time of peak temperature or spectral hardness, which is usually considered to be the moment when the expanded photosphere ``touches down'' on the NS (see Sect. 3). The decay time $\tau _{{\rm decay}}$ is determined by fitting an exponential function to the full-bandpass light curve after touch down and measuring the e-folding decay time. Since all the detectors are of a similar type (i.e., a xenon-filled proportional counter), the systematic errors introduced by using observed photon rates instead of derived calibrated energy fluxes are negligible compared to statistical errors.

Table 1 gives the duration measurements for the 32 superexpansion bursts. The durations $t_{\rm se}$ and $t_{\rm me}$are plotted as a function of $\tau _{{\rm decay}}$ in Fig. 4. The diagram reveals two important features: first, $t_{\rm me}$ is proportional to $\tau _{{\rm decay}}$ (they are approximately equal). This is not surprising; the longer the burst, the longer the flux remains near its peak value. Since the peaks are super-Eddington in these bursts, the duration of the super-Eddington phase should be proportional to the decay time (see Appendix C). Second, $t_{\rm se}$ is independent of $\tau _{{\rm decay}}$; in all bursts the superexpansion lasts a few seconds. We discuss possible explanations for the lack of correlation between $t_{\rm se}$ and $\tau _{{\rm decay}}$ in Sect. 6.3.

6 Discussion

6.1 Association between superexpansion bursts and UCXBs

All the superexpansion bursts that we find, including those in the literature, are from (candidate) UCXBs (see in 't Zand et al. 2007). A characteristic of UCXBs is that they are hydrogen deficient (e.g., Nelemans 2008). As a result, X-ray bursts from UCXBs are most likely fueled entirely by helium and/or heavier elements[*]. Furthermore, since there is no stable CNO burning in-between bursts, the freshly accreted NS envelope in an UCXB is colder than that of a hydrogen-rich system accreting at the same rate. Bursts from UCXBs therefore tend to occur at greater depth, where the thermal time is longer. This gives rise to so-called ``intermediate-duration bursts'' with durations of several tens of minutes (Cumming et al. 2006; in 't Zand et al. 2005). Because of the large and rapid energy release, the peak luminosity of helium-rich bursts (of both the short- and intermediate-duration variety) often exceeds the Eddington limit, resulting in phases of photospheric radius expansion (Cumming et al. 2006; Weinberg et al. 2006b; Paczynski 1983).

6.2 Evidence for heavy-element ashes in photosphere

The convective region that forms during an X-ray burst is well-mixed with the freshly synthesized ashes of nuclear burning. Weinberg et al. (2006b) solve for the evolution of the vertical extent of the convective region in PRE bursts with strong radiative winds. They find that the convective region extends outwards to sufficiently shallow depths that the base of the wind lies well within the ashes of burning. As a result, some ashes are ejected in the wind and exposed at the photosphere. The column density of ejected ashes, which consist primarily of heavy elements (near the Fe peak; see below), is expected to be especially large for the energetic, helium-rich bursts that exhibit superexpansion. The spectral signature of the ashes is therefore expected to be detectable at even modest spectral resolution (Weinberg et al. 2006b; see also van Paradijs 1982 and Foster et al. 1987).

We now discuss two features in the data that suggest the presence of heavy-element ashes in the photosphere: absorption edges at the end of the superexpansion phase (Sect. 6.2.1) and smaller-than-expected radii during the moderate expansion phase (Sect. 6.2.2).

6.2.1 Absorption edges

Which elements might be responsible for the observed absorption edges? We first consider the early-time edge in the spectrum of 4U 0614+09, which increases from an initial energy of $E_{\rm edge}=4.6~{\rm keV}$ to 8.5 keV within $\simeq$2 s. Since the photosphere is at large radii ( $r_{\rm ph} \ga 30$ km) during this time, the gravitational redshift should be negligible ($z\la 0.1$). Although  $r_{\rm ph}$is decreasing with time, suggesting that material is moving away from the observer and back on to the NS, the rate of decrease appears much too slow ($\sim$100 km s-1) to produce any appreciable doppler redshift[*]. This suggests that the variations in  $E_{\rm edge}$are not due to variations in redshift but rather are intrinsic to the source. One possibility is that the shift in $E_{\rm edge}$ is due to variations in which elements and ionization states dominate the absorption as the photosphere contracts and $T_{\rm eff}$ increases. If correct, bound-bound transitions should also be a source of absorption. The limited spectral resolution of the PCA makes it difficult to detect narrow X-ray absorption lines, however (such lines have never been confirmed in PCA spectra as far as we know).

We now consider the late-time 8.5 keV edge in 4U 0614+09. The measured photospheric radii at this time ( $r_{\rm ph}\approx 10$ km) imply that the photosphere is close to the NS surface and, thus, that the edge is gravitationally redshifted. For typical NS parameters (e.g., $M=1.4~M_\odot$, R=10 km) $z\approx0.3$ at the surface and the intrinsic energy of the $8.5~{\rm ~keV}$ edge would be $11~{\rm keV}$. This is close to both the hydrogen-like and helium-like edges of Ni ( $10.8~{\rm keV}$and $10.3~{\rm keV}$, respectively). That the edge may be due to Ni is supported by calculations which show that at the large ignition depth[*] implied by the intermediate duration of the burst from 4U 0614+09 ( $y_{\rm base}\sim10^{10}~{\rm g~cm}^{-2}$; Kuulkers et al. 2010), Ni is the dominant product of constant pressure helium burning (Hashimoto et al. 1983).

The 4U 1722-30 moderate expansion phase edge at $E_{\rm edge}\approx 11~{\rm keV}$ is also close to the unshifted hydrogen-like Ni edge, consistent with the large measured photospheric radius during this phase. After the moderate expansion phase, when the photosphere is at the NS surface, $E_{\rm edge}\approx 7\pm1~{\rm keV}$, consistent with a gravitationally redshifted hydrogen-like Ni edge.

We can also use the measured optical depth of the edge, $\tau _{\rm opt}$, to demonstrate that not only must the absorption be due to a heavy element such as Ni, but that its abundance must be much higher than the solar value. We do so by assuming that $\tau_{\rm opt} = \tau_{\rm bf}(E_{\rm e}) \equiv N \sigma_{\rm bf}(E_{\rm e})$, where N is the hydrogenic column density of the element above the photosphere, $\sigma_{\rm bf}(E) \simeq 6.3\times10^{-18}(E_{\rm edge}/E)^3 Z^{-2}~{\rm cm}^2$is the bound-free cross-section, and we take $E_{\rm edge}= 13.6Z^2~{\rm eV}$(see, e.g., Bildsten et al. 2003). We approximate the hydrogenic column density as $N(T, \rho, Z)= f \zeta_{\rm H} N_{\rm e}$, where f is the fraction of atoms belonging to that element (the ``number fraction''), $\zeta _{\rm H}$ is the fraction in the hydrogen-like state at a given temperature and density from Saha equilibrium (we assume an element is either fully ionized or hydrogen-like), $N_{\rm e} \approx \sigma_{\rm Th}^{-1}$ is the electron number column density, and $\sigma_{\rm Th}$ is the Thomson cross-section. Such an approximation should give a reasonable estimate of N (see, e.g., Weinberg et al. 2006b).

\begin{figure} \par\includegraphics[width=7.5cm,clip]{13952f5.ps} \end{figure} Figure 5:

Fraction of 44Ti and 56Ni in a hydrogenic state $\zeta _{\rm H}$ (top panel) and the optical depth of the edge $\tau _{\rm bf}(E_{\rm e}) \equiv N \sigma _{\rm bf}(E_{\rm e})$ (bottom panel) as a function of effective temperature (bottom axis) and blackbody radius $r_{\rm ph}\equiv (L_{\rm Edd} / 4\pi \sigma T_{\rm eff}^4)^{1/2}$ (top axis) assuming a density of $\rho =0.01~{\rm g~cm}^{-3}$. Results are shown for mass fractions of X=0.1 and 1.

Open with DEXTER

In the top panel of Fig. 5 we show $\zeta _{\rm H}$ as a function of effective temperature $kT_{\rm eff}$ and $r_{\rm ph}=(L_{\rm Edd} / 4\pi \sigma T_{\rm eff}^4)^{1/2}$ for 44Ti and 56Ni at a density[*] of $\rho =0.01~{\rm g~cm}^{-3}$. In the bottom panel we show the implied optical depth of the edge $\tau _{\rm bf}(E_{\rm e}) \equiv N \sigma _{\rm bf}(E_{\rm e})$ for mass fractions of X=0.1 and 1. As the figure shows, a mass fraction $X\ga 0.1$is required in order to obtain an optical depth as large as the measured values $\tau_{\rm opt}\ga 1$ at the observed temperatures. Furthermore, elements $Z\la22$ cannot produce sufficiently large optical depths even for X=1. A Ni (Fe) mass fraction of $X\sim0.1$ is $\sim$1000 (100) times larger than the solar abundance.

Rotational broadening is expected to be small compared to the PCA spectral resolution and the width of an absorption edge. The NS in 4U 0614+09 has a spin frequency of $\nu_{\rm spin}=415$ Hz (Strohmayer et al. 2007), resulting in a maximum relative Doppler shift of $v/c=2\pi\nu_{\rm spin}R_{\rm NS}/c \simeq 0.1$and a FWHM of the broadening profile approximately a factor 2 lower (n.b., viewing angle effects and the smaller rotation velocity of an expanded photosphere tend to further reduce the broadening). The other two bursters have no measured spin frequencies, but the highest confirmed spin frequency ever measured for a burster is only 50% larger (620 Hz; Muno et al. 2002).

6.2.2 Small radii during moderate expansion phase

Steady state models of radiative winds from NSs predict photospheric radii of $100{-}1000~{\rm km}$ for mass outflow rates of $\dot{M}\approx10^{17}{-}10^{19}~{\rm g~s}^{-1}$(Joss & Melia 1987; Nobili et al. 1994; Paczynski & Prószynski 1986). The measured photospheric radii during the moderate expansion are much smaller than this ( $r_{\rm ph} \approx 30{-}50~{\rm km}$). The models were not calculated for lower $\dot{M}$for numerical reasons and perhaps the observed radii are small because the outflow rates are $\dot{M} < 10^{17}~{\rm g~s}^{-1}$. This seems unlikely, however. From energy conservation, Paczynski & Prószynski (1986) showed that the radiatively-driven mass outflow rate from a neutron star is given by $\dot{M} \simeq \alpha \dot{M}_0$, where $\alpha\equiv (L_{\rm base} - L_{\rm Edd}) / L_{\rm Edd}$ is the excess luminosity at the base of the ignition layer relative to Eddington and $\dot{M}_0 = 1.7\times10^{18}~{\rm g~s}^{-1}$ is a constant that depends only on the neutron star mass and radius (taken to be $M=1.4~M_\odot$ and $R=10~{\rm km}$). Such a low $\dot{M}$(i.e., $\alpha \la 0.05$) would therefore seem to require fine-tuning as it would imply that all the bursts are super-Eddington by only the slightest amount.

An alternative possibility is that the outflow structure is truncated at a radius where absorption becomes sufficiently more important than electron scattering; material above this radius has a lower effective Eddington limit and is blown away. The wind models either ignored absorption (Nobili et al. 1994; Paczynski & Prószynski 1986; Ebisuzaki et al. 1983) or assumed the wind consists of solar abundances (Joss & Melia 1987). The presence of heavy element ashes in the wind can, however, significantly modify the structure of the outflow.

To see why, note that at the temperatures observed during the moderate expansion phase ( $kT_{\rm eff} \simeq 1{-}2~{\rm ~keV}$), the fraction of Ni in the hydrogen-like state is 0.001-0.4 from Saha equilibrium at a density $\rho =0.01~{\rm g~cm}^{-3}$ (this assumes the Ni is either fully ionized or hydrogen-like; Ni is the dominant product of burning at these depths, see Sect. 6.2.1). The radiative force on hydrogenic Ni in the ground state is, in the optically thin limit (i.e., ignoring line blanketing), $F_{\rm rad} =\pi h {\rm e}^2 f_{1\rightarrow 2} F(E)/ m_{\rm e} c^2$ (Bildsten et al. 2003; Michaud 1970), where the flux per unit energy at the Ly$\alpha$transition F(E) is nearly constant across the line ( $E=8.0~{\rm keV}$) and $f_{1\rightarrow2}=0.42$ is the oscillator strength for hydrogenic Ni (Fuhr et al. 1981). At the observed temperatures, the radiative acceleration on Ni is then $a_{\rm rad}\approx 10^{15}{-}10^{16}~{\rm cm~s}^{-2}$ assuming a blackbody spectrum[*], a factor of $\ga$100 larger than the gravitational acceleration at the observed photospheric radii $r_{\rm ph} \approx 30{-}50~{\rm km}$. The force acting on the bound electrons is therefore $\ga$100 times larger than that acting on the free electrons and line driving will become dynamically significant once the abundance ratio of bound to free electrons exceeds $\sim$1/100 (see, e.g., Gayley 1995). This suggests that once material reaches $\approx$ $50~{\rm km}$and a significant fraction of ions become hydrogenic, line-driving will accelerate the flow to velocities much higher than the $v\approx10^3~{\rm km~s}^{-1}$ found in the aforementioned wind models.

Since $\rho\propto v^{-1}$ in a steady state wind, the structure of the outflow above $\approx$ $50~{\rm km}$may be much more tenuous than the wind models suggest. If line-driving accelerates the material to $\sim$ $10^4{-}10^5~{\rm km~s}^{-1}$, the column density of overlying material will be a factor of $\sim$10-100 smaller than that found in the wind models. The radius of the electron scattering photosphere may therefore be smaller by the same factor, in better agreement with the observed $r_{\rm ph}$. One caveat is that it is not clear whether lines or electron scattering will be the dominant source of opacity; a wind calculation that accounts for the absorption opacity from heavy elements is therefore needed in order to reliably estimate the location of the photosphere. While the electron scattering opacity dominates the free-free and bound-free opacity for the measured temperatures and densities of the photosphere (even if the composition is primarily heavy elements; see, e.g., Cox & Giuli 1968), the bound-bound opacity may be important.

6.3 Superexpansion duration

If superexpansion is due to a super-Eddington flux driving the photosphere to large radii, as the time profiles suggest, why is the superexpansion duration $t_{\rm se}$ always short (a few seconds) and independent of the decay time $\tau_{\rm decay} \sim 10{-}1000~{\rm s}$ (see Sect. 5)? Since the longer a burst, the longer the flux remains near its peak value, one might have expected $t_{\rm se}$to increase with increasing  $\tau _{{\rm decay}}$, as is the case with the moderate expansion duration  $t_{\rm me}$.

We now describe a possible explanation for this lack of correlation between $t_{\rm se}$ and $\tau _{{\rm decay}}$. In Appendix C we show why the lack of correlation is unlikely the result of either a brief (second-long) phase of highly super-Eddington flux or hydrodynamic burning.

X-ray burst wind models have all assumed a steady state outflow (Joss & Melia 1987; Nobili et al. 1994; Paczynski & Prószynski 1986; Ebisuzaki et al. 1983) and do not therefore describe the time-dependent response of the overlying layers in the very first moments of radiative driving. These models do, however, show that it takes $\approx$$1~{\rm s}$ for time-independent conditions to be established (see $t_{\rm char}$ in Table 1 of Joss & Melia 1987). Given that $t_{\rm se} \approx 1~{\rm s}$, this suggests that the superexpansion may be the result of a transient stage in the development of the wind.

Analyzing this possibility requires a time-dependent wind calculation and is beyond the scope of this paper. It is nonetheless worth noting that the superexpansion is consistent with the ejection of a geometrically thin shell of material of initial column depth $y_{\rm ej} \gg y_{\rm ph}$, where $y_{\rm ph}\simeq 1~{\rm g~ cm}^{-2}$is the depth of the photosphere on the NS surface. This shell, which may correspond to the layer of material above where the flux first becomes super-Eddington[*], will become transparent when it reaches an expansion factor $r/R \sim (y_{\rm ej}/y_{\rm ph})^{1/2}$. Once it becomes transparent - at a time $t_{\rm se}$ according to this picture - the observer suddenly sees the underlying neutron star again. Since the wind has had enough time to reach a steady state by this time, the photosphere is located at the moderate expansion value $r_{\rm ph} \approx 30{-}50~{\rm km}$.

The nuclear energy release from He burning ($\approx$ $1~{\rm MeV~nucleon}^{-1}$) is approximately $1\%$ of the gravitational binding energy at the NS surface, and therefore at most $1\%$ of the accreted mass can be ejected. This implies $y_{\rm ej} \la 0.01 y_{\rm base}$. If we assume the velocity of the ejected material is roughly constant with radius, the initial depth of the ejected column is $y_{\rm ej} = y_{\rm ph} (v_{\rm ph} t_{\rm se} / R)^2$and we have the constraint $y_{\rm base} \ga 10^8 (v_{\rm ph} t_{\rm se} / 10^4~{\rm km})^2~{\rm g~cm}^{-2}$. Since even short duration X-ray bursts have ignition depths $y_{\rm base} > 10^8~{\rm g~cm}^{-2}$, this constraint is easily satisfied in the case of 4U 1722-30 ( $v_{\rm ph} \approx 10^3~{\rm km~s}^{-1}$and $t_{\rm se} = 5~{\rm s}$; see Sect. 3.2 and Table 1). In the case of 4U 0614+09, the only other superexpansion burst for which there is an estimate of $v_{\rm ph}$, we get the strong constraint $y_{\rm base} \ga 10^9~{\rm g~cm}^{-2}$for $v_{\rm ph} \approx 3\times10^4~{\rm km~s}^{-1}$ and $t_{\rm se} = 1.2~{\rm s}$. This burst is an intermediate-duration burst and the ignition depth inferred from the cooling time is indeed consistent with $y_{\rm base}\sim10^{10}~{\rm g~cm}^{-2}$ (Kuulkers et al. 2010).

7 Summary and conclusions

The volume and quality of data on superexpansion bursts has increased substantially since the first detailed study nearly 20 years ago (van Paradijs et al. 1990). We found 28 new superexpansion bursts in the burst catalogs and literature, several of which were detected with much higher temporal and spectral resolution than the 4 original superexpansion bursts. In studying this larger sample, we found that superexpansion bursts have the following features:

1.
At least 31 of the 32 superexpansion bursts are from (candidate) ultracompact X-ray binaries.
2.
Three PCA bursts show significant spectral deviations from the absorbed black body model that typically describe X-ray burst spectra. The spectral deviations can be explained as absorption edges, with edge energies and depths that vary with time.
3.
Superexpansion is seen in short duration bursts, intermediate-duration bursts, and superbursts and the superexpansion phase is always followed by a moderate expansion phase.
4.
The duration of the superexpansion is always a few seconds, independent of burst duration, while the duration of the moderate expansion phase is proportional to burst duration.
5.
The photospheric radius during the moderate expansion phase is significantly smaller than that predicted by models of radiation-driven X-ray burst winds.
We showed that the absorption edges and small photospheric radii of the moderate expansion phases may indicate the presence of heavy-element ashes in the wind. In particular, the edge energies and optical depths appear consistent with a redshifted hydrogen-like or helium-like Ni edge and high Ni mass fractions ($X\ga 0.1$); Ni is expected to be the dominant product of burning at the large ignition depths inferred from the duration of these bursts. While we do not have a good explanation for why the edge energies seem to shift over the course of a few seconds, we speculate that it may be due to variations in which elements and ionization states dominate as $r_{\rm ph}$ decreases and the temperature increases.

The brevity of the superexpansion and its lack of correlation with burst duration may be the result of a transient stage in the wind's development, perhaps during which a shell of material is ejected to large radii by the sudden onset of super-Eddington flux deep below the photosphere. A time-dependent wind calculation using realistic compositions and opacities is needed in order to assess the viability of this proposed explanation.

The spectral deviations seen in the PCA bursts suggest that the spectra of superexpansion bursts have the potential to provide great insight into burst and NS physics. High spectral resolution observations with sub-2 keV energy coverage, as can be achieved with Chandra or XMM-Newton, are clearly needed. The shortest burst recurrence times for X-ray sources that exhibit almost exclusively superexpansion bursts (e.g., 4U 1722-30 and 4U 1812-12) are of order 5 to 10 days (e.g., in 't Zand et al. 2007), implying required exposure times of $\sim$ $500~{\rm ks}$if one were to plan a dedicated observation. There is often some predictability to when an X-ray burst will occur (e.g., Galloway et al. 2008a; Ubertini et al. 1999) and with careful planning less demanding exposure times (say by a factor of two) may be feasible.

Acknowledgements

We are grateful to David Ballantyne for providing us with his reflection models, Craig Markwardt for guidance in the PCA background calculation, Duncan Galloway for pointing out a second RXTE burst from 4U 1722-30, Erik Kuulkers for discovering the rich RXTE burst from 4U 0614+09, Nikolai Shaposhnikov for calling our attention to background issues with the 4U 1722-30 data, and thank Lars Bildsten, Phil Chang, Duncan Galloway, Alexander Heger, Keith Jahoda, Jelle Kaastra, Laurens Keek, Frits Paerels, Tod Strohmayer and Eliot Quataert for helpful discussions.

Appendix A: PCA spectral data preparation and analysis method

Table A.1:   Details of the data (analysis) for the 3 PCA superexpansion bursts. See also Figs. 2, 3, and B.1.

Details about the PCA data collecting modes, analysis settings, and time and spectral resolution are provided in Table A.1. For 4U 0614+09 and 4U 1722-30, data were obtained in the burst catcher mode. For 4U 1820-30 standard-2 data were obtained. The PCA spectra were accumulated from all active PCUs. While the spectra for 4U 1820-30 were drawn from only the upper xenon layer (``LR1''), those of the other two bursts were from all layers (the ``burst catcher'' mode does not allow separation of PCUs or layers).

A varying time resolution was employed in the time-resolved spectroscopy, based on the resolution available, the statistical quality of the data and the changes in the spectrum. The spectra were rebinned so as to have at least 15 photons per bin in order to ensure applicability of the $\chi ^2$ statistic. Contributions from particle and cosmic backgrounds, as predicted through version 3.6 of the tool pcabackest, were subtracted.

Response matrices were generated with version 11.7 of the tool pcarmf. A systematic error of 1.5% was assumed per photon energy channel. The instrument team recently suggested[*] that the systematic error should be set to 0.5%. While our fitted parameter values do not change if we adopt their prescription, doing so increases the $\chi ^2$ values somewhat. Perhaps the larger systematic uncertainty is due to a spectrum (a few-keV black body) that is different from that of the Crab source (a power law with a photon index of 2.1) which was solely used for the calibration; this should be investigated further.

Burst spectra were corrected for detector dead time following the procedure described in the RXTE Cook Book[*]. The time resolution for such a correction is limited to 0.125 s, so interpolations were necessary for the precursor in 4U 0614+09.

The burst spectra were compared with models between 3 keV and 30 keV using XSPEC version 12.5.0 (Arnaud 1996). The 3 keV threshold signifies the photon energy below which the instrument response is not well calibrated. The upper threshold signifies the photon energy above which the burst emission is expected to be negligible. At those energies, the spectrum is expected to be dominated by the accretion flux. Thus, some handle is obtained on the accretion emission.

Accounting for the changing accretion emission is not trivial. In super-Eddington bursts, one cannot simply subtract the spectrum accumulated before the burst because the super-Eddington flux and expanding photosphere can affect the accretion disk (e.g., Ballantyne & Strohmayer 2004). Indeed, as shown in the main text, the observed flux drops below the pre-burst (i.e., accretion) flux during the superexpansion phase. The flux during the moderate expansion phase may also affect the accretion. It is difficult to differentiate accretion flux from burst flux, because the burst emission dominates over the most sensitive part of the bandpass. Only at the highest energies does the accretion emission dominate, but the statistical quality is insufficient to infer a spectral shape. We assume that the spectral shape of the accretion emission remains, throughout the burst, identical to that of the pre-burst emission and fit its (``accretion'') normalization. When possible we determined an empirical 3-30 keV spectral shape from data in a $\sim$1000 s time interval prior to the burst (this is not always exactly 1000 s since there is not always data available for a continuous 1000 s interval, see Table A.1). The data from 4U 0614+09 are consistent with a power law, and the data from 4U 1722-30 and 4U 1820-30 are consistent with a comptonized spectrum, all with low-energy absorption. This accretion model was incorporated into our full spectral model of the data.

Quoted errors on spectral parameters are single-parameter 1$\sigma$values.

Appendix B: PCA spectral model

\begin{figure} \begin{tabular}{lll} \includegraphics[height=0.70\columnwidth,ang... ...hics[height=0.655\columnwidth,angle=270]{13952fa1e.ps}\end{tabular} \end{figure} Figure B.1:

Spectral fits to the PCA bursts from 4U 0614+09 ( left plots), 4U 1722-30 ( middle plot) and 4U 1820-30 ( right plots) during time intervals when the absorbed black body plus reflection model provides a good fit to the data (see Fig. 2 for example time intervals when the black body plus reflection model fails to provide a good fit to these bursts). The upper row shows the fractional deviations for a model that includes the absorbed black body component but not the reflection or absorption edge components. The lower row shows the deviations for a model that includes the absorbed black body and reflection component but not the absorption edge component. 4U 1722-30 is not shown because at that time does a reflection component not explain the deviations. The spectra are taken during the moderate expansion. The error bars include the 1.5% systematic error.

Open with DEXTER

To understand the X-ray burst emission process, we first accumulated an optimum-quality spectrum for each burst by identifying long data stretches when the spectral shape, as measured by the flux ratio between two photon energy ranges, remains approximately constant. The times over which we accumulated data for this initial spectral study are given in Table A.1. We then tested whether the resulting spectra are consistent with the canonical burst model, consisting of black body radiation (leaving free the temperature and normalization), low-energy absorption by cold gas of cosmic abundances (following the model for atomic cross sections and cosmic abundances of Morrison & McCammon 1983; leaving free the equivalent H-atom column density $N_{\rm H}$) and accretion emission (leaving free the accretion normalization; see above). The fractional deviations of the spectra with respect to this model are shown in the upper row of Fig. B.1. Not shown are the results between 20 and 30 keV because of the large error bars in that bandpass. None of the spectra fit the model. The shapes of the deviations are generally similar with a maximum at 6 to 7 keV and a minimum between 10 and 13 keV. The amplitude of the deviations of the different bursts are similar and far larger than instrumental uncertainties (0.5% to 1.5% per channel).

One approach to modeling the deviations is to include both a broad Gaussian emission line centered between 6 and 7 keV and an absorption edge close to 10 keV. A more physically motivated approach is to account for scattering (``reflection'') and relativistic blurring of the burst's black body radiation by a hot accretion disk (Ballantyne & Strohmayer 2004; Ballantyne 2004). Ballantyne & Strohmayer (2004) used such a reflection model to fit the deviations in the 4U 1820-30 superburst. Their reflection model accounts for reprocessing of thermal photons from the neutron star by the accretion disk (including comptonization, fluorescence, recombination, and photo-electric absorption), which is allowed to come into thermal and ionization balance. The model includes a number of ionization stages of C, N, O, Mg, Si and Fe, and the parameters include the bolometric flux of the reflection, the temperature of the black body, metal abundance and the ionization degree $\xi=4\pi F_{\rm X}/n_{\rm H}$ of the scattering medium, with $F_{\rm X}$ the bolometric flux of the direct black body radiation and $n_{\rm H}$ the hydrogen number density. See Ballantyne (2004) for further details of this model.

We used the Ballantyne (2004) reflection model. In our implementation, we assume solar abundances and fit for two of the reflection parameters: $\xi$and the bolometric flux. Assuming solar abundances is only relevant to Fe since it is the only element in the model with spectral features in the PCA bandpass. The temperature is given by that of the black body component. Note that this model is quite different from reflection by a power law as commonly applied in AGN and Galactic black hole spectra. In bursts, the radiant energy per frequency decade (the ``$\nu F_\nu$'' spectrum) peaks for black bodies at photon energies where photoelectric absorption by metals is very important, unlike for power law emission in AGN and Galactic black holes (Ballantyne 2004).

The reflection model also includes a convolution function for relativistic blurring by the accretion disk following Fabian et al. (1989). It is parametrized by the power law index for the radial dependence of the emissivity (set to -3), the inner disk radius (set to 10 GM/c2with M the neutron star mass), the outer disk radius (set to 200 GM/c2) and the inclination angle (set to 30$^{\rm o}$). Whenever these parameters were left free during fitting, the improvement in the fit was marginal. For practical purposes they were, therefore, kept fixed.

The complete applied model can be written in XSPEC as: constant*(wabs1*(bbodyrad + rdblur*atable{reflection}) + wabs2*comptt/po) with constant the detector dead time factor, wabs1 and wabs2 low-energy absorption (different for the two instances in this formula), bbodyrad the Planck function, rdblur the relativistic blurring function, reflection the model for the reflection of the Planck function against the accretion disk following Ballantyne (2004), comptt a comptonization component following Titarchuk (1994) and po a power law function. The latter two components are representative of the non-burst emission. The model has six free parameters: $N_{\rm H}$, $kT_{\rm bb}$, $R_{\rm bb}$, the flux and $\xi$ of the reflection component and the accretion normalization of comptt or po expressed relative to the pre-burst value.

Including reflection in the model is highly successful in reducing the deviations in the spectra of 4U 0614+09 and 4U 1820-30 for the particular time interval specified in Table A.1 (the ``time interval of initial spectral study''). We find $\chi^2_\nu=2.3$ and 0.75, respectively (the value for 4U 1820-30 is consistent with Ballantyne & Strohmayer 2004). The remaining deviations are shown in the lower row of Fig. B.1. The black body plus reflection model does not, however, fit all the spectra of 4U 0614+09 and 4U 1820-30 (see Sect. 3.1). Furthermore, it almost never provides a good fit to the spectra of 4U 1722-30 (the middle-right panel in Fig. 2 is representative of the typical spectral deviations found at all times in black body plus reflection model fits to the 4U 1722-30 spectra).

Even when the black body plus reflection model provides a good fit, the flux of the reflection component, a free parameter, is often higher than that of the direct black body component. This is due to the fact that the fitting procedure primarily tries to fit the narrow features - the broad emission line and the absorption edge. Since the continua of the reflection and direct black body components are very similar in the PCA bandpass, their contributions are difficult to disentangle. High reflection fluxes were also found by Ballantyne & Strohmayer (2004) in the late-time burst spectra of 4U 1820-30 (see their Fig. 1). As a result of a high reflection flux, the flux of the direct black body component becomes so low that the black body radius becomes substantially lower than 10 km. This is physically unrealistic. Without a proper model for the geometry of the accretion disk and independent measurements of the iron abundance in the donor star, it is impossible to meaningfully constrain the reflection flux in an independent manner.

We calculated bolometric luminosities and emission region radii by fitting the spectra without the reflection (or edge) component. After fitting, the absorption and the accretion normalization was set to zero, the deadtime correction set to 1, and the response matrix in XSPEC set to a dummy value. The flux could then be estimated in a broader energy range than the PCA bandpass. The unabsorbed flux was calculated between 0.05 and 30 keV, essentially a bolometric bandpass for a black body with a temperature between 0.5 and 3 keV. Since the fits are often formally unacceptable, no errors were calculated.

We tried several other functions to model the spectra. These include combinations of two different black bodies, combinations of one black body with a power law (with a free spectral index), gauss function or relativistic iron line (following Laor 1991, model laor in XSPEC), and single reflection models of a power law against a neutral or ionized disk (following Magdziarz & Zdziarski 1995, models pexrav/pexriv in XSPEC). While some of these models fit some of the spectra reasonably well, they only do so over limited time intervals in any given burst. A broken power law fits the data with the same goodness ( $\chi^2_\nu$) at any time, but there is no physical basis for such a model.

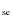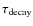
Appendix C: Ruling out alternative explanations for the lack of correlation between t $_{{\rm se}}$and $\tau _{{\rm decay}}$

Here we first consider the possibility that the transition between the superexpansion phase and the moderate expansion phase is due not to a shell ejection, as suggested in Sect. 6.3, but rather to a transition in the luminosity at the NS surface. In particular, if the luminosity exceeds not only the local Eddington luminosity, $L_{\rm Edd}\equiv 4\pi G M c / \kappa_0$, but also the Eddington luminosity at infinity, $L_{\rm Edd, \infty}\simeq L_{\rm Edd} (1+z)^2$, a strong radiation-driven wind will form ( $\kappa_0=0.2~{\rm cm^2~g}^{-1}$is the hydrogen-free electron scattering opacity). Such a wind can potentially drive the photosphere to very large radii ($\ga$ $100~{\rm km}$). If, however, $L_{\rm Edd} < L < L_{\rm Edd, \infty}$, a comparatively mild quasi-static expansion is sufficient to reduce the luminosity at the photosphere below $L_{\rm Edd}$(Hanawa & Sugimoto 1982; Paczynski & Prószynski 1986; Paczynski 1983). In this case, the PRE will be less extreme. This suggests that perhaps the large radius expansion factors reached during the superexpansion occur because initially $L>L_{\rm Edd, \infty}$. Then, after a time $t_{\rm se} \approx~{\rm seconds}$, the luminosity decreases to $L_{\rm Edd} < L < L_{\rm Edd, \infty}$ and the photosphere retreats closer to the NS surface, marking the start of the moderate expansion phase. This phase continues for a duration of order the cooling time after which the luminosity decreases to $L<L_{\rm Edd}$ and the photosphere settles on to the NS surface.

To test this idea, we carry out time-dependent cooling calculations for a range of ignition depths. To solve the heat transport equation we use the technique described in Weinberg & Bildsten (2007); Cumming & Macbeth (2004) carry out similar calculations for superbursts. We assume that the atmosphere is radiative and initially at its peak temperature, in accord with models of the rise of X-ray bursts (see e.g., Weinberg et al. 2006b; Cumming & Bildsten 2000). We assume a peak temperature at the base of the ignition layer $y_{\rm base}$ of $T_{\rm base, initial} = f T_{\rm max}$, where f is factor less than but of order unity and $T_{\rm max}=(3 g y_{\rm base} / a)^{1/4}$is the critical temperature at which radiation pressure completely dominates ( g=(1+z)GM/R2 is the gravitational acceleration and a is the radiation constant). We chose the value of f by solving for $T_{\rm base, initial}$ such that the fluence (the cooling curve integrated over the duration of the burst) equals the total nuclear energy release $E=4\pi R^2 y_{\rm base} Q_{\rm nuc} / (1+z)$ assuming $Q_{\rm nuc}=1.6~{\rm MeV~nucleon}^{-1}$, corresponding to helium burning completely to nickel. Although our conclusions are not sensitive to the exact value of f, for reference, we find $f\approx 0.8{-}0.9$.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13952fa2.ps} \end{figure} Figure C.1:

Model calculations of the radiative cooling following the burst rise. The solid lines show the luminosity L for ignition depths $y_{\rm base}=3\times 10^8, 10^9,$ and $10^{10}~{\rm g~cm}^{-2}$ with f=0.88, 0.85, and 0.78, respectively. The values for f were chosen such that the fluence equals the nuclear energy released in burning the entire He column to Ni. The Eddington limit at the NS surface and at infinity (assuming z=0.31 and $M=1.4~M_\odot$) are drawn as dotted lines.

Open with DEXTER

In Fig. C.1 we show time profiles of the calculated luminosity L for three ignition depths $y_{\rm base}$. The dotted lines mark $L_{\rm Edd}$ and $L_{\rm Edd, \infty}$ for a 1.4 $M_\odot$NS and an opacity $\kappa_0=0.2~{\rm cm^2~g}^{-1}$. An observer would see an Eddington-limited light curve where $L>L_{\rm Edd}$ (the excess luminosity is used to drive the outward expansion of the overlying layers) and a light curve that follows the plotted luminosity where $L<L_{\rm Edd}$.

As the figure shows, the profiles all have the same shape regardless of $y_{\rm base}$ and f: an early flat phase followed by a break and a steep decay. The factor f primarily determines the overall vertical scale while $y_{\rm base}$ determines the thermal time of the ignition layer and therefore the location of the break. The key result is that the early-time light curve is very flat, barely decreasing until after the break, at which point it rapidly falls below $L_{\rm Edd}$. Such a light curve cannot explain the features of the superexpansion as there is no second-long, depth-independent phase during which $L>L_{\rm Edd, \infty}$.

The light curve is flat because we assumed that the initial profile was the radiative profile ( $T\propto y^n$with $n\approx 1/4$) and therefore $L\propto T^4/y$ is constant until the thermal wave reaches $y_{\rm base}$and the ignition layer begins to cool. If we had assumed a shallower initial profile, the early-time flux would decrease with time (see, e.g., the superburst calculations of Cumming & Macbeth 2004 who assume an initial profile with n=1/8corresponding to an isobaric deflagration). However, absent any strong motivation for assuming a non-radiative initial profile, we conclude that a variation in the early time L is unlikely to explain the lack of correlation between $t_{\rm se}$ and $\tau _{{\rm decay}}$.

Since the superexpansion phase always occurs within seconds of burst onset, perhaps it is associated not with post-peak cooling, as assumed above, but rather with the physics of the burning during the burst rise. Due to their larger ignition depths and helium mass fractions, the peak energy generation rate in superexpansion bursts can be considerably higher than in ordinary short-duration bursts. If the ignition is deep enough, the heating time due to burning $t_{\rm heat} = ({\rm d}\!\ln T_{\rm b}/{\rm d}t)^{-1}$ can become shorter than the local dynamical time $t_{\rm dyn} \approx 10^{-6}~{\rm s}$. Such hydrodynamic burning could drive strong shocks through the upper layers of the atmosphere (Zingale et al. 2001; Weinberg et al. 2006a). However, when we solve the rise using the prescription described in Weinberg et al. (2006b) assuming an initially pure He layer, we find that $t_{\rm heat} > t_{\rm dyn}$unless $y_{\rm base} \ga 10^{11}~{\rm g~cm}^{-2}$. This suggests that strong shocks do not form during the rise of superexpansion bursts as they ignite at $y_{\rm base} \la 10^{10}~{\rm g~cm}^{-2}$.

References

  1. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
  2. Ballantyne, D. R. 2004, MNRAS, 351, 57 [NASA ADS] [CrossRef] [Google Scholar]
  3. Ballantyne, D. R., & Strohmayer, T. E. 2004, ApJ, 602, L105 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bildsten, L. 1998, in The many faces of neutron stars, ed. A. Alpar, L. Buccheri, & J. van Paradijs, NATO ASI (Dordrecht: Kluwer), 419 [Google Scholar]
  5. Bildsten, L., Salpeter, E. E., & Wasserman, I. 1992, ApJ, 384, 143 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bildsten, L., Chang, P., & Paerels, F. 2003, ApJ, 591, L29 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cox, J. P., & Giuli, R. T. 1968, Principles of stellar structure [Google Scholar]
  8. Cumming, A., & Bildsten, L. 2000, ApJ, 544, 453 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cumming, A., & Macbeth, J. 2004, ApJ, 603, L37 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cumming, A., Macbeth, J., Zand, J. J. M. i., & Page, D. 2006, ApJ, 646, 429 [NASA ADS] [CrossRef] [Google Scholar]
  11. Ebisuzaki, T., Hanawa, T., & Sugimoto, D. 1983, PASJ, 35, 17 [NASA ADS] [Google Scholar]
  12. Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
  13. Falanga, M., Chenevez, J., Cumming, A., et al. 2008, A&A, 484, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Foster, A. J., Fabian, A. C., & Ross, R. R. 1987, MNRAS, 228, 259 [Google Scholar]
  15. Fuhr, J. R., Martin, G. A., Wlese, W. L., & Younger, S. M. 1981, J. Phys. Chem. Ref. Data, 10, 305 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fujimoto, M. Y., Hanawa, T., & Miyaji, S. 1981, ApJ, 247, 267 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fujimoto, M. Y., Sztajno, M., Lewin, W. H. G., & van Paradijs, J. 1987, ApJ, 319, 902 [CrossRef] [Google Scholar]
  18. Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008a, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
  19. Galloway, D. K., Özel, F., & Psaltis, D. 2008b, MNRAS, 387, 268 [Google Scholar]
  20. Gayley, K. G. 1995, ApJ, 454, 410 [NASA ADS] [CrossRef] [Google Scholar]
  21. Grindlay, J., Gursky, H., Schnopper, H., et al. 1976, ApJ, 205, L127 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hanawa, T., & Sugimoto, D. 1982, PASJ, 34, 1 [NASA ADS] [Google Scholar]
  23. Hashimoto, M.-A., Hanawa, T., & Sugimoto, D. 1983, PASJ, 35, 1 [NASA ADS] [Google Scholar]
  24. Heasley, J. N., Janes, K. A., Zinn, R., et al. 2000, AJ, 120, 879 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hoffman, J., Lewin, W., Doty, J., et al. 1978, ApJ, 221, L57 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hoffman, J. A., Lewin, W. H. G., & Doty, J. 1977, ApJ, 217, L23 [NASA ADS] [CrossRef] [Google Scholar]
  27. in 't Zand, J. J. M., Verbunt, F., Kuulkers, E., et al. 2002, A&A, 389, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. in 't Zand, J. J. M., Cumming, A., van der Sluys, M. V., Verbunt, F., & Pols, O. R. 2005, A&A, 441, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. in 't Zand, J. J. M., Jonker, P. G., & Markwardt, C. B. 2007, A&A, 465, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. in 't Zand, J. J. M., Bassa, C. G., Jonker, P. G., et al. 2008, A&A, 485, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Jager, R., Mels, W. A., Brinkman, A. C., et al. 1997, A&AS, 125, 557 [Google Scholar]
  32. Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
  33. Jonker, P. G., Bassa, C. G., & Wachter, S. 2007, MNRAS, 377, 1295 [Google Scholar]
  34. Joss, P. C., & Melia, F. 1987, ApJ, 312, 700 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kuulkers, E., den Hartog, P. R., in 't Zand, J. J. M., et al. 2003, A&A, 399, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Kuulkers, E., in 't Zand, J. J. M., Atteia, J., et al. 2010, A&A, 514, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Lamb, D. Q., & Lamb, F. K. 1978, ApJ, 220, 291 [NASA ADS] [CrossRef] [Google Scholar]
  38. Laor, A. 1991, ApJ, 376, 90 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lewin, W., van Paradijs, J., & Taam, R. 1995, in X-ray binaries, ed. W. Lewin, J. van Paradijs, & E. van den Heuvel (Cambridge: Cambridge U.P.), 175 [Google Scholar]
  40. Lewin, W. H. G., Vacca, W. D., & Basinska, E. M. 1984, ApJ, 277, L57 [NASA ADS] [CrossRef] [Google Scholar]
  41. Lewin, W. H. G., van Paradijs, J., & Taam, R. E. 1993, Space Sci. Rev., 62, 223 [NASA ADS] [CrossRef] [Google Scholar]
  42. London, R. A., Taam, R. E., & Howard, W. M. 1986, ApJ, 306, 170 [Google Scholar]
  43. Madej, J., Joss, P. C., & Rózanska, A. 2004, ApJ, 602, 904 [NASA ADS] [CrossRef] [Google Scholar]
  44. Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
  45. Majczyna, A., Madej, J., Joss, P. C., & Rózanska, A. 2005, A&A, 430, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Maraschi, L., & Cavaliere, A. 1977, in X-ray Binaries and Compact Objects, 127 [Google Scholar]
  47. Michaud, G. 1970, ApJ, 160, 641 [NASA ADS] [CrossRef] [Google Scholar]
  48. Molkov, S., Revnivtsev, M., Lutovinov, A., & Sunyaev, R. 2005, A&A, 434, 1069 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Molkov, S. V., Grebenev, S. A., & Lutovinov, A. A. 2000, A&A, 357, L41 [NASA ADS] [Google Scholar]
  50. Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
  51. Muno, M. P., Chakrabarty, D., Galloway, D. K., & Psaltis, D. 2002, ApJ, 580, 1048 [NASA ADS] [CrossRef] [Google Scholar]
  52. Nelemans, G. 2008, in Hydrogen-Deficient Stars, ed. A. Werner, & T. Rauch, ASP Conf. Ser., 391, 273 [Google Scholar]
  53. Nobili, L., Turolla, R., & Lapidus, I. 1994, ApJ, 433, 276 [Google Scholar]
  54. Paczynski, B. 1983, ApJ, 267, 315 [NASA ADS] [CrossRef] [Google Scholar]
  55. Paczynski, B., & Prószynski, M. 1986, ApJ, 302, 519 [NASA ADS] [CrossRef] [Google Scholar]
  56. Pavlov, G. G., Shibanov, I. A., & Zavlin, V. E. 1991, MNRAS, 253, 193 [NASA ADS] [CrossRef] [Google Scholar]
  57. Smale, A. P. 2001, ApJ, 562, 957 [NASA ADS] [CrossRef] [Google Scholar]
  58. Strohmayer, T., & Bildsten, L. 2006, New views of thermonuclear bursts (Compact stellar X-ray sources), 113 [Google Scholar]
  59. Strohmayer, T., Markwardt, C., & Kuulkers, E. 2007, ApJL, accepted [arXiv:0711.4018] [Google Scholar]
  60. Strohmayer, T. E., & Brown, E. F. 2002, ApJ, 566, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  61. Swank, J., Becker, R., Boldt, E., et al. 1977, ApJ, 212, L73 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tawara, Y., Hayakawa, S., & Kii, T. 1984a, PASJ, 36, 845 [NASA ADS] [Google Scholar]
  63. Tawara, Y., Kii, T., Hayakawa, S., et al. 1984b, ApJ, 276, L41 [NASA ADS] [CrossRef] [Google Scholar]
  64. Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
  65. Ubertini, P., Bazzano, A., Cocchi, M., et al. 1999, ApJ, 514, L27 [NASA ADS] [CrossRef] [Google Scholar]
  66. van Paradijs, J. 1982, A&A, 107, 51 [NASA ADS] [Google Scholar]
  67. van Paradijs, J., Dotani, T., Tanaka, Y., & Tsuru, T. 1990, PASJ, 42, 633 [NASA ADS] [Google Scholar]
  68. Weinberg, N. N., & Bildsten, L. 2007, ApJ, 670, 1291 [NASA ADS] [CrossRef] [Google Scholar]
  69. Weinberg, N. N., Bildsten, L., & Brown, E. F. 2006a, ApJ, 650, L119 [NASA ADS] [CrossRef] [Google Scholar]
  70. Weinberg, N. N., Bildsten, L., & Schatz, H. 2006b, ApJ, 639, 1018 [NASA ADS] [CrossRef] [Google Scholar]
  71. Woosley, S. E., & Taam, R. E. 1976, Nature, 263, 101 [NASA ADS] [CrossRef] [Google Scholar]
  72. Woosley, S. E., Heger, A., Cumming, A., et al. 2004, ApJS, 151, 75 [NASA ADS] [CrossRef] [Google Scholar]
  73. Zdziarski, A. A., Gierlinski, M., Wen, L., & Kostrzewa, Z. 2007, MNRAS, 377, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  74. Zingale, M., Timmes, F. X., Fryxell, B., et al. 2001, ApJS, 133, 195 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... otherwise[*]
This is multiplicative model edge in XSPEC.
... fits[*]
For some spectra the edge can be satisfactorily fit by allowing for unrealistic values of 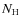$N_{\rm H}$, the black body temperature and the accretion flux. However, for the 4U 0614+091 burst, the edge immediately after the superexpansion has such a low energy (see below) that a good fit cannot be obtained even if one allows for unrealistic values of these standard spectral parameters.
... elements[*]
It is unclear whether free-falling 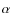$\alpha$ particles, in the absence of protons, will spall heavier accreted nuclei already present in the NS atmosphere to such a degree that significant amounts of protons are produced (cf., Bildsten et al. 2003,1992).
... redshift[*]
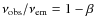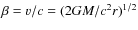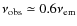If instead it was a radial free-fall, the redshift could be significant even at these large radii. The ratio of observed to emitted frequency would be $\nu_{\rm obs}/\nu_{\rm em} =1-\beta$ where $\beta=v/c=(2 GM/c^2r)^{1/2}$ is the free fall velocity. Thus, for $r\simeq30~{\rm km}$ have $\nu_{\rm obs}\simeq0.6 \nu_{\rm em}$.
... depth[*]
We choose to express depth in terms of the mass contained in a column of unit cross-sectional area.
... density[*]
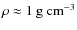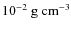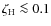In the wind models, $d\ln \rho/d\ln r \ga -3$ and $\rho\approx 1~{\rm g~ cm}^{-3}$ at r=R (see Paczynski & Prószynski 1986); since the observed expansion factors are $\approx$3-5 during the moderate expansion phase, we expect the photospheric density to be $\approx$ $10^{-2}~{\rm g~cm}^{-3}$. For $\zeta_{\rm H}\la0.1$, the optical depth $\tau_{\rm bf}$ scales almost linearly with $\rho$.
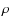... spectrum[*]
The spectra of type I bursts are somewhat harder than a blackbody at the observed 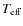$T_{\rm eff}$ (Majczyna et al. 2005; Pavlov et al. 1991; Madej et al. 2004; London et al. 1986). The radiative force acting on hydrogenic ions may therefore be larger than our estimates, although the ionization fraction will also be smaller.
... super-Eddington[*]
During the burst rise, the flux first exceeds the Eddington limit at some depth deep below the photosphere. This is because the electron scattering opacity increases towards the surface due to the temperature-dependent Klein-Nishina corrections (Paczynski 1983). A given flux can therefore be sub-Eddington in the deeper layers and at a certain point become super-Eddington as it diffuses upward into lower density, cooler material.
... suggested[*]
http://www.universe.nasa.gov/xrays/programs/rxte/pca/doc/rmf/pcarmf-11.7/
... Book[*]
http://heasarc.gsfc.nasa.gov/docs/xte/recipes/pca_deadtime.html
Copyright ESO 2010

All Tables

Table 1:   Measurements of 32 bursts with superexpansion.

Table A.1:   Details of the data (analysis) for the 3 PCA superexpansion bursts. See also Figs. 2, 3, and B.1.

All Figures

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{13952f1.ps} \end{figure} Figure 1:

Time profiles of the 2-30 keV photon flux of 24 X-ray bursts detected from 4U 1722-30 with BeppoSAX WFC (this includes 21 bursts with precursor, see Table 1, and three without at MJD 50521.804, 50527.181 and 50532.411). The photon flux is scaled between -1 and 4 phot s-1 cm-2. The horizontal dotted lines indicate a flux level of 0 phot s-1 cm-2. The MJD indicated in each panel refers to t=0 s. The profiles have been aligned to the start time of the precursor.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[height=0.675\columnwidth,angle=270]{13... ...includegraphics[height=0.615\columnwidth,angle=270]{13952f2f.ps} }\end{figure} Figure 2:

Spectral fits to the PCA bursts from 4U 0614+09 and 4U 1722-30 during time intervals when the absorbed black body plus reflection model fails to fit the data (see Fig. B.1 for example time intervals when the black body plus reflection model provides a good fit to these bursts). Left plots: the 4U 0614+09 spectrum between 1.65 and 1.78 s after burst onset (this is the second data point after the superexpansion phase in Fig. 3). Middle plots: the 4U 0614+09 spectrum between 2.53 and 2.65 s after burst onset (ninth data point). Right plots: the 4U 1722-30 spectrum for the 7 s long interval indicated by the grey bar in Fig. 3. The upper panels show the observed photon flux (crosses) and the fitted black body plus reflection model (histogram). The middle panels show the fractional deviation of the data points from the black body plus reflection model. The lower panels show the deviations after an absorption edge is included in the model.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.3cm,angle=0]{13952f3a.ps}\includegra... ...gle=0]{13952f3b.ps}\includegraphics[width=6cm,angle=0]{13952f3c.ps} \end{figure} Figure 3:

Time profiles of various spectral parameters for 3 superexpansion bursts detected with RXTE-PCA from 4U 0614+09 ( left; see also Kuulkers et al. 2010), 4U 1722-30 ( center; see also Molkov et al. 2000) and 4U 1820-30 (right; see also Ballantyne & Strohmayer 2004; Strohmayer & Brown 2002). Time is in seconds since burst onset (see Table A.1). Top panels: total PCA countrate for the xenon layers (solid line, in units of 104 s-1) and propane layer (dot-dashed grey line, in units of 1250 s-1), after subtracting the pre-burst levels. The horizontal dashed lines mark a count rate of zero. Second panels: bolometric flux of the fitted black body if no reflection component is included, corrected for detector dead time and for absorption. The errors were not determined, but they become large when kT<1 keV. Third panels: black body temperature in keV. Fourth panels: black body radius assuming isotropic emission. Assumed distances: 3.2 kpc (4U 0614+09; Kuulkers et al. 2010), 9.5 kpc (4U 1722-30; Kuulkers et al. 2003) and 7.6 kpc (4U 1820-30; Kuulkers et al. 2003); Fifth and sixth panels: absorption edge energy $E_{\rm edge}$ in keV and optical depth $\tau _{\rm opt}$. Bottom panels: reduced $\chi ^2$ value for each fit to the black body + reflection + edge model. We left out the data for 4U 1820-30 between 2000 and 2500 s, because these are not understood (see Ballantyne & Strohmayer 2004). The grey vertical bars for 4U 0614+09 and 4U 1722-30 delimit the time intervals for the spectra shown in Fig. 2. $N_{\rm H}$ was fixed for 4U 0614+09 and 4U 1820-30 and free for 4U 1722-30 because a fixed value did not yield good fits.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{13952f4.ps} \end{figure} Figure 4:

Duration of radius expansion phases versus decay time $\tau _{{\rm decay}}$ for each superexpansion burst. For data, see Table 1. Crosses mark the duration of a burst's superexpansion phase ( $t_{\rm se}$) and asterisks mark the duration of its moderate expansion phase ( $t_{\rm me}$). The dashed line marks the relationships $t_{\rm se},t_{\rm me}=\tau _{\rm decay}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{13952f5.ps} \end{figure} Figure 5:

Fraction of 44Ti and 56Ni in a hydrogenic state $\zeta _{\rm H}$ (top panel) and the optical depth of the edge $\tau _{\rm bf}(E_{\rm e}) \equiv N \sigma _{\rm bf}(E_{\rm e})$ (bottom panel) as a function of effective temperature (bottom axis) and blackbody radius $r_{\rm ph}\equiv (L_{\rm Edd} / 4\pi \sigma T_{\rm eff}^4)^{1/2}$ (top axis) assuming a density of $\rho =0.01~{\rm g~cm}^{-3}$. Results are shown for mass fractions of X=0.1 and 1.

Open with DEXTER
In the text

  \begin{figure} \begin{tabular}{lll} \includegraphics[height=0.70\columnwidth,ang... ...hics[height=0.655\columnwidth,angle=270]{13952fa1e.ps}\end{tabular} \end{figure} Figure B.1:

Spectral fits to the PCA bursts from 4U 0614+09 ( left plots), 4U 1722-30 ( middle plot) and 4U 1820-30 ( right plots) during time intervals when the absorbed black body plus reflection model provides a good fit to the data (see Fig. 2 for example time intervals when the black body plus reflection model fails to provide a good fit to these bursts). The upper row shows the fractional deviations for a model that includes the absorbed black body component but not the reflection or absorption edge components. The lower row shows the deviations for a model that includes the absorbed black body and reflection component but not the absorption edge component. 4U 1722-30 is not shown because at that time does a reflection component not explain the deviations. The spectra are taken during the moderate expansion. The error bars include the 1.5% systematic error.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13952fa2.ps} \end{figure} Figure C.1:

Model calculations of the radiative cooling following the burst rise. The solid lines show the luminosity L for ignition depths $y_{\rm base}=3\times 10^8, 10^9,$ and $10^{10}~{\rm g~cm}^{-2}$ with f=0.88, 0.85, and 0.78, respectively. The values for f were chosen such that the fluence equals the nuclear energy released in burning the entire He column to Ni. The Eddington limit at the NS surface and at infinity (assuming z=0.31 and $M=1.4~M_\odot$) are drawn as dotted lines.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.