EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 520 (September-October 2010) A&A, 520 (2010) A79 Full HTML
Free Access
Issue
A&A
Volume 520, September-October 2010
Article Number A79
Number of page(s) 12
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/200913725
Published online 06 October 2010
A&A 520, A79 (2010)

Chromospheric activity and rotation of FGK stars in the solar vicinity[*],[*]

An estimation of the radial velocity jitter

R. Martínez-Arnáiz1 - J. Maldonado2 - D. Montes1 - C. Eiroa2 - B. Montesinos3

1 - Universidad Complutense de Madrid, Facultad de Ciencias Físicas, Dpt. Astrofísica, av. Complutense s/n. 28040 Madrid, Spain
2 - Universidad Autónoma de Madrid, Departamento de Física Teórica, Módulo 15, 28049 Cantoblanco, Madrid, Spain
3 - LAEX, CAB (CSIC-INTA), ESAC Campus, PO BOX 78, 28691 Villanueva de la Cañada, Madrid, Spain

Received 24 November 2009 / Accepted 27 January 2010

Abstract
Context. Chromospheric activity produces both photometric and spectroscopic variations that can be mistaken as planets. Large spots crossing the stellar disc can produce planet-like periodic variations in the light curve of a star. These spots clearly affect the spectral line profiles, and their perturbations alter the line centroids creating a radial velocity jitter that might ``contaminate'' the variations induced by a planet. Precise chromospheric activity measurements are needed to estimate the activity-induced noise that should be expected for a given star.
Aims. We obtain precise chromospheric activity measurements and projected rotational velocities for nearby ($d \leq 25$ pc) cool (spectral types F to K) stars, to estimate their expected activity-related jitter. As a complementary objective, we attempt to obtain relationships between fluxes in different activity indicator lines, that permit a transformation of traditional activity indicators, i.e., Ca II H & K lines, to others that hold noteworthy advantages.
Methods. We used high resolution ($\sim$50 000) echelle optical spectra. Standard data reduction was performed using the IRAF ECHELLE package. To determine the chromospheric emission of the stars in the sample, we used the spectral subtraction technique. We measured the equivalent widths of the chromospheric emission lines in the subtracted spectrum and transformed them into fluxes by applying empirical equivalent width and flux relationships. Rotational velocities were determined using the cross-correlation technique. To infer activity-related radial velocity (RV) jitter, we used empirical relationships between this jitter and the $ R'_{{\rm HK}}$ index.
Results. We measured chromospheric activity, as given by different indicators throughout the optical spectra, and projected rotational velocities for 371 nearby cool stars. We have built empirical relationships among the most important chromospheric emission lines. Finally, we used the measured chromospheric activity to estimate the expected RV jitter for the active stars in the sample.

Key words: solar neighbourhood - stars: late-type - stars: activity - stars: chromospheres - stars: rotation - planetary systems

1 Introduction

Exoplanetary science is living a golden era characterized by the enormous rate at which new exoplanets are being discovered. This impressive advancement would not have been possible without parallel technological developments. Improved precision in both radial velocity and photometric measurements has extended the area around the star in which a planet can be found and has increased the probability of detecting low mass exoplanets. These improvements have created, however, a new and noteworthy problem, i.e., the possibility of misidentifying planets. Chromospheric activity, in particular, the presence of spots and/or alteration of the granulation pattern in active regions, create a time-variable photometric and spectroscopic signature (Saar & Donahue 1997; Santos et al. 2000; Saar 2003) that might be misinterpreted as an exoplanet. Moreover, the minimum detectable mass of a planet orbiting a star is limited by the rms velocity jitter caused by stellar sources (Narayan et al. 2005). Therefore, a thorough analysis of activity levels, as only different activity indicators can provide, must be performed for those stars that constitute the natural targets of planet-search surveys.

When searching for exoplanets using the radial velocity (RV) technique, the possibility of jitter caused by chromospheric activity must be considered. When modeling stellar activity, Saar & Donahue (1997) were the first to quantitatively estimate the impact of stellar spots on the RV curve and showed that they could produce peak-to-peak RV amplitudes of up to a few hundred  m s-1, depending on spot size and the rotational velocity of the star. Subsequent studies (Saar et al. 2003; Santos et al. 2000; Desort et al. 2007; Paulson et al. 2004) obtained similar results. Several attempts to reduce RV noise levels by using an activity-based correction have been made (Saar et al. 2003; Saar & Donahue 1997; Saar & Fischer 2000; Santos et al. 2000; Wright 2005; Saar et al. 1998). To use these corrections and to test and calibrate the relations, high precision, homogeneous chromospheric activity measurements are needed.

Transit searches for exoplanets are also affected by the temporal evolution and modulation of active regions across the stellar disc. The amplitude of variations can reach more than 1% when a large spot crosses the solar disc at activity maximum. This decrease in signal, combined with the modulation caused by stellar rotation can mimic the signal of a planet orbiting the star. Therefore Sun-like variability, not to mention that of stars more active than the Sun, can significantly affect the detection performance of photometric planet searches (Aigrain et al. 2004; Baliunas et al. 1997; Henry et al. 1997,2000).

Hence, chromospheric activity is a proxy for predicting variability levels expected for a star, therefore allowing the estimation of a lower limit for planet detections in its vicinity. In this paper, we present spectroscopic-based chromospheric activity measurements for 371 nearby ($d \leq 25$ pc), cool (spectral types F to K) stars. These stars are the natural targets for exoplanet searches: their proximity ensures the ability to get an adequate signal-to-noise ratio (hereafter S/N), and solar-like stars are more likely to host so-called habitable planets (Turnbull & Tarter 2003; Kasting et al. 1993; Doyle et al. 1998). In this study, we considered not only the traditional chromospheric activity indicators, i.e., $ R'_{{\rm HK}}$ or H$\alpha$, but also other less common indicators, such as the Ca II IRT lines, which allow us to exploit peak-to-peak RV amplitude variations caused by spots being less significant at longer wavelengths (Reiners et al. 2010; Desort et al. 2007).

2 The stellar sample

The stellar sample comprises 371 cool stars in the solar vicinity, constrained to be at distances closer than 25 pc (see Table A1). Distances were obtained from the Hipparcos Catalogue (ESA 1997) and the New Reduction of the Raw Data (van Leeuwen 2007). The spectral type distribution of the sample is 56 F type stars, 126 G type stars, 186 K stars, and 3 M type stars. Since our study is based on solar-like stars, only F, G and K spectral types stars with trigonometric parallax $\pi \geq 40$ mas were retrieved. To avoid misclassified stars, we used colour index as a complementary criteria, i.e., B-V colour index in the range 0.25-0.58 mag (F stars), 0.52-0.81 mag (G stars), and 0.74-1.40 mag (K stars). To establish the main-sequence character of the stars, we used a cutoff of $\pm$1 mag from the main sequence (Wright 2005). Finally, stars in multiple systems were removed from the sample. We used the CCDM (Dommanget & Nys 1994,2002) and SB9 (Pourbaix et al. 2004) catalogues to identify astrometric and spectroscopic binaries, respectively.

These stars are potential targets for present and future projects that aim to detect Earth-like planets or exo-solar analogues to the Edgeworth-Kuiper Belt. In this context, most of our stars will be observed in the framework of DUNES (DUst around NEarby Stars), an approved Herschel Open Time Key Project with the aim of detecting cool faint dusty disks, at flux levels as low as the Solar EKB. Some preliminary results can be found in Martínez-Arnáiz et al. (2009), Maldonado et al. (2010), and Montes et al. (2010).

Table 1:   A constant for FOCES, 2dcoudé (McDonald), FEROS and SARG spectra.

3 Observations and data reduction

The present work is based on data extracted from high resolution echelle spectra. Most of the spectra were obtained in severalobserving runs but we also used S4N spectra (Allende Prieto et al. 2004). The latter have similar spectral resolution ($\sim$45 000) to those obtained by us and were consequently used in an analogous manner to measure and analyse the stellar parameters and properties of the stars.

Observations were obtained at two different observatories: the German-Spanish Astronomical Observatory, CAHA, (Almería, Spain) and La Palma Observatory (La Palma, Spain). Observations were taken at the former with the 2.2 m telescope using the Fibre optics Cassegrain Echelle Spectrograph (FOCES) (Pfeiffer et al. 1998) with a $2048 \times 2048 24$ $\mu$m SITE$\sharp$1d-15, and at the latter with the 3.5 m Telescopio Nazionale Galileo (TNG) using the Spectrografo di Alta Resoluzione Galileo (SARG), the grid R4 (31.6 lines/mm), the red cross-dispersor (200 lines/mm), and a CCD detector mosaic of total surface $2048 \times 4096$ and 13.5 $\mu$m pixels.

We carried out four observing runs at CAHA (July 2005, January 2006, December 2006 and February-May 2007). FOCES spectra have a wavelength range from 3600 to 10 700 Å in 106 orders with a typical resolution of 40 000 (reciprocal dispersion from 0.08-0.13 Å/pixel in the red and blue region of the spectrum, respectively). The total number of stars observed using this spectrograph is 198. At La Palma Observatory, we performed three observing runs (February 2006, April 2007 and, November 2008). SARG spectra have a wavelength range from 5540 to 7340 Å in 50 orders with a resolution of 57 000 (reciprocal dispersion from 0.01 to 0.04 Å/pixel in the red and blue region of the spectrum, respectively). We observed 129 stars using the SARG spectrograph.

As mentioned before, we used S4N (Allende Prieto et al. 2004) spectra. These spectra were taken between October 2000 and November 2001 in six observing runs at the Harlan J. Smith 2.7 m telescope (McDonald Observatory) and two at the 1.52 m telescope at La Silla (Chile). At McDonald Observatory, the 2dcoudé (Tull et al. 1995) spectrograph with the Tektronix $2048 \times 2048$ 24 $\mu$m CCD detector was used. The spectral coverage was 3600-5100 Å  with a typical resolution of 50 000. At La Silla Observatory, the Fiber-fed Extended Range Optical Spectrograph (FEROS) (Kaufer et al. 2000) with the CCD detector EEV  $2048 \times 2048$ 15 $\mu$m was used. The wavelength coverage in this case is 3500-9200 Å  and the resolution $\sim$45 000. The total number of studied S4N stars is 106. Of them, 79 were observed at McDonald Observatory, while the rest were observed with FEROS at La Silla Observatory.

All the observed stars and the corresponding spectrograph used are listed in Table A1. We note that some stars were observed more than once and using different spectrographs.

For the reduction, we used the standard procedures in the IRAF (Image Reduction and Analysis Facility) package (bias subtraction, extraction of the scattered light produced in the optical system, division by the normalized flat-field, and wavelength calibration). After the reduction process, the spectrum was normalized to the continuum order by order by fitting a polynomial function to remove the general shape of the aperture spectra.

4 Analysis and results

4.1 Rotational velocities

The determination of rotational velocities for stars in exoplanet surveys is crucial. Radial velocity variations induced by chromospherically active regions on the stellar surface are modulated by the rotation period of the star (Baliunas et al. 1997; Henry et al. 1997,2000). Obtaining the rotational velocity of the star is thus essential to test whether detected RV variations have a stellar or a planetary origin.

The widths and shapes of spectral lines contain information that allow us to deduce physical information about the star, including its rotation rate. To measure this width, the most commonly used parameter is the the line FWHM (Full Width Half Maximum) because it can be easily measured. The Fourier domain offers, however, some advantages over the wavelength one. Signatures of certain physical processes, such as the Doppler-shift distribution produced by rotation or macroturbulence, are more readily detected in that domain. The cross-correlation function (CCF) was therefore used to measure rotational velocities. The width ($\sigma $) of the CCF peak for a star when correlated with itself depends on the instrumental profile and several broadening mechanisms such as gravity, effective temperature, or rotation. To measure the rotational contribution, and hence determine the star's projected rotational velocity, the contribution of other broadening mechanisms has to be modelled. For $v \sin{i} \leq 50$ km s-1, the CCF is well approximated by a Gaussian (Soderblom et al. 1989) and consequently the rotational broadening corresponds to a quadratic broadening of the CCF. In that case, the observed width of the CCF can be written as (see Queloz et al. 1998, and references therein)

\begin{displaymath}\sigma_{\rm obs}^{\rm 2}=\sigma_{\rm rot}^{\rm 2}+\sigma_{\rm0}^{\rm 2}, \end{displaymath} (1)

where $\sigma_{\rm rot}$ is the rotational broadening and $\sigma _{\rm0}$ is the width of the CCF of a similar non-rotating star. Projected rotational velocities, $v \sin{i}$, can be derived from the above expression as

\begin{displaymath}v~\sin~i=A\left(\sigma_{\rm obs}^{\rm 2}-\sigma_{\rm0}^{\rm 2}\right)^{\rm 1/2}, \end{displaymath} (2)

where A is a coupling constant that depends on the spectrograph and its configuration. To determine A for each spectrograph, non-rotating stars were used[*]. Their spectra were broadened from v  $\sin{i} = 1$ km s-1 to 50 km s-1 using the program JSTARMOD[*]. The value of $\sigma_{\rm obs}$ was then determined as the equivalent width of the first peak in the CCF. The constant A was found by fitting the relation $v \sin i ^{\rm 2}$ vs. $\sigma_{\rm obs}^{\rm 2}$. The stars used to compute A, the measurements, and the mean values for each spectrograph are shown in Table 1.

It is well known that $\sigma _{\rm0}$ is a function of the broadening mechanisms present in the atmosphere of the star, except rotation (Melo et al. 2004). Since the broadening mechanisms are a function of the temperature and gravity, we may expect the colour index, B-V to depend on $\sigma _{\rm0}$, for stars in the main sequence. To determine this dependence, we created morphed spectra with no rotational velocity using the ATLAS9 code by Kurucz (1993) adapted to operate on a linux platform by Sbordone et al. (2004) and Sbordone (2005). Temperatures vary from 3500 K to 6500 K (in intervals of 250 K). Since the stars were selected to be on the main sequence, $\log g$ was fixed to be 4.5. Solar metallicity was assumed. The morphed spectra were broadened to match the instrumental profile of the real spectra using the FWHM of the calibration arc lines, which is a good approximation of the broadening for the instruments used. Given that each spectrograph has a different resolving power, different instrumental broadenings were applied to obtain a calibration curve for each instrument. These curves are shown in Fig. 1.

Color indices, B-V, were obtained from the Tycho-2 Catalogue (Høg et al. 2000) using the transformation from $B_{\rm T}$ and $V_{\rm T}$ to Johnson indices (see Sect. 1.3 from Hipparcos Catalogue, ESA 1997) and are listed in Table A1.

\begin{figure} \par\includegraphics[width=9.cm, keepaspectratio]{13275fg1.ps} \end{figure} Figure 1:

Calibration between $\sigma _{\rm0}$ and colour index B-V, where $\sigma _{\rm0}$ represents the ``natural'' broadening of the spectrum lines and was obtained from synthetic spectra covering the spectral range of the observed stars. Given that the instrumental profile also contributes as a broadening mechanism and considering that each spectrograph has a different one, we had to derive a calibration relationship for each of them.

Open with DEXTER

Once A and $\sigma _{\rm0}$ were known for each star, v $\sin{i}$ could be directly derived by measuring $\sigma_{\rm obs}$, i.e., width of the CCF of the star when correlated with itself. Values for stars in the sample can be found in Table A1. For slow rotating stars, it is important to mention that sometimes, the value of $\sigma _{\rm0}$ is larger than that of $\sigma_{\rm obs}$. In that case, $v \sin{i}$ cannot be measured using this method and we only provide an upper limit. This value was chosen by considering the minimum v $\sin{i}$ that could be measured with the same spectrograph for a star of the same spectral type, i.e., the same $\sigma _{\rm0}$.

4.2 Chromospheric activity

We analyse different activity indicators throughout the optical spectra (from Ca II H&K to Ca II IRT). These lines form at different heights in the chromosphere hence provide information about different stellar properties. Some lines are present only during high energy processes such as flares. As shown in previous work (see Montes et al. 2001,2000, and references therein), by performing a simultaneous analysis of different optical chromospheric activity indicators, a detailed study of the chromosphere's structure can be achieved and it becomes possible to discriminate between structures such as plages, prominences, flares, and microflares. The spectra used in this work have a spectral range that covers plages from Ca II H & K to Ca II IRT lines, including the Balmer lines.

4.2.1 Equivalent widths and fluxes

To determine the chromospheric contribution to the spectrum, and thus the chromospheric activity, the contribution of the photosphere must be removed. In order to achieve this, we used the spectral subtraction technique, described in detail by Montes et al. (1995a,2000). This technique has been extensively used before because it permits the detecion of weak emission features in the cores of chromospheric lines. In addition, it is the most effective means of identifying other chromospheric activity indicators such as the Balmer lines or the Ca II IRT, where no calibrations of the photospheric minimum flux exists (Montes et al. 1996b; Barden 1985; López-Santiago et al. 2003; Montes et al. 2000; Gálvez et al. 2002; Montes et al. 1995a; Frasca & Catalano 1994; Gálvez et al. 2009; Gunn & Doyle 1997; Lázaro & Arévalo 1997; Montes et al. 2001; Gálvez et al. 2007; López-Santiago et al. 2010; Hall & Ramcey 1992; Huenemoerder et al. 1989; Montes et al. 1997). Inactive, slowly rotating stars, observed in the same observing run as the active stars, were used as reference to construct a morphed spectrum for each active star, using the program JSTARMOD. The program builds the morphed spectrum by shifting and broadening the reference spectrum to match that of the target star. This implies that the reference star must have a lower rotation rate than but a similar spectral type to the target star. A compilation of the inactive, slowly rotating stars used as references can be found in Table 2. Reference stars were initially chosen from the literature but some inactive, slowly rotating stars of the sample were also used as reference after confirming that they did not show chromospheric activity. To ensure that those stars were inactive, their values of total flux in Ca II H & K were compared to the lower boundary defined by Rutten (1984), which is traditionally used to correct flux measurements from the basal chromospheric flux (see Fig. 3). Maximum differences of 0.25 (F type stars), 0.3 (G type stars) and 0.35 (K type stars) in $\log (F_{\rm H} + F_{\rm K})$ values between the stars used as references and the lower boundary of Rutten (1984) were allowed. The morphed spectrum was subtracted from that of the active star, obtaining a spectrum in which only the chromospheric contribution is present, i.e., the subtracted spectrum. The excess emission EW of the activity indicator lines were obtained from that spectrum. To estimate the errors in the measured EW, we followed Montes et al. (2001) and considered JSTARMOD's typical internal precisions (0.5-2 km s-1 in velocity shifts and $\pm$5 km s-1 in $v \sin{i}$), the rms in regions outside the chromospheric features (typically 0.01-0.03), and the standard deviations. The estimated errors for relatively strong emitters are in the range of 10-20% but for low activity stars errors are larger. Taking into consideration that S/N is lower in the blue spectral region, errors in the chromospheric features at these wavelengths are larger.

Table 2:   Inactive stars used as references in the subtraction technique to measure chromospheric activity.

In Fig. 2, we plot an histogram for the total number of stars of each spectral type and the number that could be classified as active (displaying chromospheric features in the spectrum) or not active. In Table A2, we give the excess emission EW and its error for the active stars in the sample. Of the complete sample of stars analysed (371 stars), 173 presented chromospheric activity features in their spectra. Of them, 8 were F type stars (14% of the analysed F stars), 38 G type stars (30% of the G type stars), 126 K type stars (68% of the analysed K stars) and 1 M star (33% of the analysed M stars). From the remaining, 193 could be classified as inactive because of the lack of any chromospheric activity feature in their spectra. Of them, 48 are F type stars (86% of the analysed F stars), 88 G type stars (70% of the total G type stars), and 57 K stars (31% of the analysed K type stars). The remaining 5 stars could not be classified as either active or inactive because of the low S/N of their spectra. We have included a column (Col. # 8) in Table A1 to specify whether the star can be considered as active or not active. In 6 cases (5 K stars and 1 M star), we could not measure chromospheric activity due to the lack of a suitable non-active reference star to perform the subtraction technique, but chromospheric activity features were clearly present in the spectra. These stars were classified as active (and indicated with * in Table A1) but chromospheric activity was not measured. It is also important to mention that due to the configuration used with the SARG spectrograph the spectral range corresponding to Ca II H & K was not covered and these lines could not be measured.

We must comment on eight special cases: HIP 3093, HIP 3765, HIP 7981, HIP 54646, HIP 60866, HIP 62523, HIP 77408 and HIP 85810. These stars were observed more than once and with different instruments. Chromospheric activity features were detected in at least one of the observations, but not in all of them. Therefore, the stars are labelled as active and inactive depending on the observing run. In six of the cases (HIP 3093, HIP 3765, HIP 54646, HIP 60866, HIP 77408 and HIP 85810), the level of activity (when measured) is very low, which points to the use of a different reference star as the explanation for the inability to detect emission features in the subtracted spectrum. Two of these stars (HIP 3093 and HIP 3765) show levels of chromospheric activity so low that are generally considered inactive and used as reference stars to subtract the photospheric contribution from the spectrum. In the remaining cases, HIP 7981 and HIP 62523, variability appears to be the cause. The star HIP 7981 was previously classified as variable by Hall et al. (2007). Both stars were observed in three observing runs, two of them closer in time than the other. The stars exhibit no chromospheric emission features in observations carried out during the same epoch, whereas they do in data for other epoch. This indicates that the lack of features appears to be real and not attributable to a different choice of the reference star.

\begin{figure} \par\includegraphics[width=9cm,clip]{13275fg2.ps} \end{figure} Figure 2:

Number of active (black) and inactive (grey) stars in the sample for each spectral type.

Open with DEXTER
Variability therefore presents itself as a plausible explanation of the lack of detected activity in two of the observations. These stars are marked with $\star$ in Table A1. Fluxes can be derived from the measured EW by correcting the continuum flux

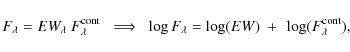
\begin{displaymath}F_{\rm\lambda}=EW_{\rm\lambda}~F_{\rm\lambda}^{\rm cont}\;\; ... ...F_{\rm\lambda} = \log (EW)~+~\log(F_{\rm\lambda}^{\rm cont}) , \end{displaymath} (3)

where the continuum flux, $F_{\lambda}^{\rm cont}$, is obviously dependent on the wavelength and must therefore be determined for the region where the activity indicator line appears. We used the empirical relationships between $F_{\lambda}^{\rm cont}$ and colour index, B-V, (Hall 1996) to compute $F_{\lambda}^{\rm cont}$ for each line and star. We note that the aforementioned relationships are linear for the spectral type range of the sample stars. In Table A3, we give the absolute flux at the stellar surface and its error for the active stars in the sample.

4.2.2 $ R'_{{\rm HK}}$ index

Chromospheric activity has been traditionally studied using the $ R'_{{\rm HK}}$ index, defined as the ratio of the emission from the chromosphere in the cores of the Ca II H & K to the total bolometric emission of the star, where the prime denotes that subtraction of the photospheric contribution has been performed. It was first used by Noyes et al. (1984). This index was first measured using observed flux indices in the core of Ca II H & K (corrected from the continuum signal) with the Mount Wilson H-K spectrophotometer (Vaughan et al. 1978). These fluxes were corrected from the photospheric contribution using an empirical calibration with the colour index B-V (Noyes et al. 1984). Finally, the Ca II H and K line-core flux measurements were corrected from the minimum surface flux using a calibration with the colour index B-V (Rutten 1984), thus providing a measurement of the chromospheric contribution associated with magnetic activity. In principle, we could derive $ R'_{{\rm HK}}$ directly from the measured fluxes in Ca II H & K lines using the subtraction technique

\begin{displaymath} R'_{\rm HK} = \frac{F'_{\rm H} + F'_{\rm K}}{\sigma T_{\rm eff}^{\rm 4}}\cdot \end{displaymath} (4)

When the subtraction technique is applied, the residual chromospheric contribution of the reference star is also subtracted from the spectrum of the target star. The source of possible differences between the fluxes obtained using the subtraction technique and those obtained with the traditional method, is the difference in chromospheric emission between our reference stars and those used by Rutten (1984) to compile his calibration. In Fig. 3, we have plotted the total surface flux in the Ca II H & K lines for the reference stars used in this work, and the Rutten (1984) calibration for main sequence stars. The values of total surface flux in the Ca II H & K lines for the reference stars have been obtained from Duncan et al. (1991), Henry et al. (1996), Wright et al. (2004), and Jenkins et al. (2006) and are included in Table 2. We note that all our reference stars have Ca II H & K fluxes close to the lower boundary defined by Rutten (1984) adopted in subsequent studies. The maximum difference between the surface fluxes of the stars used as references in the present study and the Rutten (1984) calibration is 0.2 dex, with the exception of K5 to K7 stars for which it is 0.35 dex. Since these differences account for differences of only 0.2 dex (0.35 dex for K5 to K7 stars) in $ R'_{{\rm HK}}$, we can assume that the values of $ R'_{{\rm HK}}$ obtained using the subtraction technique are comparable to those obtained with the traditional method.

\begin{figure} \par\includegraphics[width=9cm,clip]{13275fg3.ps} \end{figure} Figure 3:

Ca II H & K surface flux vs colour index B-V. Small dots represent Duncan et al. (1991) and Wright et al. (2004) data. To represent the stars considered as reference in this work, we have used different symbols according to the source of $F_{\rm H} +F_{\rm K}$ values: circles for Duncan et al. (1991) data, squares for Henry et al. (1996) data, crosses for Wright et al. (2004) data, and triangles for Jenkins et al. (2006) data. The curve represents the surface flux boundary obtained by Rutten (1984).

Open with DEXTER

To determine the effective temperatures needed to convert total flux in Ca II H & K into $ R'_{{\rm HK}}$, we used the empirical calibrations with the colour index B -V provided by Gray (2008), which holds for the spectral type range of the target stars ( $0.00 \leq B -V \leq 1.5$).

Table 3:   Comparison of the classification of the stars as active or inactive with previous results.

\begin{figure} \par\includegraphics[width=9cm,clip]{13275fg4.ps} \end{figure} Figure 4:

Comparison of $ R'_{{\rm HK}}$ index obtained in this paper and that obtained with the Mount Wilson H-K spectrophotometer (Vaughan et al. 1978) and similar techniques. Different symbols are used for Duncan et al. (1991), Strassmeier et al. (2000), Wright et al. (2004), Hall et al. (2007), and Mamajek & Hillenbrand (2008) data. In the lower panel, we have plotted $\sigma $ (as described in the text).

Open with DEXTER

4.3 Comparison with previous results

To test whether the transformation is consistent with those values of $ R'_{{\rm HK}}$ computed using photometry (or a technique to mimic photometric results using spectroscopic data), we compared our data to those obtained by Duncan et al. (1991), Strassmeier et al. (2000), Wright et al. (2004), Hall et al. (2007), and Mamajek & Hillenbrand (2008). The comparison is plotted in Fig. 4, where

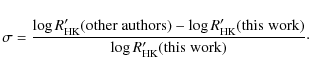
\begin{displaymath}\sigma = \frac{\log R'_{\rm HK} ({\rm other\;authors)} - \log... ...K} ({\rm this\;work)}}{\log R'_{\rm HK} (\rm this\;work)}\cdot \end{displaymath} (5)

The dispersion observed in Fig. 4 is compatible with variations in activity levels with time. To determine if there are systematic differences between our data and any of the five data sets analysed, we have plotted $\sigma $ in Fig. 4. The closer the value of $\sigma $ to 0, the smaller the difference between our values and those from other authors. In addition, we performed a Kolmogorov-Smirnov test to determine whether our data and those obtained by other authors are equivalent. The values of the estatistical estimator D obtained when applying the Kolmogorov-Smirnov test with Mt. Wilson (n = 59), Strassmeier (n = 37), Wright (n = 38), Hall (n = 19) and Mamajek (n = 31) data are 0.152, 0.351, 0.236, 0.263 and 0.322, respectively. These results indicate that the null hypothesis, i.e., both samples are equivalent, could not be rejected at a level of significance less than 65 % in the Mt. Wilson, Wright, and Hall cases. This clearly means that $\log R'_{\rm HK}$ values obtained using the traditional method are equivalent to those obtained in this study. As might be expected, discrepancies are larger when we compare our results with those presented in Mamajek & Hillenbrand (2008), because the latter constitutes a compilation of values obtained from different sources. Differences between our results and Strassmeier et al. (2000) are also larger than the rest. Again this is not surprising, taking into account that the method used to correct from the photospheric contribution is different than in the rest of the cases. The Strassmeier et al. (2000) values therefore do not necessarily reproduce the original $\log R'_{\rm HK}$ values. It is also important to note that discrepancies are larger for less active stars, in particular for stars with measured $\log R'_{\rm HK} \le -4.9$. This result is again expectated considering that for stars with low activity levels, errors in the photospheric contribution correction become more apparent.

Table 4:   Stars for which our classification as active or inactive differs from that of other authors.

We also compared our results with those obtained by the mentioned authors (Wright et al. 2004; Hall et al. 2007; Strassmeier et al. 2000; Mamajek & Hillenbrand 2008; Duncan et al. 1991). In Table 3, we summarise the number of active and inactive targets that we share with the mentioned authors as well as the number for which our classification is convergent. As mentioned in Sect. 4.2.1 we classified a star as active when chromospheric features were present in the spectrum. To classify the stars observed by other authors, we used Saar & Brandenburg (1999) criterion to differentiate between active ( $\log R'_{\rm HK} > - 4.75$) and inactive ( $\log{R'_{\rm HK}} \leq -4.75$) stars with the exception of Strassmeier et al. (2000) data, for which the author provides his own classification. For Duncan et al. (1991), we obtained similar results for 84% of the inactive and 77% active stars. We obtained similar results to Strassmeier et al. (2000) data for 95% of the inactive stars and 84% of the active ones. Concerning Wright et al. (2004) and based on the Saar & Brandenburg (1999) criterion, we reached agreement for 88% of the active stars and 91% of the inactive ones. For the Hall et al. (2007) data, we obtained similar results for 89% of the inactive stars and 67% of the active ones. Finally, when comparing our results to those of Mamajek & Hillenbrand (2008), we reached an agreement for 87% of the common inactive stars, and for 85% of the actives ones.

In Table 4, we give details of the values of $\log R'_{\rm HK}$ found for those stars for which our classification as active or inactive differs from that of Duncan et al. (1991), Strassmeier et al. (2000), Wright et al. (2004), Hall et al. (2007), or Mamajek & Hillenbrand (2008). We note that with the exception of HIP 41484, which was classified as a high-activity variable by Hall et al. (2007), in all cases the measured values correspond to the low activity domain ( $\log{R'_{\rm HK}} \leq -4.40$). It is important to mention that we classify a star as active or inactive after inspecting the spectrum from which the photospheric contribution has been subtracted. This means that every star showing chromospheric activity features will be considered active, regardless of the weakness of the activity levels that we measure. On the other hand, Saar & Brandenburg (1999) criterion is based on the value obtained after measuring the activity. This implies that some of the stars that we have considered as active (because they show emission features in the spectrum) should be reclassified as inactive after applying the aforementioned criterion. We prefer to maintain our criterion, and consider inactive only those stars that did not exhibit emission features in the subtracted spectrum. Taking this into account, we can consider the agreement between data obtained in the present work and that previously reported as fairly good.

4.4 Spectral types

As mentioned in Sect. 4.2.1, when performing the subtraction technique to measure chromospheric activity the use of a reference non-active star with similar physical properties (temperature and surface gravity) to those of the target star is necessary. Therefore, we were able to determine the spectral types of the target stars by comparing their spectra with those of the reference stars. The process began by assuming a spectral type for each star and applying the subtraction technique using as a reference an inactive star of similar spectral type and luminosity class. We then compared the non-chromospheric lines of the original and morphed spectra to test whether the spectral types of the star and that of the reference were really the same. In this way, we could correct the assumed spectral type of each star. We estimate the errors to be of one spectral subtype.

In theory, if both stars have the same spectral type, the resultant (subtracted) spectrum should be null. In reality, the subtracted spectrum exhibit some noise, because of the small differences in metallicity and/or gravity and when the S/N of one of the spectra is low. Nevertheless, small differences in metallicity (only population I stars were observed) and gravity (the cutoff of $\pm$1 mag from the Main Sequence (see Sect. 2) corresponds to variations of $\pm$0.2 in $\log g$) are lower than those produced by the difference of one spectral subtype, which is the estimated error in the spectral type determination. Our results are shown in Table A1.

5 Discussion

5.1 Flux-flux relationships

Although chromopsheric activity has been traditionally studied using the $ R'_{{\rm HK}}$ index, we have already pointed out that longer wavelengths provide noteworthy advantages when exoplanet searches are to be performed. The impact of chromospheric active regions on radial velocity variations appear to be smaller when the red region of the spectrum is considered (Desort et al. 2007). Moreover, the S/N in the red region of the spectrum is higher for cool stars. We have measured activity levels using activity tracers throughout the optical spectrum, including the IRT Ca II lines.

After measuring chromospheric activity in different indicator lines, we have analysed the relationships between their fluxes. This approach was first introduced to study the magnetic structure of cool stars (Schrijver 1987; Rutten et al. 1991) by comparing fluxes in chromospheric and coronal indicator lines. Subsequent studies generalised the method and analysed the relationship among different chromospheric indicators. The most widely studied relationship is that between H$_{\alpha}$ core emission and the total surface flux in Ca II H & K lines (Strassmeier et al. 1990; Walkowicz & Hawley 2009; Robinson et al. 1990; Cincunegui et al. 2007). Several studies have obtained fluxes in other chromospheric indicators lines, such as the Ca II infrared triplet, for binary (Montes et al. 1996b,1995b,1996a) and single (Busà et al. 2007; Thatcher & Robinson 1993; López-Santiago et al. 2005) stars. The aforementioned studies were either centred on a specific spectral type range (Walkowicz & Hawley 2009; Thatcher & Robinson 1993) or analysed the relation between total fluxes, instead of that between each of the indicator lines.

Table 5:   Linear fit coefficients for each flux-flux relationship.

We have obtained empirical power-law relations between pairs of chromospheric indicator lines by fitting the data shown in Figs. 5 and Table A1 to an equation

\begin{displaymath}\log F_{\rm 1} = c_{\rm 1} + c_{\rm 2} \log F_{\rm 2}, \end{displaymath} (6)

where $F_{\rm 1}$ and $F_{\rm 2}$ are the fluxes of two different lines. We present the coefficients and the correlation coefficient (R) of such relationships in Table 5.

In this context, the present study represents a significant extension in terms of spectral type range and number of stars. Moreover, we present relationships between each pair of chromospheric indicator lines in the optical range. These relationships have an enormous potential given that they permit the transformation between any pair of chromospheric activity indicator lines, in particular the transformation of Ca II H & K fluxes to other more convenient ones. They might be extremely useful when using traditional photometric activity data, i.e., similar to that obtained by Vaughan et al. (1978), or when using spectroscopic data in which not all the chromospheric features are present. We have used them to obtain $\log R'_{\rm HK}$ when Ca II H or K lines could not be measured (see Sect. 5.2).

\begin{figure} \par\includegraphics[width=9cm,clip]{13275fg5a.ps}\includegraphics[width=9cm,clip]{13275fg5b.ps} \end{figure} Figure 5:

Flux-flux relationship between the total flux in H&K Ca II and Ca II IRT ( left) and the total flux in H&K Ca II and Ca II IRT ( right). Symbol sizes increase with increasing rotational velocity (triangles are used when $v \sin{i}$ could not be determined). Colors are used to discern different spectral types.

Open with DEXTER

5.2 Predicted radial velocity jitter

The most fruitful technique for detecting extrasolar planets has been the radial velocity method. As instrumental improvements and technique refinements have improved precisions in the m s-1 domain, the analysis and minimization of the impact of RV noise sources has become more important. There are two different kinds of RV perturbations: the random and systematic measurement effects, and the intrinsic stellar variations. The former can be reduced by improving spectrographs and performing robust statistical analysis. The latter, however, includes several phenomena (Saar 2009) and must be handled carefully. The RV noise sources can lead to a false planet detection (if they produce a periodic signal over a few orbital periods) or prevent planet detection (if the perturbation is larger than the orbital RV variation). Following Narayan et al. (2005), the minimum detectable exoplanet mass with the RV method is

\begin{displaymath} M_{\rm min} \propto M_{\rm p}N^{\rm -1/2}_{\rm obs}(\sigma^{... ...gma^{\rm 2}_{\rm rv})^{\rm 1/2}P^{\rm 1/3}M^{\rm 2/3}_{\rm *}, \end{displaymath} (7)

where $M_{\rm p}$ is the planet mass, $M_{\rm *}$ is the stellar mass, N is the number of observations, P is the orbital period, and $\sigma_{\rm i}$ and $\sigma_{\rm rv}$ are the rms instrumental error and rms velocity jitter caused by stellar sources, respectively. Therefore, for a given system, the minimum detectable mass will be limited by the number of observations and the dominant noise source, $\sigma_{\rm i}$ or $\sigma_{\rm rv}$. Since spectrographs have been improved to achieve $\sigma_{\rm i} \sim 1$ m s-1, the true limiting factor in Eq. (7) is the intrinsic stellar noise.

Stellar RV variations are produced by different magnetic-activity-related phenomena: convection (Saar 2009), starspots (Saar & Donahue 1997), magnetic plage/network (Saar 2003) and flares (Reiners 2009; Saar 2009). Although bisector analysis may sometimes lead to the confirmation of a planet orbiting a star even when RV jitter is present (Setiawan et al. 2007,2008; Sozzetti et al. 2006), the latter technique is not always successful (Huélamo et al. 2008; Figueira et al. 2010). Several authors have studied the impact of activity on RV jitter using $ R'_{{\rm HK}}$ as a proxy (Paulson et al. 2002; Saar et al. 2003; Santos et al. 2010; Paulson & Yelda 2006; Santos et al. 2000; Wright 2005; Saar et al. 1998). In particular, Saar et al. (1998) and Santos et al. (2000) compiled empirical relationships between $\sigma_{\rm rv}$ and $ R'_{{\rm HK}}$ for stars in the Lick vr survey (Marcy & Butler 1998) and the Geneva extrasolar planet search programme. We used these relationships to obtain the expectable RV jitter for the active stars in the sample. Results are given in Table A4. We note that, while Santos et al. (2000) obtained individual relationships for G and K stars, Saar et al. (1998) found that both type of stars exhibited similar trend. Agreement between the values obtained using each method is therefore fairly good except for K stars, which present larger $\sigma_{\rm rv}$ values for Saar et al. (1998) than for Santos et al. (2000) relationships.

It is important to mention that both relationships were obtained using stars with moderate activity levels (- $5.0 \leq \log R'_{\rm HK} \leq -4.0$). We assumed that the linear fit holds for more active stars and applied the relations to five stars that have $\log R'_{\rm HK} > - 4.0$. Whether this is valid or not is an open question that must be studied by recalibrating these relations by including a wider variety of activity levels. In our study, we considered chromospheric activity measurements in spectral ranges that contain some advantages for cool stars, i.e. the Ca II IRT lines. New calibrations with different indices would be very beneficial to the community. In the context of this aim, our sample represents a large and varied (in terms of activity levels and activity indicators) set of stars but due to the unavailability of  $\sigma_{rv}$ data (not public) we could not perform this analysis.

By applying the aforementioned empirical relationships and the derived values of $ R'_{{\rm HK}}$, we calculated the expected RV jitter for the stars in the sample, which we present in Table A4. For stars for which both Ca II H and Ca II K could be measured, $ R'_{{\rm HK}}$ could be directly derived as described in Sect. 4.2.2. However, in some cases, measurement of one of the Ca II lines (or both) was not possible due to low S/N or the presence of cosmic rays. In these cases, we used the empirical relationships obtained in Sect. 5.1 to transform the total flux in Ca II IRT into Ca II (H + K) flux. We chose to use the Ca II IRT index because the dispersion between both indices is clearly lower than in the relation between the Ca II (H + K) and H$\alpha$ fluxes. However, when one or more lines in the triplet could not be measured, we used the flux in H$\alpha$ to infer that in Ca II (H + K). It is important to mention that the stars observed with the SARG spectrograph constitute a special case. With the configuration of the spectrograph we used, the spectral range containing Ca II H & K is not available in the spectrum. The photospheric contribution correction for the orders containing the Ca II IRT lines was also less accurate than in the H$\alpha$ order. Consequently, we chose to use the empirical relationship between Ca II (H + K) and H$\alpha$ for these stars. The $ R'_{{\rm HK}}$ values obtained are given in Table A3. As mentioned in Sect. 4.3, discrepancies between our derived values of $\log R'_{\rm HK}$ and those obtained using a traditional method become important for stars with low activity levels. Given that the Saar et al. (1998) and Santos et al. (2000) relationships were obtained using traditional $\log R'_{\rm HK}$ data, the results obtained when applying them to the least active stars should be interpreted carefully. We have marked all stars with $\log R'_{\rm HK} \le -4.9$ in Table A3 with the symbol \ddag.

We cross-correlated our sample with the exoplanet database[*] and found that out of the total sample of 371 stars, 17 have confirmed exoplanets orbiting around them. As expected, all of them are either inactive stars, i.e., HIP 1499 (HD 1461 b), HIP 7513 ($\upsilon$ And b), HIP 43587 (55 Cnc b), HIP 49699 (HD 87883 b), HIP 53721 (47 UMa b), HIP 64924 (61 Vir b), HIP 65721 (70 Vir b), HIP 109378 (HD 210277 b) and HIP 116727 ($\gamma$ Cep b); or have very low activity levels, i.e., HIP 3093 (HD 3651 b), HIP 10138 (Gl 86 b), HIP 16537 ($\epsilon$ Eri b), HIP 71395 (HD 128311 b), HIP 80337 (HD 147513 b), HIP 99711 (HD 192263 b) and HIP 113357 (51 Peg b). For HIP 40693 (HD 69830 b), chromospheric activity could not be measured because of the lack of an inactive reference star to apply the subtraction technique, but chromospheric features were visible in the spectrum. The stars with known extrasolar planets are marked with \dag  in Table A1.

5.3 Applicability to transit searches

Transit searches for exoplanets are also affected by the presence of active regions on the surface of a star (Baliunas et al. 1997; Henry et al. 1997,2000). Aigrain et al. (2004) used a Sun-based model to predict the ``stellar background'' using chromospheric activity (as given by $ R'_{{\rm HK}}$). In the solar case, the noise spectrum for chromospheric irradiance variations at frequencies lower than $\sim$8 mHz, commonly referred to as ``solar background'', is frequently modelled by a sum of power laws, in which the number of terms, N, varies from one to five depending on the frequency coverage (Andersen et al. 1994), i.e.,

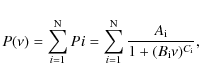
\begin{displaymath}P(\nu) = \sum_{i=1}^{\rm N} P_{\rm }i = \sum_{i=1}^{\rm N} \frac{A_{\rm i}}{1+(B_{\rm i}\nu)^{C_{\rm i}}}, \end{displaymath} (8)

where $\nu$ is frequency, $A_{\rm i}$ is the amplitude of the ith component, Bi is its characteristic timescale, and $C_{\rm i}$ is the slope of the power law. For a given component, the power remains approximately constant on timescales longer than B, and declines for shorter timescales. Each power law corresponds to a separate class of physical phenomena with a different characteristic timescale. The fitting of solar data (Aigrain et al. 2004) uncovers three components. The first component corresponds to active regions ( $\tau \simeq 1.3 \times 10^5$ s), whose amplitude both increases and correlates with the Ca II K-line index (Aigrain et al. 2004; Andersen et al. 1994). The second component is related to super- and meso-granulation with typical timescales of hours, but no detailed models of these phenomena have been developed to date. The third component is the superposition of variability on timescales of a few minutes, related to granulation and higher frequency effects, such as oscillations and photon noise.

This model can be applied to other stars (Aigrain et al. 2004) to predict the expected ``stellar background''. According to Aigrain et al. (2004), the amplitude of the first power law A1is correlated with emission in the Ca II H & K lines, i.e. $ R'_{{\rm HK}}$, and can be written as follows

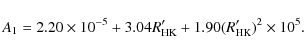
\begin{displaymath}A_{\rm 1} = 2.20 \times 10^{\rm -5} + 3.04 R'_{\rm HK} + 1.90 (R'_{\rm HK})^2 \times 10^{\rm 5}. \end{displaymath} (9)

We refer the reader to Aigrain et al. (2004) for a detailed derivation of the aforementioned formula and the other two parameters ($B_{\rm i}$ and $C_{\rm i}$). Chromospheric activity measurements, such as those presented in this work, can be therefore used as a proxy to infer the expected amplitude variation of active stars and thus to establish a lower limit to planet detection.

6 Summary and conclusions

We have used high resolution spectroscopic observations to measure the chromospheric activity and the projected rotational velocities for 371 nearby cool stars. For the fraction presenting chromospheric activity (173 stars out of 371), we have analysed the relationship between pairs of chromospheric activity indicator lines, compiling empirical relations to be used when not all the chromospheric features are included in the spectral range. We have applied these relationships to obtain values of $\log R'_{\rm HK}$ when the Ca II H & K spectral region was not available in the spectrum.

To test the applicability of the results to planet searches, we have calculated the RV jitter one should expect for each of the active stars in the sample. As previously pointed out, those values must be applied carefully because magnetic activity is variable and a simple subtraction of the activity-related ``signal'' is not possible. They have to be used as an estimation of the activity-related noise one should expect for a star and thus used to set the minimum detectable mass for a planet orbiting the star or to determine the minimal amplitude variation that could indicate the existence of a planet. Our results represent an important resource in terms of target selection for exoplanet searches surveys.

Acknowledgements
R. Martínez-Arnáiz acknowledges support from the Spanish Ministerio de Educación y Ciencia (currently the Ministerio de Ciencia e Innovación), under the grant FPI20061465-00592 (Programa Nacional Formación Personal Investigador) and projects AYA2008-00695 (Programa Nacional de Astronomía y Astrofísica), AYA2008-01727 (Programa Nacional de Astronomía y Astrofísica), AstroMadrid S2009/ESP-1496. This research has made use of the SIMBAD database and VizieR catalogue access tool, operated at CDS, Strasbourg, France. We also thank the anonymous referee for his/her valuable suggestions on how to improve the manuscript.

Appendix A: Tables of results

The stellar and line parameters are published in electronic format only available at CDS, Table A1, contains the Hipparcos number (Col. #1), the spectrograph used to observe the star (Col. #2), the modified Julian date (MJD) of the observation (Col. #3), the right ascension and declination (Col. #4 and #5), colour index (B-V) (Col. #6), spectral type (Col. #7), and projected rotational velocity, v $\sin{i}$ (Col. #8). Col. #9 specifies whether the star may be classified as active or non active. We note that for some stars in Col. #8, only upper limits are given. As mentioned in the text, for very slowly rotating stars, the value of $\sigma _{\rm0}$ can be higher than that of $\sigma_{\rm obs}$. In those cases, we give the minimum value that could be measured with the same spectrograph and for a star of the same spectral type.

The chromospheric activity results are listed in two different tables. Table A2 contains the excess emission EW as measured in the subtracted spectrum, whereas Table A3 includes the excess fluxes derived in this work. In both tables, Cols. #1 , #2, and #3 contain the Hipparcos number of the star, the spectrograph used to observe it, and the modified Julian date of the observation, respectively. In Cols. #4, #5, #6, #7, #8, and #9, excess emission (or fluxes) for Ca II K, Ca II H, H$\alpha$, and Ca II IRT $\lambda$4898 Å, Ca II IRT $\lambda$8542 Å  and Ca II IRT $\lambda$8662 Å  are given. Table A3 has an additional column containing $\log R'_{\rm HK}$. As mentioned in the text, for those stars with measured values of both Ca II H and Ca II K lines, $\log R'_{\rm HK}$ was derived directly as described in Sect. 4.2.2. When it was not possble to measure one or both of the Ca II lines, we used the empirical relationships between the total flux in Ca II (H + K) and H$\alpha$ or Ca II IRT obtained in the present work (see Fig. 5 and Table 5). Given that the relationship between Ca II (H + K) and Ca II IRT clearly exhibits lower dispersion, we used it when possible, i.e. when measuring the three lines in the Ca II infrared triplet was possible. In the remaining cases, including all the stars observed with SARG (infrared orders are strongly affected by fringing), we used the relationship between Ca II (H + K) and H$\alpha$.

Predicted radial velocity variations, i.e., jitter (based on Santos et al. 2000; Saar et al. 1998), are given in Table A4. It contains only those stars for which $\log R'_{\rm HK}$ could be derived. Columns #1, #2, and #3 contain the same information as that of Tables A2 and A3. The spectral type and $\log R'_{\rm HK}$ for each star are listed in Cols. #4 and #5. Columns #6 and #7 contain the $\sigma_{\rm rv}$ values (within 1$\sigma $) obtained using Saar et al. (1998) and Santos et al. (2000) relationships, respectively.

Online Material we have also included Fig. A1 with plots of the flux-flux relationships among different chromospheric activity indicators.

References

  1. Aigrain, S., Favata, F., & Gilmore, G. 2004, A&A, 414, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Allende Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Andersen, B. N., Leifsen, T. E., & Toutain, T. 1994, Sol. Phys., 152, 247 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baliunas, S. L., Henry, G. W., Donahue, R. A., Fekel, F. C., & Soon, W. H. 1997, ApJ, 474, L119 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barden, S. C. 1985, ApJ, 295, 162 [NASA ADS] [CrossRef] [Google Scholar]
  6. Busà, I., Aznar Cuadrado, R., Terranegra, L., Andretta, V., & Gomez, M. T. 2007, A&A, 466, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Cincunegui, C., Díaz, R. F., & Mauas, P. J. D. 2007, A&A, 469, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Desort, M., Lagrange, A.-M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Dommanget, J., & Nys, O. 1994, Communications de l'Observatoire Royal de Belgique, 115 [Google Scholar]
  10. Dommanget, J., & Nys, O. 2002, VizieR Online Data Catalog, 1274, 0 [Google Scholar]
  11. Doyle, L. R., Billingham, J., & DeVincenzi, D. L. 1998, Acta Astron., 42, 599 [CrossRef] [Google Scholar]
  12. Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJ Suppl., 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
  13. ESA. 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
  14. Figueira, P., Pepe, F., Melo, C. H. F., et al. 2010, A&A, 511, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Frasca, A., & Catalano, S. 1994, A&A, 284, 883 [NASA ADS] [Google Scholar]
  16. Gálvez, M. C., Montes, D., Fernández-Figueroa, M. J., et al. 2002, A&A, 389, 524 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gálvez, M. C., Montes, D., Fernández-Figueroa, M. J., de Castro, E., & Cornide, M. 2007, A&A, 472, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Gálvez, M. C., Montes, D., Fernández-Figueroa, M. J., De Castro, E., & Cornide, M. 2009, AJ, 137, 3965 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres, Third Ed. (Cambridge University Press) [Google Scholar]
  20. Gunn, A. G., & Doyle, J. G. 1997, A&A, 318, 60 [NASA ADS] [Google Scholar]
  21. Hall, J. C. 1996, Publications of the ASP, 108, 313 [Google Scholar]
  22. Hall, J. C., & Ramcey, L. W. 1992, AJ, 104, 1942 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hall, J. C., Lockwood, G. W., & Skiff, B. A. 2007, AJ, 133, 862 [NASA ADS] [CrossRef] [Google Scholar]
  24. Henry, G. W., Baliunas, S. L., Donahue, R. A., Soon, W. H., & Saar, S. H. 1997, ApJ, 474, 503 [NASA ADS] [CrossRef] [Google Scholar]
  25. Henry, G. W., Baliunas, S. L., Donahue, R. A., Fekel, F. C., & Soon, W. 2000, ApJ, 531, 415 [NASA ADS] [CrossRef] [Google Scholar]
  26. Henry, T. J., Soderblom, D. R., Donahue, R. A., & Baliunas, S. L. 1996, AJ, 111, 439 [NASA ADS] [CrossRef] [Google Scholar]
  27. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
  28. Huélamo, N., Figueira, P., Bonfils, X., et al. 2008, A&A, 489, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Huenemoerder, D. P., & Barden, S. C. 1984, in BAAS, 16, 510 [Google Scholar]
  30. Huenemoerder, D. P., Buzasi, D. L., & Ramsey, L. W. 1989, AJ, 98, 1398 [NASA ADS] [CrossRef] [Google Scholar]
  31. Jenkins, J. S., Jones, H. R. A., Tinney, C. G., et al. 2006, MNRAS, 372, 163 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  33. Kaufer, A., Stahl, O., Tubbesing, S., et al. 2000, in Optical and IR Telescope Instrumentation and Detectors, ed. M. Iye, & A. F. Moorwood, Proc. SPIE, 4008, 459 [Google Scholar]
  34. Kurucz, R. L. 1993, in Peculiar versus Normal Phenomena in A-type and Related Stars, ed. M. M. Dworetsky, F. Castelli, & R. Faraggiana, ASP Conf. Ser., 44, IAU Colloq., 138, 87 [Google Scholar]
  35. Lázaro, C., & Arévalo, M. J. 1997, AJ, 113, 2283 [NASA ADS] [CrossRef] [Google Scholar]
  36. López-Santiago, J., Montes, D., Fernández-Figueroa, M. J., & Ramsey, L. W. 2003, A&A, 411, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. López-Santiago, J., Montes, D., Fernández-Figueroa, M. J., Gálvez, M. C., & Crespo-Chacón, I. 2005, in 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, ed. F. Favata, G. A. J. Hussain, & B. Battrick, ESA SP, 560, 775 [Google Scholar]
  38. López-Santiago, J., Montes, D., Gálvez-Ortiz, M. C., et al. 2010, A&A, 514, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Maldonado, J., Martínez-Arnáiz, R., Eiroa, C., & Montes, D. 2010, in Proc. Pathways towards habitable planets, ed. V. Coudé du Foresto, D. M. Gelino, & I. Ribas, ASP Conf. Ser., 430 [Google Scholar]
  40. Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
  41. Marcy, G. W., & Butler, R. P. 1998, ARA&A, 36, 57 [NASA ADS] [CrossRef] [Google Scholar]
  42. Martínez-Arnáiz, R., Maldonado, J., Montes, D., et al. 2009, in The Ages of Stars, Proc. IAU Symp., 258 (Cambridge University Press) [Google Scholar]
  43. Melo, C., Pasquini, L., & de Medeiros, J. R. 2004, in Stellar Rotation, ed. A. Maeder, & P. Eenens, IAU Symp., 215, 455 [Google Scholar]
  44. Montes, D., de Castro, E., Fernandez-Figueroa, M. J., & Cornide, M. 1995a, A&AS, 114, 287 [Google Scholar]
  45. Montes, D., Fernandez-Figueroa, M. J., de Castro, E., & Cornide, M. 1995b, A&A, 294, 165 [NASA ADS] [Google Scholar]
  46. Montes, D., Fernandez-Figueroa, M. J., Cornide, M., & De Castro, E. 1996a, in Cool Stars, Stellar Systems, and the Sun, ed. R. Pallavicini, & A. K. Dupree, ASP Conf. Ser., 109, 657 [Google Scholar]
  47. Montes, D., Fernandez-Figueroa, M. J., Cornide, M., & de Castro, E. 1996b, A&A, 312, 221 [NASA ADS] [Google Scholar]
  48. Montes, D., Martin, E. L., Fernandez-Figueroa, M. J., Cornide, M., & de Castro, E. 1997, A&AS, 123, 473 [Google Scholar]
  49. Montes, D., Fernández-Figueroa, M. J., De Castro, E., et al. 2000, A&AS, 146, 103 [Google Scholar]
  50. Montes, D., López-Santiago, J., Fernández-Figueroa, M. J., & Gálvez, M. C. 2001, A&A, 379, 976 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Montes, D., Martínez-Arnáiz, R., Maldonado, J., & Eiroa, C. 2010, in Proc. Towards Other Earths: perspectives and limitations in the ELT era, ed. N. C. Santos, C. Melo, L. Pasquini, & A. Glindemann, DVD,http://www.astro.up.pt/investigacao/conferencias/toe2009/DVD/TOE/ [Google Scholar]
  52. Narayan, R., Cumming, A., & Lin, D. N. C. 2005, ApJ, 620, 1002 [NASA ADS] [CrossRef] [Google Scholar]
  53. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
  54. Paulson, D. B., & Yelda, S. 2006, PASP, 118, 706 [NASA ADS] [CrossRef] [Google Scholar]
  55. Paulson, D. B., Saar, S. H., Cochran, W. D., & Hatzes, A. P. 2002, AJ, 124, 572 [NASA ADS] [CrossRef] [Google Scholar]
  56. Paulson, D. B., Cochran, W. D., & Hatzes, A. P. 2004, AJ, 127, 3579 [Google Scholar]
  57. Pfeiffer, M. J., Frank, C., Baumueller, D., Fuhrmann, K., & Gehren, T. 1998, A&AS, 130, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Queloz, D., Allain, S., Mermilliod, J.-C., Bouvier, J., & Mayor, M. 1998, A&A, 335, 183 [NASA ADS] [Google Scholar]
  60. Reiners, A. 2009, A&A, 498, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Reiners, A., Bean, J. L., Huber, K. F., et al. 2010, ApJ, 710, 432 [NASA ADS] [CrossRef] [Google Scholar]
  62. Robinson, R. D., Cram, L. E., & Giampapa, M. S. 1990, ApJS, 74, 891 [NASA ADS] [CrossRef] [Google Scholar]
  63. Rutten, R. G. M. 1984, A&A, 130, 353 [NASA ADS] [Google Scholar]
  64. Rutten, R. G. M., Schrijver, C. J., Lemmens, A. F. P., & Zwaan, C. 1991, A&A, 252, 203 [NASA ADS] [Google Scholar]
  65. Saar, S. H. 2003, in Scientific Frontiers in Research on Extrasolar Planets, ed. D. Deming & S. Seager, ASP Conf. Ser., 294, 65 [Google Scholar]
  66. Saar, S. H. 2009, in AIP Conf. Ser. 1094, ed. E. Stempels, 152 [Google Scholar]
  67. Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
  68. Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
  69. Saar, S. H., & Fischer, D. 2000, ApJ, 534, L105 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  70. Saar, S. H., Butler, R. P., & Marcy, G. W. 1998, ApJ, 498, L153 [Google Scholar]
  71. Saar, S. H., Hatzes, A., Cochran, W., & Paulson, D. 2003, in The Future of Cool-Star Astrophysics: 12th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (2001 July 30-August 3), ed. A. Brown, G. M. Harper, & T. R. Ayres (University of Colorado), 12, 694 [Google Scholar]
  72. Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
  73. Santos, N. C., Gomes da Silva, J., Lovis, C., & Melo, C. 2010, A&A, 511, A54, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Sbordone, L. 2005, Mem. Soc. Astron. Itali. Suppl., 8, 61 [Google Scholar]
  75. Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. Itali. Suppl., 5, 93 [Google Scholar]
  76. Schrijver, C. J. 1987, A&A, 172, 111 [NASA ADS] [Google Scholar]
  77. Setiawan, J., Weise, P., Henning, T., et al. 2007, ApJ, 660, L145 [NASA ADS] [CrossRef] [Google Scholar]
  78. Setiawan, J., Henning, T., Launhardt, R., et al. 2008, Nature, 451, 38 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  79. Soderblom, D. R., Pendleton, J., & Pallavicini, R. 1989, AJ, 97, 539 [NASA ADS] [CrossRef] [Google Scholar]
  80. Sozzetti, A., Udry, S., Zucker, S., et al. 2006, A&A, 449, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Strassmeier, K., Washuettl, A., Granzer, T., Scheck, M., & Weber, M. 2000, A&AS, 142, 275 [Google Scholar]
  82. Strassmeier, K. G., Fekel, F. C., Bopp, B. W., Dempsey, R. C., & Henry, G. W. 1990, ApJS, 72, 191 [NASA ADS] [CrossRef] [Google Scholar]
  83. Thatcher, J. D., & Robinson, R. D. 1993, MNRAS, 262, 1 [NASA ADS] [Google Scholar]
  84. Tull, R. G., MacQueen, P. J., Sneden, C., & Lambert, D. L. 1995, Publ. ASP, 107, 251 [NASA ADS] [Google Scholar]
  85. Turnbull, M. C., & Tarter, J. C. 2003, ApJS, 145, 181 [NASA ADS] [CrossRef] [Google Scholar]
  86. van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data (Springer), 449 [Google Scholar]
  87. Vaughan, A. H., Preston, G. W., & Wilson, O. C. 1978, PASP, 90, 267 [NASA ADS] [CrossRef] [Google Scholar]
  88. Walkowicz, L. M., & Hawley, S. L. 2009, AJ, 137, 3297 [NASA ADS] [CrossRef] [Google Scholar]
  89. Wright, J. T. 2005, PASP, 117, 657 [NASA ADS] [CrossRef] [Google Scholar]
  90. Wright, J. T., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2004, ApJS, 152, 261 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... vicinity[*]
Based on observations made with the 2.2 m telescope at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto (Spain) and the Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Istituto Nazionale de Astrofisica Italiano (INAF), in the Spanish Observatorio del Roque de los Muchachos. This research has been supported by the Programa de Acceso a Infraestructuras Científicas y Tecnológicas Singulares (ICTS).
...[*]
Tables A1 to A4 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/520/A79
... used[*]
Slow rotating stars with well known v $\sin{i}$.
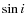...JSTARMOD[*]
JSTARMOD is a modified version of the Fortran code STARMOD developed at the Penn State University (Barden 1985; Huenemoerder & Barden 1984). The modified code, implemented by López-Santiago, admits as input echelle spectra obtained with a CCD with more than 2048 pixels.
... database[*]
http://exoplanet.eu
Copyright ESO 2010

All Tables

Table 1:   A constant for FOCES, 2dcoudé (McDonald), FEROS and SARG spectra.

Table 2:   Inactive stars used as references in the subtraction technique to measure chromospheric activity.

Table 3:   Comparison of the classification of the stars as active or inactive with previous results.

Table 4:   Stars for which our classification as active or inactive differs from that of other authors.

Table 5:   Linear fit coefficients for each flux-flux relationship.

All Figures

  \begin{figure} \par\includegraphics[width=9.cm, keepaspectratio]{13275fg1.ps} \end{figure} Figure 1:

Calibration between $\sigma _{\rm0}$ and colour index B-V, where $\sigma _{\rm0}$ represents the ``natural'' broadening of the spectrum lines and was obtained from synthetic spectra covering the spectral range of the observed stars. Given that the instrumental profile also contributes as a broadening mechanism and considering that each spectrograph has a different one, we had to derive a calibration relationship for each of them.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13275fg2.ps} \end{figure} Figure 2:

Number of active (black) and inactive (grey) stars in the sample for each spectral type.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13275fg3.ps} \end{figure} Figure 3:

Ca II H & K surface flux vs colour index B-V. Small dots represent Duncan et al. (1991) and Wright et al. (2004) data. To represent the stars considered as reference in this work, we have used different symbols according to the source of $F_{\rm H} +F_{\rm K}$ values: circles for Duncan et al. (1991) data, squares for Henry et al. (1996) data, crosses for Wright et al. (2004) data, and triangles for Jenkins et al. (2006) data. The curve represents the surface flux boundary obtained by Rutten (1984).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13275fg4.ps} \end{figure} Figure 4:

Comparison of $ R'_{{\rm HK}}$ index obtained in this paper and that obtained with the Mount Wilson H-K spectrophotometer (Vaughan et al. 1978) and similar techniques. Different symbols are used for Duncan et al. (1991), Strassmeier et al. (2000), Wright et al. (2004), Hall et al. (2007), and Mamajek & Hillenbrand (2008) data. In the lower panel, we have plotted $\sigma $ (as described in the text).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13275fg5a.ps}\includegraphics[width=9cm,clip]{13275fg5b.ps} \end{figure} Figure 5:

Flux-flux relationship between the total flux in H&K Ca II and Ca II IRT ( left) and the total flux in H&K Ca II and Ca II IRT ( right). Symbol sizes increase with increasing rotational velocity (triangles are used when $v \sin{i}$ could not be determined). Colors are used to discern different spectral types.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.