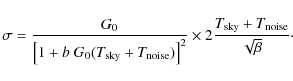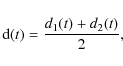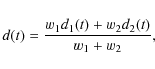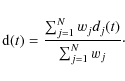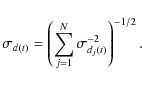| Issue |
A&A
Volume 520, September-October 2010
Pre-launch status of the Planck mission
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 16 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200912849 | |
| Published online | 15 September 2010 | |
Pre-launch status of the Planck mission
Planck pre-launch status: Low Frequency Instrument calibration and expected scientific performance
A. Mennella1 - M. Bersanelli1 - R. C. Butler2 - F. Cuttaia2 - O. D'Arcangelo3 - R. J. Davis4 - M. Frailis5 - S. Galeotta5 - A. Gregorio6 - C. R. Lawrence7 - R. Leonardi8 - S. R. Lowe4 - N. Mandolesi2 - M. Maris5 - P. Meinhold8 - L. Mendes9 - G. Morgante2 - M. Sandri2 - L. Stringhetti2 - L. Terenzi2 - M. Tomasi1 - L. Valenziano2 - F. Villa2 - A. Zacchei5 - A. Zonca10 - M. Balasini11 - C. Franceschet1 - P. Battaglia11 - P. M. Lapolla11 - P. Leutenegger11 - M. Miccolis11 - L. Pagan11 - R. Silvestri11 - B. Aja12 - E. Artal12 - G. Baldan11 - P. Bastia11 - T. Bernardino13 - L. Boschini11 - G. Cafagna11 - B. Cappellini10 - F. Cavaliere1 - F. Colombo11 - L. de La Fuente12 - J. Edgeley4 - M. C. Falvella14 - F. Ferrari11 - S. Fogliani5 - E. Franceschi2 - T. Gaier7 - F. Gomez15 - J. M. Herreros15 - S. Hildebrandt15 - R. Hoyland15 - N. Hughes16 - P. Jukkala16 - D. Kettle4 - M. Laaninen17 - D. Lawson4 - P. Leahy4 - S. Levin15 - P. B. Lilje18 - D. Maino1 - M. Malaspina2 - P. Manzato5 - J. Marti-Canales19 - E. Martinez-Gonzalez13 - A. Mediavilla12 - F. Pasian5 - J. P. Pascual12 - M. Pecora11 - L. Peres-Cuevas20 - P. Platania3 - M. Pospieszalsky21 - T. Poutanen22,23,24 - R. Rebolo16 - N. Roddis4 - M. Salmon13 - M. Seiffert7 - A. Simonetto3 - C. Sozzi3 - J. Tauber20 - J. Tuovinen25 - J. Varis25 - A. Wilkinson4 - F. Winder4
1 - Università degli Studi di Milano, Dipartimento di Fisica, via
Celoria 16, 20133 Milano, Italy
2 - INAF-IASF - Sezione di Bologna, via Gobetti 101, 40129 Bologna,
Italy
3 - CNR - Istituto di Fisica del Plasma, via Cozzi 53, 20125 Milano,
Italy
4 - Jodrell Bank Centre for Astrophysics, School of Physics &
Astronomy, University of Manchester, Manchester, M13 9PL, UK
5 - INAf - Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143
Trieste, Italy
6 - Università degli Studi di Trieste, Dipartimento di Fisica, via
Valerio 2, 34127 Trieste, Italy
7 - Jet Propulsion Laboratory, California Institute of Technology, 4800
Oak Grove Drive, Pasadena, CA 91109, USA
8 - University of California at Santa Barbara, Physics Department,
Santa Barbara CA 93106-9530, USA
9 - Planck Science Office, European Space Agency,
ESAC, PO box 78, 28691 Villanueva de la Caada, Madrid, Spain
10 - INAF-IASF - Sezione di Milano, via Bassini 15, 20133 Milano, Italy
11 - Thales Alenia Space Italia, S.S Padana Superiore 290, 20090
Vimodrone (Milano), Italy
12 - Departamento de Ingeniera de Comunicaciones, Universidad de
Cantabria, Avenida De Los Castros, 39005 Santander, Spain
13 - Instituto de Fisica De Cantabria, Consejo Superior de
Investigaciones Cientificas, Universidad de Cantabria, Avenida De Los
Castros, 39005 Santander, Spain
14 - Agenzia Spaziale Italiana, Viale Liegi 26, 00198 Roma, Italy
15 - Instituto de Astrofisica de Canarias, vía Láctea, 38200 La Laguna
(Tenerife), Spain
16 - DA-Design Oy, Keskuskatu 29, 31600 Jokioinen, Finland
17 - Ylinen Electronics Oy, Teollisuustie 9 A, 02700 Kauniainen, Finland
18 - Institute of Theoretical Astrophysics, University of Oslo, PO box
1029 Blindern, 0315 Oslo, Norway
19 - Joint ALMA Observatory, Las Condes, Santiago, Chile
20 - Research and Scientific Support Dpt, European Space Agency, ESTEC,
Noordwijk, The Netherlands
21 - National Radio Astronomy Observatory, 520 Edgemont Road,
Charlottesville VA 22903-2475, USA
22 - University of Helsinki, Department of Physics, PO Box 64 (Gustaf
Hllstrmin katu 2a), 00014 Helsinki, Finland
23 - Helsinki Institute of Physics, PO Box 64 (Gustaf Hllstrmin katu
2a), 00014 Helsinki, Finland
24 - Metsähovi Radio Observatory, Helsinki University of Technology,
Metshovintie 114 02540 Kylmälä, Finland
25 - MilliLab, VTT Technical Research Centre of Finland, Tietotie 3,
Otaniemi, Espoo, Finland
Received 8 July 2009 / Accepted 12 January
2010
Abstract
We present the calibration and scientific performance parameters of the
Planck Low Frequency Instrument (LFI) measured
during the ground cryogenic test campaign. These parameters
characterise the instrument response and
constitute our optimal pre-launch knowledge of the LFI scientific
performance. The LFI shows excellent 1/f
stability
and rejection of instrumental systematic effects; its measured noise
performance shows that LFI is the most sensitive
instrument of its kind. The calibration parameters will be updated
during flight operations until the
end of the mission.
Key words: cosmic microwave background - telescopes - space vehicles: instruments - instrumentation: detectors - instrumentation: polarimeters - submillimeter: general
1 Introduction
The Low Frequency Instrument (LFI) is an array of 22 coherent differential receivers at 30, 44, and 70 GHz onboard the European Space Agency PlanckThe LFI shares the focal plane of the Planck telescope with the High Frequency Instrument (HFI), an array of 52 bolometers in the 100-857 GHz range, cooled to 0.1 K. This wide frequency coverage, necessary for optimal component separation, constitutes a unique feature of Planck and a formidable technological challenge, because it requires the integration of two different technologies with different cryogenic requirements in the same focal plane.
Excellent noise performance is obtained with receivers based
on indium phosphide high electron mobility transistor
amplifiers, cryogenically cooled to 20 K by a vibrationless
hydrogen sorption cooler, which provides more than 1 W of
cooling power at 20 K. The LFI thermal design has been driven
by an optimisation of receiver sensitivity and
available cooling power; in particular, radio frequency (RF)
amplification is divided between a 20 K front-end unit and
a ![]() 300 K
back-end unit connected by composite waveguides (Bersanelli et al. 2010).
300 K
back-end unit connected by composite waveguides (Bersanelli et al. 2010).
The LFI has been developed following a modular approach in which the various sub-units (e.g., passive components, receiver active components, electronics) have been built and tested individually before proceding to the next integration step. The final integration and testing phases have been the assembly, verification, and calibration of both the individual radiometer chains (Villa et al. 2010) and the integrated instrument.
In this paper, we focus on the calibration, i.e., the set of parameters that provides our most accurate knowledge of the instrument's scientific performance. After an overview of the calibration philosophy, we focus on the main calibration parameters measured during test campaigns performed at instrument and satellite levels. Information concerning the test setup and data analysis methods is provided where necessary, with references to appropriate technical articles for further details. The companion article that describes the LFI instrument (Bersanelli et al. 2010) is the most central reference for this paper.
The naming convention that we use for receivers and individual channels is given in Appendix A.
2 Overview of the LFI pseudo-correlation architecture
We briefly summarise the LFI pseudo-correlation architecture. Further details and a more complete treatment of the instrument can be found in Bersanelli et al. (2010).In the LFI, each receiver couples with the Planck
telescope secondary mirror by means of a corrugated feed horn feeding
an orthomode transducer (OMT) that divides the incoming wave into two
perpendicularly polarised components, which
propagate through two independent pseudo-correlation receivers with
HEMT (high electron mobility transistor) amplifiers
divided into a cold (![]() 20 K)
and a warm (
20 K)
and a warm (![]() 300 K)
stage connected by composite waveguides.
300 K)
stage connected by composite waveguides.
A schematic of the LFI pseudo-correlation receiver is shown in
Fig. 1.
In each radiometer connected to an OMT arm, the sky signal and the
signal from a stable reference load thermally
connected to the HFI 4 K shield (Valenziano
et al. 2009) are coupled to cryogenic low-noise HEMT
amplifiers by means of a 180![]() hybrid. One of the two signals runs through a switch that applies a
phase shift, which oscillates between 0
and 180
hybrid. One of the two signals runs through a switch that applies a
phase shift, which oscillates between 0
and 180![]() at a frequency of 4096 Hz. A second phase switch is present in
the second radiometer leg to ensure symmetry, but it does not introduce
any phase shift. The signals are then recombined by a
second 180
at a frequency of 4096 Hz. A second phase switch is present in
the second radiometer leg to ensure symmetry, but it does not introduce
any phase shift. The signals are then recombined by a
second 180![]() hybrid coupler, producing a sequence of sky-load outputs alternating at
twice the frequency of the phase
switch.
hybrid coupler, producing a sequence of sky-load outputs alternating at
twice the frequency of the phase
switch.
![\begin{figure}\par\includegraphics[width=8cm]{12849fg1.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg8.png)
|
Figure 1: Schematic of the LFI pseudo-correlation architecture. |
| Open with DEXTER | |
In the back-end of each radiometer (see bottom part of Fig. 1), the RF signals are further amplified, filtered by a low-pass filter and then detected. After detection, the sky and reference load signals are integrated and digitised in 14-bit integers by the LFI digital acquisition electronics (DAE) box.
According to the scheme described above, the radiometric differential power output from each diode can be written as
where the gain modulation factor, r, minimises the
effect of the input signal offset between the sky (![]() 2.7 K)
and the reference load (
2.7 K)
and the reference load (![]() 4.5 K).
The effect of reducing the offset in software and the way r
is estimated from
flight data are discussed in detail in Mennella
et al. (2003).
4.5 K).
The effect of reducing the offset in software and the way r
is estimated from
flight data are discussed in detail in Mennella
et al. (2003).
3 Calibration philosophy
The LFI calibration plan was designed to ensure optimal measurement of all parameters characterising the instrument response. Calibration activities have been performed at various levels of integration, from single components, to the integrated instrument and the entire satellite. The inherent redundancy of this approach provided maximum knowledge about the instrument and its subunits, as well as calibration at different levels.Table 1 gives the main LFI instrument parameters and the integration levels at which they have been measured. Three main groups of calibration activities are identified: (i) basic calibration (Sect. 5.1); (ii) receiver noise properties (Sect. 5.2); and (iii) susceptibility (Sect. 5.3).
A particular point must be made about the front-end bias tuning, which is not part of calibration but is nevertheless a key step in setting the instrument scientific performance. To satisfy tight mass and power constraints, power bias lines have been divided into four common-grounded power groups, with no bias voltage readouts. Only the total drain current flowing through the front-end amplifiers is measured and is available in the housekeeping telemetry. This design has important implications for front-end bias tuning, which depends critically on the satellite electrical and thermal configuration. Therefore, front-end bias tuning has been repeated at all integration stages, and will also be repeated in-flight before the start of nominal operations. Details about bias tuning performed at the various integration levels can be found in Davis et al. (2009), Varis et al. (2009), Villa et al. (2010), and Cuttaia et al. (2009).
Table 1: Main instrument parameters and stages at which they have been measured.
4 Instrument-level cryogenic environment and test setup
The LFI receivers and the integrated instrument were tested in 2006 at the Thales Alenia Space-Italia laboratories located in Vimodrone (Milano). Custom-designed cryo-facilities were developed to reproduce as closely as possible flight-like thermal, electrical, and data interface conditions (Terenzi et al. 2009a). Table 2 compares the main expected flight thermal conditions with those reproduced during tests on individual receivers and on the integrated instrument.During the integrated instrument tests, the temperature of the sky and reference loads was much higher than expected in flight (18.5 K vs. 3-4.5 K) as can be seen from the table. To compensate for this, receiver-level tests were conducted with the sky and reference loads at two temperatures, one near flight, the other near 20 K (Villa et al. 2010). During the instrument-level tests, parameters that depend on the sky and reference load temperatures (such as the white noise sensitivity and the photometric calibration constant) could be extrapolated to flight conditions.
4.1 Thermal setup
A schematic of the LFI cryo-facility with the main thermal interfaces is shown in Fig. 2. The LFI was installed face-down, with the feed-horns directed towards an ECCOSORB ``sky-load'' and the back-end unit resting upon a tilted support. The entire instrument was held in place by a counterweight system that allowed slight movements to compensate for thermal contractions during cooldown. The reference loads were mounted on a mechanical structure reproducing the HFI external interfaces inserted in the middle of the front-end unit.
We summarise here and in Table 3 the main characteristics and issues of the testing environment. Further details about the sky load thermal design can be found in Terenzi et al. (2009a).
![\begin{figure}\par\includegraphics[width=8cm]{12849fg2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg11.png)
|
Figure 2: LFI cryo-chamber facility. The LFI is mounted face-down with the feed horn array facing the eccosorb sky-load. |
| Open with DEXTER | |
Front-end unit. The front-end unit and the LFI main
frame were cooled by a large copper flange simulating
the sorption cooler cold-end interface. The flange was linked to the
20 K cooler by means of ten large copper braids. Its
temperature was controlled by a PID controller, and was stable to ![]() 35 mK
at temperatures
35 mK
at temperatures ![]() 25.5 K
at
the control stage. The thermal control system was also used in the
susceptibility test to change the temperature of the
front end in steps (see Sect 5.3).
25.5 K
at
the control stage. The thermal control system was also used in the
susceptibility test to change the temperature of the
front end in steps (see Sect 5.3).
Sky load. The sky load was thermally linked to the 20 K cooler through a gas heat switch that could be adjusted to obtain the necessary temperature steps during calibration tests. One of the sensors mounted on the central region of the load did not work correctly during the tests and results from the thermal modelling were used to describe its thermal behaviour.
Reference loads. These were installed on an aluminium structure thermally anchored to the 20 K cooler by means of high conductivity straps. An upper plate held all 70 GHz loads, while the 30 and 44 GHz loads were attached to three individual flanges. Two thermometers on the bottom flange were used to measure and control the temperature of the entire structure. Five other sensors monitored the temperatures of the aluminum cases of the reference loads. The average temperature of the loads was around 22.1 K, with typical peak-to-peak stability of 80 mK.
Radiative shroud. The LFI was enclosed in a thermal shield intercepting parasitics and providing a cold radiative environment. The outer surface was highly reflective, while the inner surface was coated black to maximise radiative coupling. Two 50 K refrigerators cooled the thermal shield to temperatures in the range 43-70 K, depending on the distance to the cryocooler cold head, as measured by twelve diode sensors.
Back-end unit. The warm back-end unit was
connected to a water circuit with temperature stabilised
by a proportional-integral-derivative (PID) controller; this stage was
affected by diurnal temperature
instabilities of the order of ![]() 0.5 K peak-to-peak. The effect of these
temperature instabilities was visible in
the total power voltage output from some detectors, but was almost
completely removed by differencing.
0.5 K peak-to-peak. The effect of these
temperature instabilities was visible in
the total power voltage output from some detectors, but was almost
completely removed by differencing.
Table 2: Summary of main thermal conditions.
Table 3: LFI cryo-facility thermal performance.
5 Measured calibration parameters and scientific performance
We present the main calibration and performance parameters (see Table 1).During the instrument-level test campaign, we experienced two failures:
one on the 70 GHz radiometer LFI18M-0,
and the other on the 44 GHz radiometer LFI24M-0.
The LFI18M-0 failure was caused by a phase switch
that cracked during cooldown. At the end of the test campaign and just
before instrument delivery to ESA,
the radiometer LFI18M-0 was replaced with a
flight spare. In the second case, the problem was a
defective electrical contact to the amplifier
![]() (gate 2 voltage)
line, which was repaired after the end of
the test. Subsequent room-temperature tests as well cryogenic ground
satellite tests (Summer
2008) and in-flight calibration (Summer 2009) showed full
functionality, confirming the successful repair of
LFI18M-0 and LFI24M-0.
Because these two radiometers were in a failed state during the test
campaign,
we generally show no results for them. The only exception is the
calibrated noise per frequency channel reported in
Table 6,
where:
(gate 2 voltage)
line, which was repaired after the end of
the test. Subsequent room-temperature tests as well cryogenic ground
satellite tests (Summer
2008) and in-flight calibration (Summer 2009) showed full
functionality, confirming the successful repair of
LFI18M-0 and LFI24M-0.
Because these two radiometers were in a failed state during the test
campaign,
we generally show no results for them. The only exception is the
calibrated noise per frequency channel reported in
Table 6,
where:
- for LFI18M-0, we assume the same noise parameters obtained for LFI18S-1; and
- for LFI24M-0, we use the noise parameters measured during single-receiver tests before integration into the instrument array.
5.1 Basic calibration
5.1.1 Experimental setup
These parameters were determined by means of tests in which the
radiometric average voltage output,
![]() ,
was recorded for various input antenna temperature levels,
,
was recorded for various input antenna temperature levels,
![]() .
Although straightforward in
principle, these tests required the following conditions in the
experimental setup and in the measurement procedure to
maximise the achieved accuracy in the recovered parameters:
.
Although straightforward in
principle, these tests required the following conditions in the
experimental setup and in the measurement procedure to
maximise the achieved accuracy in the recovered parameters:
- the sky load temperature distribution had to be accurately known;
- temperature steps had to be sufficiently large (at least a few Kelvin) to dominate over variations caused by 1/f noise or other instabilities;
- the reference load temperature had to remain stable during the change in the sky load temperature or, alternatively, variations had to be taken into account in the data analysis, especially in the determination of receiver isolation;
- data points must be acquired at multiple input temperatures to increase the accuracy of the estimates of response linearity.
On the other hand, these conditions were not as well-met during instrument-level tests:
- the total number of available temperature controllers allowed us to place only three sensors on the sky load, one on the back metal-plate, one on the side, and one on the tip of the central pyramid. The input temperature was then determined using the measurements from these three sensors in a dedicated thermal model of the sky load itself;
- the minimum and maximum temperatures that could be set without impacting the focal plane and reference load temperatures were 17.5 K and 30 K, half the range obtained during receiver-level tests;
- the time needed to change the sky load temperature by a few Kelvin was large, of the order of several hours, because of its high thermal mass. This limited to three the number of temperature steps that could be performed in the available time.
Table 4 summarises temperatures for the three temperature steps considered in these tests. The sky load temperature (antenna temperature) has been determined from the sky load thermal model using temperature sensor data. The reference load temperature is a direct measurement converted into antenna temperature. Front-end and back-end unit temperatures are direct temperature sensor measurements averaged over all sensors.
Table 4: Main temperatures during basic calibration.
5.1.2 Photometric calibration, noise temperature, and linearity
Noise temperatures and calibration constants can be calculated by
fitting the ![]() data
with the most representative model (Mennella et al. 2009;
Daywitt
1989)
data
with the most representative model (Mennella et al. 2009;
Daywitt
1989)
where
In Table 8,
we summarise the best-fit parameters obtained for all the LFI
detectors. The nonlinearity parameter b for
the 70 GHz receivers is ![]() 10-3, consistent with zero
within
the measurement uncertainty. The 30 and 44 GHz
receivers show some compression at high input temperatures. This
nonlinearity arises from the back-end RF amplification stage and
detector diode, which show compression down to very low
input powers. The nonlinear response has been thoroughly tested both on
the individual back end modules
(Mennella et al. 2009)
and during the RCA calibration campaign (Villa
et al. 2010) and has been shown to closely
reproduce Eq. (2).
10-3, consistent with zero
within
the measurement uncertainty. The 30 and 44 GHz
receivers show some compression at high input temperatures. This
nonlinearity arises from the back-end RF amplification stage and
detector diode, which show compression down to very low
input powers. The nonlinear response has been thoroughly tested both on
the individual back end modules
(Mennella et al. 2009)
and during the RCA calibration campaign (Villa
et al. 2010) and has been shown to closely
reproduce Eq. (2).
5.1.3 Isolation
Isolation was estimated from the average radiometer voltage outputs,
![]() and
and
![]() ,
at the two
extreme sky load temperatures (Steps 1 and 3 in
Table 4)
,
at the two
extreme sky load temperatures (Steps 1 and 3 in
Table 4)![]() . Equations used to
calculate isolation
values and uncertainties are reported in Appendix B.
. Equations used to
calculate isolation
values and uncertainties are reported in Appendix B.
In Fig. 3, we summarise the measured isolation for all detectors and provide a comparison with similar measurements performed on individual receiver chains. The results show large uncertainties in isolation measured during instrument-level tests, caused by 1/f noise instabilities in the total power datastreams that were not negligible in the time span between the various temperature steps, which was of the order of a few days.
![\begin{figure}\par\mbox{ \includegraphics[width = 4.3cm]{12849fg3.ps} \includegr...
...{12849fg5.ps} \includegraphics[width = 4.3cm]{12849fg6.ps} }
\par
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg27.png)
|
Figure 3: Summary of measured isolation compared with the same measurements performed at receiver level (Villa et al. 2010). |
| Open with DEXTER | |
Apart from the limitations given by the measurement setup, the results show that isolation lies in the range -10 dB to -20 dB, which is globally within the requirement of -13 dB.
5.2 Noise properties
The pseudo-correlation design of the Planck-LFI receivers has been optimised to minimise the effects of 1/f gain variations in the radiometers.
The white noise sensitivity of the receivers is essentially independent of the reference load temperature level (Seiffert et al. 2002) and can be written, in its most general form, as
where
For data obtained from a single diode output, K=1
for unswitched data and K=2 for differenced data.
The factor of 2 for differenced data is the product of one ![]() from the difference and another
from the difference and another ![]() from the halving of the sky integration time. When we average the two
(calibrated) outputs of each radiometer, we gain back a factor
from the halving of the sky integration time. When we average the two
(calibrated) outputs of each radiometer, we gain back a factor ![]() ,
so that the final radiometer sensitivity is given by Eq. (3)
with
,
so that the final radiometer sensitivity is given by Eq. (3)
with ![]() .
.
Figure 4 shows the effectiveness of the LFI pseudo-correlation design (see Meinhold et al. 2009). After differencing, the 1/f knee frequency is reduced by more than three orders of magnitude, and the white noise sensitivity scales almost perfectly with the three values of the constant K. The following terminology is used in the figure:
- Total power data: datastreams acquired without operating the phase switch;
- Modulated data: datastreams acquired in nominal, switching conditions before taking the difference in Eq. (1);
- Diode differenced data: differenced datastreams for each diode;
- Radiometer differenced data: datastreams obtained from a weighted average of the two diode differenced datastreams for each radiometer (see Eq. (E.2)).
![\begin{figure}\par\includegraphics[width=15.5cm,clip]{12849fg7n.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg33.png)
|
Figure 4: Amplitude spectral densities of unswitched and differenced data streams. The pseudo-correlation differential design reduces the 1/f knee frequency by three orders of magnitude. The white noise level scales almost perfectly with K. |
| Open with DEXTER | |
5.2.1 Overview of main noise parameters
If we consider a typical differenced data noise power spectrum, P(f), we can identify three main characterisics:
- 1.
- The white noise plateau, where
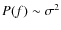 .
The white noise sensitivity is given by
.
The white noise sensitivity is given by 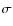 (in units of K s1/2),
and the noise effective bandwidth by
(in units of K s1/2),
and the noise effective bandwidth by
where is the voltage DC level,
is the voltage DC level, 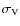 the uncalibrated white noise sensitivity and
the term in square brackets represents the effect of compressed voltage
output (see
Appendix C).
the uncalibrated white noise sensitivity and
the term in square brackets represents the effect of compressed voltage
output (see
Appendix C).
- 2.
- The 1/f noise tail, characterised by a
power spectrum
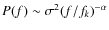 described
by two parameters: the knee frequency, fk,
defined as the frequency where the 1/f and white
noise
contribute equally, and the slope
described
by two parameters: the knee frequency, fk,
defined as the frequency where the 1/f and white
noise
contribute equally, and the slope 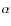 .
.
- 3.
- Spurious frequency spikes. These are a common-mode additive effect caused by interference between scientific and housekeeping data in the analog circuits of the data acquisition electronics box (see Sect. 5.2.5).
5.2.2 Test experimental conditions
The test used to determine instrument noise was a long-duration (2-day)
acquisition during which the instrument
ran undisturbed in its nominal mode. Target temperatures were set at
![]() K
and
K
and ![]() K.
The front-end unit was at 26 K, maintained to be stable to
K.
The front-end unit was at 26 K, maintained to be stable to ![]() 10 mK.
10 mK.
The most relevant instabilities were a 0.5 K peak-to-peak 24-hour fluctuation in the back-end temperature and a 200 mK drift in the reference load temperature caused by a leakage in the gas gap thermal switch that was refilled during the last part of the acquisition (see Fig. 5).
The effect of the reference load temperature variation was clearly identified in the differential radiometric output (see Fig. 6) and removed from the radiometer data before differencing. The effect of the back-end temperature was removed by correlating the radiometric output with temperature sensor measurements.
5.2.3 White noise sensitivity and noise effective bandwidth
There are four sources of white noise that determines the final
sensitivity: (i) the input sky signal; (ii)
the RF part of the receiver (active components and resistive losses);
(iii) the back-end electronics after the detector
diode![]() ; and
(iv) signal quantisation performed in the digital processing unit.
; and
(iv) signal quantisation performed in the digital processing unit.
Signal quantisation can significantly increase the noise level
if ![]() ,
where q represents
the quantisation step and
,
where q represents
the quantisation step and ![]() the noise level before quantisation. Previous optimisation studies (Maris et al. 2004)
demonstrated that a quantisation ratio
the noise level before quantisation. Previous optimisation studies (Maris et al. 2004)
demonstrated that a quantisation ratio
![]() is enough to satisfy telemetry requirements without
significantly increasing the noise level. This has been verified during
calibration tests using the so-called
``calibration channel'', i.e., a data channel containing about 15
minutes per day of unquantised data from each
detector. The use of the calibration channel allowed a comparison
between the white noise level before and after
quantisation and compression for each detector. Table 9
summarises these
results and shows that digital quantisation caused an increase in the
signal white noise of less than 1%.
is enough to satisfy telemetry requirements without
significantly increasing the noise level. This has been verified during
calibration tests using the so-called
``calibration channel'', i.e., a data channel containing about 15
minutes per day of unquantised data from each
detector. The use of the calibration channel allowed a comparison
between the white noise level before and after
quantisation and compression for each detector. Table 9
summarises these
results and shows that digital quantisation caused an increase in the
signal white noise of less than 1%.
We report in Fig. 7 the white noise effective bandwidth calculated according to Eq. (4) . Our results indicate that the noise effective bandwidth is smaller than the requirement by 20%, 50%, and 10% at 30, 44, and 70 GHz, respectively. Non-idealities in the in-band response (ripples) causing bandwidth narrowing are discussed in Zonca et al. (2009).
![\begin{figure}
\par\includegraphics[width = 8.8 cm]{12849fg8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg45.png)
|
Figure 5: Thermal instabilities during the long duration acquisition. Top: drift in the reference load temperature caused by leakage in the gas cap thermal switch. The drop towards the end of the test coincides with refill of the thermal switch. Bottom: 24-h back-end temperature fluctuation. |
| Open with DEXTER | |
It is useful to extrapolate these results to the expected in-flight
sensitivity of the instrument at the
nominal temperature of 20 K when observing a sky signal of ![]() 2.73 K
in thermodynamic temperature. This estimate
has been performed in two different ways. The first uses measured noise
effective bandwidths and noise temperatures in
the radiometer equation, Eq. (3).
The second starts from measured uncalibrated noise,
which is then calibrated in temperature units, corrected for the
different focal plane temperature in test conditions,
and extrapolated to
2.73 K
in thermodynamic temperature. This estimate
has been performed in two different ways. The first uses measured noise
effective bandwidths and noise temperatures in
the radiometer equation, Eq. (3).
The second starts from measured uncalibrated noise,
which is then calibrated in temperature units, corrected for the
different focal plane temperature in test conditions,
and extrapolated to ![]() 2.73 K
input using the radiometeric response equation, Eq. (2).
The
details of the extrapolation are given in Appendix D.
2.73 K
input using the radiometeric response equation, Eq. (2).
The
details of the extrapolation are given in Appendix D.
Table 5 indicates the sensitivity per radiometer estimated according to the two procedures. The sensitivity per radiometer was obtained using a weighted noise average from the two detectors of each radiometer (see Appendix E). Because radiometers LFI18M-0 and LFI24M-0 were not working during the tests, we estimated the sensitivity per frequency channel by considering the white noise sensitivity of LFI24M-0, which was later repaired, measured during receiver-level tests, while for LFI18M-0, which was later replaced by a spare unit, we assumed the same sensitivity as for LFI18S-1. Further details about the white noise sensitivity of individual detectors are reported in Meinhold et al. (2009).
![\begin{figure}
\par\includegraphics[width=17cm]{12849fg9.eps}
\vspace{-3mm} \end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg46.png)
|
Figure 6: Calibrated differential radiometric outputs (downsampled to 1 Hz) for all LFI detectors during the long duration test. Temperature sensor data in antenna temperature units are superimposed (thin black line) on the calibrated radiometric data. |
| Open with DEXTER | |
Table 5:
White noise sensitivities per radiometer in
![]() .
.
We provide in Table 6 the sensitivity per frequency channel estimated using the two procedures and compared with the LFI requirement.
Table 6:
White noise sensitivities per frequency channel in ![]() K
K![]() s1/2.
s1/2.
![\begin{figure}
\par\includegraphics[width=9cm]{12849fg10.ps}
\vspace{-3mm}\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg47.png)
|
Figure 7: Noise effective bandwidths calculated during instrument-level measurements. The three lines indicate the 70 GHz, 44 GHz, and 30 GHz requirements. |
| Open with DEXTER | |
5.2.4 1/f noise parameters
The 1/f noise properties of the LFI differenced data were determined more accurately during instrument-level than receiver-level tests for two reasons: (i) the test performed in this phase was the longest of all the test campaign; and (ii) because of the greater temperature stability, especially compared to the 70 GHz receivers cryofacility (Villa et al. 2010).
Summarised in Table 7, the results show very good 1/f noise stability of the LFI receivers, almost all with a knee frequency well below the required 50 mHz.
Table 7: Summary of knee frequency and slope.
5.2.5 Spurious frequency spikes
During the FM test campaign, we found unwanted frequency spikes in the radiometeric data at frequencies of the order of a few hertz. The source of the problem was recognised to be in the backend data acquisition electronics box, where unexpected crosstalk between the circuits handling housekeeping and radiometric data affected the radiometer voltage output downstream of the detector diode.
In Fig. 8, this is clearly shown in spectra of unswitched data acquired from the 70 GHz detector LFI18S-10 with the housekeeping data acquisition activated and deactivated. Because the disturbance is added to receiver signal at the end of the radiometric chain it acts as a common mode effect on both the sky and reference load data so that its effect in differenced data is reduced by several orders of magnitude bringing it well below the radiometer noise level.
![\begin{figure}(a)\includegraphics[width=8cm]{12849fg11.eps}\\
\vspace{0.4cm}
...
....4cm}
(d)\includegraphics[width=8cm]{12849fg14.eps}
\vspace{-2mm}\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg50.png)
|
Figure 8:
DAE-only and radiometer noise amplitude density spectra in
|
| Open with DEXTER | |
Further analysis of these spikes has shown that the disturbance is synchronized in time. By binning the data synchronously, we obtain a template of the disturbance, which allows its removal in the time-domain (Meinhold et al. 2009). The feasibility of this approach has been proven using data acquired during the full satellite test campaign in Liege, Belgium during July and August, 2008.
Therefore, because the only way to eliminate the disturbance in hardware would be to operate the instrument without any housekeeping information, our baseline approach is that, if necessary, the residual effect will be removed from the data in the time domain after measuring the disturbance shape from the flight data.
5.3 Radiometric suceptibility to front-end temperature instabilities
Thermal fluctuations in the receivers result in gain changes in the amplifiers and noise changes in the (slightly emissive) passive components (e.g., horns, OMTs, waveguides). These changes mimic the effect of changes in sky emission, expecially at fluctuation frequencies near the satellite spin frequency. The most important source of temperature fluctuations for LFI is the sorption cooler (Bhandari et al. 2004; Wade et al. 2000).
For small temperature fluctuations in the focal plane, the radiometric response is linear (Terenzi et al. 2009b; Seiffert et al. 2002), so the spurious antenna temperature fluctuation in the differential receiver output can be written as
where the transfer function
The analytical form of
If we consider the systematic error budget in Bersanelli et al. (2010),
it is possible to derive a requirement for
the radiometric transfer function,
![]() ,
in order to maintain the final peak-to-peak error per
pixel
,
in order to maintain the final peak-to-peak error per
pixel ![]()
![]() K (see
Appendix F).
During instrument-level
calibration activities, dedicated tests were performed to estimate
K (see
Appendix F).
During instrument-level
calibration activities, dedicated tests were performed to estimate
![]() and compare it with theoretical
estimates and similar tests performed on individual receivers.
and compare it with theoretical
estimates and similar tests performed on individual receivers.
5.3.1 Experimental setup
During this test, the focal plane temperature was varied in steps
between between 27 and 34 K. The sky and
reference load temperatures were
![]() K
and
K
and ![]() K.
The reference load
temperature showed a non-negligible coupling with the focal plane
temperature (as shown in
Fig. 9)
so that the effect of this variation had to be removed from the data
before calculating
the thermal transfer function.
K.
The reference load
temperature showed a non-negligible coupling with the focal plane
temperature (as shown in
Fig. 9)
so that the effect of this variation had to be removed from the data
before calculating
the thermal transfer function.
![\begin{figure}
\par\includegraphics[width=8.5cm]{12849fg15.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg60.png)
|
Figure 9: Behaviour of focal plane ( top), sky load ( middle), and reference load ( bottom) temperatures during the thermal susceptibility tests. |
| Open with DEXTER | |
Although the test lasted more than 24 h, it was difficult to reach a clean steady state plateau after each step because of the high thermal mass of the instrument. Furthermore, for some detectors the bias tuning was not yet optimised, so that only data from a subset of detectors could be compared with similar measurements performed at receiver-level.
In Fig. 10,
we summarise our results by comparing predicted and measured transfer
functions
for the tested detectors. Predicted transfer functions were calculated
using the list of parameters provided in
Appendix G,
derived from receiver-level tests. In the same figure, we also plot the
thermal susceptibility requirement rescaled to the experimental test
conditions with a scale factor given by the ratio
| (7) |
where
Figure 10 shows that transfer functions measured during instrument-level tests are compliant with scientific requirements and reflect theoretical predictions, with the exception of LFI22 and LFI23, which were more susceptible to front-end temperature fluctuations than expected. In general, results from the instrument-level test campaign confirm the design expectations, and suggest that the level of temperature instabilities in the focal plane will not represent a significant source of systematic errors in the final scientific products. This has been further verified during satellite thermal-vacuum tests conducted with the flight model sorption cooler (see Sect. 6.4).
![\begin{figure}\mbox{ \includegraphics[width=4.2cm]{12849fg16.ps} \includegraphic...
...2cm]{12849fg18.ps} \includegraphics[width=4.2cm]{12849fg19.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg62.png)
|
Figure 10: Measured and predicted radiometric thermal transfer functions, with the scientific requirement rescaled to the experimental conditions of the test. The comparison is possible only for the subset of radiometers that was tuned at the time of this test. |
| Open with DEXTER | |
6 Comparison with satellite-level test results
The final cryogenic ground test campaign was conducted at the Centre Spatial de Liège (CSL) with the LFI and the HFI integrated onboard Planck. To reproduce flight temperature conditions, the satellite was enclosed in an outer cryochamber cooled to liquid nitrogen temperatures, and surrounded by an inner thermal shield atDuring the CSL tests, we verified instrument functionality, tuned front-end biases and back-end electronics, and assessed scientific performance in the closest conditions to flight attainable on the ground. Front-end bias tuning made use of the ability of the 4 K cooler system to provide several different stable temperatures to the reference loads in the range of 24 K down to the nominal 4 K (Cuttaia et al. 2009).
A detailed description of satellite-level tests is beyond the scope of this paper; here we focus on the comparison of the main performance parameters measured during instrument and satellite tests, and show that despite differences in test conditions the overall behaviour was reproduced.
6.1 White noise sensitivity
Calibrated white noise sensitivities were determined during
satellite-level tests by exploiting a ![]() 80 mK
variation in the sky load temperature caused by the periodic helium
refills of the chamber. This variation allowed us
to estimate the photometric calibration constant by correlating the
differenced voltage datastream
80 mK
variation in the sky load temperature caused by the periodic helium
refills of the chamber. This variation allowed us
to estimate the photometric calibration constant by correlating the
differenced voltage datastream
![]() from
each detector with the sky load temperature
from
each detector with the sky load temperature
![]() (in antenna temperature units).
(in antenna temperature units).
To extrapolate the calibrated sensitivity from the
4.5 K input temperature in the test to flight conditions, we
calculated the ratio
using the noise temperature found from the non-linear model fit from the receiver-level test campaign (Villa et al. 2010). This ratio ranges from a minimum of
In Fig. 11, we summarise graphically the in-flight sensitivity estimates from the three tests. In the following plots the sensitivity values are provided with errorbars, with the following meanings:
- errorbars in sensitivities estimated from satellite-level data represent the statistical error in the calibration constants calculated from the various temperature jumps and propagated through the sensitivity formulas. They represent genuine statistical uncertainties;
- errorbars in sensitivities estimated from receiver and instrument level tests data represent the uncertainty coming from the calculation performed according to the two different methods described in Sect. 5.2.3 and Appendix D. In this case, errorbars do not have specific statistical significance, but nevertheless provide an indication of the uncertainties in the estimate.
After a thorough bias tuning activity conducted during in-flight calibration (see Cuttaia et al. 2009), a new bias configuration was found that normalised the white noise sensitivity of these two receivers, as expected. A full description of the in-flight calibration results and scientific performance will be given in a forthcoming dedicated paper.
![\begin{figure}\par\includegraphics[width=9cm]{12849fg20.ps}\\
\mbox{ }\\
\includegraphics[width=9cm]{12849fg21.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg66.png)
|
Figure 11: Summary of in-flight sensitivities per radiometer estimated from receiver, instrument, and satellite-level test campaigns. |
| Open with DEXTER | |
6.2 Noise stability
During satellite-level tests, receiver noise stability was determined from stable data acquisitions lasting several hours with the instruments in their tuned and nominal conditions. Figure 12 summarises 1/f knee frequencies measured at instrument and satellite levels compared with the 50 mHz requirement, and shows that the noise stability of all channels is within requirements, with the single marginal exception of LFI23S-11. The slope ranged from a minimum of 0.8 to a maximum of 1.7.
During satellite-level tests, there was substantial
improvement in the noise stability relative to instrument-level
tests, in some cases with a reduction in knee frequency of more than a
factor of 2. This can be partly explained by the
almost perfect signal input balance achieved in the CSL cryo-facility,
which was much less than 1 K compared to the
![]() 3 K
obtained in the instrument cryo-facility. Some improvement was also
expected because of the much
higher thermal stability of the CSL facility. In particular
fluctuations of the sky and reference loads in CSL were
about two order of magnitudes less than those in the instrument
facility
(see Table 3).
Because the highly balanced input achieved in CSL will
not be reproduced in-flight, we expect that the flight knee frequencies
will be slightly higher (although similar)
than those measured in CSL.
3 K
obtained in the instrument cryo-facility. Some improvement was also
expected because of the much
higher thermal stability of the CSL facility. In particular
fluctuations of the sky and reference loads in CSL were
about two order of magnitudes less than those in the instrument
facility
(see Table 3).
Because the highly balanced input achieved in CSL will
not be reproduced in-flight, we expect that the flight knee frequencies
will be slightly higher (although similar)
than those measured in CSL.
![\begin{figure}\par\mbox{\includegraphics[width=4.2cm]{12849fg22.ps} \includegrap...
...cm]{12849fg24.ps} \includegraphics[width=4.2cm]{12849fg25.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg67.png)
|
Figure 12: Summary of 1/f knee frequencies measured at instrument and satellite levels. |
| Open with DEXTER | |
6.3 Isolation
Isolation (see Eq. (B.3)) was measured during the satellite tests by changing the reference load temperature by 3.5 K. Figure 13 compares the isolation measured during receiver- and satellite-level tests. Several channels exceed the -13 dB requirement; a few are marginally below. One channel, LFI21S-1, showed poor isolation of only -7 dB. This result is consistent with the high value of the calibrated white noise measured for this channel (see Sect. 6.1), supporting the hypothesis of non-optimal biasing of that channel.
![\begin{figure}\par\mbox{\includegraphics[width=4.2cm]{12849fg26.ps} \includegrap...
...cm]{12849fg28.ps} \includegraphics[width=4.2cm]{12849fg29.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg68.png)
|
Figure 13: Summary of isolation measured at receiver and satellite levels. |
| Open with DEXTER | |
6.4 Thermal susceptibility
As mentioned in Sect. 4.3, the most important source of
temperature fluctuations in the LFI focal plane is the
sorption cooler. The satellite-level test provided the first
opportunity to measure the performance of the full Planck
thermal system. Fluctuations at the interface between the sorption
cooler and the LFI were measured to be about 100 mK
peak-to-peak. Using methods described in Mennella
et al. (2002), we infer that the effect of these
fluctuations will be
less than 1 ![]() K
per pixel in the maps, in line with the scientific requirements
outlined in Bersanelli
et al. (2010).
K
per pixel in the maps, in line with the scientific requirements
outlined in Bersanelli
et al. (2010).
Table 8: Best-fit non-linear model parameters.
Table 9: Impact of quantisation and compression on white noise sensitivity.
7 Conclusions
The LFI was integrated and tested in thermo-vacuum conditions at the Thales Alenia Space Italia laboratories, located in Vimodrone (Milano), during the summer of 2006. The test goals were a wide characterisation and calibration of the instrument, ranging from functionality to scientific performance assessment.The LFI was fully functional, apart from two failed components in LFI18M-0 and LFI24M-0 that have now been fixed (one replaced and the other repaired) after the cryogenic test campaign, recovering full functionality.
Measured instrument parameters are consistent with
measurements performed on individual receivers. In particular, the
LFI shows excellent 1/f stability and
rejection of instrumental systematic effects. Although the very
ambitious
sensitivity goals have not been fully met, the measured performance
makes LFI the most sensitive instrument of its kind,
a factor of 2 to 3 superior to WMAP![]() at
the same frequencies. In particular at 70 GHz, near the
minimum of the foreground emission for both temperature and
polarisation anisotropy, the combination of sensitivity and angular
resolution of LFI will provide a clean
reconstruction of the temperature power spectrum up to
at
the same frequencies. In particular at 70 GHz, near the
minimum of the foreground emission for both temperature and
polarisation anisotropy, the combination of sensitivity and angular
resolution of LFI will provide a clean
reconstruction of the temperature power spectrum up to
![]() (Mandolesi et al. 2010).
(Mandolesi et al. 2010).
After the instrument test campaign, the LFI was integrated with the HFI and the satellite. Between June and August 2008, Planck was tested at the CSL in flight-representative, thermo-vacuum conditions, and showed to be fully functional.
Planck was launched on May 14![]() from the Guyane Space Centre in Kourou and has reached its observation
point,
L2. In-flight testing and calibration is underway, and will provide the
final instrument tuning and scientific
performance assessment. After 17 years, Planck
is almost ready to begin recording the first light of the Universe.
from the Guyane Space Centre in Kourou and has reached its observation
point,
L2. In-flight testing and calibration is underway, and will provide the
final instrument tuning and scientific
performance assessment. After 17 years, Planck
is almost ready to begin recording the first light of the Universe.
The Planck-LFI project is developed by an Interntional Consortium lead by Italy and involving Canada, Finland, Germany, Norway, Spain, Switzerland, UK, USA. The Italian contribution to Planck is supported by the Italian Space Agency (ASI). The work in this paper has been supported by in the framework of the ASI-E2 phase of the Planck contract. The US Planck Project is supported by the NASA Science Mission Directorate. In Finland, the Planck-LFI 70 GHz work was supported by the Finnish Funding Agency for Technology and Innovation (Tekes).
Appendix A: LFI receiver and channel naming convention
The various receivers are labelled LFI18 to LFI28, as shown in Fig. A.1. The radiometers connected to the two OMT arms are labelled M-0 (``main'' OMT arm) and S-1 (``side'' OMT arm), while the two output detectors from each radiometer are labelled as 0 and 1. Therefore LFI18S-10, for example, refers to detector 0 of the side arm of receiver LFI18, and LFI24M-01 refers to detector 1 of the main arm of receiver LFI24.
![\begin{figure}\par\includegraphics[width=7.5cm,clip]{12849fg30.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg75.png)
|
Figure A.1: Feed horns in the LFI focal plane. Each feed horn is tagged by a label running from LFI18 to LFI28. LFI18 through LFI23 are 70 GHz receivers, LFI24 through LFI26 are 44 GHz receivers, and both LFI27 and LFI28 are 30 GHz receivers. |
| Open with DEXTER | |
Appendix B: Receiver isolation: definition, scientific
requirements, and measurements
B.1 Definition and requirement
In Sect. 2,
it is shown that the output of the LFI pseudo-correlation
receivers is a sequence of sky and reference load signals alternating
at twice the phase switch frequency. If the
pseudo-correlator is not ideal, the separation after the second hybrid
is not perfect and a certain level of mixing
between the two signals will be present in the output. Typical
limitations on isolation are (i) imperfect hybrid phase
matching; (ii) front-end gain amplitude mismatch; and (iii) mismatch in
the insertion loss in the two switch states
(Seiffert et al. 2002).
A more general relationship representing the receiver power output can
be written as
where the parameter
We now consider the receiver scanning the sky and therefore
measuring a variation in the sky signal given
by the CMB, ![]() .
If we define
.
If we define
![]() and
develop Eq. (B.1)
in series up to the first order in
and
develop Eq. (B.1)
in series up to the first order in ![]() ,
we see that the
differential power output is proportional to
,
we see that the
differential power output is proportional to
| (B.2) |
where
If we assume 10% (corresponding to
![]() )
as the maximum acceptable loss in the CMB signal due to imperfect
isolation and consider typical values for the LFI receivers (
)
as the maximum acceptable loss in the CMB signal due to imperfect
isolation and consider typical values for the LFI receivers (
![]() K and
K and
![]() ranging from 10 to 30 K), we find
ranging from 10 to 30 K), we find
![]() equivalent to -13 dB, which corresponds to the requirement for
LFI receivers.
equivalent to -13 dB, which corresponds to the requirement for
LFI receivers.
B.2 Measurement
If ![]() and
and ![]() are the voltage output variations induced by
are the voltage output variations induced by
![]() ,
then it is easy to see from Eq. (B.1)
(with the approximation
,
then it is easy to see from Eq. (B.1)
(with the approximation
![]() )
that
)
that
If the reference load temperature is not perfectly stable but varies by an amount
Measuring the isolation accurately, however, is generally difficult and requires a very stable environment. Any change in
To estimate the accuracy in our isolation measurements, we
first calculated the uncertainty caused by a systematic
error in the reference load voltage output,
![]() .
If we substitute in
Eq. (B.4)
.
If we substitute in
Eq. (B.4)
![]() with
with
![]() and develop an expression to first order in
and develop an expression to first order in
![]() ,
we obtain
,
we obtain
where we indicate by
We estimated ![]() in our measurement conditions. Because the three temperature steps were
implemented
in about one day, we evaluated the total power signal stability on this
timescale from a long-duration acquisition
in which the instrument was left running undisturbed for about two
days. For each detector datastream, we first
removed spurious thermal fluctuations by performing a correlation
analysis with temperature sensor data then we
calculated the peak-to-peak variation in the reference load datastream.
in our measurement conditions. Because the three temperature steps were
implemented
in about one day, we evaluated the total power signal stability on this
timescale from a long-duration acquisition
in which the instrument was left running undisturbed for about two
days. For each detector datastream, we first
removed spurious thermal fluctuations by performing a correlation
analysis with temperature sensor data then we
calculated the peak-to-peak variation in the reference load datastream.
Appendix C: Calculation of noise effective bandwidth
The well-known radiometer equation applied to the output of a single diode in the Planck-LFI receivers links the white noise sensitivity to sky and noise temperatures and the receiver bandwidth. It reads (Seiffert et al. 2002)
In the case of a linear response, i.e., if
which is commonly used to estimate the receiver bandwidth,
If the response is linear and the noise is purely radiometric (i.e., all the additive noise from back-end electronics is negligible and there are no non-thermal noise inputs from the source), then
In contrast, if the receiver output is compressed, from Eq. (2) we have that
By combining Eqs. (2), (C.3) and (C.5) we find that
which shows that
Appendix D: White noise sensitivity calibration and extrapolation to flight conditions
We now detail the calculation needed to convert the uncalibrated white
noise sensitivity measured on the ground to
the expected calibrated sensitivity for in-flight conditions. The
calculation starts from the general radiometric output
model in Eq. (2),
which can be written in the following form
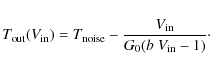
|
(D.1) |
Our starting point is the raw datum, which is a couple of uncalibrated white noise levels for the two detectors in a radiometer measured with the sky load at a temperature
From the measured uncalibrated white noise level in
Volt s1/2, we attempt to derive a
calibrated white noise
level extrapolated to input temperature equal to
![]() and with the front.end unit at a temperature of
and with the front.end unit at a temperature of
![]() .
This is achieved in three steps:
.
This is achieved in three steps:
- 1.
- extrapolation to nominal front-end unit temperature;
- 2.
- extrapolation to nominal input sky temperature;
- 3.
- calibration in units of K s1/2.
D.1 Step 1-extrapolate uncalibrated noise to nominal front end unit temperature
This is a non-trivial step to be performed if we wich to consider all the elements in the extrapolation. Here we focus on a zero-order approximation based on the following assumptions:
- 1.
- the radiometer noise temperature is dominated by the
front-end noise temperature, such that
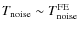 ;
;
- 2.
- we neglect any effect on the noise temperature given by resistive losses of the front-end passive components;
- 3.
- we assume the variation in
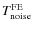 to be linear in
to be linear in
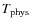 .
.
where
From the radiometer equation we have that
where
![\begin{displaymath}\eta = \frac{\partial T_{\rm noise}^{\rm FE}}
{\partial T_{\...
..._{\rm noise}(T_{\rm test}))\right]^{-1}
\Delta T_{\rm phys}.
\end{displaymath}](/articles/aa/full_html/2010/12/aa12849-09/img129.png)
|
(D.5) |
D.2 Step
2 - extrapolate uncalibrated noise to
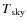
From this point, we consider quantities such as
![]() ,
white noise level, and G0,
extrapolated to
the nominal front-end temperature using Eqs. (D.2),
(D.3),
and (D.4).
Therefore, we now omit the superscript ``nom'' so that, for example,
,
white noise level, and G0,
extrapolated to
the nominal front-end temperature using Eqs. (D.2),
(D.3),
and (D.4).
Therefore, we now omit the superscript ``nom'' so that, for example,
![]() .
.
We now start from the radiometer equation in which, for each
detector, the white noise spectral density is given by
We now attempt to find a similar relationship for the uncalibrated white noise spectral density linking
where
If we refer to
D.3 Step 4-calibrate extrapolated noise
From Eqs. (D.7)
and (2),
we obtain
If we call
![\begin{displaymath}\sigma^{\rm cal} = \frac{\left[1+b~ G_0(T_{\rm sky}+T_{\rm noise})\right]^2}{G_0} \sigma.
\end{displaymath}](/articles/aa/full_html/2010/12/aa12849-09/img143.png)
|
(D.11) |
Appendix E: Weighted noise averaging
According to the LFI receiver design, the output from each radiometer
is produced by combinating signals from two corresponding detector
diodes. We consider two differenced and calibrated datastreams coming
from two detectors of a radiometer leg, d1(t)
and d2(t).
The simplest way to combine the two outputs is to take a straight
average, i.e.,
so that the white noise level of the differenced datastream is given by
An alternative to Eq. (E.1)
is given by a weighted average in which weights are represented by the
inverse of the noise levels of the two diode datasteams, i.e.,
or, more generally, in the case where we average more than two datastreams,
For noise-weighted averaging, we choose the weights
Appendix F: Thermal susceptibility scientific requirement
Temperature fluctuations in the LFI focal plane arise primarily from
variations in the sorption cooler system
driven by the cycles of the six cooler compressors that ``pump''![]() the hydrogen in the
high-pressure piping line towards the cooler cold-end. These
fluctuations exhibit a frequency spectrum dominated by a
period of
the hydrogen in the
high-pressure piping line towards the cooler cold-end. These
fluctuations exhibit a frequency spectrum dominated by a
period of ![]() 1 h,
corresponding to the global warm-up/cool-down cycle of the six
compressors.
1 h,
corresponding to the global warm-up/cool-down cycle of the six
compressors.
An active PID temperature stabilisation assembly at the
interface between the cooler cold-end and the focal
plane, achieves stabilities of the order of 80-100 mK
peak-to-peak with a frequency spectrum dominated by the single
compressor frequency (![]() 1 mHz)
and the frequency of the whole assembly (
1 mHz)
and the frequency of the whole assembly (![]() 0.2 mHz).
0.2 mHz).
These fluctuations propagate through the focal plane
mechanical structure, so that the true temperature
instabilities at the level of the feed-amplifier systems (the term
![]() in
Eq. (6))
are significantly damped. The LFI thermal model (Tomasi et al. 2010)
shows that the fluctuations in the front-end modules are of the level
of
in
Eq. (6))
are significantly damped. The LFI thermal model (Tomasi et al. 2010)
shows that the fluctuations in the front-end modules are of the level
of ![]() 10 mK
and dominated by the
``slowest'' components (i.e., those with frequencies
10 mK
and dominated by the
``slowest'' components (i.e., those with frequencies ![]() 10-2 Hz).
10-2 Hz).
If we take into account that slow fluctuations in the antenna
temperature time stream are damped further by a
factor ![]() 103
by the scanning strategy and map-making (Mennella
et al. 2002), we can easily see from
Eq. (6)
that a receiver susceptibility
103
by the scanning strategy and map-making (Mennella
et al. 2002), we can easily see from
Eq. (6)
that a receiver susceptibility
![]() is required
to maintain the final peak-to-peak error per pixel
is required
to maintain the final peak-to-peak error per pixel ![]()
![]() K.
K.
Appendix G: Front-end temperature susceptibility parameters
Temperature susceptibility parameters are summarised in Table G.1.
Table G.1: Temperature susceptibility parameters.
References
- Bersanelli, M., Cappellini, B., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhandari, P., Prina, M., Bowman, R. C., et al. 2004, Cryogenics, 44, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Cuttaia, F., Menella, A., Stringhetti, L., et al. 2009, JINST, 4, T12013 [NASA ADS] [Google Scholar]
- Davis, R., Wilkinson, A., Davies, R., et al. 2009, JINST, 4, T12002 [NASA ADS] [Google Scholar]
- Daywitt, W. 1989, Radiometer equation and analysis of systematic errors for the NIST automated radiometers, Tech. Rep. NIST/TN-1327, NIST [Google Scholar]
- Dupac, X., & Tauber, J. 2005, A&A, 430, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandolesi, N., Bersanelli, M.., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- Maris, M., Maino, D., Burigana, C., et al. 2004, A&A, 414, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, P., Riti, J.-B., & de Chambure, D. 2004, in 5th International Conference on Space Optics, ed. B. Warmbein, ESA SP, 554, 323 [Google Scholar]
- Meinhold, P., Leonardi, R., Aja, B., et al. 2009, JINST, 4, T12009 [Google Scholar]
- Mennella, A., Bersanelli, M., Burigana, C., et al. 2002, A&A, 384, 736 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennella, A., Bersanelli, M., Seiffert, M., et al. 2003, A&A, 410, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennella, A., Villa, F., Terenzi, L., et al. 2009, JINST, 4, T12011 [NASA ADS] [Google Scholar]
- Seiffert, M., Mennella, A., Burigana, C., et al. 2002, A&A, 391, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauber, J. A., Norgaard-Nielsen, H. U., Ade, P. A. R., et al. 2010, A&A, 520, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terenzi, L., Lapolla, M., Laaninen, M., et al. 2009a, JINST, 4, T12015 [NASA ADS] [Google Scholar]
- Terenzi, L., Salmon, M., Colin, A., et al. 2009b, JINST, 4, T12012 [Google Scholar]
- Tomasi, M., Cappellini, B., Gregorio, A., et al. 2010, JINST, 5, T01002 [Google Scholar]
- Valenziano, L., Cuttaia, F., De Rosa, A., et al. 2009, JINST, 4, T12006 [Google Scholar]
- Varis, J., Hughes, N., Laaninen, M., et al. 2009, JINST, 4, T12001 [NASA ADS] [Google Scholar]
- Villa, F., Bersanelli, M., Burigana, C., et al. 2002, in Experimental Cosmology at Millimetre Wavelengths, ed. M. de Petris, & M. Gervasi, AIP Conf. Ser., 616, 224 [Google Scholar]
- Villa, F., Terenzi, L., Sandri, M., et al. 2010, A&A, 520, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, L., Bhandari, P., Bowman, J. R., et al. 2000, in Advances in Cryogenic Engineering, 45A, ed. Q.-S. Shu et al. (Kluwer Academic/Plenum New York), 499 [Google Scholar]
- Zonca, A., Franceschet, C., Battaglia, P., et al. 2009, JINST, 4, T12010 [Google Scholar]
Footnotes
- ...Planck
![[*]](/icons/foot_motif.png)
- Planck http://www.esa.int/Planck is a project of the European Space Agency - ESA - with instruments provided by two scientific Consortia funded by ESA member states (in particular the lead countries: France and Italy) with contributions from NASA (USA), and telescope reflectors provided in a collaboration between ESA and a scientific Consortium led and funded by Denmark.
- ... 15 months
![[*]](/icons/foot_motif.png)
- There are enough consumables onboard to allow operation for an additional year.
- ...)
![[*]](/icons/foot_motif.png)
- The slight compression found in the output of the 30 and 44 GHz receivers is caused by the back-end amplifier and diode, which operated in the same conditions during both test campaigns.
- ...)
![[*]](/icons/foot_motif.png)
- The test can be conducted, in principle, also by changing the reference load temperature. In the instrument cryofacility, however, this was not possible because only the sky load temperature could be controlled.
- ...
diode
![[*]](/icons/foot_motif.png)
- The additional noise introduced by the analog electronics is generally negligible compared to the intrisic noise of the receiver, and its impact was further mitigated by the variable gain stage after the diode.
- ... WMAP
![[*]](/icons/foot_motif.png)
- Calculated for the final resolution element per unit integration time.
- ... ``pump''
![[*]](/icons/foot_motif.png)
- The sorption cooler does not use mechanical compressors to generate a high pressure flow, but a process of absorption-desorption of hydrogen into six hydride beds, the ``compressors'' being controlled by a temperature modulation of the beds themselves.
All Tables
Table 1: Main instrument parameters and stages at which they have been measured.
Table 2: Summary of main thermal conditions.
Table 3: LFI cryo-facility thermal performance.
Table 4: Main temperatures during basic calibration.
Table 5:
White noise sensitivities per radiometer in
![]() .
.
Table 6:
White noise sensitivities per frequency channel in ![]() K
K![]() s1/2.
s1/2.
Table 7: Summary of knee frequency and slope.
Table 8: Best-fit non-linear model parameters.
Table 9: Impact of quantisation and compression on white noise sensitivity.
Table G.1: Temperature susceptibility parameters.
All Figures
![\begin{figure}\par\includegraphics[width=8cm]{12849fg1.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg8.png)
|
Figure 1: Schematic of the LFI pseudo-correlation architecture. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=8cm]{12849fg2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg11.png)
|
Figure 2: LFI cryo-chamber facility. The LFI is mounted face-down with the feed horn array facing the eccosorb sky-load. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\mbox{ \includegraphics[width = 4.3cm]{12849fg3.ps} \includegr...
...{12849fg5.ps} \includegraphics[width = 4.3cm]{12849fg6.ps} }
\par
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg27.png)
|
Figure 3: Summary of measured isolation compared with the same measurements performed at receiver level (Villa et al. 2010). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=15.5cm,clip]{12849fg7n.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg33.png)
|
Figure 4: Amplitude spectral densities of unswitched and differenced data streams. The pseudo-correlation differential design reduces the 1/f knee frequency by three orders of magnitude. The white noise level scales almost perfectly with K. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width = 8.8 cm]{12849fg8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg45.png)
|
Figure 5: Thermal instabilities during the long duration acquisition. Top: drift in the reference load temperature caused by leakage in the gas cap thermal switch. The drop towards the end of the test coincides with refill of the thermal switch. Bottom: 24-h back-end temperature fluctuation. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{12849fg9.eps}
\vspace{-3mm} \end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg46.png)
|
Figure 6: Calibrated differential radiometric outputs (downsampled to 1 Hz) for all LFI detectors during the long duration test. Temperature sensor data in antenna temperature units are superimposed (thin black line) on the calibrated radiometric data. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12849fg10.ps}
\vspace{-3mm}\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg47.png)
|
Figure 7: Noise effective bandwidths calculated during instrument-level measurements. The three lines indicate the 70 GHz, 44 GHz, and 30 GHz requirements. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}(a)\includegraphics[width=8cm]{12849fg11.eps}\\
\vspace{0.4cm}
...
....4cm}
(d)\includegraphics[width=8cm]{12849fg14.eps}
\vspace{-2mm}\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg50.png)
|
Figure 8:
DAE-only and radiometer noise amplitude density spectra in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{12849fg15.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg60.png)
|
Figure 9: Behaviour of focal plane ( top), sky load ( middle), and reference load ( bottom) temperatures during the thermal susceptibility tests. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\mbox{ \includegraphics[width=4.2cm]{12849fg16.ps} \includegraphic...
...2cm]{12849fg18.ps} \includegraphics[width=4.2cm]{12849fg19.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg62.png)
|
Figure 10: Measured and predicted radiometric thermal transfer functions, with the scientific requirement rescaled to the experimental conditions of the test. The comparison is possible only for the subset of radiometers that was tuned at the time of this test. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=9cm]{12849fg20.ps}\\
\mbox{ }\\
\includegraphics[width=9cm]{12849fg21.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg66.png)
|
Figure 11: Summary of in-flight sensitivities per radiometer estimated from receiver, instrument, and satellite-level test campaigns. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\mbox{\includegraphics[width=4.2cm]{12849fg22.ps} \includegrap...
...cm]{12849fg24.ps} \includegraphics[width=4.2cm]{12849fg25.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg67.png)
|
Figure 12: Summary of 1/f knee frequencies measured at instrument and satellite levels. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\mbox{\includegraphics[width=4.2cm]{12849fg26.ps} \includegrap...
...cm]{12849fg28.ps} \includegraphics[width=4.2cm]{12849fg29.ps} }
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg68.png)
|
Figure 13: Summary of isolation measured at receiver and satellite levels. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=7.5cm,clip]{12849fg30.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12849-09/Timg75.png)
|
Figure A.1: Feed horns in the LFI focal plane. Each feed horn is tagged by a label running from LFI18 to LFI28. LFI18 through LFI23 are 70 GHz receivers, LFI24 through LFI26 are 44 GHz receivers, and both LFI27 and LFI28 are 30 GHz receivers. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010



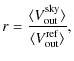
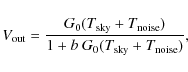
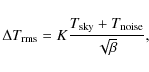
![\begin{displaymath}\beta = {(K V_{\rm DC} / \sigma_{\rm V})^2 \over \left[ 1 + b~ G_0(T_{\rm sky}+T_{\rm noise})\right]^{2}},
\end{displaymath}](/articles/aa/full_html/2010/12/aa12849-09/img36.png)
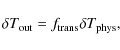
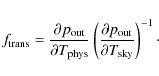

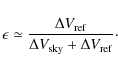
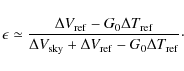
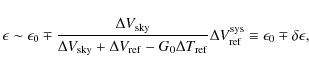
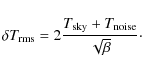
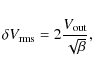
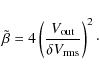

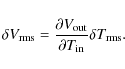
![$\displaystyle 4\left(\frac{T_{\rm sky}+T_{\rm noise}}{\delta T_{\rm rms}}\right)^2
\left[ 1 + b~ G_0(T_{\rm sky}+T_{\rm noise})\right]^2$](/articles/aa/full_html/2010/12/aa12849-09/img109.png)

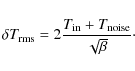
![\begin{displaymath}\sigma=\frac{V_{{\rm out}}}{\sqrt{\beta }}\left[1+
b~ G_0\left(T_{{\rm in}}+T_{\rm noise}\right)\right]^{-1},
\end{displaymath}](/articles/aa/full_html/2010/12/aa12849-09/img134.png)
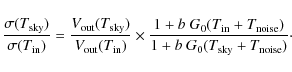
![\begin{displaymath}\rho = \frac{
T_{\rm sky}+T_{\rm noise}}{T_{\rm in}+T_{\rm n...
... noise})}{1+b~ G_0
(T_{\rm sky}+T_{\rm noise})}\right]^2\cdot
\end{displaymath}](/articles/aa/full_html/2010/12/aa12849-09/img139.png)