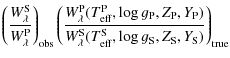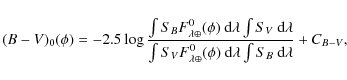| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 57 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200810284 | |
| Published online | 05 October 2010 | |
VLT multi-object spectroscopy of 33 eclipsing binaries in the Small Magellanic Cloud
New distance and depth of the SMC, and a
record-breaking apsidal motion![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
P. North1 - R. Gauderon1 - F. Barblan2 - F. Royer3
1 - Laboratoire d'astrophysique, École Polytechnique Fédérale de
Lausanne (EPFL),
Observatoire de Sauverny, 1290 Versoix, Switzerland
2 - Geneva Observatory, Geneva University, 1290 Sauverny, Switzerland
3 - GEPI, UMR 8111 du CNRS, Observatoire de Paris-Meudon, 92195 Meudon
Cedex, France
Received 29 May 2008 / Accepted 12 May 2010
Abstract
Aims. Our purpose is to provide reliable stellar
parameters for a significant sample of eclipsing binaries, which are
representative of a whole dwarf and metal-poor galaxy. We also aim at
providing a new estimate of the mean distance to the SMC and of its
depth along the line of sight for the observed field of view.
Methods. We use radial velocity curves obtained with
the ESO FLAMES facility at the VLT and light curves from the OGLE-II
photometric survey. The radial velocities were obtained by
least-squares fits of the observed spectra to synthetic ones, excluding
the hydrogen Balmer lines.
Results. Our sample contains 23 detached,
9 semi-detached and 1 overcontact systems. Most
detached systems have properties consistent with stellar evolution
calculations from single-star models at the standard SMC metalicity Z
= 0.004, though they tend to be slightly overluminous. The few
exceptions are probably due to third-light contribution or insufficient
signal-to-noise ratio. The mass ratios are consistent with a flat
distribution, both for detached and semi-detached/contact binaries.
A mass-luminosity relation valid from ![]() 4 to
4 to ![]() 18
18
![]() is derived. The uncertainties are in the
is derived. The uncertainties are in the ![]() 2 to
2 to ![]() 11%
range for the masses, in the
11%
range for the masses, in the ![]() 2 to
2 to ![]() 5%
range for the radii and in the
5%
range for the radii and in the ![]() 1 to
1 to ![]() 6%
range for the effective temperatures. The average distance modulus is
19.11
6%
range for the effective temperatures. The average distance modulus is
19.11 ![]() 0.03 (66.4
0.03 (66.4 ![]() 0.9 kpc). The moduli derived from the V
and from the I data are consistent within
0.01 mag. The
0.9 kpc). The moduli derived from the V
and from the I data are consistent within
0.01 mag. The ![]() depth
of the SMC is, for our field, of 0.25 mag or 7.6 kpc
under the assumption of a Gaussian distribution of stars along the line
of sight. Three systems show significant apsidal motion, one of them
with an apsidal period of 7.6 years, the shortest known to
date for a detached system with main sequence stars.
depth
of the SMC is, for our field, of 0.25 mag or 7.6 kpc
under the assumption of a Gaussian distribution of stars along the line
of sight. Three systems show significant apsidal motion, one of them
with an apsidal period of 7.6 years, the shortest known to
date for a detached system with main sequence stars.
Key words: stars: early-type - binaries: eclipsing - binaries: spectroscopic - stars: fundamental parameters - Magellanic Clouds - stars: distances
1 Introduction
Since the late 1990s, the usefulness of extragalactic eclipsing binaries has been emphasized in a number of papers. The reader can notably refer to the excellent reviews from Clausen (2004) and Guinan (2004, 2007). The two major contributions of eclipsing binaries (hereafter EBs) to astrophysics are to provide first of all fundamental mass and radius measurements for the component stars, which are needed to test stellar evolution models, and second precise distance moduli (DMi). The latter are obtained from the luminosities that in turn are computed from the absolute radii and effective temperatures. Until a purely geometrical distance determination is feasible, Paczynski (2001) considers that detached EBs are the most promising distance indicators to the Magellanic Clouds. Besides, Wyithe & Wilson (2002, hereafter WW02) remarked that semi-detached EBs are even more promising, because their parameters are better constrained.
The renewed interest in extragalactic EBs, especially EBs in the Magellanic Clouds, has been stimulated by the release of a huge number of light curves as a byproduct of automated microlensing surveys (EROS, MACHO, OGLE) with 1-m class telescopes. As photometry is only half the story, high-resolution spectrographs attached to 4-m class or larger telescopes had to be used to obtain reliable radial velocity (RV) curves. Four B-type EB systems belonging to the Large Magellanic Cloud (LMC) were accurately characterized in a series of papers from Guinan et al. (1998), Ribas et al. (2000, 2002) and Fitzpatrick et al. (2002, 2003). More recently, from high resolution, high S/N spectra obtained with UVES at the ESO VLT, the analysis of eight more LMC systems was presented by González et al. (2005). A corner stone in the study of EBs in the SMC was set up with the release of two papers from Harries et al. (2003, hereafter HHH03) and Hilditch et al. (2005, hereafter HHH05), giving the fundamental parameters of a total of 50 EB systems of spectral types O and B. The spectroscopic data were obtained with the 2dF multi-object spectrograph on the 3.9-m Anglo-Australian Telescope. To our knowledge this is the first use of multi-object spectroscopy in the field of extragalactic EBs. Recently, even the distance to large spiral galaxies were measured on the basis of two EBs in M31 (Ribas et al. 2005; Vilardell et al. 2010) and one in M 33 (Bonanos et al. 2006).
The huge asymmetry between the number of EB light curves published so far and the very small number of RV curves is striking. If one considers the SMC, the new OGLE-II catalog of EBs in the SMC (Wyrzykowski et al. 2004) contains 1350 light curves, and currently only 50 of these systems have moderately reliable RV curves. This paper reduces this imbalance a little by releasing the analysis of 28 more EB systems plus revised solutions for 5 systems previously described by HHH03 and HHH05. The RV measurements were derived from muti-object spectroscopic observations made with the VLT FLAMES facility.
Another strong motivation for increasing the number of fully
resolved binaries is to settle the problem of the distribution of the
mass ratio of detached binaries with early B primaries.
Recently, two papers were published supporting different conclusions:
van Rensbergen et al. (2006),
whose work is based on the 9th Catalogue of Spectroscopic
Binaries (Pourbaix et al. 2004),
support the view that the q-distribution
(where q is the mass ratio) follows a
decreasing power law (
![]() );
however, from the examination of the homogeneous sample of the
21 detached systems characterized by HHH03 and HHH05,
Pinsonneault & Stanek
(2006) draw the
conclusion that the proportion of close detached systems with mass
ratio q > 0.87 far outnumbers what can be
expected from either a Salpeter or a flat q-distribution
(the ``twins'' hypothesis). Finally, let us mention
that the q-distribution of semi-detached
(i.e. evolved) systems is no more settled, the statistics
strongly depending on the method used to find the mass ratios,
i.e. from the light curve solution or from
SB2 spectra (van Rensbergen et al. 2006).
);
however, from the examination of the homogeneous sample of the
21 detached systems characterized by HHH03 and HHH05,
Pinsonneault & Stanek
(2006) draw the
conclusion that the proportion of close detached systems with mass
ratio q > 0.87 far outnumbers what can be
expected from either a Salpeter or a flat q-distribution
(the ``twins'' hypothesis). Finally, let us mention
that the q-distribution of semi-detached
(i.e. evolved) systems is no more settled, the statistics
strongly depending on the method used to find the mass ratios,
i.e. from the light curve solution or from
SB2 spectra (van Rensbergen et al. 2006).
Although the controversy about the characteristic distance to the SMC seems to be solved in favor of a mid position between the ``short'' and the ``long'' scales, distance data and line-of-sight depth remain vital for a comparison with theoretical models concerning the three-dimensional structure and the kinematics of the SMC (Stanimirovic et al. 2004).
Our contribution provides both qualitative and quantitative improvements over previous studies. Thanks to the VLT GIRAFFE facility, spectra were obtained with a resolution three times that in HHH03/05's study. Another strong point is the treatment of nebular emission. The SMC is known to be rich in H II regions (Fitzpatrick 1985; Torres & Carranza 1987). Consequently, strong Balmer lines in emission are very often present in the spectra of the binary systems under study. Therefore, it was rapidly clear that it was essential to find a consistent way to deal with this ``third component'' polluting most double-lined (SB2) spectra.
We present the observations in Sect. 2. The reduction of the spectroscopic data and the interpretation of both photometric and spectroscopic data are described in Sect. 3, where the errors are also discussed in detail. The sample as a whole is discussed in relation with the SMC properties in Sect. 4, while the individual binary systems are described in the Appendix.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{10284fg1.eps}
\vspace*{6.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg29.png)
|
Figure 1:
Positions of the 33 binaries in the 1
|
| Open with DEXTER | |
2 Observations
The targets, astrometry included, were selected from the first OGLE
photometric catalog. The GIRAFFE field of view (FoV) constrained to
choose systems inside a 25![]() -diameter
circle. Other constraints were
-diameter
circle. Other constraints were ![]() mag, at least
15 well-behaved detached light curves (for the SMC field) and
finally seven bump cepheids in the FoV (for another program). The
positions in the sky of 33 objects studied in this paper are
shown in Fig. 1.
The epoch, exposure time, air mass, seeing and age of moon for each of
the 16 CCD frames are gathered in Table 1.
mag, at least
15 well-behaved detached light curves (for the SMC field) and
finally seven bump cepheids in the FoV (for another program). The
positions in the sky of 33 objects studied in this paper are
shown in Fig. 1.
The epoch, exposure time, air mass, seeing and age of moon for each of
the 16 CCD frames are gathered in Table 1.
The relation between our own 1-33 labeling and the OGLE names can be found in Table 3, which lists the basic parameters of the systems. The coordinates are from Wyrzykowski et al. (2004). The orbital periods and epochs of the primary minimum are close to those listed by Wyrzykowski et al. (2004), but the periods were improved as far as possible with the radial velocity curves determined in this work. That was worth the effort, because spectroscopic observations were performed more than three years after the last photometric ones. The times of the photometric minima are quite sharply defined, which means that the uncertainty on the period (mentioned between parentheses in Table 3) is based on the uncertainty of the spectroscopically defined epoch of the primary minimum. The latter is quite precise for circular orbits; for eccentric orbits, it is less accurate, because the Kepler equation had to be solved and the solution is affected by the uncertainty on the eccentricity. We have decided here to adopt the dynamic definition of the primary and secondary components, rather than the photometric one. In other words, the primary component is always the more massive one, and the primary minimum always corresponds to the eclipse of the primary by the secondary component. As a consequence, it may happen that the so-called primary minimum is not the deeper one. Figure 2 shows the histogram of the periods. The strong observational bias in favor of short periods is conspicuous.
For all but two binaries, the light curves come from the new version of the OGLE-II catalog of eclipsing binaries detected in the SMC (Wyrzykowski et al. 2004). This catalog is based on the Difference Image Analysis (DIA) catalog of variable stars in the SMC (see http://sirius.astrouw.edu.pl/ ogle/ogle2/smc_ecl/index.html). The data were collected from 1997 to 2000. The systems 4 121084 and 5 100731 were selected from the first version of the catalog (standard PSF photometry), but for an unknow reason they do not appear anymore in the new version. Nevertheless, they were retained as there is no objective reason to exclude them.
The DIA photometry is based on I-band
observations (between 202 and 312 points per curve). B and
V light curves were also used in spite of a
much poorer sampling (between 22-28 points/curve and
28-46 points/curve in B
and V respectively). To give an
idea of the accuracy of the OGLE photometry,
the objects studied here have an average I magnitude
and scatter in the range 15.083 ![]() 0.009 to 18.159
0.009 to 18.159 ![]() 0.047. These values were calculated from the best-fitting synthetic
light curves. For the two other bands, we get 14.701
0.047. These values were calculated from the best-fitting synthetic
light curves. For the two other bands, we get 14.701 ![]() 0.011 to 18.090
0.011 to 18.090 ![]() 0.025 for B and 14.966
0.025 for B and 14.966 ![]() 0.009 to 18.173
0.009 to 18.173 ![]() 0.023 for V. The quality of an observed
light curve can be better expressed by comparing the depth of the
primary minimum
0.023 for V. The quality of an observed
light curve can be better expressed by comparing the depth of the
primary minimum
![]() to the average rms scatter
to the average rms scatter ![]() .
These ratios are shown in Table 16. This permits
us to classify the light curves into five categories: low
(
.
These ratios are shown in Table 16. This permits
us to classify the light curves into five categories: low
(
![]() ),
low-to-medium (
),
low-to-medium (
![]() ),
medium (
),
medium (
![]() ),
medium-to-high (
),
medium-to-high (
![]() )
and high (
)
and high (
![]() )
quality. According to this scheme, most I-band
light curves (58%) belong to the low-to-medium and medium
quality categories, one-third (33%) in the medium-to-high and
high quality categories, and the remaining 9% in the poor
quality category. This classification scheme is not useful for the
other bands, the low sampling is the limiting factor.
)
quality. According to this scheme, most I-band
light curves (58%) belong to the low-to-medium and medium
quality categories, one-third (33%) in the medium-to-high and
high quality categories, and the remaining 9% in the poor
quality category. This classification scheme is not useful for the
other bands, the low sampling is the limiting factor.
The VLT FLAMES/GIRAFFE spectroscopy was obtained by one of us
(FR) during eight consecutive nights from
2003 November 16 to 23. The spectrograph was
used in the low resolution (LR2) Medusa mode: resolving power R=6400,
bandwidth ![]() Å
centered on 4272 Å. The most prominent absorption lines in the
blue part of early-B stars spectra are: H
Å
centered on 4272 Å. The most prominent absorption lines in the
blue part of early-B stars spectra are: H![]() ,
He I
,
He I
![]() ,
H
,
H![]() ,
He I
,
He I
![]() ,
H
,
H![]() ,
He I
,
He I
![]() ,
and He I
,
and He I
![]() .
For late-O stars, He II
.
For late-O stars, He II
![]() and He II
and He II
![]() gain in importance. Two fields, one in the SMC and one in the LMC, were
observed in turn at a rate of four exposures per night with an
integration time of 2595 s for all but one epoch. Thus we
attained 16 spectra per target, with a total of
104 targets in the SMC and 44 in the LMC. The LMC
SB2 systems are being analyzed and will be presented in
another paper.
gain in importance. Two fields, one in the SMC and one in the LMC, were
observed in turn at a rate of four exposures per night with an
integration time of 2595 s for all but one epoch. Thus we
attained 16 spectra per target, with a total of
104 targets in the SMC and 44 in the LMC. The LMC
SB2 systems are being analyzed and will be presented in
another paper.
Beside the spectra of the objects, 21 sky spectra
were obtained for each exposure in the SMC. The parameters related to
the spectroscopic observations are gathered in Table 1. The observed
signal-to-noise ratios (S/N)
were determined for each smoothed spectrum (see
Sect. 3.1)
in the continuum between 4195 and 4240 Å. Two values
are presented in Table 11
for each object: the highest and lowest S/N values
for an exposure of 2595 s. Not surprisingly, the short
exposure of 707 s (due to a technical problem) was useful for
the brightest objects only. For a given binary with ![]() s,
the ratio of the
highest S/N to the
lowest S/N is
s,
the ratio of the
highest S/N to the
lowest S/N is ![]() 2.
2.
Table 1: Spectroscopic observations: epochs, heliocentric Julian dates at mid exposure, exposure times and sky conditions.
3 Data reductions and analysis
3.1 Spectroscopic data reduction
The basic reduction and calibration steps including velocity correction
to the heliocentric reference frame for the spectra were performed with
the GIRAFFE Base Line Data Reduction Software (BLDRS) (see
http://girbldrs.sourceforge.net). Sky subtraction, a critical step for
faint objects, was done as follows: for each epoch an average sky
spectrum was computed from the 21 sky spectra measured over
the whole FoV. For a given epoch the sky level was found to vary
slightly across the field, but interpolating between spectra was not
considered a valuable alternative. Local sky variations with respect to
the average spectrum are given in Table 8. The
values
![]() are read as follows: for example, the sky position labeled S19 is on
average (i.e. over all epochs)
are read as follows: for example, the sky position labeled S19 is on
average (i.e. over all epochs) ![]() 20% brighter than the mean
(i.e. over all sky positions) sky spectrum. The variations were found
to be between about -11 and +35%. Normalization to the
continuum, cosmic-rays removal and Gaussian smoothing (
20% brighter than the mean
(i.e. over all sky positions) sky spectrum. The variations were found
to be between about -11 and +35%. Normalization to the
continuum, cosmic-rays removal and Gaussian smoothing (
![]() pix) were performed
with standard NOAO/PyRAF tasks.
pix) were performed
with standard NOAO/PyRAF tasks.
The first 60 Å of the spectra, i.e. for wavelengths
between 3940 and 4000 Å, were suppressed. The reason
is that below ![]() 4000 Å
the S/N is getting very poor and
therefore there is no reliable way to place the continuum. Furthermore,
the region around H
4000 Å
the S/N is getting very poor and
therefore there is no reliable way to place the continuum. Furthermore,
the region around H![]() was found to be strongly contaminated by the interstellar Ca II H
and K absorption lines. The last few Å
(above 4565 Å) were found equally unusable because of
a strongly corrupted signal.
was found to be strongly contaminated by the interstellar Ca II H
and K absorption lines. The last few Å
(above 4565 Å) were found equally unusable because of
a strongly corrupted signal.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10284fg2.eps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg52.png)
|
Figure 2: Histogram of periods of our sample of 33 eclipsing binaries in 0.5 day bins. |
| Open with DEXTER | |
3.2 Analysis
For historical reasons, the analysis has been made in essentially two steps.First, RG did a complete analysis of all systems, using the
KOREL code (Hadrava 1995,
2004) to obtain
both the radial velocity curves and the separated spectra of the
individual components. Then, the simultaneous analysis of light and RV
curves was made with the 2003 version of the Wilson-Devinney (WD)
Binary Star Observables Program (Wilson & Devinney 1971; Wilson 1979, 1990) via the PHOEBE
interface (Prsa & Zwitter 2005).
However, simulations performed following the referee's request
regarding this early version of the work showed that the
amplitude ![]() of the RV curve and the mass ratio
of the RV curve and the mass ratio ![]() were not recovered with the expected robustness. More details about
these simulations are given below (Sect. 3.5.1).
Although on average the proper values are recovered, one particular
solution may be off by as much as five percent (one sigma) or
ten percent (two sigma), which was deemed unsatisfactory
were not recovered with the expected robustness. More details about
these simulations are given below (Sect. 3.5.1).
Although on average the proper values are recovered, one particular
solution may be off by as much as five percent (one sigma) or
ten percent (two sigma), which was deemed unsatisfactory![]() .
.
Thus, a second, almost independent analysis was made by PN,
using a least-squares fit of synthetic binary spectra to observed unsmoothed
spectra for the RV determinations. The latter technique seemed
much more robust according to the same simulation: the ![]() and
and ![]() amplitudes
were recovered to better than one percent - at least for the
particular binary that was simulated - and the dispersion of
the values of the small eccentricity (
amplitudes
were recovered to better than one percent - at least for the
particular binary that was simulated - and the dispersion of
the values of the small eccentricity (
![]() )
is no
higher than two percent. Small systematic errors may result from
temperature or rotation mismatch, but they remain smaller than the
uncertainties of the previous analysis.
)
is no
higher than two percent. Small systematic errors may result from
temperature or rotation mismatch, but they remain smaller than the
uncertainties of the previous analysis.
We took the opportunity of this new analysis to define a more objective determination of the effective temperatures of the components. Instead of a visual fit of a spectrum close to quadrature, we used a least-squares fit of synthetic binary spectra to all observed spectra falling out of eclipses. Then, the error on the effective temperatures could be naturally defined as the rms scatter of the results. More details are given in the next sections and in the following discussion of individual binaries.
3.3 Photometry: quality check
The quality of the I-band light curves was
discussed in Sect. 2.
Despite the high range of rms scatter, we can expect a very
accurate determination of the out-of-eclipse I-magnitude
because of the large number of data points (![]() 300). This is not the case
with the B- and V-bands.
A much poorer sampling can lead to erroneous zero-level
computation in the light-curve analysis step and result in wrong
color-index determination. Therefore, it is necessary to
perform a quality check
of the photometric data. This was done in the form of color-color
diagrams of our sample. Figure 3 presents
the three diagrams that can be obtained from the three color
indices
300). This is not the case
with the B- and V-bands.
A much poorer sampling can lead to erroneous zero-level
computation in the light-curve analysis step and result in wrong
color-index determination. Therefore, it is necessary to
perform a quality check
of the photometric data. This was done in the form of color-color
diagrams of our sample. Figure 3 presents
the three diagrams that can be obtained from the three color
indices
![]() ,
,
![]() and
and
![]() .
These are the values at quadratures, i.e. an average value
characterizing a ``hybrid'' star of intermediate properties with
respect to the two components of a particular system. Not surprisingly,
most binaries are found on a relatively narrow linear strip.
For any diagram, the scatter of the objects is low because the
reddening line is almost parallel to the sequence. For example, the
ratio EB-V
/ EV-I
= 0.81, determined from Eq. (11) in
Sect. 3.12,
is close to 0.69, the slope of the
sequence
.
These are the values at quadratures, i.e. an average value
characterizing a ``hybrid'' star of intermediate properties with
respect to the two components of a particular system. Not surprisingly,
most binaries are found on a relatively narrow linear strip.
For any diagram, the scatter of the objects is low because the
reddening line is almost parallel to the sequence. For example, the
ratio EB-V
/ EV-I
= 0.81, determined from Eq. (11) in
Sect. 3.12,
is close to 0.69, the slope of the
sequence
![]() vs.
vs. ![]() .
Nevertheless, four outliers appear, which are marked with open symbols.
In principle there is a possibility to restore a bad color
index, as illustrated by the example of the
system 5 261267: inspecting the three light curves,
one can suspect that the cause of the discrepancy lies in a poorly
sampled V-band light curve in the out-of-eclipse
domain. The other two light curves (B and I)
seem more reliable. Therefore, only the B-I color-index
is reliable for this system. But the two other indices, B-V
and V-I, can safely be
interpolated from the B-I value
under the assumption that the system lies on the linear strip. The
method is illustrated by the dashed lines in the diagrams.
Of course, this reconstruction of two bad indices from a good
one is not possible, unless only one of the three light curves is
unreliable (either B or V).
In this particular example, the situation is not so clear-cut because
the reconstructed indices (
B-V=-0.129
and V-I=-0.139)
would imply a
.
Nevertheless, four outliers appear, which are marked with open symbols.
In principle there is a possibility to restore a bad color
index, as illustrated by the example of the
system 5 261267: inspecting the three light curves,
one can suspect that the cause of the discrepancy lies in a poorly
sampled V-band light curve in the out-of-eclipse
domain. The other two light curves (B and I)
seem more reliable. Therefore, only the B-I color-index
is reliable for this system. But the two other indices, B-V
and V-I, can safely be
interpolated from the B-I value
under the assumption that the system lies on the linear strip. The
method is illustrated by the dashed lines in the diagrams.
Of course, this reconstruction of two bad indices from a good
one is not possible, unless only one of the three light curves is
unreliable (either B or V).
In this particular example, the situation is not so clear-cut because
the reconstructed indices (
B-V=-0.129
and V-I=-0.139)
would imply a ![]() value
that is too low. Therefore, all four outliers will be excluded from the
final estimate of the distance modulus.
value
that is too low. Therefore, all four outliers will be excluded from the
final estimate of the distance modulus.
On the upper right diagram of Fig. 3, red crosses indicate the intrinsic colors computed below (Sect. 3.11). Their positions, slightly below the regression line of the sequence, is entirely compatible with the reddening arrow and the observed colors, which inspires confidence regarding the color excesses determined in Sect. 3.11.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg61.png)
|
Figure 3: Observed (reddened) color-color diagrams of our sample. These are the brightest out-of-eclipse values from Table 3. They were determined from the best light-curve fits. The low scatter is due to a reddening line almost parallel to the main sequence (see upper right panel). Note that some values (open symbol) are doubtful as they lie off the linear trend. The dashed lines illustrate how to recover correct B-V and V-I indices from doubtful ones, under the assumption that the B-I index is reliable, for the system 5 261267. |
| Open with DEXTER | |
3.4 Synthetic spectra
Except for the first two steps of the analysis, i.e. (a) the simultaneous ``disentangling'' of the composite spectra and retrieving of the RV curves through the KOREL code (Hadrava 1995, 2004) and (b) the simultaneous analysis of the light and RV curves through the WD/PHOEBE code, the search for the parameters of a binary relies heavily on synthetic spectra. Indeed, the systemic velocity, the projected rotational velocities, the ratio of radii, and the primary temperature are found by comparing the observed spectra (separated and composite) with a library of synthetic spectra. Actually, two libraries were used. For objects with effective temperatureThe grids with a metalicity suitable for the SMC, Z
= 0.004, i.e. one-fifth of the solar metalicity, were chosen.
Concerning the BSTAR2006 library, we took the grid with a
microturbulent
velocity of 2 km s-1. Both
grids of spectra are based on NLTE line-blanketed model atmospheres.
The temperature step is 1000 K below ![]() and 2500 K for early-O stars. We
restrained to surface gravities
and 2500 K for early-O stars. We
restrained to surface gravities ![]() (0.25 dex step). The spectra were convolved with the
appropriate rotational profiles (
(0.25 dex step). The spectra were convolved with the
appropriate rotational profiles (
![]() =
30, 40, 50, 75, 100, 150, 200, 250 and 300 km s-1)
and with a Gaussian instrumental profile (resolution of
0.67 Å) by means of the program ROTIN3
(http://nova.astro.umd.edu/Synspec43/synspec-frames-rotin.html).
Besides a grid of continuum-normalized spectra, a grid of flux spectra
was generated for color indices calculation through synthetic
photometry.
=
30, 40, 50, 75, 100, 150, 200, 250 and 300 km s-1)
and with a Gaussian instrumental profile (resolution of
0.67 Å) by means of the program ROTIN3
(http://nova.astro.umd.edu/Synspec43/synspec-frames-rotin.html).
Besides a grid of continuum-normalized spectra, a grid of flux spectra
was generated for color indices calculation through synthetic
photometry.
Formally, a normalized synthetic composite spectrum is
computed at a given orbital phase ![]() from the normalized j-component spectra
from the normalized j-component spectra ![]() ,
the radial velocities of both components
,
the radial velocities of both components
![]() and the light dilution factors
and the light dilution factors
![]() :
:
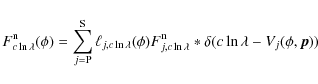
|
(1) |
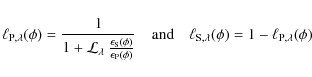
|
(2) |
where
|
(3) |
We checked that
3.5 Radial velocities
As explained above (Sect. 3.2), the radial velocities were determined with two independent methods. As a first step, a ``disentangling'' method was used, which allowed us to give a first estimate of the parameters of all systems. As a second and final step, a least-squares method was used. Each step is described below.
3.5.1 First step: spectrum ``disentangling''
Simon & Sturm (1994)
were the first to propose a method allowing the simultaneous recovery
of the individual spectra of the components and of the radial
velocities. Another method aimed at the same results, but using Fourier
transforms to save computing time, was proposed almost simultaneously
by Hadrava (1995).
The advantages of these methods are that they need no hypothesis about
the nature of the components of the binary system, except that their
individual spectra remain constant with time. Contrary to the
correlation techniques, no template is needed.
In addition to the radial velocities and orbital elements, one
gets the individual spectra of the
components (``disentangling''), with a signal-to-noise ratio which
significantly exceeds that of the observed composite spectra.
For instance, for a binary system with two components of equal
brightness and observed 16 times with S/N=50,
the signal-to-noise ratio of each separated spectrum would be S/N=4 ![]() 50
50 ![]() 0.5=100 (the factor 0.5 takes account of the two
components). That is important, because the nature of the components
can then be determined safely. In this work we use this
advantage to determine the effective temperatures of some components,
but for brighter binaries observed at higher resolution and S/N,
it would also be possible to determine photospheric
abundances. Other details about these techniques and their applications
(including abundance determinations) can be found in e.g. Hensberge
et al. (2000),
Pavlovski & Hensberge (2005)
and Hensberge & Pavlovski (2007).
0.5=100 (the factor 0.5 takes account of the two
components). That is important, because the nature of the components
can then be determined safely. In this work we use this
advantage to determine the effective temperatures of some components,
but for brighter binaries observed at higher resolution and S/N,
it would also be possible to determine photospheric
abundances. Other details about these techniques and their applications
(including abundance determinations) can be found in e.g. Hensberge
et al. (2000),
Pavlovski & Hensberge (2005)
and Hensberge & Pavlovski (2007).
The radial velocities were determined from the lines of He I
(![]() 4471,
4471, ![]() 4388,
4388, ![]() 4144,
4144, ![]() 4026) only.
We preferred to avoid the H Balmer lines (as did
Fitzpatrick et al. 2002)
because their large width makes them more sensitive to systematics due
e.g. to wrong placement of the continuum, and because of
moderate to strong nebular emission polluting most systems (only
6/33 systems were found devoid of any emission). Consequently,
four regions with a width of 80 Å centered on the four He I lines
were cut from each spectrum of the series.
Since the KOREL code uses the Fourier transform of the spectra, both
edges of each spectral region were fixed to 1 by hammering of
the signal to 1 with a cosine bell function (Hanning window).
KOREL was run with out-of-eclipse spectra only, although the
line-strength factors, i.e. the contributions of each
component to the system continuum, could in principle be obtained as
results of the KOREL analysis. However, for most of our spectra the S/N
was too low to provide reliable results. Therefore,
the selection was performed with the out-of-eclipse phase
ranges given by the light curves. The period P
was taken from Table 3
and has slightly improved values compared to those of Wirzykowski
et al. (2004),
as explained in Sect. 2.
A first estimate of the epoch of periastron passage T0,
of the eccentricity e and of the
longitude of periastron
4026) only.
We preferred to avoid the H Balmer lines (as did
Fitzpatrick et al. 2002)
because their large width makes them more sensitive to systematics due
e.g. to wrong placement of the continuum, and because of
moderate to strong nebular emission polluting most systems (only
6/33 systems were found devoid of any emission). Consequently,
four regions with a width of 80 Å centered on the four He I lines
were cut from each spectrum of the series.
Since the KOREL code uses the Fourier transform of the spectra, both
edges of each spectral region were fixed to 1 by hammering of
the signal to 1 with a cosine bell function (Hanning window).
KOREL was run with out-of-eclipse spectra only, although the
line-strength factors, i.e. the contributions of each
component to the system continuum, could in principle be obtained as
results of the KOREL analysis. However, for most of our spectra the S/N
was too low to provide reliable results. Therefore,
the selection was performed with the out-of-eclipse phase
ranges given by the light curves. The period P
was taken from Table 3
and has slightly improved values compared to those of Wirzykowski
et al. (2004),
as explained in Sect. 2.
A first estimate of the epoch of periastron passage T0,
of the eccentricity e and of the
longitude of periastron
![]() were determined from the light curves. For the eccentric systems, a
first solution was found neglecting apsidal motion. The only orbital
parameters allowed to converge were the primary semi-amplitude
were determined from the light curves. For the eccentric systems, a
first solution was found neglecting apsidal motion. The only orbital
parameters allowed to converge were the primary semi-amplitude ![]() and the mass ratio q. For each system,
KOREL was run with a grid of values
and the mass ratio q. For each system,
KOREL was run with a grid of values
![]() .
The solution with the minimum sum of squared residuals as defined by
Hadrava (2004)
was retained as the best solution. For eccentric systems,
a second run was performed letting
.
The solution with the minimum sum of squared residuals as defined by
Hadrava (2004)
was retained as the best solution. For eccentric systems,
a second run was performed letting ![]() , q,
T0 and
, q,
T0 and ![]() free to converge (e is determined by
photometry). We note that the four spectral regions were analyzed
simultaneously, i.e. in a single run of KOREL. Each region was
weighted according to the S/N of
each He I line (
free to converge (e is determined by
photometry). We note that the four spectral regions were analyzed
simultaneously, i.e. in a single run of KOREL. Each region was
weighted according to the S/N of
each He I line (
![]() ).
To circumvent the difficulty of measuring
the S/Ns inside the lines, they
were estimated from the values calculated with the GIRAFFE
Exposure Time Calculator of the ESO. The calculated values were then
normalized to the measured value between 4195 and
4240 Å. The non-Keplerian correction and Rossiter effect were
calculated from the WD/PHOEBE solution.
).
To circumvent the difficulty of measuring
the S/Ns inside the lines, they
were estimated from the values calculated with the GIRAFFE
Exposure Time Calculator of the ESO. The calculated values were then
normalized to the measured value between 4195 and
4240 Å. The non-Keplerian correction and Rossiter effect were
calculated from the WD/PHOEBE solution.
Beside the simultaneous retrieving of RV curves, orbital
parameters and separated spectra, the KOREL code is able to separate
the spectra for a given orbital solution (![]() ,
q, T0
and
,
q, T0
and ![]() fixed). A final run of KOREL with this mode was then used to
distinguish the regions around the Balmer and He II 4200
and 4542 lines. Indeed, He II lines
and a number of Si III-IV lines
are very useful to set the temperature of hot components.
fixed). A final run of KOREL with this mode was then used to
distinguish the regions around the Balmer and He II 4200
and 4542 lines. Indeed, He II lines
and a number of Si III-IV lines
are very useful to set the temperature of hot components.
3.5.2 Testing the robustness by simulations
In order to test possible biases on the determination of ![]() and q by KOREL, we simulated ten sets of
nine out-of-eclipse composite spectra of the
system 5 266131. We used the fitted radial velocity
curves to shift the synthetic spectra of each component and added them
at the observed
phases with the adopted luminosity ratio in the B band.
We used the synthetic spectra with parameters closest to the observed
ones from the grid of Munari et al. (2005).
A Gaussian noise was added to the composite synthetic spectra,
so that the signal-to-noise ratio varied from 37
to 71 (see Table 11) and assuming
that the S/N ratio is
inversely proportional to the seeing given in Table 1. The KOREL code
was run on each of these ten simulated datasets, and the averages of
the resulting
and q by KOREL, we simulated ten sets of
nine out-of-eclipse composite spectra of the
system 5 266131. We used the fitted radial velocity
curves to shift the synthetic spectra of each component and added them
at the observed
phases with the adopted luminosity ratio in the B band.
We used the synthetic spectra with parameters closest to the observed
ones from the grid of Munari et al. (2005).
A Gaussian noise was added to the composite synthetic spectra,
so that the signal-to-noise ratio varied from 37
to 71 (see Table 11) and assuming
that the S/N ratio is
inversely proportional to the seeing given in Table 1. The KOREL code
was run on each of these ten simulated datasets, and the averages of
the resulting
![]() and q values were computed. We found
and q values were computed. We found ![]() and
and ![]() instead of the input values 223.4
instead of the input values 223.4 ![]()
![]() and 0.889
and 0.889 ![]() 0.039 respectively. The simulation then gives
0.039 respectively. The simulation then gives ![]() instead of the input 263.0
instead of the input 263.0 ![]()
![]() .
Thus, the parameters obtained from the simulated spectra agree with the
input value to within
.
Thus, the parameters obtained from the simulated spectra agree with the
input value to within ![]() ,
which means that there is no danger of a significant systematic error.
However, the rms scatter of the
,
which means that there is no danger of a significant systematic error.
However, the rms scatter of the
![]() and q parameters proved disappointingly
large, about
and q parameters proved disappointingly
large, about
![]() and 0.044 respectively. This means that the uncertainty on the
RV amplitude reaches about 5%, which translates
into 15% for the masses.
and 0.044 respectively. This means that the uncertainty on the
RV amplitude reaches about 5%, which translates
into 15% for the masses.
3.5.3 Second step: least-squares RV determination
On the basis of the first analysis, we selected two synthetic spectra
from the OSTAR2002 and BSTAR2006 libraries for the two components of
each system, with the parameters closest to the estimations.
A chi-square was computed as the quadratic sum of the
differences between the observed spectrum and the composite synthetic
one for arbitrary radial velocities. However, we did not use the
complete spectra: the hydrogen Balmer lines were suppressed because of
their extended width and because they were mixed with nebular emission
in a number of cases. A SuperMongo (Lupton & Monger 2000) procedure
implementing the amoeba minimization algorithm was
used, letting the two radial velocities and the blue intensity ratio
free to converge. The radial velocities are essentially constrained by
five He I lines (
![]() ,
4026, 4144, 4388 and 4471).
Convergence was generally fast and robust, in the sense that
the results did not depend on the initial guess values. Some iterations
were necessary, however, to clearly identify the primary and
secondary components, so that the proper model was attributed
to the proper component.
,
4026, 4144, 4388 and 4471).
Convergence was generally fast and robust, in the sense that
the results did not depend on the initial guess values. Some iterations
were necessary, however, to clearly identify the primary and
secondary components, so that the proper model was attributed
to the proper component.
A preliminary analysis of the radial velocities was then performed with an interactive code (Lucke & Mayor 1980), which allowed us to assess the quality of the RV curves (especially the rms scatter of the residuals) and obtain first orbital elements.
3.5.4 Simulations
The same ten sets of nine composite synthetic spectra described above
were used to test the least-squares method of
RV determination. The results proved very encouraging, because
they follow distributions whose sigma amounts to only 0.8
and 0.6% of the means for the amplitudes ![]() and
and ![]() respectively. The sigma of the eccentricity distribution
is 1.8% of e=0.036,
and the argument of the periastron has
respectively. The sigma of the eccentricity distribution
is 1.8% of e=0.036,
and the argument of the periastron has ![]() .
.
The effect of a mismatch was tested through template spectra
with effective temperatures lower by 3300 K, respectively
4080 K for the primary and secondary components, compared to
the temperatures used to build the artificial ``observed'' spectra (the
projected rotational velocities were also lower by about
40 km s-1). The amplitudes
changed by +1.1, resp. +0.3% only for the
primary and secondary components. Increasing the temperatures
by 2700, resp. 1860 K (and the ![]() by 40 km s-1) lead to relative
differences
by 40 km s-1) lead to relative
differences ![]() %
and
%
and ![]() %.
Thus, the mismatch that can be expected will not induce
systematic errors much larger than about one percent, which is in
general smaller than the random
error. Because of its robustness we adopted the least-squares technique
for the RV determination rather than the results of the KOREL
code. However, we are aware that the above comparison between the two
techniques may not be quite fair, because the KOREL code recovers the
individual spectra from the data, while the least-squares fit uses
external template spectra. In that sense the advantage of the
least-squares fit may prove somewhat artificial.
%.
Thus, the mismatch that can be expected will not induce
systematic errors much larger than about one percent, which is in
general smaller than the random
error. Because of its robustness we adopted the least-squares technique
for the RV determination rather than the results of the KOREL
code. However, we are aware that the above comparison between the two
techniques may not be quite fair, because the KOREL code recovers the
individual spectra from the data, while the least-squares fit uses
external template spectra. In that sense the advantage of the
least-squares fit may prove somewhat artificial.
3.6 Apsidal motion
The WD code allows us to determine the time derivative
![]() of the argument of the periastron. That possibility was used for all
eccentric systems but one 4 175333, which has the lowest
eccentricity of all. The systems for which a significant apsidal motion
was found in that way were examined further by subdividing the
photometric data into four consecutive time series, which we analyzed
with an interactive version of the EBOP16 code (Etzel 1980). The
of the argument of the periastron. That possibility was used for all
eccentric systems but one 4 175333, which has the lowest
eccentricity of all. The systems for which a significant apsidal motion
was found in that way were examined further by subdividing the
photometric data into four consecutive time series, which we analyzed
with an interactive version of the EBOP16 code (Etzel 1980). The ![]() angle
(if precise enough) and the
angle
(if precise enough) and the ![]() quantities
ajusted for each time series were then examined for systematic
variation. That allowed us to better visualize the effect of apsidal
motion on the light curves and to better assess its significance.
quantities
ajusted for each time series were then examined for systematic
variation. That allowed us to better visualize the effect of apsidal
motion on the light curves and to better assess its significance.
3.7 Wilson-Devinney analysis
3.7.1 First step
For each system, a preliminary photometric solution had been found
(before taking the radial velocities into account) by the application
of the method of multiple subsets (MMS) (Wilson & Biermann 1976). The groups of
subsets used were essentially the same as those advocated by Wyithe
& Wilson (2001,
2002)
(Table 2).
![]() , t0,
, t0,
![]() and q
were fixed; e was fixed to 0 for
clearly non-eccentric systems; a could be
included in any subset because it does not correlate with any other
parameter. That allowed us to provide fairly
precise values of e and
and q
were fixed; e was fixed to 0 for
clearly non-eccentric systems; a could be
included in any subset because it does not correlate with any other
parameter. That allowed us to provide fairly
precise values of e and ![]() which were then introduced into the KOREL analysis. Then, all three
light curves and both RV curves provided by KOREL were
simultaneously analyzed with the WD code. That does not imply
though that photometric and spectroscopic data were analyzed in a
really simultaneous way, because the results from the preliminary light
curve analysis were used in the KOREL analysis; it is rather
an iterative analysis. The I light curve
is the most constraining one, thanks to the large number of points, but
the B and V light
curves are very important too, because they provide accurate
out-of-eclipse B and V magnitudes.
The mass ratio q was fixed to the value
found by KOREL. The semi-major orbital axis a,
treated as a free parameter, allows us to scale the masses and radii.
In a first run, the temperature of the primary was
arbitrarily fixed to 26 000 K. Second-order
parameters such as albedos and gravity darkening exponents were fixed
to 1.0. Metallicities
which were then introduced into the KOREL analysis. Then, all three
light curves and both RV curves provided by KOREL were
simultaneously analyzed with the WD code. That does not imply
though that photometric and spectroscopic data were analyzed in a
really simultaneous way, because the results from the preliminary light
curve analysis were used in the KOREL analysis; it is rather
an iterative analysis. The I light curve
is the most constraining one, thanks to the large number of points, but
the B and V light
curves are very important too, because they provide accurate
out-of-eclipse B and V magnitudes.
The mass ratio q was fixed to the value
found by KOREL. The semi-major orbital axis a,
treated as a free parameter, allows us to scale the masses and radii.
In a first run, the temperature of the primary was
arbitrarily fixed to 26 000 K. Second-order
parameters such as albedos and gravity darkening exponents were fixed
to 1.0. Metallicities
![]() were set at -0.5. The limb-darkening coefficients of the
logarithmic law were automatically interpolated after each fit from the
van Hamme tables (van Hamme 1993).
The code needs an estimation of the standard deviations of the observed
curves in order to assign a weight to each curve. These
were set at -0.5. The limb-darkening coefficients of the
logarithmic law were automatically interpolated after each fit from the
van Hamme tables (van Hamme 1993).
The code needs an estimation of the standard deviations of the observed
curves in order to assign a weight to each curve. These ![]() 's were
calculated from the sums of squares of residuals of the individual
curves, as advocated by Wilson and van Hamme (2004). These values
were refined for subsequent runs.
's were
calculated from the sums of squares of residuals of the individual
curves, as advocated by Wilson and van Hamme (2004). These values
were refined for subsequent runs.
Table 2: Method of multiple subsets: groups of parameters allowed to converge for each model.
A finetuning run was performed with the primary temperature found after analyzing the observed spectra. The standard uncertainties of the whole set of parameters were estimated in a final iteration by letting them free to converge.
Table 3: Basic parameters of the observed eclipsing binaries: identifying number (Fig. 1), OGLE identifying code, coordinates, orbital period, epoch of primary minimum (see text), infrared and (B-V) and (V-I) color indices.
The standard procedure described above is sufficient for
symmetric light curves only. For systems with a small
depression before the primary minimum, which is occasionally the case
with semi-detached systems, it is necessary to introduce a cool spot
onto the primary component. Obviously, this step is performed after
obtaining the symmetric best-fit solution. The spot is characterized by
four parameters, i.e. colatitude, longitude, angular radius
and temperature factor. Because the observed feature can be described
by a large number of combinations of the four parameters related to the
spot (high degeneracy), the spot was arbitrarily put onto the equator
of the primary (i.e. colatitude of ![]() ), and the
three other parameters were optimized alternately
following the MMS. If there was a high propensity to diverge,
one of the three free parameters was set to an arbitrary value, and the
MMS was performed on the two remaining parameters.
), and the
three other parameters were optimized alternately
following the MMS. If there was a high propensity to diverge,
one of the three free parameters was set to an arbitrary value, and the
MMS was performed on the two remaining parameters.
In this first step, the WD analysis was performed with the
photometric convention, according to which the primary star is the one
that is eclipsed near phase zero, i.e. the star with the
higher mean surface brightness in a given passband (
![]() ).
It followed that in some cases q
may not necessarily be
).
It followed that in some cases q
may not necessarily be ![]() .
We finally adopted the dynamic convention
.
We finally adopted the dynamic convention ![]() in order to avoid confusion.
in order to avoid confusion.
The orbit was considered as circular for the detached systems when the eccentricity given by the WD code was lower than its estimated error.
3.7.2 Second step
Both photometric and RV curves were simultaneously analyzed, fixing the
effective temperature of the primary component to the spectroscopic
value (see below for the determination of the latter).
For semi-detached and contact systems, there is no need to fix
any other parameter. For detached systems, however, the ratio
of radii is very poorly constrained by photometry alone when the
eclipses are partial, which is the case of all detached systems in our
sample. Therefore, we adopted the brightness ratio determined by
spectroscopy, and fixed the potential of the primary,
![]() ,
to a value for which the brightness ratio in the blue band
matched the spectroscopic one within the uncertainties. The potential
depends on both radius and mass, but the latter is constrained by the
RV curve, so that fixing a potential is equivalent to
fixing a radius. In some cases it was not possible to
reproduce the spectroscopic brightness ratio without degrading the
photometric fit, so we gave priority to the latter.
,
to a value for which the brightness ratio in the blue band
matched the spectroscopic one within the uncertainties. The potential
depends on both radius and mass, but the latter is constrained by the
RV curve, so that fixing a potential is equivalent to
fixing a radius. In some cases it was not possible to
reproduce the spectroscopic brightness ratio without degrading the
photometric fit, so we gave priority to the latter.
3.8 Systemic velocity and projected rotational velocities
3.8.1 First step
The component spectra of the four regions centered on the He I lines
were normalized with the help of the KORNOR program (Hadrava 2004). The systemic
velocity
![]() was found from the separated spectra of the four regions centered on
the He I lines. The observed
spectra were cross-correlated via the IRAF
was found from the separated spectra of the four regions centered on
the He I lines. The observed
spectra were cross-correlated via the IRAF
![]() task against synthetic spectra computed for the estimated
task against synthetic spectra computed for the estimated
![]() ,
,
![]() and
and
![]() .
The
.
The ![]() values were obtained
as the S/N-weighted averages of
the individual velocities calculated for each line.
values were obtained
as the S/N-weighted averages of
the individual velocities calculated for each line.
The projected rotational velocities, ![]() ,
were tentatively measured by calibrating the full widths at
half-maximum (hereafter FWHM) of the He I lines
against a grid of (FWHM,
,
were tentatively measured by calibrating the full widths at
half-maximum (hereafter FWHM) of the He I lines
against a grid of (FWHM, ![]() ) values
obtained from synthetic spectra (Hensberge et al. 2000). The FWHMs
were computed from Gaussian or Voigt profiles
fitting via the IRAF
) values
obtained from synthetic spectra (Hensberge et al. 2000). The FWHMs
were computed from Gaussian or Voigt profiles
fitting via the IRAF ![]() task. The
task. The ![]() values
retrieved by this method were often found unsatisfactory when comparing
observed and synthetic spectra retrospectively. The problem was the
high sensitivity of the FWHM measurement to the
continuum placement. Therefore, a synchronous rotational velocity was
assumed for most circular binaries unless profile fitting proved this
hypothesis wrong. In any case, this assumption is certainly justified
for short-period systems, i.e. binaries with
values
retrieved by this method were often found unsatisfactory when comparing
observed and synthetic spectra retrospectively. The problem was the
high sensitivity of the FWHM measurement to the
continuum placement. Therefore, a synchronous rotational velocity was
assumed for most circular binaries unless profile fitting proved this
hypothesis wrong. In any case, this assumption is certainly justified
for short-period systems, i.e. binaries with ![]() (North & Zahn 2003),
where the ratio (R/a) is
the star radius divided by the separation. For eccentric
systems, pseudo-synchronization was assumed (Mazeh 2008,
Eq. (5.1)). For a given star, its pseudo-synchronous
rotational velocity is computed from its radius and the
pseudo-synchronization frequency of the binary. This equilibrium
frequency, which is close to the orbital periastron frequency, is given
in Hut (1981).
(North & Zahn 2003),
where the ratio (R/a) is
the star radius divided by the separation. For eccentric
systems, pseudo-synchronization was assumed (Mazeh 2008,
Eq. (5.1)). For a given star, its pseudo-synchronous
rotational velocity is computed from its radius and the
pseudo-synchronization frequency of the binary. This equilibrium
frequency, which is close to the orbital periastron frequency, is given
in Hut (1981).
3.8.2 Second step
Contrary to the first step, when the KOREL code was used, we do not need to define the systemic velocity a posteriori here. The least-squares method directly provides ``absolute'' radial velocities (i.e. not only relative ones), even though mismatch might bias them by a few km s-1. Thus the systemic velocity (given in Table 11) naturally flows from the WD analysis, which includes the RV curves.
As in the first step, rotational velocities were derived from the assumption of synchronous (for circular orbits) or pseudo-synchronous (for eccentric orbits) spin motion. No clear departure from this assumption could be seen on the spectra.
3.9 Spectroscopic luminosity and ratio of radii
3.9.1 First step
As mentioned above, and as emphasized repeatedly by Andersen
et al. (e.g. 1980)
and rediscovered by Wyithe & Wilson (2001, hereafter WW01),
the ratio of radii ![]() of an EB with partial eclipses is poorly constrained by its
light curve. The ratio of monochromatic luminosities
of an EB with partial eclipses is poorly constrained by its
light curve. The ratio of monochromatic luminosities
![]() is equally poorly recovered in fitting light curves of simulated EBs
(i.e. EBs with previously known parameters). On the contrary,
the surface brightness ratio and consequently the derived effective
temperature ratio
is equally poorly recovered in fitting light curves of simulated EBs
(i.e. EBs with previously known parameters). On the contrary,
the surface brightness ratio and consequently the derived effective
temperature ratio
![]() is,
in general, reliably recovered. The sum of the radii
is,
in general, reliably recovered. The sum of the radii
![]() is also very well constrained. The poor constraining of k
is very well illustrated by Fig. 3 in
González et al. (2005).
is also very well constrained. The poor constraining of k
is very well illustrated by Fig. 3 in
González et al. (2005).
Because our sample comprises only systems with partial
eclipses,
![]() ,
k must be determined to find reliable radii
and surface gravities. We followed the procedure described in González
et al. (2005).
The ratio of the monochromatic luminosities can be expressed by
Eq. (4)
(Hilditch 2001):
,
k must be determined to find reliable radii
and surface gravities. We followed the procedure described in González
et al. (2005).
The ratio of the monochromatic luminosities can be expressed by
Eq. (4)
(Hilditch 2001):
where Rj is the radius,
For given masses, metallicities and helium abundances, it should in principle be possible to derive a purely spectroscopic solution for the two radii and the two effective temperatures, from the analysis of a set of four lines. If we further assume that the sum of the radii is known from the light-curves analysis as well as the temperature ratio, the analysis of only two lines is sufficient to determine a mixed photometric-spectroscopic ratio of radii. However, because EWs are sensitive to a possible continuum misplacement, we preferred to fit the observed line profiles with a synthetic composite spectrum or to determine the ratio of the EWs of two different lines in the same component. The latter methods are more reliable than a blind application of Eq. (4) to estimate the effective temperatures, at least for spectra with moderate S/N.
For a given chemical composition, true undiluted EWs depend on
both the effective temperature and the surface gravity of the stars.
Moreover, this dependence is not always monotonic even if we restrict
the sample to late O and early B stars, because the
He I lines have a maximum strength
at ![]() 20 000 K.
Consequently, in order to avoid the hassle of working with
non-explicit equations, for a given line, Eq. (4) was solved
with the photometric temperature ratio and the true EW values
corresponding to the photometric
20 000 K.
Consequently, in order to avoid the hassle of working with
non-explicit equations, for a given line, Eq. (4) was solved
with the photometric temperature ratio and the true EW values
corresponding to the photometric ![]() and a first guess of
and a first guess of ![]() .
.
![]() ,
,
![]() and
a first
guess of
and
a first
guess of
![]() are then used to compute the ratio of radii k.
Combining k and
are then used to compute the ratio of radii k.
Combining k and ![]() ,
the new Rj
and
,
the new Rj
and ![]() values are obtained
straightforwardly. The small error introduced into the chain
values are obtained
straightforwardly. The small error introduced into the chain ![]() because we used approximate values for the true EWs could be removed
after iterating one more time.
because we used approximate values for the true EWs could be removed
after iterating one more time.
Nevertheless, this method is not very efficient when the
observed EWs have large uncertainties, as for a composite
spectrum of low S/N.
There, a more pragmatic approach consists in optimizing both ![]() and
and ![]() in a single step by looking for the best-fitting synthetic composite
spectrum for a given pair (
in a single step by looking for the best-fitting synthetic composite
spectrum for a given pair (
![]() ,
,
![]() )
and the
)
and the ![]() and
and ![]() constraints.
constraints.
3.9.2 Second step
Here the luminosity ratio in the blue is simply one of the three parameters determined by the non-linear least-squares algorithm amoeba, the other two parameters are the effective temperatures (see more details below, Sect. 3.10). So the luminosity ratio is determined in a very homogeneous way, and an error estimate naturally arises through the rms scatter of the resulting values. This does not guarantee, however, that the results are free from any bias. One may specifically suspect that in the temperature regime where the strengths of all lines (H and He ones) vary in unison with the temperature, some degeneracy may arise between the temperatures and the luminosity ratio. That temperature regime spans roughly from 22 000 to 30 000 K, which means that the luminosity ratio of the majority of systems may be fragile. Nevertheless, a posteriori examination of the resulting HR diagrams does not confirm this fear, even though a few systems fail to match the evolutionary tracks.
3.10 Effective temperatures
Once reliable ![]() and
and ![]() values
were found, a way for setting the temperature of the primary
must be found (the temperature of the secondary is a
by-product via the photometric temperature ratio).
values
were found, a way for setting the temperature of the primary
must be found (the temperature of the secondary is a
by-product via the photometric temperature ratio).
For late O and early B stars, the H![]() and H
and H![]() Balmer lines are far better temperature indicators than He I lines
(Huang & Gies 2005,
2005).
Therefore, the most direct way to determine the effective temperatures
of both components of a given system would consist in calibrating the
equivalent widths measured on the normalized separated spectra with
those obtained with a library of synthetic spectra. Unfortunately, this
is not always possible because of the high proportion of systems
contaminated by H
Balmer lines are far better temperature indicators than He I lines
(Huang & Gies 2005,
2005).
Therefore, the most direct way to determine the effective temperatures
of both components of a given system would consist in calibrating the
equivalent widths measured on the normalized separated spectra with
those obtained with a library of synthetic spectra. Unfortunately, this
is not always possible because of the high proportion of systems
contaminated by H![]() and H
and H![]() nebular
emission lines. Thus, most spectra of individual components are
unreliable around the Balmer lines.
nebular
emission lines. Thus, most spectra of individual components are
unreliable around the Balmer lines.
3.10.1 First step
A safer method consists in comparing an observed composite spectrum
close to quadrature with a synthetic composite spectrum computed at the
same orbital phase. The spectra retained for the temperature
determination are those with ![]() or
or ![]() .
This method is quite sensitive to the continuum placement.
A low S/N
and/or strong emission lines can hinder a reliable profile fitting.
.
This method is quite sensitive to the continuum placement.
A low S/N
and/or strong emission lines can hinder a reliable profile fitting.
Another method is a variant of the traditional spectral
type vs. temperature calibration. In the traditional method,
the line strengths ratio of two lines are measured and compared with
the values obtained from a series of reference spectra whose spectral
types are known. The effective temperature is then found via a spectral
type - ![]() calibration
scale. As emphasized by HHH03/05, this technique is efficient
for O-B1 stars but far less straightforward for later types.
Above this limit, the relative strength of the He II 4542
and Si III 4553 lines is
a
reliable tool, as is the relative strength of the Si IV 4089-4116
and He I 4121 lines.
For temperatures below
calibration
scale. As emphasized by HHH03/05, this technique is efficient
for O-B1 stars but far less straightforward for later types.
Above this limit, the relative strength of the He II 4542
and Si III 4553 lines is
a
reliable tool, as is the relative strength of the Si IV 4089-4116
and He I 4121 lines.
For temperatures below ![]() 29-30 000 K,
the problem is the lack of exploitable metallic lines. Unfortunately,
the faint Si II lines are totally
undetectable. For later B stars, the only detectable metallic
line is Mg II 4481, but this line
is often severely buried in the noise for most components.
29-30 000 K,
the problem is the lack of exploitable metallic lines. Unfortunately,
the faint Si II lines are totally
undetectable. For later B stars, the only detectable metallic
line is Mg II 4481, but this line
is often severely buried in the noise for most components.
3.10.2 Second step
The method is qualitatively speaking the same as that of the first step, consisting in fitting a composite synthetic spectrum to the observed one near quadrature. However, the least-squares fit method allows us in principle to use all out-of-eclipse spectra, and provides a much more objective estimate of the temperatures. Because the radial velocities are known, the only parameters which have to be fit are the effective temperatures of both components and the blue luminosity ratio. As mentioned in Sect. 3.9.2, the fit is quite robust at both ends of the temperature range of our sample: at the cool end, the He I lines increase in strength with temperature, while the H I Balmer lines decrease; in addition, the Mg II line decreases very fast. At the hot end, both H and He I lines decrease with temperature, but the He II lines begin to appear. All lines vary more or less in parallel in the intermediate range, which may lead to degeneracy when the S/N ratio is poor.
For all systems with a significant nebular emission in the core of the hydrogen Balmer lines, we simply removed a 4 Å wavelength interval centered on the emission line in both observed and synthetic composite spectra. But, contrary to the synthetic spectra used for RV determinations, here we include the H Balmer lines in the fit, except for their very centers.
The rms scatter of the fitted effective temperatures is
typically on the order of 1000 K, and is even smaller
than that for one third of the sample. Although formally the error bar
on ![]() should be set to that scatter divided by the square root of the number
of spectra, we chose to put it equal to the scatter itself. Indeed,
visual examination of the observed and model spectra show that the
temperature effect is often very subtle, so we feel this
choice is more realistic.
should be set to that scatter divided by the square root of the number
of spectra, we chose to put it equal to the scatter itself. Indeed,
visual examination of the observed and model spectra show that the
temperature effect is often very subtle, so we feel this
choice is more realistic.
The fit proved to depend somewhat on the normalization of the spectra. The latter were first normalized with an automatic procedure with fixed continuum regions. Then, another automatic procedure was used, which corrected the first normalization with the help of a pair of synthetic spectra with preliminary stellar parameters. That normalization resulted in a slightly higher continuum and was found satisfactory in general, except for the bluer end of the spectrum. A final normalization was made by hand, which was adopted in most cases, but not in all, because the continuum proved sometimes too high. The temperature determination was run on the automatically normalized spectra as well as on the manually normalized ones. The results were found to depend little on the normalization, which was not unexpected because the last two normalizations did not differ much from one another.
The average temperatures were computed on all out-of-eclipse spectra on the one hand, and on a selection of those for which the RV difference is greater than 300 km s-1 (250 or even 200 km s-1 for longer period systems) on the other hand. The selection often resulted in a smaller scatter of the temperature, though not in every case. The average temperature was weighted with the inverse of the chi-square provided by the amoeba procedure.
3.11 Synthetic photometry and reddening
Intrinsic (B-V) color indices are
needed for two purposes: the computation of the EB-V color
excess for a given system and the computation of the B-band
bolometric corrections BCB
of the individual components. In the first case, (B-V)0 is
phase-dependent and characterizes the binary as a whole, while in the
second case (B-V)0j
is the usual (constant) color characteristic of a given star. Both
types of color indices were computed from synthetic photometry,
i.e. from synthetic stellar spectra and the response functions
of the filters. The general formula for the phase-dependent (B-V)0
of a binary is given by
where SX is the response function of the X-band filter (Bessell 1990),
where
A similar procedure was used to compute the (V-I)0 color indices, taking CV-I = 1.268 and the appropriate response functions SV and SI. This index is needed for the determination of the distance modulus from the I-band photometric observations.
Alternatively, the intrinsic color index (B-V)0
could be estimated via a color-temperature relation from the
literature. Because this kind of calibration is established with stars
from the solar neighborhood (e.g. Flower 1996), the
coefficients of the fit are in turn representative of stars with a
solar metalicity. Consequently, synthetic photometry with Z
= 0.004 spectra was
considered more reliable for our objects. Both (B-V)0
and (V-I)0
were computed for a grid of temperatures and surface gravities. Because
the fluxes are not given beyond 7500 Å in the OSTAR2002
library (which contains fluxes for stars hotter than
30 000 K), we had to complement the flux distribution
of stars hotter than 30 000 K by the appropriate
Kurucz fluxes![]() to be able to compute the (V-I)0 index.
We chose the grid with a metalicity of -0.5. Because of that
inhomogeneity, the (V-I)0 indices
of binary systems hosting components with
to be able to compute the (V-I)0 index.
We chose the grid with a metalicity of -0.5. Because of that
inhomogeneity, the (V-I)0 indices
of binary systems hosting components with ![]() K
may be slightly less reliable than those of the other systems (the
systems 4 110409, 4 121084,
4 175149, 5 32412, 5 38089 and
5 266015 are
in this case). For a given object, the color indices were
linearly interpolated from these grids.
K
may be slightly less reliable than those of the other systems (the
systems 4 110409, 4 121084,
4 175149, 5 32412, 5 38089 and
5 266015 are
in this case). For a given object, the color indices were
linearly interpolated from these grids.
To estimate the uncertainties, however, the following
first-order approximations valid for early-B stars of intermediate ![]() values
were used (see Sect. 3.13):
values
were used (see Sect. 3.13):
Table 4: Intrinsic color indices at quadrature computed by synthetic photometry.
Once the color excess ![]() is determined, one must make an assumption about the value of the
extinction parameter
is determined, one must make an assumption about the value of the
extinction parameter ![]() .
This parameter is assumed equal to the standard value 3.1
.
This parameter is assumed equal to the standard value 3.1 ![]() 0.3 for each system. Note that this
parameter suffers from a rather large uncertainty. For the SMC
bar, Gordon et al. (2003)
propose the mean value
0.3 for each system. Note that this
parameter suffers from a rather large uncertainty. For the SMC
bar, Gordon et al. (2003)
propose the mean value ![]()
![]() 0.13 from a sample of four stars with
0.13 from a sample of four stars with
![]() ranging from 2.4
ranging from 2.4 ![]() 0.3
to 3.3
0.3
to 3.3 ![]() 0.38.
Nevertheless, because of the small size of Gordon et al.'s
sample, the more conservative standard value was retained
here.
Moreover, the contribution of
0.38.
Nevertheless, because of the small size of Gordon et al.'s
sample, the more conservative standard value was retained
here.
Moreover, the contribution of
![]() to the total error budget for the DMi is low. The difference
to the total error budget for the DMi is low. The difference
![]() between a DM calculated with Gordon et al.'s value
and the
standard value is given by
between a DM calculated with Gordon et al.'s value
and the
standard value is given by ![]() .
Thus, with
.
Thus, with ![]() ,
the DM is slightly increased by 0.036 mag if
,
the DM is slightly increased by 0.036 mag if ![]() is adopted.
is adopted.
In order to determine the distance modulus from the I-band
data, the ratio of the absorptions in the infrared and optical
bands AI
/ AV is
calculated from the relationship
| (8) |
with
3.12 Distance modulus: V- or I-band approach?
There are two ways of determining the distance modulus of a particular
system, depending on whether one takes visual or infrared data:
The safest choice is to take the expression which leads to the value with the smallest uncertainty. The I-band magnitude at quadrature is far more reliable than the V-band value because there is typically
Consequently, the I-band calculation must be preferred, at least for system for which there is a reliable way to obtain the (V-I)0 index. We have seen that this is the case for systems where both components have
In order to check the purely synthetic intrinsic (V-I)
index, both V- and I-band
formulations of Eq. (9)
can be used to derive the following relation between the two color
excesses:
A simple modification of this equation gives
This is a semi-empirical dereddening, as EB-V is calculated from a synthetic intrinsic (B-V) index. The (V-I)0 indices so obtained agree within 0.01-0.02 mag for four of the six hot binaries; the difference reaches 0.03 mag for the system 5 32412, but this is less than the estimated error of the distance modulus. For 5 38089, the difference is 0.06 mag, but this system has abnormal colors and so will be excluded from the statistics of the distance moduli.
3.13 Uncertainties
3.13.1 Distance modulus and related parameters
The calculus of the uncertainties in a number of parameters relies on
some assumptions and simplifications. These points are discussed below.
The uncertainty in the distance modulus of a particular
binary
![]() is determined via the standard rules of the propagation
of errors for independent variables,
is determined via the standard rules of the propagation
of errors for independent variables,
This expression was easily derived from the infrared formulation of Eq. (9). The uncertainty in the I magnitude (
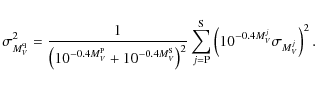
|
(14) |
The absolute visual magnitude of a component is found through the absolute bolometric magnitudes
There is now an important point emphasized by Clausen (2000).
with the associated uncertainty
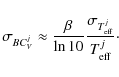
|
(17) |
Combining Eqs. (15) and (16) and expressing
![\begin{displaymath}%
\sigma^{2}_{M_{V}^{j}} \approx
\frac{1}{\left( \ln 10 \righ...
..._{{\rm eff}}^{j}}}{T_{{\rm eff}}^{j}} \right)^{2} \right]\cdot
\end{displaymath}](/articles/aa/full_html/2010/12/aa10284-08/img313.png)
|
(18) |
Thus the uncertainty in
The uncertainties in the intrinsic color indices at
quadrature, (B-V)0
and (V-I)0,
are estimated by the approximation for early-B stars given in
Sect. 3.11.
Since the color indices relate not to a single star, but to a binary
system, one defines an ``equivalent'' effective temperature
![]() of the system (which is the effective temperature of a single star with
the same color index as the system) by inverting Eq. (7). Then,
a rough estimate of the error on the intrinsic color index is
obtained by propagating the error on
of the system (which is the effective temperature of a single star with
the same color index as the system) by inverting Eq. (7). Then,
a rough estimate of the error on the intrinsic color index is
obtained by propagating the error on
![]() ,
which is identified with that on
,
which is identified with that on
![]() ,
the temperature of the primary. In general,
the error on the absolute magnitude of the system will by far
outweigh the other terms on the right side of Eq. (13).
,
the temperature of the primary. In general,
the error on the absolute magnitude of the system will by far
outweigh the other terms on the right side of Eq. (13).
3.13.2 Masses and radii
Masses and radii heavily depend on the radial velocity
semi-amplitudes Kj.
The WD code does not directly provide the errors of the masses
and radii, but only those of the semi-major axis a,
of the mass ratio q, the
inclination i, the effective
temperature of the secondary, and the potentials. It is in
principle possible to derive the errors of the masses from those
of a and q with
the third Kepler law (which gives the total mass) and the appropriate
propagation formulae.
However, the resulting errors tend to appear underestimated,
so we preferred to use the errors of ![]() given by the bina code that was used for a
preliminary interpretation of the RV curves alone. The errors
of the masses are then obtained through the formula
given by the bina code that was used for a
preliminary interpretation of the RV curves alone. The errors
of the masses are then obtained through the formula
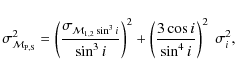
|
(19) |
and may be twice larger than those obtained from WD. Still, they have to be considered rather as lower limits to the real uncertainties, because they are based only on the scatter of the radial velocities around the fitted curve. Systematic errors may arise, however, from the choice of the template spectra used to obtain the RV values, and from the unavoidable fact that these synthetic spectra can never perfectly match the real ones.
The relation between the uncertainties in the masses and
pertaining variables can be found in Hilditch (2001),
for example. The absolute radius of component j
is obtained from

|
(20) |
where a is the semi-major axis and rj the relative radius of component j. The relative radii are considered as functions of two independent variables, the sum
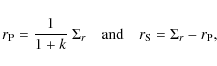
|
(21) |
with the associated uncertainties
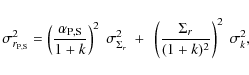
|
(22) |
where
The spectroscopic ratio of radii k is
obtained by inverting Eq. (4)
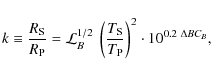
|
(23) |
where
| (24) | ||
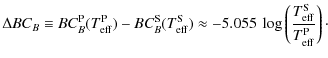
|
(25) |
Therefore, the ratio of radii can be written as
|
(26) |
Neglecting the uncertainties of the empirical coefficients in the expression for the bolometric correction, the error of k is then
![$\displaystyle %
\left(\frac{\sigma_{k}}{k}\right)^{2} \approx \frac{1}{4}
\left...
...\sigma_{T_{{\rm eff}}^{{\rm S}}}}{T_{{\rm eff}}^{{\rm S}}}\right)^2\right]\cdot$](/articles/aa/full_html/2010/12/aa10284-08/img332.png)
|
(27) |
4 Results and discussion
The I-band light curves and the best-fit solutions
are shown in Figs. 17-19. The
RV curves are shown in Figs. 20-22. The mass-![]() diagrams
are shown in Figs. 23-25. The
HR diagrams are shown in Figs. 26-28. The parameters
found from the WD/PHOEBE analysis are given in Tables 11 (orbital
parameters) and 12
(temperature ratios, potentials and luminosity ratios). The
astrophysical parameters of the primary and secondary components are
given in Tables 13
and 14,
respectively. Absolute magnitudes and distance moduli are given in
Table 15.
Finally, the rms scatters of the light curves and RV curves
are summarized in Tables 16
and 17.
diagrams
are shown in Figs. 23-25. The
HR diagrams are shown in Figs. 26-28. The parameters
found from the WD/PHOEBE analysis are given in Tables 11 (orbital
parameters) and 12
(temperature ratios, potentials and luminosity ratios). The
astrophysical parameters of the primary and secondary components are
given in Tables 13
and 14,
respectively. Absolute magnitudes and distance moduli are given in
Table 15.
Finally, the rms scatters of the light curves and RV curves
are summarized in Tables 16
and 17.
4.1 Common systems with HHH03/05
Table 5: Comparison of our solutions (NGBR) for the five binaries in common with HHH03/05.
Table 6: Comparison of our results (NGBR) with the light-curves solutions of Wyithe & Wilson (2001,2002, WW01, WW02) and Graczyk (2003, dG03).
Five systems are the same in HHH03/05's sample and ours: two detached systems (4 163552 and 5 038089) and three semi-detached ones (4 110409, 5 026631 and 5 277080). The comparison of a number of parameters is shown in Table 5. The good news is that we agree on the model, i.e. the configuration of the system in relation with the Roche lobes. The bad news is that in several cases we disagree on most parameters, except for the inclination, a purely photometric parameter. There is nothing surprising about that, as we have the same light curves.
The first system, 4 110409, shows a fair agreement for the
masses (excellent for the primary, within ![]() for the secondary), the radii (within
for the secondary), the radii (within ![]() )
and the surface gravities (
)
and the surface gravities (![]() or better). By contrast, the effective temperatures differ by
as much as 7000 (primary) and 6000 K (secondary), those given
by HHH05 being clearly underestimated.
or better). By contrast, the effective temperatures differ by
as much as 7000 (primary) and 6000 K (secondary), those given
by HHH05 being clearly underestimated.
The second system, 5 163552, shows a good agreement of the
temperatures, the estimates by HHH05 being only ![]() K
higher than ours. On the other hand, the masses given by HHH05 are
K
higher than ours. On the other hand, the masses given by HHH05 are ![]() larger
than ours, and their radii are larger too. Part of the problem might
arise from HHH05 neglecting the third light. In addition,
HHH05 may have been more sensitive to crowding effects on their
RV curves, since the diameter of the 2dF fibers they used
is
larger
than ours, and their radii are larger too. Part of the problem might
arise from HHH05 neglecting the third light. In addition,
HHH05 may have been more sensitive to crowding effects on their
RV curves, since the diameter of the 2dF fibers they used
is
![]() ,
while the diameter of the FLAMES/GIRAFFE fibers is only
,
while the diameter of the FLAMES/GIRAFFE fibers is only ![]() .
But nebular emission may be the main
reason for the discrepancy: HHH05 overestimate the amplitude of both
RV curves (compared to our estimate), and indeed nebular
emission can mimick a wider separation of Balmer lines near
quadratures.
.
But nebular emission may be the main
reason for the discrepancy: HHH05 overestimate the amplitude of both
RV curves (compared to our estimate), and indeed nebular
emission can mimick a wider separation of Balmer lines near
quadratures.
For the semi-detached system 5 26631, there is a perfect
agreement about the mass of the primary, while the mass of the
secondary given by HHH05 is ![]() larger than ours. Their solution appears less realistic than ours,
because they obtain a mass ratio close to unity, which would be
exceptional for a semi-detached system. Similarly, we agree on the
radius of the primary, while HHH05 overestimate the radius of the
secondary. HHH05 estimate temperatures lower by
larger than ours. Their solution appears less realistic than ours,
because they obtain a mass ratio close to unity, which would be
exceptional for a semi-detached system. Similarly, we agree on the
radius of the primary, while HHH05 overestimate the radius of the
secondary. HHH05 estimate temperatures lower by ![]() K
(primary) and by
K
(primary) and by ![]() K
(secondary) than we. The amplitude of their RV curve is
overestimated for the primary, but slightly lower than ours for the
secondary. Again, nebular emission might be responsible for the
discrepancy.
K
(secondary) than we. The amplitude of their RV curve is
overestimated for the primary, but slightly lower than ours for the
secondary. Again, nebular emission might be responsible for the
discrepancy.
The fourth system, 5 38089, shows a very large discrepancy in the mass estimates: for the secondary, it amounts to 63% if we take our value as the reference. Both masses are overestimated by HHH03, while the radius of the primary perfectly agrees, and that of the secondary is significantly overestimated. On the other hand, the temperatures nearly perfectly agree (within 2%) for the primary, and slightly disagree (by 1840 K) for the secondary. It appears that HHH03 have strongly overestimated the amplitude of the RV curve of the primary, while that of the secondary is much closer to ours. Here, one cannot invoke any systematic effect linked with nebular emission, since the latter cannot be seen on our spectra. On the other hand, this system has peculiar color indices (Fig. 3) and its position is unsatisfactory in our own HR diagram. Crowding problems causing what could be called ``spectroscopic third light'' are probably the main source of problems in both studies, and may have been enhanced in that of HHH03 by the wider 2dF fiber.
The last system, 5 277080, holds the record of mass discrepancy: compared to our values, HHH05 overestimate the mass by factors as large as 1.8 and 2.3 for the primary and the secondary respectively. The radii are overestimated as well, but by a much smaller amount. The temperatures differ by more than 4000 K. Nebular emission cannot be the culprit, since it remains undetectable in our spectra.
The problem lies in the RV curves and the separated spectra.
There are three basic spectroscopic parameters on which all the
subsequent analysis is built: the two velocity semi-amplitudes
and one of the temperatures (the other one being constrained by the
photometric mean surface brightness ratio). If the velocity
semi-amplitudes are wrong, the masses, radii, q-ratio,
![]() -values and
luminosities are wrong. The luminosities are obviously highly dependent
on the temperatures, despite a partial cancelling of a possible error
by the bolometric correction (see Sect. 3.13). We are
confident of our values for the velocity semi-amplitudes and the
primary temperature. The RV curves of the five systems shared
with HHH03/05 are shown in Figs. 20-22. They are well
sampled, there are good constraints at the quadratures and the
-values and
luminosities are wrong. The luminosities are obviously highly dependent
on the temperatures, despite a partial cancelling of a possible error
by the bolometric correction (see Sect. 3.13). We are
confident of our values for the velocity semi-amplitudes and the
primary temperature. The RV curves of the five systems shared
with HHH03/05 are shown in Figs. 20-22. They are well
sampled, there are good constraints at the quadratures and the ![]() curves
are flat (except for 5 277080 where some systematics appears).
Consequently, there is no reason to doubt the quality of our velocity
semi-amplitudes. The RV curves are not shown in HHH03/05,
nevertheless there are certainly two reasons to suspect that they have
a poorer quality than ours. The first one is instrument-related.
As already mentioned, our instrumental setup has a better
resolution (0.67 Å instead of 2 Å).
Moreover, for the systems in common, our data have a higher S/N
(typically a factor of about two, from the S/N-calculators
of the respective instruments), in spite of a lower S/N
on average for the whole sample, as we observed mostly fainter
systems. Thus our raw data are intrinsically better. The second reason
is related to the measurement of the radial velocities. Our radial
velocities were determined exclusively from the He I lines
mentioned in Sect. 3.5.
From the procedure described in HHH03/05, it seems clear that
in most cases (i.e. with no conspicuous emission lines) both
Balmer and He I and/or the whole
spectrum were used to determine the radial velocities. One can suspect
that unrecognized nebular emission in the H I lines
is partly responsible for bad RV measurements. Actually, in a
number of cases, nebular emission in the Balmer lines can easily be
confused with the typical ``SB2 cleavage'' of blended lines.
Because the separation of a composite spectrum is tightly linked to the
radial velocities, the quality of the component spectra and their
subsequent use for fixing the temperature of one component will be
badly influenced by poorly determined radial velocities.
curves
are flat (except for 5 277080 where some systematics appears).
Consequently, there is no reason to doubt the quality of our velocity
semi-amplitudes. The RV curves are not shown in HHH03/05,
nevertheless there are certainly two reasons to suspect that they have
a poorer quality than ours. The first one is instrument-related.
As already mentioned, our instrumental setup has a better
resolution (0.67 Å instead of 2 Å).
Moreover, for the systems in common, our data have a higher S/N
(typically a factor of about two, from the S/N-calculators
of the respective instruments), in spite of a lower S/N
on average for the whole sample, as we observed mostly fainter
systems. Thus our raw data are intrinsically better. The second reason
is related to the measurement of the radial velocities. Our radial
velocities were determined exclusively from the He I lines
mentioned in Sect. 3.5.
From the procedure described in HHH03/05, it seems clear that
in most cases (i.e. with no conspicuous emission lines) both
Balmer and He I and/or the whole
spectrum were used to determine the radial velocities. One can suspect
that unrecognized nebular emission in the H I lines
is partly responsible for bad RV measurements. Actually, in a
number of cases, nebular emission in the Balmer lines can easily be
confused with the typical ``SB2 cleavage'' of blended lines.
Because the separation of a composite spectrum is tightly linked to the
radial velocities, the quality of the component spectra and their
subsequent use for fixing the temperature of one component will be
badly influenced by poorly determined radial velocities.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg4.eps}\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg516.png)
|
Figure 4:
Photometric vs. spectroscopic values of the B luminosity
ratio (full symbol: detached; open symbol: semi-detached/contact). The
dotted line corresponds to |
| Open with DEXTER | |
An important point of divergence in the methodology used to ``solve'' a binary is the use (or non-use) of the spectral B luminosity ratio. Comparing the spectral and photometric values of the B luminosity ratio actually reveals that they often disagree for detached systems. The reason is the near-degeneracy of the ratio of radii with the inclination in the case of partial eclipses (Wyithe & Wilson 2001). In principle, the photometric luminosity ratio of semi-detached systems should be better constrained, because they have fewer free photometric parameters than the detached ones (see Fig. 3 in Wyithe & Wilson 2001 and 2002). The regression shown in Fig. 4 clearly shows that the spectroscopic and photometric ratios of the population of semi-detached systems agree fairly well, except that the slope is slightly lower than one. The latter fact may arise because the secondary tidal distortion is larger than that of the primary: the total luminosity, which is the parameter provided by the WD code, may be lower than suggested by the apparent brightness at the quadrature. Among the detached systems, Fig. 4 shows only those for which the spectroscopic and photometric luminosity ratios were found to agree, so the good match is artificial.
Thus, the spectroscopic luminosity ratios were adopted systematically for the detached systems, except where they agree with the photometric one within the uncertainties (full dots in Fig. 4). For the semi-detached and contact ones, the photometric ratio was preferred. In HHH05, the spectroscopic ratio was only used to settle the case between two conflicting photometric solutions.
Finally, it must be emphasized that the quality of our spectral analysis is owed to a great extent to the excellent library of synthetic NLTE O- and B-spectra.
4.2 Nebular emission and kinematics
H![]() and H
and H![]() emission lines are visible in most binary spectra of our sample. FWHM
values and heliocentric radial velocities are presented in
Table 7.
These are mean values inferred from spectra close to conjunction in
order to separate the real emission from the ``SB2 cleavage''.
The strengths are not indicated, because in normalized spectra the
nebular lines are diluted by the stellar continua. Therefore it would
not be possible to compare line strengths measured on two spectra of
two different systems. Even in the case of two spectra of the same
binary at two different epochs the strength measurement is not reliable
because of the dependence of the
diluting stellar continuum on the seeing
emission lines are visible in most binary spectra of our sample. FWHM
values and heliocentric radial velocities are presented in
Table 7.
These are mean values inferred from spectra close to conjunction in
order to separate the real emission from the ``SB2 cleavage''.
The strengths are not indicated, because in normalized spectra the
nebular lines are diluted by the stellar continua. Therefore it would
not be possible to compare line strengths measured on two spectra of
two different systems. Even in the case of two spectra of the same
binary at two different epochs the strength measurement is not reliable
because of the dependence of the
diluting stellar continuum on the seeing![]() .
.
Table 7:
Nebular emission: mean radial velocities and mean FWHM
of the H![]() and H
and H![]() lines
(the quoted uncertainties are standard deviations).
lines
(the quoted uncertainties are standard deviations).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{10284fg5.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg594.png)
|
Figure 5:
Histogram of the mean heliocentric radial velocities of the nebular H |
| Open with DEXTER | |
It is beyond the scope of this paper to make a detailed kinematic study
of the SMC. Nevertheless, it is interesting to examine the
distribution of the 20 RVs derived from the nebular H![]() lines
listed in Table 7.
The distribution is illustrated in Fig. 5.
The 5 km s-1-binned histogram
shows a bimodal distribution with two modes at 145-150 and
160-165 km s-1. Because the
size of the sample is modest, one can wonder about the significance of
this observation. Therefore, the RVs of the
nebular lines in the sky spectra were also investigated
(21 spectra per epoch). The H
lines
listed in Table 7.
The distribution is illustrated in Fig. 5.
The 5 km s-1-binned histogram
shows a bimodal distribution with two modes at 145-150 and
160-165 km s-1. Because the
size of the sample is modest, one can wonder about the significance of
this observation. Therefore, the RVs of the
nebular lines in the sky spectra were also investigated
(21 spectra per epoch). The H![]() data are presented
in Table 8.
It is evident that the RV-distribution shows two peaks as
well, at 140-145 and 160-165 km s-1
(Fig. 6).
Therefore, these
observations provide compelling evidence that the nebular H II
of the SMC displays a bimodal velocity distribution (at least
in our small 25
data are presented
in Table 8.
It is evident that the RV-distribution shows two peaks as
well, at 140-145 and 160-165 km s-1
(Fig. 6).
Therefore, these
observations provide compelling evidence that the nebular H II
of the SMC displays a bimodal velocity distribution (at least
in our small 25
![]() -diameter field).
-diameter field).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{10284fg6.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg595.png)
|
Figure 6:
Histogram of the mean heliocentric radial velocities of the nebular H |
| Open with DEXTER | |
Comparing the systemic velocities of our 33 systems with the combined
nebular H II velocities
(41 values) shows that the two samples have very different
distributions. The nebular velocities were fitted by two Gaussian
functions of equal amplitudes with modes at 145.2 and
161.4 km s-1 and standard
deviations of 3.44 and 4.14 km s-1,
respectively. The corresponding FWHMs are about one
fifth of a resolution element (![]() 47 km s-1).
The systemic velocities are best fitted with a Gaussian function
centered on 162 km s-1 with a
standard deviation of 12.9 km s-1.
That last fit is less convincing than for the H I,
because there are less data and the velocity dispersion is 3-4
47 km s-1).
The systemic velocities are best fitted with a Gaussian function
centered on 162 km s-1 with a
standard deviation of 12.9 km s-1.
That last fit is less convincing than for the H I,
because there are less data and the velocity dispersion is 3-4 ![]() higher. More nebular and systemic velocity data from the analysis of
the remaining SB1 systems contained in the GIRAFFE field are
expected to substantially improve the statistics.
higher. More nebular and systemic velocity data from the analysis of
the remaining SB1 systems contained in the GIRAFFE field are
expected to substantially improve the statistics.
Note that the observed bimodal distribution of H II
is compatible with the kinematic study of H I
in the SMC by Stanimirovic et al. (2004), even though
the gas we see in our work is certainly hotter than the gas observed at
21 cm wavelength. Indeed, the authors mention the existence of
a bimodal velocity field with central velocities of 137 and
174 km s-1. Interestingly,
Fitzpatrick (1985)
already mentioned two H I complexes with
velocities 134 and 167 km s-1,
which our emitting gas is probably related with. Figure 7 shows the mean
(heliocentric) velocity field obtained from nebular H II
data. Filled and open symbols correspond to binary and sky (nebular)
data, respectively. The size of the symbol is drawn according to the
value of the radial velocity. A cross indicates the position
of a binary without significant emission. The map has the same
orientation as in Fig. 1.
We can tentatively draw an oblique line from the NE to the
SW corner demarcating high-velocity points from low-velocity
points. This line has a ![]() slope in the EN (clockwise) direction. On the east (i.e. left)
side of this line, nebular RVs are greater than
slope in the EN (clockwise) direction. On the east (i.e. left)
side of this line, nebular RVs are greater than ![]() .
This velocity gradient is consistent with Fig. 3 in
Stanimirovic et al., i.e. the velocity of H I
increases from west to east in this part of the SMC. Therefore, the hot
and cool phases of the gas seem to share very similar spatial and
kinematic distributions.
.
This velocity gradient is consistent with Fig. 3 in
Stanimirovic et al., i.e. the velocity of H I
increases from west to east in this part of the SMC. Therefore, the hot
and cool phases of the gas seem to share very similar spatial and
kinematic distributions.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10284fg7.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg598.png)
|
Figure 7: Velocity field of the H II gas. The size of symbol is proportional to the value of the velocity. Values higher than 155 km s-1 are given in red (electronic version only). Filled symbols are for binary systems, while open symbols are for skies. Crosses are for binary systems without emission. |
| Open with DEXTER | |
Table 8:
Sky positions: astrometry, sky background excesses (see Sect. 4.2) and
mean radial velocities derived from the H![]() emission line.
emission line.
4.3 Comparison with evolutionary models and the mass-luminosity relation
The comments of the individual systems are given in Sect. A. Here, the
collective properties of the sample are examined more thoroughly. For
each of the 33 systems, Table 9 lists the
differences
![]() between the evolutionary mass interpolated, in the HR diagram,
in the evolutionary tracks from Charbonnel et al. (1993), and the
observed dynamical mass determined from the simultaneous RV-curves and
light-curves analysis. Figure 9
shows these differences versus the observed masses for the
23 binaries with a detached configuration. The agreement
between the observed and evolutionary masses is acceptable, though some
systematics does appear. The most discrepant objects are the secondary
components of 5 38089 and 5 123390, and the primary
of 5 38089. These systems have a
peculiar position in the HR diagram, perhaps because of
third-light contamination.
between the evolutionary mass interpolated, in the HR diagram,
in the evolutionary tracks from Charbonnel et al. (1993), and the
observed dynamical mass determined from the simultaneous RV-curves and
light-curves analysis. Figure 9
shows these differences versus the observed masses for the
23 binaries with a detached configuration. The agreement
between the observed and evolutionary masses is acceptable, though some
systematics does appear. The most discrepant objects are the secondary
components of 5 38089 and 5 123390, and the primary
of 5 38089. These systems have a
peculiar position in the HR diagram, perhaps because of
third-light contamination.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg8.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg642.png)
|
Figure 8: Comparison between two kinematic tracers: radial velocities of nebular H II ( left) and systemic velocities of binary systems ( right). The data are arranged in 5 km s-1 bins. The best-fitting double-Gaussian and Gaussian models are over-plotted. |
| Open with DEXTER | |
For comparison, the sample of 18 detached systems of HHH05 is
shown in Fig. 10.
Figures 9
and 10
are drawn to the same scale. Besides the very large scatter of HHH05's ![]() values
(they span a range of almost
values
(they span a range of almost ![]() ),
the most striking feature is the correlation between
),
the most striking feature is the correlation between ![]() and the observed mass for a number of primary and secondary components,
especially between 7 and
and the observed mass for a number of primary and secondary components,
especially between 7 and
![]() .
Explaining this trend is not straightforward, but it might be related
to the temperature determination. Indeed, HHH05 mentioned in their
Sect. 3.1.2 that, while the O-B1 stars were easy to
classify, later B-type stars were not, due to the absence of
He II lines and to the
lack of detectable metal lines. We faced the same difficulty, but with
considerably less severe consequences. The larger telescope and better
resolution clearly have brought a dramatic improvement in the quality
of the results.
.
Explaining this trend is not straightforward, but it might be related
to the temperature determination. Indeed, HHH05 mentioned in their
Sect. 3.1.2 that, while the O-B1 stars were easy to
classify, later B-type stars were not, due to the absence of
He II lines and to the
lack of detectable metal lines. We faced the same difficulty, but with
considerably less severe consequences. The larger telescope and better
resolution clearly have brought a dramatic improvement in the quality
of the results.
There is a slight trend in our mass residuals: first of all,
most ![]() values are positive. Second, while the mass difference is negligible
for low masses (around
values are positive. Second, while the mass difference is negligible
for low masses (around ![]() ),
it seems to gradually increase to almost
),
it seems to gradually increase to almost ![]() at about
at about
![]() .
The single point at
.
The single point at ![]() corresponds to
corresponds to ![]() only, but it is not sufficient to define the possible relation beyond
only, but it is not sufficient to define the possible relation beyond ![]() .
It might be part of a parallel sequence defined by four other
stars. One may speculate that if real, the latter sequence
might correspond to e.g. systems for which the sky background
was overestimated, which would have caused an underestimate
of
.
It might be part of a parallel sequence defined by four other
stars. One may speculate that if real, the latter sequence
might correspond to e.g. systems for which the sky background
was overestimated, which would have caused an underestimate
of
![]() .
The main trend is surprising, because the more massive systems are also
more luminous on average and
so appear brighter, because they all lie at about the same distance.
Hence the signal-to-noise ratio of their spectra is higher, and the
determination of the
.
The main trend is surprising, because the more massive systems are also
more luminous on average and
so appear brighter, because they all lie at about the same distance.
Hence the signal-to-noise ratio of their spectra is higher, and the
determination of the ![]() should be more reliable. On the other hand,
should be more reliable. On the other hand, ![]() is better constrained in stars cooler than
is better constrained in stars cooler than ![]() K,
because the He I lines
increase in strength with increasing temperature, while the H I Balmer
lines decrease. In hotter stars, both the H I
and He I lines decrease
with increasing temperature, so that even a slight error in
the continuum placement or (equivalently) in the sky subtraction may
cause a significant error in
K,
because the He I lines
increase in strength with increasing temperature, while the H I Balmer
lines decrease. In hotter stars, both the H I
and He I lines decrease
with increasing temperature, so that even a slight error in
the continuum placement or (equivalently) in the sky subtraction may
cause a significant error in
![]() .
At the hot end of the temperature range of our sample
(i.e. for
.
At the hot end of the temperature range of our sample
(i.e. for ![]() K),
the effective temperature is again better constrained, thanks to the
fast raise of He II lines.
Therefore, one may expect that the least reliable
temperatures - hence the least reliable
luminosities - will occur for stars with intermediate
K),
the effective temperature is again better constrained, thanks to the
fast raise of He II lines.
Therefore, one may expect that the least reliable
temperatures - hence the least reliable
luminosities - will occur for stars with intermediate ![]() or masses. This might explain why the scatter of the
or masses. This might explain why the scatter of the ![]() values
in Fig. 9
is large between 7 and
values
in Fig. 9
is large between 7 and
![]() .
.
Table 9: Comparison with theoretical evolutionary models: difference between the evolutionary and observed masses.
That ![]() in most cases is not easy to explain. Possible explanations can
be grouped into three categories:
in most cases is not easy to explain. Possible explanations can
be grouped into three categories:
- Systematic error in the
 determination:
as mentioned above, the temperature determination is very sensitive to
continuum placement or sky subtraction, especially when all lines vary
in the same way with
determination:
as mentioned above, the temperature determination is very sensitive to
continuum placement or sky subtraction, especially when all lines vary
in the same way with  .
The continuum has been determined both automatically and manually for
each star, and we verified that the least-squares fit used to determine
the temperature always gives the same result, unless the continuum is
clearly wrong. All fits were done under visual monitoring, so the
quality of the continuum placement could be judged with confidence.
In addition, plotting the estimated temperature against the
sum of the squared residuals generally results in a horizontal line,
as shown in Sect. A (the
system 5 180576 is a notable exception). This is
proof that the
.
The continuum has been determined both automatically and manually for
each star, and we verified that the least-squares fit used to determine
the temperature always gives the same result, unless the continuum is
clearly wrong. All fits were done under visual monitoring, so the
quality of the continuum placement could be judged with confidence.
In addition, plotting the estimated temperature against the
sum of the squared residuals generally results in a horizontal line,
as shown in Sect. A (the
system 5 180576 is a notable exception). This is
proof that the  determination
does not depend on the SNR of the spectra or, in other words,
that the continuum was defined in the same way, whatever the SNR of the
spectrum. The normalization and the temperature determination were done
(in the so-called second step) on the original unsmoothed
spectra. In order to further explore the possible role of the
SNR, we smoothed the spectra of the system 4 121110
with a 3-points boxcar (0.6 Å wide) and performed the
determination
does not depend on the SNR of the spectra or, in other words,
that the continuum was defined in the same way, whatever the SNR of the
spectrum. The normalization and the temperature determination were done
(in the so-called second step) on the original unsmoothed
spectra. In order to further explore the possible role of the
SNR, we smoothed the spectra of the system 4 121110
with a 3-points boxcar (0.6 Å wide) and performed the
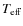 determination
again. The result was the same within
determination
again. The result was the same within  K, which confirms
that it is insensitive to the SNR of the spectra, because the latter
was improved by a factor of
K, which confirms
that it is insensitive to the SNR of the spectra, because the latter
was improved by a factor of  in this test. Therefore, it is doubtful that the explanation
resides in the way the continuum was defined.
in this test. Therefore, it is doubtful that the explanation
resides in the way the continuum was defined.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fg9.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg657.png)
Figure 9: Detached systems: difference between evolutionary mass and observed mass vs. observed mass. Filled symbols: primary; open symbols: secondary. The point in the inset in the lower left corner shows the median error bars for the mass of the primary. The vertical bar does not include the errors on luminosity and
 (hence on the interpolated mass), so it must be considered as
a lower limit.
(hence on the interpolated mass), so it must be considered as
a lower limit.
Open with DEXTER The sky subtraction may be more problematic. Indeed, we have seen that the sky does vary slightly in the FLAMES field, and all we could do was to subtract an average sky spectrum from the stellar spectra. Underestimating the sky would have left some continuum flux, which would have slightly diluted the stellar absorption lines, leading to an overestimate of
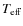 .
The only cure to this problem would have been to use the IFUs instead
of the MEDUSA fibres, to be able at least in principle to measure the
sky surrounding each object. But this would have come at the expense of
a drastic reduction of the number of targets. Although sky subtraction
can explain some of the scatter we see in Fig. 9,
it remains a riddle why this could lead to a systematic
overestimate of
.
The only cure to this problem would have been to use the IFUs instead
of the MEDUSA fibres, to be able at least in principle to measure the
sky surrounding each object. But this would have come at the expense of
a drastic reduction of the number of targets. Although sky subtraction
can explain some of the scatter we see in Fig. 9,
it remains a riddle why this could lead to a systematic
overestimate of
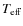 (causing the overestimate of L and,
ultimately, of the interpolated
(causing the overestimate of L and,
ultimately, of the interpolated
 ). Because an average sky was
subtracted, one would expect as many negative values of
). Because an average sky was
subtracted, one would expect as many negative values of
 as positive ones. However, the sky positions had been chosen on the DSS
chart on the basis of their ``darkness'', so that the selected
skies may be darker than
those that typically surround the targets.
as positive ones. However, the sky positions had been chosen on the DSS
chart on the basis of their ``darkness'', so that the selected
skies may be darker than
those that typically surround the targets.
- Inadequacy of the stellar evolution models:
in Figs. 26-28 we plot not only
the evolutionary tracks for the metalicity Z=0.004
of Charbonnel et al. (1993),
but also those at Z=0.001 (Schaller et al.
1992).
It is interesting to see that the more metal-poor models are
slightly more luminous and hotter, and some systems fit them better.
It is possible that some stars have indeed a metalicity
approching Z=0.001 (especially for the light
elements, which are the main contributors to Z),
as shown e.g. by Peters & Adelman (2006). However,
it is doubtful that all our systems have such a low
metalicity, and a look at the HR diagrams shows that this
explanation cannot hold for all of them.
Also plotted in Figs. 26-28 are the evolutionary tracks of Claret & Gimenez (1998) for a helium content Y=0.28 and a metalicity Z=0.004. These models have a helium enhancement
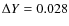 relative to those of Charbonnel et al. (1993), because the
latter have Y=0.252. One can see that increasing
the helium content increases the luminosity, withouth changing much the
temperature. Again, some stars would fit better these models than the
standard ones, while others (like the components of 4 175333)
would need a helium enhancement so large as to make this solution
untenable.
relative to those of Charbonnel et al. (1993), because the
latter have Y=0.252. One can see that increasing
the helium content increases the luminosity, withouth changing much the
temperature. Again, some stars would fit better these models than the
standard ones, while others (like the components of 4 175333)
would need a helium enhancement so large as to make this solution
untenable.
- Inadequacy of the synthetic spectra: if
the true metalicity of most systems is close to Z=0.004
and the helium content is normal, and if the standard evolutionary
models can be trusted, then the synthetic spectra used to estimate the
effective temperatures may be suspected. An overestimate
of
 would certainly have resulted from the use of LTE atmosphere
models: as shown by Hunter et al. (2007) in their
Table 13,
the temperatures of stars analyzed by Kilian-Montenbruck
et al. (1994)
on the basis of LTE atmosphere models and
non-LTE line formation calculations are about
29 000 K, instead of the
26 000-27 000 K derived with
NLTE models. Nevertheless, the synthetic spectra we used are
precisely based on the
latter, so that no obvious bias on temperatures is expected.
With the FASTWIND code Massey et al. (2009) found
temperatures of O stars
would certainly have resulted from the use of LTE atmosphere
models: as shown by Hunter et al. (2007) in their
Table 13,
the temperatures of stars analyzed by Kilian-Montenbruck
et al. (1994)
on the basis of LTE atmosphere models and
non-LTE line formation calculations are about
29 000 K, instead of the
26 000-27 000 K derived with
NLTE models. Nevertheless, the synthetic spectra we used are
precisely based on the
latter, so that no obvious bias on temperatures is expected.
With the FASTWIND code Massey et al. (2009) found
temperatures of O stars  K
hotter than those obtained by Bouret et al. (2003), who used the
TLUSTY and CMFGEN codes. Part of the discrepancy might be explained,
however, by moonlight continuum contamination in the spectra
of Bouret et al. (2003).
On the other hand, Mokiem et al. (2006, 2007) found
temperatures
K
hotter than those obtained by Bouret et al. (2003), who used the
TLUSTY and CMFGEN codes. Part of the discrepancy might be explained,
however, by moonlight continuum contamination in the spectra
of Bouret et al. (2003).
On the other hand, Mokiem et al. (2006, 2007) found
temperatures
 K hotter than those
of Massey et al. (2009),
and they also used FASTWIND. Finally, Massey et al. (2009) still find some
mass discrepancy for their LMC stars. Therefore, some debate
still exists regarding the temperature scales, though the above
references all deal with O stars, rather than with the
B stars we are more concerned with. Unfortunately, similar
studies for metal poor B stars in the range we are interested
in (
K hotter than those
of Massey et al. (2009),
and they also used FASTWIND. Finally, Massey et al. (2009) still find some
mass discrepancy for their LMC stars. Therefore, some debate
still exists regarding the temperature scales, though the above
references all deal with O stars, rather than with the
B stars we are more concerned with. Unfortunately, similar
studies for metal poor B stars in the range we are interested
in (
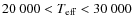 K)
are lacking, so it is difficult to assess the reliability of
the temperature scale. One may expect, however, that it is more
reliable than for O stars, because the NLTE effects
are less important.
K)
are lacking, so it is difficult to assess the reliability of
the temperature scale. One may expect, however, that it is more
reliable than for O stars, because the NLTE effects
are less important.
The OSTAR2002/BSTAR2006 libraries we used are recent and are probably the best available. The only reservation one could possibly raise is the choice of the microturbulence (2 km s-1 for
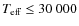 K
and 10 km s-1 for
K
and 10 km s-1 for 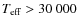 K),
which may be a rough approximation of reality.
K),
which may be a rough approximation of reality.
Conversely, even perfectly realistic models may prove inappropriate, if superficial abundance anomalies exist in the components of our binary systems. It is well known that early B-type stars may show a large overabundance of helium - the so-called helium-rich stars, of which HD 37776 is the prototype - but no example is known among components of close binaries. In any case, stronger He lines would mimick a lower effective temperature, while it seems that the temperatures are overestimated. Thus, only helium-weak stars could explain an overestimate of temperatures, but none are known at such large masses.
The astrophysical parameters of our sample of detached
binaries allow us to give a mass-luminosity relation for the SMC valid
for masses between ![]() 4
and
4
and ![]() 18
18
![]() .
A linear regression fit gives, on all 46 points:
.
A linear regression fit gives, on all 46 points:
with a rms of 0.095 (see the red line in Fig. 11). This is almost exactly the same relation as that obtained by Gonzáles et al. (2005) for the LMC. The mass-luminosity diagram is plotted in Fig. 11 together with the isochrones computed from the Geneva models for Z = 0.004 and Y = 0.252 (Charbonnel et al. 1993). All objects are within the
Most stars lie below the 50 Myr isochrone. The
exceptions are some low-mass objects (
![]() ),
i.e. both components of 5 111649 and of
4 175333. These two systems appear to be
),
i.e. both components of 5 111649 and of
4 175333. These two systems appear to be ![]() 70 Myr
old. They clearly bias the regression line to a low value of the slope.
Graczyk (2003)
adopts the relation
70 Myr
old. They clearly bias the regression line to a low value of the slope.
Graczyk (2003)
adopts the relation
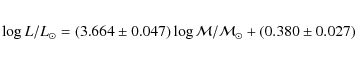
for the LMC and the SMC, which is shown as the full blue line in Fig. 11. The latter relation appears slightly too steep: it clearly runs above unevolved stars with
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg11.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg667.png)
|
Figure 11: Mass-luminosity relation for our 23 detached systems. Full dots represent the primary components, while open dots represent the secondary ones. The dotted lines are the isochrones with age of 0, 5, 10, 20, 30, 40, 50 and 70 Myr for Z = 0.004 (Charbonnel et al. 1993). The red line is a simple least-squares fit of all 46 points, without weighing. The steeper blue line is the relation adopted by Graczyk (2003) for the LMC and SMC. |
| Open with DEXTER | |
4.4 Apsidal motion
Four of the nine eccentric systems have a negligible or marginal
(i.e.
![]() )
apsidal motion, while four others show a formally significant one (see
Table 11);
the apsidal motion of the ninth system was arbitrarily fixed
to a value close to the theoretical expectation. Interestingly, the
system 5 266131 has a very fast apsidal motion, and
probably holds the record among those hosting non-degenerate components
(Petrova & Orlov 1999;
Bulut & Demircan 2007).
Note also that in two of these systems (5 123390 and
5 266131), the relative radius
of the primary component is very close to, or even slightly
exceeds, the limiting radius above which orbital circularization occurs
quickly (North & Zahn 2003,
2004): they have
)
apsidal motion, while four others show a formally significant one (see
Table 11);
the apsidal motion of the ninth system was arbitrarily fixed
to a value close to the theoretical expectation. Interestingly, the
system 5 266131 has a very fast apsidal motion, and
probably holds the record among those hosting non-degenerate components
(Petrova & Orlov 1999;
Bulut & Demircan 2007).
Note also that in two of these systems (5 123390 and
5 266131), the relative radius
of the primary component is very close to, or even slightly
exceeds, the limiting radius above which orbital circularization occurs
quickly (North & Zahn 2003,
2004): they have ![]() and 0.281 respectively, while the limiting radius is
and 0.281 respectively, while the limiting radius is
![]() .
Thus, those systems are caught in the act of circularizing their orbit,
and indeed their eccentricities are among the smallest of all our
eccentric binaries.
.
Thus, those systems are caught in the act of circularizing their orbit,
and indeed their eccentricities are among the smallest of all our
eccentric binaries.
In order to compare our observed apsidal rotation rates with
those predicted by theory, we used Eqs. (1) to (8) of
Claret & Giménez (1993),
which allow us to obtain the average tidal-evolution constant ![]() of the system from the orbital and stellar parameters, including the
measured apsidal period
of the system from the orbital and stellar parameters, including the
measured apsidal period ![]() .
On the other hand, we used the grid of stellar models for the
metalicity Z=0.004 computed by Claret (2005). After
interpolation in surface gravity and mass of the theoretical
.
On the other hand, we used the grid of stellar models for the
metalicity Z=0.004 computed by Claret (2005). After
interpolation in surface gravity and mass of the theoretical ![]() values,
the same formulae were used to obtain the predicted average constant
values,
the same formulae were used to obtain the predicted average constant ![]() .
We corrected for the relativistic precession term, even though it is
small for short periods (Mazeh 2008),
because it contributes no more than 2% to the total precession
period. The result is
shown in Fig. 12,
where we plot
.
We corrected for the relativistic precession term, even though it is
small for short periods (Mazeh 2008),
because it contributes no more than 2% to the total precession
period. The result is
shown in Fig. 12,
where we plot
![]() as a function of
as a function of
![]() .
The one-to-one relation is the straight diagonal line, and three
systems fall on or very close to it. Two other systems are
clearly discrepant. One of the latter, 5 95557, has a formally
significant, but small apsidal motion; the masses are not very
precisely determined, which may explain part of the difference.
It is quite possible that the apsidal motion of
5 95557 is affected by the gravitational perturbation of a
small, unseen third companion. The other discrepant
system 5 123390, is only marginally so,
because it is only
.
The one-to-one relation is the straight diagonal line, and three
systems fall on or very close to it. Two other systems are
clearly discrepant. One of the latter, 5 95557, has a formally
significant, but small apsidal motion; the masses are not very
precisely determined, which may explain part of the difference.
It is quite possible that the apsidal motion of
5 95557 is affected by the gravitational perturbation of a
small, unseen third companion. The other discrepant
system 5 123390, is only marginally so,
because it is only ![]() away from the equality line. In any case, one has to keep in mind that
the error bars shown represent lower limits of the real
uncertainties, because they include only the error on the apsidal
period, while errors on the masses and radii of the components also
contribute. The latter errors certainly dominate for 5 266131,
which lies below the equality line. The open dot represents the
system 5 265970, for which an
apsidal motion close to the theoretical value was assumed.
away from the equality line. In any case, one has to keep in mind that
the error bars shown represent lower limits of the real
uncertainties, because they include only the error on the apsidal
period, while errors on the masses and radii of the components also
contribute. The latter errors certainly dominate for 5 266131,
which lies below the equality line. The open dot represents the
system 5 265970, for which an
apsidal motion close to the theoretical value was assumed.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg12.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg677.png)
|
Figure 12:
Observed versus theoretical apsidal constant |
| Open with DEXTER | |
It would be easy to significantly reduce the error bar on the
average
![]() by reobserving with photometry the few systems showing significant
apsidal motion. Further spectroscopic data would be needed as well to
obtain more precise masses and radii, in order to determine a
meaningful value of
by reobserving with photometry the few systems showing significant
apsidal motion. Further spectroscopic data would be needed as well to
obtain more precise masses and radii, in order to determine a
meaningful value of
![]() .
That would bring an additional constraint on the metalicity and on the
extent of overshooting, for instance.
.
That would bring an additional constraint on the metalicity and on the
extent of overshooting, for instance.
4.5 Distribution of the mass ratios of the detached systems: do binaries really like to be twins?
From the 21 detached systems of the HHH03/05 sample, Pinsonneault
& Stanek (2006)
suggest that the proportion of massive detached systems with a mass
ratio close to unity is far higher than what would be expected from a
classic Salpeter-like (
![]() )
or a flat (
)
or a flat (
![]() )
q-distribution. This statement is based on two
arguments. The first is the striking difference between the median mass
ratio of the detached sample (q = 0.87) and of the
semi-detached/contact sample (q = 0.65). The
surprising point is not the low q-value for the
semi-detached sample, which is expected for a post mass-transfer
system, but rather the high proportion of systems with q
> 0.85 in the detached sample. Moreover, they argue that this
difference is real, i.e. not due to an observational bias such
as the easier detection of systems with components of similar size and
brightness. Their argument is that, beside the detached binaries with q
> 0.85, there are two detached systems with a q-value
as low as
)
q-distribution. This statement is based on two
arguments. The first is the striking difference between the median mass
ratio of the detached sample (q = 0.87) and of the
semi-detached/contact sample (q = 0.65). The
surprising point is not the low q-value for the
semi-detached sample, which is expected for a post mass-transfer
system, but rather the high proportion of systems with q
> 0.85 in the detached sample. Moreover, they argue that this
difference is real, i.e. not due to an observational bias such
as the easier detection of systems with components of similar size and
brightness. Their argument is that, beside the detached binaries with q
> 0.85, there are two detached systems with a q-value
as low as ![]() 0.55.
Indeed, it seems to be a very strong argument in favor of the
reality of a population of twins, because the observation of detached
systems with such a low q value would mean
that the cut-off value of the q distribution
of the detached systems is small enough (
0.55.
Indeed, it seems to be a very strong argument in favor of the
reality of a population of twins, because the observation of detached
systems with such a low q value would mean
that the cut-off value of the q distribution
of the detached systems is small enough (![]() )
to exclude an observational bias. Let us recall that the
cut-off value is the q value, which marks
the transition between a
double-lined and a single-lined binary (SB2-SB1 transition),
i.e. a function of the resolution and of the S/N,
besides stellar parameters. Therefore, as our sample of
23 detached systems is comparable with, and even slightly
larger than HHH03/05's, this is an excellent opportunity to compare
both statistics and thus to shed some light on the controversial topic
of the q distribution of detached and
semi-detached/contact systems.
)
to exclude an observational bias. Let us recall that the
cut-off value is the q value, which marks
the transition between a
double-lined and a single-lined binary (SB2-SB1 transition),
i.e. a function of the resolution and of the S/N,
besides stellar parameters. Therefore, as our sample of
23 detached systems is comparable with, and even slightly
larger than HHH03/05's, this is an excellent opportunity to compare
both statistics and thus to shed some light on the controversial topic
of the q distribution of detached and
semi-detached/contact systems.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fg13.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg681.png)
|
Figure 13:
Distribution of the 33 observed mass ratios (solid: detached, dashed:
semi-detached/contact) with 0.05 bins. The best flat
distribution is over-plotted for each category (detached and
semi-detached or contact systems). Both distributions are truncated at
a cut-off value of |
| Open with DEXTER | |
The q-distributions for our detached and
semi-detached/contact binaries are given in Fig. 13. One sees that
the two samples have quite different distributions. The
semi-detached/contact distribution is patchy because of the small size
of the sample (10 objects), but it seems to be compatible with
a constant law. The cumulative probability distribution of the
mass ratios (Fig. 14,
top) confirms that it is consistent with a flat distribution, limited
to the interval 0.44
< q < 0.76. The statistics of
semi-detached system is not discussed by Pinsonneault & Stanek (2006). The subject was
computationally investigated by van Rensbergen et al. (2006, 2008, 2010). Interestingly,
they mention that 45% of the observed Algols have a mass ratio
in the 0.4-1 range. The low-value for this range coincides with the
observed cut-off of our small sample. Through our experience in
processing spectral data, we assume that this is the detection
threshold for SB2 systems, but van Rensbergen et al.
consider this value not as an observational bias but rather as a
parameter of real astrophysical relevance, because they include both
the SB1 and SB2 systems in their observed
q-distribution. Indeed, their models of
``conservative'' evolution (i.e. no mass lost by the system)
produce an overwhelming majority of Algols with ![]() .
On the other hand, they have better reproduced the observed Algolid q-distribution
(from Budding et al.'s catalog 2004) assuming a
``liberal'' model of evolution, i.e. a lot of mass
loss and a little loss of angular momentum during mass transfer. Their
simulations clearly depict a distribution with a broad peak in the
0.25-0.55 range and rapidly decreasing for higher q-values
(see Fig. 5
in van Rensbergen et al. 2010).
We found the same number of semi-detached systems with q
> 0.55 as with q < 0.55, which seems
to disagree with the above simulations. Nevertheless, the disagreement
would be much alleviated if our sample included the
SB1 systems. Van Rensbergen et al. consider that the q-distribution
of the detached Algol-progenitor systems obeys a power law of
the type
.
On the other hand, they have better reproduced the observed Algolid q-distribution
(from Budding et al.'s catalog 2004) assuming a
``liberal'' model of evolution, i.e. a lot of mass
loss and a little loss of angular momentum during mass transfer. Their
simulations clearly depict a distribution with a broad peak in the
0.25-0.55 range and rapidly decreasing for higher q-values
(see Fig. 5
in van Rensbergen et al. 2010).
We found the same number of semi-detached systems with q
> 0.55 as with q < 0.55, which seems
to disagree with the above simulations. Nevertheless, the disagreement
would be much alleviated if our sample included the
SB1 systems. Van Rensbergen et al. consider that the q-distribution
of the detached Algol-progenitor systems obeys a power law of
the type ![]() (for early B-type primaries). This is not very different from a flat
distribution, considering the rather narrow range of mass ratios
sampled by our 23 detached systems. Indeed the latter can be
considered as progenitors of Algols because of their short orbital
periods. Figures 13
and 14
(top) show that the q-distribution of
these systems is very well modeled by a flat distribution truncated at q
= 0.72, and we have verified that the power law adopted by van
Rensbergen et al. would fit the observed q-distribution
as well as a constant. The higher value for the SB1-SB2 cut-off
compared to semi-detached systems is related to the almost q3-dependence
of the luminosity ratio for main-sequence stars. Let us mention that a
flat q-distribution is assumed by most population
synthesis studies (Pinsonneault & Stanek 2006).
(for early B-type primaries). This is not very different from a flat
distribution, considering the rather narrow range of mass ratios
sampled by our 23 detached systems. Indeed the latter can be
considered as progenitors of Algols because of their short orbital
periods. Figures 13
and 14
(top) show that the q-distribution of
these systems is very well modeled by a flat distribution truncated at q
= 0.72, and we have verified that the power law adopted by van
Rensbergen et al. would fit the observed q-distribution
as well as a constant. The higher value for the SB1-SB2 cut-off
compared to semi-detached systems is related to the almost q3-dependence
of the luminosity ratio for main-sequence stars. Let us mention that a
flat q-distribution is assumed by most population
synthesis studies (Pinsonneault & Stanek 2006).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fg14.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg683.png)
|
Figure 14: Top: cumulative probability distribution as a function of the mass ratio for our 23 detached (solid line) and 10 semi-detached/contact (dotted line) binaries. The dashed oblique line plotted over the detached distribution represents a flat distribution with a cutoff at q = 0.72. For the semi-detached/contact systems, a flat distribution with a cutoff at q=0.43provides a reasonable fit as well. Bottom: cumulative probability distribution for HHH03/05's 21 detached binaries. The over-plotted flat distribution with a cutoff at q = 0.5 shows the incompatibility of a flat distribution with the HHH03/05 data. There is a similar figure in Pinsonneault & Stanek (2006). They show that the data are best-fitted with a 55% flat-45% twin distribution (not shown in this figure). |
| Open with DEXTER | |
The cumulative probability distribution of the mass ratios of
detached systems for the HHH03/05 data is given in
Fig. 14
(bottom). A similar figure is shown in Pinsonneault &
Stanek. This distribution differs significantly from ours on two
points: the low cut-off value of ![]() 0.5 and the relatively strong
deviation from a flat distribution. The low cut-off is rather
surprising. The mean
apparent magnitude of the HHH03/05 sample (
0.5 and the relatively strong
deviation from a flat distribution. The low cut-off is rather
surprising. The mean
apparent magnitude of the HHH03/05 sample (
![]() mag)
is 1.38 mag lower than ours (
mag)
is 1.38 mag lower than ours (
![]() mag).
A rough estimation of the ratio of our mean S/N
to their mean S/N,
taking into account our twice bigger telescope and longer exposure time
via Eq. (3.2) of Hilditch (2001),
gives a ratio of
mag).
A rough estimation of the ratio of our mean S/N
to their mean S/N,
taking into account our twice bigger telescope and longer exposure time
via Eq. (3.2) of Hilditch (2001),
gives a ratio of ![]() 0.8.
That means that our mean spectral S/N
is 20% smaller than theirs despite the bigger optics because
of significantly
fainter targets. Nevertheless, their 20%-better S/N
hardly explains a luminosity ratio cut-off of
0.8.
That means that our mean spectral S/N
is 20% smaller than theirs despite the bigger optics because
of significantly
fainter targets. Nevertheless, their 20%-better S/N
hardly explains a luminosity ratio cut-off of ![]() 1/8 to be compared with our
1/8 to be compared with our ![]() 1/3-value
(for detached main-sequence binaries,
1/3-value
(for detached main-sequence binaries, ![]() ).
Moreover, the instrumental resolution of the LR2 setup in MEDUSA mode
is three times the value of the 2dF spectrograph with the
1200B grating. Therefore, either our sample is deficient
in low-q systems or there are some badly determined q-values
in one of the samples. The first explanation cannot be entirely ruled
out because of the small-sample statistics. Nevertheless, the
comparison of the RV-related parameters for the five systems common to
both HHH03/05's program and ours can certainly help to settle the
issue.
).
Moreover, the instrumental resolution of the LR2 setup in MEDUSA mode
is three times the value of the 2dF spectrograph with the
1200B grating. Therefore, either our sample is deficient
in low-q systems or there are some badly determined q-values
in one of the samples. The first explanation cannot be entirely ruled
out because of the small-sample statistics. Nevertheless, the
comparison of the RV-related parameters for the five systems common to
both HHH03/05's program and ours can certainly help to settle the
issue.
Can the ``twin hypothesis'' be excluded by our data? The
thorough study by Lucy (2006)
points to a negative answer. He discusses both the ``weak''
hypothesis (
![]() )
of an excess of binary systems with q > 0.8
relative to a constant distribution, and the ``strong''
hypothesis (
)
of an excess of binary systems with q > 0.8
relative to a constant distribution, and the ``strong''
hypothesis (
![]() )
of an excess of systems with q > 0.95.
He shows that
)
of an excess of systems with q > 0.95.
He shows that ![]() is confirmed for binary systems in our Galaxy with an accurate enough
mass ratio (
is confirmed for binary systems in our Galaxy with an accurate enough
mass ratio (
![]() ). Therefore,
it would be of great interest to test the same hypothesis in
another galaxy, and our study might, at first sight, be considered a
second step towards that goal, after HHH03/05. But a realistic typical
error on our q values is
). Therefore,
it would be of great interest to test the same hypothesis in
another galaxy, and our study might, at first sight, be considered a
second step towards that goal, after HHH03/05. But a realistic typical
error on our q values is ![]() ,
and our sample of 15 systems with q
> 0.84 is so small, relative to the 102 systems used by
Lucy, as to render any confirmation or rejection of
,
and our sample of 15 systems with q
> 0.84 is so small, relative to the 102 systems used by
Lucy, as to render any confirmation or rejection of
![]() impossible. Our data might be more useful to constrain
impossible. Our data might be more useful to constrain
![]() ,
but extensive simulations would be necessary to estimate the detection
biases, and this effort does not appear justified by our small sample.
Therefore, the twin hypothesis remains an open question as far as the
SMC (and any galaxy other than ours) is concerned.
,
but extensive simulations would be necessary to estimate the detection
biases, and this effort does not appear justified by our small sample.
Therefore, the twin hypothesis remains an open question as far as the
SMC (and any galaxy other than ours) is concerned.
4.6 Extinction and distances
4.6.1 Color excess and extinction
The histogram of the 28 color excesses is given in Fig. 15. Note that one
system (5 196565) does not have B and V light
curves and four systems have an unreliable observed B-V index
(see Sect. 3.3).
The mean value is ![]()
![]() 0.051 mag with individual values in the range
0.052-0.252 mag. By comparison, for four
stars in the bar, Gordon et al. (2003) found values
ranging from 0.147 to 0.218 mag. From their
extinction map across the SMC, Zaritsky et al. (2002) give EB-V
0.051 mag with individual values in the range
0.052-0.252 mag. By comparison, for four
stars in the bar, Gordon et al. (2003) found values
ranging from 0.147 to 0.218 mag. From their
extinction map across the SMC, Zaritsky et al. (2002) give EB-V ![]() 0.05-0.25 mag. Sasselov et al. (1997) found a mean
value of
0.05-0.25 mag. Sasselov et al. (1997) found a mean
value of ![]()
![]() 0.009 mag. Thus, our results agree very well with these
previous determinations. In order to investigate the spatial
variation of the extinction across the studied field, EB-V was
plotted against
0.009 mag. Thus, our results agree very well with these
previous determinations. In order to investigate the spatial
variation of the extinction across the studied field, EB-V was
plotted against ![]() ,
the distance to the optical center along the projected axis
(not shown). No correlation was found. The GIRAFFE
field is likely too small to detect a trend, if any.
,
the distance to the optical center along the projected axis
(not shown). No correlation was found. The GIRAFFE
field is likely too small to detect a trend, if any.
![\begin{figure}
\par\includegraphics[width=7.5cm]{10284fg15.eps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg693.png)
|
Figure 15: Histogram of color excesses of 28 binaries in 0.025 bins. The best Gaussian fit is over-plotted. |
| Open with DEXTER | |
4.6.2 Distance
The parameters relevant to the determination of the distance moduli are
shared between Tables 4
(synthetic photometry) and 15.
The DM was computed in both V- and I-band,
as explained in Sect. 3.12. One
system (5 196565) has no value because of only one
available light curve. Fortunately, for most systems the difference
between the two computations of the individual DM is low and
well within the uncertainties. As expected in Sect. 3.12, the I-values
have a slightly lower absolute uncertainty. The discrepancy between the
V and I moduli is
negligible: ![]() mag
with a scatter
mag
with a scatter ![]() mag
for the 28 reliable systems.
mag
for the 28 reliable systems.
The DMi were checked for a possible dependence upon a number
of parameters: apparent visual magnitude, absolute visual magnitude,
systemic velocity, color excess and distance to the optical center
along the projected axis. Statistical tests were performed (calculus of
the Spearman rank correlation coefficient, followed by a Student
T test) and no significant correlation was found. The ![]() vs.
vs.
![]() and
and ![]() vs.
vs. ![]() diagrams are shown in Fig. 16 (bottom).
In order to calculate an unbiased mean DM, the
HR diagrams (Figs. 26-28) of the
individual systems were used to select the systems suitable for this
purpose. This is actually a more objective criterion than relying
solely on the quality of the light curves and spectra. Therefore, eight
objects with strong discrepancies with theoretical models were
conservatively discarded from the sample of 27 binaries (which
remain from the initial sample of 33 binaries, after
suppression of stars with unreliable or no color index,
or with a third light, see below). Some of the primaries of
these eight systems may have luminosities really higher or lower than
expected, but we can lucidly assume that most discrepancies are the
direct consequences of low S/N
data and/or third light contamination. These suspicious systems are
indicated by open symbols in Fig. 16.
diagrams are shown in Fig. 16 (bottom).
In order to calculate an unbiased mean DM, the
HR diagrams (Figs. 26-28) of the
individual systems were used to select the systems suitable for this
purpose. This is actually a more objective criterion than relying
solely on the quality of the light curves and spectra. Therefore, eight
objects with strong discrepancies with theoretical models were
conservatively discarded from the sample of 27 binaries (which
remain from the initial sample of 33 binaries, after
suppression of stars with unreliable or no color index,
or with a third light, see below). Some of the primaries of
these eight systems may have luminosities really higher or lower than
expected, but we can lucidly assume that most discrepancies are the
direct consequences of low S/N
data and/or third light contamination. These suspicious systems are
indicated by open symbols in Fig. 16.
From the sample of 33 objects, six at least must be discarded for the computation of the mean distance modulus: 5 196565 because of the total lack of B and V data, 4 163552 because of a third light contribution, and four systems which do not have reliable observed color indices (5 038089, 5 180185, 5 261267 and 5 277080). At that stage, there remain 27 systems with presumably good distance moduli, without consideration of their HR diagrams. Removing further the eight systems which have a dubious position in the HR diagram (i.e. 4 113853, 4 121084, 4 121110, 4 175149, 4 175333, 5 95557, 5 123390 and 5 185408) leaves us with only 19 systems, a bit more than half of the initial sample. By ``dubious position'' we mean systems for which the error bar of the mass does not overlap that of the luminosity/temperature on the HR diagram. A third subsample was defined, which contains the nine ``best'' systems, defined as those detached systems for which either the luminosity/temperature error bar overlaps the Z=0.004 evolutionary track, or the mass error bar overlaps the representative point of the corresponding component for at least one of the components. These systems are 4 121461, 4 160094, 5 16658, 5 32412, 5 100731, 5 111649, 5 265970, 5 266131 and 5 266513.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg16.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg697.png)
|
Figure 16:
Top: distribution of the V-
(left) and I-band (right)
distance moduli. The distribution of the whole sample of
27 systems with good colors and presumably without third light
(dashed line) is shown. Only binaries with good HR diagrams
are selected for the smaller statistics. The best-fitting Gaussian
curves for the 19-binary distributions are over-plotted. Bottom:
distance modulus vs. absolute visual magnitude (left)
and distance modulus vs. apparent visual magnitude (right).
The estimated magnitude cut-off for a mean extinction is indicated by
the diagonal solid line; the dashed lines correspond to the cut-off
lines for |
| Open with DEXTER | |
Another important point is to identify possible biases acting upon the
DM distribution. Actually, there is a small magnitude cut-off.
This is the apparent magnitude cut-off, close to ![]() mag.
It almost coincides with the apparent magnitude of
5 266513, the faintest binary
of our sample, whose spectra have (smoothed) S/N
in the 18-50 range. This V cut-off sets a
higher limit for the absolute magnitude a binary should have in order
to be seen across the whole depth of the SMC field. If we take
mag.
It almost coincides with the apparent magnitude of
5 266513, the faintest binary
of our sample, whose spectra have (smoothed) S/N
in the 18-50 range. This V cut-off sets a
higher limit for the absolute magnitude a binary should have in order
to be seen across the whole depth of the SMC field. If we take ![]() 19.5 as the
upper limit for the DM, we find that the
19.5 as the
upper limit for the DM, we find that the ![]() cut-off
is -1.82
cut-off
is -1.82 ![]() 0.16 mag
with
0.16 mag
with ![]()
![]() 0.051 mag. The cut-off strip for
0.051 mag. The cut-off strip for ![]() mag
is indicated in Fig. 16
(bottom-left). Systems to the right of the oblique
lines are too faint to be observed as SB2 with good enough spectra.
mag
is indicated in Fig. 16
(bottom-left). Systems to the right of the oblique
lines are too faint to be observed as SB2 with good enough spectra.
For example, in spite of a reliable solution, the binary
4 175333 should be discarded from the calculus of the mean DM
in order to remove the observational bias just discussed. Indeed, with ![]() and
and ![]() ,
this system would not be perceived as an SB2 if it were more distant,
i.e. if it had
,
this system would not be perceived as an SB2 if it were more distant,
i.e. if it had ![]() (see Fig. 16,
bottom-left). Indeed this object had already been
discarded on the basis of the peculiar position of its components in
the HR diagram.
(see Fig. 16,
bottom-left). Indeed this object had already been
discarded on the basis of the peculiar position of its components in
the HR diagram.
At the other end of the ![]() -spectrum,
there is a second cut-off, but this one does not bias the
DM-distribution. This is the cut-off of the luminosity function,
responsible for the depleted left-part of Fig. 16 (bottom-right).
Close to
-spectrum,
there is a second cut-off, but this one does not bias the
DM-distribution. This is the cut-off of the luminosity function,
responsible for the depleted left-part of Fig. 16 (bottom-right).
Close to ![]() mag,
this is roughly the low-limit for late O stars: intrinsically
brighter stars should be earlier O stars, but they are very
scarce, so the probability of finding one in a sample of
33 objects is very low.
mag,
this is roughly the low-limit for late O stars: intrinsically
brighter stars should be earlier O stars, but they are very
scarce, so the probability of finding one in a sample of
33 objects is very low.
The histograms of the individual DMi in V and I are shown in Fig. 16 (top-left). For a given band, both the whole sample (i.e. the 27 systems remaining after the exclusion of the obviously problematic ones) and the ``good systems'' (i.e. the 19 best ones) distributions are plotted. Although eight systems are considered as less reliable, one can see that all but three (4 175149, 4 175333 and 5 123390) discarded values are within the ``good systems'' range of DMi. This range spans 0.45 mag, from 18.87 to 19.32. The modes of the V and I distributions of the ``good systems'' are 19.15 and 19.20 respectively. In addition the distribution of the nine ``best'' systems is plotted in red.
One can wonder to which extent the average value of the DMs is
the most pertinent indicator of the mean distance of our stars. There
is a ![]() to 0.1 mag deviation between the modal and mean values of the
distributions (for both V and I),
but we verified that these distributions, despite their apparent
asymmetry, do not depart from Gaussians in a significant way.
Because the modal value is not a robust one for these small samples, we
rather considered the weighted average and the median values.
to 0.1 mag deviation between the modal and mean values of the
distributions (for both V and I),
but we verified that these distributions, despite their apparent
asymmetry, do not depart from Gaussians in a significant way.
Because the modal value is not a robust one for these small samples, we
rather considered the weighted average and the median values.
The average and median distance moduli for the three subsamples defined above are given in Table 10 for the V and I bands. The average values are weighted by the reciprocal variance of the individual moduli. The rms scatter is given besides each average value; besides each median value is given the width of the distribution, defined as half the difference between the upper and lower quartiles.
Table 10: Summary of the average and median distance moduli, for the three subsamples defined in the text.
We see that the V and I
distance moduli of any given subsample are perfectly consistent. More
surprisingly, the sample of all 27 systems has a slightly
shorter distance modulus than the two other subsamples, while it
contains many systems with high positive ![]() values
(see Sect. 4.3).
Likewise, the sample of the nine best systems (i.e. those
which match the standard Z=0.004 evolutionary
tracks best) have the same distance modulus as the sample of the
19 good systems. These results suggest that the components
which are overluminous with respect to their Z=0.004
track are not necessarily overluminous in reality. Otherwise, if their
luminosity were overestimated, they should also lie at a larger
apparent distance.
values
(see Sect. 4.3).
Likewise, the sample of the nine best systems (i.e. those
which match the standard Z=0.004 evolutionary
tracks best) have the same distance modulus as the sample of the
19 good systems. These results suggest that the components
which are overluminous with respect to their Z=0.004
track are not necessarily overluminous in reality. Otherwise, if their
luminosity were overestimated, they should also lie at a larger
apparent distance.
Finally, combining both V and I
results, we adopt
as the most probable average distance modulus for our sample. That value is 0.20
4.6.3 Distance according to the detached systems versus distance according to the others
In the context of a search for systematic effects, one may wonder
whether detached systems give a different distance modulus than the
semi-detached or contact ones. Separating our 19 ``good''
systems into a group of 13 detached ones and a group of
6 semi-detached ones, we computed the weighted average
distance modulus (in the I band)
for each group. For the detached systems we
obtain ![]()
![]() 0.04 mag; the error is the rms scatter divided by
0.04 mag; the error is the rms scatter divided by ![]() .
For the semi-detached and contact ones, we obtain
.
For the semi-detached and contact ones, we obtain ![]()
![]() 0.05 mag. Thus, our 6 semi-detached and contact
systems are, on average, 0.08 mag remoter than our
13 detached systems. Given the error bars, the difference is
not significant since it amounts to only about
0.05 mag. Thus, our 6 semi-detached and contact
systems are, on average, 0.08 mag remoter than our
13 detached systems. Given the error bars, the difference is
not significant since it amounts to only about ![]() .
.
Nevertheless, we looked at the distance moduli determined by
HHH03/05 to see whether a similar difference exists in their data.
Interestingly, almost the same difference appears: for
21 detached systems, one has ![]()
![]() 0.06, while for the 29 others one has
0.06, while for the 29 others one has ![]()
![]() 0.05. So, here too, the semi-detached and contact systems are
remoter than the detached ones on average, and by a similar amount, of
0.06 mag. The effect is only on the order of
0.05. So, here too, the semi-detached and contact systems are
remoter than the detached ones on average, and by a similar amount, of
0.06 mag. The effect is only on the order of ![]() ,
so it is formally not significant. The coincidence between our
results and those of HHH03/05 remains intriguing, however.
,
so it is formally not significant. The coincidence between our
results and those of HHH03/05 remains intriguing, however.
4.6.4 Depth
The observed dispersion of the DMi is the convolution of the true depth
of our population of binaries with the average uncertainty of the DM
determined for one binary system. Hence, under the assumption of a
Gaussian distribution of both the cosmic and the error standard
deviations, the true ![]() depth
is given by the quadratic difference between the observed standard
deviation of the
moduli and the typical error on the modulus of an individual system.
The observed standard deviation being 0.144 mag, and taking
the average of the squares of the estimated errors as representative of
the typical error, the
depth
is given by the quadratic difference between the observed standard
deviation of the
moduli and the typical error on the modulus of an individual system.
The observed standard deviation being 0.144 mag, and taking
the average of the squares of the estimated errors as representative of
the typical error, the ![]() depth
becomes
depth
becomes ![]() mag
rms (
mag
rms (![]() 3.9 kpc),
since the average variance of an individual I distance
modulus is 0.00479 mag2. Groenewegen
gives 0.11 mag (3.4 kpc) as the intrinsic
3.9 kpc),
since the average variance of an individual I distance
modulus is 0.00479 mag2. Groenewegen
gives 0.11 mag (3.4 kpc) as the intrinsic ![]() spread for his sample of SMC Cepheids, so our result perfectly
agrees with his. The HHH05 sample (29 binaries)
displays a higher dispersion,
spread for his sample of SMC Cepheids, so our result perfectly
agrees with his. The HHH05 sample (29 binaries)
displays a higher dispersion, ![]() 0.28 mag (
0.28 mag (![]() 7.8 kpc),
but the authors consider that value as an overestimate. Our depth
estimate is only 15% higher than that of Groenewegen (2000).
7.8 kpc),
but the authors consider that value as an overestimate. Our depth
estimate is only 15% higher than that of Groenewegen (2000).
4.6.5 Temperature scale and distance modulus
We have seen that a suspicion remains, that the effective temperatures
may have been overestimated in a number of systems. What is the effect
of such an overestimate on the resulting distance modulus? For the sake
of simplicity, let us consider a single star rather than a
binary system. Its distance modulus can be written (under the
assumption that we use the V magnitude) as
![\begin{eqnarray*}m-M&=&V_q+2.5~\log\left(10^{-0.4~M_V}\right)-3.1~E_{B-V} \\
&...
...\rm bol}-BC)}\right) \\
&& -~3.1~\left[(B-V)_q-(B-V)_0\right],
\end{eqnarray*}](/articles/aa/full_html/2010/12/aa10284-08/img725.png)
because
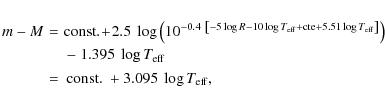
where we have taken into account that the radius is constant. Introducing a second star will essentially leave the result unchanged, because the ratio of the temperatures will appear (as well as the ratio of radii), which can be considered constant. Therefore, by differentiating the last equation above, one finally gets a very simple relation between a change
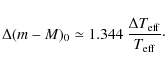
|
(30) |
For 4 175333, for instance, the temperature excess is especially large because it reaches
A quick estimate of the average temperature-excess of the nine ``best'' systems leads to an average modulus excess of about 0.04 mag, so that the corrected distance modulus would be reduced to 19.07, which still remains rather long compared to the frequently quoted value of 18.9. In any case, it appears difficult to reduce the distance modulus to less than 19.0. Thus, our data do favor the ``long'' rather than the ``short'' distance scale to the Magellanic Clouds.
5 Conclusions
Our first goal was to extract the fundamental stellar parameters
characterizing 33 SB2 systems and then to test the
reliability of stellar evolution models at low metalicity. We showed
that most components of detached systems have properties in fair
agreement with the predictions of the Geneva single-star models at Z
=0.004, although several systems appear slightly overluminous for their
mass. From the subsample of detached systems, we give a mass-luminosity
relation valid for masses between ![]() and
and ![]() .
Despite the lack of evolutionary cross checks, the semi-detached
binaries appear to satisfy the typical morphology of Algol-like
systems: a main-sequence primary with a large, less massive
and more evolved secondary companion.
.
Despite the lack of evolutionary cross checks, the semi-detached
binaries appear to satisfy the typical morphology of Algol-like
systems: a main-sequence primary with a large, less massive
and more evolved secondary companion.
Our binaries were then used as primary standard candles.
Average distance moduli obtained from the I-band
data show no systematic difference compared to values obtained from the
V data. For each band, the frequency
distribution of the DMi is not significantly different from a Gaussian.
Combining V and I results
and considering both the mean and the median values, we adopt ![]()
![]() 0.03 as the average DM for the 19 most reliable systems. We
showed that even if we correct the effective temperatures for a
possible overestimate (hence revising the luminosity of our systems
downwards), the average DM would still remain above 19.00,
so that our results support the long distance scale to the
Magellanic Clouds rather than the short one. The true depth of our
sample is estimated to be 2
0.03 as the average DM for the 19 most reliable systems. We
showed that even if we correct the effective temperatures for a
possible overestimate (hence revising the luminosity of our systems
downwards), the average DM would still remain above 19.00,
so that our results support the long distance scale to the
Magellanic Clouds rather than the short one. The true depth of our
sample is estimated to be 2 ![]()
![]() (
(![]() 7.6 kpc),
if we consider the
7.6 kpc),
if we consider the ![]() interval as
representative.
interval as
representative.
We found a significant apsidal motion for at least three systems. For one system, the apsidal motion might be affected by an unseen third companion, but at least two other systems most probably owe it to the stellar structure of their components alone. The observed and predicted precession rates perfectly agree for the latter two systems, which are now circularizing their orbit, and the agreement extends to one or two other systems showing much less precise apsidal motion. The system 5 266131 probably shows the largest precession motion of all systems hosting main sequence stars, which is exclusively due to the non-point mass nature of the components.
Beside the astrophysical parameters and the distance moduli,
other interesting results were obtained. We showed that the twin
hypothesis for massive binaries is not supported by our results,
although they are not strong enough to reject it either. Our sample of
23 detached systems agrees quite well with a standard flat
mass-ratio spectrum. There is a clear cut-off of the q-distribution
at
![]() .
Therefore, the high proportion of detached binaries with a
q value close to unity is more probably the
result of an observational bias. The discrepancy observed by
Pinnsonneault & Stanek (2006)
may well be due to a number of underestimated mass ratios in the
HHH03/05 sample. The distribution of the mass ratios of the
semi-detached/contact binaries is consistent with a flat distribution
restricted to the interval
0.4 < q < 0.8. The sample is too
small (10 objects) to tell more.
.
Therefore, the high proportion of detached binaries with a
q value close to unity is more probably the
result of an observational bias. The discrepancy observed by
Pinnsonneault & Stanek (2006)
may well be due to a number of underestimated mass ratios in the
HHH03/05 sample. The distribution of the mass ratios of the
semi-detached/contact binaries is consistent with a flat distribution
restricted to the interval
0.4 < q < 0.8. The sample is too
small (10 objects) to tell more.
Another important result is the bimodal distribution of the
radial velocity of the H II gas,
with peak values at 145.2 ![]() 0.5 and 161.4
0.5 and 161.4 ![]() 0.6 km s-1.
0.6 km s-1.
Finally, we emphasize that the accomplishment of this project was possible thanks to the public availability of the OGLE-II catalog of EB light curves, the OSTAR2002/ BSTAR2006 libraries of synthetic spectra, the KOREL code and the PHOEBE interface to the WD codes.
AcknowledgementsThis work was supported by the Swiss National Fund for Scientific Research. RG warmly thanks K. Pavlovski and S. Ilijic for fruitful discussions and skilled advice during his one-week stay at the Department of Physics of the University of Zagreb (Croatia) in September 2005. P. Hadrava and A. Prsa are thanked for their help with the program KOREL and the PHOEBE interface to the WD program respectively. We are indebted to Prof. André Blecha (now retired) for having led the creation of the Data Reduction Software of the FLAMES-GIRAFFE instrument, which allowed PN and FR to obtain Guaranteed Time Observations, part of which are analyzed here. P.N. thanks Dr. Paul Bartholdi, who had initiated him to the SM macro amoeba. We also thank the anonymous referee of a previous version of this paper; one of his remarks led to a re-analysis of our spectra, which resulted in more robust masses and effective temperatures. Finally, we thank W. van Rensbergen for constructive remarks.
References
- Andersen, J. 1975a, A&A, 44, 349
- Andersen, J. 1975b, A&A, 44, 355
- Andersen, J. 1975c, A&A, 44, 445
- Andersen, J., Clausen, J. V., & Nordtsröm, B. 1980, in Close binary stars: observations and interpretation, ed. M. J. Plavec, D. M. Popper, R. K. Ulrich (Dordrecht: Reidel), IAU Symp., 88, 81
- Bessell, M. S. 1990, PASP, 102, 1181
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231
- Bonanos, A. Z., Stanek, K. Z., Kudritzki, R. P., et al. 2006, ApJ, 652, 313
- Bono, G., Caputo, F., & Marconi, M. 2001, MNRAS, 325, 1353
- Bouret, J.-C., Lanz, T., Hillier, D. J., et al. 2003, ApJ, 95, 1182
- Budding, E., Erdem, A., Cicek, C., et al. 2004, A&A, 217, 263
- Bulut, I., & Demircan, O. 2007, MNRAS, 378, 179
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245
- Charbonnel, C., Meynet, G., Maeder, A., Schaller, G., & Schaerer, D. 1993, A&AS, 101, 415
- Claret, A. 2005, A&A, 440, 647
- Claret, A., & Giménez, A. 1993, A&A, 277, 502
- Claret, A., & Giménez, A. 1998, A&AS, 133, 123
- Clausen, J. V. 2000, in From Extrasolar Planets to Cosmology: The VLT Opening Symp.: Proc. ESO Symposium Held at Antofagasta, Chile, 1-4 March 1999, ed. J. Bergeron, & A. Renzini (Springer-Verlag), 225
- Clausen, J. V. 2004, NewAR, 48, 679
- De Mink, S. E., Pols, O. R., & Hilditch, R. W. 2007, A&A, 467, 1181
- Etzel, P. B. 1980, EBOP User's Guide, 3rd Ed., UCLA Astronomy & Astrophysics
- Fitzpatrick, E. L. 1985, ApJS, 59, 77
- Fitzpatrick, E. L., Ribas, I., Guinan, E. F., et al. 2002, ApJ, 564, 260
- Fitzpatrick, E. L., Ribas, I., Guinan, E. F., Maloney, F. P., & Claret, A. 2003, ApJ, 587, 685
- Flower, P. J. 1996, ApJ, 469, 355
- González, J. F., Ostrov, P., Morrell, N., & Minniti, D. 2005, ApJ, 624, 946
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279
- Graczyk, D. 2003, MNRAS, 342, 1334
- Groenewegen, M. A. T. 2000, A&A, 363, 901
- Guinan, E. F. 2004, NewAR, 48, 647
- Guinan, E. F. 2007, 2007, in ASP Conf. Ser., 370, 125
- Guinan, E. F., Fitzpatrick, E. L., DeWarf, L. E., et al. 1998, ApJ, 509, L21
- Hadrava, P. 1995, A&AS, 114, 393
- Hadrava, P. 2004, Publ. Astron. Inst. ASCR, 92, 15
- Harries, T. J., Hilditch, R. W., & Howarth, I. D. 2003, MNRAS, 339, 157
- Hensberge, H. H., & Pavlovski, K. 2007, in Binary stars as critical tools & tests in contemporary astrophysics, ed. W. I. Hartkopf, E. F. Guinan, P. Harmanec (Cambridge University Press), IAU Symp., 240, 136
- Hensberge, H., Pavlovski, K., & Verschueren, W. 2000, A&A, 358, 553
- Hilditch, R. W. 2001, An Introduction to Close Binary Stars (Cambridge University Press)
- Hilditch, R. W., Howarth, I. D., & Harries, T. J. 2005, MNRAS, 357, 304 (HHH05)
- Huang, W., & Gies, D. R. 2006a, ApJ, 648, 580
- Huang, W., & Gies, D. R. 2006b, ApJ, 648, 591
- Hunter, I., Dufton, P. L., Smartt, S. J., et al. 2007, A&A, 466, 277
- Hut, P. 1981, A&A, 99, 126
- Ilijic, S., Hensberge, H., Pavlovski, K., & Freyhammer, L. M. 2004, in ASP Conf. Ser., 318, 111
- Jaschek, C., & Jaschek, M. 1987, The Classification of Stars (Cambridge University Press)
- Kilian-Montenbruck, J., Gehren, T., & Nissen, P. E. 1994, A&A, 291, 757
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83
- Lucke, P. B., & Mayor, M. 1980, A&A, 92, 182
- Lucy, L. B. 2006, A&A, 457, 629
- Lupton, R. H., & Monger, P. 2000, SuperMongo Graphics and Computational Package, Princeton Astronomical Observatory and MacMaster University
- Massey, P., Zangari, A. M., Morrell, N. I., et al. 2009, ApJ, 692, 618
- Mazeh, T. 2008, EAS Publications Series, 29, 1
- Mokiem, M. R., de Koter, A., Evans, C. J. et al. 2006, A&A, 456, 1131
- Mokiem, M. R., de Koter, A., Evans, C. J., et al. 2007, A&A, 465, 1003
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127
- North, P., & Zahn, J.-P. 2003, A&A, 405, 677
- North, P., & Zahn, J.-P. 2004, New Astron. Rev., 48, 677
- Paczynski, B. 2001, AcA, 51, 81
- Pavlovski, K., & Hensberge, H. H. 2005, A&A, 439, 309
- Peters, G. J., & Adelman, S. J. 2006, Astrophysics in the Far Ultraviolet: Five Years of Discovery with FUSE, ed. G. Sonneborn, H. Moos, & B.-G. Andersson, ASPC, 348, 136
- Petrova, A. V., & Orlov, V. V. 1999, AJ, 117, 587
- Pinsonneault, M. H., & Stanek, K. Z. 2006, ApJ, 639, L67
- Pourbaix, D., Tokovinin, A., Batten, A., et al. 2004, A&A, 424, 727
- Prsa, A. 2006, PHOEBE Scientific Reference, Univ. of Ljubljana, available in electronic form at http://phoebe.fiz.uni-lj.si/
- Prsa, A., & Zwitter, T. 2005, ApJ, 628, 426
- Ribas, I., Guinan, E. F., Fitzpatrick, E. L., et al. 2000, ApJ, 528, 692
- Ribas, I., Fitzpatrick, E. L., Maloney, F. P., Guinan, E. F., & Udalski, A. 2002, ApJ, 574, 771
- Ribas, I., Jordi, C., Vilardell, F., et al. 2005, ApJ, 635, 37
- Sasselov, D. D., Beaulieu, J. P., Renault, C., et al. 1997, A&A, 324, 471
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269
- Simon, K. P., & Sturm, E. 1994, A&A, 281, 286
- Stanimirovic, S., Staveley-Smith, L., & Jones, P. A. 2004, ApJ, 604, 176
- Torres, G., & Carranza, G. J. 1987, MNRAS, 226, 513
- van Hamme, W. 1993, AJ, 106, 2096
- van Rensbergen, W., De Loore, C., & Jansen, K. 2006, A&A, 446, 1071
- van Rensbergen, W., De Greve, J. P., De Loore, C., & Mennekens, N. 2008, A&A, 487, 1129
- van Rensbergen, W., De Greve, J. P., Mennekens, N., Jansen, K., & De Loore, C. 2010, A&A, 510, A13
- Vilardell, F., Ribas, I., Jordi, C., Fitzpatrick, E. L., & Guinan, E. F. 2010, A&A, 509, 70
- Wilson R. E. 1979, ApJ, 234, 1054
- Wilson R. E. 1990, ApJ, 356, 613
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605
- Wilson, R. E., & Biermannn, P. 1976, A&A, 48, 349
- Wilson R. E., & van Hamme, W. 2004, Computing Binary Stars Observables, Gainesville, Univ. Florida, available in electronic form at ftp://ftp.astro.ufl.edu/pub/wilson/
- Wyithe, J. S. B., & Wilson, R. E. 2001, ApJ, 559, 260
- Wyithe, J. S. B., & Wilson, R. E. 2002, ApJ, 571, 293
- Wyrzykowski, L., Udalski, A., Kubiak, M., et al. 2004, AcA, 54, 1
- Zaritsky, D., Harris, J., Thompson, I. B., Grebel, E. K., & Massey, P. 2002, AJ, 123, 855
Online Material
Table 11: Orbital parameters.
Table 12: Wilson-Devinney analysis, as obtained on the basis of both photometry and spectroscopy.
Table 13: Astrophysical parameters for the primary components.
Table 14: Astrophysical parameters for the secondary components.
Table 15: Distance determination.
Table 16: Light curves: ratio of the primary minimum to the rms (I-band), rms scatters and minimum chi-squared values from WD/PHOEBE code.
Table 17: Radial velocity curves: rms scatters.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg17.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1809.png)
|
Figure 17:
I-band light curves with |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg18.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1810.png)
|
Figure 18: Same as Fig. 17, for 12 more stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg19.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1811.png)
|
Figure 19: Same as Fig. 17, for nine more stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg20.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1812.png)
|
Figure 20:
Radial velocity data and best-fitting RV curves.The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg21.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1813.png)
|
Figure 21: Same as Fig. 20, for 12 more stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg22.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1814.png)
|
Figure 22: Same as Fig. 20, for nine more stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg23.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1815.png)
|
Figure 23: Mass-surface gravity diagrams: the positions of the primary and the secondary components are indicated by filled and open symboles, respectively. The lines ares isochrones from Charbonnel et al. (1993) at Z = 0.004, with ages of 3, 5, 10, 20, 30, 40, 50 and 100 Myr. See text for comments on individual stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg24.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1816.png)
|
Figure 24: Same as Fig. 23, for 12 more stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg25.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1817.png)
|
Figure 25: Same as Fig. 23, for nine more stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg26.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1818.png)
|
Figure 26:
HR diagrams: the positions of the primary and the secondary components
are indicated by filled and open symbols, respectively. The primary is
the component with the larger mass. The evolutionary tracks from
Charbonnel et al. (1993)
at Z = 0.004, corresponding to the observed masses,
are indicated by solid (primary) and dashed black lines (secondary).
Since
these authors adopt a helium content Y=0.24+3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg27.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1819.png)
|
Figure 27: Same as Fig. 26, for 12 more stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg28.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1820.png)
|
Figure 28: Same as Fig. 26, for nine more stars. |
| Open with DEXTER | |
Appendix A: The individual binaries
Each system is discussed thoroughly in this section. We give details concerning the light-curve solution, the radial-velocity solution, the temperature and luminosity-ratio determinations and the characteristics of the spectra. Also discussed are the positions of the components in the mass-surface gravity plane and the temperature-luminosity (HR) diagram. A review of the distances and collective properties of the whole sample of 33 binaries is given in Sect. 4. Except where otherwise stated, we mean the I-band light curve when we refer to the light curve of a specific system.
A.1 4 110409
With a difference of 0.04 mag in the brightness level between
phase 0.25 and phase 0.75, this semi-detached system
displays the most asymmetric light curve among all systems studied
here.
The light curve is bright (
![]() mag) and of high
quality, with a low rms scatter combined with a deep primary eclipse (
mag) and of high
quality, with a low rms scatter combined with a deep primary eclipse (
![]()
![]() 65).
This EB-type light curve shows a relatively strong depression occurring
just before the primary minimum. Actually, this is strong evidence for
absorption by a gas stream stemming from the (inner) L1 Lagrangian
point and seen in projection against the primary surface (HHH05).
As a consequence, the use of a ``simple'' symmetric model for
the light-curve fit is not satisfactory, resulting in a rather poor fit
despite the intrinsic quality of the observations. Therefore, this
solution was subsequently improved by adding a cool spot on the equator
of the primary component (see Sect. 3.7). The
parameters of the spot are: a colatitude of
65).
This EB-type light curve shows a relatively strong depression occurring
just before the primary minimum. Actually, this is strong evidence for
absorption by a gas stream stemming from the (inner) L1 Lagrangian
point and seen in projection against the primary surface (HHH05).
As a consequence, the use of a ``simple'' symmetric model for
the light-curve fit is not satisfactory, resulting in a rather poor fit
despite the intrinsic quality of the observations. Therefore, this
solution was subsequently improved by adding a cool spot on the equator
of the primary component (see Sect. 3.7). The
parameters of the spot are: a colatitude of ![]() rad (fixed),
a longitude of 0.569 rad, an angular radius of
0.3 rad and a temperature factor of 0.6,
i.e. the effective temperature of the spot is 0.6
that of the rest of the stellar surface. Although this
new synthetic light curve gives a far more satisfactory fit, the
rad (fixed),
a longitude of 0.569 rad, an angular radius of
0.3 rad and a temperature factor of 0.6,
i.e. the effective temperature of the spot is 0.6
that of the rest of the stellar surface. Although this
new synthetic light curve gives a far more satisfactory fit, the ![]() curve
reveals that this system is certainly more complex than this ``one
circular cool spot'' model. Actually, there are still some
discrepancies at the bottom of the eclipses and just after the
secondary minimum. Nevertheless, this model is certainly sufficient to
reliably set the inclination, the brightness
ratio of the components and the maximum out-of-eclipse flux. On the
finding chart, the image of this star is slightly elongated in the
EW direction, suggesting a blend with another, fainter star,
which would lie
curve
reveals that this system is certainly more complex than this ``one
circular cool spot'' model. Actually, there are still some
discrepancies at the bottom of the eclipses and just after the
secondary minimum. Nevertheless, this model is certainly sufficient to
reliably set the inclination, the brightness
ratio of the components and the maximum out-of-eclipse flux. On the
finding chart, the image of this star is slightly elongated in the
EW direction, suggesting a blend with another, fainter star,
which would lie ![]() or slightly farther away to the West. Nevertheless, no clear sign
of a third light is seen in the lightcurve.
or slightly farther away to the West. Nevertheless, no clear sign
of a third light is seen in the lightcurve.
The RV curves are well constrained with 11 out-of-eclipse spectra and notably observations close to phase 0.75. This system was previously studied by HHH05. There are significant differences between their RV parameters and ours. Our RV semi-amplitudes are 135 and 259 km s-1, to be compared to their values of 160 and 247 km s-1. Besides a lower S/N and resolving power than us, in this particular case the discrepancy is certainly due to their admitted lack of observations close to the quadratures. Consequently, our value for the mass ratio, q = 0.52, is certainly more secure than theirs (0.65).
We found a spectroscopic B luminosity ratio of 1.45. This is higher than the photometric value (1.29), perhaps because of the large distortion of the Roche lobe filling companion. Interestingly, the brighter, i.e. primary, component has lower monochromatic luminosities than the secondary component: even though the primary has a higher bolometric luminosity, it emits mostly in the UV part of the spectrum, so that its I luminosity, for instance, is lower than for the secondary.
The most interesting parts of the separated spectra of both
components are presented in Fig. A.1.
As a consequence of the low B luminosity
of the primary, the spectrum of the latter is the noisier of the pair.
Not surprisingly, in both spectra the most prominent features are the H
I and He I lines.
It is tempting to identify a number of features in the primary
spectrum with the C II 4267, O II 4276-4277,
Si III 4553, Si IV 4089
and Si IV 4116 lines.
Nevertheless, both the lack of positive identification of the He II 4542
line for a ![]() 14
14
![]() star
and the noisy profile of the He I lines
mean that one must be careful in not over-interpreting a spectrum of
rather poor quality. The better secondary spectrum displays cleaner
features. The He I 4471 and Mg II 4481
lines allow us to secure the temperature of the secondary.
star
and the noisy profile of the He I lines
mean that one must be careful in not over-interpreting a spectrum of
rather poor quality. The better secondary spectrum displays cleaner
features. The He I 4471 and Mg II 4481
lines allow us to secure the temperature of the secondary.
By fixing the photometric temperature and B luminosity ratios, a least-squares fit of the 11 out-of-eclipse spectra provided a primary temperature very close to 32 500 K, that is to say 7000 K more than what was determined by HHH05.
Both mass-![]() and the HR diagrams are typical of a massive Algol-type binary. The
brighter and more massive component of the system appears to be close
to the zero-age main sequence (ZAMS), while the secondary component is
larger and far more luminous than a non-evolved star of the same mass.
and the HR diagrams are typical of a massive Algol-type binary. The
brighter and more massive component of the system appears to be close
to the zero-age main sequence (ZAMS), while the secondary component is
larger and far more luminous than a non-evolved star of the same mass.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA1a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{10284fgA1b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1823.png)
|
Figure A.1:
Sections of the separated spectra of the primary and secondary
components of the binary 4 110409. The scale on the
vertical axis is adapted to the size of the features in each section.
The red line represents the best-fit synthetic spectrum shifted to the
systemic velocity. Besides prominent H I
and He I lines, Mg II
and Si III lines are visible in
the spectrum of the secondary. The spectrum of the primary is far less
convincing; nevertheless Si IV lines
seem to be present next to H |
| Open with DEXTER | |
A.2 4 113853
The best fit was obtained with a semi-detached model. Because of a
moderate rms scatter (0.017) combined with shallow eclipses (![]() 0.18 mag)
if not purely ellipsoidal variations, the light curve of this binary is
one of the poorest of the whole sample. This low amplitude is due to a
low inclination (
0.18 mag)
if not purely ellipsoidal variations, the light curve of this binary is
one of the poorest of the whole sample. This low amplitude is due to a
low inclination (![]() 60
60
![]() ).
The
).
The ![]() curve
reveals that the profiles of the eclipses are not perfectly
symmetrical. The quality of the data is not sufficient, though, to
trace the possible astrophysical cause of this asymmetry. On the
finding chart, the star seems fairly well isolated.
curve
reveals that the profiles of the eclipses are not perfectly
symmetrical. The quality of the data is not sufficient, though, to
trace the possible astrophysical cause of this asymmetry. On the
finding chart, the star seems fairly well isolated.
Despite only seven out-of-eclipse spectra, the RV curves are rather well constrained with observations close to both quadratures.
The S/N of the composite spectra are low (25-65) and there is a sizeable nebular emission in the Balmer lines. Because of the lack of metallic lines and the severe contamination of the Balmer lines by nebular emission, which hinders the ``disentangling'' procedure, the separated spectra of the components were not used. The least-squares fit was performed, letting both temperatures and the B luminosity ratio free to converge. It provided a temperature ratio remarkably close to the photometric one, and a spectroscopic B luminosity ratio of 0.68, which also perfectly agreed with the photometric ratio (0.68). Thus, fixing the temperature and luminosity ratios to the photometric values was unnecessary for determining a reliable temperature of the primary.
Both the mass-![]() and the HR diagrams show an evolved system with a primary component
seemingly half-way between the ZAMS and the terminal-age main sequence
(TAMS). On the HR diagram the primary lies much higher than
the evolutionary track corresponding to its mass. Whether this is due
to a temperature overestimate (linked e.g. with an
underestimated sky background) or to some evolutionary effect remains
to be examined. Besides, the distance modulus perfectly agrees with the
currently accepted value for the SMC.
and the HR diagrams show an evolved system with a primary component
seemingly half-way between the ZAMS and the terminal-age main sequence
(TAMS). On the HR diagram the primary lies much higher than
the evolutionary track corresponding to its mass. Whether this is due
to a temperature overestimate (linked e.g. with an
underestimated sky background) or to some evolutionary effect remains
to be examined. Besides, the distance modulus perfectly agrees with the
currently accepted value for the SMC.
A.3 4 117831
This faint system has a low-to-medium quality light curve of the
EA type. There is a slight ellipsoidal variation between the
eclipses, and the latter have a similar depth (![]() 0.4 mag). This is a
close detached system with similar components. The finding chart
suggests a possible slight blend with a fainter star located some
0.4 mag). This is a
close detached system with similar components. The finding chart
suggests a possible slight blend with a fainter star located some ![]() to the East of the system. No clear sign of a third light is
seen in the lightcurves though.
to the East of the system. No clear sign of a third light is
seen in the lightcurves though.
The RV curves are well constrained with 12 out-of-eclipse spectra and observations close to phase 0.25 and phase 0.75. The mass ratio close to one (q = 0.98) is indicative of a binary with ``twin'' components.
The separated spectra have a quality too poor to see any
useful metallic line. The Mg II 4481
and C II 4267 are barely visible.
The separation of the Balmer lines was hindered by the strong emission.
A first least-squares fit provided both temperatures and a
poorly constrained spectroscopic B luminosity
ratio of 0.97 ![]() 0.11.
The WD code converged to a higher luminosity ratio
(1.17
0.11.
The WD code converged to a higher luminosity ratio
(1.17 ![]() 0.05),
even when we tried to minimize it by fixing the potential of the
primary. The temperature of the primary was finally set by a fit where
the ratio of temperatures was fixed to the photometric value, and the
luminosity ratio assumed equal to one. The small number of photometric
data in the minima, especially the primary one, probably makes the
photometric
luminosity ratio unreliable and explains why the radius of the primary
component appears slightly smaller than that of the secondary one.
0.05),
even when we tried to minimize it by fixing the potential of the
primary. The temperature of the primary was finally set by a fit where
the ratio of temperatures was fixed to the photometric value, and the
luminosity ratio assumed equal to one. The small number of photometric
data in the minima, especially the primary one, probably makes the
photometric
luminosity ratio unreliable and explains why the radius of the primary
component appears slightly smaller than that of the secondary one.
According to the mass-![]() diagram, the age of the system is about 50 Myr, assuming the
standard SMC metalicity Z=0.004. The positions of
both components in the HR diagram agree to within the error bars with
the evolutionary tracks.
diagram, the age of the system is about 50 Myr, assuming the
standard SMC metalicity Z=0.004. The positions of
both components in the HR diagram agree to within the error bars with
the evolutionary tracks.
This system was studied by Wyithe et al. 2002 (see Table 6). Their results were not constrained by spectroscopy, thus it is not surprising that they found a very different solution. They considered this system as a semi-detached binary with a photometric mass ratio of 0.157. Our spectroscopic results completely rule out that model.
A.4 4 121084
This system displays deep eclipses (>0.6 mag) of similar depth. A slight ellipsoidal variation is visible. This is clearly a close detached system with slightly distorted twin components. No clear sign of crowding is seen on the finding chart, except possibly with very faint neighbor stars.
The RV curves are well constrained with nine out-of-eclipse observations regularly distributed around the quadratures.
The composite spectra are polluted by strong nebular emission
in both H![]() and H
and H![]() lines.
Nevertheless, the widely separated Balmer lines allow a reliable
temperature and luminosity ratio determination. The separated spectra
are useful to confirm the rather high
lines.
Nevertheless, the widely separated Balmer lines allow a reliable
temperature and luminosity ratio determination. The separated spectra
are useful to confirm the rather high ![]() values
of the components. Not surprisingly, no metallic lines are visible
because of the moderate S/N
combined with fast rotational velocities. The potential of the primary
was fixed so that the luminosity ratio given by the WD code
matched the spectroscopic one. The temperature of the primary was
obtained by fixing the temperature ratio to the
photometric one.
values
of the components. Not surprisingly, no metallic lines are visible
because of the moderate S/N
combined with fast rotational velocities. The potential of the primary
was fixed so that the luminosity ratio given by the WD code
matched the spectroscopic one. The temperature of the primary was
obtained by fixing the temperature ratio to the
photometric one.
Both stars lie on the ZAMS, both in the mass-![]() and HR diagrams. On the HR diagram, however, they are
clearly more luminous and hotter than their expected positions for a
metalicity Z=0.004. They would better agree with
the ZAMS and evolutionary tracks for Z=0.001,
as many other systems do. Moving the representative
points to the their expected positions for Z=0.004
would
require a 2000 K decrease in effective temperature; that seems
high, but the residuals between the observed and synthetic composite
spectra show only very subtle changes. Only a modest systematic effect
might be responsible.
and HR diagrams. On the HR diagram, however, they are
clearly more luminous and hotter than their expected positions for a
metalicity Z=0.004. They would better agree with
the ZAMS and evolutionary tracks for Z=0.001,
as many other systems do. Moving the representative
points to the their expected positions for Z=0.004
would
require a 2000 K decrease in effective temperature; that seems
high, but the residuals between the observed and synthetic composite
spectra show only very subtle changes. Only a modest systematic effect
might be responsible.
A.5 4 121110
The medium-to-high quality light curve shows a deep (![]() 0.5 mag)
primary eclipse. A slight ellipsoidal variation is visible
between the eclipses. This is again a close detached system with
slightly distorted components. No star closer than
0.5 mag)
primary eclipse. A slight ellipsoidal variation is visible
between the eclipses. This is again a close detached system with
slightly distorted components. No star closer than
![]() is seen on the finding chart, except for a very faint one lying about
is seen on the finding chart, except for a very faint one lying about ![]() away to the SW.
away to the SW.
The RV curves are well constrained with 11 out-of-eclipse spectra.
There is strong nebular emission in both Balmer lines. The
spectroscopic B luminosity ratio
(0.415 ![]() 0.047)
nicely agrees with the photometric one (0.424), without any
need for fixing the potential of the primary. The temperature of the
primary was fitted after fixing the temperature and luminosity ratios
to their photometric values, as ususal. The Si III 4553
line is clearly visible on the separated spectrum of the primary. The
lack of Mg II 4481 confirms the
relatively high temperature of the primary. The spectrum of the
secondary is too noisy for the
identification of metallic lines.
0.047)
nicely agrees with the photometric one (0.424), without any
need for fixing the potential of the primary. The temperature of the
primary was fitted after fixing the temperature and luminosity ratios
to their photometric values, as ususal. The Si III 4553
line is clearly visible on the separated spectrum of the primary. The
lack of Mg II 4481 confirms the
relatively high temperature of the primary. The spectrum of the
secondary is too noisy for the
identification of metallic lines.
On the mass-![]() diagram, the stars match an isochrone corresponding to about
7-8 Myr. In the HR diagram, the positions of both
components are above the Z=0.004 evolutionary
tracks but are consistent with the lower metalicity ones (Z=0.001).
Increasing the helium content would also help to reconcile their
positions with the evolutionary tracks, unless a systematic effect
raises
the apparent effective temperatures.
diagram, the stars match an isochrone corresponding to about
7-8 Myr. In the HR diagram, the positions of both
components are above the Z=0.004 evolutionary
tracks but are consistent with the lower metalicity ones (Z=0.001).
Increasing the helium content would also help to reconcile their
positions with the evolutionary tracks, unless a systematic effect
raises
the apparent effective temperatures.
A.6 4 121461
This is an eccentric system with two (relatively) widely separated
components. Both eclipses are very similar in depth and width. With ![]() mag,
this is one of the faintest systems in our sample. Nevertheless, the
finding chart indicates no crowding problem whatsoever.
No significant apsidal motion was found on the basis of
photometry. An analysis with the EBOP code shows that the
mag,
this is one of the faintest systems in our sample. Nevertheless, the
finding chart indicates no crowding problem whatsoever.
No significant apsidal motion was found on the basis of
photometry. An analysis with the EBOP code shows that the ![]() value
depends critically on the
value
depends critically on the ![]() quantity,
which is poorly constrained, while the more robust
quantity,
which is poorly constrained, while the more robust ![]() quantity
is such that
quantity
is such that ![]() and thus does not constrain
and thus does not constrain ![]() very tightly. Figure A.2
suggests a marginal decrease of
very tightly. Figure A.2
suggests a marginal decrease of
![]() with time which, if real, could only be due to gravitational
perturbations from a third body, because
with time which, if real, could only be due to gravitational
perturbations from a third body, because ![]() ,
while pure tidal effects always result in
,
while pure tidal effects always result in ![]() .
We have assumed no apsidal motion.
.
We have assumed no apsidal motion.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1832.png)
|
Figure A.2:
Variation with time of the |
| Open with DEXTER | |
This system is one of the two in our sample with 16 out-of-eclipse spectra, of which 15 were used (the eighth has too poor SNR). There is a sufficient number of observations close to the quadratures.
The composite spectra are very noisy. The separated spectra
are of a very poor quality, with no exploitable metallic lines. There
is strong nebular emission. Letting the temperature of both components
free to converge (together with the B luminosity
ratio) resulted in very uncertain
values, so we fixed the temperature ratio to the photometric
one to estimate the temperature of the primary. The rotational
velocities were fixed to the pseudosynchronized values.
A luminosity ratio of 0.95 ![]() 0.06 was found on the basis of the spectra, which agrees well with the
photometric one (0.91
0.06 was found on the basis of the spectra, which agrees well with the
photometric one (0.91 ![]() 0.03) obtained without fixing the
potential of the primary. The photometric luminosity ratio was adopted,
which results in almost identical radii for the components. This
results in a slightly lower surface gravity for the secondary component
than for the primary because of the mass ratio, but this difference is
not significant.
0.03) obtained without fixing the
potential of the primary. The photometric luminosity ratio was adopted,
which results in almost identical radii for the components. This
results in a slightly lower surface gravity for the secondary component
than for the primary because of the mass ratio, but this difference is
not significant.
On the mass-![]() diagram, this system lies close to the ZAMS but might be up to
15-20 Myr old. The positions of the stars in the
HR diagram agree within the error bars with the evolutionary
tracks, although they tend to lie too high, as is the case of
other systems.
diagram, this system lies close to the ZAMS but might be up to
15-20 Myr old. The positions of the stars in the
HR diagram agree within the error bars with the evolutionary
tracks, although they tend to lie too high, as is the case of
other systems.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fgA3a.eps}\hspace*{7mm}
\includegraphics[width=8cm,clip]{10284fgA3b.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1833.png)
|
Figure A.3:
Example of observed spectra close to a quadrature. Both spectra are at
the same scale. The red line represents the composite synthetic
spectrum of the binary system, i.e. the addition of the scaled
and velocity-shifted synthetic spectra of the two components for the
corresponding orbital phase. Besides a low S/N,
the spectrum of 4 121461 shows strong nebular emission in the
Balmer lines. From the best fit the B luminosity
ratio was found to be |
| Open with DEXTER | |
A.7 4 159928
This system presents low-to-medium quality light curves of the
EW type with eclipses of unequal depth. The rms scatter of the
light curve is rather low, but the minima are not very deep (
![]() mag).
It can be inferred from this that the system comprises close,
strongly distorted components of unequal brightness. The best-fitting
model corresponds to a
semi-detached binary with a low inclination, close to
mag).
It can be inferred from this that the system comprises close,
strongly distorted components of unequal brightness. The best-fitting
model corresponds to a
semi-detached binary with a low inclination, close to
![]() .
The finding chart shows a well isolated target, except for a quite
faint neighbor at about
.
The finding chart shows a well isolated target, except for a quite
faint neighbor at about
![]() to the NNE.
to the NNE.
There are only eight out-of-eclipse spectra, but they are close to the two quadratures.
A spectroscopic luminosity ratio of 0.45 was found in the B band,
which is higher than the photometric value (0.36). The
temperature of the primary was determined by fixing the temperature and
luminosity ratios to the photometric values, after suppression of the
very strong nebular emission lines. The Si III 4553
line is the only metallic line clearly visible in the
separated spectrum of the primary. The spectrum of the secondary shows
no exploitable metallic line. The Mg II 4481
is barely visible. The synchronized values for ![]() are close to 200 km s-1 and
therefore all but the strongest lines are buried in the noise.
are close to 200 km s-1 and
therefore all but the strongest lines are buried in the noise.
Both the mass-![]() and HR diagrams show positions typical of a semi-detached system with
an evolved secondary component. The primary is slightly overluminous
relative to the evolutionary track of a single star.
and HR diagrams show positions typical of a semi-detached system with
an evolved secondary component. The primary is slightly overluminous
relative to the evolutionary track of a single star.
A.8 4 160094
This detached system of moderate eccentricity presents low-to-medium
quality light curves with rather shallow eclipses (
![]() mag).
Except for a few very faint neighbors, the target seems free from
crowding on the finding chart.
mag).
Except for a few very faint neighbors, the target seems free from
crowding on the finding chart.
There are 11 out-of-eclipse spectra. Both quadratures are well covered by the observations.
The ![]() of the primary was determined together with that of the secondary and
with the B luminosity ratio. The
temperature of the secondary proved rather ill-defined, so the
photometric temperature ratio was used to define it,
as usual. The potential of the primary was fixed to a value
that implies a luminosity ratio close to the spectroscopic one.
No metallic lines are visible in the very noisy separated
spectra. The nebular emission is strong in both H I lines.
of the primary was determined together with that of the secondary and
with the B luminosity ratio. The
temperature of the secondary proved rather ill-defined, so the
photometric temperature ratio was used to define it,
as usual. The potential of the primary was fixed to a value
that implies a luminosity ratio close to the spectroscopic one.
No metallic lines are visible in the very noisy separated
spectra. The nebular emission is strong in both H I lines.
Despite the moderate quality of the photometric and
spectroscopic data, the positions of both stars fall right on the ZAMS
in the mass-![]() diagram.
In the HR diagram, their position agree well with the
evolutionary tracks, though they appear slightly overluminous.
diagram.
In the HR diagram, their position agree well with the
evolutionary tracks, though they appear slightly overluminous.
A notable characteristic of this system is its fast apsidal
motion ![]()
![]() 1.9
1.9
![]() yr-1.
Figure A.4
shows the
yr-1.
Figure A.4
shows the ![]() product as a function of time, as obtained using the EBOP
code. The solid line represents the WD solution, which appears
consistent with the EBOP results, even though the latter would be
compatible with a faster apsidal motion coupled with a slightly smaller
eccentricity. Further discussion of this result is deferred to
Sect. 4.
product as a function of time, as obtained using the EBOP
code. The solid line represents the WD solution, which appears
consistent with the EBOP results, even though the latter would be
compatible with a faster apsidal motion coupled with a slightly smaller
eccentricity. Further discussion of this result is deferred to
Sect. 4.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA4.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1839.png)
|
Figure A.4:
Variation with time of the |
| Open with DEXTER | |
A.9 4 163552
This is one of the five systems with ![]() mag,
displaying a high-quality light curve of the EB type. The eclipses have
very similar depths (
mag,
displaying a high-quality light curve of the EB type. The eclipses have
very similar depths (![]() mag),
indicating that the temperature ratio is very close to unity. Some
faint neighbors are seen on the finding chart about
mag),
indicating that the temperature ratio is very close to unity. Some
faint neighbors are seen on the finding chart about
![]() from the target, and it is difficult to judge whether closer neighbors
might lurk
within the relatively large spot left by this bright system. According
to the light curve, there is a substantial third-light contribution to
this system: we find
from the target, and it is difficult to judge whether closer neighbors
might lurk
within the relatively large spot left by this bright system. According
to the light curve, there is a substantial third-light contribution to
this system: we find ![]() ,
while Graczyk (2003,
hereafter dG03) found
,
while Graczyk (2003,
hereafter dG03) found ![]() .
A significant ellipsoidal variation is indicative of tidally distorted
components, though the system is still in a detached
configuration.
.
A significant ellipsoidal variation is indicative of tidally distorted
components, though the system is still in a detached
configuration.
There are only nine out-of-eclipse spectra, but the RV curves are well constrained near quadratures.
The observed spectra of this binary were roughly corrected for
the presence of a third component, by subtracting a constant
from the normalized spectra. The value of the constant was adjusted
until the effective temperatures obtained from the least-squares fit to
the corrected spectra give a reasonable match to the evolutionary
tracks at the metalicity Z=0.004 in the
HR diagram. A constant of 0.1 only proved
sufficient to this purpose, which is widely different from
dG03's photometric estimate of the third light, ![]() .
On the other hand, our WD analysis resulted in
.
On the other hand, our WD analysis resulted in ![]() ,
which is more consistent with our rough
spectroscopic estimate. Actually, a first attempt to analyze
this system resulted in highly overluminous components. This was
interpreted as a clear sign that the observed spectra were
severely contaminated by the object responsible for the photometric
third light.
,
which is more consistent with our rough
spectroscopic estimate. Actually, a first attempt to analyze
this system resulted in highly overluminous components. This was
interpreted as a clear sign that the observed spectra were
severely contaminated by the object responsible for the photometric
third light.
The separated spectrum of the primary shows a faint Mg II 4481 line and a noisy Si III 4553 line. These lines were used to constrain the temperature of the primary. The Si III 4553 line is visible in the spectrum of the secondary too.
This system was studied by HHH05, dG03 (see his Fig. 6) and WW02. Only dG03 took the third-light contribution into account. Not surprisingly, our photometric solution is very close to theirs.
Since we adjusted the amount of third light so that the
primary component have a realistic luminosity, the HR diagram shows a
primary close to the stellar evolutionary track of a 9.6
![]() star, and a secondary close to the evolutionary track of a
9.1
star, and a secondary close to the evolutionary track of a
9.1
![]() star. Their positions are clearly far from the zero-age main sequence.
From the mass-
star. Their positions are clearly far from the zero-age main sequence.
From the mass-![]() diagram,
the age of the system is estimated to be 20 Myr.
As the position of the primary was inferred from the expected
position in the HR diagram, the proposed solution is not
entirely reliable and thus is not used for the determination of the
mean distance modulus of the
SMC (see Sect. 4.6).
diagram,
the age of the system is estimated to be 20 Myr.
As the position of the primary was inferred from the expected
position in the HR diagram, the proposed solution is not
entirely reliable and thus is not used for the determination of the
mean distance modulus of the
SMC (see Sect. 4.6).
A.10 4 175149
The medium-to-high quality light curve of this system is of the
EB type; unfortunately, most of the right part of each eclipse
is missing. That is due to a period very close to 2 days
exactly. The minima are fairly deep (
![]() mag),
well-defined and of unequal depth. There is a strong ellipsoidal
variation. The binary is a semi-detached system, with distorted
components of different brightnesses. A slight depression
occurring before the primary eclipse is indicative of a gas stream.
However, we did not venture into adding a spot on the primary in order
to mimick this effect, because we felt that the large gaps in the light
curve already limit the reliability of the proposed solution.
mag),
well-defined and of unequal depth. There is a strong ellipsoidal
variation. The binary is a semi-detached system, with distorted
components of different brightnesses. A slight depression
occurring before the primary eclipse is indicative of a gas stream.
However, we did not venture into adding a spot on the primary in order
to mimick this effect, because we felt that the large gaps in the light
curve already limit the reliability of the proposed solution.
This system is close to the edge of the CCD used in the OGLE II survey, so it was also listed under the designation 5 38079 in the OGLE database. Thanks to that circumstance, there are 574 photometric I magnitudes instead of less than 300. An examination of the OGLE finding chart reveals that this binary is clearly blended.
This is the second system with 16 out-of-eclipse spectroscopic observations. Because of the 2-day period, all these observations took place before the quadratures. Nevertheless, the RV curves seem to be sufficiently constrained.
A spectroscopic B luminosity ratio of 1.39
was found, though with a large scatter (
![]() ). This is higher than the
photometric value (1.18). The separated spectra are fairly
good.
The spectrum of the hot primary component displays the He II 4200
and 4542 lines. The Si III 4553
and a faint Si IV 4089 lines are
equally visible. These lines provide strong constraints for the
temperature of the primary. The best-fitting primary temperature was
obtained after fixing the temperature and luminosity ratios to the
photometric values.
). This is higher than the
photometric value (1.18). The separated spectra are fairly
good.
The spectrum of the hot primary component displays the He II 4200
and 4542 lines. The Si III 4553
and a faint Si IV 4089 lines are
equally visible. These lines provide strong constraints for the
temperature of the primary. The best-fitting primary temperature was
obtained after fixing the temperature and luminosity ratios to the
photometric values.
The mass-![]() diagram shows the typical oblique orientation of the segment connecting
the components of an evolved binary. The HR diagram shows a
highly overluminous primary, relative to the evolutionary track of a
11.8
diagram shows the typical oblique orientation of the segment connecting
the components of an evolved binary. The HR diagram shows a
highly overluminous primary, relative to the evolutionary track of a
11.8
![]() star, and an evolved secondary far more luminous than a main-sequence
star of 7.8
star, and an evolved secondary far more luminous than a main-sequence
star of 7.8
![]() .
One may wonder whether the strange position of the primary is due to an
unrecognized third light, both in photometry and spectroscopy,
or to some evolutionary effect. In any case, there is no
obvious third light in the light curve.
.
One may wonder whether the strange position of the primary is due to an
unrecognized third light, both in photometry and spectroscopy,
or to some evolutionary effect. In any case, there is no
obvious third light in the light curve.
A.11 4 175333
This slightly eccentric system presents low-to-medium quality light
curves of the EA type. This is one of the few systems with ![]() mag.
Consequently, the
mag.
Consequently, the ![]() curve
shows a relatively high scatter. The minima are of unequal depth.
A slight ellipsoidal variation is visible. This is clearly a
detached system with components of unequal brightness. The target
appears perfectly isolated on the finding chart.
curve
shows a relatively high scatter. The minima are of unequal depth.
A slight ellipsoidal variation is visible. This is clearly a
detached system with components of unequal brightness. The target
appears perfectly isolated on the finding chart.
There are 14 out-of-eclipse spectra. The observations well constrain the RV curves.
This system was studied by WW01. That they consider the eclipses as total (while we consider them as partial) and their lack of spectroscopic constraints on their ratio of radii account for the differences between their solution and ours. The evidence for total eclipses does not appear compelling, so additional photometry would be needed to settle the issue. We found a spectroscopic B luminosity ratio of 0.55, slightly lower than that finally adopted taking photometry into account. The separated spectrum of the primary shows a noisy Mg II 4481 line. The spectrum of the secondary is too noisy to detect any metallic line. The temperature of the primary was fitted with the temperature and luminosity ratios fixed to the photometric values. The fit with both temperatures free to converge, together with the luminosity ratio, gave a rather large scatter of about 1600 K and a secondary temperature about 900 K cooler. In spite of the partial eclipses, there was no need to fix the potential of the primary in order to find a B luminosity ratio that matches the spectroscopic value, so the photometric value of the luminosity ratio was adopted.
On the mass-![]() diagram, both stars fall right on the 20 Myr isochrone. On the
HR diagram, however, both stars appear significantly
overluminous relative to their evolutionary tracks, suggesting that the
effective temperatures may be overestimated by at least
2000 K! Strangely
enough, the color excess of this system appears to be small (
E(B-V)=0.07)
and the distance modulus (18.6) clearly smaller than the
accepted value for the SMC (
diagram, both stars fall right on the 20 Myr isochrone. On the
HR diagram, however, both stars appear significantly
overluminous relative to their evolutionary tracks, suggesting that the
effective temperatures may be overestimated by at least
2000 K! Strangely
enough, the color excess of this system appears to be small (
E(B-V)=0.07)
and the distance modulus (18.6) clearly smaller than the
accepted value for the SMC (
![]() ). If the effective
temperatures had indeed been overestimated, this would have implied
both an intrinsic color that is too blue and an intrinsic luminosity
that is too large (hence a more negative absolute
magnitude), so one would rather expect a high color excess and
a high distance modulus.
). If the effective
temperatures had indeed been overestimated, this would have implied
both an intrinsic color that is too blue and an intrinsic luminosity
that is too large (hence a more negative absolute
magnitude), so one would rather expect a high color excess and
a high distance modulus.
A.12 5 016658
This close detached system presents medium quality light curves with eclipses of equal depths, and is composed of tidally distorted twin components. The finding chart reveals no crowding problem.
There are 11 out-of-eclipse spectra. The RV curves are well constrained by the observations around phase 0.25.
This system was studied by WW01. As for the previous binary,
the differences observed between their (photometric) solution and ours
is due to their lack of a spectroscopic constraint on the ratio of
radii, and because they assume total eclipses. Evidence for the latter
is not compelling, however, and awaits further photometric measurements
for confirmation. A spectroscopic B luminosity
ratio of ![]() 0.60
was found, which guided the choice of the potential of the primary
component in the WD analysis. The Mg II 4481
line is clearly visible on the separated spectrum of the primary. The
spectrum of the secondary is too noisy to show any metallic line. The
best-fitting primary temperature was obtained simultaneously with the
temperature of the secondary, which appeared quite compatible (within
300 K) with the photometric one (i.e. given the
spectroscopic primary temperature and the photometric temperature
ratio), and with the luminosity ratio. The photometric temperature
ratio was adopted.
0.60
was found, which guided the choice of the potential of the primary
component in the WD analysis. The Mg II 4481
line is clearly visible on the separated spectrum of the primary. The
spectrum of the secondary is too noisy to show any metallic line. The
best-fitting primary temperature was obtained simultaneously with the
temperature of the secondary, which appeared quite compatible (within
300 K) with the photometric one (i.e. given the
spectroscopic primary temperature and the photometric temperature
ratio), and with the luminosity ratio. The photometric temperature
ratio was adopted.
On the mass-![]() diagrams, both stars fall on the 30 Myr isochrone within the
errors. On the HR diagram, the primary has a position
compatible with its evolutionary track within errors, though it appears
slightly too luminous. The secondary is slightly hotter than the
primary, and is more overluminous; still, it remains
compatible with its evolutionary track if the errors on both luminosity
and mass are considered.
diagrams, both stars fall on the 30 Myr isochrone within the
errors. On the HR diagram, the primary has a position
compatible with its evolutionary track within errors, though it appears
slightly too luminous. The secondary is slightly hotter than the
primary, and is more overluminous; still, it remains
compatible with its evolutionary track if the errors on both luminosity
and mass are considered.
A.13 5 026631
This system presents a medium-quality light curve of the EW type with
minima of unequal depth. This is clearly a semi-detached system with
strongly distorted components of unequal brightness.
It presents the second-lowest inclination of the sample with ![]() ,
implied by the rather small amplitude of the light curve.
No blend is apparent on the finding chart, except
for two or three very faint neighbors at about
,
implied by the rather small amplitude of the light curve.
No blend is apparent on the finding chart, except
for two or three very faint neighbors at about
![]() .
.
There are only eight out-of-eclipse spectra, but these are sufficiently constraining to get reliable RV curves.
A spectroscopic B luminosity ratio of 0.74
was found, while the photometric value is 0.50. The separated
spectra show no useful metallic lines. This is due notably to the high ![]() values
(
values
(![]() 190 km s-1).
The temperature of the primary was obtained by fixing the temperature
and luminosity ratios to the photometric values.
190 km s-1).
The temperature of the primary was obtained by fixing the temperature
and luminosity ratios to the photometric values.
The mass-![]() and HR diagrams show the typical positions for the components of a
semi-detached system, with the primary near its expected evolutionary
track and an overluminous secondary. The primary is slightly
overluminous relative to its track, as is often the case in
this work, while the secondary is slightly below its track,
a rare occurrence.
and HR diagrams show the typical positions for the components of a
semi-detached system, with the primary near its expected evolutionary
track and an overluminous secondary. The primary is slightly
overluminous relative to its track, as is often the case in
this work, while the secondary is slightly below its track,
a rare occurrence.
This binary was studied by HHH05. Their primary temperature
(25 500 K) and mass ratio (![]() 1) differ significantly from
our values.
1) differ significantly from
our values.
A.14 5 032412
This wide, detached system presents medium-to-high quality light curves with minima of unequal depth, betraying components of unequal brightness. The target appears well isolated on the finding chart.
There are 13 out-of-eclipse spectra. The RV curves are very
well constrained and the rms scatters are low. Interestingly, both the
light and velocity curves indicate a negligible eccentricity,
in spite of the small relative radii of the components,
as if circularization had taken place during the protostellar
phase. Note that this is the most massive system of our whole sample:
its total mass reaches ![]() .
.
A spectroscopic B luminosity ratio of 0.55 was found. The separated spectra are of high quality (Fig. A.5), even for the H I lines. Beside the H I and He I lines, the following lines are visible in the spectrum of the primary: He II 4200 and 4542 (strong), Si IV 4089, Si IV 4116, O II 4185, Si IV 4212, O II 4276-7 and Si III 4553. An effective temperature of about 35 000 K was inferred from the best-fitting synthetic spectrum.
The following metallic lines are visible in the separated spectrum of the secondary: Si IV 4089, Si IV 4116, O II 4185, O II 4190, C II 4267, O II 4276-7, O II 4415-7, Mg II 4481 and Si III 4553. He II 4542 is clearly visible too. Comparing the relative depths of Mg II 4481 with He I 4472, He II 4542 with Si III 4553, C II 4267 with O II 4276-7, Si IV 4089 and Si IV 4116 with He I 4121 allows us to estimate an effective temperature close to 31 000 K. Thanks to the good SNR of the spectra, fitting simultaneously the temperatures of the components and the luminosity ratio resulted in a temperature ratio very close to the photometric one. Nevertheless, the adopted temperatures are those obtained by imposing the photometric ratio.
The mass-![]() diagram shows a very young binary with both components on the ZAMS. On
the HR diagram, the positions of both components agree fairly
well with the stellar evolutionary tracks of 17.1 and
13.1
diagram shows a very young binary with both components on the ZAMS. On
the HR diagram, the positions of both components agree fairly
well with the stellar evolutionary tracks of 17.1 and
13.1
![]() stars. However, the primary appears slightly overluminous relative to
its track.
stars. However, the primary appears slightly overluminous relative to
its track.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA5a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{10284fgA5b.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1851.png)
|
Figure A.5:
Sections of the separated spectra of the primary and secondary
components of the binary 5 032412. The scale on the
vertical axis is adapted to the size of the features in each section.
The red line represents a velocity-shifted synthetic spectrum of the
star. Beside prominent H I and He I lines,
He II, O II, Mg
II, Si III
and Si IV lines are visible in
both spectra. The strong He II 4542,
next to a smaller Si III 4553 line,
and the He II 4200 line confirm
the high temperature of the primary ( |
| Open with DEXTER | |
A.15 5 038089
This bright detached system presents medium-quality light curves with eclipses of very similar depth. Therefore, the components are very similar.
This system has abnormal color indices (see Table 3 and Fig. 3), which suggests the presence of a third light. An examination of the OGLE finding chart reveals that this binary is clearly blended, though with much fainter stars.
There are 11 out-of-eclipse spectra. The RV curves are very well constrained and the rms scatter is remarkably low.
A spectroscopic B luminosity ratio of 0.68 was found. The eclipses are not very deep, so we fixed the potential of the primary to reproduce this luminosity ratio. The separated spectra shown in Fig. A.6 are very similar. Strong He II 4200 and 4552 lines are visible in both spectra. The following metallic lines are equally identifiable (Fig. A.6): O II 4076, Si IV 4089, Si IV 4116, O II 4185, O II 4190, C II 4267, O II 4276, O II 4415-4417, Si III 4553. This wealth of lines allows us to determine the temperatures of both components with a great accuracy. From the best-fitting synthetic spectra, we found 30 400 K and 30 800 K for the effective temperature of the primary and secondary, respectively. This is very close (i.e. within 200 K) to the temperatures estimated from the composite spectra by imposing the photometric temperature and luminosity ratios; thus, one can safely conclude from this example that the two methods are equivalent.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA6a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{10284fgA6b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1852.png)
|
Figure A.6: Sections of the separated spectra of the primary and secondary components of the binary 5 038089. The scale on the vertical axis is adapted to the size of the features in each section. The red line represents a velocity-shifted synthetic spectrum of the star. Beside prominent H I and He I lines, He II and a number of fainter metallic lines (C II, O II, Si III, Si IV) are visible. The relative intensities of the He II 4542 and Si III 4553 are very useful to constrain the temperature of the two stars. |
| Open with DEXTER | |
The high quality of the spectroscopic observations allowed us to
estimate the astrophysical parameters with a greater accuracy than for
most systems in our sample. On the mass-![]() diagram, both
components lie just above the 10 Myr isochrone; their
respective positions suggest that the ratio of radii may be slightly
underestimated. The HR diagram shows that both stars are
significantly overluminous with respect to the evolutionary tracks
of 13.0 and 11.7
diagram, both
components lie just above the 10 Myr isochrone; their
respective positions suggest that the ratio of radii may be slightly
underestimated. The HR diagram shows that both stars are
significantly overluminous with respect to the evolutionary tracks
of 13.0 and 11.7
![]() stars. Invoking the blending of the binary with a third-light
contributor does not seem to help much. No clear sign of a
third light can be seen in the lightcurve; this is admittedly a weak
argument, since the light curve of a detached system with weak
proximity effects cannot constrain a third light well. But,
in addition, a third light will not much change the
relative radii of the components, and the effective temperatures seem
well constrained by the relative intensities of several lines,
so that the luminosities should remain unaffected.
Furthermore, the quality of the radial velocity curves is so good, that
it is difficult to imagine how the masses could be biased otherwise
than through the inclination angle i.
A third light would
make the photometric minima less deep and so it would mimick a
lower i. Since the RV amplitudes
give the product
stars. Invoking the blending of the binary with a third-light
contributor does not seem to help much. No clear sign of a
third light can be seen in the lightcurve; this is admittedly a weak
argument, since the light curve of a detached system with weak
proximity effects cannot constrain a third light well. But,
in addition, a third light will not much change the
relative radii of the components, and the effective temperatures seem
well constrained by the relative intensities of several lines,
so that the luminosities should remain unaffected.
Furthermore, the quality of the radial velocity curves is so good, that
it is difficult to imagine how the masses could be biased otherwise
than through the inclination angle i.
A third light would
make the photometric minima less deep and so it would mimick a
lower i. Since the RV amplitudes
give the product ![]() ,
underestimating i is equivalent to overestimating
,
underestimating i is equivalent to overestimating
![]() ,
while we would need the reverse to explain the HR diagram we
see. A test with the EBOP code confirms this qualitative
argument: assuming a third light
,
while we would need the reverse to explain the HR diagram we
see. A test with the EBOP code confirms this qualitative
argument: assuming a third light ![]() changes the radius of the primary by -0.26% only (keeping the
ratio of radii constant), so that the luminosity decreases by
half a percent, while the inclination is increased by more than three
degrees, lowering the masses by 3.6%. That would imply
evolutionary tracks with a luminosity about 0.05 dex lower
(or 11%) in the HR diagram. Finally, the distance
modulus of this system is very close to that expected for the SMC.
Therefore, for a third light to be the cause of
the inconsistency, it can only be via the RV curves,
the amplitude of which should be biased to low values by a stationary
third spectrum.
changes the radius of the primary by -0.26% only (keeping the
ratio of radii constant), so that the luminosity decreases by
half a percent, while the inclination is increased by more than three
degrees, lowering the masses by 3.6%. That would imply
evolutionary tracks with a luminosity about 0.05 dex lower
(or 11%) in the HR diagram. Finally, the distance
modulus of this system is very close to that expected for the SMC.
Therefore, for a third light to be the cause of
the inconsistency, it can only be via the RV curves,
the amplitude of which should be biased to low values by a stationary
third spectrum.
This binary was part of the first release of 10 bright SMC systems by HHH03. Comparing our results with theirs, we see that we have similar estimates for the mass ratio and temperatures of the stars, but markedly different values for the masses and radius of the secondary. A photometric solution was proposed by dG03, who do not recommend it for distance determination because its components do not fall into their mass-luminosity relation.
A.16 5 095337
This is a close but detached system, with tidally distorted components
of unequal brightness. The ![]() curve suggests that
the primary eclipse is not perfectly reproduced by the synthetic light
curve, but there is no obvious third-light contribution. The finding
chart shows some blends with two or three fainter stars at
curve suggests that
the primary eclipse is not perfectly reproduced by the synthetic light
curve, but there is no obvious third-light contribution. The finding
chart shows some blends with two or three fainter stars at
![]() or so.
or so.
There are 10 out-of-eclipse spectra. The RV curves are well constrained with observations close to both quadratures.
A spectroscopic B luminosity ratio of 0.66
was found. The separated spectra are of poor quality. Because of the
low S/N and the high
![]() (
(![]() 200 km s-1),
no metallic line can be positively identified. There is some
nebular emission in the Balmer lines. The best-fitting synthetic
spectra allowed us to simultaneously estimate the temperatures of the
primary and the secondary, whose ratio agrees quite well with the
photometric one. In addition, the spectroscopic B luminosity
ratio perfectly matches the photometric one, so that the
potential of
both the primary and the secondary were left free to converge.
200 km s-1),
no metallic line can be positively identified. There is some
nebular emission in the Balmer lines. The best-fitting synthetic
spectra allowed us to simultaneously estimate the temperatures of the
primary and the secondary, whose ratio agrees quite well with the
photometric one. In addition, the spectroscopic B luminosity
ratio perfectly matches the photometric one, so that the
potential of
both the primary and the secondary were left free to converge.
On the mass-![]() diagram, both components define a segment which is perfectly parallel
and very close to the 10 Myr isochrone. On the
HR diagram, however, both components appear strongly
overluminous compared to the evolutionary tracks of 8.7 and
7.6
diagram, both components define a segment which is perfectly parallel
and very close to the 10 Myr isochrone. On the
HR diagram, however, both components appear strongly
overluminous compared to the evolutionary tracks of 8.7 and
7.6
![]() stars. Decreasing the effective temperatures by about 1300 K
would reconcile the luminosities with the tracks. However, this looks
difficult. The emission in both Balmer lines was suppressed on
a 4 Å range centered on each emission line, and we
verified that increasing that range to 8 Å does not change the
estimated temperature in a significant way. Thus, either this system
suffers from some bias on the RV curves, or its metalicity is
closer to Z=0.001 than to Z=0.004.
stars. Decreasing the effective temperatures by about 1300 K
would reconcile the luminosities with the tracks. However, this looks
difficult. The emission in both Balmer lines was suppressed on
a 4 Å range centered on each emission line, and we
verified that increasing that range to 8 Å does not change the
estimated temperature in a significant way. Thus, either this system
suffers from some bias on the RV curves, or its metalicity is
closer to Z=0.001 than to Z=0.004.
A.17 5 095557
This is the system with the highest eccentricity, displaying a medium-quality light curve with minima of unequal depths. The target is perfectly isolated on the finding chart.
There are 11 out-of-eclipse spectra. The RV curves are well constrained with observations close to both quadratures, but the fit is not very good and, unfortunately, most spectra are grouped in the phase interval with the smaller amplitude.
A spectroscopic B luminosity ratio of ![]() 0.5 was
found when limiting the fit to the seven spectra for which the radial
velocity difference
0.5 was
found when limiting the fit to the seven spectra for which the radial
velocity difference ![]() .
This ratio increases to 0.63 if all eleven spectra are taken
into account, so that this quantity is rather poorly constrained. The
separated spectra are of very poor quality. This is probably partly
due to the low S/N of the
observed spectra, and partly to some inaccuracies in the orbital
parameters. The temperature of the secondary given by the fits to the
composite spectra is about 1000 K higher than the photometric
estimate, which was adopted. The pseudosynchronized values of
.
This ratio increases to 0.63 if all eleven spectra are taken
into account, so that this quantity is rather poorly constrained. The
separated spectra are of very poor quality. This is probably partly
due to the low S/N of the
observed spectra, and partly to some inaccuracies in the orbital
parameters. The temperature of the secondary given by the fits to the
composite spectra is about 1000 K higher than the photometric
estimate, which was adopted. The pseudosynchronized values of
![]() were adopted.
were adopted.
An apsidal motion is detected at the ![]() significance level,
and the WD result is confirmed by the variation of the
significance level,
and the WD result is confirmed by the variation of the ![]() quantity
as given by the EBOP code. The photometric data were divided into four
sets and the fits were obtained by fixing the inclination, the ratio of
radii and the relative radius of the primary. The result is displayed
in Fig. A.7
and suggests that the apsidal motion is real. The adopted apsidal
motion seems underestimated in that figure, but the constraint imposed
by the RV curves has to be kept in mind. On the mass-
quantity
as given by the EBOP code. The photometric data were divided into four
sets and the fits were obtained by fixing the inclination, the ratio of
radii and the relative radius of the primary. The result is displayed
in Fig. A.7
and suggests that the apsidal motion is real. The adopted apsidal
motion seems underestimated in that figure, but the constraint imposed
by the RV curves has to be kept in mind. On the mass-![]() diagram,
the two components lie right on the 30 Myr isochrone, despite
the rather large uncertainty of the masses. In the
HR diagram both components appear clearly overluminous with
regard to their respective evolutionary tracks, as in many other
systems.
diagram,
the two components lie right on the 30 Myr isochrone, despite
the rather large uncertainty of the masses. In the
HR diagram both components appear clearly overluminous with
regard to their respective evolutionary tracks, as in many other
systems.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA7.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1859.png)
|
Figure A.7:
Same as Fig. A.4,
but for the system 5 95557. The filled black dots
represent independent |
| Open with DEXTER | |
A.18 5 100485
This is a detached system with ``twin'' components and a circular
orbit. The finding chart reveals no crowding problem, because the
closest neighbor is found at about
![]() .
.
There are 13 out-of-eclipse spectra. The RV curves are well constrained, with observations close to both quadratures and small residuals.
A spectroscopic B luminosity ratio of 0.93
was found, which matches the photometric value (0.97) rather
well. The separated spectra are very similar. The following metallic
lines can positively be identified: C II 4267,
Mg II 4481 and Si III 4553.
These lines allowed us to estimate a temperature close to ![]() 22 000 K
for each component. The least-squares fit, performed with both
temperatures and the luminosity ratio free to converge, provided a
temperature ratio very close to the photometric one.
22 000 K
for each component. The least-squares fit, performed with both
temperatures and the luminosity ratio free to converge, provided a
temperature ratio very close to the photometric one.
The two components lie right on the 20 Myr isochrone
on the mass-![]() diagram,
and they are compatible within the errors with their respective
evolutionary tracks in the HR diagram. Here again, however,
they are slightly overluminous, unless their metalicity
is low.
diagram,
and they are compatible within the errors with their respective
evolutionary tracks in the HR diagram. Here again, however,
they are slightly overluminous, unless their metalicity
is low.
A.19 5 100731
This system presents low-to-medium quality light curves of the
EW type, with the smallest amplitudes among those in our
sample. This is another case of a binary seen in an unfavourable
inclination (![]() 60
60
![]() ).
The finding chart shows a perfectly isolated target.
).
The finding chart shows a perfectly isolated target.
The most satisfying fit of the light curves was obtained with an overcontact model.
There are only eight out-of-eclipse spectra. Nevertheless, these observations are sufficiently constraining to get reliable RV curves.
Spectroscopy gives a B luminosity ratio of
![]() ,
while the photometric ratio amounts to
,
while the photometric ratio amounts to ![]() .
As usual, the latter was preferred, especially because of the
strong constraints provided by a Roche-lobe-filling pair. The separated
spectra have a low S/N, and a
least-squares fit to the composite spectra with both temperatures free
provided two temperatures close to 23 000 K.
However, the scatter of the secondary temperature was high,
so the photometric temperature ratio was adopted and fixed.
.
As usual, the latter was preferred, especially because of the
strong constraints provided by a Roche-lobe-filling pair. The separated
spectra have a low S/N, and a
least-squares fit to the composite spectra with both temperatures free
provided two temperatures close to 23 000 K.
However, the scatter of the secondary temperature was high,
so the photometric temperature ratio was adopted and fixed.
The mass-![]() diagram shows a secondary component more evolved than the primary,
as expected. On the HR diagram, both components
appear to be underluminous with respect to their evolutionary tracks,
though only by a little amount. This is an exceptional occurrence.
diagram shows a secondary component more evolved than the primary,
as expected. On the HR diagram, both components
appear to be underluminous with respect to their evolutionary tracks,
though only by a little amount. This is an exceptional occurrence.
A.20 5 106039
This system is a typical semi-detached one. There is a small depression occurring just before the eclipse of the primary, which is strong evidence for a gas stream. We did not attempt to model that stream with a cool spot on the primary, because the distortion of the light curve remains relatively mild. The target appears perfectly isolated on the finding chart.
There are nine out-of-eclipse spectra. The RV curves are well constrained with observations close to both quadratures.
A spectroscopic B luminosity ratio of 1.03
was found, which excellently agrees with the photometric
value (1.01). The following metallic lines are visible in the
separated spectrum of the primary: C II 4267,
Mg II 4481 (faint) and Si III 4553.
A stronger Mg II 4481
line is equally visible in the spectrum of the secondary. From these
lines, the primary temperature was estimated to be close
to 25 500 K. The least-squares fit,
performed with temperature and luminosity ratios fixed to the
photometric values, provided a primary temperature
![]() K
higher.
K
higher.
The position of the primary component in the
HR diagram is in fair agreement with the theoretical
evolutionary track of a 8.6
![]() star, though it is slightly overluminous. The evolved secondary
component is overluminous with respect to the track of a single star of
the same mass.
star, though it is slightly overluminous. The evolved secondary
component is overluminous with respect to the track of a single star of
the same mass.
A.21 5 111649
This is a detached system with very slightly distorted twin components.
There is a group of bright stars close to the target in the finding
chart, but they are remote enough (
![]() )
that no third light should be expected from them.
)
that no third light should be expected from them.
There are 10 out-of-eclipse spectra. The RV curves are not well sampled because the period of 2.95955 days is very close to an integer number of days, but the scatter is small, thanks to the slow projected rotational velocities induced by the relatively long period.
A spectroscopic B luminosity ratio of 0.89
was found, which was imposed (via the potential of the primary) to
define the ratio of radii. Indeed, the small amplitude of the light
curve prevents a purely photometric ratio to be well constrained. Noisy
C II 4267 and Mg II 4481
lines are visible in the separated spectrum of the secondary. The
temperature of the primary was determined from a fit with fixed
temperature and luminosity ratios. According to both spectroscopy and
photometry, the secondary appears marginally hotter than the primary,
the temperature difference being about ![]() .
.
Both components have a very similar mass (![]() 5.4
5.4
![]() ),
and according to the mass-
),
and according to the mass-![]() diagram,
the empirical mass contrast appears a bit too high to match the
diagram,
the empirical mass contrast appears a bit too high to match the ![]() Myr
isochrone. Interestingly, both components lie right on the Terminal Age
Main Sequence (TAMS), where evolution is so fast that a theoretical
lower limit to the mass ratio can be settled.
Starting from the purely empirical surface gravities, and increasing
their difference by two sigma (so that
Myr
isochrone. Interestingly, both components lie right on the Terminal Age
Main Sequence (TAMS), where evolution is so fast that a theoretical
lower limit to the mass ratio can be settled.
Starting from the purely empirical surface gravities, and increasing
their difference by two sigma (so that ![]() and
and ![]() ),
one can read the corresponding masses along the
),
one can read the corresponding masses along the ![]() isochrone. Assuming that both stars have not yet passed the ``hook''
that marks the end of the main sequence, the resulting mass ratio is q=0.98.
But it is quite possible that the primary has just passed the hook
while the secondary has not, in which case q=0.966.
In both cases, the mass ratio is closer to one than the value directly
obtained from the RV curves by 0.03 to 0.04.
Therefore, this system can be considered as hosting real twins.
isochrone. Assuming that both stars have not yet passed the ``hook''
that marks the end of the main sequence, the resulting mass ratio is q=0.98.
But it is quite possible that the primary has just passed the hook
while the secondary has not, in which case q=0.966.
In both cases, the mass ratio is closer to one than the value directly
obtained from the RV curves by 0.03 to 0.04.
Therefore, this system can be considered as hosting real twins.
The position of the primary in the HR diagram agrees almost perfectly with the theoretical evolutionary track, especially if the star has just evolved beyond the ``hook''. That of the secondary, however, is a bit too high, as if its mass were underestimated.
A.22 5 123390
This slightly eccentric system (e = 0.042) presents
low-to-medium quality light curves with a small amplitude. This is
clearly a detached system with components of unequal brightness. The
finding chart shows a neighbor at about ![]() to the SW of the binary, which might have polluted the spectra
slightly.
to the SW of the binary, which might have polluted the spectra
slightly.
There are 14 out-of-eclipse spectra. The RV curves have a small rms scatter and are very well constrained by the observations.
A spectroscopic B luminosity ratio of 0.58
was found. The separated spectra are of fairly good quality. The
following metallic lines are visible in both spectra: O II 4076,
C II 4267, O II 4276,
O II 4415-4417, Mg II 4481
and Si III 4553. For the primary,
the best-fitting temperature for these lines is ![]() 26 000 K.
The least-squares fit of the composite spectra gave temperatures of
28 400 and
26 260 K for the primary and secondary respectively,
but with a large scatter. A plot of the fitted temperatures
versus the unnormalized chi-square shows that in some cases the fit
switched components, i.e. attributed the high temperature to
the secondary and vice versa, which partly explains the large
scatter (see Fig. A.8).
Strangely enough, the photometric ratio of temperatures is close to
one, so that the temperatures become 27 840 and
28 320 K for the primary and secondary component
respectively when fitted while keeping this ratio fixed. Taken at face
value, however, Fig. A.8
rather suggests 29 000 and 25 000 K.
26 000 K.
The least-squares fit of the composite spectra gave temperatures of
28 400 and
26 260 K for the primary and secondary respectively,
but with a large scatter. A plot of the fitted temperatures
versus the unnormalized chi-square shows that in some cases the fit
switched components, i.e. attributed the high temperature to
the secondary and vice versa, which partly explains the large
scatter (see Fig. A.8).
Strangely enough, the photometric ratio of temperatures is close to
one, so that the temperatures become 27 840 and
28 320 K for the primary and secondary component
respectively when fitted while keeping this ratio fixed. Taken at face
value, however, Fig. A.8
rather suggests 29 000 and 25 000 K.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1869.png)
|
Figure A.8: Temperature of the primary (black dots) and of the secondary (red dots) component of the system 5 123390, obtained by fitting composite synthetic spectra to the observed ones, versus the quality of the fit. The trends are roughly horizontal, at least for good fits, which inspires confidence. In a few cases, the components are exchanged (see text). |
| Open with DEXTER | |
According to the mass-![]() diagram, this binary is
diagram, this binary is ![]() 12 Myr
old. The position of the primary component in the HR diagram is a bit
too high with regard to its evolutionary track. The secondary component
is much too luminous, falling on the track of the primary!
If the purely spectroscopic temperatures were adopted, the
primary would be even more overluminous, but the secondary would fall
right on its track.
12 Myr
old. The position of the primary component in the HR diagram is a bit
too high with regard to its evolutionary track. The secondary component
is much too luminous, falling on the track of the primary!
If the purely spectroscopic temperatures were adopted, the
primary would be even more overluminous, but the secondary would fall
right on its track.
There is a marginally significant apsidal motion of
4.75 ![]() 1.63
1.63
![]() yr-1.
We show in Fig. A.9
the
yr-1.
We show in Fig. A.9
the ![]() quantity found with
the EBOP code on the basis of the I magnitudes.
There is indeed a slight trend corresponding to an increase of
quantity found with
the EBOP code on the basis of the I magnitudes.
There is indeed a slight trend corresponding to an increase of ![]() with time.
with time.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA9.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1870.png)
|
Figure A.9:
Same as Fig. A.4,
but for the system 5 123390. The filled black dots
represent independent |
| Open with DEXTER | |
A.23 5 180185
The EA-type light curves of this system are irregularly sampled,
because the period is close to 5.5 days, and there
are only very few data in the primary minimum. This is a typical
well-detached system with twin components and a small eccentricity. The
finding chart reveals a slightly fainter neighbor about ![]() away from the target, i.e. far enough that its influence on
the spectra may be considered negligible.
away from the target, i.e. far enough that its influence on
the spectra may be considered negligible.
This system has unreliable color indices (see Table 3 and Fig. 3).
There are 12 out-of-eclipse spectra. The RV curves are excellent and well constrained by the observations, with the smallest residuals seen in our sample. The formal errors on the resulting amplitudes are smaller than one percent, allowing mass estimates to within 2-3%.
A spectroscopic B luminosity ratio of 0.63
was found, which is close to the value given by the
WD analysis and finally adopted (0.71). This is the
system with the longest period (![]() days) in our sample.
The long period is responsible for the low
days) in our sample.
The long period is responsible for the low ![]() values
(
values
(![]() 40 km s-1)
compatible with synchronous rotation. As a consequence, the
separated spectra of this binary show rather sharp lines. The following
metallic lines are visible in both spectra: C II 4267,
Mg II 4481 and Si III 4553.
The temperature of the primary was obtained as usual by fixing the
temperature and luminosity ratios to the photometric values, despite
the small number of points in the minima. The secondary has a slightly
hotter temperature than the primary.
40 km s-1)
compatible with synchronous rotation. As a consequence, the
separated spectra of this binary show rather sharp lines. The following
metallic lines are visible in both spectra: C II 4267,
Mg II 4481 and Si III 4553.
The temperature of the primary was obtained as usual by fixing the
temperature and luminosity ratios to the photometric values, despite
the small number of points in the minima. The secondary has a slightly
hotter temperature than the primary.
Both components are fairly well aligned on the 50 Myr
isochrone in the mass-![]() diagram,
although the primary should be slightly more evolved. On the
HR diagram, the secondary falls right on its track, while the
luminosity of the primary appears too low. This might be due to an
unreliable temperature ratio, because of the small number of
photometric points in the minima.
diagram,
although the primary should be slightly more evolved. On the
HR diagram, the secondary falls right on its track, while the
luminosity of the primary appears too low. This might be due to an
unreliable temperature ratio, because of the small number of
photometric points in the minima.
A.24 5 180576
This system presents low quality light curves of the EB type.
The depths of both minima are rather low and the rms scatter is high.
This is a detached system with components of unequal brightness and a
circular orbit. The finding chart shows a close neighbor at
about
![]() to the NNW, which might have distorted the temperature estimate of the
binary components.
to the NNW, which might have distorted the temperature estimate of the
binary components.
There are 12 out-of-eclipse spectra. The RVs curves are rather good and well constrained by the observations.
A spectroscopic B luminosity ratio of 0.42
was found. This is close to the value reached by the final
WD analysis. The observed composite spectra are very noisy (
![]() )
and are
contaminated by nebular emission. The separated spectra are of a rather
poor quality. This is partly due to the low reliability of the
continuum placement. The C II 4267
and Mg II 4481 lines are visible
in the spectrum of the primary. The temperature of the primary,
determined from a least-squares fit where the temperature and
luminosity ratios were fixed, depends on the quality
of the fit, as shown by Fig. A.10. We
adopted the temperature of the primary corresponding to the
best
)
and are
contaminated by nebular emission. The separated spectra are of a rather
poor quality. This is partly due to the low reliability of the
continuum placement. The C II 4267
and Mg II 4481 lines are visible
in the spectrum of the primary. The temperature of the primary,
determined from a least-squares fit where the temperature and
luminosity ratios were fixed, depends on the quality
of the fit, as shown by Fig. A.10. We
adopted the temperature of the primary corresponding to the
best ![]() ,
in view of the roughly linear correlation between
,
in view of the roughly linear correlation between
![]() and
and ![]() ,
but without attempting to extrapolate the relation to
,
but without attempting to extrapolate the relation to ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1875.png)
|
Figure A.10: Effective temperatures of the system 5 180576 obtained from a fit to the composite spectra, keeping the temperature and luminosity ratios fixed. Black dots are for the primary, red dots for the secondary. Note that the two curves should be considered as one and the same, since their ratio is constant. |
| Open with DEXTER | |
In the mass-![]() diagram, the components are perfectly aligned along the 15 Myr
isochrone. The position of the primary component in the
HR diagram appears slightly too high relative to the
corresponding evolutionary track, while the secondary falls right on
its track.
diagram, the components are perfectly aligned along the 15 Myr
isochrone. The position of the primary component in the
HR diagram appears slightly too high relative to the
corresponding evolutionary track, while the secondary falls right on
its track.
A.25 5 185408
This system presents medium quality light curves of the
EA type. The minima are of similar depth and there is some
ellipsoidal variation. This is a typical detached system with closely
similar components, with medium quality light curves and low amplitude
minima of similar depth. The orbit is
circular. The I-band light curve was cleaned from
five outliers before the PHOEBE/WD analysis. The finding chart shows a
well isolated target, the closest neighbor is found at about ![]() to the WNW.
to the WNW.
There are 12 out-of-eclipse spectra. The RV curves are excellent, especially in view of the faintness of the object, and well constrained by the observations.
A spectroscopic B luminosity ratio of ![]() 0.64 was
found. The WD analysis tended to raise this value and the
potential of the primary had to be fixed to keep it close to the
spectroscopic one. The C II 4267,
Mg II 4481 and Si III 4553
lines are visible in both separated spectra. The temperatures were
obtained by fixing the temperature and luminosity ratios to the
photometric values.
0.64 was
found. The WD analysis tended to raise this value and the
potential of the primary had to be fixed to keep it close to the
spectroscopic one. The C II 4267,
Mg II 4481 and Si III 4553
lines are visible in both separated spectra. The temperatures were
obtained by fixing the temperature and luminosity ratios to the
photometric values.
On the mass-![]() diagram, the components are fairly well aligned on the 10 Myr
isochrone. On the HR diagram, both components are
significantly overluminous with respect to their respective
evolutionary tracks, as is often the case.
diagram, the components are fairly well aligned on the 10 Myr
isochrone. On the HR diagram, both components are
significantly overluminous with respect to their respective
evolutionary tracks, as is often the case.
A.26 5 196565
This detached eccentric system presents medium quality light curves
with eclipses of similar depth. The V and B data
are missing in the OGLE database. The finding chart shows a neighbor of
similar brightness as the target about ![]() to the S, raising some concern regarding possible spectral
pollution. The results do not confirm these fears, though.
to the S, raising some concern regarding possible spectral
pollution. The results do not confirm these fears, though.
There are 13 out-of-eclipse spectra. The RV curves are very good and well constrained by the observations, in spite of a lack of observations where the expected amplitude reaches its maximum.
A spectroscopic B luminosity ratio of ![]() 0.41 was
found, and the potential of the primary was adjusted and fixed in the
WD analysis to maintain that value. The C II 4267
and Mg II 4481 lines are visible
in both separated spectra. The least-squares fit of composite synthetic
spectra to the observed ones provided a temperature ratio higher than
that provided by the photometry, and a primary temperature of
20 960
0.41 was
found, and the potential of the primary was adjusted and fixed in the
WD analysis to maintain that value. The C II 4267
and Mg II 4481 lines are visible
in both separated spectra. The least-squares fit of composite synthetic
spectra to the observed ones provided a temperature ratio higher than
that provided by the photometry, and a primary temperature of
20 960 ![]() 600 K. Fixing the temperature ratio to
the photometric value resulted in the slightly hotter primary
temperature that has been adopted.
600 K. Fixing the temperature ratio to
the photometric value resulted in the slightly hotter primary
temperature that has been adopted.
The mass-![]() diagram suggests that the secondary has a radius too large with regard
to the primary, as if the luminosity ratio was overestimated:
while the primary lies close to the 40 Myr isochrone, the
secondary lies on the 50 Myr one. On the HR diagram,
however, each component has a position compatible with its respective
evolutionary track within the error bars, though the primary is
slightly overluminous while the secondary is slightly underluminous.
diagram suggests that the secondary has a radius too large with regard
to the primary, as if the luminosity ratio was overestimated:
while the primary lies close to the 40 Myr isochrone, the
secondary lies on the 50 Myr one. On the HR diagram,
however, each component has a position compatible with its respective
evolutionary track within the error bars, though the primary is
slightly overluminous while the secondary is slightly underluminous.
This system was studied by WW01. Their relative radius of the primary (0.204) is very close to ours (0.200) but their radius of the secondary (0.116) is smaller than ours (0.150). The difference arises because they consider the eclipses as total, while we consider them as partial. Additional accurate photometry in both minima would be welcome to settle the question.
A.27 5 261267
This is a typical semi-detached system with high-quality light curves
and eclipses of unequal depths. The ![]() curve shows no
detectable depression before the primary eclipse. Although the finding
chart shows a few neighbors, they all lie beyond
curve shows no
detectable depression before the primary eclipse. Although the finding
chart shows a few neighbors, they all lie beyond ![]() of the target.
of the target.
This system has peculiar color indices (see Table 3 and Fig. 3). Since it lies near the edge of the CCD in the OGLE-II survey, it is also listed under the name 6 11806 in the corresponding database. Thus, there are more than 600 data points in the I-band light curve, instead of about 300.
There are 10 out-of-eclipse spectra, which constrain the RV curves relatively well.
Both photometric and spectroscopic ratios are very similar (![]() 0.4).
Because of the relatively high
0.4).
Because of the relatively high
![]() (>150 km s-1) and
moderate S/N of the
observations, there are no exploitable metallic lines in the separated
spectra. The temperature of the primary was obtained,
as usual, by least-squares fit to the composite
spectra, after fixing the temperature and luminosity ratios to the
values given by a preliminary WD analysis.
(>150 km s-1) and
moderate S/N of the
observations, there are no exploitable metallic lines in the separated
spectra. The temperature of the primary was obtained,
as usual, by least-squares fit to the composite
spectra, after fixing the temperature and luminosity ratios to the
values given by a preliminary WD analysis.
The mass-![]() and HR diagrams are typical of a massive Algol-type binary. The primary
is overluminous relative to the evolutionary track of an isolated star
of the same mass, as are other semi-detached systems like
4 113853 and 5 277080.
and HR diagrams are typical of a massive Algol-type binary. The primary
is overluminous relative to the evolutionary track of an isolated star
of the same mass, as are other semi-detached systems like
4 113853 and 5 277080.
A.28 5 265970
This slightly eccentric detached system has medium-to-high quality
light curves of the EA type. The sampling of the light-curve
is incomplete, due to an orbital period close to 3.5 days.
In particular, the depth of the secondary minimum is
ill-defined. Therefore, the photometric temperature ratio and
inclination are not very reliable. Actually, there is a correlation
between
these two parameters, in the sense that an increase of
inclination implies a decrease of the temperature ratio. The finding
chart shows a well defined target, but with an only slightly fainter
neighbor about
![]() to the NW.
to the NW.
This system lies near the edge of the OGLE-II CCD, and so was measured also on the adjacent chip under the name 6 17345, so that there are as many as 586 data points in the I band. The two data sets were merged after applying a small magnitude offset to each. With the EBOP code the fitted magnitude at quadrature and its error were defined for each set, then the mean magnitude at quadrature weighted by the inverse of the variance was computed. Finally, the appropriate offset was applied to each of the two sets to adjust it to this mean magnitude.
There are 10 out-of-eclipse spectra. The RV curves are quite good and well constrained by the observations.
Because of the loose constraints on the light curves, the proposed solution for this system heavily relies on the spectroscopic observations. Nevertheless, the proposed solution meets the spectroscopic and photometric constraints very well, so we consider it as close to reality.
A spectroscopic B luminosity ratio of ![]() 0.23 was
found from the usual least-squares fit, which provides the temperature
of the primary with an excellent internal precision. The temperature of
the secondary is much less certain, because of the small luminosity
ratio. In order to maintain the
luminosity ratio to the spectroscopic value in the
WD analysis, one has to fix the potential of the primary to an
appropriate value, and the temperature ratio converges to a lower value
than the spectroscopic one, but still compatible with it given the
errors. Thus the photometric temperature ratio was adopted, and the
temperature of the primary was determined in the usual way.
0.23 was
found from the usual least-squares fit, which provides the temperature
of the primary with an excellent internal precision. The temperature of
the secondary is much less certain, because of the small luminosity
ratio. In order to maintain the
luminosity ratio to the spectroscopic value in the
WD analysis, one has to fix the potential of the primary to an
appropriate value, and the temperature ratio converges to a lower value
than the spectroscopic one, but still compatible with it given the
errors. Thus the photometric temperature ratio was adopted, and the
temperature of the primary was determined in the usual way.
A number of metallic lines are identifiable in both separated spectra: C II 4267, O II 4276, O II 4415-17, Mg II 4481 and Si III 4553. There is no emission in the Balmer lines.
The positions of the stars in the mass-![]() diagram are not quite mutually consistent: the ratio of radii should be
decreased in order to bring the two components on the same isochrone,
which would correspond to about 26 Myr. In the
HR diagram, the primary component matches its theoretical
evolutionary track surprisingly well, while the secondary has a
position consistent with its
track within the error bar. The spectroscopic constraints, which are
strong, are well fulfilled, but additional photometric data would be
useful to improve our solution. This system is especially interesting,
because the primary is very close to the TAMS while the secondary is
much less evolved.
diagram are not quite mutually consistent: the ratio of radii should be
decreased in order to bring the two components on the same isochrone,
which would correspond to about 26 Myr. In the
HR diagram, the primary component matches its theoretical
evolutionary track surprisingly well, while the secondary has a
position consistent with its
track within the error bar. The spectroscopic constraints, which are
strong, are well fulfilled, but additional photometric data would be
useful to improve our solution. This system is especially interesting,
because the primary is very close to the TAMS while the secondary is
much less evolved.
We applied the EBOP code on four subset of the total time
series, after fixing all parameters to their average value, except
inclination, ![]() ,
,
![]() ,
magnitude at quadrature and phase shift. No significant trend
can be seen in Fig. A.11,
which does not prove, however, that
,
magnitude at quadrature and phase shift. No significant trend
can be seen in Fig. A.11,
which does not prove, however, that ![]() remains constant with time. The less reliable
remains constant with time. The less reliable ![]() quantity does not
differ significantly from zero according to the EBOP code. In the
WD solution, we have arbitrarily imposed a low value
quantity does not
differ significantly from zero according to the EBOP code. In the
WD solution, we have arbitrarily imposed a low value ![]()
![]()
![]() which roughly corresponds to the theoretical prediction.
which roughly corresponds to the theoretical prediction.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA11.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1881.png)
|
Figure A.11:
Same as Fig. A.4,
but for the system 5 265970. The horizontal dashed
line shows the weighted average of the |
| Open with DEXTER | |
A.29 5 266015
This system presents high-quality light curves of the EB type with minima of unequal depth. Its bright I-band light curve is perfectly well sampled. The small depression occurring just before the primary eclipse is indicative of a semi-detached system with a secondary component filling its Roche lobe and pouring matter onto the primary component. However, the amplitude of this effect was judged too small to justify an attempt to model it through a spot.
There are 10 out-of-eclipse spectra. The RV curves are well constrained by the observations.
A spectroscopic B luminosity ratio of 0.61
was found, rather remote from the photometric value (0.49),
as is often the case in semi-detached systems. The separated
spectra of both components have a decent S/N
(Fig. A.12).
Nevertheless, the ![]() being high (>150 km s-1),
the small metallic lines are not very conspicuous. The
He I 4120 and He II 4542 lines
are visible in the spectrum of the primary. The Si III line
appears in both spectra. This is one of the few systems with apparently
no significant nebular emission lines, therefore the separated Balmer
lines can be used to find the temperature of the primary. The spectral
features of the primary point to a 32 000 K
star, which is confirmed by the usual least-squares fit.
being high (>150 km s-1),
the small metallic lines are not very conspicuous. The
He I 4120 and He II 4542 lines
are visible in the spectrum of the primary. The Si III line
appears in both spectra. This is one of the few systems with apparently
no significant nebular emission lines, therefore the separated Balmer
lines can be used to find the temperature of the primary. The spectral
features of the primary point to a 32 000 K
star, which is confirmed by the usual least-squares fit.
The positions of the stars in the mass-![]() and HR diagrams are coherent with an evolved system having
undergone mass exchange. The primary component is close to the track
corresponding to a 15.6
and HR diagrams are coherent with an evolved system having
undergone mass exchange. The primary component is close to the track
corresponding to a 15.6
![]() star.
star.
This system was studied by WW02. As with most semi-detached systems they studied, their photometric mass ratio proved to be unreliable.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fA12a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{10284fA12b.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1882.png)
|
Figure A.12:
Sections of the separated spectra of the primary and secondary
components of the binary 5 266015. The scale on the
vertical axis is adapted to the size of the features in each section.
The red line represents a velocity-shifted synthetic spectrum of the
star.
Beside prominent H I and He I lines,
He II, O II, Mg
II, Si III
and Si IV lines are visible in
both spectra. The strong He II 4542,
next to a smaller Si III 4553 line,
and the He II 4200 line
confirm the high temperature of the primary ( |
| Open with DEXTER | |
A.30 5 266131
The most striking feature of this slightly eccentric detached system (
![]() )
is its huge apsidal motion, which explains the apparently very bad I-band
)
is its huge apsidal motion, which explains the apparently very bad I-band
![]() curve.
An examination of the OGLE finding chart revealed that this
binary is slightly blended, but a posteriori, this does not
seem to have distorted the results.
curve.
An examination of the OGLE finding chart revealed that this
binary is slightly blended, but a posteriori, this does not
seem to have distorted the results.
This system lying close to the edge of the CCD in the OGLE-II survey, it also exists under the name 6 22883, which doubles the number of data points in the I band. The magnitude at quadrature was determined using the EBOP code for each of the two data sets; the two resulting values agreeing within one thousandth of a magnitude, the two data sets were merged without applying any magnitude offset.
There are 10 out-of-eclipse spectra, which constrain quite well the RV curves.
A spectroscopic B luminosity ratio of ![]() 0.65 was
found. As usual with the well detached systems, the potential
of the primary was fixed at a value which preserves this luminosity
ratio through the WD analysis. The S/N
of the separated spectra are too low to allow any useful metallic
line to be seen. Since the temperature ratio is well constrained by the
photometric data, the temperature of the primary was determined by
fixing this ratio at its photometric value. There is no nebular
emission in the Balmer lines.
0.65 was
found. As usual with the well detached systems, the potential
of the primary was fixed at a value which preserves this luminosity
ratio through the WD analysis. The S/N
of the separated spectra are too low to allow any useful metallic
line to be seen. Since the temperature ratio is well constrained by the
photometric data, the temperature of the primary was determined by
fixing this ratio at its photometric value. There is no nebular
emission in the Balmer lines.
The mass-![]() diagram suggests that the ratio of radii has been slightly
underestimated, since the secondary has a surface gravity too large
compared to the primary. Still, the positions of both components are
compatible, within the errors, with an isochrone
at 7-8 Myr. The HR diagram shows a good
match between the positions of both components and the evolutionary
tracks of single 9.0 and 7.7
diagram suggests that the ratio of radii has been slightly
underestimated, since the secondary has a surface gravity too large
compared to the primary. Still, the positions of both components are
compatible, within the errors, with an isochrone
at 7-8 Myr. The HR diagram shows a good
match between the positions of both components and the evolutionary
tracks of single 9.0 and 7.7
![]() stars. However, both components are slightly overluminous relative to
their respective tracks.
stars. However, both components are slightly overluminous relative to
their respective tracks.
The apsidal motion amounts to ![]()
![]() yr-1,
as shown by the
yr-1,
as shown by the ![]() values
obtained with the EBOP code for four successive subsets of the whole
time serie in the I band. That value is
confirmed by the WD analysis. The run of
values
obtained with the EBOP code for four successive subsets of the whole
time serie in the I band. That value is
confirmed by the WD analysis. The run of ![]() versus
time is shown in Fig. A.13,
together with the best-fit curve provided by the WD code. The
reality of a very fast apsidal motion is beyond any doubt.
It is further discussed in Sect. 4.
versus
time is shown in Fig. A.13,
together with the best-fit curve provided by the WD code. The
reality of a very fast apsidal motion is beyond any doubt.
It is further discussed in Sect. 4.
A.31 5 266513
This a close detached system with similar components, according to its
medium quality light curves with minima of similar depth. The finding
chart shows a slightly fainter star at ![]() to the W of the target.
to the W of the target.
There are 10 out-of-eclipse spectra. The RV curves are well constrained by the observations, though the noise is rather large because this system is the faintest in our sample.
A spectroscopic B luminosity ratio of 0.73 was found, but with a large scatter of 0.09. The potential of the primary was fixed so that the WD analysis preserves a ratio close to that value. The separated spectra have a low S/N and no metallic lines are exploitable. Moreover, the Balmer lines are polluted by nebular emission. The photometric temperature ratio is rather well defined, thanks to the large depth of the minima, and was fixed for the determination of the temperature of the primary, as usual for most detached systems.
The mass-![]() diagram shows the two components fairly well aligned along the
diagram shows the two components fairly well aligned along the ![]() Myr
isochrone. On the HR diagram, the primary lies almost exactly
on its evolutionary track, while the secondary is slightly
overluminous, though its position is quite compatible with the
evolutionary tracks within the errors. The luminosity ratio (hence the
ratio of radii) seems to have been slightly overestimated.
Myr
isochrone. On the HR diagram, the primary lies almost exactly
on its evolutionary track, while the secondary is slightly
overluminous, though its position is quite compatible with the
evolutionary tracks within the errors. The luminosity ratio (hence the
ratio of radii) seems to have been slightly overestimated.
A.32 5 277080
This system is a typical semi-detached binary with high-quality light curves of the EB type. A small depression before the primary eclipse signals the possible presence of a mass-transfer stream. The effect is small enough for us not to deem it worth the effort to model it through a cool spot on the primary.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA13.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1887.png)
|
Figure A.13: Same as Fig. A.4, but for the system 5 266131. The solid line is the best fit provided by the WD code. |
| Open with DEXTER | |
This system has peculiar color indices (see Table 3 and
Fig. 3).
Indeed, an examination of the OGLE finding chart revealed that this
binary is strongly blended with a brighter star lying ![]() to the SW of the target.
to the SW of the target.
There are 11 out-of-eclipse spectra. Because of an orbital period close to two days, there are no observations before the quadratures. Yet the RV curves are rather well constrained. This is one of the few systems without nebular emission in the Balmer lines.
A spectroscopic B luminosity ratio of 0.7 was found. This is higher than the photometric ratio (0.57), as seems to be often the case of semi-detached systems. The separated spectra are fairly good. A number of metallic lines are visible in the spectrum of the primary: O II 4185, C II 4267, O II 4276-7, Mg II 4481 and Si III 4553. The Mg II 4481 line is the only metallic line detectable in the spectrum of the secondary. The temperature of the primary was determined after fixing the temperature and luminosity ratios to their photometric values.
The positions of the stars in the mass-![]() and HR diagrams are typical of Algol-type system with a
secondary more evolved than the primary. The primary component,
however, is much more luminous than expected from the
evolutionary track of a single star of the same mass, and we cannot
guarantee that its effective temperature has not been overestimated.
The peculiar HR diagram might
be the result of the blend mentioned above with a nearby bright star.
and HR diagrams are typical of Algol-type system with a
secondary more evolved than the primary. The primary component,
however, is much more luminous than expected from the
evolutionary track of a single star of the same mass, and we cannot
guarantee that its effective temperature has not been overestimated.
The peculiar HR diagram might
be the result of the blend mentioned above with a nearby bright star.
A.33 5 283079
This is a typical detached system with twin components and a circular
orbit. The target appears just isolated on the finding chart, with a
companion of similar brightness about ![]() away from it to the SE.
away from it to the SE.
There are 10 out-of-eclipse spectra. The RV curves
are well defined and constrained by the observations. There is probably
a faint nebular emission in both H![]() and H
and H![]() lines.
lines.
With a spectroscopic B luminosity ratio close to 1.0, a mass ratio of 1.003 and a temperature ratio of 0.997, this is the system with the most similar components in our sample. Thus it is probably a real pair of ``twins'', i.e. it has a mass ratio higher than 0.95. This is why the choice of the primary is undecided in this system: which component is the primary was decided on the basis of an early iteration, and it is only in the last iteration that we obtained q=1.003 > 1. The potential of the primary was fixed in the WD analysis, in order to keep the B luminosity ratio close to 0.99. The separated spectra are noisy and the C II 4267 and Mg II 4481 are barely visible. The temperature of the primary was determined by fixing the temperature ratio to 0.997 and the luminosity ratio to 0.99.
On the mass-![]() diagram, both components lie on the 3 Myr isochrone,
so this system is very young. On the HR diagram, they
are slightly overluminous with respect to the evolutionary tracks, but
still within the error bars. On the other hand, the components lie
exactly on the metal-poor tracks (Z=0.001).
diagram, both components lie on the 3 Myr isochrone,
so this system is very young. On the HR diagram, they
are slightly overluminous with respect to the evolutionary tracks, but
still within the error bars. On the other hand, the components lie
exactly on the metal-poor tracks (Z=0.001).
Footnotes
- ... motion
![[*]](/icons/foot_motif.png)
- Based on observations made with the FLAMES-GIRAFFE multi-object spectrograph mounted on the Kuyen VLT telescope at ESO-Paranal Observatory (Swiss GTO programme 072.A-0474A; PI: P. North).
- ...
![[*]](/icons/foot_motif.png)
- Tables 11-17, Figs. 17-28 and Appendix are only available in electronic form at http://www.aanda.org
- ... unsatisfactory
![[*]](/icons/foot_motif.png)
- This should not be interpreted as a criticism of the KOREL code, but only as a warning that this code should be used in a very careful way. See also Sect. 3.5.4 for a remark about the other method.
- ... fluxes
![[*]](/icons/foot_motif.png)
- See http://kurucz.harvard.edu/grids.html
- ... seeing
![[*]](/icons/foot_motif.png)
- Note that the sky subtracted from the stellar spectra was limited to the continuum component. Therefore, sky subtraction did not alter the nebular emission lines.
All Tables
Table 1: Spectroscopic observations: epochs, heliocentric Julian dates at mid exposure, exposure times and sky conditions.
Table 2: Method of multiple subsets: groups of parameters allowed to converge for each model.
Table 3: Basic parameters of the observed eclipsing binaries: identifying number (Fig. 1), OGLE identifying code, coordinates, orbital period, epoch of primary minimum (see text), infrared and (B-V) and (V-I) color indices.
Table 4: Intrinsic color indices at quadrature computed by synthetic photometry.
Table 5: Comparison of our solutions (NGBR) for the five binaries in common with HHH03/05.
Table 6: Comparison of our results (NGBR) with the light-curves solutions of Wyithe & Wilson (2001,2002, WW01, WW02) and Graczyk (2003, dG03).
Table 7:
Nebular emission: mean radial velocities and mean FWHM
of the H![]() and H
and H![]() lines
(the quoted uncertainties are standard deviations).
lines
(the quoted uncertainties are standard deviations).
Table 8:
Sky positions: astrometry, sky background excesses (see Sect. 4.2) and
mean radial velocities derived from the H![]() emission line.
emission line.
Table 9: Comparison with theoretical evolutionary models: difference between the evolutionary and observed masses.
Table 10: Summary of the average and median distance moduli, for the three subsamples defined in the text.
Table 11: Orbital parameters.
Table 12: Wilson-Devinney analysis, as obtained on the basis of both photometry and spectroscopy.
Table 13: Astrophysical parameters for the primary components.
Table 14: Astrophysical parameters for the secondary components.
Table 15: Distance determination.
Table 16: Light curves: ratio of the primary minimum to the rms (I-band), rms scatters and minimum chi-squared values from WD/PHOEBE code.
Table 17: Radial velocity curves: rms scatters.
All Figures
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{10284fg1.eps}
\vspace*{6.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg29.png)
|
Figure 1:
Positions of the 33 binaries in the 1
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10284fg2.eps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg52.png)
|
Figure 2: Histogram of periods of our sample of 33 eclipsing binaries in 0.5 day bins. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg3.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg61.png)
|
Figure 3: Observed (reddened) color-color diagrams of our sample. These are the brightest out-of-eclipse values from Table 3. They were determined from the best light-curve fits. The low scatter is due to a reddening line almost parallel to the main sequence (see upper right panel). Note that some values (open symbol) are doubtful as they lie off the linear trend. The dashed lines illustrate how to recover correct B-V and V-I indices from doubtful ones, under the assumption that the B-I index is reliable, for the system 5 261267. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg4.eps}\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg516.png)
|
Figure 4:
Photometric vs. spectroscopic values of the B luminosity
ratio (full symbol: detached; open symbol: semi-detached/contact). The
dotted line corresponds to |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{10284fg5.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg594.png)
|
Figure 5:
Histogram of the mean heliocentric radial velocities of the nebular H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{10284fg6.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg595.png)
|
Figure 6:
Histogram of the mean heliocentric radial velocities of the nebular H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10284fg7.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg598.png)
|
Figure 7: Velocity field of the H II gas. The size of symbol is proportional to the value of the velocity. Values higher than 155 km s-1 are given in red (electronic version only). Filled symbols are for binary systems, while open symbols are for skies. Crosses are for binary systems without emission. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg8.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg642.png)
|
Figure 8: Comparison between two kinematic tracers: radial velocities of nebular H II ( left) and systemic velocities of binary systems ( right). The data are arranged in 5 km s-1 bins. The best-fitting double-Gaussian and Gaussian models are over-plotted. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fg9.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg657.png)
|
Figure 9:
Detached systems: difference between evolutionary mass and observed
mass vs. observed mass. Filled symbols: primary; open symbols:
secondary. The point in the inset in the lower left corner shows the
median error bars for the mass of the primary. The vertical bar does
not include the errors on luminosity and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fg10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg658.png)
|
Figure
10: Same as Fig. 9, for the detached systems of Hilditch et al. (2005). |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg11.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg667.png)
|
Figure 11: Mass-luminosity relation for our 23 detached systems. Full dots represent the primary components, while open dots represent the secondary ones. The dotted lines are the isochrones with age of 0, 5, 10, 20, 30, 40, 50 and 70 Myr for Z = 0.004 (Charbonnel et al. 1993). The red line is a simple least-squares fit of all 46 points, without weighing. The steeper blue line is the relation adopted by Graczyk (2003) for the LMC and SMC. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg12.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg677.png)
|
Figure 12:
Observed versus theoretical apsidal constant |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fg13.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg681.png)
|
Figure 13:
Distribution of the 33 observed mass ratios (solid: detached, dashed:
semi-detached/contact) with 0.05 bins. The best flat
distribution is over-plotted for each category (detached and
semi-detached or contact systems). Both distributions are truncated at
a cut-off value of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fg14.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg683.png)
|
Figure 14: Top: cumulative probability distribution as a function of the mass ratio for our 23 detached (solid line) and 10 semi-detached/contact (dotted line) binaries. The dashed oblique line plotted over the detached distribution represents a flat distribution with a cutoff at q = 0.72. For the semi-detached/contact systems, a flat distribution with a cutoff at q=0.43provides a reasonable fit as well. Bottom: cumulative probability distribution for HHH03/05's 21 detached binaries. The over-plotted flat distribution with a cutoff at q = 0.5 shows the incompatibility of a flat distribution with the HHH03/05 data. There is a similar figure in Pinsonneault & Stanek (2006). They show that the data are best-fitted with a 55% flat-45% twin distribution (not shown in this figure). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm]{10284fg15.eps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg693.png)
|
Figure 15: Histogram of color excesses of 28 binaries in 0.025 bins. The best Gaussian fit is over-plotted. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fg16.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg697.png)
|
Figure 16:
Top: distribution of the V-
(left) and I-band (right)
distance moduli. The distribution of the whole sample of
27 systems with good colors and presumably without third light
(dashed line) is shown. Only binaries with good HR diagrams
are selected for the smaller statistics. The best-fitting Gaussian
curves for the 19-binary distributions are over-plotted. Bottom:
distance modulus vs. absolute visual magnitude (left)
and distance modulus vs. apparent visual magnitude (right).
The estimated magnitude cut-off for a mean extinction is indicated by
the diagonal solid line; the dashed lines correspond to the cut-off
lines for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg17.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1809.png)
|
Figure 17:
I-band light curves with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg18.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1810.png)
|
Figure 18: Same as Fig. 17, for 12 more stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg19.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1811.png)
|
Figure 19: Same as Fig. 17, for nine more stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg20.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1812.png)
|
Figure 20:
Radial velocity data and best-fitting RV curves.The |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg21.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1813.png)
|
Figure 21: Same as Fig. 20, for 12 more stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg22.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1814.png)
|
Figure 22: Same as Fig. 20, for nine more stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg23.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1815.png)
|
Figure 23: Mass-surface gravity diagrams: the positions of the primary and the secondary components are indicated by filled and open symboles, respectively. The lines ares isochrones from Charbonnel et al. (1993) at Z = 0.004, with ages of 3, 5, 10, 20, 30, 40, 50 and 100 Myr. See text for comments on individual stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg24.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1816.png)
|
Figure 24: Same as Fig. 23, for 12 more stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg25.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1817.png)
|
Figure 25: Same as Fig. 23, for nine more stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg26.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1818.png)
|
Figure 26:
HR diagrams: the positions of the primary and the secondary components
are indicated by filled and open symbols, respectively. The primary is
the component with the larger mass. The evolutionary tracks from
Charbonnel et al. (1993)
at Z = 0.004, corresponding to the observed masses,
are indicated by solid (primary) and dashed black lines (secondary).
Since
these authors adopt a helium content Y=0.24+3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg27.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1819.png)
|
Figure 27: Same as Fig. 26, for 12 more stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{10284fg28.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1820.png)
|
Figure 28: Same as Fig. 26, for nine more stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA1a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{10284fgA1b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1823.png)
|
Figure A.1:
Sections of the separated spectra of the primary and secondary
components of the binary 4 110409. The scale on the
vertical axis is adapted to the size of the features in each section.
The red line represents the best-fit synthetic spectrum shifted to the
systemic velocity. Besides prominent H I
and He I lines, Mg II
and Si III lines are visible in
the spectrum of the secondary. The spectrum of the primary is far less
convincing; nevertheless Si IV lines
seem to be present next to H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA2.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1832.png)
|
Figure A.2:
Variation with time of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10284fgA3a.eps}\hspace*{7mm}
\includegraphics[width=8cm,clip]{10284fgA3b.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1833.png)
|
Figure A.3:
Example of observed spectra close to a quadrature. Both spectra are at
the same scale. The red line represents the composite synthetic
spectrum of the binary system, i.e. the addition of the scaled
and velocity-shifted synthetic spectra of the two components for the
corresponding orbital phase. Besides a low S/N,
the spectrum of 4 121461 shows strong nebular emission in the
Balmer lines. From the best fit the B luminosity
ratio was found to be |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA4.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1839.png)
|
Figure A.4:
Variation with time of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA5a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{10284fgA5b.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1851.png)
|
Figure A.5:
Sections of the separated spectra of the primary and secondary
components of the binary 5 032412. The scale on the
vertical axis is adapted to the size of the features in each section.
The red line represents a velocity-shifted synthetic spectrum of the
star. Beside prominent H I and He I lines,
He II, O II, Mg
II, Si III
and Si IV lines are visible in
both spectra. The strong He II 4542,
next to a smaller Si III 4553 line,
and the He II 4200 line confirm
the high temperature of the primary ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA6a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{10284fgA6b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1852.png)
|
Figure A.6: Sections of the separated spectra of the primary and secondary components of the binary 5 038089. The scale on the vertical axis is adapted to the size of the features in each section. The red line represents a velocity-shifted synthetic spectrum of the star. Beside prominent H I and He I lines, He II and a number of fainter metallic lines (C II, O II, Si III, Si IV) are visible. The relative intensities of the He II 4542 and Si III 4553 are very useful to constrain the temperature of the two stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA7.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1859.png)
|
Figure A.7:
Same as Fig. A.4,
but for the system 5 95557. The filled black dots
represent independent |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA8.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1869.png)
|
Figure A.8: Temperature of the primary (black dots) and of the secondary (red dots) component of the system 5 123390, obtained by fitting composite synthetic spectra to the observed ones, versus the quality of the fit. The trends are roughly horizontal, at least for good fits, which inspires confidence. In a few cases, the components are exchanged (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA9.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1870.png)
|
Figure A.9:
Same as Fig. A.4,
but for the system 5 123390. The filled black dots
represent independent |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA10.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1875.png)
|
Figure A.10: Effective temperatures of the system 5 180576 obtained from a fit to the composite spectra, keeping the temperature and luminosity ratios fixed. Black dots are for the primary, red dots for the secondary. Note that the two curves should be considered as one and the same, since their ratio is constant. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA11.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1881.png)
|
Figure A.11:
Same as Fig. A.4,
but for the system 5 265970. The horizontal dashed
line shows the weighted average of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fA12a.eps}\hspace*{3mm}
\includegraphics[width=8.5cm,clip]{10284fA12b.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1882.png)
|
Figure A.12:
Sections of the separated spectra of the primary and secondary
components of the binary 5 266015. The scale on the
vertical axis is adapted to the size of the features in each section.
The red line represents a velocity-shifted synthetic spectrum of the
star.
Beside prominent H I and He I lines,
He II, O II, Mg
II, Si III
and Si IV lines are visible in
both spectra. The strong He II 4542,
next to a smaller Si III 4553 line,
and the He II 4200 line
confirm the high temperature of the primary ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10284fgA13.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa10284-08/Timg1887.png)
|
Figure A.13: Same as Fig. A.4, but for the system 5 266131. The solid line is the best fit provided by the WD code. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.