| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 7 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201014819 | |
| Published online | 20 September 2010 | |
The Swift Burst Analyser
I. BAT and XRT spectral and flux evolution of gamma ray bursts
P. A. Evans1 - R. Willingale1 - J. P. Osborne1 - P. T. O'Brien1 - K. L. Page1 - C. B. Markwardt2,3,4 - S. D. Barthelmy2 - A. P. Beardmore1 - D. N. Burrows5 - C. Pagani1 - R. L. C. Starling1 - N. Gehrels2 - P. Romano6
1 - Department of Physics and Astronomy, University of Leicester, Leicester, LE1 7RH, UK
2 - NASA/Goddard Space Flight Center, Astrophysics Science Division, Greenbelt, MD 20771, USA
3 - CRESST/Center for Research and Exploration in Space Science and
Technology, 10211 Wincopin Circle, Suite 500, Columbia, MD 21044, USA
4 - Department of Astronomy, University of Maryland College Park, College Park, MD 20742, USA
5 - Department of Astronomy and Astrophysics, 525 Davey Lab., Pennsylvania State University, University Park, PA 16802, USA
6 - INAF, Istituto di Astrofisica Spaziale e Fisica Cosmica, via U La Malfa 153, 90146 Palermo, Italy
Received 19 April 2010 / Accepted 15 June 2010
Abstract
Context. Gamma ray burst models predict the broadband
spectral evolution and the temporal evolution of the energy flux.
In contrast, standard data analysis tools and data repositories
provide count-rate data, or use single flux conversion factors for all
of the data, neglecting spectral evolution.
Aims. We produce Swift BAT and XRT light curves in flux units, where the spectral evolution is accounted for.
Methods. We have developed software to use the hardness ratio
information to track spectral evolution of GRBs, and thus to convert
the count-rate light curves from the BAT and XRT instruments on Swift into accurate, evolution-aware flux light curves.
Results. The Swift Burst Analyser website![]() contains BAT, XRT and combined BAT-XRT flux light curves in three energy regimes for all GRBs observed by the Swift
satellite. These light curves are automatically built and updated when
data become available, are presented in graphical and plain-text
format, and are available for download and use in research.
contains BAT, XRT and combined BAT-XRT flux light curves in three energy regimes for all GRBs observed by the Swift
satellite. These light curves are automatically built and updated when
data become available, are presented in graphical and plain-text
format, and are available for download and use in research.
Key words: gamma-ray burst: general - methods: data analysis - catalogs
1 Introduction
Gamma ray bursts are the most powerful explosions known, and the Swift satellite (Gehrels et al. 2004) has revolutionised our understanding of them, both in filling some gaps in our knowledge and raising new questions and challenges to theory. See Zhang (2007) for a recent review of GRBs and the advances made by Swift.
One of the difficulties inherent in confronting theory with the wealth of data that Swift has produced is that models predict how the flux and spectrum of a GRB or its afterglow will evolve, whereas the data are in units of count rate over some bandpass; in the presence of spectral evolution the count-rate cannot be seen as a proxy for the flux.
It is thus desirable to create GRB flux light curves![]() which employ a time-dependent flux conversion factor to account for spectral evolution. Also, since the bandpasses of the Swift Burst Alert Telescope (BAT; Barthelmy et al. 2005; bandpass: 15-350 keV) and X-ray Telescope (XRT; Burrows et al. 2005;
bandpass: 0.3-10 keV), are close to each other, it is often
informative to consider the two instruments' data together,
extrapolated to a single bandpass, be it the XRT band
(e.g.O'Brien et al. 2006; Willingale et al. 2007) or part of the BAT bandpass (e.g. 15-25 keV, Sakamoto et al. 2007).
which employ a time-dependent flux conversion factor to account for spectral evolution. Also, since the bandpasses of the Swift Burst Alert Telescope (BAT; Barthelmy et al. 2005; bandpass: 15-350 keV) and X-ray Telescope (XRT; Burrows et al. 2005;
bandpass: 0.3-10 keV), are close to each other, it is often
informative to consider the two instruments' data together,
extrapolated to a single bandpass, be it the XRT band
(e.g.O'Brien et al. 2006; Willingale et al. 2007) or part of the BAT bandpass (e.g. 15-25 keV, Sakamoto et al. 2007).
We have therefore created the Swift Burst Analyser. In
this first paper relating to the facility, we present an online
repository of BAT and XRT unabsorbed flux light curves in three energy
regimes: 0.3-10 keV flux, 15-50 keV flux, and the flux
density at 10 keV. The Burst Analyser provides BAT and
XRT flux light curves separately and combined; an example is
shown in Fig. 1.
It also includes a time evolution history for each instrument of
the counts-to-flux conversion factor, and of the spectral photon
index,
![]() (i.e. for a power-law spectrum with the number of photons at energy E is given by
(i.e. for a power-law spectrum with the number of photons at energy E is given by
![]() ).
In addition, we provide BAT flux light curves where spectral
evolution is not included, for comparison with the non-evolving
XRT data already available online
).
In addition, we provide BAT flux light curves where spectral
evolution is not included, for comparison with the non-evolving
XRT data already available online![]() (Evans et al. 2007, 2009). One example of the advantage of considering spectral evolution is shown in Fig. 2;
for GRB 060729 the rapid decay phase is steeper when viewed in
flux space with spectral evolution accounted for, which allows us to
see the turn-on of the afterglow. (Note that Grupe et al. 2007, 2010 also accounted for spectral evolution in their analysis of this GRB. The evolution-induced dip
feature shown in Fig. 2
is less prominant in the 0.3-10 keV band which is why it is not
seen in their analysis.) We consider the physical interpretation of GRB
light curves enabled by our new method in Paper II (Evans
et al., in prep.).
(Evans et al. 2007, 2009). One example of the advantage of considering spectral evolution is shown in Fig. 2;
for GRB 060729 the rapid decay phase is steeper when viewed in
flux space with spectral evolution accounted for, which allows us to
see the turn-on of the afterglow. (Note that Grupe et al. 2007, 2010 also accounted for spectral evolution in their analysis of this GRB. The evolution-induced dip
feature shown in Fig. 2
is less prominant in the 0.3-10 keV band which is why it is not
seen in their analysis.) We consider the physical interpretation of GRB
light curves enabled by our new method in Paper II (Evans
et al., in prep.).
All of the data created by the Burst Analyser are available from: http://www.swift.ac.uk/burst_analyser. This includes graphical plots and the data in plain-text format.
In this paper we introduce the Swift Burst Analyser. In Sect. 2 we explain how the light curves are created and spectral evolution accounted for. Section 3 highlights the limitations of our method and some recommended checks users should apply. We also give details of when the light curves are created and how they can be accessed (Sect. 4), and the usage policy (Sect. 5).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14819fig1.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14819-10/Timg4.png)
|
Figure 1: An example of a flux density light curve from the Burst Analyser. The spectrally-evolving BAT-XRT flux light curve of GRB 061121, is shown as unabsorbed flux density at 10 keV; the lower panel shows the evolution of the photon index of the power-law spectrum. The last 3 BAT data points suffer from a poorly-constrained spectrum; see Sect. 3.4 for details. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14819fig2.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14819-10/Timg5.png)
|
Figure 2: The flux density light curve of GRB 060729 from the Burst Analyser. Accounting for spectral evolution shows the flux decline during the steep decay to be more rapid than in count space, and reveals the turn-on of the afterglow. |
| Open with DEXTER | |
2 Creation procedure
The process of creating the light curves comprises three phases: generating count-rate light curves and hardness ratios, determining the counts-to-flux conversion factors, and converting the count-rate light curves into flux units. Throughout the descriptions of thes phases, any FTOOLS used were called with the default parameters unless explicitly stated otherwise.
2.1 Count-rate light curves and hardness ratios
The XRT count-rate light curves used by the Burst Analyser are taken from the Swift XRT Light Curve Repository2, and their creation has been documented in detail by Evans et al. (2007, 2009) and will not be repeated here. The hardness ratios are taken from the same place, but are first binned up to contain a minimum of 20 counts per band per bin (on the repository the minimum is 15 counts). This helps to reduce the effect of statistical fluctuations in the hardness ratio on the final light curve.
For BAT, the BATGRBPRODUCT script (part of the Swift software![]() ) is first executed. Among the products created by this script are a measure of
) is first executed. Among the products created by this script are a measure of
![]() and the time range over which it was determined; a spectrum corresponding to this interval (hereafter, ``the
and the time range over which it was determined; a spectrum corresponding to this interval (hereafter, ``the
![]() spectrum'');
and an event list of BAT data extending to 2000 s either side of
the trigger. From this event list a 4-ms binned 15-150 keV
light curve is extracted using the BATBINEVT tool, supplied with relevant detector mask file created by BATGRBPRODUCT. Signal-to-noise-ratio (SNR)-binned
light curves are built from this 4-ms light curve using a custom
script. The ``noise'' on the input bins is the Poisson error in the
count-rate (see the BAT Software Guide
spectrum'');
and an event list of BAT data extending to 2000 s either side of
the trigger. From this event list a 4-ms binned 15-150 keV
light curve is extracted using the BATBINEVT tool, supplied with relevant detector mask file created by BATGRBPRODUCT. Signal-to-noise-ratio (SNR)-binned
light curves are built from this 4-ms light curve using a custom
script. The ``noise'' on the input bins is the Poisson error in the
count-rate (see the BAT Software Guide![]() for more information), and when rebinning the light curve this is
propagated by adding in quadrature, as standard. The algorithm of
the SNR-binning script is described below and illustrated in Fig. 3;
in essence it bins the most significant parts of the light curve
first, to maximise the time-resolution in those bins. In detail
the algorithm is thus:
for more information), and when rebinning the light curve this is
propagated by adding in quadrature, as standard. The algorithm of
the SNR-binning script is described below and illustrated in Fig. 3;
in essence it bins the most significant parts of the light curve
first, to maximise the time-resolution in those bins. In detail
the algorithm is thus:
- 1.
- set n=1;
- 2.
- bin the light curve (or light-curve sections) into new bins of n original 4-ms bins. If any 4-ms bins are left over at the end of the light curve (or section), append them to the last new bin in the curve (or section);
- 3.
- search for any of these new bins with SNR above the threshold;
- 4.
- save any above-threshold new bins in the output light curve;
- 5.
- split the light curve into sections, separated by times which were saved to the output light curve in the previous step;
- 6.
- if at least one new above-threshold bin was found during this pass, increase n by one; otherwise, double n;
- 7.
- if n corresponds to a bin size of
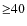 s simply add every 40-s long bin to the output light curve;
s simply add every 40-s long bin to the output light curve;
- 8.
- if there are still bins in the original light curve which have not been assigned to the output light curve, go back to step 2. Otherwise, save the output light curve.
| Figure 3: A demonstration of the SNR binning algorithm. In the first pass (1) the bins marked in black were above the SNR threshold. For the second pass (2) the sub-threshold input bins were grouped in twos. One of these groups was found to be above threshold. In the third pass (3) the input bins were grouped in threes (with left-over input bins appended if necessary, meaning that some of the groups contain four input bins) and two of these were above threshold. This continues until all of the input bins are above threshold (i.e. the whole plot is black) or the input bins are grouped into new bins of 40-s or longer, at which point they are all added to the output light curve. |
|
| Open with DEXTER | |
This results in a light curve in which bins are either above some SNR threshold, or 40 s in duration. This upper limit on bin size is set to preserve some information about the behaviour of the light curve during low-flux periods. Any bins which had SNR < 3 (regardless of the input SNR threshold) are flagged as unreliable, and not be shown in the online plots but they are included in the online data files (on lines beginning with an ``!'' - the comment-line delimiter for QDP). Using this above algorithm, light curves with SNR thresholds of 4-7 are created.
The BAT-XRT combined light curve will necessarily be presented in log-log space most of the time, thus data at ![]() are not shown. Although one could simply use the light curve just
created and ignore the bins before the trigger time, this will result
in sub-optimal binning of the light
curve. Instead a second set of light curves are built using the above
algorithm, but given an input 4-ms-binned light curve which only
contains data after the trigger time.
are not shown. Although one could simply use the light curve just
created and ignore the bins before the trigger time, this will result
in sub-optimal binning of the light
curve. Instead a second set of light curves are built using the above
algorithm, but given an input 4-ms-binned light curve which only
contains data after the trigger time.
As well as the SNR-binned light curve, constant time-binned 15-150 keV light curves are also created, using BATBINEVT. These are nominally created for bin sizes of 4 ms, 64 ms, 1 s and 10 s, but if
![]() s then the light curves with bin size longer than
s then the light curves with bin size longer than
![]() will not be built.
Also, if
will not be built.
Also, if
![]() s
the 4-ms binned light curve is not built, since this rapidly becomes
extremely large. These light curves are accumulated only over the time
range:
s
the 4-ms binned light curve is not built, since this rapidly becomes
extremely large. These light curves are accumulated only over the time
range:
| (1) |
where
A BAT hardness ratio defined as (25-50 keV)/(15-25 keV) is also created using the SNR-binning algorithm above, except that the SNR in both
bands must be above the threshold before an output bin is created. The
input 4-ms light curves in these bands are created with BATBINEVT. By default a hardness ratio with a SNR threshold of 5 is created. If this fails to produce at least two bins with SNR ![]() 3
the threshold is reduced to 4, and if necessary further to 3.
Even if there are still fewer than three bins with an SNR
3
the threshold is reduced to 4, and if necessary further to 3.
Even if there are still fewer than three bins with an SNR ![]() 3
this hardness ratio will be used. The errors on the hardness ratio are
calculated assuming that the individual bands' errors are Gaussian.
3
this hardness ratio will be used. The errors on the hardness ratio are
calculated assuming that the individual bands' errors are Gaussian.
2.2 Counts-to-flux conversion factors
In order to convert the count-rate light curves (described above) into flux light curves, a time-evolving counts-to-flux conversion factor is needed. We do not have sufficient photons to create spectra with a reasonable time-resolution, so instead we assume a spectral shape and use the hardness ratios to track the evolution. GRB spectra tend to be power-laws, or broken power-laws. For the BAT data is has been found that sometimes a cut-off power-law best describes the data (Sakamoto et al. 2008).
We therefore fit the BAT
![]() spectrum with both power-law and cut-off power-law spectral models. If the latter gives a
spectrum with both power-law and cut-off power-law spectral models. If the latter gives a
![]() value at least nine lower than the former (i.e. a 3-
value at least nine lower than the former (i.e. a 3-![]() improvement) then a cut-off power-law model is used in all of the
counts-to-flux conversion factor
calculations (for BAT and XRT). This occurs for 15 per cent
of GRBs; for the rest a power-law model is used. Note that using a
single hardness ratio, we cannot track both the spectral index and the
cut-off energy, but we lack the statistics to use multiple hardness
ratios; we therefore keep the cut-off energy fixed at the value
determined in the above fit, allowing no evolution of this parameter.
This may introduce a systematic error or bias in our counts-to-flux
conversion factors (hereafter ``CF''), which is discussed
in Sect. 3.2.
improvement) then a cut-off power-law model is used in all of the
counts-to-flux conversion factor
calculations (for BAT and XRT). This occurs for 15 per cent
of GRBs; for the rest a power-law model is used. Note that using a
single hardness ratio, we cannot track both the spectral index and the
cut-off energy, but we lack the statistics to use multiple hardness
ratios; we therefore keep the cut-off energy fixed at the value
determined in the above fit, allowing no evolution of this parameter.
This may introduce a systematic error or bias in our counts-to-flux
conversion factors (hereafter ``CF''), which is discussed
in Sect. 3.2.
In addition to the emission model, an absorption model must also be determined. Following the XRT spectrum repository (Evans et al. 2009), we take the absorption model to consist of a PHABS component with the Galactic column density (from Kalberla et al. 2005) and a second PHABS component to represent the absorption local to the burst. If the redshift of the GRB is in the public domain, this component is a ZPHABS with the redshift of the GRB.
Table 1:
The phase spaces used to interpolate from hardness ratio (HR) to
counts-to-flux conversion factors (CF) and spectral photon index (
![]() ).
).
For GRBs with XRT data we can use the XRT data to determine the values of these absorption components. Butler & Kocevski (2007a)
note that absorption derived from early-time XRT data, when strong
spectral evolution is present, can be misleading. Therefore,
if there are at least 200 X-ray photons detected at T>4000 s
post-trigger, a new spectrum is built using only the data from
this time (using the software presented in Evans et al. 2009). If there are fewer than 200 late-time
photons, the absorption values are taken from the XRT spectrum on the repository![]() . If there are no XRT data the Galactic absorption component is taken from Kalberla et al. (2005), and the intrinsic component is assumed to have
. If there are no XRT data the Galactic absorption component is taken from Kalberla et al. (2005), and the intrinsic component is assumed to have
![]()
![]() and lie at z=2.23; these being the mean values from the XRT catalogue (Evans et al. 2009). The absorption values used, and their provenance, are given on the Burst Analyser web page for each GRB.
and lie at z=2.23; these being the mean values from the XRT catalogue (Evans et al. 2009). The absorption values used, and their provenance, are given on the Burst Analyser web page for each GRB.
The spectral model thus determined is loaded into XSPEC and the photon index of the (cut-off) power-law,
![]() ,
is stepped from -1 to 5 in steps of 0.1. For each
,
is stepped from -1 to 5 in steps of 0.1. For each
![]() value
the hardness ratio, unabsorbed 0.3-10 keV flux, unabsorbed
15-50 keV flux, model normalisation and count-rate predicted by
the model are recorded
value
the hardness ratio, unabsorbed 0.3-10 keV flux, unabsorbed
15-50 keV flux, model normalisation and count-rate predicted by
the model are recorded![]() . This gives a look-up table of hardness ratio versus conversion factors (and
. This gives a look-up table of hardness ratio versus conversion factors (and
![]() values). The
hardness ratios and count-rates are determined for the bands used in Sect. 2.1,
i.e. for BAT the hardness ratio is
(25-50 keV)/(15-25 keV) and the count-rate is determined over
the 15-150 keV range. For XRT the hardness ratio is
(1.5-10 keV/0.3-1.5 keV). The normalisation of the power-law
and cut-off power-law models in XSPEC is defined as the flux density at 1 keV, in units of photons keV-1
values). The
hardness ratios and count-rates are determined for the bands used in Sect. 2.1,
i.e. for BAT the hardness ratio is
(25-50 keV)/(15-25 keV) and the count-rate is determined over
the 15-150 keV range. For XRT the hardness ratio is
(1.5-10 keV/0.3-1.5 keV). The normalisation of the power-law
and cut-off power-law models in XSPEC is defined as the flux density at 1 keV, in units of photons keV-1
![]() s-1. A normalisation of one is thus equivalent to 662.5
s-1. A normalisation of one is thus equivalent to 662.5 ![]() Jy. This can then be extrapolated to give the flux density at 10 keV using either:
Jy. This can then be extrapolated to give the flux density at 10 keV using either:
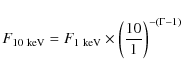
|
(2) |
for the power-law model, or
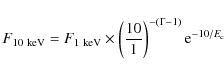
|
(3) |
for the cut-off power-law, where
Given these look-up tables, the hardness ratios created in Sect. 2.1 can be converted instead into time evolution histories of conversion factors. For each bin in the original hardness
ratio, the conversion factors and
![]() value
appropriate to that hardness are determined by interpolating within
this lookup table. The uncertainties in the hardness are also
propagated by interpolating the 1-
value
appropriate to that hardness are determined by interpolating within
this lookup table. The uncertainties in the hardness are also
propagated by interpolating the 1-![]() limits
on the hardness ratios. For BAT data, because the bins may not
exceed 40-s in duration, it is possible for some bins to have
negative hardness ratios (from Poisson fluctuations of low significance
bins). It is impossible for the lookup table to contain negative
values, so these bins are skipped (and will be interpolated across
in Sect. 2.3). Some bins
may have positive hardness ratio values, but negative lower limits. In
this case the error-bar on the conversion factor (or
limits
on the hardness ratios. For BAT data, because the bins may not
exceed 40-s in duration, it is possible for some bins to have
negative hardness ratios (from Poisson fluctuations of low significance
bins). It is impossible for the lookup table to contain negative
values, so these bins are skipped (and will be interpolated across
in Sect. 2.3). Some bins
may have positive hardness ratio values, but negative lower limits. In
this case the error-bar on the conversion factor (or
![]() )
will be truncated at a hardness ratio tending to zero. See Sect. 3.4 for more information.
)
will be truncated at a hardness ratio tending to zero. See Sect. 3.4 for more information.
In order to make the (linear) interpolation as accurate as possible it is preferable to perform it in a phase-space that gives an approximately linear relationship between hardness ratio and the conversion factor. By inspecting look-up tables we thus chose the phase-spaces given in Table 1 for the interpolation.
For some GRBs, there were too few photons for even a single hardness
ratio bin to be created for XRT. This is most commonly the case for
bursts detected by missions other than Swift, which are often not observed by XRT until many hours after the trigger. In these cases
![]() and the
conversion factors were determined from the same spectrum used to
obtain the absorption details (above); this does not allow for spectral
evolution (see Sect. 3.5).
and the
conversion factors were determined from the same spectrum used to
obtain the absorption details (above); this does not allow for spectral
evolution (see Sect. 3.5).
2.3 Flux light curves
For each bin in each count-rate light curve created in Sect. 2.1, a counts-to-flux conversion factor is determined by interpolating the time evolution histories of conversion factors created in Sect. 2.2. For BAT this interpolation is done in linear time space, for XRT log(time) space (since BAT includes negative times and a small time range, whereas XRT only has times after the trigger and covers many decades); the conversion factor is interpolated in log space for both instruments since it covers several decades. The count-rate and error are then multiplied by the conversion factor to give the flux for each bin. For BAT data, some hardness ratio bins with negative values of the ratio may have been skipped (Sect. 2.2) in which case the conversion factor is simply interpolated across this gap. Because GRBs show strong spectral evolution at early times, it is unwise to extrapolate the hardness ratio beyond times where we have a reliable measurement. Thus any light curve bins that occur after the end of the final valid (i.e. positive-valued) hardness ratio bin are discarded and not converted into flux. At later times the spectral evolution is minimal (Butler & Kocevski 2007b), thus for XRT any light curve bins which occur after the final hardness ratio bin are converted to flux using the conversion factors from the final hardness bin.
The uncertainty in the conversion factor is not propagated into
the flux light curve. This is because it is in part a systematic effect
and it will dilute the significance of genuine variability in the light
curve. However, we require this information to determine whether
features in the flux light curves are believable or not. Therefore,
in addition to the basic flux light curve plots, we produce plots
with subpanels showing either the conversion factor and its error, or
the derived photon index (
![]() )
and its errors. Users can use these to consider how much weight should be applied to any given features.
)
and its errors. Users can use these to consider how much weight should be applied to any given features.
As noted in Sect. 2.1, for BAT SNR-binned light curves the maximum permitted bin duration is 40 s, which can result in some low significance (SNR < 3) bins. These are not shown in the online plots, however they appear in the data files as lines beginning with an exclamation mark.
For BAT we also create a flux light curve with no spectral
evolution (for XRT this is already provided by the Light Curve
Repository). The creation is analogous to the light curves described
above, but instead of using the hardness ratio to determine the
conversion factor, a single conversion is used for all bins. This
is taken from the model fitted to the
![]() spectrum. There are thus no sub-plots available for the non-evolving spectrum, instead the spectral model and conversion
factors used are given on the Burst Analyser results page for each GRB.
spectrum. There are thus no sub-plots available for the non-evolving spectrum, instead the spectral model and conversion
factors used are given on the Burst Analyser results page for each GRB.
3 Caveats and checks
Although substantial efforts have been made, by human analysis of the data products, to ensure that these products are reliable and accurate, there are some assumptions inherent to the light-curve creation process which may introduce artefacts. These are both predictable and identifiable. Several of the issues concern the uncertainty involved in extrapolating the BAT or XRT data beyond the range covered by the instrument; if there is any reason to question the assumptions involved in the light-curve creation process, we recommend that users consider the data in their ``own'' bands (i.e. the BAT data in the 15-50 keV range and the XRT data in the 0.3-10 keV range). For the combined BAT-XRT light curve the ``safest'' data to use is the flux density at 10 keV, as, for this dataset, the spectral extrapolation is minimal, as is the associated uncertainty.
In order to determine whether the data are reliable or potentially prone to inaccuracies, there are five questions that should be asked of a dataset.
3.1 Is 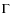 discontinuous between BAT and XRT?
discontinuous between BAT and XRT?
An integral part of the flux conversion is the assumption of a spectral shape (Sect. 2.2).
This can be a power-law or cut-off power-law, but in each case when the
flux is extrapolated outside an instrument's bandpass (i.e. beyond
the band over which the shape was determined) there is an implicit
assumption that the power-law index remains the same. The temporal
evolution of the photon index (
![]() )
as determined from the hardness ratios can be seen as a sub-plot on the
light curves; the default display of the web pages shows this sub-plot.
If the BAT and XRT data show discontinuous
)
as determined from the hardness ratios can be seen as a sub-plot on the
light curves; the default display of the web pages shows this sub-plot.
If the BAT and XRT data show discontinuous
![]() values
then the spectral shape changes between bands and the BAT flux
extrapolated to the XRT
band will be unreliable, and vice-versa. This discontinuity is present
in about 20 per cent of cases. Although the flux density is
not immune to this effect, is will be less strongly affected since it
lies close to both bandpasses. This is demonstrated in Fig. 4.
values
then the spectral shape changes between bands and the BAT flux
extrapolated to the XRT
band will be unreliable, and vice-versa. This discontinuity is present
in about 20 per cent of cases. Although the flux density is
not immune to this effect, is will be less strongly affected since it
lies close to both bandpasses. This is demonstrated in Fig. 4.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{14819fig4a.eps}\...
...ps}\par\includegraphics[angle=-90,width=8.9cm,clip]{14819fig4c.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14819-10/Timg24.png)
|
Figure 4:
Combined BAT-XRT light curve of GRB 060510B. The
|
| Open with DEXTER | |
3.2 Is the BAT spectral fit a cut-off power-law?
As noted in Sect. 2.2, in
some cases a cut-off power-law gives a better spectral fit than a
power-law (in the 465 BAT light curves created for the Burst
Analyser up to GRB 100316D, 67 required
cut-off power-laws), however in these cases we do not allow the
high-energy cut-off to vary. If the cut-off energy moves to lower
energies with time, then at later times the flux above the cut-off will
be overestimated; the inverse is true if the cut-off energy evolves to
harder energies. To investigate the magnitude of this problem we
created a series of BAT spectra for a range of
![]() and cut-off energy (
and cut-off energy (![]() )
values. For each spectrum we determined the hardness ratio and
count-to-flux conversion factors as in Sect. 2.2.
Then, for each spectrum with a hardness ratio in the range 0.9-0.92
(i.e. spectra of approximately equal hardness), we show in
Fig. 5 how the conversion factor and
)
values. For each spectrum we determined the hardness ratio and
count-to-flux conversion factors as in Sect. 2.2.
Then, for each spectrum with a hardness ratio in the range 0.9-0.92
(i.e. spectra of approximately equal hardness), we show in
Fig. 5 how the conversion factor and
![]() necessary to generate such a hardness ratio vary with
necessary to generate such a hardness ratio vary with ![]() .
As can be seen, the
.
As can be seen, the ![]() dependence is not large (note the linear axes). For example, if
dependence is not large (note the linear axes). For example, if ![]() was frozen at 80 keV, but in reality at late times it was
60 keV, the conversion factors would be inaccurate by up to
5 per cent. For more extreme examples of
was frozen at 80 keV, but in reality at late times it was
60 keV, the conversion factors would be inaccurate by up to
5 per cent. For more extreme examples of
![]() variation
(e.g. from 80 keV to 40 keV) these inaccuracies can
reach 50 per cent; however only when extrapolating outside of
the BAT band. The conversion from BAT counts to 15-50 keV flux is
never off by more than 2 per cent.
variation
(e.g. from 80 keV to 40 keV) these inaccuracies can
reach 50 per cent; however only when extrapolating outside of
the BAT band. The conversion from BAT counts to 15-50 keV flux is
never off by more than 2 per cent.
The range of cut-off energies is limited to 40-100 keV in Fig. 5 because at higher energies the 15-50 keV spectrum (whence the hardness ratio is obtained) is insensitive to the cut-off energy, and with lower values the hard band has so few counts that we cannot obtain a hardness ratio. For the XRT we do not see evidence for the cut-off power-law spectra, so freezing the cut-off energy should not affect the XRT flux conversions; except that if the cut-off energy were actually evolving through the 15-50 keV region the use of a fixed energy would lead to the XRT 15-50 keV flux values being overestimates.
In summary, for the ![]() 15
per cent of GRBs where a cut-off power-law is preferred to a power-law
to fit the BAT spectrum, the flux extrapolated outside of the
instruments' bandpasses may be subject to inaccuracies of a factor of
at most two.
15
per cent of GRBs where a cut-off power-law is preferred to a power-law
to fit the BAT spectrum, the flux extrapolated outside of the
instruments' bandpasses may be subject to inaccuracies of a factor of
at most two.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14819fig5.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14819-10/Timg26.png)
|
Figure 5:
The effect of the cut-off energy on the conversion factors and
|
| Open with DEXTER | |
3.3 Are the 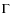 values outside the range 0-4?
values outside the range 0-4?
Although there is considerable scatter in the
![]() values found from BAT and XRT data, values outside the range
values found from BAT and XRT data, values outside the range ![]() 0-4 are not generally seen (see, for example, the Swift Data Table
0-4 are not generally seen (see, for example, the Swift Data Table![]() ; the BAT catalogue, Sakamoto et al. 2008; the XRT catalogue, Evans et al. 2009); thus if the
; the BAT catalogue, Sakamoto et al. 2008; the XRT catalogue, Evans et al. 2009); thus if the
![]() sub-plot shows values outside this range it may indicate a low SNR hardness ratio point rather than a real value of
sub-plot shows values outside this range it may indicate a low SNR hardness ratio point rather than a real value of
![]() and users should double-check the size of the errors on
and users should double-check the size of the errors on
![]() and the conversion factor. Recall that the errors on the conversion
factor are not propagated into the flux errors (see Sect. 3.4
for more). Most light curves show one or two bins with these
``extreme'' values; usually they are the last few bins in that BAT
light curve and it is safe to disregard them.
and the conversion factor. Recall that the errors on the conversion
factor are not propagated into the flux errors (see Sect. 3.4
for more). Most light curves show one or two bins with these
``extreme'' values; usually they are the last few bins in that BAT
light curve and it is safe to disregard them.
Note also that the hardness-ratio-to-conversion-factor look-up table is only created for
![]() values
in the range -1 to 5; if a data point has a value
outside of this range then the conversion factor has been extrapolated
rather than interpolated, and may be less reliable.
values
in the range -1 to 5; if a data point has a value
outside of this range then the conversion factor has been extrapolated
rather than interpolated, and may be less reliable.
3.4 Are the errors on 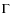 or the conversion factor large or
asymmetric?
or the conversion factor large or
asymmetric?
As discussed in Sect. 2.3, the uncertainty on the hardness ratio is propagated to the uncertainty on the conversion factor, but not into the final error-bar on the flux values. This is because, where the spectral evolution is not large, these errors are systematic in nature and tend to wash out genuine variability. However, if the errors on the conversion factor (visible in the sub-plots) are large compared to the actual flux values, users should not ascribe weight to apparently discrepant points. For example if a single data point lies significantly above the rest of the light curve and has a conversion factor which is inconsistent with the other conversion factor values and has a large error, the apparently discrepant flux is almost certainly the result of a poorly constrained spectral index, whose error is not reflected in the final light curve. To minimise confusion caused by these datapoints, any bin with ``unreliable'' conversion factors are not shown in the default online plots; in the datafile they are indicated by lines beginning with ``!#''. An ``unreliable'' conversion factor is defined as one where the error (positive or negative) is larger than two dex, or where the conversion factor is consistent with zero.
Because the hardness ratio errors were determined assuming Gaussian statistics in each BAT band, low SNR
hardness bins can have negative error-bars which extend below zero.
However, the hardness-ratio-to-conversion-factor look up table cannot
contain negative hardness ratio values. Thus any datapoints
corresponding to hardness ratios consistent with zero
(i.e. non-detections in one of the bands) will have uncertainties
on their
![]() and conversion factor values which are truncated where the hardness
ratio goes to zero. This can usually be spotted by a strongly
asymmetric error on
and conversion factor values which are truncated where the hardness
ratio goes to zero. This can usually be spotted by a strongly
asymmetric error on
![]() or the conversion factor. Further, the hardness ratio and its corresponding
or the conversion factor. Further, the hardness ratio and its corresponding
![]() and conversion factors is viewable online and users can easily check if
and when it becomes unreliable. There is no straightforward means of
determining what the uncertainty in conversion factor should be at such
times; it should instead be considered unconstrained and users are
advised to ignore these datapoints. As with ``extreme'' values of
and conversion factors is viewable online and users can easily check if
and when it becomes unreliable. There is no straightforward means of
determining what the uncertainty in conversion factor should be at such
times; it should instead be considered unconstrained and users are
advised to ignore these datapoints. As with ``extreme'' values of
![]() (Sect. 3.3), most light curves contain a few bins which are subject to this issue, typically at the end of the BAT data.
(Sect. 3.3), most light curves contain a few bins which are subject to this issue, typically at the end of the BAT data.
3.5 Do most/all of the bins for BAT or XRT have the same 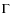 or
conversion factor value?
or
conversion factor value?
For low SNR datasets, there may be only one or two hardness ratio points. In this case the
![]() sub-plots will show very little evolution. This is the case for
sub-plots will show very little evolution. This is the case for ![]() 3 per cent of BAT light curves and
3 per cent of BAT light curves and ![]() 20 per cent of XRT light curves - many of the latter are GRBs detected by other missions which Swift
did not observe until several hours after the trigger. For
BAT-triggered GRBs, only 13 per cent of XRT hardness ratios
have fewer than three bins. This is not a problem, it simply
highlights a lack of information due to the low significance of the
data, but users should note in this case that the light curves tend
towards the non-evolving ones; we lack the data quality necessary to
track the spectral evolution.
20 per cent of XRT light curves - many of the latter are GRBs detected by other missions which Swift
did not observe until several hours after the trigger. For
BAT-triggered GRBs, only 13 per cent of XRT hardness ratios
have fewer than three bins. This is not a problem, it simply
highlights a lack of information due to the low significance of the
data, but users should note in this case that the light curves tend
towards the non-evolving ones; we lack the data quality necessary to
track the spectral evolution.
4 Data availability and creation policy
The data are all available online from: http://www.swift.ac.uk/burst_analyser/. The top-level page provides various means of choosing a specific burst, alternatively the trigger number or target ID of the object (if known) can be appended to the above URL.
The light curves exist both as plots (in postscript and png
[Portable Network Graphics] format) and as text files. For each GRB
there are up to four categories of light curve available: BAT-XRT
combined data (only includes data after the trigger time), BAT-only
data, XRT-only data, and
a BAT light curve with no spectral evolution. For bursts where BAT or
XRT data do not exist, not all of the above will be created.
As discussed in Sects. 2.1 and 2.3
there are
several different BAT-binning criteria used, and the light curves may
have no sub-plot, or a panel showing the conversion factor or
![]() value
for each bin. Note that these values are the interpolated values; at
the start of the four light curve sections is an option to view the measured hardness ratio, and its representation as
value
for each bin. Note that these values are the interpolated values; at
the start of the four light curve sections is an option to view the measured hardness ratio, and its representation as
![]() or conversion factors. Each light curve is also created in three
different bands: the 0.3-10 keV flux, 15-50 keV flux, and
flux density at 10 keV. The web page by default presents a single
light curve (flux density, with a
or conversion factors. Each light curve is also created in three
different bands: the 0.3-10 keV flux, 15-50 keV flux, and
flux density at 10 keV. The web page by default presents a single
light curve (flux density, with a
![]() sub-plot)
for each of the categories, however users can change which plots are
shown. As noted above, some BAT data points are considered unreliable,
either from a low SNR (in the SNR-binned light
curves), or because the uncertainty in the flux conversion is high.
These are not shown in the default plot (alhough they are in the
corresponding text file), however an option to show such points is
given on the web pages. The conversion factor time evolution histories
and a tar archive containing all of the data for the GRB in question
are also available to download. Full documentation supporting these web
pages and downloadable files is also provided online at: http://www.swift.ac.uk/burst_analyser/docs.php. This page also contains a list of any changes made after publication of this paper.
sub-plot)
for each of the categories, however users can change which plots are
shown. As noted above, some BAT data points are considered unreliable,
either from a low SNR (in the SNR-binned light
curves), or because the uncertainty in the flux conversion is high.
These are not shown in the default plot (alhough they are in the
corresponding text file), however an option to show such points is
given on the web pages. The conversion factor time evolution histories
and a tar archive containing all of the data for the GRB in question
are also available to download. Full documentation supporting these web
pages and downloadable files is also provided online at: http://www.swift.ac.uk/burst_analyser/docs.php. This page also contains a list of any changes made after publication of this paper.
The light curves are automatically created and updated via CRON
jobs which run every ten minutes. These check both BAT and XRT data to
determine whether products need to be built or updated. For BAT data
the products will be built for the first time once data appear on on
the
quick-look site![]() (typically a few hours after the trigger), and updated when the ONTIME
keyword of these data increases. For XRT data the products will be
built or updated whenever the X-ray light curve from the Light Curve
Repository2 is created or updated.
(typically a few hours after the trigger), and updated when the ONTIME
keyword of these data increases. For XRT data the products will be
built or updated whenever the X-ray light curve from the Light Curve
Repository2 is created or updated.
Users can determine when a product was last updated from the web page for the GRB. At the top of the page, beneath the GRB name, are given details of the last dataset which was used to create the product. Also, in the footer bar at the base of the page, the time (in UT) when the page was last created is also specified.
5 Usage
The Burst Analyser data products are publically available and may be freely used. Users should consider the caveats in this paper (Sect. 3), and online (through the documentation link, above) before using the Burst Analyser data in any scientific medium.
Wherever these data products are used we ask that this paper be cited. The suggested wording is: ``for details of how these light curves were produced, see Evans et al. (2010)''.
Please also include the following paragraph in the Acknowledgements section: ``this work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester''.
AcknowledgementsThis work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester. P.A.E., J.P.O., K.L.P., A.P.B., C.P. and R.L.C.S. acknowledge STFC support, D.N.B., acknowledges support from NASA contract NAS5-00136.
References
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Sp. Sci. Rev., 120, 143 [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Sp. Sci. Rev., 120, 165 [Google Scholar]
- Butler, N. R., & Kocevski, D. 2007a, ApJ, 663, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, N. R., & Kocevski, D. 2007b, ApJ, 668, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Gronwall, C., Wang, X.-Y., et al. 2007, ApJ, 662, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Burrows, D. N., Wu, X.-F., et al. 2010, ApJ, 711, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmaan, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O'Brien, P. T., Willingale, R., Osborne, J., et al. 2006, ApJ, 647, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Hill, J. E., Yamazaki, R., et al. 2007, ApJ, 669, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Barthelmy, S. D., Barbier, L., et al. 2008, ApJS, 175, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R. 2007, ApJ, 662, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. 2007, ChJAA, 7, 1 [Google Scholar]
Footnotes
- ... website
![[*]](/icons/foot_motif.png)
- http://www.swift.ac.uk/burst_analyser
- ... curves
![[*]](/icons/foot_motif.png)
- We create light curves in units both of flux and flux density; however for concision, we use the collective phrase, ``flux light curves'' to refer to both types.
- ... online
![[*]](/icons/foot_motif.png)
- http://www.swift.ac.uk/xrt_curves
- ... software
![[*]](/icons/foot_motif.png)
- http://swift.gsfc.nasa.gov/docs/software/lheasoft/download.html
- ... Guide
![[*]](/icons/foot_motif.png)
- http://swift.gsfc.nasa.gov/docs/swift/analysis/bat_swguide_v6_3.pdf
- ... repository
![[*]](/icons/foot_motif.png)
- http://www.swift.ac.uk/xrt_spectra
- ... recorded
![[*]](/icons/foot_motif.png)
- The count-rate is the observed, i.e. absorbed count rate.
- ... Table
![[*]](/icons/foot_motif.png)
- http://swift.gsfc.nasa.gov/docs/swift/archive/grb_table/
- ... site
![[*]](/icons/foot_motif.png)
- http://www.swift.ac.uk/access/ql.php
All Tables
Table 1:
The phase spaces used to interpolate from hardness ratio (HR) to
counts-to-flux conversion factors (CF) and spectral photon index (
![]() ).
).
All Figures
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14819fig1.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14819-10/Timg4.png)
|
Figure 1: An example of a flux density light curve from the Burst Analyser. The spectrally-evolving BAT-XRT flux light curve of GRB 061121, is shown as unabsorbed flux density at 10 keV; the lower panel shows the evolution of the photon index of the power-law spectrum. The last 3 BAT data points suffer from a poorly-constrained spectrum; see Sect. 3.4 for details. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{14819fig2.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14819-10/Timg5.png)
|
Figure 2: The flux density light curve of GRB 060729 from the Burst Analyser. Accounting for spectral evolution shows the flux decline during the steep decay to be more rapid than in count space, and reveals the turn-on of the afterglow. |
| Open with DEXTER | |
| In the text | |
| |
Figure 3: A demonstration of the SNR binning algorithm. In the first pass (1) the bins marked in black were above the SNR threshold. For the second pass (2) the sub-threshold input bins were grouped in twos. One of these groups was found to be above threshold. In the third pass (3) the input bins were grouped in threes (with left-over input bins appended if necessary, meaning that some of the groups contain four input bins) and two of these were above threshold. This continues until all of the input bins are above threshold (i.e. the whole plot is black) or the input bins are grouped into new bins of 40-s or longer, at which point they are all added to the output light curve. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{14819fig4a.eps}\...
...ps}\par\includegraphics[angle=-90,width=8.9cm,clip]{14819fig4c.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14819-10/Timg24.png)
|
Figure 4:
Combined BAT-XRT light curve of GRB 060510B. The
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14819fig5.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14819-10/Timg26.png)
|
Figure 5:
The effect of the cut-off energy on the conversion factors and
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


