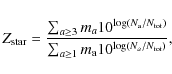EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 519 (September 2010) A&A, 519 (2010) A64 Full HTML
Free Access
Issue
A&A
Volume 519, September 2010
Article Number A64
Number of page(s) 12
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201014471
Published online 14 September 2010
A&A 519, A64 (2010)

An in-depth spectroscopic analysis of the Blazhko star RR Lyrae[*]

I. Characterisation of the star: abundance analysis and fundamental parameters

K. Kolenberg1 - L. Fossati2 - D. Shulyak3 - H. Pikall1 - T. G. Barnes4 - O. Kochukhov5 - V. Tsymbal6

1 - Institut für Astronomie, Universität Wien, Türkenschanzstrasse 17, 1180 Wien, Austria
2 - Department of Physics and Astronomy, Open University, Walton Hall, Milton Keynes, MK7 6AA, UK
3 - Institute of Astrophysics, Georg-August-University, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
4 - The University of Texas at Austin, McDonald Observatory, 1 University Station, C1402, Austin, Texas, 78712-0259, USA
5 - Department of Astronomy and Space Physics, Uppsala University, 751 20 Uppsala, Sweden
6 - Tavrian National University, Vernadskiy's Avenue 4, Simferopol, Crimea 95007, Ukraine

Received 19 March 2010 / Accepted 19 April 2010

Abstract
Context. The knowledge of accurate stellar parameters is a keystone in several fields of stellar astrophysics, such as asteroseismology and stellar evolution. Although the fundamental parameters can be derived from both spectroscopy and multicolour photometry, the results obtained are sometimes affected by systematic uncertainties. Stellar pulsation reaches high amplitudes in RR Lyrae stars, and as a consequence the stellar parameters vary significantly over the pulsation cycle. The abundances of the star, however, are not expected to change.
Aims. We present a self-consistent spectral analysis of the pulsating star RR Lyr, which is the primary target of our study of the Blazhko effect.
Methods. We used high-resolution and high signal-to-noise ratio spectra to carry out a consistent parameter determination and abundance analysis for RR Lyr. The LL MODELS code was employed for model atmosphere calculations, while the SYNTH3 and WIDTH9 codes were used for line profile calculations and LTE abundance analysis. We describe in detail the methodology adopted to derive the fundamental parameters and the abundances. From a set of available high-resolution spectra of RR Lyr, we selected the phase of maximum radius at which the spectra are least disturbed by the pulsation. Using the abundances determined at this phase as a starting point, we expect to be able to determine the fundamental parameters determined at other phases more accurately.
Results. The set of fundamental parameters obtained in this work fits the observed spectrum accurately. From the abundance analysis, we find clear indications of a depth-dependent microturbulent velocity, that we quantify.
Conclusions. We confirm the importance of a consistent analysis of relevant spectroscopic features, the application of advanced model atmospheres, and the use of up-to-date atomic line data for determining stellar parameters. These results are crucial for further studies, e.g., detailed theoretical modelling of the observed pulsations.

Key words: stars: fundamental parameters - stars: individual: RR Lyr - stars: oscillations - stars: variables: RR Lyrae - stars: abundances

1 Introduction

The modelling of pulsational signals requires the knowledge of stellar parameters and primarily accurate values of the effective temperature ( $T_{{\rm eff}}$) and metallicity (Z). The determination of fundamental parameters can be performed by different methods (some examples for stars from B- to G- type are Fuhrmann et al. 1997; Przybilla et al. 2006; and Fossati et al. 2009) that do not always provide consistent results. Thus, it is important to choose a methodology that allows us to constrain the parameters of the star from the available observables (usually photometry and spectroscopy) in the most robust and reliable way.

RR Lyr is the prototype and eponym of its class of pulsating stars. RR Lyrae stars play a crucial role as distance indicators. Their evolutionary stage (He burning in core, H burning in shell) makes them useful tracers of Galactic history. These classical pulsators display radial oscillations (the simplest type of pulsation) with large amplitudes that make them useful touchstones for theoretical modelling. RR Lyr is one of the most well-studied stars of its class. Nearly a century ago, Shapley (1916) discovered that it exhibits a strong Blazhko effect, i.e., a (quasi-)periodic modulation of its light curve shape in amplitude and phase. The Blazhko effect in RR Lyr has been closely followed over the past century, and changes have been reported in both the strength and the duration of its Blazhko cycle (Szeidl 1988; Kolenberg et al. 2006). Some well-studied stars even exhibit multiple (variable) modulation periods (see, e.g., LaCluyzé et al. 2004). Despite numerous attempts to model the phenomenon, the Blazhko effect has eluded a satisfactory explanation so far. High-precision photometry from ground-based or space-borne precise instruments also indicate that Blazhko modulation may be a far more common phenomenon than initially thought: as many as half of the Galactic RRab stars may be modulated (Jurcsik et al. 2009; Szabo et al. 2009; Kolenberg et al. 2010).

To constrain the viable models for the Blazhko effect, it is vital to obtain accurate values for the fundamental parameters (and their variations) of modulated and non-modulated RR Lyrae stars. This has been the main motivation of the study presented in this article.

RR Lyr is the only star of its class to have a directly determined parallax, measured with the HST/FGS, by Benedict et al. (2002), to be $\pi$(FGS $) = 3.82 \pm 0.2$ mas ( $d = 262 \pm 13$ pc). When a small ISM correction of Av = 0.07 is applied, this distance results in an $M_{v}^{\rm RR} \simeq +0.61_{-0.11}^{+0.10}$ mag, which corresponds to $\simeq$ $49 \pm 5~L_{\odot}$.

Table 1:   Basic data of the observations of RR Lyr.

Fundamental parameters of RR Lyr have been obtained by several authors with a variety of methods (e.g., Lambert et al. 1996; Manduca et al. 1981; Siegel 1982; for a summary see Kolenberg 2002). The published fundamental parameters of RR Lyr display a considerable range in both $T_{{\rm eff}}$ and \ensuremath{\log g} because of the large pulsation amplitudes. According to these analyses, RR Lyr's $T_{{\rm eff}}$ varies over its 13h36min pulsation cycle between approximately 6250 and 8000 K and its \ensuremath{\log g} between 2.5 and 3.8 (extreme values). Superimposed on the large variation, the Blazhko cycle leads to an additional variation in the fundamental parameters. Jurcsik et al. (2008) showed also that the mean properties of modulated RR Lyrae stars change over the Blazhko cycle. Element abundances of RR Lyr were obtained previously by, e.g., Clementini et al. (1996), Lambert et al. (1996), and Takeda et al. (2006).

The main goal of the present work is to perform a self-consistent atmospheric and abundance analysis of RR Lyr that reproduces all of its photometric and spectroscopic data. Furthermore, we investigate the degree to which the derived fundamental parameters depend on the applied methods. Considering the structure of the available models, especially the position of the convective zones and the zones of nuclear fusion, the measured abundances of the star are not expected to change over the pulsation (and the Blazhko) cycle. Hence, if the abundances are accurately determined at one phase in the pulsation cycle, they can be of help in determining (or at least constraining) the fundamental parameters at other phases. In this paper, we select the optimal phase for determining the abundances of the star. This is the first of a series of papers that will be devoted to a detailed spectroscopic study of RR Lyr. In forthcoming papers, we will discuss the spectral variations over the pulsation and Blazhko cycle of the star.

2 Observations and spectral data reduction

A total of 64 spectra of RR Lyr were obtained between June 26th and August 27th, 2004 with the Robert G. Tull Coudé Spectrograph on the 2.7-m telescope of McDonald Observatory. This is a cross-dispersed échelle spectrograph yielding a two-pixel resolving power $R \simeq 60~000$ for the configuration used here. Table 1 lists the observing time, exposure time, the signal-to-noise ratio (SNR) per resolution element for each acquired spectrum, and the phases in the pulsation and Blazhko cycles. For the determination of the phases we used the ephemerides derived by Kolenberg et al. (2006). To minimize smearing of the spectral features by pulsation, each spectrum was limited to an exposure time of 960 s. Two spectra have shorter exposures as a result of being stopped due to cloud. The SNR per resolution element of the obtained spectra varies according to the brightness of the star (given the fixed integration time) and the weather conditions during the observation. Spectra ID319-328 were inadvertently taken at the wrong blaze angle and thus have a low SNR.

Bias frames and flat-field frames were obtained at the start of each night, and Th-Ar spectra were observed frequently during each night for calibration purposes. The spectra were reduced using the Image Reduction and Analysis Facility (IRAF[*], Tody 1993). Each spectrum, normalised by fitting a low order polynomial to carefully selected continuum points, covers the wavelength range 3633-10 849 Å, with several gaps between the orders at wavelengths greater than 5880 Å.

The normalisation of the hydrogen lines was important because we used them to derive $T_{{\rm eff}}$. The H$\alpha$ absorption line was not covered by our spectra, and the orders adjacent to H$\beta$were affected by a spectrograph defect that prevented a proper normalization. We were able to perform a reliable normalisation of the H$\gamma $ line using the artificial flat-fielding technique described by Barklem et al. (2002). This approach assumes that the relation between the blaze shapes of the different échelle orders is a smoothly changing function of the order number. On this basis, one can establish the apparent blaze shapes by fitting polynomials to continuum points in several orders above and below the hydrogen line. In a subsequent step, a 2-D polynomial surface was fitted to these empirical blaze functions, and the continuum in the orders containing the H$\gamma $ line was determined by interpolation.

This normalisation procedure was performed on two spectra taken close to the optimal phase. We used a surface fit to 3-4 orders on both sides of the broad hydrogen line to determine the continuum in the H$\gamma $ spectral orders. The accuracy of this normalisation technique is attested by both a close agreement between the normalised overlapping H$\gamma $ profiles and the lack of discrepancy between observations of RR Lyr obtained at similar pulsation phases.

Simultaneously with the spectroscopic campaign, we obtained photometric data in Johnson V by means of a multi-site campaign. The photometric data were published by Kolenberg et al. (2006). They were used for accurate determination of the pulsation frequencies and phases in the pulsation and Blazhko cycle.

3 The models

3.1 The pulsation model

To determine the dynamical properties of the atmosphere at the most quiescent phases theoretically, we used the so-called Vienna Nonlinear Pulsation Code (Feuchtinger 1999). For the unperturbed starting model, we assumed the parameter values of $0.65~M_{\odot}$, $50~L_{\odot}$, $T_{\rm eff}=6600$ K, and a typical Pop II chemical composition of Y=0.239 and Z=0.001, which collectively correspond to a limit cycle with the observed period of pulsation. The kinetic energy of the atmosphere (defined as the part of the photosphere where $\tau = 2/3$ to the outer boundary of our model, see Fig. 1) shows 2 local minima, where the first - roughly at phase 0.35 - corresponds to the phase of maximum photospheric radius. The flow ceases and the whole envelope starts to contract again to reach its minimal radius shortly after minimum light. Although the velocities in the atmosphere are low, we are aware that the atmosphere is not static at any point during the stellar pulsation, which conflicts with what is assumed in most model atmosphere codes. But there are phases during which the dynamical effects are smaller, which are those we are interested in for abundance analysis. We note that the pulsation model does not take into account the Blazhko modulation in the star.

\begin{figure} \par\includegraphics[width=8cm,clip]{figures/14471fg1.ps} \end{figure} Figure 1:

RR Lyr model bolometric luminosity ( upper panel), photospheric radius ( middle panel), and atmospheric kinetic energy ( lower panel) as a function of the pulsational phase. By convention, phase 0 corresponds to the maximum of the luminosity. The two full vertical lines correspond to the phases of both maximum radius (the phase we declare as most quiescent) and minimum light (usually adopted for the spectroscopic analysis).

Open with DEXTER

3.2 The model atmosphere

To compute model atmospheres of RR Lyr, we employed the LL MODELS stellar model atmosphere code (Shulyak et al. 2004). For all the calculations, local thermodynamical equilibrium (LTE) and plane-parallel geometry were assumed. Both of these assumptions need to be evaluated in our particular case.

The LTE assumption may be questionable because of the low plasma density and shock waves in the RR Lyr atmosphere. To reduce the uncertainties in the spectroscopic analysis, we implement our model atmospheres at phases where the dynamical effects in the star's atmosphere are expected to be small. We refer the reader to the next section for more explanation. Ignoring LTE may also lead to systematic errors in the abundance analysis. However, a detailed non-LTE analysis is beyond the scope of the present paper.

The atmospheres of giants are extended because of their large radii, and sphericity effects may thus become important for the stellar atmosphere modelling. For instance, based on a detailed model atmosphere analysis, Heiter & Eriksson (2006) recommended using spherically symmetric models for abundance analysis of stars with $\log g \leqslant 2$ and 4000 K  $\leqslant T_{\rm eff} \leqslant 6500$ K. Taking into account the estimated gravitational acceleration of RR Lyr of $\log g=2.4$ (see next section), one can expect the sphericity effects to be small enough not to significantly influence the abundance analysis. The estimated errors in the Fe abundance based on theoretical Fe I lines presented in Heiter & Eriksson (2006) indeed do not exceed 0.1 dex for the model with $T_{\rm eff}=6500$ and $\log g=1$. A $\log g=2.4$ value for RR Lyr thus justifies the use of plane-parallel model atmospheres for abundance analysis.

We used the VALD database (Piskunov et al. 1995; Kupka et al. 1999; Ryabchikova et al. 1999) as a source of atomic line parameters for opacity calculations with the LL MODELS code. Finally, convection was implemented according to the Canuto & Mazzitelli (1991a,b) model of convection (see Heiter et al. 2002, for more details).

4 The optimal phase

During the pulsation cycle, the spectral lines of RR Lyr change dramatically. In particular, when a shock wave passes through the atmosphere, it is possible to observe line broadening, line doubling, line disappearance, and sometimes even line emission (Preston et al. 1965; Chadid & Gillet 1996; Chadid et al. 2008; Preston 2009). This is obviously the sign of a very non-quiescent atmosphere, which in principle cannot be modelled with a static model atmosphere, such as ATLAS and LL MODELS. In practice, a model atmosphere code that is able to realistically model the atmosphere of a variable star such as RR Lyr, given both its chemical and pulsational peculiarity, does not yet exist. Therefore we are forced to use a static model atmosphere. To analyse the star in the most consistent way, we decided to study RR Lyr when its atmosphere is as close as possible to that of a non-variable star.

In the past, RR Lyrae stars were always analysed by studying spectra obtained close to the phase of minimum light because it was believed that this was the phase at which the star's atmosphere is ``at its quietest''. The adoption of static model atmospheres for the analysis of RR Lyrae stars was then justified by demonstrating that the results obtained at different phases were all in agreement with each other. At the ``quiescent phase'', we generally suppose that a) there are no shock-waves or any other fast plasma motions in the atmosphere that distort the line profiles and b) pressure stratification is as close as possible to its hydrostatic analog.

Picturing a homogeneously pulsating sphere, the most quiescent phase is associated with both phases of minimum and maximum radius. In the case of an oversimplified pulsation model, these also correspond to the minimum and maximum light in the star's luminosity variation. At these extreme positions in the pulsation, the atmosphere comes to a halt and, due to zero gas velocity, the pressure stratification at these phases is closest to the hydrostatic case (but not necessarily the same!). Furthermore, since the plasma velocities are negligible, the kinetic energy should be zero as well. For RR Lyrae stars, and especially those of type RRab (fundamental mode pulsators) with strongly nonlinear light curves (resembling a saw-tooth function), the phase of maximum light is short-lived and known to be accompanied by shock-waves. Thus, in previous works the quiescent phase was associated with the phase of minimum light. However, the assumption that all atmospheric layers move synchronously because they are rigidly bound to each other is wrong. Realistic models show that at minimum radius, radiation is blocked in deeper layers and ready to migrate into the outer layers and accelerate both the photosphere and the atmosphere.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{figures/14471fg2.ps} \end{figure} Figure 2:

Radial plots showing gas velocity u in units of the sound speed (the so-called Mach number) shown for the phase of maximum radius (left) and minimum light (right).

Open with DEXTER
Looking at both pulsational models and a large sample of stellar spectra, obtained at different phases, we found that there is a quiescent phase very close to the phase of maximum radius, where the radial velocity derived from the metallic lines corresponds to the stellar gamma velocity. On the light curve, this corresponds to a phase on the descending branch of the light variation. Figure 1 shows the calculated bolometric light curve, the photospheric radius variation, and the atmospheric kinetic energy as a function of the pulsation phase. The two vertical lines correspond to the phases of maximum stellar radius and of minimum light. As mentioned above, the expansion of the model envelope is not homologous. We see different waves running in and out - some even steepening to become shock waves.

Minimum light is a less fortunate choice for obtaining undistorted line profiles, as parts of the atmosphere still move with supersonic speed (e.g., Mach 3 in Fig. 2). Figure 2 shows radial plots covering approximately the outer 270 (of 400 total) radial mesh points in the Vienna pulsation model. For the phases of both maximum radius and minimum light, the gas velocity u (in units of the local sound) speed is plotted. At maximum radius (left panel in Fig. 2), the photosphere starts to move towards the model's center, while parts of the envelope still move outwards. All velocities are below sound speed. At minimum light (right panel in Fig. 2) - which occurs before minimum radius - we see the transition between super- and subsonic inflow, sometimes called a shock, at the photosphere. This distorts the spectra and makes them less suited to our detailed analysis.

We note that the most quiescent phase, i.e., the phase of maximum radius, is actually very short-lived. A spectroscopic observation has to be well-timed (within, say, half an hour) to catch the spectral lines without distortion. The integration times also cannot exceed a few percent of the pulsation period, to avoid smearing of the spectra due to a pulsation-induced Doppler effect. Integration times not much longer than 15 min taken within the appropriate (narrow) phase interval are recommended. This places constraints on the obtained SNR, and therefore, this study could only be performed with telescopes larger than 2-m. At minimum light, the star is not at its quietest, and the shock wave associated with the bump phase (Gillet & Crowe 1988) close to minimum light will also distort the spectral line profiles in RRab stars.

Figure 1 clearly shows that the phase corresponding to minimum light occurs before a local minimum of the atmospheric kinetic energy, while at the phase of maximum radius the stellar atmosphere is very close to the other local minimum of kinetic energy.

This picture is also confirmed by the observations. Figure 3 compares the line profile of RR Lyr in the region around 4500 Å and the bisector of the Ti II line at $\sim $4501 Å as observed at the phases close to both maximum radius and minimum light. The main difference between the two line profiles is given by the line broadening, which is an indicator of the atmospheric activity: to a quiet phase correspond narrow spectral lines.

The spectral line broadening as a function of phase is shown in Fig. 4. This figure displays the full width at half maximum (FWHM) measured for four strong spectral features as a function of the pulsational phase. For each of the four lines, we obtained a clear minimum close to the phase of maximum radius (between 0.2 and 0.3). This plot also shows the rapid changes in the FWHM caused by the shock waves. The observed peaks in FWHM close to the pulsation phases $\sim $0.65 and $\sim $0.9 have been interpreted as arising from two shocks, a weaker and a stronger shock, respectively, propagating through the star's atmosphere and compressing the turbulent gas (Fokin et al. 1999). Fokin & Gillet (1997) and Fokin et al. (1999) showed that their RR Lyr models exhibit very strong shocks[*] up to Mach 25 in the highest part of the star's atmosphere (see Fig. 3 in Fokin et al. 1999).

\begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg3.ps} \end{figure} Figure 3:

Left panel: comparison between a part of the RR Lyr spectrum as observed close to the phase of maximum radius (full line) and close to the phase of minimum light (dashed line). Right panel: comparison between the bisectors of the Ti II line at $\sim $4501 Å as observed close to the phase of maximum radius (full line) and close to the phase of minimum light (dashed line). The dotted line shows the zero velocity, for comparison. The velocity scale is in ${\rm m~s}^{-1}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg4.ps} \vspace*{-2mm} \end{figure} Figure 4:

Full width at half maximum (FWHM) in Å as a function of pulsational phase measured for three Fe II lines and one Ti II line. The minimum is in correspondance with the phase of maximum radius. The typical uncertainty in the FWHM is of $\sim $0.01 Å, but also depends on the SNR of each spectrum. The two peaks visible at about phase 0.65 and 0.9 are due to two propagating shock waves (Fokin et al. 1999).

Open with DEXTER

The line bisectors, shown in Fig. 3, also illustrate that the line asymmetry changes with the pulsational phase, according to a trend similar to that exhibited by the FWHM. This point will be described in more detail in the next paper.

In practice, it is not trivial to predict exactly when the star will be at maximum radius, because of the Blazhko effect and other (possibly longer) periodicities involved in the pulsation. To find the appropriate spectrum for analysis, we investigated all the available spectra obtained close to the phase of maximum radius (determined with the simultaneous photometry) and selected those of the minimum FWHM and line asymmetry. In the end, the two spectra with numbers 258 and 260 were obtained very close to the phase of maximum radius and showed a comparable line broadening and a very small line asymmetry. We decided to perform a detailed analysis of spectrum number 260 because of its higher SNR. Our simultaneous photometry (Kolenberg et al. 2006) confirmed that this spectrum was recorded around pulsation phase $\phi = 0.28$.

5 Fundamental parameters and abundance analysis

In general, a fundamental parameter determination begins from a derivation of $T_{{\rm eff}}$ and \ensuremath{\log g} from photometric indices. For RR Lyr, this operation is not trivial. In Sect. 4, we assumed that the atmosphere of RR Lyr can be at best simplified as ``static'' only at the phase of maximum radius. It is therefore at this phase that we made use of the photometric indices and the static model atmosphere grids to determine the fundamental parameters.

As a starting point of our analysis, we decided to take the parameters derived by other authors who analysed spectra of RR Lyr obtained at a similar phase. In particular, Takeda et al. (2006) derived the fundamental parameters spectroscopically from high resolution spectra of RR Lyr, one of them obtained not far from the phase of maximum radius. These parameters can be taken only as a starting point because the star was observed at a different Blazhko phase[*]. We explore the effect of Blazhko modulation on the spectra of RR Lyr in a forthcoming paper.

We used the parameters given by Takeda et al. (2006) for their spectrum taken at pulsation phase $\phi=0.36$ ( $T_{{\rm eff}}$ = $6040\pm40$ K, \ensuremath{\log g} =  $2.09\pm0.1$ dex) as our starting point. We performed an iterative process to improve and test the parameters as described in the following. In our analysis, every time any of the parameters $T_{{\rm eff}}$, \ensuremath{\log g}, $\upsilon _{{\rm mic}}$, or abundances changed during the iteration process, we calculated a new model by implementing the most recently determined quantities. We did the same for the abundances. While the results of the abundance analysis depend upon the assumed model atmosphere, the atmospheric temperature-pressure structure itself depends upon the adopted abundances. We therefore recalculated the model atmosphere every time the abundances had been changed, even if the other model parameters remained unchanged. This procedure ensured that the model structure was consistent with the assumed abundances.

5.1 The effective temperature

We performed the $T_{{\rm eff}}$ determination by fitting synthetic line profiles, calculated with SYNTH3 (Kochukhov 2007), to the observed profile of the H$\gamma $ line, the only hydrogen line for which it was possible to make a reliable normalisation. In the temperature range expected for RR Lyr, hydrogen lines are very sensitive to temperature variations and depend very little on \ensuremath{\log g} variations. In particular, this is expected when the stellar $T_{{\rm eff}}$ is close to its minimum. In the case of RR Lyr the use of hydrogen lines as $T_{{\rm eff}}$ indicators is very important because these lines describe the stellar structure more effectively than any other line, being formed in a wide region of the stellar atmosphere, and the line wings are free from non-LTE effects. The $T_{{\rm eff}}$ obtained with this procedure is $T_{{\rm eff}}$ = $6125 \pm 50$ K. We note that these error bars are what we obtain from the fitting of the hydrogen line profile. Since there are model uncertainties that are not taken into account in this fitting procedure, these error bars are probably underestimated. Figure 5 shows the comparison between the observed H$\gamma $ line profile and the synthetic profiles calculated with the adopted stellar parameters, as well as the synthetic profiles obtained by either increasing or decreasing $T_{{\rm eff}}$ by 50 K.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg5.ps} \end{figure} Figure 5:

Comparison between the observed H$\gamma $ line profile (solid line) and synthetic profiles calculated with the final adopted $T_{{\rm eff}}$ =6125 K (red line) and with $T_{{\rm eff}}$ = 6175 K (green line) and $T_{{\rm eff}}$ = 6075 K (blue line). The red line agrees very well with the observed spectrum.

Open with DEXTER

Figure 5 shows a clear wavelength shift in the observed H$\gamma $ core relative to its wings and to the metal lines formed in deeper layers. This is caused by a velocity gradient in the outer layers of the star (Van Hoof & Struve 1953; Mathias et al. 1995 for RR Lyr).

Another spectroscopic indicator for $T_{{\rm eff}}$ is provided by the analysis of metallic lines. In particular, $T_{{\rm eff}}$ is determined by eliminating the correlation between line abundance and line excitation potential ( $\chi_{{\rm excit}}$) for a given ion/element. This procedure can lead to erroneous parameters, in particular for stars such as RR Lyr where non-LTE effects could be large and the $\upsilon _{{\rm mic}}$ determination is complicated by the pulsation (see Sect. 6.1). For this reason, we decided not to take this indicator into account in our analysis, but to use it just as a check of the adopted $T_{{\rm eff}}$ value. This check pointed towards values comparable to the one we found from the H$\gamma $ line profile fitting.

5.2 The surface gravity

The surface gravity can be derived using two independent methods: based on line profile fitting of gravity-sensitive metal lines with developed wings, and based on the ionisation balance of several elements. For RR Lyrae stars, the Mg I lines are the most suitable lines for the first method. Described in Fuhrmann et al. (1997), the first method assumes that the wings of the Mg I lines at $\lambda\lambda$ 5167, 5172, and 5183 Å are very sensitive to \ensuremath{\log g} variations. We decided to use this method only as a check of \ensuremath{\log g} and not of the parameter determination. The first reason for doing this is the large uncertainty in the \ensuremath{{\upsilon}\sin i} and $\upsilon_{{\rm macro}}$ values that, given the available spectral resolution and SNR, could not be precisely determined. Another reason is the slight line asymmetry (clearly visible for the strong lines, such as Mg I), which makes precise line profile fitting impossible. A third reason is the uncertainty in the $\upsilon _{{\rm mic}}$ value, which will be discussed in detail in Sect. 6.1. The comparison is particularly difficult because the Mg abundance is about 1 dex below solar, which ensures that the wings of these lines are not very pronounced.

The second method for surface gravity determination assumes ionisation equilibrium, but this method is extremely sensitive to the non-LTE effects present for each ion/element. Since we are unable to apply the line profile fitting to the Mg I lines with developed wings, we assume ionisation equilibrium to determine \ensuremath{\log g}, comparing the result with that obtained for the Mg I lines. In adopting the ionisation equilibrium, for some elements we also took into account the non-LTE corrections predicted by various authors for some specific elements in solar-type metal-poor stars. From the ionisation equilibrium, we obtained \ensuremath{\log g} = $2.4\pm0.2$. This value was derived using only the lines with an equivalent width smaller than 75 mÅ, to minimise both the non-LTE effects and the uncertainty in the $\upsilon _{{\rm mic}}$ (both being more pronounced for the strong lines), and to assure a large enough number of lines, in particular for iron. We compared this value with those for the observed profiles of the Mg I lines with developed wings and obtained a good agreement, in particular when we adopt a depth-dependent $\upsilon _{{\rm mic}}$ (see Sect. 6.1). For this comparison, we used the line parameters of the Mg I lines adopted by Ryabchikova et al. (2009).

Our value for the surface gravity is consistent with the ionisation equilibrium of Fe I/Fe II and a few other elements, such as Si I/Si II and Ti I/Ti II. For Ca and V, we do not infer ionisation equilibrium, even within the error bars, but we measured only one line for both Ca II and V I. Taking into account the non-LTE corrections for Ca I ($\sim $+0.1-0.2) and Ca II (almost in LTE) given by Mashonkina et al. (2006), ionisation equilibrium is indeed then found for that element. In the case of chromium, several Cr I and Cr II lines have theoretically calculated oscillator strengths, which may influence the final abundance results.

Since RR Lyr's effective temperature is too low for it to exhibit a sufficient number of He lines (though they are detected - see Preston 2009), we are unable to measure the atmospheric He abundance. Ryabchikova et al. (2009) tested the effect of a strong He depletion in the atmosphere of the solar-type star HD 49933, concluding that a depleted He abundance would affect only the \ensuremath{\log g} determination and leave $T_{{\rm eff}}$ unchanged within the error bars of 0.2 dex. We also tested the effect of a He overabundance for RR Lyr. If we assume X=0.5 and Y=0.49, we find a general abundance decrease, e.g., Fe decreases 0.3 dex. In addition, we observe a variation in the pressure-sensitive lines such as the Mg I lines with extended wings leading to changes in \ensuremath{\log g} that do not exceed our error bars.

5.3 LTE abundance analysis

Our main source of the atomic parameters of spectral lines is the VALD database. The LTE abundance analysis was based on equivalent widths, analysed with a modified version (Tsymbal 1996) of the WIDTH9 code (Kurucz 1993). We opted for equivalent widths because of the small line asymmetry and the uncertainty about the form of the microturbulent velocity, making the synthetic line profile fitting more uncertain. We intend to analyse in the same consistent way the other collected spectra of RR Lyr, which exhibit a far more pronounced line asymmetry, and therefore will be analysed mostly using equivalent widths.

In total, about 700 lines were measured with equivalent widths, but after a check against both the solar spectrum and the spectrum of HD 49933 (Ryabchikova et al. 2009), we chose to keep 617 lines of 26 different elements and 32 different ions. We also tried to keep a set of lines uniformly distributed over the range of equivalent widths, wavelength, and excitation potentials, in particular for important ions such as Fe I, for which we kept 284 lines. We used nearly all unblended spectral lines with accurate atomic parameters, except lines in spectral regions where the continuum normalisation was too uncertain. RR Lyr shows a strong underabundance for almost every measured ion/element. For this reason, it was possible to infer only approximate abundance values or upper limits to the abundance of some ions whose lines were too weak to measure equivalent widths. For these measurements, we used synthetic line profile fitting, since these lines were too shallow to manifest both any visible line asymmetry and $\upsilon _{{\rm mic}}$ dependence.

Microturbulence was determined by minimizing the correlation between equivalent width and abundance for several ions. We used mainly Fe I lines since this is the ion that provides the largest number of lines within a wide range in equivalent widths, but the correlations obtained with Ti I, Ti II, Cr I, Cr II, Fe II, and Ni I were also taken into account. Using all the available lines, we could not find a unique value for the $\upsilon _{{\rm mic}}$ able to completely remove the correlation between equivalent width and abundance. In particular, it was possible to effectively remove this correlation using only the lines with an equivalent width smaller than 75 mÅ, while the stronger lines exhibited a steep abundance increase with increasing equivalent width. Using only the lines with an equivalent width of less than 75 mÅ  we obtained a $\upsilon _{{\rm mic}}$ of $2.4\pm0.3$  ${\rm km~s}^{-1}$, while using all available lines we obtained a value of $3.1\pm0.5$  ${\rm km~s}^{-1}$. In this last case, the plot shows that the correlation is only statistically minimised, as it yields an underestimated abundance for the medium-strength lines and an overestimated abundance for the strong lines (see lower plot of Fig. 6).

In the literature, several authors mentioned the possibility of a depth-dependent $\upsilon _{{\rm mic}}$ for RR Lyrae stars (Clementini et al. 1996; Takeda et al. 2006). Therefore, given the impossibility of finding a clear $\upsilon _{{\rm mic}}$ value, we decided to derive the profile of a depth-dependent $\upsilon _{{\rm mic}}$ using the available measured lines. This part of the work is discussed in Sect. 6.1.

The full set of derived abundances, adopting both a constant and a depth dependent $\upsilon _{{\rm mic}}$, is shown in Table 2. The last column of Table 2 indicates the solar abundances by Asplund et al. (2005) for comparison.

\begin{figure} \par\includegraphics[width=8.4cm,clip]{figures/14471fg6.ps} \end{figure} Figure 6:

Plots of individual abundances for 284 Fe I lines versus the measured equivalent width for RR Lyr, adopting a constant (open circles) and depth-dependent (open squares) $\upsilon _{{\rm mic}}$. The same dependence for 108 common Fe I lines in the spectrum of HD 49933 is shown by crosses. We applied an arbitrary vertical shift for visualisation purposes.

Open with DEXTER

Table 2:   LTE atmospheric abundances for RR Lyr.

The stellar metallicity (Z) is defined as follows

\begin{displaymath} Z_{\rm star}=\frac{\sum_{a \geq 3}m_{a}10^{\log(N_{\rm a}/N_... ...tot})}}{\sum_{a \geq 1}m_{\rm a}10^{\log(N_{a}/N_{\rm tot})}}, \end{displaymath} (1)

where a is the atomic number of an element with atomic mass ma. Making use of the abundances obtained from the performed analysis and assuming the depth-dependent $\upsilon _{{\rm mic}}$, we derived a metallicity of $Z = 0.003 \pm 0.002$ dex. For elements that were not analysed, we adopted the solar abundances of Asplund et al. (2005). However, if we assume an underabundance of -1.0 dex for all elements that were not analysed, excluding H and He, the resulting Z value remains practically unchanged. We note that in the pulsation model we used a metallicity value of Z = 0.001. This is almost the lowest value consistent with what we obtain from our spectrum. However, we have to keep in mind that we do not take into account NLTE effects in our analysis, and that these effects may influence our result. In general, for metal-poor stars such as RR Lyr, the NLTE correction is negative, meaning that the abundance in NLTE is lower, so the true Z may be lower too (between 0.003 and 0.001). The effect of NLTE on the abundances was illustrated by, e.g., Takeda et al. (2006) for oxygen. Using the solar Fe abundance value of Asplund et al. (2005), we obtain [Fe/H $]=-1.41 \pm 0.11$ for RR Lyr. This is in good agreement with the value [Fe/H]=-1.39 obtained by Beers et al. (2000), who list typical errors of 0.1-0.2 dex.

We used spectral synthesis with SYNTH3 to check the hyperfine structure (hfs) effects on the abundance determination of Mn, Cu, Zn, Ba, and Pr. For each measured line of these elements, hfs effects are smaller than 0.01 dex, except for the Ba II line at $\lambda$ 6141 Å for which the hfs correction is -0.1 dex, bringing the line abundance closer to the mean Ba abundance. The hfs calculations for barium were taken from McWilliam (1998), who does not list the parameters for the Ba line at $\lambda$ 6496 Å, for which, however, we do not expect any significant hfs effect (Mashonkina & Zhai 2006).

The abundance uncertainties given in Table 2 are the standard deviation from the mean abundance (hence no uncertainties are given if the abundances were derived from a single line). More realistic error bars for each element/ion can be found in Ryabchikova et al. (2009) where a rigorous derivation of the abundance uncertainties is given on the basis of the adopted uncertainties in the stellar parameters. This direct comparison is possible because RR Lyr and HD 49933 have a similar $T_{{\rm eff}}$ and in particular similar values of the uncertainties in both $T_{{\rm eff}}$ and  \ensuremath{\log g}.

Given the quality of the data and the slight line asymmetry, it was not possible to obtain definite values for both \ensuremath{{\upsilon}\sin i} and $\upsilon_{{\rm macro}}$, but just to constrain their values. We found that \ensuremath{{\upsilon}\sin i} lies between 0 and 9  ${\rm km~s}^{-1}$, and $\upsilon_{{\rm macro}}$ between 6 and 11  ${\rm km~s}^{-1}$. In particular, for the minimum given \ensuremath{{\upsilon}\sin i} we obtained the maximum $\upsilon_{{\rm macro}}$ and vice versa, as both effects contribute to line broadening. We note that the spectral lines cannot be explained by only the effects of rotational broadening ( \ensuremath{{\upsilon}\sin i}). The constraints on \ensuremath{{\upsilon}\sin i} that we obtained are in good agreement with those obtained by Kolenberg (2002) through analysis of the line profile variations of the star. They are also in accord with the findings by Peterson et al. (1996), who measured the line widths for 27 RR Lyrae (of which 8 are RRab) variables via cross-correlation analysis. They estimated an upper limit of 10 km s-1 to \ensuremath{{\upsilon}\sin i} in all cases.

6 Discussion

6.1 A depth-dependent microturbulent velocity

As previously mentioned, we calculated the profile of a depth-dependent $\upsilon _{{\rm mic}}$ on the basis of the available equivalent widths obtained for several Fe I lines spanning a large range of values. A depth-dependent $\upsilon _{{\rm mic}}$ was previously suggested by several authors, such as Takeda et al. (2006), who found evidence that ``strongly suggest that the microturbulence increases with height in the atmosphere of RR Lyrae stars, and that a simple application of the $\upsilon _{{\rm mic}}$ value derived from weak/medium-strength lines to stronger lines may result in an overestimation of the abundances''.

Figure 6 displays the line abundance as a function of the measured equivalent width for all the measured Fe I lines in the spectrum of RR Lyr, calculated by assuming constant (bottom) and depth-dependent (middle) $\upsilon _{{\rm mic}}$. It is clear that the use of a constant $\upsilon _{{\rm mic}}$ leads to an underestimation of the abundance of the medium-strength lines and an overestimation for the strong lines. In Fig. 6, we included as comparison the line abundance as a function of the measured equivalent width in HD 49933 for the set of common Fe I lines. This demonstrates that the observed behaviour does not depend on the set of adopted lines.

We believe that this phenomenon could be explained by both strong non-LTE effects and a depth-dependent $\upsilon _{{\rm mic}}$. Generally speaking, non-LTE effects are stronger for deep lines than for shallow lines, and adopting line formation in LTE would lead to a higher abundance, in agreement with what we observe here. Gehren et al. (2001) showed that for solar-type stars there is a substantial Fe I underpopulation leading to stronger Fe line wings when LTE is assumed, while Fe II is in LTE, but Gehren et al. (2001) adopted a model atom for Fe that did not include high-excitation levels. Mashonkina et al. (2009) analysed the Fe I/Fe II ionisation equilibrium in four solar-type stars and in the Sun concluding that the inclusion of the high-excitation levels in the Fe I model atom substantially reduced the non-LTE effects. RR Lyr is a metal-poor giant for which non-LTE effects are expected to be stronger than in solar-type stars. If the deviation we measure were caused by non-LTE effects, it should only produce a deviation of about 0.5 dex for the stronger lines. We believe that the non-LTE effects are only partially responsible for the obtained deviation, because we observe it in all measured ions with a similar magnitude and always in the same direction. These ions include those for which non-LTE effects are supposed to be weak, such as Fe II, which shows deviations even stronger than those registered for Fe I. We note that non-LTE effects work differently for different ions, leading to deviations in both directions and with a wide range of magnitudes. For this reason, we believe that a depth-dependent $\upsilon _{{\rm mic}}$ is mostly responsible for the observed deviations. A depth-dependent $\upsilon _{{\rm mic}}$ is also supported by modelling RR Lyr stars as shown by Fokin et al. (1999), who observed pulsation-dependent variations in the microturbulent velocity (see their Fig. 3).

The depth-dependent $\upsilon _{{\rm mic}}$ profile was obtained by fitting[*] the line abundance in the plane equivalent width versus line abundance. We performed this procedure for Fe I, given its large number of measured lines, and then tested the solution with the other ions. For each line, the code searches the most likely individual line abundance, assuming a certain dependence of the microturbulent velocity on the atmospheric depth. This dependence is varied to minimise the dispersion between the observed and the theoretical line widths over the whole set of measured spectral lines. Since the equivalent widths are of lines that formed in a small fraction of the stellar atmosphere, it is impossible to obtain a $\upsilon _{{\rm mic}}$ value at each atmospheric depth. For this reason, it was necessary to speculate about the analytic form of the $\upsilon _{{\rm mic}}$ dependence on the atmospheric depth. We tested both a step-like function and a low-degree polynomial function. We chose the latter because of the unrealistically steep and large step needed for the step-like function.

Figure 7 shows the profile obtained for the depth-dependent $\upsilon _{{\rm mic}}$ in comparison with the sound speed calculated by LL MODELS. According to the results of Fokin et al. (1999), the $\upsilon _{{\rm mic}}$ should always be subsonic due to strong dissipation effects. In Fig. 7 this is the case, except for the region between $\log\tau_{\rm 5000}$ equal to -3.5 and -5.5 $\upsilon _{{\rm mic}}$, where $\upsilon _{{\rm mic}}$ becomes supersonic. This, however, should be interpreted with caution since the numerical calculation of the sound speed with the LL MODELS code may be affected by accuracy loss in the uppermost layers where the thermodynamic variables (such as pressure and density) are slowly changing functions of atmospheric depth. We also note that our empirical estimation of the $\upsilon _{{\rm mic}}$ may contain systematic uncertainties, and thus the supersonic regime shown in Fig. 7 may have little to do with reality. Nevertheless, the general behaviour of $\upsilon _{{\rm mic}}$ with depth (i.e., strong increase in superficial layers) plausibly reflects a real physical phenomenon.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg7.ps} \end{figure} Figure 7:

Comparison between the profile of the microturbulent velocity (full line) and of the sound speed (dashed line) as a function of atmospheric depth.

Open with DEXTER

Assuming a depth-dependent $\upsilon _{{\rm mic}}$, the abundances of most ions change, in particular those with a large number of strong lines. As expected, for most of the ions the abundance increases instead of decreasing. This phenomenon is explained by our adopted value of constant $\upsilon _{{\rm mic}}$ being overestimated because it was obtained by statistically minimising the correlation abundance versus equivalent width. Because we have a large number of middle-strength lines, a small number of strong lines and an overestimated $\upsilon _{{\rm mic}}$ we obtained an underestimated abundance (see the bottom plot of Fig. 6). When applying the depth-dependent $\upsilon _{{\rm mic}}$, the middle-strength lines (responsible for the underestimated abundance) yield an abundance similar to the shallow and strong lines, thus leading to a higher final abundance. This effect is visible for ions with a large number of lines, such as Fe I. For elements with a few lines and some of them very strong, such as Ba II, the final abundance instead decreases, with a considerable decrease also in the standard deviation.

6.2 Comparison with previous determinations

Since we propose a different approach to the analysis of RR Lyrae stars to determine their physical parameters, it is important to compare our results with those previously obtained by other authors. The main publications on this topic containing an abundance analysis and parameter determination of RR Lyr itself are Clementini et al. (1995), Lambert et al. (1996), and Takeda et al. (2006).

Clementini et al. (1995) analysed several field RR Lyrae stars to derive broad band photometric calibrations for both fundamental parameters and metallicity. Their spectra of RR Lyr covered a large wavelength range with a moderate resolution ( $R\sim38~000$) and a high SNR (probably assumed per pixel) of about 460. They observed RR Lyr at pulsational phases of 0.70 and 0.73, around minimum light. Since they did not identify any systematic difference between the two spectra, they summed them to obtain one high-SNR spectrum. They compared the $T_{{\rm eff}}$ value obtained from broad band photometry by several other authors between 1975 and 1994, and, taking into account these comparisons, they built their own calibration leading to a $T_{{\rm eff}}$ value of $6222\pm115$ K. They derived the surface gravity from the stellar mass and radius, obtaining a \ensuremath{\log g} value of $2.8\pm0.2$ dex. The microturbulent velocity was derived in the usual way (minimisation of the correlation between line abundance and equivalent widths) obtaining a value of 4.2 $\pm$ 0.2  ${\rm km~s}^{-1}$. Clementini et al. (1995) also mentioned the possibility of a depth-dependent $\upsilon _{{\rm mic}}$, but they concluded that, if it were present, a $\upsilon _{{\rm mic}}$ depth-dependency would only be small and affect the abundances by just 0.1 dex (0.2 dex for the elements with a large number of strong lines). We confirm this estimate in our present work (see Table 2). Most of their abundances are for LTE, except for oxygen and sodium that were analysed assuming non-LTE. Table 3 shows a comparison between the abundances obtained by Clementini et al. (1995) and those derived in this work. The comparison shows a rather close agreement between the two sets of abundances, where for only Al I, Sc II, Mn I, and Zn I we find a small disagreement.

Table 3:   Comparison between the atmospheric ion abundances relative to the Sun obtained by Clementini et al. (1995) and in this work.

Lambert et al. (1996) observed a set of RR Lyrae stars with a spectral resolution of 23 000 to obtain narrow and broad band photometric calibrations for fundamental parameters and metallicity. RR Lyr was observed at eight different phases, one of them close to the phase of minimum light and one close to the phase of maximum radius. The spectrum obtained close to the phase of maximum radius has a SNR (assumed per pixel) of $\sim $100. For each phase, they derived the fundamental parameters from both photometry (adopting previously existing calibrations) and spectroscopy. From the photometric calibration that they obtained, for the spectrum at a phase close to maximum radius, $T_{{\rm eff}}$ = 6350 $\pm$ 200 K and \ensuremath{\log g} = 2.6 $\pm$ 0.2 dex, while from spectroscopy they derived $T_{{\rm eff}}$ = 6200 $\pm$ 200 K and \ensuremath{\log g} = 2.3 $\pm$ 0.2 dex. Lambert et al. (1996) found a constant $\upsilon _{{\rm mic}}$ throughout the stellar atmosphere, but they also obtained a rather constant $\upsilon _{{\rm mic}}$ throughout the pulsation cycle (between 3.6 $\pm$ 0.3  ${\rm km~s}^{-1}$ and 4.4 $\pm$ 0.5  ${\rm km~s}^{-1}$). This result is surprising because several pulsation models of RR Lyrae stars exhibit large variations in the $\upsilon _{{\rm mic}}$ during the pulsational cycle. We will study this issue in detail in the forthcoming work. In general, the high value obtained by Lambert et al. (1996) shows the turbulent motions present in the atmosphere and agrees with the large value we also obtained when a constant $\upsilon _{{\rm mic}}$ is assumed. Lambert et al. (1996) derived the Ca and Fe abundance for both LTE and non-LTE, adopting only the lines that are not deeper than 100 mÅ. In LTE, they obtained $\log (N_{\rm Fe}/N_{\rm tot})=-6.06$ dex and $\log (N_{\rm Ca}/N_{\rm tot})=-6.89$ dex. In non-LTE, they obtained a correction of about 0.2 dex for Fe I and no correction for Fe II, but, as mentioned in Sect. 6.1, we believe that the non-LTE correction for Fe I is much smaller. The non-LTE correction they obtained for Ca I was $\sim $0.05 dex. Both the Fe and Ca abundances presented by Lambert et al. (1996) are in good agreement with what we obtained. There is the possibility that the higher $T_{{\rm eff}}$ and $\upsilon _{{\rm mic}}$ relative to what we adopted compensate each other leading to values very close to those obtained with a lower $T_{{\rm eff}}$ and $\upsilon _{{\rm mic}}$.

Takeda et al. (2006) analysed five spectra of RR Lyr to derive spectroscopically the fundamental parameters and the abundances of O, Si, and Fe. The spectra were obtained at high resolution ( $R\sim60~000$) with a rather high SNR ($\sim $350-400), but for a very limited wavelength range intended to cover mainly the oxygen triplet at $\lambda\lambda\sim7770$ Å. One of these five spectra was obtained at a pulsational phase close to the phase of maximum radius. The fundamental parameters were derived by minimising the correlations of line abundance with both excitation potential ( $T_{{\rm eff}}$) and ionisation equilibrium ( \ensuremath{\log g}). The hydrogen line wings were used as check of the parameters determined, the inverse of the strategy we applied. For this phase, they obtained $T_{{\rm eff}}$ = 6040 $\pm$ 40 K, \ensuremath{\log g} = 2.09 $\pm$ 0.1 dex, and $\upsilon _{{\rm mic}}$ = 3.0 $\pm$ 0.1  ${\rm km~s}^{-1}$. The $\upsilon _{{\rm mic}}$ value obtained by Takeda et al. (2006) is in very good agreement with what we have found using a constant $\upsilon _{{\rm mic}}$. They also strongly suggest the presence of a depth-dependent $\upsilon _{{\rm mic}}$ for RR Lyrae stars. Takeda et al. (2006) analysed two sets of oxygen lines in non-LTE obtaining two values for the O abundance of -4.11 dex and -4.00 dex. We believe that the difference between their two obtained values is due to their adopting a constant $\upsilon _{{\rm mic}}$. The strong infrared oxygen triplet is very sensitive to the adopted $\upsilon _{{\rm mic}}$. The O abundance we obtained is very close to -4.00 dex assuming both a constant and a depth-dependent $\upsilon _{{\rm mic}}$. Takeda et al. (2006) also derived the Si and Fe abundance in LTE, obtaining respectively -5.93 dex and -5.82 dex. These two values do not match our results very well (we obtain a higher Si abundance and a lower Fe abundance). We are not able to explain this difference since it cannot be due to the small differences in the adopted stellar parameters.

The effective temperatures determined in these studies may not be directly comparable because the analysed spectra were obtained at different Blazhko phases. A more reasonable comparison can be done for the surface gravity because it is supposed to change less during the pulsation cycle.

What clearly emerges is a systematic difference between the \ensuremath{\log g} inferred from both stellar mass and radius and from the ionisation equilibrium. The ionisation equilibrium leads to a lower \ensuremath{\log g} than that derived by the assumed stellar mass and radius. Our \ensuremath{\log g} value lies in-between and is well validated by the fit of the magnesium lines with developed wings. This method is independent of both the ionisation equilibrium and the assumed stellar mass and radius.

The other parameters that can be directly compared are the elemental abundances. We do not expect these to vary within the pulsation cycle, unless the pulsation is able to bring material from the inner core up to the stellar atmosphere, a possibility that we deem unlikely. Comparing the abundances obtained in the three aforementioned studies and in our work, we note good agreement but for a few exceptions. This means that if static models could be applied to RR Lyrae stars, they may be applicable to many phases (not all!), but we will tackle this issue in our forthcoming work on the analysis of the other acquired spectra of RR Lyr.

From the point of view of the atmospheric modelling, the main difference between earlier work and ours is the adoption of an abundance-dependent model atmosphere for an RR Lyrae type star. The impact of depth-dependent microturbulent velocity and individual chemistry is shown in Fig. 8. As expected, strong underabundance makes the temperature in the surface layers higher compared to solar or scaled solar models. Introduction of the depth-dependent $\upsilon _{{\rm mic}}$ affects the strongest spectral features, leading to weaker absorption at their line centre. This, in turn, decreases the line absorption coefficient and thus leads to a further increase in the temperature. For instance, the temperature difference between models computed with constant and depth-dependent microturbulent velocities (see Fig. 7) can amount to as much as 300 K. On the other hand, only the strongest lines are affected by this modification in model temperature structure and thus the statistical results of abundance analysis are not affected that much, as shown in Table 2.

In contrast, line profile analysis of strong lines must be performed with appropriate models that account for the effect of depth-dependent microturbulence. Finally, we do not find any noticeable difference in temperature structure between the scaled-solar model ([M/H]=-1.5), which corresponds to the mean underabundance we found for Fe, and individual abundance models. This allows us to use scaled abundance models to mimic the temperature structure of the star as a first guess. We note, however, that the metallicity is the result of an abundance analysis, which is not known in the beginning. This methodological difficulty is automatically removed using an iterative procedure of abundance analysis as applied in this study.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg8.eps} \end{figure} Figure 8:

Comparison of temperature structures of models computed under different assumptions about microturbulent velocity $\upsilon _{{\rm mic}}$ and abundances (see the legend on the plot). Depth-dependent $\upsilon _{{\rm mic}}$ was taken from Fig. 7. For all the models we took $T_{{\rm eff}}$ =6125, \ensuremath{\log g} =2.4.

Open with DEXTER

7 Conclusions

Fundamental-mode RR Lyrae (RRab) stars pulsate with high velocities, which, in certain phases, leads to a distortion of their spectral features. The aim of this study has been to determine a set of self-consistent and accurate parameters and abundances for RR Lyr, the prototype and brightest member of its class. To achieve this, we collected a set of high-resolution spectroscopic data at our disposal, obtained with the Robert G. Tull Coudé Spectrograph on the 2.7-m telescope of McDonald Observatory. To derive the most reliable abundances for the star, we determined the phase in RR Lyr's pulsation cycle at which the atmosphere is ``at its most quiescent'', the phase of maximum radius. Our assumptions were strengthened by the Vienna Nonlinear Pulsation Code. With observations taken at the phase of maximum radius, the fundamental parameters and the element abundances of RR Lyr were determined by means of an iterative process. For the determination of the effective temperature, we used synthetic line profile fitting to the H$\gamma $ line and obtained $T_{{\rm eff}}$ = $6125 \pm 50$ K (error bars from the fitting procedure only). For the \ensuremath{\log g} determination, we used the condition of ionisation equilibrium and obtained a \ensuremath{\log g} value of $2.4\pm0.2$ at the phase of maximum radius. The LTE abundance analysis based on element abundances versus equivalent widths could not fit the element abundances with a single microturbulent velocity ( $\upsilon _{{\rm mic}}$) value. A depth-dependent $\upsilon _{{\rm mic}}$is physically plausible for RR Lyrae atmospheres and was previously suggested (but never derived or quantified) by several authors. In this work, we have derived, for the first time, the depth-dependent $\upsilon _{{\rm mic}}$ profile and quantified the expected abundance variation. By assuming a depth-dependent $\upsilon _{{\rm mic}}$, we obtained closer agreement between the element abundances and equivalent widths. In general, the adoption of a fixed $\upsilon _{{\rm mic}}$ value (which is too high) leads to an underestimation of the element abundances by 0.06 dex (maximum value). Nevertheless, RR Lyr is shown to be underabundant in all heavy elements, in agreement with previous studies.

RR Lyr, the eponym of its class, is one of the most well-studied RR Lyrae stars. However, many intricacies of its pulsation remain poorly understood, and to accurately model the star, we have to take into account complex physics that we are only beginning to uncover. The star is an asteroseismic target of the Kepler Mission (Borucki et al. 2009) through the Kepler Asteroseismic Science Consortium (KASC, see also Gilliland et al. 2010). Besides finding that the star exhibits amplitude and phase modulation (the so-called Blazhko effect), Kolenberg et al. (2010) detected, for the first time, the occurrence of half-integer frequencies in the star, i.e., peaks at $\frac{1}{2} f_0, \frac{3}{2} f_0, \frac{5}{2} f_0$ etc., with f0 the main pulsation frequency. This phenomenon (``period doubling'') may be caused by instabilities in the star and connected to the mysterious Blazhko effect (see Szabó et al. 2010, in preparation). To further explore theoretical models of RR Lyr, it is necessary to know the physical parameters of the star with the highest accuracy possible.

For this reason, an in-depth analysis of the star's atmospheric motions is very timely. We intend to expand this analysis in our forthcoming publications of the star. Our study clearly illustrates that it is crucial to use the appropriate models to correctly interpret the spectral data of RR Lyrae stars, and that high-quality observations can contribute to improving those models.

Acknowledgements

We kindly thank the referee of this paper, Dr. George Preston, for constructive comments. K.K. is a Hertha Firnberg Fellow, supported by the Austrian Science Foundation (FWF project T359-N2 and FWF stand-alone project P19962). L.F. has received support from the Austrian Science Foundation (FWF project P19962). His research at the Open University (UK) is funded by an STFC Rolling Grant. D.S. is supported by Deutsche Forschungsgemeinschaft (DFG) Research Grant RE1664/7-1. O.K. is a Royal Swedish Academy of Sciences Research Fellow supported by grants from the Knut and Alice Wallenberg Foundation and the Swedish Research Council. We kindly thank Stefano Bagnulo and John Landstreet for the useful discussions and comments during the preparation of the draft.

References

  1. Asplund, M., Grevesse, N., & Sauval, A. J. 2005, ASP Conf. Ser., 336, 25 [Google Scholar]
  2. Barklem, P. S., Stempels, H. C., Allende Prieto, C., et al. 2002, A&A, 385, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Beers, T. C., Chiba, M., Yoshii, Y., et al. 2000, AJ, 119, 2866 [NASA ADS] [CrossRef] [Google Scholar]
  4. Benedict, G. F., McArthur, B. E., Fredrick, L. W., et al. 2002, AJ, 123, 473 [NASA ADS] [CrossRef] [Google Scholar]
  5. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  6. Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
  7. Canuto, V. M., & Mazzitelli, I. 1992, ApJ, 389, 724 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chadid, M., & Gillet, D. 1996, A&A, 308, 481 [NASA ADS] [Google Scholar]
  9. Chadid, M., Vernin, J., Gillet, D. 2008, A&A, 491, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Clementini, G., Carretta, E., Gratton, R., et al. 1995, AJ, 110, 2319 [NASA ADS] [CrossRef] [Google Scholar]
  11. Feuchtinger, M. U. 1999, A&A, 351, 103 [NASA ADS] [Google Scholar]
  12. Fokin, A. B., & Gillet, D. 1997, A&A, 325, 1013 [NASA ADS] [Google Scholar]
  13. Fokin, A. B., Gillet, D., & Chadid, M. 1999, A&A, 344, 930 [NASA ADS] [Google Scholar]
  14. Fossati, L., Ryabchikova, T., Bagnulo, S., et al. 2009, A&A, 503, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Fuhrmann, K., Pfeiffer, M., Frank, C., Reetz, J., & Gehren, T. 1997, A&A, 323, 909 [NASA ADS] [Google Scholar]
  16. Gehren, T., Butler, K., Mashonkina, L., Reetz, J., & Shi, J. 2001, A&A, 366, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gillet, D., Crowe, R. A. 1988, A&A, 199, 242 [NASA ADS] [Google Scholar]
  18. Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [NASA ADS] [CrossRef] [Google Scholar]
  19. Jurcsik, J., Hurta, Zs., Sódor, Á., et al. 2009, MNRAS, 397, 350 [NASA ADS] [CrossRef] [Google Scholar]
  20. Heiter, U., & Eriksson, K. 2006, A&A, 452, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Heiter, U., Kupka, F., van't Veer-Menneret, C., et al. 2002, A&A, 392, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Kochukhov, O. 2007, Spectrum synthesis for magnetic, chemically stratified stellar atmospheres, Physics of Magnetic Stars, 109, 118 [Google Scholar]
  23. Kolenberg, K. 2002, Ph.D. Thesis, University of Leuven, http://www.ster.kuleuven.be/pub/kolenberg_phd/ [Google Scholar]
  24. Kolenberg, K., Smith, H. A., Gazeas, K. D., et al. 2006, A&A, 459, L577 [Google Scholar]
  25. Kolenberg, K., Szábo, R., Kurtz, D. W., et al. 2010, ApJ, 713, 198 [Google Scholar]
  26. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  27. Kurucz, R. 1993, ATLAS9: Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13 (Cambridge: Smithsonian Astrophysical Observatory) [Google Scholar]
  28. LaCluyzé, A., Smith, H. A., Gill, E.-M., et al. 2004, AJ, 127, 1653 [NASA ADS] [CrossRef] [Google Scholar]
  29. Lambert, D. L., Heath, J. E., Lemke, M., & Drake, J. 1996, ApJS, 103, 183 [NASA ADS] [CrossRef] [Google Scholar]
  30. Manduca, A., Bell, R. A., Barbes, T. G., et al. 1981, ApJ, 250, 312 [NASA ADS] [CrossRef] [Google Scholar]
  31. Mashonkina, L., & Zhao, G. 2006, A&A, 456, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Mashonkina, L., Korn, A. J., & Przybilla, N. 2006, A&A, 461, 261 [Google Scholar]
  33. Mashonkina, L., Gehren, T., Shi, J., Korn, A., & Grupp, F. 2009, Fe I/Fe II ionization equilibrium in cool stars: NLTE versus LTE, Chemical Abundances in the Universe: Connecting First Stars to Planets, ed. K. Cunha, M. Spite, & B. Barbuy, Proc. IAU Symp., 265, 197 [Google Scholar]
  34. Mathias, P., Gillet, D., Fokin, A. B., & Chadid, M. 1995, A&A, 298, 843 [NASA ADS] [Google Scholar]
  35. McWilliam, A. 1998, AJ, 115, 1640 [NASA ADS] [CrossRef] [Google Scholar]
  36. Peterson, R. C., Carney, B. W., & Latham, D. W. 1996, ApJ, 465, 47 [Google Scholar]
  37. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
  38. Preston, G. W. 2009, A&A, 507, 1621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Preston, G. W., Smak, J., & Paczynski, B. 1965, ApJS, 12, 99 [NASA ADS] [CrossRef] [Google Scholar]
  40. Przybilla, N., Butler, K., Becker, S. R., & Kudritzki, R. P. 2006, A&A, 445, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., Kupka, F., & Weiss, W. W. 1999, Phis. Scr. T, 83, 162 [Google Scholar]
  42. Ryabchikova, T. A., Fossati, L., & Shulyak, D. 2009, A&A, 506, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Siegel, M. J. 1982, PASP, 94, 122 [NASA ADS] [CrossRef] [Google Scholar]
  44. Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz Ch., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Szeidl, B. 1988, in: Multimode Stellar Pulsations, ed. G. Kovacs, L. Szabados, & B. Szeidl, Kultura, 45 [Google Scholar]
  46. Takeda, Y., Honda, S., Aoki, W., et al. 2006, PASJ, 58, 389 [NASA ADS] [Google Scholar]
  47. Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes (San Francisco: ASP), ASP Conf. Ser., 52, 173 [Google Scholar]
  48. Tsymbal, V. V. 1996, in Model Atmospheres and Spectral Synthesis, ed. S. J., Adelman, F., Kupka, & W. W., Weiss, ASP Conf. Ser., 108, 198 [Google Scholar]
  49. Van Hoof, A., & Struve, O. 1953, PASP, 65, 158 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... RR Lyrae[*]
Data obtained with the 2.7-m telescope at McDonald Observatory, Texas, US.
... (IRAF[*]
IRAF (http://iraf.noao.edu/) is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation.
... shocks[*]
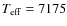Fokin & Gillet (1997) note that the theoretical velocities and the shock amplitudes are very sensitive to model parameters. They used parameters different from ours: $T_{\rm eff} = 7175$ K, $L = 62~L_{\odot}$, $M = 0.578~M_{\odot}$, X = 0.7, and Y = 0.299. The model generated with the Vienna Nonlinear Pulsation Code shows a maximum, during one pulsation cycle, of 4.7 Mach outward and -3.1 Mach inward, which corresponds to gas velocities of 35 and -23 km s-1. Owing to artificial viscosity, we can assume that the star undergoes stronger shocks than our models. The artificial tensor viscosity used broadens the shock region and underestimates any possible heating phenomena. The position of the outer boundary condition is crucial to the maximum velocity, because shock waves steepen when they run outwards towards lower density. 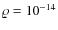Fokin's model continues until $\varrho = 10^{-14}$, while the Vienna models we used stop at about 10-10.
... phase[*]
Fundamental parameters obtained at different Blazhko phases are not necessarily equal to one another, although they are obtained at the same pulsation phase.
... fitting[*]
The code adopts an LTE plane-parallel model atmosphere calculated using subroutines of the SynthV code (Tsymbal 1996) and the DUNLSF minimisation procedure of the IMSL numerical libraries package.

All Tables

Table 1:   Basic data of the observations of RR Lyr.

Table 2:   LTE atmospheric abundances for RR Lyr.

Table 3:   Comparison between the atmospheric ion abundances relative to the Sun obtained by Clementini et al. (1995) and in this work.

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{figures/14471fg1.ps} \end{figure} Figure 1:

RR Lyr model bolometric luminosity ( upper panel), photospheric radius ( middle panel), and atmospheric kinetic energy ( lower panel) as a function of the pulsational phase. By convention, phase 0 corresponds to the maximum of the luminosity. The two full vertical lines correspond to the phases of both maximum radius (the phase we declare as most quiescent) and minimum light (usually adopted for the spectroscopic analysis).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{figures/14471fg2.ps} \end{figure} Figure 2:

Radial plots showing gas velocity u in units of the sound speed (the so-called Mach number) shown for the phase of maximum radius (left) and minimum light (right).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg3.ps} \end{figure} Figure 3:

Left panel: comparison between a part of the RR Lyr spectrum as observed close to the phase of maximum radius (full line) and close to the phase of minimum light (dashed line). Right panel: comparison between the bisectors of the Ti II line at $\sim $4501 Å as observed close to the phase of maximum radius (full line) and close to the phase of minimum light (dashed line). The dotted line shows the zero velocity, for comparison. The velocity scale is in ${\rm m~s}^{-1}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg4.ps} \vspace*{-2mm} \end{figure} Figure 4:

Full width at half maximum (FWHM) in Å as a function of pulsational phase measured for three Fe II lines and one Ti II line. The minimum is in correspondance with the phase of maximum radius. The typical uncertainty in the FWHM is of $\sim $0.01 Å, but also depends on the SNR of each spectrum. The two peaks visible at about phase 0.65 and 0.9 are due to two propagating shock waves (Fokin et al. 1999).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg5.ps} \end{figure} Figure 5:

Comparison between the observed H$\gamma $ line profile (solid line) and synthetic profiles calculated with the final adopted $T_{{\rm eff}}$ =6125 K (red line) and with $T_{{\rm eff}}$ = 6175 K (green line) and $T_{{\rm eff}}$ = 6075 K (blue line). The red line agrees very well with the observed spectrum.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{figures/14471fg6.ps} \end{figure} Figure 6:

Plots of individual abundances for 284 Fe I lines versus the measured equivalent width for RR Lyr, adopting a constant (open circles) and depth-dependent (open squares) $\upsilon _{{\rm mic}}$. The same dependence for 108 common Fe I lines in the spectrum of HD 49933 is shown by crosses. We applied an arbitrary vertical shift for visualisation purposes.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg7.ps} \end{figure} Figure 7:

Comparison between the profile of the microturbulent velocity (full line) and of the sound speed (dashed line) as a function of atmospheric depth.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figures/14471fg8.eps} \end{figure} Figure 8:

Comparison of temperature structures of models computed under different assumptions about microturbulent velocity $\upsilon _{{\rm mic}}$ and abundances (see the legend on the plot). Depth-dependent $\upsilon _{{\rm mic}}$ was taken from Fig. 7. For all the models we took $T_{{\rm eff}}$ =6125, \ensuremath{\log g} =2.4.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.