EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 519 (September 2010) A&A, 519 (2010) A57 Full HTML
Free Access
Issue
A&A
Volume 519, September 2010
Article Number A57
Number of page(s) 6
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201014008
Published online 14 September 2010
A&A 519, A57 (2010)

The apsidal-motion test of stellar structure and evolution: an update

A. Claret1 - A. Giménez2

1 - Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
2 - Centro de Astrobiologia (CSIC-INTA), 28850 Torrejón de Ardoz, Madrid, Spain

Received 7 January 2010 / Accepted 18 May 2010

Abstract
Aims. The recent revision of a sample of 94 double-lined eclipsing binaries with accurate absolute dimensions provides a set of 18 systems with eccentric orbits that are precise enough to carry out an updated apsidal motion test of stellar structure. The availability of these new high-quality observational data, together with improved stellar models, that include the latest opacities, stellar compressibility, resonances, and rotation, has triggered the comparison presented in this paper between theoretical and observed apsidal motion rates.
Methods. The applicability of the adopted stellar models to the sample of eclipsing binaries with accurate absolute dimensions and eccentric orbits was checked with two classical tests of the good agreement between the predicted and observed effective temperatures of the component stars and a fit to a common isochrone of their position in the H-R diagram. For this comparison, stellar models were computed for the observed individual masses and incorporated the most recent input physics available, including the effects of rotation and convective core overshooting.
Results. The final comparison of the theoretical and observed weighted internal-structure constants k2 shows good agreement and no systematic effects. Observational evidence does not show more massive cores than predicted by the models as has been suggested, and this result is independent of the evolutionary status.

Key words: binaries: eclipsing - stars: evolution - stars: rotation

1 Introduction

For quite a while apsidal motions in eclipsing binary systems have been used to test the internal structure of the stars (see e.g. Giménez 2007, for a summary of the history of such studies). The Newtonian contribution to the observed apsidal motion, which contains the internal structure parameter, is highly dependent on the stellar radii (R5). Therefore, only systems that accurately determine their absolute dimensions can be used to test the models. In order to check the capability of the adopted evolutionary models to reproduce the observed apsidal motion rates, we first make certain that they can fit the masses, radii, and effective temperatures of both components at the same age in the H-R diagram. This constraint has not always been fulfilled satisfactorily, at least at the required level of precision, and has been indicated as the most probable source of the earlier claimed discrepancies between theory and observations. These discrepancies have suggested that the models were less concentrated in mass toward their centre than the real stars (see e.g. Claret & Giménez 1993, for a review of the problem). Claret & Giménez (1993) introduced stellar rotation and core overshooting in their theoretical models and, for the first time, no significant discrepancy was detected when considering binary systems with a good determination of their absolute dimensions. The present paper provides a revision of such a comparison using only data with masses and radii determined with precisions better than $2\%$, thus significantly improving the reliability of the test. For consistency, the latest stellar models with the capability to compute internal structure constants were used in the comparison as described below.

In addition to the classical contribution to the apsidal motion rate due to static tides, dynamic tides can cause significant deviations in the theoretical predictions due to the effects of the compressibility of the stellar fluid when the systems are near synchronism. For higher rotational angular velocities, additional deviations due to resonances appear when the forcing frequencies of the dynamic tides come into the range of the free oscillation modes of the component stars. Claret & Willems (2002) introduced such effects in the theoretical calculation of the apsidal-motion rates. Besides the contributions of tidal and rotational distortions to the rate of secular apsidal motion, there is also a general relativistic contribution (Levi-Civita 1937) that can be important for binaries with high orbital eccentricities and small relative radii as shown by Giménez (1985).

Very recently, Torres et al. (2010) have revised the absolute dimensions of 94 double-lined eclipsing binaries systems (DLEBS). Eighteen of them have eccentric orbits and show apsidal motion with period determinations adequate for a detailed apsidal-motion test of stellar structure. The availability of this new data sample, together with the latest improvements in the stellar models with respect to earlier studies (including the opacities, stellar compressibility, resonances, and rotation) led us to the analysis in this paper, following the preliminary indications already given by Torres et al. (2010), with the aim of a global comparison between predicted and observed apsidal-motion rates. To reduce internal errors, we carried out such a revision, which updates the earlier paper by Claret & Giménez (1993), using stellar models computed precisely for the observed individual masses, rather than interpolating within a grid for an adopted initial chemical composition, as in our previous paper.

2 The observational data

Table 1 shows the more relevant astrophysical parameters concerning apsidal motion for the 18 systems with good absolute dimensions and apsidal-motion rates. As mentioned in Claret & Willems (2002), ``searching for appropriate systems is not only a bibliographical survey since it is sometimes hard to separate true good quality data from those presenting only apparent small errors''. Fortunately, the orbital elements and the absolute dimensions of the systems displayed in Table 1 were all re-analysed (using homogeneous methodology) by Torres et al. (2010). Therefore, they are sometimes slightly refined if compared with the original sources. The covered mass range is 0.8-23 $M_{\odot}$, and the mean error in radius is around $1{-}2\%$, which we can consider precise enough for our purpose. The systems with high relativistic contributions were excluded from our comparison of the log  k2 values, because the Newtonian contribution in these cases is comparable to the uncertainty of the apsidal-motion rate, and no significant conclusions can be drawn when compared with the predictions derived from the stellar models. For the sake of clarity, we have not included the rotational velocities in Table 1. Such information can be obtained from the paper of Torres et al. (2010).

Table 1:   Revised astrophysical parameters and orbital elements of EBS showing apsidal motion.

3 The stellar models

Stellar models were generated using the Granada evolutionary code by Claret (2004). We refer the readers to this paper to identify the main differences between such a code and those previously used by Claret & Giménez (1993) and Claret & Willems (2002). Since no system in our sample is a fast rotator, standard models are an acceptable approximation. We do not consider rotation directly in our models and the corrections by rotation on the internal structure constant k2 are computed as indicated by Claret (1999). This is the same approach as was adopted in Claret & Giménez (1993). In addition, the component stars are all well detached and evolutionary models of single stars suit our needs rather than current binary models. For systems showing a convective core we considered core overshooting described as an extra mixing beyond the classical Schwarzchild criterion. This extra mixing produces stellar models with longer main-sequence lifetimes because more fuel is available in the core. Other mechanisms may also increase the core size, as for example internal gravity waves or rotation. For the excess distance, we use $d_{\rm over} = \alpha_{\rm ov} H_{\rm }$, where $H_{\rm p}$ is the pressure scale height taken at the edge of the convective core as given by Schwarzschild's criterion, and $\alpha_{\rm ov}$ is a free parameter. Core overshooting was key in decreasing the discrepancies between the theoretical and observed apsidal-motion rates in previous studies (see for example, Claret & Giménez 1991, 1993). The dependence of $\alpha_{\rm ov}$ on stellar mass was considered following the results by Claret (2007). Selected double-line eclipsing binary systems, strategically positioned in the HR diagram, were used to infer the mass dependence of the core overshooting parameter. One of the main conclusions by Claret (2007) is that core overshooting (or equivalently other mechanisms such as induced mixing by rotation) seems to be necessary to match the absolute dimensions of key double-lined eclipsing binaries as well as the colour-magnitude diagrams of some clusters. For models with convective envelopes, we adopted the mixing-length theory to describe them with $\alpha = 1.68$, as calibrated using the Sun.

All the models were computed by adopting the primordial helium content derived by Claret & Willems (2002), $Y_{\rm p} = 0.238 \pm 0.011$, with a mean enrichment law of $\Delta Y/\Delta Z \approx 2.0$ using the value of Z that best fits the observed effective temperatures, except in the case of V636 Cen for which the actual observed Z was assumed. Concerning opacities, for high temperatures the code uses the set of tables provided by Iglesias & Rogers (1996), completed with the computations by Alexander & Ferguson (1994) for lower temperatures. Individual models for the precise observed masses were computed so that no interpolation was necessary in mass.

Mass loss was considered during the main-sequence and for red giants. Given the evolutionary status and the masses of the our sample of DLEBS, the formalism by Nieuwenhuijzen & de Jager (1990) was considered for all models except for the Wolf-Rayet stage (Nugis & Lamers et al. 2000) or for red giants with masses lower than 4 $M_{\odot}$ (Reimers 1977). On the other hand, concerning opacities, we have performed preliminary tests adopting the more recent Alexander opacities and the differences are not significant with respect to the comparison with absolute dimensions and internal structure constant k2. Therefore, they do not affect our main comparison and conclusions. The nuclear input data was also revised with respect to the evolutionary code used by Claret & Giménez (1993), which only treated the basic nuclear reactions. Instead, a more general network was introduced for more advanced stages of evolution (47 isotopes). As such a subroutine is very time-consuming, we adopted a less extensive network that follows the evolution of 13 isotopes: 1H, 4He, 12C, 13C, 14N, 16O, 17O, 18O, 20Ne, 22Ne, 24Mg, 25Mg, and 26Mg. Recent measurements of the nuclear reaction 14N(p, $\gamma$)15O (Runkle 2003; Formicola et al. 2004) were also incorporated into the code. Summarizing, the main differences between the present models and those in our 1993 paper are: new opacity tables, a more extensive nuclear network, a wider mass range, and more accurate computations of the envelopes decreasing the triangle size in the HR diagram to $\Delta$log  $T_{\rm eff} = 0.001 $and $\Delta$log L = 0.004 or less.

3.1 The internal structure constants

To compute the theoretical internal structure constants kj to be compared with the observed values, we integrated the models using the differential equations of Radau as given by

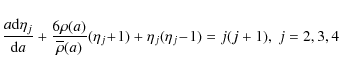
\begin{displaymath}{a{\rm d}\eta_{j}\over {\rm d}a}+ {6\rho(a)\over\overline\rho... ..._{j}\!+\!1)}+ {\eta_{j}(\eta_{j}\!-\!1)} = {j(j+1}), ~ j=2,3,4 \end{displaymath} (1)

where,

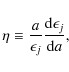
\begin{displaymath}\eta \equiv {{a}\over{\epsilon_{j}}} {{\rm d}\epsilon_{j}\over{{\rm d}a}}, \end{displaymath} (2)

and a is the mean radius of the configuration, $\epsilon_j$ measure of the deviation from sphericity, $\rho(a)$ the mass density at the distance a from the centre, and $\overline\rho(a)$ the mean mass density within a sphere of radius a. The result is expressed as the internal structure constants in the form

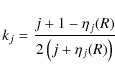
\begin{displaymath}k_{j} = {{j +1 - \eta_{j}(R)}\over{2\left(j+\eta_{j}(R)\right)}} \end{displaymath} (3)

where R refers to the values of $\eta_{j}$ at the star's surface. The contribution of j=3 and 4 are very small, so we generally only use k2.

It is nevertheless well known that rotating models are more mass concentrated than the standard ones. Stothers (1974) was the first to investigate this effect, and in 1993, Claret & Giménez made a first attempt to evaluate the influence of stellar rotation on k2. Later, Claret (1999) introduced a more elaborated method to treat rotation in the Granada code. This method follows Kippenhahn & Thomas (1970) by considering three contributions to the total gravitational potential: the spherical symmetric one, the one due to rotation, and the integral describing the distortion. A detailed description of the numerical method is given by Claret (1999). The resulting correction of the internal structure constant due to stellar rotation is then given by $\Delta {\rm log} k_2 \equiv {\rm log} k_{2, \rm stan} - \lambda$, where $\lambda=2V^{2}/(3gR)$, g is the surface gravity, and V is the rotational velocity. Nevertheless, the effects of the induced mixing were not included in our rotating models.

The classical formula for the apsidal-motion rates is derived under some simplifications that also require some revision. In particular, the assumption that the star readjusts its shape instantaneously during the revolution is only valid when the orbital period is much longer than the periods of the low-order modes of oscillation. There has been some research on the role of resonances and stellar compressibility (see e.g. Papaloizou & Pringle 1980; Quataert et al. 1996; Smeyers & Willems 2001; Willems & Claret 2002). These results were applied systematically to the apsidal-motion scenario for the first time by Claret & Willems (2002). In the present paper we apply the same formalism. The contribution of the dynamic tides were calculated for each system as a function of $\omega/\omega_P$, where $\omega$ is the angular velocity and $\omega_P$ the angular velocity at periastron. An example of this test for the case of EM Car is shown in Fig. 1. The relative deviation between the classical rate of apsidal motion and that one given by the theory of dynamic tides is

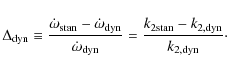
\begin{displaymath}\Delta_{\rm dyn} \equiv {{\dot{\omega}_{\rm stan} - \dot{\ome... ...{{k_{2\rm stan} - k_{\rm 2,dyn}} \over {k_{\rm 2,dyn}}} \cdot \end{displaymath} (4)

\begin{figure} \par\includegraphics[height=8.cm,width=8.cm,clip]{fig1.eps} \end{figure} Figure 1:

The effects of dynamic tides in the apsidal-motion constant of EM Car. The vertical dashed line denotes the observed value of the angular velocitiy.

Open with DEXTER

\begin{figure} \par\includegraphics[height=6cm,width=8cm,clip]{fig2.eps} \vspace*{-3mm} \end{figure} Figure 2:

Examples of the fitting process: theoretical isochrones for EM Car, V539 Ara, and IT Cas.

Open with DEXTER

\begin{figure} \par\includegraphics[height=7.6cm,width=7.6cm,clip]{fig3.eps} \end{figure} Figure 3:

Evolutionary ages inferred for each individual component of the systems in Table 1.

Open with DEXTER

\begin{figure} \par\includegraphics[height=7.6cm,width=7.6cm,clip]{fig4.eps} \vspace*{-4mm} \end{figure} Figure 4:

Theoretical and observed apsidal-motion constant for the systems in Table 1.

Open with DEXTER

4 Comparison with the observations

4.1 Ages and effective temperatures

Apsidal motion can only be considered to be a robust test of stellar structure if the adopted stellar models are able to reproduce the astrophysical parameters of the selected DLEBS with the necessary accuracy. The observed masses, radii, and effective temperatures of both components must simultaneously fit a common isochrone as given by the models. A comparison of only effective temperatures/isochrones has been carried out in several papers in the literature by testing different stellar models, including our own code (see for example, Lastennet & Valls-Gabaud 2002). They find that the different stellar models predict similar absolute dimensions and ages. Further comparisons are also shown in the paper by Torres et al. (2010). An example of this test is shown in Fig. 2. The apsidal motion test is thus an additional parameter in the overall comparison of stellar structure models with observations. It requires calculating of the internal structure constant k2 in the models, and the main reason to use only our own codes is that there are no other updated stellar models providing k2 for the mass range and evolutionary status of our observational sample. Given that the chemical composition is not known accurately for our sample, this increases the number of free parameters, but an enrichment law has been adopted, together with the best value of Z, thereby optimizing the fit of the effective temperatures. In this comparison of the absolute dimensions with the models, we have obtained an average value of Z of 0.018 $\pm$ 0.003, very similar to the one already adopted in our 1993 paper (Z = 0.02). This difference is probably due to the different opacity tables, as well as the revised absolute dimensions. On the other hand, it should be noted that the influence of the mixing-length parameter $\alpha$ is not significant, given the involved effective temperatures in our sample of DLEBS.

A more extensive comparison between the ages of the primaries and secondaries derived from the theoretical models is shown in Fig. 3. The agreement is very good; i.e. the ages of both components coincide as required within the involved uncertainties, and this is true along more than 2 orders of magnitude in age. For three systems, the fit of a common isochrone is not totally satisfactory, namely V760 Sco, AG Per and $\zeta$ Phe. These systems were already identified in previous studies as showing problems with their location on the H-R diagram (Claret & Giménez 1993; Claret & Willems 2002). However, the case of $\zeta$ Phe is found to be in better agreement with the theoretical predictions than in our earlier papers. This improvement is mainly due to the use of Z as a free parameter instead of adopting it to be 0.02, but also, in a minor way, due to the new models - mainly the more recent opacity tables - and the revised absolute dimensions. A metallicity of 0.015 was found for $\zeta$ Phe and 0.018 for V760 Sco, which could be verified by future spectroscopic observations. In the cases of V760 Sco and AG Per the identified discrepancy in age between the component stars may be related to their youth. The problem of fitting a common age for young systems is a well known problem essentially because the density of isochrones, within given error bars of the absolute dimensions, increases very rapidly towards the ZAMS. A different case is EK Cep, since one of its components is still in the pre main-sequence phase, while the other is on the main sequence so the problem of the selection of the best isochrone is thus avoided. Difficulties with the analysis of EK Cep, in the sense of not being able to fit the observed parameters with available models, led Yildiz (2003) to find a solution by assuming that the stellar core, which contains 52% of the total mass, rotates 65 times faster than the outer layers. However, the adopted assumptions by Yildiz present some problems. For example, such a redistribution of the angular velocity for EK Cep A, which is a very young star, seems very unlikely. Moreover, the author use the approximation by Kopal to compute k2 instead of integrating Radau's equation. The old approximation by Kopal, derived when numerical models were not available, is known to provide artificially lower values of k2. Owing to problems with the empirical determination of its effective temperatures, Claret (2006) adopted a different approach to compare the observations with the theoretical models by using the effective temperature ratio, which is a better determined parameter than the absolute values from the light-curve analysis. Such an approach is supported observationally by the inconsistency found in the photometric distances for both components of EK Cep. We have found that the standard models are able to reproduce the effective temperature ratio, masses, radii, and apsidal-motion rate for the same isochrone. A similar situation was found in the case of PV Cas.

4.2 The apsidal-motion test

It is not possible to separate the individual contribution of each component to the total apsidal-motion rate. Instead of individual contributions, we have the mean apsidal-motion constant as a function of the stellar masses mi, the stellar radii Ri, the eccentricity e, the orbital period P, and the apsidal-motion period U:

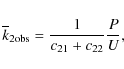
\begin{displaymath}{\overline k_{2 \rm obs}} = {1\over {c_{2 1} + c_{2 2}}} {P\over U}, \end{displaymath} (5)

where

\begin{displaymath}{c_{2 i}} \!=\! \left[\! \left({\omega_{i}\over{\omega_{K}}}\... ..._{i}}}~g(e) \right]\!\! {\left({R_{i}\over{A}}\right)^{\!\!5}} \end{displaymath} (6)

where A is the semi-major axis of the orbit, while f and g are functions of the orbital eccentricity given by

f(e) = (1 - e2)-2 (7)

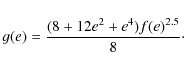
\begin{displaymath}{g(e)} = {(8 + 12e^2 + e^4) f(e)^{2.5}\over{8}}\cdot \end{displaymath} (8)

Here, ${\omega_{i}/{\omega_{K}}}$ is the ratio between the rotational angular velocity of component i and the average orbital angular velocity. In addition, we have

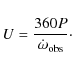
\begin{displaymath}{U} = {360 P\over{\dot\omega_{\rm obs}}}\cdot \end{displaymath} (9)

The value of $\dot\omega$ to be used in the equations above, in order to derive the observational internal structure average constant of each system is that due to the Newtonian contribution, i.e. the one induced by the non-sphericity of the component stars. The total apsidal motion rate also includes the term predicted by General Relativity, for which the observational data have to be corrected. The relativistic contribution to the advance of the periastron is caused by the correction of the Newtonian two-body equation of gravitational field deviating from the pure inverse square law of the separation, and it does not depend on the tidal/rotational distortion (see e.g. Giménez 1985). It can be easily computed using the expression derived by Levi-Civita (1937),

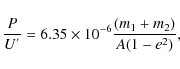
\begin{displaymath}{P\over U^{'}} = {6.35\times10^{-6}} {{(m_1 + m_2)}\over {A(1 - e^2)}}, \end{displaymath} (10)

where U' is apsidal-motion period corresponding to the relativistic correction. The Newtonian apsidal-motion rate to be compared with theoretical models of the internal structure is thus

\begin{displaymath}{\dot\omega_{\rm newt}} = {\dot\omega_{\rm obs}} - {\dot\omega_{\rm GR}}. \end{displaymath} (11)

Some binary systems, like DI Her, have shown apsidal motion rates that are too slow when compared with theoretical predictions that cannot be explained as the result to problems with the Newtonian contribution since the relativistic terms dominates in their apsidal motion. The case of AS Cam, which also presents similar discrepancies, is not relevant here because of the large uncertainties in its absolute dimensions and apsidal motion rate. These anomalies have sometimes been interpreted as a failure of General Relativity. However, it does not seems the case since several investigations of other relativistic systems (Claret 1997; Wolf et al. 2010; Torres et al. 2010) have shown that the General Relativity correction is fully valid. In addition, the anomaly in the apsidal motion rate of DI Her has recently been explained as coming from a misalignment of the spin and orbital axes of the component stars (Albrecht et al. 2009; Claret et al. 2010). These results give confidence that Eqs. (10) and (11) can be used without problems of introducing any systematic effect in the comparison of the Newtonian contributions.

Equations (5) and (11) can now be combined to allow us to compare the observational apsidal-motion constants with the theoretical values as derived from stellar evolutionary models, using a weighted average value as given by

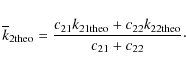
\begin{displaymath}{\overline k_{2 \rm theo}} = {c_{2 1}k_{2 1 \rm theo} + c_{2 2}k_{2 2 \rm theo} \over {c_{2 1} + c_{2 2}}}\cdot \end{displaymath} (12)

Of course, as mentioned before, we first apply the corrections by rotation, dynamic tides, stellar compressibility, and relativistic term to the systems given in Table 1 using the procedures described above. To derive the rotational contribution (Eq. (4)) to the total apsidal-motion, we adopt the observed rotational velocities quoted by Torres et al. (2010). The rotational velocities of the systems obtained through measurements of the line broadening of selected absorption features of the respective spectra. However, for two systems, namely V478 Cyg and CW Cep, such measurements are not available. For these cases, we assumed that both components of each system are synchronized with the orbital velocities at periastron, where the tidal forces are stronger. On the other hand, the system V636 Cen is represented twice (lower left corner of Fig. 4) because we adopted two solutions for the corresponding evolutionary models: one adopting the standard solar mixing-length model ( $\alpha = 1.68$) and another one, to the left, with two values for $\alpha$ (1.4 and 1.0, for the primary and the secondary, respectively; see Clausen et al. 2009, for additional details). The standard solar mixing-length models are marginally in better agreement with the observations concerning apsidal motion but they do not reproduce the absolute dimensions as well as the tuned models do. However, this question is still open. To fully understand and describe the properties of the envelopes, it will be necessary to investigate many more systems in the mass range of V636 Cen.

The comparison between the theoretical and the observed apsidal-motion constant k2 is shown in Fig. 4. We can consider the comparison to be reasonably good within the involved uncertainties since the theoretical models are found to be able to satisfactorily reproduce the observed apsidal-motion rates. One important characteristic of Fig. 4 is that no systematic effects can be detected; i.e., the differences between the theoretical and observed k2 are not correlated with any other parameter, such as mass or the evolutionary status of the system, because the dispersion of the points is consistent with the observational errors. Basically the same process as followed by Claret & Giménez (1993) has been adopted here, aso we refer the readers to that paper for more details. The different data sample limited to systems with accurate absolute dimensions better than $2\%$, the more modern revised stellar models, and the effects of stellar compressibility, define the main differences. Our results confirm the expectations from the previous paper. Indeed the comparison of the properties of the systems common to both papers shows excellent agreement. But the much smaller error bars in the $\log {k_2}$ values of the present paper allow the first robust test and a discussion of the behaviour of specific systems.

5 Conclusions

We have compared the observed astrophysical parameters of double-lined eclipsing binaries, including apsidal-motion rates, with theoretical stellar model predictions. The code used to generate such models incorporates updated input physics like stellar rotation, recent opacities tables, effects of stellar compressibility, dynamic tides, mass loss, and moderate core overshooting.

Before comparing the theoretical and observed apsidal-motion rates in our sample, adopted from Torres et al. (2010), a careful test of the absolute dimensions and the predicted values by theoretical stellar models was performed to guarantee that the apsidal-motion test is really significant. We found good agreement between the ages of both components, computed individually, as well as good fits between the theoretical and observed effective temperatures.

A subsequent comparison was made between the theoretical and observed apsidal-motion rates by means of the internal structure constant, k2. No systematic differences were found between the observed and theoretical predictions. This result indicates that, when we adopt double-lined eclipsing binaries with very good determination of their absolute dimensions and apsidal-motion rates, together with theoretical models based on modern tools, the apsidal motion test is fully successful within the limit of the involved uncertainties and with no requirements for additional free parameters.

We expect that additional absolute dimensions and apsidal-motion rates will be available in the near future so that it will be possible to check and extend the capability of our theoretical stellar models to investigate all relevant aspects of stellar/tidal evolution more deeply.

Acknowledgements
The Spanish MEC (AYA2006-06375, AYA2009-14000-C03-01) is gratefully acknowledged for its support during the development of this work. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and of NASA's Astrophysics Data System Abstract Service.

References

  1. Albrecht, S., Reffert, S., Snellen, I. A. G., & Winn, J. N. 2009, Nature, 461, 373 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
  3. Andersen, J. 1983, A&A, 118, 255 [NASA ADS] [Google Scholar]
  4. Andersen, J., & Clausen, J. V. 1989, A&A, 213, 183 [NASA ADS] [Google Scholar]
  5. Andersen, J., & Giménez, A. 1985, A&A, 145, 206 [NASA ADS] [Google Scholar]
  6. Andersen, J., Clausen, J. V., Nordström, B., & Reipurth, B. 1983, A&A, 121, 271 [NASA ADS] [Google Scholar]
  7. Andersen, J., Clausen, J. V., Nordström, B., & Popper, D. M. 1985, A&A, 151, 329 [NASA ADS] [Google Scholar]
  8. Andersen, J., Clausen, J. V., & Giménez, A. 1993, A&A, 277, 439 [NASA ADS] [Google Scholar]
  9. Barembaum, M. J., & Etzel, P. B. 1995, AJ, 109, 2680 [NASA ADS] [CrossRef] [Google Scholar]
  10. Claret, A. 1997, A&A, 327, 11 [NASA ADS] [Google Scholar]
  11. Claret, A. 1999, A&A, 350, 56 [NASA ADS] [Google Scholar]
  12. Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Claret, A. 2006, A&A, 445, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Claret, A. 2007, A&A, 475, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Claret, A., & Giménez, A. 1991, A&A, 244, 319 [NASA ADS] [Google Scholar]
  16. Claret, A., & Giménez, A. 1993, A&A, 277, 487 [NASA ADS] [Google Scholar]
  17. Claret, A., & Willems, B. 2002, A&A, 388, 518 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Claret, A., Giménez, A., & Martin, E. L. 1995, A&A, 302, 741 [NASA ADS] [Google Scholar]
  19. Claret, A., Torres, G., & Wolf, M. 2010, A&A, 515, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Clausen, J. V. 1996, A&A, 308, 151 [NASA ADS] [Google Scholar]
  21. Clausen, J. V., & Giménez, A. 1991, A&A, 241, 98 [NASA ADS] [Google Scholar]
  22. Clausen, J. V., Giménez, A., & Scarfe, C. 1986, A&A, 167, 287 [NASA ADS] [Google Scholar]
  23. Clausen, J. V., Bruntt, H., Claret, A., et al. 2009, A&A, 502, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys. Lett. B, 591, 61 [NASA ADS] [CrossRef] [Google Scholar]
  25. Giménez, A. 1985, ApJ, 297, 405 [NASA ADS] [CrossRef] [Google Scholar]
  26. Giménez, A. 2007, in Binary Stars as Critical Tools and Tests in Contemporary Astrophysics, ed. W. I. Hartkopf, E. F. Guinan, & P. Harmanec, IAU Symp., 240, 290 [Google Scholar]
  27. Giménez, A., & Clausen, J. V. 1994, A&A, 291, 795 [NASA ADS] [Google Scholar]
  28. Giménez, A., Clausen, J. V., & Jensen, K. S. 1986, A&A, 159, 157 [NASA ADS] [Google Scholar]
  29. Holmgren, D. E., Hill, G., & Fisher, W. 1991, A&A, 248, 129 [NASA ADS] [Google Scholar]
  30. Kippenhahn, R., & Thomas, R. C. 1970, in Stellar Rotation, ed. A. Slettebak (Dordrecht, Holland: D. Reidel, Publ. Co.), 20 [Google Scholar]
  31. Lacy, C. H. S., & Frueh, M. L. 1985, ApJ, 295, 569 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lacy, C. H. S., Torres, G., Latham, D. W., Zakirov, M. M., & Arzumanyants, G. C. 1997, AJ, 114, 1206 [Google Scholar]
  33. Lastennet, E., & Valls-Gabaud, D. 2002, A&A, 396, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Levi-Civita, T. 1937, Am. J. Math., 59, 225 [Google Scholar]
  35. Martin, E. L., & Rebolo, R. 1993, A&A, 274, 274 [NASA ADS] [Google Scholar]
  36. Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
  37. Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
  38. Papaloizou, J., Pringle, J. E. 1980, MNRAS, 193, 603 [NASA ADS] [CrossRef] [Google Scholar]
  39. Pavlovski, K., & Southworth, J. 2009, MNRAS, 394, 1519 [NASA ADS] [CrossRef] [Google Scholar]
  40. Popper, D. M. 1974, ApJ, 188, 559 [NASA ADS] [CrossRef] [Google Scholar]
  41. Popper, D. M. 1987a, AJ, 93, 672 [NASA ADS] [CrossRef] [Google Scholar]
  42. Popper, D. M. 1987b, ApJ, 313, L81 [NASA ADS] [CrossRef] [Google Scholar]
  43. Popper, D. M., & Etzel P. B. 1981, AJ, 86, 102 [NASA ADS] [CrossRef] [Google Scholar]
  44. Popper, D. M., & Hill, G. 1991, AJ, 101, 600 [NASA ADS] [CrossRef] [Google Scholar]
  45. Quataert, E. J., Kumar, P., & Ao, C. O. 1996, ApJ, 463, 284 [NASA ADS] [CrossRef] [Google Scholar]
  46. Reimers, D. 1977, A&A, 61, 217 [NASA ADS] [Google Scholar]
  47. Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
  48. Runkle, R. C. 2003, Ph.D. Thesis, University of North Carolina [Google Scholar]
  49. Smeyers, P., & Willems, B. 2001, A&A, 373, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
  51. Stickland, D. J., Koch, R. H., & Pfeiffer, R. J. 1992, The Observatory, 112, 277 [NASA ADS] [Google Scholar]
  52. Stothers, R. 1974, ApJ, 194, 651 [NASA ADS] [CrossRef] [Google Scholar]
  53. Svarícek, P., Wolf, M., Claret, A., et al. 2008, A&A, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
  55. Vaz, L. P. R., Andersen, J., & Claret, A. 2007, 469, 285 [Google Scholar]
  56. Wachmann, A. A. 1974, A&A, 34, 317 [NASA ADS] [Google Scholar]
  57. Willems, B., & Claret, A. 2002, A&A, 382, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Wolf, M. 2000, A&A, 356, 134 [NASA ADS] [Google Scholar]
  59. Wolf, M., & Zejda, M. 2005, A&A, 437, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Wolf, M., Kucáková, H., Kolasa, M., et al. 2006, A&A, 456, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Wolf, M., Claret, A., Kotková, L., et al. 2010, A&A, 509, 18 [Google Scholar]
  62. Yildiz, M. 2003, A&A, 409, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Zasche, P., & Wolf, M. 2007, AN, 328, 928 [Google Scholar]

All Tables

Table 1:   Revised astrophysical parameters and orbital elements of EBS showing apsidal motion.

All Figures

  \begin{figure} \par\includegraphics[height=8.cm,width=8.cm,clip]{fig1.eps} \end{figure} Figure 1:

The effects of dynamic tides in the apsidal-motion constant of EM Car. The vertical dashed line denotes the observed value of the angular velocitiy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=6cm,width=8cm,clip]{fig2.eps} \vspace*{-3mm} \end{figure} Figure 2:

Examples of the fitting process: theoretical isochrones for EM Car, V539 Ara, and IT Cas.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=7.6cm,width=7.6cm,clip]{fig3.eps} \end{figure} Figure 3:

Evolutionary ages inferred for each individual component of the systems in Table 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=7.6cm,width=7.6cm,clip]{fig4.eps} \vspace*{-4mm} \end{figure} Figure 4:

Theoretical and observed apsidal-motion constant for the systems in Table 1.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.