EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 519 (September 2010) A&A, 519 (2010) A21 Full HTML
Free Access
Issue
A&A
Volume 519, September 2010
Article Number A21
Number of page(s) 13
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913569
Published online 07 September 2010
A&A 519, A21 (2010)

Particle acceleration in a transient magnetic reconnection event

M. Gordovskyy - P. K. Browning - G. E. Vekstein

Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, Manchester M13 9PL, UK

Received 29 October 2009 / Accepted 12 April 2010

Abstract
Context. In the present paper, we investigate particle acceleration by direct electric field in solar flares.
Aims. Proton and electron kinetics are considered based on MHD simulations of magnetic reconnection, with the aim of determining the properties of accelerated particles in a time-dependent reconnecting event model.
Methods. At first, we considered several two-dimensional numerical models of forced reconnection in the initially force-free Harris current sheet. The electric and magnetic fields from these models were then used to study proton and electron motion with the guiding centre, test particle approach.
Results. It is shown that protons and electrons can be accelerated to very high energies up to tens of MeV in the present model. The energy spectra for both particle species are combinations of exponential and rather hard power-law shapes. Also, protons and electrons are ejected from the CS in different directions.

Key words: Sun: flares - magnetohydrodynamics (MHD) - acceleration of particles

1 Introduction

Solar flares are the most energetic explosive events in the Solar System releasing up to $\sim$1026 J on time scales of $\sim$10-100 s. A substantial part of this energy (up to 10-30%) is carried by non-thermal, high-energy particles. Observations show that electrons and ions in major flares can be accelerated to the energies of $\sim$10-100 MeV and 100 MeV-1 GeV, respectively (see Lin & Hudson 1976; Mandzhavaridze & Ramaty 1993; Aschwanden 2002; Lin et al. 2008, and references therein). In the past decade, advances in observational techniques have provided a large amount of high-quality data concerning high-energy particles. However, a self-consistent model of particle acceleration that could satisfy all the phenomenological constraints is still a major theoretical problem.

Several mechanisms of particle acceleration have been considered in the context of the solar corona and geomagnetic tail (see e.g. Benz 2008, for review). The most widely considered are acceleration by $\vec{B}$-parallel electric field in either a single current sheet (CS) (e.g. Speiser 1965; Smith 1980; Martens & Young 1990; Zhu & Parks 1993) or fragmented CS (Vlahos et al. 2004; Turkmani et al. 2005; Bian & Browning 2008) acceleration by plasma waves (e.g. Smith 1977; Miller & Roberts 1995; Miller et al. 1996; Pryadko & Petrosian 1997), shocks (Decker & Vlahos 1986; Miteva & Mann 2007) and collapsing magnetic traps (e.g. Brown & Hoyng 1975; Kovalev & Somov 2002; Aulanier et al. 2005; Karlicky & Barta 2007).

At the same time, observations reveal that sources of non-thermal radiation in many flares have different spectra and show different intensity variations (see e.g. Takakura et al. 1995; Emslie et al. 2003; Fletcher et al. 2007), which is hard to explain based on a single acceleration mechanism. It is, therefore, likely that particle acceleration is a multi-stage process with several mechanisms being dominant during different stages and/or at different locations (see e.g. de Jager 1986; Gordovskyy et al. 2005; Brown et al. 2009). Nevertheless, the super-Dreicer electric field is still widely considered as the mechanism responsible for acceleration of charged particles near the primary energy release site in the corona. This seems natural since magnetic reconnection is well established as the primary process of energy release in solar flares. At the same time, additional mechanisms, such as acceleration by plasma waves and shocks, may be dominant in the lower corona and chromosphere.

\begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg01.eps}\vspace*{2mm} \end{figure} Figure 1:

The model sketch ( left panel) and initial magnetic field and current density ( right panel).

Open with DEXTER

A basic model of acceleration by the electric field in CS was suggested by Speiser (1965). A number of authors (e.g. Martens & Young 1990; Litvinenko & Somov 1993; Litvinenko 1996) analytically studied particle acceleration by the electric field in CS and estimated energies gained by adiabatic and non-adiabatic particles. However, the analytical approach is limited to simple electric and magnetic field configurations, while numerical simulations are needed for more complex cases.

The majority of numerical studies use the test particle approach to the problem. For example, Sato et al. (1982) simulated particle trajectories in using numerical RCS model that allowed determination of the resulting particle energies and pitch angles. Kliem (1994) used the test-particle approach to study acceleration by fragmentary electric field in the reconnection region and shows that particles can be accelerated to near-relativistic energies within $\sim$10-2 s. Miller (1997) considered test-particle acceleration by the fast-mode wave and find that pitch angle scattering is essential for electron acceleration. A self-consistent approach combining analytically derived magnetic and electric field configurations with test-particle calculations was used by Browning & Vekstein (2001) to study particle motion in a 2D model and determine the resulting energy spectra. Zharkova & Gordovskyy (2004) considered particle orbits in simple non-neutral CS and show that, in the presence of a strong longitudinal magnetic field, electrons and protons may be ejected separately. Dalla & Browning (2006) investigated particle orbits around three-dimensional null-point and find that two populations of accelerated particles are produced: trapped particles remaining in the vicinity of the null-point and particles escaping the configuration in two symmetric jets along field lines near the spine. Hannah & Fletcher (2006) calculated full trajectories in a simple configuration with hyperbolic x-point and constant electric field and find that most particles are accelerated within few gyro-periods and also show that the presence of guiding field increases the number of accelerated particles.

Similarly, Petkaki & MacKinnon (2007) have studied test-particle trajectories in the vicinity of X-point but with an oscillating electric field. They found that in most cases the final energy spectra are bi-modal with protons and electrons accelerated up to $\sim$10 MeV and $\sim$1 MeV, respectively. However, the test particle approach has a number of limitations (see e.g. Wood & Neukirch 2005). The major one is that the effect of electric and magnetic fields produced by moving particles is ignored. This effect may be ignored if the number of accelerated particles remains much smaller than the total number of particles. However, if these numbers are comparable the induced fields should be taken into account.

Alternatively, particle motion can be studied using the particle-in-cell approach (see e.g. Birdsall & Langdon 1991). The main advantage of this method is self-consistent treatment of particles and fields. Thus, the PIC approach was used to investigate the acceleration of electrons in RCS by Drake et al. (2005). They show that density cavities occurring along separatrices support parallel electric fields accelerating plasma. Later, Tsiklauri & Haruki (2007) performed PIC simulations of magnetic reconnection near x-point. They show that a substantial amount of magnetic energy can be converted into heat and energy of non-thermal particles in the collisionless regime, thereby avoiding the uncertainty in resistivity required in classic MHD simulations. Siversky & Zharkova (2009) studied proton and electrons trajectories near CS midplane and find that a strong self-induced electric field may prevent protons and electrons from being ejected separately.

However, the PIC approach also has several serious limitations, such as a very small simulation region and difficulties in considering populations of particles with very different q/m ratios (see e.g. Siversky & Zharkova 2009). That is why the test particle approach is still vital, especially when considering large-scale models with an evolution time scale that is much longer than the Alfvén time.

In the present paper, we investigate how particle acceleration changes during the evolution of a reconnecting current sheet. For this purpose, we consider the model of forced reconnection (Hahm & Kulsrud 1985; Vekstein & Jain 1998; Jain et al. 2005) performing 2.5D MHD simulations of reconnection in initially stationary non-neutral Harris CS (Sect. 2). The electric and magnetic fields from the MHD simulations were used to calculate a large number of electron and proton trajectories in the guiding-centre approximation (GCA) (Northrop 1963). The obtained trajectories were then used to deduce the energy spectra of ejected particles and their ejection directions (Sect. 3). The results are summarised in Sect. 4.

The primary motivation of this paper is to explain the origin of high-energy particles in solar flares. However, the results have implications for other contexts where charged particles are accelerated by electric field associated with magnetic reconnection. These include, for example, the heliosheath, AGN jets, pulsar magnetospheres, etc. (e.g., de Gouveia Dal Pino & Lazarian 2000; Birk et al. 2001; Lazarian & Opher 2009).

2 MHD simulations of forced reconnection

The aim here is to perform MHD simulations of the magnetic field, electric current, and plasma velocity evolution arising in forced magnetic reconnection. The considered model represents a single reconnection event triggered by a transient external perturbation (Hahm & Kulsrud 1985). Such a perturbation, in the context of solar corona, might result from displacement of coronal loop footpoints, emergence of new magnetic flux or propagating coronal wave.

2.1 Problem formulation and main equations

Consider a 2.5D model where magnetic field $\vec{B}=\{B_x,B_y,B_z\}$, current density $\vec{j} = \{j_x,j_y,j_z\}$, velocity $\vec{v}=\{v_x,v_y,v_z\}$, density $\rho$, gas pressure p, and resistivity $\eta$ depend on two coordinates, x and y. The model is infinite and periodic in the x-direction (with the period lx) and bounded from the top and bottom (by y=-y1 and y=+y1) (Fig. 1).

Evolution of this model is considered using the standard set of resistive MHD equations (e.g. Priest 1982):

                              $\displaystyle \frac{\partial \rho}{\partial t}$ = $\displaystyle - \vec{\nabla} \cdot (\rho \vec{v})$ (1)
$\displaystyle \frac{\partial \vec{v}}{\partial t}$ = $\displaystyle - (\vec{v} \cdot \vec{\nabla}) \vec{v} - \frac 1{\rho} \vec{j} \times \vec{B} - \frac 1{\rho}\vec{\nabla}p$ (2)
$\displaystyle \frac{\partial w}{\partial t}$ = $\displaystyle - (\vec{v} \cdot \vec{\nabla})w - (\gamma-1)w\; \vec{\nabla} \cdot \vec{v} + \frac {\eta}{\rho} j^2$ (3)
$\displaystyle \frac{\partial \vec{B}}{\partial t}$ = $\displaystyle \vec{\nabla} \times [\vec{v} \times \vec{B}] - \vec{\nabla} \times (\eta \vec{j})$ (4)
$\displaystyle \vec{j}$ = $\displaystyle \frac 1{\mu_0} [\vec{\nabla} \times \vec{B}],$ (5)

where w is the specific internal energy density related to pressure and density as $p=(\gamma-1)\rho w$ and $\mu_0$ is the magnetic permeability. The electric field may be deduced as $\vec{E} = -\vec{v} \times \vec{B} + \eta \vec{j}$. In this model the effects of thermal conduction, radiation and viscosity are ignored; however, the numerical viscosity is added into the numerical code to regularise the solution (see Sect. 2.2 for method description).

Let us introduce characteristic length L0 (which is equal to the model half-width), density $\rho_0$, and magnetic field B0. Using these values the dimensionless coordinates can be defined as $X = x \; L_0^{-1}$ and $Y = y\; L_0^{-1}$ and dimensionless operator nabla as $\nabla^* = \nabla\; L_0$. The dimensionless velocity can be defined as $V = v\; v_{\rm A}^{-1}$ and time as $\tau = t\; t_{\rm A}^{-1}$, where $v_{\rm A}$ is the characteristic Alfvén velocity $v_{\rm A} = B_0/\sqrt{\mu_0 \rho_0}$ and $t_{\rm A}$ is the characteristic Alfvén time $t_{\rm A} = L_0 /v_{\rm A}$. The dimensionless density, pressure, and specific internal energy can be defined as $R = \rho\; \rho_0^{-1}$, $P = p\; \mu_0 B_0^{-2}$, and $W = w\; v_{\rm A}^{-2}$. The dimensionless magnetic and electric field are defined as $B^* = B\; B_0^{-1}$ and $E^* = E\; v_{\rm A}^{-1} B_0^{-1}$, and dimensionless current density is defined as $J = j \; \mu_0 L_0 B_0^{-1}$. Finally, the dimensionless resistivity can be introduced as the inverse local Lundquist number $S^{-1} = \eta \; \mu_0^{-1} L_0^{-1} v_{\rm A}^{-1}$.

The initial magnetic field configuration is a force-free Harris sheet defined as

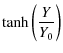
$\displaystyle B_x^*(\tau =0)$ = $\displaystyle \tanh \left(\frac Y{Y_0}\right)$ (6)
$\displaystyle B_y^*(\tau =0)$ = 0 (7)
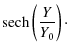
$\displaystyle B_z^*(\tau =0)$ = $\displaystyle \ensuremath{{\rm sech}}\left(\frac Y{Y_0}\right)\cdot$ (8)

As a result, the corresponding current density is
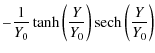
              $\displaystyle J_x(\tau =0)$ = $\displaystyle -\frac 1{Y_0} \tanh \left(\frac Y{Y_0}\right) \ensuremath{{\rm sech}}\left(\frac Y{Y_0}\right)$ (9)
$\displaystyle J_y(\tau =0)$ = 0 (10)
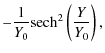
$\displaystyle J_z(\tau =0)$ = $\displaystyle -\frac 1{Y_0} \ensuremath{{\rm sech}} ^2 \left(\frac Y{Y_0}\right),$ (11)

where Y0 is the initial characteristic width of the current sheet (CS). The current density varies with Y as $J(\tau =0) = \frac 1{Y_0} \ensuremath{{\rm sech}}\left( \frac Y {Y_0} \right)$. Thus, the initial maximum current in the system is $J_{\max}(\tau =0) = \frac 1{Y_0}$ (see Fig. 1). The initial plasma density and pressure are uniform. Such a force-free magnetic field configuration is more relevant to the solar corona than the neutral Harris sheet, in which the magnetic forces are balanced by thermal pressure and the magnetic field vanishes near the CS mid-plane.

The resistivity in the model is defined as a step-like function:

             S-1 = $\displaystyle 0, \;\;\; J < J_{\rm cr},$  
S-1 = $\displaystyle S^{-1}_1, \;\;\; J \geq J_{\rm cr},$ (12)

i.e., the local resistivity is non-zero only if the local current density is greater than some critical value $J_{\rm cr}$. In all the simulations, this critical current is set to be slightly higher than the maximum current of the initial state ( $J_{\rm cr} = 1.02 J_{\max}(\tau =0)$), therefore the initial state of the system is a steady one. This approach may be regarded as modelling the reconnection triggered by current-dependent micro-instability. This also has the advantage of eliminating global resistive diffusion, which occurs when resistivity is uniform.

Furthermore, we consider forced magnetic reconnection (Hahm & Kulsrud 1985; Vekstein & Jain 1998; Jain et al. 2005), whereby the reconnection in the initially stable configuration is triggered by a transient spatially varying displacement of the top and bottom boundaries. This is done by applying plasma flow perpendicular to these boundaries and periodic in the x-direction during the time $\tau_{\rm p}$:

                Vy(y= -y1) = $\displaystyle \frac{\Delta}{\tau_{\rm p}} \cos \left( \frac{2\pi}{L_x} X \right) \left[1-\cos \left(\frac{2\pi}{\tau_{\rm p}} \tau \right) \right]$  
Vy(y= +y1) = $\displaystyle - \frac{\Delta}{\tau_{\rm p}} \cos \left( \frac{2\pi}{L_x} X \right) \left[1-\cos \left(\frac{2\pi}{\tau_{\rm p}} \tau \right) \right],$ (13)

while the two other components of velocity remain zero ( $V_{x,z}(y=\pm y_1)=0$). Here, Lx=lx/L0 is the period of boundary deformation in the x-direction (Fig. 1). The duration of the perturbing impulse is longer than the characteristic Alfvén time (i.e., $\tau_{\rm p} \gg 1$) so that the deformation is effectively quasi-static and the displacement amplitude is smaller than the model scale length (i.e., $\Delta \ll 1$).

At the end of the impulse ( $\tau =\tau_{\rm p} $), the magnetic field lines near the top and bottom boundaries are deformed as $\delta Y = \Delta \cos \left( \frac{2\pi}{L_x} X \right)$ and $\delta Y = -\Delta \cos \left( \frac{2\pi}{L_x} X \right)$, respectively, and the two boundaries become closed with all the three components of velocity and the component of current perpendicular to the boundaries (Jy) are set to zero. Therefore, after the perturbation impulse ends, the Poynting flux through these boundaries becomes zero.

2.2 Method of solution and adopted parameters

The set of Eqs. (1)-(5) is solved numerically using the Lare2d MHD code (Arber et al. 2001) in a 2D domain of size $4L_0 \times 2L_0$ with a uniform grid of $256\times128$ grid points. The initial conditions were set as $\vec{B^*} = [\tanh(Y/Y_0);0;\ensuremath{{\rm sech}} (Y/Y_0)]$, R=1, $W=7.5\times 10^{-3}$ (corresponding to the dimensionless pressure P=0.01; i.e., it is magnetically dominated plasma with $\beta = 0.01$). Periodic boundary conditions were applied to the left and right boundaries ( X= - Lx/2=-2 and X= + Lx/2= 2, respectively), while the conditions at the top and bottom boundaries ($Y= \pm 1$) were

    \begin{eqnarray*}&&\hspace*{-4mm}\frac{\partial B^*_x}{\partial Y}(Y=\pm 1) = \f... ...al W}{\partial Y}(Y=\pm 1) =0\\ &&\hspace*{-4mm}R(Y=\pm 1) = 1. \end{eqnarray*}


Physically, these conditions mean that there is no electric current or plasma motion at the top and bottom boundaries; i.e., it is the ``rigid wall'' boundary.

In the present study we performed several experiments for different initial CS thicknesses Y0 and resistivity S-11. In all the experiments, the horizontal period of boundary deformation was Lx=4. The duration of impulse was $\tau_{\rm p} =16$, and the amplitude of boundary deformation was $\Delta=0.1$. The initial CS characteristic width Y0 was set equal to 0.25, 0.32, or 0.40 (the corresponding critical current values $J_{\rm cr}$ were 4.1, 3.2, and 2.6, respectively). The resistivity S-11 was set to $1.0\times 10^{-4}$, $3.2\times 10^{-4}$, $1.0\times 10^{-3}$, or $3.2\times 10^{-3}$.

Finally, in order to reduce the numerical noise associated with high gradients, we used the shock viscosity (see Arber et al. 2001, and references therein). The advantage of this regularisation method over the uniform viscosity smoothing is that the shock viscosity only acts in the vicinity of high ${\vec{\nabla}} v$ so that the numerical dissipation is minimal. In all the experiments the plasma heating due to the numerical viscosity was at least a factor of 20 lower than plasma heating due to current dissipation.

2.3 Forced magnetic reconnection in Harris CS

Magnetic field, current density, and velocity field from one of the numerical experiments are shown in Fig. 2, while the magnetic, kinetic, and internal energies, and the maximum current versus time are plotted in Fig. 3. Using these plots one can distinguish two main characteristic stages of the CS evolution.

At first, as the boundary flow is applied ( $0 < \tau < \tau_{\rm p} $), the magnetic field is deformed, leading to the enhancement of current density to $J > J_{\rm cr}$in a region around the centre of the domain. During this time, both magnetic energy and total energy in the domain increase slightly (Fig. 3). This occurs because of the energy input of the boundary displacement and is expected from the analytical model of forced reconnection. This phase corresponds to the ``ideal'' equilibrium in the analytical models, which include tangential magnetic field discontinuity and infinite current at the resonant surface (Hahm & Kulsrud 1985; Vekstein & Jain 1998). As the result of the current density enhancement, the reconnection starts in the central region, forming a rather long and thin diffusion layer with plasma inflow in the vertical direction and outflow in the horizontal direction (Fig. 2b). Then, the horizontal size of the CS gradually decreases while plasma outflow becomes organised in four separatrix jets (Figs. 2c-e). These features are very similar to the standing shock waves in the Petschek reconnection model.

\begin{figure} \par\includegraphics[width=15.5cm,clip]{13569fg02.eps} \end{figure} Figure 2:

Evolution of the current sheet with the initial width Y0=0.25 and dimensionless resistivity $S^{-1}=3.2\times 10^{-4}$. Left panels show the magnetic field lines in x-y plane and the current density (greyscale). Right panels show the absolute magnitude of plasma velocity (greyscale) and flow direction (arrows). Panels a- g) correspond to the times t=0, $t=16t_{\rm A}$, $t=32t_{\rm A}$, $t=48t_{\rm A}$, $t=64t_{\rm A}$, $t=96t_{\rm A}$, and $t=160t_{\rm A}$, respectively. It should be noted that the colour scale for current density and velocity (shown on the left) changes between panels to enhance the contrast.

Open with DEXTER

During the reconnection near the X-point the magnetic energy $\mathcal{E}_{\rm m}$ quickly decreases because it is converted mostly into internal energy (Fig. 3). The rate at which the magnetic energy dissipates depends on the resistivity as ${\rm d}\mathcal{E}_{\rm m}/{\rm d}t \sim \eta_1^{-0.6}$ (see Fig. 5), which is in a good agreement with the analytical estimations (Hahm & Kulsrud 1985; Vekstein & Jain 1998).

As the field reconnects, magnetic islands start to form around o-points located at the left and right boundaries of the domain. This is already evident as early as the end of the boundary displacement impulse (Fig. 2b). As expected, the islands grow in size as the reconnection proceeds, reaching a size comparable to the width of the domain (2 L0) as the field relaxes to the final ``reconnected'' equilibrium. There is little change in the size of the islands after $\sim$ $100 t_{\rm A}$ (Figs. 2f, g).

Outflow from the reconnection region around the x-point results in the concentration of magnetic field and current around the magnetic islands (Figs. 2f, g). The current density in these regions is much lower than it was in the primary current sheet and it stays very close to the value of critical current $J_{\rm cr}$ (Fig. 3d). The reconnection rate is nearly zero, and the magnetic field topology and magnetic energy in the domain practically do not change during this stage.

Comparison of magnetic energy variation in different numerical experiments (Fig. 4) shows that the final energy in the system depends on the initial CS width Y0, hence on the critical current value $J_{\rm cr}$. Thus, the final magnetic energy in the initially wide CS Y0=0.4) is nearly the same as the initial magnetic energy. In the intermediate case of Y0=0.32, the magnetic energy drops by $\sim$$2{-}4 \%$, and in the case of initially thin CS (Y0=0.25), the magnetic energy in the final state is $\sim$$10\%$ lower than the initial magnetic energy.

It should be noted that these ratios are very model dependent. Indeed, this ratio of the released magnetic energy to the magnetic energy of the initial state will be lower for a larger numerical box. Nevertheless, this comparison reveals the important fact that the magnetic energy of the final state is hardly affected by the magnitude of resistivity S-11, which agrees with the analytical theory of forced reconnection. It also shows that the total energy release is greater for smaller initial CS thickness Y0. Considering that this parameter determines the maximum value of force-free parameter $\alpha$ in the model ( $\alpha_{\max} = 1/y_0$), one can conclude that our results are in good agreement with the previous analytical works (Vekstein & Jain 1998; Jain & Vekstein 1999) showing similar dependence.

\begin{figure} \par\includegraphics[width=16cm,clip]{13569fg03.eps} \vspace*{-2mm} \end{figure} Figure 3:

Magnetic, kinetic, internal energies, and maximum current density versus time for the model shown in Fig. 2. The dashed line in the lower right panel denotes the critical current value. The magnetic, kinetic, and internal energies (panels a- c), respectively) are non-dimensionalised with respect to $\mu _0^{-1} B_0^2 L_0^2$, and the current density (panel d) with respect to $\mu _0^{-1} B_0 L_0^{-1}$; time is measured in terms of $t_{\rm A}$ (see Sect. 2.1).

Open with DEXTER

\begin{figure} \par\includegraphics[width=16cm,clip]{13569fg04.eps} \vspace*{-2mm} \end{figure} Figure 4:

Variation of magnetic energy with time for different initial CS widths and different model resistivity's. Solid, dashed and dot-dashed lines are for Y0=0.40, 0.32 and 0.25, respectively. Panels a-d) are for the dimensionless resistivity S-1=10-4, $3.2\times 10^{-4}$, $1.02\times 10^{-3}$, and $3.2\times 10^{-3}$, respectively. The magnetic energy is nondimensionalised with respect to $\mu _0^{-1} B_0^2 L_0^2$; time is measured in terms of $t_{\rm A}$ (see Sect. 2.1).

Open with DEXTER

3 Particle motion in guiding centre approximation

3.1 Main equations

We assume that particle acceleration time in the present model is shorter than the characteristic time of MHD system evolution ($\sim$ $10 t_{\rm A}$); therefore, test particle trajectories may be calculated using quasi-static approach in which magnetic and electric time do not change with time. The validity of this assumption can be checked a posteriori.

The adopted characteristic scale length in our MHD model is L0=104 m; therefore, the width of the CS (in x-direction) during the fast magnetic energy release is $\sim$104 m, while its thickness (in y-direction) is about 102-103 m. The characteristic magnetic field is set to B0=10-2 T, and the characteristic plasma density is $\rho_0 = 4\times 10^{-11}$ kg m-3 (corresponding to the particle density of $n = 2.4\times 10^{10}$ cm-3). These magnitudes are close to those normally accepted in magnetic reconnection models and other models concerning the solar corona. These basic values allow us to calculate other characteristic quantities in the model. Thus, the characteristic Alfvén speed is $v_{\rm A}=1.4\times 10^6$ m s-1, the Alfvén time is $t_{\rm A}=7.1\times 10^{-3}$ s, and characteristic electric field $E_0 = v_{\rm A} B_0 = 1.4\times 10^4$ V m-1. Finally, the characteristic plasma temperature is $T_0 = 1.2\times 10^8$ K (assuming that the average particle mass is $\mu_{\rm m} = 0.5 m_{\rm p}$, as in fully ionised pure hydrogen plasma); i.e., the initial temperature in the MHD simulations in Sect. 2 was $\sim$0.6 MK.

Now let us consider proton and electron gyro-periods ( $\mathcal{T} = \frac{2\pi m}{qB}$) and gyro-radii ( $R_{\rm g} = \frac{mv}{qB}$). This is done in Table 1 for different particle energies and magnetic fields. It can be seen that for all the considered magnetic field and particle energy values, the proton and electron gyro-radii are much smaller than the model scale length, and the particle gyro-periods are much shorter than the model characteristic Alfvén time. Therefore, the proton and electron motion in the present model can be considered in the guiding centre (GC) approximation. This approach has previously been used to study particle acceleration in RCS by many authors (see e.g. Browning & Vekstein 2001; Wood & Neukirch 2005; Giuliani et al. 2005). It is important to note that the present adiabatic approach is valid because we consider non-neutral RCS; i.e., the magnetic field is non-zero everywhere. Non-adiabatic effects, such as particle motion in the vicinity of the magnetic null-point (e.g. Dalla & Browning 2006) or in a very thin CS (e.g. Zharkova & Gordovskyy 2004) can make a substantial difference for particle acceleration, especially for protons and heavier ions.

Particle motion in the GC approximation in stationary electric and magnetic fields is governed by the following set of equations (e.g. Northrop 1963):

                                    $\displaystyle \frac{{\rm d} \vec{r}}{{\rm d}t}$ = $\displaystyle \vec{u} + v_{\vert\vert} \vec{b}$ (14)
$\displaystyle \vec{u}$ = $\displaystyle \vec{u}_E + \frac mq \frac {v^2_{\vert\vert}}B [\vec{b} \times (\... ...t\vec{\nabla})\vec{b}] + \frac mq \frac \mu B [\vec{b} \times (\vec{\nabla} B)]$  
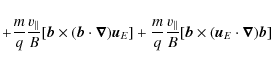
    $\displaystyle +\frac mq \frac {v_{\vert\vert}}B [\vec{b} \times (\vec{b}\cdot \...  
    $\displaystyle +\frac mq \frac 1B [\vec{b} \times (\vec{u}_E\cdot \vec{\nabla})\vec{u}_E]$ (15)
$\displaystyle \frac{{\rm d} v_{\vert\vert}}{{\rm d}t}$ = $\displaystyle \frac qm \vec{E}\cdot \vec{b} - \mu (\vec{b} \cdot \vec{\nabla}B)+ v_{\vert\vert} \vec{u}_E\cdot ((\vec{b}\cdot\vec{\nabla})\vec{b})$  
    $\displaystyle + \vec{u}_E\cdot ((\vec{u}_E\cdot\vec{\nabla})\vec{b})$ (16)
$\displaystyle \frac{{\rm d}\mu }{{\rm d}t}$ = 0. (17)

Here $\vec{r}$, $\vec{u}$, and v|| are the particle gyro-centre position, drift velocity across the field lines, and velocity along the field lines, respectively; $\vec{b}=\frac{\vec{B}}B$ is the magnetic field direction vector; $\vec{u}_E = \frac {\vec{E}\times\vec{b}}{B}$ is the drift velocity perpendicular to electric and magnetic fields ($E\times B$ drift). Finally, $\mu$ is the magnetic moment per mass unit $\mu = \frac{u_{\rm g}^2}{2B}$, where $u_{\rm g}$ is the particle gyration velocity.

\begin{figure} \par\includegraphics[width=6cm,clip]{13569fg05.eps} \end{figure} Figure 5:

Relation between the magnetic dissipation rate during the reconnection around x-point and resistivity S-1. Solid squares are for the model with initial characteristic CS thickness Y0 = 0.32, open circles are for Y0=0.25. Power-law approximation (dashed lines) gives the power-law index 0.65 for the first case and 0.61 for the second case.

Open with DEXTER

Table 1:   Proton and electron gyro-periods and gyro-radii.

3.2 Method of solution

When solving the set of Eqs. (14)-(17), the same scaling is used as in the MHD model (Sect. 2). The dimensionless magnetic moment is introduced as $M=\mu B_0 v_{\rm A}^{-2}$, while the dimensionless full drift velocity and $E\times B$ drift velocity are introduced as $\vec{U} = \vec{u} v_{\rm A}^{-1}$ and $\vec{U}_E = \vec{u}_E v_{\rm A}^{-1}$, respectively. Finally, the particle mass-to-charge ratio is expressed using the parameter $\epsilon = \frac mq v_{\rm A} L_0^{-1} B_0^{-1}$. Effectively, this parameter is of the same order of magnitude as the ratio of the particle characteristic gyro-period to the characteristic Alfvén time ( $\mathcal{T}/t_{\rm A} = 2\pi \epsilon$) or the ratio of the particle characteristic gyro-radius (the gyro-radius of particle with $v_{\rm g} = v_{\rm A}$) to the model scale length. Therefore, this value has to be much lower than 1, otherwise the GC approximation becomes invalid. In the present model, the parameter $\epsilon$ is $1.47\times 10^{-4}$ for protons and $-8.02\times 10^{-8}$ for electrons.

The set of Eqs. (22-24) is solved using a numerical code (the GCA code) based on the second-order Runge-Kutta (predictor-corrector) scheme. As an input the GCA code takes series of snapshots from the MHD simulations with the Lare2d code. Each snapshot contains electric and magnetic fields and their spatial derivatives defined on the same grid as in MHD simulations for a given time instant.

Since the GCA code requires electric field, magnetic field, and their derivatives to be defined at any location, it uses simple linear 2D interpolation as follows. Given a function f defined on a 2D discrete grid (x(i),y(j)) and some position $(x_{\rm p},y_{\rm p})$ with $x_i < x_{\rm p} < x_{i+1}$ and $y_j < y_{\rm p} < y_{j+1}$, we then define the value of function f at $(x_{\rm p},y_{\rm p})$ as

                       $\displaystyle f(x_{\rm p},y_{\rm p})$ = (1-sx)(1-sy)fi,j + sx (1- sy) fi+1,j  
    +(1-sx) sy fi,j+1 + sx sy fi+1,j+1, (18)

where $s_x=\frac{x_{\rm p}-x_i}{x_{i+1}-x_i}$ and $s_y=\frac{y_{\rm p}-y_j}{y_{j+1}-y_j}$.

Approximately 105 test particle trajectories are calculated for every considered MHD snapshot for both protons and electrons. The initial positions of test particles are uniformly distributed within the phase space: 32 positions along the x-axis, 16 positions along the y-axis, 32 positions for initial particle velocity V (from $0.2 V_{\rm th}$ to $6.4 V_{\rm th}$, where $V_{\rm th} = \sqrt{2 k_{\rm B} T_0/m_{\rm p/e}}/v_{\rm A}$), and 8 for pitch angle V||/V (from -1 to 1).

Each test particle assigned with the statistical weight $\chi$ depending on the initial velocity as $\chi = V^2 \exp(-V^2/V_{\rm th}^2)$). This weight is taken into account when calculating the energy spectra. Therefore, the initial velocity distribution is a Maxwellian corresponding to the characteristic temperature T0. The trajectory calculation is run until a test particle crosses one of the four domain boundaries ( $X = \pm l_x/2$, $Y= \pm 1$). If a particle remains in the domain for $10 t_{\rm A}$, it is assumed to be ``frozen'' and calculation ends.

It should be noticed that, in contrast to the MHD model in Sect. 2, the simulation domain for particle trajectories is not treated as periodic in the x-direction; i.e., a particle crossing the $X = \pm L_x/2$ boundaries is considered to be ejected. Physically, this means that we study what energy is gained by particle by one CS in the periodic structure. (Very recently we performed several experiments with particles moving in the periodic domain. We will discuss these results in a forthcoming paper.)

\begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg06.eps} \end{figure} Figure 6:

Trajectories of protons starting with thermal velocities $v_{\rm ini} = 0.1 v_{\rm A}$ from six locations uniformly distributed along the Y=-0.4;Z=0 line. The left panel is for protons starting with large magnetic moments ( $v_{\vert\vert}=0.1 v_{\rm ini}$) and the right panel is for protons starting with small magnetic moments ( $v_{\vert\vert}=0.8 v_{\rm ini}$). The magnetic and electric fields are taken from the model with Y0=0.25 and S-11 = 10-3 at $t=32t_{\rm A}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg07.eps} \end{figure} Figure 7:

Trajectories of electrons starting with thermal velocities $v_{\rm ini} = 3.9 v_{\rm A}$. All other parameters are the same as in Fig. 6.

Open with DEXTER

\begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg08.eps} \vspace*{1.75mm} \end{figure} Figure 8:

Trajectories of protons starting with thermal velocities $v_{\rm ini} = 0.1 v_{\rm A}$. The snapshot is taken at $t=96t_{\rm A}$. All other parameters are the same as in Fig. 6.

Open with DEXTER
\begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg09.eps} \end{figure} Figure 9:

The same as in Fig. 8 but for electrons starting with thermal velocities $3.9 v_{\rm A}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=15cm,clip]{13569fg10.eps} \end{figure} Figure 10:

The electron ( left panels) and proton ( middle panels) energy spectra for the model with initial CS width Y0 = 0.4 and dimensionless resistivity $S^{-1}_1 = 3.2 \times 10^{-4}$for different stages of the RCS evolution. The solid lines show the spectra of particles leaving the system, dashed lines show the spectra of remaining particles. Note that the colour scale for the current density (shown on the right) changes between panels to enhance the contrast. Upper panels correspond to the time $t=16t_{\rm A}$ while lower panels correspond to $t=128t_{\rm A}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=15cm]{13569fg11.eps} \end{figure} Figure 11:

The energy spectra for the model with Y0=0.25 and $S^{-1}_1 = 3.2 \times 10^{-4}$. All other parameters are the same as in Fig. 10. Upper panels correspond to the time $t=16t_{\rm A}$, while lower panels correspond to $t=128t_{\rm A}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=15cm]{13569fg12.eps} \end{figure} Figure 12:

The energy spectra for the model with Y0=0.25 and $S^{-1}_1 = 3.0 \times 10^{-3}$. All other parameters are the same as in Fig. 10. Upper panels correspond to the time $t=8t_{\rm A}$, while lower panels correspond to $t=32t_{\rm A}$.

Open with DEXTER

3.3 Particle trajectories

Figures 6, 7 show typical trajectories of particles injected from different positions along the x-axis with thermal velocities from outside the magnetic diffusion region ( $Y_{\rm ini} = -0.4$) during the X-point reconnection stage, while Figs. 8, 9 show trajectories of particles injected with the same initial characteristics during the O-point stage of the CS evolution.

In general, the trajectories obtained in the present study are in good agreement with previous, similar works (see e.g. Wood & Neukirch 2005). It can be seen that particle trajectories mostly follow the magnetic field lines, while $E\times B$ drift and other drifts can be considered as the secondary effects.

The significant exception are particles moving in the X-point configuration (Figs. 6, 7) in the inflow area (below the centre of the domain) where the strong plasma velocity gives rise to a $\vec{v} \times \vec{B}$ electric field, which, in turn, leads to $E\times B$ drift in the y-direction. As a result, protons that have quite low thermal velocities of $\sim$ $0.1 v_{\rm A}$ move across the field lines (Figs. 6a, b) and the high-$\mu$ electrons (Fig. 7a) (thermal velocities $\sim$ $4 v_{\rm A}$) also show noticeable drift in the y-direction. Another significant case of $E\times B$ drift can be observed in large-$\mu$ protons moving around the O-points (Fig. 8a). They are oscillating along the field lines, while slightly moving towards the centre of the domain (in the inflow region) or towards the centre of the o-points (in the outflow region). In all cases, the $E\times B$ drift represents the bulk plasma motion: inflow in the y-direction into the diffusion region in the case of X-point (see velocity panels in Figs. 2d, e) and outflow in the x-direction in the case of O-point.

Comparison of trajectories corresponding to high-$\mu$ particles (i.e. with the large pitch angles $v_{\rm g}/v_{\vert\vert}$, left panels in Figs. 7-9) and to those with small magnetic moments (small pitch angles, right panels in Figs. 7-9) shows that particles with large magnetic moments undergo some mirroring. Thus, the electrons with large magnetic moments oscillate along the field lines in the inflow region (Fig. 7a), and both protons and electrons with large pitch angles (Figs. 8a and 9a) oscillate along the field lines both in the inflow and outflow regions in o-point configuration. This occurs because the particles with low parallel velocity are more affected by the field convergence. This effect is not apparent in protons in the X-point configuration (Fig. 6) since their parallel velocities ( $\vec{v}\cdot \vec{b})$ are lower than the $E\times B$ drift velocity; however, note that the change in magnetic moment (pitch angle) between the left and righthand panels still noticeably affects some trajectories.

The majority of particles leave the domain with energies close to their initial energies. Only a tiny fraction of particles manage to get close to the diffusion region near the centre of the domain or close to one of the separatrix jets where strong parallel electric field accelerates them to the velocities $\sim$10-103 higher than the initial thermal velocity.

It is found that the acceleration time for electrons is approximately $0.1t_{\rm A}$, while it is about $1t_{\rm A}$ for protons. Both values are substantially lower than the characteristic evolution time in the MHD model $\sim$ $10 t_{\rm A}$. Therefore, the quasistatic approach used in particle trajectory simulations is valid.

3.4 Particle energy spectra

The particle kinetic energy is calculated as

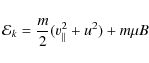
\begin{displaymath}\mathcal{E}_{k} = \frac m2 (v_{\vert\vert}^2+u^2) + m\mu B \end{displaymath} (19)

where v|| is the particle parallel velocity, and u is particle drift velocity (though, for high-energy particles outside the diffusion region, the kinetic energy of parallel motion is dominant, $\frac m2 v_{\vert\vert}^2 \gg \frac m2 u^2$ and $\frac m2 v_{\vert\vert}^2 \gg m\mu B$). The final energy spectra of test particles at the end of each time ``snapshot'' calculated taking into account their statistic weight $\chi$ are shown in Figs. 9-11 both for particles ejected from the domain and those remaining.

The proton and electron spectra appear very similar during the whole evolution of MHD system, which can be easily explained. Indeed, when acceleration occurs in a region with a size comparable to particle gyro-radius, the non-adiabatic effects play a significant role, particle behaviour depends strongly on particle mass, and proton and electron trajectories are completely different (see e.g. Zharkova & Gordovskyy 2004). However, when the scales of magnetic and electric field variations are much larger than particle gyroradii (which is the case in the present study), the non-adiabatic effects may be ignored, and protons and electrons behave rather similarly. Litvinenko (1996) estimated the energy gained by electrons in CS with a strong longitudinal magnetic field as $\mathcal{E} \approx eaE B_{\vert\vert}/B_{\bot}$, where a is the CS thickness, B|| is the longitudinal magnetic field (Bz in our model CS) and $B_{\bot}$ is the transversal magnetic field (By in our model). This energy does not depend on the particle mass; therefore, once protons are ``adiabatic'' (i.e. their gyro-radii are much smaller than the field's scale length), their energies are approximately the same as for electrons. The small noticeable difference is most likely due to the difference in the initial thermal velocities, which are comparable to the drift velocity uE for protons and much higher than uE for electrons (see discussion in Vekstein & Browning 1997; Browning & Vekstein 2001).

\begin{figure} \par\includegraphics[width=15cm]{13569fg13.eps} \end{figure} Figure 13:

Integrated energy spectra of protons leaving the simulation domain compared with the initial thermal spectrum (solid line). The dashed lines are for resistivity $S^{-1}_1 = 3.2 \times 10^{-4}$ and dot-dot-dashed lines for $S^{-1}_1 = 1.0\times 10^{-3}$. Panel a) is for the initial CS thickness Y0 = 0.40 and panel  b) is for Y0=0.25.

Open with DEXTER

\begin{figure} \par\includegraphics[width=15cm]{13569fg14.eps} \end{figure} Figure 14:

The same as in Fig. 13 but for electrons.

Open with DEXTER

It can be seen that substantial acceleration of particles occurs mostly during the X-point reconnection stage when the parallel electric field is very strong. During this stage the spectra are a combination of thermal distribution with high-energy, nearly power-law tails ( $N \sim \mathcal{E}^{-\gamma}$). The spectral indices measured near $\mathcal{E}=100$ keV are very low (i.e., the spectra are very hard), $\gamma$ is between 1.0 and 1.5.

Maximum energies in the final energy spectra mostly depend on the electric field, which, in turn, depends mostly on the resistivity in the system. Thus, when the dimensionless resistivity is S-11 = 10-4, protons and electrons are accelerated up to the energies $\sim$1-3 MeV. In the case of intermediate resistivity $S^{-1}_1 = 3.2 \times 10^{-4}$ the maximum energies are $\sim$5-10 MeV, and in the case of strong resistivity S-11 = 10-3 the maximum energies reach $\sim$20-30 MeV.

During the O-point stage, the energies are much lower. Thus, particles are accelerated to energies $\sim$50-200 keV, and at least the electrons accelerated during this stage will be observable owing to the hard X-ray emission. The high-energy parts of spectra at this stage are softer than those during the X-point stage, and spectral indices $\gamma$ measured near $\mathcal{E}=100$ keV are $\gamma=$1.5-3.0.

The number of particles accelerated to high energies is larger during the early stages of reconnection, and then this number gradually decreases. Thus, the fraction of electrons and protons accelerated to the energies >10 keV during the early evolution of MHD system is approximately 10$\%$ (of total number of particles) reaching up to 25$\%$. During the O-point stage this number reduces to $3{-}5\%$.

It should be noted that some of the particles remaining in the domain longer than $10 t_{\rm A}$ and considered as ``frozen'' may eventually leave the domain. However, since the energy spectrum of ``frozen'' particles is similar to those of ejected ones, this should not lead to substantial change in the energy spectra of ejected particles. The quoted energies strongly depend on the adopted scaling parameters (Sect. 2.2). Furthermore, in the case of power-law energy distribution, the maximum energy also strongly depends on the number of test particles used in simulations. As a result, the maximum proton and electron energies shown above should be taken with caution. Finally, the proportion of ejected particles should depend on the size of the simulation domain (taking the uniform distribution of test particle initial positions into account); i.e., increase in size of the simulation domain will lead to a lower portion of particles accelerated to high energies.

\begin{figure} \par\includegraphics[width=15cm,clip]{13569fg15.eps} \vspace*{2.5mm} \end{figure} Figure 15:

The number density ( left panels) and average energy ( right panels) for protons at their final positions in the model with Y0=0.25 and $S^{-1}=3.2\times 10^{-4}$ during different stages of the RCS evolution. Corresponding times are shown in the graph. Upper panels correspond to the time $t=8t_{\rm A}$, while lower panels correspond to $t=128t_{\rm A}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=15cm,clip]{13569fg16.eps} \end{figure} Figure 16:

The same as in Fig. 15 but for electrons.

Open with DEXTER

The MHD configuration considered in Sect. 2 relaxes to its final state in $\sim$100 $t_{\rm A}$time, which, taking the scaling introduced in Sect. 3.1 into account, corresponds to $\sim$1 s. This time is comparable to the time necessary for high-energy particles to reach the solar chromosphere in order to produce hard X-ray and, possibly, $\gamma$-ray emission. Therefore, it may be possible that the energy spectra deduced from the observed non-thermal radiation are instead associated with the cumulative spectra of energy particles, i.e., energy spectra of all electrons or protons accelerated during the current sheet evolution.

Let us consider the cumulative spectra obtained from our simulations by adding all the ejected protons or electrons from t=0 to $t=256 t_{\rm A}$ (Figs. 13 and 14). It can be seen that the cumulative spectra are similar to the instantaneous spectra shown in Figs. 10-12: the high-energy (>1 keV) part is the power-law tail of the initial thermal distribution. The maximum energy varies from $\sim$1 MeV for lower resistivity to $\sim$10 MeV for higher resistivity. Similar to the instantaneous spectra, the cumulative spectra are quite hard: the spectral indices vary slightly around the 1.5 value. Another interesting feature that can be seen on the cumulative spectra is the small gap at 1-10 keV between ``thermal'' bumps and power-law, high-energy parts. In principle, this gap might be responsible for the broken power-law shapes often observed in hard X-ray spectra at similar energies (Kontar et al. 2002). On the other hand, it is known that this distribution of particles with positive dN/dE is unstable, and the spectrum should get flat because of the wave-particle interaction well before the particles reach dense layers of the solar atmosphere.

3.5 Geometry of particle ejection from the CS

Figures 15, 16 show the distributions of number density and average energy for the test particles at their final positions (with the test particle statistical weights $\chi$ taken into account) for one typical model. The highest values are observed near the left and right boundaries of the domain representing leaving particles. Comparison of particle distributions with magnetic field and flow pattern shows that the leaving particle concentrations near the boundaries correspond to the locations where the separatrices cross the domain boundaries; i.e., most of particles leaving the domain move along (or with) the separatrix jets.

However, it is interesting to note the asymmetry of particle ejection. Thus, Fig. 15 shows that high-energy protons leaving the domain through the left boundary are ejected predominantly at y >0, while there are virtually no high-energy protons at the corresponding location in y < 0 semi-space. At the same time, protons leaving through the right boundary are ejected mostly in y<0 semi-space.

High-energy electrons (Fig. 16) are also ejected asymmetrically, similar to the protons. However, those electrons leaving through the left boundary are predominantly ejected into y <0 semi-space, while electrons leaving through the right boundary are mostly ejected in y >0 semi-space.

This finding is very similar to the results by Zharkova & Gordovskyy (2004) who showed the asymmetry of proton and electron ejection in the presence of guiding field using the full trajectory calculations. The effect of proton and electron separation can be explained easily. Indeed, particles are accelerated by the parallel electric field $(\vec{E}\cdot\vec{b})$. Since bx changes its sign at y=0, the value of $(\vec{E}\cdot\vec{b})$ would have opposite signs in y >0 and y<0 semi-spaces. Therefore, x components of particle velocities in y>0 and y<0 would be opposite as well, as observed in the experiments.

4 Conclusions

We considered forced reconnection using 2D3V MHD simulations. In this model the initially stationary force-free Harris sheet is perturbed by external boundary deformation. This eventually leads to the reconnection near the X-point and creation of magnetic islands, which is in good agreement with previous analytical models (Hahm & Kulsrud 1985; Vekstein & Jain 1998) and numerical simulations (Jain et al. 2005).

Series of magnetic and electric field ``snapshots'' from the MHD simulations were used to calculate particle trajectories in the guiding centre approximation. Based on the obtained trajectories, proton and electron energy spectra were deduced for various stages of CS evolution for different sets of model parameters. It was found that majority of particles leave the domain with initial thermal energies while a few particles reach the diffusion region near the x-point and leave the simulation domain with energies much higher than initially. Both protons and electrons were found to be accelerated to the energies $\sim$107 eV. The characteristic acceleration time is $\sim$ $0.1t_{\rm A}$ for electrons and $\sim$ $1t_{\rm A}$ for protons.

The number of accelerated particles strongly varies during the RCS evolution. The most effective acceleration is during the X-point stage when $\sim$$10\%$ of test particles are accelerated. Since only a minority of particles are accelerated, the test-particle approach is, therefore, valid in the present study.

The resulting energy spectra of ejected particles are superpositions of the initial Maxwellian one and high-energy power-law part. The spectral indices of power-law part $\gamma$ vary with time. During the reconnection near x-point the spectra are very hard with $\gamma \approx 1.0{-}1.5$ becoming softer ( $\gamma \approx 2.0{-}2.5$) when particles are accelerated by the weak current formed around the magnetic islands.

Similar to papers by Zhu & Parks (1993) and Zharkova & Gordovskyy (2004), protons and electrons are found to be ejected into different directions, depending on the direction of the guiding field Bz. This potentially can lead to a separation of electrons and ions in the current sheet, which in turn may contribute to the asymmetry of hard X-ray sources observed in flares.

It should be noted that the acceleration model considered in the present work alone is not sufficient to explain the wide variety of observational features related to high-energy particles, especially in major solar flares. Most likely, particles are accelerated by a combination of different mechanisms that dominate in different locations and/or during different stages of the flare.

Acknowledgements
We are grateful to Tony Arber and Chris Brady for providing the Lare2d code and helpful discussion. This work is supported by the Science and Technology Facilities Council (UK), grant ST/F003064/1.

References

  1. Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, M. 2001, J. Comp. Phys., 171, 151 [Google Scholar]
  2. Aulanier, G., Pariat, E., & Demoulin, P. 2005, A&A, 444, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Aschwanden, M. J. 2002, Space Sci. Rev., 101, 1 [NASA ADS] [CrossRef] [Google Scholar]
  4. Benz, A. O. 2008, Living Rev. Sol. Phys., 5, 1 [Google Scholar]
  5. Bian, N., & Browning, P. K. 2008, ApJ, 687, L111 [NASA ADS] [CrossRef] [Google Scholar]
  6. Birdsall, C. K., & Langdon, A. B. 1991, Plasma Physics via Computer simulations (IOP Publishing) [Google Scholar]
  7. Birk, G. T., Crusius-Watzel, A. R., & Lesch, H. 2001, ApJ, 559, 96 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brown, J. C., & Hoyng, P. 1975, ApJ, 200, 734 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brown, J. C., Turkmani, R., Kontar, E. P., MacKinnon, A. L., & Vlahos, L. 2009, A&A, 508, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Browning, P. K., & Vekstein, G. E. 2001, JGR, 106, 18677 [Google Scholar]
  11. Dalla, S., & Browning, P. K. 2006, ApJ, 640, L99 [NASA ADS] [CrossRef] [Google Scholar]
  12. Decker, R. B., & Vlahos, L. 1986, ApJ, 306, 710 [NASA ADS] [CrossRef] [Google Scholar]
  13. Drake, J. F., Shay, M. A., Thongthai, W., & Swisdak, M. 2005, Phys. Rev. Lett., 94, 095001 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Emslie, A. G., Kontar, E. P., Krucker S., & Lin, R. P. 2003, ApJ, 595, L107 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fletcher, L., Hannah, I. G., Hudson, H. S., & Metcalf, T. R. 2007, ApJ, 656, 1187 [NASA ADS] [CrossRef] [Google Scholar]
  16. Giuliani, P., Neukirch, T., & Wood, P. 2005, ApJ, 635, 636 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gordovskyy, M., Zharkova, V. V., Voitenko, Yu. M., & Goosens, M. 2005, Adv. Space Sci., 35, 1743 [Google Scholar]
  18. de Gouveia Dal Pino, E. M., & Lazarian, A. 2000, ApJ, 536, L31 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  19. Hahm, T. S., & Kulsrud, R. M. 1985, Phys. Fluids, 28, 2412 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hannah, I., & Fletcher, L. 2006, Sol. Phys., 236, 59 [NASA ADS] [CrossRef] [Google Scholar]
  21. Heerikhuisen, J., Litvinenko, Yu. E., & Craig, I. J. D. 2002, ApJ, 566, 512 [NASA ADS] [CrossRef] [Google Scholar]
  22. de Jager, C. 1986, Space Sci. Rev., 44, 43 [NASA ADS] [Google Scholar]
  23. Jain, R., Browning, P. K., & Kusano, K. 2005, Phys. Plasm., 12, 012904 [Google Scholar]
  24. Jain, R., & Vekstein, G. E. 1999, Ap&SS, 264, 113 [NASA ADS] [CrossRef] [Google Scholar]
  25. Karlicky, M., & Barta, M. 2007, Adv. Space Res., 39, 1427 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kliem, B. 1994, ApJS, 90, 719 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kovalev, V. A., & Somov, B. V. 2002, Astr. Lett., 28, 488 [Google Scholar]
  28. Kress, B. T., Hudson, M. K., Looper, M. D., Lyon, J. G., & Goodrich, C. C. 2008, JASTP, 70, 1727 [NASA ADS] [Google Scholar]
  29. Lazarian, A., & Opher, M. 2009, ApJ, 703, 8 [NASA ADS] [CrossRef] [Google Scholar]
  30. Lin, R. P. 2008, AIP Conf. Proc., 1039, 52 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lin, R. P., & Hudson, H. S. 1976, Sol. Phys., 50, 153 [NASA ADS] [CrossRef] [Google Scholar]
  32. Litvinenko, Yu. E. 1996, ApJ, 462, 997 [NASA ADS] [CrossRef] [Google Scholar]
  33. Litvinenko, Yu. E., & Somov, B. V. 1993, Sol. Phys., 146, 127 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mandzhavidze, N., & Ramaty, R. 1993, Nuclear Phys. B, 33A, 141 [Google Scholar]
  35. Martens, P. C. H., & Young, A. 1990, ApJS, 73, 333 [NASA ADS] [CrossRef] [Google Scholar]
  36. Miller, J. A. 1997, ApJ, 491, 939 [NASA ADS] [CrossRef] [Google Scholar]
  37. Miller, J. A., & Roberts, D. A. 1995, ApJ, 452, 912 [NASA ADS] [CrossRef] [Google Scholar]
  38. Miller, J. A., Larosa, T. N., & Moore, R. L. 1996, ApJ, 461, 445 [NASA ADS] [CrossRef] [Google Scholar]
  39. Miteva, R., & Mann, G. 2007, A&A, 474, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Northrop, T. 1963, The Adiabatic Motion of Charged Particles (Interscience) [Google Scholar]
  41. Petkaki, P. & MacKinnon, A. L. 2007, A&A, 472, 623 [Google Scholar]
  42. Priest, E. R. 1982, Solar Magnetohydrodynamics (D. Reidel) [Google Scholar]
  43. Pryadko, J. M., & Petrosian, V. 1997, ApJ, 482, 774 [NASA ADS] [CrossRef] [Google Scholar]
  44. Sato, T., Matsumoto, H., & Nagai, K. 1982, JGR, 87, 6089 [Google Scholar]
  45. Siversky, T. V., & Zharkova, V. V. 2009, J. Plasma Phys., 75, 619 [NASA ADS] [CrossRef] [Google Scholar]
  46. Smith, D. F. 1977, ApJ, 217, 644 [NASA ADS] [CrossRef] [Google Scholar]
  47. Smith, D. F. 1980, Sol. Phys., 66, 135 [NASA ADS] [CrossRef] [Google Scholar]
  48. Speiser, T. W. 1965, JGR, 70, 4219 [Google Scholar]
  49. Takakura, T., Kosugi, T., Sakao, T., et al. 1995, PASJ, 47, 355 [NASA ADS] [Google Scholar]
  50. Tsiklauri, D., & Haruki, T. 2007, Phys. Plasm., 14, 112905 [Google Scholar]
  51. Turkmani, R., Vlahos, L., Galsgaard, K., Cargill, P. J., & Isliker, H. 2005, ApJ, 620, L59 [NASA ADS] [CrossRef] [Google Scholar]
  52. Vekstein, G. E., & Browning, P. K. 1997, Phys. Plasm., 4, 2261 [Google Scholar]
  53. Vekstein, G. E., & Jain, R. 1998, Phys. Plasm., 5, 1506 [Google Scholar]
  54. Vlahos, L., Isliker, H., & Lepreti, F. 2004, ApJ, 608, 540 [NASA ADS] [CrossRef] [Google Scholar]
  55. Wood, P., & Neukirch, T. 2005, Sol. Phys., 226, 73 [NASA ADS] [CrossRef] [Google Scholar]
  56. Zharkova, V. V., & Gordovskyy, M. 2004, ApJ, 604, 884 [NASA ADS] [CrossRef] [Google Scholar]
  57. Zhu, Z., & Parks, G. 1993, JGR, 98, 7603 [Google Scholar]

All Tables

Table 1:   Proton and electron gyro-periods and gyro-radii.

All Figures

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg01.eps}\vspace*{2mm} \end{figure} Figure 1:

The model sketch ( left panel) and initial magnetic field and current density ( right panel).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.5cm,clip]{13569fg02.eps} \end{figure} Figure 2:

Evolution of the current sheet with the initial width Y0=0.25 and dimensionless resistivity $S^{-1}=3.2\times 10^{-4}$. Left panels show the magnetic field lines in x-y plane and the current density (greyscale). Right panels show the absolute magnitude of plasma velocity (greyscale) and flow direction (arrows). Panels a- g) correspond to the times t=0, $t=16t_{\rm A}$, $t=32t_{\rm A}$, $t=48t_{\rm A}$, $t=64t_{\rm A}$, $t=96t_{\rm A}$, and $t=160t_{\rm A}$, respectively. It should be noted that the colour scale for current density and velocity (shown on the left) changes between panels to enhance the contrast.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{13569fg03.eps} \vspace*{-2mm} \end{figure} Figure 3:

Magnetic, kinetic, internal energies, and maximum current density versus time for the model shown in Fig. 2. The dashed line in the lower right panel denotes the critical current value. The magnetic, kinetic, and internal energies (panels a- c), respectively) are non-dimensionalised with respect to $\mu _0^{-1} B_0^2 L_0^2$, and the current density (panel d) with respect to $\mu _0^{-1} B_0 L_0^{-1}$; time is measured in terms of $t_{\rm A}$ (see Sect. 2.1).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{13569fg04.eps} \vspace*{-2mm} \end{figure} Figure 4:

Variation of magnetic energy with time for different initial CS widths and different model resistivity's. Solid, dashed and dot-dashed lines are for Y0=0.40, 0.32 and 0.25, respectively. Panels a-d) are for the dimensionless resistivity S-1=10-4, $3.2\times 10^{-4}$, $1.02\times 10^{-3}$, and $3.2\times 10^{-3}$, respectively. The magnetic energy is nondimensionalised with respect to $\mu _0^{-1} B_0^2 L_0^2$; time is measured in terms of $t_{\rm A}$ (see Sect. 2.1).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6cm,clip]{13569fg05.eps} \end{figure} Figure 5:

Relation between the magnetic dissipation rate during the reconnection around x-point and resistivity S-1. Solid squares are for the model with initial characteristic CS thickness Y0 = 0.32, open circles are for Y0=0.25. Power-law approximation (dashed lines) gives the power-law index 0.65 for the first case and 0.61 for the second case.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg06.eps} \end{figure} Figure 6:

Trajectories of protons starting with thermal velocities $v_{\rm ini} = 0.1 v_{\rm A}$ from six locations uniformly distributed along the Y=-0.4;Z=0 line. The left panel is for protons starting with large magnetic moments ( $v_{\vert\vert}=0.1 v_{\rm ini}$) and the right panel is for protons starting with small magnetic moments ( $v_{\vert\vert}=0.8 v_{\rm ini}$). The magnetic and electric fields are taken from the model with Y0=0.25 and S-11 = 10-3 at $t=32t_{\rm A}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg07.eps} \end{figure} Figure 7:

Trajectories of electrons starting with thermal velocities $v_{\rm ini} = 3.9 v_{\rm A}$. All other parameters are the same as in Fig. 6.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg08.eps} \vspace*{1.75mm} \end{figure} Figure 8:

Trajectories of protons starting with thermal velocities $v_{\rm ini} = 0.1 v_{\rm A}$. The snapshot is taken at $t=96t_{\rm A}$. All other parameters are the same as in Fig. 6.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{13569fg09.eps} \end{figure} Figure 9:

The same as in Fig. 8 but for electrons starting with thermal velocities $3.9 v_{\rm A}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm,clip]{13569fg10.eps} \end{figure} Figure 10:

The electron ( left panels) and proton ( middle panels) energy spectra for the model with initial CS width Y0 = 0.4 and dimensionless resistivity $S^{-1}_1 = 3.2 \times 10^{-4}$for different stages of the RCS evolution. The solid lines show the spectra of particles leaving the system, dashed lines show the spectra of remaining particles. Note that the colour scale for the current density (shown on the right) changes between panels to enhance the contrast. Upper panels correspond to the time $t=16t_{\rm A}$ while lower panels correspond to $t=128t_{\rm A}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm]{13569fg11.eps} \end{figure} Figure 11:

The energy spectra for the model with Y0=0.25 and $S^{-1}_1 = 3.2 \times 10^{-4}$. All other parameters are the same as in Fig. 10. Upper panels correspond to the time $t=16t_{\rm A}$, while lower panels correspond to $t=128t_{\rm A}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm]{13569fg12.eps} \end{figure} Figure 12:

The energy spectra for the model with Y0=0.25 and $S^{-1}_1 = 3.0 \times 10^{-3}$. All other parameters are the same as in Fig. 10. Upper panels correspond to the time $t=8t_{\rm A}$, while lower panels correspond to $t=32t_{\rm A}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm]{13569fg13.eps} \end{figure} Figure 13:

Integrated energy spectra of protons leaving the simulation domain compared with the initial thermal spectrum (solid line). The dashed lines are for resistivity $S^{-1}_1 = 3.2 \times 10^{-4}$ and dot-dot-dashed lines for $S^{-1}_1 = 1.0\times 10^{-3}$. Panel a) is for the initial CS thickness Y0 = 0.40 and panel  b) is for Y0=0.25.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm]{13569fg14.eps} \end{figure} Figure 14:

The same as in Fig. 13 but for electrons.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm,clip]{13569fg15.eps} \vspace*{2.5mm} \end{figure} Figure 15:

The number density ( left panels) and average energy ( right panels) for protons at their final positions in the model with Y0=0.25 and $S^{-1}=3.2\times 10^{-4}$ during different stages of the RCS evolution. Corresponding times are shown in the graph. Upper panels correspond to the time $t=8t_{\rm A}$, while lower panels correspond to $t=128t_{\rm A}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm,clip]{13569fg16.eps} \end{figure} Figure 16:

The same as in Fig. 15 but for electrons.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.