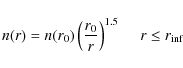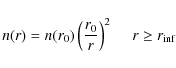| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200913112 | |
| Published online | 14 September 2010 | |
The solar type protostar IRAS16293-2422: new constraints on the physical structure
N. Crimier1 - C. Ceccarelli1 - S. Maret1 - S. Bottinelli2 - E. Caux1 - C. Kahane1 - D. C. Lis3 - J. Olofsson1
1 - Laboratoire d'Astrophysique, Observatoire de Grenoble, 38041 Grenoble, France
2 - CESR-UPS, Centre National de la Recherche Scientifique, Toulouse, France
3 - California Institute of Technology, MC 301-17, Pasadena, CA 91125, USA
Received 12 August 2009 / Accepted 23 March 2010
Abstract
Context. The low mass protostar IRAS16293-2422 is a
prototype Class 0 source in studies of the chemical structure during
the initial phases of life of solar type stars.
Aims. To derive the chemical structure accurately, a precise
determination of the source physical structure is required. The goal of
this study is to derive the structure of IRAS16293-2422.
Methods. We reanalyzed all available continuum data (single dish
and interferometric, from millimeter to MIR) to derive accurate density
and dust temperature profiles. Using ISO observations of water, we also
reconstructed the gas temperature profile.
Results. Our analysis shows that the envelope surrounding
IRAS16293-2422 is described well by the Shu ``inside-out'' collapsing
envelope model or a single power-law density profile with index equal
to 1.8. In contrast to some previous studies, our analysis does not
show evidence of a large (![]() 800 AU in diameter) cavity.
800 AU in diameter) cavity.
Conclusions. Although IRAS16293-2422 is a multiple system
composed of two or three objects, our reconstruction will be useful in
deriving the chemical structure of the large cold envelope surrounding
these objects and the warm component, treated here as a single source,
from single-dish observations of molecular emission.
Key words: stars: formation - ISM: molecules - ISM: abundances
1 Introduction
Understanding how our Sun and the Solar System formed is arguably one of
the major goals of modern astrophysics. Many different approaches
contribute to our understanding of the past history of the Solar
System. Analyzing the relics of the ancient eons, comets, and
meteorites, is one. Studying present-day objects similar to the progenitor of the
Sun is another. Here we pursue the latter approach and
analyze in detail the case of one of the most well-studied solar-type
protostars, IRAS16293-2422 (hereinafter IRAS16293). IRAS16293 is a
Class 0 protostar in the ![]() Ophiuchus complex at 120 pc from the
Sun (Loinard et al. 2008) that has played a similar role as
a prototype for solar-type protostars in astrochemical studies as
Orion KL for high-mass protostars. This is because of its
proximity and the strength of the lines of molecular emission
(e.g., van Dishoeck et al. 1995; Blake et al. 1994; Walker et al. 1986; Mundy et al. 1992, to mention just
a few representative works from the previous
decades). It was in this source that the
phenomenon of the ``super-deuteration''
Ophiuchus complex at 120 pc from the
Sun (Loinard et al. 2008) that has played a similar role as
a prototype for solar-type protostars in astrochemical studies as
Orion KL for high-mass protostars. This is because of its
proximity and the strength of the lines of molecular emission
(e.g., van Dishoeck et al. 1995; Blake et al. 1994; Walker et al. 1986; Mundy et al. 1992, to mention just
a few representative works from the previous
decades). It was in this source that the
phenomenon of the ``super-deuteration''![]() was first
discovered, by detecting a surprisingly abundant amount of multiply
deuterated molecules: formaldehyde, hydrogen sulfide, methanol, and
water (Vastel et al. 2003; Butner et al. 2007; Parise et al. 2003; Ceccarelli et al. 1998). The
first hot corino (Ceccarelli et al. 2007; Bottinelli et al. 2004) was also discovered in this source, with the detection of
several abundant complex organic molecules in the region where the
dust grain mantles sublimate (Cazaux et al. 2003; Bottinelli et al. 2004; Ceccarelli et al. 2000b).
was first
discovered, by detecting a surprisingly abundant amount of multiply
deuterated molecules: formaldehyde, hydrogen sulfide, methanol, and
water (Vastel et al. 2003; Butner et al. 2007; Parise et al. 2003; Ceccarelli et al. 1998). The
first hot corino (Ceccarelli et al. 2007; Bottinelli et al. 2004) was also discovered in this source, with the detection of
several abundant complex organic molecules in the region where the
dust grain mantles sublimate (Cazaux et al. 2003; Bottinelli et al. 2004; Ceccarelli et al. 2000b).
Unsurprisingly, IRAS16293 has therefore been the target of several studies to reconstruct its physical structure, namely its dust and gas density and temperature profiles (Ceccarelli et al. 2000a; Schöier et al. 2004; Jørgensen et al. 2005; Schöier et al. 2002), the mandatory first step to correctly evaluate the abundance of molecular species across the envelope. Ceccarelli et al. (2000a) used water and oxygen lines observations obtained with the Infrared Space Observatory (ISO) to derive the gas and dust density and temperature profile. In contrast, Schöier et al. (2002) used the dust continuum observations to derive the structure of the envelope. Moreover, Ceccarelli et al. assumed the semi-analytical solution by Shu and coworkers (Adams & Shu 1986; Shu 1977) to fit the observational data, while Schöier et al. (2002) assumed a single power law for the density distribution, and a posteriori verified that the Shu's solution also reproduced the observational data. The two methods lead to similar general conclusions: a) the envelope of IRAS16293 is centrally peaked and has a density distribution in overall agreement with the inside-out collapse picture (Shu 1977); b) there is a region, about 300 AU in diameter, where the dust mantles sublimate (giving rise to the phenomenon of the hot corino, mentioned above). However, the two different methods, unsurprisingly, also lead to some notable differences. For example, the gas density differs by about a factor 3 in the region where the ice sublimation is predicted to occur, leading to differences in the derived abundances of several molecular species.
Subsequent studies have built on the early ones to improve the derivation of the physical structure of IRAS16293. First, the study by Schöier et al. (2004), based on interferometric OVRO observations, concluded that the envelope has a large central cavity, about 800 AU in diameter. Using new Spitzer data, Jørgensen et al. (2005), then concluded that the envelope has an even larger central cavity, about 1200 AU in diameter. This large central cavity has a great impact on the whole interpretation of the hot corino of IRAS16293, because it predicts the absence of the mantle sublimation region. If the predicted cavity is real, the observed complex organic molecules must have an origin other than grain mantle sublimation from thermally heated dust. In addition to raising an important point in itself, Schöier et al. and Jørgensen et al. illustrate the paramount importance of correctly understanding the physical structure of the source in order to assess the chemical structure and all that follows.
In the present work, we therefore re-analyzed the
available data on IRAS16293 from scratch, considering, in
addition, the distance to this source estimated
by Loinard et al. (2008) (120 pc instead of 160 pc, as assumed in Ceccarelli
et al. 2000a, Schöier et al. 2002, 2004, and Jørgensen et al. 2005). This new
analysis is necessary and timely because of two important
observational projects having IRAS16293 as a target: a) the unbiased
spectral survey in the 3, 2, 1, and 0.8 mm bands just obtained at the
IRAM and JCMT telescopes (``The IRAS16293-2422 Millimeter And
Sub-millimeter Spectral Survey''![]() ;
Caux et al. 2010, in prep.), and b) the unbiased spectral survey between 500 and 2000
GHz that will shortly be performed with the heterodyne instrument HIFI aboard
the Herschel Space Observatory (HSO) launched in May 2009 (the
Herschel Guaranteed Time Key Program CHESS - Chemical Herschel Surveys
of Star Forming Regions
;
Caux et al. 2010, in prep.), and b) the unbiased spectral survey between 500 and 2000
GHz that will shortly be performed with the heterodyne instrument HIFI aboard
the Herschel Space Observatory (HSO) launched in May 2009 (the
Herschel Guaranteed Time Key Program CHESS - Chemical Herschel Surveys
of Star Forming Regions![]() ).
The two projects, involving large international teams, will provide an
accurate census of the molecular inventory of IRAS16293, the largest
ever obtained for a solar type protostar. To convert the observations
into an accurate chemical composition across the IRAS16293 envelope,
the dust and gas density and temperature profiles have first to be
determined accurately. Deriving these profiles is the goal of the
present article.
).
The two projects, involving large international teams, will provide an
accurate census of the molecular inventory of IRAS16293, the largest
ever obtained for a solar type protostar. To convert the observations
into an accurate chemical composition across the IRAS16293 envelope,
the dust and gas density and temperature profiles have first to be
determined accurately. Deriving these profiles is the goal of the
present article.
We conclude this section by addressing the problem of the binarity of
IRAS16293 and how it agrees with the analysis we present here. As soon
as interferometric observations became available it was realized that
IRAS16293 is indeed a proto-binary system (Mundy et al. 1992; Wootten 1989),
composed of two sources: A (the south source) and B (the north
source) separated by ![]() 4'', i.e.,
4'', i.e., ![]() 500
AU at 120 pc. While source B is the brightest in the continuum, source
A is often, but not always, the brightest in the molecular emission
(e.g., Chandler et al. 2005). The most
recent observations show that IRAS16293 is indeed a triple system, the
source A being composed of two objects, A1 and A2, of 0.5 and 1.5
500
AU at 120 pc. While source B is the brightest in the continuum, source
A is often, but not always, the brightest in the molecular emission
(e.g., Chandler et al. 2005). The most
recent observations show that IRAS16293 is indeed a triple system, the
source A being composed of two objects, A1 and A2, of 0.5 and 1.5 ![]() ,
respectively (Loinard et al. 2009).
While it is clear that the multiple nature of IRAS16293 cannot be
neglected in general, the two projects mentioned above involve
observations with single-dish telescopes, so that much of the structure
on small scal es is smeared out in these observations. The molecular
line emission will be dominated by the cold envelope, which fills the
telescope beam, and by any warm component at the interior of the
envelope. The major goal here is to provide a reliable estimate of the
envelope temperature and
density profiles of both the gas and dust components, up to the scales
where the approximation of a spherical symmetry is valid. We later
discuss the size of these scales, based on the available
observations.
,
respectively (Loinard et al. 2009).
While it is clear that the multiple nature of IRAS16293 cannot be
neglected in general, the two projects mentioned above involve
observations with single-dish telescopes, so that much of the structure
on small scal es is smeared out in these observations. The molecular
line emission will be dominated by the cold envelope, which fills the
telescope beam, and by any warm component at the interior of the
envelope. The major goal here is to provide a reliable estimate of the
envelope temperature and
density profiles of both the gas and dust components, up to the scales
where the approximation of a spherical symmetry is valid. We later
discuss the size of these scales, based on the available
observations.
The article is organized as follows. Section 2 discusses the derivation of the dust density and temperature distribution, based on the analysis of all available continuum data. Section 3 describes the derivation of the gas temperature profile, and the constraint of the abundance of a major gas coolant with the help of ISO. Finally, Sect. 4 discusses and summarizes the results of the presented study.
2 Dust temperature and density profiles
2.1 The data set
The present analysis is based on the continuum emission from the envelope that forms/surrounds the protostar IRAS16293. Three types of observations are considered: maps of the emission, a spectral energy distribution (SED), and interferometric observations at 1 and 3 mm. All data used had been retrieved from archives, except the map at 350- i)
- Continuum emission profiles
We used the maps of the dust continuum emission at 350
 m (obtained at the Caltech Submillimeter Observatory; CSO), and 450 and 850
m (obtained at the Caltech Submillimeter Observatory; CSO), and 450 and 850  m (obtained at the James Clerk Maxwell Telescope; JCMT). The 450 and 850
m (obtained at the James Clerk Maxwell Telescope; JCMT). The 450 and 850 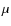 m maps had been retrieved from the JCMT archive (website). The beam sizes are 7.5'' and 14.8'' at 450 and 850
m maps had been retrieved from the JCMT archive (website). The beam sizes are 7.5'' and 14.8'' at 450 and 850 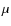 m, respectively. Based on the many previous JCMT published observations, the calibration uncertainty and noise levels are
m, respectively. Based on the many previous JCMT published observations, the calibration uncertainty and noise levels are
 10% and 0.04 Jy beam-1 at 850
10% and 0.04 Jy beam-1 at 850  m and
m and
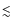 30% and 0.3 Jy beam-1 at 450
30% and 0.3 Jy beam-1 at 450 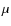 m, respectively.
m, respectively.
Observations of the 350
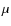 m
continuum emission toward IRAS 16293 reported here were carried out in
2003 February using the SHARC II facility bolometer camera of the
Caltech Submillimeter Observatory (CSO) on Mauna Kea in Hawaii (Dowell et al. 2003). SHARC II is a
m
continuum emission toward IRAS 16293 reported here were carried out in
2003 February using the SHARC II facility bolometer camera of the
Caltech Submillimeter Observatory (CSO) on Mauna Kea in Hawaii (Dowell et al. 2003). SHARC II is a
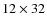 pixel filled array with a field of view of
pixel filled array with a field of view of
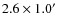 .
The data were taken during excellent submillimeter weather conditions
(a 225 GHz zenith opacity of 0.04, corresponding to less
than 1 mm of precipitable water). The observations were carried out
using the ``box-scan'' scanning mode
.
The data were taken during excellent submillimeter weather conditions
(a 225 GHz zenith opacity of 0.04, corresponding to less
than 1 mm of precipitable water). The observations were carried out
using the ``box-scan'' scanning mode![[*]](/icons/foot_motif.png) . Five 10 min scans were reduced together using the CRUSH software package (Kovács 2008)
to produce the final calibrated image. Telescope pointing was checked
by observing Juno, Vesta, or Mars, immediately before or after the
science observations and the measured offsets were applied during data
reduction. The data were taken before the CSO Dish Surface Optimization
system (DSOS) become operational. The shape of the telescope beam was
determined from the pointing images of Vesta and Mars. It contains a
diffraction-limited main beam with a FWHM diameter of 9
. Five 10 min scans were reduced together using the CRUSH software package (Kovács 2008)
to produce the final calibrated image. Telescope pointing was checked
by observing Juno, Vesta, or Mars, immediately before or after the
science observations and the measured offsets were applied during data
reduction. The data were taken before the CSO Dish Surface Optimization
system (DSOS) become operational. The shape of the telescope beam was
determined from the pointing images of Vesta and Mars. It contains a
diffraction-limited main beam with a FWHM diameter of 9
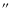 and an error beam with a FWHM diameter of 22
and an error beam with a FWHM diameter of 22
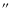 ,
with relative peak intensities of 0.8 and 0.2, respectively. This size of the error beam is consistent with earlier 350
,
with relative peak intensities of 0.8 and 0.2, respectively. This size of the error beam is consistent with earlier 350 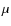 m measurements using the SHARC I camera (Hunter 1997).
m measurements using the SHARC I camera (Hunter 1997).
We obtained continuum emission profiles as a function of the distance from the center of the envelope, by averaging the map emission over annuli at the same distance. In each case, we adopted a radial sampling corresponding to the half of the resolution of the instrument. The uncertainties in the continuum emission profiles were evaluated taking into account the calibration uncertainty, noise levels, and the non-sphericity of the source. The resulting profiles, normalized to the peak emission, are shown in Fig. 1. We note that the 450 and 850
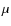 m profiles are
identical to those reported by Schöier et al. (2002).
m profiles are
identical to those reported by Schöier et al. (2002).
![\begin{figure}
\par\includegraphics[width=12cm,angle=0]{13112f01.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg24.png)
Figure 1: Continuum emission profiles at 850
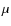 m ( left bottom
panel), 450
m ( left bottom
panel), 450 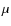 m (right upper panel) and 350
m (right upper panel) and 350 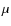 m (left upper panel), plus the SED (right bottom panel). The curves show the emission predicted by two
models with different density profiles (see text for more details):
the solid thick line is the best-fit of the maps and SED data
obtained by a density profile with a 2-indexes power law with
m (left upper panel), plus the SED (right bottom panel). The curves show the emission predicted by two
models with different density profiles (see text for more details):
the solid thick line is the best-fit of the maps and SED data
obtained by a density profile with a 2-indexes power law with
 and
and
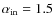 in the outer and inner
envelope respectively (Shu-like density distribution); the dashed
line is the best-fit obtained by a single power-law index,
in the outer and inner
envelope respectively (Shu-like density distribution); the dashed
line is the best-fit obtained by a single power-law index,
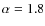 .
The dotted-dashed lines show the telescope beam
profiles adopted.
.
The dotted-dashed lines show the telescope beam
profiles adopted.
Open with DEXTER - ii)
- Spectral energy distribution
Table 1 reports the SED obtained by considering all the data available in the literature (plus the 350
 m point obtained by us; see above). The
millimeter and submillimeter data points were obtained by
integrating the maps over the entire envelope. The integrated flux at
1.3 mm was that quoted in Saraceno et al. (1996). We retrieved the IRAS fluxes
from the IRAS Point Source Catalog v2.1
m point obtained by us; see above). The
millimeter and submillimeter data points were obtained by
integrating the maps over the entire envelope. The integrated flux at
1.3 mm was that quoted in Saraceno et al. (1996). We retrieved the IRAS fluxes
from the IRAS Point Source Catalog v2.1![[*]](/icons/foot_motif.png) .
.
Table 1: The spectral energy distribution of IRAS 16293-2422.
IRAS 16293 was observed with the InfraRed Spectrograph (IRS) installed aboard the Spitzer Space Telescope as part of the ``From Molecular Cores to Planet Forming DIsks'' (Evans & c2d Team 2005; Evans et al. 2003) Legacy Program (AOR: 11826944, PI: Neal Evans). We used the observations obtained with the Long-High (LH) module (20-37
 m, R = 600) on
2004 July 29, in staring mode. The data reduction was performed using the
c2d pipeline S15.3.0 (Lahuis et al. 2006) with the pre-reduced (BCD)
data. Since the MIPS map at 24
m, R = 600) on
2004 July 29, in staring mode. The data reduction was performed using the
c2d pipeline S15.3.0 (Lahuis et al. 2006) with the pre-reduced (BCD)
data. Since the MIPS map at 24 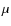 m shows that the IRAS16293
emitting region (
m shows that the IRAS16293
emitting region ( 30-40'') is larger than the LH module field of
view (11.1''
30-40'') is larger than the LH module field of
view (11.1''  22.3''), we adopted the full aperture extraction
method in the pipeline. In addition, we corrected the derived flux
level for the missing flux by comparing the IRS spectrum integrated on
the MIPS bandwith and the integrated MIPS flux. We note that this method
assumes that the source emission has a similar distribution across the whole
IRS wavelength interval,
22.3''), we adopted the full aperture extraction
method in the pipeline. In addition, we corrected the derived flux
level for the missing flux by comparing the IRS spectrum integrated on
the MIPS bandwith and the integrated MIPS flux. We note that this method
assumes that the source emission has a similar distribution across the whole
IRS wavelength interval,  21-37
21-37 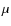 m. The correction factor
derived by this method is 22% in the flux.
m. The correction factor
derived by this method is 22% in the flux.
- iii)
- Interferometric continuum data
Observations of the 3 and 1.3 mm continuum were obtained with the IRAM Plateau de Bure Interferometer (PdBI) in 2004 and are described in detail in Bottinelli et al. (2004). They were obtained using the B and C configurations of the PdBI array, resulting in a spatial resolution of about 0.8''.
2.2 Adopted model
We obtained the best-fit to the continuum data, described in the previous section, by using the 1D radiative transfer code DUSTY (Ivezic & Elitzur 1997), which has been extensively used in similar works (including Jørgensen et al. 2002, 2005 Schöier et al. 2004,2002). Briefly, providing as input the temperature of the central object and a dust density profile, DUSTY self-consistently computes the dust temperature profile and the dust emission. A comparison between the computed 350, 450, and 850In this work, we consider two cases for the density distribution. In
the first, we assume a broken power-law density profile as
in the Shu (1977) solution
where

|
(3) |
In both cases, n(r0) is the density at r0, and the envelope starts at a radius
In addition to the above parameters, the opacity of the dust as a function of wavelength is a parameter of DUSTY. Following numerous previous studies (Evans et al. 2001; Shirley et al. 2002; Schöier et al. 2002; Young et al. 2003; Van Der Tak et al. 1999), we adopted the dust opacity calculated by Ossenkopf & Henning (1994), namely their OH5 dust model, which refers to grains coated by ice. Again, the basic result, though, does not substantially depend on the choice of the dust opacity model.
As explained in Ivezic & Elitzur (1997), DUSTY gives scale-free results, so that the source bolometric luminosity
![]() and the distance are required to compare the DUSTY output with actual
observations. We assumed the lastest estimate of the distance to the
and the distance are required to compare the DUSTY output with actual
observations. We assumed the lastest estimate of the distance to the ![]() Ophiuchus cloud, namely 120 pc (see Introduction), and we derived the
bolometric luminosity by integrating the observed emission over the
full spectrum, optimizing the resulting
Ophiuchus cloud, namely 120 pc (see Introduction), and we derived the
bolometric luminosity by integrating the observed emission over the
full spectrum, optimizing the resulting ![]() (see below).
(see below).
We computed grids of models for both cases described above. The summary of the covered parameter space is reported in Table 2.
Table 2: Range and step of the DUSTY input parameters.
The best-fit model was found by minimizing the2.3 Results
a) Brightness profiles and SED analysis
Table 3 lists the best-fit model parameters for the two models described in the previous section as well as the parameters obtained by Schöier et al. (2002) for comparison. Figure 1 compares the solutions to the observed data (maps and SED).
Table 3: Summary of the dust radiative transfer analysis.
The results of this part of the analysis are:- The bolometric luminosity, obtained by minimizing the
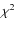 ,
is
22
,
is
22 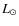 rather then 14
rather then 14 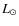 ,
the value obtained by simply
scaling the bolometric luminosity adopted by Ceccarelli et al. (2000b) and
Schöier et al. (2002) to a distance of 120 pc instead of 160 pc.
,
the value obtained by simply
scaling the bolometric luminosity adopted by Ceccarelli et al. (2000b) and
Schöier et al. (2002) to a distance of 120 pc instead of 160 pc.
- The single power-law and Shu-like density distributions can both
reproduce the observations, the maps, and the SED data, including the
IR part of the spectrum (Fig. 1). They provide similar best-fit
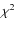 values,
although the Shu-like distribution reproduces more accurately the 450
values,
although the Shu-like distribution reproduces more accurately the 450 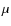 m
profile. Also the derived physical parameters are substantially
similar for the two models.
m
profile. Also the derived physical parameters are substantially
similar for the two models.
- The observed data, including the Spitzer data between 20 and 40
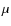 m, do not imply that a large cavity must be present (Jørgensen et al. 2005). Our solution using higher luminosity (22 instead of
14
m, do not imply that a large cavity must be present (Jørgensen et al. 2005). Our solution using higher luminosity (22 instead of
14 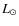 )
also can reproduce the MIR Spitzer observations. Figure 2 compares the MIR Spitzer and IRAS observations with the emission predicted by our models and those of Jørgensen et al. (2005) and Schöier et al. (2002).
)
also can reproduce the MIR Spitzer observations. Figure 2 compares the MIR Spitzer and IRAS observations with the emission predicted by our models and those of Jørgensen et al. (2005) and Schöier et al. (2002).
![\begin{figure}
\par\includegraphics[width=9cm,angle=0]{13112f02.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg51.png)
|
Figure 2:
MIR Spitzer and IRAS fluxes as a function of the wavelength. The two crosses represent the integrated fluxes at 23.7 and 25 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,angle=90]{13112f03.ps}\\ [2mm]
\includegraphics[width=9cm,angle=90]{13112f04.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg52.png)
|
Figure 3: Dust temperature ( upper panel) and H2 density ( lower panel) profiles from the best-fit obtained in the two cases Shu-like (solid line) and single power-law density distribution (dashed line). |
| Open with DEXTER | |
b) Interferometric data analysis
The previous analysis considers single dish data, which at best have a spatial resolution of 8'', equivalent to a radius of ![]() 1000 AU.
To constrain the inner region in greater detail, we used 1 and
3 mm continuum interferometric observations obtained with the
Plateau de Bure interferometer (PdBI) described in the previous
section. To compare the model predictions with the observations, we
produced synthetic maps for each model, to which we added the predicted
emission from the envelope plus the emission of the two Gaussian-like
sources A and B. The parameters used to represent the emission of the
sources A and B were extracted from the interferometric maps at 1.3 and
3 mm and reported in Table 4. We then used the UV_FMODEL task in Gildas
1000 AU.
To constrain the inner region in greater detail, we used 1 and
3 mm continuum interferometric observations obtained with the
Plateau de Bure interferometer (PdBI) described in the previous
section. To compare the model predictions with the observations, we
produced synthetic maps for each model, to which we added the predicted
emission from the envelope plus the emission of the two Gaussian-like
sources A and B. The parameters used to represent the emission of the
sources A and B were extracted from the interferometric maps at 1.3 and
3 mm and reported in Table 4. We then used the UV_FMODEL task in Gildas![]() to compute visibility tables with the same
to compute visibility tables with the same ![]() plane coverage as the actual observations.
plane coverage as the actual observations.
Table 4: Integrated flux and full width at half maximum ( FWHM) of the Gaussians used to model the emission of the sources A and B at 1.3 and 3 mm.
Table 5 reports the
![]() values obtained using the observed and modeled visibility amplitudes at
1.3 mm. The comparison is performed for each of the three models
of the envelope, i.e., the single power-law density distribution, the
Shu-like density distribution, and the central cavity of Schöier et al. (2004).
We tested cases in which the envelope is centered on one of the two
sources or on the mid-way point between the two sources. The
values obtained using the observed and modeled visibility amplitudes at
1.3 mm. The comparison is performed for each of the three models
of the envelope, i.e., the single power-law density distribution, the
Shu-like density distribution, and the central cavity of Schöier et al. (2004).
We tested cases in which the envelope is centered on one of the two
sources or on the mid-way point between the two sources. The
![]() values are computed over more than 104 points. The 2D representation of the visibility amplitudes observed and modeled in
values are computed over more than 104 points. The 2D representation of the visibility amplitudes observed and modeled in ![]() plan is difficult to read. Therefore to illustrate the comparison
between the visibility amplitudes observed and modeled, we averaged the
visibility amplitudes over the same
plan is difficult to read. Therefore to illustrate the comparison
between the visibility amplitudes observed and modeled, we averaged the
visibility amplitudes over the same ![]() radius and plotted them in Fig. 4. We note that the error bars shown in Fig. 4
represent only the measurement errors. The standard deviations
resulting from the radial average are meaningless in this case due to
its non-sphericial geometry (caused by the sources A and B).
Figure 4 attempts to illustrate the comparison between the observations and the models, our conclusions being based on the
radius and plotted them in Fig. 4. We note that the error bars shown in Fig. 4
represent only the measurement errors. The standard deviations
resulting from the radial average are meaningless in this case due to
its non-sphericial geometry (caused by the sources A and B).
Figure 4 attempts to illustrate the comparison between the observations and the models, our conclusions being based on the
![]() in Table 5. The computations were performed considering all the visibility amplitudes obtained in the
in Table 5. The computations were performed considering all the visibility amplitudes obtained in the ![]() plane before the azimuthal average.
plane before the azimuthal average.
The interferometric data are dominated by the two components of the
IRAS16293 binary system. However, regarding the envelope contribution -
which is relevant to the present work - in
the case where the envelope is centered on the mid-way point between
the sources A and
B, the visibilities at ![]() radii lower than about 80 k
radii lower than about 80 k![]() are not
reproduced well by the single power-law density profiles. Our solution
with the Shu-like density profile and the solution with a cavity
(suggested by Schöier et al. 2004) provides far closer agreement. However, when envelope is centered on either B or A,
all three models give similar results (Fig. 4), and reproduce
the observed visibilities well. Since with the data available in the
literature there is no way to know whether the envelope is centered on
one of the two sources (A or B) or just on the mid-way point between them, either of the
two solutions (centered on a source or on the mid-way point
between A and B) is equally plausible. In other words, we
are affected by a degeneracy dominated by the parameters relative to
the binarity of the source. The interferometric data can be
reproduced without a cavity.
We note that the 3 mm PdBI observations do not provide additional information.
We emphasize that the above analysis of the interferometric data is
directly applicable to the OVRO data that led Schöier et al. (2004) to suggest
the presence of a cavity. The OVRO data probe visibility amplitudes
lower than about 60 k
are not
reproduced well by the single power-law density profiles. Our solution
with the Shu-like density profile and the solution with a cavity
(suggested by Schöier et al. 2004) provides far closer agreement. However, when envelope is centered on either B or A,
all three models give similar results (Fig. 4), and reproduce
the observed visibilities well. Since with the data available in the
literature there is no way to know whether the envelope is centered on
one of the two sources (A or B) or just on the mid-way point between them, either of the
two solutions (centered on a source or on the mid-way point
between A and B) is equally plausible. In other words, we
are affected by a degeneracy dominated by the parameters relative to
the binarity of the source. The interferometric data can be
reproduced without a cavity.
We note that the 3 mm PdBI observations do not provide additional information.
We emphasize that the above analysis of the interferometric data is
directly applicable to the OVRO data that led Schöier et al. (2004) to suggest
the presence of a cavity. The OVRO data probe visibility amplitudes
lower than about 60 k![]() ,
a range also probed by the PDBI
data. Therefore, as shown above, they can be reproduced by assuming
that the envelope is centered on either source A or B without the
necessity of assuming a cavity.
,
a range also probed by the PDBI
data. Therefore, as shown above, they can be reproduced by assuming
that the envelope is centered on either source A or B without the
necessity of assuming a cavity.
Table 5:
![]() values obtained comparing the visibility amplitudes observed and modeled at 1.3 mm.
values obtained comparing the visibility amplitudes observed and modeled at 1.3 mm.
![\begin{figure}
\par\includegraphics[width=15cm,angle=0]{13112f05.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg56.png)
|
Figure 4:
Visibility amplitudes as a function of the |
| Open with DEXTER | |
c) Summary of the continuum data analysis
Both the single dish and interferometric continuum data can be reproduced by either of the two models we considered: a Shu-like and single power-law density distribution. Furthermore, no cavity is required to explain the data, neither the Spitzer MIR data (Jørgensen et al. 2005) nor the interferometric data (Schöier et al. 2004).
Therefore, the Shu-like density profile (which has a physical interpretation), with no cavity, is adopted as our reference model for the study of the gas temperature and water line predictions.
3 Gas temperature profile
3.1 Adopted method
We computed the gas temperature profile using the CHT96 code described in Ceccarelli et al. (1996) (see also Ceccarelli et al. 2000a; Maret et al. 2002; Crimier et al. 2009). Briefly, the code computes the gas equilibrium temperature at each point of the envelope, by equating the heating and cooling terms at each point of the envelope. Following the method described in Ceccarelli et al. (1996), we considered heating from the gas compression (due to the collapse), dust-gas collisions, and photo-pumping of H2O and CO molecules by the IR photons emitted by the warm dust close to the center![\begin{displaymath}\beta = \frac{k_{\rm d}}{k_{\rm L} + k_{\rm d}} +
\frac{k_{...
...m d} \right)
\Delta L_{\rm th} \right]} {\Delta L_{\rm th}}
\end{displaymath}](/articles/aa/full_html/2010/11/aa13112-09/img59.png)
|
(4) |
where

|
(5) |
in the infalling region of the envelope (where
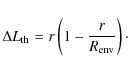
|
(6) |
In addition, H2O and CO molecules can be pumped by absorption of the NIR photons emitted by the innermost warm dust. Since the densities and temperatures of the regions of the envelope targeted by this study are not enough to populate the levels in the vibrational states, the effect of the NIR photons is an extra heating of the gas, as described in Ceccarelli et al. (1996). We note that the code takes into account the dust with temperatures up to 1500 K.
The code has a number of parameters that influence the gas equilibrium
temperature. First, the dust temperature, assumed to be the
output of the previous step analysis (Sect. 2). Second,
since the infall heating depends on the velocity gradient across the
envelope and the cooling depends on the gas lines (which can be and sometimes are
optically thick), the velocity field across the envelope is
also a parameter of the code. Here we assumed that the infall velocity
field corresponds to the free fall velocity field with a 2 ![]() source at the center of the envelope (Loinard et al. 2009). Third, we
adopted the ``standard'' cosmic ray ionization rate, namely
source at the center of the envelope (Loinard et al. 2009). Third, we
adopted the ``standard'' cosmic ray ionization rate, namely
![]() s-1, although in practcie this parameter is
unimportant. Finally, given the contributions of the H2O, CO, and OI
to the gas cooling, their respective abundances are important
parameters of the model. Previous theoretical studies have shown that
the O abundance is constant across the envelope, except in the very
inner regions, where the gas temperature exceeds about 250 K, and
endothermic reactions that form OH and H2O become very efficient
(Doty et al. 2004; Ceccarelli et al. 1996; Doty & Neufeld 1997). Unfortunately, this parameter is very
poorly constrained by observations (because of the difficulty in
observing the O fine structure lines and their being easily
excited in the foreground molecular cloud and its associated PDR
(see e.g., Caux et al. 1999; Liseau et al. 1999). Here we assumed that the atomic O abundance
is equal to
s-1, although in practcie this parameter is
unimportant. Finally, given the contributions of the H2O, CO, and OI
to the gas cooling, their respective abundances are important
parameters of the model. Previous theoretical studies have shown that
the O abundance is constant across the envelope, except in the very
inner regions, where the gas temperature exceeds about 250 K, and
endothermic reactions that form OH and H2O become very efficient
(Doty et al. 2004; Ceccarelli et al. 1996; Doty & Neufeld 1997). Unfortunately, this parameter is very
poorly constrained by observations (because of the difficulty in
observing the O fine structure lines and their being easily
excited in the foreground molecular cloud and its associated PDR
(see e.g., Caux et al. 1999; Liseau et al. 1999). Here we assumed that the atomic O abundance
is equal to
![]() and verified a posteriori that the O fine
structure line emission is consistent with the ISO observations. We
note, however, that O is never the dominant coolant except, perhaps,
in a very small region of the envelope (Ceccarelli et al. 2000a; Maret et al. 2002). In contrast, CO, is the main coolant in the outer envelope, but, since
the cooling lines are heavily optically thick, its abundance does not
play an important role (in the regime where it is higher than about
and verified a posteriori that the O fine
structure line emission is consistent with the ISO observations. We
note, however, that O is never the dominant coolant except, perhaps,
in a very small region of the envelope (Ceccarelli et al. 2000a; Maret et al. 2002). In contrast, CO, is the main coolant in the outer envelope, but, since
the cooling lines are heavily optically thick, its abundance does not
play an important role (in the regime where it is higher than about
![]() with respect to H2). We, therefore, assumed a
canonical
with respect to H2). We, therefore, assumed a
canonical
![]() CO abundance across the
envelope
CO abundance across the
envelope![]() .
.
Finally, water is an important coolant in the inner region, where the
grain mantles sublimate, injecting into the gas phase large quantities
of water molecules. Based on previous studies, we approximated
the H2O abundance with a step function: the abundance is
![]() in the region where the dust temperature exceeds 100 K, and
in the region where the dust temperature exceeds 100 K, and
![]() elsewhere. Both
elsewhere. Both
![]() and
and
![]() are found by comparing the
theoretical predictions with the ISO observations (see Sect.
3.2). We note that, to solve the water level
population statistical equilibrium equations, we used the collisional
coefficients between H2O and H2 computed by
Faure et al. (2007). We assumed that the ortho-to-para H2 ratio is at the
local thermal equilibrium (LTE) in each part of the envelope.
Finally, we assumed a H2O ortho-to-para ratio equal to 3.
are found by comparing the
theoretical predictions with the ISO observations (see Sect.
3.2). We note that, to solve the water level
population statistical equilibrium equations, we used the collisional
coefficients between H2O and H2 computed by
Faure et al. (2007). We assumed that the ortho-to-para H2 ratio is at the
local thermal equilibrium (LTE) in each part of the envelope.
Finally, we assumed a H2O ortho-to-para ratio equal to 3.
3.2 Results
To constrain the water abundance, a necessary step in predicting the
gas temperature profile, we used the ISO observations of the water
lines towards IRAS16293 (Ceccarelli et al. 2000a,1998) and compared them
with the model predictions obtained for different H2O abundance
profiles. We computed a grid of models with
![]() and
and
![]() varying
between
varying
between
![]() and
and
![]() .
.
![\begin{figure}
\par\rotatebox{0}{\includegraphics[width=9cm]{13112f06.ps}}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg74.png)
|
Figure 5:
Reduced- |
| Open with DEXTER | |
![\begin{figure}
\par\rotatebox{0}{\includegraphics[width=8.2cm]{13112f07.ps}}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg79.png)
|
Figure 6:
Ratio of the observed to predicted H2O line flux versus the upper level energy in cm-1. In these computations, we used the dust temperature and density profiles of the Shu-like model of Table 3 and an H2O abundance equal to
|
| Open with DEXTER | |
The results for the single power-law density profile are similar, the upper limit to the inner H2O abundance being a factor ten lower (because of the higher density in the inner part predicted by this model).
![\begin{figure}
\par\includegraphics[width=10cm,angle=90]{13112f08.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg80.png)
|
Figure 7: Dust (solid line) and gas (dashed line) temperature profiles of the best-fit model obtained assuming a Shu-like density distribution (see text). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=90]{13112f09.ps}\\ [2mm]
\par\includegraphics[width=9.4cm,angle=90]{13112f10.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg81.png)
|
Figure 8:
Heating ( top panel) and cooling ( bottom panel) rates as function of the radius, computed assuming that the inner H2O abundance is equal to
|
| Open with DEXTER | |
Table 6: Predictions of the line fluxes (after subtraction of the continuum) of the water lines observable with the Herschel spectrometer HIFI.
Table 7: Predictions of the line fluxes (after subtraction of the continuum) of the water lines observable with the Herschel spectrometer PACS.
Figure 7 shows the dust
and gas temperature profiles for the Shu-like density distribution. Gas
and dust are thermally coupled across the whole envelope, the largest
difference (<10![]() )
between them occuring in the infall region, where
)
between them occuring in the infall region, where
![]() .
Figure 8
shows the heating and cooling terms across the envelope. The heating is
totally dominated by the compression in the entire collapsing region,
and by the collisions between the dust and the gas in the outer
envelope. We note that the H2O and CO photo-pumping plays
only a minor role. The cooling is dominated by the water line emission
in the inner region (where the ice sublimate), by the dust-gas
collisions in a large intermediate region, and by the CO line emission
in the very outer envelope. These results are very similar to those of Ceccarelli et al. (2000a).
We note that low-lying water lines could possibly be contaminated by
the outflow driven by the source. This effect could possibly lead to an
overestimate of the outer water abundance. Since the ISO water lines
are spectrally unresolved, it is impossible to address this question
using the ISO data.
.
Figure 8
shows the heating and cooling terms across the envelope. The heating is
totally dominated by the compression in the entire collapsing region,
and by the collisions between the dust and the gas in the outer
envelope. We note that the H2O and CO photo-pumping plays
only a minor role. The cooling is dominated by the water line emission
in the inner region (where the ice sublimate), by the dust-gas
collisions in a large intermediate region, and by the CO line emission
in the very outer envelope. These results are very similar to those of Ceccarelli et al. (2000a).
We note that low-lying water lines could possibly be contaminated by
the outflow driven by the source. This effect could possibly lead to an
overestimate of the outer water abundance. Since the ISO water lines
are spectrally unresolved, it is impossible to address this question
using the ISO data.
Tables 7 and 6 list the
predicted fluxes of the water lines that will be observable with HSO,
for the best-fit model (H2O abundance in the outer
envelope equal to
![]() )
with H2O abundance in the inner
envelope equal to
)
with H2O abundance in the inner
envelope equal to
![]() ,
but also for the case with a larger H2O inner
envelope abundance (
,
but also for the case with a larger H2O inner
envelope abundance (
![]() ).
).
4 Discussion and conclusions
Our new analysis of the single dish and interferometric continuum
observations of the envelope of IRAS16293 has confirmed that an envelope of
about 2 ![]() surrounds the proto-binary system of
IRAS16293. The envelope can be described with a Shu-like density
distribution, corresponding to the gas collapsing towards a 2
surrounds the proto-binary system of
IRAS16293. The envelope can be described with a Shu-like density
distribution, corresponding to the gas collapsing towards a 2 ![]() central star. The luminosity of IRAS16293 has been re-evaluated to be
22
central star. The luminosity of IRAS16293 has been re-evaluated to be
22 ![]() for a distance of 120 pc.
for a distance of 120 pc.
Both the single dish and interferometric data have been able to be reproduced by an
envelope with an inner radius between 20 and 30 AU, equivalent to
about 0.4'' and smaller than the radius at which the dust
temperature reaches 100 K (the ice mantle sublimation temperature)
namely 75 to 85 AU. We have found that our analysis can reproduce the
full SED, including the Spitzer MIR data, without the necessity of a
central cavity of 800 AU radius (Jørgensen et al. 2005). The difference between
our models and previous ones (based on the Schöier et al. 2002, initial
model) is the higher bolometric luminosity (kept as a free parameter
in our models) and the lower optical thickness of the envelope (
![]() ,
namely twice as smaller as in the Schöier's models). These differences
help to ensure that the predicted MIR radiation flux agrees with the
observed one. Finally, the interferometric data, being dominated by the
two components of the binary system, do not provide significant
constraints on the envelope structure, with one exception. They exclude
the case of an envelope with a single power-law density profile
centered on the mid-way point between the two sources. Based on this
assumption, Schöier et al. (2004)
suggested the presence of a cavity 800 AU in diameter. Since no data
constrains where
the center of the envelope is located, we favor the solution with the
envelope centered on one of the two sources. In addition, the Shu-like
model fits the PDBI data slightly better and is thus our preferred
solution.
,
namely twice as smaller as in the Schöier's models). These differences
help to ensure that the predicted MIR radiation flux agrees with the
observed one. Finally, the interferometric data, being dominated by the
two components of the binary system, do not provide significant
constraints on the envelope structure, with one exception. They exclude
the case of an envelope with a single power-law density profile
centered on the mid-way point between the two sources. Based on this
assumption, Schöier et al. (2004)
suggested the presence of a cavity 800 AU in diameter. Since no data
constrains where
the center of the envelope is located, we favor the solution with the
envelope centered on one of the two sources. In addition, the Shu-like
model fits the PDBI data slightly better and is thus our preferred
solution.
As already noted by Ceccarelli et al. (2000a), the ISO data do not permit us to constrain the inner H2O abundance because the detected lines are optically thick and cover a relatively small range of upper-level energies (![]() 300 cm-1).
The outer-envelope water abundance is also relatively
poorly constrained. In addition, the relatively low spectral resolution
of ISO does not allow us to determine whether some lines are
contaminated by the emission from the outflow. The future observations
with the HIFI spectrometer aboard the Herschel Space Observatory,
launched in May 2009, will certainly constrain more tightly the water
abundance profile across the IRAS16293 envelope, helping us to
understand the distribution of water in the protostars similar to the
Sun's progenitor. On the one hand, the water abundance in the outer
envelope (0.7-
300 cm-1).
The outer-envelope water abundance is also relatively
poorly constrained. In addition, the relatively low spectral resolution
of ISO does not allow us to determine whether some lines are
contaminated by the emission from the outflow. The future observations
with the HIFI spectrometer aboard the Herschel Space Observatory,
launched in May 2009, will certainly constrain more tightly the water
abundance profile across the IRAS16293 envelope, helping us to
understand the distribution of water in the protostars similar to the
Sun's progenitor. On the one hand, the water abundance in the outer
envelope (0.7-
![]() )
derived from the ISO observations here is consistent with some previous estimates of water abundance in cold gas (e.g., Cernicharo et al. 1997) but only marginally consistent with other low estimates (e.g., Snell et al. 2000), so the new Herschel/HIFI observations, with their significantly higher
spatial and spectral resolution, will be crucial in settling the question. On the other hand, the inner envelope abundance (<
)
derived from the ISO observations here is consistent with some previous estimates of water abundance in cold gas (e.g., Cernicharo et al. 1997) but only marginally consistent with other low estimates (e.g., Snell et al. 2000), so the new Herschel/HIFI observations, with their significantly higher
spatial and spectral resolution, will be crucial in settling the question. On the other hand, the inner envelope abundance (<
![]() )
is lower than expected if all ice in the
mantles sublimates (see Ceccarelli et al. 2000a). In this case, the Herschel/HIFI observations will also help us to understand this point.
)
is lower than expected if all ice in the
mantles sublimates (see Ceccarelli et al. 2000a). In this case, the Herschel/HIFI observations will also help us to understand this point.
As stated in the Introduction, the main aim of our study was to provide as accuratly as possible estimates of the dust and gas temperature profiles of the cold envelope of IRAS16293 and its warm inner component, also known as the hot corino, to interpret the data observed in two large projects, TIMASSS and CHESS (see Introduction). We are aware that the proposed description is unable to account for the multiple nature of the IRAS16293 system. However it has the merit of allowing the interpretation of the single-dish observations in the upcoming projects, despite its limitation. A more detailed analysis will only be possible once the relevant molecular emission is observed with interferometers, resolving the two components of the system. Before this, the analysis based on a single warm component and cold envelope is the only viable one and allows a first understanding of the chemical composition of a system that will eventually form a star and planetary system like our own.
AcknowledgementsWe warmly thank Laurent Loinard for the very useful discussions on the interferometric data of IRAS16293. We acknowledge the financial support by PPF and the Agence Nationale pour la Recherche (ANR), France (contract ANR-08-BLAN-0225). The CSO is supported by the National Science Foundation, award AST-0540882.
References
- Adams, F. C., & Shu, F. H. 1986, ApJ, 308, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, G. A., van Dishoek, E. F., Jansen, D. J., Groesbeck, T. D., & Mundy, L. G. 1994, ApJ, 428, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Bottinelli, S., Ceccarelli, C., Neri, R., et al. 2004, ApJ, 617, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Butner, H. M., Charnley, S. B., Ceccarelli, C., et al. 2007, ApJ, 659, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Caux, E., Ceccarelli, C., Castets, A., et al. 1999, A&A, 347, L1 [NASA ADS] [Google Scholar]
- Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 471, 400 [Google Scholar]
- Ceccarelli, C., Castets, A., Loinard, L., Caux, E., & Tielens, A. G. G. M. 1998, A&A, 338, L43 [NASA ADS] [Google Scholar]
- Ceccarelli, C., Castets, A., Caux, E., et al. 2000a, A&A, 355, 1129 [NASA ADS] [Google Scholar]
- Ceccarelli, C., Loinard, L., Castets, A., Tielens, A. G. G. M., & Caux, E. 2000b, A&A, 357, L9 [NASA ADS] [Google Scholar]
- Ceccarelli, C., Maret, S., Tielens, A. G. G. M., Castets, A., & Caux, E. 2003, A&A, 410, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Caselli, P., Herbst, E., Tielens, A. G. G. M., & Caux, E. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 47 [Google Scholar]
- Cernicharo, J., Lim, T., Cox, P., et al. 1997, A&A, 323, L25 [NASA ADS] [Google Scholar]
- Chandler, C. J., Brogan, C. L., Shirley, Y. L., & Loinard, L. 2005, ApJ, 632, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Crimier, N., Ceccarelli, C., Lefloch, B., & Faure, A. 2009, A&A, 506, 1229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doty, S. D., & Neufeld, D. A. 1997, ApJ, 489, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Doty, S. D., Schöier, F. L., & van Dishoeck, E. F. 2004, A&A, 418, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dowell, C. D., Allen, C. A., Babu, R. S., et al. 2003, in SPIE Conf. Ser. 4855, ed. T. G. Phillips, & J. Zmuidzinas, 73 [Google Scholar]
- Evans, N. J., & c2d Team. 2005, BAAS, 37, 1323 [NASA ADS] [Google Scholar]
- Evans, II, N. J., Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., Crimier, N., Ceccarelli, C., et al. 2007, A&A, 472, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, T. R. 1997, PhD Thesis, California Institute of Technology [Google Scholar]
- Ivezic, Z., & Elitzur, M. 1997, MNRAS, 287, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, J. K., Lahuis, F., Schöier, F. L., et al. 2005, ApJ, 631, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, A. 2008, in SPIE Conf. Ser., 7020 [Google Scholar]
- Lahuis, F., Kessler-Silacci, J. E., Evans, N. J., I., et al. 2006, c2d Spectroscopy Explanatory Supplement, Tech. Rep., Pasadena: Spitzer Science Center [Google Scholar]
- Liseau, R., White, G. J., Larsson, B., et al. 1999, A&A, 344, 342 [NASA ADS] [Google Scholar]
- Loinard, L., Torres, R. M., Mioduszewski, A. J., & Rodríguez, L. F. 2008, ApJ, 675, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Rodriguez, L., Pech, G., et al. 2009, BAAS, 41, 296 [NASA ADS] [Google Scholar]
- Maret, S., Ceccarelli, C., Caux, E., Tielens, A. G. G. M., & Castets, A. 2002, A&A, 395, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mundy, L. G., Wootten, A., Wilking, B. A., Blake, G. A., & Sargent, A. I. 1992, ApJ, 385, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Parise, B., Simon, T., Caux, E., et al. 2003, A&A, 410, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Ceccarelli, C., & Maret, S. 2005, A&A, 441, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandell, G., & Weintraub, D. A. 2001, ApJS, 134, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Saraceno, P., Andre, P., Ceccarelli, C., Griffin, M., & Molinari, S. 1996, A&A, 309, 827 [NASA ADS] [Google Scholar]
- Schöier, F. L., Jørgensen, J. K., van Dishoeck, E. F., & Blake, G. A. 2002, A&A, 390, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., Jørgensen, J. K., van Dishoeck, E. F., & Blake, G. A. 2004, A&A, 418, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shirley, Y. L., Evans, II, N. J., & Rawlings, J. M. C. 2002, ApJ, 575, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Snell, R. L., Howe, J. E., Ashby, M. L. N., et al. 2000, ApJ, 539, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, T., Silk, J., & Hollenbach, D. J. 1983, ApJ, 275, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Van Der Tak, F. F. S., van Dishoeck, E. F., Evans, II, N. J., Bakker, E. J., & Blake, G. A. 1999, ApJ, 522, 991 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Blake, G. A., Jansen, D. J., & Groesbeck, T. D. 1995, ApJ, 447, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Phillips, T. G., Ceccarelli, C., & Pearson, J. 2003, ApJ, 593, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, C. K., Lada, C. J., Young, E. T., Maloney, P. R., & Wilking, B. A. 1986, ApJ, 309, L47 [Google Scholar]
- Wootten, A. 1989, ApJ, 337, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Young, C. H., Shirley, Y. L., Evans, II, N. J., & Rawlings, J. M. C. 2003, ApJS, 145, 111 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... ``super-deuteration''
![[*]](/icons/foot_motif.png)
- The super-deuteration refers to the exceptionally high abundance ratio of D-bearing molecules with respect to their H-bearing isotopologues found in low mass protostars, with observed D-molecule/H-molecule ratios reaching the unity (see e.g., the review in Ceccarelli et al. 2007).
- ... Survey''
![[*]](/icons/foot_motif.png)
- http://www-laog.obs.ujf-grenoble.fr/heberges/timasss/
- ...
![[*]](/icons/foot_motif.png)
- http://www-laog.obs.ujf-grenoble.fr/heberges/chess/
- ... mode
![[*]](/icons/foot_motif.png)
- see http://www.submm.caltech.edu/sharc/
- ... v2.1
![[*]](/icons/foot_motif.png)
- http://irsa.ipac.caltech.edu/cgi-bin/Gator/nph-dd?catalog=iraspsc
- ...
![[*]](/icons/foot_motif.png)
- The temperature at the inner radius
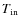 defines the radius at which the integration starts. The DUSTY codes
requires the temperature rather than the radius because it is based on
a scale-free algorithm.
defines the radius at which the integration starts. The DUSTY codes
requires the temperature rather than the radius because it is based on
a scale-free algorithm.
- ... SED
![[*]](/icons/foot_motif.png)
- We note that the dust optical
thickness
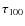 affects the shape of the SED, so in general it enters into the determination of the bolometric luminosity.
affects the shape of the SED, so in general it enters into the determination of the bolometric luminosity.
- ... Gildas
![[*]](/icons/foot_motif.png)
- http://iram.fr/IRAMFR/GILDAS/doc/html/mis-html/node13.html
- ... center
![[*]](/icons/foot_motif.png)
- Cosmic ray ionization is a minor heating term in the protostellar envelopes.
- ...
envelope
![[*]](/icons/foot_motif.png)
- We note that it possible that a region where CO abundance is lower, because of the freezing onto the dust grains, exists. However, the gas cooling is relatively insensitive to this lower abundance for the reasons explained in the text.
All Tables
Table 1: The spectral energy distribution of IRAS 16293-2422.
Table 2: Range and step of the DUSTY input parameters.
Table 3: Summary of the dust radiative transfer analysis.
Table 4: Integrated flux and full width at half maximum ( FWHM) of the Gaussians used to model the emission of the sources A and B at 1.3 and 3 mm.
Table 5:
![]() values obtained comparing the visibility amplitudes observed and modeled at 1.3 mm.
values obtained comparing the visibility amplitudes observed and modeled at 1.3 mm.
Table 6: Predictions of the line fluxes (after subtraction of the continuum) of the water lines observable with the Herschel spectrometer HIFI.
Table 7: Predictions of the line fluxes (after subtraction of the continuum) of the water lines observable with the Herschel spectrometer PACS.
All Figures
![\begin{figure}
\par\includegraphics[width=12cm,angle=0]{13112f01.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg24.png)
|
Figure 1:
Continuum emission profiles at 850 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,angle=0]{13112f02.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg51.png)
|
Figure 2:
MIR Spitzer and IRAS fluxes as a function of the wavelength. The two crosses represent the integrated fluxes at 23.7 and 25 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,angle=90]{13112f03.ps}\\ [2mm]
\includegraphics[width=9cm,angle=90]{13112f04.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg52.png)
|
Figure 3: Dust temperature ( upper panel) and H2 density ( lower panel) profiles from the best-fit obtained in the two cases Shu-like (solid line) and single power-law density distribution (dashed line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,angle=0]{13112f05.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg56.png)
|
Figure 4:
Visibility amplitudes as a function of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\rotatebox{0}{\includegraphics[width=9cm]{13112f06.ps}}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg74.png)
|
Figure 5:
Reduced- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\rotatebox{0}{\includegraphics[width=8.2cm]{13112f07.ps}}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg79.png)
|
Figure 6:
Ratio of the observed to predicted H2O line flux versus the upper level energy in cm-1. In these computations, we used the dust temperature and density profiles of the Shu-like model of Table 3 and an H2O abundance equal to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=10cm,angle=90]{13112f08.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg80.png)
|
Figure 7: Dust (solid line) and gas (dashed line) temperature profiles of the best-fit model obtained assuming a Shu-like density distribution (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=90]{13112f09.ps}\\ [2mm]
\par\includegraphics[width=9.4cm,angle=90]{13112f10.ps}
\end{figure}](/articles/aa/full_html/2010/11/aa13112-09/Timg81.png)
|
Figure 8:
Heating ( top panel) and cooling ( bottom panel) rates as function of the radius, computed assuming that the inner H2O abundance is equal to
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.