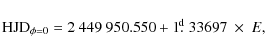EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 518 (July-August 2010) A&A, 518 (2010) A48 Full HTML
Free Access
Issue
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
Article Number A48
Number of page(s) 12
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201014460
Published online 02 September 2010
A&A 518, A48 (2010)

Photospheric and chromospheric activity on the young solar-type star HD 171488 (V889 Herculis)[*],[*]

A. Frasca1 - K. Biazzo1,2 - Zs. Kovári3 - E. Marilli1 - Ö. Çakirli4,5

1 - INAF, Osservatorio Astrofisico di Catania, via S. Sofia, 78, 95123 Catania, Italy
2 - INAF, Osservatorio Astrofisico di Arcetri, L.go E. Fermi, 5, 50125 Firenze, Italy
3 - Konkoly Observatory, 1525 Budapest, PO Box 67, Hungary
4 - Ege University, Science Faculty, Astronomy and Space Sciences Dept., 35100 Bornova, Izmir, Turkey
5 - TÜBITAK National Observatory, Akdeniz University Campus, 07058 Antalya, Turkey

Received 18 March 2010 / Accepted 4 May 2010

Abstract
Aims. We present the results of contemporaneous spectroscopic and photometric monitoring of the young solar-type star V889 Herculis ( $P_{\rm rot}\simeq 1.337$ days) aimed at studying surface inhomogeneities at both photospheric and chromospheric levels.
Methods. Echelle FOCES spectra ($R\simeq$40000) and Johnson BV photometry have been performed in August 2006, with a good coverage of rotational phases. Spectral type, rotational velocity, metalicity, and gravity were determined with a code developed by us (ROTFIT) and a library of high-resolution spectra of slowly-rotating reference stars. The metalicity was measured from the analysis of iron lines with the MOOG code. The spectral subtraction technique was applied to the most relevant chromospheric diagnostics included in the FOCES spectral range, namely Ca II IRT, H$\alpha $, He ID3, H$\beta $, and Ca II H&K lines.
Results. A simple model with two large high-latitude spots is sufficient to reproduce the B and V light curves as well as the radial velocity modulation if a temperature difference between photosphere and spots of about 1500K is used. A Doppler-imaging analysis of photospheric lines basically confirms a similar spot distribution. With the help of an analogous geometric two-spot model, we are able to reproduce the observed modulations in the residual chromospheric emissions adopting different values of ratios between the flux of plages and the quiet chromosphere (about 5 for H$\alpha $ and 3 for Ca II diagnostics). Facular regions of solar type appear to be the main responsible features for the modulations of chromospheric diagnostics. Both the spot/plage model and the cross-correlation between the light curve and the chromospheric line fluxes display a significant lead effect of plages with respect to spots (from 20 $\hbox{$^\circ$ }$ to 40 $\hbox{$^\circ$ }$ in longitude), as already observed in some active solar-type stars and RS CVn systems.
Conclusions. The contemporaneous monitoring of photospheric and chromospheric diagnostics in the young and rapidly rotating solar-type star HD 171488 allowed us to detect active regions which have nearly the same location at both atmospheric layers, with plages slightly leading spots in longitudes. These active regions are similar to the solar ones in some respects, because the spot temperature is close to that of sunspot umbrae and the plage flux-contrast is consistent with the average solar values. The main differences with respect to the Sun are larger sizes and higher latitudes.

Key words: stars: activity - starspots - stars: chromospheres - stars: rotation - stars: individual: HD 171488

1 Introduction

Young solar-mass stars just arrived on the Zero-Age Main Sequence (ZAMS) or on their way to it are in a very important phase of their life. Indeed, at this time they start to spin up approaching the ZAMS when they get free from their circumstellar disks. Thereafter, the disks can start to ``condense'', giving rise to proto-planetary systems, and the stars experience angular momentum loss resulting from a magnetized stellar wind. It is therefore very important to define the physical conditions that affect the subsequent evolution of the star and of its environment. In addition to the basic stellar parameters ( $T_{\rm eff}$, $\log g$, [Fe/H]), it is of fundamental importance to know the rotation rate and the level and behavior of the star's magnetic activity.

Fast rotators with an age of about 100 Myr likely originate from a less efficient disk-locking during their T Tau phase, but they also suggest a reduced effect of magnetic braking. It has been proposed that the rate of angular momentum loss decreases or at least saturates at high rotation rates (MacGregor & Brenner 1991; Barnes & Sofia 1996). Saturation of magnetic activity is witnessed by the typical behavior of X-ray emission and other activity signatures as a function of the rotation speed (Randich 1997; Krishnamurthi et al. 1997). Periodic variability of saturated fast-rotating stars is present both in the optical continuum (e.g., Marilli et al. 1997; Stassun et al. 2004) and in the X-ray band (Flaccomio et al. 2005). This rises questions about the true extent of saturation in fast-rotating stars. It is intriguing that very fast rotating stars, for which a ``super saturation" regime, i.e. a slight decline of magnetic activity with the increase of rotation rate, is displayed (Prosser et al. 1996), still show organized magnetic topologies but inefficient angular momentum losses (Stepien et al. 2004).

For all these reasons we consider it mandatory to investigate the surface topology of magnetic active regions on fast-rotating young stars, also because of the implications on the stability and early evolution of planetary systems.

The source HD 171488 (=V889 Herculis) is a young fast-rotating solar analog that has been the subject of several studies in the last decade. Its kinematic properties indicate that HD 171488 is a member of the Local Association, a stream of young stars with ages ranging from 20 to 150 Myr (Montes et al. 2001). It is probably the brightest single early-G type star that is rotating fast enough for mapping its photosphere through Doppler imaging (DI). Strassmeier et al. (2003) made the first dedicated photometric and spectroscopic study of HD 171488 in which they defined its astrophysical parameters, concluding that it is a single G0V main-sequence star with an age of about 30-50 Myr based on both its position on the HR diagram and the lithium content. They also made the first reconstruction of its photosphere through the DI technique, showing a big polar spot with additional high-latitude features. Subsequent works based on DI have always found a polar spot (Jeffers & Donati 2008; Marsden et al. 2006). From long-term photometry and DI, two active longitudes separated by about 180$^{\circ}$ seem to be persistent for several years (Huber et al. 2009; Järvinen et al. 2008). Jeffers & Donati (2008) found a high solar-type differential rotation with the equator lapping the poles every 12-13 days. Järvinen et al. (2008) found instead a much weaker differential rotation.

Despite the number of works devoted to this object in the last few years, which are mainly based on DI or Zeeman-DI, a simultaneous detailed investigation of the chromospheric and photospheric inhomogeneities has not been performed so far.

In the present work we analyze contemporaneous BV photometry and high-resolution spectra of HD 171488. We determined the main parameters of the photospheric spots by means of the DI technique applied to a few suitable absorption lines and of a spot model for simultaneous solution of light and radial velocity curves. The behavior of chromospheric inhomogeneities was investigated with the Ca  II H & K ( $\lambda=3968.49$ Å, 3933.68 Å), H$\epsilon $ ( $\lambda= 3970$.074 Å), H$\alpha $ ( $\lambda=6562.849$ Å), and Ca  II infrared triplet (IRT; $\lambda=8498.06$ Å, 8542.14 Å, 8662.17 Å) lines.

The work is organized as follows. In Sect. 2 we describe the observations and data reduction. The spectral classification, rotational and radial velocities, evolutionary status, and metalicity are discussed in Sect. 3. The diagnostics of photospheric and chromospheric activity are analyzed in Sects. 4 and 5, respectively. A short discussion of the behavior of photospheric and chromospheric activity is presented in Sect. 6. Section 7 contains our conclusions.

2 Observations and reduction

2.1 Spectroscopy

We observed HD 171488 at the 2.2-m Cassegrain telescope of the Calar Alto Observatory (CAHA, Sierra de Los Filabres, Spain) with the Fiber Optics Cassegrain Échelle Spectrograph (FOCES; Pfeiffer et al. 1998) during four nights from 13 to 16 August, 2006. The $2048\times2048$ CCD detector Site#1d (pixel size = 24 $\mu$m) allowed us to achieve with an exposure time of 15 min a signal-to-noise (S/N) ratio in the range 80-160 for HD 171488 ( $V\simeq7\hbox{$.\!\!^{\rm m}$ }4$), depending on airmass and sky conditions.

The spectral resolution, as evaluated from the full-width-at-half-maximum (FWHM) of the emission lines of the Th-Ar calibration lamp, was in the range 0.15-0.22 Å from the blue to the red, yielding a resolving power $R=\lambda/\Delta\lambda~\simeq~$40 000.

The data reduction was performed with the ECHELLE task of the IRAF[*] package, following the scheme summarized by Biazzo et al. (2009).

To remove the telluric water vapor lines at the H$\alpha $ and Na  I D2 wavelengths, we used the procedure described by Frasca et al. (2000), adopting as telluric template a high-S/N spectrum of V889 Herculis (A7 IV, $v\sin i=196$ km s-1), acquired during our observing run.

2.2 Photometry

The photometric observations were performed in the B and V Johnson filters with the 91-cm Cassegrain telescope at the M. G. Fracastoro station (Serra La Nave, Mt. Etna, Italy) of the Osservatorio Astrofisico di Catania (OACt). The observations were made with a photon-counting refrigerated photometer equipped with an EMI 9893QA/350 photomultiplier, cooled to  $-15~^\circ$C. The dark-current noise of the detector, operated at this temperature, is about 1 count/s.

The solar analog HD 171488 was observed from 14 to 21 August 2006 for a total of eight nights, along with V889 Herculis ( $V=6\hbox{$.\!\!^{\rm m}$ }84$, B-V=1.06, Oja 1987), which was used as a comparison star (C) for the differential photometry and V889 Herculis ( $V=5\hbox{$.\!\!^{\rm m}$ }79$, B-V=0.00, present work) and V889 Herculis ( $V=8\hbox{$.\!\!^{\rm m}$ }43$, B-V=0.57, present work) as check (Ck1, Ck2) stars. We adopted HD 171286 as the local standard for the determination of the photometric instrumental ``zero points''. Several standard stars selected from the list of Landolt (1992) were also observed during the run to determine the transformation coefficients to the Johnson standard system. The observed magnitudes were corrected for atmospheric extinction using the seasonal average coefficients for the Serra La Nave Observatory.

The data were reduced by means of the photometric data reduction package PHOT designed for the photoelectric photometry of the OACt (Lo Presti & Marilli 1993). The photometric errors, estimated from measurements of standard stars with a brightness comparable to the program stars, are typically $\sigma_V \approx 0\hbox{$.\!\!^{\rm m}$ }010$ and $\sigma_{B-V} \approx 0\hbox{$.\!\!^{\rm m}$ }014$.

In order to improve the photometric precision we averaged four consecutive measurements of the variable and adopted the standard deviation, ranging from about 0.005 to 0.015 mag, as an error estimate for each of the mean photometric points.

The photometric data are reported in Table 5.

3 Astrophysical parameters

Thanks to the high resolution and the wide wavelength coverage of the FOCES spectra, we redetermined spectral type, effective temperature, gravity, metalicity, radial and rotational velocity and quoted these values in Table 1 along with literature values. The evolutionary status of HD 171488 was also checked.

Table 1:   Physical parameters of HD 171488 from the literature and present work.

3.1 Spectral type and rotational velocity

The spectral type and the $v\sin i$ of HD 171488 was derived through the IDL[*] code ROTFIT (Frasca et al. 2006). The code simultaneously finds the spectral type and the $v\sin i$ of the target searching for, into a library of standard star spectra, the spectrum which is best fitting (minimum of the residuals) the target one, after the rotational broadening by convolution with a rotational profile of increasing $v\sin i$ at steps of 0.5 km s-1. We acquired spectra of a very small sample of standard stars (nine objects) with FOCES during our run. Thus, we preferred to use a library of 185 ELODIE Archive standard stars well distributed in effective temperature, spectral type, and gravity, and in a suitable range of metalicities (Prugniel & Soubiran 2001) that have nearly the same resolution ($R\simeq$ 42 000) as our FOCES spectra. We found for HD 171448 a G2V spectral type, a nearly solar metalicity, [Fe/H $]=+0.01\pm0.09$, $\log g=4.30\pm0.15$, and $T_{\rm eff}=5750\pm130$ K (see Table 1), as average parameters of the best ten standard stars per each echelle order. This temperature range encompasses all the previous $T_{\rm eff}$ values from the literature.

We remark that our temperature determination is not strongly affected by starspots due to their low contribution to the observed flux in the spectral range of the observations. Indeed, as shown by Frasca et al. (2005), for large spot-photosphere temperature differentials the star's integrated emission is dominated by non-spotted photospheric flux. In their Appendix A Frasca et al. (2005) outline a formalism for evaluating the mean temperature observed from a star in a given spectral region with a given spot filling-factor and photosphere-spot temperature difference, $\Delta T$. Adopting $T_{\rm eff}=5800$ K, $\Delta T=1500$ K, and a filling-factor of 0.1, which is likely an overestimation, the measured temperature would be at most only 50 K cooler than the true photospheric temperature. Thus we conclude that the ``undisturbed'' photospheric temperature must be of about 5800 K, and we adopted this value for the following analysis.

For the $v\sin i$ determination, we chose as ``non-rotating'' templates three stars with spectral type similar to HD 171488 observed with FOCES during the same run, namely V889 Herculis (F8V), V889 Herculis (F9V-IV), and V889 Herculis (G2V). We found $v\sin i=37.1\pm$1.0  km s-1 as the average of different echelle orders and these three templates, which agrees very well with the literature values reported in Table 1. However, using the ROTFIT code with the ELODIE templates, we found a nearly equal value of 37.4  km s-1.

Examples of the application of the ROTFIT code to two different spectral regions are shown in Fig. 7, where the very good agreement between observed and standard spectra is apparent.

3.2 Radial velocity

We measured the heliocentric radial velocity ($V_{\rm r}$) by means of the cross-correlation technique, (e.g., Simkin 1974; Gunn et al. 1996), taking advantage of the wide spectral coverage offered by FOCES. The radial velocity standard star $\alpha $ Ari ( $V_{\rm r}=-14.2$  km s-1), observed in the same run, was used as template. We cross-correlated each spectral order of the FOCES spectra of HD 171488 with the template with the IRAF task FXCOR, avoiding the orders with low S/N ratio or contaminated by broad and/or chromospheric lines (e.g., H$\alpha $, Na  II D2, Ca  II H&K) or by prominent telluric features. We ended up with 60 orders useful for the calculation of the cross-correlation functions (CCFs). The radial velocities listed in Table 2 per spectrum are weighted averages of the values of the 60 chosen orders with weights $w_i = 1/\sigma_i^2$, where $\sigma_i$ is the error for the ith order evaluated by FXCOR. The average value over the entire observing run is $V_{\rm r}=-23.3\pm0.2$ km s-1, which closely agrees with previous determinations. Anyway, the individual values of $V_{\rm r}$ display a clear rotational modulation (see Fig. 6) as already found by Huber et al. (2009) and explained in terms of a ``Rossiter-McLaughlin'' effect caused by starspots instead of eclipses, as in the original formulation (e.g., Rossiter 1924).

3.3 Evolutionary status, lithium abundance and age

We checked the evolutionary status of HD 171488 by means of its position in the Hertzsprung-Russell (HR) diagram (Fig. 1) and the lithium content. We used the evolutionary tracks calculated by Palla & Stahler (1999) for the pre-main sequence phase. The unspotted photospheric temperature of 5800 K was adopted. To derive the stellar luminosity we firstly evaluated the interstellar extinction $A_{\rm V}\simeq 0.03$ mag (quite negligible) from the Hipparcos parallax ( $\pi=26.87\pm0.89$ mas, Perryman et al. 1997), assuming a mean extinction of 0.7 mag/kpc. Then the de-reddened V0 magnitude at maximum brightness (spottedness minimum) was converted into absolute magnitude $M_{\rm V}$ with the parallax and subsequently converted into bolometric magnitude by using the bolometric correction tabulated by Flower (1996) as a function of the effective temperature. The bolometric magnitude of the Sun, $M_{\rm bol} = 4.64$ (Cox 2000), was used to express the stellar luminosity in solar units ( $L\simeq 1.2~L_{\odot}$).

The comparison with the evolutionary tracks and isochrones of Palla & Stahler (1999) indicates that HD 171488 is a post-T Tau or ZAMS star with an age of $\approx$ 50 Myr, a mass of about 1.08 $M_{\odot}$, and a radius $R\simeq~1.1~R_{\odot}$, in good agreement with previous determinations. The comparison with the Siess et al. (2000) evolutionary tracks leads to slightly higher values of mass ( $M\simeq 1.16~M_{\odot}$) and age (70-100 Myr) that are, however, still consistent with the former within the errors.

Table 2:   Radial velocities and parameters of the subtracted spectra.

\begin{figure} \par\includegraphics[width=8.4cm,clip]{14460f1.ps} \end{figure} Figure 1:

Position of HD 171488 on the HR diagram. The evolutionary tracks and isochrones of Palla & Stahler (1999) are shown by continuous and dotted lines, respectively. The birth line of Palla & Stahler (1999) is displayed by a dashed line.

Open with DEXTER

Another evidence of the youth of our object is given by the Li I $\lambda6707.8$ absorption line. Indeed, lithium is strongly depleted from the stellar atmospheres of late-type stars when mixing mechanisms pull it deeply in their convective layers, and a deep Li  I $\lambda $6707.8 photospheric absorption line is generally considered as a youth indicator (e.g., Soderblom et al. 1998).

The equivalent width of the lithium $\lambda $6707.8 line, $W_{\rm Li\textsc{i}}=224\pm8$ mÅ, is the average value of all the EWs measured in each FOCES spectrum. We derived a lithium abundance $A_{\rm Li}= 3.2$ by interpolation of the NLTE curves of growth tabulated by Pavlenko & Magazzù (1996). A contribution of 9 mÅ due to the FeI $\lambda $ 6707.4 Å line, evaluated according to the empirical correction proposed by Soderblom et al. (1993), $\Delta EW_{\rm Li} ({\rm m\AA})=20~(B-V)_0-3$, was subtracted before calculating the abundance. Although the lithium content cannot be simply converted into star age, HD 171488 seems to be slightly more lithium-rich than the stars in Pleiades upper envelope of the same temperature. The lithium abundance indicates an age in the range 50-150 Myr, in agreement with the position on the HR diagram.

3.4 Metalicity

The iron abundance was measured in the local thermodynamic equilibrium (LTE) assumption with the 2002 version of MOOG (Sneden 1973) and a grid of 1D model atmospheres by Kurucz (1993). The LTE iron abundance was derived by means of equivalent widths of 31 Fe I and Fe II lines in the 5000-6800 Å range measured with a Gaussian fitting procedure with the IRAF task SPLOT. For the analysis we used the prescriptions given by Randich et al. (2006). We refer the interested reader to that paper for a detailed description of the procedure, line list, and $\sigma$-clipping criteria.

The effective temperature was determined by imposing that the iron abundance does not depend on the excitation potentials of the lines. The microturbulence velocity $\xi$ was determined by imposing that the iron abundance is independent of the equivalent widths of Fe I lines. The surface gravity $\log g$ was determined by imposing the Fe I/Fe II ionization equilibrium. The initial value for the effective temperature was the one we adopted as undisturbed photospheric $T_{\rm eff}=5800$ K (Sect. 3.1). For the surface gravity we adopted as starting value the one derived by means of the ROTFIT code for spectral synthesis ( $\log g=4.3$; Sect. 3.1). The initial microturbulence velocity was set to be 1.5 km s-1. Final astrophysical parameters were $T_{\rm eff}=5850\pm100$ K, $\log g=4.3\pm0.2$, $\xi=1.8\pm0.2$ km s-1, i.e. the effective temperature and gravity did not change appreciably, while the iron abundance was $\rm [Fe/H]=+0.15\pm0.07$, which agrees with the value provided by ROTFIT taking the errors into account, but it is noticeably higher than the value of -0.5 suggested by Strassmeier et al. (2003).

4 Photospheric activity

\begin{figure} \par\mbox{\includegraphics[width=6.5cm,clip]{14460f2a.ps}\hspace{4mm} \includegraphics[width=6.5cm,clip]{14460f2b.ps} } \end{figure} Figure 2:

Doppler maps (top panels), line-profile fits (middle panels), and light-curve fits (bottom panels) for Ca  I-$\lambda $6439 (left panels) and Fe  I-$\lambda $6411 (right panels). The arrows below each map indicate the phases of spectroscopic observations.

Open with DEXTER

4.1 Light curve and spot modeling

The photometric data acquired contemporaneously to the spectroscopic ones allowed us to obtain a light-curve showing a rotational modulation due to spots (Fig. 6). The rotational phases were derived according to the Järvinen et al. (2008) ephemeris

\begin{displaymath}{\rm HJD}_{\phi=0} = 2~449~950.550+1\hbox{$.\!\!^{\rm d}$ }33697~\times~E , \end{displaymath} (1)

where the rotational period ( $P_{\rm rot}$) is nearly identical to the value of 1.3371 days found by Strassmeier et al. (2003). With a periodogram analysis and a CLEAN deconvolution algorithm (Roberts et al. 1987) we found a period of $1.37\pm0.12$ days that is fully consistent with the value of Järvinen et al. (2008), taking the limited time span of our data into account.

The V light-curve has a slightly asymmetric shape with a maximum brightness $V_{\rm max}\simeq 7\hbox{$.\!\!^{\rm m}$ }40$ at about phase 0.4, a minimum around 0.0 phase, and a variation amplitude $\Delta V\simeq0.07 $ mag. Its shape is very similar to that shown by Järvinen et al. (2008) in their Fig. 2 for the mean epoch 2006.79.

For a first reconstruction of the photospheric inhomogeneities, we used MACULA (Frasca et al. 2005), a spot model code which assumes circular dark or bright spots on the surface of a spherical limb-darkened star. The flux contrast between spotted areas and quiet photosphere ( $F_{\rm sp}/F_{\rm ph}$) is evaluated through the PHOENIX NextGen (Hauschildt et al. 1999) atmosphere models adopting T=5800 K for the quiet photosphere. With only two photometric bands and the rather small amplitude of the light curve it is not easy to derive the spot temperature. Thus we preferred to fix the spot temperature, $\Delta T=1500$ K, close to the values found for high latitude spots by Strassmeier et al. (2003) and Järvinen et al. (2008) with DI technique, and let the spot area and location be free to vary. In order to minimize the degrees of freedom and still allowing the code to reproduce an asymmetric light curve, only two spots have been put on the photosphere. We adopted the same inclination of the rotation axis used by Strassmeier et al. (2003), $i=55^\circ$. We also exploited the information contained in the radial velocity searching for a solution of the B, V light curves that simultaneously reproduce the $V_{\rm r}$ behavior. The synthetic curves are displayed by dotted lines superimposed to the data in Fig. 6 and the spot parameters are quoted in Table 4. The light curves alone mainly constrains the spot longitudes and areas, with only a raw indication of latitudes. Anyway, the broad light modulation, as well as the shape and amplitude of radial velocity variations, force the spots to have high latitudes ($75^\circ$ and $60^\circ$) as found in previous studies. This simple model will be also applied to the chromospheric line-fluxes curves in Sect. 6 for the study of the spatial relation between photospheric and chromospheric active regions (ARs).

4.2 Doppler imaging

For a more accurate surface reconstruction we used the Doppler imaging code TEMPMAP by Rice et al. (1989). It performs a full LTE spectrum synthesis by solving the equation of transfer through a set of model atmospheres (Kurucz 1993) at all aspect angles and for a given set of chemical abundances. Simultaneous inversions of the spectral lines as well as of two photometric band-passes (Johnson B and V in the present case) are then carried out using maximum-entropy regularization.

The 10 available spectra collected over three rotations cover the whole rotational phase, i.e., they can be used to reconstruct one single Doppler image. The last spectrum from the time series was excluded due to an insufficient S/N ratio.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{14460f3.ps} % \end{figure} Figure 3:

Average map from the two single-line inversions in Fig. 2.

Open with DEXTER
\begin{figure} \par\includegraphics[width=16cm,height=10cm,clip]{14460f4.ps} % \end{figure} Figure 4:

Top of each panel: examples of observed, continuum-normalized spectra of HD 171488 (solid line) in the H$\alpha $, H$\beta $, He  I D3, and Ca  II IRT regions together with the non-active stellar template (dotted line). Bottom of each panel: the difference spectra of the two upper spectra. The hatched area represents the excess emission (absorption for He  I D3) that has been integrated to get the net equivalent width.

Open with DEXTER

Doppler imaging was performed within the 6392-6440 Å spectral range using two lines, the Fe   I-6411, and Ca   I-6439 lines. The quality of the data with a low S/N ratio did not allow us to use other lines in the domain. The individual reconstructions as well as the average map are shown in Figs. 2 and 3, respectively. The maps revealed a similar spot distribution, i.e., mainly cool polar spots with temperature contrasts of up to $\approx$1500 K with respect to the undisturbed surface of 5800 K. Some low-latitude features are also recovered, however, with significantly weaker contrast ranging from $\approx$300 K (Ca   I-6439) to a maximum of $\approx$500 K (Fe   I-6411). Numerous bright features also appeared as mirroring of dominant cool spots, thus most of them are believed to be artifacts.

Despite small differences, the resulting Ca and Fe maps agree very well (cf. the average map in Fig. 3). The overall structure reveals a dominant cool polar spot with a broad appendage extending in longitude between $\sim$ $180^{\circ}{-}300^{\circ}$ and another cool region, at a mid-latitude of $\sim$ $60^\circ$, centered at a longitude $\phi\simeq 45^{\circ}$. This result is reminiscent of the maps obtained by Järvinen et al. (2008), where a similar temperature distribution was recovered over several years. Moreover, the polar spot/appendage is consistent with the high-latitude circular spot (# 2) found by modeling our light curve with MACULA, while the # 1 region found by the light-curve model at $\phi=10^{\circ}$ (see Table 4) matches well the lump of the polar spot at $\sim0^{\circ}$ phase along with the mid-latitude spot at $\phi=45^{\circ}$.

\begin{figure} \par\includegraphics[width=13cm,height=11cm,clip]{14460f5.eps} \end{figure} Figure 5:

Top panel: example of an observed, continuum-normalized spectrum of HD 171488 (solid line) in the Ca  II H & K region together with the non-active stellar template (dotted line). Bottom panels: the difference spectrum. H$\epsilon $ emission is barely visible in the raw spectrum, but it is clearly emphasized in the residuals.

Open with DEXTER

5 Chromospheric activity

The wide wavelength range of FOCES allowed us to study the chromosphere of HD 171488 by using several lines from the near UV to the NIR wavelengths (namely, Ca  II H & K, H$\beta $, He  I D3, H$\alpha $, Ca  II IRT), which provide information on different atmospheric levels, from the region of temperature minimum to the upper chromosphere. To derive the chromospheric losses, we used the ``spectral synthesis'' technique, based on the comparison between the target spectrum and an observed spectrum of a non-active standard star (called ``reference spectrum''). The difference between the observed and the reference spectrum provides as residual the net chromospheric line emission, which can be integrated to produce an emission equivalent width, $W^{\rm em}$ (see, e.g., Barden 1985; Montes et al. 1995; Herbig 1985; Frasca & Catalano 1994).

The non-active star used as a reference for the spectral subtraction is V889 Herculis (=V889 Herculis), a G2 V star (B-V=0.62) with a very low activity level, as indicated by the low value of the Ca  II Mt. Wilson index (S=0.156, Duncan et al. 1991), close to the value for the quiet Sun (S=0.159, Oranje 1983), and by the deepest H$\alpha $ core among the G-type stars investigated by Herbig (1985). This star was also observed with FOCES during the same run as HD 171488. In Fig. 4 we show an example of a spectrum of HD 171488 in the H$\alpha $, H$\beta $, He  I D3, and Ca  II IRT regions together with the standard-star spectrum rotationally broadened to $v\sin i=37$ km s-1, which mimics the active star in absence of chromospheric activity. The Ca  II H & K region is displayed in Fig. 5. The H$\alpha $, H$\beta $, and Ca  II IRT profiles are clearly filled-in by emission. The Ca  II IRT $\lambda $8542 line displays a small emission reversal in its core. The He  I $\lambda $5876 line appears as an absorption feature. The Ca  II H & K cores exhibit strong emission features and H$\epsilon $ emission is also visible (Fig. 5).

The values of emission equivalent widths, $W^{\rm em}$, in the different chromospheric diagnostics are listed in Table 2 along with their errors.

We also evaluated the total radiative losses in the chromospheric lines following the guidelines by Frasca & Catalano (1994), i.e. by multiplying the average $W^{\rm em}$ by the continuum surface flux at the wavelength of the line. The latter was evaluated for all the stars of the spectrophotometric atlas of Gunn & Stryker (1983) with the angular diameters calculated through the Barnes & Evans (1976) relation. The continuum flux of HD 171488 was found by interpolating the values for the Gunn & Stryker (1983) stars at B-V=0.62. As a check, we also used the synthetic low-resolution NextGen spectra (Hauschildt et al. 1999) by interpolating the tabulated continuum fluxes at the star temperature. We found nearly identical values of the continuum flux (within 5%) with the two methods. The average chromospheric line fluxes are reported in Table 3.

Table 3:   Radiative chromospheric losses, $\chi ^2$, and probability for the line-flux modulations.

For evaluating the significance of the $W^{\rm em}$ modulations we used simple $\chi ^2$ tests. If the data are totally uncorrelated with the rotational phase, no significant $\chi ^2$ difference is expected between a fit of a smooth periodic function and that of a constant function (the weighted average of the data). As a fitting function, we used a Fourier polynomial of degree 2, which is able to reproduce asymmetrical curves. Additionally, we calculated the probability $P_{\chi^2<\chi^2_0}$ that in a $\chi ^2$ distribution with n-p-1 degrees of freedom (with n the number of data points and p the number of fitting parameters) a random variable is less than the measured $\chi^2_0$. A low value of $P_{\chi^2<\chi^2_0}$ for the periodic function assures a statistically significant modulation. The $\chi ^2$ and $P_{\chi^2<\chi^2_0}$ values are also reported in Table 3.

\begin{figure} \par\mbox{\includegraphics[width=6.cm,height=8cm,clip]{14460f6a.e... ...mm} \includegraphics[width=6.cm,height=8cm,clip]{14460f6b.eps} } \end{figure} Figure 6:

Left panels, from top to bottom: V magnitude, $W^{\rm em}_{\rm H\alpha }$, $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-IRT}$, and $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-H+K}$ versus the rotational phase. Note the clear anti-correlation of the photospheric (V light curve) and chromospheric diagnostics. The dotted lines represent the solution of spot/plage model. Right panels, from top to bottom: B magnitude, radial velocity, $W^{\rm em}_{\rm H\beta }$, and $W_{\rm He\textsc {i}}$ versus the rotational phase.

Open with DEXTER

5.1 H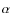$\alpha $ line

The H$\alpha $ line is one of the most useful and easily accessible indicators of chromospheric emission related to solar and stellar activity. Its source function is photoionization-dominated in the quiet chromospheres of the Sun and solar-like stars, but it can become collision-dominated in very active stars or inside ARs. As a consequence, H$\alpha $ is useful for detecting chromospheric solar and stellar plages, thanks to their high contrast against the surrounding chromosphere.

All our FOCES spectra of HD 171488 always show an H$\alpha $ absorption profile with a considerable filling-in of the core. The residual H$\alpha $ profile is almost symmetric (see Fig. 4). The values of the residual emission $W^{\rm em}_{\rm H\alpha }$ are plotted as a function of the rotational phase in Fig. 6, where a smooth rotational modulation anti-correlated with the light curve is apparent. The results of the $\chi ^2$ analysis, summarized in Table 3, assure the statistical significance of the observed H$\alpha $ rotational modulation.

5.2 H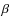$\beta $ line

When compared with the non-active template, the H$\beta $ profile of HD 171488 also appears filled in by core emission. This contribution is, however, much smaller than for the H$\alpha $ line, as expected from the lower transition probabilities for H$\beta $ and the higher photospheric flux at 4861 Å.

The results of the $\chi ^2$ analysis (Table 3) indicate that the small-amplitude variation displayed by $W^{\rm em}_{\rm H\beta }$ is not statistically significant.

As a further test we calculated the Spearman's rank-correlation coefficient between $W^{\rm em}_{\rm H\beta }$ and $W^{\rm em}_{\rm H\alpha }$ by means of the IDL procedure RCORRELATE (Press et al. 1986). We found a very low correlation coefficient $\rho=6\times10^{-8}$ with a significance 1.0, which means no correlation. We remark that this could be due to the faintness of the residual emission that prevents us from clearly detecting variations over the errors.

On the basis of the H$\alpha $ and H$\beta $ flux we evaluated a Balmer decrement $F_{\rm H\alpha}/F_{\rm H\beta}~\simeq~2.7~\pm~0.6$. As suggested by Hall & Ramsey (1992), high values of the Balmer decrement ($\sim$10) are typical of solar prominences seen off-limb (e.g., Landman & Mongillo 1979), whereas solar plages or flares have always values of about 1-2 (e.g., Chester 1991). Indeed, the theoretical NLTE model developed by Buzasi (1989) leads to high Balmer decrement values, ranging from 3 to 15 for prominence-like structures viewed away from the stellar disk, while values in the range 1-2 are found for plage-like structures.

The Balmer decrement measured for HD 171488 suggests that the emission in the Balmer lines is basically due to magnetic surface regions analog to solar plages, and eventual prominences play a marginal role.

5.3 Helium D3 line

The He  I $\lambda $ 5876 (D3) line is another useful diagnostics of chromospheric activity in the optical domain. It is particularly helpful for F-type stars in which the other activity indicators in the optical/IR range are more difficult to be observed due to the strong continuum flux (e.g., Rachford & Foight 2009). Both in these stars and in the moderately active G an K-type stars, this line is normally seen as an absorption feature (e.g., Huenemoerder 1986; Biazzo et al. 2007). The He  I absorption implies a temperature of $\sim$10 000 K in the layer where the line is formed, i.e. this line, as in the Sun, is a diagnostics of the upper chromosphere.

The adopted reference spectrum (72 Her) does not show any He  I absorption nor emission, as expected on the basis of its very low activity level. In this case, the spectral subtraction technique, cleaning the spectrum from nearby photospheric absorption lines, allows us to emphasize the He  I line of HD 171488, which appears as an excess absorption in the residual spectra (see Fig. 4), and to measure its equivalent width, $W_{\rm HeI}$. For $W_{\rm HeI}$ we adopted the usual convention that an absorption line has a positive equivalent width.

As seen in Table 2 and Fig. 6, the D3 line is always in absorption with small variations only possibly correlated with the star rotation.

As for the H$\beta $, the $\chi ^2$ test indicates that there is no significant rotational modulation of $W_{\rm HeI}$. However, the rank-correlation coefficient with the H$\alpha $, $\rho=-0.345$ with a significance 0.298, indicates a marginal anti-correlation between $W^{\rm em}_{\rm H\alpha }$ and $W_{\rm HeI}$, in the sense that the He  I absorption is slightly weaker when the net H$\alpha $ emission gets stronger.

Table 4:   Spots and plages parameters.

5.4 Ca II H&K lines

The Ca II H & K lines show strong emission cores that appear nearly symmetric in all spectra without any detectable trace of self-absorption. H$\epsilon $ emission is barely seen only in the few best spectra and become more evident after the subtraction of the non-active template (Fig. 5). Thus, we could not investigate the behavior of H$\epsilon $ with the star rotation as we did for SAO 51891 (Biazzo et al. 2009).

The absorption wings of each of the two Ca  II lines span two échelle orders and it was necessary to merge them following the guidelines of Frasca et al. (2000) before proceeding with the spectral subtraction analysis. The non-active template was built up with the same merging procedure from the FOCES spectrum of 72 Her broadened at $v\sin i=37.1$ km s-1. No emission in the core of the Ca  II H and K lines of the template is visible (Fig. 5, upper panel), as expected from the very low chromospheric activity level reported in the literature (see above).

We measured the equivalent widths by integrating the emission profiles in the subtracted spectra, as for H$\alpha $. We disentangled the contribution of the H$\epsilon $ line from the Ca  II H by fitting Voigt functions to both profiles. The sum of the net equivalent widths of H and K lines, $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-H+K}$, displays a significant modulation with the star rotation (bottom left panel in Fig 6) that is not as outstanding as that of H$\alpha $, but its reliability is testified by the results of the $\chi ^2$ tests (Table 3). The rank-correlation coefficient, $\rho=0.567$ with a significance 0.112, supports a rotational modulation of the Ca  II H+K emission correlated with the H$\alpha $ one.

We calculated the radiative chromospheric losses in the H & K lines analogously as done for H$\alpha $. In particular, we used two 10 Å-wide bands centered at 3910 and 4010 Å, i.e. at the two sides of the H & K lines, to perform the flux calibration, following the prescriptions by Frasca et al. (2000). The ratio of the residual peak intensities, $r_{\rm K}/r_{\rm H}\simeq~1.08\pm0.015$, is higher than typical values measured in the quiet solar chromosphere ( $r_{\rm K}/r_{\rm H}\simeq1.05$), but it is lower than what it is found in solar plages ( $r_{\rm K}/r_{\rm H}\simeq1.20$, e.g. Linsky 1970). If the solar analogy is valid, this would mean that we are observing at all phases a ``mixture'' of quiet chromosphere and ARs.

5.5 Ca II IRT lines

The lines of the Ca II infrared triplet, which share the upper level of the H and K transitions, present some advantages compared to the Ca II H & K lines. They lie in a spectral region with a well-defined continuum, making the normalization easier during the data reduction. Moreover, they are not significantly affected by telluric lines and are less affected by atmospheric extinction than the visible and ultraviolet lines. As such, they have become very useful chromospheric diagnostics in recent years also thanks to the high sensitivity of the new detectors to the near infrared.

A filled-in Ca II IRT-3 ( $\lambda 8862$) line profile is shown by Busà et al. (2007) who measured a net equivalent width (after the subtraction of a synthetic profile) of 0.511 Å that is higher than the values measured by us, ranging from 0.350 to 0.402 Å. The total contribution of the three IRT lines measured by Busà et al. (2007) in 2002 is 1.46 Å, which is significantly higher than the values measured by us (1.01-1.16 Å, see Table 2). This could be due to a higher activity level during the Busà et al. observations or, more likely, to the different photospheric template used by them, which is apparently deeper in its core than our own.

Measurements of the residual EW of Ca  II IRT-3 line (after the subtraction of a solar spectrum broadened at the star's $v\sin i$) are also reported by Järvinen et al. (2008) for 2001, 2002, and 2005 epochs. They found values comparable to our determinations in 2001 and 2002 and a larger EW, on average, in 2005. Moreover, they detected also a modulation of the residual EW anti-correlated with the contemporaneous light curve in the last season.

We found a nice rotational modulation of the net equivalent widths of the IRT lines, which becomes more evident if we consider the total emission of the triplet $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-IRT}$ (see Fig. 6) that closely follows the H$\alpha $ trend. The statistical significance of the rotational modulation is assured both from the $\chi ^2$ analysis (Table 3) and from the strong correlation with the $W^{\rm em}_{\rm H\alpha }$ curve ( $\rho=0.755$ with a significance 0.007).

The flux ratio F8542/F8498=1.7, indicative of high optical depths, is in the range of the values (1.5-3) found by Chester (1991) in solar plages. Solar prominences have instead values of $F_{8542}/F_{8498}\sim 9$, typical of an optically-thin emission source. This result confirms what we found for HD 171488 from the H$\alpha $/H$\beta $ flux ratio.

6 Plage modeling

The chromospheric line-flux variations contain valuable information on the surface inhomogeneities at this atmospheric level simultaneous to the photospheric diagnostics.

We applied our spot-model IDL code, MACULA (Frasca et al. 2005), to the curves of $W^{\rm em}_{\rm H\alpha }$, $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-IRT}$, and $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-H+K}$, with the aim of further investigating the main parameters of the chromospheric plages and the degree of spot-plage correlation. Given the scatter in the data, two bright spots (plages) are fully sufficient to reproduce the observed variations.

An important parameter that enters in the plage model is the flux contrast between plages and surrounding chromosphere ( $F_{\rm plage}/F_{\rm chrom}$). Values of $F_{\rm plage}/F_{\rm chrom}$ $\approx~2$, which can be deduced averaging solar plages in H$\alpha $ (e.g., Ellison 1952; LaBonte 1986b), are too low for reproducing the $\sim$23% variation of $W^{\rm em}_{\rm H\alpha }$. Indeed, very large plages, covering a large fraction of the stellar surface, would be required with such a low flux contrast, and they do not provide a good fit of the observed modulation on the basis of the $\chi ^2$. On the other hand, very high values of flux contrast ( $F_{\rm plage}/F_{\rm chrom}~\ga 10$) would imply very small plages producing top-flattened modulations that are not observed. In order to achieve a good fit, a flux contrast of 5 was adopted.

The solutions essentially provide the longitude of the plages, giving only rough estimates of their latitude and size. We searched for the best solution starting with the values of longitude, latitude, and radii of the photospheric active regions and found that only the longitude of the plage at lower latitude must change appreciably. The plage radii are, however, strongly dependent on the assumed flux contrast $F_{\rm plage}/F_{\rm chrom}$. This means that only the combined information between plage sizes and flux contrast, i.e. some kind of plage ``luminosity'' in units of the quiet chromosphere ( $L_{\rm plage}/L_{\rm quiet}$) can be deduced as a meaningful parameter. We remark that the $W^{\rm em}$ level of the quiet chromosphere is also a rather uncertain parameter, because it depends on the plage distribution, which can give a non-negligible contribution also at the phase of minimum $W^{\rm em}$. The solution of the H$\alpha $ light curve is displayed with a dotted line in Fig. 6 along with the observed $W^{\rm em}_{\rm H\alpha }$ values.

For the solution of the $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-IRT}$ and $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-H+K}$ curves we had to use a lower plage contrast with the same radii used for the H$\alpha $ curve, namely $F_{\rm plage}/F_{\rm chrom}=3.3$ for the former and and 3.1 for the latter. This is consistent with the variation amplitude of about 14% and 11% for the $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-IRT}$ and $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-H+K}$, respectively. The solutions of the $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-IRT}$ and $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-H+K}$ light curves are also displayed with dotted lines in Fig. 6 and the parameters of the spots and plages, as recovered by our model, are listed in Table 4. The values of plage contrast in H$\alpha $ and Ca  II are nearly the same as those found by Frasca et al. (2000) for HD 206860, another young ( ${\rm age}\sim300$ Myr) early-G type star.

Considering the aforementioned size/contrast degeneracy, this would imply that in these very active solar-type stars the plages are brighter (compared to the adjacent quiet chromosphere) when observed in the H$\alpha $ compared to the Ca  II K line. This result is not in contradiction to what is known from observations of solar ARs in UV emission lines, for which the enhancement of intensity inside plages increases with the temperature of line formation (e.g., Noyes et al. 1970). As mentioned above, the flux contrast for H$\alpha $ solar plages, as measured from residual line-core intensity, $F_{\rm plage}/F_{\rm chrom}\approx1.5{-}2.5$ (e.g., Ellison 1952; LaBonte 1986b), is much lower than the value derived by us for HD 171488 and HD 206860, while $F_{\rm plage}/F_{\rm chrom}\simeq3$ found for the Ca II plages falls in the range found for the solar plages (e.g., LaBonte 1986a; Ayres et al. 1986). Anyway, for a proper comparison with solar plages we must consider that for the latter the residual photospheric flux in the line core is not removed, and indeed it is not easily distinguished from the true chromospheric emission at the low activity level of the quiet Sun. This photospheric contribution is higher in the core of H$\alpha $ than in the H&K Ca II lines, giving rise to a contrast drop. To deal with this we made our values of the H$\alpha $ and Ca II emission equivalent widths comparable with the solar determinations by adding back the photospheric contribution at the bottom of the lines as measured in the non-active template.

We found a strongly reduced amplitude, $\sim$12%, for the H$\alpha $ curve for which our model derives a plage flux contrast of 1.8, in line with the average solar values. For the Ca II H&K residual intensity, the modulation drops from $\sim$11% to $\sim$7%, which lowers the plage contrast from 3.1 to 2.5. This would imply that for very active solar-type stars the plage contrast (with respect to their ``quiet'' chromosphere) is analogous to what is found for the Sun, but the overall chromospheric flux is much higher and the plages are bigger. This gives rise to the large amplitudes of the line-flux modulations observed for very active stars.

Another interesting result of our plage model is that the longitude of the plage at lower latitude (that giving the highest contribution in the flux curves) is higher than that of the corresponding spot by about 20-40$^{\circ}$, i.e. the plage is preceding the spot in the sense of star's rotation. This result is found in all the chromospheric diagnostics for which a significant modulation has been detected and is confirmed by the simple cross-correlation of the light curve with the $W^{\rm em}$ modulations. We found a deep minimum of the CCF for the correlation between V-light curve and $W^{\rm em}_{\rm H\alpha }$ with a phase shift of the H$\alpha $ with respect to the V curve of 0.094 in phase units, which translates into a longitude difference of about +34$^{\circ}$. Slightly smaller phase shifts are found for Ca  II IRT (0.070) and Ca  II H+K (0.052), corresponding to a longitude difference of about 20$^{\circ}$ between plage and spot.

Lead and lag between plages and spots have been suggested to explain phase shifts between photometric light curves and chromospheric indicators that are not exactly in anti-phase. Radick et al. (1987) found spots leading plages by about 19$^{\circ}$ in the Hyades star V889 Herculis (G0 V), while Catalano et al. (2000) found both lead and lag in the active components of a few RS CVn systems, with a tendency for spots to lead plages. The Sun itself, when observed as a star in the integrated light of the C  II chromospheric line ($\lambda~$133.5 nm) from UARS SOLSTICE experiment, displays alternating positive and negative longitude shifts with respect to the spot photocenters (Catalano et al. 1998).

7 Conclusion

We performed an accurate analysis of high-resolution spectra and contemporaneous BV photometry of the nearby young solar-type star HD 171488 with the main aim to characterize the behavior of spots and plages on its surface. Revised astrophysical parameters, such as $T_{\rm eff}$, $\log g$, [Fe/H], rotational and heliocentric radial velocity, and lithium abundance, were also determined and were found to agree closely with previous determinations from the literature, with the exception of the metalicity, for which we did not find a sub-solar abundance as suggested by Strassmeier et al. (2003). Both the position on the HR diagram and the lithium abundance give an estimate of about 50 Myr for the age of HD 171488, confirming it as a young Sun on its way to the ZAMS.

We were able to find a clear radial velocity modulation with an amplitude of about 500 m s-1 due to a ``Rossiter-McLaughlin'' effect caused by starspots. A spot modeling of the B and V light curves, performed with our code MACULA, is also able to reproduce the radial velocity modulation by adopting only two high-latitude spots 1500 K cooler than the quiet photosphere. A more accurate surface reconstruction was also performed by applying the Doppler imaging analysis to two photospheric spectral lines and the B and V light curves. The method provides maps that essentially confirm the large polar spotted area with a temperature difference $\Delta T\simeq$ 1500 K with respect to the unspotted photosphere.

Chromospheric activity was also studied with different spectral diagnostics. Equivalent widths of the residual emissions in the cores of H$\alpha $, Ca II H&K, and Ca II IRT lines show clear modulations with the rotational phase and are ascribed to active chromospheric regions analog to solar plages. A small but significant emission in the H$\beta $ core, as well as an absorption feature corresponding to the He I $\lambda5876$ line, are emphasized by the subtraction of the non-active template and are additional proofs of the high activity level of HD 171488 also in the upper chromosphere. Due to the fairly large relative errors, no clear rotational modulation could be detected in the H$\beta $ and He I line fluxes. The average Balmer decrement, measured as the ratio of H$\alpha $ to H$\beta $ flux, confirms that the observed chromospheric emission is mainly coming from extended facular regions.

The H$\alpha $ and Ca II flux curves are well fitted by a model with two circular bright spots (plages), also performed with MACULA, with sizes similar to the underlying spots and a flux contrast of 5 for the H$\alpha $ and about 3 for the Ca II H&K and IRT fluxes, as expected from the different modulation amplitude. The flux curves are nearly anticorrelated with the photometry, even if the plage at a lower latitude precedes in longitude, by about 20 $\hbox{$^\circ$ }$-40 $\hbox{$^\circ$ }$, the corresponding photospheric spot. This finding is not anomalous, because lead and lag between plages and spots have been observed in the Sun and are frequently invoked as the cause of phase shifts between light curves and chromospheric line fluxes observed both in young active stars and in RS CVn systems.

Acknowledgements

The authors are grateful to the anonymous referee for a careful reading of the paper and valuable comments. We thank the CAHA and OACt teams for the assistance during the observations. This work has been supported by the Italian Ministero dell'Istruzione, Università e Ricerca (MIUR) and by the Regione Sicilia which are gratefully acknowledged. The ESO Scientific Visitor Programme enabled Z.s.K. and K.B. to visit ESO Garching during the preparation of the paper. Z.s.K. acknowledges the support of the Hungarian OTKA grants K-68626 and K-81421. This research has made use of SIMBAD and VIZIER databases, operated at CDS, Strasbourg, France.

References

  1. Ayres, T. R., Testerman, L., & Brault, J. W. 1986, ApJ, 304, 542 [NASA ADS] [CrossRef] [Google Scholar]
  2. Barden, S. C. 1985, ApJ, 295, 162 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barnes, S., & Sofia, S. 1996, ApJ, 462, 746 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barnes, T. G., & Evans, D. S. 1976, MNRAS, 174, 489 [NASA ADS] [CrossRef] [Google Scholar]
  5. Biazzo, K., Frasca, A., Henry, G. W., Catalano, S., & Marilli, E. 2007, ApJ, 656, 474 [NASA ADS] [CrossRef] [Google Scholar]
  6. Biazzo, K., Frasca, A., Marilli, E., et al. 2009, A&A, 499, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Busà, I., Aznar Cuadrado, R., Terranegra, L., et al. 2007, A&A, 466, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Buzasi, D. L. 1989, Ph.D. Thesis, Pennsylvania State Univ. [Google Scholar]
  9. Catalano, S., Lanza, A. F., Brekke, P., Rottmann, G. J., & Hoyng, P., 1998, in Cool Stars, Stellar Systems and the Sun, ed. R. A Donahue, & J. A. Bookbinder, ASP Conf. Ser., 154, 584 [Google Scholar]
  10. Catalano, S., Rodonò, M., Cutispoto, G., et al. 2000, in Variable Stars as Essential Astrophysical Tools, ed. C. Formula banoglu (Kluwer Academic Publishers), 687 [Google Scholar]
  11. Chester, M. M. 1991, Ph.D. Thesis, Pennsylvania State Univ. [Google Scholar]
  12. Cutispoto, G., Pastori, L., & Pasquini, L. 2002, A&A, 384, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Cox, A. N. 2000, Allen's Astrophysical Quantities, 4th edn. (New York: AIP Press and Springer-Verlag) [Google Scholar]
  14. Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
  15. Ellison, M. A. 1952, MNRAS, 112, 679 [NASA ADS] [Google Scholar]
  16. Fekel, F. C. 1997, PASP, 109, 514 [NASA ADS] [CrossRef] [Google Scholar]
  17. Flaccomio, E., Micela, G., Sciortino, S., et al. 2005, ApJS, 160, 450 [NASA ADS] [CrossRef] [Google Scholar]
  18. Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
  19. Frasca, A., & Catalano, S. 1994, A&A, 284, 883 [NASA ADS] [Google Scholar]
  20. Frasca, A., Freire Ferrero, R., Marilli, E., & Catalano, S. 2000, A&A, 364, 179 [NASA ADS] [Google Scholar]
  21. Frasca, A., Biazzo, K., Catalano, S., et al. 2005, A&A, 432, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Frasca, A., Guillout, P., Marilli, E., et al. 2006, A&A, 454, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gunn, J., & Stryker, L. L. 1983, ApJS, 52, 121 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gunn, A. G., Hall, J. C., Lockwood, G. W., & Doyle, J. G. 1996, A&A, 305, 146 [NASA ADS] [Google Scholar]
  25. Hall, J. C., & Ramsey, L. W. 1992, AJ, 104, 1942 [NASA ADS] [CrossRef] [Google Scholar]
  26. Harlan, E. A. 1969, AJ, 74, 916 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., & Alexander, D. R. 1999, ApJ, 525, 871 [NASA ADS] [CrossRef] [Google Scholar]
  28. Herbig, G. H. 1985, ApJ, 289, 269 [NASA ADS] [CrossRef] [Google Scholar]
  29. Huenemoerder, D. P. 1986, AJ, 92, 673 [NASA ADS] [CrossRef] [Google Scholar]
  30. Huber, K. F., Wolter, U., Czesla, S., et al. 2009, A&A, 501, 715 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Järvinen, S. P., Korhonen, H., Berdyugina, S. V., et al. 2008, A&A, 488, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Jeffers, S. D., & Donati, J.-F. 2008, MNRAS, 390, 635 [NASA ADS] [CrossRef] [Google Scholar]
  33. Krishnamurthi, A., Pinsonneault, M. H., Barnes, S., & Sofia, S. 1997, ApJ, 480, 303 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kurucz, R. L. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid, Kurucz CD-ROM # 13 [Google Scholar]
  35. LaBonte B. J. 1986a, ApJS, 62, 229 [NASA ADS] [CrossRef] [Google Scholar]
  36. LaBonte B. J. 1986b, ApJS, 62, 241 [NASA ADS] [CrossRef] [Google Scholar]
  37. Landman, D. A., & Mongillo, M. 1979, ApJ, 230, 581 [NASA ADS] [CrossRef] [Google Scholar]
  38. Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
  39. Linsky, J. L. 1970, Sol. Phys., 11, 355 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lo Presti, C., & Marilli, E. 1993, PHOT - Photometrical Data Reduction Package. Internal report of Catania Astrophysical Observatory N. 2/1993 [Google Scholar]
  41. MacGregor, K. B., & Brenner, M. 1991, ApJ, 376, 204 [NASA ADS] [CrossRef] [Google Scholar]
  42. Marilli, E., Catalano, S., & Frasca, A. 1997, Mem. Soc. Astron. Ital., 68, 895 [NASA ADS] [Google Scholar]
  43. Marsden, S. C., Donati, J.-F., Semel, M., Petit, P., & Carter, B. D. 2006, MNRAS, 370, 468 [NASA ADS] [CrossRef] [Google Scholar]
  44. Montes, D., Fernández-Figueroa, M. J., De Castro, E., & Cornide, M. 1995, A&AS, 109, 135 [NASA ADS] [Google Scholar]
  45. Montes, D., López-Santiago, J., Gálvez, M. C., et al. 2001, MNRAS, 328, 45 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  46. Noyes, R. W., Withbroe, G. L., & Kirshner, R. P. 1970, Sol. Phys., 11, 388 [NASA ADS] [CrossRef] [Google Scholar]
  47. Oja, T. 1987, A&AS, 71, 561 [Google Scholar]
  48. Oranje, B. J. 1983, A&A, 124, 43 [NASA ADS] [Google Scholar]
  49. Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pavlenko, Y. V., & Magazzù, A. 1996, A&A, 311, 961 [NASA ADS] [Google Scholar]
  51. Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
  52. Pfeiffer, M. J., Frank, C., Baumueller, D., et al. 1998, A&AS, 130, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1986, Numerical Recipes [Google Scholar]
  54. Prosser, C. F., Randich, S., Stauffer, J. R., Schmitt, J. H. M. M., & Simon, T. 1996, AJ, 112, 1570 [NASA ADS] [CrossRef] [Google Scholar]
  55. Prugniel, P., & Soubiran, C. 2001, A&A, 369, 1048 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Rachford, B. L., & Foight, D. R. 2009, ApJ, 698, 786 [NASA ADS] [CrossRef] [Google Scholar]
  57. Radick, R. R., Thompson, D. T., Lockwood, G. W., Duncan, D. K., & Baggett, W. E. 1987, ApJ, 321, 459 [NASA ADS] [CrossRef] [Google Scholar]
  58. Randich, S. 1997, Mem. Soc. Astron. Ital., 68, 971 [Google Scholar]
  59. Randich, S., Sestito, P., Primas, F., et al. 2006, A&A, 450, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Rice, J. B., Wehlau, W. H., & Khokhlova, V. L. 1989, A&A, 208, 179 [NASA ADS] [Google Scholar]
  61. Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968 [NASA ADS] [CrossRef] [Google Scholar]
  62. Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
  63. Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 385, 593 [NASA ADS] [Google Scholar]
  64. Simkin, S. M. 1974, A&A, 31, 129 [NASA ADS] [Google Scholar]
  65. Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
  66. Soderblom, D. R., Jones, B. F., & Balachandran, S., et al. 1993, AJ, 106, 1059 [NASA ADS] [CrossRef] [Google Scholar]
  67. Soderblom, D. R., King, J. R., & Henry, T. J. 1998, AJ, 116, 396 [NASA ADS] [CrossRef] [Google Scholar]
  68. Stassun, K. G., Ardila, D. R., Barsony, M., Basri, G., & Mathieu, R. D. 2004, AJ, 127, 3537 [NASA ADS] [CrossRef] [Google Scholar]
  69. Stepien, K., Schmitt, J. H. M. M., & Voges, W. 2001, A&A, 370, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Strassmeier, K. G., Pichler, T., Weber, M., & Granzer, T. 2003, A&A, 411, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Online Material

Table 5:   BV Johnson photometry of HD 171488.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{14460f7.ps} % \end{figure} Figure 7:

Observed FOCES spectrum of HD 171488 in the Mg  Ib triplet ( upper panel) and 5600 Å ( lower panel) spectral regions together with the ELODIE standard spectrum broadened at 37.1 km s-1 overplotted with a thin/red line. In each box the difference (observed - synthetic) is also displayed with a dotted line around zero ordinate.

Open with DEXTER

Footnotes

... (V889 Herculis)[*]
Based on observations collected at Calar Alto Astronomical Observatory (Spain) and Catania Astrophysical Observatory (Italy).
...[*]
Table 5 and Fig. 7 are only available in electronic form at http://www.aanda.org
... IRAF[*]
IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of the Universities for Research in Astronomy, inc. (AURA) under cooperative agreement with the National Science Foundation.
... IDL[*]
IDL (Interactive Data Language) is a registered trademark of ITT Visual Information Solutions.

All Tables

Table 1:   Physical parameters of HD 171488 from the literature and present work.

Table 2:   Radial velocities and parameters of the subtracted spectra.

Table 3:   Radiative chromospheric losses, $\chi ^2$, and probability for the line-flux modulations.

Table 4:   Spots and plages parameters.

Table 5:   BV Johnson photometry of HD 171488.

All Figures

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{14460f1.ps} \end{figure} Figure 1:

Position of HD 171488 on the HR diagram. The evolutionary tracks and isochrones of Palla & Stahler (1999) are shown by continuous and dotted lines, respectively. The birth line of Palla & Stahler (1999) is displayed by a dashed line.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=6.5cm,clip]{14460f2a.ps}\hspace{4mm} \includegraphics[width=6.5cm,clip]{14460f2b.ps} } \end{figure} Figure 2:

Doppler maps (top panels), line-profile fits (middle panels), and light-curve fits (bottom panels) for Ca  I-$\lambda $6439 (left panels) and Fe  I-$\lambda $6411 (right panels). The arrows below each map indicate the phases of spectroscopic observations.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{14460f3.ps} % \end{figure} Figure 3:

Average map from the two single-line inversions in Fig. 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,height=10cm,clip]{14460f4.ps} % \end{figure} Figure 4:

Top of each panel: examples of observed, continuum-normalized spectra of HD 171488 (solid line) in the H$\alpha $, H$\beta $, He  I D3, and Ca  II IRT regions together with the non-active stellar template (dotted line). Bottom of each panel: the difference spectra of the two upper spectra. The hatched area represents the excess emission (absorption for He  I D3) that has been integrated to get the net equivalent width.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=13cm,height=11cm,clip]{14460f5.eps} \end{figure} Figure 5:

Top panel: example of an observed, continuum-normalized spectrum of HD 171488 (solid line) in the Ca  II H & K region together with the non-active stellar template (dotted line). Bottom panels: the difference spectrum. H$\epsilon $ emission is barely visible in the raw spectrum, but it is clearly emphasized in the residuals.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=6.cm,height=8cm,clip]{14460f6a.e... ...mm} \includegraphics[width=6.cm,height=8cm,clip]{14460f6b.eps} } \end{figure} Figure 6:

Left panels, from top to bottom: V magnitude, $W^{\rm em}_{\rm H\alpha }$, $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-IRT}$, and $W^{\rm em}_{\rm Ca\mbox{\fontsize{5pt}{7pt}\selectfont II}-H+K}$ versus the rotational phase. Note the clear anti-correlation of the photospheric (V light curve) and chromospheric diagnostics. The dotted lines represent the solution of spot/plage model. Right panels, from top to bottom: B magnitude, radial velocity, $W^{\rm em}_{\rm H\beta }$, and $W_{\rm He\textsc {i}}$ versus the rotational phase.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{14460f7.ps} % \end{figure} Figure 7:

Observed FOCES spectrum of HD 171488 in the Mg  Ib triplet ( upper panel) and 5600 Å ( lower panel) spectral regions together with the ELODIE standard spectrum broadened at 37.1 km s-1 overplotted with a thin/red line. In each box the difference (observed - synthetic) is also displayed with a dotted line around zero ordinate.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.