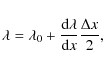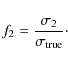| Issue |
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014428 | |
| Published online | 01 September 2010 | |
Counter-dispersed slitless-spectroscopy technique:
planetary nebula velocities in the halo of NGC 1399![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
E. K. McNeil1,2,3 - M. Arnaboldi2 - K.C. Freeman1 - O. E. Gerhard3 - L. Coccato3 - P. Das3
1 - Mt Stromlo Observatory, Australian National University, Cotter Road, Weston Creek, ACT 2611, Australia
2 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
3 - Max Planck Institute for Extraterrestrial Physics,
Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
Received 15 March 2010 / Accepted 4 May 2010
Abstract
Aims. Using a counter-dispersed slitless spectroscopy
technique, we detect and measure the line-of-sight velocities of
187 planetary nebulae (PNe) around one of the nearest cD galaxies,
NGC 1399, with FORS1 on the VLT.
Methods. We describe the method for identifying and classifying
the emission-line sources and the procedure for computing their J2000
coordinates and velocities. The number of PN detections and the errors
in the velocity measurements (37 km s-1) indicate that this technique is comparable to other methods.
Results. We present the spatial distribution of the PNe and a
basic analysis of their velocities. The PN two-dimensional velocity
field shows marginal rotation consistent with other studies. We also
find a low-velocity substructure in the halo and a flatter
velocity-dispersion profile compared to previous observations that
extends to ![]() 400
400
![]() .
The detection of a low-velocity subcomponent underscores the importance
of discrete velocity tracers for the detection of un-mixed components.
.
The detection of a low-velocity subcomponent underscores the importance
of discrete velocity tracers for the detection of un-mixed components.
Conclusions. The new velocity-dispersion profile is in good
agreement with revised velocity dispersions for the red globular
clusters in NGC 1399. The outer parts of this profile are
consistent with one of the dynamical models, which corresponds to a
circular velocity of ![]() 340 km s-1 and a rescaled B-band mass-to-light ratio of
340 km s-1 and a rescaled B-band mass-to-light ratio of ![]() 20 at 7
20 at 7![]() radius. These measurements trace the kinematics of the outer halo and
disentangle the heterogenous populations in the Fornax Cluster core.
The new data set the stage for a revised dynamical model of the outer
halo of NGC 1399.
radius. These measurements trace the kinematics of the outer halo and
disentangle the heterogenous populations in the Fornax Cluster core.
The new data set the stage for a revised dynamical model of the outer
halo of NGC 1399.
Key words: galaxies: clusters: individual: NGC 1399 - galaxies: elliptical and lenticular, cD - techniques: spectroscopic
1 Introduction
An important key to understanding the formation and evolution of
galaxies is to examine the kinematics of the halo where the orbits have
long dynamical timescales and the mass profile is dominated by dark
matter. In disk galaxies, HI measurements generally provide
line-of-sight velocities out to the edges (Rubin et al. 1977; Bosma 1978).
Measuring kinematics in the outer parts of early-type galaxies is more
complicated since HI measurements are usually unavailable, and the
signal-to-noise of the integrated-light spectra drops off before the
mass profile flattens. Specifically, long-slit spectra provide
measurements for the first 2-3 ![]() (Kronawitter et al. 2000), multi-object spectroscopy provides line-of-sight velocity distributions out to 3
(Kronawitter et al. 2000), multi-object spectroscopy provides line-of-sight velocity distributions out to 3 ![]() (Proctor et al. 2009) and IFUs can take measurements at 4
(Proctor et al. 2009) and IFUs can take measurements at 4 ![]() (Weijmans et al. 2009; Murphy & Gebhardt 2007).
Discrete tracers like planetary nebulae provide the necessary kinematic
information to examine the regions beyond these limits and learn about
the formation history of the outer regions of elliptical galaxies (Hui et al. 1995; Arnaboldi et al. 1996).
(Weijmans et al. 2009; Murphy & Gebhardt 2007).
Discrete tracers like planetary nebulae provide the necessary kinematic
information to examine the regions beyond these limits and learn about
the formation history of the outer regions of elliptical galaxies (Hui et al. 1995; Arnaboldi et al. 1996).
The planetary nebula (PN) stage occurs at the end of a star's life when
the atmosphere has been ejected and is subsequently ionized by UV
radiation from the exposed stellar core. Due to the extreme rarefaction
of the gas in the atmosphere, these objects emit up to 15% of
their light at [OIII] (![]() 5007) (Dopita et al. 1992), which allows their detection and velocity measurement out to a distance of 100 Mpc (Gerhard et al. 2005). Moreover, the PN number density traces the light in early-type galaxies (Coccato et al. 2009).
Because they follow the same spatial distribution as stars, PNe provide
kinematics that are directly related to integrated light measurements.
We are able to use planetary nebulae as kinematic tracers out to more
than 7
5007) (Dopita et al. 1992), which allows their detection and velocity measurement out to a distance of 100 Mpc (Gerhard et al. 2005). Moreover, the PN number density traces the light in early-type galaxies (Coccato et al. 2009).
Because they follow the same spatial distribution as stars, PNe provide
kinematics that are directly related to integrated light measurements.
We are able to use planetary nebulae as kinematic tracers out to more
than 7 ![]() for measuring the dark matter distribution and angular momentum content in the halo (de Lorenzi et al. 2009; Romanowsky et al. 2003; Douglas et al. 2007; Napolitano et al. 2009; de Lorenzi et al. 2008; Coccato et al. 2009; Méndez et al. 2001).
for measuring the dark matter distribution and angular momentum content in the halo (de Lorenzi et al. 2009; Romanowsky et al. 2003; Douglas et al. 2007; Napolitano et al. 2009; de Lorenzi et al. 2008; Coccato et al. 2009; Méndez et al. 2001).
In general, globular clusters follow a different spatial distribution so their kinematics do not trace the same population as the stars (Harris 1991; Brodie & Strader 2006; Ashman & Zepf 1998). The globular cluster system is dominated by the blue component of a bimodal color distribution in most galaxies. The radial distribution of this component is flatter than the integrated light from the stars. However, in many galaxies including NGC 1399, the red globular cluster sample does follow the integrated light (Schuberth et al. 2009; Brodie & Strader 2006), and we expect the kinematics of this subset to be comparable to those of the integrated light and the PNe.
Traditionally, PNe are detected using an on-band/off-band technique (Ciardullo et al. 1989). The sky is imaged through a narrow-band filter centered at the redshifted
[OIII] ![]() 5007 line
and then again in a broad band that does not contain any brightemission
lines. PNe are too faint to detect in the broad-band image, but they
appear in the narrow-band image. Foreground stars appear in both
narrow- and broad-band images, so the wide filter is used to
distinguish them from the PNe. Once the positions are measured from the
on-band image, the velocities are then typically obtained using
multi-slit or fibre spectroscopy (Doherty et al. 2009; Arnaboldi et al. 2004).
5007 line
and then again in a broad band that does not contain any brightemission
lines. PNe are too faint to detect in the broad-band image, but they
appear in the narrow-band image. Foreground stars appear in both
narrow- and broad-band images, so the wide filter is used to
distinguish them from the PNe. Once the positions are measured from the
on-band image, the velocities are then typically obtained using
multi-slit or fibre spectroscopy (Doherty et al. 2009; Arnaboldi et al. 2004).
More recently, a number of techniques have been developed that allow detection and velocity measurement to be done in the same observing run. Méndez et al. (2001) identify PNe using narrow- and broad-band images, but then follow with a dispersed image in the same run. The velocity of each PN can be calculated from the difference between the object's position in the narrow-band frame and the dispersed frame. This technique has also been applied to NGC 1344, another Fornax galaxy, by Teodorescu et al. (2005). We compare the efficiency of those observations to ours in Sect. 3.3.1.
The PN Spectrograph (PN.S) is an instrument on the William Herschel Telescope dedicated to measuring PN velocities in nearby galaxies (Douglas et al. 2002). The pupil is split in half before being dispersed in opposite directions in twin spectrographs. A combination of the two exposures, which are simultaneously generated, allows identification of emission-line objects and the measurement of their velocities using the separation between the positions in the two spectral images.
For extremely faint samples in distant galaxies, observing the entire field through slits significantly reduces the signal from the sky. Multislit Imaging Spectroscopy involves a grid of slits that are stepped until the entire field has been spectrally imaged. These types of observations have detected samples of intracluster PNe 100 Mpc away (Arnaboldi et al. 2007; Gerhard et al. 2005; Ventimiglia et al. 2008).
The counter-dispersed slitless technique in this paper uses only two exposures for each field to obtain positions and velocities of PNe in the cD galaxy, NGC 1399. The field is first observed with a dispersed image. Next the spectrograph is rotated 180 degrees and the same field is exposed again, this time with the dispersion in the opposition direction. As in the PN.S observations, the velocity is a function of the separation between the position of the PN in the two frames. In this way, the slitless technique avoids the two-stage selection and measurement process. Because there are no slits or fibres, the light loss is reduced. The number of measurable PN velocities is not limited by the number of available fibres or the restrictive geometry of the slits.
NGC 1399 is a cD galaxy in the Fornax cluster (Schombert 1986). It is one of the closest cD galaxies and therefore promises one of the best kinematic data sets for the outer halo. Located near the center of their clusters, cD galaxies are believed to form through accretion and mergers with other cluster members. As such, these galaxies are valuable clues to the formation history of galaxies and the evolution of clusters (Hausman & Ostriker 1978).
![\begin{figure}
\par\includegraphics[width=9cm]{14428fg1}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg15.png)
|
Figure 1: DSS image of NGC 1399 overlaid with the five observed fields. The fields were intentionally overlapped in order to confirm consistent astrometry and velocity calibration across the observations. NGC 1404 is seen in field 7. |
| Open with DEXTER | |
This paper describes the latest kinematic data for the outer parts of the galaxy. It is part of a larger project intended to dynamically model the galaxy using PNe and X-ray constraints. NGC 1399 is well studied with kinematic measurements from long-slit spectra (Saglia et al. 2000). Previous to this work, the radial extent of the PN kinematics was limited to the velocities from Arnaboldi et al. (1994) at 24 kpc. The current sample measures more than 4 times as many PN velocities out to more than twice the radius. The resulting kinematics provide a significant improvement in understanding the velocity field of the halo.
![\begin{figure}
\par\includegraphics[angle=270, width=17cm,clip]{14428fg2}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg16.png)
|
Figure 2: Part of the central field (field 5). The top frame is the W0 exposure and the bottom frame is the counter-dispersed E180 exposure after rotating back in the computer. The diffuse light at the top center of each frame is the southern tip of the bright central region of NGC 1399. In these images, the stars appear as streaks in the x-direction (the direction of dispersion). Examples of planetary nebula candidates are circled. Notice that there is a small difference in the PNs' x-positions in the W0 and E180 fields due to their velocity. The arrows point to emission-line objects that are associated with some continuum - these are background galaxies. |
| Open with DEXTER | |
We describe our observations in Sect. 2 before moving on to the
data reduction, the image registration and the detection of planetary
nebula in Sect. 3. We discuss the measurement of the PN velocities
in Sect. 4, and Sect. 5 addresses the technique for mapping
the astrometry on spectral images. The analysis of the sample,
including discussions of objects associated with NGC 1404 and a
low-velocity subcomponent, is covered in Sect. 6. We explore the
kinematics of the halo of NGC 1399 in Sect. 7 and give a
summary of this work in Sect. 8. Throughout the paper, we assume
the distance from Tonry et al. (2001) of 19.95 Mpc, which means that 1
![]() corresponds to 96.7 pc.
corresponds to 96.7 pc.
2 Observations
2.1 Instrumental set-up
Observations of five fields around NGC 1399 were carried out with FORS1 (Appenzeller et al. 1998) on the 8-m VLT at Paranal Observatory during the nights of 25-27 Nov. 2000. The five fields represent a subset of theTable 1: Observing log*.
We used the 600B grating with a measured mean dispersion of 1.19 Å pix-1.
The interference filter, FILT_503_5+86, is centered near the wavelength
of the redshifted [OIII] emission at the systemic velocity of
NGC 1399 (1425 km s-1, Graham et al. 1998). The filter, with a FWHM
of 60 Å, limits the length of the spectra of continuum sources
which would otherwise cover much of the field. It allows detection of
PNe with velocities within ![]() 1800 km s-1 of the systemic velocity. For some fields, bright stars were masked out.
1800 km s-1 of the systemic velocity. For some fields, bright stars were masked out.
With this instrumental configuration, the direction of dispersion is along the horizontal axis (x-axis) depicted in Fig. 2. Because of the slitless technique, both axes have spatial information. In the focal plane, the presence of the grism causes an anamorphic distortion resulting in a contraction in the direction of dispersion (see discussion in Sect. 2.3).
2.2 Observing mode
In this technique, the positions and velocities are obtained using two narrow-band, dispersed exposures of the same field. In the first, an image is acquired at position angle (PA) 0![\begin{figure}
\par\includegraphics[width=17cm,clip]{14428fg3}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg30.png)
|
Figure 3: Schematic describing the
counter-dispersed imaging technique. In the field shown, there are four
stars (shown as rainbow continuum sources) and 3 planetary nebulae
(shown as small emission-line dots). The first frame shows the W0 field
with dispersion to the right. The second frame, E180
|
| Open with DEXTER | |
2.3 Calibrations
The position of each PN in the dispersed image is a combination of its position on the sky, its line-of-sight velocity and the distortion from the instrument; we must quantify and separate these contributions in order to measure the velocity. The grism introduces an anamorphic distortion into the field that needs to be corrected before we measure velocities. Also, the dispersion changes as a function of position and the filter bandpass is dependent on the location in the field.We used three sets of daytime calibration frames based on a
![]() grid of slitlets imaged through the narrowband [OIII] filter. In
the first set, the slitlets are imaged in undispersed white light. This
gives us the positions of the slitlets in the grid. In the second set,
the white light is dispersed. This set determines the filter bandpass
as a function of position on the CCD. The final set is illuminated with
a dispersed HeAr lamp. There are three lines covered by our bandpass:
grid of slitlets imaged through the narrowband [OIII] filter. In
the first set, the slitlets are imaged in undispersed white light. This
gives us the positions of the slitlets in the grid. In the second set,
the white light is dispersed. This set determines the filter bandpass
as a function of position on the CCD. The final set is illuminated with
a dispersed HeAr lamp. There are three lines covered by our bandpass:
![]() and
and
![]() .
This frame is used to evaluate the anamorphic distortion and to measure the local dispersion.
.
This frame is used to evaluate the anamorphic distortion and to measure the local dispersion.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14428fg4}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg33.png)
|
Figure 4:
Calibration frames. Each vertical line is comprised of
19 nearly-adjacent slitlets. Using this
|
| Open with DEXTER | |
The daytime calibration exposures for the following steps were taken over three days where each slitlet position was exposed once in each configuration (image of the slitlet, dispersed white-light spectrum, and dispersed HeAr spectrum). The slitlets are formed by 19 pairs of moveable fingers, each calibrated at 10 positions across the field. All of the positions were co-added to create a master white-light image, a master white-light spectrum, and a master HeAr lamp spectrum. The three master calibration frames are shown in Fig. 4. The image processing and analysis necessary for these calibrations was done in IRAF and Mathematica. The y-position is taken to be the vertical center of each slitlet. To measure the position in the dispersion direction, 40 rows were summed along the slitlet and a Gaussian was fit - the x-position is taken to be the mean of the Gaussian. See Sect. 4.4.2 for a discussion of how well it is possible to measure the central wavelength of the filter bandpass.
2.3.1 Mapping the anamorphic distortion
The first calibration step is to use the x, y-positions from the image of the slitlets in the first calibration frame and the positions of the brightest line (Effectively, this transformation converts the data from the spectral
into the image plane. We define the spectral and image planes like Arnaboldi et al. (2007);
the spectral plane is the dispersed image as observed, and the image
plane has been corrected for the distortion introduced by the grism
thereby making an undispersed, distortion-corrected image for one
wavelength (
![]() ).
The PN identification and velocity measurement were done on the
image-plane images because they are distortion-corrected.
).
The PN identification and velocity measurement were done on the
image-plane images because they are distortion-corrected.
2.3.2 Calculating the local dispersion
Next, we measure the distance between the 5015.67 Å and 5085.82 Å lines in the dispersed HeAr lamp image to derive the local dispersion. We assume that the dispersion is linear on this scale. The two-dimensional, 2nd-order function describing the dispersion at each of the 190 calibration slitlets is fit with surfit, and we interpolate to get a measurement of the local dispersion at any location.
Because we measure the dispersion in the non-distortion-corrected (spectral) calibration frame, we multiply the local dispersions by the linear term from the geomap solution in Sect. 2.3.1 when we apply them to relate position to wavelength. This is possible because the higher-order terms are small compared to the linear term of the anamorphic-distortion fit. This converts our dispersions from the measured spectral-plane dispersions to image-plane dispersions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg5}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg35.png)
|
Figure 5:
Anamorphic distortion. Each black point represents the location of the
midpoint of a slitlet in the undispersed image frame. The red points
are the corresponding slitlets as measured using the |
| Open with DEXTER | |
2.3.3 Measuring the bandpass shift
![\begin{figure}
\par\includegraphics[angle=270,width=8cm,clip]{14428fg6}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg36.png)
|
Figure 6:
Bandpass shift as a function of position on the CCD. The shift is
measured by comparing the measured center of the bandpass to the
location of the |
| Open with DEXTER | |
Finally, we map the bandpass shift as a function of position. We do
this by comparing the Gaussian center of the dispersed white light to
the position of the ![]() 5015.67 line.
We expect there to be an underlying smooth, 2D function that
describes the bandpass shift caused by the presence of an interference
filter at a small inclination in a converging beam. We modeled this
function with a 2D cubic using Mathematica and now we can evaluate
the bandpass at any location on the CCD. Figure 6
shows the measured bandpass shift across the CCD in light blue. The
smooth red surface represents the model for the underlying smooth
function that determines the local bandpass. The rms of the residuals
is less than 1 pixel.
5015.67 line.
We expect there to be an underlying smooth, 2D function that
describes the bandpass shift caused by the presence of an interference
filter at a small inclination in a converging beam. We modeled this
function with a 2D cubic using Mathematica and now we can evaluate
the bandpass at any location on the CCD. Figure 6
shows the measured bandpass shift across the CCD in light blue. The
smooth red surface represents the model for the underlying smooth
function that determines the local bandpass. The rms of the residuals
is less than 1 pixel.
When we align the W0 and E180 images using the stars, we must first
correct for the bandpass shift. In the W0 and E180 images of the
same star, the light path is different causing different bandpass
shifts in the two images. In general, the location of a star in our
images is measured with a 2D Gaussian using the n2gaussfit
task in IRAF. For each star used in the alignment, we evaluate the
two-dimensional cubic function at that location and apply the shift to
the n2gaussfit coordinates. The bandpass shift is measured in
the spectral plane, but we want to register image-plane images.
Therefore, using geoxytran, we apply the anamorphic distortion correction from geomap
to obtain the distortion-corrected bandpass-shifted location of each
star. These new coordinates are used to obtain the rigid shift that
will be applied to the distortion-corrected images before calculating
the velocity of the PNe. Because we measure the center of the filter
relative to the ![]() 5015.67 line, it becomes our fiducial wavelength. The E180 and W0 images will be aligned on the x,y positions
of this wavelength in the stars, and the wavelength of the PNe
emissions will be measured relative to that line.
5015.67 line, it becomes our fiducial wavelength. The E180 and W0 images will be aligned on the x,y positions
of this wavelength in the stars, and the wavelength of the PNe
emissions will be measured relative to that line.
3 Data reduction, registration and identification of emission-line sources
3.1 Data reduction
The data reduction for the counter-dispersed technique was carried out in IRAF. Each field is imaged with three-1200s exposures at each position angle. The frames are bias subtracted and flat fielded individually. The sky flats were taken at twilight using the narrow-band filter and the grism. The three frames at each PA were combined using imcombine with a standard sigma-clipping for cosmic-ray removal.The result is a total of 10 combined, bias-subtracted, flat-fielded frames - 5 at
PA = W0 and 5 at PA = E180. We subtract the background from each frame by smoothing with fmedian
and subtracting the smoothed background from the spectral image. Next
each of the frames is corrected for anamorphic distortion using IRAF
task geotran as described in Sect. 2.3.1 - this transforms the frame from the spectral to the image plane. We rotate the E180 image by 180![]() so that the stars are in comparable positions in the W0 and E180
so that the stars are in comparable positions in the W0 and E180
![]() frames; the calibration frames are no longer applicable to E180
frames; the calibration frames are no longer applicable to E180
![]() because the direction of dispersion is opposite.
because the direction of dispersion is opposite.
3.2 Registering the images
We must now register the W0 and E1803.3 Identification of emission-line objects
In these images, emission-line sources are easily distinguished from stars because they appear as points instead of streaks. For the identification we rely on the W0, E180![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg7}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg37.png)
|
Figure 7:
Examples of the three classes of emission-line objects identified in our sample. Each frame is 1
|
| Open with DEXTER | |
We identify three kinds of emission-line objects:
- those that are point-like in both wavelength and space - these are planetary nebula candidates;
- those emission-line sources that are associated with a continuum - these are background galaxy candidates including some Lyman-
 galaxies at z=3.1. These objects can be either point-like or extended in the spatial direction;
galaxies at z=3.1. These objects can be either point-like or extended in the spatial direction;
- those with resolved or double emission in wavelength. They can be extended or point-like in the spatial direction. These are also background galaxies and include some [OII] emitters.
Table 2: Breakdown of emission-line objects.
3.3.1 The efficiency of the technique
We found a total of 187 PNe in the five fields, including 146 bound to NGC 1399. As a point of comparison, Teodorescu et al. (2005) applied a related technique to NGC 1344, another Fornax galaxy, using the VLT and found 197 PNe. In their technique (summarized in Méndez et al. 2001), each field is imaged with broad- and narrow-band filters, and then a grism is added and the narrow-band image is dispersed. The velocity would be measured from the separation between the PNe in the narrow-band image and the dispersed, narrow-band image.As elliptical galaxies in the same cluster, we expect the PN detection efficiencies in these two galaxies to scale with their color and luminosity. NGC 1399 is red compared to NGC 1344 (B-V=0.95 versus B-V=0.87 based on the extinction-corrected total luminosities published by de Vaucouleurs et al. 1991). According to Hui et al. (1993), the difference in color would indicate that the luminosity specific PN number density of NGC 1399 is only 43% of that of NGC 1344. Also NGC 1399 is almost a full magnitude brighter which should have the effect of nearly doubling the number of PN detected in NGC 1399. Finally, Teodorescu et al. covered the area around NGC 1344 uniformly, while the NGC 1399 observations only covered 5/9ths of the proposed grid. We can estimate the number of detections we are missing by symmetrizing the detections from the fields we do have. This would increase our sample by about 55 PNe.
If we adjust our detection rate for the difference in color, magnitude and coverage, we would have detected 224 PNe, which is similar to the 197 NGC 1344-bound objects found by Teodorescu et al. (2005). We conclude that the counter-dispersed spectroscopy technique described in this paper provides an efficient strategy for collecting large PN velocity samples in the local volume and is comparable to the singly-dispersed imaging technique (Teodorescu et al. 2005; Méndez et al. 2001).
4 Planetary nebula velocities
4.1 Velocity calibration
The data reduction and the registration were done using the positions of the stars. As continuum sources, their spectra are approximated by the nearly-symmetrical filter curve (see discussion in Sect. 4.4.2) and adjusted to compensate for the filter bandpass shift. Unlike stellar continuum sources, planetary nebulae are not subject to the filter bandpass shift and their positions on the CCD are dependent on both their positions in the sky and their velocities. The counter-dispersion causes each PN to appear in different places in the W0 and E180where
Using this calibration, we generate line-of-sight velocity measurements for the PNe in our sample. The mean measured velocity is different from the systemic velocity of the galaxy - this indicates a zero-point offset in the calibration which is discussed in Sect. 4.4. First, in Sect. 4.2 we will determine the errors. In Sect. 4.3, we seek to demonstrate that the velocities are internally consistent and therefore represent an accurate 2D relative-velocity field.
4.2 Errors on the velocity measurements
The individual velocity errors are a combination of the errors in reduction, registration and measurement. The total error is calculated using 17 duplicates - these are PN that are detected in the overlap region between two fields. For each set of two fields, the mean difference in the duplicates is estimated (see Sect. 4.5) and the individual velocity errors for our sample are determined from the standard deviation of the differences between all the pairs from overlapping areas. We measure an rms in the difference of 52 km s-1, corresponding to an individual velocity error of 37 km s-1. This value is comparable to the 40 km s-1 error on the velocities in Méndez et al. (2001), but it is larger than the 20 km s-1 errors in the Planetary Nebula Spectrograph data (Douglas et al. 2002).4.3 Testing the internal consistency of the velocity calibration
Due to the complexity of the calibrations for counter-dispersed imaging, we seek to confirm that our velocity calibration is correct. The following three tests confirm that the velocity calibration does not depend on the distance of the PN from the center of the galaxy, the x,y position of the PN on the CCD or the velocity of the PN.
In the first test, we computed a running average of the velocity as a function of radius for the PNe in the central field (field 5). Assuming point symmetry, we expect to see a flat mean-velocity curve since the running average relies on averaged annular bins. Since it is not physically possible for the annular bins to have a velocity gradient, a rising or falling curve would indicate that our velocity calibration depends incorrectly on radius. In Fig. 8, we observe a flat running average, which indicates that our velocity calibration is not dependent on the distance to the center of the galaxy.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{14428fg8}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg42.png)
|
Figure 8: Velocity distribution of our central field's PN candidates as a function of radius. The red line marks the running average computed with 20 PNe in an annular bin. The lack of a trend in the average indicates that the velocity calibration does not vary with radius. |
| Open with DEXTER | |
In the second test we looked for a trend in the velocity as a function of position on the CCD. We compared our velocities with those from Arnaboldi et al. (1994) using 14 objects in common between the two samples with a mean difference of 166 km s-1. We show the dependence in the difference as a function of x and y in Fig. 9, and we do not see a scaling with position.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg9}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg43.png)
|
Figure 9:
14 PNe in common between our sample and the 1994 NTT sample as a
function of position on the CCD. The triangles represent the difference
in velocity as a function of x-position and the open circles show it as a function of y-position. The lack of a trend in either distribution indicates that the velocity calibration is not a function of x or y on the CCD. The mean difference in velocity is 166 km s-1 with |
| Open with DEXTER | |
The final test is the measured difference between the mean velocity of NGC 1399 PNe and the mean of the NGC 1404 candidates that we can see in field 7. If our velocity calibration were scaled with velocity, we would expect to see the difference in the means of the two galaxies scaled proportionately. Using a maximum likelihood technique we fit the PNe in field 7 with two normal distributions, one for each galaxy. See Fig. 10.
We see a difference of ![]() km s-1 between the peaks of NGC 1399 and NGC 1404. The fit shown in Fig. 10 finds the peaks at
km s-1 between the peaks of NGC 1399 and NGC 1404. The fit shown in Fig. 10 finds the peaks at
![]() km s-1 and
km s-1 and
![]() km s-1. This separation is consistent with the separation of the values in the literature of 522 km s-1 (Graham et al. 1998).
The spatial selection caused by the boundaries of field 7 may influence
the mean velocity of the NGC 1404 objects detected. As
discussed in Sect. 6.2, NGC 1404 displays rotation; according to Graham et al. (1998)
it would have the effect of lowering the velocities that we detect in
NGC 1404 which would account for the slightly smaller measured
separation. Our conclusion is that the velocity calibration does not
change as a function of distance to the center of the galaxy, position
in the field or velocity. We conclude that we are accurately measuring
relative velocities with this technique. We discuss the determination
of the absolute velocity in the next section.
km s-1. This separation is consistent with the separation of the values in the literature of 522 km s-1 (Graham et al. 1998).
The spatial selection caused by the boundaries of field 7 may influence
the mean velocity of the NGC 1404 objects detected. As
discussed in Sect. 6.2, NGC 1404 displays rotation; according to Graham et al. (1998)
it would have the effect of lowering the velocities that we detect in
NGC 1404 which would account for the slightly smaller measured
separation. Our conclusion is that the velocity calibration does not
change as a function of distance to the center of the galaxy, position
in the field or velocity. We conclude that we are accurately measuring
relative velocities with this technique. We discuss the determination
of the absolute velocity in the next section.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg10}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg47.png)
|
Figure 10: Histogram of velocities in field 7 is overplotted with the modeled velocity distribution. The model is a maximum-likelihood fit to the unbinned velocity distribution. We can compare the separation between the peaks to the difference in the published systemic velocities of NGC 1399 and NGC 1404. In this figure, we have applied the systematic shift of 166 km s-1 discussed in Sect. 4.4. After the shift, the fitted galaxy velocities are 1426 km s-1 and 1917 km s-1. |
| Open with DEXTER | |
4.4 Calculating absolute velocities
As described in Sect. 4.3, the measured instrumental velocities are relative velocities. Absolute velocities are necessary to compare these measurements with other kinematic tracers. The mean velocity of the current sample is 1197 km s-1. Using a friendless outlier algorithm, we remove 12 low-velocity planetary nebulae that we believe are not virialized and therefore do not trace the mass of NGC 1399 (See Sect. 6.3). The mean instrumental velocity for the 146 PNe associated with NGC 1399 is| Figure 11: Comparison of the current velocity measurements with those from the NTT measurements (Arnaboldi et al. 1994). These 17 objects were detected in both samples. For the middle range of NTT values, we see a consistent agreement with the more recent data. At the fast and slow extremes, the agreement deviates. In this figure, we have already applied an offset of 166 km s-1, which is the mean offset in the 14 PNe at the center of the distribution (shown with the dashed line). |
|
| Open with DEXTER | |
We compare the VLT counter-dispersed-technique velocities with the 1994 NTT multi-object-spectroscopy measurements (Arnaboldi et al. 1994). As shown in Fig. 11,
a comparison indicates that the offset is constant for objects in the
center of the NTT velocity distribution. Relying on the 14 out of
17 objects that were detected in both samples in this range, we
calculate a systematic offset of 166 km s-1. The dispersion in the difference, 88 km s-1, is consistent with the combination in quadrature of the errors in the VLT and NTT samples: i.e.
![]() .
As the distribution in Fig. 9 illustrates, the offset between the previous work and this velocity calculation is not dependent on position on the CCD.
.
As the distribution in Fig. 9 illustrates, the offset between the previous work and this velocity calculation is not dependent on position on the CCD.
The error in the offset is calculated from the dispersion,
![]() km s-1. When we apply the shift with this error to our measured values, we find a mean velocity of
km s-1. When we apply the shift with this error to our measured values, we find a mean velocity of ![]() km s-1 for our sample of PNe in NGC 1399. This is consistent with Graham et al. (1998) where
km s-1 for our sample of PNe in NGC 1399. This is consistent with Graham et al. (1998) where
![]() km s-1 (NED) and Richtler et al. (2004) where
km s-1 (NED) and Richtler et al. (2004) where
![]() km s-1
for the GCs. Since the offset is constant, our measurements stand
alone as relative velocities. For absolute velocities, we rely upon the
adjustment of 166 km s-1 based on the NTT values.
km s-1
for the GCs. Since the offset is constant, our measurements stand
alone as relative velocities. For absolute velocities, we rely upon the
adjustment of 166 km s-1 based on the NTT values.
4.4.1 Comparison to X-Shooter
X-Shooter is a new, multi-wavelenth, medium-resolution, single-target spectrograph for the VLT (D'Odorico 2008). It is designed to cover a wavelength range of ![]() 3000-24800 using three arms: UVB (
3000-24800 using three arms: UVB (![]() 3000-5595), VIS (
3000-5595), VIS (![]() 5595-10240) and NIR (
5595-10240) and NIR (![]() 10240-24800).
As part of the commissioning observations, we received observations of
one of our PNe from the UVB and VIS arms. We were able to resolve the
double [OIII] emission at
10240-24800).
As part of the commissioning observations, we received observations of
one of our PNe from the UVB and VIS arms. We were able to resolve the
double [OIII] emission at ![]() 4958.9 and
4958.9 and ![]() 5006.8.
The long wavelength range and a multitude of skylines gives us a
wavelength calibration with 1 Å precision and yielding a measured
velocity for this PN of
5006.8.
The long wavelength range and a multitude of skylines gives us a
wavelength calibration with 1 Å precision and yielding a measured
velocity for this PN of ![]() km s-1. Having accounted for the systematic offset of 166 km s-1 discussed in Sect. 4.4, this value is consistent with the measurement of
km s-1. Having accounted for the systematic offset of 166 km s-1 discussed in Sect. 4.4, this value is consistent with the measurement of ![]() km s-1 from the counter-dispersed images.
km s-1 from the counter-dispersed images.
4.4.2 Understanding the velocity offset
In Sect. 4.3 we demonstrated that the velocity calibration is internally self-consistent. Now we discuss the systematic offset. Relative to the measurements from Arnaboldi et al. (1994), we see a difference of 166 km s-1. We explored several possibilities for the origin of this offset.
The first possibility questioned the assumption that the short stellar
spectra are symmetrical in wavelength. Depending on the temperature of
the star, it seemed possible that metal lines were creating an
asymmetrical feature on the blue side of the stellar spectrum as seen
through the filter. Our assumption of symmetry is important because we
are using the locations of stars in W0 and E180
![]() to
register the images. If asymmetry caused a systematic shift of the
center of the filter bandpass by say 2 pixels, it would introduce
an error in the mean velocity of 131 km s-1.
to
register the images. If asymmetry caused a systematic shift of the
center of the filter bandpass by say 2 pixels, it would introduce
an error in the mean velocity of 131 km s-1.
This issue was resolved by comparing the measured center of the filter to the measured center of a stellar template point-by-point multiplied with the filter bandpass. The centers were obtained by fitting Gaussians. The stellar templates are ATLAS9 model atmospheres with log (g) = 4.5, no rotation and solar metallicity (Munari et al. 2005). We covered a range of 4000-8000 K. A typical fit to the filter and the filter-template combination is shown in Fig. 12. We conclude that, over this range of temperatures, the fitted center of the stellar spectrum compared to the Gaussian fit to the filter differs by less than 0.3 Å or 20 km s-1 and therefore the absorption lines are not the cause of the zero-point offset.
![\begin{figure}
\par\includegraphics[angle=90,width=9cm,clip]{14428fg12.eps}\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg57.png)
|
Figure 12: Comparison of the filter to a stellar template as seen through the filter. The filter response curve is shown as the dotted line and fit with a dashed Gaussian. The solid, gray line represents a 5500 K [Fe/H] = 0 stellar template (Munari et al. 2005) as seen through the filter. Notice the asymmetry caused by metal lines in the blue end of the spectrum. Comparing the dash-dotted Gaussian stellar fit to the dashed fit to the filter, we see that the measured position of the center will not be significantly affected by the absorption (<0.3 Å). |
| Open with DEXTER | |
The second possibility for the cause of the velocity offset is the
influence of temperature on the filter bandpass. Interference filters
in convergent beams generally experience a shift of 1 Å to the
blue for every 5 ![]() C drop in ambient temperature (Jacoby 1989).
Since the calibration frames are taken during the day, they could have
introduced a systematic shift. However, according to the condition
report, the dome was climate controlled to the night temperature during
the day. We conclude that the temperature did not affect the velocity
measurement.
C drop in ambient temperature (Jacoby 1989).
Since the calibration frames are taken during the day, they could have
introduced a systematic shift. However, according to the condition
report, the dome was climate controlled to the night temperature during
the day. We conclude that the temperature did not affect the velocity
measurement.
After completing the astrometry and confirming its accuracy to 0
![]() 3 in the dispersion direction (see Sect. 5),
we recalculated the velocities using celestial coordinates. This
approach cuts out the registration of the images since the astrometry
is completed independently for the two frames. Additionally, the
stellar astrometry confirms that we understand the geometry of each
plane (W0 and E180) independently. For each PN, we obtained
3 in the dispersion direction (see Sect. 5),
we recalculated the velocities using celestial coordinates. This
approach cuts out the registration of the images since the astrometry
is completed independently for the two frames. Additionally, the
stellar astrometry confirms that we understand the geometry of each
plane (W0 and E180) independently. For each PN, we obtained
![]() (J2000) in the W0 and E180 frames. After calculating the separation in arcseconds, we used the plate scale (0.25
(J2000) in the W0 and E180 frames. After calculating the separation in arcseconds, we used the plate scale (0.25
![]() /pix) from the astrometry to convert to a separation in pixels and subsequently Ångstroms using the local dispersion (
/pix) from the astrometry to convert to a separation in pixels and subsequently Ångstroms using the local dispersion (![]() 1.2 Å/pix). The technique did not improve the agreement between our measurements and the 1994 NTT values.
1.2 Å/pix). The technique did not improve the agreement between our measurements and the 1994 NTT values.
In conclusion, we have examined several sources for the velocity offset and none of them are viable. We are unable to account for this difference between our measurements and the literature. Because we are confident that our velocities are internally consistent, we approach them as accurate relative velocities.
4.5 Mosaicking the individual pointings on a global velocity field
Some of the fields have regions of overlap, and there are 17 PNe detected in these regions. We use these duplicated detections to try to understand if the systematic velocity offset is global or if it changes field to field. We compared velocity measurements from each overlap region to determine the offset necessary to make the two fields in question consistent.
With the central field (field 5) defined as our benchmark, we adjusted two fields (field 2 and field 4) using PNe duplicated in field 5. We applied a high-sigma criterion for rejecting the outliers. Field 2, the topmost field, contained only 3 usable PN duplicates for this purpose, and we calculated an offset of 18 km s-1 between the objects in field 2 and field 5. Field 4, just to the east of the central field, contains 10 duplicates, and we calculated an offset of -24 km s-1 between the objects in field 4 and field 5. We apply the calculated difference to each field creating a global velocity field from the three local ones. Since these adjustments are on the order of the error in the velocity measurement, we find these three fields consistent with a global systematic offset. The duplicates are summarized in Table 3.
The two southernmost fields do not contain reliable overlap with the fields above (see Fig. 1). We created a smoothed, symmetrized velocity field using the now-consistent velocities from the three known fields (see Sect. 7.1 regarding the construction of this velocity fields). By assuming point symmetry of the PNe in fields 2, 4, and 5 and smoothing, we create a velocity field that covers the southern pointing (field 8). The field was evaluated at the location of 16 observed field 8 PN candidates thereby creating an equal number of phantom PNe. We then adjusted the mean velocity of the field 8 candidates to match the mean velocities of our phantom PNe by adding 47 km s-1. Now, having made the field 8 velocities consistent with the rest of the field, we used 3 duplicate PNe to calibrate the velocities of the field 7 candidates, adding 55 km s-1 to bring them onto the same plane as fields 2, 4, 5, and 8. There is one PN in common between field 4 and field 7, but we favored the more robust adjustment to field 8 instead. This procedure ensures that the velocity measurements in all of our fields are self-consistent.
Table 3: Duplicated detections from regions of overlap between fields.
4.6 The separation of NGC 1399 and NGC 1404
As shown in Fig. 1, the central part of NGC 1404 is observed in the southeast field (field 7). The PNe in this field come from both NGC 1399 and NGC 1404. The published mean velocities of these galaxies differ by over 500 km s-1, but, due to the dispersions, it isn't possible to separate the PNe unambiguously by their velocities. We have adopted a probability of membership method that assigns each PN to a galaxy only if it has 95% probability of belonging.The first criterion of membership is the relative surface brightness contribution from the two galaxies at the location of the PN. The light profile of NGC 1399 is taken from Dirsch et al. (2003). The light profile for NGC 1404 is an r1/4-law fit to photometry data from the same paper. The location of the planetary was then projected onto the major axis of each galaxy and both light profiles were evaluated at the respective radii. The ratio of flux at the projected distance of the PN is the ratio of probability of membership based on light alone.
The second criterion is the relative likelihood that an object of a given velocity belongs to the velocity distribution of NGC 1399 versus NGC 1404. The total velocity distribution of field 7 was fitted with two Gaussians through a maximum likelihood technique (Fig. 10). Then, reversing the technique, the relative likelihood of membership for each velocity was calculated. The ratio of likelihoods provides a ratio of probability of membership from velocity only.
Our two criteria were multiplied to produce a ratio of probability of membership value. A planetary is assigned membership if it is 19 times more likely to belong to one galaxy than the other (95% confidence interval). The 95% confidence criterion results in only 6 objects of ambiguous membership. If we lower our standard to 60% confidence of membership we would have 2 ambiguous PNe - 2 more PNe would belong to NGC 1404 and 2 more to NGC 1399. We retain the more stringent criteria. In order to examine the specific cases of the ambiguous PNe, see the figures in Sect. 6.1. The Field 7 candidates contribute 9 members of NGC 1399, 23 members of NGC 1404, and 6 of ambiguous membership. This analysis results in a total of 146 NGC 1399 planetary nebulae in our sample.
5 Astrometry
The astrometry was performed using the imcoords package in IRAF. We visually matched stars from USNO-B (Monet et al. 2003) to those in our images (about 10 per field). Because they are spectral images, for each star we fitted a 2-dimensional Gaussian and shifted the location to account for the local bandpass shift before building up a matrix of star positions. It is not necessary to correct for the anamorphic distortion because that transformation is folded into the mapping from the spectral plane to the celestial plane. Our images are described with a 2nd-order solution relative to the USNO-B stars. We expect our absolute astrometry to be no better than the errors on the USNO-B coordinates which isTo check the validity of our astrometry we selected several stars that
were not used in the astrometric fit and compared their calculated VLT
(i.e. this sample) positions to the USNO-B coordinates. The residuals
are <0
![]() 4.
We also completed an astrometric plate solution for a narrow-band NTT
image covering roughly the same field. When we compare the NTT
astrometry to the USNO coordinates, the residuals are 0
4.
We also completed an astrometric plate solution for a narrow-band NTT
image covering roughly the same field. When we compare the NTT
astrometry to the USNO coordinates, the residuals are 0
![]() 3
- comparable to those for the VLT data. This indicates that the
spectral imagery of the VLT data does not cause an unpredictable
behavior in the geometry that would affect our velocity calibration.
3
- comparable to those for the VLT data. This indicates that the
spectral imagery of the VLT data does not cause an unpredictable
behavior in the geometry that would affect our velocity calibration.
For each planetary nebula, we average the position in the W0 and E180
![]() frames to get velocity-independent position coordinates. We applied the astrometric solution to these coordinates yielding an
frames to get velocity-independent position coordinates. We applied the astrometric solution to these coordinates yielding an
![]() (J2000) catalog for the emission-line objects. This catalog will be included in a subsequent paper.
(J2000) catalog for the emission-line objects. This catalog will be included in a subsequent paper.
5.1 Comparison to X-Shooter
As discussed in Sect. 4.4.1, a PN from our sample was included in the commissioning data for the UVB and VIS arms of X-Shooter. The pointing coordinates for the PN were taken from the astrometric solution from the counter-dispersed images. The slit placement required a blind offset because PNe would not be visible in an acquisition exposure. As expected, the PN lands 1/3 of the way along the 106 The PN velocity sample
6.1 Phase-space diagrams
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg13}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg61.png)
|
Figure 13: The locations of the PNe
in space. PNe moving faster than the systemic velocity are marked with
black crosses. Those moving slower than the systemic velocity of
NGC 1399 are marked with black circles. The low-velocity objects
are marked with solid red squares. Blue crosses indicate objects
associated with NGC 1404 and green crosses mark the ambiguous PNe
that are not assigned to either galaxy. North is up and the major axis
lies at 110 |
| Open with DEXTER | |
In this section we view the PN 2D velocity field in various projections in phase space in order to investigate the kinematic properties of the galaxy. In particular, we present our PN sample in four subcomponents: those associated with NGC 1399, those associated with NGC 1404, those ambiguous ones that have not been assigned to a galaxy and a low-velocity subcomponent which we believe is not bound to either galaxy. The NGC 1404 and ambiguous candidates are defined in Sect. 4.6 and the low-velocity subcomponent is defined in Sect. 6.3. The spatial locations of the planetary nebulae are shown in Fig. 13. Notice that the positions are primarily limited by the locations of the five pointings shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg14}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg62.png)
|
Figure 14:
Phase space distribution. The NGC 1399 planetary nebulae
velocities are shown as a function of radius in black. The 12
low-velocity objects are marked in red. The open blue circles show the
NGC 1404 PNe and the green squares are those of ambiguous
membership (see Sect. 4.6).
The systemic velocities of the two galaxies are marked in dashed
(NGC 1399) and dotted (NGC 1404) lines. The position of
NGC 1404 is marked with a solid blue line at r=588
|
| Open with DEXTER | |
Comparing the line-of-sight velocity to the projected radius in Fig. 14,
we see the main NGC 1399 population in black with the measured
systemic velocity of this subcomponent marked with the black dashed
line. Notice the paucity of PNe at 300
![]() - this is caused by the spatial coverage of the survey. There is a low-velocity subcomponent moving at about 700 km s-1 slower than the galaxy. Referring back to Fig. 13, these objects are distributed across the north-central regions of our observations. As confirmed in Fig. 8, the average velocity of the main population is constant at all radii.
- this is caused by the spatial coverage of the survey. There is a low-velocity subcomponent moving at about 700 km s-1 slower than the galaxy. Referring back to Fig. 13, these objects are distributed across the north-central regions of our observations. As confirmed in Fig. 8, the average velocity of the main population is constant at all radii.
6.2 PN kinematics of NGC 1404
The PNe assigned to NGC 1404 (marked in blue in Fig. 13) dominate the sample in the southwest. In Fig. 14, these objects are found at large radii, around the systemic velocity of NGC 1404 (1947 km s-1; Graham et al. 1998). As illustrated in Fig. 10, the fitted mean velocity for the NGC 1404 PNe in this sample is
![]() km s-1. Graham et al. (1998) report rotation in NGC 1404 that could cause the PNe that we are detecting to be up to 100 km s-1 slower than the systemic velocity of NGC 1404. This may contribute to the
km s-1. Graham et al. (1998) report rotation in NGC 1404 that could cause the PNe that we are detecting to be up to 100 km s-1 slower than the systemic velocity of NGC 1404. This may contribute to the ![]() 30 km s-1 difference between the fit shown in Fig. 10 and the mean velocity value in the literature.
30 km s-1 difference between the fit shown in Fig. 10 and the mean velocity value in the literature.
6.3 Low-velocity subpopulation
We selected the 12 low-velocity objects from our sample using a high-sigma clipping algorithm similar to the technique in Merrett et al. (2006). It is an iterative outlier test that rejects objects that lie >In the high-sigma clipping algorithm, we assign PNe membership in either NGC 1399 or the low-velocity subcomponent. It is possible or even likely that one or two of the objects assigned to the subcomponent are actually members of NGC 1399. However, in most of the analysis in this paper, it is important to define the sample as a discrete set of objects, and the results will not change significantly based on the misclassification of one or two objects. This is not the case for the calculation of the velocity dispersion, which is sensitive to outliers in the wings of the distribution. The velocity dispersion calculation employs a robust fitting technique which is detailed in Sect. 7.2.1.
The low-velocity objects are remarkable in that they are not uniformly distributed over the entire galaxy, but rather concentrated in the north-central parts. Considering the asymmetric placement of the fields and the relatively small numbers of PNe in some of the outer fields, we considered the possibility of a selection from the filter. Because it is an interference filter at an angle in a converging beam, the bandpass function is not centered on the CCD, as shown in Fig. 6. We examined the 50% transmission edges of the filter as a function of distance from the intersection of the plane of the CCD with the axis of the filter, as seen in Fig. 15. We conclude that the filter is not causing the asymmetry in the velocity distribution. The most recent globular cluster (GC) work also shows a handful of low velocity objects in the sample removed with a tracer-mass-estimator method (Schuberth et al. 2009), which supports our claim that we are seeing a real substructure.
A low-velocity subcomponent is difficult to detect with integrated light measurements. Based on the phase-space distribution of the low-velocity PNe, we can infer that the subcomponent would manifest itself as an asymmetric feature in the line profile. This retrograde tail would be visible in the h3 value from integrated light measurements. Saglia et al. (2000) present h3 values of about -0.1 at large radii along the minor-axis slit. These measurements agree with the asymmetry in the PN distribution tending towards low velocities, but they do not provide an estimate for the amount of light or the mean velocity of the subcomponent.
The origin of the low-velocity subcomponent is unknown. The mean velocity is similar to the systemic velocity of NGC 1396 (![]() km s-1, Drinkwater et al. 2001),
an elliptical galaxy to the west of NGC 1399, and their spatial
distribution is consistent with their association with the outer halo
of this galaxy. Unfortunately, our observations do not extend to the
west, so we lack more conclusive evidence. The low-velocity globular
clusters are dominated by blue metal-poor members. This is consistent
with the possibility of the low-velocity material originating from a
stripped galaxy. We do not detect a velocity gradient in the
low-velocity PNe, so it seems unlikely that these objects are being
currently stripped as part of a interaction between the two galaxies.
The photometry of NGC 1399 from the OBEY survey (Tal et al. 2009) indicates a smooth light distribution down to the surface brightness limit of V=27.7 mag arcsec-2,
so the stellar component accompanying the low-velocity PNe must be
extremely diffuse across our fields. This corroborates the indication
from the velocity gradient that we are not seeing a clearly defined
stream of PNe from an infalling galaxy.
km s-1, Drinkwater et al. 2001),
an elliptical galaxy to the west of NGC 1399, and their spatial
distribution is consistent with their association with the outer halo
of this galaxy. Unfortunately, our observations do not extend to the
west, so we lack more conclusive evidence. The low-velocity globular
clusters are dominated by blue metal-poor members. This is consistent
with the possibility of the low-velocity material originating from a
stripped galaxy. We do not detect a velocity gradient in the
low-velocity PNe, so it seems unlikely that these objects are being
currently stripped as part of a interaction between the two galaxies.
The photometry of NGC 1399 from the OBEY survey (Tal et al. 2009) indicates a smooth light distribution down to the surface brightness limit of V=27.7 mag arcsec-2,
so the stellar component accompanying the low-velocity PNe must be
extremely diffuse across our fields. This corroborates the indication
from the velocity gradient that we are not seeing a clearly defined
stream of PNe from an infalling galaxy.
In any case, the asymmetry in the velocity distribution indicates that the low-velocity PNe are not currently phase-mixed with NGC 1399. Like in M 87 (Doherty et al. 2009), we see a superposition of kinematic components in the halo of this central cluster galaxy. This reflects the complexity of galaxy superpositions and interactions in cluster cores. The subcomponents could not have been disentangled without discrete velocity tracers; having PN velocities is therefore important for deriving a complete picture of the kinematics in the outer halos of brightest cluster galaxies. The detection of subcomponents in galaxy halos is not restricted to cD galaxies. In cases like M31 or the MW, these structures can be traced with red giant branch (RGB) stars. In nearby clusters, we are unable to detect individual RGB stars, but it is possible to measure the velocities of individual PNe. Globular cluster velocities can also be used outside the local group, but we emphasize that PNe hold an important role because they are the only individual stars visible at several Mpc and they trace the stellar population directly.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg15}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg67.png)
|
Figure 15: The detection limits imposed by the filter. This figure shows all of the PNe detected in our five fields. The black circles represent the ones associated with NGC 1399, the low-velocity subcomponent and the unassigned PNe. NGC 1404 PNe are marked with a blue open circle. The dotted line marks the systemic velocity of NGC 1399 (Graham et al. 1998). The red and blue squares trace the red and blue 50% transmission limits of the filter respectively. At small distances, the mean wavelength is near the mean wavelength of the galaxy. As the bandpass shifts at the edges of the CCD, the sample gets closer to the edge of the filter. Since there are no detections at or near the edge of the bandpass, we conclude the filter is not blocking the high-velocity counterpart to the low-velocity subpopulation. Moreover, we are detecting NGC 1404 PNe at these high velocities - it would be possible to see NGC 1399 ones at the same wavelength if they existed. |
| Open with DEXTER | |
7 Kinematics of the halo of NGC 1399
7.1 Rotation
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg16.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg68.png)
|
Figure 16:
NGC 1399 halo velocities. This smoothed, symmetrized velocity map
shows the location of each PN with an x. The photometric major axis is
vertical in this configuration. The map indicates rotation of |
| Open with DEXTER | |
Now we consider the kinematic properties of the main NGC 1399
sample. The smoothed, symmetrized velocity map shown in Fig. 16
illustrates the rotation in the observed fields. It is made by
reflecting the entire sample (defined as the PNe which are not
classified as members of NGC 1404, the low-velocity subcomponent
or the ambiguous objects) in x, y and velocity and then smoothing using an adaptive Gaussian kernel smoothing as described in Coccato et al. (2009).
The velocity field was fit with a cosine function in order to derive
the direction and amplitude of rotation as a function of radius. The
measured values for these quantities and their errors (computed by
means of Monte Carlo simulations) are obtained using the same process
described in Coccato et al. (2009) and are listed in Table 4. We observe rotation of ![]() 20 km s-1 along an axis offset from the photometric major axis (PA = 110
20 km s-1 along an axis offset from the photometric major axis (PA = 110![]() ). Additionally, the kinematic major axis displays a strong twist in the outer regions similar to those described in Coccato et al. (2009).
). Additionally, the kinematic major axis displays a strong twist in the outer regions similar to those described in Coccato et al. (2009).
This analysis is consistent with the low-amplitude of rotation (<30 km s-1 along the major axis) observed by Saglia et al. (2000) inside 1![]() .
In contrast to the rotation result from Arnaboldi et al. (1994), we see only a low amplitude of rotation in the outer parts - rotation of
.
In contrast to the rotation result from Arnaboldi et al. (1994), we see only a low amplitude of rotation in the outer parts - rotation of ![]() 20 km s-1 is a fraction of their value. A comparison to the globular cluster system's rotation can be found in Sect. 7.3.2.
20 km s-1 is a fraction of their value. A comparison to the globular cluster system's rotation can be found in Sect. 7.3.2.
Table 4: Rotation of the Halo of NGC 1399.
7.2 The velocity dispersion
Using the new PN velocities, we trace the dispersion out to large radii. PNe are particularly good for this task because they extend well beyond the integrated-stellar-light measurements, and their number density follows the light where they overlap (Coccato et al. 2009).
7.2.1 Robust fitting
Due to possible contamination from the low-velocity subcomponent, the
dispersion is calculated using a robust fitting technique. We begin by
measuring the standard deviation of the data. To avoid using the tails
of the distribution, we estimate the dispersion using only objects
within 2 standard deviations (![]() )
and then scale the measured dispersion using a factor generated in a Monte Carlo simulation of the same process. A 2
)
and then scale the measured dispersion using a factor generated in a Monte Carlo simulation of the same process. A 2![]() limit is selected because we are confident that the contamination is
not significant within this range. A step-by-step description of the
process follows in the next two paragraphs.
limit is selected because we are confident that the contamination is
not significant within this range. A step-by-step description of the
process follows in the next two paragraphs.
Based on the number of PNe in each annular bin, 53 objects are drawn at
random from a Gaussian distribution with the measured mean and
dispersion of the data. Objects at greater than 2![]() are rejected and the dispersion of the remaining objects is measured.
This process is repeated 10 000 times creating a Monte Carlo
distribution of dispersion values. The mean of the 10 000
dispersion values is used to calculate a scaling, f2, between the dispersion as measured within 2
are rejected and the dispersion of the remaining objects is measured.
This process is repeated 10 000 times creating a Monte Carlo
distribution of dispersion values. The mean of the 10 000
dispersion values is used to calculate a scaling, f2, between the dispersion as measured within 2![]() (
(
![]() )
and the known input dispersion (
)
and the known input dispersion (
![]() ). We define
). We define
The dispersion of the 10 000 measurements gives the error in our dispersion values,
Returning to the data, a 2![]() limit is applied to each radial bin and the dispersion is calculated
for the PNe within this limit. This dispersion is then scaled by the
factor defined in Eq. (2). Since we expect the initial estimate for 2
limit is applied to each radial bin and the dispersion is calculated
for the PNe within this limit. This dispersion is then scaled by the
factor defined in Eq. (2). Since we expect the initial estimate for 2![]() to be influenced by the outliers, we repeat this process until the dispersion estimate stabilizes. The error,
to be influenced by the outliers, we repeat this process until the dispersion estimate stabilizes. The error,
![]() ,
is
,
is
![]() the dispersion of the Monte Carlo distribution.
the dispersion of the Monte Carlo distribution.
Figure 17 shows the
line-of-sight velocity dispersion as a function of projected radius
calculated with the robust-fitting technique. The calculated values are
included in Table 5. The
radial limits of the bins are set such that all the bins have about the
same number of objects (53 or 54). We discuss the dispersion, ![]() ,
rather than
,
rather than
![]() ,
but they are approximately equivalent since the rotation velocity is low. The velocity error has been subtracted in quadrature.
,
but they are approximately equivalent since the rotation velocity is low. The velocity error has been subtracted in quadrature.
7.2.2 Comparison to previous PN measurements
In contrast to the previous measurements (Arnaboldi et al. 1994), the velocity dispersion from the new observations is much lower and much flatter. There could be several contributing factors to this change. Compared to the 1994 values, this sample is four times larger, has more precise measurements and does not have a problem with the extreme velocities as described in Fig. 11. Moreover, the robust fitting treatment has a significant effect on the dispersion. This is shown as the difference between the red squares and the red line in Fig. 17.In summary, this reassessment of the velocity dispersion implies a lower value than the previously published measurements. In the latest NGC 1399 data, there is no evidence of an upturn in the dispersion which would have indicated a growing influence from the cluster potential.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14428fg17} %
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg78.png)
|
Figure 17: Dispersion profile of NGC 1399. The new data are shown as red squares in the outer regions. The instrumental dispersion has been subtracted in quadrature. For comparison, we have shown the calculation of the dispersions without using the robust fitting (red dashed line). The black circles represent integrated light measurements from Saglia et al. (2000) (solid = major axis, hollow = minor axis). The minor axis is projected for comparison to the major axis. The PN measurements from Arnaboldi et al. (1994) are in green, rising steeply. The outermost integrated light point, a blue triangle, is from P. Saha (private communication), and it shows good agreement with a profile extrapolated from Saglia et al.'s (2000) major axis dispersion measurement and the new PN kinematics. The black lines are various models from Kronawitter et al. (2000) (see discussion in text). |
| Open with DEXTER | |
7.3 Other tracers
7.3.1 Integrated light
The current PN dispersion values agree well with the major-axis values described in Saglia et al. (2000). One side of the parallel-to-minor-axis values does not agree well with the PN measurements, which suggests that there may be preferential contamination from non-phase-mixed PNe in this measurement. See Fig. 17.
The new PN measurements agree well with the outermost dispersion
measurement from integrated light - less than 200 km s-1 at 163
![]() (Saha, private communication). This value, marked with a blue triangle in Fig. 17,
is derived from one all-night, carefully-sky-subtracted, long-slit
observation taken with the RGO spectrograph on the Anglo-Australian
Telescope. This measurement is included in Table 5.
Approximately equal time was spent on the target and the sky. The
current PN sample is in good agreement with the largest-radius
integrated light measurement confirming the consistency of these
tracers.
(Saha, private communication). This value, marked with a blue triangle in Fig. 17,
is derived from one all-night, carefully-sky-subtracted, long-slit
observation taken with the RGO spectrograph on the Anglo-Australian
Telescope. This measurement is included in Table 5.
Approximately equal time was spent on the target and the sky. The
current PN sample is in good agreement with the largest-radius
integrated light measurement confirming the consistency of these
tracers.
Table 5: New velocity dispersion measurements in the outer halo of NGC 1399.
![\begin{figure}
\includegraphics[width=17cm,clip]{14428fg18}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg79.png)
|
Figure 18:
Globular cluster dispersion profile of NGC 1399. The black dots
represent the same integrated light measurements described in Fig. 17. The magenta crosses connected with a dotted line mark the GC dispersion values from Schuberth et al. (2009). After applying the decontamination algorithm from Sect. 4.6
to Schuberth et al.'s RI sample and also removing two low-velocity
GCs based on the tracer-mass estimator method in that paper, we measure
the dispersions shown in magenta squares. An instrumental dispersion of
70 km s-1 has been subtracted in quadrature. This dispersion profile is in excellent agreement with one of the models from Kronawitter et al. (2000), as discussed in Sect. 7.4. Lingering contamination from NGC 1404 seems to have strongly influenced the velocity dispersion profile from Schuberth et al. (2009) around 250
|
| Open with DEXTER | |
7.3.2 Globular clusters
NGC 1399 has a rich globular cluster system with about 7000 objects (Dirsch et al. 2003). Their abundance makes them potentially valuable tracers, but only the red subsample follows the radial distribution of the light and the PNe (see Fig. 15 in Schuberth et al. 2009). We consider the velocity dispersion from the red clusters only - the blue clusters have a higher dispersion which goes hand-in-hand with their flatter spatial distribution. Although the entire GC system is moving in the same potential as the PNe and stars, the different spatial distribution of the clusters requires different kinematics if they are to be in equilibrium.
The GC dispersions included in Schuberth et al. (2009) are higher than the PNe and Saha's integrated light value. These values are shown with magenta crosses in Fig. 18.
The difference seems to be highly influenced by contamination from
NGC 1404. The decontamination in that paper is based on a cut in
radius - any objects within 3
![]() of NGC 1404 were not included.
of NGC 1404 were not included.
We apply the two-fold decontamination algorithm (as described in Sect. 4.6) to the red GC sample (RI in Schuberth et al. 2009) which leads to a sample of NGC 1399 GCs that has 10 fewer objects than RIII in Schuberth et al. (2009), although some of the objects that were rejected by Schuberth et al. (2009)
were kept in our sample. We also reject two low-velocity GCs from the
RI sample based on the tracer-mass estimator (TME) algorithm from Schuberth et al. (2009).
The GCs are rebinned to have an equal number of objects in each bin,
but the dispersion values fall within one error bar if we use the bin
limits described in Table A.1 of Schuberth et al. (2009). After the decontamination, the TME outlier rejection and the subsequent rebinning, the measured dispersions drop to ![]() 200 km s-1 and are in excellent agreement with the PNe. See Fig. 19. The revised GC velocity dispersion values based on the two-fold decontamination are included in Table 5.
200 km s-1 and are in excellent agreement with the PNe. See Fig. 19. The revised GC velocity dispersion values based on the two-fold decontamination are included in Table 5.
The globular cluster rotation analysis is summarized in Sect. 7 of Schuberth et al. (2009). In agreement with the PNe, they find marginal rotation for the red sample. The red globular cluster rotation is ![]() km s-1 at an azimuthal angle of
km s-1 at an azimuthal angle of
![]() degrees,
but a rotation of this amplitude could be measured from randomized data
with probabilty 27% - this is interpreted as insignificant rotation.
They find rotation of 110
degrees,
but a rotation of this amplitude could be measured from randomized data
with probabilty 27% - this is interpreted as insignificant rotation.
They find rotation of 110 ![]() 53 km s-1 at
53 km s-1 at
![]() in the blue sample, but we do not expect the blue GCs to agree with the
rotation of the PNe and the integrated light based on the spatial
distribution and kinematics shown in Figs. 14 and 15 of Schuberth et al. (2009).
While there is disagreement about the position angle, the planetary
nebula and globular cluster kinematics agree that the amplitude of any
rotation in NGC 1399 would be small.
in the blue sample, but we do not expect the blue GCs to agree with the
rotation of the PNe and the integrated light based on the spatial
distribution and kinematics shown in Figs. 14 and 15 of Schuberth et al. (2009).
While there is disagreement about the position angle, the planetary
nebula and globular cluster kinematics agree that the amplitude of any
rotation in NGC 1399 would be small.
7.3.3 Fornax cluster galaxies
Just as PNe and globular clusters can be used to trace the mass distribution of a galaxy, cluster members allow us to estimate the cluster's mass. NGC 1399's position at the core of the Fornax cluster leaves open two possibilities for the dispersion profile at extremely large radii; the halo of a cluster's central galaxy could be dynamically separate from the cluster, or it could be part of it. For example, in the case of the Virgo cluster core, M87 displays a truncation at 160 kpc, where the velocity dispersion of the galaxy drops below 80 km s-1 (Doherty et al. 2009) while the potential determined from the X-rays is already dominated by the cluster mass distribution, implying that the central galaxy is dynamically separate from the cluster. If a central galaxy is not truncated, then it may be difficult to define the boundary between the galaxy and the cluster since the velocity dispersion of the galaxy could rise with radius to become similar to that of the cluster.Photometry of NGC 1399 from Schombert (1986) indicates that
there is no truncation, at least in the stellar mass, up to a radius
of about 300kpc. The component of the Fornax cluster centered on NGC
1399 has a dispersion of 370 km s-1 (Drinkwater et al. 2001). As
discussed by Drinkwater et al., the dwarf galaxies in Fornax
constitute a distinct population with a much higher dispersion than
the giants (
![]() km s-1 compared to
km s-1 compared to
![]() km s-1). Figure 19 shows the velocity dispersion for likely
Fornax Cluster members taken from Ferguson (1989). These values
agree very well with Drinkwater et al. The most distant dispersion
measurements of NGC 1399 available come from the GCs - the profile
seems to be falling at 1000
km s-1). Figure 19 shows the velocity dispersion for likely
Fornax Cluster members taken from Ferguson (1989). These values
agree very well with Drinkwater et al. The most distant dispersion
measurements of NGC 1399 available come from the GCs - the profile
seems to be falling at 1000
![]() (Schuberth et al. 2009). At
(Schuberth et al. 2009). At ![]() 2000
2000
![]() ,
the dispersion profile is not well understood. Bergond et al. (2007) see an indication of the onset of the cluster potential (Bergond et al. 2007), but Schuberth et al. (2008)
interpret the same data as being part of the NGC 1399 system with
a falling dispersion profile. Current observations do not bridge the
space between the last GCs (
,
the dispersion profile is not well understood. Bergond et al. (2007) see an indication of the onset of the cluster potential (Bergond et al. 2007), but Schuberth et al. (2008)
interpret the same data as being part of the NGC 1399 system with
a falling dispersion profile. Current observations do not bridge the
space between the last GCs (![]() 2000
2000
![]() )
and the first
dispersion estimate from the cluster members at nearly
3000
)
and the first
dispersion estimate from the cluster members at nearly
3000
![]() .
At the radial limit of our sample (500
.
At the radial limit of our sample (500
![]() ), the PN
dispersion reaches 220 km s-1 indicating that these PNe are
not in the regime dominated by the cluster potential, but still
within the NGC 1399 halo. Mass models based on ASCA and Rosat X-ray
data (Ikebe et al. 1996; Paolillo et al. 2002) indicate that the transition
to the cluster potential might be at around 500
), the PN
dispersion reaches 220 km s-1 indicating that these PNe are
not in the regime dominated by the cluster potential, but still
within the NGC 1399 halo. Mass models based on ASCA and Rosat X-ray
data (Ikebe et al. 1996; Paolillo et al. 2002) indicate that the transition
to the cluster potential might be at around 500
![]() .
However,
these mass models may not be consistent with the globular cluster
kinematics (Schuberth et al. 2009); this issue requires more work.
.
However,
these mass models may not be consistent with the globular cluster
kinematics (Schuberth et al. 2009); this issue requires more work.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14428fg19}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg86.png)
|
Figure 19: Dispersion profile representing the best values for each type of tracer. As in Fig. 17, the new PNe data are shown as red squares and the black circles represent integrated-light measurements from Saglia et al. (2000) (solid = major axis, hollow = minor axis). The last integrated-light measurement (blue triangle) agrees well with the new PNe dispersions. For comparison, the red GC sample from Schuberth et al. (2009) has been decontaminated with the same technique as the PNe and is displayed with magenta asterisks. The black asterisks represent Fornax Cluster dispersions (Ferguson 1989). The solid line shows the best model for the PN data from Kronawitter et al. (2000). |
| Open with DEXTER | |
7.4 Dynamical models
A full dynamical model based on the new PN and GC data is deferred to
a subsequent paper. Here we only compare the data briefly to a range
of models from Kronawitter et al. (2000). These models were
constructed based on absorption line kinematics reaching 100
![]() ,
assuming spherical symmetry. The anisotropy of the orbit
distribution was constrained by line profile shape measurements
inside 80
,
assuming spherical symmetry. The anisotropy of the orbit
distribution was constrained by line profile shape measurements
inside 80
![]() .
Best-fitting distribution functions were
constructed in a sequence of potentials including that of the stars
with constant mass-to-light ratio and an additional logarithmic halo
potential. Best fit composite potentials and confidence regions were
determined from the combined fit to all the absorption line data.
The lines overlayed on Fig. 17 represent several of the
models from Kronawitter et al. (2000); note that that their
projected velocity-dispersion profiles are available only to
.
Best-fitting distribution functions were
constructed in a sequence of potentials including that of the stars
with constant mass-to-light ratio and an additional logarithmic halo
potential. Best fit composite potentials and confidence regions were
determined from the combined fit to all the absorption line data.
The lines overlayed on Fig. 17 represent several of the
models from Kronawitter et al. (2000); note that that their
projected velocity-dispersion profiles are available only to
![]() .
The long-dashed model at the top represents the best fit
to the photometry and integrated-light kinematics described in
Saglia et al. (2000). At the bottom, the dotted line shows a
self-consistent model with constant mass-to-light ratio. The
short-dashed line near the middle shows an intermediate model that is
consistent with the inner integrated light data as well as the
outer-most PN point. The best match to all of the velocity dispersion
points from the current PN sample and also to the globular cluster
points for
.
The long-dashed model at the top represents the best fit
to the photometry and integrated-light kinematics described in
Saglia et al. (2000). At the bottom, the dotted line shows a
self-consistent model with constant mass-to-light ratio. The
short-dashed line near the middle shows an intermediate model that is
consistent with the inner integrated light data as well as the
outer-most PN point. The best match to all of the velocity dispersion
points from the current PN sample and also to the globular cluster
points for
![]() is provided by a model at the low-mass end
of the Kronawitter et al. (2000) confidence range, shown with a
solid line in Figs. 17 and 18. This line
represents the velocity-dispersion profile of a mildly radially
anisotropic (
is provided by a model at the low-mass end
of the Kronawitter et al. (2000) confidence range, shown with a
solid line in Figs. 17 and 18. This line
represents the velocity-dispersion profile of a mildly radially
anisotropic (
![]() )
spherical model with a central
B-band mass-to-light ratio of M/LB=12, a dark matter halo with
circular velocity
)
spherical model with a central
B-band mass-to-light ratio of M/LB=12, a dark matter halo with
circular velocity
![]() km s-1 for
km s-1 for
![]() and a
mildly increasing M/LB-profile, reaching
and a
mildly increasing M/LB-profile, reaching
![]() at
at
![]() (see Fig. 20). Outside 100
(see Fig. 20). Outside 100
![]() the
anisotropy of this model is not necessarily a good approximation for
the halo of NGC 1399, however, because of the shallow luminosity
density profile the velocity dispersions are insensitive to
anisotropy (Gerhard 1993; Churazov et al. 2010). Nonetheless, this
model is only indicative; more detailed dynamical modeling is
needed to explore the full range of anisotropy and mass profiles
consistent with the new data.
the
anisotropy of this model is not necessarily a good approximation for
the halo of NGC 1399, however, because of the shallow luminosity
density profile the velocity dispersions are insensitive to
anisotropy (Gerhard 1993; Churazov et al. 2010). Nonetheless, this
model is only indicative; more detailed dynamical modeling is
needed to explore the full range of anisotropy and mass profiles
consistent with the new data.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14428fg20}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg94.png)
|
Figure 20: Top: circular velocity curve for the model from Kronawitter et al. (2000) that best fits the inner absorption line kinematics, the PN velocity dispersions and the red GC velocity dispersions (solid line). This corresponds to the model shown with a solid line in Figs. 17 and 18. The dotted line shows the circular velocity curve of a constant mass-to-light ratio model. Bottom: B-band mass-to-light ratio profile for the best-fit model. |
| Open with DEXTER | |
8 Summary and conclusion
Using counter-dispersed, slitless spectroscopy from FORS1 on the VLT, we detected 411 emission-line objects around NGC 1399, including 146 PNe associated with NGC 1399, 23 associated with NGC 1404, 12 low-velocity PNe, 6 unassigned PNe and 224 background galaxies, and we measured the line-of-sight velocities of the PNe. This technique, applied for the first time on an 8-m class telescope, measures individual velocities with errors of less than 40 km s-1 at nearly 20 Mpc distance. It provides an efficient way of sampling the velocity field in the outer halos of galaxies, particularly because it does not require a two-stage detection-and-measurement process. In this paper we described the reduction technique specifically developed for the astrometry and velocity calibration of these observations. The new PN velocity measurements allow us to examine the kinematics of the outer halo of the cD galaxy NGC 1399.
The 146 PNe in NGC 1399 show weak rotation. The kinematic
major axis is offset from the photometric major axis and displays a
twist at large radii. The small amplitude of rotation confirmed the
result from Saglia et al. (2000). The PN velocity-dispersion profile flattens at about
220 km s-1 extending to ![]() 40 kpc.
The PNe dispersions show good agreement with the major-axis
integrated-light values and the globular cluster sample (Schuberth et al. 2009) after the NGC 1404 objects have been removed using a different method.
40 kpc.
The PNe dispersions show good agreement with the major-axis
integrated-light values and the globular cluster sample (Schuberth et al. 2009) after the NGC 1404 objects have been removed using a different method.
A comparison to the sequence of dynamical models constructed by
Kronawitter et al. (2000) from inner absorption line kinematics
indicates that the PNe in the outer regions of NGC 1399 are
consistent with a model with a B-band central mass-to-light ratio
of 12 and a dark matter halo with a circular velocity of
![]() km s-1. This comparison highlights the importance of having
kinematics at large radii to distinguish between the various
models. This paper establishes the most up-to-date data set with
integrated light, PNe and GCs, which will constrain new dynamical
models to be constructed in a subsequent paper.
km s-1. This comparison highlights the importance of having
kinematics at large radii to distinguish between the various
models. This paper establishes the most up-to-date data set with
integrated light, PNe and GCs, which will constrain new dynamical
models to be constructed in a subsequent paper.
The PN kinematics of the halo support the role of cD galaxies in
hierarchical structure formation within clusters. The multi-component
sample is comprised of objects associated with NGC 1399, NGC 1404 and
a low-velocity sub-group at ![]() 800 km s-1. At the
cluster core, we expect to find a heterogenous population including
stars left over from previous accretion, merger or tidal stripping
events; these stars are still in the process of phase-mixing. The
superposition of the various components on the NGC 1399 field
underscores the complexity of velocity measurements in cluster cores
and the necessity of using discrete tracers to detect these
components.
800 km s-1. At the
cluster core, we expect to find a heterogenous population including
stars left over from previous accretion, merger or tidal stripping
events; these stars are still in the process of phase-mixing. The
superposition of the various components on the NGC 1399 field
underscores the complexity of velocity measurements in cluster cores
and the necessity of using discrete tracers to detect these
components.
These results have opened valuable opportunities for further research on the formation and evolution of elliptical galaxies and on the dynamical structure of NGC 1399 and the Fornax cluster core in particular. The ambiguity of the source of the low-velocity data underlines the importance of understanding the kinematics of the western region of NGC 1399 and the implications on the dynamics of the Fornax cluster core. Given that the outer regions of early-type galaxies are dark-matter dominated and the orbits in this range have long dynamical time scales, the PN kinematics will provide valuable constraints on dynamical studies of this galaxy. The new data indicates that at large radii we must be aware of contamination in the wings of the velocity distribution as we look towards modeling the galaxy. Using these new PN data and the existing GC and integrated light observations, the dynamical modeling of NGC 1399 will be described in a future paper. Modeling NGC 1399 is a particularly exciting prospect because of existing X-ray data providing an independent assessment of the potential. The estimate of the orbital anisotropy will shed light on the formation of the halos of brightest cluster galaxies. Finally, given the success of this technique, we will apply the developed reduction processes to other systems to further explore the kinematics of the halos of early-type galaxies using PNe as discrete tracers.
AcknowledgementsWe thank the anonymous referee for his/her useful comments. We wish to thank R. Saglia and P. Saha for the use of their published and unpublished integrated light dispersions respectively. We thank S. D'Odorico and the X-Shooter team for the commissioning observations of one of the PNe in this sample. We thank M. Fabricius for his help with the analysis of the integrated light spectra. We are grateful to Y. Schuberth for generously sharing the globular cluster velocity catalogs. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. E. McNeil acknowledges support from the Max-Planck Institute for Ex. Physics and ESO Director Discretionary Funds 2009 during a 10-month visit to the Garching campus. P. Das was supported by the DFG Cluster of Excellence.
References
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Hui, X., Capaccioli, M., & Ford, H. 1994, The Messenger, 76, 40 [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Mendez, R. H., et al. 1996, ApJ, 472, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Gerhard, O., Aguerri, J. A. L., et al. 2004, ApJ, 614, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Gerhard, O., Okamura, S., et al. 2007, PASJ, 59, 419 [NASA ADS] [Google Scholar]
- Ashman, K. M., & Zepf, S. E. 1998, Globular Cluster Systems (Cambridge University Press) [Google Scholar]
- Bergond, G., Athanassoula, E., Leon, S., et al. 2007, A&A, 464, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosma, A. 1978, Ph.D. Thesis, Groningen Univ. [Google Scholar]
- Brodie, J. P., & Strader, J. 2006, ARA&A, 44, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Tremaine, S., Forman, W., et al. 2010, MNRAS, 359 [Google Scholar]
- Ciardullo, R., Jacoby, G. H., Ford, H. C., & Neill, J. D. 1989, ApJ, 339, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- de Lorenzi, F., Gerhard, O., Saglia, R. P., et al. 2008, MNRAS, 385, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- de Lorenzi, F., Gerhard, O., Coccato, L., et al. 2009, MNRAS, 395, 76 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, S&T, 82, 621 [Google Scholar]
- Dirsch, B., Richtler, T., Geisler, D., et al. 2003, AJ, 125, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- D'Odorico, S. 2008, The Messenger, 134, 12 [NASA ADS] [Google Scholar]
- Doherty, M., Arnaboldi, M., Das, P., et al. 2009, A&A, 502, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dopita, M. A., Jacoby, G. H., & Vassiliadis, E. 1992, ApJ, 389, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, N. G., Arnaboldi, M., Freeman, K. C., et al. 2002, PASP, 114, 1234 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, N. G., Napolitano, N. R., Romanowsky, A. J., et al. 2007, ApJ, 664, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Drinkwater, M. J., Gregg, M. D., & Colless, M. 2001, ApJ, 548, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, H. C. 1989, AJ, 98, 367 [Google Scholar]
- Gerhard, O., Arnaboldi, M., Freeman, K. C., et al. 2005, ApJ, 621, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O. E. 1993, MNRAS, 265, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., Colless, M. M., Busarello, G., Zaggia, S., & Longo, G. 1998, A&AS, 133, 325 [Google Scholar]
- Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hausman, M. A., & Ostriker, J. P. 1978, ApJ, 224, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, X., Ford, H. C., Ciardullo, R., & Jacoby, G. H. 1993, ApJ, 414, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, X., Ford, H. C., Freeman, K. C., & Dopita, M. A. 1995, ApJ, 449, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Ikebe, Y., Ezawa, H., Fukazawa, Y., et al. 1996, Nature, 379, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H. 1989, ApJ, 339, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Kronawitter, A., Saglia, R. P., Gerhard, O., & Bender, R. 2000, A&AS, 144, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Méndez, R. H., Riffeser, A., Kudritzki, R.-P., et al. 2001, ApJ, 563, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Merrett, H. R., Merrifield, M. R., Douglas, N. G., et al. 2006, MNRAS, 369, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, J., & Gebhardt, K. 2007, BAAS, 38, 747 [NASA ADS] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Coccato, L., et al. 2009, MNRAS, 393, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Paolillo, M., Fabbiano, G., Peres, G., & Kim, D. 2002, ApJ, 565, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Proctor, R. N., Forbes, D. A., Romanowsky, A. J., et al. 2009, MNRAS, 398, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Richtler, T., Dirsch, B., Gebhardt, K., et al. 2004, AJ, 127, 2094 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 301, 1696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rubin, V. C., Thonnard, N., & Ford, Jr., W. K. 1977, ApJ, 217, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Saglia, R. P., Kronawitter, A., Gerhard, O., & Bender, R. 2000, AJ, 119, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J. M. 1986, ApJS, 60, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Schuberth, Y., Richtler, T., Bassino, L., & Hilker, M. 2008, A&A, 477, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tal, T., van Dokkum, P. G., Nelan, J., & Bezanson, R. 2009, AJ, 138, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Teodorescu, A. M., Méndez, R. H., Saglia, R. P., et al. 2005, ApJ, 635, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Ventimiglia, G., Arnaboldi, M., & Gerhard, O. 2008, Astron. Nachr., 329, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Weijmans, A.-M., Cappellari, M., Bacon, R., et al. 2009, MNRAS, 398, 561 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... NGC 1399
![[*]](/icons/foot_motif.png)
- Based on observations made with the VLT at Paranal Observatory under programme ID 066.B-0278.
- ...
![[*]](/icons/foot_motif.png)
- Line of sight velocities is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/518/A44
All Tables
Table 1: Observing log*.
Table 2: Breakdown of emission-line objects.
Table 3: Duplicated detections from regions of overlap between fields.
Table 4: Rotation of the Halo of NGC 1399.
Table 5: New velocity dispersion measurements in the outer halo of NGC 1399.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm]{14428fg1}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg15.png)
|
Figure 1: DSS image of NGC 1399 overlaid with the five observed fields. The fields were intentionally overlapped in order to confirm consistent astrometry and velocity calibration across the observations. NGC 1404 is seen in field 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270, width=17cm,clip]{14428fg2}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg16.png)
|
Figure 2: Part of the central field (field 5). The top frame is the W0 exposure and the bottom frame is the counter-dispersed E180 exposure after rotating back in the computer. The diffuse light at the top center of each frame is the southern tip of the bright central region of NGC 1399. In these images, the stars appear as streaks in the x-direction (the direction of dispersion). Examples of planetary nebula candidates are circled. Notice that there is a small difference in the PNs' x-positions in the W0 and E180 fields due to their velocity. The arrows point to emission-line objects that are associated with some continuum - these are background galaxies. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14428fg3}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg30.png)
|
Figure 3: Schematic describing the
counter-dispersed imaging technique. In the field shown, there are four
stars (shown as rainbow continuum sources) and 3 planetary nebulae
(shown as small emission-line dots). The first frame shows the W0 field
with dispersion to the right. The second frame, E180
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14428fg4}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg33.png)
|
Figure 4:
Calibration frames. Each vertical line is comprised of
19 nearly-adjacent slitlets. Using this
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg5}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg35.png)
|
Figure 5:
Anamorphic distortion. Each black point represents the location of the
midpoint of a slitlet in the undispersed image frame. The red points
are the corresponding slitlets as measured using the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8cm,clip]{14428fg6}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg36.png)
|
Figure 6:
Bandpass shift as a function of position on the CCD. The shift is
measured by comparing the measured center of the bandpass to the
location of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg7}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg37.png)
|
Figure 7:
Examples of the three classes of emission-line objects identified in our sample. Each frame is 1
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{14428fg8}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg42.png)
|
Figure 8: Velocity distribution of our central field's PN candidates as a function of radius. The red line marks the running average computed with 20 PNe in an annular bin. The lack of a trend in the average indicates that the velocity calibration does not vary with radius. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg9}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg43.png)
|
Figure 9:
14 PNe in common between our sample and the 1994 NTT sample as a
function of position on the CCD. The triangles represent the difference
in velocity as a function of x-position and the open circles show it as a function of y-position. The lack of a trend in either distribution indicates that the velocity calibration is not a function of x or y on the CCD. The mean difference in velocity is 166 km s-1 with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg10}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg47.png)
|
Figure 10: Histogram of velocities in field 7 is overplotted with the modeled velocity distribution. The model is a maximum-likelihood fit to the unbinned velocity distribution. We can compare the separation between the peaks to the difference in the published systemic velocities of NGC 1399 and NGC 1404. In this figure, we have applied the systematic shift of 166 km s-1 discussed in Sect. 4.4. After the shift, the fitted galaxy velocities are 1426 km s-1 and 1917 km s-1. |
| Open with DEXTER | |
| In the text | |
| |
Figure 11: Comparison of the current velocity measurements with those from the NTT measurements (Arnaboldi et al. 1994). These 17 objects were detected in both samples. For the middle range of NTT values, we see a consistent agreement with the more recent data. At the fast and slow extremes, the agreement deviates. In this figure, we have already applied an offset of 166 km s-1, which is the mean offset in the 14 PNe at the center of the distribution (shown with the dashed line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=9cm,clip]{14428fg12.eps}\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg57.png)
|
Figure 12: Comparison of the filter to a stellar template as seen through the filter. The filter response curve is shown as the dotted line and fit with a dashed Gaussian. The solid, gray line represents a 5500 K [Fe/H] = 0 stellar template (Munari et al. 2005) as seen through the filter. Notice the asymmetry caused by metal lines in the blue end of the spectrum. Comparing the dash-dotted Gaussian stellar fit to the dashed fit to the filter, we see that the measured position of the center will not be significantly affected by the absorption (<0.3 Å). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg13}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg61.png)
|
Figure 13: The locations of the PNe
in space. PNe moving faster than the systemic velocity are marked with
black crosses. Those moving slower than the systemic velocity of
NGC 1399 are marked with black circles. The low-velocity objects
are marked with solid red squares. Blue crosses indicate objects
associated with NGC 1404 and green crosses mark the ambiguous PNe
that are not assigned to either galaxy. North is up and the major axis
lies at 110 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg14}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg62.png)
|
Figure 14:
Phase space distribution. The NGC 1399 planetary nebulae
velocities are shown as a function of radius in black. The 12
low-velocity objects are marked in red. The open blue circles show the
NGC 1404 PNe and the green squares are those of ambiguous
membership (see Sect. 4.6).
The systemic velocities of the two galaxies are marked in dashed
(NGC 1399) and dotted (NGC 1404) lines. The position of
NGC 1404 is marked with a solid blue line at r=588
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg15}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg67.png)
|
Figure 15: The detection limits imposed by the filter. This figure shows all of the PNe detected in our five fields. The black circles represent the ones associated with NGC 1399, the low-velocity subcomponent and the unassigned PNe. NGC 1404 PNe are marked with a blue open circle. The dotted line marks the systemic velocity of NGC 1399 (Graham et al. 1998). The red and blue squares trace the red and blue 50% transmission limits of the filter respectively. At small distances, the mean wavelength is near the mean wavelength of the galaxy. As the bandpass shifts at the edges of the CCD, the sample gets closer to the edge of the filter. Since there are no detections at or near the edge of the bandpass, we conclude the filter is not blocking the high-velocity counterpart to the low-velocity subpopulation. Moreover, we are detecting NGC 1404 PNe at these high velocities - it would be possible to see NGC 1399 ones at the same wavelength if they existed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{14428fg16.ps}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg68.png)
|
Figure 16:
NGC 1399 halo velocities. This smoothed, symmetrized velocity map
shows the location of each PN with an x. The photometric major axis is
vertical in this configuration. The map indicates rotation of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14428fg17} %
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg78.png)
|
Figure 17: Dispersion profile of NGC 1399. The new data are shown as red squares in the outer regions. The instrumental dispersion has been subtracted in quadrature. For comparison, we have shown the calculation of the dispersions without using the robust fitting (red dashed line). The black circles represent integrated light measurements from Saglia et al. (2000) (solid = major axis, hollow = minor axis). The minor axis is projected for comparison to the major axis. The PN measurements from Arnaboldi et al. (1994) are in green, rising steeply. The outermost integrated light point, a blue triangle, is from P. Saha (private communication), and it shows good agreement with a profile extrapolated from Saglia et al.'s (2000) major axis dispersion measurement and the new PN kinematics. The black lines are various models from Kronawitter et al. (2000) (see discussion in text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=17cm,clip]{14428fg18}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg79.png)
|
Figure 18:
Globular cluster dispersion profile of NGC 1399. The black dots
represent the same integrated light measurements described in Fig. 17. The magenta crosses connected with a dotted line mark the GC dispersion values from Schuberth et al. (2009). After applying the decontamination algorithm from Sect. 4.6
to Schuberth et al.'s RI sample and also removing two low-velocity
GCs based on the tracer-mass estimator method in that paper, we measure
the dispersions shown in magenta squares. An instrumental dispersion of
70 km s-1 has been subtracted in quadrature. This dispersion profile is in excellent agreement with one of the models from Kronawitter et al. (2000), as discussed in Sect. 7.4. Lingering contamination from NGC 1404 seems to have strongly influenced the velocity dispersion profile from Schuberth et al. (2009) around 250
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14428fg19}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg86.png)
|
Figure 19: Dispersion profile representing the best values for each type of tracer. As in Fig. 17, the new PNe data are shown as red squares and the black circles represent integrated-light measurements from Saglia et al. (2000) (solid = major axis, hollow = minor axis). The last integrated-light measurement (blue triangle) agrees well with the new PNe dispersions. For comparison, the red GC sample from Schuberth et al. (2009) has been decontaminated with the same technique as the PNe and is displayed with magenta asterisks. The black asterisks represent Fornax Cluster dispersions (Ferguson 1989). The solid line shows the best model for the PN data from Kronawitter et al. (2000). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14428fg20}
\end{figure}](/articles/aa/full_html/2010/10/aa14428-10/Timg94.png)
|
Figure 20: Top: circular velocity curve for the model from Kronawitter et al. (2000) that best fits the inner absorption line kinematics, the PN velocity dispersions and the red GC velocity dispersions (solid line). This corresponds to the model shown with a solid line in Figs. 17 and 18. The dotted line shows the circular velocity curve of a constant mass-to-light ratio model. Bottom: B-band mass-to-light ratio profile for the best-fit model. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.