EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 518 (July-August 2010) A&A, 518 (2010) A3 Full HTML
Free Access
Issue
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
Article Number A3
Number of page(s) 4
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201014374
Published online 18 August 2010
A&A 518, A3 (2010)

Milne-Eddington inversion of the Fe I line pair at 630 nm
(Research Note)

D. Orozco Suárez1 - L. R. Bellot Rubio2 - J. C. del Toro Iniesta2

1 - National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
2 - Instituto de Astrofísica de Andalucía (CSIC), Apdo. Correos 3004, 18080 Granada, Spain

Received 8 March 2010 / Accepted 26 May 2010

Abstract
Context. The iron lines at 630.15 and 630.25 nm are often used to determine the physical conditions of the solar photosphere. A common approach is to invert them simultaneously under the Milne-Eddington approximation. The same thermodynamic parameters are employed for the two lines, except for their opacities, which are assumed to have a constant ratio.
Aims. We aim at investigating the validity of this assumption, since the two lines are not exactly the same.
Methods. We use magnetohydrodynamic simulations of the quiet Sun to examine the behavior of the ME thermodynamic parameters and their influence on the retrieval of vector magnetic fields and flow velocities.
Results. Our analysis shows that the two lines can be coupled and inverted simultaneously using the same thermodynamic parameters and a constant opacity ratio. The inversion of two lines is significantly more accurate than single-line inversions because of the larger number of observables.

Key words: radiative transfer - polarization - line: profiles - Sun: surface magnetism - Sun: photosphere - methods: data analysis

1 Introduction

Both solar physics and radiative transfer owe much to the Milne-Eddington (ME) approximation. In an incredibly simplistic description of spectral line formation, which provides useful hints for understanding the behavior of spectral lines that form in solar and stellar atmospheres. It also offers a key diagnostics to infer the physical conditions of the plasma. This is particularly true when magnetic fields are present. The first solution of the radiative transfer equation in the presence of a magnetic field was derived adopting the ME assumption that all physical quantities relevant to line formation are constant with depth (Rachkovsky 1962b,a; Unno 1956). Under these conditions, the solution is analytic and therefore, by simply varying the model parameters, one gains an understanding of the Stokes line profiles' behavior. Similarly, the analytic character of the ME solution allows perturbative analyses like those performed by Landi Degl'Innocenti & Landolfi (1983), who studied the influence of velocity gradients, or Orozco Suárez & Del Toro Iniesta (2007), who calculated the sensitivities of ME Stokes profiles to the various model parameters. Inversion codes of the radiative transfer equation are diagnostic tools that become simpler under the ME hypothesis. Since the pioneering work by Harvey et al. (1972) and Auer et al. (1977), and after improvements by Landolfi & Landi Degl'Innocenti (1982) and Landolfi et al. (1984), a number of ME inversion codes have been developed. These include the HAO code (Skumanich & Lites 1987; Lites & Skumanich 1990), MELANIE (Socas-Navarro 2001), HELIX (Lagg et al. 2004), MILOS (Orozco Suárez & Del Toro Iniesta 2007), and VFISV (Borrero et al. 2010).

Strictly speaking, the ME model is applicable to just one spectral line. The reason is that the so-called thermodynamic parameters of the model are meant to characterize the behavior of the specific line under consideration. The line-to-continuum opacity ratio, $\eta _0$, the Doppler width of the line, $\Delta \lambda _{\rm D}$, and the damping parameter, a, govern the shape of the Stokes profiles (i.e., they are the parameters of the Voigt and Faraday-Voigt functions). In turn, the source-fuction terms, S0 and S1, control the continuum level, the line depression, and the Stokes amplitudes. However, many investigations are based upon the simultaneous ME inversion of spectral line pairs, like the well-known Fe I doublet at 630 nm (e.g., Lites et al. 1993) or the Mg I b lines at 517.2 and 518.3 nm (Lites et al. 1988). These inversions are reported to use no extra free parameters as compared to single-line inversions, based on the similarities between the two lines belonging to the same multiplet: the opacities for each line are specified in the ratio of their respective oscillator strengths, while the Doppler widths and the damping parameters are assumed to be identical for the two lines. S0 and S1 are also the same for both lines because they lie very close in wavelength.

This strategy has been widely used for more than 20 years to analyze the Fe I 630 nm measurements taken with instruments such as the Advanced Stokes Polarimeter (Elmore et al. 1992) or the spectropolarimeter aboard the Hinode satellite (Kosugi et al. 2007; Tsuneta et al. 2008; Lites et al. 2007). The simultaneous inversion has been shown to provide better results than single-line inversions (e.g., Lites et al. 1994). The better performance is easy to understand: if the observables reproduced by the inversion are doubled, the results can be expected to be more accurate (at least by a factor $\sqrt{2}$). However, the two lines do not have exactly the same atomic parameters (see Table 1). For this reason, they are formed at slightly different heights, where different physical conditions may exit (e.g. Martínez González et al. 2006). In view of these differences and of the large excursions of $\eta _0$, a, and $\Delta \lambda _{\rm D}$ in the real solar photosphere, both horizontally and vertically, one may wonder whether the simultaneous ME inversion of the two lines is valid and what the limitations are. General inversion codes not relying on the ME approximation perform exact line transfer calculations, so they are able to invert the two lines without inconsistencies. The purpose of the present Research Note is to check the ME case using the excellent test bench offered by modern magnetohydrodynamic (MHD) simulations.

Table 1:   Atomic data for the Fe I 630 nm lines.

2 Influence of the ME thermodynamic parameters

Trade-offs among the ME thermodynamic parameters have been reported and found not to be very important for the inference of vector magnetic fields and line-of-sight (LOS) velocities (e.g., Westendorp Plaza et al. 1998; Lites & Skumanich 1990). An explanation of this phenomenon has been given by Orozco Suárez & Del Toro Iniesta (2007). Therefore, the first question we should answer is whether or not the thermodynamic parameters of the lines need to be the same to obtain similar LOS velocities, $v_{\rm LOS}$, magnetic field strengths, B, inclinations, $\gamma$, and azimuths, $\varphi$, from their individual analysis.

To investigate this, we synthesized realistic Stokes profiles for the two Fe I lines at 630 nm using simulations performed with the MPS/University of Chicago Radiative MHD code. This code solves the MHD equations for compressible and partially ionized plasmas. Further information about the simulations can be found in Vögler (2003) and Vögler et al. (2005). The snapshot used here belongs to a mixed-polarity simulation run with an average magnetic field strength of $\langle B \rangle \simeq 140$ G at $\log ~\tau_{500} =-1$. We generated the Stokes spectra of the two lines from the MHD models using the SIR code (Ruiz Cobo & Del Toro Iniesta 1992), as explained by Orozco Suárez et al. (2010). We then inverted the two lines separately with the MILOS code. The inversion was carried out assuming a one-component model atmosphere (magnetic filling factor unity) and zero macroturbulent velocity. No noise was added to the Stokes profiles.

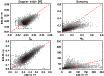
Figure 1 shows scatter plots of $\Delta \lambda _{\rm D}$, a, S0, and $\eta _0$ as inferred from the inversion of the two lines. The results for S1 are very similar to those for S0, with less scatter. In this and other figures, the gray colors inform about the pixel density, with black meaning higher values. Over-plotted are dashed lines representing one-to-one correspondences, except for $\eta _0$ where the ratio $\eta_{0,2}~/~\eta_{0,1}=0.327$ is indicated (1 and 2 stand for the 630.15 and the 630.25 lines, respectively; see below). The plots include all pixels in the simulation snapshot ( $288 \times 288$), independently of the polarization signal. Obviously, the thermodynamic parameters are far from being the same for the two lines. The scatter is large for $\Delta \lambda _{\rm D}$ and S0, although they show a linear correlation with a slope close to unity. For $\eta _0$ and a the scatter is dramatic; differences of up to a factor 3 for a and of more than one order of magnitude for $\eta _0$can be seen. Indeed, the $\eta _0$ values obtained for the 630.15 nm line span the full range of variation of the line-to-continuum opacity ratio in real solar atmospheres (see, e.g., Fig. 11 of Westendorp Plaza et al. 1998).

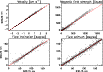
Do these discrepancies between the thermodynamic parameters affect the magnetic and velocity inferences? The answer to this question is negative, as can be seen in Fig. 2, where $v_{\rm LOS}$, B, $\gamma$, and $\varphi$ are displayed as inferred from the individual inversion of the 630.15 and 630.25 nm lines. Despite the strong scatter in the thermodynamics, the results from both lines are remarkably similar. Therefore, we have to conclude that although the thermodynamic parameters of ME inversions may have little meaning, it is possible to establish approximate relations between the parameters of the two lines for use in simultaneous inversions, as we shall see in the next section.

\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{14374Fig1.eps}} \vspace*{3.5mm} \end{figure} Figure 1:

$\Delta \lambda _{\rm D}$, a, S0, and $\eta _0$ parameters from the inversion of the Fe I line at 630.25 nm vs. those obtained from the 630.15 nm line. The dashed lines represent one-to-one correspondences. In the bottom right panel the dashed line represents $\eta _{0,2}/\eta _{0,1} = 0.327$. Both lines are inverted separately.

Open with DEXTER

\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{14374Fig2.eps}} \vspace*{3.5mm}\end{figure} Figure 2:

Line-of-sight velocity, magnetic field strength, inclination, and azimuth from the inversion of the 630.25 nm line vs those from the inversion of the line at 630.15 nm. Both lines are inverted separately.

Open with DEXTER

3 Understanding the simultaneous inversion

Since iron is mostly ionized and local thermodynamic equilibrium conditions prevail in the solar photosphere, the dependence of the logarithmic derivative of $\eta _0$ on temperature (the most important quantity in line formation) is linear with the excitation potential $\chi$ and the ionization potential I, and quadratic with the temperature. $\Delta \lambda _{\rm D}$ is proportional to the square root of temperature and does not depend on the atomic parameters of the line. Assuming van der Waals broadening for the calculation of the damping coefficient, an intricate (but weak) dependence of a on $\chi$, along with a proportionality with the 7/10-th power of temperature, is obtained (see, e.g., Gray 2008).

\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{14374Fig3.eps}} \end{figure} Figure 3:

$\eta _0$ values retrieved from the inversion of the Fe I lines at 630.15 and 630.25 nm. The dashed line represents the theoretical ratio $\eta _{0,2}/\eta _{0,1} = 0.327$. The solid line stands for a multi-polynomial fit. The inset zooms in the dotted box.

Open with DEXTER

Neglecting the differences induced by the slightly different excitation potentials of both lines, the a and $\Delta \lambda _{\rm D}$ ratios are proportional to $\lambda_{0,2}/\lambda_{0,1}$. Thus, the damping and Doppler width can safely be assumed to be equal for both lines, which is also the case for S0and S1, because the Planck function should not present significant differences in such a short wavelength interval. $\eta _0$ is proportional to the square of the central wavelength of the line and to its gf value. Therefore, $\eta_{0,2}/\eta_{0,1} \approx (g_2 ~ f_2 ) / (g_1 ~ f_1$), where g is the multiplicity of the lower level and f the oscillator strength. Note that this ratio is independent of the temperature or other thermodynamic quantities, so it should not change with height in the atmosphere even if the opacity varies by orders of magnitude. With the parameters of Table 1, the opacity ratio for the Fe I 630 nm lines turns out to be $\eta_{0,2}~/~\eta_{0,1}=0.327$. This is the value implemented in MILOS. The HAO code and MELANIE use similar ratios[*].

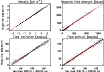
\begin{figure} \par\resizebox{9cm}{!}{\includegraphics{14374Fig4.eps}} \end{figure} Figure 4:

Magnetic field strength, inclination, azimuth, and LOS velocity from the the inversion of the 630.25 nm line vs those from the simultaneous inversion of the two lines. The latter inversion was done assuming the same model atmosphere (total of nine free parameters) for the two lines, with their $\eta _0$ values coupled.

Open with DEXTER

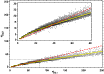
To check the validity of this estimate, we inverted the 630.25 nm line again but forcing S0, S1, $\Delta \lambda _{\rm D}$, and a to be equal to those obtained from the previous inversion of the 630.15 nm line. The remaining model parameters were allowed to vary freely. Figure 3 shows the $\eta _0$ values retrieved from the inversion. The dashed line represents the ratio $\eta_{0,2}~/~\eta_{0,1}=0.327$. The solid line corresponds to a multi-polynomial fit y = a[1]x3 + a[2]x2+ a[3]x with $a = [ 1 \times10^{-4}$, ${-}9.3\times10^{-3}, 0.5]$ for $\eta_{0,1} \leqslant 38$ and y = b[1]x + b[2] with b = [ 0.23,4.1] for $\eta_{0,1} > 38$. Note that the theoretical ratio provides a fair description of the relationship between the two $\eta _0$ values in the range where most of the points are located (to stress the differences, the inset zooms in on the boxed area). Since the exact values of the thermodynamical parameters are not very important for the determination of the magnetic field vector and the LOS velocity, we conclude that it is safe to use a constant opacity ratio to invert the two lines simultaneously without increasing the number of free parameters.

The final consistency proof is shown in Fig. 4, where the parameters obtained from the inversion of Fe I 630.25 nm are plotted against those coming from the simultaneous inversion of the two lines as coupled through their theoretical $\eta _0$ ratio. The scatter is very small for B and v $_{\rm LOS}$and somewhat larger for $\gamma$ and $\varphi$, but still much smaller than that of Fig. 2. This suggests that the accuracy of analyses based on one single line (e.g., Bommier et al. 2009) could be improved by adding the other line.

Acknowledgements
We thank an anonymous referee for raising the issue investigated in this paper. Our work has been supported by the Spanish MICINN through projects AYA2009-14105-C06-06 and PCI2006-A7-0624, by Junta de Andalucía through project P07-TEP-2687 (including European FEDER funds), and by the Japan Society for the Promotion of Science.

References

  1. Auer, L. H., House, L. L., & Heasley, J. N. 1977, Sol. Phys., 55, 47 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bard, A., Kock, A., & Kock, M. 1991, A&A, 248, 315 [NASA ADS] [Google Scholar]
  3. Bommier, V., Martínez González, M., Bianda, M., et al. 2009, A&A, 506, 1415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Borrero, J. M., & Bellot Rubio, L. R. 2002, A&A, 385, 1056 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2010, Sol. Phys., 35 [Google Scholar]
  6. Elmore, D. F., Lites, B. W., Tomczyk, S., et al. 1992, Proc. SPIE, 1746, 22 [NASA ADS] [CrossRef] [Google Scholar]
  7. Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press) [Google Scholar]
  8. Harvey, J., Livingston, W., & Slaughter, C. 1972, Line Formation in the Presence of Magnetic Fields, 227 [Google Scholar]
  9. Kosugi, T., Matsuzaki, K., & Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
  10. Lagg, A., Woch, J., Krupp, N., & Solanki, S. K. 2004, A&A, 414, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Landi Degl'Innocenti, E., & Landolfi, M. 1983, Sol. Phys., 87, 221 [NASA ADS] [Google Scholar]
  12. Landolfi, M., & Landi Degl'Innocenti, E. 1982, Sol. Phys., 78, 355 [NASA ADS] [CrossRef] [Google Scholar]
  13. Landolfi, M., Landi Degl'Innocenti, E., & Arena, P. 1984, Sol. Phys., 93, 269 [NASA ADS] [CrossRef] [Google Scholar]
  14. Lites, B. W., & Skumanich, A. 1990, ApJ, 348, 747 [NASA ADS] [CrossRef] [Google Scholar]
  15. Lites, B. W., Skumanich, A., Rees, D. E., & Murphy, G. A. 1988, ApJ, 330, 493 [NASA ADS] [CrossRef] [Google Scholar]
  16. Lites, B. W., Elmore, D. F., Seagraves, P., & Skumanich, A. P. 1993, ApJ, 418, 928 [NASA ADS] [CrossRef] [Google Scholar]
  17. Lites, B. W., Martinez Pillet, V., & Skumanich, A. 1994, Sol. Phys., 155, 1 [NASA ADS] [CrossRef] [Google Scholar]
  18. Lites, B. W., Elmore, D. F., Streander, K. V., et al. 2007, ASP Conf. Series, 369, 55 [NASA ADS] [Google Scholar]
  19. Martínez González, M. J., Collados, M., & Ruiz Cobo, B. 2006, A&A, 456, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Orozco Suárez, D., & Del Toro Iniesta, J. C. 2007, A&A, 462, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Orozco Suárez, D., Bellot Rubio, L. R., Vögler, A., & Del Toro Iniesta, J. C. 2010, A&A, 518, A2 [Google Scholar]
  22. Rachkovsky, D. N. 1962a, Izv. Krymsk. Astrofiz. Obs., 27, 148 [Google Scholar]
  23. Rachkovsky, D. N. 1962b, Izv. Krymsk. Astrofiz. Obs., 28, 259 [Google Scholar]
  24. Ruiz Cobo, B., & Del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
  25. Skumanich, A., & Lites, B. W. 1987, ApJ, 322, 473 [Google Scholar]
  26. Socas-Navarro, H. 2001, ASP Conf. Ser., 236, 487 [NASA ADS] [Google Scholar]
  27. Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
  28. Unno, W. 1956, PASJ, 8, 108 [NASA ADS] [Google Scholar]
  29. Vögler, A. 2003, Ph.D. Thesis, University of Göttingen, Germany, http://webdoc.sub.gwdg.de/diss/2004/voegler/ [Google Scholar]
  30. Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Westendorp Plaza, C., Del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 1998, ApJ, 494, 453 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... ratios[*]
The opacity ratio depends basically upon f, which is known with limited precision and varies from one source to the next. This causes an uncertainty in the theoretical opacity ratio. For example, the laboratory measurements of Bard et al. 1991 give 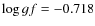$\log gf= -0.718$ for Fe I 630.15 nm, rather than the -0.75 specified in Table 1. With this oscillator strength, the theoretical ratio would be 0.301 (closer to the values retrieved from the inversion, but only at the high $\eta _0$ end).
Copyright ESO 2010

All Tables

Table 1:   Atomic data for the Fe I 630 nm lines.

All Figures

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{14374Fig1.eps}} \vspace*{3.5mm} \end{figure} Figure 1:

$\Delta \lambda _{\rm D}$, a, S0, and $\eta _0$ parameters from the inversion of the Fe I line at 630.25 nm vs. those obtained from the 630.15 nm line. The dashed lines represent one-to-one correspondences. In the bottom right panel the dashed line represents $\eta _{0,2}/\eta _{0,1} = 0.327$. Both lines are inverted separately.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{14374Fig2.eps}} \vspace*{3.5mm}\end{figure} Figure 2:

Line-of-sight velocity, magnetic field strength, inclination, and azimuth from the inversion of the 630.25 nm line vs those from the inversion of the line at 630.15 nm. Both lines are inverted separately.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{14374Fig3.eps}} \end{figure} Figure 3:

$\eta _0$ values retrieved from the inversion of the Fe I lines at 630.15 and 630.25 nm. The dashed line represents the theoretical ratio $\eta _{0,2}/\eta _{0,1} = 0.327$. The solid line stands for a multi-polynomial fit. The inset zooms in the dotted box.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{9cm}{!}{\includegraphics{14374Fig4.eps}} \end{figure} Figure 4:

Magnetic field strength, inclination, azimuth, and LOS velocity from the the inversion of the 630.25 nm line vs those from the simultaneous inversion of the two lines. The latter inversion was done assuming the same model atmosphere (total of nine free parameters) for the two lines, with their $\eta _0$ values coupled.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.