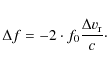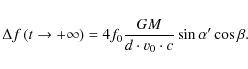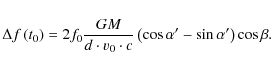| Issue |
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
|
|
|---|---|---|
| Article Number | L156 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201014325 | |
| Published online | 03 September 2010 | |
LETTER TO THE EDITOR
Pre-flyby estimates of the precision of the mass determination of asteroid (21) Lutetia from Rosetta radio tracking
M. Pätzold1 - T. P. Andert2 - B. Häusler2 - S. Tellmann1 - J. D. Anderson3 - S. W. Asmar3 - J.-P. Barriot4 - M. K. Bird5
1 - Rheinisches Institut für Umweltforschung,
Abteilung Planetenforschung, an der Universität zu Köln, Aachener
Strasse 209, 50931 Köln, Germany
2 -
Institut für Raumfahrttechnik,
Universität der Bundeswehr München,
Werner-Heisenberg-Weg 150, Neubiberg, Germany
3 -
Jet Propulsion Laboratory, California Institute for Technology,
4800 Oak Grove Drive, Pasadena, CA 91109, USA
4 -
Géosciences du Pacifique Sud,
Université de la Polynésie française,
BP 6570, 98702 FAA'A,
Tahiti, Polynésie Française, France
5 -
Argelander Institut für Astronomie,
Universität Bonn,
Auf dem Hügel 71,
53121 Bonn, Germany
Received 26 February 2010 / Accepted 16 June 2010
Abstract
The Rosetta spacecraft will fly by its second target asteroid (21)
Lutetia on 10 July 2010. Simulations based on the currently
known size of Lutetia and assumptions on the bulk density show that
tracking of two radio-carrier frequencies at X-band (8.4 GHz) and S-band
(2.3 GHz) during the flyby will determine the mass at less
than 1% accuracy. Derivation of the asteroid volume by camera
observation will drive the uncertainty in derivation of the bulk
density. Mass and bulk density provide valuable clues that might help
resolve the difficulties in determining the taxonomic class of the
asteroid.
Key words: minor planets, asteroids: general - minor planets, asteroids: individual: (21) Lutetia
1 Introduction
The Rosetta spacecraft was launched on 2 March 2004 to intercept comet 67P/Churyumov-Gerasimenko in 2014 and to orbit and escort the nucleus from its aphelion to perihelion in late 2015. The postponement of the Rosetta launch from January 2003 to March 2004 made it necessary to change the mission entirely, starting with the new target comet 67P/Churyumov-Gerasimenko and a new cruise trajectory. New target asteroids were also selected: asteroids (2867) Steins and (21) Lutetia (Barucci et al. 2005).
During the cruise to its target, Rosetta has flown by Earth three times and once by Mars. After its second Earth flyby, Rosetta encountered the small asteroid (2867) Steins on 5 September 2008. Following its last Earth flyby in November 2009, Rosetta is en route to encounter the asteroid (21) Lutetia on 10 July 2010. Apart from the various cometary science objectives, the Rosetta Radio Science Investigation (RSI) experiment (Pätzold et al. 2007,2009) will also focus on the mass and bulk density determination of the asteroid (21) Lutetia.
An asteroid's mass can be determined to high precision by analysing the spacecraft´s radio tracking data (distance/range and velocity/range rate or Doppler frequency). The gravitational attraction of the asteroid acting on the spacecraft during the flyby steadily perturbs the flyby trajectory by an amount proportional to the mass of the asteroid. The magnitude of the perturbation also depends on the flyby distance, the relative velocity between spacecraft and asteroid, and the geometry (e.g. Anderson et al. 1992; Pätzold et al. 2001).
Lutetia is comparable to the target asteroid (140) Siwa of the old Rosetta mission, for which a mass determination to a precision of 1% was deemed possible at a flyby distance of 3500 km (Pätzold et al. 2001). Based on the experience of three close Mars Express/Phobos flybys (Andert et al. 2010) and improved software tools for data processing and orbit determination developed at the University of the German Armed Forces in Munich, Germany, this work estimates the feasibility and precision of the Lutetia mass determination in July 2010 and studies the implications for the bulk density, porosity and origin.
The bulk density, as determined from the mass and the volume of the body, is an important parameter to understand the asteroid's composition, internal structure and porosity. Bulk densities, however, are affected by the body's porosity and are not necessarily an immediate indicator of the asteroid type. So far, precise masses of only few asteroids have been determined. The masses of Ceres, Pallas and Vesta have been estimated from their influence on the motion of Mars (Standish & Hellings 1989). Other estimates of asteroid mass have been derived from analyses of the motion of moons around 145 Ida (Belton et al. 1995) and 45 Eugenia (Merline et al. 1999) or by analysing trajectory perturbations of the NEAR spacecraft flying by asteroid Mathilde (Yeomans et al. 1997) or by spacecraft orbiting about the asteroids Eros (Yeomans et al. 2000) and Itokawa (Abe et al. 2006). A large fraction of asteroid mass derivations with various levels of precision were obtained from the analysis of the gravitational perturbations during close approaches between asteroids (Mouret et al. 2007; Baer & Chesley 2008).
Mass determinations of large asteroids like Lutetia may also be
relevant for the accuracy of the ephemerides of the inner planets in
the solar system. Lutetia may be a massive asteroid and is considered a
major perturber of the Martian orbit![]() . The future ESA mission Gaia will derive masses from many asteroids from their mutual perturbations (Mignard et al. 2007).
Lutetia is, in fact, a major perturber of several smaller asteroids. A
precise mass determination for Lutetia may help to improve the
dynamical modelling of asteroid orbit perturbations (Mouret et al. 2007).
. The future ESA mission Gaia will derive masses from many asteroids from their mutual perturbations (Mignard et al. 2007).
Lutetia is, in fact, a major perturber of several smaller asteroids. A
precise mass determination for Lutetia may help to improve the
dynamical modelling of asteroid orbit perturbations (Mouret et al. 2007).
The uncertainty in the volume determination by radar techniques or imaging from flyby spacecraft typically ranges from 15% to 20%. The error in the volume is thus the driver for the precision in the bulk density. Only orbiting spacecraft allow a volume determination of a few percent (Abe et al. 2006). An overview of known masses, volumes, and bulk densities has been published by Britt et al. (2002).
2 Flyby geometry

|
Figure 1:
Encounter geometry in the flyby plane. The LOS to Earth and the trajectory form an angle
|
| Open with DEXTER | |
The attracting forces from the asteroid acting on the spacecraft during
the flyby will perturb the trajectory and change the relative flyby
velocity. Figure 1 shows a schematic representation of the flyby plane formed by the asteroid and the flyby trajectory.
The attracting force, and hence the
![]() vector, is directed toward the asteroid from any point along the trajectory. The
vector, is directed toward the asteroid from any point along the trajectory. The
![]() vector
is composed of two perpendicular components, one along the trajectory
and the other one across the trajectory. Both components are projected
into the line-of-sight (LOS) to Earth. The LOS forms an angle
vector
is composed of two perpendicular components, one along the trajectory
and the other one across the trajectory. Both components are projected
into the line-of-sight (LOS) to Earth. The LOS forms an angle ![]() with the trajectory and is not necessarily in the same plane as formed
by the asteroid and the trajectory; in fact the Earth is 3
with the trajectory and is not necessarily in the same plane as formed
by the asteroid and the trajectory; in fact the Earth is 3![]() above the flyby plane. This geometry angle
above the flyby plane. This geometry angle ![]() is an important parameter because it directly influences the magnitude of the
is an important parameter because it directly influences the magnitude of the
![]() component along LOS observable via the Doppler effect. There is a first
order analytical solution for the change in velocity
component along LOS observable via the Doppler effect. There is a first
order analytical solution for the change in velocity ![]() ,
which describes these dependencies (Pätzold et al. 2001):
,
which describes these dependencies (Pätzold et al. 2001):
where
where
The
![]() is observed via the Doppler effect. If ignoring relativistic effects,
the shift in the radio carrier frequency due to the perturbed velocity
is
is observed via the Doppler effect. If ignoring relativistic effects,
the shift in the radio carrier frequency due to the perturbed velocity
is
The factor 2 considers that the radio link is operated in the two-way mode and that the Doppler shift is induced on the uplink and the downlink. Rosetta radio tracking during the Lutetia flyby will be performed using two carrier frequencies at X-band (8.4 GHz) and S-band (2.3 GHz). The received carrier frequencies will be recorded at a ground station antenna on Earth for eight hours centred on the time of closest approach.
In practice, the spacecraft orbital elements after the last manoeuvre before closest approach will be computed from the radio tracking directly after this manoeuvre. The post-manoeuvre trajectory will be extrapolated by solving the equation of motion for Rosetta to many hours after closest approach, assuming that the asteroid and its perturbing forces are not present. This extrapolated unperturbed trajectory, the gravity attraction of all planets acting on Rosetta, the knowledge of the precise location of the ground station on the surface, the Earth rotation, plate tectonics, solid Earth tides, the position of the antenna phase centres on ground, and relativistic propagation effects, all provide the basis for the computation of the relative velocity vector along the line-of-sight (LOS). This leads to a predicted Doppler shift and, together with the transmitted carrier frequency, to a predicted received frequency for all times during and after the flyby.
Frequency residuals are computed by subtracting the predicted received frequency from the true observed frequency. If there is no influence by the asteroid then the frequency residuals are zero or show a bias from relative velocity contributions not considered in the prediction. Any changes from zero between the pre-encounter predicted and the post-encounter observed Doppler shift is assumed to be caused by the perturbing force of gravity attraction acting on the spacecraft.
One may derive from Eqs. (1)-(3) for
![]() that
that
The dependencies are clear: slow and close flybys at the optimal geometry angle
At the time of closest approach
![]() ,
however,
,
however,
For
To prepare the Rosetta/Lutetia flyby and to assess whether a mass
determination of Lutetia is feasible and at what precision, the flyby
has been simulated according to (1) for ![]() 4 h about closest approach. The asteroid mass for the simulation was
4 h about closest approach. The asteroid mass for the simulation was
![]() (
(
![]() solar masses), corresponding to a bulk density of 2000 kg/m3
(ranging between the common bulk densities of a C-type and an M-type
asteroid) and a mean spherical radius of 47.9 km (Tedesco
et al. 2004). Random frequency noise of 12 mHz (1-sigma),
observed during frequent Rosetta payload checkouts, has been added to
account for a foreseeable measurement uncertainty (Fig. 2). A model with GM as the free parameter was fit by a non-linear least-squares procedure, yielding
solar masses), corresponding to a bulk density of 2000 kg/m3
(ranging between the common bulk densities of a C-type and an M-type
asteroid) and a mean spherical radius of 47.9 km (Tedesco
et al. 2004). Random frequency noise of 12 mHz (1-sigma),
observed during frequent Rosetta payload checkouts, has been added to
account for a foreseeable measurement uncertainty (Fig. 2). A model with GM as the free parameter was fit by a non-linear least-squares procedure, yielding
![]() (error 2.9%). This scenario assumed continuous radio tracking during
(error 2.9%). This scenario assumed continuous radio tracking during ![]() 4 h about the time closest approach and is considered as the reference case.
4 h about the time closest approach and is considered as the reference case.

|
Figure 2:
Simulated flyby scenario |
| Open with DEXTER | |

|
Figure 3: Simulated flyby scenario with tracking stop 20 min before closest approach and no post-encounter tracking. The difference between the simulation (solid curve) and the fit to the data (dashed line) after the flyby is obvious. |
| Open with DEXTER | |

|
Figure 4: Simulated flyby scenario with tracking stop 20 min before closest approach and resumption of tracking one hour after closest approach. |
| Open with DEXTER | |
Table 1: Results from different simulated flyby scenarios for Rosetta at asteroid Lutetia.
The steerable Rosetta High Gain Antenna (HGA) will maintain Earth
pointing during the encounter approach phase. Shortly before closest
approach, however, the HGA will reach its articulation limit and the
spacecraft must turn its attitude by nearly 180![]() in order to allow further tracking. A tracking gap will thus occur
around the time of closest approach until the spacecraft is able to
re-establish the two-way radio link with Earth.
in order to allow further tracking. A tracking gap will thus occur
around the time of closest approach until the spacecraft is able to
re-establish the two-way radio link with Earth.
It is important to assess the influence of this tracking gap on the precision of the derived mass solution compared to the reference case. A number of simulations have been performed, assuming an early end of tracking before closest approach and no (immediate) resumption of tracking after closest approach (Fig. 3 and Table 1). One obvious consequence of these suboptimal scenarios is a large increase in the uncertainty of the GM solution of up to 26%.
Simulations assuming a tracking interruption of about an hour about closest approach show much better results (Fig. 4 and Table 1) and show comparable precision to the reference case. It was concluded from these simulations that the tracking must be resumed shortly after closest approach.
3 Discussion and conclusions
Currently, Rosetta radio tracking is the only way to derive precise mass information on the asteroid. A recent search for a satellite of (21) Lutetia, the presence of which would enable an alternate mass determination of comparable accuracy from the orbit period, was negative down to a diameter of roughly 6 km (Busch et al. 2009). Despite the suboptimal flyby geometry, the mass determination of asteroid (21) Lutetia is feasible to a precision of a few percent, assuming the noise conditions are similar to those observed during several in-flight payload checkouts.
If observations from the Rosetta camera OSIRIS are used to determine the size and the volume of Lutetia, the bulk density may be derived from the known mass and volume. The precision of the bulk density will be driven by the precision of the volume estimate. The size and the shape of Lutetia will not be entirely visible during the Rosetta flyby. This will constrain the volume derivation, probably at an error of 10% to 30%. This is similar to the observations by Drummond et al. (2009), where one axis was not visible but will be visible sometime in the next 12 months. This will improve the volume determination and the bulk density well after the Rosetta flyby. For a given volume, the bulk density will provide clues to the nature and type of Lutetia and will help for understanding the inconclusive taxanomic derivations of this asteroid.
The taxonomic asteroid type of Lutetia, C-type, M-type or X-type, is currently under discussion (e.g. Lazzarin et al. 2009). M-type asteroids are thought to be remnants or debris of former larger differentiated bodies, containing mostly heavy metallic material. In contrast to earlier paradigms (Margot & Brown 2003), there are currently no M-type asteroids known to have high porosities and low densities (Lupishko 2006; Descamps et al. 2008). A high mass determination for Lutetia (and thus high density) might therefore favour an M-type asteroid. C-type asteroids are known to have high porosities and low bulk densities in the range 1300-1600 kg/m3. A low mass (low density) determination might then imply a C-type asteroid (Britt et al. 2002). An asteroid is classified as X-type if its spectral characteristics are not fully consistent with the other usual types.
There are two mass estimates for (21) Lutetia from asteroid orbit determination (Baer et al. 2008) of
![]() solar masses
(
solar masses
(
![]() )
and from perturbations of the Mars orbit by large asteroids (Fienga et al. 2009) of
)
and from perturbations of the Mars orbit by large asteroids (Fienga et al. 2009) of
![]() solar masses (
solar masses (
![]() ).
These estimates are two to three times higher than the value used in
the simulation, implying a higher density by the same factor for a
volume based on a spherical radius of 47.9 km. Keck II 10-m
observations with adaptive optics of (21) Lutetia (Drummond et al. 2009)
revealed a highly ellipsoidal body with semi-major axes larger than
thought before. Although the error of the shortest axis is very high,
the actual volume could be 50% higher than the one used in our
simulations. A more massive body may be encountered in July 2010,
considerably improving the signal-to-noise ratio.
).
These estimates are two to three times higher than the value used in
the simulation, implying a higher density by the same factor for a
volume based on a spherical radius of 47.9 km. Keck II 10-m
observations with adaptive optics of (21) Lutetia (Drummond et al. 2009)
revealed a highly ellipsoidal body with semi-major axes larger than
thought before. Although the error of the shortest axis is very high,
the actual volume could be 50% higher than the one used in our
simulations. A more massive body may be encountered in July 2010,
considerably improving the signal-to-noise ratio.
Rosetta radio tracking should be recorded by the same ground station during the entire Lutetia flyby to avoid residual biases at the interfaces of visibility. The flyby is fully visible by the ESA and NASA ground station complexes near Madrid, Spain. To achieve an improved signal-to-noise ratio, RSI has also requested tracking time from the 70-m DSN antenna DSS-63. Finally, in response to the RSI request to reduce the tracking gap, the Rosetta Flight Control Team (FCT) has confirmed the feasibility of no longer tracking 5 min before closest approach and resuming tracking one hour after closest approach.
New filter techniques, first applied to the data of two MEX/Phobos flybys (Andert et al. 2010), promise further improvements in the precision of mass determination. The assumed frequency noise level of 12 mHz in the simulations is considered as conservative. RSI is confident that a better signal-to-noise ratio from a larger antenna than the usual 35-m ground station antennas and new filter techniques may improve the mass solution of (21) Lutetia to a precision below one percent.
AcknowledgementsThe German part of the Rosetta Radio Science Investigations Experiment is funded by the DLR Bonn-Oberkassel under grants 50QM0701 and 50QM1002. The US part is funded by a contract with NASA. We thank all colleagues involved in the Rosetta project at ESOC, ESAC, ESTEC, the ESA-ESTRACK network, and the NASA-Deep Space Network for their valuable and continuous support.
References
- Abe, S., Mukai, T., Hirata, N., et al. 2006, Science, 312, 1344 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Anderson, J. D., Armstrong, J. W., Campbell, J. K., et al. 1992, Space Sci. Rev., 60, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Andert, T. P., Rosenblatt, P., Pätzold, M., et al. 2010, Geophys. Res. Lett., 37, 9202 [Google Scholar]
- Baer, J., & Chesley, S. R. 2008, Celest. Mech. Dyn. Astron., 100, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Baer, J., Milani, A., Chesley, S., & Matson, R. D. 2008, BAAS, 40, 493 [NASA ADS] [Google Scholar]
- Barucci, M. A., Fulchignoni, M., Fornasier, S., et al. 2005, A&A, 430, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belton, M. J. S., Chapman, C. R., Thomas, P. C., et al. 1995, Nature, 374, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Britt, D. T., Yeomans, D., Housen, K., & Consolmagno, G. 2002, Asteroids III, 485 [Google Scholar]
- Busch, M. W., Kulkarni, S. R., & Conrad, A. 2009, Icarus, 203, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Descamps, P., Marchis, F., Pollock, J., et al. 2008, Icarus, 196, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Drummond, J. D., Conrad, A., Merline, W., & Carry, B. 2009, in AAS/Division for Planetary Sciences Meeting Abstracts, 41, 59.07 [Google Scholar]
- Fienga, A., Laskar, J., Morley, T., et al. 2009, A&A, 507, 1675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazzarin, M., Marchi, S., Moroz, L. V., & Magrin, S. 2009, A&A, 498, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lupishko, D. F. 2006, Sol. System Res., 40, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Margot, J. L., & Brown, M. E. 2003, Science, 300, 1939 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Merline, W. J., Close, L. M., Dumas, C., et al. 1999, Nature, 401, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F., Cellino, A., Muinonen, K., et al. 2007, Earth Moon and Planets, 101, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Mouret, S., Hestroffer, D., & Mignard, F. 2007, A&A, 472, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pätzold, M., Häusler, B., Aksnes, K., et al. 2007, Space Sci. Rev., 128, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Pätzold, M., Häusler, B., Aksnes, K., et al. 2009, in Rosetta, ESA's mission to the origin of the solar system, ed. R. Schulz, C. Alexander, H. Boehnhard, & K. H. Glassmeier (Springer Science, Business Media) [Google Scholar]
- Pätzold, M., Wennmacher, A., Häusler, B., et al. 2001, A&A, 370, 1122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Standish, E. M., & Hellings, R. W. 1989, Icarus, 80, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E. F., Noah, P. V., Noah, M., & Price, S. D. 2004, NASA Planetary Data System, 12 [Google Scholar]
- Yeomans, D. K., Antreasian, P. G., Barriot, J., et al. 2000, Science, 289, 2085 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yeomans, D. K., Barriot, J., Dunham, D. W., et al. 1997, Science, 278, 2106 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Footnotes
All Tables
Table 1: Results from different simulated flyby scenarios for Rosetta at asteroid Lutetia.
All Figures

|
Figure 1:
Encounter geometry in the flyby plane. The LOS to Earth and the trajectory form an angle
|
| Open with DEXTER | |
| In the text | |

|
Figure 2:
Simulated flyby scenario |
| Open with DEXTER | |
| In the text | |

|
Figure 3: Simulated flyby scenario with tracking stop 20 min before closest approach and no post-encounter tracking. The difference between the simulation (solid curve) and the fit to the data (dashed line) after the flyby is obvious. |
| Open with DEXTER | |
| In the text | |

|
Figure 4: Simulated flyby scenario with tracking stop 20 min before closest approach and resumption of tracking one hour after closest approach. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



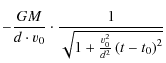
![$\displaystyle -\frac{GM}{d\cdot v_{\rm0}}\cdot\left[1+\frac{\frac{v_{\rm0}}{d}\...
...\rm0}\right)}{\sqrt{1+\frac{v_{\rm0}^2}{d^2}\left(t-t_{\rm0}\right)^2}} \right]$](/articles/aa/full_html/2010/10/aa14325-10/img21.png)