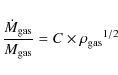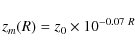EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 518 (July-August 2010) A&A, 518 (2010) A56 Full HTML
Free Access
Issue
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
Article Number A56
Number of page(s) 11
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201014304
Published online 02 September 2010
A&A 518, A56 (2010)

The dilution peak, metallicity evolution, and dating of galaxy interactions and mergers

M. Montuori1 - P. Di Matteo2 - M. D. Lehnert2 - F. Combes3 - B. Semelin3

1 - SMC-ISC-CNR & Physics Department, Univ. Roma ``La Sapienza'', Pl. Aldo Moro 2, 00185 Rome, Italy
2 - Observatoire de Paris, section de Meudon, GEPI, 5 Place Jules Jannsen, 92195 Meudon, France
3 - Observatoire de Paris, LERMA, CNRS, UPMC, 61 Avenue de l'Observatoire, 75014 Paris, France

Received 22 February 2010 / Accepted 18 May 2010

Abstract
Strong inflows of gas from the outer disk to the inner kiloparsecs are induced during the interaction of disk galaxies. This inflow of relatively low-metallicity gas dilutes the metallicity of the circumnuclear gas. This process is critical for the galaxy evolution. We have investigated several aspects of the process as the timing and duration of the dilution and its correlation with the induced star formation. We analysed major (1:1) gas-rich interactions and mergers, spanning a range of initial orbital characteristics. Star formation and metal enrichment from SNe are included in our model. Our results show that the strongest trend is between the star formation rate and the dilution of the metals in the nuclear region; i.e., the more intense the central burst of star formation, the more the gas is diluted. This trend comes from strong inflows of relatively metal-poor gas from the outer regions of both disks, which fuels the intense star formation and lowers the overall metallicity for a time. The strong inflows happen on timescales of about 108 years or less (i.e., on an internal dynamical time of the disk in the simulations), and the most intense star formation and lowest gas phase metallicities are seen generally after the first pericentre passage. As the star formation proceeds and the merger advances, the dilution reduces and enrichment becomes dominant - ultimately increasing the metallicity of the circumnuclear gas to a level higher than the initial metallicities of the merging galaxies. The ``fly-bys'' - pairs that interact but do not merge - also cause some dilution. We even see some dilution early in the merger or in the ``fly-bys'' and thus do not observe a strong trend between the nuclear metallicities and separation in our simulations until the merger is well advanced. We also analyse the O and Fe enrichment of the ISM, and show that the evolution of the $\rm\alpha/Fe$ ratios, as well as the dilution of the central gas metallicity, can be used as a clock for dating the interaction.

Key words: galaxies: interactions - galaxies: formation - galaxies: evolution

1 Introduction

Understanding how galaxy interactions and mergers shape the ensemble population of galaxies in the local universe is crucial for our understanding of galaxy evolution. It has been recognised for several decades that mergers may play an important role in the evolution of galaxies, especially for the early types (e.g., Toomre 1977). While there have been many observations and theoretical studies of ``first-order'' effects in interactions and mergers (such as morphological and kinetical evolution and star formation), much less work has been done on second order effects such as the evolution of metallicity.

Recently, we have undertaken the study of the evolution of metallicity in major dry (i.e., gas poor) mergers, showing that they can lead to metallicity gradients in agreement with those of local ellipticals (Di Matteo et al. 2009). However, in gas-poor mergers, the evolution of the local galaxy metallicity is driven only by the mixing of stars during the coalescence process. Gas can alter the properties of the final remnant significantly, affecting both the final gas phase and stellar metal abundance and ratios. In particular, gas phase metallicity can play an important role in constraining our understanding of the complex interaction between gas flows and star formation in interactions and mergers and allow us to constrain the relative time scales of the different epochs (i.e., date the merger/interaction).

If the progenitor disks have strong gas metallicity gradients, as observed in many galaxies in the local universe (Dinerstein 1996; Shields 1990), one would expect that interaction-induced gas inflows will drive a noticeable amount of gas into the central regions from the outer disk and thus initially lower the circumnuclear gas phase metallicity. Outflows of gas ejected in tidal tails may contribute to modifying the metallicity profile of the final merger remnant. Subsequent star formation (and outflows) may increase (decrease) the gas phase circumnuclear metallicity. The exact timing of the inflows versus the initiation of intense star formation and subsequent metal enrichment may provide robust constraints on the underlying physical mechanisms that determine the rate and relative timing of gas flows and star formation within the models. Comparing the evolution of the metallicity and its relationship to both inflows and star formation will allow us to constrain the dissipation time scales, the star formation evolution, the time delay between the onset of inflows, sufficient to dilute the metallicity, etc.

In the past few years, a number of studies have investigated the role played by interactions and environment in determining the gas phase metallicities of galaxies. Donzelli & Pastoriza (2000) show that merging galaxies have on average higher excitation in their optical emission line spectra than interacting pairs, and attribute this difference to lower gas metallicity in the mergers. Márquez et al. (2002) studied a sample of more than one hundred spiral galaxies, ranging from isolated to interaction with strong morphological distortions, and show that the [NII]/H$\alpha$ ratios, used as a metallicity indicator, indicate a clear trend from the metallicity to morphological type, with earlier type spirals showing higher ratios, while they found no trend with the status of the interaction. Recently, Kewley et al. (2006) have derived the luminosity-metallicity relation for a sample of local galaxy pairs and compared it with that of nearby field galaxies. They found that pairs with small projected separations ( $s < 20~{\rm kpc}~h^{-1}$) have systematically lower metallicities than either isolated galaxies or pairs with larger separations, for a given luminosity. They also found a correlation between gas metallicity and burst strengths - all galaxies in their interacting sample with strong central bursts having close companions and metallicities lower than the comparable field galaxies or pairs with wider separations. Rupke et al. (2008), in a study of strong interactions with high star formation rates (ultra-luminous infrared galaxies), found that the metal abundance in these intense starbursts is a factor of two lower than that of galaxies of comparable luminosity and mass. These results have been generally explained by gas inflows induced by the interaction, which dilute the pre-existing nuclear gas to produce a lower metallicity than that observed for wider separated pairs or isolated systems. More recently, Peeples et al. (2008,2009) have studied, respectively, a sample of low-mass, high-metallicity and high-mass, low-metallicity outliers from the mass-metallicity relation of star-forming galaxies selected from the Sloan Digital Sky Survey (SDSS). They showed that the low-mass, high-metallicity outliers are usually isolated galaxies, with no evident companion or strong interactions. On the other hand, the high-mass, low-metallicity outlierts typically consist of systems that have high star formation rates and evidence for disturbed morphologies.

However, Cooper et al. (2008) found a strong metallicity-density relation for star forming galaxies in the local universe, with the more metal-rich galaxies apparently favouring regions of higher galaxy overdensity (see also Ellison et al. 2009). They conclude that the discrepancy found with the other studies (including those just discussed) is due to the fact that the number of close pairs ( $s < 100~{\rm kpc}~h^{-1}$) in the SDSS sample constitutes only a tiny fraction of the whole sample (less than 1% of galaxies). In this case, close pairs with low central metallicity could not contribute significantly to the scatter found in the mass-metallicity relation. Of course it can be difficult to discern trends in the gas phase metallicity during a merger when studying large samples of galaxies in SDSS as other factors may dominate the overall mass-metallicity relationship and its scatter. A confirmation that the mass-metallicity relation is affected by interactions only for close pairs showing signs of strong disturbances has been found by Michel-Dansac et al. (2008), who pointed out that, in such pairs, the gas metallicity depends on the mass ratio of the two interacting systems: less massive members are systematically enriched, while a galaxy in interaction with a comparable stellar mass companion shows a metallicity lower than that of a galaxy in isolation. So while mergers and interactions alone may not drive the overall scatter in the mass-metallicity relationship, it may be a contributing factor. All these studies suggest that the dilution and enrichment of the ISM in the central regions of disk galaxies strongly depend on the exact timing of the different processes at play: gas inflows, interaction-driven star formation, gas consumption, feedback and subsequent enrichment.

While a number of numerical studies have investigated the response of the gaseous component of galaxies during tidal interactions and the subsequent star formation such interactions induce (Di Matteo et al. 2008; Cox et al. 2008; Di Matteo et al. 2007; Kapferer et al. 2005; Mihos & Hernquist 1994a; Cox et al. 2006; Iono et al. 2004; Springel 2000), little attention has been given to the detailed evolution of the metal content during galaxy encounters. Using a galaxy pair catalogue from cosmological simulations, Perez et al. (2006) have shown that the O/H abundance ratio in the central regions of close galaxy pairs ( $s < 50~{\rm kpc}~h^{-1}$) shows a lower level of enrichment than the mean O/H abundance ratio of a control sample, thus confirming the role played by gas inflow in diluting the metal content of the nuclear regions. Recently, Rupke et al. (2010) have analysed simulations of major galaxy mergers, studying the dilution of the gas metallicity in the nuclear regions due to gas inflow. They found a dilution of about 0.1-0.3 dex, happening shortly after the first pericentre passage between the two galaxies. However, their models do not include either star formation prescriptions or metal enrichment, so that while it has been possible to give predictions about the strength of the dilution, nothing is still known about the role played by interaction-induced star formation in the metal dilution and then subsequent enrichement. Moreover, the exact timing of the dilution peak and its correlation with the increase in the amplitude of the star formation have not been studied yet in any detail.

2 Models and initial conditions

Here we study mergers and flybys involving two massive Sbc galaxies, having a mass ratio 1:1. The Sbc galaxies (hereafter called gSb) are composed of a spherical dark matter halo and a spherical bulge, represented by Plummer spheres (Binney & Tremaine 1987) with total masses $M_{\rm H}=1.7$ $\times $ $10^{11}~M_{\odot}$ and $M_{\rm B}=11.5$ $\times $ $10^9~M_{\odot}$ and core radii $r_{\rm H}=12~{\rm kpc}$ and $r_{\rm B}=1~{\rm kpc}$ respectively. The stellar disk is represented by a Miyamoto-Nagai density profile (Binney & Tremaine 1987) with mass M*=40.6 $\times $ $10^9~M_{\odot}$, vertical and radial scale lengths given respectively by $h_{*}=0.5~{\rm kpc}$ and $a_{*}=5~{\rm kpc}$. The galaxies initially contain a gas mass $M_{\rm gas}=0.2~M_{*}$, redistributed in a Miyamoto-Nagai disk with vertical and radial scale lengths given respectively by $h_{\rm gas}=0.2~{\rm kpc}$ and $a_{\rm gas}=6~{\rm kpc}$. For each pair of interacting galaxies, we performed 24 simulations, varying the galaxies orbital initial conditions (initial orbital energy E and angular momentum L) and taking into account both direct and retrograde orbits. The initial orbital parameters (initial distance between the two galaxies, initial relative velocity, specific angular momentum, orbital energy and spin) for the different runs are fully described in Table 7 of Chilingarian et al. (2010), and we refer the reader to this paper for their complete description.

\begin{figure} \par\includegraphics[width=7cm,angle=270]{14304fg1.ps}\includegra... ...270]{14304fg3.ps}\includegraphics[width=7cm,angle=270]{14304fg4.ps} \end{figure} Figure 1:

The dynamics of the gas during the interaction and subsequent merger of two gSb galaxies for several orbits (shown with different colours). (First panel): relative distance of the two galaxy centres versus time for some simulated orbits. (Second panel): gas mass inside 2 kpc from one of the two galaxy centres versus time. (Third panel): evolution of the star formation rate (SFR) relative to the rate for the corresponding initial galaxies evolved in isolation. (Fourth panel): evolution of the central gas metallicity. The metallicity has been normalised to that of the initial galaxies used in the merger simulations evolved isolated. In the second, third, and fourth panel, squares and asterisks respresent respectively the time of the first pericentre passage and the time of final coalescence for the different orbits.

Open with DEXTER

We chose a reference frame with its origin at the barycentre of the system and x-y plane corresponding to the orbital plane. For each interacting pair, we have kept the disk of one of the two galaxies in the orbital plane ( $i_1 = 0 \hbox{$^\circ$ }$), and varied the inclination i2 of the companion disk, considering: $i_2 = 0 \hbox{$^\circ$ }$, $i_2 = 45 \hbox{$^\circ$ }$, $i_2 = 75 \hbox{$^\circ$ }$, and $i_2 = 90\hbox{$^\circ$ }$. The orbital angular momentum can be parallel (direct orbit) or anti-parallel (retrograde orbit) to the z-axis of the reference frame.

All the simulations (96 in total) were run using the Tree-SPH code described in Semelin & Combes (2002). Each galaxy contains a total of $N_{\rm TOT}=120~000$ particles, equally redistributed among gas, stars and dark matter. A Plummer potential is used to soften gravity at small scales, with constant softening lengths of $\epsilon=280$ pc for all particles. The gas is modelled as isothermal, with a temperature $T_{\rm gas}= 10^4~{\rm K}$. The assumption of an isothermal ISM is justified by the short cooling times in the gaseous disk at the resolution of our models, such that fluctuations in the gas temperature, those due to SN explosions for example, would be quicky radiated away (see the discussion in, e.g., Mihos & Hernquist 1996).

We refer the reader to Semelin & Combes (2002) for a detail description of and the tests performed to validate the code. Other tests have been presented in Di Matteo et al. (2008). The equations of motion are integrated using a leapfrog algorithm with a fixed time step of $\Delta t = 5$ $\times $  $10^5~{\rm yr}$.

\begin{figure} \par\includegraphics[width=7cm,angle=270]{14304fg5.ps}\includegra... ...ps}\includegraphics[width=7cm,angle=270]{14304fg8.ps} \vspace*{3mm} \end{figure} Figure 2:

Same as Fig. 1, but for the simulations of ``flybys''. Note that simulations resulting in starbursts with higher intensities also have gas phase metallicities with higher dilution. Even in flybys, the star formation rate and dilution of the metallicity are related.

Open with DEXTER

2.1 Star formation and metal enrichment

The numerical recipes used to implement star formation and metal enrichment have been fully described elsewhere (Chilingarian et al. 2010; Di Matteo et al. 2007), thus here we only summarise those features that are most directly relevant to our analysis. Star formation efficiency has been parametrised as:

\begin{displaymath}% \frac{\dot{M}_{\rm gas}}{M_{\rm gas}}=C\times {\rho_{\rm gas}}^{1/2} \end{displaymath} (1)

where $M_{\rm gas}$ is the gas mass of a particle, and $\rho_{\rm gas}$ the local gas density. The constant $C=0.3~{\rm pc}^{3/2}~M_{\odot}^{-1/2}~{\rm Gyr}^{-1}$ has been chosen such that the isolated disk galaxies form stars at an average rate of ${\sim}1~M_{\odot}~{\rm yr}^{-1}$. Once the star formation recipe is defined, we apply it to gas particles, using the hybrid method described in Mihos & Hernquist (1994b).

The effect of star formation on the surrounding interstellar medium has been implemented as follows. For each star-forming hybrid particle, we evaluate the fraction of stars formed with masses ${>}8~M_{\odot}$, adopting a Miller & Scalo (1979) initial mass function (IMF), and we assume that stars above this mass threshold instantaneously become supernovae. Each of the SN leave behind a remnant of  $1.4~M_{\odot}$ and releases their remaining mass to the surrounding ISM. The mass released also enriches the surrounding gas with metals. This is done assuming a yield $y=M_{\rm ret}/M_{*}$ = 0.02, where  $M_{\rm ret}$ is the total mass of all reprocessed metals and M* the total mass in stars. For each gas particle, the return of mass and metals is applied to the ith neighbour gas particle, using a weight wi based on the smoothing kernel. The metallicity is initially distributed in a gradient of the form:

\begin{displaymath}% z_{m}(R)= z_{0} \times 10^{-0.07 ~R} \end{displaymath} (2)

with R the particle distance from the galaxy centre and $z_{0}=3~z_{\odot}$ (Lemasle et al. 2008; Kennicutt et al. 2003; Magrini et al. 2007), evolves with time, as star formation proceeds.

Supernovae explosions also inject energy into the surrounding ISM. This is taken into account assuming that a fraction,  $\epsilon_{\rm kin}$, of the energy,  $E_{\rm SN}$, released by a SNe goes into kinetic energy giving a radial kick to the velocities of neighbouring gas particles. The value of  $\epsilon_{\rm kin}$has been chosen such that the total amount of kinetic energy received by a gas particle due to the contribution from all the surrounding neighbours, is less than 1 km s-1, thus preventing a rapid growth of the vertical thickness of the gaseous disk. A more detailed description of the implementation of feedback recipes used in our code is given in Chilingarian et al. (2010); Semelin & Combes (2002).

3 Results

3.1 Gas flows: where and when

It is known that close passages of galaxies can destabilise galaxy disks, producing asymmetries, such as bars, which are efficient mechanisms for driving gas into the circumnuclear region of a galaxy, producing a burst of star formation (Combes 2008; Iono et al. 2004). If, prior to the interaction, the gas is distributed in the disk with a negative metallicity gradient, with the outer regions being relatively more metal poor than the inner ones as observed in local galaxies (Dinerstein 1996; Shields 1990), then a portion of this low-metallicity gas will fall into the nuclear regions, diluting the pre-existing gas with gas of lower metallicity. This dilution will last until the star formation, which is enhanced by the gas inflow, releases reprocessed metals to enrich the gas.

This cycle (dilution and enrichment) is shown in Figs. 1 and 2 for some of our galaxy merger simulations. For the analysis of the effect of mergers on the metallicity of galaxies, we have defined the metallicity dilution (often referred to as simply dilution) as  $z/z_{\rm iso}< 1$, where z is the metallicity of a galaxy in the pair during the merger or flyby and  $z_{\rm iso}$ is the corresponding value for the same galaxy evolved isolated. Both z and  $z_{\rm iso}$are measured in apertures of 1-2 kpc and thus represent the evolution of the metallicity for the nuclear or circumnuclear regions of galaxies (which also corresponds reasonably well with the aperture sizes used to estimate the metallicities of galaxies; see discussion in the Sect. 1).

We find that as soon as the two galaxies have undergone their first pericentre passage, an intense inflow of gas, lasting for 300-400 Myr, takes place. A detailed discussion of the mechanism generating the gas inflows we observe in our simulations is given in Di Matteo et al. (2007). They show that each close passage of the two interacting galaxies is accompanied by the amplification of stellar asymmetries - stellar bars. These stellar bars are responsible of removing angular momentum from gas, transferring it to the stellar component, and in regulating the subsequent inflow of gas in the inner kpc. We note that this result has already been discussed in several previous studies using simulations (see for example Mihos & Hernquist 1994a,b, Mihos & Hernquist 1996). This mechanism does not require any stellar feedback to work, that is, the gas inflows are a natural consequence of the dynamics of the interaction and the redistribution of the angular momentum that is induced during the progression of the merger (Rupke et al. 2010; Di Matteo et al. 2008). This intense inflows can deposit in few 108 ys into the central ( $r\le 2~{\rm kpc}$) regions ${\sim}2{-}3$ $\times $ $10^9~M_{\odot}$ of gas, originally located before the interaction at an average distance of $6{-}7~{\rm kpc}$ from the galaxy centre. The amount and origin of the inflowing gas obviously depends on characteristics of the merger like orbital parameters of the interaction and gas fraction (see Di Matteo et al. 2007, for a discussion). In all cases, this inflow of gas fuels the first increase in the star formation rate during the merging process. A second, sometimes even stronger peak of SF takes place in the final phases of the interaction when the two galaxies are close to coalescence.

\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{14304fg9.ps} \end{figure} Figure 3:

The duration that the circumnuclear metallicity is below 0.8 (shown in red) and between 0.8 and 1.0 (shown in black) relative to an isolated simulated spiral with the same properties as the individual merging galaxies. We chose 0.8 as the threshold because this is the span of the most extreme metallicity offset observed in nearby mergers (e.g. Rupke et al. 2008; Kewley et al. 2006).

Open with DEXTER

The time of strong enhancement in the SFR also coincides with the time of high-dilution. Typically, we find that the dilution lasts for 2 $\times $ 109 years, with half of the sample substaining a $z/z_{\rm iso}\le 0.8$ for less than 5 $\times $ 108 (Fig. 3). In the case of fly-bys, this dilution is still visible far after the pericentre passage, when the separation between the two galaxies is several hundreds of kpc. We emphasise that the gas redistribution and subsequent dilution takes place on scales of several kiloparsecs and is not due to the effects of stellar feedback which typically act over much smaller physical scales. Moreover, significant star formation is initiated only after a substantial gas inflow has occurred. So feedback from SNe explosion has little effect on the inflowing gas and certainly is unable to prevent substantial inflows of gas initially.

A possible concurrent physical mechanism for redistributing metals in the interstellar medium of the galaxy could be through gas diffusion, which is not included in our code[*]. At scales of hundreds of parsecs (which corresponds roughly to our numerical resolution), the diffusion law can take the form of a heat equation, with a diffusion coefficient D=9.25 $\times $ $10^{26}~{\rm cm}^2~{\rm s}^{-1}$(see Martínez-Serrano et al. 2008). This means that the typical timescale for diffusing metals from the outer regions of the disk (R = 7 kpc[*]) is $T_{\rm diff}=R^2/D \ge 10^{10}~{\rm yr}$. This timescale is significantly longer than the average inflow timescale which is of-order 300-400 Myr. Thus, we can safely assert that the process of dilution of the central gas metallicity studied here is driven by interaction-driven inflows rather than metal diffusion.

Once the gas inflow and the corresponding burst of star formation is over, the re-processed gas released by SNe explosions starts to enrich the central metallicity, so that the $z/z_{\rm iso}$ ratio becomes greater than one (Figs. 1 and 2, fourth panel). We checked that during the interaction, the contrast in the gas density between the nuclear region and the outer disk are sufficient to result in gas depletion times that are significantly lower than the times typically required to re-enrich the ISM in metals. This substantiates our interpretation that the dilution in the metallicity of gas in the nucleus is due to strong merger-driven gas inflows.

3.2 Relationship between the star formation and metallicity

We have seen that the dilution of the gas-phase metallicity takes place at approximately the same time as the strongest enhancement in the star formation. In general, we find that the peak of SF and the maximum dilution are roughly coeval, with a delay between the two of 108 yr at most. This correlation between the starburst phase and the strong dilution is clearly seen in the results of the simulations shown in Fig. 4. The maximum dilution is reached in the simulations at approximately the peak in the star formation rate. In this phase, the higher SFR, which is a sign of the strongest gas inflow are indeed associated with the strongest dilution as would be expected. We note that a strong correlation between metallicity and central burst strength has been observed by Kewley et al. (2006) in a sample of galaxy pairs. Specifically, they pointed out that all five galaxies in the pairs sample with strong central bursts have close companions and metallicities lower than the comparable field galaxies.

Before the peak in the star formation rate, galaxies tend to populate a region of low to moderate SFRs and dilutions (typically $0.7 \le z/z_{\rm iso}\le 1$; see Fig. 4). During the burst phase and peak of star formation rate, the ejecta of the SNe starts to enrich the gas, and indeed, once the burst is over, galaxies have low star formation rates and high-metallicities (Fig. 4). The first two phases of the relation between star formation and dilution are associated with before, during, and after the first pericentre passage and then close to final coalescence of the merging galaxies, the last phase in the metallicity evolution is always associated with well after their first pericentre passage and is near or after coalescence. This final state of the interaction is true whether one considers mergers or simply flybys.

\begin{figure} \par {\hspace*{2.5cm}\includegraphics[width=8cm,angle=270]{14304f... ...\includegraphics[width=4.cm,angle=0]{14304fg18.ps} }\vspace*{1mm} \end{figure} Figure 4:

The star formation rate, $M_{\odot }$  ${\rm yr^{-1}}$, versus the relative metallicity of the interaction and merger. As in Fig. 1, the metallicity is shown relative to an isolated disk with the same initial conditions as the galaxies used in the merger simulations. The blue asterisks indicate times when the star formation is near its peak, while green triangles represent galaxies before their peak star formation and red dots represent galaxies that are past their peak of star formation and are in the final stages of the merger. In the bottom panels, we show the morphologies of the merger pairs in each region of the diagram to indicate the range of morphologies seen in the simulations.

Open with DEXTER

3.3 Relationship between separation and metallicity

While the correlation between SFR (at the peak of intensity) and metallicity dilution is quite remarkable, we expect a larger scatter when plotting the dilution as a function of the physical distance of galaxies in the pairs, especially for those at the smallest separations. This is because the interacting pair can be in a number of different evolutionary states at any given distance, except for perhaps the smallest separations. For example, a galaxy at moderate separations of several 10 s of kpc could be in an initial encounter and before first pericentre passage when the circumnuclear metallicity is largely unchanged. Or it could be just after the first pericentre passage when its circumnuclear gas could be highly diluted (Fig. 5). This causes a range of possible metallicity dilutions, from $z/z_{\rm iso}=1$ to $z/z_{\rm iso}\sim0.5$ (Fig. 5, right panel), with an average value of $z/z_{\rm iso}=0.75$. At the smallest separations, say less than 10-20 kpc, but still distinguishable systems, galaxies are likely to be either near the pericentre passage or near final coalescence. This leads to both a strong dilution and, on average, lower circumnuclear metallicity (see Fig. 5). At very small separations, less than about 4 kpc, galaxies can be near first pericentre passage or near coalescence which in either case have relatively large dilution and relatively low-metallicity, or can have coalesced and be strong enriched by supernovae ejecta and have relatively high-metallicity. We show this in Fig. 5 where in the smallest separation bin, if we include galaxy pairs with projected separations of less than 4 kpc we find a net average increase in the metallicity (i.e., z>1, with an average value of $z/z_{\rm iso} \sim 1.2$) while if we exclude such systems, we find a net decrease in the circumnuclear metallicity ( $z/z_{\rm iso} \sim 0.7$). This indicates the predominance of the metal enriched mergers at small projected separations.

Kewley et al. (2006) have shown that galaxy pairs with small projected separations ( $4~{\rm kpc}~h^{-1} \le s\le 20~{\rm kpc}~h^{-1}$) and strong bursts of star formation have metallicities lower than the comparable field galaxies. Note that in this analysis we are considering the physical (3D) distance between the two galaxies, and not their projected separation. Considering the effects of projection would likely contribute to increasing the scatter in the relation between metallicity and separation.

\begin{figure} \par\includegraphics[width=6cm,angle=270]{14304fg19.ps}\includegraphics[width=6cm,angle=270]{14304fg20.ps} \end{figure} Figure 5:

(Left panel:) the physical 3-dimensional separation of the galaxy pairs and mergers versus their relative circumnuclear metallicity. The black line represents the average relation, for physical distances greater than 4 kpc and binned every 10 kpc. The blue line represents the average relation when in addition including mergers with physical separations below 4 kpc in the smallest bin (0-10 kpc). (Right panel:) evolution of two mergers (blue and green curves) and a fly-by (red curve) in the metallicity-distance plane. The simulations suggest that even at wide separations there are gas inflows which dilute the metallicities of the nuclear regions and that this dilution persists until the pairs are strongly interacting, overlapping, and near or after coalescence. During the final merging process, a wide range of metallicities can be observed but on average will show a much higher metallicity than if they had not interacted or merged.

Open with DEXTER

3.4 O and Fe enrichment

\begin{figure} \par\includegraphics[width=7cm,angle=270]{14304fg21.ps}\includegr... ...\includegraphics[width=7cm,angle=270]{14304fg24.ps} \vspace*{1.5mm} \end{figure} Figure 6:

Rate of oxygen and iron released in the ISM by SNe II and SNeIa explosions (in units of $M_{\odot }$ yr-1) as a function of time two different simulations whose star formation histories are shown in Fig. 1. The first and final two panels show the ejection rate of oxygen and iron for the star formation history in Fig. 1 represented by the orange and red curves respectively. For the iron release, we separate the contribution from SNeIa (red curve) and SNe II (grey curve) for each of the two simulations. The black arrows in each panel represent the time of the first pericentre passage and final coalescence. Since the enrichment is instantaneous (i.e., no delay for the evolutionary times of the type II supernovae, the evolution of the star formation and ejecta rate are synchronous.

Open with DEXTER

Our simulations do not track the evolution of individual elements directly in the code. However, to track their evolution in an approximate way, we can use some simple arguments to give an estimate of the amount of iron and $\alpha$ elements, like oxygen, released in the ISM by type I and II SNe. At a given time, t, during the evolution of a galaxy, the rate of oxygen mass released in the ISM by SNe II can be estimated by:

\begin{displaymath}% {\rm O}_{\rm SNeII}(t)[M_{\odot}/{\rm yr}]=m_{\rm O,SNeII}R_{\rm SNeII}M_*(t) \end{displaymath} (3)

where $m_{\rm O,SNeII}$ is the total mass of oxygen ejected averaged over the initial stellar mass by a type II SNe, $R_{\rm SNeII}$, is the number of SNe II per unit mass of star formation, and M*(t) is the mass of stars formed at time t. Similarly, the rate of iron mass ejected on average in the ISM by SNe II explosions is given by:

\begin{displaymath}% {\rm Fe}_{\rm SNeII}(t)[M_{\odot}/{\rm yr}]=m_{\rm Fe,SNeII}R_{\rm SNeII}M_*(t). \end{displaymath} (4)

The progenitors of SNe II have very short lifetimes, less than a few 10 Myr, so that we can assume that the SNe II rate follows closely the star formation rate of the galaxy, and so that the release of oxygen and iron by SNe II in the ISM is approximately instantaneous[*].

The stars formed at time t contributes also in enriching the ISM with Fe released through type Ia SNe, which are the product of a thermonuclear detonation of a white dwarf accreting matter from a companion star. While the progenitors of SNe II have very short lifetimes, the time delay between the birth of the progenitors of SNe Ia and their explosion can be quite long, of the order of 1 Gyr or more depending on the progenitors, the binary parameters, etc. (Strolger et al. 2010). We will assume delay time between the birth of their progenitors and the explosion is uniformly distributed between 1 and 4 Gyr after the birth of the parent population, thus obtaining that, at any time t, the amount of iron released by SNeIa is:

\begin{displaymath}% {\rm Fe}_{\rm SNeIa}(t)[M_{\odot}/{\rm yr}]=m_{\rm Fe,SNeIa}R_{\rm SNeIa}M_*(t-\tau). \end{displaymath} (5)

where $\tau $ is the delay time between the birth of the progenitors and the detonation of the type Ia supernova. For the supernovae rates  $R_{\rm SNeIa}$ and  $R_{\rm SNeII}$ we have used the values in Strolger et al. (2010), while the synthesised masses  $m_{\rm Fe,SNeIa}, m_{\rm Fe,SNeII}$ and  $m_{\rm O,SNeIa}$ are derived from Table 3 in Iwamoto et al. (1999). The amount of oxygen released by a SNe Ia is about 0.1 times lower than the iron and we will neglect its contribution in the following estimations. In Fig. 6, we show the rate at which O and Fe are ejected into the ISM during some of the simulated mergers. We caution the reader that we are showing the global values, i.e. evaluated over the whole galaxy. The intense episodes of star formation are accompanied by intense peaks of O and Fe release, which coincide with the first phases of the encounter, soon after the first pericentre passage, and with the merging phase. During the burst of star formation, the ISM is enriched mostly in oxygen (the  $\rm O_{SNeII}$ ejection rate is about a factor 30 greater than that of $\rm Fe_{SNeII}$). If a second burst of star formation occurs in the simulation, a concomitant second peak of O and Fe release will also take place in the final phases of the interaction causing further relative enrichment of oxygen.

We note that if the coalescence of the two galaxies happens on a short time scale (i.e., less than 1 Gyr after the first pericentre passage), there is not enough time to enrich the ISM by SNe Ia. This means that the stellar population forming during the final burst forms from gas still relatively enhanced in $\alpha$-elements (see Fig. 6, second panel). If, in turn, the merger happens on longer time scales (i.e., longer than 1 Gyr), the iron released by SNe Ia explosions has time to lower the [ $\rm\alpha/Fe$] ratio of the ISM, and the stellar population formed in the merging phase will be less enhanced in $\alpha$ elements (Fig. 6, fourth panel).

The O and Fe ejected into the ISM obviously affects the ratio between these two elements (Fig. 7). Assuming that the initial galaxies have percentages of O and Fe similar to the Sun, as star formation proceeds during the interaction, the mass ratio of these two elements changes: in particular the oxygen abundance increases, until the iron release from SNeIa explosions inverts the trend. Note that the influence of the iron release from SNe Ia on the populations of new stars formed during the merger depends on the delay time between the birth of the parent population and the onset of SNe Ia - shorter delay times cause a more rapid decline in the O/Fe ratio. We caution the reader that in all our discussion of the relative abundance of $\alpha$-elements, we are neglecting any possible contribution from SNe Ia from the pre-existing old stellar population. This is of course an important simplification of these models which we will investigate in future studies.

\begin{figure} \par\includegraphics[angle=270,width=4.3cm,clip]{14304fg25.ps}\includegraphics[angle=270,width=4.3cm,clip]{14304fg26.ps} \end{figure} Figure 7:

The evolution of the oxygen over iron mass ratio for two of our galaxy mergers, whose rate of mass release in the ISM is shown in Fig. 6. For each panel, three different curves are shown corresponding to three different delay times for onset of SNeIa, $\tau $: $\tau $ = 1-4 Gyr (black curve), $\tau $ = 1-3 Gyr (dark grey) and $\tau $ = 1-2 Gyr (light grey), as indicated in the legends. The black arrows in each panel represent the time of first pericentre passage and coalescence.

Open with DEXTER

4 Discussion

Overall, our results are not surprising. It has been known for the last few decades that mergers of gas-rich massive galaxies lead to transformations in the morphological type (Barnes 1992; Barnes & Hernquist 1991) and drive strong inflows of gas into the circumnuclear region (Barnes 2002; Di Matteo et al. 2007; Braine & Combes 1993; Barnes & Hernquist 1996; Casoli et al. 1991). These inflows are a result of strong tidal torques, dissipation, and strong asymmetries in the stellar distribution (e.g., bars; see Barnes 2002; Barnes & Hernquist 1996) leading to efficient star formation (Di Matteo et al. 2007). While the infall of gas in mergers has been discussed within the context of simulations and observations (Barnes 2002; Di Matteo et al. 2007; Braine & Combes 1993; Barnes & Hernquist 1996; Casoli et al. 1991), currently, there has been only limited quantitative attempts to address the relationship between infall, star formation, and the metallicity (e.g., Rupke et al. 2010; Perez et al. 2006). The trends we find in the simulations are fascinating and explain a number of important phenomenon that have been observed in interacting and merging galaxies. Metallicity changes during the merger event is a powerful way of testing the timing and strength of the gas inflows and ultimately in understanding the fate of post-merger/interacting galaxies.

Overall, we find broad agreement with the results of our simulations for the evolution of the metallicity and what is observed. We find for example that the net decrease in the metallicity is a few tenths of a dex, which is comparable to what is observed in merging and interacting galaxies (Sol Alonso et al. 2010; Michel-Dansac et al. 2008; Rupke et al. 2008; Kewley et al. 2006). In addition, as is likely observed, our simulations show that the peak of the star formation is close in time to the minimum in the circumnuclear metallicity (Rodrigues et al. 2008; Rupke et al. 2008). The trends could be explained entirely by the strength of the gas inflows of relatively metal-poor gas from the outer regions of the disks which both fuel star formation and dilute the metal content of the gas in and around the nucleus. The strength of the inflows likely depends both on the initial gas content of the disks, how it is distributed, the characteristics of the orbits through which the galaxies merge, and the mass ratios of the galaxies. Here we concentrated on the modelling a range of orbital parameters and a 20$\%$ gas fractions. Subsequent papers will focus on varying the mass ratios, gas fraction, and gas distributions.

The simulation results suggest that the strongest star formation and dilution of the initial nuclear metallicity occurs around pericentre passage of the merger. This effect has been observed in that the star formation at small separations exhibit a tail to high H$\alpha$ equivalent widths (e.g., Woods et al. 2006; Barton et al. 2000). At this time, we also expect the minimum in the metallicity to occur. This expect relationship has been emphasised in Kewley et al. (2006) based on a study of pairs of galaxies. The sample of Kewley et al. (2006) is particularly appropriate for this type of study as it is a robust sample of pairs of interacting galaxies and show generally a modest increase in their star formation rates and modest likely dilutions. For example, their most intense starbursts, which show significant offsets in metallicity, only have offsets of about 0.2-0.3 dex compared to non-interacting galaxies with similar B-band absolute magnitudes. This is the amount we find in our simulations.

We can explain the full range of circumnuclear metallicities observed in more violent mergers in the local (Rupke et al. 2008) or distant universe (Rodrigues et al. 2008). By violent mergers, we mean in this context galaxies which are luminous in the infrared and have star formation rates several to almost 100 times that of the Milky Way. These are the most appropriate for comparison because, as we have shown, as the merger advances, the star formation rate will decrease and the metallicity increases reaching values that are higher than the initial metallicities.

To show that our models can reproduce the data, we have made a monte-carlo simulation of the metallicity distribution we might obtain if we observed a set of galaxies near their maximum star formation rate and allow for a range in their properties and the intrinsic scatter in the mass-metallicity relationship. For such a comparison sample, we would naturally draw on the most violent star-forming galaxies in the local universe which are major mergers. This is the point in our simulations, where we get the most significant influx of material into the circumnuclear regions and near the peak of star formation. At this stage, we can dilute the circumnuclear gas with relatively metal poor gas from the outer disk decreasing the overall metallicity by about a factor of 2 and relatively brief time (of-order an internal dynamical time of about 108 yrs). Thus, in our simple monte-carlo approach to the metallicity estimates, we allow for a decrease of 0.3 $\pm$ 0.1 dex. We make this allowance as we only have single metallicity gradient in all our models (-0.1 dex kpc-1). However, metallicity gradients in spiral galaxies range from about 0.0 to -0.2 dex kpc-1. To allow for this variation, we have assigned a range in the metallicity allowed of 0.1 dex. We do not know the nature of the progenitors either. They could have a range of initial circumnuclear metallicities and the mass metallicity relationship has a significant scatter 0.15 dex (Tremonti et al. 2004). Thus we allow for an additional source of scatter of 0.15 dex to reflect the scatter in the mass-metallicity relation. Finally, there is also measurement uncertainties which are about 0.1 dex (Rupke et al. 2008).

We assume that each source of scatter is Gaussian and that each can be linearly combined. This assumption is appropriate since (at the metallicities observed here) the uncertainty in the metallicity is not correlated to the metallicity, our numerical simulations are completely independent of the data, and the scatter in the mass-metallicity relationship is intrinsic. One such monte-carlo simulation is shown in Fig. 8 but all reproduce the data from Rupke et al. (2008) reasonably well. Unfortunately, Rupke et al. (2008) did not actually estimate masses directly for their sample but used a random set of masses generated from a typical mass and scatter from the literature were then assigned. While we could have used their masses directly which would have made the agreement look more spectacular, the reality is that we have simply reproduced the scatter in the metallicity by making a set of simple assumptions. Thus this agreement between the data and model should not be taken literally but demonstrates that numerical simulations of the type run here can reproduce the spread in metallicity without making any assumptions beyond suggesting that the highest levels of star formation in a merger occurs near the peak in the strength of the gas flows something that every model over the last decades has shown and can be argued on robust physical grounds.

\begin{figure} \par\includegraphics[width=8cm,clip]{14304fg27.ps} \end{figure} Figure 8:

Monte-carlo simulation of the metallicity distribution predicted by the models compared to the data from Rupke et al. (2008). The up-side down triangles are the simulated results (see text for details), the blue stars and red circle are galaxy values taken directly from Rupke et al. (2008) as described there. Unfortunately, Rupke et al. (2008) did not actually measure the mass of any of the individual galaxies but used a single mass allowing for some scatter (see that paper for details). We have approximately reproduced their mass distribution for this comparison.

Open with DEXTER

In addition to investigating the general evolution of the metallicity, we also adopted a crude model for the evolution of Oxygen and Iron during mergers and interactions. We were motivated to make these simplistic estimates by the fact that following the evolution of $\alpha$ elements like Oxygen can be used to ``date'' mergers. In analogy with studies of the stellar populations of early type galaxies, bulges, or in components of the Milky Way such as the thick disk and bulge, [O/Fe] or [$\alpha$/Fe] ratios can be used as a chronometer telling us over what timescale the bulk of the (luminosity-weighted) stellar population formed (e.g., Zoccali et al. 2006; Thomas et al. 2005). Our hope was that even a crude model such as the one we have adopted could provide useful information about how observationally we might go about dating mergers and interactions.

How this might work is that if the galaxy is in the early phases of merging, we would expect to see both overall low-metallicity and depending on the distribution of [$\alpha$/Fe] in initial disks, evidence of what radii the gas came from through its abundance ratios. The bulge of our galaxies, at least in the stars, is enriched in $\alpha$ elements relative to the sun (Lecureur et al. 2007; Zoccali et al. 2008; Ryde et al. 2010). Moreover, the disk of our Milky Way appears to have an enhancement out to relatively large radii but this ratio depends on the radius (see Acharova et al. 2010, and references therein). Of course these measurements are for the stellar metal abundances, not for the gas phase so the comparison is not completely fair. It does however at least suggests a possible trend that may be useful in determining the radii at which freshly deposited gas came from. At any rate, we may therefore expect in the early stages, a mild $\alpha$ enhancement in the gas. As the merger proceeds, this enhancement will become more pronounced, until the late stages where it will begin to lessen as the type Ia SNe become more important. An interesting question is how much of this enhanced material makes its way into each generation of star formation. While in principle this can happen quickly as the star formation lasts for several 100 Myr (several crossing times) sufficient for the metals to mix with the ambient gas, it is not clear if this actually happens. If it does, then we would predict that a majority of the stars formed would be $\alpha$ enhanced but may have metallicities lower than stars formed from gas before the burst occurred. Only after about 1-2 Gyr or so would both the metallicity increase above what an isolated galaxy would have and would the $\alpha$ enhancement begin to lessen. Of course this exact time scale is uncertain for both the metallicity and $\alpha$ enhance because we do not have a firm understanding of the delay time for type Ia SNe.

Taken at face value, the results of our simulations would suggest that we can make realistic bulges and early-type galaxies. It is well known that the bulge of the Milky Way is both metal-rich (typically about [Fe/H] $\sim$ -0.3 to 0.3 with a mean of about 0) (Zoccali et al. 2008) and is $\alpha$ enhanced (Lecureur et al. 2007; Zoccali et al. 2008; Ryde et al. 2010). Both of these results are consistent with our simulations modulo the uncertainty in the delay times of type Ia SNe, and the mass and characteristics of pre-existing bulges in the merging galaxies (see Pipino et al. 2009). This general result appears to hold generally for bulges, namely they are metal-rich and $\alpha$ enhanced (Thomas et al. 2005) and normalizing for their mass differences, very similar to early type galaxies (Thomas et al. 2005). Interestingly, there is some evidence for a radial gradient in the average metallicity of the stars in the galactic bulge (Zoccali et al. 2008). Depending on the initial conditions, this may be consistent with our simulations. In the simulations it is likely there is a gradient in the star formation with radius as the strongest gas flows and most intense star formation is in the deepest part of the potential well. However, a complete discussion of the metallicity, $\alpha$ enhancement, and radial gradients in bulges and early-type galaxies is beyond the scope of this paper, our simulation results are at least consistent with these general properties of spheroids. We will address these questions in more detail in a subsequent manuscript.

Finally, these results have important implications for our understanding of metallicity evolution of galaxies as observed at high-redshift. Since we have found that during the most intense phases of star formation, the gas phase metallicity can be reduced (diluted) by infalling material from the outer regions of the merging galaxies. Mergers and interactions are known to play an important role in initiating intense starbursts in the distant universe (Law et al. 2007,2009; Epinat et al. 2009; Nesvadba et al. 2008). In order to estimate gas phase metallicities of distant galaxies, they must have high surface brightnesses in their emission line gas (see Lehnert et al. 2009, and references therein ). It is now reasonably well established that the mass-metallicity relation appears to have evolved over the last 10 Gyr (Erb et al. 2006; Rodrigues et al. 2008; Mannucci et al. 2009; Queyrel et al. 2009; Savaglio et al. 2005; Halliday et al. 2008). However, combining the possible limitations in the observations due to surface brightness dimming and the importance of mergers in initiating intense (high surface brightness) starbursts, it may be the determinations of the evolution in metallicity may be strongly influenced by dilution. If this is so, we would predict that, if the importance of mergers increases with redshift (e.g., de Ravel et al. 2009), we should see both a decrease in the average metallicity and an increase in the scatter in the mass-metallicity relation with increasing redshift. While we have no modelled a full range of initial conditions, our results here suggest that this increasing scatter would be about several tenths of a dex which is less than a factor of 2 more than the scatter in the relation for local galaxies (Gallazzi et al. 2005).

5 Conclusions

In this work, we have studied the dilution and subsequent enrichment of the interstellar medium during interactions and mergers of disk galaxies of comparable mass. Our models, which include star formation and chemical enrichment, have made it possible to follow, for the first time, the evolution of the circumnuclear gas phase metallicity from the initial interaction until the coalescence phase, thus significantly improving the existing simulations and leading to insight between star formation, gas inflows and dilution, and metallicity evolution in mergers and interactions.

Our main results can be summarised as follows:

  • The dilution of the gas initially in circumnuclear regions of the merger pairs starts just after the first pericentre passage, as the disk is destabilised and gas flows inwards. For mergers, usually a second dilution peak is observed in the final phase of coalescence. A significative dilution can take place also in fly-bys, just after their close passage, mimicking to some extent what we observe in our merger simulations. Thus even flybys may be important for the star formation and evolution of galaxies.

  • On average, the amplitude of the metallicity dilution we find (0.2-0.3 dex) is in agreement with observations (Rupke et al. 2008; Kewley et al. 2006).

  • The strongest correlation we found is between the maximum in the SFR and the strength of the circumnuclear dilution - pairs experiencing the strongest bursts also show the strongest circumnuclear dilution. This can be explained in terms of interaction-driven gas inflows from the outer disk regions into the galaxy centre.

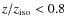  • The dilution phase (defined as $z/z_{\rm iso} <0.8$) is very rapid, half of the sample sustains this high dilution phase for less than 5 $\times $ 108 years.

  • The gas inflow causes concomitant enhanced star formation; such enhanced star formation releases a significant amount of enriched material in the ISM. This enrichment results in merger remnants which have higher final circumnuclear metallicities than the corresponding galaxies evolved in isolation. The same can happen for fly-bys which experience enhanced star formation rates.

  • Type Ia and II SNe formed during the interaction release O and Fe in the ISM, thus changing the average mass ratio of these two elements. In particular, we note that, if the merger takes place on short time scales (lower than the typical delay time of SNe Ia, which unfortunately is not well constrained), the stellar population formed during the last SF burst forms from an 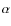$\alpha$-enriched ISM, while, for mergers with longer time scales, SNeIa can have the time to release a sufficient amount of iron in the gas. The resulting stellar population has thus lower values of $\rm [\alpha/Fe]$ ratios.

  • The circumnuclear metallicity, as well as the [ 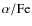$\rm\alpha/Fe$] ratios, can be used as an indicator of the timing of merger/interaction state, thus helping in disentangle projection effects, i.e., galaxies which appears close in projection, but that are not strongly interacting. The remnants of these mergers appear qualitatively consistent with what is known about the bulge of our galaxy, other nearby galaxies, and early type galaxies generally. Thus, in agreement with many authors, it appears when considering chemical evolution that mergers can reproduce early type systems.

  • If mergers play a significant role in the galaxies that have had their metallicities determined at high-redshift, then it is possible that dilution is signficantly affecting these estimates.

Acknowledgements
P.D.M. is supported by a grant from the French Agence Nationale de la Recherche (ANR). These simulations are available as part of the GalMer simulation data base (http://galmer.obspm.fr). The authors wish to thank the referee for their constructive and helpful comments and A. Pipino for a critical reading of an early version of this manuscript and helpful suggestions.

Appendix A: Metallicity evolution in the isolated galaxy

\begin{figure} \par\includegraphics[width=6cm,angle=270]{14304fg28.ps} \end{figure} Figure A.1:

Metallicity profiles of the gas in the gSb galaxy simulation which were evolved in isolation (i.e., did not experience a merger or interaction during the simulation). The profiles are given at different times, as indicated in the labels.

Open with DEXTER

Since the goal of this paper is to investigate the role interactions and mergers play in the gas phase metallicity evolution, it is essential to study the evolution of the gas properties of simulated galaxies that did not experience a merger or interaction (i.e., an isolated galaxy). This is essential to distinguish between secular processes that drive the evolution of galaxies from the effects that occur during the interaction and merger process. For the isolated galaxy simulation, initial metallicity profile (given in Eq. (2)) evolves rapidly in the first 500 Myr of evolution, due to the compression of gas into density waves and inflow into the central regions (Fig. A.2). At this time, spiral arms and a bar are formed, as clearly shown in the maps of the stellar distribution (Fig. A.3). The galaxy models studied in this paper were not evolved in isolation before starting the interaction. However, as shown in Figs. A.1 and A.2, tidally driven gas inflows from the outer disk take place after the pericentre passage (with our initial choice of the orbital parameters, this corresponds to around 400 Myr from the beginning of the simulation) and in the merging phase (between 1 and 3 Gyr with the exact timing depending on the orbital characteristics). By this time - 400 Myr - the metallicity profile has already reached an equilibrium configuration (see Fig. A.1), and the galaxy has relaxed.

\begin{figure} \par\mbox{\includegraphics[width=2cm,angle=0]{14304fg29.ps}\inclu... ...ps}\includegraphics[width=2cm,angle=0]{14304fg35.ps}\hspace*{1cm}}\end{figure} Figure A.2:

From top-left to bottom-right: maps of the gas distribution of the model gSb galaxy evolved in isolation. Maps are shown from t=0 to t=3 Gyr in steps of 500 Myr. Each map is 40 kpc $\times $ 40 kpc in size.

Open with DEXTER

\begin{figure} \par\mbox{\includegraphics[width=2cm,angle=0]{14304fg36.ps}\inclu... ...ps}\includegraphics[width=2cm,angle=0]{14304fg42.ps}\hspace*{1cm}}\end{figure} Figure A.3:

From top-left to bottom-right: maps of the stellar distribution of the gSb galaxy model evolved in isolation. Maps are shown for every 500 Myr over t=0 to t=3 Gyr. Each map is 40 kpc $\times $ 40 kpc in size.

Open with DEXTER

References

  1. Acharova, I. A., Lépine, J. R. D., Mishurov, Y. N., et al. 2010, MNRAS, 402, 1149 [NASA ADS] [CrossRef] [Google Scholar]
  2. Sol Alonso, M., Michel-Dansac, L., & Lambas, D. G. 2010, A&A, 514, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Barnes, J. E. 1992, ApJ, 393, 484 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barnes, J. E. 2002, MNRAS, 333, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barnes, J. E. 2004, MNRAS, 350, 798 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barnes, J. E., & Hernquist, L. E. 1991, ApJ, 370, L65 [NASA ADS] [CrossRef] [Google Scholar]
  7. Barnes, J. E., & Hernquist, L. 1996, ApJ, 471, 115 [NASA ADS] [CrossRef] [Google Scholar]
  8. Barton, E. J., Arnold, J. A., Zentner, A. R., Bullock, J. S., & Wechsler, R. H. 2007, ApJ, 671, 1538 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barton, E. J., Geller, M. J., & Kenyon, S. J. 2000, ApJ, 530, 660 [NASA ADS] [CrossRef] [Google Scholar]
  10. Barton Gillespie, E., Geller, M. J., & Kenyon, S. J. 2003, ApJ, 582, 668 [NASA ADS] [CrossRef] [Google Scholar]
  11. Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton Univ. Press) [Google Scholar]
  12. Braine, J., & Combes, F. 1993, A&A, 269, 7 [NASA ADS] [Google Scholar]
  13. Casoli, F., Dupraz, C., Combes, F., & Kazes, I. 1991, A&A, 251, 1 [NASA ADS] [Google Scholar]
  14. Chien, L.-H., Barnes, J. E., Kewley, L. J., & Chambers, K. C. 2007, ApJ, 660, L105 [Google Scholar]
  15. Chilingarian, I., Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2010, A&A, in press [Google Scholar]
  16. Combes, F. 2008, in Proceedings of Formation and Evolution of Galaxy Bulges, July 2007, ed. M. Bureau, E. Athanassoula, & B. Barbuy, IAU Symp., 245, 151 [Google Scholar]
  17. Cooper, M. C., Tremonti, C. A., Newman, J. A., & Zabludoff, A. I. 2008, MNRAS, 390, 245 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cox, T. J., Jonsson, P., Primack, J. R., & Somerville, R. S. 2006, MNRAS, 373, 1013 [NASA ADS] [CrossRef] [Google Scholar]
  19. Cox, T. J., Jonsson, P., Somerville, R. S., Primack, J. R., & Dekel, A. 2008, MNRAS, 384, 386 [NASA ADS] [CrossRef] [Google Scholar]
  20. de Ravel, L., Le Fèvre, O., Tresse, L., et al. 2009, A&A, 498, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Dinerstein, H. L. 1996, in Cosmic Abundances, ed. S. S. Holt, & G. Sonneborn (San Francisco: ASP), ASP Conf. Ser., 99, 337 [Google Scholar]
  22. Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2007, A&A, 468, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Di Matteo, P., Bournaud, F., Martig, M., et al. 2008, A&A, 492, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Di Matteo, P., Pipino, A., Lehnert, M. D., Combes, F., & Semelin, B. 2009, A&A, 499, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Donzelli, C. J., & Pastoriza, M. G. 2000, AJ, 120, 189 [NASA ADS] [CrossRef] [Google Scholar]
  26. Ellison, S. L., Simard, L., Cowan, N. B., et al. 2009, MNRAS, 396, 1257 [NASA ADS] [CrossRef] [Google Scholar]
  27. Epinat, B., Contini, T., Le Fèvre, O., et al. 2009, A&A, 504, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [NASA ADS] [CrossRef] [Google Scholar]
  30. Halliday, C., Daddi, E., Cimatti, A., et al. 2008, A&A, 479, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Iono, D., Yun, M. S., & Mihos, J. C. 2004, ApJ, 616, 199 [NASA ADS] [CrossRef] [Google Scholar]
  32. Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  33. Kannappan, S. J., Jansen, R. A., & Barton, E. J. 2004, AJ, 127, 1371 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kapferer, W., Knapp, A., Schindler, S., Kimeswenger, S., & van Kampen, E. 2005, A&A, 438, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Kennicutt, R. C. Jr., Bresolin, F., & Garnett, D. R. 2003, ApJ, 591, 801 [CrossRef] [Google Scholar]
  36. Kewley, L. J., Geller, M. J., & Barton, E. J. 2006, AJ, 131, 2004 [NASA ADS] [CrossRef] [Google Scholar]
  37. Law, D. R., Steidel, C. C., Erb, D. K., et al. 2007, ApJ, 669, 929 [NASA ADS] [CrossRef] [Google Scholar]
  38. Law, D. R., Steidel, C. C., Erb, D. K., et al. 2009, ApJ, 697, 2057 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Lehnert, M. D., Nesvadba, N. P. H., Tiran, L. L., et al. 2009, ApJ, 699, 1660 [NASA ADS] [CrossRef] [Google Scholar]
  41. Lemasle, B., François, P., Piersimoni, A., et al. 2008, A&A, 490, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Magrini, L., Vílchez, J. M., Mampaso, A., Corradi, R. L. M., & Leisy, P. 2007, 470, 865 [Google Scholar]
  43. Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, 398, 1915 [NASA ADS] [CrossRef] [Google Scholar]
  44. Márquez, I., Masegosa, J., Moles, M., et al. 2002, A&A, 393, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Martínez-Serrano, F. J., Serna, A., Domínguez-Tenreiro, R., et al. 2008, MNRAS, 388, 39 [Google Scholar]
  46. Michel-Dansac, L., Lambas, D. G., Alonso, M. S., & Tissera, P. 2008, MNRAS, 386, L82 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mihos, J. C., & Hernquist, L. 1994a, ApJ, 431, L9 [NASA ADS] [CrossRef] [Google Scholar]
  48. Mihos, J. C., & Hernquist, L. 1994b, ApJ, 437, 611 [NASA ADS] [CrossRef] [Google Scholar]
  49. Mihos, J. C., & Hernquist, L. 1996, ApJ, 464, 641 [NASA ADS] [CrossRef] [Google Scholar]
  50. Miller, G. E., & Scalo, J. M. 1979, ApJS, 41, 513 [NASA ADS] [CrossRef] [Google Scholar]
  51. Nesvadba, N. P. H., Lehnert, M. D., Davies, R. I., Verma, A., & Eisenhauer, F. 2008, A&A, 479, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Peeples, M. S., Pogge, R. W., & Stanek, K. Z. 2008, ApJ, 685, 904 [NASA ADS] [CrossRef] [Google Scholar]
  53. Peeples, M. S., Pogge, R. W., & Stanek, K. Z. 2009, ApJ, 695, 259 [NASA ADS] [CrossRef] [Google Scholar]
  54. Perez, M. J., Tissera, P. B., Scannapieco, C., Lambas, D. G., & de Rossi, M. E. 2006, A&A, 459, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Pipino, A., Devriendt, J. E. G., Thomas, D., et al. 2009, A&A, 505, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Queyrel, J., Contini, T., Pérez-Montero, E., et al. 2009, A&A, 506, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Ryde, N., Gustafsson, B., Edvardsson, B., et al. 2010, A&A, 509, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Rodrigues, M., Hammer, F., Flores, H., et al. 2008, A&A, 492, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Rupke, D. S. N., Veilleux, S., & Baker, A. J. 2008, ApJ, 674, 172 [NASA ADS] [CrossRef] [Google Scholar]
  60. Rupke, D. S. N., Kewley, L. J., & Barnes, J. E. 2010, ApJ, 710, L156 [NASA ADS] [CrossRef] [Google Scholar]
  61. Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] [Google Scholar]
  62. Semelin, B., & Combes, F. 2002, A&A, 388, 826 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Shields, G. A. 1990, ARA&A, 28, 525 [NASA ADS] [CrossRef] [Google Scholar]
  64. Springel, V. 2000, MNRAS, 312, 859 [NASA ADS] [CrossRef] [Google Scholar]
  65. Strolger, L. G., Dahlen, T., & Riess, A. G. 2010, ApJ, 713, 32 [NASA ADS] [CrossRef] [Google Scholar]
  66. Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
  67. Toomre, A. 1977, ARA&A, 15, 437 [CrossRef] [Google Scholar]
  68. Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
  69. Woods, D. F., Geller, M. J., & Barton, E. J. 2006, AJ, 132, 197 [NASA ADS] [CrossRef] [Google Scholar]
  70. Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Footnotes

... code[*]
We thank the referee for pointing out the importance of diffusion in this problem.
... = 7 kpc[*]
This is the average distance from the galaxy centre of the gas that strongly participates in the interaction-driven inflow.
... instantaneous[*]
Any possible time delay would result into a time-shift between the SFR peak and the oxygen and SNeII-Fe peak.

All Figures

  \begin{figure} \par\includegraphics[width=7cm,angle=270]{14304fg1.ps}\includegra... ...270]{14304fg3.ps}\includegraphics[width=7cm,angle=270]{14304fg4.ps} \end{figure} Figure 1:

The dynamics of the gas during the interaction and subsequent merger of two gSb galaxies for several orbits (shown with different colours). (First panel): relative distance of the two galaxy centres versus time for some simulated orbits. (Second panel): gas mass inside 2 kpc from one of the two galaxy centres versus time. (Third panel): evolution of the star formation rate (SFR) relative to the rate for the corresponding initial galaxies evolved in isolation. (Fourth panel): evolution of the central gas metallicity. The metallicity has been normalised to that of the initial galaxies used in the merger simulations evolved isolated. In the second, third, and fourth panel, squares and asterisks respresent respectively the time of the first pericentre passage and the time of final coalescence for the different orbits.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,angle=270]{14304fg5.ps}\includegra... ...ps}\includegraphics[width=7cm,angle=270]{14304fg8.ps} \vspace*{3mm} \end{figure} Figure 2:

Same as Fig. 1, but for the simulations of ``flybys''. Note that simulations resulting in starbursts with higher intensities also have gas phase metallicities with higher dilution. Even in flybys, the star formation rate and dilution of the metallicity are related.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{14304fg9.ps} \end{figure} Figure 3:

The duration that the circumnuclear metallicity is below 0.8 (shown in red) and between 0.8 and 1.0 (shown in black) relative to an isolated simulated spiral with the same properties as the individual merging galaxies. We chose 0.8 as the threshold because this is the span of the most extreme metallicity offset observed in nearby mergers (e.g. Rupke et al. 2008; Kewley et al. 2006).

Open with DEXTER
In the text

  \begin{figure} \par {\hspace*{2.5cm}\includegraphics[width=8cm,angle=270]{14304f... ...\includegraphics[width=4.cm,angle=0]{14304fg18.ps} }\vspace*{1mm} \end{figure} Figure 4:

The star formation rate, $M_{\odot }$  ${\rm yr^{-1}}$, versus the relative metallicity of the interaction and merger. As in Fig. 1, the metallicity is shown relative to an isolated disk with the same initial conditions as the galaxies used in the merger simulations. The blue asterisks indicate times when the star formation is near its peak, while green triangles represent galaxies before their peak star formation and red dots represent galaxies that are past their peak of star formation and are in the final stages of the merger. In the bottom panels, we show the morphologies of the merger pairs in each region of the diagram to indicate the range of morphologies seen in the simulations.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6cm,angle=270]{14304fg19.ps}\includegraphics[width=6cm,angle=270]{14304fg20.ps} \end{figure} Figure 5:

(Left panel:) the physical 3-dimensional separation of the galaxy pairs and mergers versus their relative circumnuclear metallicity. The black line represents the average relation, for physical distances greater than 4 kpc and binned every 10 kpc. The blue line represents the average relation when in addition including mergers with physical separations below 4 kpc in the smallest bin (0-10 kpc). (Right panel:) evolution of two mergers (blue and green curves) and a fly-by (red curve) in the metallicity-distance plane. The simulations suggest that even at wide separations there are gas inflows which dilute the metallicities of the nuclear regions and that this dilution persists until the pairs are strongly interacting, overlapping, and near or after coalescence. During the final merging process, a wide range of metallicities can be observed but on average will show a much higher metallicity than if they had not interacted or merged.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,angle=270]{14304fg21.ps}\includegr... ...\includegraphics[width=7cm,angle=270]{14304fg24.ps} \vspace*{1.5mm} \end{figure} Figure 6:

Rate of oxygen and iron released in the ISM by SNe II and SNeIa explosions (in units of $M_{\odot }$ yr-1) as a function of time two different simulations whose star formation histories are shown in Fig. 1. The first and final two panels show the ejection rate of oxygen and iron for the star formation history in Fig. 1 represented by the orange and red curves respectively. For the iron release, we separate the contribution from SNeIa (red curve) and SNe II (grey curve) for each of the two simulations. The black arrows in each panel represent the time of the first pericentre passage and final coalescence. Since the enrichment is instantaneous (i.e., no delay for the evolutionary times of the type II supernovae, the evolution of the star formation and ejecta rate are synchronous.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=4.3cm,clip]{14304fg25.ps}\includegraphics[angle=270,width=4.3cm,clip]{14304fg26.ps} \end{figure} Figure 7:

The evolution of the oxygen over iron mass ratio for two of our galaxy mergers, whose rate of mass release in the ISM is shown in Fig. 6. For each panel, three different curves are shown corresponding to three different delay times for onset of SNeIa, $\tau $: $\tau $ = 1-4 Gyr (black curve), $\tau $ = 1-3 Gyr (dark grey) and $\tau $ = 1-2 Gyr (light grey), as indicated in the legends. The black arrows in each panel represent the time of first pericentre passage and coalescence.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{14304fg27.ps} \end{figure} Figure 8:

Monte-carlo simulation of the metallicity distribution predicted by the models compared to the data from Rupke et al. (2008). The up-side down triangles are the simulated results (see text for details), the blue stars and red circle are galaxy values taken directly from Rupke et al. (2008) as described there. Unfortunately, Rupke et al. (2008) did not actually measure the mass of any of the individual galaxies but used a single mass allowing for some scatter (see that paper for details). We have approximately reproduced their mass distribution for this comparison.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6cm,angle=270]{14304fg28.ps} \end{figure} Figure A.1:

Metallicity profiles of the gas in the gSb galaxy simulation which were evolved in isolation (i.e., did not experience a merger or interaction during the simulation). The profiles are given at different times, as indicated in the labels.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=2cm,angle=0]{14304fg29.ps}\inclu... ...ps}\includegraphics[width=2cm,angle=0]{14304fg35.ps}\hspace*{1cm}}\end{figure} Figure A.2:

From top-left to bottom-right: maps of the gas distribution of the model gSb galaxy evolved in isolation. Maps are shown from t=0 to t=3 Gyr in steps of 500 Myr. Each map is 40 kpc $\times $ 40 kpc in size.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=2cm,angle=0]{14304fg36.ps}\inclu... ...ps}\includegraphics[width=2cm,angle=0]{14304fg42.ps}\hspace*{1cm}}\end{figure} Figure A.3:

From top-left to bottom-right: maps of the stellar distribution of the gSb galaxy model evolved in isolation. Maps are shown for every 500 Myr over t=0 to t=3 Gyr. Each map is 40 kpc $\times $ 40 kpc in size.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.