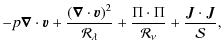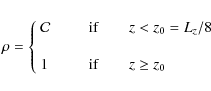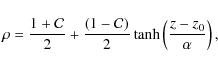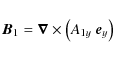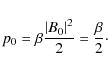EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 518 (July-August 2010) A&A, 518 (2010) A57 Full HTML
Free Access
Issue
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
Article Number A57
Number of page(s) 9
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913652
Published online 02 September 2010
A&A 518, A57 (2010)

Spontaneous non-steady magnetic reconnection within the solar environment

L. Bettarini1 - G. Lapenta1,2,3

1 - Centrum voor Plasma-Astrofysica, Departement Wiskunde, Katholieke Universiteit Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
2 - Leuven Mathematical Modeling & Computational Science Centre, Katholieke Universiteit Leuven, Belgium
3 - Leuven Centre for Aero & Space Science, Technology and Applications, Katholieke Universiteit Leuven, Belgium

Received 12 November 2009 / Accepted 4 May 2010

Abstract
Context. A fundamental step to produce realistic models of the solar phenomena requiring fast (and high power) triggering events is to understand the feasibility of a spontaneous transition from a slow to a fast reconnection regime in the solar environment and its macroscopic evolution within the theoretical framework of pure resistive magnetohydrodynamics.
Aims. We show the dynamical evolution of a reconnecting force-free magnetic field in a ``simplified'' solar atmosphere (high chromosphere-low corona) described by a pressure-balanced configuration with a variable density modeling the transition region. Magnetic reconnection plays a fundamental role in this region and we show the efficient working of a non-steady and self-feeding reconnection process whose development as determined by characteristic solar parameters (global resistivity, global viscosity, plasma beta) is followed.
Methods. This work presents a 2.5-dimensional simulation study of the instability of force-free current-sheets located in a medium with a strong density variation along the current layer. In order to reach the needed high resolution and to reduce the influence of spurious numerical effects, we use a code with a fully-implicit-particle (or Flip) algorithm to solve an Eulerian-Lagrangian formulation of resistive and viscous magnetohydrodynamics equations.
Results. The initial force-free configuration is observed to undergo a two-stage evolution consisting of an abrupt regime transition from a slow to a fast reconnection process, which leads the system to a final chaotic configuration. Yet the onset of the fast phase is not determined by any anomalous enhancement in the plasma's local resistivity. An asymmetric development of the whole structure is observed and the related magnetic field topology and energetic features are described.
Conclusions. This mechanism can be used as a simple but effective model of several (explosive) processes taking place from the high chromosphere up to the low corona. Our simplified model of the solar atmosphere allows us to obtain a realistic oriented path for the evolution of the overall flow and reconnecting current-sheet. In the present work, the numerical experiment provides key information and observables (like the energetic fluxes) to be compared with observations.

Key words: magnetohydrodynamics (MHD) - methods: numerical - Sun: atmosphere - Sun: coronal mass ejections (CMEs) - Sun: flares - magnetic fields

1 Introduction

Magnetic reconnection is a fundamental mechanism that plays a major role both in the dynamics of astrophysical objects and in the evolution of several structures in the solar environment, in planetary magnetospheres and in the heliosphere. Here, indeed, a broad range of phenomena undergoes a multi-stage evolution determined by a rapid transition from a slow to a fast and often bursty dynamics, which presents typical magnetic reconnection marks such as the change in the magnetic field-line connectivity, the formation of high-velocity plasma jets, plasma heating, and particle accelerations (Biskamp 1993).

Magnetic reconnection is believed to be the key process underlying the evolution of a number of processes that take place in the solar environment. It may in particular be the responsible for the release of magnetic flux and plasma in the corona and in the interstellar medium during solar explosive phenomena. In general, a catastrophic loss of mechanical equilibrium of the underlying coronal magnetic structure is required, and magnetic reconnection plays a role either in triggering the initiating eruption or in the aftermath of the event by characterizing the subsequent evolution and related structures like post CME's current-sheets (Lin et al. 2004; Forbes & Lin 2000). In the case of a flare evolution, the free energy of the solar magnetic field (which exceeds the energy of the solar atmosphere potential field) is released. This excess energy is connected with currents that flow in the corona from the photosphere, throughout the chromosphere and the transition region and the flare process is the process of the rapid variation of these currents.

From Yohkoh X-ray telescope observations (Shibata 1996) we have evidence consistent with the reconnection model of solar flares (Tsuneta 1996). In particular, the onboard soft X-ray telescope revealed many jet-like features in which the out-flowing plasma is associated with a change in the magnetic field topology of the underlying X-ray emitting structure and with the rise of an X-type neutral point location as the reconnection process goes on. Recently Hinode observations have yielded a more detailed picture of the X-jet formation and dynamics (Cirtain et al. 2007) which suggest that the heating of the solar chromosphere and corona may be related to small-scale ubiquitous reconnection (Shibata et al. 2007). Karpen et al. (1998) provided a detailed scenario for the formation of current-sheets and their dissipation through reconnection during a chromospheric erupting event. They pointed out that magnetic reconnection occurs in a bursty and intermittent mode whose unknown physical mechanism is in contrast with the well-known Sweet-Parker (SP) and Petschek (PE) models of reconnection, and it is essential to explain the time evolution of flaring events. Their 2.5-dimensional numerical simulations of magnetic reconnection in the lower solar atmosphere also showed the formation of two-sided outflows, whose dynamics and acceleration should be affected by the vertical density variation from the chromosphere to corona's upper layers. These bi-directional jets have been observed in the form of simultaneous blue and red Doppler shifts, and they are characteristic structures present in most of the UV explosive solar events (Aschwanden 2006, and references therein).

Large-scale chromosphere/corona models are carried out within magnetohydrodynamics (MHD). Yet it is widely accepted that to obtain a fast reconnection regime in MHD, it is necessary to have a localized enhancement of the plasma resistivity (Kliem et al. 2000; Scholer 1989; Hautz & Scholer 1987). Indeed, it is believed that the description of a plasma as a resistive fluid is not sufficient to obtain the fast reconnection rate expected by the models, as for instance of the above mentioned structures. On the other hand, the microscopic mechanisms leading to the formation of the invoked anomalous resistivity depend on several factors and have not been conclusively identified. New insights into this topic have been recently given by Baty et al. (2006), who claim to have maintained a PE-like reconnection process in two-dimensional time-dependent MHD simulations without the use of a significantly high localized resistivity. However, the onset of this process still depends on a non-uniform if small resistivity. Furthermore, Nitta (2007) shows that it is possible to have a self-similar reconnection process in MHD with a continuous transition from a slow reconnection regime to a fast one by increasing the magnetic Reynolds number. He considers a new series of solutions of two-dimensional MHD equations on a wide range of the magnetic Reynolds number, that is from about 10 to 2100. The reconnecting structures change according to the regime the system undergoes, passing from an X-point configuration, to an X-O-X point, that is two X-points with a magnetic islands placed in between. Finally, for the slowest regime at the highest Reynolds number the magnetic islands collapse and form a long current-sheet with a Y profile.

On the other hand, Lapenta (2008) observes the spontaneous development of a fast reconnection mechanism on macroscopic scales. A two-dimensional current-sheet evolves through two different stages, that is a first slow very elongated SP layer is followed by a rapid transition to a fast chaotic reconnection process, and the system does not need anomalous resistivity nor driven flows to undergo this evolution. This MHD bursty process, which leads to a chaotic final state, is due to the destabilization of the SP layer via the tearing instability as predicted in previous theoretical studies (Loureiro et al. 2007; Furth et al. 1963; Bulanov et al. 1979). The resulting chaotic reconnection phase is fast and has the fundamental property of being independent both from the Lundquist number as well as from the dynamic Reynolds number. In order to observe this dynamics, the horizontal size of our numerical box must be large with respect to the thickness of the forming SP layer, and a high Lundquist number has also to be considered. This allows the SP layer to expand till the instability driving the system to a chaotic reconnection regime sets in. During this phase, an outflow pattern determining a circulation loop feeding-back reconnection regions is observed. The net results obtained by the development of this process are that (a) it is much faster, developing on scales on the order of the Alfvén time, and (b) the areas of reconnection become distributed chaotically over a macroscopic region. Furthermore, recent three-dimensional MHD numerical analyses (Kowal et al. 2009) test and confirm the investigation on the effects of turbulence on MHD magnetic reconnection (Kowal et al. 2009; Lazarian & Vishniac 1999): in the presence of weakly stochastic magnetic fields, the speed of the process is independent both of Ohmic and anomalous resistivity.

The above described picture does not include the effects of a density gradient either parallel or orthogonal to the two-dimensional current-sheet. In compressible conditions, the presence of a density variation may influence the onset and the evolution of reconnecting field lines and the resulting jet formation and acceleration. By introducing a stratification caused by a gravitational field, the reconnection process evolves toward a traditional two-dimensional pattern passing through an initial stage, whose features and duration depend on the imposed stratification (Galsgaard & Roussev 2002). In general, a lower reconnection rate is found and it decreases according to a faster magnetic field expansion, which produces a more complex reconnection dynamics.

We primarily aim to study the spontaneous fast chaotic reconnection process in the presence of a strong density gradient modeling the solar atmosphere from the high chromosphere to the low corona. There, the rapid density variation, which is balanced by the temperature gradient, is well approximated with a constant plasma pressure (Syrovatskii 1981). Hence, the gravitational field can be neglected and a force-free configuration of the magnetic field is usually assumed. This reconnection process via a chaotic evolution is a promising candidate to explain the cross-scale process that links the small-scale reconnection dynamics to the triggering and ejection of large-scale explosive phenomena, such as solar flares and coronal mass ejections (CME hereafter) (Tajima & Shibata 2002). We move from the two-dimensional MHD model of a current-sheet in the high chromosphere/low corona provided by Yokoyama & Shibata (2001), and we determine the conditions and the features of a spontaneous transition from a slow reconnection regime to a fast dynamics leading to a chaotic macroscopic state of the reconnection site.

In sections below we introduce the numerical setup, the initial conditions, the perturbations, and the parameters for our analysis (Sect. 2). In Sects. 3 and 4 we present the results of the simulations for the several cases. We observe the development of a two-stage process with the onset of a fast reconnection. The dynamics proceeds with the fracture of the initial reconnection site in several structures, determining a final turbulent state. Moreover, the density jump from the chromosphere to the corona is critical in giving an asymmetric development of the global structure, determining an oriented path for the overall flow and current-density evolution. We also observe an overall final accelerating jet outward to the upper layers of the corona. In Sect. 5 we summarize the results, draw our conclusions and point to fundamental open questions and future directions.

2 Numerical settings

We define a vertical or stream-wise direction (z), oriented away from the sun, wherein open boundary conditions are set at z = 0 and Lz, and a horizontal or cross-stream direction (x) with reflecting boundary conditions. Hence, we numerically solve the viscous-resistive compressible 2.5-dimensional MHD equations. In dimensionless form we have this set of equations

                                  $\displaystyle \frac{\partial \rho}{\partial t}$ = $\displaystyle -\boldsymbol{\nabla}\cdot \rho {\vec{v}}$ (1)
$\displaystyle \rho \frac{\partial {\vec{v}}}{\partial t}$ = $\displaystyle - \rho \left({\vec{v}} \cdot \boldsymbol{\nabla}\right) {\vec{v}}... ...bol{\nabla}\right) {\vec{B}}\right] + \frac{1}{\mathcal R_\nu} \Delta {\vec{v}}$ (2)
$\displaystyle \frac{\partial B}{\partial t}$ = $\displaystyle \boldsymbol{\nabla}\times \left({\vec{v}} \times {\vec{B}}\right) + \frac{1}{\mathcal S} \Delta {\vec{B}}$ (3)
$\displaystyle \rho \frac{\partial \mathcal I}{\partial t}$ = $\displaystyle -p \boldsymbol{\nabla}\cdot {\vec{v}} + \frac{\left(\boldsymbol{\... ...{\Pi \cdot \Pi}{\mathcal R_\nu} + \frac{{\vec{J}} \cdot {\vec{J}}}{\mathcal S},$ (4)

where $\rho$ is the mass density, ${\vec{B}}$ is the magnetic field, ${\vec{v}}$ is the fluid velocity, $\mathcal I$ is the specific internal energy, ${\vec{J}}$ is the current density, p is the fluid pressure, and $\Pi$ is the symmetric rate-of-strain tensor defined as

\begin{displaymath}% \Pi = \frac{1}{2} \left[\boldsymbol{\nabla}{\vec{v}} + \boldsymbol{\nabla}{\vec{v}}^T\right]. \end{displaymath} (5)

In Eqs. (2)-(4), $\mathcal R_\lambda ({=}v_0 L_0/\lambda)$ and $\mathcal R_\nu ({=} \rho_0 v_0 L_0/\nu)$ are the Reynolds numbers, measuring respectively the global kinematic $(\lambda)$ and dynamic viscosity ($\nu$) in the numerical box (see below for the definition of $v_0, \rho_0$ and L0). In our simulations we always consider $\mathcal R_\lambda = \mathcal R_\nu$, and we accordingly refer only to the dynamic Reynolds number $\mathcal R_\nu$. The quantity $\mathcal S ~ ({=} v_{\rm A} L_0/\eta$, where $v_{\rm A}$ is the the Alfvén velocity) is the Lundquist number, which gives a measure of the global explicit resistivity ($\eta$) we set within the domain. We use an ideal equation of state with polytropic index $\gamma = 5/3$ so that $p = \rho ~ (\gamma-1) ~ \mathcal I$. In general, numerical simulations represent an infinite class of systems. We normalize our set of equations by means of characteristic quantities $(\rho_0, L_0, v_0)$ with reasonable values for the region of the high chromosphere/low solar corona: the number density $\rho_0/m \approx 10^9~\ensuremath{\mbox{cm}^{-3}} $ where m is the mean particle mass, the length scale $L_0 \approx 1000{-}2000~\ensuremath{\mbox{km}} $ where $L_0 = \mbox{current-sheet width} = L_x/20 = L_z/80$ and $v_{\rm A} = v_0 \approx 400{-}600~\ensuremath{\mbox{km} ~ \mbox{s}^{-1}} $ (approximately three times the sound speed, that is $v_{\rm S} = 130{-}200~\ensuremath{\mbox{km} ~ \mbox{s}^{-1}} $). Consequently we get a time scale of $t_{\rm A} = L/v_{\rm A} \approx 1.5{-}5~\ensuremath{\mbox{s}} $, a normalization scale for the magnetic field of B0 = 6-9 G and a unit for the temperature, $T_0 = 1{-}2.2 \times 10^6~\ensuremath{\mbox{K}} $.

\begin{figure} \par\includegraphics[width=3.5cm,clip]{aa13652-09-fig1.eps} \end{figure} Figure 1:

Schematic reconstruction of our basic system: it is possible to visualize the initial stream-wise component of the magnetic field (in blue and red) and the density step at Lz/8.

Open with DEXTER

To solve Eqs. (1)-(4) we use the code FLIP MHD (Brackbill 1991). We consider 600 (in x) $\times$ 960 (in z) Lagrangian markers initially arrayed in a $3 \times 3$ uniform formation in each of the $200\ \times\ 320$ cells of our numerical grid. This has the sizes

\begin{displaymath}% \begin{array}{ll} x \in [-10,10] & \quad \mbox{with} ~ {\r... ...\in [0,80] & \quad \mbox{with} ~ {\rm d}z = 0.25. \end{array} \end{displaymath} (6)

As shown in Fig. 1, our system consists in a current-sheet determined by a force-free field configuration given by the equations
  B0z(x) = $\displaystyle \tanh x$ (7)
B0y(x) = $\displaystyle -{\rm sech~}x,$ (8)

which implies that the current-sheet width is equal to the normalization length L and is resolved by 30 Lagrangian markers. As already pointed out in the introduction, our computational domain has transversal sizes large enough to allow a complete development of the system dynamics. The density is modeled as a step function

\begin{displaymath}% \rho = \left\{ \begin{array}{ll} \mathcal C & \qquad \mbox... ...& \\ 1 & \qquad \mbox{if} \qquad z \ge z_0 \end{array}\right. \end{displaymath} (9)

or as a hyperbolic tangent function

\begin{displaymath}% \rho = \frac{1+\mathcal C}{2}+\frac{\left(1-\mathcal C\right)}{2} \tanh\left(\frac{z-z_0}{\alpha}\right), \end{displaymath} (10)

where $\mathcal C$ is the ratio between the density in the region 0 < z < Lz/8 (modeling the high chromosphere) and that in Lz/8 < 0 < Lz (the low corona), and we choose it to range from 102 up to 105 as considered in Yokoyama & Shibata (2001). In Eq. (9), z0 is the position of the discontinuity resembling the transition region, whereas in Eq. (10) it represents the transition region's center; the parameter $\alpha$ allows us to assume different thicknesses of the transition region.

Reconnection is set in by a magnetic field perturbation defined by the out-of-plane component of the magnetic vector potential

\begin{displaymath}% {\vec{B}}_1 = \boldsymbol{\nabla}\times \left(A_{1y} ~\boldsymbol{{e}}_y\right) \end{displaymath} (11)

with
                         A1y = $\displaystyle \varepsilon \exp\left[-\kappa_x \left(x-x_{\rm p}\right)^2-\kappa_z \left(z-z_{\rm p}\right)^2\right]$  
    $\displaystyle \times \cos\left[\kappa_x \left(x-x_{\rm p}\right)\right] \cos\left[\kappa_z \left(z-z_{\rm p}\right)\right]$ (12)

providing a GEM-like perturbation (Birn et al. 2001) but localized in $(x, z) = (x_{\rm p}, z_{\rm p})$ by the exponential factor. We referred to the model and simulations of Yokoyama & Shibata (2001), but with the intention to study the possibility of a natural-evolving slow-fast reconnection transition in the low corona with the development of a final turbulent state. After performing a few test simulations, we accordingly set the initial perturbation amplitude $(\varepsilon)$ to 0.5 and the perturbation wave-numbers in the x $(\kappa_x)$ and z $(\kappa_z)$ direction to $\pi/L_x$ and $\pi/4 L_z$ respectively. In general we consider that the perturbation is located exactly at the center of the x- and z-axis, which means for the low corona: $(x_{\rm p}, z_{\rm p}) = (0, L_z/2)$. Other cases with different $z_{\rm p}$ (Lz/8, Lz/4, 0) but always $x_{\rm p} = 0$ have been considered and performed.

3 Simulation parameters

3.1 Viscosity and resistivity

Figure 2 shows the reconnected flux as a function of the simulation time for several different values of the Lundquist and dynamic Reynolds number, both ranging from 102 to $\infty$, even though the actual upper limit is given by the intrinsic numerical effects. The plasma $\beta$ is set to 0.2 for these simulations (see Sect. 3.2). As we used a non-selfconsistent perturbation that is not an eigenstate of the system, we had a small transient time of about a decade of time steps. The system displays the same behavior, except for very low $\mathcal S$ or $\mathcal R_\nu$: this undergoes a two-stage evolution consisting of a slow reconnection phase followed by a rapid increase of the reconnected flux, which corresponds to a fast reconnecting regime. The viscosity and resistivity affect the dynamics of the system in a different way. Viscosity is effective only when it is set to high values $(\mathcal R_\nu = 10^2)$. Resistivity has the main role in determining both the behavior of the system in the first slow phase and in switching it to a fast regime. If $\mathcal S$ is too low, as described by the dotted line in the above mentioned figure, the system remains in a steady-state reconnection process where the corresponding width of our current-sheet is constant in time until the end of the simulation. By increasing $\mathcal S$, the slow phase shortens and we observe the triggering of a fast regime whose starting point and dynamical features appear to be independent of the value of resistivity. If we increase $\mathcal S$ further until the numerical dissipation dominates $(\mathcal S \rightarrow \infty)$, the two-stage evolution continues (as long as viscosity has a negligible value).

\begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig2.eps} \end{figure} Figure 2:

Big plot: reconnected flux as a function of the simulation time for different values of the Lundquist number, $\mathcal S$, and the dynamic Reynolds number, $\mathcal R_\nu$. In all cases but $(\mathcal S, \mathcal R_\nu) = (10^2, 10^4)$ (dotted line), we can observe an abrupt transition from a slow reconnection process to a fast regime. Small plot: detailed view of the slow SP regime.

Open with DEXTER

As long as the reconnection process remains in the first slow reconnection regime, although the system does not reach the strict steady state described by the SP theory, the reconnection system's morphology and the scaling of the current sheet thickness for different values of the resistivity agrees reasonably well with the SP theory. The scaling of the reconnection rate, $\mathcal M$, prescribed by SP theory is $\mathcal M = \mathcal S^{-1/2} = \delta/\mathcal L$, where $\delta$ and $\mathcal L$ are the thickness and the length of the diffusion region, respectively. In Fig. 3 we show the ratio $\mathcal L/\delta$ as a function of time for the case with the Lundquist and the Reynolds numbers set to $\mathcal S = \mathcal R_\nu = 10^4$. As already pointed out, the perturbation is not an eigenstate of the system and therefore the current-sheet evolves in time, that is the length of the diffusion region, $\mathcal L$, increases and correspondingly its thickness, $\delta$, decreases: it breaks when it reaches the value of hundreds corresponding to the value consistent with the SP theory (square-root of 104).

\begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig3.eps}\vspace*{3.5mm} \end{figure} Figure 3:

Diffusion region's aspect ratio (length/width) as a function of the simulation time for the case with the Lundquist number and the dynamic Reynolds number set to $\mathcal S = \mathcal R_\nu = 10^4$.

Open with DEXTER

In the subsequent discussion, the focus will be on $\mathcal S = \mathcal R_\nu = 10^4$. We point out that this process is not affected by the numerical resistivity. Figure 4 shows the reconnection rate as a function of time, and different methods are used and compared. As suggested in Dorelli & Birn (2001), the rate can be computed by time-derivative of the reconnected flux obtained by means of the out-of-plane component of the vector potential at the mid axis, Ay at x = 0, or by the value of the out-of-plane component of the electric field, Ey (dashed line) at the X-point: their difference provides a measure of the numerical effects acting on the system, and from Fig. 4 is evident that the computed rates are equal.

\begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig4.eps} \end{figure} Figure 4:

Reconnected rate as a function of the simulation time $(\mathcal S = \mathcal R_\nu = 10^4)$: the solid line corresponds to the rate computed as the time-derivative of the reconnected flux obtained by the out-of-plane magnetic vector potential, Ay; the dashed line corresponds to the rate computed by the out-of-plane component of the electric field, Ey.

Open with DEXTER

3.2 The plasma beta

As previously pointed out we consider the simplified assumption, which is yet reasonable for the solar environment, that a temperature gradient is provided in order to balance the density variation. Hence, we have an overall uniform and constant initial plasma pressure

\begin{displaymath}% p_0 = \beta \frac{\left\vert B_0\right\vert^2}{2} = \frac{\beta}{2}\cdot \end{displaymath} (13)

In Fig. 5 we show the reconnected flux as a function of the simulation time for different values of the beta parameter ranging from 0.2 to 2. As the Alfvén velocity is fixed, the change of $\beta$ implies that we are varying the compressibility of our system. In the first slow and diffusive SP reconnection regime, the difference in the compressibility does not influence the evolution at all. Indeed, the dynamics depends on the global system's resistivity/viscosity, which is fixed by $\mathcal R_\nu = \mathcal S = 10^4$. Yet, as soon as we observe the triggering of the second faster reconnection phase, which corresponds to system's structure evolving on smaller and smaller length-scales (see below), it is evident that for higher compressibility the slope of the reconnected flux becomes steeper and hence the corresponding reconnection rate becomes faster. Accordingly the main features of the fast reconnection phase critically depend on the compressive effects in the system and no longer on the global resistivity/viscosity. For the realistic simulation below we consider the accepted value $\beta = 0.2$ to place the current-sheet approximately in the high chromosphere/low corona (Yokoyama & Shibata 2001; Gary 2001).

\begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig5.eps} \end{figure} Figure 5:

Reconnected flux as a function of the simulation time for different values of the beta parameter with the Lundquist number and the dynamic Reynolds number set to $\mathcal S = \mathcal R_\nu = 10^4$.

Open with DEXTER

4 Results and discussion

The evolution of a current-sheet in the presence of an orthogonal strong density variation is characterized by a two-stage evolution whose main features are described in Fig. 6. The contour of the out-of-plane component of the current density (Jy) is shown superposed on the same component of the magnetic vector potential (solid black lines) at four different instants. At about $t \approx 18{-}20$ (top panel), the system is evolving according to the SP theory (see Sect. 3.1) and the slow reconnection regime proceeds with the elongation and thinning of the current sheet in the low density region (second panel of Fig. 6, $t \approx 36$). As described in the previous work by Bulanov et al. (1979) and in recent ones (Skender & Lapenta 2010; Loureiro et al. 2007), the system reaches a configuration where the ratio between the length and the width of the current sheet makes it tearing-unstable. This is also evident in Fig. 3 where diffusion region's aspect ratio is shown as a function of the simulation time: at about $t \approx 40$ a maximum is reached, the instability process rapidly evolves and the initially formed SP diffusion region starts to destabilize. Due to the disruption of the main current sheet, several structures form which in turn determine a reconnection site (third panel from the top of Fig. 6, $t \approx 52$): these drive the initial configuration to smaller and smaller scales (bottom panel). During this process the presence of the strong density gradient produces an asymmetric development determining an oriented path for the overall flow and current density evolution. As the two-stage reconnection proceeds, we observe the slow upward movement of the initial diffusion region determined by the accumulation of the magnetic flux due to the asymmetric configuration of the system. This confirms at MHD scales the preliminary results shown recently in particle-in-cell simulations of collisionless magnetic reconnection in asymmetric configurations (Oka et al. 2008). The diffusion region breaks up into several parts and the islands that form start to move forward and backward, pushed by the reconnection jets. A chaotic configuration is more and more evident both in the most intense current-density region still in fragmentation and in the macro-structure emitted toward the upper layers of the corona and that resembles the turbulent reconnection as proposed by Tajima & Shibata (2002) or Lazarian & Vishniac (1999). Furthermore, due to the density wall there is the buildup of a magnetic flux of opposite polarity and post-disruption arcades form in the low corona. As the process goes on, converging motions toward the polarity inversion line lead to the shrinking of the current-sheet at the base of these growing magnetic structures. This situation probably leads to a release of magnetic energy in the solar atmosphere via a new reconnection process.

\begin{figure} \par\includegraphics[width=14cm,clip]{aa13652-09-fig6a.eps}\vspac... ...2.36mm} \par\includegraphics[width=14cm,clip]{aa13652-09-fig6d.eps} \end{figure} Figure 6:

Contour of the out-of-plane current density, Jy, (in color) superposed on the same component of the vector potential (solid black lines) at four different instants ( from top to bottom): t = 17, 36, 53, 96. Here the density is modeled as a discontinuity with the step located at z = Lz/8 = 10. For a better visualization, only the central part of the numerical box is shown in the images.

Open with DEXTER

The onset of a macroscopic circulation pattern linking all the small reconnection sites sustains the strong increase of the reconnection rate as seen in Fig. 2 (for $\mathcal S = 10^4$). The net effect is an overall acceleration of the system that drags all structures forward and therefore expells plasma in the upper corona. In Fig. 7, the contour of the out-of-plane magnetic vector potential at $t \approx 96$ is shown with the velocity field superposed and represented by properly scaled arrows: we can observe the well-developed circulation pattern during the multiple reconnection process and the effective acceleration reconnection jet. The motions driving the post-disruption arcades rising in the low corona are also evident.

\begin{figure} \par\includegraphics[width=14cm,clip]{aa13652-09-fig7.eps} \end{figure} Figure 7:

Contour of the out-of-plane magnetic vector potential at $t \approx 96$(solid colored lines). The velocity field is also shown and is represented by properly scaled arrows. For a better visualization, only the central part of the numerical box is shown in the image.

Open with DEXTER

4.1 Reconnection fluxes

The energy transfers provide information on the structures moving down toward the high chromosphere or up toward the upper layers of the solar corona. We consider the flux of the Poynting vector, the enthalpy flux and the kinetic flux, respectively defined as

        $\displaystyle {\vec{S}}$ = $\displaystyle {\vec{E}} \times {\vec{B}}$ (14)
$\displaystyle {\vec{H}}$ = $\displaystyle (\mathcal I + p) ~ {\vec{v}}$ (15)
$\displaystyle {\vec{K}}$ = $\displaystyle \frac{1}{2} \rho ~ \vert{\vec{v}}\vert^2 ~ {\vec{v}}$ (16)

through a surface extended from x = -5 to x = +5 and located at z = 20 (downward flux) and z = 80, the higher boundary (upward flux). In Fig. 8 one can see these profiles as a function of time through the two-stage process: the top panel describes the upward flux, whereas the bottom panel describes the downward flux. The mass flux through the same surfaces is shown as reference. We observe that the fast process determines a sensitive rise in the upward mass flux associated with an increase of the kinetic and enthalpy fluxes: the multiple chaotically-moving plasmoids accelerate upward and the plasma is characterized by an increase of the compressional heating effects. The chaotic fast stage shows an initial increase of all fluxes, and a weak maximum is reached. Later, a real impulsive event occurs, which has a duration of about $\Delta t \approx 10$, which is $15 \div 50~\ensuremath{\mbox{s}} $ according to the normalization values provided in Sect. 2. Hence, we obtain from Fig. 8 that the dimensionless values of the energy fluxes associated with the impulse are $\rho ~ v_z \approx 4$, $H_z \approx 3$, $K_z \approx 1$. So, we obtain from definitions (14)-(16) and by again using the normalization values for our set of simulations, we obtain thefollowing physical values for the energy fluxes associated with the impulse
                       $\displaystyle \rho ~ v_z$ $\textstyle \approx$ $\displaystyle 0.8 \div 2.4 \times 10^{16}~\ensuremath{\mbox{particle}/\mbox{cm}^2~\mbox{s}} $ (17)
Hz $\textstyle \approx$ $\displaystyle 0.6 \div 6.6 \times 10^8~\ensuremath{\mbox{erg}/\mbox{cm}^2~\mbox{s}} $ (18)
Kz $\textstyle \approx$ $\displaystyle 0.2 \div 2.2 \times 10^8~\ensuremath{\mbox{erg}/\mbox{cm}^2~\mbox{s}} .$ (19)

These values show a reasonable agreement with observations of solar explosive phenomena (Tsuneta 1996; Shibata 1996). The Poynting up-flux increases during most of the fast process and reaches a constant value of about $S_z \approx 1.2$, that is $0.2 \div 2.6 \times 10^8~\ensuremath{\mbox{erg}/\mbox{cm}^2~\mbox{s}} $, but it drops out in the impulsive phase. This means that the rapid emission of a highly structured accelerating mass toward the upper layers of the corona does not come with a corresponding impulsive release of magnetic energy that is instead converted into the other forms of energy. This is consistent with Takeuchi & Shibata (2001) who showed that in the later stage of a (simulated) reconnection event at the photospheric level slow waves carry more energy than Alfvén waves do. With regard to the downward-fluxes, only small variations are observed. This behavior is caused by the density gradient that, as already discussed, allows the pile-up of magnetic flux with the formation of post-disruption arcades. In Fig. 9, we show the contour of the specific internal energy at $t \approx 96$ with respect to its initial value, $\mathcal I/\mathcal I(t=0)$. The turbulent configuration of the most dense structures whose internal energy rapidly increased during the evolution is evident. In particular, we note the high values obtained on the post-disruption arcades in the low corona.

\begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig8.eps} \end{figure} Figure 8:

Top panel: energy and mass fluxes through a surface extended from x = -5 to x = +5 and located at the higher boundary, z = 80 = Lz (upward fluxes). Bottom panel: same as the top panel, but the surface for the computation of the fluxes is located at z = 20 (downward fluxes).

Open with DEXTER

\begin{figure} \par\includegraphics[width=14cm,clip]{aa13652-09-fig9.eps} \end{figure} Figure 9:

Contour of the specific internal energy with respect its initial value, $\mathcal I/\mathcal I(t=0)$, at t = 96. For a better visualization, only the central part of the numerical box is shown.

Open with DEXTER

4.2 Effect of perturbation location

As already pointed out at the end of Sect. 2, we performed simulations with different values of $z_{\rm p}$, but found no substantial qualitative differences as a function of the position of the initial perturbation, at least in the cases considered. For instance, if the perturbation is located in the transition region ( $x_{\rm p} = 0$ and $z_{\rm p} = L_z/8$) modeled as a discontinuity between the chromosphere and the corona, we observe the same current-sheet dynamics as described in the previous sections, even though two clear differences can be observed in Fig. 10, where the out-of-plane current density (in color) and magnetic vector potential (solid black lines) are shown for this case at $t \approx 96$:

  • the density step does not allow the current-sheet to develop into the high chromosphere at all and this determines that the whole structure is elongated toward upper coronal layers. The accelerating jet still presents a chaotic internal structure, but it has a wider aperture with respect the previous cases;
  • the motion of the overall structure toward the upper coronal layer again allows the formation of post-disruption arcades that develop slower than they do in the previous cases. By the end of the simulation we are not able to determine any visible sign of a starting reconnection process at the base of the corona $(L_z \approx 10)$.
The upward fluxes in this case do not change with respect the previous ones, while the downward fluxes are affected by the presence of the density step, which determines the accumulation of magnetic flux that encompasses the surface through which the flux is computed.

\begin{figure} \par\includegraphics[width=14cm,clip]{aa13652-09-fig10.eps} \end{figure} Figure 10:

Contour of the out-of-plane current density, Jy, (in color) superposed on the same component of the vector potential (solid black lines) at t = 96. Here the density is modeled as a discontinuity with the step located at z = Lz/8 = 10 and the initial perturbation is located at $x_{\rm p} = 0, z_{\rm p} = L_z/8$. For a better visualization, only the central part of the numerical box is shown.

Open with DEXTER

If the density is modeled by a hyperbolic tangent, the same dynamics is observed as long as a steep profile is considered: the smoother the slope of the density function, the less sensitive the accumulation of magnetic flux, the rise of the main reconnection site and the overall acceleration of system. Finally, with a very low density variation, we recovered the results obtained by Lapenta (2008), even though open boundary conditions instead of periodic settings alter the detail of the evolution.

5 Conclusions

We presented a 2.5-dimensional model of the current-sheet evolution located in the solar atmosphere, in particular across the region where the chromosphere and the corona meet. There magnetic reconnection plays a fundamental role in solar plasma dynamics and we tested a new reconnection mechanism embedded in a simplified solar atmosphere, where the transition region is modeled as a density step or a hyperbolic tangent variation of the density and temperature. Previous studies of such systems, most of which focused on triggering events and dynamics of solar flares (Yokoyama & Shibata 2001), on filaments (Lin et al. 2008) or on the evolution and observations of current-sheets forming in the aftermath of coronal mass ejections (Bemporad et al. 2006; Poletto et al. 2004), always demanded the presence of locally enhanced plasma resistivity to explain the rapid increase of the reconnection rate to allow the fast evolution underlying explosive phenomena in the solar atmosphere. Yet we here demonstrate by means of high-resolution simulations

  • A natural two-stage evolution of a current-sheet with a spontaneous transition from a low to a fast reconnection regime can occur within the solar corona without the need to include any anomalous effect and in the presence of a strong density gradient.
  • An asymmetric evolution determined by the density (temperature) variation from the chromosphere and the solar corona is observed: the global dynamics reported resembles the tearing evolution of solar structures both just before and immediately after observed and/or modeled explosive phenomena. Despite our simplified model of the solar atmosphere, we obtain magnetic field configurations with a preferential oriented path for the overall flow and current density evolution as well as observables (mass and energy fluxes) resembling the picture so far provided by observations.
  • A macroscopic turbulent state is reached by our system and this should be further investigated as the properties of this final configuration can give us important insights and constrains that are fundamental to distinguish among several turbulent models of current layer-like structures within the solar atmosphere.
Several observational clues can be mentioned to support the scenario described here. For example hard X-ray and radio emissions present many properties during solar flares ascribed to small-scale, fragmented, bursty magnetic reconnections (Aschwanden 2002). Post-CME current-sheets are observed to have a much larger thickness than what the MHD theory prescribes (Bemporad 2008). Chaotic magnetic reconnection in a current-sheet could explain this observed behavior.

From the observational point of view, important information to improve the model of turbulent reconnection and to compare observational data with numerical results can be obtained from the analysis of the frequency distribution of time scales in the chaotic evolution of current-sheets. Indeed, this kind of study could distinguish between a fractal current-sheet evolution or turbulent reconnection, because the former process is scale-free and generally produces power law distributions, while turbulent processes are controlled by incoherent random processes and hence they generally give exponential distributions (Aschwanden 2006). In the future, an ``expanding box'' setting (Rappazzo et al. 2005; Grappin et al. 1993) of our simulations may be considered in order to follow the evolution of the current-sheet in a simpler cartesian geometry with spherical effects included. This would allow us also to properly study the formation and evolution of outward and downward flows as seen in H$\alpha$ observations of highly dynamic filaments and surges in active regions (Lin et al. 2008). Moreover, a better understanding of the above-mentioned events as well as of other highly-dynamic process, like for instance solar spicules (Takeuchi & Shibata 2001), demands a more detailed model of the solar atmosphere with the inclusion of the photosphere, at least as boundary condition constraining the dynamics determined by our reconnection mechanism and the related energy fluxes.

Acknowledgements
The research leading to these results has received funding from the European Commission's Seventh Framework Programme (FP7/2007-2013) under the grant agreement n$^\circ$ 218816 (SOTERIA project, www.soteria-space.eu). The simulations shown were conducted using processors on the VIC cluster of the Vlaams Supercomputer Centrum at K.U. Leuven (Belgium). The authors are grateful to J. Birn for the suggestion of the methods to measure the reconnection rate. We are also grateful to the anonymous referee for comments and suggestions.

References

  1. Aschwanden, M. J. 2002, Space Sci. Rev., 101, 1 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aschwanden, M. J. 2006, Physics of the solar corona: an introduction with problems and solutions (Springer Science & Business) [Google Scholar]
  3. Baty, H., Priest, E. R., & Forbes, T. G. 2006, Phys. Plasmas, 13, 022312 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bemporad, A. 2008, ApJ, 689, 572 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bemporad, A., Poletto, G., Suess, S. T., et al. 2006, ApJ, 638, 1110 [Google Scholar]
  6. Birn, J., Drake, J. F., Shay, M. A., et al. 2001, J. Geophys. Res., 106, 3715 [Google Scholar]
  7. Biskamp, D. 1993, Nonlinear magnetohydrodynamics, Cambridge Monograph on Plasma Physics (Cambridge: Cambridge University Press) [Google Scholar]
  8. Brackbill, J. U. 1991, J. Comp. Phys., 96, 163 [Google Scholar]
  9. Bulanov, S. V., Sakai, D.-I., & Syrovatskii, S. I. 1979, Sov. J. Plasma Phys., 5, 280 [NASA ADS] [Google Scholar]
  10. Cirtain, J. W., Golub, L., Lundquist, L., et al. 2007, Science, 318, 1580 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  11. Dorelli, J. C., & Birn, J. 2001, Phys. Plasmas, 8, 4010 [NASA ADS] [CrossRef] [Google Scholar]
  12. Forbes, T., & Lin, J. 2000, J. Atmos. Solar-Terr. Phys., 62, 1499 [Google Scholar]
  13. Furth, H. P., Killeen, J., & Rosenbluth, M. N. 1963, Phys. Fluids, 6, 459 [NASA ADS] [CrossRef] [Google Scholar]
  14. Galsgaard, K., & Roussev, I. 2002, A&A, 383, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Gary, G. A. 2001, Sol. Phys., 203, 71 [NASA ADS] [CrossRef] [Google Scholar]
  16. Grappin, R., Velli, M., & Mangeney, A. 1993, Phys. Rev. Lett., 70, 2190 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  17. Hautz, R., & Scholer, M. 1987, Geophys. Res. Lett., 14, 969 [NASA ADS] [CrossRef] [Google Scholar]
  18. Karpen, J. T., Antiochos, S. K., DeVore, C. R., & Golub, L. 1998, ApJ, 495, 491 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kliem, B., Karlicky, M., & Benz, A. O. 2000, A&A, 360, 715 [NASA ADS] [Google Scholar]
  20. Kowal, G., Lazarian, A., Vishniac, E. T., & Otmianowska-Mazur, K. 2009, ApJ, 700, 63 [NASA ADS] [CrossRef] [Google Scholar]
  21. Lapenta, G. 2008, Phys. Rev. Lett., 100, 235001 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  22. Lazarian, A., & Vishniac, E. T. 1999, ApJ, 517, 700 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lin, J., Raymond, J. C., & van Ballegooijen, A. A. 2004, ApJ, 602, 422 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lin, Y., Martin, S., Engvold, O., Rouppe van der Voort, L., & van Noort, M. 2008, Adv. Space Res., 42, 803 [NASA ADS] [CrossRef] [Google Scholar]
  25. Loureiro, N. F., Schekochihin, A. A., & Cowley, S. C. 2007, Phys. Plasmas, 14, 100703 [NASA ADS] [CrossRef] [Google Scholar]
  26. Nitta, S.-Y. 2007, ApJ, 663, 610 [NASA ADS] [CrossRef] [Google Scholar]
  27. Oka, M., Fujimoto M., Nakamura, T. K. M., Shinohara, I., & Nishikawa, K.-I. 2008, Phys. Rev. Lett., 101, 205004 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  28. Poletto, G., Suess, S. T., Bemporad, A., et al. 2004, ApJ, 613, L173 [NASA ADS] [CrossRef] [Google Scholar]
  29. Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R. B. 2005, ApJ, 633, 474 [NASA ADS] [CrossRef] [Google Scholar]
  30. Scholer, M. 1989, J. Geophys. Res., 94, 8805 [NASA ADS] [CrossRef] [Google Scholar]
  31. Shibata, K. 1996, Adv. Space Res., 17, 9 [NASA ADS] [CrossRef] [Google Scholar]
  32. Shibata, K., Nakamura, T., Matsumoto, T., et al. 2007, Science, 318, 1591 [Google Scholar]
  33. Skender, M., & Lapenta, G. 2010, Phys. Plasmas, 17, 022905 [NASA ADS] [CrossRef] [Google Scholar]
  34. Syrovatskii, S. I. 1981, ARA&A, 19, 163 [NASA ADS] [CrossRef] [Google Scholar]
  35. Tajima, T., & Shibata, K. 2002, Plasma Astrophys. (Perseus Books Group) [Google Scholar]
  36. Takeuchi, A., & Shibata, K. 2001, ApJ, 546, L73 [NASA ADS] [CrossRef] [Google Scholar]
  37. Tsuneta, S. 1996, ApJ, 456, 840 [NASA ADS] [CrossRef] [Google Scholar]
  38. Yokoyama, T., & Shibata, K. 2001, ApJ, 549, 1160 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=3.5cm,clip]{aa13652-09-fig1.eps} \end{figure} Figure 1:

Schematic reconstruction of our basic system: it is possible to visualize the initial stream-wise component of the magnetic field (in blue and red) and the density step at Lz/8.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig2.eps} \end{figure} Figure 2:

Big plot: reconnected flux as a function of the simulation time for different values of the Lundquist number, $\mathcal S$, and the dynamic Reynolds number, $\mathcal R_\nu$. In all cases but $(\mathcal S, \mathcal R_\nu) = (10^2, 10^4)$ (dotted line), we can observe an abrupt transition from a slow reconnection process to a fast regime. Small plot: detailed view of the slow SP regime.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig3.eps}\vspace*{3.5mm} \end{figure} Figure 3:

Diffusion region's aspect ratio (length/width) as a function of the simulation time for the case with the Lundquist number and the dynamic Reynolds number set to $\mathcal S = \mathcal R_\nu = 10^4$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig4.eps} \end{figure} Figure 4:

Reconnected rate as a function of the simulation time $(\mathcal S = \mathcal R_\nu = 10^4)$: the solid line corresponds to the rate computed as the time-derivative of the reconnected flux obtained by the out-of-plane magnetic vector potential, Ay; the dashed line corresponds to the rate computed by the out-of-plane component of the electric field, Ey.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig5.eps} \end{figure} Figure 5:

Reconnected flux as a function of the simulation time for different values of the beta parameter with the Lundquist number and the dynamic Reynolds number set to $\mathcal S = \mathcal R_\nu = 10^4$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{aa13652-09-fig6a.eps}\vspac... ...2.36mm} \par\includegraphics[width=14cm,clip]{aa13652-09-fig6d.eps} \end{figure} Figure 6:

Contour of the out-of-plane current density, Jy, (in color) superposed on the same component of the vector potential (solid black lines) at four different instants ( from top to bottom): t = 17, 36, 53, 96. Here the density is modeled as a discontinuity with the step located at z = Lz/8 = 10. For a better visualization, only the central part of the numerical box is shown in the images.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{aa13652-09-fig7.eps} \end{figure} Figure 7:

Contour of the out-of-plane magnetic vector potential at $t \approx 96$(solid colored lines). The velocity field is also shown and is represented by properly scaled arrows. For a better visualization, only the central part of the numerical box is shown in the image.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{aa13652-09-fig8.eps} \end{figure} Figure 8:

Top panel: energy and mass fluxes through a surface extended from x = -5 to x = +5 and located at the higher boundary, z = 80 = Lz (upward fluxes). Bottom panel: same as the top panel, but the surface for the computation of the fluxes is located at z = 20 (downward fluxes).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{aa13652-09-fig9.eps} \end{figure} Figure 9:

Contour of the specific internal energy with respect its initial value, $\mathcal I/\mathcal I(t=0)$, at t = 96. For a better visualization, only the central part of the numerical box is shown.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14cm,clip]{aa13652-09-fig10.eps} \end{figure} Figure 10:

Contour of the out-of-plane current density, Jy, (in color) superposed on the same component of the vector potential (solid black lines) at t = 96. Here the density is modeled as a discontinuity with the step located at z = Lz/8 = 10 and the initial perturbation is located at $x_{\rm p} = 0, z_{\rm p} = L_z/8$. For a better visualization, only the central part of the numerical box is shown.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.