EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 518 (July-August 2010) A&A, 518 (2010) A2 Full HTML
Free Access
Issue
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
Article Number A2
Number of page(s) 11
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913421
Published online 18 August 2010
A&A 518, A2 (2010)

Applicability of Milne-Eddington inversions to high spatial resolution observations of the quiet Sun[*]

D. Orozco Suárez1,2 - L. R. Bellot Rubio1 - A. Vögler3 - J. C. del Toro Iniesta1

1 - Instituto de Astrofísica de Andalucía (CSIC), Apdo. Correos 3004, 18080 Granada, Spain
2 - National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
3 - Sterrenkundig Instituut, Utrecht University, Postbus 80000, 3508 TA Utrecht, The Netherlands

Received 8 October 2009 / Accepted 26 May 2010

Abstract
Context. The physical conditions of the solar photosphere change on very small spatial scales both horizontally and vertically. Such a complexity may pose a serious obstacle to the accurate determination of solar magnetic fields.
Aims. We examine the applicability of Milne-Eddington (ME) inversions to high spatial resolution observations of the quiet Sun. Our aim is to understand the connection between the ME inferences and the actual stratifications of the atmospheric parameters.
Methods. We use magnetoconvection simulations of the solar surface to synthesize asymmetric Stokes profiles such as those observed in the quiet Sun. We then invert the profiles with the ME approximation. We perform an empirical analysis of the heights of formation of ME measurements and analyze the uncertainties brought about by the ME approximation. We also investigate the quality of the fits and their relationship with the model stratifications.
Results. The atmospheric parameters derived from ME inversions of high-spatial resolution profiles are reasonably accurate and can be used for statistical analyses of solar magnetic fields, even if the fit is not always good. We also show that the ME inferences cannot be assigned to a specific atmospheric layer: different parameters sample different ranges of optical depths, and even the same parameter may trace different layers depending on the physical conditions of the atmosphere. Despite this variability, ME inversions tend to probe deeper layers in granules than in intergranular lanes.

Key words: magnetic fields - instrumentation: high angular resolution - Sun: photosphere

1 Introduction

The solar spectrum carries information about the properties of our star. In general, a broad range of atmospheric layers contribute to the shape of the spectral lines, making it difficult to extract this information directly. Both the measurement process and the method of analysis introduce uncertainties in the physical quantities retrieved from the observations. Sources of error are photon noise and instrumental effects such as limited spectral resolution, wavelength sampling, and angular resolution, but also the simplifications and approximations of the model used to interpret the measurements.

In this paper we evaluate the merits of Milne-Eddington (ME) inversions for the analysis of the polarization line profiles emerging from the solar atmosphere. The ME approximation does not account for vertical variations of the parameters (Rachkovsky 1962,1967; Unno 1956), so it cannot accurately describe the solar plasma when rapid changes in height are present. What then is the significance of the ME parameters?

To answer this question it is necessary to simulate the processes of line formation and data inversion. Usually one prescribes a set of model atmospheres, performs spectral synthesis calculations, inverts the synthetic profiles, and compares the results with the known input. A common approach is to use ME models both to generate the spectra and to invert them (e.g., Borrero et al. 2007; Norton et al. 2006). In that case the analysis is internally consistent and the uncertainties of the retrieved ME parameters are mostly due to the noise and, to a smaller extent, to the convergence of the algorithm, provided that the spectral resolution and wavelength sampling are appropriate. Uncertainties caused by photon noise are known as statistical errors and can be evaluated by means of numerical tests or, more efficiently, by using ME response functions (Del Toro Iniesta et al. 2010; Orozco Suárez & Del Toro Iniesta 2007). However, they represent only a small fraction of the total error. Another source of error is the very assumption of height-independent parameters, which leads to symmetric line profiles. What happens when realistic (i.e., asymmetric) Stokes spectra are analyzed in terms of ME models? Do the uncertainties of the retrieved parameters increase significantly? Answering these questions is the aim of the present work.

A first study of the capabilities and limitations of ME inversions was carried out by Westendorp Plaza et al. (1998) with simple (non-ME) model atmospheres. They made a quantitative comparison of results obtained with the ME code of the High Altitude Observatory (Lites & Skumanich 1990; Skumanich & Lites 1987) and the SIR code (Stokes Inversion based on Response functions, Ruiz Cobo & Del Toro Iniesta 1992). The main conclusion of their work was that ME inversions provide accurate values of the physical parameters averaged along the line of sight, at least when the stratifications are smooth.

More recently, Khomenko & Collados (2007b) have investigated whether the magnetic field stratification itself can be determined reliably through inversion of high-resolution data. To that end, they synthesized the Stokes profiles of the Fe I 630 nm lines with the help of MHD models and inverted them with SIR, allowing for vertical gradients of the atmospheric parameters. The analysis showed that SIR is able to recover the actual magnetic stratification for fields as weak as 50 G if there is no noise. This work extends the results of Westendorp Plaza et al. (1998) to the case in which the stratifications are not smooth.

To determine the uncertainties associated with ME inversions of asymmetric Stokes profiles we use state-of-the-art magnetohydrodynamic simulations (Sect. 2). Our goal is to describe the solar photosphere as realistically as possible. We construct model atmopheres from the simulations and synthesize the emerging Stokes profiles of the Fe I 630.2 nm lines (Sect. 3). The SIR code is used for the spectral synthesis, so the profiles are asymmetric. Finally, we apply an ME inversion to the data (Sect. 4). The spatial sampling of the MHD models $0\hbox{$.\!\!^{\prime\prime}$ }0287$ is preserved in our numerical experiments. There are two reasons why we neglect the effects of solar instrumentation: first, they have already been studied before (e.g., Orozco Suárez et al. 2007, 2010a,b); second, this sampling is close to critical for the observations to be delivered by large telescopes like the Advanced Technology Solar Telescope[*] (Wagner et al. 2006) and the European Solar Telescope[*] (Collados 2008). We invert the profiles with the MILOS code (Orozco Suárez & Del Toro Iniesta 2007)[*]. A direct comparison of the retrieved and true parameters allows us to determine the effective ``heights of formation'' of the ME parameters (Sect. 5) and to quantify the errors caused by the ME approximation (Sect. 6). The conclusions of our work are given in Sect. 7. For completeness, the results of ME inversions are compared with those of tachogram/magnetogram-like analyses in the Appendix.

2 Magnetohydrodynamic simulations

We use radiative MHD simulations performed with MURaM, the MPS/University of Chicago RAdiative MHD code (Vögler et al. 2005; Vögler 2003). This code solves the 3D time-dependent MHD equations for a compressible and partially ionized plasma taking into account non-grey radiative energy transport and opacity binning (Nordlund 1982).

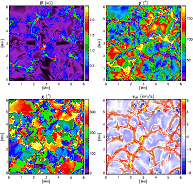
\begin{figure} \par\mbox{\resizebox{8.5cm}{!}{\includegraphics{13421Fig1a.ps}}\r... ...1Fig1c.ps}}\resizebox{8.5cm}{!}{\includegraphics{13421Fig1d.ps}} }\end{figure} Figure 1:

Magnetic field strength, inclination, azimuth, and LOS velocity at $\tau =1$ in a simulation snapshot with $\langle B \rangle=140$ G. Negative velocities represent upflows.

Open with DEXTER

Among other problems, MURaM has been employed to study facular brightenings (Keller et al. 2004), the relation between G-band bright points and magnetic flux concentrations (Shelyag et al. 2004; Schüssler et al. 2003), the emergence of magnetic flux tubes from the upper convection zone to the photosphere (; Cheung et al. 2007), the strongly inclined magnetic fields of the internetwork (Schüssler & Vögler 2008), umbral dots (Schüssler & Vögler 2006), solar pores (Cameron et al. 2007), and even full sunspots (Rempel et al. 2009a,b). MURaM has also been used to evaluate the diagnostic potential of spectral lines (Shelyag et al. 2007; Khomenko et al. 2005a; Khomenko & Collados 2007b,a; Khomenko et al. 2005b), the validity of visible lines for the study of internetwork magnetic fields at high spatial resolution (Orozco Suárez et al. 2007), and the continuum contrast of the solar granulation (Danilovic et al. 2008).

In this paper we consider a 5-min sequence of a mixed-polarity simulation run representing a network region with an average magnetic field strength $\langle B \rangle=140$ G at $\log ~ \tau=-1$[*]. The cadence is 10 s, so we have 30 snapshots. A bipolar distribution of vertical fields with $\langle B \rangle=200$ G was used to initialize the simulations. Additional details about this particular run can be found in Khomenko et al. (2005a).

The computational box has 288 $\times$ 288 $\times$ 100 grid points and covers 6000 km in the horizontal direction and 1400 km in the vertical direction. The model extends from z=-800 to z=600 km, with z=0 km the average of the heights where $\tau =1$. The spatial grid sampling is 0 $.\!\!^{\prime\prime}$0287, implying an equivalent resolution of 0 $.\!\!^{\prime\prime}$057 (41.6 km) on the solar surface. The simulation provides the density, the linear momentum density vector, the total energy density, the magnetic field vector, the temperature, and the gas pressure at every grid point. The time-averaged radiation flux density leaving the top of the box has the solar value $F_{\odot}=6.34$ $\times$ 1010 erg s-1 cm-2.

3 Spectral synthesis

In order to compute synthetic Stokes profiles we solve the radiative transfer equation (RTE) for polarized light. The calculations are carried out with the SIR code with the opacity routines of Wittmann (1974). The spectral synthesis is accomplished in two steps: first, the input model atmospheres are built from the MHD simulations; then, the RTE is solved.

3.1 MHD models and spectral line synthesis

The parameters needed for the spectral synthesis are the temperature, electron pressure, line-of-sight (LOS) velocity, magnetic field strength, inclination and azimuth, and optical depth. The simulations provide most of them. However, the electron pressure and optical depth need to be computed from the local temperature, gas pressure, and density by solving the Saha and Boltzmann equations. The optical depth scale is set up assuming that z=600 km (the top of the computational box) corresponds to $\log\tau=-4.9$. This value has been taken from the Harvard-Smithsonian Reference Atmosphere (HSRA, Gingerich et al. 1971). Finally, the resulting stratifications are interpolated to an evenly spaced optical depth grid using second-order polynomials. The grid extends from $\log{\tau}=-4$ to 2 with $\Delta\log\tau=0.05$. This range of optical depths encompasses the formation region of all photospheric lines, except the cores of the strongest ones.

Figure 1 displays maps of the field strength, inclination, azimuth, and LOS velocity at $\tau =1$ for one simulation snapshot. In the velocity map the granulation pattern is clearly visible, with granular upflows that are weaker than the intergranular downflows. Some of the small-scale intergranular structures have velocities of up to 6  ${\rm km}~{\rm s}^{-1}$.

The field strength map shows strong flux concentrations in the intergranular lanes. Granules also harbor magnetic fields, but they seldom exceed 300 G. There is a tight correlation between the field strength and inclination in these simulations: the intergranular fields tend to be vertical, whereas the granules exhibit more horizontal fields. Finally, the azimuth map is dominated by granular-sized structures with diameters of 1 $^{\prime\prime}$-2 $^{\prime\prime}$ (0.7-1.5 Mm).

\begin{figure} \par\includegraphics[width=8cm,clip]{13421Fig2a.ps}\vspace*{3mm} \includegraphics[width=8cm,clip]{13421Fig2b.ps} \end{figure} Figure 2:

Probability density functions for the magnetic field strength and field inclination at $\log\tau=-1$.

Open with DEXTER

Figure 2 depicts the probability density functions (PDFs)[*] of the magnetic field strength and inclination at optical depth $\log\tau=-1$, averaged over the 30 available snapshots. The field strength PDF increases rapidly toward weak fields, indicating that most pixels have magnetic fields of the order of hectogauss. The distribution peaks at about 20 G. The inclination PDF shows some vertical fields and a larger occurrence of horizontal fields. The simulation run was seeded with mixed-polarity vertical fields; therefore, the distribution is rather symmetric about $\gamma=90\ensuremath{^\circ}\/$.

Table 1:   Atomic parameters of the spectral lines.

Once we have constructed model atmospheres for each of the 288 $\times$ 288 pixels and for all the snapshots, we use them to compute the Stokes profiles of Fe I 630.15 and 630.25 nm. The atomic parameters used in the calculations are given in Table 1. The $\log gf$ values have been taken from the VALD database (Piskunov et al. 1995), except for Fe I 630.25 nm which is not available in VALD and comes from a fit to the solar spectrum using the two-component model of Borrero & Bellot Rubio (2002). The collisional broadening coefficients $\alpha$ and $\sigma$ due to neutral hydrogen atoms have been evaluated following the procedure of Anstee & O'Mara (1995) and Barklem et al. (2000,1998). The abundances have been taken from Thévenin (1989), i.e., a value of 7.46 is employed for iron.

3.2 Synthesis results

Figure 3 shows a continuum map of the simulated region. The rms contrast, computed as the standard deviation divided by the mean, is 14.8% at 630 nm. This contrast exceeds the typical values obtained from ground-based observations; the speckle-reconstructed G-band images taken at the Dunn Solar Telescope, for example, show contrasts of 14.1% (Uitenbroek et al. 2007). Nevertheless, the agreement is reasonable because the observed values are degraded by instrumental effects (e.g., Danilovic et al. 2008; Wedemeyer-Böhm & Rouppe van der Voort 2009).

We have compared the temporally and spatially averaged intensity profiles with the corresponding ones in the Fourier Transform Spectrometer (FTS) atlas of the quiet Sun by Brault & Neckel (1987) and Neckel (1999, see Fig. 4). For the comparison, the simulated profiles have been first normalized to unity and then displaced in wavelength to correct for the solar gravitational redshift (see Lopresto et al. 1980). Also, an additional minor correction to the wavelength shift has been allowed to improve the fits. The figure shows that the widths of the synthetic profiles are very similar to those measured in the FTS atlas. However, the bottom panels indicate that the simulations do not completely reproduce the line asymmetries: the differences between observed and synthetic profiles are small (of the order of 2.5%), but not zero.

In summary, despite some differences between the FTS and the synthetic profiles, the simulations appear to explain the observations rather well. Therefore, we hope that they also produce sufficiently realistic polarization spectra, in particular with regard to their asymmetries.

\begin{figure} \par\includegraphics[width=9cm,clip]{13421Fig3.eps} \end{figure} Figure 3:

Continuum intensity map for the simulation snapshot depicted in Fig. 1. The wavelength is 630 nm.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13421Fig4.ps} \end{figure} Figure 4:

Average intensity profiles from the simulations (solid) and the FTS atlas (dashed), for the Fe I lines at 630.2 nm. The bottom panel shows the intensity differences (FTS - simulation) in percent.

Open with DEXTER

4 ME inversion of the Stokes profiles

To determine the vector magnetic field and the LOS velocity we perform ME inversions. Given the high spatial and temporal resolution of the simulations, the macroturbulence is set to zero and the filling factor to unity, i.e., the magnetic atmosphere is assumed to occupy the whole pixel (one-component model atmospheres). A total of nine quantities are determined from the inversion: the thermodynamic parameters S0, S1, $\eta_0$, $\Delta\lambda_{\rm D}$, and a (representing the intercept and the slope of the source function, the line-to-continuum opacity ratio, the Doppler width, and the damping parameter), the strength, inclination, and azimuth of the magnetic field vector (B, $\gamma$, and $\chi$), and the line-of-sight velocity ( $v_{\rm LOS}$). The Stokes profiles are taken from a single snapshot of the simulation. No noise is added to the spectra to better isolate the uncertainties due to the ME approximation.

The Fe I lines at 630 nm belong to the same multiplet and are formed under very similar thermodynamic conditions. Hence, we can reliably assume that the ME thermodynamic parameters are the same for both lines except for $\eta_0$. A simultaneous inversion with no extra free parameters is thus possible using a constant $\eta_0$ ratio and the same  $\Delta\lambda_{\rm D}$ and a values for the two lines. This is the strategy implemented in several ME codes (for details, see Orozco Suárez et al. 2010b).

We use the same initial guess model for all the pixels, stopping the inversion when convergence is achieved or 200 iterations have been performed. The initial model is given by S0=0.2, S1=0.8, $\eta_0=6.5$, $\Delta \lambda_{\rm D}=30$ mÅ, a=0.03, B=200 G, $\gamma=20$ \ensuremath{^\circ}, $\chi=20$ \ensuremath{^\circ}, and $v_{\rm LOS}=0.25$  ${\rm km}~{\rm s}^{-1}$.

5 Understanding ME inferences

\begin{figure} \par\includegraphics[width=17cm,clip]{13421Fig5.eps} \vspace*{2mm} \end{figure} Figure 5:

Examples of MHD atmospheres and simulated profiles (black) and ME fits (red) for three different pixels. Left panels: magnetic field strength, inclination, azimuth, and LOS velocity stratifications. The red horizontal lines indicate the inversion results. Right panels: Stokes I, Q, U and V profiles synthesized from the MHD simulations without noise (black) and ME fits (red). Cases  a)- c) correspond to (x,y) = (1.75, 1.08), (2.90, 2.58), and (1.67, 1.73) Mm in Figs. 6 and 7.

Open with DEXTER

The line asymmetries observed in the solar atmosphere imply that there are vertical gradients of the physical parameters, because the line wings trace relatively deep layers and the core is formed higher in the atmosphere. By contrast, the ME fits are strictly symmetric and deliver height-independent atmospheric parameters. Thus, it is important to verify that the ME model can indeed be used for the analysis of observations at very high spatial resolution.

Figure 5 shows the magnetic field strength, inclination, azimuth, and LOS velocity stratifications in three pixels of the simulation snapshot, labeled (a)-(c). The figure also displays the corresponding Stokes I, Q, U, and V profiles. The results of the ME inversions are overplotted in red. Case (a) shows symmetric Stokes profiles, in (b) the profiles are rather asymmetric, and (c) shows three-lobed Stokes V spectra together with anomalous linear polarization signals. (a) represents a strong field case and (b) and (c) correspond to weak fields. In the three examples the atmospheric quantities undergo large variations with optical depth.

The ME fit is good in (a) and worse in (b) and (c). Clearly, as the asymmetry level increases, the ME model has more difficulties to reproduce the profiles. The misfits are obvious in Stokes Q, U, and V, and less dramatic in Stokes I.

The models retrieved from the inversion are shown in the left panels of Fig. 5 (red lines). The height-independent ME parameters can be interpreted as averages of the actual stratifications weighted by the corresponding response functions (Westendorp Plaza et al. 1998). In general it is difficult to confirm this by simply looking at the atmospheric stratifications, but case (c) provides a particularly clear example. This case represents a pixel whose ME fit is not satisfactory. The analysis of the stratifications shows that the profiles arise from an atmosphere that has sharp discontinuities in field strength, inclination, azimuth, and LOS velocity, located more or less at the same optical depth. The two parts of the atmosphere separated by the discontinuity leave clear signatures in the emergent Stokes V spectra, to the point that the magnetic and kinematic properties of the plasma above and below the discontinuity can roughly be guessed from a simple inspection of the profiles: there is a weak field associated with small velocites and a stronger field showing large redshifts. Surprisingly, however, the ME model returned by the inversion seems to describe only the weak field.

To understand why this happens, it is important to realize that the inversion algorithm uses all the wavelength samples to determine the best-fit ME parameters. As mentioned before, different wavelength positions across the line trace different atmospheric layers. Thus, the ME inversion is forced to return average parameters along the LOS in order to fit the whole line profile reasonably well without any bias toward better fits in the core or the wings. This favors the weak field component of the atmosphere because it occupies most of the line-forming region in this particular example.

\begin{figure} \par\hspace*{1.5mm}\includegraphics[width=8cm,clip]{13421Fig6a.ps... ...ps}\hspace*{5mm} \includegraphics[width=7.85cm,clip]{13421Fig6d.ps} \end{figure} Figure 6:

Top: optical depths at which the inferred ME parameters coincide with the real magnetic field strength and LOS velocity stratifications (left and right, respectively). Bottom: magnetic field strengths retrieved from the ME inversion and normalized continuum intensities (left and right, respectively).

Open with DEXTER

Figure 5 demonstrates that the ME model parameters coincide with the real stratifications at specific optical depths. This allows us to define the effective ``height of formation'' of the ME parameters.

Formation-height maps have been calculated by taking the optical depth at which the stratification is closer to the inferred ME parameter. The formation heights are constrained to be in the range from $\log\tau=0$ to -2 because this interval includes most of the layers to which the Fe I lines are sensitive. When more than one value of the MHD stratification coincides with the corresponding ME parameter, we select the one located deeper in the atmosphere. The optical depth of the minimum (or maximum) of the MHD stratification is taken if the ME parameter is smaller (or larger) than all stratification values. Even then the formation height is not allowed to go outside of the interval from $\log\tau=0$ to -2.

Figure 6 shows the results for the magnetic field strength and the LOS velocity. For convenience, we also display the continuum image and the field strengths retrieved from the inversion. Different colors indicate different atmospheric layers. There are clear differences between the two maps: the granular centers are predominantly green ( $\log\tau\in[-0.7,-1.2]$) in the velocity map and green-red ( $\log\tau\in[-0.3,-0.7]$) in the field strength map, demonstrating that the ME inversion extracts the velocities from higher optical depths than the magnetic fields, at least in granules. The intergranular lanes tend to show blue colors in the two maps ( $\log\tau\in[-1.3,-1.7]$). The sharp red-yellow discontinuities observed at the border of granules in the velocity map have little meaning since they are a result of the way we estimate formation heights. These regions have zero velocities (Fig. 1) and also zero velocity gradients along the LOS, which makes our algorithm select layers close to the bottom of the photosphere (limited to $\log\tau=0$). Both maps exhibit significant pixel-to-pixel differences, especially the field-strength map. This ``noise'' is caused by MHD stratifications with many jumps in the vertical direction.

In summary, ME inversions provide results that cannot be assigned to a constant optical depth. The same parameter may show formation-height differences of up to 1-1.5 dex across the FOV. Also, the heights to which the ME parameters refer change depending on the parameter, as predicted by Del Toro Iniesta & Ruiz Cobo (1996) and Sánchez Almeida et al. (1996). In the case of the Fe I 630.2 nm lines, we find mean optical depths of $\log\tau = -1.0$ and -1.1 for the LOS velocity and the field strength, respectively. This includes granular and intergranular regions. If only intergranular regions are considered, the mean optical depths move $\sim$0.2 dex toward higher layers. The rms variation of the formation heights is 0.4 and 0.5 dex, respectively.

6 Inversion results

Below we compare the ME inversion results with the original MHD models. To that end we use the atmospheric parameters of the simulations at $\log\tau=-1$. This layer corresponds to the average formation height of the ME parameters. As such, it represents the best choice for a ``reference model''.

Figure 7 displays maps of the magnetic field strength, inclination, azimuth, and LOS velocity in the reference model (left column) and the models retrieved from the inversion (right column). To better visualize the details we only show a small area of about 9 Mm2. The strong resemblance between the reference parameters and the ME models is obvious: the shapes of the different structures are well reproduced and only small differences can be recognized. Sometimes the inversion yields bad results for the inclination and azimuth, but this happens mainly in areas with weak polarization signals.

From a visual inspection of the maps, one can say that the ME inversion is able to determine the magnetic field vector satisfactorily. Even structures with field strengths as low as 100 G are well recovered. To make more precise statements, Fig. 8 shows the parameters inferred from the fit vs. the MHD parameters at $\log\tau=-1$. These scatter plots allow us to estimate the uncertainties that can be expected from the use of the ME approximation, since no noise has been added to the profiles (Sect. 4).

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13421Fig7.eps} \end{figure} Figure 7:

From top to bottom: magnetic field strength, inclination, azimuth, and LOS velocity. The left column represents the MHD parameters at $\log\tau=-1$. The right column shows the results of the ME inversion of the Fe I lines at 630.2 nm.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13421Fig8.eps} \end{figure} Figure 8:

Scatter plots of the magnetic field strength, inclination, azimuth and LOS velocity inferred from the ME inversion vs. the MHD parameters at $\log\tau=-1$. The dashed lines represent one-to-one correspondences. The red dots are the mean values of the parameters in small, evenly-spaced bins along the X-axis. The blue lines represent the rms fluctuations of the parameters in those bins.

Open with DEXTER

As can be seen, the scatter is larger for the magnetic field inclination and azimuth. The mean values of the parameters[*] (red dots) show that the magnetic field strength is really close to that in the reference model from 0 to 500 G. For stronger fields the retrieved values are slightly underestimated, although the deviation does not exceed $\sim$250 G. The red lines indicate maximum rms fluctuations of about $\sim$80 G in the whole range of strengths. The inclination shows rms fluctuations smaller than 10 \ensuremath{^\circ} for vertical fields and 15 \ensuremath{^\circ} for inclined fields. The rms variation in the azimuth is about 15 \ensuremath{^\circ}. The LOS velocity panel shows that the retrieved velocity is some 200-300  ${\rm m}~{\rm s}^{-1}$ lower than the reference velocities for receding flows (intergranular lanes). The rms values are lower than $\sim$500  ${\rm m}~{\rm s}^{-1}$ in the full velocity range.

The scatter observed in the various panels of Fig. 8 originates from the use of ME model atmospheres (unable to fit asymmetric Stokes profiles) and the pixel-to-pixel variations of the formation height of the ME parameters, as explained in the previous section. The deviation of the ME field strengths from a one-to-one correspondence with the MHD models can easily be understood by looking at the top panel of Fig. 6 and recalling that we have chosen the atmospheric layer at $\log\tau=-1$ as a reference. In those spatial locations where the optical depth assigned to the retrieved ME parameter is smaller than the optical depth of the reference layer, the resulting field strength will ``apparently'' be underestimated. These spatial locations are associated with strong flux concentrations; in the MHD models they spread out with height, therefore we retrieve weaker fields.

The rms differences between the inversion results and the MHD models tell us how much a single ME parameter could deviate from the real value, but only if the mean differences are zero or close to zero. Non-zero mean differences indicate that systematic errors exist. For this reson, when the mean difference is larger than the standard deviation, the former should be preferred as a better estimate of the true error.

The choice of $\log\tau=-1$ for the reference model is appropriate because it produces the lower mean and rms values on average. To illustrate this, Fig. 9 represents histograms of the differences between the inferred parameters and the MHD model at three optical depths ($\log\tau$ = -0.5,-1,-1.5, coded in black, red, and green, respectively).

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13421Fig9.eps} \end{figure} Figure 9:

Normalized histograms of the differences between the inferred ME model parameters and the real ones taken at different optical depths.

Open with DEXTER

For the magnetic field strength, the histogram corresponding to $\log\tau=-1$ peaks around zero. The maximum shifts toward negative values when the inversion results are compared with deeper layers (fields are underestimated on average) and toward positive values when the comparison is made with higher layers (over-estimating the strength). The full width at half maximum (FWHM) of the distribution is about 30 G for $\log\tau=-1$, and increases up to $\sim$45 and $\sim$50 G for $\log\tau=-1.5$ and -0.5, respectively. These effects are less pronounced for the field inclination: the peaks of the histograms are located at zero and the FWHM varies from 6 \ensuremath{^\circ} ( $\log\tau=-1.5$) to $\sim$13 \ensuremath{^\circ}and $\sim$23 \ensuremath{^\circ} ( $\log\tau=-1$ and -0.5, respectively). The larger FWHMs originate from the extended wings of the distributions. The azimuth histogram does not vary when the comparison is made with different optical depths. Then the FWHM is about 20 \ensuremath{^\circ}.

The histograms of the LOS velocity differences show larger variations. The one corresponding to $\log\tau=-1$ has the smaller FWHM (${\sim}500$  ${\rm m}~{\rm s}^{-1}$). It also features a long tail toward negative values caused by pixels located in intergranular lanes. The asymmetry of the histograms around the location of the peaks changes dramatically when we compare the inversion results with different atmospheric layers. For instance, if the reference layer is taken at $\log\tau=-0.5$, the histogram is a clear combination of two different distributions, one representing granular centers (higher and narrower) and the other representing intergranular lanes (smaller in amplitude and broader).

7 Summary and conclusions

We have analyzed radiative MHD simulations of the quiet Sun. We have used them to synthesize Stokes line profiles in three different spectral regions (525.0, 617.3, and 630.2 nm). The comparison of the synthetic profiles with the FTS atlas suggests that the simulations quite satisfactorily describe the physical conditions of the solar photosphere, although the MHD models are slightly hotter than the HSRA around $\tau =1$.

After synthesizing the Stokes profiles, the applicability of ME inversions to high spatial resolution observations has been examined. We have considered the case of the Fe I lines at 630.2 nm. The analysis of the profiles by means of ME inversions has allowed us to characterize the uncertainties that can be expected from the ME approximation. For this reason, the synthetic profiles were not degraded by noise, instrumental effects, or spatial resolution.

The main limitation of ME inversions is that they provide constant atmospheric parameters, whereas the MHD models feature physical properties that change with height. This limitation means that ME models are unable to reproduce spectral line asymmetries. Consequently, the ME inferences cannot be assigned to a specific optical depth. Depending on the conditions of the atmosphere, the retrieved ME parameters sample different layers.

However, from a statistical point of view we conclude that ME inversions provide fair estimates of the physical conditions prevailing at $\log\tau \sim -1$. The rms uncertainty is smaller than 30 G for the magnetic field strength, 13 \ensuremath{^\circ} and 20 \ensuremath{^\circ} for the field inclination and azimuth, and 500  ${\rm m}~{\rm s}^{-1}$ for the LOS velocity. Thus, ME inversions are appropriate for statistical analyses of the solar photosphere. This be said, it is important to realize that the errors may be large for individual pixels, even if the best-fit profiles reproduce the observations satisfactorily (the field strength in case a of Fig. 5 is a good example of this).

Finally, we stress that the uncertainties associated with the ME approximation are larger than those due to photon noise (Del Toro Iniesta et al. 2010; Orozco Suárez et al. 2006). However, the noise has another undesirable effect: it hides the weaker polarization signals. This has not been considered in our study.

Acknowledgements
This work has been funded by the Spanish MICINN through projects AYA2009-14105-C06-06 (including European FEDER funds) and PCI2006-A7-0624, by Junta de Andalucía through project P07-TEP-2687, and by the Japan Society for the Promotion of Science.

References

  1. Anstee, S. D., & O'Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
  2. Barklem, P. S., Anstee, S. D., & O'Mara, B. J. 1998, PASA, 15, 336 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barklem, P. S., Piskunov, N., & O'Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  4. Beckers, J. M., & Brown, T. M. 1978, in Future solar optical observations needs and constraints, Proc. JOSO Workshop, ed. G. Godoli, 106, 189 [Google Scholar]
  5. Borrero, J. M., & Bellot Rubio, L. R. 2002, A&A, 385, 1056 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Borrero, J. M., Tomczyk, S., Norton, A., et al. 2007, Sol. Phys., 240, 177 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brault, J., & Neckel, H. 1987, Spectral atlas of solar absolute disk-averaged and disk-center intensity from 3290 to 12 510 Å (Hamburg: Hamburg Univ.) ftp.hs.uni-hamburg.de/pub/outgoing/FTS-atlas [Google Scholar]
  8. Brown, T. 1981, in Solar instrumentation: What's next?, ed. R. B. Dunn (NSO: Sunspot, NM), 150 [Google Scholar]
  9. Cameron, R., Schüssler, M., Vögler, A., & Zakharov, V. 2007, A&A, 474, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cauzzi, G., Smaldone, L. A., Balasubramaniam, K. S., & Keil, S. L. 1993, Sol. Phys., 146, 207 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cheung, M. C. M. 2006, Ph.D. Thesis, University of Göttingen, Germany, http://webdoc.sub.gwdg.de/diss/2006/cheung/ [Google Scholar]
  12. Cheung, M. C. M., Schüssler, M., & Moreno-Insertis, F. 2007, A&A, 467, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Collados, M. 2008, Proc. SPIE, 7012, 70120J [CrossRef] [Google Scholar]
  14. Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Del Toro Iniesta, J. C. 2003, Introduction to Spectropolarimetry (Cambridge, UK: Cambridge University Press) [Google Scholar]
  16. Del Toro Iniesta, J. C., & Ruiz Cobo, B. 1996, Sol. Phys., 164, 169 [NASA ADS] [CrossRef] [Google Scholar]
  17. Del Toro Iniesta, J. C., Tarbell, T. D., & Ruiz Cobo, B. 1994, ApJ, 436, 400 [NASA ADS] [CrossRef] [Google Scholar]
  18. Del Toro Iniesta, J. C., Orozco Suárez, D., & Bellot Rubio, L. R. 2010, ApJ, 711, 312 [NASA ADS] [CrossRef] [Google Scholar]
  19. Domínguez Cerdeña, I., Kneer, F., & Sánchez Almeida, J. 2003, ApJ, 582, L55 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fernandes, D. N. 1992, Ph.D. Thesis, Stanford University, USA [Google Scholar]
  21. Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
  22. Keller, C. U., Schüssler, M., Vögler, A., & Zakharov, V. 2004, ApJ, 607, L59 [NASA ADS] [CrossRef] [Google Scholar]
  23. Khomenko, E., & Collados, M. 2007a, ApJ, 659, 1726 [NASA ADS] [CrossRef] [Google Scholar]
  24. Khomenko, E., & Collados, M. 2007b, Mem. Soc. Ast. Ital., 78, 166 [NASA ADS] [Google Scholar]
  25. Khomenko, E. V., Shelyag, S., Solanki, S. K., & Vögler, A. 2005a, A&A, 442, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Khomenko, E. V., Martínez González, M. J., Collados, M., et al. 2005b, A&A, 436, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Landi Degl'Innocenti, E. 1992, in Solar Observations: Techniques and Interpretation, ed. F. Sanchez, M. Collados, & M. Vázquez (Cambridge: Cambridge University Press), 71 [Google Scholar]
  28. Landi Degl'Innocenti, E., & Landolfi, M. 2004, Polarization in spectral lines (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
  29. Lites, B. W., & Skumanich, A. 1990, ApJ, 348, 747 [NASA ADS] [CrossRef] [Google Scholar]
  30. Lites, B. W., Skumanich, A., Rees, D. E., & Murphy, G. A. 1988, ApJ, 330, 493 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lopresto, J. C., Chapman, R. D., & Sturgis, E. A. 1980, Sol. Phys., 66, 245 [NASA ADS] [CrossRef] [Google Scholar]
  32. Martínez Pillet, V., Bonet, J. A., Collados, M. V., et al. 2004, Proc. SPIE, 5487, 1152 [NASA ADS] [CrossRef] [Google Scholar]
  33. Norton, A. A., Graham, J. P., Ulrich, R. K., et al. 2006, Sol. Phys., 239, 69 [Google Scholar]
  34. Neckel, H. 1999, Sol. Phys., 184, 421 [NASA ADS] [CrossRef] [Google Scholar]
  35. Nordlund, A. 1982, A&A, 107, 1 [NASA ADS] [Google Scholar]
  36. Orozco Suárez, D., & Del Toro Iniesta, J. C. 2007, A&A, 462, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Orozco Suárez, D., Bellot Rubio, L. R., & Del Toro Iniesta, J. C. 2006, ASP Conf. Ser., 358, 197 [NASA ADS] [Google Scholar]
  38. Orozco Suárez, D., Bellot Rubio, L. R., & Del Toro Iniesta, J. C. 2007, ApJ, 662, L31 [NASA ADS] [CrossRef] [Google Scholar]
  39. Orozco Suárez, D., Bellot Rubio, L. R., Martínez Pillet, V., et al. 2010a, A&A, in press [arXiv:1006.5510] [Google Scholar]
  40. Orozco Suárez, D., Bellot Rubio, L. R., & Del Toro Iniesta, J. C. 2010b, A&A, 518, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
  42. Rachkovsky, D. N. 1962, Izv. KrymskoiAstrofiz. Obs., 27, 148 [Google Scholar]
  43. Rachkovsky, D. N. 1967, Izv. KrymskoiAstrofiz. Obs., 37, 56 [Google Scholar]
  44. Rees, D. E., & Semel, M. D. 1979, A&A, 74, 1 [NASA ADS] [Google Scholar]
  45. Rempel, M., Schüssler, M., & Knölker, M. 2009a, ApJ, 691, 640 [NASA ADS] [CrossRef] [Google Scholar]
  46. Rempel, M., Schüssler, M., Cameron, R. H., & Knölker, M. 2009b, Science, 325, 171 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  47. Ruiz Cobo, B., & Del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
  48. Sánchez Almeida, J., Ruiz Cobo, B., & Del Toro Iniesta, J. C. 1996, A&A, 314, 295 [NASA ADS] [Google Scholar]
  49. Scherrer, P. H., & SDO/HMI Team 2002, BAAS, 34, 735 [NASA ADS] [Google Scholar]
  50. Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
  51. Schüssler, M., & Vögler, A. 2006, ApJ, 641, L73 [NASA ADS] [CrossRef] [Google Scholar]
  52. Schüssler, M., & Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Schüssler, M., Shelyag, S., Berdyugina, S., Vögler, A., & Solanki, S. K. 2003, ApJ, 597, L173 [NASA ADS] [CrossRef] [Google Scholar]
  54. Semel, M. 1967, Ann. Astrophys., 30, 513 [Google Scholar]
  55. Shelyag, S., Schüssler, M., Solanki, S. K., Berdyugina, S. V., & Vögler, A. 2004, A&A, 427, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Shelyag, S., Schüssler, M., Solanki, S. K., & Vögler, A. 2007, A&A, 469, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Skumanich, A., & Lites, B. W. 1987, ApJ, 322, 473 [Google Scholar]
  58. Thévenin, F. 1989, A&AS, 77, 137 [Google Scholar]
  59. Uitenbroek, H. 2003, ApJ, 592, 1225 [NASA ADS] [CrossRef] [Google Scholar]
  60. Uitenbroek, H., Tritschler, A., & Rimmele, T. 2007, ApJ, 668, 586 [NASA ADS] [CrossRef] [Google Scholar]
  61. Unno, W. 1956, PASJ, 8, 108 [NASA ADS] [Google Scholar]
  62. Vögler, A. 2003, Ph.D. Thesis, University of Göttingen, Germany, http://webdoc.sub.gwdg.de/diss/2004/voegler/ [Google Scholar]
  63. Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Wagner, J., Rimmele, T. R., Keil, S., et al. 2006, Proc. SPIE, 6267, 9 [NASA ADS] [Google Scholar]
  65. Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Westendorp Plaza, C., Del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 1998, ApJ, 494, 453 [NASA ADS] [CrossRef] [Google Scholar]
  67. Wittmann, A. 1974, Sol. Phys., 35, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Online Material

\begin{figure} \par\includegraphics[width=17cm,clip]{13421FigApp.eps} \end{figure} Figure 10:

Scatter plots of the longitudinal magnetic field, Bz (first two rows), of the LOS velocity (third row), and of the magnetic field inclination (fourth row), as functions of their corresponding values in the MHD simulations at $\log\tau=-1$. The first column refers to results obtained with the 630.15 nm line; the second column displays results obtained with the 630.25 nm line; results with the two lines at the same time are shown in the third column. Color and line codes are the same as in Fig. 8. The mean value of the rms difference between the inferences and the simulations at $\log\tau=-1$ is given in the upper left corner of each panel.

Open with DEXTER

Appendix A: Milne-Eddington vs. classical proxies

The study of the solar atmosphere relies on the availability of precise magnetic fields and LOS velocities. Thus, one needs robust diagnostics in order to extract this information from the Stokes spectra. Classical methods such as tachogram techniques, the weak field approximation, and the center-of-gravity technique represent an alternative to Stokes inversions.

For some of these methods, the random errors induced by photon noise have been estimated not to exceed $\sim$20 m s-1 in the case of the LOS velocity or $\sim$10 G for the magnetic flux (see e.g., Scherrer et al. 1995; Scherrer & SDO/HMI Team 2002; Martínez Pillet 2007). However, like in the case of ME inversions, systematic uncertainties coming from the hypotheses underlying the technique are expected to be larger than the random errors themselves. A thorough study, similar to the one we have performed for the ME technique, is thus in order. We carry out such an analysis in this Appendix for the Fourier tachometer technique (Brown 1981; Beckers & Brown 1978)[*], the center-of-gravity method (Rees & Semel 1979; Semel 1967), and the weak field approximation (Landi Degl'Innocenti & Landolfi 2004; Landi degl'Innocenti 1992).

Both the center-of-gravity method and the weak-field approximation are applied to the whole profiles while the Fourier tachometer uses only four wavelength samples across the Stokes I profile (-9, -3, 3, and 9 pm). The center-of-gravity technique extracts the longitudinal component of the magnetic field, Bz, from the separation between the barycenters of the Stokes I+V and I-Vprofiles. Bz can also be obtained with the weak-field approximation through a proportionality between the Stokes V profile and the wavelength derivative of Stokes I. The transverse component of the field, in turn, is derived through a proportionality between Stokes L and the second wavelength derivative of Stokes I[*]. Regression fits are used between the circular (linear) polarization profiles and the first (second) derivatives of the intensity profiles for increased accuracy. Then, the magnetic inclination is obtained from the ratio between the transverse and longitudinal components of the field.

Figure 10 summarizes the results. Each column refers to a different set of lines: Fe I 630.15 nm (left), Fe I 630.25 nm (middle), and the two lines simultaneously considered (i.e., ME inversion; right). The labels on the ordinates are self-explanatory, while the abscissae give the values of the corresponding quantities at $\log\tau=-1$.

The less accurate method turns our to be the weak-field approximation: the inferred magnetic inclinations show larger rms fluctuations than the ME ones, and the longitudinal component of the field displays a clear saturation for fields stronger than 1000-1100 G when calculated with the line at 630.25 nm. For Bz values above 1 kG, the weak field inferences resulting from the 630.15 nm line seem to be closer to the MHD values at $\log\tau=-1$than the ME ones. Nevertheless, they present a larger scatter. The center-of-gravity method looks very robust and, indeed, it presents less scatter than ME inversions for the longitudinal field component and the LOS velocity (only the results from the 630.15 nm line are shown; the results for 630.15 nm are very similar). The good performance of the center-of-gravity method was noticed earlier by Cauzzi et al. (1993) and Uitenbroek (2003). Unfortunately, this technique does not provide information about the field inclination. The LOS velocities resulting from the tachometer are fairly comparable to those of the ME inversion. The scatter is similar in both cases.

In summary, the ME inversion seems to be the more complete and accurate technique, although none of the others can be discarded. In particular, a combination of the center-of-gravity technique for calculating Bz and  $v_{\rm LOS}$ along with the weak field approximation for the magnetic inclination may represent a suitable alternative which is much less expensive in terms of computing resources. It is important to note, however, that the results of our study are only valid when the magnetic field is spatially resolved. Further investigation is needed to check the applicability of these techniques when the field is unresolved. This additional investigation is important in view of the theoretical deviations predicted by Landi Degl'Innocenti & Landolfi (2004).

Footnotes

... Sun[*]
Figure 10 and appendix are only available in electronic form at http://www.aanda.org
... Telescope[*]
http://atst.nso.edu/
... Telescope[*]
http://www.iac.es/project/EST/
...(Orozco Suárez & Del Toro Iniesta 2007)[*]
MILOS is programmed in IDL and can be downloaded from our website, http://spg.iaa.es/download.asp
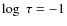
...$\log ~ \tau=-1$[*]
All optical depths refer to the continuum opacity at 500 nm.
... (PDFs)[*]
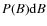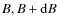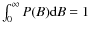The PDF is defined such that $P(B){\rm d}B$ is the probability of finding a magnetic field B in the interval [ $B,B+{\rm d}B$]. The integral of the PDF is unity, i.e.,  $\int_0^{\infty} P(B){\rm d}B = 1$.
... parameters[*]
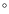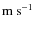The average values have been calculated by taking bins along the X-axis of size 28 G, 3 \ensuremath{^\circ}, and 115  ${\rm m}~{\rm s}^{-1}$, depending on the physical quantity.
...)[*]
We in fact use the formula proposed by Fernandes (1992).
...I[*]
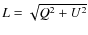Stokes L is the total linear polarization, $L=\sqrt{Q^2+U^2}$.

All Tables

Table 1:   Atomic parameters of the spectral lines.

All Figures

  \begin{figure} \par\mbox{\resizebox{8.5cm}{!}{\includegraphics{13421Fig1a.ps}}\r... ...1Fig1c.ps}}\resizebox{8.5cm}{!}{\includegraphics{13421Fig1d.ps}} }\end{figure} Figure 1:

Magnetic field strength, inclination, azimuth, and LOS velocity at $\tau =1$ in a simulation snapshot with $\langle B \rangle=140$ G. Negative velocities represent upflows.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13421Fig2a.ps}\vspace*{3mm} \includegraphics[width=8cm,clip]{13421Fig2b.ps} \end{figure} Figure 2:

Probability density functions for the magnetic field strength and field inclination at $\log\tau=-1$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13421Fig3.eps} \end{figure} Figure 3:

Continuum intensity map for the simulation snapshot depicted in Fig. 1. The wavelength is 630 nm.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13421Fig4.ps} \end{figure} Figure 4:

Average intensity profiles from the simulations (solid) and the FTS atlas (dashed), for the Fe I lines at 630.2 nm. The bottom panel shows the intensity differences (FTS - simulation) in percent.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{13421Fig5.eps} \vspace*{2mm} \end{figure} Figure 5:

Examples of MHD atmospheres and simulated profiles (black) and ME fits (red) for three different pixels. Left panels: magnetic field strength, inclination, azimuth, and LOS velocity stratifications. The red horizontal lines indicate the inversion results. Right panels: Stokes I, Q, U and V profiles synthesized from the MHD simulations without noise (black) and ME fits (red). Cases  a)- c) correspond to (x,y) = (1.75, 1.08), (2.90, 2.58), and (1.67, 1.73) Mm in Figs. 6 and 7.

Open with DEXTER
In the text

  \begin{figure} \par\hspace*{1.5mm}\includegraphics[width=8cm,clip]{13421Fig6a.ps... ...ps}\hspace*{5mm} \includegraphics[width=7.85cm,clip]{13421Fig6d.ps} \end{figure} Figure 6:

Top: optical depths at which the inferred ME parameters coincide with the real magnetic field strength and LOS velocity stratifications (left and right, respectively). Bottom: magnetic field strengths retrieved from the ME inversion and normalized continuum intensities (left and right, respectively).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13421Fig7.eps} \end{figure} Figure 7:

From top to bottom: magnetic field strength, inclination, azimuth, and LOS velocity. The left column represents the MHD parameters at $\log\tau=-1$. The right column shows the results of the ME inversion of the Fe I lines at 630.2 nm.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13421Fig8.eps} \end{figure} Figure 8:

Scatter plots of the magnetic field strength, inclination, azimuth and LOS velocity inferred from the ME inversion vs. the MHD parameters at $\log\tau=-1$. The dashed lines represent one-to-one correspondences. The red dots are the mean values of the parameters in small, evenly-spaced bins along the X-axis. The blue lines represent the rms fluctuations of the parameters in those bins.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13421Fig9.eps} \end{figure} Figure 9:

Normalized histograms of the differences between the inferred ME model parameters and the real ones taken at different optical depths.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{13421FigApp.eps} \end{figure} Figure 10:

Scatter plots of the longitudinal magnetic field, Bz (first two rows), of the LOS velocity (third row), and of the magnetic field inclination (fourth row), as functions of their corresponding values in the MHD simulations at $\log\tau=-1$. The first column refers to results obtained with the 630.15 nm line; the second column displays results obtained with the 630.25 nm line; results with the two lines at the same time are shown in the third column. Color and line codes are the same as in Fig. 8. The mean value of the rms difference between the inferences and the simulations at $\log\tau=-1$ is given in the upper left corner of each panel.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.