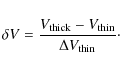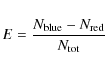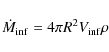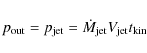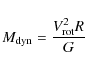| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 50 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014252 | |
| Published online | 06 August 2010 | |
A comparative study of high-mass cluster forming clumps![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
A. López-Sepulcre - R. Cesaroni - C. M. Walmsley
INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
Received 12 February 2010 / Accepted 21 April 2010
Abstract
Aims. We have searched for star formation activity (mainly infall and outflow signatures) in a sample of high-mass molecular clumps (M > 100 ![]() )
in different evolutionary stages and with a wide range of surface
densities, with the aim of looking for evolutionary trends and testing
observationally recent theoretical models which predict the need for a
minimum surface density to form high-mass stars.
)
in different evolutionary stages and with a wide range of surface
densities, with the aim of looking for evolutionary trends and testing
observationally recent theoretical models which predict the need for a
minimum surface density to form high-mass stars.
Methods. Our sample has been selected from single-dish
1.2 mm continuum surveys and is composed of 48 massive
molecular clumps, of which 29 are IR-loud and 19 are IR-dark.
Each of these has been mapped in the HCO+(1-0), HCN(1-0) and C18O(2-1)
transitions with the IRAM-30 m telescope on Pico Veleta (Spain).
We derive basic parameters (mass, momentum, kinetic energy) for the
clumps and their associated outflows and examine the HCO+(1-0) line profiles for evidence of infall or expansion.
Results. Molecular outflows have been detected in 75% of our targets from the presence of high-velocity wings in the HCO+(1-0) spectra. These are equally frequent and massive (between ![]() 1 and
1 and ![]() 100
100 ![]() )
in IR-dark and IR-loud clumps, implying similar levels of star
formation activity in both kinds of objects. A surface density
threshold at
)
in IR-dark and IR-loud clumps, implying similar levels of star
formation activity in both kinds of objects. A surface density
threshold at
![]() g cm-2
has been found above which the outflow detection rate increases
significantly and the outflows are on average more massive. The infall
detection rate in our sample is low, but significantly higher in the
IR-dark sub-sample. Our clump mass estimates using the mm dust
emission and C18O(2-1) are sensitive to the temperature, but assuming a value of 15 K for the IR-dark sub-sample, we find evidence that C18O is depleted by a factor
g cm-2
has been found above which the outflow detection rate increases
significantly and the outflows are on average more massive. The infall
detection rate in our sample is low, but significantly higher in the
IR-dark sub-sample. Our clump mass estimates using the mm dust
emission and C18O(2-1) are sensitive to the temperature, but assuming a value of 15 K for the IR-dark sub-sample, we find evidence that C18O is depleted by a factor ![]() 4.5. The HCO+(1-0)
to HCN(1-0) integrated intensity ratios measured reveal a greater
dispersion about the mean value in the IR-dark sub-sample than in the
IR-loud by a factor of about 5. We find that a considerable number
of IR-dark sources are self-absorbed in HCN(1-0) suggesting that
radiative transport effects in the ground state transitions have an
important influence on the integrated intensity ratio.
4.5. The HCO+(1-0)
to HCN(1-0) integrated intensity ratios measured reveal a greater
dispersion about the mean value in the IR-dark sub-sample than in the
IR-loud by a factor of about 5. We find that a considerable number
of IR-dark sources are self-absorbed in HCN(1-0) suggesting that
radiative transport effects in the ground state transitions have an
important influence on the integrated intensity ratio.
Conclusions. Our results indicate that, in terms of outflow
frequency and energetics, both IR-dark and IR-loud molecular clumps
present equivalent signatures of star formation activity, and that the
formation of high-mass stars requires sufficiently high clump surface
densities. The higher infall detection rate measured for the IR-dark
subsample suggests that these objects could be associated with the
onset of star formation.
Key words: stars: formation - ISM: clouds - ISM: jets and outflows - ISM: molecules
1 Introduction
High-mass stars have a deep impact on their environment, shaping the
physical and chemical properties of the interstellar medium. Despite
the key role they play in the evolution of galaxies, their formation
mechanism is still poorly understood. O-B stars reach the zero-age
main sequence still in the accretion phase, and the radiation pressure
they exert is expected to overcome the gravitational infall of
material, thus preventing the stars from accumulating masses greater
than ![]() 8
8 ![]() (Palla & Stahler 1993).
Several models have been proposed to explain the formation of high-mass
stars. These include accretion driven formation through massive disks
(e.g. Krumholz et al. 2009; McKee & Tan 2003; Yorke & Sonnhalter 2002; Keto et al. 2002), competitive accretion in dense clusters (Bonnell et al. 2004), and merging of low-mass protostars (Bonnell & Bate 2002).
(Palla & Stahler 1993).
Several models have been proposed to explain the formation of high-mass
stars. These include accretion driven formation through massive disks
(e.g. Krumholz et al. 2009; McKee & Tan 2003; Yorke & Sonnhalter 2002; Keto et al. 2002), competitive accretion in dense clusters (Bonnell et al. 2004), and merging of low-mass protostars (Bonnell & Bate 2002).
Table 1: Details of the 1.2 mm surveys from which our source sample has been selected.
From an observational point of view, the rareness of O-B stars and therefore the higher distances, their fast evolution towards the Zero-Age Main Sequence (ZAMS), and the high dust extinction involved complicate the study of high-mass star formation. Moreover, massive stars form in molecular clumps together with clusters of low-mass stars, causing considerable confusion in the observations. In spite of this, a number of deeply embedded massive disk/outflow systems (see Cesaroni et al. 2007) have been identified, lending support to the accretion models. However, the statistics is very poor and it is not clear whether this is the general mechanism to form high-mass stars. Furthermore, a detailed picture of the different evolutionary phases of massive star formation is still lacking.
In the last years, several (sub)millimetre continuum and line
surveys have been conducted towards high-mass star forming regions
(SFRs; e.g. Beuther et al. 2002a; Bronfman et al. 1996).
The targets of these surveys have been mostly molecular clumps selected
on the basis of their infrared (IR) spectral energy distributions
and/or maser emission, and are known to harbour one or more massive
young stellar objects (YSOs) which are already formed. These objects
will be referred to as IR-loud clumps hereafter. Nevertheless,
to understand the formation of massive stars, it is also
necessary to study the earliest phases of this process. These have been
suggested to take place within IR-dark clouds (IRDCs; Rathborne
et al. 2006), which are detected in absorption against the bright, diffuse mid-IR Galactic background (Perault et al. 1996; Egan et al. 1998). A limited number of surveys towards these regions in the (sub)millimetre continuum (Carey et al. 2000; Rathborne et al. 2006) and in several line transitions (Carey et al. 1998; Simon et al. 2006) have measured high densities (n>105 cm-3) and very low temperatures (T<20 K). They have sizes of several parsecs and typically contain a number of smaller condensations (![]() 0.5 pc)
detected as dust emission peaks at mm wavelengths within the more
diffuse and extended IRDC (Rathborne et al. 2006). Following the nomenclature proposed by Bergin & Tafalla (2007), we will refer to these condensations as IR-dark clumps. IRDCs are considered potential cluster and high-mass SFRs (see Menten et al. 2005, for a review), and are therefore excellent candidates for studying the initial conditions of massive star formation.
0.5 pc)
detected as dust emission peaks at mm wavelengths within the more
diffuse and extended IRDC (Rathborne et al. 2006). Following the nomenclature proposed by Bergin & Tafalla (2007), we will refer to these condensations as IR-dark clumps. IRDCs are considered potential cluster and high-mass SFRs (see Menten et al. 2005, for a review), and are therefore excellent candidates for studying the initial conditions of massive star formation.
In this context, we have conducted a survey with the IRAM-30 m
telescope towards a sample of parsec-sized high-mass molecular clumps
which include IR-dark as well as IR-loud clumps. The aim is to search
for signatures of star formation activity, mainly in the form of
outflow and infall, in order to obtain a comparative picture of
the evolutionary stages of both kinds of objects. An additional
motivation for this survey has been the claim by Krumholz & McKee (2008) that only clumps with surface densities greater than ![]() 0.7 g cm-2 can form stars more massive than 10
0.7 g cm-2 can form stars more massive than 10 ![]() .
Our sample contains sources with surface densities ranging from
.
Our sample contains sources with surface densities ranging from ![]() 0.1 to
0.1 to ![]() 10 g cm-2, and this allows us to check Krumholz & McKee's prediction observationally.
10 g cm-2, and this allows us to check Krumholz & McKee's prediction observationally.
In Sect. 2 we describe our sample and molecular line observations; maps and spectra are presented in Sect. 3; clump masses, outflow and infall parameters are derived in Sect. 4; in Sect. 5 we discuss our results; and finally, Sect. 6 summarises the main conclusions of this survey.
2 The sample and observations
2.1 The sample
The observed sample has been selected from several single-dish surveys at 1.2 mm and is composed of 49 high-mass molecular clumps, of which 18 are IR-dark clumps selected from the survey of Rathborne et al. (2006), and 31 are IR-loud clumps, selected from the surveys of Beuther et al. (2002a), Faúndez et al. (2004) and Hill et al. (2005). Table 1 summarises the main characteristics of these surveys.
For each source, we have computed the surface density, ![]() ,
from the clump mass, M, distance, d, and deconvolved angular diameter,
,
from the clump mass, M, distance, d, and deconvolved angular diameter, ![]() :
:
in accordance with the definition of
The selection criteria applied by us are the following:
- declination higher than
 ,
to be observable with the IRAM-30 m telescope;
,
to be observable with the IRAM-30 m telescope;
- mass larger than 100
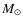 ,
to exclude low-mass star forming regions;
,
to exclude low-mass star forming regions;
- distance smaller than 4 kpc, to obtain clump angular
diameters greater than the IRAM-30 m beam at 3 mm, assuming
typical diameters of
 1 pc (
1 pc ( 25'').
25'').
Table 2: Observed sample.
Figure 1 presents a plot of surface density, ![]() ,
against clump mass, M,
for all the sources in our sample. IR-loud and IR-dark sources are
plotted in different panels. For both types of objects we find points
above and below the
,
against clump mass, M,
for all the sources in our sample. IR-loud and IR-dark sources are
plotted in different panels. For both types of objects we find points
above and below the ![]() threshold given by Krumholz & McKee (2008), although the majority lie below this threshold. It is worth noting, however, that our
threshold given by Krumholz & McKee (2008), although the majority lie below this threshold. It is worth noting, however, that our ![]() values represent an average across the whole clump, which may in reality contain smaller, denser cores.
values represent an average across the whole clump, which may in reality contain smaller, denser cores.
Ignoring the extra sources, three sources belonging to the sample of Beuther et al. (2002a) have masses below 100 ![]() .
The reason is that the mass of the clumps reported in such paper were derived using an dust opacity of
.
The reason is that the mass of the clumps reported in such paper were derived using an dust opacity of ![]() 0.2 cm2 g-1 (see the authors' erratum: Beuther et al. 2005). Therefore, we have re-calculated the masses from the continuum emission at 1.2 mm using a dust opacity of 1 cm2 g-1 (Ossenkopf & Henning 1994), which is that adopted in Rathborne et al. (2006), Faúndez et al. (2004) and Hill et al. (2005), in order to homogenise the whole sample. This has produced, for the sources selected from Beuther et al. (2002a), masses smaller than the original ones by a factor
0.2 cm2 g-1 (see the authors' erratum: Beuther et al. 2005). Therefore, we have re-calculated the masses from the continuum emission at 1.2 mm using a dust opacity of 1 cm2 g-1 (Ossenkopf & Henning 1994), which is that adopted in Rathborne et al. (2006), Faúndez et al. (2004) and Hill et al. (2005), in order to homogenise the whole sample. This has produced, for the sources selected from Beuther et al. (2002a), masses smaller than the original ones by a factor ![]() 5.
5.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{14252fg1.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg41.png)
|
Figure 1:
Surface density, |
| Open with DEXTER | |
2.2 Observations and data reduction
The IRAM-30 m telescope near Pico Veleta (Granada, Spain) was used
on August 4-8, 2008 to map our sample in the HCO+(1-0), HCN(1-0), and C18O(2-1) lines. The rest frequency, and the typical system temperature,
![]() ,
and 1
,
and 1![]() rms of the spectra are listed in Table 3.
rms of the spectra are listed in Table 3.
For each source, single pointing observations in wobbler mode were made
before proceeding with the On-The-Fly (OTF) mapping, in order to check
the presence of the HCO+(1-0)
and/or HCN(1-0) emission lines. Such spectra were obtained with a
wobbler throw of 120'' and an integration time of 4 min. The OTF
maps have sizes of 1' ![]() 1'
and were obtained with the single beam A100, B100, A230 and B230
receivers. All the lines were covered at both low and high spectral
resolution using a 1 MHz filterbank with 1024 channels and an
autocorrelator (VESPA). The former was split into 4 sections of
256 channels, used separately with each of the four receivers. The
angular resolution of the images is 29'' for the HCO+(1-0) and HCN(1-0) lines, and 12'' for C18O(2-1).
The OTF dump time was 2 s, and the sampling interval 4''.
Most of the maps were scanned twice, once along the RA and once
along the Dec, to avoid scanning effects on the resulting
images.
1'
and were obtained with the single beam A100, B100, A230 and B230
receivers. All the lines were covered at both low and high spectral
resolution using a 1 MHz filterbank with 1024 channels and an
autocorrelator (VESPA). The former was split into 4 sections of
256 channels, used separately with each of the four receivers. The
angular resolution of the images is 29'' for the HCO+(1-0) and HCN(1-0) lines, and 12'' for C18O(2-1).
The OTF dump time was 2 s, and the sampling interval 4''.
Most of the maps were scanned twice, once along the RA and once
along the Dec, to avoid scanning effects on the resulting
images.
Table 3: Observed lines.
The data were reduced using the programs CLASS and GREG of the GILDAS software package developed by the IRAM and the Observatoire de Grenoble. The spectra have been smoothed to a resolution of 0.5 km s-1 to improve the signal to noise ratio.
2.2.1 Emission at the OFF position
Six sources suffer from emission at the OFF position in the
OTF spectra. As a result, these spectra present an
artificial ``dip'' or absorption feature which can affect the numbers
obtained in the calculations. When possible, this effect has been
corrected or at least minimised by fitting a negative Gaussian to the
spectra at positions in the map where the real emission was below 3![]() ,
and subtracting such a Gaussian from each spectrum in the OTF map.
This method has not produced a good result in any case for the HCN(1-0)
line, where 3 Gaussians are needed, and thus the correction has
not been applied to this line. Table 4 lists the sources displaying emission at the OFF position, the line wing affected (B for blue, R for
red), the number of scans affected (1 or 2), and the lines
for which it was possible to apply a correction. Note that for
G24.33+0.1M2 and G35.39-0.3M4, only one of the two OTF scans are
affected by emission at the OFF position because the problem was
spotted in time during the observations, and the coordinates of the
OFF position were changed before the beginning of the second
OTF scan.
,
and subtracting such a Gaussian from each spectrum in the OTF map.
This method has not produced a good result in any case for the HCN(1-0)
line, where 3 Gaussians are needed, and thus the correction has
not been applied to this line. Table 4 lists the sources displaying emission at the OFF position, the line wing affected (B for blue, R for
red), the number of scans affected (1 or 2), and the lines
for which it was possible to apply a correction. Note that for
G24.33+0.1M2 and G35.39-0.3M4, only one of the two OTF scans are
affected by emission at the OFF position because the problem was
spotted in time during the observations, and the coordinates of the
OFF position were changed before the beginning of the second
OTF scan.
Table 4: Sources affected by emission at OFF position.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{14252fg2.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg43.png)
|
Figure 2: Example of emission at OFF for the HCO+(1-0) spectrum in 05358+3543. Black: spectrum without correction; the line displays an artificial absorption at -20 km s-1. Green: the same spectrum after having applied the Gaussian correction (see text). |
| Open with DEXTER | |
Figure 2 illustrates the problem and the solution. It shows the average HCO+(1-0) spectrum of 05358+3543 before applying any correction (black). The line is absorbed at ![]() -20 km s-1
due to the presence of emission at the OFF position. In green the
corrected average spectrum is shown, and the absorption feature has
disappeared.
-20 km s-1
due to the presence of emission at the OFF position. In green the
corrected average spectrum is shown, and the absorption feature has
disappeared.
2.2.2 Wrong systemic velocity
There are five IR-dark sources for which the systemic velocity differs considerably (![]() 50 km s-1) from that reported in Rathborne et al. (2006, based on 13CO(1-0) data). This can be seen by comparing the value of
50 km s-1) from that reported in Rathborne et al. (2006, based on 13CO(1-0) data). This can be seen by comparing the value of
![]() in Table 2 (centre velocity used for the observations) to that given in Table A.2
(velocity obtained from a Gaussian fit to the line, see below).
Unfortunately, for two of these sources, namely G24.33+0.1M4 and
G24.60+0.1M2, the C18O(2-1) line falls outside the velocity
limits of the VESPA unit used in the observations. Therefore, in these
two cases, the 1 MHz resolution C18O(2-1) spectra have been used to obtain maps and derive the parameters presented in this paper.
in Table 2 (centre velocity used for the observations) to that given in Table A.2
(velocity obtained from a Gaussian fit to the line, see below).
Unfortunately, for two of these sources, namely G24.33+0.1M4 and
G24.60+0.1M2, the C18O(2-1) line falls outside the velocity
limits of the VESPA unit used in the observations. Therefore, in these
two cases, the 1 MHz resolution C18O(2-1) spectra have been used to obtain maps and derive the parameters presented in this paper.
3 Maps and spectra
3.1 Clump maps and spectra
The three lines were detected in wobbler mode with signal to noise
ratios greater than 5 towards all of our targets. OTF line
integrated maps are presented in Fig. B.1, where the (0, 0) position corresponds to the coordinates listed in Table 2 (i.e. the 1.2 mm dust emission peak). The 1![]() rms value, first contour level, and contour step of each map are listed in Table A.1. Note that in some cases, especially in IR-dark sources where the emission is weaker, the C18O(2-1)
clump is poorly defined and the map is noisy. This is to be expected,
since the observations were conducted during summer and their quality
is very susceptible to the atmospheric conditions at this wavelength
(1.2 mm). There are two sources, namely G25.04-0.2M4 and
22570+5912_2, for which the C18O(2-1) maps are not presented
because, due to their high noise, they display no clear emission of the
clump. Therefore, these will not be considered in the calculations
derived from the C18O(2-1) emission, although their respective map 1
rms value, first contour level, and contour step of each map are listed in Table A.1. Note that in some cases, especially in IR-dark sources where the emission is weaker, the C18O(2-1)
clump is poorly defined and the map is noisy. This is to be expected,
since the observations were conducted during summer and their quality
is very susceptible to the atmospheric conditions at this wavelength
(1.2 mm). There are two sources, namely G25.04-0.2M4 and
22570+5912_2, for which the C18O(2-1) maps are not presented
because, due to their high noise, they display no clear emission of the
clump. Therefore, these will not be considered in the calculations
derived from the C18O(2-1) emission, although their respective map 1![]() rms values are shown in Table A.1 The HCO+(1-0)
and HCN(1-0) integrated maps have lower angular resolution, but are
less noisy and the distribution of the emission is fairly clear for the
whole sample.
rms values are shown in Table A.1 The HCO+(1-0)
and HCN(1-0) integrated maps have lower angular resolution, but are
less noisy and the distribution of the emission is fairly clear for the
whole sample.
The dashed contour in each map of Fig. B.1 marks the half power level of the integrated emission. The black solid contour denotes an arbitrarily defined clump region which has been used to obtain average spectra and, in the case of C18O(2-1), to derive clump masses (see below): in many cases this corresponds to the half power contour (dashed), but it may vary between the 40% and the 80% level depending on the intensity and morphology of the source. In some cases where the C18O(2-1) emission is weak and patchy, the corresponding HCO+(1-0) or HCN(1-0) clump region contour has been assigned to them, as indicated in the figure caption.
In general, for the IR-loud sub-sample, the sizes and shapes of the IR-loud HCO+(1-0) and HCN(1-0) clumps are very similar, and the peak positions of the HCO+(1-0), HCN(1-0) and C18O(2-1) maps are the same within ![]() 10'',
with few exceptions such as G28.28-0.35 and 20332+4124. The same cannot
be said for the IR-dark sub-sample, where it is more common to find
that the clump sizes, shapes, and/or positions are different in the HCO+(1-0) and HCN(1-0) maps (e.g. G19.27M1 and M2), and the C18O(2-1) emission may trace a different region with respect to HCO+(1-0) and HCN(1-0) (e.g. G24.08M2, G24.60M1). This will be discussed in more detail in Sect. 5.
10'',
with few exceptions such as G28.28-0.35 and 20332+4124. The same cannot
be said for the IR-dark sub-sample, where it is more common to find
that the clump sizes, shapes, and/or positions are different in the HCO+(1-0) and HCN(1-0) maps (e.g. G19.27M1 and M2), and the C18O(2-1) emission may trace a different region with respect to HCO+(1-0) and HCN(1-0) (e.g. G24.08M2, G24.60M1). This will be discussed in more detail in Sect. 5.
We have found some sources for which the peak of the emission is offset
with respect to the centre of the map (and thus the 1.2 mm dust
emission peak position) by more than ![]() 20''. In particular, three cases, each of which shows two clearly separated components in the integrated maps (Fig. B.1), need to be mentioned here:
20''. In particular, three cases, each of which shows two clearly separated components in the integrated maps (Fig. B.1), need to be mentioned here:
- 1.
- The maps of G192.59-0.04 contain two components: the northern one coincides in coordinates with G192.58-0.04, and the southern one with G192.60-0.05. Therefore this source does not have HCO+(1-0), HCN(1-0) or C18O(2-1) counterparts, and will not be considered hereafter.
- 2.
- 18507+0121 corresponds to the southern component; the northern one is actually the IR-dark clump G34.43+0.2M1.
- 3.
- 22570+5912_2 corresponds to the south-western component; the north-eastern clump corresponds to 22570+ 5912_1.
Figure B.2 presents the HCO+(1-0), HCN(1-0) and C18O(2-1) spectra for all the clumps. Each of these has been obtained by averaging the line emission over the clump region (black contour in Fig. B.1). The C18O(2-1) spectra of the two sources mentioned above for which no C18O map is shown in Fig. B.1 are also presented in Fig. B.2 because, although the maps are useless to define the shape and emission distribution of the clump, the C18O(2-1) integrated emission averaged over the whole map results in a visible line from which the systemic velocity of the clump can be measured. We note that the HCN(1-0) line has three hyperfine (HF) components, with an expected proportion between the central, red and blue component intensities of 5:3:1, respectively (Townes & Schawlow 1955), although this is not necessarily what one sees in real spectra, due to optical depth and/or non-LTE effects (Kwan & Scoville 1975).
Many of the HCO+(1-0) and HCN(1-0) spectra display self-absorbed profiles and thus the optically thinner C18O(2-1) line has been used to define the systemic velocity of the clumps. Table A.2 presents the results from the Gaussian fit to the C18O(2-1) spectrum at the peak coordinates of each integrated map. Analogous Gaussian fits have been performed to the HCO+(1-0) spectra, masking the self-absorption and high-velocity wings when present. The values are listed in Table A.3. Note that the peak coordinates in the C18O(2-1) and the HCO+(1-0) integrated maps of a given source may not coincide with each other exactly. In these cases the line parameters in Tables A.2 and A.3 correspond to slightly different positions in the maps. For those sources where the C18O(2-1) emission is too weak or without C18O(2-1) map in Fig. B.1, the Gaussian fit has been made at the HCO+(1-0) peak coordinates for both the C18O(2-1) and the HCO+(1-0) lines, as specified in the table. In general, the peak velocity agrees within 1 km s-1 between the HCO+(1-0) and the C18O(2-1) lines.
As mentioned in Sect. 2.2.2, five IR-dark sources have velocities which differ considerably (by ![]() 50 km s-1) from the ones reported by Rathborne et al. (2006) and used during the observations. For these, and for other three IR-dark clumps for which the discrepancy is
50 km s-1) from the ones reported by Rathborne et al. (2006) and used during the observations. For these, and for other three IR-dark clumps for which the discrepancy is ![]() 15 km s-1, a new kinematic distance has been recalculated using the Galaxy rotation curve of Brand (1986), which assumes a solar Galactocentric distance of 8.5 kpc. The resulting near and far distances (
15 km s-1, a new kinematic distance has been recalculated using the Galaxy rotation curve of Brand (1986), which assumes a solar Galactocentric distance of 8.5 kpc. The resulting near and far distances (
![]() and
and
![]() ,
respectively) are listed in Table 5, together with the old distance,
,
respectively) are listed in Table 5, together with the old distance,
![]() .
Note that the new distances are all greater than 4 kpc and
therefore fall outside our distance selection criterium. For the
purposes of this paper, we will adopt
.
Note that the new distances are all greater than 4 kpc and
therefore fall outside our distance selection criterium. For the
purposes of this paper, we will adopt
![]() ,
because IR-dark clumps are absorption features against the mid-IR
Galactic background emission and therefore it is likely that they are
located at the near distance. This change in distance implies different
masses from the ones presented in Table 2,
and will be taken into account in the calculations and figures in the
remainder of this paper. By contrast, the surface density,
,
because IR-dark clumps are absorption features against the mid-IR
Galactic background emission and therefore it is likely that they are
located at the near distance. This change in distance implies different
masses from the ones presented in Table 2,
and will be taken into account in the calculations and figures in the
remainder of this paper. By contrast, the surface density, ![]() ,
remains unchanged, so in practice the affected points in Fig. 1 shift horizontally towards the right.
,
remains unchanged, so in practice the affected points in Fig. 1 shift horizontally towards the right.
Table 5: New distances computed for eight IR-dark clumps.
3.2 Outflow maps
The presence of molecular outflows has been assessed by searching for high-velocity wings in the HCO+(1-0) spectrum that results from averaging all the spectra within the clump region (Fig. B.2). It is worth noting that the use of HCO+ implies we are tracing the outflow in the near vicinity (the envelope) of the source driving it. With other molecules such as the more commonly used CO, one is more sensitive to the outer, lower density, high-velocity outflowing material (see Sect. 5.2.3).
Without distinguishing here between IR-dark and IR-loud
sources, or between high and low clump surface density, we have
identified a total of 19 sources with clear high-velocity HCO+(1-0) wings (extending up to ![]() 10 km s-1
or more with respect to the line peak velocity) indicative of outflows.
Out of the remaining 29 sources, 17 are also considered to be
driving molecular outflows because, although the HCO+(1-0)
wings are not as extended, the blue- and red-shifted lobes are
spatially separated. This is compatible with a bipolar outflow oriented
almost perpendicular to the line-of-sight (l.o.s.).
10 km s-1
or more with respect to the line peak velocity) indicative of outflows.
Out of the remaining 29 sources, 17 are also considered to be
driving molecular outflows because, although the HCO+(1-0)
wings are not as extended, the blue- and red-shifted lobes are
spatially separated. This is compatible with a bipolar outflow oriented
almost perpendicular to the line-of-sight (l.o.s.).
Adding all up, an outflow detection rate of 75% is obtained for our sample. Outflow maps are presented in Fig. B.3. In these maps, the blue and red wing emission of the HCO+(1-0) line (solid and dashed contours, respectively) are superimposed on either the C18O(2-1) integrated emission or the HCO+(1-0) integrated emission when the former is too noisy (grey scale). In a few cases, despite the presence of extended HCO+(1-0) wings, there is no clear outflow bipolarity in the maps (e.g. 23139+5939). This could be explained by an outflow directed close to the l.o.s., or by confusion due to the superposition of many outflows.
4 Properties derived from the C18O(2-1) and HCO+(1-0) lines
4.1 Clump mass estimates
From the emission integrated under the C18O(2-1) line we have estimated the molecular mass contained within the clump region of each C18O(2-1) map presented in Fig. B.1 (
![]() ,
Table A.4, Col. 5). A C18O abundance dependent on the Galactocentric distance,
,
Table A.4, Col. 5). A C18O abundance dependent on the Galactocentric distance,
![]() ,
has been assumed (Wilson & Rood 1994):
,
has been assumed (Wilson & Rood 1994):
We have adopted [CO]/[H2] = 10-4, and an excitation temperature,
An estimate of the virial mass,
![]() ,
of each of these clumps, has been obtained from the C18O(2-1) line
,
of each of these clumps, has been obtained from the C18O(2-1) line ![]() (Table A.2), and from the angular diameter of the C18O clump, D (Table A.4), using Eq. (3) of MacLaren et al. (1988),
assuming uniform density accross the clump. Given the variety of
morphologies displayed by our sample sources, the major source of
uncertainty in the derivation of this quantity is the clump size. We
estimate an average uncertainty of 50% on the clump sizes, and
this same error applies to the virial mass determination. The resulting
values are also listed in Table A.4.
For comparison, this table presents also the mass of the clumps
derived from the dust emission at 1.2 mm. For the eight
sources listed in Table 5, this has been modified to account for the new distance.
(Table A.2), and from the angular diameter of the C18O clump, D (Table A.4), using Eq. (3) of MacLaren et al. (1988),
assuming uniform density accross the clump. Given the variety of
morphologies displayed by our sample sources, the major source of
uncertainty in the derivation of this quantity is the clump size. We
estimate an average uncertainty of 50% on the clump sizes, and
this same error applies to the virial mass determination. The resulting
values are also listed in Table A.4.
For comparison, this table presents also the mass of the clumps
derived from the dust emission at 1.2 mm. For the eight
sources listed in Table 5, this has been modified to account for the new distance.
The issue of clump masses will be covered in more detail in Sect. 5.1.
4.2 Derivation of outflow parameters
A comparison between the optically thick HCO+(1-0) line and the optically thinner C18O(2-1)
is helpful, not only to define the clump systemic velocity and to
discriminate between self-absorption and multiple components in the
former, but also to define the HCO+ line wings.
For each source with an outflow detection, the low-velocity limits
have generally been defined where the C18O(2-1) line intensity falls below 2![]() .
In a few cases where also the C18O(2-1) line displays non-Gaussian extended wings, the beginning of these on the spectra of Fig. B.2 has been chosen as low-velocity limits. The high-velocity limits have been chosen where the HCO+(1-0) line intensity falls below 2
.
In a few cases where also the C18O(2-1) line displays non-Gaussian extended wings, the beginning of these on the spectra of Fig. B.2 has been chosen as low-velocity limits. The high-velocity limits have been chosen where the HCO+(1-0) line intensity falls below 2![]() .
The outflow velocity ranges thus defined (
.
The outflow velocity ranges thus defined (
![]() and
and
![]() ,
respectively) are presented in Table A.5 and have been used both to obtain the outflow maps in Fig. B.3 and to compute the outflow parameters.
,
respectively) are presented in Table A.5 and have been used both to obtain the outflow maps in Fig. B.3 and to compute the outflow parameters.
Table A.5 also lists, for the blue and red emission, the outflow velocities,
![]() and
and
![]() ,
and the deconvolved lobe sizes,
,
and the deconvolved lobe sizes, ![]() and
and ![]() .
By outflow velocity we mean the difference between the high-velocity limit of the outflow velocity range
.
By outflow velocity we mean the difference between the high-velocity limit of the outflow velocity range ![]() ,
and the systemic velocity,
,
and the systemic velocity,
![]() ,
of the C18O(2-1) clump (Table A.2). Typical values of this quantity are
,
of the C18O(2-1) clump (Table A.2). Typical values of this quantity are ![]() 10 km s-1,
although higher values have also been found. The most extreme case is
18316-0602, with blue and red wings that extend
beyond 20 km s-1.
10 km s-1,
although higher values have also been found. The most extreme case is
18316-0602, with blue and red wings that extend
beyond 20 km s-1.
Following the procedure described in López-Sepulcre et al. (2009; Eqs. (4)-(6)), the outflow mass, momentum and energy of the outflow (
![]() ,
,
![]() and
and
![]() ,
respectively) have been derived from the emission integrated under
,
respectively) have been derived from the emission integrated under
![]() and
and
![]() ,
and spatially integrated over the area defined by the 5
,
and spatially integrated over the area defined by the 5![]() contour
level of the corresponding outflow lobe. Note that in many cases the
maps are not large enough to cover all such area.
As a result, part of the outflow emission is lost, but in no
case is this loss significant because the blue and red lobe half power
contours are always within the limits of the map. Therefore, the effect
on the numbers derived is negligible. In the calculations, we have
adopted a HCO+ abundance relative to H2 of 5
contour
level of the corresponding outflow lobe. Note that in many cases the
maps are not large enough to cover all such area.
As a result, part of the outflow emission is lost, but in no
case is this loss significant because the blue and red lobe half power
contours are always within the limits of the map. Therefore, the effect
on the numbers derived is negligible. In the calculations, we have
adopted a HCO+ abundance relative to H2 of 5 ![]() 10-9 (Irvine et al. 1987) and
10-9 (Irvine et al. 1987) and
![]() K (the numbers increase by a factor 1.5 and 2 for
K (the numbers increase by a factor 1.5 and 2 for
![]() and 30 K, respectively), and the emission in the line wings has
been assumed optically thin. We derive a median outflow mass and energy
of 10
and 30 K, respectively), and the emission in the line wings has
been assumed optically thin. We derive a median outflow mass and energy
of 10 ![]() and 0.21
and 0.21 ![]() 1046 erg, respectively.
1046 erg, respectively.
A kinematic timescale has been estimated for each outflow lobe from
![]() ,
where r is the deconvolved projected spatial size of the lobe, and
,
where r is the deconvolved projected spatial size of the lobe, and
![]() is the outflow velocity defined above. The average of the numbers
obtained for the blue and red lobes produces the kinematic timescale
presented in Table A.6, typically a few 104 yr. For G24.33+0.1M1 only the red wing emission has been considered to derive
is the outflow velocity defined above. The average of the numbers
obtained for the blue and red lobes produces the kinematic timescale
presented in Table A.6, typically a few 104 yr. For G24.33+0.1M1 only the red wing emission has been considered to derive
![]() because the blue wing is blended with an absorption feature due to the
emission at the OFF position, as pointed out in
Sect. 2.2.1. and Tables A.5 and A.6. We note that, as a consequence, the outflow parameters derived for this source are lower limits.
because the blue wing is blended with an absorption feature due to the
emission at the OFF position, as pointed out in
Sect. 2.2.1. and Tables A.5 and A.6. We note that, as a consequence, the outflow parameters derived for this source are lower limits.
Finally, the outflow parameters
![]() (mass loss rate),
(mass loss rate),
![]() (mechanical force), and
(mechanical force), and
![]() (mechanical luminosity) have been determined.
(mechanical luminosity) have been determined.
All the outflow parameters derived as described here are listed in Table A.6. With the exception of the outflow mass,
![]() ,
these are subject to an uncertainty due to the lack of knowledge of the
outflow axis inclination with respect to the l.o.s., i. For an inclination of 45
,
these are subject to an uncertainty due to the lack of knowledge of the
outflow axis inclination with respect to the l.o.s., i. For an inclination of 45![]() the outflow parameters do not change much:
the outflow parameters do not change much:
![]() and
and ![]() ,
for instance, remain the same, while E and
,
for instance, remain the same, while E and
![]() increase by a factor 2. Quantities which depend strongly on the outflow velocity, such as E and
increase by a factor 2. Quantities which depend strongly on the outflow velocity, such as E and
![]() ,
are most affected by the inclination: for
,
are most affected by the inclination: for
![]() these increase by about an order of magnitude or more. Table 6
lists the factors by which each parameter must be multiplied to correct
for several inclinations. Clearly this is, together with the HCO+ abundance, one of the major sources of uncertainty in the determination of outflow parameters.
these increase by about an order of magnitude or more. Table 6
lists the factors by which each parameter must be multiplied to correct
for several inclinations. Clearly this is, together with the HCO+ abundance, one of the major sources of uncertainty in the determination of outflow parameters.
Table 6: Factors to multiply by the projected outflow-related parameters, as a function of outflow inclination, i.
4.3 Identification of infall candidates: the asymmetry parameter 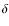 V
V
The profiles of optically thick lines arising from regions undergoing
infall have stronger blue-shifted emission than red-shifted emission,
provided the excitation temperature decreases outwards from the centre
of the region (e.g. Anglada et al. 1987; Zhou 1992).
In order to analyse quantitatively the presence of infall in our
sample sources, we have used the nondimensional asymmetry
parameter ![]() ,
defined by Mardones et al. (1997) as the velocity difference between the peaks of an optically thick and an optically thin line, in units of the
,
defined by Mardones et al. (1997) as the velocity difference between the peaks of an optically thick and an optically thin line, in units of the ![]() of the optically thin line:
of the optically thin line:
Our optically thin and thick lines are C18O(2-1) and HCO+(1-0), respectively. To compute this quantity, we have first fitted a Gaussian to the C18O(2-1) line at the peak coordinates of the HCO+(1-0) integrated map (Col. 2 of Table A.7) to obtain
By definition, negative values of ![]() correspond to blue asymmetric HCO+(1-0) line profiles and therefore potential infall candidates. Positive values of
correspond to blue asymmetric HCO+(1-0) line profiles and therefore potential infall candidates. Positive values of ![]() correspond
to red asymmetric profiles, which could be interpreted as expansion. We
have considered the line asymmetry to be significant only when
correspond
to red asymmetric profiles, which could be interpreted as expansion. We
have considered the line asymmetry to be significant only when
![]() ,
where
,
where
![]() is the typical error we derive for the asymmetry parameter
is the typical error we derive for the asymmetry parameter ![]() .
Therefore, we define as infall candidates those sources for which
.
Therefore, we define as infall candidates those sources for which
![]() ,
labelled B in Table A.7. On the other hand, sources with
,
labelled B in Table A.7. On the other hand, sources with
![]() display a significantly red asymmetry and are labelled R in Table A.7.
display a significantly red asymmetry and are labelled R in Table A.7.
5 Discussion
5.1 Clump masses
Figure 3 presents a plot of virial mass,
![]() ,
against clump mass derived from the emission under the C18O(2-1) line,
,
against clump mass derived from the emission under the C18O(2-1) line,
![]() (see Sect. 4.1), with IR-dark and IR-loud sources (filled
circles) plotted in different panels. The error bars on the bottom
right corner of each panel represent the uncertainties of the
quantities plotted according to what is described in Sect. 4.1.
For comparison, also the high-mass molecular clumps studied by
Hofner et al. (2000) in the C17O molecule
are plotted with the IR-loud sources (crosses) in this figure. While
most of the sources of the Hofner et al. sample have larger clump
masses than virial masses, the opposite holds for the majority of our
IR-loud sources. This feature is even more pronounced for the IR-dark
sub-sample. Indeed, we find that the virial masses are greater than the
clump masses by an average factor of 4.7 for the IR-dark clumps,
and only 2.2 for the IR-loud.
(see Sect. 4.1), with IR-dark and IR-loud sources (filled
circles) plotted in different panels. The error bars on the bottom
right corner of each panel represent the uncertainties of the
quantities plotted according to what is described in Sect. 4.1.
For comparison, also the high-mass molecular clumps studied by
Hofner et al. (2000) in the C17O molecule
are plotted with the IR-loud sources (crosses) in this figure. While
most of the sources of the Hofner et al. sample have larger clump
masses than virial masses, the opposite holds for the majority of our
IR-loud sources. This feature is even more pronounced for the IR-dark
sub-sample. Indeed, we find that the virial masses are greater than the
clump masses by an average factor of 4.7 for the IR-dark clumps,
and only 2.2 for the IR-loud.
As described in Sect. 4.1, our clump masses,
![]() ,
have been derived from the emission under the C18O(2-1)
line assuming it is optically thin. If this is not the case, our
masses have been underestimated. For example, accounting for an
optical depth of 1.9 in the C18O(2-1) line of the IR-loud clumps would result in a horizontal shift of all the IR-loud points towards the
,
have been derived from the emission under the C18O(2-1)
line assuming it is optically thin. If this is not the case, our
masses have been underestimated. For example, accounting for an
optical depth of 1.9 in the C18O(2-1) line of the IR-loud clumps would result in a horizontal shift of all the IR-loud points towards the
![]() line and thus to a situation in which the clumps are virialised. By contrast, one would need an optical depth of
line and thus to a situation in which the clumps are virialised. By contrast, one would need an optical depth of ![]() 4.8 to virialise the IR-dark subsample. This would indicate that the C18O(2-1) emission is optically thicker for the IR-dark clumps than for the IR-loud, by a factor of
4.8 to virialise the IR-dark subsample. This would indicate that the C18O(2-1) emission is optically thicker for the IR-dark clumps than for the IR-loud, by a factor of ![]() 2.5.
However, there is no particular reason to expect higher optical depths
in IR-dark clumps, especially in a sample like ours, where both IR-dark
and IR-loud sources cover the same range of column densities.
2.5.
However, there is no particular reason to expect higher optical depths
in IR-dark clumps, especially in a sample like ours, where both IR-dark
and IR-loud sources cover the same range of column densities.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg3.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg78.png)
|
Figure 3:
Virial mass,
|
| Open with DEXTER | |
Figure 4 shows the mass derived from the dust continuum emission at 1.2 mm,
![]() ,
plotted against
,
plotted against
![]() .
In spite of the large scattering, it is clear that the points representing IR-loud sources cluster around the
.
In spite of the large scattering, it is clear that the points representing IR-loud sources cluster around the
![]() line,
while almost all the points representing IR-dark clumps lie above and
to the left of this line, i.e., the region where
line,
while almost all the points representing IR-dark clumps lie above and
to the left of this line, i.e., the region where
![]() .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg4.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg81.png)
|
Figure 4:
Clump mass derived from the continuum emission at 1.2 mm,
|
| Open with DEXTER | |
We will now explore three possibilities that may explain this result.
The first one is an overestimate of the clump mass and size obtained
from the mm continuum as opposed to that obtained from the C18O(2-1)
emission. A higher sensitivity in the continuum at 1.2 mm may
allow detection of more extended emission and therefore larger sizes
and masses. However, once more, this should have the same effect in
both the IR-loud and IR-dark subsamples, while we find a systematic
difference between the two:
![]() is smaller than
is smaller than
![]() only for the IR-dark clumps. Furthermore, we find that the ``dust'' sizes are similar to the ``C18O'' sizes for our whole sample, independently of the presence of IR emission. This can also be inferred from Fig. 5,
where, to get rid of any effect due to the different sizes measured in
the two tracers, we have plotted the surface density derived from the
dust emission at 1.2 mm,
only for the IR-dark clumps. Furthermore, we find that the ``dust'' sizes are similar to the ``C18O'' sizes for our whole sample, independently of the presence of IR emission. This can also be inferred from Fig. 5,
where, to get rid of any effect due to the different sizes measured in
the two tracers, we have plotted the surface density derived from the
dust emission at 1.2 mm,
![]() (the same as
(the same as ![]() in Fig. 1), as a function of the surface density derived from the C18O(2-1) emission,
in Fig. 1), as a function of the surface density derived from the C18O(2-1) emission,
![]() .
The same behaviour found in Fig. 4 is present in this plot:
.
The same behaviour found in Fig. 4 is present in this plot:
![]() is systematically greater than
is systematically greater than
![]() only for IR-dark sources. Therefore, this result cannot be explained by mm continuum clumps having larger measured sizes than C18O clumps.
only for IR-dark sources. Therefore, this result cannot be explained by mm continuum clumps having larger measured sizes than C18O clumps.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg82.png)
|
Figure 5:
Surface density derived from the continuum emission at 1.2 mm,
|
| Open with DEXTER | |
A second and more plausible explanation is a lower C18O abundance in IR-dark clumps. From the ratio between the column densities obtained from the C18O(2-1)
and the dust continuum emission at 1.2 mm, we measure a median
depletion factor of 4.5 for our IR-dark subsample. This agrees
with what reported by Fontani et al. (2006), who found CO was depleted in their sample of IR-dark clumps by a median factor of ![]() 3. They argue that the low temperatures present in IR-dark clumps may cause CO to be trapped in H2O ice on dust grains, leading to lower CO abundances. The fact that we have assumed the same C18O abundance
for both IR-loud and IR-dark clumps, without taking into account that
this molecule may be depleted in the latter, may lead to underestimated
IR-dark clump masses. A C18O underabundance also explains why the C18O emission is weaker and the C18O clumps do not show a clear morphology in many of our IR-dark clumps.
3. They argue that the low temperatures present in IR-dark clumps may cause CO to be trapped in H2O ice on dust grains, leading to lower CO abundances. The fact that we have assumed the same C18O abundance
for both IR-loud and IR-dark clumps, without taking into account that
this molecule may be depleted in the latter, may lead to underestimated
IR-dark clump masses. A C18O underabundance also explains why the C18O emission is weaker and the C18O clumps do not show a clear morphology in many of our IR-dark clumps.
There is a third important factor that needs to be examined, and this
is temperature. We have assumed a low excitation temperature (
![]() K) for all the IR-dark clumps when computing
K) for all the IR-dark clumps when computing
![]() ,
which is also the dust temperature adopted by Rathborne et al. (2006)
to derive the clump masses from the continuum emission at 1.2 mm.
It is likely that this temperature has been underestimated at
least in some cases, which results in an overestimated
,
which is also the dust temperature adopted by Rathborne et al. (2006)
to derive the clump masses from the continuum emission at 1.2 mm.
It is likely that this temperature has been underestimated at
least in some cases, which results in an overestimated
![]() and an underestimated
and an underestimated
![]() .
.
As an example, let us consider one of the most massive IR-dark clumps in our sample: G34.43+0.2M1. Rathborne et al. (2008) estimate a dust temperature of 34 K for this source. Table 7 lists the values of
![]() and
and
![]() of G34.43M1 for temperatures of 15 and 34 K. When using 34 K instead of 15 K,
of G34.43M1 for temperatures of 15 and 34 K. When using 34 K instead of 15 K,
![]() becomes smaller by a factor
becomes smaller by a factor ![]() 2, and
2, and
![]() increases by 25%, approximately. Although at 34 K
increases by 25%, approximately. Although at 34 K
![]() still exceeds
still exceeds
![]() by a factor
by a factor ![]() 5,
the discrepancy is not as large as at 15 K. This example
demonstrates how the choice of temperature can affect the calculation
of clump masses, and that in the case of our IR-dark clumps, an
underestimate of
5,
the discrepancy is not as large as at 15 K. This example
demonstrates how the choice of temperature can affect the calculation
of clump masses, and that in the case of our IR-dark clumps, an
underestimate of
![]() and
and
![]() may in part explain the appearance of Fig. 4, at least for some of the sources (e.g. G34.43M1, G24.60M2).
may in part explain the appearance of Fig. 4, at least for some of the sources (e.g. G34.43M1, G24.60M2).
Table 7:
![]() and
and
![]() derived for G24.33+0.1M1 for two different temperatures.
derived for G24.33+0.1M1 for two different temperatures.
In conclusion, we believe that the behaviour of the IR-dark sub-sample in Fig. 3 is not real, but results from either an overestimate in the C18O abundance when computing
![]() ,
or an underestimate in the excitation and dust temperatures
adopted (or a combination of both). While the choice of
temperature affects both
,
or an underestimate in the excitation and dust temperatures
adopted (or a combination of both). While the choice of
temperature affects both
![]() and
and
![]() ,
only
,
only
![]() is affected by the uncertainties on the C18O abundance. Therefore, we conclude that the clump mass computed from the 1.2 mm continuum emission,
is affected by the uncertainties on the C18O abundance. Therefore, we conclude that the clump mass computed from the 1.2 mm continuum emission,
![]() ,
is more reliable than the one obtained from the C18O(2-1) emission,
,
is more reliable than the one obtained from the C18O(2-1) emission,
![]() ,
and we will thus make use of the former in Sects. 5.2 and 5.3.
,
and we will thus make use of the former in Sects. 5.2 and 5.3.
Indeed, if we plot
![]() ,
against
,
against
![]() instead of
instead of
![]() (Fig. 6), we obtain similar trends for both IR-dark and IR-loud clumps. In this case
(Fig. 6), we obtain similar trends for both IR-dark and IR-loud clumps. In this case
![]() and
and
![]() are
comparable for our sources, and thus our clumps are on average
virialised. An interesting feature of this figure, if one
considers both IR-loud and IR-dark sources, including those of Hofner
et al., is that
are
comparable for our sources, and thus our clumps are on average
virialised. An interesting feature of this figure, if one
considers both IR-loud and IR-dark sources, including those of Hofner
et al., is that
![]() generally exceeds the virial mass for
generally exceeds the virial mass for
![]() ,
while this is not so evident for smaller masses. This suggests that the
most massive molecular clumps are more unstable under gravitational
collapse than the lowest mass clumps, unless the former are
magnetically supported. According to Eq. (8) of Fontani
et al. (2002; see also McKee et al. 1993), magnetic fields of 1 or a few mG are sufficient to stabilise the most massive clumps (
,
while this is not so evident for smaller masses. This suggests that the
most massive molecular clumps are more unstable under gravitational
collapse than the lowest mass clumps, unless the former are
magnetically supported. According to Eq. (8) of Fontani
et al. (2002; see also McKee et al. 1993), magnetic fields of 1 or a few mG are sufficient to stabilise the most massive clumps (
![]() ). However, bear in mind that Hofner et al. used the less abundant C17O molecule,
and it is therefore likely that they were tracing a more internal
region of the clump undergoing collapse. The same consideration applies
also to Fig. 3.
). However, bear in mind that Hofner et al. used the less abundant C17O molecule,
and it is therefore likely that they were tracing a more internal
region of the clump undergoing collapse. The same consideration applies
also to Fig. 3.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg86.png)
|
Figure 6:
Virial mass,
|
| Open with DEXTER | |
5.2 Molecular outflows
5.2.1 Outflow detection rate
As mentioned in Sect. 3.2, a total outflow detection rate of 75% has been measured in our sample. If we distinguish between IR-dark and IR-loud clumps, very similar detection rates are found, of 79% and 73%, respectively.
In Fig. 7 we show a plot of surface density against mass,
![]() ,
in which outflow detections are represented by filled circles, and
non-detections by open circles. IR-dark and IR-loud clumps are plotted
in two different panels, as in Fig. 1. We remind the reader that, unlike Fig. 1, the eight IR-dark sources listed in Table 5
are plotted here with the corrected mass values according to the new
distances. This plot illustrates the high outflow detection rate
measured for both IR-dark and IR-loud sources, a finding which
indicates that star formation takes place actively in both kinds of
objects. The most remarkable result is that we can define an empirical
outflow threshold at
,
in which outflow detections are represented by filled circles, and
non-detections by open circles. IR-dark and IR-loud clumps are plotted
in two different panels, as in Fig. 1. We remind the reader that, unlike Fig. 1, the eight IR-dark sources listed in Table 5
are plotted here with the corrected mass values according to the new
distances. This plot illustrates the high outflow detection rate
measured for both IR-dark and IR-loud sources, a finding which
indicates that star formation takes place actively in both kinds of
objects. The most remarkable result is that we can define an empirical
outflow threshold at
![]() g cm-2
under which the outflow detection rate falls considerably, both for
IR-dark and IR-loud sources. Indeed, the detection rate for both
sub-samples is is of 100% above
g cm-2
under which the outflow detection rate falls considerably, both for
IR-dark and IR-loud sources. Indeed, the detection rate for both
sub-samples is is of 100% above
![]() g cm-2, and 56% below it. This threshold is marked with a dashed line in Fig. 7 under the dotted line at
g cm-2, and 56% below it. This threshold is marked with a dashed line in Fig. 7 under the dotted line at
![]() g cm-2, which defines the theoretical prediction made by Krumholz & McKee (2008).
g cm-2, which defines the theoretical prediction made by Krumholz & McKee (2008).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{14252fg7.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg88.png)
|
Figure 7:
Molecular outflow detections for the IR-dark (top) and IR-loud (bottom) sub-samples. Plot of surface density, |
| Open with DEXTER | |
The histogram in Fig. 8 also evidences the increase of the outflow detection rate with surface density, starting from only a 30% for sources with
![]() g cm-2, and growing rapidly towards saturation at 100% for the highest
g cm-2, and growing rapidly towards saturation at 100% for the highest ![]() values.
This implies that sufficiently high surface densities are required for
active star formation to occur. For the sample under study,
values.
This implies that sufficiently high surface densities are required for
active star formation to occur. For the sample under study,
![]() g cm-2 is found to be high enough for this. This value is smaller than the theoretical
g cm-2 is found to be high enough for this. This value is smaller than the theoretical
![]() g cm-2 required for high-mass star formation according to Krumholz & McKee (2008).
However, parsec-sized molecular clumps like the ones in our sample are
not likely to be homogeneous, but may contain a number of smaller
fragments, not resolved by our single-dish observations, which may be
massive and dense enough to satisfy Krumholz & McKee's prediction.
Moreover, one must evaluate the outflow masses to find out whether the
driving sources are indeed high-mass YSOs (see below).
In short, our empirical
g cm-2 required for high-mass star formation according to Krumholz & McKee (2008).
However, parsec-sized molecular clumps like the ones in our sample are
not likely to be homogeneous, but may contain a number of smaller
fragments, not resolved by our single-dish observations, which may be
massive and dense enough to satisfy Krumholz & McKee's prediction.
Moreover, one must evaluate the outflow masses to find out whether the
driving sources are indeed high-mass YSOs (see below).
In short, our empirical
![]() g cm-2
threshold supports Krumholz & McKee's idea and gives a measure of
the minimum surface density that a molecular clump needs to undergo
effective star or cluster formation.
g cm-2
threshold supports Krumholz & McKee's idea and gives a measure of
the minimum surface density that a molecular clump needs to undergo
effective star or cluster formation.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{14252fg8.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg90.png)
|
Figure 8: Molecular outflow detection rate as a function of surface density for the whole sample. |
| Open with DEXTER | |
5.2.2 Outflow parameters against clump mass and surface density
To investigate how the outflow parameters vary with clump mass, we have plotted the outflow mass,
![]() ,
momentum,
,
momentum,
![]() ,
and kinetic energy,
,
and kinetic energy,
![]() against clump mass,
against clump mass,
![]() (Fig. 9).
Our sample sources are represented by circles, open if they are
IR-loud, and filled if they are IR-dark. Different colours have been
used to mark different ranges of surface densities:
(Fig. 9).
Our sample sources are represented by circles, open if they are
IR-loud, and filled if they are IR-dark. Different colours have been
used to mark different ranges of surface densities:
![]() g cm-2 (black),
g cm-2 (black), ![]() between 0.3 and 0.7 g cm-2 (green) and
between 0.3 and 0.7 g cm-2 (green) and
![]() g cm-2 (blue). For comparison, the sample sources from the outflow surveys conducted by López-Sepulcre et al. (2009; black crosses) and Beuther et al. (2002b;
red crosses) are also plotted. For the latter, only the sources
with no distance ambiguity, and which do not overlap our sample are
represented. For consistency with these two surveys,
g cm-2 (blue). For comparison, the sample sources from the outflow surveys conducted by López-Sepulcre et al. (2009; black crosses) and Beuther et al. (2002b;
red crosses) are also plotted. For the latter, only the sources
with no distance ambiguity, and which do not overlap our sample are
represented. For consistency with these two surveys,
![]() K
has been assumed to calculate the outflow parameters, and therefore the
corresponding outflow parameter values presented in Table A.6, obtained for
K
has been assumed to calculate the outflow parameters, and therefore the
corresponding outflow parameter values presented in Table A.6, obtained for
![]() K, have been multiplied by a factor 2 (see Sect. 4.2). The error bars on the top-left corners of the
K, have been multiplied by a factor 2 (see Sect. 4.2). The error bars on the top-left corners of the
![]() and
and
![]() plots correspond to a correction for an arbitrary inclination of 60
plots correspond to a correction for an arbitrary inclination of 60
![]() (see Table 6).
(see Table 6).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg9.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg93.png)
|
Figure 9:
Outflow mass (bottom), total outflow momentum (middle) and outflow kinetic energy (top)
against mass of the clump derived from the dust emission. Filled
circles represent IR-dark sources, while open circles represent IR-loud
sources. Different colours are used to mark sources with
|
| Open with DEXTER | |
A general look at the
![]() plot reveals that our detected molecular outflows are massive, with masses ranging between a few and
plot reveals that our detected molecular outflows are massive, with masses ranging between a few and ![]() 100
100 ![]() ,
similar to the ones detected by Beuther et al. (2002b).
This suggests that the sources powering them are also massive, although
high-resolution imaging is needed to confirm this and to test for
possible multiplicity of the outflows. The behaviour of the points
indicate that more massive clumps drive more massive outflows. This
trend is also evidenced by the dotted line, which represents our least
squares fit to all the points plotted:
,
similar to the ones detected by Beuther et al. (2002b).
This suggests that the sources powering them are also massive, although
high-resolution imaging is needed to confirm this and to test for
possible multiplicity of the outflows. The behaviour of the points
indicate that more massive clumps drive more massive outflows. This
trend is also evidenced by the dotted line, which represents our least
squares fit to all the points plotted:
![]() .
The dashed line, on the other hand, corresponds to the relation
.
The dashed line, on the other hand, corresponds to the relation
![]() ,
which is the best fit to the Beuther et al. data, and represents
also a fair fit to both our data and those from López-Sepulcre
et al. (2009).
The good correlation between outflow mass and clump mass is a
remarkable finding, and the fact that it holds for several orders of
magnitude suggests that the character of star formation, in this case
in the form of outflows, remains unchanged within a wide range of clump
masses, including the most massive ones. This result is also reflected
in Fig. 10, where to avoid distance dependency, we have plotted
,
which is the best fit to the Beuther et al. data, and represents
also a fair fit to both our data and those from López-Sepulcre
et al. (2009).
The good correlation between outflow mass and clump mass is a
remarkable finding, and the fact that it holds for several orders of
magnitude suggests that the character of star formation, in this case
in the form of outflows, remains unchanged within a wide range of clump
masses, including the most massive ones. This result is also reflected
in Fig. 10, where to avoid distance dependency, we have plotted
![]() against
against
![]() .
It is worth noting in this plot the upper limit of
.
It is worth noting in this plot the upper limit of
![]() ,
an indicator that up to about 20% of the clump mass can be
affected by molecular outflows. This suggests that outflow feedback can
be important in the process of high-mass star/cluster formation, which
supports the theoretical results obtained by Wang et al. (2010).
,
an indicator that up to about 20% of the clump mass can be
affected by molecular outflows. This suggests that outflow feedback can
be important in the process of high-mass star/cluster formation, which
supports the theoretical results obtained by Wang et al. (2010).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg10.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg98.png)
|
Figure 10:
Ratio between outflow mass and clump mass,
|
| Open with DEXTER | |
If we focus only on our sources in Fig. 9,
we find that IR-dark and IR-loud clumps contain equally massive
outflows, with no apparent segregation between the two types of
objects. Furthermore, no clear difference in outflow mass can be
seen among the three different surface density ranges. Overall, this
plot suggests that our outflow-bearing sources may be treated as a
homogeneous sample in which the outflow mass increases with the mass of
the clump, and neither the surface density nor the membership of the
IR-dark or IR-loud subsample influence strongly the mass of the
molecular outflows. Similar trends are found in the
![]() and
and
![]() plots.
plots.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg11.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg102.png)
|
Figure 11:
Outflow mass loss rate (bottom), mechanical force of the outflow (middle) and mechanical luminosity of the outflow (top)
against mass of the clump derived from the dust emission. Filled
circles represent IR-dark sources, while open circles represent IR-loud
sources. Different colours are used to mark sources with
|
| Open with DEXTER | |
For completeness, also the outflow parameters
![]() ,
,
![]() ,
and
,
and
![]() ,
plotted against the mass of the clump are shown in Fig. 11. The same symbology as in Fig. 9 applies here. The error bars correspond to a correction for an outflow inclination varying from 30
,
plotted against the mass of the clump are shown in Fig. 11. The same symbology as in Fig. 9 applies here. The error bars correspond to a correction for an outflow inclination varying from 30
![]() (lower error bar) to 60
(lower error bar) to 60
![]() (upper error bar). The behaviour of the points is very similar to that in Fig. 11.
(upper error bar). The behaviour of the points is very similar to that in Fig. 11.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg12.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg103.png)
|
Figure 12:
Outflow mass against surface density of the clump. IR-dark sources are
represented by filled circles, and IR-loud by open circles. The two
vertical dashed lines mark the theoretical (
|
| Open with DEXTER | |
In order to examine in more detail the role of the surface density on the outflow parameters, we present in Fig. 12 a plot of outflow mass,
![]() ,
as a function of surface density,
,
as a function of surface density, ![]() .
As expected from Figs. 9 and 11, the points are very scattered and they do not show a trend as clear as the one found for
.
As expected from Figs. 9 and 11, the points are very scattered and they do not show a trend as clear as the one found for
![]() .
However, for almost all the sources with
.
However, for almost all the sources with
![]() g cm-2, the outflow masses are
g cm-2, the outflow masses are ![]() 10
10 ![]() ,
whereas below 0.3 g cm-2
the presence of lower mass outflows is more common (about 30%).
Therefore, while low surface density clumps may drive outflows with a
wide range of masses, from
,
whereas below 0.3 g cm-2
the presence of lower mass outflows is more common (about 30%).
Therefore, while low surface density clumps may drive outflows with a
wide range of masses, from ![]() 1 to
1 to ![]() 100
100 ![]() ,
high surface density clumps favour only the most massive outflows in
this range. Again, no distinction is found between IR-dark and
IR-loud sources, and thus we can conclude that IR-loud and IR-dark
clumps are very similar in terms of outflow frequency, mass and
energetics.
,
high surface density clumps favour only the most massive outflows in
this range. Again, no distinction is found between IR-dark and
IR-loud sources, and thus we can conclude that IR-loud and IR-dark
clumps are very similar in terms of outflow frequency, mass and
energetics.
5.2.3 Comparison with a CO survey
The present survey has made use of the HCO+(1-0) line to
derive outflow parameters, instead of the more commonly used
CO molecule. This section is aimed at comparing our outflow
parameters to those derived from the CO(2-1) line by Beuther
et al. (2002b) for eight IR-loud clumps that are common to both studies. Table 8 lists the sources as well as their respective
![]() ,
,
![]() ,
and
,
and
![]() derived by us and by Beuther et al. We note that the values presented have been computed for
derived by us and by Beuther et al. We note that the values presented have been computed for
![]() K, which is the excitation temperature assumed by Beuther et al. (2002b).
K, which is the excitation temperature assumed by Beuther et al. (2002b).
Table 8: Comparison of outflow mass, momentum and kinetic energy between this study and that of Beuther et al. (2002b).
On average, the outflow mass, momentum, and kinetic energy obtained by
Beuther et al. are greater than the ones derived by us by a
factor 1.5, 5, and 17, respectively. In other
words, the discrepancy is larger the more the parameter depends on
the velocity. This finding is illustrated in Fig. 13,
which presents a comparative plot for each of the three outflow
parameters under analysis. The outflow masses are similar for the two
surveys, although Beuther et al. report slightly higher values.
This may be caused in part by the fact that we, unlike Beuther
et al., have assumed optically thin conditions and thus obtain
lower limit values to the outflow mass. An overestimate of the
assumed HCO+ abundance by a factor 1.5 is another
possible explanation for the discrepancy. The greater differences found
for the outflow momentum and kinetic energy are most likely explained
by the more extended wings of the CO(2-1) line with respect to the HCO+(1-0) line.
![]() and especially
and especially
![]() are more sensitive to the higher velocity channels of the line wings,
and so it is expected that a line with broader wings will produce higer
values of moment and kinetic energy of the outflow.
are more sensitive to the higher velocity channels of the line wings,
and so it is expected that a line with broader wings will produce higer
values of moment and kinetic energy of the outflow.
In summary, while we obtain similar outflow masses, the less extended outflow wings of the HCO+(1-0) line produces underestimated outflow momenta and kinetic energies. Even though this effect can be noticed in the upper panel of Fig. 9, where the points representing our sources appear to ``sink'' slightly with respect to the points corresponding to the other two surveys, the overall trend of the plot remains unchanged, and so do the conlusions drawn in the previous sections.
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{14252fg13.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg112.png)
|
Figure 13:
Comparison between our derived outflow mass,
|
| Open with DEXTER | |
5.3 Infall
According to the definition of infall candidate given in
Sect. 4.3, the infall detection rate in our sample is
low: 13% for IR-loud clumps, and 32% for IR-dark clumps.
Unlike the outflow detections, there seems to be no correlation at all
between the detection of infall and the surface density, ![]() ,
of the clump. All the infall candidates except one (G34.77-0.6M2),
present also molecular outflows. The low infall detection rate measured
is illustrated in Fig. 14, where we present a plot of surface density against clump mass,
,
of the clump. All the infall candidates except one (G34.77-0.6M2),
present also molecular outflows. The low infall detection rate measured
is illustrated in Fig. 14, where we present a plot of surface density against clump mass, ![]() vs.
vs.
![]() ,
in which sources with a significantly blue asymmetric HCO+(1-0)
line (i.e., infall candidates) are represented as blue circles,
and sources with significant red asymmetry are represented as red
circles. We find that blue asymmetries are less abundant than red
asymmetries, which implies that either clear large-scale infall
signatures are difficult to detect, or this phase has a relatively
short time scale.
,
in which sources with a significantly blue asymmetric HCO+(1-0)
line (i.e., infall candidates) are represented as blue circles,
and sources with significant red asymmetry are represented as red
circles. We find that blue asymmetries are less abundant than red
asymmetries, which implies that either clear large-scale infall
signatures are difficult to detect, or this phase has a relatively
short time scale.
The low percentage of infall candidates we obtain may be understood if one imagines an evolutionary picture starting with a prestellar infalling clump that subsequently forms a cluster of YSOs, leading to the appearance of winds and outflows which can gradually become more dominant at large scales and cause the velocity field of the region to become more chaotic with time. As a result, the optically thick molecular lines such as HCO+(1-0) are less likely to display a clear infall profile as star formation activity inside the clump evolves.
Despite the low overall infall detection rate, this is significantly higher in the IR-dark subsample, which suggests, according to the picture mentioned above, that these are more likely to be associated with the onset of star formation and may thus represent an early evolutionary stage of star formation with respect to IR-loud clumps.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg14.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg113.png)
|
Figure 14:
HCO+(1-0) line asymmetries for the IR-dark (top) and IR-loud (bottom) sub-samples. Plot of surface density, |
| Open with DEXTER | |
A parameter which provides a quantitative idea of whether a sample
is dominated by blue or red asymmetries is the blue excess, E, defined by Mardones et al. (1997) as:
where
5.3.1 Comparison with another survey
To try to understand the disagreement between our E values and those obtained by the above cited authors, we have made a comparative analysis of the derived ![]() for nine of our IR-loud sources which also belong to the sample studied by Fuller et al. (2005). The sources and their respective
for nine of our IR-loud sources which also belong to the sample studied by Fuller et al. (2005). The sources and their respective ![]() values are listed in Table 9. In addition, Fig. 15 presents a comparative plot of each pair of
values are listed in Table 9. In addition, Fig. 15 presents a comparative plot of each pair of ![]() values, where the limits of the significant blue and red asymmetry regions have been marked at
values, where the limits of the significant blue and red asymmetry regions have been marked at
![]() with dot-dashed lines. We have assumed a typical error of 0.05 on
with dot-dashed lines. We have assumed a typical error of 0.05 on ![]() for
the sources of Fuller et al., as reported by the authors. We
find there is good agreement between our numbers and those derived by
Fuller et al., in the sense that, within the errors, all the
points fall inside one of the three quadrants intersected by the
equality line (dashed), and therefore have the same type of line
asymmetry. This analysis leads to the conclusion that, at least for the
IR-loud sub-sample, our
for
the sources of Fuller et al., as reported by the authors. We
find there is good agreement between our numbers and those derived by
Fuller et al., in the sense that, within the errors, all the
points fall inside one of the three quadrants intersected by the
equality line (dashed), and therefore have the same type of line
asymmetry. This analysis leads to the conclusion that, at least for the
IR-loud sub-sample, our ![]() values
are as reliable as those obtained in similar surveys. Consequently, our
low percentage of infall candidates among IR-loud clumps is to be
regarded as valid as the high percentages reported in other surveys.
values
are as reliable as those obtained in similar surveys. Consequently, our
low percentage of infall candidates among IR-loud clumps is to be
regarded as valid as the high percentages reported in other surveys.
Table 9:
Comparison between our ![]() and the one derived by Fuller et al. (2005) from HCO+(1-0).
and the one derived by Fuller et al. (2005) from HCO+(1-0).
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{14252fg15.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg123.png)
|
Figure 15:
Comparison of the asymmetry parameter, |
| Open with DEXTER | |
5.3.2 Asymmetry parameter distribution
As expected from Fig. 14, the histogram in Fig. 16
reveals a higher population of red asymmetric sources with respect to
the one with blue asymmetries. For the IR-loud clumps, there is a
central peak of sources without significant asymmetry, a feature
reported also by Fuller et al. (2005).
However, this central peak is not present for the IR-dark sub-sample,
which in addition displays more scattering and reaches more extreme
values of ![]() .
It is not straightforward to interpret this interesting result
only from our observations. A more complete analysis of infall
would require knowledge of the excitation temperature gradient present
within the clumps. This finding highlights the complexity and diversity
present among IR-dark clumps, and encourages further investigation of
this kind of objects.
.
It is not straightforward to interpret this interesting result
only from our observations. A more complete analysis of infall
would require knowledge of the excitation temperature gradient present
within the clumps. This finding highlights the complexity and diversity
present among IR-dark clumps, and encourages further investigation of
this kind of objects.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg124.png)
|
Figure 16:
Histograms of the asymmetry parameter |
| Open with DEXTER | |
Table 10: Infall and accretion rates, and ratio between the two quantities.
5.3.3 Infall rates
For the sources identified as infall candidates, we provide a rough estimate of the infall rate,
![]() ,
using the following equation:
,
using the following equation:
where
An approach to estimate the mass accretion rate,
![]() ,
towards the protostars is described in Beuther et al. (2002b) and López-Sepulcre et al. (2009). We can derive this quantity for the infall candidates from the outflow mass loss rates,
,
towards the protostars is described in Beuther et al. (2002b) and López-Sepulcre et al. (2009). We can derive this quantity for the infall candidates from the outflow mass loss rates,
![]() .
Considering the molecular outflows to be momentum driven, the following equation holds:
.
Considering the molecular outflows to be momentum driven, the following equation holds:
where
A comparison between the infall rates derived from Eq. (5) and the accretion rates calculated from Eq. (6) reveals differences of between 2 and 4 orders of magnitude, as can be seen in the last column of Table 10. As we have mentioned above, our infall rates are overestimates, but the discrepancies between
![]() and
and
![]() are huge. Nevertheless, it is likely that the former represents
the infalling material onto the whole protocluster, while the latter
corresponds to the material being accreted towards individual
protostars and therefore yields much smaller values. If this is
the case, it is worth noting in Table 10 that the ratio
are huge. Nevertheless, it is likely that the former represents
the infalling material onto the whole protocluster, while the latter
corresponds to the material being accreted towards individual
protostars and therefore yields much smaller values. If this is
the case, it is worth noting in Table 10 that the ratio
![]() is on average higher for the IR-dark sources by about an order of
magnitude. Even though the number of sources analysed here is very
small and therefore the statistics is poor, this result is interesting.
According to Tomisaka (1998),
while the accretion rate remains constant during the accretion phase,
the outflow rate increases with time until it reaches about one third
of the accretion rate (which is what we have assumed in the
determination of
is on average higher for the IR-dark sources by about an order of
magnitude. Even though the number of sources analysed here is very
small and therefore the statistics is poor, this result is interesting.
According to Tomisaka (1998),
while the accretion rate remains constant during the accretion phase,
the outflow rate increases with time until it reaches about one third
of the accretion rate (which is what we have assumed in the
determination of
![]() ). In this scenario, the greater
). In this scenario, the greater
![]() ratios
obtained for the IR-dark clumps support the idea that these objects are
in an earlier evolutionary phase in which, while the whole clump is
actively undergoing infall, the outflows formed within it are
still young and have not attained their maximum outflow mass loss
rate yet.
ratios
obtained for the IR-dark clumps support the idea that these objects are
in an earlier evolutionary phase in which, while the whole clump is
actively undergoing infall, the outflows formed within it are
still young and have not attained their maximum outflow mass loss
rate yet.
Table 11: Specific angular momentum of 4 sources at two different scales.
5.4 Velocity gradients
In half of our sample we detect C18O(2-1) velocity gradients. The corresponding velocity maps are shown in Fig. B.4.
It is not easy to tell whether these velocity gradients are due to
rotation, multiple components or outflowing motions, but a comparison
between the orientation of the velocity gradient and that of the
outflow axis (when present) might give a hint. There are four cases in
which the velocity gradient is roughly perpendicular to the outflow
axis: 18236-1205, 18316-0602, G34.43+0.2M1, and 19095+0930.
For these sources, the interpretation of a rotating envelope
perpendicular to the bipolar outflow is plausible. In other cases,
such as G23.60+0.0M1, the velocity gradient is parallel to the outflow
axis and therefore it likely traces the outflowing gas. However, we
have estimated a ``dynamical mass'' for all the sources with a velocity
gradient, assuming they are rotating structures, from the following
equation:
where
Assuming the velocity gradient present in the four sources above is due
to rotational motions, we can study the conservation of the specific
angular momentum, l, on them. Using
![]() in Table A.4, and the radius, r of each clump presented in Table 11, we derive the values of l reported in Col. 4 of the same table, which range between 0.07 and 0.15 km s-1 pc. These values can be compared with the initial specific angular momentum of the parental clumps,
in Table A.4, and the radius, r of each clump presented in Table 11, we derive the values of l reported in Col. 4 of the same table, which range between 0.07 and 0.15 km s-1 pc. These values can be compared with the initial specific angular momentum of the parental clumps,
![]() .
Under the assumption that the initial clump angular momentum is due to
the Galactic differential rotation, i.e. for an angular velocity
.
Under the assumption that the initial clump angular momentum is due to
the Galactic differential rotation, i.e. for an angular velocity
![]() s-1 (Clemens 1985), and that the molecular clumps were formed from larger spheres of gas at a density of 1 cm-3 (typical of the interstellar medium), we derive, for each of the four sources, the initial clump radius,
s-1 (Clemens 1985), and that the molecular clumps were formed from larger spheres of gas at a density of 1 cm-3 (typical of the interstellar medium), we derive, for each of the four sources, the initial clump radius,
![]() ,
and initial specific angular momentum,
,
and initial specific angular momentum,
![]() ,
listed in Table 11. The latter are on the order of a few km s-1 pc,
between one and two orders of magnitude higher than the (sub)parsec
scale values. This indicates that there is a loss of specific angular
momentum when going from large scales (i.e.
,
listed in Table 11. The latter are on the order of a few km s-1 pc,
between one and two orders of magnitude higher than the (sub)parsec
scale values. This indicates that there is a loss of specific angular
momentum when going from large scales (i.e. ![]() 10 pc) to scales of about 1 pc or less, a result which was already found by López-Sepulcre et al. (2009)
for G10.62-0.38, and which supports magnetic braking as a mechanism
that removes angular momentum from the clump during its collapse
(e.g. Mouschovias & Morton 1985; Galli et al. 2006). A more complete analysis of the conservation of l, such as the one carried out by Ohashi et al. (1999, see their Fig. 2) for a sample of low-mass protostars, requires further measurements at smaller scales.
10 pc) to scales of about 1 pc or less, a result which was already found by López-Sepulcre et al. (2009)
for G10.62-0.38, and which supports magnetic braking as a mechanism
that removes angular momentum from the clump during its collapse
(e.g. Mouschovias & Morton 1985; Galli et al. 2006). A more complete analysis of the conservation of l, such as the one carried out by Ohashi et al. (1999, see their Fig. 2) for a sample of low-mass protostars, requires further measurements at smaller scales.
5.5 HCO+(1-0) versus HCN(1-0)
HCN and HCO+ are commonly used as tracers of the dense
gas from which ``bursts'' of star formation emanate both in the
Galactic and extragalactic contexts (Wu et al. 2005; Gao & Solomon 2004).
They have the advantage relative to CO that their dipole moments are
high and hence that even their 3 mm transitions trace gas of
density above ![]() 104 cm-3.
On the other hand, they both are ``minor species'' in that they in
general trace a small fraction of C, N, O and hence their
abundances tend to be more sensitive to the quirks of chemistry
(CO in contrast takes up essentially all gas phase C). One
test of the stability of their abundances is to
examine the variability of the [HCO+]/[HCN] ratio or,
more practically, of the intensity ratio of their 3 mm
transitions and in this section, we consider the dispersion in our
observed values of this ratio.
104 cm-3.
On the other hand, they both are ``minor species'' in that they in
general trace a small fraction of C, N, O and hence their
abundances tend to be more sensitive to the quirks of chemistry
(CO in contrast takes up essentially all gas phase C). One
test of the stability of their abundances is to
examine the variability of the [HCO+]/[HCN] ratio or,
more practically, of the intensity ratio of their 3 mm
transitions and in this section, we consider the dispersion in our
observed values of this ratio.
It should be noted while doing this that, as we shall see, abundance ratio variations are not the only factor causing variations in R = I(HCO+(1-0))/I(HCN(1-0)), where I is the velocity integrated intensity of the line specified in brackets. Radiative transport as well perhaps as temperature variations may also be important and these must be considered. One should also realise that there are notable chemical differences between HCN and HCO+. Most obviously, the HCO+ abundance is linked via ion-molecule reactions to that of CO as well as to the general ionization equilibrium. HCN on the other hand is linked to the hydocarbon chemistry as well as to the amount of nitrogen in the gas phase. Thus elemental depletion onto dust grains (as presumably in IR-dark clumps) can have a considerable effect on the abundance of species like HCN and one can expect abundance variations linked to grain temperature (see the recent discussion of Hily-Blant et al. 2010, for example).
With this in mind, we have computed R for each of our sample sources from the velocity-integrated emission under the HCO+(1-0) and HCN(1-0) lines at the same offset coordinates used for the calculation of ![]() (Col. 2 in Table A.7). The resulting values and their errors are listed in Table A.8.
(Col. 2 in Table A.7). The resulting values and their errors are listed in Table A.8.
![\begin{figure}
\par\includegraphics[width=8cm]{14252fg17.eps}\hspace*{3mm}
\includegraphics[width=8cm]{14252fg18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg142.png)
|
Figure 17: Ratio of HCO+(1-0) to HCN(1-0) line emission against clump mass (left) and against surface density (right). |
| Open with DEXTER | |
When plotting this quantity as a function of clump mass or surface
density for IR-dark and IR-loud sources separately (Fig. 17), the difference between the two types of objects is evident: even though there is no clear correlation between R and
![]() or
or ![]() for either of the two sub-samples, the points corresponding to the
IR-dark clumps are more spread, spanning a larger range, and the
average ratio is higher. The mean ratios and standard deviations for
the IR-dark and IR-loud subsamples are, respectively, 1.3
for either of the two sub-samples, the points corresponding to the
IR-dark clumps are more spread, spanning a larger range, and the
average ratio is higher. The mean ratios and standard deviations for
the IR-dark and IR-loud subsamples are, respectively, 1.3 ![]() 1.0 and 0.74
1.0 and 0.74 ![]() 0.21. Thus there is much more dispersion in the IR-dark than in the IR-loud sub-sample.
0.21. Thus there is much more dispersion in the IR-dark than in the IR-loud sub-sample.
As can be seen from the histograms in Fig. 18, the emission of both the HCO+(1-0) and HCN(1-0) lines is generally weaker among the IR-dark clumps, which is not so unexpected taking into account that they are colder. However, the HCN(1-0) emission has been found to be particularly weak relative to the HCO+(1-0) emission in many IR-dark sources, as evidenced by some maps and spectra in Figs. B.1 and B.2.
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{14252fg19.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg143.png)
|
Figure 18: Histogram of the HCO+(1-0) (left) and HCN(1-0) (right) velocity-integrated line emission. |
| Open with DEXTER | |
Considering the IR-loud sub-sample, R covers a range of values between 0.3 and 1.1. There are two IR-dark clumps (G19.27+0.1M2 and G23.60+0.0M2) that fall below this range. These are actually the weakest HCO+(1-0) emitters in the whole sample, but not the weakest HCN(1-0) emitters, and hence the low R values. On the other hand, eight IR-dark sources lie above R = 1.1. Examining the spectra and maps of these sources, one notes that (a) there are a few cases (examples are G19.27+0.1M1 and G25.04-0.2M4) where there is an offset of more than 10'' between the HCN and HCO+ peaks and (b) there are some spectra where there appears to be severe self-absorption of the blue wing of the HCN line. Examples of the latter are the four IR-dark sources G24.33+0.1M4, G24.60+0.1M2, G25.04-0.2M1, and G25.04-0.2M2 and we compare in Fig. 19 the HCO+ and HCN spectra. While the hyperfine splitting of HCN renders the interpretation difficult, the evidence suggests strong self absorption in HCN due presumably to a foreground low density layer with relatively large HCN abundance. This as well as the offsets between map peaks suggests to us the presence of abundance gradients with density and we conclude that it would be very helpful to obtain maps in higher J transitions of these species to compare with the present results. It would certainly also be useful to obtain observations of the 13C isotopomers of HCN and HCO+.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg20.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg144.png)
|
Figure 19: HCN(1-0) spectrum (black) superimposed on the HCO+(1-0) spectrum (green) of the IR-dark sources G24.33+0.1M4, G24.60+0.1M2, G25.04-0.2M1, and G25.04-0.2M2. The dashed vertical line marks the peak velocity of the C18O(2-1) spectrum. We note that the velocity in the case of the HCN(1-0) line has been calculated with respect to the main hyperfine component. The three purple vertical lines mark the positions of the HCN(1-0) satellite components. |
| Open with DEXTER | |
In conclusion, the diversity of R values measured for the IR-dark clumps contrasts with the relative uniformity of R found in the IR-loud subsample. We suspect that this reflects abundance gradients within IR-dark clumps possibly linked to freeze out of heavy elements upon grain surfaces at low dust temperatures. We note in this context that some IRDCs are known to have a ``nitrogen-rich'' chemistry with strong ammonia and N2H+ emission (Wang et al. 2008; Pillai et al. 2006; Fontani et al. 2006). In local clouds, this is linked to freeze out of CO at high densities and low temperatures and it seems reasonable to assume that an analogous process operates in IR-dark clumps. IR-loud sources probably have larger grain temperatures at which CO and other volatile species evaporate.
Finally, our findings have also relevance for the extragalactic community, who make use of the HCN molecule to estimate the amount of dense molecular gas and correlate it to the star formation rate in galaxies (see Wu et al. 2005, for a Galactic and extragalactic analysis on the matter). It is interesting that our mean value for the HCO+(1-0) to HCN(1-0) ratio of 0.74 for the IR-loud sub-sample is not greatly different than that (a median of 0.86) found by Krips et al. (2008) for a sample of AGN and starburst galaxies (though with a variation from 0.48 to 1.5). As remarked above concerning the IR-dark sub-sample, a thorough study of the HCO+/HCN abundance ratio in our sample would be interesting in its own right as well as producing useful insight into the mechanisms operating in extragalactic starbursts.
6 Summary
We mapped in HCO+(1-0), HCN(1-0), and C18O(2-1) a sample of 19 IR-dark and 30 IR-loud high-mass molecular clumps with the IRAM-30 m telescope near Pico Veleta (Spain), to search for star formation activity signatures, such as infalling motions and molecular outflows, and try to look for evolutionary trends and constraints on the formation of massive stars.
Our main conclusions are the following:
- 1.
- An estimate of the clump masses has been derived from the emission under the C18O(2-1)
line. For the IR-loud clumps, these agree with the masses derived
from the dust continuum emission at 1.2 mm. By contrast, the C18O-derived
masses of the IR-dark clumps are systematically smaller than the
continuum-derived masses, due to either underestimated excitation
temperatures, and/or CO depletion in these regions. Considering
the latter, we obtain a median CO depletion factor of 4.5 for
our IR-dark sub-sample. Taking this into account, we find the clump
masses are comparable to the virial masses in the whole sample, and
that
 becomes greater than
becomes greater than
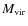 for the most massive objects, indicating they may be unstable under
gravitational collapse. We estimate that a magnetic field of a few mG
is sufficient to support these clumps against collapse.
for the most massive objects, indicating they may be unstable under
gravitational collapse. We estimate that a magnetic field of a few mG
is sufficient to support these clumps against collapse.
- 2.
- From the presence of high-velocity HCO+(1-0) wings,
we have detected molecular outflows in 75% of our sample sources.
For these, the outflow parameters have been derived, finding
they are high-mass outflows (i.e., between a few and
 100
100 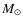 )
and thus likely to be driven by massive YSOs. We find molecular
outflows are as common, massive and energetic among IR-dark sources as
they are among IR-loud sources, indicating both kinds of objects are
equally active in the formation of stars and clusters.
In addition, our data allows us to set an empirical outflow
threshold surface density at
)
and thus likely to be driven by massive YSOs. We find molecular
outflows are as common, massive and energetic among IR-dark sources as
they are among IR-loud sources, indicating both kinds of objects are
equally active in the formation of stars and clusters.
In addition, our data allows us to set an empirical outflow
threshold surface density at
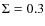 g cm-2
below which the detection rate falls considerably, and the outflows are
less massive and energetic on average. This lends support to the
theoretical prediction made by Krumholz & McKee (2008),
who establish a minimum clump surface density for high-mass star
formation to occur. A good correlation is found between outflow
parameters and clump mass, with more massive and energetic outflows
corresponding to more massive molecular clumps. Our results also
indicate that up to a 20% of the clump mass can be affected by
molecular outflows, and therefore outflow feedback may be an important
factor in the process of high-mass star/cluster formation.
g cm-2
below which the detection rate falls considerably, and the outflows are
less massive and energetic on average. This lends support to the
theoretical prediction made by Krumholz & McKee (2008),
who establish a minimum clump surface density for high-mass star
formation to occur. A good correlation is found between outflow
parameters and clump mass, with more massive and energetic outflows
corresponding to more massive molecular clumps. Our results also
indicate that up to a 20% of the clump mass can be affected by
molecular outflows, and therefore outflow feedback may be an important
factor in the process of high-mass star/cluster formation.
- 3.
- The presence of infall has been assessed by looking for blue-shifted asymmetries in the HCO+(1-0) line profiles. With this method, infall detection rates of 13% for the IR-loud, and 32% for the IR-dark clumps have been measured. The higher number of infall candidates in the IR-dark sub-sample suggests these objects are more likely associated with the accretion phase and thus may represent the onset of star or cluster formation. A more detailed study of the kinematics and temperature distribution within the molecular clumps in our sample is necessary to interpret correctly the HCO+(1-0) line profiles.
- 4.
- About half of our sample sources present C18O(2-1) velocity gradients. In four cases these are perpendicular to the outflow axis, and could therefore represent a rotating envelope around the bipolar outflow. The low dynamical masses implied by the velocity gradients measured suggest that rotation is not dynamically relevant in our sample. We also conclude from our estimates of specific angular momentum in these clumps that this quantity is at least an order of magnitude lower than that expected on the basis of differential galactic rotation and hence that magnetic braking has led to angular momentum loss.
- 5.
- On average, the HCO+(1-0) to HCN(1-0) line ratio is greater and presents much more scattering in the IR-dark sub-sample. Inspection of the clump morphologies in the integrated maps indicates that these two molecules may trace different regions of the IR-dark clumps. This, together with the discovery of a number of IR-dark sources which display highly self-absorbed HCN(1-0) line profiles, suggests that the ground state lines are sensitive to foreground material at low density, and points to abundance gradients with density.
A.L.S. acknowledges support from the FP6 Marie-Curie Research Training Network ``Constellation: the origin of stellar masses'' (MRTN-CT-2006-035890). We thank the staff of IRAM-Granada, who provided help during the observations. Many thanks to Marco Padovani for reading the manuscript and providing helpful suggestions. We are grateful to our referee, Henrik Beuther, for his comments and suggestions which have undoubtedly improved our paper.
References
- Anglada, G., Rodríguez, L. F., Canto, J., et al. 1987, A&A, 186, 280 [NASA ADS] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002a, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Sridharan, T. K., et al. 2002b, A&A, 383, 892 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2005, ApJ, 633, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., & Bate, M. R. 2002, MNRAS, 336, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Vine, S. G., & Bate, M. R. 2004, MNRAS, 349, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Brand, J. 1986, Ph.D. Thesis, Leiden University [Google Scholar]
- Bronfman, L., Nyman, L. Å, & May, J. 1996, A&AS, 115, 81 [Google Scholar]
- Carey, S. J., Clark, F. O., Egan, M. P., et al. 1998, ApJ, 508, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Feldman, P. A., Redman, R. O., et al. 2000, ApJ, 543, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Galli, D., Lodato, L., Walmsley, C. M., & Zhang, Q. 2007, PPV (Tucson: Univ. Arizona Press), 197 [Google Scholar]
- Clemens, D. P. 1985, ApJ, 295, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Egan, M. P., Shipman, R. F., Price, S. D., et al. 1998, ApJ, 494, 199 [Google Scholar]
- Faúndez, S., Bronfman, L., Garay, G., et al. 2004, A&A, 426, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Cesaroni, R., Caselli, P., & Olmi, L. 2002, A&A, 389, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Caselli, P., Crapsi, A., et al. 2006, A&A, 460, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuller, G. A., Williams, S. J., & Sridharan, T. K. 2005, A&A, 442, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, D., Lizano, S., Shu, F. H., & Allen, A. 2006, ApJ, 647, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., & Solomon, M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, T., Burton, M. G., Minier, V., et al. 2005, MNRAS, 363, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Walmsley, C. M., Pineau des Forêts, G., & Flower, D. 2010, A&A, 513, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hofner, P., Wyrowski, F., Walmsley, C. M., & Churchwell, E. 2000, ApJ, 536, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E. 2002, ApJ, 580, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Krips, M., Neri, R., García-Burillo, S., et al. 2008, ApJ, 677, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2008, Nature, 451, 1082 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., et al. 2009, Science 323, 754 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kwan, J., & Scoville, N. 1975, ApJ, 195, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Irvine, W. M., Goldsmith, P. F., & Hjalmarson, Å. 1987, ASSL, 134, 561 [Google Scholar]
- Liszt, H., Lucas, R., & Black, J. H. 2004, A&A, 428, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sepulcre, A., Codella, C., Cesaroni, R., et al. 2009, A&A, 499, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacLaren, I., Richardson, K. M., & Wolfendale, A. W. 1988, ApJ, 333, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Mardones, D., Myers, P. C., Tafalla, M., et al. 1997, ApJ, 489, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J., Rodríguez, L. F., & Reipurth, B. 1998, ApJ, 502, 337 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- McKee, C. F., Zweibel, E. G., Goodman, A. A., & Heiles, C. 1993, in Protostars and Planets III, ed. E. H. Levy, & J. I. Lunine, 327 [Google Scholar]
- Menten, K. M., Pillai, T., & Wyrowski, F. 2005, in Massive Star Birth: A crossroads of Astrophysics, ed. R. Cesaroni, M. Felli, E. Churchwell, & C. M. Walmsley (Cambridge: Cambridge Univ. Press), Proc. IAU, 227, 23 [Google Scholar]
- Mouschovias, T. C., & Morton, S. A. 1985, ApJ, 298, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Ohashi, N. 1999, in Star Formation, ed. T. Nakamoto, NRO, 129 [Google Scholar]
- Ossenkopf, V., & Henning, Th. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Palla, F., & Stahler, S. 1993, ApJ, 418, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Pérault, M., Omont, A., Simon, G., et al. 1996, A&A, 315, L165 [NASA ADS] [Google Scholar]
- Pillai, T., Wyrowski, F., Carey, S. J., & Menten, K. M. 2006, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Simon, R., & Jackson, J. M. 2007, ApJ, 662, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., Zhang, Q., & Simon, R. 2008, ApJ, 689, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJ, 653, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Sridharan, T. K., Beuther, H., Saito, M., et al. 2005, ApJ, 634, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Tomisaka, K. 1998, ApJ, 502, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Townes, C. H., & Schawlow, A. L. 1955, Microwave Spectroscopy (New York: McGraw-Hill) [Google Scholar]
- Wilson, T. L., & Rood, R. T. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Zhang, Q., Pillai, T., et al. 2008, ApJ, 672, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, P., Li, Z. Y., Abel, T., & Nakamura, F. 2010, ApJ, 709, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., & Evans II, N. J. 2003, ApJ, 592, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., Evans II, N. J., Gao, Y., et al. 2005, ApJ, 635, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W., & Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, S. 1992, ApJ, 394, 204 [NASA ADS] [CrossRef] [Google Scholar]
Online Material
Appendix A: Tables
Table A.1:
1![]() rms values, first contour, and contour step of the clump maps in Fig. B.1 (grey scale).
rms values, first contour, and contour step of the clump maps in Fig. B.1 (grey scale).
Table A.2:
Gaussian fit to C18O(2-1) spectra at peak coordinates![]() .
.
Table A.3:
Gaussian fit to HCO+(1-0) spectra at peak coordinates![]() .
.
Table A.4: Deconvolved C18O(2-1) clump diameter, Galactocentric distance and various mass estimates.
Table A.5: Outflow detection, velocity range of the HCO+(1-0) wings and lobe sizes.
Table A.6: Total outflow energetics and kinematics.
Table A.7: Spectral line velocities, line asymmetry, and infall rate.
Table A.8:
HCO+(1-0) to HCN(1-0) line ratios![]() .
.
Appendix B: Figures
![\begin{figure}
\par\includegraphics[width=13cm,clip]{14252fgb1.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg153.png)
|
Figure B.1: Contour maps of the molecular clumps. IR-dark and IR-loud sources are labelled IRD and IRL, respectively. Black dashed lines represent the half power contours and black solid lines the clump regions (see text), defined as follows. Left panels: HCO+(1-0) emission. Clump regions: 50% (G189), 60% (05358, G192.58), 70% (G192.60), and 80% (G213) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% (G189), 60% (05358, G192.58), and 70% (G213, G192.60) power contours. Right panels: C18O(2-1) emission. Clump regions: 60% (G189, G192.58), 70% (G213, G192.60), and HCO+(1-0) 60% (05358) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{14252fgb2.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg154.png)
|
Figure B.1: continued. We note that G192.59 has not been detected by our observations: the two components seen in the maps represent G192.58 (northern) and G192.60 (southern). Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (18151_2), 60% (18151_1), and 70% (18151_3, G18.15) power contours; in the cases of 18151_3, and G18.15 it has been manually cut to include only the central component. Central panels: HCN(1-0) emission. Clump regions: 60% (18151_2, 18151_1) and 70% (18151_3, G18.15) power contours; in the cases of 18151_3 it has been manually cut to include only the central component. Right panels: C18O(2-1) emission. Clump regions: 50% (18151_3, 18151_1, G18.15) and HCO+(1-0) 50% (18151_2) power contours; in the cases of 18151_3 and G18.15 it has been manually cut to include only the central component. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb3.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg155.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 60% (18223, 18228, G19.27M1), 70% (G18.18), and HCN(1-0) 60% (G19.27M2) power contours. Central panels: HCN(1-0) emission. Clump regions: 60% (18223, G19.27M2, G19.27M1), 70% (18228), and 80% (G18.18) power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (18223), 70% (G18.18, 18228), and HCN(1-0) 60% (G19.27M2, G19.27M1) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb4.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg156.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (18264), 60% (G23.60M1, 18316, G23.60M2), and 70% (18236) power contours. Central panels: HCN(1-0) emission. Clump regions 60% power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (G23.60M2), 60% (18264, 18316), 70% (18236), and 80% (G23.60M2) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg157.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (18317), 60% (G24.08M2, G24.33M1, G24.33M4) and 80% (G24.33M2) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% (18317, G24.08M2, G24.33M1), 60% (G24.33M1), and 80% (G24.33M2) power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (G24.08M2), 60% (18317, G24.33M1), 70% (G24.33M2), and 80% (G24.33M4) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg158.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (G24.60M2) and 70% (G24.60M1, G25.04M1, G25.04M4, G25.04M2) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% (G24.60M2, G24.60M1), 60% (G25.04M1, G25.04M4), and 70% (G25.04M2) power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (G24.60M2), 60% (G24.60M1), 70% (G25.04M1), HCO+(1-0) 70%, and HCN(1-0) 60% (G25.04M4) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb7.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg159.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 40% (G34.43M3), 60% (18507), and 70% (G28.28, G34.43M1, G34.24) power contours; in the case of 18507 it has been manually cut to include only the southern component. Central panels: HCN(1-0) emission. Clump regions: 50% (18507, G34.43M3), 60% (G34.43M1), and 70% (G28.28, G34.24) power contours; in the case of 18507 it has been manually cut to include only the southern component. Right panels: C18O(2-1) emission. Clump regions: 40% (G34.43M1), 50% (G28.28, 18507), 80% (G34.24), and HCO+(1-0) 40% (G34.43M3) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb8.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg160.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (18517, G34.77M2, 19035) and 60% (G35.39M4, G38.95M1) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% (G35.39M4, 19035), 60% (18517, G34.77M2), and 70% (G38.95M1) power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (18517, G38.95M1, 19035), HCO+(1-0) 60% (G35.39M4), and HCN(1-0) 60% (G34.77M2) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb9.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg161.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): the 50% (19095, 20216, 22570_2) and 60% (20332, 22134) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (19095, 20332, 22134), 60% (20216), and HCO+(1-0) 50% (22570_2) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb10.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg162.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 40% (23151) and 50% (22570_1, 23033, 23139) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (23033, 23139, 23151) and 60% (22570_1) power contours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{14252fgb11.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg163.png)
|
Figure B.2: Average spectra. For each source, the peak velocity from the Gaussian fit to the C18O(2-1) line at the peak coordinates (see Table A.2) is marked with a dashed vertical line. The purple vertical solid lines mark the positions of the HCN(1-0) hyperfine components. IR-dark and IR-loud sources are labelled IRD and IRL, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb12.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg164.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb13.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg165.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{14252fgb14.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg166.png)
|
Figure B.2: continued. G24.33+0.1M1: Note the blue-shifted absorption due to emission at the OFF position (see text and Table 4). G24.33+0.1M4: The C18O(2-1) line falls outside the limits of the VESPA unit and therefore the spectra obtained with the 1 MHz backend have been used instead (spectral resolution: 1.4 km s-1). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{14252fgb15.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg167.png)
|
Figure B.2: continued. G24.60+0.1M2: The C18O(2-1) line falls outside the limits of the VESPA unit and therefore the spectra obtained with the 1 MHz backend have been used instead (spectral resolution: 1.4 km s-1). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg168.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb17.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg169.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg170.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{14252fgb19.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg171.png)
|
Figure B.3:
Outflow maps. IR-dark and IR-loud sources are labelled IRD and IRL, respectively. Blue-shifted (solid contours) and red-shifted (dashed contours) HCO+(1-0) integrated wing emission, with contours starting from 5 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb20.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg172.png)
|
Figure B.3:
continued. Blue-shifted (solid contours) and red-shifted (dashed contours) HCO+(1-0) integrated wing emission, with contours starting from 8 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb21.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg173.png)
|
Figure B.4: C18O(2-1) velocity maps. The arrows indicate the orientation of the bipolar outflow, where present (solid for the blue lobe, dashed for the red lobe). IR-dark and IR-loud sources are labelled IRD and IRL, respectively. Sources with no outflow detection are labelled ``NO'', and sources with an outflow detection but no clear orientation are labelled ``ORI''. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb22.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg174.png)
|
Figure B.4: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm]{14252fgb23.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg175.png)
|
Figure B.4: continued. |
| Open with DEXTER | |
Footnotes
- ... clumps
![[*]](/icons/foot_motif.png)
- Based on observations carried out with the IRAM 30-m telescope at Pico Veleta (Granada, Spain). IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
- ...
![[*]](/icons/foot_motif.png)
- Appendices A and B are only available in electronic form at http://www.aanda.org
All Tables
Table 1: Details of the 1.2 mm surveys from which our source sample has been selected.
Table 2: Observed sample.
Table 3: Observed lines.
Table 4: Sources affected by emission at OFF position.
Table 5: New distances computed for eight IR-dark clumps.
Table 6: Factors to multiply by the projected outflow-related parameters, as a function of outflow inclination, i.
Table 7:
![]() and
and
![]() derived for G24.33+0.1M1 for two different temperatures.
derived for G24.33+0.1M1 for two different temperatures.
Table 8: Comparison of outflow mass, momentum and kinetic energy between this study and that of Beuther et al. (2002b).
Table 9:
Comparison between our ![]() and the one derived by Fuller et al. (2005) from HCO+(1-0).
and the one derived by Fuller et al. (2005) from HCO+(1-0).
Table 10: Infall and accretion rates, and ratio between the two quantities.
Table 11: Specific angular momentum of 4 sources at two different scales.
Table A.1:
1![]() rms values, first contour, and contour step of the clump maps in Fig. B.1 (grey scale).
rms values, first contour, and contour step of the clump maps in Fig. B.1 (grey scale).
Table A.2:
Gaussian fit to C18O(2-1) spectra at peak coordinates![]() .
.
Table A.3:
Gaussian fit to HCO+(1-0) spectra at peak coordinates![]() .
.
Table A.4: Deconvolved C18O(2-1) clump diameter, Galactocentric distance and various mass estimates.
Table A.5: Outflow detection, velocity range of the HCO+(1-0) wings and lobe sizes.
Table A.6: Total outflow energetics and kinematics.
Table A.7: Spectral line velocities, line asymmetry, and infall rate.
Table A.8:
HCO+(1-0) to HCN(1-0) line ratios![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{14252fg1.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg41.png)
|
Figure 1:
Surface density, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{14252fg2.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg43.png)
|
Figure 2: Example of emission at OFF for the HCO+(1-0) spectrum in 05358+3543. Black: spectrum without correction; the line displays an artificial absorption at -20 km s-1. Green: the same spectrum after having applied the Gaussian correction (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg3.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg78.png)
|
Figure 3:
Virial mass,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg4.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg81.png)
|
Figure 4:
Clump mass derived from the continuum emission at 1.2 mm,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg82.png)
|
Figure 5:
Surface density derived from the continuum emission at 1.2 mm,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg86.png)
|
Figure 6:
Virial mass,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{14252fg7.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg88.png)
|
Figure 7:
Molecular outflow detections for the IR-dark (top) and IR-loud (bottom) sub-samples. Plot of surface density, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{14252fg8.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg90.png)
|
Figure 8: Molecular outflow detection rate as a function of surface density for the whole sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg9.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg93.png)
|
Figure 9:
Outflow mass (bottom), total outflow momentum (middle) and outflow kinetic energy (top)
against mass of the clump derived from the dust emission. Filled
circles represent IR-dark sources, while open circles represent IR-loud
sources. Different colours are used to mark sources with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg10.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg98.png)
|
Figure 10:
Ratio between outflow mass and clump mass,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{14252fg11.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg102.png)
|
Figure 11:
Outflow mass loss rate (bottom), mechanical force of the outflow (middle) and mechanical luminosity of the outflow (top)
against mass of the clump derived from the dust emission. Filled
circles represent IR-dark sources, while open circles represent IR-loud
sources. Different colours are used to mark sources with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg12.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg103.png)
|
Figure 12:
Outflow mass against surface density of the clump. IR-dark sources are
represented by filled circles, and IR-loud by open circles. The two
vertical dashed lines mark the theoretical (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{14252fg13.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg112.png)
|
Figure 13:
Comparison between our derived outflow mass,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg14.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg113.png)
|
Figure 14:
HCO+(1-0) line asymmetries for the IR-dark (top) and IR-loud (bottom) sub-samples. Plot of surface density, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{14252fg15.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg123.png)
|
Figure 15:
Comparison of the asymmetry parameter, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg124.png)
|
Figure 16:
Histograms of the asymmetry parameter |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{14252fg17.eps}\hspace*{3mm}
\includegraphics[width=8cm]{14252fg18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg142.png)
|
Figure 17: Ratio of HCO+(1-0) to HCN(1-0) line emission against clump mass (left) and against surface density (right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{14252fg19.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg143.png)
|
Figure 18: Histogram of the HCO+(1-0) (left) and HCN(1-0) (right) velocity-integrated line emission. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14252fg20.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg144.png)
|
Figure 19: HCN(1-0) spectrum (black) superimposed on the HCO+(1-0) spectrum (green) of the IR-dark sources G24.33+0.1M4, G24.60+0.1M2, G25.04-0.2M1, and G25.04-0.2M2. The dashed vertical line marks the peak velocity of the C18O(2-1) spectrum. We note that the velocity in the case of the HCN(1-0) line has been calculated with respect to the main hyperfine component. The three purple vertical lines mark the positions of the HCN(1-0) satellite components. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{14252fgb1.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg153.png)
|
Figure B.1: Contour maps of the molecular clumps. IR-dark and IR-loud sources are labelled IRD and IRL, respectively. Black dashed lines represent the half power contours and black solid lines the clump regions (see text), defined as follows. Left panels: HCO+(1-0) emission. Clump regions: 50% (G189), 60% (05358, G192.58), 70% (G192.60), and 80% (G213) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% (G189), 60% (05358, G192.58), and 70% (G213, G192.60) power contours. Right panels: C18O(2-1) emission. Clump regions: 60% (G189, G192.58), 70% (G213, G192.60), and HCO+(1-0) 60% (05358) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{14252fgb2.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg154.png)
|
Figure B.1: continued. We note that G192.59 has not been detected by our observations: the two components seen in the maps represent G192.58 (northern) and G192.60 (southern). Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (18151_2), 60% (18151_1), and 70% (18151_3, G18.15) power contours; in the cases of 18151_3, and G18.15 it has been manually cut to include only the central component. Central panels: HCN(1-0) emission. Clump regions: 60% (18151_2, 18151_1) and 70% (18151_3, G18.15) power contours; in the cases of 18151_3 it has been manually cut to include only the central component. Right panels: C18O(2-1) emission. Clump regions: 50% (18151_3, 18151_1, G18.15) and HCO+(1-0) 50% (18151_2) power contours; in the cases of 18151_3 and G18.15 it has been manually cut to include only the central component. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb3.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg155.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 60% (18223, 18228, G19.27M1), 70% (G18.18), and HCN(1-0) 60% (G19.27M2) power contours. Central panels: HCN(1-0) emission. Clump regions: 60% (18223, G19.27M2, G19.27M1), 70% (18228), and 80% (G18.18) power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (18223), 70% (G18.18, 18228), and HCN(1-0) 60% (G19.27M2, G19.27M1) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb4.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg156.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (18264), 60% (G23.60M1, 18316, G23.60M2), and 70% (18236) power contours. Central panels: HCN(1-0) emission. Clump regions 60% power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (G23.60M2), 60% (18264, 18316), 70% (18236), and 80% (G23.60M2) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb5.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg157.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (18317), 60% (G24.08M2, G24.33M1, G24.33M4) and 80% (G24.33M2) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% (18317, G24.08M2, G24.33M1), 60% (G24.33M1), and 80% (G24.33M2) power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (G24.08M2), 60% (18317, G24.33M1), 70% (G24.33M2), and 80% (G24.33M4) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb6.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg158.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (G24.60M2) and 70% (G24.60M1, G25.04M1, G25.04M4, G25.04M2) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% (G24.60M2, G24.60M1), 60% (G25.04M1, G25.04M4), and 70% (G25.04M2) power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (G24.60M2), 60% (G24.60M1), 70% (G25.04M1), HCO+(1-0) 70%, and HCN(1-0) 60% (G25.04M4) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb7.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg159.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 40% (G34.43M3), 60% (18507), and 70% (G28.28, G34.43M1, G34.24) power contours; in the case of 18507 it has been manually cut to include only the southern component. Central panels: HCN(1-0) emission. Clump regions: 50% (18507, G34.43M3), 60% (G34.43M1), and 70% (G28.28, G34.24) power contours; in the case of 18507 it has been manually cut to include only the southern component. Right panels: C18O(2-1) emission. Clump regions: 40% (G34.43M1), 50% (G28.28, 18507), 80% (G34.24), and HCO+(1-0) 40% (G34.43M3) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb8.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg160.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 50% (18517, G34.77M2, 19035) and 60% (G35.39M4, G38.95M1) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% (G35.39M4, 19035), 60% (18517, G34.77M2), and 70% (G38.95M1) power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (18517, G38.95M1, 19035), HCO+(1-0) 60% (G35.39M4), and HCN(1-0) 60% (G34.77M2) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb9.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg161.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): the 50% (19095, 20216, 22570_2) and 60% (20332, 22134) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (19095, 20332, 22134), 60% (20216), and HCO+(1-0) 50% (22570_2) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{14252fgb10.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg162.png)
|
Figure B.1: continued. Left panels: HCO+(1-0) emission. Clump regions (black solid contours): 40% (23151) and 50% (22570_1, 23033, 23139) power contours. Central panels: HCN(1-0) emission. Clump regions: 50% power contours. Right panels: C18O(2-1) emission. Clump regions: 50% (23033, 23139, 23151) and 60% (22570_1) power contours. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{14252fgb11.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg163.png)
|
Figure B.2: Average spectra. For each source, the peak velocity from the Gaussian fit to the C18O(2-1) line at the peak coordinates (see Table A.2) is marked with a dashed vertical line. The purple vertical solid lines mark the positions of the HCN(1-0) hyperfine components. IR-dark and IR-loud sources are labelled IRD and IRL, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb12.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg164.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb13.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg165.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{14252fgb14.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg166.png)
|
Figure B.2: continued. G24.33+0.1M1: Note the blue-shifted absorption due to emission at the OFF position (see text and Table 4). G24.33+0.1M4: The C18O(2-1) line falls outside the limits of the VESPA unit and therefore the spectra obtained with the 1 MHz backend have been used instead (spectral resolution: 1.4 km s-1). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{14252fgb15.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg167.png)
|
Figure B.2: continued. G24.60+0.1M2: The C18O(2-1) line falls outside the limits of the VESPA unit and therefore the spectra obtained with the 1 MHz backend have been used instead (spectral resolution: 1.4 km s-1). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb16.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg168.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb17.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg169.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb18.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg170.png)
|
Figure B.2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{14252fgb19.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg171.png)
|
Figure B.3:
Outflow maps. IR-dark and IR-loud sources are labelled IRD and IRL, respectively. Blue-shifted (solid contours) and red-shifted (dashed contours) HCO+(1-0) integrated wing emission, with contours starting from 5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb20.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg172.png)
|
Figure B.3:
continued. Blue-shifted (solid contours) and red-shifted (dashed contours) HCO+(1-0) integrated wing emission, with contours starting from 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb21.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg173.png)
|
Figure B.4: C18O(2-1) velocity maps. The arrows indicate the orientation of the bipolar outflow, where present (solid for the blue lobe, dashed for the red lobe). IR-dark and IR-loud sources are labelled IRD and IRL, respectively. Sources with no outflow detection are labelled ``NO'', and sources with an outflow detection but no clear orientation are labelled ``ORI''. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14252fgb22.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg174.png)
|
Figure B.4: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{14252fgb23.eps}
\end{figure}](/articles/aa/full_html/2010/09/aa14252-10/Timg175.png)
|
Figure B.4: continued. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



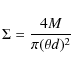
![\begin{displaymath}%
\frac{[{\rm C}^{16}{\rm O}]}{[{\rm C}^{18}{\rm O}]} = 58.8~R_{\rm gal} + 37.1.
\end{displaymath}](/articles/aa/full_html/2010/09/aa14252-10/img48.png)