EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 517 (July 2010) A&A, 517 (2010) A62 Full HTML
Free Access
Issue
A&A
Volume 517, July 2010
Article Number A62
Number of page(s) 4
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201014215
Published online 06 August 2010
A&A 517, A62 (2010)

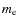Constraints on variation in $\alpha $ and $\textit{m}_{\rm e}$ from WMAP 7-year data

S. J. Landau1,[*] - G. Scóccola2,[*]

1 - Departamento de Física, FCEyN, Universidad de Buenos Aires, Ciudad Universitaria - Pab. 1, 1428 Buenos Aires, Argentina
2 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild Str. 1, Postfach 1317, 85741 Garching, Germany

Received 8 February 2010 / Accepted 4 May 2010

Abstract
Aims. We update the constraints on the time variation of the fine structure constant $\alpha $ and the electron mass $m_{\rm e}$, using the latest CMB data, including the 7-yr release of WMAP.
Methods. We made statistical analyses of the variation of each one of the constants and of their joint variation, together with the basic set of cosmological parameters. We used a modified version of CAMB and COSMOMC to account for these possible variations.
Results. We present bounds on the variation of the constants for different data sets, and show how results depend on them. When using the latest CMB data plus the power spectrum from Sloan Digital Sky Survey LRG, we find that $\alpha / \alpha_0=0.986 \ \pm \ 0.007$ at 1-$\sigma $ level, when the 6 basic cosmological parameters were fitted, and only variation in $\alpha $ was allowed. The constraints in the case of variation of both constants are $ \alpha / \alpha_0= 0.986 \ \pm \ 0.009$ and $m_{\rm e} / m_{\rm e0} = 0.999 \ \pm \ 0.035$. In the case of only variation in $m_{\rm e}$, the bound is $m_{\rm e} / m_{{\rm e}0}=0.964 \pm 0.025$.

Key words: cosmic background radiation - cosmological parameters - early Universe

1 Introduction

The variation of fundamental constants over cosmological time scales is a prediction of theories that attempt to unify the four interactions in nature, like string derived field theories, related brane-world theories and Kaluza-Klein theories (see Uzan 2003; García-Berro et al. 2007, and references therein). Many observational and experimental efforts have been made to put constraints on such variations. Most of the reported data are consistent with null variation of fundamental constants. Although there have been recent claims for time variation of the fine structure constant ($\alpha $) and of the proton to electron mass ratio ( $\mu = \frac{m_{\rm p}}{m_{\rm e}}$) (Reinhold et al. 2006; Murphy et al. 2003), independent analyses of similar data give null results (Malec et al. 2010; King et al. 2008; Srianand et al. 2004; Thompson et al. 2009). On the other hand, a recent analysis of ammonia spectra in the Milky Way suggests a spatial variation of $\mu$ (Molaro et al. 2009; Levshakov et al. 2010).

Unifying theories predict variation of all coupling constants, being all variations related in general to the rolling of a scalar field. Therefore, the relationship between variations of coupling constants depends on the unifying model. In this paper we adopt a phenomenological approach and analyse the possible variation of $\alpha $ and/or $m_{\rm e}$ at the time of the formation of neutral hydrogen without assuming any theoretical model. Nakashima et al. (2010) have considered also the variation in the proton mass ($m_{\rm p}$). This quantity affects mainly the baryon mass density and the baryon number density. Their results confirm the strong degeneracy with the baryon density. Therefore, we will not consider the variation in $m_{\rm p}$ in this work.

Cosmic microwave background radiation (CMB) is one of the most powerful tools to study the early universe and in particular, to put bounds on possible variations in the fundamental constants between early times and the present. Changing $\alpha $ or $m_{\rm e}$ at recombination affects the differential optical depth of the photons due to Thompson scattering, changing therefore Thompson scattering cross section and the ionization fraction. The signatures on the CMB angular power spectrum due to varying fundamental constants are similar to those produced by changes in the cosmological parameters, i.e. changes in the relative amplitudes of the Doppler peaks and a shift in their positions. Moreover, an increment in $\alpha $ or $m_{\rm e}$ decreases the high-$\ell$ diffusion damping, which is due to the finite thickness of the last-scattering surface, and thus, increases the power on very small scales (Hannestad 1999; Kaplinghat et al. 1999).

Recent analyses of CMB data (earlier than the WMAP seven-year release) including a possible variation in $\alpha $ have been performed by Martins et al. (2010); Menegoni et al. (2009); Scóccola et al. (2009,2008); Nakashima et al. (2010), and including a possible variation in $m_{\rm e}$ have been performed by Scóccola et al. (2009); Nakashima et al. (2010); Scóccola et al. (2008).

In our previous works, we have also analyzed the dependence of the updated recombination scenario (that includes the recombination of helium, and was implemented in R ECFAST following Wong et al. 2008) on $\alpha $ and $m_{\rm e}$, and show that these dependencies are not relevant for WMAP data.

In this paper we adopt a phenomenological approach and analyse the possible variation in $\alpha $ and/or $m_{\rm e}$ without assuming any theoretical model. We use WMAP seven-year release, together with other recent CMB data. We also combine CMB data with other cosmological data sets: i) the power spectrum of the Sloan Digital Sky Survery DR7 LRG; ii) a recent constraint of the Hubble constant H0 with data from the Hubble Space Telescope. In Sect. 2 we describe the method and data sets we used in the statistical analysis. We present and discuss our results in Sect. 3. We conclude in Sect. 4.

2 Statistical analysis

We performed our statistical analysis by exploring the parameter space with Monte Carlo Markov chains generated with the CosmoMC code (Lewis & Bridle 2002) which uses the Boltzmann code CAMB (Lewis et al. 2000) and R ECFAST to compute the CMB power spectra. We modified them in order to include the possible variation in $\alpha $ and $m_{\rm e}$ at recombination.

We use data from the WMAP 7-year temperature and temperature-polarization power spectrum (Larson et al. 2010), and other CMB experiments such as CBI (Readhead et al. 2004), ACBAR (Kuo et al. 2004), BOOMERANG (Jones et al. 2006; Piacentini et al. 2006), BICEP (Chiang et al. 2010) and QUAD (Brown et al. 2009). In order to reduce degeneracies of the cosmological parameters, we combine the CMB data sets with other cosmological data: i) the power spectrum of the Sloan Digital Sky Survey LRG (Reid et al. 2010) and ii) the recent constraint on the Hubble constant, $H_0= 74.2 \ \pm \ 3.6$ km s-1 Mpc-1, presented by Riess et al. (2009).

We have considered a spatially-flat cosmological model with adiabatic density fluctuations, and the following parameters:

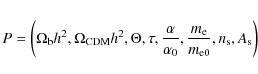
\begin{eqnarray*}P=\left(\Omega_{\rm b} h^2, \Omega_{\rm CDM} h^2, \Theta, \tau,... ...0}, \frac{m_{\rm e}}{m_{{\rm e}0}}, n_{\rm s}, A_{\rm s}\right) \end{eqnarray*}


where $\Omega _{\rm b} h^2 $ is the baryon density and $\Omega_{\rm CDM} h^2$ is the dark matter density, both in units of the critical density; $\Theta$ gives the ratio of the co-moving sound horizon at decoupling to the angular diameter distance to the surface of last scattering (and is related to the Huble constant H0); $\tau $ is the reionization optical depth; $n_{\rm s}$ the scalar spectral index; and $A_{\rm s}$ is the amplitude of the density fluctuations.

We have performed statistical analyses using the data mentioned above and considering variation of only one constant ($\alpha $ or $m_{\rm e}$) and variation of both constants. We present our results in the next section.

3 Results and discussion

Results for the variation of the constants in the case when only one constant is allowed to vary are shown in Table 1 and for the case when both are allowed to vary, are presented in Table 2. The obtained values are consistent with no variation of $\alpha $ or $m_{\rm e}$ at recombination. The obtained errors are at the same percent level than those obtained by Martins et al. (2010); Menegoni et al. (2009); Scóccola et al. (2009,2008) using WMAP-5 year release. The parameter space has higher dimension when both constants are allowed to vary. Therefore, limits on $\alpha $ and $m_{\rm e}$ are more stringent in the case were only one constant is allowed to vary. Results for the cosmological parameters have similar values for all of the analyses. Therefore, we only report the values obtained in the case where both $\alpha $ and $m_{\rm e}$ were allowed to vary and the data from CMB and the power spectrum of the SDSS DR7 were considered (see Table 3). The mean values and errors for the cosmological parameters are in agreement within 1-$\sigma $ with those obtained by the WMAP collaboration (Larson et al. 2010) with no variation of fundamental constants.

Table 1:   Mean values and 1-$\sigma $ errors for the analysis with variation of only $\alpha $, and only $m_{\rm e}$.

Table 2:   Mean values and 1-$\sigma $ errors for the analysis with the joint variation of $\alpha $ and $m_{\rm e}$.

Table 3:   Mean values and 1$\sigma $ errors for the cosmological parameters using all CMB data and the SDSS DR7 power spectrum.

In Fig. 1 we show the 68% and 95% c.l. constraints for $\alpha /\alpha _0$ versus H0, for the analysis of the variation of $\alpha $ alone. The results correspond to different data sets: all the CMB data alone; all the CMB data plus the H0 prior taken from Riess et al. (2009); and all the CMB data plus the power spectrum from Sloan Digital Sky Survery DR7 LRG (Reid et al. 2010). The large degeneracy between $\alpha /\alpha _0$ and H0 from CMB data is reduced when another data set is added. However, since the value of H0 obtained from the extra data sets are different, the obtained constraint on $\alpha /\alpha _0$ depends strongly on the data chosen for the analysis. Nevertheless, the results are consistent within 1-$\sigma $.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg1.eps} \end{figure} Figure 1:

68% and 95% c.l. constraints for $\alpha /\alpha _0$ versus H0, for the analysis of the variation of $\alpha $ alone. Results from different data sets.

Open with DEXTER

In Fig. 2 we present the constraints for $\alpha /\alpha _0$ versus $\tau $ and in Fig. 3 we present the constraints for $\alpha /\alpha _0$ versus $\Omega _{\rm b} h^2 $. There are degeneracies among these parameters. The contours change because of the different mean value of $\alpha /\alpha _0$ obtained with different data sets.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg2.eps} \end{figure} Figure 2:

68% and 95% c.l. constraints for $\alpha /\alpha _0$ versus $\tau $, for the analysis of the variation of $\alpha $ alone. Results from different data sets.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg3.eps} \end{figure} Figure 3:

68% and 95% c.l. constraints for $\alpha /\alpha _0$ versus $\Omega _{\rm b} h^2 $, for the analysis of the variation of $\alpha $ alone. Results from different data sets.

Open with DEXTER

In Fig. 4 we present the result for the case where only $m_{\rm e}$ was allowed to vary. The degeneracy between $m_{\rm e}/m_{\rm e0}$and H0 is larger than between $\alpha /\alpha _0$ and H0, making impossible to find reliable constraints using CMB data alone. When another data set is added, the bounds result tighter, but the mean value for $m_{\rm e}/m_{\rm e0}$ depends strongly on which data set was added. Results are marginally consistent at 1-$\sigma $.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg4.eps} \end{figure} Figure 4:

68% and 95% c.l. constraints for $m_{\rm e}/m_{\rm e0}$ versus H0, for the analysis of the variation of $m_{\rm e}$ alone. Results from different data sets.

Open with DEXTER

The constraints on $m_{\rm e}/m_{\rm e0}$ versus $\tau $ are shown in Fig. 5, and on $m_{\rm e}/m_{\rm e0}$ versus $\Omega _{\rm b} h^2 $ are shown in Fig. 6. In both cases, the results depend on the data set added to CMB data in the statistical analysis.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg5.eps} \end{figure} Figure 5:

68% and 95% c.l. constraints for $m_{\rm e}/m_{\rm e0}$ versus $\tau $, for the analysis of the variation of $m_{\rm e}$ alone. Results from different data sets.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg6.eps} \end{figure} Figure 6:

68% and 95% c.l. constraints for $m_{\rm e}/m_{\rm e0}$ versus $\Omega _{\rm b} h^2 $, for the analysis of the variation of $m_{\rm e}$ alone. Results from different data sets.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg7.eps} \end{figure} Figure 7:

68% and 95% c.l. constraints for the joint variation of $\alpha $ and $m_{\rm e}$ from different data sets.

Open with DEXTER

In Fig. 7 we show the posterior distribution for $\alpha /\alpha _0$ and $m_{\rm e}/(m_{\rm e})_0$, for the case of joint variation of these quantities, marginalized over the cosmological parameters. The results correspond to different data sets. The difference in the contours is mainly due to the large degeneracy of $m_{\rm e}$ and H0, and the different H0 values derived from the Sloan power spectrum and from the H0 prior. We see that the mean value of $m_{\rm e}$ is more affected than the mean value of $\alpha $. These results can also be seen in Table 2.

A variation of $\alpha $ or $m_{\rm e}$ affects the recombination scenario (see Scóccola et al. 2009, for example). As a consequence, the angular diameter distance at recombination is modified if any of these constants varies. This results in a change in the Doppler peak positions and heights (see Kaplinghat et al. 1999, for example). This explains the degeneracy between $\alpha $ and $m_{\rm e}$ shown in Fig. 7 and confirmed by the correlation coefficient. On the other hand, the degeneracy between $\alpha $ or $m_{\rm e}$ with the baryon mass density or the Hubble constant can be explained since these effects are similar to a change in the cosmological parameters. A variation in $\alpha $ and/or $m_{\rm e}$ at recombination, affects mainly the binding energy of hydrogen. This quantity is proportional to $m_{\rm e} \alpha^2$. When only one constant is allowed to vary, its influence on the parameter estimation is similar, regardless of the constant. However, when a joint variation analysis is performed, the results are different for $\alpha $ and $m_{\rm e}$, due to the power with which they enter the hydrogen binding energy. In particular, in Fig. 7, we note that the bounds on $\alpha $ are not affected when including additional data sets to the CMB data. This is due to the fact that $\alpha $ is no longer correlated with H0, as it was shown previously (see, for example, Landau et al. 2008).

4 Conclusions

In this paper we have updated the constraints on the time variation of the fine structure constant $\alpha $ and the electron mass $m_{\rm e}$during recombination epoch, using the latest CMB data, including the 7-yr release of WMAP. We perform several statistical analyses adding two different data sets; the H0 prior taken from Riess et al. (2009); and the power spectrum from Sloan Digital Sky Survery DR7 LRG (Reid et al. 2010). The bounds on the variation of the constants are tighter than previous results because of the higher precision of the new data used in this work.

Our results show no variation of the constants at recombination time. We also emphasize that the constraints depend strongly on which data set we choose in the analysis, due to the large degeneracy between $\alpha $ or $m_{\rm e}$ and H0. Yet, the results are consistent within 1-$\sigma $.

Acknowledgements
The research leading to these results has received funding from the European Community's Seventh Framework Programme ([FP7/2007-2013] under grant agreement No. 237739), and PICT 2007-02184 from Agencia Nacional de Promoción Científica y Tecnológica, Argentina. The authors would like to thank H. C. Chiang for help with compiling the BICEP dataset in COSMOMC.

References

  1. Brown, M. L., Ade, P., Bock, J., et al. 2009, ApJ, 705, 978 [NASA ADS] [CrossRef] [Google Scholar]
  2. Chiang, H. C., Ade, P. A. R., Barkats, D., et al. 2010, ApJ, 711, 1123 [NASA ADS] [CrossRef] [Google Scholar]
  3. García-Berro, E., Isern, J., & Kubyshin, Y. A. 2007, A&AR, 14, 113 [NASA ADS] [CrossRef] [Google Scholar]
  4. Hannestad, S. 1999, Phys. Rev. D, 60, 023515 [NASA ADS] [CrossRef] [Google Scholar]
  5. Jones, W. C., Ade, P. A. R., Bock, J. J., et al. 2006, ApJ, 647, 823 [NASA ADS] [CrossRef] [Google Scholar]
  6. Kaplinghat, M., Scherrer, R., & Turner, M. 1999, Phys. Rev. D, 60, 023516 [NASA ADS] [CrossRef] [Google Scholar]
  7. King, J. A., Webb, J. K., Murphy, M. T., & Carswell, R. F. 2008, Phys. Rev. Lett., 101, 251304 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  8. Kuo, C. L., Ade, P. A. R., Bock, J. J., et al. 2004, ApJ, 600, 32 [NASA ADS] [CrossRef] [Google Scholar]
  9. Landau, S. J., Mosquera, M. E., Scóccola, C. G., & Vucetich, H. 2008, Phys. Rev. D, 78, 083527 [NASA ADS] [CrossRef] [Google Scholar]
  10. Larson, D., Dunkley, J., Hinshaw, G., et al. 2010, ApJS, accepted [arXiv:1001.4635] [Google Scholar]
  11. Levshakov, S. A., Molaro, P., Lapinov, A. V., et al. 2010, A&A, 512, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
  13. Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [NASA ADS] [CrossRef] [Google Scholar]
  14. Malec, A. L., Buning, R., Murphy, M. T., et al. 2010, MNRAS, 403, 1541 [NASA ADS] [CrossRef] [Google Scholar]
  15. Martins, C. J. A. P., Menegoni, E., Galli, S., Mangano, G., & Melchiorri, A. 2010, [arXiv:1001.3418] [Google Scholar]
  16. Menegoni, E., Galli, S., Bartlett, J. G., Martins, C. J. A. P., & Melchiorri, A. 2009, Phys. Rev. D, 80, 087302 [NASA ADS] [CrossRef] [Google Scholar]
  17. Molaro, P., Levshakov, S. A., & Kozlov, M. G. 2009, Nuclear Physics B Proc. Suppl., 194, 287 [Google Scholar]
  18. Murphy, M. T., Webb, J. K., & Flambaum, V. V. 2003, MNRAS, 345, 609 [NASA ADS] [CrossRef] [Google Scholar]
  19. Nakashima, M., Ichikawa, K., Nagata, R., & Yokoyama, J. 2010, J. Cosmology and Astro-Particle Physics, 1, 30 [Google Scholar]
  20. Piacentini, F., Ade, P. A. R., Bock, J. J., et al. 2006, ApJ, 647, 833 [NASA ADS] [CrossRef] [Google Scholar]
  21. Readhead, A. C. S., Mason, B. S., Contaldi, C. R., et al. 2004, ApJ, 609, 498 [NASA ADS] [CrossRef] [Google Scholar]
  22. Reid, B. A., Percival, W. J., Eisenstein, D. J., et al. 2010, MNRAS, 404, 60 [NASA ADS] [CrossRef] [Google Scholar]
  23. Reinhold, E., Buning, R., Hollenstein, U., et al. 2006, Phys. Rev. Lett., 96, 151101 [NASA ADS] [CrossRef] [Google Scholar]
  24. Riess, A. G., Macri, L., Casertano, S., et al. 2009, ApJ, 699, 539 [NASA ADS] [CrossRef] [Google Scholar]
  25. Scóccola, C. G., Landau, S. J., & Vucetich, H. 2008, Phys. Lett. B, 669, 212 [NASA ADS] [CrossRef] [Google Scholar]
  26. Scóccola, C. G., Landau, S. J., & Vucetich, H. 2009, Mem. della Soc. Astron. Italiana, 80, 814 [Google Scholar]
  27. Srianand, R., Chand, H., Petitjean, P., & Aracil, B. 2004, , 92, 121302 [Google Scholar]
  28. Thompson, R. I., Bechtold, J., Black, J. H., et al. 2009, ApJ, 703, 1648 [NASA ADS] [CrossRef] [Google Scholar]
  29. Uzan, J. 2003, Rev. Mod. Phys., 75, 403 [NASA ADS] [CrossRef] [Google Scholar]
  30. Wong, W. Y., Moss, A., & Scott, D. 2008, MNRAS, 386, 1023 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

...[*]
Member of the Carrera del Investigador Científico y Tecnológico, CONICET.
...[*]
Marie Curie fellow.

All Tables

Table 1:   Mean values and 1-$\sigma $ errors for the analysis with variation of only $\alpha $, and only $m_{\rm e}$.

Table 2:   Mean values and 1-$\sigma $ errors for the analysis with the joint variation of $\alpha $ and $m_{\rm e}$.

Table 3:   Mean values and 1$\sigma $ errors for the cosmological parameters using all CMB data and the SDSS DR7 power spectrum.

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg1.eps} \end{figure} Figure 1:

68% and 95% c.l. constraints for $\alpha /\alpha _0$ versus H0, for the analysis of the variation of $\alpha $ alone. Results from different data sets.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg2.eps} \end{figure} Figure 2:

68% and 95% c.l. constraints for $\alpha /\alpha _0$ versus $\tau $, for the analysis of the variation of $\alpha $ alone. Results from different data sets.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg3.eps} \end{figure} Figure 3:

68% and 95% c.l. constraints for $\alpha /\alpha _0$ versus $\Omega _{\rm b} h^2 $, for the analysis of the variation of $\alpha $ alone. Results from different data sets.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg4.eps} \end{figure} Figure 4:

68% and 95% c.l. constraints for $m_{\rm e}/m_{\rm e0}$ versus H0, for the analysis of the variation of $m_{\rm e}$ alone. Results from different data sets.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg5.eps} \end{figure} Figure 5:

68% and 95% c.l. constraints for $m_{\rm e}/m_{\rm e0}$ versus $\tau $, for the analysis of the variation of $m_{\rm e}$ alone. Results from different data sets.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg6.eps} \end{figure} Figure 6:

68% and 95% c.l. constraints for $m_{\rm e}/m_{\rm e0}$ versus $\Omega _{\rm b} h^2 $, for the analysis of the variation of $m_{\rm e}$ alone. Results from different data sets.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{14125fg7.eps} \end{figure} Figure 7:

68% and 95% c.l. constraints for the joint variation of $\alpha $ and $m_{\rm e}$ from different data sets.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.