Characterization of Kepler early-type targets

G. Catanzaro; A. Frasca; J. Molenda-Żakowicz; E. Marilli

doi:10.1051/0004-6361/201014189

Home

All issues

Volume 517 (July 2010)

A&A, 517 (2010) A3

Full HTML

Free Access

Issue		A&A Volume 517, July 2010


Article Number		A3
Number of page(s)		9
Section		Catalogs and data
DOI		https://doi.org/10.1051/0004-6361/201014189
Published online		23 July 2010

A&A 517, A3 (2010)

Characterization of Kepler early-type targets ^,

G. Catanzaro¹ - A. Frasca¹ - J. Molenda-Zakowicz² - E. Marilli¹

1 - INAF - Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
2 - Astronomical Institute of the University of Wroc $\l$ aw, ul. Kopernika 11, 51-622. Wroc $\l$ aw, Poland

Received 3 February 2010 / Accepted 18 March 2010

Abstract
Context. Stellar pulsation offers a unique opportunity to constrain the intrinsic parameters of stars and unveil their inner structure. The Kepler satellite is collecting an enormous amount of data of unprecedent photometric precision, which will allow us to test theory and obtain a very precise tomography of stellar interiors.
Aims. We attempt to determine the stars' fundamental parameters ( $T_{\rm eff}$ , $\log g$ , $v\sin i$ , and luminosity) needed for computing asteroseismic models and interpreting Kepler data. We report spectroscopic observations of 23 early-type Kepler asteroseismic targets, 13 other stars in the Kepler field, that had not been selected to be observed.
Methods. We measured the radial velocity by performing a cross-correlation with template spectra to help us identify non-single stars. Spectral synthesis was performed to derive the stellar parameters of our target stars, and the state-of-the-art LTE atmospheric models were computed. For all the stars of our sample, we derived the radial velocity, $T_{\rm eff}$ , $\log g$ , $v\sin i$ , and luminosities. For 12 stars, we performed a detailed abundance analysis of 20 species, for 16, we could derive only the [Fe/H] ratio. A spectral classification was also performed for 17 stars in the sample.
Results. We identify two double-lined spectroscopic binaries, HIP 96299 and HIP 98551, the former of which is an already known eclipsing binary, and two single-lined spectroscopic binaries, HIP 97254 and HIP 97724. We also report two suspected spectroscopic binaries, HIP 92637 and HIP 96762, and the detection of a possible variability in the radial velocity of HIP 96277. Two of our program stars are chemically peculiar, namely HIP 93941, which we classify as B2 He-weak, and HIP 96210, which we classify as B6 Mn. Finally, we find that HIP 93522, HIP 93941, HIP 93943, HIP 96210 and HIP 96762, are very slow rotators ( $v\sin i < 20$ km s^-1) which makes them very interesting and promising targets for asteroseismic modeling.

Key words: stars: early-type - stars: abundances - stars: fundamental parameters - binaries: spectroscopic

1 Introduction

Kepler is a NASA space mission that was successfully launched on 6 March 2009. Its primary goal is the detection of Earth-size and larger planets orbiting around stars similar to the Sun by means of the method of photometric transits (see Borucki et al. 2009a). Kepler photometry will also be used to detect pulsations in stars selected as Kepler asteroseismic targets by the Kepler Asteroseismic Science Consortium, KASC. The study of their pulsational properties will allow us to investigate their internal structure and to derive accurate stellar radii by means of asteroseismic methods (see Christensen-Dalsgaard et al. 1997). The first results of the Kepler mission, published by Borucki et al. (2009b), confirm the expected high precision of the acquired data, which allows to discover Earth-size planets on Earth-like orbit around stars as faint as 12 mag.

In reality, most of the atmospheric parameters, such as $T_{\rm eff}$ , $\log g$ , and metallicity needed by theoreticians to compute asteroseismic models, come from the Kepler Input Catalogue (KIC), which is based on calibrated photometry. Therefore, any determination of these atmospheric parameters based on ground-based spectroscopic data of Kepler targets is valuable and important. In this paper, we present a detailed spectroscopic analysis of 34 stars of spectral type earlier than F selected in 2007 from the list of candidate Kepler targets with Hipparcos parallaxes provided by Molenda-Zakowicz et al. (2006). At that time, the Kepler mission was still in preparation and the exact position of the Kepler field of view had not been fixed. As a result, it was not known which of our targets would be finally observed by Kepler. Thus we decided to acquire spectra of all the stars with Hipparcos data that were potential asteroseismic targets in the sky region where Kepler was to have been pointed. After defining the mission, 65% of the stars proposed by us were selected as Kepler asteroseismic targets by the steering committee of the KASC. Some results concerning cool stars were published by Molenda-Zakowicz et al. (2008,2007).

For each star, we derive the parameters needed to construct asteroseismic models, i.e., the effective temperature, surface gravity, and the metal abundance. Dealing with asteroseismic radius determination, which means combining stellar atmospheric parameters with large frequency spacing, Stello et al. (2009) show that an accuracy in $T_{\rm eff}$ of $\approx$ 200 K is enough to guarantee an error in the radius of smaller than 4 $\%$ for stars as hot as $\approx$ 6400 K. The same authors also show that the most important parameter is metallicity, an accuracy of $\sigma$ [Fe/H] $\approx$ 0.15 dex corresponding to an error in the radius on the order of 2 $\%$ . To achieve this accuracy, moderate- or high-resolution spectroscopy is fully adequate.

Projected rotational velocity ( $v\sin i$ ) is another essential parameter for constraining asteroseismic models. It provides information about the possible multiplet splitting caused by rapid rotation that could change the structure of the frequency spectrum. In this sense, stars with low values of $v\sin i$ are the most promising asteroseismic targets for Kepler.

Finally, for all our program stars we measure the radial velocity, RV. This can be used to detect new spectroscopic binaries for which we may need to correct the stars' Kepler magnitudes, as well as the magnitudes and colors obtained form ground-based data, for the presence of the secondary component. These corrections are important when deriving the stars' effective temperature and luminosity from photometry. Treating a binary system as a single star may indeed result in the computation of an incorrect asteroseismic model, a spurious interpretation of the frequency spectrum, and a wrong determination of the radius of the star and of any eventual planet. The presence of an unknown component can also influence the frequency pattern of the star with its own frequencies and make our interpretation of the power spectrum totally wrong.

2 Observation and data reduction

2.1 Photometry

The photometric observations were carried out in the Strömgren uvby $\beta$ system with the 91-cm Cassegrain telescope at M.G. Fracastoro station (Serra La Nave, Mt. Etna, 1735 m a.s.l.) of the INAF - Osservatorio Astrofisico di Catania (OAC). The observations were performed with a photon-counting photometer equipped with an EMI 9893QA/350 photomultiplier, cooled to $-15\hbox{$^\circ$ }$ . Owing to poor weather and technical problems, we could observe only 14 of our targets along with three stars in the same field used to determine the zero points (see Table 1). The observations were performed on 2008 December 1 and 2009 June 6 and 7.

A set of uvby standard stars of known Strömgren indices (Lindemann & Hauck 1973) and V magnitude were nightly observed to transform the instrumental magnitudes of the targets into the Strömgren photometric system. Both the V magnitude and Strömgren photometric indices of all the target stars that we were able to observe are given in Table 2.

Table 1: Magnitudes and colors of the zero-point stars from Hauck & Mermilliod (1998).

The average errors are 0.010, 0.010, 0.020, and 0.020 mag for V, b-y, m₁, and c₁, respectively. For the beta index, we find a typical error of 0.020.

Table 2: V magnitude and Strömgren parameters for a subset of the program stars.

2.2 Spectroscopy

The spectra of our program stars were acquired on 13 nights between June 18 and September 17, 2007 and on three nights from July to October 2009 (see Table 3) at the M.G. Fracastoro station of OAC. We used the 91-cm telescope and FRESCO, the fiber-fed REOSC echelle spectrograph of OAC which allows us to obtain spectra in the range of 4300-6800 Å with a resolution R= 21 000. The spectra were recorded on a thinned, back-illuminated (SITE) CCD with $1024 \times 1024$ pixels of 24 $\mu$ m size, whose typical readout noise is about 8 e^- and gain is 2.5 e^-/ADU.

The reduction of spectra, which included the subtraction of the bias frame, trimming, correcting for the flat-field and the scattered light, the extraction of the orders, and the wavelength calibration, was performed using the NOAO/IRAF package. The amount of scattered light correction was about 10 ADU. After dividing the extracted spectra by a flat-field, the residual shape of the spectrum had been removed by dividing each spectral order by a Legendre function of a low order. Typical signal-to-noise ratio (SNR) of our spectra is $\sim$ 50. Finally, the IRAF package rvcorrect was used to compute the velocity correction for the Earth's motion, which moved the spectra into the heliocentric rest frame.

The V magnitudes of our targets range from about 9 to 11 mag since the sample was optimized for stars that are bright enough to have high signal-to-noise ratio in Kepler photometry but do not saturate Kepler CCDs. We acquired spectra for 23 stars falling onto the active pixels of Kepler CCDs, and for 13 stars that had not previously been observed by Kepler or that occupied the gaps on the CCDs or that were not selected as asteroseismic targets by the KASC.

3 Radial velocity

We measured the radial velocity, RV, of our program stars with the IRAF task fxcor by means of the method of cross-correlation (see, e.g., Fitzpatrick 1993; Tonry & Davis 1979) between each order of the echelle spectra of the targets and the corresponding echelle order of the spectrum of HR 1389 (A2IV-V, $v_{\rm hel}=38.97~\rm km~s^{-1}$ ) or $\iota$ Psc (F7 V, $v_{\rm hel}=5.4~ \rm km~s^{-1}$ ) (see Fekel 1999; Nordström et al. 2004) selected as RV standard stars. We excluded from the analysis all spectral ranges heavily affected by telluric absorption lines (e.g., the O₂ band $\lambda$ 6276-6315). For a precise evaluation of the centroids of the CCF peaks in each echelle order, we fitted them with a Gaussian function. To deblend the two CCF peaks seen in SB2 systems, a two-Gaussian fit algorithm was applied.

The radial velocity of program stars were calculated by averaging RV measurements from all the echelle orders with the usual instrumental weight $W_{\rm i}=\sigma_{\rm i}^{-2}$ . The $\sigma_{\rm i}$ values were computed by fxcor, which takes into account the height of the fitted peak and the antisymmetric noise as described by Tonry & Davis (1979). The standard errors in the weighted means were computed on the basis of the errors $\sigma_{\rm i}$ in the RV values for each order (see, e.g., Topping 1972).

We list the radial velocities of our program stars along with their uncertainties in Table 3.

Table 3: Stellar parameters derived for the 23 Kepler asteroseismic targets in the KIC Catalogue and 13 other stars in Kepler field of view, but not yet selected as mission targets.

4 Determination of the atmospheric parameters

We determined the effective temperature, $T_{\rm eff}$ , and surface gravity, $\log g$ , of our program stars by minimizing the difference between the observed and the synthetic H $\beta$ profiles. For the goodness-of-fit parameter, we used $\chi^2$ defined as

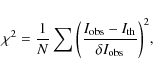
$\begin{displaymath}\displaystyle \chi^2 = \frac{1}{N} \sum \bigg(\frac{I_{\rm obs} - I_{\rm th}}{\delta I_{\rm obs}}\bigg)^2, \end{displaymath}$

where N is the total number of points, $I_{\rm obs}$ and $I_{\rm th}$ are the intensities of the observed and computed profiles, respectively, and $\delta I_{\rm obs}$ is the photon noise. Errors were estimated to be the variation in the parameters that increases the $\chi^2$ by unity. As starting values of $T_{\rm eff}$ and $\log g$ , we determined the effective temperature and gravity from our Strömgren photometry according to the grid of Moon & Dworetsky (1985). The photometric colors were dereddened with the Moon (1985) algorithm. For stars not photometrically observed by us, we used the values quoted by Molenda-Zakowicz et al. (2006). We also proceeded with the determination of rotational velocities by matching Mg II $\lambda$ 4481 Å profile with a synthetic one. The results of our calculations are reported in Cols. 6-8 of Table 3.

$\begin{figure} \par\includegraphics[width=8.9cm,clip]{14189fg1.ps} \vspace*{2mm} \end{figure}$	Figure 1: Example of fitting the synthetic to the observed H $\beta$ lines for four stars from our sample having different rotational velocities and/or different effective temperatures.
Open with DEXTER

In Fig. 1, we show four examples of fitting the synthetic H $\beta$ profile to the observed line in stars with different rotational velocities. The theoretical profiles were computed with SYNTHE (Kurucz & Avrett 1981) on the basis of ATLAS9 (Kurucz 1993) atmosphere models. All the models were computed using solar opacity distribution function (ODF) and microturbulence velocity $\xi$ = 2 km s^-1. All main sequence or slightly evolved stars ( $\log g \geq$ 3.0) have microturbulences between 1.5 and 3.5 km s^-1 (e.g., Gray et al. 2001, and references therein). Neglecting this small dependence on $\xi$ , we can introduce a systematic error not larger than 0.1 dex into the abundance determination.

In Fig. 2, we placed the program stars with parallax errors smaller than 50% on the $\log T_{\rm eff}$ - $\log L/L_\odot$ diagram that we constructed using effective temperatures derived in this paper and the luminosities calculated from both the V magnitudes and the parallaxes reported by van Leeuwen (2007) and listed in Table 3. We evaluated the interstellar extinction $A_{\rm V}$ on the basis the star's distance, assuming a mean extinction of 1.7 mag/kpc on the Galactic plane ( $\vert b\vert < 5\hbox{$^\circ$ }$ ) and 0.7 mag/kpc out of the plane. The de-reddened magnitude was converted into absolute magnitude $M_{\rm V}$ with the parallax and subsequently converted into bolometric magnitude by using the bolometric correction tabulated by Flower (1996) as a function of the effective temperature. The bolometric magnitude of the Sun, $M_{\rm bol} = 4.64$ (Drilling & Landolt 1999), was used to express the stellar luminosity in solar units. The uncertainty in the stellar luminosity accounts for the parallax error.

As can be seen in the figure, most stars are located on the main sequence or slightly above it. Only two stars fall below the main sequence, accounting also for the errors in $T_{\rm eff}$ and luminosity, namely HIP 96343 and HIP 93941. The first lies near the position of metal poor stars, but this is incosistent with its iron abundance ([Fe/H] $\sim0.5$ , see Table 5). This inconsistency could be attributed to the companion star at 9 $\hbox{$^{\prime\prime}$ }$ , which may have affected the observed spectrum leading to wrong stellar parameters. The discrepancy is far more evident for HIP 93941, whose position in the $\log T_{\rm eff}$ - $\log L/L_\odot$ diagram is inconsistent with the star's surface gravity (see Table 3). We discuss this star in more detail in Sect. 5.1.

$\begin{figure} \par\includegraphics[width=8.45cm,clip]{14189fg2.ps} \vspace*{6mm} \end{figure}$

Figure 2:

HR diagram of the stars with relative parallax error $\le$ 50 $\%$ . Light-grey (cyan) dots represent the targets for which a detailed abundance analysis has been performed. Evolutionary tracks for stellar masses ranging from 1.5 to 4.0 solar masses (Siess et al. 2000) have been also displayed (thick lines have been used for the post-main sequence portion of each track). The isochrones at 25 and 50 Myr are plotted with dotted and dash-dotted lines, respectively.

Open with DEXTER

4.1 Spectral classification

We performed a spectral classification of our program stars following the guidelines of Hernández et al. (2004), who apply their scheme to low-resolution spectra. For this purpose, we degraded the resolution of the observed spectra from R = 21 000 to R = 3 000 by convolving the spectra with a Gaussian kernel of the appropriate width. We then, measured the equivalent widths (EW), of H $\gamma$ , He I $\lambda$ 4471, He I $\lambda$ 5876, Mg II $\lambda$ 4481, and other photospheric lines useful to the spectral classification of hot stars. Finally, we assigned spectral types to our program stars using the relation between EW and the spectral type tabulated by Hernández et al. (2004). The uncertainty in our determinations, derived from the agreement between different diagnostics, is typically one spectral subclass but can reach two subclasses for rapid rotators and/or stars that have spectrograms of low signal-to-noise ratio. The spectral types assigned by us to 17 of our program stars are listed in the fifth column of Table 3. The remaining 19 stars had too high $v\sin i$ , too low SNR in their spectrograms, or too low temperature for measuring helium and Mg II lines, and remained unclassified.

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{14189fg3.ps} \end{figure}$	Figure 3: Abundance patterns derived for 12 stars (see Table 4). For the sake of clarity, we excluded from the plot all the chemical elements with Z > 28 (i.e., nickel).
Open with DEXTER

Table 4: Chemical abundances computed for all the low-rotating stars ( $v \sin i <$ 90 km s^-1) of our sample.

5 Metal abundances

We determined stellar abundances of our program stars by computing synthetic spectra that reproduce the observed ones. We therefore, divided the measured spectrograms into several intervals, each 25 Å wide, and derived the abundances in each interval by performing a $\chi^2$ minimization of the difference between the observed and synthetic spectrum. We adopted lists of spectral lines and atomic parameters from Castelli & Hubrig (2004), who updated the parameters listed originally by Kurucz & Bell (1995).

We computed the abundances relative to the solar standard values given by Asplund et al. (2005). For each element, we calculated the uncertainty in the abundance to be the standard deviation of the mean obtained from individual determinations in each interval of the analyzed spectrum. For elements whose lines occurred in one or two intervals only, the error in the abundance ( $\sim$ 0.1 dex) was evaluated by varying the effective temperature and gravity within their uncertainties given in Table 3, $[ T_{\rm eff}~\pm~ \delta T_{\rm eff}]$ and $[\log g~\pm~\delta \log g]$ , and computing the abundance for $T_{\rm eff}$ and $\log g$ values in these ranges. In Table 4, we list the abundances derived with the method described above and applied to 12 stars from Table 3 for which $v\sin i$ does not exceed 90 km s^-1.

Table 5: Iron abundances computed for all the rapid-rotating stars.

For stars with $v\sin i > 90$ km s^-1, the lines are too broad to attempt this kind of analysis and we derived only iron abundance from the equivalent widths of Fe II $\lambda \lambda$ 5018.44, 5316.615 Å. The latter were converted into abundances using WIDTH9 (Kurucz & Avrett 1981) and the ATLAS9 atmospheric models. The results obtained for rapid rotators are listed in Table 5.

For all stars apart from HIP 93941, HIP 95092, HIP 96061, and HIP 96210, which we discuss below, the metal abundances derived in this paper agree with the solar one to within the error bars. We illustrate this in Fig. 3, in which we plot the abundance patterns of elements with the atomic number $Z \le 28$ , derived for the twelve stars listed in Table 4. The heavier elements are not shown for the sake of the clarity in the diagrams.

5.1 HIP 93941

This star was classified to be spectral type B2 (with an uncertainty of two spectral sub-classes) for the first time in this paper. Our classification is consistent with the star's ultraviolet magnitudes (see Carnochan & Wilson 1983) measured by the sky survey S2/68 telescope on-board the ESRO TD1 satellite (Boksenberg et al. 1973) and with its H $\beta$ photoelectric photometry by Deutschman et al. (1976).

Our detailed abundance analysis indicates that HIP 93941 has significant overabundances of silicon ( $\approx$ 2 dex), chromium ( $\approx$ 1.6 dex), and nitrogen ( $\approx$ 1.5 dex), as well as moderate overabundances of calcium, titanium, and iron (all $\approx$ 1 dex) and an underabundance of magnesium. This specific pattern of element abundances resembles the abundances measured in the He-weak star $\alpha$ Scl (see López-García et al. 2001). Taking into account its very low projected rotational velocity, $v\sin i$ = 10 km s^-1, which is typical of this class of stars, we suspected that HIP 93941 is a He-weak star. Thus, to confirm this kind of peculiarity, we attempted to derive the helium abundance by performing a spectral synthesis of the HeI 4471 Å line. According to Leone & Lanzafame (1998), the behavior of this line is quite independent of the microturbulence, and NLTE effects are small for $T_{\rm eff}<20~000$ K. For HIP 93941, we derive an helium abundance [He] = $-0.30~\pm~0.10$ . The error was evaluated by computing the abundance for $T_{\rm eff}$ and $\log g$ within the intervals $[ T_{\rm eff}~\pm~ \delta T_{\rm eff}]$ and $[\log g~\pm~\delta \log g]$ . This make HIP 93941 a very interesting target for the asteroseismic part of the Kepler mission because pulsations have not yet been detected in He-weak stars.

5.2 HIP 95092 and HIP 96061

For these main-sequence stars, normal abundances were derived. The only exception is titanium, which is underabundant by $\approx$ 1 dex in HIP 95092 and overabundant by $\approx$ 1 dex in HIP 96061. Similar anomalies have also been observed in other normal A-type stars, i.e., Vega (Lemke 1989) or $\beta$ Pic (Holweger et al. 1997), so we can consider HIP 95092 and HIP 96061 as normal stars.

5.3 HIP 96210

HIP 96210 shows a general overabundance of carbon, oxygen, and all iron-peak elements with a particularly strong overabundance of manganese ( $\approx$ 2.2 dex) and a strong underabundance of magnesium. With respect to the manganese abundance, and taking into account the values of $T_{\rm eff}$ and $\log g$ for this star, HIP 96210 should be classified as a member of the group of HgMn chemically peculiar stars (see, e.g., Jaschek & Jaschek 1987). We note, however, that this classification needs to be confirmed in additional observations because the spectral range of our data does not cover the blue region of the spectrum around the Hg I $\lambda$ 3984 Å, which is an important diagnostic for this kind of peculiarity.

6 Stars variable in radial velocity

Around 50% of stars of all spectral types are binaries (see Petrie 1960). This also concerns stars selected as Kepler asteroseismic targets. Since an additional component influences the star's magnitude and colors, the contribution from the secondary star has to be computed and removed from the Kepler data before the asteroseismic analysis can begin.

Below, we discuss eight stars that we find to be variable in radial velocity either in our observations or by comparing our results with those published in the literature. In all cases, additional observations are required to study these systems in more detail, and to confirm that the other stars are singles or to eventually detect new spectroscopic binaries among them.

6.1 Double-lined spectroscopic binaries

HIP 96299

This star was discovered to be an eclipsing binary with a period of 10.0486 days by Hartman et al. (2004). We found that it also appears as a double-lined spectroscopic binary. This makes HIP 96299 a very interesting target for the Kepler asteroseismic study since for SB2 eclipsing binaries it is possible to derive accurate values for the mass of the two components, which is a basic ingredient for constraining evolutionary and asteroseismic models. As we acquired only one spectrogram of this star, further observations are needed to obtain its radial-velocity curve and determine its orbital solution.

HIP 98551

This star, which was not selected as a Kepler asteroseismic target, is the second double-lined spectroscopic binary discovered by ourselves. As in the previous case, we have only one spectrogram of this target. HIP 98551 is not known to exhibit eclipses.

6.2 Single-lined spectroscopic binaries

For single-lined binary stars, we cannot derive the masses of the components in the above-mentioned way. We need instead to calculate the systems' mass function: this can be used to estimate the magnitude and color indices of the secondary component of the system and allows us to calculate the duplicity corrections for the primary. In Table 6, we list five stars that we find to be variable in RV. The table also includes the two SB2 systems discussed in Sect.6.1, and an already known SB1 system, namely HIP 98814.

HIP 92637

This star was observed spectroscopically by Dworetsky et al. (1982), who used the X-spectrograph mounted on the 1.5 telescope at Mount Wilson during May-August 1975 with the aim of classifying to the MK system the ``ultraviolet objects'' from the S2/68 experiment. Dworetsky et al. (1982) classify HIP 92637 as B4V:, which is in a rough agreement with our classification, and measure the star's radial velocity, to be $27 \pm 36$ km s^-1. The measurement of RV by Dworetsky et al. (1982) is very inaccurate but still differs significantly from the RV measured in our spectra. We then classify HIP 92637 as a suspected SB1, which should be targeted by future observations.

Table 6: Spectroscopic binaries and stars with possible RV variations.

HIP 96277

The RV of this star shows a peak-to-peak scatter in our three spectra of the order of three times the average uncertainty in our measurements. Therefore, we classify it as a possible SB1 and note that additional observations are needed to confirm this finding.

HIP 96762

This star was observed by Fehrenbach & Burnage (1990) with the objective prism at the Observatorie de Haute-Provence. The radial velocity measured by these authors, $24 \pm 6$ km s^-1, notwithstanding the relatively large uncertainty, is higher than the RV reported in the present paper ( $16.5 \pm 1.1$ km s^-1) by 1.2 $\sigma_{RV}$ . As such, this is another suspected SB1 system.

HIP 97254

This is another star observed by Fehrenbach & Burnage (1990). The significant difference between the RV measured by these authors and that reported in this paper, $\Delta RV\simeq 13$ km s^-1 (i.e., more than 3 $\sigma_{RV}$ ), allows us to conclude that HIP 97254 is a new SB1 system.

HIP 97724

For this star also the radial velocity measured by Fehrenbach & Burnage (1990) differs significantly from the value measured by ourselves. Therefore, we classify HIP 97724 as the second new SB1 star in our sample.

HIP 98814

This star was discovered to be an eclipsing binary of the Algol type by Ceraski (1904). The spectroscopic study of Struve (1946) showed that HIP 98814 is a single-lined spectroscopic binary with a circular orbit of semi-amplitude K = 68 km s^-1 and an orbital period of 3.3177 days. Our single data-point, $RV = -40.70 \pm 3.51$ , phased with the orbital period of 3.3178 d determined by Hartman et al. (2004) from photometric observations, follows the RV curve of Struve (1946), which has a rather large scatter being based on old plate spectra.

We note that the RV curve obtained by Struve (1946) remains the only determination available to date for this star. Two subsequent spectrograms acquired by Etzel & Olson (1993) at the Mount Laguna Observatory (San Diego, California, USA) were used by the authors to derive the star's projected rotational velocity, of $41 \pm 7$ km s^-1, which is in a very good agreement with the value reported in the present paper. Etzel & Olson (1993) do not provide the RV for HIP 98814 obtained from their data.

7 Conclusions

We have discussed the atmospheric and kinematical properties of 23 Kepler asteroseismic targets and an additional 13 stars falling in the Kepler field of view that had not been selected as mission targets. We measured the stars' radial velocity and the projected rotational velocity, and derived the effective temperature, the surface gravity, and the abundances of up to 20 different species. In this last task, the number of analyzed species depended on the SNR of the individual spectrograms and the rotational velocity of the target.

We identified two double-lined spectroscopic binaries, HIP 96299 and HIP 98551, two single-lined spectroscopic binaries, HIP 97254 and HIP 97724, two suspected SB1 systems, HIP 92637 and HIP 96762, and one star, HIP 96277, whose tentative variations in RVhave to be confirmed with additional observations. More spectra are needed to measure the radial-velocity curves of these stars and compute the systems' orbital solutions, as well as attempt to detect secondary components in high-resolution spectrograms of the SB1 stars. SB2 systems, especially those that are also eclipsing binaries, are important asteroseismic targets for Kepler since for them it is possible to compute the masses of the components, which places strong constraints on the asteroseismic models that fit the observed frequency spectrum.

For 17 stars in our sample, we computed a MK spectral classifications and for 28 stars we performed an abundance analysis. We also discovered two stars that are chemically peculiar, namely, HIP 96210, which we classified as a suspected HgMn star, and HIP 93941, classified as He-weak. A full, detailed analysis of the abundances of the Kepler targets will require acquisition of high-resolution, spectrograms of high signal-to-noise ratio covering a wide part of the optical domain, which is planned for the most interesting Kepler targets. However, such high-quality data could be probably obtained only for a quite small fraction of all the stars observed by Kepler, due to their faintness and the availability of high-resolution echelle spectrographs at large-aperture telescopes in the northern hemisphere.

Therefore, we emphasize the importance of low- and medium-resolution spectroscopic and multicolor photometric observations of Kepler targets, which can be acquired for a high number of stars with medium-sized telescopes and will allow us to maximize the scientific output of the mission.

Finally, we draw attention to five Kepler targets, HIP 93522, 93941, 93943, 96210, and 96762, which are of very low projected rotational velocity ( $v\sin i < 20$ km s^-1). Were they to be true slowly-rotating stars (not nearly pole-on fast rotators), they would be very promising targets for asteroseismology since an unambiguous interpretation of the observed frequency spectrum would then be possible. We note that HIP 93941, 96210 and 96762 are B-type stars, which makes them even more interesting because so slowly rotating stars of this spectral class are rare.

Acknowledgements

J.M.Z. acknowledges the MNiSW grant N203 014 31/2650 and thanks the Astronomical Institute of the University of Wroc $\l$ aw for financial support. We made use of the SIMBAD database, operated at CDS, Strasbourg, France, and the NASA's Astrophysics Data System.

References

Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ASP Conf. Ser., ed. T. G. Barnes III, & F. N. Bash, 336, 25 [Google Scholar]
Boksenberg, A., Evans, R. G., Fowler, R. G., et al. 1973, MNRAS, 163, 291 [NASA ADS] [Google Scholar]
Borucki, W. J., Koch, D., Batalha, N., et al. 2009, in Transiting Planets, Proc. IAU Symp., 253, 289 [Google Scholar]
Borucki, W. J., Koch, D., Jenkins J., et al. 2009, Science, 325, 709 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Brancewicz, H. K., & Dworak, T. Z. 1980, Acta Astron., 30, 501 [Google Scholar]
Carnochan, D. J., & Wilson, R. 1983, MNRAS, 202, 317 [NASA ADS] [Google Scholar]
Castelli, F., & Hubrig, S. 2004, A&A, 425, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ceraski, W. 1904, Astron. Nachr., 166, 77 [NASA ADS] [CrossRef] [Google Scholar]
Christensen-Dalsgaard, J., Arentoft, T., Brown, T. M., et al. 2007, Commun. Asteroseismol., 150, 350 [NASA ADS] [CrossRef] [Google Scholar]
Drilling, J. S., & Landolt, A. U. 1999, in Allen's Astrophysical Quantities, 4th edn., ed. A. N. Cox (Los Alamos, NM), 381 [Google Scholar]
Cutri R. M., Skrutskie M. F., Van Dyk S., et al. 2003, 2MASS All-Sky Catalog of Point Sources, University of Massachusetts and Infrared Processing and Analysis Center, California Institute of Technology [Google Scholar]
Deutschman, W. A., Davis, R. J., & Schild R. E. 1976, ApJS, 30, 97 [NASA ADS] [CrossRef] [Google Scholar]
Dworetsky, M. M., Whitelock, P. A., & Carnochan, D. J. 1982, MNRAS, 201, 901 [NASA ADS] [Google Scholar]
Etzel, P. B., & Olson E. C. 1993, AJ, 106, 1200 [NASA ADS] [CrossRef] [Google Scholar]
Fekel, F. C. 1999, in Precise Stellar Radial Velocities, ed. J. B. Hearnshaw, & C. D. Scarfe, IAU Coll. 170, ASP Conf. Ser., 185, 378 [Google Scholar]
Fitzpatrick, M. J.1993, in Astronomical Data Analysis Software and System II, ed. R. J. Hanish, R. V. J. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 472 [Google Scholar]
Fehrenbach, Ch., & Burnage, R. 1990, A&AS, 83, 91 [Google Scholar]
Fehrenbach, Ch., Duflot, M., Mannone, C., Burnage, R., & Genty V. 1997, A&AS, 124, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
Giuricin, G., Mardirossian, F., & Mezzetti, M. 1983, ApJS, 52, 35 [NASA ADS] [CrossRef] [Google Scholar]
Gray, R. O., Graham, P. W., & Hoyt, S. R., AJ, 121, 2159 [Google Scholar]
Hall, D. S., & Wawrukiewicz, A. S. 1972, PASP, 84, 541 [NASA ADS] [CrossRef] [Google Scholar]
Hartman, J. D., Bakos, G., Stanek, K. Z., & Noyes, R. W. 2004, AJ, 128, 1761 [NASA ADS] [CrossRef] [Google Scholar]
Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Hernández, J., Calvet, N., Briceño, C., Hartmann, L., & Berlind P. 2004, AJ, 127, 1682 [NASA ADS] [CrossRef] [Google Scholar]
Holweger, H., Hempel, M., van Thiel, T., & Kaufer, A. 1997, A&A, 320, L49 [NASA ADS] [Google Scholar]
Jaschek, C., & Jaschek, M. 1987, The classification of stars (Cambridge: University Press) [Google Scholar]
Kopal, Z. 1956, Annales d'Astrophysique, 19, 298 [Google Scholar]
Kurucz, R. L. 1993, A new opacity-sampling model atmosphere program for arbitrary abundances, in Peculiar versus normal phenomena in A-type and related stars, IAU Coll., 138, ed. M. M. Dworetsky, F. Castelli, R. Faraggiana, ASP Conf. Ser., 44, 87 [Google Scholar]
Kurucz, R. L., & Avrett E. H. 1981, SAO Special Rep., 391 [Google Scholar]
Kurucz, R. L., & Bell B. 1995, Kurucz CD-ROM No. 23 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
Lemke, M. 1989, A&A, 225, 125 [Google Scholar]
Leone, F., & Lanzafame, A. C. 1998, A&A, 330, 306 [NASA ADS] [Google Scholar]
Lindemann, E., & Hauck, B. 1973, A&AS, 11, 119 [NASA ADS] [Google Scholar]
López-García, Z., Adelman, S. J., & Pintado, O. I. 2001, A&A, 367, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Molenda-Zakowicz, J., Arentoft, T., Kjeldsen, H., & Bonanno, A., 2006, Proc. SOHO 18/GONG 2006/HELAS I, ESA SP-624, ed. K. Fletcher, & M. Thompson, Published on CDROM, 110.1 [Google Scholar]
Molenda-Zakowicz, J., Frasca, A., Latham, D. W., & Jerzykiewicz M. 2007, Acta Astron., 57, 301 [NASA ADS] [Google Scholar]
Molenda-Zakowicz, J., Frasca, A., & Latham, D. W. 2008, Acta Astron., 58, 419 [NASA ADS] [Google Scholar]
Moon, T. T. 1985, Communications from the University of London Obs., No. 78 [Google Scholar]
Moon, T. T., & Dworetsky, M. M. 1985, MNRAS, 217, 305 [NASA ADS] [CrossRef] [Google Scholar]
Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Petrie, R. M. 1960, AJ, 65, 55 [NASA ADS] [CrossRef] [Google Scholar]
Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 385, 593 [NASA ADS] [Google Scholar]
Stello, D., Chaplin, W. J., Bruntt, H., et al. 2009, ApJ, 700, 1589 [NASA ADS] [CrossRef] [Google Scholar]
Struve, O. 1946, AJ, 104, 253 [Google Scholar]
The Hipparcos Catalogue 1997, ESA SP-1200 [Google Scholar]
Tonry, J., & Davis, M. 1979, AJ, 84, 1511 [NASA ADS] [CrossRef] [Google Scholar]
Topping, J. 1972, Errors of Observation and Their Treatment (Chapman and Hall Ltd.), 89 [Google Scholar]
van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Footnotes

... targets: Based on observations collected with the telescope at the M.G. Fracastoro station of the INAF - Osservatorio Astrofisico di Catania.
...: Reduced spectra are only available in electronic form atthe CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/517/A3
... KASC: http://astro.phys.au.dk/KASC
... package: IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc.

Copyright ESO 2010

All Tables