EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 517 (July 2010) A&A, 517 (2010) A18 Full HTML
Free Access
Issue
A&A
Volume 517, July 2010
Article Number A18
Number of page(s) 6
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201014076
Published online 27 July 2010
A&A 517, A18 (2010)

Launching of jets by cold, magnetized disks in Kerr metric

A. Sadowski - M. Sikora

N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland

Received 15 January 2010 / Accepted 16 April 2010

Abstract
We confirm Cao's discovery that in the vicinity of fast rotating black holes jets can be launched centrifugally by cold, magnetized disks even for nearly vertically shaped magnetic flux surfaces. Outflows produced under such extreme conditions are investigated via studying kinematics of test particles in the force-free magnetosphere approximation. Implications of a possibility of magneto-centrifugal launching of very well collimated central outflows around the fast rotating black holes are discussed in the general context of the jet formation scenarios in AGNs.

Key words: black hole physics - accretion, accretion disks - magnetic fields

1 Introduction

According to a popular class of astrophysical jet models they are powered by the rotational energy of accretion disks and mass loaded via ``magnetocentrifugal'' forces. For Newtonian accretion disks such models require the poloidal magnetic field lines to be inclined towards the geometrically thin accretion disk by less than 60 degrees, independently of the distance from the central object (Blandford & Payne 1982). For disks around black holes (BHs) this angle depends on the radius and the BH spin (Cao 1997; Lyutikov 2009). The effect is that the smaller the distance and the larger BH spin, the larger the angle. At the inner edge of a Keplerian disk (located at the marginally stable orbit - $r_{\rm ms}$) and for the maximal BH spin it approaches $90^{\circ}$. We confirm these results and investigate the kinematics of test particles in the fixed force-free magnetosphere. Our paper is organized as follows. General equations describing the particle kinematics are derived in Sect. 2. The geometry of the effective equipotential surfaces and of ``light cylinders'' are presented in Sect. 3. The kinematics of test particles and its dependence on the BH spin and the launching distance is illustrated in Sect. 4. The results are discussed in a general context of the production of relativistic jets in active galactic nuclei in Sect. 5 and are summarized in Sect. 6.

2 A rigid rotation of particle trajectories in the Kerr metric

It is convenient to investigate the kinematics of particles forced by magnetic fields to move on rigidly rotating trajectories in a frame co-rotating with magnetic field lines. In a frame like this the norm of a 4-velocity, uiui=-1, is in the Kerr metric given by

$\displaystyle % \left(g_{tt} + 2 g_{t\phi} \Omega_0 + g_{\phi\phi} \Omega_0^2\r... ...t(u^t\right)^2 + 2 \left(g_{t\phi} + g_{\phi\phi}\Omega_0 \right) u^t u^{\phi'}$    
$\displaystyle + g_{\phi\phi} \left(u^{\phi'}\right)^2 + g_{rr} \left(u^r\right)^2 + g_{\theta\theta} \left(u^{\theta}\right)^2$ = -1,
(1)

where $\phi' = \phi - \Omega_0 t$, $u^{\phi'} = u^{\phi} - \Omega_0 u^t$, $\Omega_0 =$ const., the t, $\phi$, r, and $\theta$ are the Boyer-Lindquist coordinates, and $g_{ik} = g_{ik}(r,\theta; a)$ are the Kerr metric components. Throughout the paper the following quantities are expressed in dimensionless units: radius r: r/(GM/c2), BH spin a*= J/(GM2/c), and angular velocity $\Omega_0: \Omega_0/(c^3/GM)$, where M and J are the BH mass and angular momentum, respectively.

For a particle trajectory, which in the rotating frame is described by functions $r = r(\theta)$ and $\phi' = \phi'(\theta)$, the r and $\phi'$ components of the particle 4-velocity are $u^{r} = r_{,\theta} u^{\theta}$ and $u^{\phi'} = {\phi'}_{,\theta} u^{\theta}$, respectively. Then the norm of the 4-velocity reads

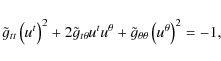
\begin{displaymath}% \tilde g_{tt} \left(u^t\right)^2 +2\tilde g_{t\theta} u^tu^{\theta} +\tilde g_{\theta\theta} \left(u^{\theta}\right)^2 = -1, \end{displaymath} (2)

where
                        $\displaystyle \tilde g_{tt}$ = $\displaystyle g_{tt} + 2g_{t\phi}\Omega_0 + g_{\phi\phi}\Omega_0^2,$ (3)
$\displaystyle % \tilde g_{t\theta}$ = $\displaystyle \left(g_{t\phi} + g_{\phi\phi} \Omega_0\right) {\phi'}_{,\theta},$ (4)
$\displaystyle % \tilde g_{\theta\theta}$ = $\displaystyle g_{\theta\theta} + g_{rr} \left(r_{,\theta}\right)^2 + g_{\phi\phi} \left({\phi'}_{,\theta}\right)^2.$ (5)

Noting that

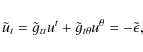
\begin{displaymath}% \tilde u_t = \tilde g_{tt} u^t + \tilde g_{t\theta} u^{\theta} = -\tilde \epsilon, \end{displaymath} (6)

where $\tilde \epsilon$ is the specific energy of a particle moving along a rigidly rotating trajectory, one can find inserting ut from Eq. (6) into (2) that

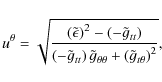
\begin{displaymath}% u^{\theta} = \sqrt{{\left(\tilde \epsilon\right)^2 - \left(... ...\tilde g_{\theta\theta} + \left(\tilde g_{t\theta}\right)^2}}, \end{displaymath} (7)

and
                            ut = $\displaystyle {\tilde \epsilon \over \left(-\tilde g_{tt}\right)} + {\tilde g_{t\theta} \over \left(-\tilde g_{tt}\right)} ~ u^{\theta}$  
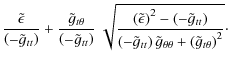
  = $\displaystyle {\tilde \epsilon \over \left(-\tilde g_{tt}\right)} + {\tilde g_{... ...g_{tt}\right)\tilde g_{\theta\theta} + \left(\tilde g_{t\theta}\right)^2}}\cdot$ (8)

Hence, the kinematics of a test particle is fully determined for a fixed particle trajectory and a given constant of motion $\tilde \epsilon$. This kinematics can be illustrated in the locally non-rotating frame (Bardeen et al. 1972), i.e. the frame of zero-angular-momentum-observers (ZAMO). In this frame the line element is

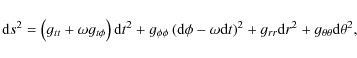
\begin{displaymath}% {\rm d}s^2 = \left(g_{tt} + \omega g_{t\phi}\right) {\rm d}... ...ight)^2 + g_{rr}{\rm d}r^2 + g_{\theta\theta} {\rm d}\theta^2, \end{displaymath} (9)

where $\omega= -g_{t\phi}/g_{\phi\phi}$ is the angular velocity of ``the dragged inertial frames''. Then the projection of the 4-velocity onto the orthonormal tetrad of the local Minkowski space can be used to calculate the Lorentz factor and velocity components of a particle in the ZAMO frame:
$\displaystyle \gamma$ = $\displaystyle u^{(t)} = u^t ~ \sqrt{-g_{tt} + g_{t\phi}^2/g_{\phi\phi}},$ (10)
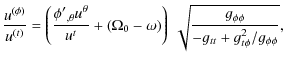
$\displaystyle % v^{(\phi)}$ = $\displaystyle {u^{(\phi)} \over u^{(t)}} = \left({{\phi'}_{,\theta} u^{\theta} ... ...ga\right)\right)~ \sqrt{g_{\phi\phi} \over -g_{tt} + g_{t\phi}^2/g_{\phi\phi}},$ (11)
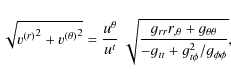
                                 v(p) $\textstyle \equiv$ $\displaystyle \sqrt{{v^{(r)}}^2 + {v^{(\theta)}}^2} = {u^{\theta} \over u^t} ~ ... (12)

where the physical velocities v(i) are expressed in speed of light units.

3 Effective potential

An effective potential defined as the minimum energy of test particles forced to rotate with a given angular velocity $\Omega _0$ is $V_{\rm eff} = \sqrt{-\tilde g_{tt}}$ (obtained from Eq. (7) setting $u^\theta=0$). Its equipotential surfaces, $V_{\rm eff}(r,\theta)={\rm const}.$, are illustrated in Fig. 1[*]. They are enclosed between the inner and outer ``light cylinders'' given by $\tilde g_{tt} = 0$ (Lyutikov 2009). Locations of the inner and outer light cylinders in the equatorial plane are presented in Fig. 2. For a given spin the cylinders coincide at the photon orbit. For a*>0.91 and the angular velocity $\Omega _0$ corresponding to the marginally stable orbit $r_{\rm ms}$ the outer light cylinder is enclosed by the BH ergosphere. In Fig. 3 we show the dependence of the equatorial and asymptotic locations of the outer light cylinder on the BH spin for $\Omega _0$ calculated at the marginally stable orbit. The asymptotic radius is always close to its equatorial plane value (e.g. 14.7M vs. 13.6M for a non-rotating BH).

\begin{figure} \par\subfigure[$a^*=0$ ]{\includegraphics[width=8cm,clip]{aa14076... ...udegraphics[width=8cm,clip]{aa14076-10-fig1b.eps} } \vspace*{1.5mm} \end{figure} Figure 1:

Equipotential surfaces of the effective potential $(V_{\rm eff} = \sqrt{-\tilde g_{tt}})$ for $\Omega _0=\Omega _0(r=r_{\rm ms},a^*)$ for a non-rotating ( top) and spinning ( bottom panel) BHs. The thick solid lines represent $V_{\rm eff}(r,\theta )=V_0\equiv V_{\rm eff}(r=r_{\rm ms},\theta =\pi /2)$ being the effective potential crossing the equator at $r=r_{\rm ms}$. The dashed lines present locations of the inner and outer light cylinders. The thin solid lines are drawn for the following values of the effective potential: $\frac69$, $\frac79$, $\frac89$, $\frac{10}9$, $\frac{11}9V_{0}$.

Open with DEXTER

Equipotential surfaces, ${\rm d}V_{\rm eff}=0$, intersect the equatorial plane at angles

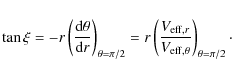
\begin{displaymath}% \tan \xi = -r \left({\rm d}\theta \over {\rm d}r \right)_{\... ...f},r} \over V_{{\rm eff},\theta} \right)_{\theta = \pi/2}\cdot \end{displaymath} (13)

Because $V_{{\rm eff},\theta}\vert _{\theta=\pi/2} = 0$, while $V_{{\rm eff},r}\vert _{\theta=\pi/2} = 0$only at r=r0 at which the Keplerian law is satisfied, i.e.

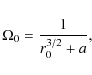
\begin{displaymath}% \Omega_0 = {1 \over r_0^{3/2} +a}, \end{displaymath} (14)

this angle is $\xi = \pi/2$ for all radii, but r=r0. At r=r0 this angle can be found by applying in Eq. (13) the L'Hospital's rule and by noting that $V_{{\rm eff},r\theta}\vert _{\theta=\pi/2}=0$. This gives
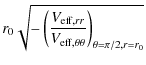
                 $\displaystyle % \tan{\xi_0}$ = $\displaystyle r_0 \sqrt{-\left(V_{{\rm eff},rr} \over V_{{\rm eff},\theta\theta} \right)_{\theta=\pi/2, r=r_0}}$  
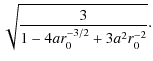
  = $\displaystyle \sqrt{3 \over 1-4a r_0^{-3/2} + 3a^2 r_0^{-2}}\cdot$ (15)

This formula fully agrees with the formula obtained by Cao (1997) and Lyutikov (2009). The dependence of $\xi _0$ on the radius r0 and on the BH spin is shown in Fig. 4.

\begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig2.eps}\vspace*{1.5mm} \end{figure} Figure 2:

Locations of the inner and outer light cylinders for $\theta =\pi /2$ as a function of radius r0 defining the angular velocity $\Omega _0$. Inner and outer cylinders are represented by curves below and above the dashed line r=r0, respectively. Dotted curves denote locations of light cylinders for $r_0<r_{\rm ms}$. Profiles for three values of the BH spin (-0.999, 0, 0.999) are presented.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig3.eps}\vspace*{1.5mm} \end{figure} Figure 3:

Locations of the light cylinders for $\Omega _0=\Omega _0(r=r_{\rm ms})$ versus BH spin. The location of the outer light cylinder is shown for the equatorial plane (thick, dashed line) as well as its asymptotic $(\theta \rightarrow 0)$ value (thin, dashed line).

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig4.eps} \end{figure} Figure 4:

Critical angle $\xi _0$ dependence on the radius r0. Profiles are shown for different BH spins, starting at the marginally stable orbits.

Open with DEXTER

4 Kinematics of test particles in a force-free magnetosphere

4.1 Purely poloidal magnetic fields

For a strong dynamical domination of large-scale magnetic fields driven by an accretion disk, test particles are restricted to move along magnetic field lines. Being anchored to a differentially rotating accretion disk, the poloidal magnetic field generates differentially rotating magnetosphere. Trajectories of test particles can then be identified with magnetic field lines rotating with an angular velocity of their foot-points (Ferraro 1937). For purely poloidal magnetic fields these trajectories are planar $(\phi'={\rm const}.)$ in the co-rotating frame, the metric component $\tilde g_{t\theta} = 0$ and Eqs. (7) and (8) are reduced to

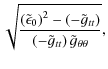
                 $\displaystyle u^{\theta}$ = $\displaystyle \sqrt{ {\left(\tilde \epsilon_0\right)^2 - \left(-\tilde g_{tt}\right) \over \left(-\tilde g_{tt}\right) \tilde g_{\theta\theta}}},$ (16)
ut = $\displaystyle {\tilde \epsilon_0 \over \left(-\tilde g_{tt}\right)},$ (17)

where $\tilde \epsilon_0^2 = - \tilde g_{tt} (\theta=\pi/2, r=r_0)$, $\tilde g_{ik} = \tilde g_{ik}(\theta, r(\theta; r_0))$, and $r(\theta; r_0)$ is the shape of the magnetic field surface, which is determined by the shape of poloidal magnetic field lines.

Test particles can be pulled from the cold disk by centrifugal forces provided the inclination of magnetic field surfaces at the foot-point is smaller than $\xi _0$ and they can proceed further provided the shape of poloidal magnetic field lines satisfies the condition $-\tilde g_{tt} < \tilde \epsilon_0^2$.

Examples of kinematics of the test particles are plotted in Fig. 5. The illustrated cases are calculated for magnetic field lines that are anchored at the marginally stable orbit and have the shape

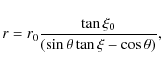
\begin{displaymath}% r = r_0 {\tan{\xi_0} \over \left(\sin{\theta} \tan{\xi} - \cos{\theta}\right)}, \end{displaymath} (18)

which in the coordinate plane ( $r\cos{\theta}$, $r\sin{\theta}$) is the straight line anchored at r=r0 and inclined at the angle $\xi $. The presented velocities and Lorentz factors were calculated in the locally non-rotating frame (see Eqs. (10)-(12)). As we can see from Eq. (8), the particles which are forced to move on rigidly rotating planar trajectories approach the speed of light at the light cylinder. This simply demonstrates that no physical solution exists on and beyond light cylinders for purely poloidal magnetic field structures.

\begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig5.eps} \end{figure} Figure 5:

Dynamics of a particle moving along purely poloidal magnetic field lines achored at $r_{\rm ms}$ and inclined at different angles for non-spinning (solid) and spinning (dashed lines) BHs. The horizontal axis represents the vertical coordinate z.

Open with DEXTER

\begin{figure} \par\subfigure[$a^*=0,\quad\xi=60^{\circ}$ ]{\includegraphics[wid... ...\circ}$ ]{\includegraphics[width=8cm,clip]{aa14076-10-fig6b.eps} }\end{figure} Figure 6:

Velocity components and the Lorentz factor $\gamma $ of particles moving along magnetic field lines with non-zero azimuthal component anchored at $r_{\rm ms}$ and inclined at the critical angle $\xi =\xi _0$ for non-spinning ( top) and spinning ( bottom panel) BHs. The poloidal and azimuthal velocity components are marked by dotted and dashed lines, respectively. The solid curves present the Lorentz factor profiles.

Open with DEXTER

4.2 Force-free magnetosphere with non-zero azimuthal magnetic field component

These constraints do not apply if a toroidal magnetic field component (induced by poloidal electrical currents) is taken into account. In this case Ferraro's law about iso-rotation still applies, i.e. magnetic field lines and therefore particle trajectories still rotate rigidly, but, due to the toroidal magnetic component the rotating trajectories are not planar and the test particles may pass the light cylinder sliding on magnetic field lines in the opposite direction to the rotation of magnetic field surfaces, i.e. with ${\rm d}\phi'/{\rm d}t <0$, which takes place if ${\phi'}_{,\theta} <0$. This can be concluded from Eq. (8) after rewriting it in the form

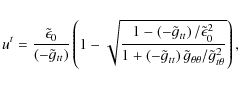
\begin{displaymath}% u^t = {\tilde \epsilon_0 \over \left(-\tilde g_{tt}\right)}... ...ight) \tilde g_{\theta\theta} /\tilde g_{t\theta}^2}}\right), \end{displaymath} (19)

where the metric functions $\tilde g_{ik}$ are calculated along trajectories $r=r(\theta; r_0)$ and $\phi'= \phi'(\theta; r_0)$. At the light cylinder both denominator and numerator ( $-\tilde g_{tt}$ and the expresion in brackets) become zero, and applying L'Hospital's rule one can check that ut and, therefore, $\gamma $ given by Eq. (10) is finite. Hence, the test particle can pass the light cylinder and proceed further provided

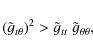
\begin{displaymath}% \left(\tilde g_{t\theta}\right)^2 > \tilde g_{tt} ~ \tilde g_{\theta\theta}, \end{displaymath} (20)

i.e. for respectively high negative values of ${\phi'}_{,\theta}$,

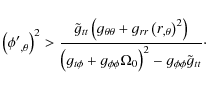
\begin{displaymath}% \left({\phi'}_{,\theta}\right)^2 > {\tilde g_{tt} \left(g_{... ...{\phi\phi}\Omega_0\right)^2 - g_{\phi\phi} \tilde g_{tt}}\cdot \end{displaymath} (21)

Examples of kinematics of test particles for a helical magnetic field structure are illustrated in Fig. 6. The velocity components and the Lorentz factor are computed for $r(\theta; r_0)$ given by Eq. (18) and for

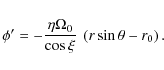
\begin{displaymath}% \phi' = -{\eta \Omega_0 \over \cos{\xi}}~ \left(r \sin{\theta} - r_0\right). \end{displaymath} (22)

This choice of particle trajectories corresponds with the poloidal and toroidal magnetic field components scaling as $B_{\rm p} \sim 1/$ $(r \sin{\theta})^2$ and $B_{\phi} \sim 1/(r \sin{\theta})$, respectively, and equating at the Alfvenic radius which in the force-free limit approaches the light cylinder, $r\sin{\theta}\approx1/\Omega_0$ (in Fig. 7 we plot a visualisation of such a shape of the magnetic field lines).

The upper panel of Fig. 6 presents the velocity and Lorentz factor profiles for a non-spinning BH. The particle is initially at rest with respect to the disk - its poloidal velocity component in the ZAMO frame is zero, while its azimuthal velocity corresponds to the Keplerian angular velocity at r0. Once the particle leaves the equilibrium it starts to be centrifugally accelerated along the magnetic field line. The poloidal velocity component rapidly increases. Because the magnetic field lines are inclined also in the azimuthal direction the particle starts to slide along them in the direction opposite to the disk rotation. Therefore, its angular velocity decreases below the initial value $\Omega _0$. The corresponding profile of the physical velocity in the azimuthal direction $v^{(\phi)}$ is shown. The light cylinder is crossed at $z\approx14~{\rm M}$ with both velocity components close to 0.5c. The profile of the Lorentz $\gamma $ factor is shown by the solid line (please note the vertical scale for $\gamma $ is marked on the right axis). Initially, it corresponds to the Keplerian angular velocity ar $r_{\rm ms}$ ( ${\approx} 1.2$ for a*=0 case). At the light cylinder $\gamma\approx 1.7$. The bottom panel of Fig. 6 presents a similar study of particle dynamics for a rotating BH case. Its behavior is similar, with exception that the $\gamma $ factor is initially strongly dominated by the azimuthal velocity component.

\begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig8.eps} \end{figure} Figure 7:

Shape of the magnetic field lines with $\eta =1.0$ for $\xi =30^{\circ }$ (the thickest solid line), $\xi =45^{\circ }$ and $\xi =60^{\circ }$ (the thinnest solid line). For the latter $(\xi =60^{\circ })$ two other curves are presented for $\eta =0.95$ (dotted line) and $\eta =1.05$ (dashed line). All lines are anchored at $r_{\rm ms}$ and the BH has zero spin. The black spot denotes the location of the BH horizon.

Open with DEXTER

We show the dependence of the test particle kinematics on $\xi $, r0 and $\eta $ in Fig. 8. The upper panel shows that the lower the inclination angle $\xi $, the more rapid the particle acceleration. The middle panel presents the dependence on the $\eta $ parameter, which determines the magnetic field line torsion. The higher the value of $\eta $, the larger the azimuthal component of the particle trajectory. As a result, the particle `slides' more easily in the azimuthal direction, making the centrifugal acceleration less efficient. Finally, the lower panel presents the dependence on the radius r0 defining the location of the magnetic field line foot-point.

The particle kinematics illustrated in this section has an exemplary character and may be applied only to the regions where the structure of the outflow is strongly dominated by the magneto-dynamics. For low mass loading rates, such a force-free approximation can be used to study the matter kinematics even far beyond the light cylinder. However, for high mass-loading rates the force-free approximation can break down even in the sub-Alfvénic region, deep within the light cylinder. In other words, as long as the decreasing with a distance magnetic-to-matter energy flux ratio $(\sigma)$ remains ${\gg}1$, a particle inertia can be considered as a small disturbance to the force-free structure of a flow (see, e.g., Beskin & Nokhrina 2006).

\begin{figure} \par\subfigure{\includegraphics[width=8cm,clip]{aa14076-10-fig8a.... ...ludegraphics[width=8cm,clip]{aa14076-10-fig8c.eps} }\vspace*{-1mm}\end{figure} Figure 8:

Lorentz $\gamma $ factor dependence on the magnetic field line inclination angle $\xi $ ( top panel), $\eta $ parameter ( middle panel) and the r0 radius ( bottom panel) for a non-spinning BH. The vertical dashed lines denote the crossing through the outer light cylinder. If not stated otherwise the parameters are $\xi =60^{\circ }$, $\eta =1.0$ and $r=r_{\rm ms}$.

Open with DEXTER

5 Discussion

A magnetocentrifugal scenario is applicable to the production of nonrelativistic jets in ``Newtonian'' objects like YSOs (young stellar objects). However, it is not clear whether it can explain the production of relativistic jets in BH accretion systems. This is because at least in idealized, steady, axisymmetric models with an accretion disk treated only as the boundary surface, efficient centrifugal mass loading can make the outflows too heavy to be accelerated up to the observed relativistic velocities. Favored mass loading scenarios for such objects involve pair production by photon-photon interactions. For typical BH accretion systems the coronal activities are powerful enough to support density of pairs by many orders of magnitude larger than the Goldreich-Julian density (Phinney 1983; McKinney 2005) in the vicinity of the BH, which allows us to treat the outflows in the ideal MHD approximation. At the same time, the rest mass-energy density of the pair plasma is by several orders lower than energy density of magnetic fields required to power luminous large-scale jets in radio-loud objects, and this implies the formation of relativistic outflows that are at least initially strongly Poynting flux-dominated.

The e+e- jets can be powered by both rotating BHs (Blandford & Znajek 1977; Phinney 1983; Beskin 1997) and accretion disks (Blandford 1976; Lovelace 1976; Lovelace et al. 1987; Ustyugova et al. 2000). These jets need external collimation to be effectively accelerated and converted to the matter-dominated ones (Begelman & Li 1994; Vlahakis & Königl 2003; Narayan et al. 2007; Komissarov et al. 2007; Lyubarsky 2009; Porth & Fendt 2010). The collimation is often considered to be provided by slower, barionic MHD outflows launched in the accretion disk (Sol et al. 1989; Bogovalov & Tsinganos 2005; Gracia et al. 2005; Beskin & Nokhrina 2006). However, this jet structure may need modification for jets launched around fast rotating BHs if the possibility of a centrifugal launching of proton-electron outflows from the innermost portions of an accretion disk was taken into account. Because the inclination angle of the effective potential surfaces is maximal at the inner edge of a disk and rapidly drops with the radius (see Eq. (15) and Fig. 4), the p-e-dominated outflow from the innermost portions of accretion disk is embraced by the Poynting flux-dominated electron-positron outflow. They both are initially Poynting flux-dominated and then predicted to be converted to the matter-dominated ones (see, e.g., Tchekhovskoy et al. 2009; Lyubarsky 2010). This implies less relativistic spines and more relativistic sheaths of jets produced by the accretion disk around fast rotating BHs, or a respective triple jet structure if taking into account the central contribution to the outflow from the BH magnetosphere. In both cases they still may require collimation by non-relativistic MHD outflows produced by the outer portions of a disk.

The production of powerful jets by accretion disks, both centrifugally loaded and by pairs, requires strong large-scale magnetic fields. The possibility of dragging of these fields by accreting plasma, originally suggested by Bisnovatyi-Kogan & Ruzmaikin (1974), is still debated (Lubow et al. 1994; Spruit & Uzdensky 2005; Bisnovatyi-Kogan & Lovelace 2007; Rothstein & Lovelace 2008; Beckwith et al. 2009). The radial distribution of the magnetic field line inclination is another question that is related to this lack of a profound model for the magnetic field evolution in accretion disks. The radial distribution is pivotal to establish a launching distance domain of centrifugal outflows and their initial collimation. And finally, even for a fixed large-scale magnetic field intensity and geometry, the mass loading rate and therefore the terminal speed of the centrifugal outflow depends very much on details of the vertical disk structure (Wardle & Königl 1993; Li 1995; Campbell 1999; Casse & Ferreira 2000; Shalybkov & Rüdiger 2000; Ogilvie & Livio 2001; Levinson 2006), which are usually ignored due to severe uncertainties, which mostly concern the structure of radiation pressure dominated magnetized accretion disks in AGNs.

In particular the proton-electron outflow may need some initial boost to pass a potential barrier which may be produced as a result of the sub-Keplerian character of the boundary layers (due to partial losses of angular momentum taken away by the outflow) or, even for nearly Keplerian boundary layers, the disk finite height (Wardle & Königl 1993; Ogilvie 1997). This boost can be provided by heating or mechanically by some magnetic flaring activities and/or by radiation pressure of effectively super-Eddington flux. An existence of the additional potential barrier may significantly limit mass loading rate which allows proton-electron loaded outflows to reach at least mildly relativistic speeds. The resulting jet structure - a mildly relativistic proton-electron component sandwiched between the pair-dominated relativistic spine and sheath - albeit very speculative at the moment, is very promising from the observational point of view because it may explain a significant proton content of AGN jets deduced from analyses of a matter content in blazars (Sikora & Madejski 2000; Ghisellini et al. 2009) and in radio lobes of powerful radio galaxies (Stawarz et al. 2007; Perlman et al. 2010).

6 Conclusions

The main results of this paper can be summarized as follows:

-
An effective potential and light cylinders are investigated in the rigidly rotating frame in the Kerr metric. The intersection of equipotential surfaces with a geometrically thin disk at the annulus, where a given angular velocity is equal to the Keplerian velocity, gives the critical angle below which a cold outflow can be launched by centrifugal forces. The location of the outer light cylinders is shown to depend strongly on radius and BH spin. Bacause for relativistic Poynting flux-dominated outflows they coincide with the cylindrical radii of Alfvénic surfaces, their location provides approximate information on the spatial scale of the region where the poloidal and toroidal magnetic components are comparable. Noting different scalings of poloidal and toroidal components, one can use this to derive the pitch of magnetic helicity at any distance from the center, which can in turn be verified by polarization measurements (see, e.g., Marscher et al. 2008).
-
The condition for the magnetocentrifugal launching of jets obtained for Keplerian disks rotating around Kerr BHs by Cao (1997) and Lyutikov (2009) is confirmed. It tells us that the maximum inclination angle of magnetic flux surfaces at which cold matter can be extracted from the disk depends on the distance from the BH and on the BH spin. The condition shows that for very fast rotating BHs the central outflows can be launched even along almost vertically shaped magnetic surfaces.
-
We show how kinematics of test particles pulled by centrifugal forces from a Keplerian disk can be algebraicallydetermined for a given magnetic field structure in the force-free outflow approximation. Examples of test particle kinematics are illustrated and the condition for the toroidal magnetic field component is derived to allow the particle to cross the light cylinder.
-
Possible implications for a jet structure are discussed as imposed by the condition for magnetocentrifugal launching of jets by inner portions of magnetized disks around fast rotating BHs. In this case a triple-component structure of a jet can be envisaged, with a proton-electron component of a jet being sandwiched between the relativistic pair-dominated spine and sheath.

Acknowledgements
A.S. and M.S. acknowledge direct support by Polish Ph.D. NN203 304035 and MNiSW NN203 301635 grants, respectively.

References

  1. Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
  2. Beckwith, K., Hawley, J., & Krolik, J. H. 2009, ApJ, 707, 428 [NASA ADS] [CrossRef] [Google Scholar]
  3. Begelman, M. C., & Li, Z.-Y. 1994, ApJ, 426, 269 [NASA ADS] [CrossRef] [Google Scholar]
  4. Beskin, V. S. 1997, Soviet Physics Uspekhi, 40, 659 [NASA ADS] [Google Scholar]
  5. Beskin, V. S., & Nokhrina, E. E. 2006, MNRAS, 367, 375 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bisnovatyi-Kogan, G. S., & Lovelace, R. V. E. 2007, ApJ, 667, L167 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bisnovatyi-Kogan, G. S., & Ruzmaikin, A. A. 1974, Ap&SS, 28, 45 [Google Scholar]
  8. Blandford, R. D. 1976, MNRAS, 176, 465 [NASA ADS] [Google Scholar]
  9. Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
  10. Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bogovalov, S. V., & Tsinganos, K. 2005, MNRAS, 357, 918 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cao, X. 1997, MNRAS, 291, 145 [NASA ADS] [Google Scholar]
  13. Casse, F., & Ferreira, J. 2000, A&A, 361, 1178 [NASA ADS] [Google Scholar]
  14. Ferraro, V. C. A. 1937, MNRAS, 97, 458 [Google Scholar]
  15. Ghisellini, G., Tavecchio, F., Foschini, L., et al. 2010, MNRAS, 402, 497 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gracia, J., Tsinganos, K., & Bogovalov, S. V. 2005, A&A, 442, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [NASA ADS] [CrossRef] [Google Scholar]
  18. Levinson, A. 2006, ApJ, 648, 510 [NASA ADS] [CrossRef] [Google Scholar]
  19. Li, Z.-Y. 1995, ApJ, 444, 848 [NASA ADS] [CrossRef] [Google Scholar]
  20. Lovelace, R. V. E. 1976, Nature, 262, 649 [NASA ADS] [CrossRef] [Google Scholar]
  21. Lovelace, R. V. E., Wang, J. C. L., & Sulkanen, M. E. 1987, ApJ, 315, 504 [NASA ADS] [CrossRef] [Google Scholar]
  22. Lubow, S. H., Papaloizou, J. C. B., & Pringle, J. E. 1994, MNRAS, 267, 235 [NASA ADS] [Google Scholar]
  23. Lyubarsky, Y. E. 2010, MNRAS, 402, 353 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lyutikov, M. 2009, MNRAS, 396, 1545 [NASA ADS] [CrossRef] [Google Scholar]
  25. Marscher, A. P., Jorstad, S. G., D'Accangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  26. McKinney, J. C. 2005, ApJ, submitted [arXiv:astro-ph/0506368] [Google Scholar]
  27. Narayan, R., McKinney, J., & Farmer, A. 2007, MNRAS, 375, 548 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ogilvie, G. I., & Livio, M. 2001, ApJ, 553, 158 [NASA ADS] [CrossRef] [Google Scholar]
  29. Perlman, E. S., Georganopoulos, M., May, E. M., & Kazanas, D. 2010, ApJ, 708, 1 [NASA ADS] [CrossRef] [Google Scholar]
  30. Phinney, E. S. 1983, Ph.D. Thesis, Cambridge University [Google Scholar]
  31. Porth, O., & Fendt, C. 2010, ApJ, 709, 1100 [NASA ADS] [CrossRef] [Google Scholar]
  32. Rothstein, D. M., & Lovelace, R. V. E. 2008, ApJ, 677, 1221 [NASA ADS] [CrossRef] [Google Scholar]
  33. Shalybkov, D., & Rüdiger, G. 2000, MNRAS, 315, 762 [NASA ADS] [CrossRef] [Google Scholar]
  34. Sikora, M., & Madejski, G. 2000, ApJ, 534, 109 [NASA ADS] [CrossRef] [Google Scholar]
  35. Sol, H., Pelletier, G., & Asseo, E. 1989, MNRAS, 237, 411 [NASA ADS] [Google Scholar]
  36. Spruit, H. C., & Uzdensky, D. A. 2005, ApJ, 629, 960 [NASA ADS] [CrossRef] [Google Scholar]
  37. Stawarz, Ł., Cheung, C. C., Harris, D. E., & Ostrowski, M. 2007, ApJ, 662, 213 [NASA ADS] [CrossRef] [Google Scholar]
  38. Tchekhovskoy, A., McKinney, J. C., & Narayan, R. 2009, ApJ, 699, 1789 [NASA ADS] [CrossRef] [Google Scholar]
  39. Vlahakis, N., & Königl, A. 2003, ApJ, 596, 1080 [NASA ADS] [CrossRef] [Google Scholar]
  40. Wardle, M., & Koenigl, A. 1993, ApJ, 410, 218 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ustyugova, G. V., Lovelace, R. V. E., Romanova, M. M., Li, H., & Colgate, S. A. 2000, ApJ, 541, L21 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

...[*]
Please note that the topology of the equipotential surfaces for a non-rotating BH case presented in the upper panel of Fig. 1 corresponds to the topology of similar surfaces obtained in the Newtonian case by Blandford & Payne (1982).

All Figures

  \begin{figure} \par\subfigure[$a^*=0$ ]{\includegraphics[width=8cm,clip]{aa14076... ...udegraphics[width=8cm,clip]{aa14076-10-fig1b.eps} } \vspace*{1.5mm} \end{figure} Figure 1:

Equipotential surfaces of the effective potential $(V_{\rm eff} = \sqrt{-\tilde g_{tt}})$ for $\Omega _0=\Omega _0(r=r_{\rm ms},a^*)$ for a non-rotating ( top) and spinning ( bottom panel) BHs. The thick solid lines represent $V_{\rm eff}(r,\theta )=V_0\equiv V_{\rm eff}(r=r_{\rm ms},\theta =\pi /2)$ being the effective potential crossing the equator at $r=r_{\rm ms}$. The dashed lines present locations of the inner and outer light cylinders. The thin solid lines are drawn for the following values of the effective potential: $\frac69$, $\frac79$, $\frac89$, $\frac{10}9$, $\frac{11}9V_{0}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig2.eps}\vspace*{1.5mm} \end{figure} Figure 2:

Locations of the inner and outer light cylinders for $\theta =\pi /2$ as a function of radius r0 defining the angular velocity $\Omega _0$. Inner and outer cylinders are represented by curves below and above the dashed line r=r0, respectively. Dotted curves denote locations of light cylinders for $r_0<r_{\rm ms}$. Profiles for three values of the BH spin (-0.999, 0, 0.999) are presented.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig3.eps}\vspace*{1.5mm} \end{figure} Figure 3:

Locations of the light cylinders for $\Omega _0=\Omega _0(r=r_{\rm ms})$ versus BH spin. The location of the outer light cylinder is shown for the equatorial plane (thick, dashed line) as well as its asymptotic $(\theta \rightarrow 0)$ value (thin, dashed line).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig4.eps} \end{figure} Figure 4:

Critical angle $\xi _0$ dependence on the radius r0. Profiles are shown for different BH spins, starting at the marginally stable orbits.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig5.eps} \end{figure} Figure 5:

Dynamics of a particle moving along purely poloidal magnetic field lines achored at $r_{\rm ms}$ and inclined at different angles for non-spinning (solid) and spinning (dashed lines) BHs. The horizontal axis represents the vertical coordinate z.

Open with DEXTER
In the text

  \begin{figure} \par\subfigure[$a^*=0,\quad\xi=60^{\circ}$ ]{\includegraphics[wid... ...\circ}$ ]{\includegraphics[width=8cm,clip]{aa14076-10-fig6b.eps} }\end{figure} Figure 6:

Velocity components and the Lorentz factor $\gamma $ of particles moving along magnetic field lines with non-zero azimuthal component anchored at $r_{\rm ms}$ and inclined at the critical angle $\xi =\xi _0$ for non-spinning ( top) and spinning ( bottom panel) BHs. The poloidal and azimuthal velocity components are marked by dotted and dashed lines, respectively. The solid curves present the Lorentz factor profiles.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{aa14076-10-fig8.eps} \end{figure} Figure 7:

Shape of the magnetic field lines with $\eta =1.0$ for $\xi =30^{\circ }$ (the thickest solid line), $\xi =45^{\circ }$ and $\xi =60^{\circ }$ (the thinnest solid line). For the latter $(\xi =60^{\circ })$ two other curves are presented for $\eta =0.95$ (dotted line) and $\eta =1.05$ (dashed line). All lines are anchored at $r_{\rm ms}$ and the BH has zero spin. The black spot denotes the location of the BH horizon.

Open with DEXTER
In the text

  \begin{figure} \par\subfigure{\includegraphics[width=8cm,clip]{aa14076-10-fig8a.... ...ludegraphics[width=8cm,clip]{aa14076-10-fig8c.eps} }\vspace*{-1mm}\end{figure} Figure 8:

Lorentz $\gamma $ factor dependence on the magnetic field line inclination angle $\xi $ ( top panel), $\eta $ parameter ( middle panel) and the r0 radius ( bottom panel) for a non-spinning BH. The vertical dashed lines denote the crossing through the outer light cylinder. If not stated otherwise the parameters are $\xi =60^{\circ }$, $\eta =1.0$ and $r=r_{\rm ms}$.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.