| Issue |
A&A
Volume 517, July 2010
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014009 | |
| Published online | 17 August 2010 | |
Planetary nebulae abundances and stellar evolution II![[*]](/icons/foot_motif.png)
S. R. Pottasch1 - J. Bernard-Salas2
1 - Kapteyn Astronomical Institute, PO Box 800, 9700 AV
Groningen, The Netherlands
2 - Center for Radiophysics and Space
Research, Cornell University, Ithaca, NY-14850-6801, USA
Received 7 January 2010 / Accepted 5 May 2010
Abstract
Context. In recent years mid- and far infrared spectra of
planetary nebulae have been analysed and lead to more accurate
abundances. It may be expected that these better abundances lead to a
better understanding of the evolution of these objects.
Aims. The observed abundances in planetary nebulae are compared
to those predicted by the models of Karakas (2003, Thesis, Monash Univ.
Melbourne) in order to predict the progenitor masses of the various PNe
used. The morphology of the PNe is included in the comparison. Since
the central stars play an important role in the evolution, it is
expected that this comparison will yield additional information about
them.
Methods. First the nitrogen/oxygen ratio is discussed with
relation to the helium/hydrogen ratio. The progenitor mass for each PNe
can be found by a comparison with the models of Karakas. Then the
present luminosity of the central stars is determined in two ways:
first by computing the central star effective temperature and radius,
and second by computing the nebular luminosity from the hydrogen and
helium lines. This luminosity is also a function of the initial mass so
that these two values of initial mass can be compared.
Results. Six of the seven bipolar nebulae can be identified as descendants of high mass stars (4-6 ![]() )
while the seventh is ambiguous. Most of the elliptical PNe have central
stars which descend from low initial mass stars, although there are a
few caveats which are discussed. There is no observational evidence for
a higher mass for central stars which have a high carbon/oxygen ratio.
The evidence provided by the abundance comparison with the models of
Karakas is consistent with the HR diagram to which it is compared. In
the course of this discussion it is shown how ``optically thin''
nebulae can be separated from those which are ``optically thick''.
)
while the seventh is ambiguous. Most of the elliptical PNe have central
stars which descend from low initial mass stars, although there are a
few caveats which are discussed. There is no observational evidence for
a higher mass for central stars which have a high carbon/oxygen ratio.
The evidence provided by the abundance comparison with the models of
Karakas is consistent with the HR diagram to which it is compared. In
the course of this discussion it is shown how ``optically thin''
nebulae can be separated from those which are ``optically thick''.
Key words: stars: abundances - planetary nebulae: general - infrared: ISM - stars: early-type - galaxies: abundances
1 Introduction
Planetary nebulae (hereafter PNe) are an advanced stage of stellar evolution of low and intermediate mass stars. After the asymptotic giant branch (AGB) phase is completed, these stars evolve through the PN stage before ending their lives as white dwarfs. The gaseous nebula seen now as PN is the remnant of the deep convective envelope which once surrounded the core. This core is now seen as the central star of the PN. The present abundances in the nebula reveal information about the chemical processes that took place during the AGB. These processes, which have first been discussed by Iben & Renzini (1981) and Renzini & Voli (1981), change the abundances according to the mass of the star involved and the initial abundances in the star. Thus by investigating the PN abundances it may be possible to assign an initial mass to the star.
Table 1: Elemental abundance of PNe with far-infrared data in addition to optical and UV data.
Models have been made of the evolution of stars of different masses. These were initiated with the discussion of Paczynski (1971) followed by the detailed calculations of Schönberner (1983), Vassiliadis and Wood (1993) and Blöcker (1995). These models refer mostly to post AGB evolution. Models referring to evolution on the AGB have been made by several authors, e.g. Marigo et al. (2003) and Karakas (2003). The latter models predict changes in the chemical composition which have occurred during the evolution and which have been brought to the surface and subsequently expelled as the nebula. It is these models which will be used to compare with observed PN abundances because not only do they follow a star of a given mass over its entire life, but the same is done for an entire sequence of possible masses for several different initial abundances.
The purpose of the present paper is to compare these models with the abundances which we have observed. These abundances have been determined with the help of mid and far infrared observations either from ISO or Spitzer and are quite accurate because they are less affected by possible temperature variations or gradients in the nebula. These observations have already been used (Pottasch & Bernard-Salas 2008 to better determine PN abundance gradients in the galaxy. In an ideal case it might be expected that a comparison of models with observations will lead to: 1) knowledge of the individual properties of the central stars; and 2) confirmation or suggestion for improvement of the models. In practice these goals are rather difficult to reach because of shortcomings of both the observations as well as the models. On the observational side are uncertainties in the effective temperature of the central star, their distances, as well as the accuracy of the measurements. The models presently available are uncertain because the physical conditions in the actual star-nebula system is poorly known. For example, the mass loss along the AGB (and post AGB) is physically not well understood and the initial conditions may not be realistic. Thus models used for comparison are taken from different authors who may use different mass loss rates. Therefore core masses are used where possible although initial masses are given for the Karakas models because the author identifies them as such.
The abundances observed are listed in Table 1. No indication is given there of the spectrum of the central star. A few of these stars are Wolf-Rayet stars for which it may be that some of the evolutionary calculations may not apply. These are the central stars of BD+30 3639, NGC 40, NGC 5315 and NGC 6369. This can be kept in mind when making the comparisons.
The objects were selected to be IR bright (in the diaphragm of the instrument used). This was first done with the ISO spectrometer where almost all of the usable PN spectra were investigated. Later the Spitzer IR spectra of PNe have been investigated. Most of these spectra are as bright or nearly as bright as the ISO PNe. This may at first suggest a bias toward PNe with massive central stars because these initially evolve at the highest luminosity. But the period of high luminosity is expected to be very short so that very few, if any, high mass central star PNe are expected. We therefore may expect that many low mass central star PNe have been observed, not only because of much longer evolution time but also because of the much greater number of low mass objects present. It is expected that most of the observed PNe are reasonably local objects, within a few kpc of the sun.
Nevertheless a confrontation of the models with the observations, even with these limitations, can give interesting insights into the evolution of the PN system. In Sect. 2 the morphology of the nebulae will be discussed, first in relation to the nitrogen/oxygen ratio observed in the nebula, and then the helium abundance will be introduced into the discussion. In Sect. 3 the effective temperature of the central star and the various ways of determining it will be discussed. Then the luminosity of the central stars will be discussed. Because the luminosity is dependent on the distance of the nebula this will also be discussed in this section. In addition a digression will be made into the long-standing question of whether or not a nebula is ``thick'' to photons which ionize hydrogen. This can be done because two different methods of obtaining the nebular luminosity are available, one which makes no assumption concerning the nebular ``thickness'' and one which is dependent on this assumption. In Sect. 4 we investigate whether the expected relation between abundance and luminosity can be seen. Conclusions and discussion are given in the last section.
2 Morphology and abundance
There is a long history of discussion of the nebular morphology and its relation with the nebular abundance. In 1971 Greig (1971) classified the large majority of PN in two categories depending on their shape. He called these categories B (binebulous) and C (centric). He noted that the B nebulae have stronger forbidden lines of N II and O II although he did not directly relate this to abundance. Greig (1972) also noted that the B nebulae have kinematic properties indicating that they are the younger group. Several years later Peimbert (1978) classified the PN solely on the basis of the nebular abundance in four classes. His type I nebulae are nitrogen and helium rich while type II are an intermediate population having nitrogen and helium abundances close to solar. Type III, called ``high velocity'' does not have a substantially different composition as type II while type IV is a poorly understood group called ``halo'' PN which is small in number and will not concern us here.
In the five years that followed it became clear that those nebulae classified as type I also showed morphological similarities. This is summarized in an article by Peimbert & Torres-Peimbert (1983) where many, but certainly not all, the PN listed as type I show morphology given as filamentary and bipolar. The use of abundance to indicate morphology, for example by calling a nebula type I on the basis of an abundance determination, a practice which for some years was common, led to false morphological classification. The morphological classifications listed in Col. 10 of Table 1 are based on detailed study, generally based on optical photographs, which is summarized by Manchado (2003). We also adopt the system which he gives dividing PN into three classes: bipolar (B), elliptical (E) and round (R). This system is not universally used, probably because it is not obvious that there is a fundamental difference between elliptical and round. The classification given is taken mostly from Phillips (2003) who takes this mostly, but not always, from earlier discussions in the literature. Because not all our nebulae are listed by Phillips we have also used other sources (e.g. Stanghellini et al. 1993 and Manchado et al. 1996). There is general agreement as to the classification for more than 90% of the PN but there are cases of disagreement. Stanghellini et al. have classified IC 4191, NGC 5315 and NGC 6369 irregular, but we follow all other observers (e.g. Phillips 2003) in calling them E or R. There is also speculation in the literature concerning the uncertainty introduced by projection effects but we have not attempted to include this uncertainty.
2.1 Nitrogen/oxygen ratio
As discussed above, we have investigated the abundances in a large number of PNe using the mid and far infrared observations from ISO or Spitzer.The resulting abundances are summarized in Table 1, which has been taken mostly from Pottasch & Bernard-Salas (2008) but include a few new results. We regard these results as more accurate than other abundances found in the literature and have the advantage that they have been derived in the same way, which is why we have only used this sample.
A histogram of the nitrogen/oxygen (N/O) ratio for the 33 PN listed in Table 1 is plotted as Fig. 1. Six of the seven bipolar nebulae have a very high log N/O ratio, between 0 and 0.4. The single exception to this is NGC 6445 which clearly has a lower value. Of the five round nebulae (not plotted), four have values of log N/O less than -0.66. The fifth nebula (NGC 5315) has a much higher log N/O ratio (-0.05), closer to that of the bipolar PN. All the elliptical nebulae have log N/O less than -0.8, but mostly in the range -1.0 to -0.4, with the exception of M1-42. This is a rather weak nebula and has been less well studied than the other PN. Thus we confirm the correlation between shape and N/O ratio and show that the morphology seems to change at a log N/O ratio of about -0.1.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{plot1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14009-10/Timg8.png)
|
Figure 1: Histogram of the nitrogen/oxygen ratio of the PNe listed in Table 1. Round PNe are not included in this plot because of the small number of objects. |
| Open with DEXTER | |
2.2 Helium vs. N/O
The helium, nitrogen and oxygen abundances with respect to hydrogen are listed in Table 1. The values of N/O are plotted in Fig. 2 as a function of He/H. The elliptical PNe are plotted as diamonds and the bipolar PNe as asterisks. It can be seen that six of the seven bipolar nebulae lie on the upper right hand side of the figure, while NGC 6445 lies somewhat by itself with a rather low N/O ratio but a rather high value of He/H. The two elliptical PNe which have a high N/O ratio and thus lie close to the six bipolar nebulae are M1-42 and NGC 5315. The abundances predicted by Karakas (2003) for stars of different initial masses are labeled with numbers in the figure indicating the masses used. These masses are connected with lines for each of the three different values of heavy element abundance Z.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{plot2.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14009-10/Timg9.png)
|
Figure 2: The N/O abundance ratio is plotted as a function of He/H. The dashed lines connect the results of the models of Karakas for a given value of Z. The ciphers give the initial masses of the individual models. The individual measured PN abundances are from Table 1. Those referred to in the text also have their names given. |
| Open with DEXTER | |
An individual comparison between the observed abundances and those predicted by
Karakas is difficult because the initial values of helium and the heavy
elements (Z) is not known for the PNe. The value of Z can be partially computed
from the observed abundances but several important elements are not observed.
Even for observed elements such as oxygen and carbon it is possible (although
unlikely) that important
amounts are tied up in dust and therefore not observable. But still important
conclusions can be drawn from Fig. 2. First of all, the observed points appear
to lie between the curves for Z=0.02 and 0.008, i.e. there is a general
agreement between the predicted and observed abundances. Four PNe seem to be
in the range of PNe with initial mass greater
than 5 ![]() .
Three of them are bipolar nebulae: NGC 6302, NGC 6537 and
He2-111. They appear to have passed the stage of hot-bottom burning. The
fourth PN, M1-42, is difficult to compare with the theoretical curves because
the high abundances indicate that it may have a high value of Z, and perhaps
a high initial helium abundance since it lies much closer to the
galactic center than the other PNe. Three other bipolar PNe, NGC 2440, Hb5 and
Hu1-2 appear to have a slightly lower initial mass, between 4
.
Three of them are bipolar nebulae: NGC 6302, NGC 6537 and
He2-111. They appear to have passed the stage of hot-bottom burning. The
fourth PN, M1-42, is difficult to compare with the theoretical curves because
the high abundances indicate that it may have a high value of Z, and perhaps
a high initial helium abundance since it lies much closer to the
galactic center than the other PNe. Three other bipolar PNe, NGC 2440, Hb5 and
Hu1-2 appear to have a slightly lower initial mass, between 4 ![]() and
5
and
5 ![]() ,
a value of Z=0.008 or somewhat higher, and have also have
undergone hot-bottom burning, which destroys carbon to produce nitrogen and
possibly some oxygen as well. The elliptical nebula
NGC 5315 is also in this category. The three elliptical PNe NGC 6153,
NGC 6886 and NGC 2392 have rather high N/O ratios indicating initial masses
slightly above 4
,
a value of Z=0.008 or somewhat higher, and have also have
undergone hot-bottom burning, which destroys carbon to produce nitrogen and
possibly some oxygen as well. The elliptical nebula
NGC 5315 is also in this category. The three elliptical PNe NGC 6153,
NGC 6886 and NGC 2392 have rather high N/O ratios indicating initial masses
slightly above 4 ![]() .
They have different He/H ratios however which
could indicate that they are stars of different initial helium abundances. All
the other PNe are very close to the Z=0.008 curve for stars between initial
masses of 1
.
They have different He/H ratios however which
could indicate that they are stars of different initial helium abundances. All
the other PNe are very close to the Z=0.008 curve for stars between initial
masses of 1 ![]() and 4
and 4 ![]() ,
and are all elliptical PNe. The only
exception is the bipolar PN NGC 6445, whose N/O ratio indicate that it is in
this initial mass range but it has a much higher He/H ratio and therefore
difficult to understand. The large majority of the nebulae can be
interpreted with central star masses which agree with the helium and nitrogen
abundances predicted by Karakas.
,
and are all elliptical PNe. The only
exception is the bipolar PN NGC 6445, whose N/O ratio indicate that it is in
this initial mass range but it has a much higher He/H ratio and therefore
difficult to understand. The large majority of the nebulae can be
interpreted with central star masses which agree with the helium and nitrogen
abundances predicted by Karakas.
2.3 The Carbon abundance
The question now arises whether the observed carbon abundances fit
into this picture. Carbon abundances are somewhat more uncertain than
nitrogen abundances because all the observable ions are in the
ultraviolet which makes them much more dependent on correct extinction and
electron temperature determination. We lack four determinations
of carbon in these nebulae because of the very large extinction
in the ultraviolet spectrum of these nebulae which made it impossible to
measure the carbon lines. In
Fig. 3 the N/O ratio has been plotted against the C/O ratio for those PNe
with carbon abundances. The predicted values of these ratios
(Karakas 2003) as a function of stellar mass for initial
values of Z=0.004, 0.008 and 0.02 are shown as points connected by dashed
lines. It may be seen that a very similar picture emerges as that drawn from
the N/O vs. He/H plot. The only three
PNe which are close to the 5 ![]() and 6
and 6 ![]() lines
are again the bipolar nebulae NGC 6302, NGC 6537 and He2-111. M1-42
now is separated from this group and is in the neighborhood of the
two other bipolar PNe Hu1-2 and NGC 2440. In Hb5 the extinction is
too high for the carbon lines to be measured. The last bipolar nebula,
NGC 6445 is again at a position of lower initial mass. Again
NGC 5315 and NGC 6153 are at a position predicted for a mass of
4.5
lines
are again the bipolar nebulae NGC 6302, NGC 6537 and He2-111. M1-42
now is separated from this group and is in the neighborhood of the
two other bipolar PNe Hu1-2 and NGC 2440. In Hb5 the extinction is
too high for the carbon lines to be measured. The last bipolar nebula,
NGC 6445 is again at a position of lower initial mass. Again
NGC 5315 and NGC 6153 are at a position predicted for a mass of
4.5 ![]() ,
as are NGC 2392 and NGC 6886. The low helium abundance of
these two PNe placed them in a
more anomalous position in Fig. 2, but both the N/O and C/O ratios
indicate that they are evolved from stars of initial mass somewhat
more than 4
,
as are NGC 2392 and NGC 6886. The low helium abundance of
these two PNe placed them in a
more anomalous position in Fig. 2, but both the N/O and C/O ratios
indicate that they are evolved from stars of initial mass somewhat
more than 4 ![]() .
NGC 6741 has about this mass as well.
.
NGC 6741 has about this mass as well.
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{plot3b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14009-10/Timg10.png)
|
Figure 3: N/O plotted against C/O. The lines and points are the same as in the caption to Fig. 2. |
| Open with DEXTER | |
The remaining PNe have lower initial mass. When the C/O ratio greater
than unity and the log N/O ratio is less than -0.46, the initial mass is
probably between 2 ![]() and 3.5
and 3.5 ![]() .
Probably the
nebulae IC 418, IC 2165, NGC 40, NGC 7027, IC 2448, Me 2-1,
BD+30 3639 and NGC 6826 are in this category. A log C/O ratio lower
than -0.15 combined with a log N/O ratio less than -0.46 indicates an
initial mass less than 2
.
Probably the
nebulae IC 418, IC 2165, NGC 40, NGC 7027, IC 2448, Me 2-1,
BD+30 3639 and NGC 6826 are in this category. A log C/O ratio lower
than -0.15 combined with a log N/O ratio less than -0.46 indicates an
initial mass less than 2 ![]() .
The extreme example is the
central star of NGC 6210 which probably has the smallest initial mass (equal
to or less than unity). Because the initial stellar abundances are not known
this should only be taken as an indication.
.
The extreme example is the
central star of NGC 6210 which probably has the smallest initial mass (equal
to or less than unity). Because the initial stellar abundances are not known
this should only be taken as an indication.
3 Stellar mass and luminosity
After the thermally pulsing AGB phase terminates, low to intermediate mass stars evolve at near constant luminosity to higher temperature. The ejected envelope becomes ionized and it is seen as a planetary nebula. Models made of single star evolution through this phase (Schönberner 1983; Vassiliadis & Wood 1993; Blöcker 1995) show that the constant stellar luminosity is a strong function of the core mass of the star. Thus determination of the luminosity provides a second method of determining the initial stellar mass which may be compared to the mass found from the abundances in the previous section. This is the purpose of the present section. First the effective temperature will be discussed, then the radius of the central star will be found using the visual magnitude of the central star. The distance of the PN plays an important role in determining the luminosity and a subsection is devoted to this subject.
The stellar luminosity can also be determined by measurements of the planetary nebula alone, even when the central star is not visible. The measurement used is either the amount of radiation which will ionize hydrogen or the amount of radiation which will doubly ionize helium. For the first case all the hydrogen ionizing radiation must be measured i.e. no ionizing radiation can escape from the nebula without causing at least one hydrogen ionization. For the second case this must be true for radiation which doubly ionizes helium. The luminosity determined in this way can be directly compared with that determined from the measurement of the central star. This is because both methods have the same dependence on the PN distance so that the distance is unimportant in the comparison. Interesting conclusions can be drawn about the ``optical thickness'' of the nebula as well.
3.1 Stellar temperature
The effective temperature of the central stars can be determined from the
Zanstra method providing the spectral distribution of radiation resembles that
of a blackbody and that all the photons which are able to ionize both hydrogen
and ionized helium are actually absorbed, i.e. the nebula is ``optically deep''
for these radiation fields. This is because the Zanstra method compares the
total amount of ionizing radiation (every photon which ionizes hydrogen
produces a single H![]() photon and the H
photon and the H![]() flux is measured) with the
flux in the visible part of the spectrum (as measured by the stellar visual
magnitude). Consider first the stellar magnitude determination.
flux is measured) with the
flux in the visible part of the spectrum (as measured by the stellar visual
magnitude). Consider first the stellar magnitude determination.
3.1.1 Stellar magnitude
The difficulty in measuring the magnitude of the central star is the result of the presence of nebular emission in the diaphragm. This must be large enough so that the star remains in the diaphragm. This is especially difficult when the star is very faint in the visible. In recent years this situation has improved: Hubble Space Telescope (HST) measurements have become available so that the image of the star is no longer broadened by the seeing. For most of the faint central stars magnitudes from the HST are now available. These are listed in the second column of Table 4. Theseare measured values and they must still be corrected for extinction. The extinction constant C is listed in Col. 3 and the reference in Col. 4 of the table. The accuracy can be judged by comparing the two central stars for which multiple measurements are available; these are shown in Table 2,
Table 2: Comparison of measured stellar magnitudes.
where Col. (1) are the HST measurements of Wolff et al. (2000), Col. (2) are HST measurements of Ciardullo et al. (1999) and Col. (3) are the ground based measurements made by Heap & Hintzen (1990a). Very faint central stars are difficult to measure. We list the HST measurement of Matsuura et al. (2005) for NGC 6537 in Table 4 but for NGC 6302 and He2-111 the central stars are too faint or too obscured to permit measurement.
3.1.2 Stellar radius
Once the stellar magnitude is known, the stellar radius can be determined if
the distance is known. This uncertain quantity will be discussed presently; the
distances used are listed in Col. 10 of Table 4. Further it is assumed that the
stars radiate as blackbodies so that the following equation can be used:
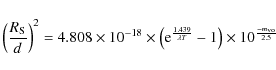
|
(1) |
where d is the distance,
3.1.3 Zanstra temperature
The Zanstra temperature measures the ratio of the amount of ionizing radiation
to the amount of radiation in the visual spectrum. ![]() (H) uses the
H
(H) uses the
H![]() flux and thus measures the amount of radiation which can ionize
hydrogen, while
flux and thus measures the amount of radiation which can ionize
hydrogen, while ![]() (HeII) measures the amount of radiation which can
completely ionize helium. In converting the ratio to a temperature it is
assumed that the stellar spectrum is a blackbody, that all the ionizing
radiation is absorbed by the nebula, and that the continuum visual flux is
measured by the stellar magnitude.
(HeII) measures the amount of radiation which can
completely ionize helium. In converting the ratio to a temperature it is
assumed that the stellar spectrum is a blackbody, that all the ionizing
radiation is absorbed by the nebula, and that the continuum visual flux is
measured by the stellar magnitude.
Zanstra temperatures have been measured for many years and several
papers have published extensive tables of these temperatures (e.g.
Phillips 2003). The most uncertain measurement in the
determination is the stellar magnitude because, as discussed above,
nebular light must be avoided. The values we have found are listed in
Cols. 5 and 6 of Table 4 and are not essentially different from those
given in the literature. One of the most discussed aspects of the
results can be seen in the table: in about 30% of the nebulae the
value of ![]() (H) is substantially lower than
(H) is substantially lower than ![]() (HeII). The
reason for this has been debated in the literature; the most often
cited reason is the assumption that the nebula is ``optically deep'' to
radiation which ionizes hydrogen is wrong and that some of this radiation
escapes the nebula without being registered. This has the consequence
that
(HeII). The
reason for this has been debated in the literature; the most often
cited reason is the assumption that the nebula is ``optically deep'' to
radiation which ionizes hydrogen is wrong and that some of this radiation
escapes the nebula without being registered. This has the consequence
that ![]() (H) is too low and that
(H) is too low and that ![]() (HeII) is the more nearly
correct value. It is difficult to confirm this because not only is the
total nebular mass uncertain, its distribution in the nebula is also
unknown. Another explanation for this difference could also be that
the stellar spectrum is not well represented by a blackbody.
(HeII) is the more nearly
correct value. It is difficult to confirm this because not only is the
total nebular mass uncertain, its distribution in the nebula is also
unknown. Another explanation for this difference could also be that
the stellar spectrum is not well represented by a blackbody.
3.1.4 Energy balance temperature
The Energy Balance method, first introduced by Stoy (1933), measures the
average excess energy per ionizing photon. This can be found from the ratio of
the intensity of collisionally excited nebular lines to H![]() .
It has the
advantage that only the nebular spectrum has to be known; no measurement of the
central star flux is necessary. It has the further advantage that it is
applicable both to optically thin as well as optically thick nebulae. The
method is also independent of the nebular model as long as all the
collisionally excited lines are measured. In practice sometimes a correction
must be made for unmeasured lines. The entire spectrum must be measured but for
most PN the visible and ultraviolet lines are the most important. For very low
temperature central stars the infrared nebular spectrum can be the most
important.
.
It has the
advantage that only the nebular spectrum has to be known; no measurement of the
central star flux is necessary. It has the further advantage that it is
applicable both to optically thin as well as optically thick nebulae. The
method is also independent of the nebular model as long as all the
collisionally excited lines are measured. In practice sometimes a correction
must be made for unmeasured lines. The entire spectrum must be measured but for
most PN the visible and ultraviolet lines are the most important. For very low
temperature central stars the infrared nebular spectrum can be the most
important.
Once the ratio of collisional line intensity to H![]() (called R) is known a
difficulty arises in interpreting this measurement in terms of a stellar
effective temperature; it is necessary to know whether the star emits as a
blackbody or some particular model atmosphere. Since this is not known it is
assumed here that the star emits as a blackbody. Preite-Martinez & Pottasch
(1983) have calculated the effective temperatures found when a variety of
model atmospheres of different effective temperatures are used as ionizing
source. They found that for a fixed value of the ratio R the model atmospheres
give a slightly lower value of effective temperature than the blackbody.
(called R) is known a
difficulty arises in interpreting this measurement in terms of a stellar
effective temperature; it is necessary to know whether the star emits as a
blackbody or some particular model atmosphere. Since this is not known it is
assumed here that the star emits as a blackbody. Preite-Martinez & Pottasch
(1983) have calculated the effective temperatures found when a variety of
model atmospheres of different effective temperatures are used as ionizing
source. They found that for a fixed value of the ratio R the model atmospheres
give a slightly lower value of effective temperature than the blackbody.
The exact status of the nebula also has an effect on the effective temperature
found. Preite-Martinez & Pottasch (1983) calculated three cases. In the
first case the nebula is optically thin to all ionizing radiation. In the
second case the nebula is optically thick to He+ ionizing radiation and in
the third case the nebula is optically thick to all ionizing radiation. These
authors compare the effective temperatures derived for 52 central star using
all of these three assumptions. They find that all three assumptions give
similar results. We have redone the calculations using the case which is thick
to He+ ionizing radiation and thin to hydrogen ionizing radiation (case
two); the effective temperatures found are listed in Col. 8 of Table 4. As can
be seen from the table, temperatures can now be found even when the central
star is unobservable. The Energy balance temperature is rather similar to
the HeII Zanstra temperature ![]() (HeII), sometimes slightly lower,
sometimes slightly higher.
(HeII), sometimes slightly lower,
sometimes slightly higher.
3.1.5 Spectroscopic temperatures
Stellar temperatures may also be obtained from a model atmosphere analysis of the spectrum. Because high resolution spectra are needed this has only been done for very bright stars. The results can be found in Mendez et al. (1988), Kudritzki et al. (1997) and Pauldrach et al. (2004). As Pauldrach et al. (2004) point out, the model atmosphere analysis is difficult; the results using hydrogen line profiles can differ according to which hydrogen line is used. Mendez et al. (1988) and Kudritzki et al. (1997) base their temperatures on the analysis of hydrogen and helium line profiles while Pauldrach et al. (2004) base their temperatures on the analysis of metal line profiles in the ultraviolet. The results are quite similar. The results are given in Table 3 where, considering the consistency of the different determinations, we estimate the error to be of the order of 10 to 15%.
Although only six spectroscopic temperatures have been measured for our
nebulae, it is interesting to compare them with what has been found from the
Zanstra and Energy Balance methods. For two of the nebulae, IC 418 and
NGC 6826, no ![]() (HeII) can be measured. In both cases there is good
agreement between the spectroscopic temperature and
(HeII) can be measured. In both cases there is good
agreement between the spectroscopic temperature and
![]() derived from
derived from
![]() (H) and
(H) and
![]() .
In two other cases, NGC 3242 and NGC 1535, there
is reasonably good agreement between the spectroscopic temperature and
.
In two other cases, NGC 3242 and NGC 1535, there
is reasonably good agreement between the spectroscopic temperature and
![]() derived from
derived from ![]() (HeII) and
(HeII) and
![]() ,
but definitely higher than
that found from
,
but definitely higher than
that found from ![]() (H). This could also be true for IC 2448 because the
spectroscopic temperature is more uncertain for this central star. It is
definitely not true for the central star of NGC 2392 where both
(H). This could also be true for IC 2448 because the
spectroscopic temperature is more uncertain for this central star. It is
definitely not true for the central star of NGC 2392 where both ![]() (HeII)
and
(HeII)
and
![]() indicate a very much higher temperature. This will presently be
discussed in more detail.
indicate a very much higher temperature. This will presently be
discussed in more detail.
Table 3: Spectroscopic temperatures.
3.1.6 Effective temperature
In Col. 8 of Table 4 the estimated value of the effective temperature
![]() is given. For those PNe where both
is given. For those PNe where both ![]() (HeII) and
(HeII) and
![]() have been
measured, they are always quite similar. Of these 27 cases the average value of
have been
measured, they are always quite similar. Of these 27 cases the average value of
![]() is similar (within 15%) to the hydrogen Zanstra temperature
is similar (within 15%) to the hydrogen Zanstra temperature
![]() (H) in 15 cases. In the other 12 cases
(H) in 15 cases. In the other 12 cases ![]() (H) is considerably
lower than
(H) is considerably
lower than
![]() ,
possibly indicating that the nebulae are optically thin.
We shall return to this subject in the next section. Four of the nebulae are
not hot enough to form a substantial amount of ionized helium. In these cases
substantial weight is given to
,
possibly indicating that the nebulae are optically thin.
We shall return to this subject in the next section. Four of the nebulae are
not hot enough to form a substantial amount of ionized helium. In these cases
substantial weight is given to
![]() which in two cases is very similar to
which in two cases is very similar to
![]() (H). In the other two cases
(H). In the other two cases
![]() is higher than
is higher than ![]() (H) and an
average of the two temperatures is used. For Mz 3 the temperature is
determined from the best fitting nebular model (see Pottasch & Surendiranath
2005c). The value of
(H) and an
average of the two temperatures is used. For Mz 3 the temperature is
determined from the best fitting nebular model (see Pottasch & Surendiranath
2005c). The value of
![]() for NGC 6302 is discussed below.
for NGC 6302 is discussed below.
Table 4: Central star magnitude, temperature and luminosity.
3.2 PN distances
Distances to PNe are uncertain because the usual method for astronomical distance determination, parallax, is applicable to only a very limited number of nebulae. In this situation two options are available. One can use less accurate methods for determining individual distances or one can assume that all nebulae have a particular property in common and use this property to obtain a statistical distance. There is an extensive literature for determining distances with the assumption that all nebulae have the same ionized mass. Especially the work of Cahn et al. (1992) or more recently the work of Stanghellini et al. (2008), which calibrates the mass using Magellanic Cloud PNe measurements, have been used. Both these determinations assume that the PNe are optically thin to hydrogen ionizing radiation but attempt to correct this assumption for the smaller high density nebulae.
The statistical distances will not be used here because PNe evolve from stars of a wide range of stellar masses and we do not wish to exclude the possibility that PNe of different stellar mass produce nebulae with different properties. Averaging any of these properties may lead to systematic errors in the individual distances found from these average properties. This in turn could introduce systematic errors in evolution calculations made using them. In addition Ciardullo et al. (1999) measured accurate distances of a small sample of binary PNe and concluded that for these nebulae the statistical distances are overestimates. Instead we determine distances using three methods which, while giving somewhat more uncertain individual distances, are much less likely to have systematic errors.
These methods are well known and are long in the literature. The first method is the expansion distances where the expansion is measured at two epochs, usually separated by 3 to 5 years. The measurements are made in both the optical (HST measurements are desirable) and at radio frequencies (VLA measurements are usually used). Expansion velocities must also be known but they cannot be measured in the plane of the sky in which the expansion is observed. The measured radial velocities are therefore used in the hope that these are very similar. In addition there may be gradients in the velocity which must be taken into account. Because the nebular density decreases between the two measured epochs, the ionization front appears to move more quickly than the matter and this must also be taken into account. A discussion with many results is given by Terzian (1997) and the effect of the ionization front is discussed by Mellema (2004). In addition, Schönberner et al.(2005) have made and applied kinematic models of several PNe to obtain expansion distances. There is general agreement for the four PNe common to the results of both Mellema (2004) and Schönberner et al.(2005), which indicate some of the expansion distances given by Terzian (1997) should be increased. The increases depend on the individual models and are thus uncertain. Both authors estimate that the results Terzian (1997) should on average increase by about 30%. These possible increases are taken into account in our distance estimates, although other methods, especially extinction distances, may place important limits on the increase. For the PNe we are discussing 9 expansion distances are known (NGC 3242, NGC 6210, NGC 6302, NGC 6543, NGC 7027, NGC 7662, IC 418, IC 2448 and BD+30 3639).
The second method is the extinction distance. In this method the extinction of field star of known distance located within a small distance from the nebula in the plane of the sky (usually less than 0.5 degrees) is measured and a plot is made of reddening as a function of distance in that direction. The reddening of the PNe is placed on this diagram and the distance read off. This method assumes that the extinction is rather uniform over the 0.5 degrees (or smaller) used, and that the PNe is located in the galactic plane where the extinction increases with distance. This is a rather time consuming process. It has been done for NGC 2440, NGC 2792, NGC 5315, NGC 5882, NGC 6543, NGC 6741, NGC 7027 and IC 2448 among the PNe we are interested in (see Gathier et al. 1986a; Martin 1994).
There is a variant of this method which instead of measuring the extinction of the PN and nearby sources, measures the 21 cm neutral hydrogen radio line absorption of the PN and nearby sources. This method has the advantage that the velocity of the absorption line is measured so that it may be ascertained whether the nebula is on the near or far side of a particular spiral arm. This method has been used for NGC 6369, NGC 6537, NGC 6886 and NGC 7027 (of the PNe which interest us). This method is again limited to PNe near the galactic plane (see Gathier et al. 1986b).
In addition use can be made of the average extinction (in magnitudes per kpc) in various directions. Such maps have been made by several authors but because a relatively limited number of stars are used, these maps are averages over relatively large areas and are more uncertain than when a small area is studied in depth. Results of this method are given for a large number of PNe by Pottasch (1984) and Sabbadin (1986). The results of these two authors generally agree when the same nebulae are compared. We will use them when no other individual distance is available.
Another method of distance determination is from the spectroscopic measurements of the central star. These measurements have already been discussed in Sect. 3.1.5 for determining the central star temperatures for which, with the exception of NGC 2392, reasonable agreement was obtained with the temperatures found from the nebular spectrum. The same discussions (Pauldrach et al. 2004; Kudritzki et al. 1997; and Mendez et al. 1988) derive the distance and mass of various bright central stars. These distances are not included in the present discussion. The reason for this is the following. The large masses and distances found by Pauldrach et al. are improbable. This has been convincingly demonstrated by Napiwotzki (2006), who found that the kinematic properties of these nebulae are inconsistent with the masses and distances given by these authors. This reasoning can be extended to the distances found by Kudritzki et al. which are very similar. Some, but not all, of the distances found by Mendez et al. (1992) are similar to those given by Pauldrach et al. and Kudritzki et al. There are six PNe in common between Mendez et al. and those used by us. For one PN, NGC 1535, the same distance is given. For two other nebulae, IC 2448 and NGC 3242 there is a strong discrepancy between the expansion distance as given by Mellema (2004) or Schönberner et al. (2005) in the sense that Mendez et al. give values of 3.5 and 1.8 kpc while the expansion distance is considerably lower, 2.1 and 0.55 kpc respectively. For the remaining 3 PNe, NGC 6826, NGC 2392 and IC 418 our individual distances are about 45% smaller than those given by Mendez et al. (1992). For the single PN for which an optical parallax is available, NGC 7293, Harris et al. (2007) measure a distance of 219 pc while Mendez et al. (1992) give the higher value of 300 pc. We regard the values of Mendez et al. as rather high and do not give tham much weight.
Distances may also be determined from the nebular spectrum. When making a model of the nebula to explain, not only the relative intensity of the lines relative to hydrogen, but the absolute hydrogen line intensities as well, the distance of the nebula is one of the unknown quantities (along with the stellar radius and temperature and the nebular density and temperature). Our experience with such models indicate that the distances determined in this way have an accuracy of about 20%. Model distances are available for NGC 2792, NGC 6826, NGC 6886, NGC 6741, NGC 6445, Hu1-2, Hb5, Me2-1 and Mz3. In addition the distance to NGC 1535 has been measured by the fact that it is a double star and the companion has a spectroscopic parallax.
In this way individual distances are known for 32 of the 33 PNe being studied. The only exception is He2-111 for which a statistical distance has been used. We feel that the distances listed in Table 4 are an improvement over the older ones shown in our previous paper.
3.2.1 Comparison with statistical distances
In the above we have discussed the reason for not using the statistical distances. Here we compare the individual distances with the statistical distances found in the literature. There are two reasons for doing this. First, to show that on average the statistical distances are not very different from the individual distances. This is to counter a possible remark when the nebular luminosities are discussed, that increasing PNe distances by a large amount is a reasonable alternative. Secondly we wish to demonstrate that bipolar PNe are affected in a different way than elliptical PNe when statistical distances are determined, thus demonstrating the bias discussed above.
There are many statistical distance scales in the literature and for clarity only two of them will be discussed here. These are the often used scale of Cahn et al. (1992, hereafter CKS) who calibrate distances using ``well known'' PNe distances, and the more recent distances of Stanghellini et al. (2008, hereafter SVV) who make use of the PNe in the Large Magellanic Cloud as calibrators. Both scales assume that all PNe are optically thin to hydrogen ionizing radiation and have the same ionized mass, but in both scales a correction to this assumption is made for nebulae considered optically thick. The differences between the distances given by these two sources is usually not large.
Of the 32 PNe (excluding He2-111 for which no individual distance is available), the individual distances to 20 nebulae are found to be the same as the statistical given by CKS, 8 PNe have larger individual distances and 4 PNe have smaller individual distances. Compared to the distances given by SSV, 14 PNe have the same distance, 2 PNe are larger than given by SSV and 11 PNe have smaller distances. Having the same distance is defined as being within 33% of the larger of the two distances. Note that in the comparison with SVV there are slightly less PNe in common.
But if only the bipolar nebulae are considered a somewhat different picture emerges. Of the 7 bipolar nebulae (again excluding He2-111) the distances to 5 of them are larger than given by CKS, 2 are at the same distance and there are no PNe at smaller distances. For SVV these numbers are 2, 3 and 0 respectively. Thus while the individual distances are rather similar to the statistical distances for the whole sample, they are on the whole larger than the statistical distances for the bipolar nebulae. This illustrates the danger of using statistical distances which averages out the differences in different classes of nebulae. For the two PNe which on the basis of the nebular abundance evolve from the most massive stars, NGC 6537 and NGC 6302, we find distances twice as high as given by CKS or SSV.
3.3 Luminosity
3.3.1 Luminosity from central star.
Once the effective temperature
![]() ,
the stellar radius, and the distance
to the PNe are known the luminosity can be calculated. Using the relation:
,
the stellar radius, and the distance
to the PNe are known the luminosity can be calculated. Using the relation:
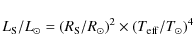
|
(2) |
the stellar luminosity given in Col. 12 of Table 4 is found. It is difficult to estimate the error of this luminosity. The distance is not well known so that the error could be as much as 30%; for individual objects it might be even higher. This introduces an error of a factor of two in the luminosity and is probably the largest error. The stellar magnitude and extinction value are probably reasonably well known and are not likely to introduce an error of more than 20% unless the wrong star has been measured. We shall return to this presently. The effective temperature, which is related to the assumption of blackbody radiation, may also be in error. An error of 10% in temperature leads to an uncertainty of 40% in luminosity.
3.3.2 Luminosity from nebular emission
The luminosity can also be determined from the emission lines of either
hydrogen or ionized helium, at least when the nebula absorbs all the ionizing
radiation. Consider hydrogen: every photon with energy greater than 13.6 eV
emitted by the central star ionizes one hydrogen atom and then produces a
single H![]() photon. Thus the H
photon. Thus the H![]() luminosity can be converted to the
total luminosity of the star above 13.6 eV. When the temperature is known this
can be converted to the total stellar luminosity. This may be written as:
luminosity can be converted to the
total luminosity of the star above 13.6 eV. When the temperature is known this
can be converted to the total stellar luminosity. This may be written as:
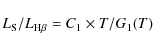
|
(3) |
where

|
(4) |
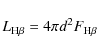
|
(5) |
and G1(T) is an integral shown as Eq. (VII-8) whose values are tabulated in Table VII-4 by Pottasch (1984).
| (6) |
where
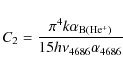
|
(7) |
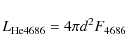
|
(8) |
where the references are the same as above.
The function T/Gx(T) has a minimum value for both hydrogen and
ionized helium. For hydrogen the function does not change by more than 25%
between temperatures of 45 000 K and 150 000 K. Within this range small errors
in the temperature will have only a reasonably small effect on the luminosity.
Outside of this range, and especially at the lower temperatures, an error in
the temperature will have a much larger effect. This should be taken into
account when comparing the luminosities determined in the different ways. For
the luminosities found from the ionized helium line, the range of temperature
where the effect is small is between 140 000 K and 800 000 K. Again a small
error in temperature will have a much large effect at lower temperatures. This
is illustrated in the PN NGC 6302. The central star, which is not visible, has
an uncertain energy balance temperature of 300 000 K (Preite-Martinez &
Pottasch 1983). The luminosity computed from the ![]() 4686 line is
7400
4686 line is
7400 ![]() .
This value is only slightly dependent on the temperature
between 200 000 K and 500 000 K. The value found from the H
.
This value is only slightly dependent on the temperature
between 200 000 K and 500 000 K. The value found from the H![]() line is
much more sensitive to the temperature and only at a value close to 300 000 K
can the same luminosity be computed. This fixes the temperature.
line is
much more sensitive to the temperature and only at a value close to 300 000 K
can the same luminosity be computed. This fixes the temperature.
The luminosities found from the H![]() line are listed in Col. 13 of Table 4, and the luminosities found the
line are listed in Col. 13 of Table 4, and the luminosities found the ![]() 4686 line are given in Col. 14 of
the same table.
4686 line are given in Col. 14 of
the same table.
3.3.3 Comparison of stellar and nebular luminosities
Both the stellar and nebular luminosities have the same dependence on the distance so that a comparison of the two does not involve the distance.
On making this comparison the general impression is of reasonably good
agreement between
the stellar and nebular luminosities. On closer inspection we can distinguish
several cases. Case 1 are those PNe where the stellar luminosity (Col. 12 in
Table 4) and the ![]() 4686 luminosity (Col. 14) agree and are both higher
than theH
4686 luminosity (Col. 14) agree and are both higher
than theH![]() luminosity. We regard these PNe as optically thin to hydrogen
ionizingradiation and optically thick to radiation which doubly ionizes helium.
For these cases we use the average of Cols. 12 and 14 as the luminosity of
the exciting star. There are eight cases: Hb5, Hu1-2, M1-42, Me2-1, NGC 2022,
NGC 5882, IC 2448 and NGC 2792. In case 2 are those nebulae where all three
luminosities agree. These are regarded as optically deep to both hydrogen and
doubly ionized helium. For these eight cases the average value of all three
luminosities is used. These are NGC 2440, NGC 5315, NGC 6445, NGC 6537,
NGC 6886, NGC 6369, NGC 6741 and NGC 7027. Then there are those nebulae
(case 3) where the stellar luminosity agrees with that determined from the
H
luminosity. We regard these PNe as optically thin to hydrogen
ionizingradiation and optically thick to radiation which doubly ionizes helium.
For these cases we use the average of Cols. 12 and 14 as the luminosity of
the exciting star. There are eight cases: Hb5, Hu1-2, M1-42, Me2-1, NGC 2022,
NGC 5882, IC 2448 and NGC 2792. In case 2 are those nebulae where all three
luminosities agree. These are regarded as optically deep to both hydrogen and
doubly ionized helium. For these eight cases the average value of all three
luminosities is used. These are NGC 2440, NGC 5315, NGC 6445, NGC 6537,
NGC 6886, NGC 6369, NGC 6741 and NGC 7027. Then there are those nebulae
(case 3) where the stellar luminosity agrees with that determined from the
H![]() luminosity, while that determined by the doubly ionized helium
luminosity is about a factor of two higher. This is probably due to the use of
a slightly too low effective temperature, since in all cases the temperature
dependence of the luminosity is quite large. The PNe involved are IC 2165,
IC 4191, NGC 6153 and NGC 6818. Here the stellar luminosity is used
(Col. 12). These PNe are considered optically thick
to all ionizing radiation fields. It is likely that NGC 7662 and NGC 3242
should be included in this group because here again the doubly ionize helium
luminosity is about twice the stellar luminosity, but because these nebulae are
optically thin to hydrogen ionizing radiation the hydrogen luminosity is lower.
Case 4 are the five PNe which have low temperature central stars and thus do
not have a HeII luminosity. Since these nebulae have low temperature central
stars the nebular luminosity is a very strong function of the temperature. For
these five PNe (BD+30 3639, IC 418, IC 40, NGC 6543 and NGC 6826) we use
an average luminosity giving double weight to luminosity determined from the
star.
luminosity, while that determined by the doubly ionized helium
luminosity is about a factor of two higher. This is probably due to the use of
a slightly too low effective temperature, since in all cases the temperature
dependence of the luminosity is quite large. The PNe involved are IC 2165,
IC 4191, NGC 6153 and NGC 6818. Here the stellar luminosity is used
(Col. 12). These PNe are considered optically thick
to all ionizing radiation fields. It is likely that NGC 7662 and NGC 3242
should be included in this group because here again the doubly ionize helium
luminosity is about twice the stellar luminosity, but because these nebulae are
optically thin to hydrogen ionizing radiation the hydrogen luminosity is lower.
Case 4 are the five PNe which have low temperature central stars and thus do
not have a HeII luminosity. Since these nebulae have low temperature central
stars the nebular luminosity is a very strong function of the temperature. For
these five PNe (BD+30 3639, IC 418, IC 40, NGC 6543 and NGC 6826) we use
an average luminosity giving double weight to luminosity determined from the
star.
We have now discussed 30 of the 33 PNe. For NGC 6210 the stellar luminosity is
twice the nebular luminosity. We will use an average value of the three
luminosities listed. The problem
concerning NGC 2392 is greater. The stellar luminosity for this object is an
order of magnitude greater than the nebular luminosity. It is also much greater
than for all the other nebulae. The problem probably lies with the temperature
we have assigned to this star. As discussed in Sect. 3.1.5 and Table 4
the spectrum of this star is not more than 50 000 K, much
less the value of 80 000 K which has been used. But a
blackbody of 50 000 K does not have enough ultraviolet
radiation to produce the observed nebular spectrum. Thus there must
be an additional source of ultraviolet radiation. This could be another
hotter
star. This has been suggested several times in the literature because
of the incompatibility of the nebular and stellar spectrum. Ciardullo
et al. (1999)
have examined HST photographs of this nebula and have found a faint star at
2.65
![]() from the bright ``central star''. This star is only seen through the
red (I) filter; it is invisible in the visible (V). It is therefore likely to
be a red star unless it has a very unusual spectrum. In any case, the stellar
luminosity listed for this star in Table 4 is certainly not correct. If one
wishes to assign a luminosity to the exciting star, we suggest using the
nebular luminosity found from the
from the bright ``central star''. This star is only seen through the
red (I) filter; it is invisible in the visible (V). It is therefore likely to
be a red star unless it has a very unusual spectrum. In any case, the stellar
luminosity listed for this star in Table 4 is certainly not correct. If one
wishes to assign a luminosity to the exciting star, we suggest using the
nebular luminosity found from the ![]() 4686 line. The PNe is clearly
optically thin to radiation capable of ionizing hydrogen.
4686 line. The PNe is clearly
optically thin to radiation capable of ionizing hydrogen.
The luminosities for NGC 1535 show a great similarity to those of NGC 2392. Again the stellar luminosity is considerably higher than the nebular luminosities and the nebula is optically thin to radiation capable of ionizing hydrogen. But in this case the effective temperature which we have assigned to the central star is not very different from the spectroscopic temperature shown in Table 3 (although only a single determination is available). It is possible that in this case the nebula is optically thin to radiation capable of doubly ionizing helium. We find it difficult to assign a luminosity to this central star.
There are 25 PNe which have both hydrogen and ionized helium Zanstra
temperatures. We define the ratio ![]() (HeII)/
(HeII)/![]() (H) as the Zanstra
ratio. Ignoring NGC 6210, there are 12 optically thick PNe and 12 optically
thin PNe as found above by a consideration of their luminosities. The Zanstra
ratio for the 12 optically thick PNe varies between 0.95 and 1.17 with a median
value of 1.03. For the 12 optically thin PNe the Zanstra ratio varies between
1.12 and 2.1 with a median value of 1.65. We conclude the assumption that the
star radiates as a blackbody is reasonable and consistent. Furthermore those
PNe with a Zanstra ratio greater than 1.2 are optically thin, while those lower
than 1.1 are optically thick. Between values 1.1 and 1.2 further information is
necessary.
(H) as the Zanstra
ratio. Ignoring NGC 6210, there are 12 optically thick PNe and 12 optically
thin PNe as found above by a consideration of their luminosities. The Zanstra
ratio for the 12 optically thick PNe varies between 0.95 and 1.17 with a median
value of 1.03. For the 12 optically thin PNe the Zanstra ratio varies between
1.12 and 2.1 with a median value of 1.65. We conclude the assumption that the
star radiates as a blackbody is reasonable and consistent. Furthermore those
PNe with a Zanstra ratio greater than 1.2 are optically thin, while those lower
than 1.1 are optically thick. Between values 1.1 and 1.2 further information is
necessary.
3.4 Core mass and the HR diagram
In the earlier discussions of the work of Karakas (2003) her various models have been identified by their initial mass, just as Karakas has done. A more direct mass to use in discussing the HR diagram is the core mass, as it avoids uncertainties in the assumed mass loss. The Z=0.008 (Z=0.02) models of Karakas labeled with the initial masses of 1, 1.5, 2.5, 4.0 and 6.0In this section the luminosities determined above are used to compare with the luminosities other models predict in order to see if they agree with the core masses given by Karakas. It would have been more consistent to compare with tracks of the original models of Karakas but she has not given post AGB tracks for these models.
The effective temperature and the luminosity of the central stars shown in
Table 4 are plotted as points in Fig. 4. The individual PN is identified on
the left side of the diagram. Several different models are plotted as solid
lines on the figure. The core mass and initial heavy element abundance Z used
in the model is shown in the diagram. Not shown on the diagram are the
phase of the helium shell flash cycle at which the ejection is assumed to
occur and the mass loss rate used in making that model. The mass loss rate in
particular is a very poorly known quantity and can result in large
uncertainties in the models. In Fig. 4 the results of Vassiliadis & Wood
(1993) are used for the core mass
![]() ,
,
![]() and
0.91
and
0.91 ![]() models (the first has Z=0.016, the two other models have
Z=0.008), and the results of Schönberner (1983) for the
models (the first has Z=0.016, the two other models have
Z=0.008), and the results of Schönberner (1983) for the
![]() model.
model.
As can be seen in the diagram, two of the three PNe (NGC 6537 and NGC 6302)
for which it was concluded
on the basis of their abundance that they originate from high mass stars,
indeed are in the high mass region of the HR diagram. The third PN (He2-111)
might also be in this region but the temperature determination is too uncertain
to be sure of this. The three other bipolar PNe, NGC 2440, Hb5 and Hu1-2 whose
abundance indicated a somewhat lower core mass, are in a
rather higher mass portion of the HR diagram. The precise value of the initial
mass agrees less well, since on the basis of the abundances we predicted in
Sect. 2 that these PNe originated from an initial mass of 4 ![]() to
5
to
5 ![]() which following Karakas (2003) corresponds to a core mass
of slightly higher than 0.8
which following Karakas (2003) corresponds to a core mass
of slightly higher than 0.8 ![]() while in the HR diagram they are in the
position of the 0.67
while in the HR diagram they are in the
position of the 0.67 ![]() track. In addition several other PNe lie in the same position. NGC 6886 has
a high N/O ratio and on this basis was suspected to originate from a higher
mass star. The bipolar PN NGC 6445, which because of its high He/H and low
N/O ratios was considered enigmatic, is also in this region. But so are
NGC 7027 and NGC 6741 whose abundances would place them in the group of
low initial mass objects. Also enigmatic are NGC 5315 and M1-42 which on the
basis of both high He/H and N/O ratios might be expected to have somewhat
higher core masses, are in the region of low mass objects on the HR diagram.
track. In addition several other PNe lie in the same position. NGC 6886 has
a high N/O ratio and on this basis was suspected to originate from a higher
mass star. The bipolar PN NGC 6445, which because of its high He/H and low
N/O ratios was considered enigmatic, is also in this region. But so are
NGC 7027 and NGC 6741 whose abundances would place them in the group of
low initial mass objects. Also enigmatic are NGC 5315 and M1-42 which on the
basis of both high He/H and N/O ratios might be expected to have somewhat
higher core masses, are in the region of low mass objects on the HR diagram.
![\begin{figure}
\par\includegraphics[width=14cm,angle=90]{hr.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14009-10/Timg34.png)
|
Figure 4:
The HR diagram. The models for core masses of 0.57, 0.67 and
0.91 |
| Open with DEXTER | |
On the other hand, the majority of PNe which on the basis of their abundances
are thought to have evolved from low mass stars, do indeed fall in the low
mass region of the HR diagram. We have checked to see whether those PNe which
are carbon rich (C/O ![]() 1) have a special position on the HR diagram, but we
find them to be at positions indistinguishable from other low initial mass
objects.
1) have a special position on the HR diagram, but we
find them to be at positions indistinguishable from other low initial mass
objects.
To summarize, there is a qualitative agreement between the two ways of
approaching stellar evolution: by either looking at the nebular
abundances or the position of the central star on the HR diagram. The
three bipolar PNe whose high N/O and He/H leads to the prediction
(Karakas 2003) that they have core masses of
0.85 ![]() to 0.95
to 0.95 ![]() are in a position on the HR diagram
that is consistent with the theoretical 0.9
are in a position on the HR diagram
that is consistent with the theoretical 0.9 ![]() tracks of
Vassiliadis & Wood (1993) or the 0.91
tracks of
Vassiliadis & Wood (1993) or the 0.91 ![]() tracks of
Blöcker (1995) (not shown in Fig. 4). The other three bipolar
PNe with somewhat lower abundances and where the predictions of
Karakas lead us to expect a slightly lower core mass, probably between
0.8
tracks of
Blöcker (1995) (not shown in Fig. 4). The other three bipolar
PNe with somewhat lower abundances and where the predictions of
Karakas lead us to expect a slightly lower core mass, probably between
0.8 ![]() and 0.88
and 0.88 ![]() ,
show less good agreement with the
model tracks. In Fig. 4 these PNe agree with the 0.67
,
show less good agreement with the
model tracks. In Fig. 4 these PNe agree with the 0.67 ![]() tracks
of Vassiliadis & Wood (1993) but they also agree with one of
the 0.6
tracks
of Vassiliadis & Wood (1993) but they also agree with one of
the 0.6 ![]() tracks of Blöcker (1995).
tracks of Blöcker (1995).
Regarding the elliptical PNe: many of the central stars fall near the
tracks of stars of core mass between 0.55 ![]() and
0.57
and
0.57 ![]() on the HR diagram. Stars of these masses are not
expected to show abundance changes which are at present observable, in
agreement with the observations. Karakas (2003) predicts a
core mass of 0.6
on the HR diagram. Stars of these masses are not
expected to show abundance changes which are at present observable, in
agreement with the observations. Karakas (2003) predicts a
core mass of 0.6 ![]() for these PNe, more in line with the value
of 0.58
for these PNe, more in line with the value
of 0.58 ![]() expected from the average measured white dwarf
masses. The reason that the observed luminosity does not agree with
that predicted from the models is not clear. If the observed
luminosity were too low, the most likely cause would be a possible
underestimate of the observed PNe distance. To obtain agreement with
the model luminosity the average distance would have to be increased
by 70%. We regard this as unlikely for an average value, although it may
occasionally occur for individual PNe.The other possibility is that the
relationship between core mass and luminosity found for the low core
mass models is not entirely correct.
expected from the average measured white dwarf
masses. The reason that the observed luminosity does not agree with
that predicted from the models is not clear. If the observed
luminosity were too low, the most likely cause would be a possible
underestimate of the observed PNe distance. To obtain agreement with
the model luminosity the average distance would have to be increased
by 70%. We regard this as unlikely for an average value, although it may
occasionally occur for individual PNe.The other possibility is that the
relationship between core mass and luminosity found for the low core
mass models is not entirely correct.
4 Summary and conclusions
We have determined the masses of a selection of 33 well-studied
nebulae PNe by comparing the observed nebular abundances with that
predicted by the evolutionary models of Karakas (2003), which
is the first systematic study of the evolution of lower mass stars.
A secondary purpose is to see whether the masses determined in this way
are consistent with the evolutionary tracks computed by
Schönberner (1983), Blöcker (1995) and Vassiliadis &
Wood (1993). The abundances used in this comparison are helium,
oxygen, nitrogen and carbon. The morphology is also considered in this
comparison but in a simplified form. The PNe are divided into two
categories: bipolar and elliptical (including round nebulae). The
result of the comparison of He vs. N/O (Sect. 2.2) indicate four PNe
have core masses greater than 0.9 ![]() ;
three of these nebulae
are bipolar (NGC 6302, NGC 6537 and He2-111). There are also four
nebulae which appear to have a slightly lower initial mass, between
0.85
;
three of these nebulae
are bipolar (NGC 6302, NGC 6537 and He2-111). There are also four
nebulae which appear to have a slightly lower initial mass, between
0.85 ![]() and 0.9
and 0.9 ![]() and have also undergone hot-bottom
burning. Again three of these PNe are bipolar (NGC 2440, Hb5 and
Hu1-2). Thus 6 of the 7 bipolar nebular in our selection have
abundances which indicate that they originated from initially high
mass stars. The only bipolar nebula which appears to be an exception
is NGC 6445 which has a high He/H ratio but a low N/O ratio which is
difficult to understand on the basis of the models of Karakas.
and have also undergone hot-bottom
burning. Again three of these PNe are bipolar (NGC 2440, Hb5 and
Hu1-2). Thus 6 of the 7 bipolar nebular in our selection have
abundances which indicate that they originated from initially high
mass stars. The only bipolar nebula which appears to be an exception
is NGC 6445 which has a high He/H ratio but a low N/O ratio which is
difficult to understand on the basis of the models of Karakas.
NGC 5315 appears to be an elliptical PN with a high mass. There are
three other elliptical nebulae which on the basis of a rather high N/O ratio
seem to originate from stars of rather high mass. These are NGC 6153, NGC 6886
and NGC 2392. A unlikely explanation is that these PNe are really bipolar seen
edge on making them look round. Two of these PNe do not have a high He/H ratio
however, making this interpretation appear too simplified. All the other
elliptical PNe have N/O and He/H ratios which do not substantially differ from
solar and therefore have a core mass of less than approximately 0.7 ![]() ,
using the evolutionary models of Karakas (2003). We cannot determine
the mass more precisely for these nebulae, except to say that in the models of
Karakas those PNe with a high carbon abundance (C/O
,
using the evolutionary models of Karakas (2003). We cannot determine
the mass more precisely for these nebulae, except to say that in the models of
Karakas those PNe with a high carbon abundance (C/O ![]() 1) have the higher
mass.
1) have the higher
mass.
An HR diagram for these nebulae was then constructed in order to see if the position of the PNe on this diagram can confirm the conclusions drawn from the comparison of the abundances with the predictions of Karakas. The effective temperature of the central stars is determined, usually with an error that is less than 10%. The determination of the luminosity can be made in two ways. First by computing it from the temperature and radius of the central star, and secondly by finding it from the nebular emission in both the hydrogen and helium lines. The second method has the additional assumption that the nebula is ``optically deep'' to ionizing radiation of hydrogen or helium. We find that the luminosity determined from the ionized helium line is usually approximately equal to the luminosity found from the central star, indicating that the nebula absorbs all radiation which can doubly ionize helium. For about 30% of the nebulae the hydrogen ionizing radiation gives a lower luminosity indicating that in these cases the nebula is ``optically thin'' to this radiation. In this way a method has been found to determine which nebulae are ``optically deep'' to the various radiation fields. Probably the largest uncertainty in the luminosity is the distance determination so that a subsection is devoted to a discussion of the distances used. The resultant HR diagram is shown in Fig. 4. The high masses found from the abundances for the six bipolar PNe are consistent with their position on the HR diagram. The position of the seventh bipolar PN, NGC 6445, is consistent with it being a high mass object, leaving its rather low N/O ratio as a problem. The position of NGC 6886 is consistent with a rather high mass. Most of the elliptical PNe have positions consistent with low core masses. The biggest problems are: 1) NGC 7027, whose HR position indicates a high mass while its abundances give a low mass; 2) NGC 5315 whose position indicates a low mass while its abundance gives a high mass. M1-42 is also a problem but its distance is very poorly known and some of the observations are not very good. NGC 2392 has a different problem since the luminosity determined from the star is improbably high. The effective temperature that we have determined for this central star does not apply to the star measured in the visual. The most likely solution is that this central star is a binary and the secondary, which is unseen in the visual, is of a much higher temperature and is responsible for the high degree of ionization found. The possible presence of a hotter star has been suspected earlier; Ciardullo et al. (1999) have looked for it but have found only a very faint nearby star. If this is the source of ionization it cannot be a main sequence star because if this was so it would be too distant to be associated with the nebula. But the ionization source could be a star which is too close to the bright star to be observed.
In general it appears that the initial masses as determined from the observed abundances in conjunction with the models of Karakas (2003) are consistent with the initial masses predicted using the evolutionary models of Schönberner (1983), Blöcker (1995) and Vassiliadis & Wood (1993). But being consistent is only a first step and both the models and the observed abundances should both be improved. Furthermore the various cases which appear to give inconsistent results must be understood before we can speak of agreement.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard-Salas, J., Pottasch, S. R., Beintema, D. A., & Wesselius, P. R. 2001, A&A, 367, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard-Salas, J., Pottasch, S. R., Feibelman, W. A., & Wesselius, P. R. 2002, A&A, 387, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard-Salas, J., Pottasch, S. R., Wesselius, P. R., & Feibelman, W. A. 2003, A&A, 406, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blöcker, T. 1995, A&A, 299, 755 [NASA ADS] [Google Scholar]
- Cahn, J. H., Kaler, J. B., & Stanghellini, L. 1992, A&AS, 94, 399 [NASA ADS] [Google Scholar]
- Ciardullo, R., Bond, H. E., Sipior, M. S., et al. 1999, AJ, 118, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Morris, P. W., & Smith, J. D. 2006, ApJ, 636, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., & Widing, K. G. 2003, Sp. Sci. Rev., 107, 665 [Google Scholar]
- Gathier, R., & Pottasch, S. R. 1988, A&A, 197, 266 [NASA ADS] [Google Scholar]
- Gathier, R., Pottasch, S. R., & Pel, J. W. 1986a, A&A, 157, 171 [NASA ADS] [Google Scholar]
- Gathier, R., Pottasch, S. R., & Goss, W. M. 1986b, A&A, 157, 191 [NASA ADS] [Google Scholar]
- Greig, W. E. 1971, A&A, 10, 161 [NASA ADS] [Google Scholar]
- Greig, W. E. 1972, A&A, 18, 70 [NASA ADS] [Google Scholar]
- Harris, H. C., Dahn, C. C., & Canzian, B. 2007, AJ, 133, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Heap, S. R., & Hintzen, P. 1990a, ApJ, 353, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Heap, S. R., Corcoron, M., Hintzen, P., et al. 1990b, in From Miras to PN, ed. M. O. Mennessier, & A. Omont, 397 [Google Scholar]
- Hummer, D. G., & Storey, P. J. 1987, MNRAS, 224, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. Jr., & Renzini, A. 1981, Phys. Proc. in Red Giants (Dordrecht: pub. Reidel) [Google Scholar]
- Karakas, A. I. 2003, Thesis, Monash Univ. Melbourne [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2003, PASA, 20, 393 [Google Scholar]
- Kudritzki, R.-P., Mendez, R. H., Puls, J., et al. 1997, ed. Habing, & Lamers, IAU Symp., 180, 64 [Google Scholar]
- Lattanzio, J. 2003, ed. S. Kwok, M. Dopita, & R. Sutherland (ASP), IAU Symp., 209, 73 [Google Scholar]
- Manchado, A. 2003, IAU Symp., 209, 431 [NASA ADS] [Google Scholar]
- Manchado, A., Guerrero, M. A., Stanghellini, L., et al. 1996, Morph. Cat. PN, (IAC) [Google Scholar]
- Marigo, P., Bernard-Salas, J., Pottasch, S. R., et al. 2003, A&A, 409, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, W. 1994, A&A, 281, 526 [NASA ADS] [Google Scholar]
- Matsuura, M., Zijlstra, A. A., Gray, M. D., et al. 2005, MNRAS, 363, 628 [NASA ADS] [Google Scholar]
- Mellema, G. 2004, A&A, 416, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendez, R. H., Kudritzki, R. P., Herrero, A., et al. 1988, A&A, 190, 113 [NASA ADS] [Google Scholar]
- Mendez, R. H., Kudritzki, R. P., & Herrero, A. 1992, A&A, 260, 329 [NASA ADS] [Google Scholar]
- Napiwotzki, R. 2006, A&A, 451, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczynski, B. 1971, Acta. Astron., 21, 417 [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Mendez, R. H. 2004, A&A, 419, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peimbert, M. 1978, IAU Symp., 76, 215 [NASA ADS] [Google Scholar]
- Peimbert, M., & Torres-Peimbert, S. 1983, IAU Symp., 103, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. P. 2003, MNRAS, 344, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Pottasch, S. R. 1984 (Dordrecht: Reidel), Plan. Neb., 105 [Google Scholar]
- Preite-Martinez, A., & Pottasch, S. R. 1983, A&A, 126, 31 [NASA ADS] [Google Scholar]
- Pottasch, S. R., & Acker, A. 1989, A&A, 221, 123 [NASA ADS] [Google Scholar]
- Pottasch, S. R., & Beintema, D. A. 1999, A&A, 347, 974 [Google Scholar]
- Pottasch, S. R., & Bernard-Salas, J. 2008, A&A, 490, 715 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., & Surendiranath, R. 2005a, A&A, 432, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., & Surendiranath, R. 2005b, A&A, 444, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., Preite-Martinez, A., Olnon, F. M., et al. 1986, A&A, 161, 363 [NASA ADS] [Google Scholar]
- Pottasch, S. R., Beintema, D. A., & Feibelman, W. A. 2000, A&A, 363, 767 [NASA ADS] [Google Scholar]
- Pottasch, S. R., Beintema, D. A., Bernard-Salas, J., & Feibelman, W. A. 2001, A&A, 387, 684 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., Beintema, D. A., Bernard-Salas, J., et al. 2002, A&A, 393, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., Beintema, D. A., Bernard-Salas, J., & Feibelman, W. A. 2003, A&A, 409, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., Beintema, D. A., Bernard-Salas, J., & Feibelman, W. A. 2004, A&A, 423, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., Beintema, D. A., & Feibelman, W. A. 2005, A&A, 436, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., Bernard-Salas, J., & Roellig, T. L. 2009, A&A, 499, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preite-Martinez, A., Acker, A., Koppen, J., et al. 1991, A&AS, 88, 121 [Google Scholar]
- Renzini, A., & Voli, M. 1983, A&A, 94, 175 [Google Scholar]
- Sabbadin, F. 1986, A&AS, 64, 579 [NASA ADS] [Google Scholar]
- Sabbadin, F., Benetti, S., Cappellaro, E., et al. 2005, A&A, 436, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönberner, D. 1983, ApJ, 273, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Schönberner, D., Jacob, R., & Steffen, M. 2005, A&A, 441, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stanghellini, L., Corradi, R. L. M., & Schwarz, H. E. 1993, A&A, 276, 463 [NASA ADS] [Google Scholar]
- Stanghellini, L., Shaw, R. A., & Villaver, E. 2008, ApJ, 689, 194 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stoy, R. H. 1933, MNRAS, 93, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Terzian, Y. 1997, ed. H. J. Habing, & H. Lamers, IAU Symp., 180, 29 [Google Scholar]
- Tylenda, R., Siodmiak, N., Gorny, S. K., et al. 2003, A&A, 405, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1994, ApJS 92, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, M. J., Code, A. D., & Groth, E. D. 2000, AJ, 119, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Zijlstra, A. A., Hoof, P. A. M., & Perley, R. A. 2008, ApJ, 681, 1296 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... II
![[*]](/icons/foot_motif.png)
- Based on observations with ISO, an ESA project with instruments funded by ESA Member States (especially the PI countries: France, Germany, the Netherlands and the United Kingdom) and with the participation of ISAS and NASA.
All Tables
Table 1: Elemental abundance of PNe with far-infrared data in addition to optical and UV data.
Table 2: Comparison of measured stellar magnitudes.
Table 3: Spectroscopic temperatures.
Table 4: Central star magnitude, temperature and luminosity.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{plot1.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14009-10/Timg8.png)
|
Figure 1: Histogram of the nitrogen/oxygen ratio of the PNe listed in Table 1. Round PNe are not included in this plot because of the small number of objects. |
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{plot2.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14009-10/Timg9.png)
|
Figure 2: The N/O abundance ratio is plotted as a function of He/H. The dashed lines connect the results of the models of Karakas for a given value of Z. The ciphers give the initial masses of the individual models. The individual measured PN abundances are from Table 1. Those referred to in the text also have their names given. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{plot3b.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14009-10/Timg10.png)
|
Figure 3: N/O plotted against C/O. The lines and points are the same as in the caption to Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,angle=90]{hr.ps}
\end{figure}](/articles/aa/full_html/2010/09/aa14009-10/Timg34.png)
|
Figure 4:
The HR diagram. The models for core masses of 0.57, 0.67 and
0.91 |
| Open with DEXTER | |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


