| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | L7 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201014796 | |
| Published online | 22 June 2010 | |
LETTER TO THE EDITOR
The double degenerate system NLTT 11748![[*]](/icons/foot_motif.png)
A. Kawka1 - S. Vennes1,2 - T. R. Vaccaro2,3
1 - Astronomický ústav, Akademie ved Ceské republiky, Fricova 298, 251 65 Ondrejov, Czech Republic
2 - Visiting Astronomer, Kitt Peak National Observatory, National
Optical Astronomy Observatory, which is operated by the Association of
Universities for Research in Astronomy (AURA) under cooperative
agreement with the National Science Foundation
3 -
Department of Physics & Astronomy, Francis Marion University, Box 100547, Florence, SC 29501, USA
Received 15 April 2010 / Accepted 18 May 2010
Abstract
We show that the extremely low-mass white dwarf NLTT 11748 (
![]() )
is in a close binary with a fainter companion. We obtained a series of
radial velocity measurements of the low-mass white dwarf using the H
)
is in a close binary with a fainter companion. We obtained a series of
radial velocity measurements of the low-mass white dwarf using the H![]() core and determined an orbital period of 5.64 h. The
velocity semi-amplitude (K=274.8 km s-1) and orbital period imply that it is a degenerate star, and that the minimum mass for the companion is
core and determined an orbital period of 5.64 h. The
velocity semi-amplitude (K=274.8 km s-1) and orbital period imply that it is a degenerate star, and that the minimum mass for the companion is
![]() (assuming a mass of
(assuming a mass of
![]() for the primary). Our analysis of Balmer line profiles shows that a
for the primary). Our analysis of Balmer line profiles shows that a
![]() white dwarf companion does not contribute more than 2% or 5% of the flux (V-band)
for helium- or hydrogen-rich surfaces, respectively. The kinematics of
the system suggest that it belongs to the Galactic halo.
white dwarf companion does not contribute more than 2% or 5% of the flux (V-band)
for helium- or hydrogen-rich surfaces, respectively. The kinematics of
the system suggest that it belongs to the Galactic halo.
Key words: binaries: close - stars: individual: NLTT 11748 - white dwarfs
1 Introduction
The high proper-motion star NLTT 11748 was identified as an extremely low mass (ELM) white dwarf by Kawka & Vennes (2009). The first ELM white dwarfs were discovered to be companions to neutron stars (e.g., van Kerkwijk et al. 1996; Bassa et al. 2003), but recent follow-up observations of ELM white dwarfs identified in colourimetric or proper motion surveys (e.g., SDSS, NLTT) often find them to be in a close binary with a white dwarf companion (e.g., SDSS J125733.63+542850.5, Marsh et al. 2010; Badenes et al. 2009; Kulkarni & van Kerkwijk 2010). The companions of several other ELM white dwarfs found to be in close binary systems are yet to be formally identified, but they are likely to be more massive white dwarfs (see, Agüeros et al. 2009a,b).
The stellar and kinematical properties of NLTT 11748 (Kawka & Vennes 2009) and of two similar objects, LP400-22 (Kilic et al. 2009; Vennes et al. 2009) and SDSS J1053+5200 (Kilic et al. 2010), also suggest that they are old halo stars. The constraints placed on their total ages help retrace the prior evolution of these systems (see Nelemans et al. 2001; Nelson et al. 2004; Tauris & Savonije 1999).
The formation of ELM white dwarfs requires that the systems go through
at least two phases of mass transfer, where the second mass transfer
phase strips the less massive companion of its outer envelope before
the helium ignition. This generic scenario appears valid whether the
more massive component is a neutron star or a white dwarf (see for
example Nelemans et al. 2001; Nelson et al. 2004). An example of a possible progenitor to an ELM white dwarf is the bright
subluminous B (sdB) star, HD 188112 (Heber et al. 2003). The subdwarf star has a lower mass than average, 0.24 versus
![]() (Zhang et al. 2009), and orbits a degenerate companion with a mass
(Zhang et al. 2009), and orbits a degenerate companion with a mass
![]() every 14.6 h. The subdwarf is a likely progenitor of a helium
white dwarf similar to NLTT 11748. On the other hand, a possible
progenitor to an ELM white dwarf with, this time, a neutron star
companion is SDSS J102347.6+003841 (Wang et al. 2009). This is a close binary comprising a G-type star and a 1.69 ms pulsar (Archibald et al. 2009) with an orbital period of 4.75 h. Although the spectral type of the visible component implies a mass of
every 14.6 h. The subdwarf is a likely progenitor of a helium
white dwarf similar to NLTT 11748. On the other hand, a possible
progenitor to an ELM white dwarf with, this time, a neutron star
companion is SDSS J102347.6+003841 (Wang et al. 2009). This is a close binary comprising a G-type star and a 1.69 ms pulsar (Archibald et al. 2009) with an orbital period of 4.75 h. Although the spectral type of the visible component implies a mass of
![]() ,
the mass ratio of the system dictates a much lower mass of
,
the mass ratio of the system dictates a much lower mass of
![]() suggesting that the star
is significantly evolved with a helium-enriched core. This system
probably represents a first link between low-mass X-ray binaries and
ELM plus neutron star binaries (Archibald et al. 2009).
suggesting that the star
is significantly evolved with a helium-enriched core. This system
probably represents a first link between low-mass X-ray binaries and
ELM plus neutron star binaries (Archibald et al. 2009).
We report new observations that help clarify the nature of the ELM white dwarf NLTT 11748. We obtained two sets of intermediate resolution spectra that show that NLTT 11748 is in a close binary system (Sect. 2). Our analysis of the spectroscopic data and a first determination of the binary parameters are presented in Sect. 3. We discuss our results in Sect. 4 and summarise in Sect. 5.
2 Observations
We observed NLTT 11748 with the FORS2 spectrograph attached to the UT1 - Antu at Paranal on UT 2009 October 22 and 23. We used the 1200R grism combined with a slit width of 1'', which provided a resolution of 3.0 Å. The spectra were obtained as part of a programme aimed at detecting and measuring magnetic fields in hydrogen-rich white dwarf stars. The observation sequence consists of two consecutive exposures with the Wollaston prism rotated by 90 degrees between them. In principle, a magnetic field may cause an apparent velocity offset in pairs of exposures, but our analysis of the radial velocity measurements excludes the effect of a magnetic field (Sect. 3.1).
We obtained additional observations with the R-C spectrograph
attached to the 4 m telescope at the Kitt Peak National
Observatory (KPNO) on UT 2010 March 4 to 6. We used the
T2KB detector and
the KPC-24 grating (860 lines/mm) in second order centred on H![]() .
We employed the GG495 filter to block out contamination from the
first order. We set the slit width to 1.5'', which provided a
resolution of 0.8 Å (full-width half-maximum).
.
We employed the GG495 filter to block out contamination from the
first order. We set the slit width to 1.5'', which provided a
resolution of 0.8 Å (full-width half-maximum).
All spectra were wavelength-calibrated using comparison arc (HeNeAr) exposures. The stability of the wavelength scale was verified through O I sky lines, which remained stable with a standard deviation of 3 km s-1. All data were reduced with standard procedures within IRAF. Figure 1 and Table 1 show our spectra and the observation log.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14796fg1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14796-10/Timg9.png)
|
Figure 1: Spectra obtained with VLT FORS2 (left) and the KPNO R-C spectrograph (right). The spectra are labeled with the orbital phase (Sect. 3.1) and the top spectra are the co-added phase-corrected spectrum for each spectrograph. |
| Open with DEXTER | |
3 Analysis
3.1 Binary parameters
We used the H![]() line centre to measure the radial velocity of NLTT 11748. We
fitted a Gaussian profile to the deep, narrow core. Repeated
measurements varying the fitting window from 2 to 5 Å
from the line centre were averaged, leaving residuals of 3
to 10 km s-1
depending on the signal-to-noise ratio of the spectrum. The velocities
were then corrected to the solar system barycentre. We verified the
procedure by cross-correlating each spectrum with a template built by
co-adding all spectra in the rest frame (see Fig. 1)
and comparing the resulting velocities to the Gaussian fits. With a
window from 6500 to 6620 Å, we found that the two methods
differ by
line centre to measure the radial velocity of NLTT 11748. We
fitted a Gaussian profile to the deep, narrow core. Repeated
measurements varying the fitting window from 2 to 5 Å
from the line centre were averaged, leaving residuals of 3
to 10 km s-1
depending on the signal-to-noise ratio of the spectrum. The velocities
were then corrected to the solar system barycentre. We verified the
procedure by cross-correlating each spectrum with a template built by
co-adding all spectra in the rest frame (see Fig. 1)
and comparing the resulting velocities to the Gaussian fits. With a
window from 6500 to 6620 Å, we found that the two methods
differ by
![]()
![]() 3.5 km s-1 for the higher quality FORS2 spectra, and
3.5 km s-1 for the higher quality FORS2 spectra, and
![]()
![]() 12.0 km s-1
for the R-C spectra. Accordingly, the FORS2 and R-C spectra
are weighted 4:1 in the orbital analysis. Table 2 lists the barycentric mid-exposure times and velocities.
12.0 km s-1
for the R-C spectra. Accordingly, the FORS2 and R-C spectra
are weighted 4:1 in the orbital analysis. Table 2 lists the barycentric mid-exposure times and velocities.
We determined the orbital parameters by fitting sinusoidal functions to the radial velocities, where
the period (P), mean systemic velocity (![]() ), the velocity semi-amplitude (K) and the initial epoch (T0) are varied. Figure 2
shows the periodogram and best-fit radial velocity curve. The
significance values are drawn at 66%, 90% and 99%. The
average of the residuals is
), the velocity semi-amplitude (K) and the initial epoch (T0) are varied. Figure 2
shows the periodogram and best-fit radial velocity curve. The
significance values are drawn at 66%, 90% and 99%. The
average of the residuals is ![]() km s-1,
commensurate with our estimates of the wavelength scale accuracy.
Although the FORS2 spectra were obtained with the Wollaston prism
in place, the low residual value excludes a significant magnetic
field. A more detailed spectropolarimetric analysis will be
reported elsewhere.
km s-1,
commensurate with our estimates of the wavelength scale accuracy.
Although the FORS2 spectra were obtained with the Wollaston prism
in place, the low residual value excludes a significant magnetic
field. A more detailed spectropolarimetric analysis will be
reported elsewhere.
Table 1: Observation log.
Table 2: Radial velocity measurements of NLTT 11748.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14796fg2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14796-10/Timg17.png)
|
Figure 2: ( Top) Periodogram of radial velocity measurements showing, in inset, an enlarged segment near the best period. ( Middle) Radial velocity measurements folded on the orbital period and compared to a sinusoidal fit (see text). ( Bottom) Residuals of the sinusoidal fit. |
| Open with DEXTER | |
The best-fit parameters are
where T0 is the initial epoch of superior conjunction of the unseen companion. We also determined the systemic velocity
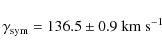
by subtracting the gravitational redshift of the white dwarf (
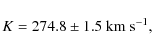
which corresponds to a mass function for the unseen companion
Adopting a mass of
We re-evaluated the kinematics of the system with the new systemic velocity to obtain (U,V,W) = (-163, -252, -29) km s-1. These updated values clearly place NLTT 11748 in the halo. Two other ELM systems whose kinematics place them in the halo are LP400-22 (Vennes et al. 2009) and SDSS J1053+5200 (Kilic et al. 2010) with the remaining systems (without a neutron star) apparently belonging to the disc (Kilic et al. 2010).
3.2 Constraints on a white dwarf companion
Although Kawka & Vennes (2009) achieved
a satisfactory fit to the Balmer line profiles, their analysis did not
consider a companion. We repeated that analysis using two composite
model grids, DA+DC or DA+DA.
We modelled the primary with a pure-hydrogen model grid (DA) and the
secondary with either a pure-helium (DC) or a DA grid. First, we
set the mass of the secondary to
![]() .
We fitted the Balmer line profiles (see Kawka & Vennes 2009,
for details of the NTT-EFOSC2 spectrum) varying three parameters:
the temperature and surface gravity of the primary (
.
We fitted the Balmer line profiles (see Kawka & Vennes 2009,
for details of the NTT-EFOSC2 spectrum) varying three parameters:
the temperature and surface gravity of the primary (
![]() )
and the effective temperature of the secondary (
)
and the effective temperature of the secondary (
![]() ). The total flux was obtained by combining the primary and secondary surface fluxes weighted by the emitting area:
). The total flux was obtained by combining the primary and secondary surface fluxes weighted by the emitting area:
![]() ,
where R is the effective radius of the composite star, and
,
where R is the effective radius of the composite star, and ![]() and
and ![]() are the primary and secondary radii computed using the evolutionary mass radius relations of Benvenuto & Althaus (1999) and Serenelli et al. (2002).
Note that the flux composition takes into account the calculated
orbital phase of the observed spectrum and the corresponding offset in
velocities between the two stars. The combined spectrum is then fitted
to the observed spectrum with
are the primary and secondary radii computed using the evolutionary mass radius relations of Benvenuto & Althaus (1999) and Serenelli et al. (2002).
Note that the flux composition takes into account the calculated
orbital phase of the observed spectrum and the corresponding offset in
velocities between the two stars. The combined spectrum is then fitted
to the observed spectrum with ![]() minimization techniques.
minimization techniques.
The best-fit parameters from the DA+DA grid are
![]()
![]() 50 K (
50 K (![]() )
and
)
and
![]()
![]() 0.15 for the primary and
0.15 for the primary and
![]() K for the secondary. The flux contribution from the secondary at 5500 Å (V-band) is
K for the secondary. The flux contribution from the secondary at 5500 Å (V-band) is ![]() % of the total flux.
But if we used the DA+DC grid we obtained an upper limit of
% of the total flux.
But if we used the DA+DC grid we obtained an upper limit of
![]() K, with a flux contribution
K, with a flux contribution ![]() %. Setting the secondary mass to
%. Setting the secondary mass to ![]() did not affect our solution for the primary, but allowed a higher
secondary temperature (+400 K). In summary, the best-fit
parameters are identical to the single star solution obtained by Kawka & Vennes (2009), and we conclude that the secondary star is much fainter than the primary star.
did not affect our solution for the primary, but allowed a higher
secondary temperature (+400 K). In summary, the best-fit
parameters are identical to the single star solution obtained by Kawka & Vennes (2009), and we conclude that the secondary star is much fainter than the primary star.
4 Discussion
If the maximum mass of a white dwarf is![\begin{figure}
\par\includegraphics[width=8cm,clip]{14796fg3.eps}\vspace{-3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14796-10/Timg42.png)
|
Figure 3: Orbital period versus mass of the visible component in binary systems containing a white dwarf and a neutron star (open triangles) or another white dwarf (open circles, this includes systems where the unseen is unknown, but has a high probability of being a more massive white dwarf). NLTT 11748, HD 188112, and SDSS J1023+0038 are marked with a filled square, circle, and triangle, respectively. These values are compared to theoretical period-mass relations for NS+WD systems of Nelson et al. (2004) and Tauris & Savonije (1999) drawn with thick and thin lines, respectively. |
| Open with DEXTER | |
Figure 3 shows the locus of the ELM binary systems in a period versus ELM mass diagram. The data from Table 3 are compared to the mass-period relations from the WD+NS binary evolutionary scenarios of Nelson et al. (2004) and Tauris & Savonije (1999). Similar trends
are also predicted for the brighter star in binary systems with two white dwarf stars (Nelemans et al. 2001). Figure 3 also includes the long period WD+NS system PSR B0820+02d (Koester & Reimers 2000). This particular system extends the apparent correlation toward higher mass (0.60 ![]()
![]() )
and longer period (1232.5 d). Table 3
first provides
the parameters of NLTT 11748, followed by the parameters of
systems containing white dwarfs with a neutron star
companion (NS+WD), and double white dwarf systems (WD+WD).
Finally, we list the parameters of the possible progenitors of ELM
white dwarf binary systems. Some scatter between the mass of the
brighter star and the orbital period is clearly visible, but a
correlation is still observed between the two parameters. The models of
Tauris & Savonije (1999) appear to better represent the
observed trend than those of Nelson et al. (2004).
The two outstanding points that are significantly off the predicted
relationship of either models are the two systems with very short
periods (SDSS J1053+5200, SDSS J1436+5010: Mullally et al. 2010; Kilic et al. 2010).
Overall, WD+WD and WD+NS systems overlap in the diagram,
so this trend alone does not allow one to distinguish between
WD+WD and WD+NS systems.
)
and longer period (1232.5 d). Table 3
first provides
the parameters of NLTT 11748, followed by the parameters of
systems containing white dwarfs with a neutron star
companion (NS+WD), and double white dwarf systems (WD+WD).
Finally, we list the parameters of the possible progenitors of ELM
white dwarf binary systems. Some scatter between the mass of the
brighter star and the orbital period is clearly visible, but a
correlation is still observed between the two parameters. The models of
Tauris & Savonije (1999) appear to better represent the
observed trend than those of Nelson et al. (2004).
The two outstanding points that are significantly off the predicted
relationship of either models are the two systems with very short
periods (SDSS J1053+5200, SDSS J1436+5010: Mullally et al. 2010; Kilic et al. 2010).
Overall, WD+WD and WD+NS systems overlap in the diagram,
so this trend alone does not allow one to distinguish between
WD+WD and WD+NS systems.
Table 3: Confirmed binary systems containing a low-mass white dwarf.
The ELM white dwarfs that are companions to neutron stars appear to be very faint (V > 20) with the brightest known ELM companion to a neutron star with an apparent magnitude of V = 19.6 (PSR J1012+5307). The binary systems containing an ELM white dwarf and either a confirmed or probable white dwarf companion are significantly brighter, with apparent visual magnitudes ranging from 16.5 up to 19.3, with NLTT 11748 the brightest of the sample. In terms of distances we find that the WD+WD sample lies within a range of 0.1-1.6 kpc at an average distance of 0.75 kpc, while the WD+NS sample lies within a range of 0.15-4.4 kpc at an average distance of 1.5 kpc. Located at a distance of 0.4 kpc and being the brightest known ELM, NLTT 11748 fits well within the relatively closer and brighter class of WD+WD systems. Moreover, NLTT 11748 is not associated with a known radio source, therefore based on these considerations alone we may conclude that the companion to NLTT 11748 is another white dwarf with a mass above average.
Indeed, after this work was submitted for publication, Steinfadt et al. (2010) announced the discovery of primary and secondary eclipses in NLTT 11748 confirming the secondary star as a white dwarf. Their analysis confirms the ELM natureof the primary star and corroborates our analysis of the binary properties. Their orbital period measurement, based on eclipse timing, agrees with our spectroscopic period within error bars. Finally, our ephemeris allows us to identifiy the primary and secondary eclipses observed by Steinfadt et al. (2010) with the corresponding orbital conjunctions.
5 Conclusions
We find that the ELM white dwarf NLTT 11748 is part of a short-period binary system (P=5.64 h). Based on our orbital analysis alone, we find that the minimum mass of the companion is
![]() .
However, the companion has independently been identified as a faint white dwarf (Steinfadt et al. 2010), and assuming a mass of
.
However, the companion has independently been identified as a faint white dwarf (Steinfadt et al. 2010), and assuming a mass of
![]() ,
we constrained the companion temperature to
,
we constrained the companion temperature to
![]() K (DA) or
K (DA) or ![]() K (DC). The kinematics of NLTT 11748 also place the system in the Galactic halo.
K (DC). The kinematics of NLTT 11748 also place the system in the Galactic halo.
A.K. and S.V. are supported by GA AV grant numbers IAA301630901 and IAA300030908, respectively, and by GA CR grant number P209/10/0967. We thank the referee for a prompt review and useful suggestions.
References
- Agüeros, M. A., Camilo, F., Silvestri, N. M., et al. 2009a, ApJ, 697, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Agüeros, M. A., Heinke, C., Camilo, F., et al. 2009b, ApJ, 700, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Archibald, A. M., Stairs, I. H., Ransom, S. M., et al. 2009, Science, 324, 1411 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Badenes, C., Mullally, F., Thompson, S. E., & Lupton, R. H. 2009, ApJ, 707, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Bassa, C. G., van Kerkwijk, M. H., & Kulkarni, S. R. 2003, A&A, 403, 1067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bassa, C. G., van Kerkwijk, M. H., Koester, D., & Verbunt, F. 2006, A&A, 456, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benvenuto, O. G., & Althaus, L. G. 1999, MNRAS, 303, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Callanan, P. J., Garnavich, P. M., & Koester, D. 1998, MNRAS, 298, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Corongiu, A., Possenti, A., Lyne, A. G., et al. 2006, ApJ, 653, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., Jacoby, B. A., & Bailes, M. 2008, AIP Conf. Proc., 983, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U., Edelmann, H., Lisker, T., & Napiwotzki, R. 2003, A&A, 411, L477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, T. J., & McCarthy, Jr., D. W. 1993, AJ, 106, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, B. A., Hotan, A., Bailes, M., Ord, S., & Kulkarni, S. R. 2005, ApJ, 629, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M., Taylor, J. H., & Ryba, M. F. 1994, ApJ, 428, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kawka, A., & Vennes, S. 2009, A&A, 506, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kilic, M., Brown, W. R., Allende Prieto, C., et al. 2009, ApJ, 695, L92 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Brown, W. R., Allende Prieto, C., & Kenyon, S. J. 2010, ApJ, 716, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, D., & Reimers, D. 2000, A&A, 364, L66 [NASA ADS] [Google Scholar]
- Kulkarni, S. R., & van Kerkwijk, M. H. 2010, ApJ, submitted [arXiv:1003.2169] [Google Scholar]
- Marsh, T. R., Gänsicke, B. T., Steeghs, D., et al. 2010, ApJL, submitted [arXiv:1002.4677] [Google Scholar]
- Mereghetti, S., Tiengo, A., Esposito, P., et al. 2009, Science, 325, 1222 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mullally, F., Badenes, C., Thomson, S. E., & Lupton, R. 2010, ApJ, 707, L51 [Google Scholar]
- Navarro, J., de Bruyn, A. G., Frail, D. A., Kulkarni, S. R., & Lyne, A. G. 1995, ApJ, 455, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, L. A., Dubeau, E., & MacCannell, K. A. 2004, ApJ, 616, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Nice, D. J., Splaver, E. M., Stairs, I. H., et al. 2005, ApJ, 634, 1242 [Google Scholar]
- Serenelli, A. M., Althaus, L. G., Rohrmann, R. D., & Benvenuto, O. G. 2002, MNRAS, 337, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Steinfadt, J. D. R., Kaplan, D. L., Shporer, A., Bildsten, L., & Howell, S. B. 2010, ApJ, 716, L146 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., & Savonije, G. J. 1999, A&A, 350, 928 [NASA ADS] [Google Scholar]
- van Kerkwijk, M. H., Bergeron, P., & Kulkarni, S. R. 1996, ApJ, 467, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Vennes, S., & Kawka, A. 2008, MNRAS, 389, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Vennes, S., Kawka, A., Vaccaro, T. R., & Silvestri, N. M. 2009, A&A, 507, 1613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbiest, J. P. W., Bailes, M., van Straten, W., et al. 2008, ApJ, 679, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Z., Archibald, A. M., Thorstensen, J. R., et al. 2009, ApJ, 703, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, N. A., Olive, J.-F., Barret, D., et al. 2004, A&A, 419, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, X., Chen, X., & Han, Z. 2009, A&A, 504, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... NLTT 11748
![[*]](/icons/foot_motif.png)
- Based on observations at the European Organisation for Astronomical Research in the Southern Hemisphere, Chile under programme ID 84.D-0862.
All Tables
Table 1: Observation log.
Table 2: Radial velocity measurements of NLTT 11748.
Table 3: Confirmed binary systems containing a low-mass white dwarf.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14796fg1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14796-10/Timg9.png)
|
Figure 1: Spectra obtained with VLT FORS2 (left) and the KPNO R-C spectrograph (right). The spectra are labeled with the orbital phase (Sect. 3.1) and the top spectra are the co-added phase-corrected spectrum for each spectrograph. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14796fg2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14796-10/Timg17.png)
|
Figure 2: ( Top) Periodogram of radial velocity measurements showing, in inset, an enlarged segment near the best period. ( Middle) Radial velocity measurements folded on the orbital period and compared to a sinusoidal fit (see text). ( Bottom) Residuals of the sinusoidal fit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14796fg3.eps}\vspace{-3mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14796-10/Timg42.png)
|
Figure 3: Orbital period versus mass of the visible component in binary systems containing a white dwarf and a neutron star (open triangles) or another white dwarf (open circles, this includes systems where the unseen is unknown, but has a high probability of being a more massive white dwarf). NLTT 11748, HD 188112, and SDSS J1023+0038 are marked with a filled square, circle, and triangle, respectively. These values are compared to theoretical period-mass relations for NS+WD systems of Nelson et al. (2004) and Tauris & Savonije (1999) drawn with thick and thin lines, respectively. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


