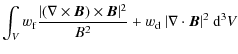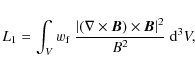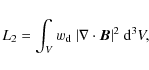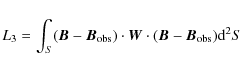| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 5 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014391 | |
| Published online | 22 July 2010 | |
How to deal with measurement errors and lacking data in nonlinear force-free coronal magnetic field modelling?
(Research Note)
T. Wiegelmann - B. Inhester
Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany
Received 9 March 2010 / Accepted 4 May 2010
Abstract
Context. The measured solar photospheric magnetic field
vector is extrapolated into the solar corona under the assumption of a
force-free plasma. In the generic case this problem is nonlinear.
Aims. We aim to improve an algorithm for computing the nonlinear
force-free coronal magnetic field. We are in particular interested to
incorporate measurement errors and to handle lacking data in the
boundary conditions.
Methods. We solve the nonlinear force-free field equations by
minimizing a functional. Within this work we extend the functional by
an additional term, which allows us to incorporate measurement errors
and treat regions with lacking observational data. We test the new code
with the help of a well known semi-analytic test case. We compare
coronal magnetic field extrapolations from ideal boundary conditions
and boundary conditions where the transversal magnetic field
information is lacking or has a poor signal-to-noise ratio in weak
field regions.
Results. For ideal boundary conditions the new code gives the
same result as the old code. The advantage of the new approach, which
includes an error matrix, is visible only for non-ideal boundary
conditions. The force-free and solenoidal conditions are fulfilled
significantly better and the solutions agrees somewhat better with the
exact solution. The new approach also relaxes the boundary and allows a
deviation from the boundary data in poor signal-to-noise ratio areas.
Conclusions. The incorporation of measurement errors in the
updated extrapolation code significantly improves the quality of
nonlinear force-free field extrapolation from imperfect boundary
conditions.
Key words: Sun: corona - Sun: photosphere - magnetic fields
1 Introduction
Because routine measurements of the coronal magnetic field are not available, we
have to rely on measurements of the photospheric magnetic field vector
to estimate the coronal magnetic field distribution. The
extrapolation of this surface field into the corona constitutes a
boundary value problem, which can be solved numerically if some
simplifying model assumptions for the coronal field are made.
Because of the low plasma ![]() in the solar corona
non-magnetic forces are often neglected to lowest order.
We have to solve the corresponding nonlinear force-free boundary value problem
in the solar corona
non-magnetic forces are often neglected to lowest order.
We have to solve the corresponding nonlinear force-free boundary value problem
where
However, in a recent joined study by DeRosa et al. (2009) which
deals with an observed
data-set (vector magnetogram taken with Hinode/SOT embedded in a
line-of-sight magnetogram from SOHO/MDI) the force-free codes did not
find consistent solutions. A major problem was that only for a part of
the model region vector magnetograms were observed (in the Hinode field-of-view, FOV) and
the transverse magnetic field component
![]() was unknown in the
remaining photospheric area. In the study, the lacking field components
were replaced by zeros, which was a simple way to treat the lacking data.
In view of the inconsistency of the results
DeRosa et al. (2009)
concluded that a successful nonlinear force-free reconstruction requires
was unknown in the
remaining photospheric area. In the study, the lacking field components
were replaced by zeros, which was a simple way to treat the lacking data.
In view of the inconsistency of the results
DeRosa et al. (2009)
concluded that a successful nonlinear force-free reconstruction requires
- 1.
- A large computational domain with a high resolution, which accommodates most of the connectivity within the coronal region under study.
- 2.
- Taking account of measurement uncertainties, in particular for the transverse field component.
- 3.
- ``Preprocessing'' of the observed vector field that approximates the physics of the photosphere-to-chromosphere interface as it transforms the observed, forced, photospheric field to a more realistic approximation of the near force-free field in the upper chromosphere,
2 Method
To solve the force-free equations, we extended the optimisation approach
introduced by Wheatland et al. (2000):
The first integral contains the conditions (1) and (2) as quadratic forms and obviously for
Here, we propose to extend the functional by adding the
surface integral over the photosphere (4) and
iterating ![]() to minimize L, which is otherwise unconstrained.
In this integral,
to minimize L, which is otherwise unconstrained.
In this integral,
![]() is a diagonal error matrix,
the elements
is a diagonal error matrix,
the elements
![]() of which are chosen inversely proportional to the local measurement
error of the respective photospheric field component
at x,y. In principle
of which are chosen inversely proportional to the local measurement
error of the respective photospheric field component
at x,y. In principle ![]() should be specified by the
instrument, and it is likely that this error distribution
will be provided along with the data for SDO/HMI vector magnetograms.
Because the line-of-sight photospheric magnetic field is
measured with much higher accuracy than the transverse field
should be specified by the
instrument, and it is likely that this error distribution
will be provided along with the data for SDO/HMI vector magnetograms.
Because the line-of-sight photospheric magnetic field is
measured with much higher accuracy than the transverse field
![]() ,
we typically set the component
,
we typically set the component
![]() to unity,
while the transverse components of
to unity,
while the transverse components of
![]() are
typically small but positive.
In regions where
are
typically small but positive.
In regions where
![]() has not been measured or where
the signal-to-noise ratio is very poor, we set
has not been measured or where
the signal-to-noise ratio is very poor, we set
![]() .
.
The boundary value problem (1) and (2)
is nonlinear, and there is no guarantee that a
solution exists for all sets of boundary values
in the sense that we can obtain L=0exactly. Boulmezaoud & Amari (2000) have shown that the full vector field
as boundary condition overdetermines the problem, and
Wiegelmann et al. (2010) investigated the influence of
photospheric measurement errors.
Observed and noisy boundary fields
![]() are
very probably inconsistent and belong to the set of boundary
values for which a strict solution does not exist.
In these cases the first integral in (4) alone could
often not be iterated to values of the order of the numerical
roundoff-error. With the new formulation (4)
we allow deviations between the model field
are
very probably inconsistent and belong to the set of boundary
values for which a strict solution does not exist.
In these cases the first integral in (4) alone could
often not be iterated to values of the order of the numerical
roundoff-error. With the new formulation (4)
we allow deviations between the model field ![]() and the observed
and the observed
![]() and so
the model field can be iterated closer to a force-free
field even if the observations are inconsistent. This
balance is controlled by the Lagrangian multiplier
and so
the model field can be iterated closer to a force-free
field even if the observations are inconsistent. This
balance is controlled by the Lagrangian multiplier ![]() .
.
2.1 Encoding of old code
The previous version of our optimisation code worked as follows (see also Wiegelmann 2004, for details):
- Set initial
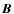 to the potential field computed from the normal component of
to the potential field computed from the normal component of
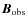 at the photospheric boundary.
at the photospheric boundary.
- Replace the transverse field component of the initial
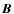 by the observed field components of
by the observed field components of
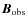 at the photospheric boundary.
at the photospheric boundary.
- Minimise L (Eq. (4)) iteratively, keeping
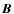 unchanged at the photospheric boundary. Only the first two terms are
influenced and the surface integral vanishes by construction
at each iteration step.
unchanged at the photospheric boundary. Only the first two terms are
influenced and the surface integral vanishes by construction
at each iteration step.
2.2 Encoding of new code
- Set initial
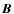 to the potential field computed from
the normal component of
to the potential field computed from
the normal component of
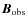 at the photospheric
boundary as above.
at the photospheric
boundary as above.
- Minimise L (Eq. (4)) iteratively without constraining
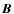 at the photospheric boundary.
The transverse magnetic field
at the photospheric boundary.
The transverse magnetic field
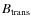 is gradually
driven towards the observations while the field relaxes
to a force-free field. If the observed field is inconsistent,
the difference
is gradually
driven towards the observations while the field relaxes
to a force-free field. If the observed field is inconsistent,
the difference
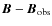 remains finite
depending on the control parameter
remains finite
depending on the control parameter 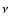 .
Where
.
Where
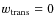 the observed field is automatically ignored.
the observed field is automatically ignored.
- Different from the old code the magnetic field is also relaxed in
the bottom boundary. Consequently the boundary values of
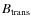 in regions with poor signal to noise ratio (
in regions with poor signal to noise ratio (
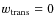 )
are automatically relaxed
towards force-free consistent values.
)
are automatically relaxed
towards force-free consistent values.
- The state L=0 corresponds to a perfect force-free and divergence-free
state and exact agreement of the boundary values
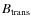 with observations
in regions with
with observations
in regions with
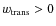 .
For inconsistent boundary data the force-free and solenoidal
conditions can still be fulfiled, but the third surface term will remain
finite. This results in some deviation of the bottom boundary data from the
observations in regions, where
.
For inconsistent boundary data the force-free and solenoidal
conditions can still be fulfiled, but the third surface term will remain
finite. This results in some deviation of the bottom boundary data from the
observations in regions, where
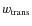 is small.
is small.
Table 1: Evaluation of the reconstruction quality.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{14391f1NEW.eps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14391-10/Timg31.png)
|
Figure 1: Magnetic fieldline plots for the reference equilibrium (panel a)), the initial potential field b) and the other panels show nonlinear force-free reconstructions with the old and new code for different cases, see text. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{14391f2NEW.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14391-10/Timg32.png)
|
Figure 2: Evolution of the entire functional L (solid line, see Eq. (4)) and its three terms (see Eq. (5)-(7)). |
| Open with DEXTER | |
3 Code testing
We tested the new code with the well known semi-analytic equilibrium from
Low & Lou (1990). These are force-free axis-symmetric equilibria in spherical
geometry, but the symmetry has broken for our tests by cutting a rectangular
obliquely orientated box out of the spherical solution. By means of a linear
shift l and a rotation angle ![]() ,
we positioned the centre of the
equilibrium solution and tilted its axis orientation relative to the cartesian
geometry of the computational domain (see Low & Lou 1990, for details).
These equilibria have become a standard for testing nonlinear force-free
extrapolation codes, (see, e.g., Tadesse et al. 2009; Wiegelmann & Neukirch 2003; Amari et al. 2006; Inhester & Wiegelmann 2006; Schrijver et al. 2006; Valori et al. 2007; Wheatland et al. 2000, for earlier studies with this
equilibrium). We here chose
l=0.3 and
,
we positioned the centre of the
equilibrium solution and tilted its axis orientation relative to the cartesian
geometry of the computational domain (see Low & Lou 1990, for details).
These equilibria have become a standard for testing nonlinear force-free
extrapolation codes, (see, e.g., Tadesse et al. 2009; Wiegelmann & Neukirch 2003; Amari et al. 2006; Inhester & Wiegelmann 2006; Schrijver et al. 2006; Valori et al. 2007; Wheatland et al. 2000, for earlier studies with this
equilibrium). We here chose
l=0.3 and
![]() for our tests and computed the equilibrium in a
box with
nx=ny=80, nz=72.
for our tests and computed the equilibrium in a
box with
nx=ny=80, nz=72.
Table 1 shows the results of these tests, where Col. 1
names the used code. The second and third column list the values of
the new parameters for the code in (4), the Lagrangian
multiplier ![]() and the matrix element
and the matrix element
![]() while
while
![]() was set to unity throughout
was set to unity throughout![]() .
.
These parameters were not present in the old code.
We treated the equilibrium field on the bottom boundary as the observed field
![]() input for both our old and new extrapolation code.
After the extrapolation, we evaluated the quality of our reconstruction by
comparing the extrapolation result with the exact reference solution
in the center 643 cube by a number of figures of merit in Table 1 Cols. 4-8.
These are the vector correlation (VC), Chauchy Schwarz (CS), normalized
vector error (NE), mean vector error (ME) and the
ratio of the computed magnetic energy and the energy of the Low and Lou
reference field (Energy). For a perfect reconstruction NE and ME are zero and all
other quantities are unity (see Schrijver et al. 2006, for a detailed explanation of these figures and the corresponding mathematical equations).
input for both our old and new extrapolation code.
After the extrapolation, we evaluated the quality of our reconstruction by
comparing the extrapolation result with the exact reference solution
in the center 643 cube by a number of figures of merit in Table 1 Cols. 4-8.
These are the vector correlation (VC), Chauchy Schwarz (CS), normalized
vector error (NE), mean vector error (ME) and the
ratio of the computed magnetic energy and the energy of the Low and Lou
reference field (Energy). For a perfect reconstruction NE and ME are zero and all
other quantities are unity (see Schrijver et al. 2006, for a detailed explanation of these figures and the corresponding mathematical equations).
We also evaluated how well the force-free condition
the divergence-free condition
and the boundary data term
are satisfied. The respective numbers are listed in Table 1 in Cols. 9 and 10. The last column displays the number of iteration steps needed to obtain the reconstruction. In practical computations L1, L2 and L3 never vanish exactly, but the code stops when
3.1 Tests with ideally measured boundary conditions
The first two rows in Table 1 show for reference the
figures of merit for the original reference solution and the initial
potential field, respectively. Rows 3-9 display test results with ideal boundary conditions
![]() from the exact solution. For the new code
we varied the Lagrangian multiplier
from the exact solution. For the new code
we varied the Lagrangian multiplier ![]() and the matrix elements
and the matrix elements
![]() .
For
.
For
![]() all pixels in the magnetogram are treated equally, which is
reasonable for perfectly measured data. Figure 1c and 1d show the respective reconstructed field lines with the old and new code
all pixels in the magnetogram are treated equally, which is
reasonable for perfectly measured data. Figure 1c and 1d show the respective reconstructed field lines with the old and new code
![]() ,
respectively.
Within a reasonable range of parameters the new code gives the same
result as the old one. If the Lagrangian multiplier
,
respectively.
Within a reasonable range of parameters the new code gives the same
result as the old one. If the Lagrangian multiplier ![]() is chosen
too small or
is chosen
too small or
![]() is nonzero mainly only for strong field regions, the
reconstructed solution is gradually decoupled from
is nonzero mainly only for strong field regions, the
reconstructed solution is gradually decoupled from
![]() and the resulting field deviates from the exact solution towards a potential field. For
and the resulting field deviates from the exact solution towards a potential field. For ![]() the code should stop immediately and return the initial
potential field for which L1=L2=0. For
the code should stop immediately and return the initial
potential field for which L1=L2=0. For
![]() the bottom boundary field is forced to agree with
the bottom boundary field is forced to agree with
![]() at every iteration step and the iteration should perform as for the old code.
at every iteration step and the iteration should perform as for the old code.
A main difference between old and new code is the evolution of the functional L during the iteration as shown in Fig. 2 panel a) and b). For the new code the force-part L1 and divergence-part L2 remain small during the entire iteration. The final state is almost identical for both implementations, however.
3.2 Tests with boundary conditions with lacking data
The main reason for the new implementation of our code is
that we need to deal with boundary data of different noise levels and qualities
or even miss some data points completely. This occurs e.g. due
to the limited field of view of some vector magnetographs like
Hinode-SOT. The line-of-sight magnetic field is usually available
for the entire solar disk, e.g. from SOHO/MDI, but the transverse
components
![]() are often not available in parts
of an active region. SDO/HMI will observe full-disk vector-magnetograms,
but
are often not available in parts
of an active region. SDO/HMI will observe full-disk vector-magnetograms,
but
![]() will suffer from a poor signal-to-noise ratio
in weak field regions. This makes
will suffer from a poor signal-to-noise ratio
in weak field regions. This makes
![]() measurements
less reliable in these regions.
measurements
less reliable in these regions.
We mimiced this effect by removing the information regarding the transverse
field in certain areas, e.g. where
![]() and
and
![]() ,
respectively. For our test field, this affects
,
respectively. For our test field, this affects
![]() and
and ![]() of the bottom boundary, respectively.
Finally as an extreme test we assigned
of the bottom boundary, respectively.
Finally as an extreme test we assigned
![]() only in
a very restricted area close to a local field concentration.
This simulates measurements with a vector magnetograph of a very small
FOV. For our test field
only in
a very restricted area close to a local field concentration.
This simulates measurements with a vector magnetograph of a very small
FOV. For our test field
![]() is then available for only
is then available for only
![]() of the bottom boundary. In the new code, the boundary area with
lacking data is marked by
of the bottom boundary. In the new code, the boundary area with
lacking data is marked by
![]() ,
in the old code
the lacking transverse field components are filled with zeros,
which implies a vertical magnetic field (see DeRosa et al. 2009, for details.)
,
in the old code
the lacking transverse field components are filled with zeros,
which implies a vertical magnetic field (see DeRosa et al. 2009, for details.)
The fieldline plots from these latter two reconstructions are
shown in Fig. 1e-h.
The comparison with the exact solution and numerical residuals
of the
![]() force and
the divergence are displayed in rows 10-18 of Table 1.
We find that the new code is closer to a force- and divergence-free field
in all cases and L1 and L2 are significantly smaller, in particular
for low values of the Lagrangian multiplier
force and
the divergence are displayed in rows 10-18 of Table 1.
We find that the new code is closer to a force- and divergence-free field
in all cases and L1 and L2 are significantly smaller, in particular
for low values of the Lagrangian multiplier ![]() .
The result of the new code
agrees also somewhat better with the original solution than the output
of the old code, but the difference is not as significant as the
difference in force-free and solenoidal conditions.
.
The result of the new code
agrees also somewhat better with the original solution than the output
of the old code, but the difference is not as significant as the
difference in force-free and solenoidal conditions.
The reason for these results is that the old and
new code react differently to inconsistent boundary conditions caused
by noisy data and by assuming a vertical field in
regions where transversal field measurements are lacking.
As seen in Fig. 2 panel c) the functional L iterated in the
old code soon reaches a stationary state at a finite value of L if the
boundary data are inconsistent.
This is different with the new code, shown in panels d) and e).
Here L1 and L2 remain very small during the entire evolution and
the inconsistency in the boundary data is absorbed in the L3 term.
L3 can also become relatively low however, because regions with
![]() (where the transverse field has a poor signal-to-noise ratio or is
even unknown) do scarcely or not at all contribute to the functional.
For a reasonably small Lagrangian multiplier
(where the transverse field has a poor signal-to-noise ratio or is
even unknown) do scarcely or not at all contribute to the functional.
For a reasonably small Lagrangian multiplier ![]() as shown in panel e)
the functionals L1 and L2 stay at a very low level (discretisation
error). The new code also relaxes the bottom boundary values
and changes the field there in order to find force-free consistent boundary
conditions. If information on
as shown in panel e)
the functionals L1 and L2 stay at a very low level (discretisation
error). The new code also relaxes the bottom boundary values
and changes the field there in order to find force-free consistent boundary
conditions. If information on
![]() are lacking in a significant
part of the magnetogram (up to
are lacking in a significant
part of the magnetogram (up to ![]() of the pixels in our
example), there is no unique solution for consistently specifying
of the pixels in our
example), there is no unique solution for consistently specifying
![]() ,
and one cannot expect the final equilibrium to
agree with the model solution. Yet we have the most probable magnetic
field model, because it is close to force- and divergence-free and agrees
with the sparse observed boundary data.
,
and one cannot expect the final equilibrium to
agree with the model solution. Yet we have the most probable magnetic
field model, because it is close to force- and divergence-free and agrees
with the sparse observed boundary data.
3.3 Influence of noise
Finally we investigate how noise influences the quality of the
reconstructed magnetic field in the last three rows of Table 1. We added a uniform noise of ![]() of the maxim transversal magnetic field onto
of the maxim transversal magnetic field onto
![]()
![]() For the old code the inconsistency in the boundary data leads to significant deviations from the force-free L1 and solenoidal condition L2. Computations with the new code lead to significantly better agreement
of the force and solenoidal condition, e.g., by almost two orders of magnitude
for a small Lagrangian multiplier
For the old code the inconsistency in the boundary data leads to significant deviations from the force-free L1 and solenoidal condition L2. Computations with the new code lead to significantly better agreement
of the force and solenoidal condition, e.g., by almost two orders of magnitude
for a small Lagrangian multiplier ![]() .
The effect of noise in the transversal
field is similar to lacking data, which is natural, as regions with a very poor
signal-to-noise ratio in
.
The effect of noise in the transversal
field is similar to lacking data, which is natural, as regions with a very poor
signal-to-noise ratio in
![]() can be as well considered as regions where we do not know
can be as well considered as regions where we do not know
![]() .
The new code still finds a force-free solution for these cases,
which are, however, more potential field like than the solution with full information. But even for
this relatively high noise level the reconstructed solution still has similarities to the
original Low and Lou reference field (error of
.
The new code still finds a force-free solution for these cases,
which are, however, more potential field like than the solution with full information. But even for
this relatively high noise level the reconstructed solution still has similarities to the
original Low and Lou reference field (error of ![]() in the vector correlation
and an under-estimation of the energy of
in the vector correlation
and an under-estimation of the energy of
![]() .) and is a significantly better
approximation than a potential field, which as an error of
.) and is a significantly better
approximation than a potential field, which as an error of ![]() and
and ![]() for
the vector correlation and energy estimate, respectively.
for
the vector correlation and energy estimate, respectively.
4 Conclusions
Different from previous implementations our new code allows us to deal with
lacking data and regions with poor signal-to-noise ratio in the extrapolation
in a systematic manner because it produces a field which is closer to
to a force- and divergence-free field and tries to match the boundary only
where it has been reliably measured.
For ideal and consistent data the extrapolation result
is identical with previous implementations of our code. This old result
could also artificially be enforced by the choice
![]() and
and
![]() .
.
For finite ![]() ,
the new code also relaxes the boundary
and allows us to fulfill the solenoidal and force-free condition
significantly better because it allows deviations between the extrapolated
boundary field and inconsistent boundary data. This deviation can be
controlled by setting the weight factors
,
the new code also relaxes the boundary
and allows us to fulfill the solenoidal and force-free condition
significantly better because it allows deviations between the extrapolated
boundary field and inconsistent boundary data. This deviation can be
controlled by setting the weight factors
![]() inversely
proportional to the measurement error or
inversely
proportional to the measurement error or
![]() ,
where
the field information is lacking.
,
where
the field information is lacking.
If no transverse magnetic field has been observed on a significant part of the
vector magnetogram, the magnetic energy of the final relaxed state is
underestimated. In an extreme case when no
![]() at all is available in the entire region, the code would
produce the initial potential field.
at all is available in the entire region, the code would
produce the initial potential field.
The work of T. Wiegelmann was supported by DLR-grant 50 OC 0501. This work was inspired by discussions with our colleagues in the NLFFF-consortium (a group of scientist sharing their experience on nonlinear force-free field modelling) during six annual workshops in the years 2004-2009.
References
- Amari, T., Boulmezaoud, T. Z., & Aly, J. J. 2006, A&A, 446, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulmezaoud, T. Z., & Amari, T. 2000, Z. Angew. Math. Phys., 51, 942 [Google Scholar]
- DeRosa, M. L., Schrijver, C. J., Barnes, G., et al. 2009, ApJ, 696, 1780 [Google Scholar]
- Fuhrmann, M., Seehafer, N., & Valori, G. 2007, A&A, 476, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inhester, B., & Wiegelmann, T. 2006, Sol. Phys., 235, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C., & Lou, Y. Q. 1990, ApJ, 352, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, T. R., Derosa, M. L., Schrijver, C. J., et al. 2008, Sol. Phys., 247, 269 [Google Scholar]
- Schrijver, C. J., Derosa, M. L., Metcalf, T. R., et al. 2006, Sol. Phys., 235, 161 [Google Scholar]
- Tadesse, T., Wiegelmann, T., & Inhester, B. 2009, A&A, 508, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valori, G., Kliem, B., & Fuhrmann, M. 2007, Sol. Phys., 245, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Wheatland, M. S., Sturrock, P. A., & Roumeliotis, G. 2000, ApJ, 540, 1150 [Google Scholar]
- Wiegelmann, T. 2004, Sol. Phys., 219, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., & Neukirch, T. 2003, Nonlin. Processes Geophys., 10, 313 [Google Scholar]
- Wiegelmann, T., Inhester, B., & Sakurai, T. 2006, Sol. Phys., 233, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Thalmann, J. K., Schrijver, C. J., Derosa, M. L., & Metcalf, T. R. 2008, Sol. Phys., 247, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Yelles Chaouche, L., Solanki, S. K., & Lagg, A. 2010, A&A, 511, A4 [Google Scholar]
Footnotes
- ... throughout
![[*]](/icons/foot_motif.png)
- We investigated several forms of
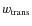 as indicated in the third column of the table. 1,0 means that
we chose
as indicated in the third column of the table. 1,0 means that
we chose
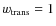 in the valid
in the valid
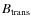 area and
0 elsewhere.
area and
0 elsewhere.
- ...
![[*]](/icons/foot_motif.png)
- This would correspond to a noise level of about 100 G for real measurements.
All Tables
Table 1: Evaluation of the reconstruction quality.
All Figures
![\begin{figure}
\par\includegraphics[width=14cm,clip]{14391f1NEW.eps}\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14391-10/Timg31.png)
|
Figure 1: Magnetic fieldline plots for the reference equilibrium (panel a)), the initial potential field b) and the other panels show nonlinear force-free reconstructions with the old and new code for different cases, see text. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{14391f2NEW.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14391-10/Timg32.png)
|
Figure 2: Evolution of the entire functional L (solid line, see Eq. (4)) and its three terms (see Eq. (5)-(7)). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.