| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201014327 | |
| Published online | 21 July 2010 | |
Observation of the full 12-hour-long transit of the exoplanet HD 80606b![[*]](/icons/foot_motif.png)
Warm-Spitzer photometry and SOPHIE spectroscopy
G. Hébrard1 - J.-M. Désert2,1 - R. F. Díaz1 - I. Boisse1 - F. Bouchy1,3 - A. Lecavelier des Etangs1 - C. Moutou4 - D. Ehrenreich5 - L. Arnold3 - X. Bonfils5,7 - X. Delfosse5 - M. Desort5 - A. Eggenberger5 - T. Forveille5 - J. Gregorio6 - A.-M. Lagrange5 - C. Lovis7 - F. Pepe7 - C. Perrier5 - F. Pont8 - D. Queloz7 - A. Santerne4 - N. C. Santos9 - D. Ségransan7 - D. K. Sing8 - S. Udry7 - A. Vidal-Madjar1
1 - Institut d'Astrophysique de Paris, UMR7095
CNRS, Université Pierre & Marie Curie, 98bis boulevard Arago, 75014
Paris, France
2 -
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
3 -
Observatoire de Haute-Provence, CNRS/OAMP, 04870 Saint-Michel-l'Observatoire, France
4 -
Laboratoire d'Astrophysique de Marseille, Univ. de Provence, CNRS (UMR6110), 38 rue F. Joliot Curie, 13388 Marseille, France
5 -
Laboratoire d'Astrophysique de Grenoble, Université Joseph-Fourier, CNRS (UMR5571), BP 53, 38041 Grenoble Cedex 9, France
6 -
CROW-observatory Portalegre, Portugal, and Atalaia.org group, Portugal
7 -
Observatoire de Genève, Université de Genève, 51 chemin des Maillettes, 1290 Sauverny, Switzerland
8 -
School of Physics, University of Exeter, Exeter, EX4 4QL, UK
9 -
Centro de Astrofísica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
Received 26 February 2010 / Accepted 5 April 2010
Abstract
We present new observations of a transit of the 111.4-day-period exoplanet HD 80606b.
Due to this long orbital period and to the orientation of the eccentric orbit (e = 0.9),
HD 80606b's transits last for about 12 hours. This makes the observation
of a full transit practically impossible from a given ground-based observatory.
With the Spitzer Space Telescope and its IRAC camera on the post-cryogenic mission,
we performed a 19-h photometric observation of
HD 80606 that covers the full 2010 January 13-14
transit as well as off-transit references
immediately before and after the event. We complement these photometric data by new
spectroscopic observations that we simultaneously performed with SOPHIE at the Haute-Provence
Observatory. This provides radial velocity measurements of the first half of the transit that was
previously uncovered with spectroscopy.
This new dataset allows the parameters of this singular planetary system to be significantly
refined. We obtained a planet-to-star radius
ratio
![]() that is more accurate but
slightly lower than the one measured from previous ground observations in the optical.
We found no astrophysical interpretations able to explain this difference
between optical and infrared radii;
we rather favor
underestimated systematic uncertainties, maybe in the ground-based composite light curve.
We detected a feature in the Spitzer light curve that could be due to a stellar spot.
We also found a transit timing about 20 minutes
earlier than the ephemeris prediction; this could be caused by actual transit-timing variations
due to an additional body in the system, or again by underestimated systematic uncertainties.
The actual angle between the spin-axis of HD 80606 and the normal to the planetary orbital plane
is found to be near
that is more accurate but
slightly lower than the one measured from previous ground observations in the optical.
We found no astrophysical interpretations able to explain this difference
between optical and infrared radii;
we rather favor
underestimated systematic uncertainties, maybe in the ground-based composite light curve.
We detected a feature in the Spitzer light curve that could be due to a stellar spot.
We also found a transit timing about 20 minutes
earlier than the ephemeris prediction; this could be caused by actual transit-timing variations
due to an additional body in the system, or again by underestimated systematic uncertainties.
The actual angle between the spin-axis of HD 80606 and the normal to the planetary orbital plane
is found to be near
![]() thanks to the fit of the Rossiter-McLaughlin anomaly,
with a sky-projected value
thanks to the fit of the Rossiter-McLaughlin anomaly,
with a sky-projected value
![]() .
This allows scenarios with
aligned spin-orbit to be definitively rejected.
Over the twenty planetary systems with measured spin-orbit angles, a few are
misaligned; this is probably the signature of two different evolution scenarios for
misaligned and aligned systems, depending whether or not
they experienced gravitational interaction with a third body.
As in the case of HD 80606, most of the planetary systems
including a massive planet are tilted;
this could be the signature
of a separate evolution scenario for massive planets compared with
Jupiter-mass planets.
.
This allows scenarios with
aligned spin-orbit to be definitively rejected.
Over the twenty planetary systems with measured spin-orbit angles, a few are
misaligned; this is probably the signature of two different evolution scenarios for
misaligned and aligned systems, depending whether or not
they experienced gravitational interaction with a third body.
As in the case of HD 80606, most of the planetary systems
including a massive planet are tilted;
this could be the signature
of a separate evolution scenario for massive planets compared with
Jupiter-mass planets.
Key words: techniques: radial velocities - techniques: photometric - stars: individual: HD 80606
1 Introduction
Among the more than 400 extrasolar planets that have been found so far, the giant planet orbiting the G5 star HD 80606 is certainly a unique case. Its eccentricity is particularly high: e = 0.93. Only one known planet possibly has a higher eccentricity, namely HD 20782b; however its high e-value is still to be confirmed as it rests on one measurement only (O'Toole et al. 2009). The comet-like orbit of HD 80606b was well established in its discovery paper by Naef et al. (2001) and has been largely confirmed by subsequent observations. Together with its 111.4-day period, the high eccentricity of HD 80606b put it on an extreme orbit: during its revolution, the planet experiences the strongly irradiated regime of a ``hot Jupiter'' at periastron (0.03 AU), and milder conditions at apoastron (0.87 AU) around which it spends most of its time, and where the planet approaches the inner boundary of the habitable zone (see Fig. 1).
| Figure 1: Schematic view of the HD 80606 system. The red dots show the positions of the planet each 24 h. |
|
| Open with DEXTER | |
As long as the inclination i of the orbit with the line of sight was unknown,
those parameters originally implied a probability of 1% for the planet to
be transiting.
In spite of this tenuous probability, an amazing chance makes the planet
HD 80606b actually transits its parent star, as seen from Earth, every 111.4 days.
This is particularly advantageous as numerous crucial studies can be
performed with photometry or spectroscopy when a planet passes in
front its parent star (planetary transits) or behind it (planetary eclipses),
especially in this case where the host star is bright (V=9.1) and
nearby (d=60 pc).
The fortunate transiting nature of HD 80606b was established in 2009 February from the
detection of a transit reported from ground observations, independently by Moutou
et al. (2009) from photometric and spectroscopic data, and by
Garcia-Melendo & McCullough (2009) and Fossey et al. (2009)
from photometric measurements. Additional observations of transits were later reported by
Winn et al. (2009a) and Hidas et al. (2010).
The 2009 February observations followed the planetary eclipse discovery reported
a few months before by Laughlin et al. (2009) from Spitzer photometric
observations at 8 ![]() m during a 30-h interval around the periastron.
Among the known transiting planets, HD 80606b has the longest period and the most eccentric
orbit. The second most extreme transiting planet is HD 17156b (P = 21.2 days and
e = 0.67). Furthermore, HD 80606b is also the most distant planet from its parent stars
when it transits: 0.3 AU compared with 0.05 AU or less for all other known cases
m during a 30-h interval around the periastron.
Among the known transiting planets, HD 80606b has the longest period and the most eccentric
orbit. The second most extreme transiting planet is HD 17156b (P = 21.2 days and
e = 0.67). Furthermore, HD 80606b is also the most distant planet from its parent stars
when it transits: 0.3 AU compared with 0.05 AU or less for all other known cases![]() .
.
In addition to the photometric detection of the HD 80606b's transit, Moutou et al. (2009)
presented its spectroscopic detection using the Rossiter-McLaughlin
effect, measured with the SOPHIE spectrograph from radial velocities
at the Haute-Provence Observatory (OHP), France.
The Rossiter-McLaughlin effect is an apparent distortion of the stellar line profiles due to the transit
of the planet in front of the rotating star. From the SOPHIE measurements, Moutou et
al. (2009) have shown the first evidence for a spin-orbit misalignment, i.e. the orbital
plane of the planet HD 80606b is not perpendicular to the spin-axis of its host star.
Using additional photometric data of the 2009 February event that allowed a better constraint
on the transit duration together with a combined analysis of the whole dataset,
Pont et al. (2009) refined the parameters of the system. They confirmed the spin-orbit
misalignment from the Rossiter-McLaughlin distortion detected with SOPHIE
and provided a measurement of the sky-projected angle between
the planetary orbital axis and the stellar rotation axis:
![]() ,
with the
confidence interval [
,
with the
confidence interval [
![]() ]
- see
also Gillon (2009). Thanks to new photometric and spectroscopic
observations of the 2009 June transit, Winn et al. (2009a) thereafter
reduced the confidence interval even more to [
]
- see
also Gillon (2009). Thanks to new photometric and spectroscopic
observations of the 2009 June transit, Winn et al. (2009a) thereafter
reduced the confidence interval even more to [
![]() ]. Thus
the spin-orbit misalignment of the HD 80606 system is now well established.
The star
HD 80606 is the component of a wide binary with HD 80607; the projected
separation of the system is about 1000 AU. The peculiar orbit of
HD 80606b could thus result from Kozai mechanism and tidal dissipation
(see e.g., Wu & Murray 2003), which can pump
the eccentricity and the inclination.
]. Thus
the spin-orbit misalignment of the HD 80606 system is now well established.
The star
HD 80606 is the component of a wide binary with HD 80607; the projected
separation of the system is about 1000 AU. The peculiar orbit of
HD 80606b could thus result from Kozai mechanism and tidal dissipation
(see e.g., Wu & Murray 2003), which can pump
the eccentricity and the inclination.
Due to the long orbital period and to the orientation of the eccentric orbit, the duration of the transit of HD 80606b is about 12 h. This should be compared to the transit duration of other known transiting exoplanets, which typically lasts less than five hours. The transit duration of HD 80606b is even longer than transits of Mercury or Venus through the Solar disk as seen from the Earth. It is thus practically impossible that a full transit of HD 80606b matches the duration of an observation night from ground. In addition, data secured before and after the transit are mandatory to obtain an accurate transit light curve, so the full sequence for HD 80606 lasts longer than a night for ground observations. Observing an entire transit of this exoplanet is thereby challenging, and only portions of a transit could be observed from a given ground-based telescope. This was the case of all the observation campaigns reported above which covered only fractions of transits. These fragmented observations induce significant uncertainties in the parameters derived from their fit.
We present here the first full photometric observation of a transit of
HD 80606b. We secured it on 2010 January 13-14 with the Spitzer space observatory
using the IRAC camera at 4.5 ![]() m in post-cryogenic mission.
Thanks to its Earth-trailing heliocentric orbit (Scoupe et al. 2006),
Spitzer allowed us to continuously observe during 19 h, enabling the coverage
of the whole 12-hour-long transit, as well as off-transit references immediately
before and after the event. We complement this photometric data by new spectroscopic
observations that we simultaneously performed with SOPHIE at OHP.
This provides radial velocity measurements of the first half of the transit, a part
that was up to now not covered by spectroscopy. Indeed,
observing the full 12-hour-long transit is even more difficult in spectroscopy
than in photometry, as the amplitude of the Rossiter-McLaughlin for HD 80606
is about 10 m s-1, whereas northern instruments able to measure radial velocities with
the required accuracy are scarce.
We also performed a ground-based photometric monitoring of HD 80606 during 2010 January.
All together, the data of this observational campaign allow the parameters of this
planetary system to be additionally refined.
m in post-cryogenic mission.
Thanks to its Earth-trailing heliocentric orbit (Scoupe et al. 2006),
Spitzer allowed us to continuously observe during 19 h, enabling the coverage
of the whole 12-hour-long transit, as well as off-transit references immediately
before and after the event. We complement this photometric data by new spectroscopic
observations that we simultaneously performed with SOPHIE at OHP.
This provides radial velocity measurements of the first half of the transit, a part
that was up to now not covered by spectroscopy. Indeed,
observing the full 12-hour-long transit is even more difficult in spectroscopy
than in photometry, as the amplitude of the Rossiter-McLaughlin for HD 80606
is about 10 m s-1, whereas northern instruments able to measure radial velocities with
the required accuracy are scarce.
We also performed a ground-based photometric monitoring of HD 80606 during 2010 January.
All together, the data of this observational campaign allow the parameters of this
planetary system to be additionally refined.
The observations and data reduction are presented in Sects. 2 and 3 for Spitzer and SOPHIE respectively. The ground-based photometry is presented in Sect. 4. The analyses and the results are presented in Sect. 5 before the discussion and conclusion in Sects. 6 and 7.
2 Spitzer photometry
2.1 Observations
We obtained Spitzer Director's Discretionary Time (DDT program #540) to observe the
2010 January transit of HD 80606b. This transit was the first observable with Spitzer since the
discovery of the transiting nature of HD 80606b in 2009 February. As Spitzer has exhausted its
cryogen of liquid coolant on 2009 May 15, our observations were performed during the first
months of the Spitzer's warm mission. Only the first two infrared channels of the IRAC camera
(Fazio et al. 2004)
are available in the post-cryogenic Spitzer. They are centered at 3.6 and 4.5 ![]() m and
cannot be observed simultaneously. We chose to observe only in one of the two
channels to avoid repointing the telescope during the transit.
This reduced overheads and
ensured that the target remained on the same part of the
detector during the full observation sequence. We opted for channel 2 at 4.5
m and
cannot be observed simultaneously. We chose to observe only in one of the two
channels to avoid repointing the telescope during the transit.
This reduced overheads and
ensured that the target remained on the same part of the
detector during the full observation sequence. We opted for channel 2 at 4.5 ![]() m because
it has the lowest noise properties. This wavelength also has a smaller limb-darkening effect
for the star.
We did not use pointing dithering, here again to maintain the target as much as possible in
the same location on the detector to reduce systematic effects due to imperfect
flat-field corrections and intra-pixel sensitivity variations.
m because
it has the lowest noise properties. This wavelength also has a smaller limb-darkening effect
for the star.
We did not use pointing dithering, here again to maintain the target as much as possible in
the same location on the detector to reduce systematic effects due to imperfect
flat-field corrections and intra-pixel sensitivity variations.
We used the Subarray mode of IRAC, which is well adapted for
bright targets. Only a
![]() -pixel part of the detector is used in this mode;
this covers a small
-pixel part of the detector is used in this mode;
this covers a small
![]() field of view (pixel size of 1.2 arcsec),
compared to the IRAC stellar mode that uses the full
field of view (pixel size of 1.2 arcsec),
compared to the IRAC stellar mode that uses the full
![]() -pixel
field. As the stellar companion HD 80607 is located only 17 arcsec to the East of HD 80606,
putting the two targets on this small field of view would have implied that their point-spread
functions (PSF) fell near the edges of the detector. This configuration is risky for accurate
photometry. We preferred to let HD 80607 out of the field of view to maintain HD 80606
on the detector, far from its edges. So we chose to put our target at the default
pointing position in the center of the subarray field of view. This position is
not on nor right next to any known hot pixels.
-pixel
field. As the stellar companion HD 80607 is located only 17 arcsec to the East of HD 80606,
putting the two targets on this small field of view would have implied that their point-spread
functions (PSF) fell near the edges of the detector. This configuration is risky for accurate
photometry. We preferred to let HD 80607 out of the field of view to maintain HD 80606
on the detector, far from its edges. So we chose to put our target at the default
pointing position in the center of the subarray field of view. This position is
not on nor right next to any known hot pixels.
The observations were secured between 2010 January 13 at 18 h and January 14 at
13 h (UT). We acquired 2488 consecutive images during a total of 19 hours.
Each image was split up into 64 frames of 0.36 seconds exposure each, taken
back-to-back.
We obtained a total of 159232 frames
during 15.9-hours effective integration time with an overhead of two seconds
between each images (15 % overheads in total).
This high efficiency is reached thanks to the use of the subarray mode and could not
be achieved in stellar mode for bright targets requiring short exposure times.
With a flux density of ![]() 200 mJy at 4.5
200 mJy at 4.5 ![]() m for HD 80606, the frame
exposure time of 0.36 sec clearly avoids saturation of the pixels. The intensities
recorded in the brightest central pixels are around 10 000 electrons.
m for HD 80606, the frame
exposure time of 0.36 sec clearly avoids saturation of the pixels. The intensities
recorded in the brightest central pixels are around 10 000 electrons.
2.2 Data reduction
We used the BCD files (Basic Calibrated Data) of each of the 159232 frames as
they are produced by the Spitzer/IRAC pipeline. They include corrections for dark
current, flat fielding, pixels non-linearity, and conversion to flux units.
To extract the light curve, we used tools and methods we developed in
Désert et al. (2009, 2010).
We found the center of the PSF of the star to a precision of
0.01 pixel through the DAOPHOT-type Photometry Procedures,
GCNTRD, from the IDL Astronomy
Library![]() ,
which computes the
stellar centroid by Gaussian fitting. We used the APER routine
to extract the raw flux of HD 80606 on each frame from the
computation of a simple aperture photometry with a radius of 4.0 pixels,
which optimized the signal-to-noise ratio of the transit light curve.
The flux integrated on these 50 pixels is
,
which computes the
stellar centroid by Gaussian fitting. We used the APER routine
to extract the raw flux of HD 80606 on each frame from the
computation of a simple aperture photometry with a radius of 4.0 pixels,
which optimized the signal-to-noise ratio of the transit light curve.
The flux integrated on these 50 pixels is ![]() 52 500 electrons.
It was corrected from the background level of
52 500 electrons.
It was corrected from the background level of
![]() electrons/pixel
that were estimated from a sky annulus with radii of 9 to 12 pixels.
The centroid of HD 80607 is located outside the field of view, but a small contribution
of its flux is detected on an edge of the detector. When estimating the background level,
we took care to use only pixels where the HD 80607's flux is negligible. It is also negligible
by comparison to the background level in the 4-pixel radius we used for the HD 80606 photometry.
Finally, the uncertainty in the background level is negligible for all the results presented
in this paper.
electrons/pixel
that were estimated from a sky annulus with radii of 9 to 12 pixels.
The centroid of HD 80607 is located outside the field of view, but a small contribution
of its flux is detected on an edge of the detector. When estimating the background level,
we took care to use only pixels where the HD 80607's flux is negligible. It is also negligible
by comparison to the background level in the 4-pixel radius we used for the HD 80606 photometry.
Finally, the uncertainty in the background level is negligible for all the results presented
in this paper.
The Spitzer/IRAC photometry is known to be systematically affected by
the so-called pixel-phase effect. This effect produces an oscillation of the
measured raw light curve due to the Spitzer telescope jitter and the intra-pixel
sensitivity variations on the IRAC detector (see e.g., Charbonneau et al. 2005;
Reach et al. 2006; Morales-Calderón et al. 2006; Ehrenreich
et al. 2007; Désert et al. 2009, 2010).
Measurements of the centroid position of the target on the detector and its variations
could be used to de-correlate the pixel-phase effect on the light curve.
We used here the method presented in Désert et al. (2009);
it has the form
![]() ,
where F and
,
where F and
![]() are the fluxes of the star before and after the pixel-phase
effect correction, and (x-x0) and (y-y0) are the position in the pixels of the source centroid on
the detector with respect to the pixel pointing position, located on [x0,y0].
Our determination of the centroid position shows a
are the fluxes of the star before and after the pixel-phase
effect correction, and (x-x0) and (y-y0) are the position in the pixels of the source centroid on
the detector with respect to the pixel pointing position, located on [x0,y0].
Our determination of the centroid position shows a ![]() -pixel oscillation with a period
of
-pixel oscillation with a period
of ![]() 70 min and a linear drift during the 19-h sequence of 0.1 and
0.2 pixel in the x- and y-direction, respectively.
70 min and a linear drift during the 19-h sequence of 0.1 and
0.2 pixel in the x- and y-direction, respectively.
In addition to the 64 frames of the image # 873 that are corrupted, we iteratively
selected and trimmed 1037 outliers by comparison to the fit of the light curve with
a transit model. Frames were considered as outliers when they were above
10 to 3![]() ,
this value was reduced by 0.1-
,
this value was reduced by 0.1-![]() steps at each iterations.
We binned the obtained transit light curve by a factor of five in
order to obtain a better computing efficiency without losing
information for the pixel phase effect.
Most of the results presented
below were obtained with the binned transit light curve.
steps at each iterations.
We binned the obtained transit light curve by a factor of five in
order to obtain a better computing efficiency without losing
information for the pixel phase effect.
Most of the results presented
below were obtained with the binned transit light curve.
We tested several radii for the aperture photometry, several areas for the background measurement, several procedures for the centroid determination and the outliers rejections. The adopted procedure reported above is the one producing the smallest errors, but all of them produced similar results.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14327f2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg28.png)
|
Figure 2: Spitzer photometry of HD 80606. From top to bottom, the three panels show the raw photometry, the photometry after correction of the pixel-phase and ramp effects, and the residuals respectively. The black points are the measurements (binned per 5 frames) and the red solid lines are the fits. The vertical dotted lines show the mid-transit, the vertical dot-dashed lines show the first and fourth contacts, and the vertical dot-dot-dashed lines show the second and third contacts. |
| Open with DEXTER | |
The upper panel of Fig. 2 shows the raw Spitzer light curve of HD 80606 after
this extraction. It clearly shows flux variations with a period of ![]() 70 min that are
due to the pixel-phase effect and telescope jitter at this period.
Its peak-to-peak amplitude represents
70 min that are
due to the pixel-phase effect and telescope jitter at this period.
Its peak-to-peak amplitude represents ![]() 1% of the
flux, which is larger than the effect seen in the channel 2 of IRAC during
the cryogenic Spitzer.
Additional variations at higher frequency and with a lower
amplitude than the one of the 70-min oscillation were seen as well
as we fitted each individual frame. They could
be due to short-term jitter of the satellite, which are apparently
not periodic. Filtering these high-frequency variations does not
significantly change our results.
Finally, a slope in the out-of-transit baseline is also seen.
This detector ramp was observed in channels 3 and 4 in pre-cryogenic Spitzer,
but was not as significant in channel 2 at that time
(see e.g., Deming et al. 2005; Knutson et al. 2007;
Désert et al. 2009, 2010).
We discarded the first thousands of frames that were the most affected
by the ramp effect (we tested several limits; see Sect. 5.1.4)
then normalized the light-curve using a time-dependent function
with the form
1% of the
flux, which is larger than the effect seen in the channel 2 of IRAC during
the cryogenic Spitzer.
Additional variations at higher frequency and with a lower
amplitude than the one of the 70-min oscillation were seen as well
as we fitted each individual frame. They could
be due to short-term jitter of the satellite, which are apparently
not periodic. Filtering these high-frequency variations does not
significantly change our results.
Finally, a slope in the out-of-transit baseline is also seen.
This detector ramp was observed in channels 3 and 4 in pre-cryogenic Spitzer,
but was not as significant in channel 2 at that time
(see e.g., Deming et al. 2005; Knutson et al. 2007;
Désert et al. 2009, 2010).
We discarded the first thousands of frames that were the most affected
by the ramp effect (we tested several limits; see Sect. 5.1.4)
then normalized the light-curve using a time-dependent function
with the form
![]() ,
where
,
where
![]() is the target flux out of transit and t is the time.
We also tried higher-degree polynomials and logarithmic baselines;
this did not significantly improve the fit.
The linear correction we adopted is not perfect; remaining uncertainties in the
actual shape of the baseline introduced errors in the system parameters
derived from the fit (see Sect. 5.1.4).
The baseline and pixel-phase-effect parameters were fitted simultaneously
with the transit-related parameters (see Sec. 5.1.3);
this allowed these effects and their uncertainties to be taken into account
in the transit parameters determination. The middle
panel of Fig. 2 shows the light curve after removal of these instrumental effects and
the lower panel shows the residuals to the fit.
is the target flux out of transit and t is the time.
We also tried higher-degree polynomials and logarithmic baselines;
this did not significantly improve the fit.
The linear correction we adopted is not perfect; remaining uncertainties in the
actual shape of the baseline introduced errors in the system parameters
derived from the fit (see Sect. 5.1.4).
The baseline and pixel-phase-effect parameters were fitted simultaneously
with the transit-related parameters (see Sec. 5.1.3);
this allowed these effects and their uncertainties to be taken into account
in the transit parameters determination. The middle
panel of Fig. 2 shows the light curve after removal of these instrumental effects and
the lower panel shows the residuals to the fit.
3 SOPHIE radial velocities
3.1 Observations
The first half of the 2010 January transit of HD 80606b was visible from Europe, so we managed to observe it with the SOPHIE spectrograph at the 1.93-m telescope of the Haute-Provence Observatory in South of France. SOPHIE is a cross-dispersed, environmentally stabilized echelle spectrograph dedicated to high-precision radial velocity measurements (Perruchot et al. 2008, Bouchy et al. 2009). Since the discovery of the transit in 2009 February, this was the first time that this part of the transit was observable from an observatory with high-precision spectroscopic capabilities. Unfortunately, the 1.93-m telescope started a technical break for maintenance and upgrades in 2009 November that was extended up to 2010 February. Due to the importance of this event, some observations could nevertheless be performed thanks to the support of the OHP staff, wich was mandatory due to the ongoing works on the telescope.
The observations were secured as part of the second sub-program of the SOPHIE Consortium
(Bouchy et al. 2009; Hébrard et al. 2010b). The night of the transit,
2010 January 13, observations could start just before 23h (UT) after technical issues were solved
and clouds disappeared, and had to be stopped 4.5 h later due to cloudy weather.
A 5.5-h sequence of good SOPHIE reference observations of HD 80606 could also be
performed on the 2010 January 15 night. 24 and 33 exposures were secured during the two
nights respectively. The exposure times ranged between 5 and 20 min, with typical
values around 9 min; we tuned it in order to maintain a constant signal-to-noise
ratio per pixel of ![]() 58 at 550 nm despite the weather changes (seeing and absorption).
58 at 550 nm despite the weather changes (seeing and absorption).
The measurements were performed with the same setup as the one we used for our observation
of the 2009 February transit (Moutou et al. 2009).
We used the fast-read-out-time mode of the CCD detector to minimize overheads.
Observations were secured in high-resolution mode allowing the resolving power
![]() to be reached. The first optical-fiber aperture was
put on the target and the second on the sky; this allowed us to check that no diffuse light
was polluting the HD 80606 spectra in these Moonless nights. Wavelength calibrations with
a thorium lamp were performed with a
to be reached. The first optical-fiber aperture was
put on the target and the second on the sky; this allowed us to check that no diffuse light
was polluting the HD 80606 spectra in these Moonless nights. Wavelength calibrations with
a thorium lamp were performed with a ![]() 2-h frequency each night, allowing the
interpolation of the spectral drift of SOPHIE for the time of each exposure. A few exposures
were performed with simultaneous thorium-lamp light in the second aperture to allow for
simultaneous wavelength calibration; those extra-calibration did not significantly improve
the radial velocity accuracy.
2-h frequency each night, allowing the
interpolation of the spectral drift of SOPHIE for the time of each exposure. A few exposures
were performed with simultaneous thorium-lamp light in the second aperture to allow for
simultaneous wavelength calibration; those extra-calibration did not significantly improve
the radial velocity accuracy.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14327f3.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg32.png)
|
Figure 3:
Radial velocities and photometry of HD 80606 as a function of the orbital phase or
the time after periastron.
Upper panel: radial velocities as measured with
ELODIE (red open squares, Moutou et al. 2009),
HRS (purple open circles, Wittenmyer et al. 2009),
HIRES (Winn et al. 2009a)
pre- and post-upgrade (green open upward and downward triangles,
respectively) and around the 2009 June transit (green filled downward triangles), and
SOPHIE during the 2009 February and 2010 January transits (blue open and filled
diamonds, respectively).
Middle panel: same as above, but enlarged around the transit phase.
Lower panel: Spitzer photometry during the 2010 January transit. The
Spitzer data are binned
per 250, i.e. one point each 100 s.
The two horizontal dotted-lines show the absorption depth expected with the
value
|
| Open with DEXTER | |
3.2 Data reduction
We used the SOPHIE pipeline (Bouchy et al. 2009) to
extract the spectra from the detector images,
to cross-correlate them with a G2-type numerical mask,
then to fit the cross-correlation functions (CCFs) by Gaussians to get the radial velocities
(Baranne et al. 1996; Pepe et al. 2002).
Each spectrum produces
a clear CCF, with a
![]() km s-1 full-width-at-half-maximum
and a contrast representing
km s-1 full-width-at-half-maximum
and a contrast representing
![]() % of the continuum.
The accuracy of the measured radial velocities is
typically around 4 m s-1. This includes photon noise
(typically
% of the continuum.
The accuracy of the measured radial velocities is
typically around 4 m s-1. This includes photon noise
(typically ![]() 2 m s-1), wavelength calibration (
2 m s-1), wavelength calibration (![]() 2 m s-1), and
guiding errors (
2 m s-1), and
guiding errors (![]() 3 m s-1) that produce motions of the input image within the
fiber (Boisse et al. 2010a). We also re-reduced the SOPHIE observations
presented in Moutou et al. (2009) to have a uniform dataset
reduced with the same version of the pipeline. There was no significant change by
comparison with the data presented in Moutou et al. (2009), except for
one of the reference exposures performed out of the transit, for which the correction
due to the Moon pollution was significantly improved. SOPHIE measurements of
HD 80606 performed in 2009 February and 2010 January have the same properties,
except for the better signal-to-noise ratios for the shorter exposure times obtained in
2010, which is largely due to the primary mirror of the telescope that was realuminized
in 2009 October.
3 m s-1) that produce motions of the input image within the
fiber (Boisse et al. 2010a). We also re-reduced the SOPHIE observations
presented in Moutou et al. (2009) to have a uniform dataset
reduced with the same version of the pipeline. There was no significant change by
comparison with the data presented in Moutou et al. (2009), except for
one of the reference exposures performed out of the transit, for which the correction
due to the Moon pollution was significantly improved. SOPHIE measurements of
HD 80606 performed in 2009 February and 2010 January have the same properties,
except for the better signal-to-noise ratios for the shorter exposure times obtained in
2010, which is largely due to the primary mirror of the telescope that was realuminized
in 2009 October.
The SOPHIE radial velocities of HD 80606 are plotted in Figs. 3 and 7 together with other data sets.
In the SOPHIE spectra, the cores of the large Ca II H & K
absorption lines of HD 80606 at 3934.8 Å and 3969.6 Å
show no chromospheric emissions. The level of the Ca II emission
corresponds to
![]() according to the SOPHIE
calibration (Boisse et al. 2010b).
For a G-type star (B-V=0.76) with this level of activity, Santos et al. (2000)
predict a dispersion below 5 m s-1 for the activity-induced stellar jitter.
According to Noyes et al. (1984) and Mamajek & Hillenbrand (2008),
this level of activity implies a stellar rotation period
according to the SOPHIE
calibration (Boisse et al. 2010b).
For a G-type star (B-V=0.76) with this level of activity, Santos et al. (2000)
predict a dispersion below 5 m s-1 for the activity-induced stellar jitter.
According to Noyes et al. (1984) and Mamajek & Hillenbrand (2008),
this level of activity implies a stellar rotation period
![]() days.
days.
4 Ground-based photometry
In order to study its intrinsic variability, HD 80606 was also observed several nights before and
after the 2010 January transit. Observations during the night of the transit were prevented by bad
weather conditions in the observing site, located in Portalegre, Portugal. We gathered a total of
nearly 23 h of observations in 10 nights spread from 2009 December 3 to 2010 January 25.
The equipment used is a 12-inch f/5.5 MEADE LX200 telescope, and a
SBIG ST8XME 9-micron-pixel CCD camera. The field is
![]() and the pixel scale is
and the pixel scale is ![]() 1.1 arcsec/pixel. Observations were taken through a Bessell
I filter, using integration times between 40 and 90 s.
1.1 arcsec/pixel. Observations were taken through a Bessell
I filter, using integration times between 40 and 90 s.
The frames were reduced with standard IRAF routines and aperture photometry was obtained for HD 80606, its companion HD 80607 and two additional reference stars located in the same field, located about 7 and 11.5 arcmin away from HD 80606. The size of the photometric aperture was varied on each night, depending on seeing conditions, to obtain the highest possible signal-to-noise ratio.
In every night, the flux ratio between HD 80606 and HD 80607 exhibits a smaller dispersion than the ratio of HD 80606 with any of the other two reference stars, or a combination of HD 80607 and the additional reference stars. Furthermore, the light curves obtained for HD 80607 - using the reference stars - also exhibit a larger dispersion than the flux ratio between HD 80606 and HD 80607. Therefore, the limits to the intrinsic variability of HD 80606 were set using only HD 80607 as reference star.
The root mean square for the different nights range from about 2.2 to 4.8 mmag, depending mainly on the weather conditions. During each night, no effect was seen due to variation of the sky level, or the position of the stars on the chip or the airmass. On the other hand, the nightly mean of our observations exhibits a dispersion of about 1.7 mmag around its mean value.
Similar photometric observations of HD 80606 were conducted in the weeks around the 2010 January
transit with the CCD camera at the 120-cm telescope of the Haute-Provence Observatory with the
setup used by Moutou et al. (2009). The filter used was
![]() with a neutral
density, and we did not defocus.
Photometric observations started on January 6 and ended on January 23, with a total of
eight sequences ranging from 30 to 120 min per night; in total, 187 images were
acquired and analyzed. Exposure times of 10 to 120 s were used to account
for varying transparency.
An observation of the transit
during the January-13 night could be performed with this instrument, on a
coverage similar to this of the SOPHIE observations reported in Sect. 3.
This ground-based photometry of a part of the transit will be studied in a
forthcoming paper.
with a neutral
density, and we did not defocus.
Photometric observations started on January 6 and ended on January 23, with a total of
eight sequences ranging from 30 to 120 min per night; in total, 187 images were
acquired and analyzed. Exposure times of 10 to 120 s were used to account
for varying transparency.
An observation of the transit
during the January-13 night could be performed with this instrument, on a
coverage similar to this of the SOPHIE observations reported in Sect. 3.
This ground-based photometry of a part of the transit will be studied in a
forthcoming paper.
The flux was extracted from aperture photometry using the GCNTRD and APER procedures (Sect. 2.2) on a 8-pixel radius (0.69 arcsec/pixel). The background was estimated from a sky annulus with radii of 10 to 12 pixels. The root mean square of flux variations ranges from 1.0 to 3.1 mmag per night, and the residual fluctuation has a standard deviation of 3.2 mmag when the transit night is excluded. This is significantly larger than what was observed in Portalegre, which may indicate a real tendency of rotational modulation, or a significant level of systematics. No attempt was done to correct for the long-term behavior in the data, which appears to be compatible with the expected rotational period of the star (as discussed in Sect. 6.5).
We conclude therefore that HD 80606 is photometrically stable at the level of a few mmag in the optical range on the timescale of several weeks.
5 Analysis
We fitted this whole dataset to refine the system parameters. As a full transit was observed with Spitzer, possible systematic effects due to the combination of transit portions secured with different ground-based instruments are expected to be reduced here. In addition, together with the new radial velocities secured at phases previously uncovered, the constraints on the spin-orbit angle would be better.
5.1 Combined fit
5.1.1 Method
We first performed a combined fit of our Spitzer photometry
of the 2010 January transit together with the available radial velocities of HD 80606.
We also included in this combined fit the timing constraint
on the eclipse as obtained from previous Spitzer measurements by Laughlin et
al. (2009) and re-analyzed by Gillon (2009).
As those data are not accurate enough to allow the ingress and egress of the eclipse
to be significantly measured, we used the estimated epochs of the mid-time of these
two events: HJD
![]() and
and
![]() .
.
We did not include in this combined
fit the radial velocity measurements secured during and near the transits.
Indeed, the Rossiter-McLaughlin observations do constrain the projected
stellar rotational velocity
![]() and the sky-projected angle
and the sky-projected angle ![]() between the planetary orbital axis and the stellar rotation axis, but they do
not significantly constrain the parameters that we measured here in the
combined fit. The analysis of the Rossiter-McLaughlin data is presented below
in Sect. 5.2 and takes into account the results of the combined
fit presented here in Sect. 5.1.
Thus, the combined fit uses the radial velocities secured with the instruments
ELODIE at OHP (Moutou et al. 2009),
HRS at HET (Wittenmyer et al. 2009),
and HIRES at Keck
(Winn et al. 2009a). This covers a 9.5-year span.
The SOPHIE data are used only for the Rossiter-McLaughlin fit.
We note that the ELODIE and SOPHIE radial velocities are absolute
heliocentric, whereas those from HIRES and HRS are relative.
between the planetary orbital axis and the stellar rotation axis, but they do
not significantly constrain the parameters that we measured here in the
combined fit. The analysis of the Rossiter-McLaughlin data is presented below
in Sect. 5.2 and takes into account the results of the combined
fit presented here in Sect. 5.1.
Thus, the combined fit uses the radial velocities secured with the instruments
ELODIE at OHP (Moutou et al. 2009),
HRS at HET (Wittenmyer et al. 2009),
and HIRES at Keck
(Winn et al. 2009a). This covers a 9.5-year span.
The SOPHIE data are used only for the Rossiter-McLaughlin fit.
We note that the ELODIE and SOPHIE radial velocities are absolute
heliocentric, whereas those from HIRES and HRS are relative.
5.1.2 Transit light curve of planets on eccentric orbit
To calculate the transit light curve with a given set of orbital parameters (period, orbital inclination,
semi major axis in unit of stellar radii, eccentricity and longitude of periastron), we calculated the
sky projected distance between the planet's and the star's center in units of stellar radius; this last result
was then directly put into the Mandel & Agol (2002) algorithm with limb darkening
coefficients.
From a theoretical model (Kurucz 1979), the three non-linear limb-darkening coefficients
at 4.5 ![]() m as defined by Sing (2010) were derived
with
m as defined by Sing (2010) were derived
with
![]() K and
K and
![]() :
c2=0.89502981,
c3= -1.1230710 and
c4=0.46541027.
The limb darkening is low at this wavelength; Désert et al. (2009)
showed that the uncertainties in the coefficients
have no significant effects on the parameters derived from the transit light curve.
:
c2=0.89502981,
c3= -1.1230710 and
c4=0.46541027.
The limb darkening is low at this wavelength; Désert et al. (2009)
showed that the uncertainties in the coefficients
have no significant effects on the parameters derived from the transit light curve.
It is worth to note that the speed of light in the system
has to be taken into account when comparing the times of the transit, the eclipse and
the periastron. The transit takes place when the planet is at ![]() 0.29 AU from the star
(see Fig. 1); this implies an apparent advance of about 2.5 min for the transit.
Similarly, the planet is at
0.29 AU from the star
(see Fig. 1); this implies an apparent advance of about 2.5 min for the transit.
Similarly, the planet is at ![]() 0.03 AU from the star at the eclipse, which implies a
delay of 15 s. Also because the
planet-observer distance decreases during the transit, the speed of light correction makes the transit
appears to last 8 s less than it really does. In the procedure we implemented this speed
of light correction.
0.03 AU from the star at the eclipse, which implies a
delay of 15 s. Also because the
planet-observer distance decreases during the transit, the speed of light correction makes the transit
appears to last 8 s less than it really does. In the procedure we implemented this speed
of light correction.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14327f4.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg45.png)
|
Figure 4:
Plot of the orbital velocity of the planet and orbit direction during the
transit. |
| Open with DEXTER | |
The orbit of HD 80606b is highly eccentric, and the transit takes place ![]() 5.7 days after the periastron,
when the planet is rapidly moving away from the star. During the transit, the star-planet distance increases
by about 5.8% between the first and the fourth contact, and the orbital velocity decreases by
about 4.1% (Fig. 4). With that in mind, it would
a priori suggest that the transit light
curve could be highly asymmetrical with for instance an egress lasting longer than the ingress. However,
during the transit, the direction of the planet motion also varies by about the same amount (upper panel
of Fig. 4). If we define
5.7 days after the periastron,
when the planet is rapidly moving away from the star. During the transit, the star-planet distance increases
by about 5.8% between the first and the fourth contact, and the orbital velocity decreases by
about 4.1% (Fig. 4). With that in mind, it would
a priori suggest that the transit light
curve could be highly asymmetrical with for instance an egress lasting longer than the ingress. However,
during the transit, the direction of the planet motion also varies by about the same amount (upper panel
of Fig. 4). If we define ![]() as the angle between the direction of the planet motion and
the line of sight,
as the angle between the direction of the planet motion and
the line of sight,
![]() is the fraction of the planet motion projected onto the sky
(see insert in Fig. 1). Between the first
contact and the last contact,
is the fraction of the planet motion projected onto the sky
(see insert in Fig. 1). Between the first
contact and the last contact,
![]() increases by about 4.3%, exactly compensating for the decrease of the
orbital velocity. As a result, the planet velocity on the sky is nearly
constant. In addition to the low variation of the apparent planet
velocity on the sky during the transit, it appears that the time
variation of this velocity is nearly symmetrical around the center of
the transit (bottom panel of Fig. 4). Consequently, the apparent velocity during the egress is extremely close to the
velocity during the ingress, the latter being only 0.004% smaller than the former. This reinforces the
apparent symmetry of the transit light curve. With the parameters of the best fit, the ingress duration
(time between first and second contact) is predicted to last only half a second more than the egress
duration (time between third and fourth contact), while both last about two hours and 45 min.
increases by about 4.3%, exactly compensating for the decrease of the
orbital velocity. As a result, the planet velocity on the sky is nearly
constant. In addition to the low variation of the apparent planet
velocity on the sky during the transit, it appears that the time
variation of this velocity is nearly symmetrical around the center of
the transit (bottom panel of Fig. 4). Consequently, the apparent velocity during the egress is extremely close to the
velocity during the ingress, the latter being only 0.004% smaller than the former. This reinforces the
apparent symmetry of the transit light curve. With the parameters of the best fit, the ingress duration
(time between first and second contact) is predicted to last only half a second more than the egress
duration (time between third and fourth contact), while both last about two hours and 45 min.
This surprising symmetry for the transit light curve of a planet on a highly eccentric orbit can be explained by considering the projection on the sky of the gravitational force from the star to the planet. Because the transited star is the same as the attracting star, the component of the gravitational force projected on the sky is close to zero during the transit. As a consequence, the apparent velocity of the planet projected on the sky is nearly constant. Even more, the projected force is also symmetrical around the star center for various positions of the planet, which explains the symmetry of the time variation of the projected velocity around the center of the transit. As a conclusion, contrary to the common-sense idea, in any configuration the transit of a planet in front of its parent star is expected to be highly symmetric, even for extremely eccentric orbits (see also Winn 2010). Our Spitzer observations confirm this result for the highly eccentric HD 80606b's orbit.
5.1.3 Free parameters
Our combined fit of the radial velocities, the Spitzer transit light curve and the eclipse timing includes 19 free parameters. We list them below, classified in four categories depending on their nature and the dataset that constrain them:
- 1.
- two free parameters constrained by photometry only:
-
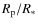 ,
the ratio of the planetary and stellar radii;
,
the ratio of the planetary and stellar radii;
- a / R*, the semimajor axis in units of stellar radius;
-
- 2.
- six free parameters constrained both by radial velocities and photometry:
-
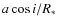 ,
the ``standard'' impact parameter, which is different (for an eccentric orbit) from the actual
impact parameter
,
the ``standard'' impact parameter, which is different (for an eccentric orbit) from the actual
impact parameter
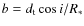 ,
where
,
where 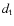 is the star-planet distance at mid-transit and i is the
inclination of the orbit;
is the star-planet distance at mid-transit and i is the
inclination of the orbit;
- P, the orbital period of the planet, which is proportional to (a/R*)3, and to the inverse
of the stellar density
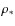 from the Kepler third law;
from the Kepler third law;
- T0, the epoch of the periastron of the planet;
-
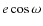 and
and
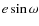 ,
which constrain the two correlated parameters
e (the eccentricity of the planetary orbit) and
,
which constrain the two correlated parameters
e (the eccentricity of the planetary orbit) and 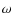 (the longitude of its periastron);
(the longitude of its periastron);
-
 ,
that depends both on the eccentricity e and on the semi-amplitude K of the
radial velocity variations - K actually is constrained by radial velocities only, and is proportional to
,
that depends both on the eccentricity e and on the semi-amplitude K of the
radial velocity variations - K actually is constrained by radial velocities only, and is proportional to
 and
(M*)2/3,
and
(M*)2/3,  and M* being the planetary
and stellar masses;
and M* being the planetary
and stellar masses;
-
- 3.
- four free parameters constrained by radial velocities only:
- 4.
- seven free parameters linked to the Spitzer light curve extraction (see Sect. 2.2):
- the two parameters
 for the baseline;
for the baseline;
- the five parameters
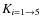 for the pixel-phase effect.
for the pixel-phase effect.
- the two parameters
Stellar evolution models remain thus mandatory to estimate M*.
Moutou et al. (2009) used isochrones to get
![]() from
from
![]() K,
K,
![]() and [Fe/H]=0.43 dex.
This accuracy is typical for stellar evolution models, from which it is difficult to predict stellar
masses at better than
and [Fe/H]=0.43 dex.
This accuracy is typical for stellar evolution models, from which it is difficult to predict stellar
masses at better than ![]() % (Fernandes & Santos 2004).
With additional constraints from the transit light curve,
Pont et al. (2009) and Winn et al. (2009a) estimated the stellar mass
of HD 80606 to
% (Fernandes & Santos 2004).
With additional constraints from the transit light curve,
Pont et al. (2009) and Winn et al. (2009a) estimated the stellar mass
of HD 80606 to
![]() and
and
![]()
![]() ,
respectively. The 2-
,
respectively. The 2-![]() disagreement between the two estimates shows that here we probably reach the limit
of the accuracy that is now achievable. Below we adopt the conservative interval
disagreement between the two estimates shows that here we probably reach the limit
of the accuracy that is now achievable. Below we adopt the conservative interval
![]()
![]() that takes into account those two studies.
that takes into account those two studies.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{old/14327f5a.ps}\par\includegraphics[width=8.8cm,clip]{old/14327f5b.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg68.png)
|
Figure 5:
Distributions of the parameters obtained for the
15 000 fits performed with the prayer bead and bootstrap (Sect. 5.1.4).
As an example, four parameters are plotted here: a/R* vs.
|
| Open with DEXTER | |
5.1.4 Best parameters and error bars
We used the Prayer Bead method (Moutou et al. 2004; Gillon et al. 2007)
as applied by Désert et al. (2009) to compute the mean values of the free
parameters and their statistic and systematic uncertainties (see examples in Fig. 5),
together with the Levenberg-Marquardt algorithm to provide the best fit at each iteration
of our procedure.
This method was applied to the Spitzer photometry to account for possible
correlated noise in the error budget. We simultaneously applied a bootstrap procedure to
the radial velocity measurements, after having quadratically added a systematic uncertainty to
the radial velocity datasets to put their corresponding reduced ![]() to unity.
Thus we quadratically added 12 m s-1
to the ELODIE uncertainties, and 5.0 and 1.7 m s-1 to the HIRES uncertainties (pre-
and post-upgrade, respectively).
In total, 15 000 shifts and fits of transit light curves and bootstraps of radial velocity errors were
produced to derive the set of parameters and to extract their means and their corresponding
standard deviations. In addition, we performed additional fits with the light curve
considering data starting at ten
different epochs before the ingress; by performing a prayer bead on 1500 shifts for each of
those ten fits, we could estimate the errors caused by the uncertainty in the shape of the
out-of-transit baseline (see Sect. 2.2).
to unity.
Thus we quadratically added 12 m s-1
to the ELODIE uncertainties, and 5.0 and 1.7 m s-1 to the HIRES uncertainties (pre-
and post-upgrade, respectively).
In total, 15 000 shifts and fits of transit light curves and bootstraps of radial velocity errors were
produced to derive the set of parameters and to extract their means and their corresponding
standard deviations. In addition, we performed additional fits with the light curve
considering data starting at ten
different epochs before the ingress; by performing a prayer bead on 1500 shifts for each of
those ten fits, we could estimate the errors caused by the uncertainty in the shape of the
out-of-transit baseline (see Sect. 2.2).
Table 1: Parameters for the HD 80606 system.
The averaged values we obtained for the seven fitted parameters linked to the Spitzer light curve extraction (Sect. 2.2) are A1 = 58818 and A2 = 6.860 for the baseline, and K1 = 0.2142, K2 = 0.1538, K3 = 0.1083, K4 = 0.0729, and K5 = 0.0050for the pixel-phase effect. However, those parameters could be different at different epochs and for different pixel locations, so this is not clear whether the Aj and Ki values we derived here could be applied to other IRAC observations with Warm-Spitzer.
The best solution of the combined fit is plotted in Fig. 3, with a ramp cut up to HJD =-2 455 210.325, i.e. the first 1.8 h of the observation were discarded, corresponding to the first 15 000 over the 159 232 unbined frames. The upper panel of Fig. 3 shows the radial velocities and the lower panel shows the Spitzer photometry binned per 250 pixels (the middle panel shows the Rossiter-McLaughlin fit that is discussed below in Sect. 5.2).
The derived parameters are reported in Table 1 together with
their error bars; they are ranked as a function of
the way they are derived. First are reported the free parameters of the combined fit that are
listed in Sect. 5.1.3 and which are constrained by photometry only,
then those that are constrained both by radial velocities and photometry,
and then those constrained by radial velocities only. In this last category,
the dispersions around the obtained radial velocity shifts are also reported.
Twelve adjusted parameters of the combined fit are reported here.
Then Table 1 shows the parameters that are directly derived from the
above free parameters of the fit, without any additional hypothesis. This includes the transit
and eclipse timings, the latest being obtained from Laughlin et al. (2009)
and Gillon (2009).
The following parameters are those that are derived by assuming the stellar mass
![]()
![]() (Sect. 5.1.3) together with the
parameters derived above and through the Kepler third law. The last parameters set
in Table 1 are those relative to the Rossiter-McLaughlin fit
that are obtained below in Sect. 5.2.
(Sect. 5.1.3) together with the
parameters derived above and through the Kepler third law. The last parameters set
in Table 1 are those relative to the Rossiter-McLaughlin fit
that are obtained below in Sect. 5.2.
The dispersion of the Spitzer photometry around the transit light curve fit represents
![]() of the stellar flux for unbinned frames.
This is the expected level of the photon noise.
The amplitude of the correlated noise as seen for different bin-sizes of the light curve
is on the order of
of the stellar flux for unbinned frames.
This is the expected level of the photon noise.
The amplitude of the correlated noise as seen for different bin-sizes of the light curve
is on the order of
![]() of the stellar flux (Fig. 6).
A bump in the light curve with an amplitude of
of the stellar flux (Fig. 6).
A bump in the light curve with an amplitude of ![]() 1 mmag
is seen just before the transit mid-time (see Sect.6.1).
It could be instrumental or due to a spot (see Sect. 6.1).
We performed fits without taking these
points into account; this did not change significantly the derived parameters.
1 mmag
is seen just before the transit mid-time (see Sect.6.1).
It could be instrumental or due to a spot (see Sect. 6.1).
We performed fits without taking these
points into account; this did not change significantly the derived parameters.
![\begin{figure}
\par\includegraphics[angle=90,width=9cm,clip]{14327f6.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg124.png)
|
Figure 6: Root mean square (RMS) of binned residuals of the Spitzer transit light curve as a function of the bin size n. The solid red line is proportional to n-1/2, as expected if only photon noise is considered. |
| Open with DEXTER | |
5.2 Rossiter-McLaughlin fit
The radial velocity measurements secured during
transits were fitted to measure the sky-projected angle ![]() between
the planetary orbital axis and the stellar rotation axis. The data we used are
the SOPHIE observations of the 2009 February transit
(Moutou et al. 2009) and the new ones we secured in
2010 January (Sect. 3). We also used
the HIRES data of the 2009 June transit (Winn et al. 2009a).
between
the planetary orbital axis and the stellar rotation axis. The data we used are
the SOPHIE observations of the 2009 February transit
(Moutou et al. 2009) and the new ones we secured in
2010 January (Sect. 3). We also used
the HIRES data of the 2009 June transit (Winn et al. 2009a).
We first measured the radial velocity shift of each dataset by comparison to the center-of-mass radial velocity references computed in Sect. 5.1. Radial velocity measurements performed near to but off the transit are mandatory to constrain those shifts. A lack of these reference observations could prohibit an accurate measurement of the spin-orbit angle. For example for the recent Rossiter-McLaughlin observation of the planetary system Kepler-8 (Jenkins et al. 2010), the paucity of off-transit observations makes it difficult to conclude if the apparent asymmetry of the Rossiter-McLaughlin shape by comparison to the Keplerian curve is due to an actual spin-orbit misalignment or to a shift due to another cause, as stellar activity and/or instrumental drifts.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14327f7.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg125.png)
|
Figure 7:
Radial velocities of HD 80606b around transits and their Rossiter-McLaughlin fit.
The upper panel shows the SOPHIE observations around the 2009 February 14 transit (Moutou
et al. 2009), the middle panel shows the HIRES observations around the
2009 June 5 transit (Winn et al. 2009a), and the lower panel shows the SOPHIE
observations around the 2010 January 13-14 transit (Sect. 3).
On each of these three panels the data are plotted together with the 1- |
| Open with DEXTER | |
For the 2009 February data of HD 80606, we used as reference the nine SOPHIE
measurements performed the nights before and after the transit night, as well
as those nine performed after the fourth contact the night of the transit.
For the 2010 SOPHIE data we used the 33 exposures obtained the January-15 night,
i.e. two days after the transit.
Finally, for the HIRES data we used the six 2009 June measurements secured before
and after the night of the transit (the 2009 June data were excluded from the HIRES
post-upgrade dataset used in Sect. 5.1 for the fit of the orbit).
The radial velocity shifts for the three datasets are reported in Table 1.
We found a shift of
![]() m s-1 between the 2009 and 2010 SOPHIE datasets, and
a shift of
m s-1 between the 2009 and 2010 SOPHIE datasets, and
a shift of
![]() m s-1 between the HIRES measured in 2009 June and the
other post-upgrade HIRES data secured more than one year earlier.
These shifts could result from a combination of instrumental effects, an unknown component
in the system and/or activity-induced jitter.
m s-1 between the HIRES measured in 2009 June and the
other post-upgrade HIRES data secured more than one year earlier.
These shifts could result from a combination of instrumental effects, an unknown component
in the system and/or activity-induced jitter.
The reference observations secured near each of the three transits
are plotted in the right panels of Fig. 7.
Using these off-transit radial velocities, we also computed the uncertainties we
had to add to the radial velocities tabulated error bars in order
to put to unity the reduced ![]() corresponding to the Keplerian fit.
We thus quadratically added 1.0 m s-1 and 2.5 m s-1 to the SOPHIE measurements
secured in 2009 and 2010 respectively, and 1.7 m s-1 to the HIRES
measurements (in agreement with the other HIRES post-upgrade
data used above, see Sect. 5.1.4).
corresponding to the Keplerian fit.
We thus quadratically added 1.0 m s-1 and 2.5 m s-1 to the SOPHIE measurements
secured in 2009 and 2010 respectively, and 1.7 m s-1 to the HIRES
measurements (in agreement with the other HIRES post-upgrade
data used above, see Sect. 5.1.4).
We modeled the Rossiter-McLaughlin anomaly shape with the analytical approach
developed by Ohta et al. (2005). The complete model has 14 parameters:
the stellar limb-darkening linear coefficient ![]() ,
the transit parameters
,
the transit parameters
![]() ,
a/R* and i,
the orbital parameters (P, T0, e,
,
a/R* and i,
the orbital parameters (P, T0, e, ![]() ,
K),
the three radial velocity shifts measured above,
and finally
,
K),
the three radial velocity shifts measured above,
and finally
![]() and
and ![]() .
We computed
.
We computed
![]() in the wavelength range 5300-6300 Å
with the same method as in Sect. 5.1.2.
The transit and orbital parameters are fixed from the results obtained
in Sect. 5.1; their uncertainties arenegligible by
comparison to those of the
two main free parameters of the Rossiter-McLaughlin fit:
in the wavelength range 5300-6300 Å
with the same method as in Sect. 5.1.2.
The transit and orbital parameters are fixed from the results obtained
in Sect. 5.1; their uncertainties arenegligible by
comparison to those of the
two main free parameters of the Rossiter-McLaughlin fit: ![]() ,
which
is constrained by the asymmetry of the anomaly, and
,
which
is constrained by the asymmetry of the anomaly, and
![]() ,
which is
constrained by its amplitude.
,
which is
constrained by its amplitude.
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{14327f8.ps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg130.png)
|
Figure 8:
Confidence interval contours for the |
| Open with DEXTER | |
The best fit is plotted in the middle panel of Fig. 3 and in
Fig. 7. It is obtained for
![]() and
and
![]() km s-1; its
km s-1; its ![]() is 117.8 for 117 degrees of freedom.
The confidence interval contours estimated from
is 117.8 for 117 degrees of freedom.
The confidence interval contours estimated from ![]() variations
(Hébrard et al. 2002) for the two correlated
variations
(Hébrard et al. 2002) for the two correlated ![]() and
and
![]() parameters are plotted in Fig. 8. The uncertainties obtained this
way are
parameters are plotted in Fig. 8. The uncertainties obtained this
way are
![]() and
and ![]() km s-1, respectively. We increased them
to take the uncertainties in the radial velocity shifts of the
three datasets with respect to the Keplerian curve computed in Sect. 5.1
into account.
Our final values are
km s-1, respectively. We increased them
to take the uncertainties in the radial velocity shifts of the
three datasets with respect to the Keplerian curve computed in Sect. 5.1
into account.
Our final values are
![]() and
and
![]() km s-1.
We checked that
the uncertainties of the parameters derived in Sect. 5.1 and used
here in the Rossiter-McLaughlin fit imply negligible uncertainties on
km s-1.
We checked that
the uncertainties of the parameters derived in Sect. 5.1 and used
here in the Rossiter-McLaughlin fit imply negligible uncertainties on ![]() and
and
![]() ;
similarly, the uncertainty in the
;
similarly, the uncertainty in the ![]() limb-darkening coefficient is negligible.
limb-darkening coefficient is negligible.
The adopted values are reported in Table 1, together with the dispersion of the radial velocities performed during the transit with respect to the Rossiter-McLaughlin fit. The dispersion is in the range 4-5 m s-1 for SOPHIE data; we have a similar dispersion around the Keplerian curve for the SOPHIE reference measurements performed before and after the transit. For the HIRES data, the dispersion around the Rossiter-McLaughlin fit is 0.8 m s-1, whereas it is twice as large (1.7 m s-1) for the 2009 June HIRES measurements performed before and after the transit. So it could remain a slight systematic in the HIRES radial velocities secured during the transit. Yet this effect is small and is detected here due to the particularly high accuracy of these measurements.
6 Discussion
6.1 Warm-Spitzer transit light curve
This planetary transit observation is among the first secured with Spitzer
in its post-cryogenic mission. This shows that accurate transit light curves
can be obtained in this second part of the observatory mission
despite enhanced ramp and pixel-phase effects.
Our Warm-Spitzer transit light curve of HD 80606 has
lower uncertainties than those obtained from
the ground. The typical durations of the pixel-phase effect (70 min) and
the planetary transit (12 h) are on time-scales different enough
to avoid significant
uncertainties of the derived system parameters due to this instrumental effect.
The transit light curve is well detected, without extra signatures of transiting
rings or satellites. According to our accuracy,
the signature of an hypothetic satellite would have been
detected up to a magnitude depth slightly below 1 mmag; this corresponds
to an upper limit of 2 ![]() on the radius.
on the radius.
A bump in the light curve is seen just before the transit mid-time with an
amplitude of ![]() 1 mmag. It could correspond to the planet occulting
a dark spot during the transit (Pont et al. 2007; Rabus et al. 2009).
The source HD 80606 is not an active star, so the probability of such an event is low.
The stability at the level of a few mmag of the stellar flux observed in the optical
(Sect. 4) would correspond to a
stability below 1 mmag at 4.5
1 mmag. It could correspond to the planet occulting
a dark spot during the transit (Pont et al. 2007; Rabus et al. 2009).
The source HD 80606 is not an active star, so the probability of such an event is low.
The stability at the level of a few mmag of the stellar flux observed in the optical
(Sect. 4) would correspond to a
stability below 1 mmag at 4.5 ![]() m, assuming dark spots are 1000-K cooler than
the stellar surface (Désert et al. 2010); so the optical
photometry cannot exclude
that the feature detected in the Spitzer light curve is due to a spot.
One can note that at the time of this feature (near 137 h after the
periastron in Fig. 3), a simultaneous feature is also
seen in the SOPHIE radial velocity data. This could argue
in favor of the interpretation of this event in terms of phenomenon at
the surface of HD 80606. This seems unlikely though, because a photometric
feature with this low flux amplitude should a priori not produce this high radial
velocity effect. The radial velocity feature is more likely an instrumental
systematic.
The feature in the Spitzer light curve is detected at a maximal value
of the pixel-phase effect (Fig. 2) so we should remain cautious
about instrumental effects. We monitored the coordinates of the
target on the subarray through the observation to test if the bump
corresponds to a particular area of the detector. This is not the case:
at the epoch of the bump, the target is located on a position of the
detector where the target passes numerous times before and after this
event, and where the pixel-phase effect apparently is well corrected
by our procedure. So we found no strong reasons to particularly
favor an instrumental effect to explain the presence of this feature
in the Spitzer light curve. The most likely explanation is the
small star spot on the surface HD 80606, above which the planet is transiting.
m, assuming dark spots are 1000-K cooler than
the stellar surface (Désert et al. 2010); so the optical
photometry cannot exclude
that the feature detected in the Spitzer light curve is due to a spot.
One can note that at the time of this feature (near 137 h after the
periastron in Fig. 3), a simultaneous feature is also
seen in the SOPHIE radial velocity data. This could argue
in favor of the interpretation of this event in terms of phenomenon at
the surface of HD 80606. This seems unlikely though, because a photometric
feature with this low flux amplitude should a priori not produce this high radial
velocity effect. The radial velocity feature is more likely an instrumental
systematic.
The feature in the Spitzer light curve is detected at a maximal value
of the pixel-phase effect (Fig. 2) so we should remain cautious
about instrumental effects. We monitored the coordinates of the
target on the subarray through the observation to test if the bump
corresponds to a particular area of the detector. This is not the case:
at the epoch of the bump, the target is located on a position of the
detector where the target passes numerous times before and after this
event, and where the pixel-phase effect apparently is well corrected
by our procedure. So we found no strong reasons to particularly
favor an instrumental effect to explain the presence of this feature
in the Spitzer light curve. The most likely explanation is the
small star spot on the surface HD 80606, above which the planet is transiting.
Our dataset results from the first joined campaign during which space-based photometry and high-precision radial velocities were carried out simultaneously. If large stellar spots are detected during a similar campaign, this would help to better understand the effect of stellar activity on radial velocity measurements. Stellar jitter indeed introduces noise in measured radial velocities and is a significant limitation in high-precision velocimetry (see e.g., Saar & Donahue 1997; Santos et al. 2000; Boisse et al. 2009; Queloz et al. 2009; Hébrard et al. 2009a). No stellar spots large enough to be spectroscopically detected were apparently seen here.
6.2 Comparison with previous measurements
The HD 80606's system parameters that we report in Table 1
have a better accuracy than previous studies
(Moutou et al. 2009; Pont et al. 2009; Gillon 2009;
Winn et al. 2009a; Hidas et al. 2010). With respect to
the ground observation of nearly all the transit phases used by Winn et al. (2009a),
the uncertainties presented here are better by factors two to five.
Exceptions are the parameters e, ![]() and K for which the error bars
are not significantly reduced. This is because most of the
constraints on these three parameters come from the radial velocity
on a 9.5-year time span already used by previous studies.
and K for which the error bars
are not significantly reduced. This is because most of the
constraints on these three parameters come from the radial velocity
on a 9.5-year time span already used by previous studies.
For most of the parameters, the revised, more accurate values agree
within 1![]() with those previously published.
There is a
with those previously published.
There is a ![]() disagreement on the inclination i
of the orbit, which is found in our study to be slightly lower; this
implies a more grazing transit, a larger impact parameter b, and a
slightly longer duration for ingress and egress (
disagreement on the inclination i
of the orbit, which is found in our study to be slightly lower; this
implies a more grazing transit, a larger impact parameter b, and a
slightly longer duration for ingress and egress (![]() 10 min longer).
The a/R*-ratio is also found to be 5% smaller, a shift by 2
10 min longer).
The a/R*-ratio is also found to be 5% smaller, a shift by 2![]() according
the error bars from Winn et al. (2009a).
according
the error bars from Winn et al. (2009a).
The projected stellar rotational velocity we found,
![]() km s-1,
is slightly higher than the value obtained by Winn et al. (2009a) from the
Rossiter-McLaughlin fit of their HIRES data:
km s-1,
is slightly higher than the value obtained by Winn et al. (2009a) from the
Rossiter-McLaughlin fit of their HIRES data:
![]() km s-1.
Whereas we also used their HIRES in our analysis, our different result
is explained because we used additional SOPHIE data and measured a
smaller
km s-1.
Whereas we also used their HIRES in our analysis, our different result
is explained because we used additional SOPHIE data and measured a
smaller
![]() ratio (see Sect. 6.3). In addition,
a difference with the study by Winn et al. (2009a) is the shift of
ratio (see Sect. 6.3). In addition,
a difference with the study by Winn et al. (2009a) is the shift of
![]() m s-1
that we found between the HIRES data secured near the transit and the other
ones (Sect. 5.2); this implies a slightly larger amplitude for the
Rossiter-McLaughlin anomaly, thus a larger
m s-1
that we found between the HIRES data secured near the transit and the other
ones (Sect. 5.2); this implies a slightly larger amplitude for the
Rossiter-McLaughlin anomaly, thus a larger
![]() .
The value
.
The value
![]() km s-1 that we measured nonetheless
agrees with those found from synthetic spectral fitting:
km s-1 that we measured nonetheless
agrees with those found from synthetic spectral fitting:
![]() and
and
![]() km s-1 by Valenti & Fischer (2005) and Winn
et al. (2009a), respectively.
The discrepancy noted and discussed by several authors (Winn et al. 2005;
Triaud et al. 2009; Hirano et al. 2010; Simpson et al. 2010)
between the
km s-1 by Valenti & Fischer (2005) and Winn
et al. (2009a), respectively.
The discrepancy noted and discussed by several authors (Winn et al. 2005;
Triaud et al. 2009; Hirano et al. 2010; Simpson et al. 2010)
between the
![]() measured from the Rossiter-McLaughlin effect and from the
spectral modeling of line broadening is negligible for such a slow-rotating star like HD 80606.
measured from the Rossiter-McLaughlin effect and from the
spectral modeling of line broadening is negligible for such a slow-rotating star like HD 80606.
The stellar radius we measured,
![]() ,
is slightly
larger than that obtained by Winn et al. (2009a), namely
,
is slightly
larger than that obtained by Winn et al. (2009a), namely
![]() .
Both values remain in agreement
with the one deduced by Moutou et al. (2009) from relationships between stellar
radius, luminosity, temperature, gravity and mass, namely
.
Both values remain in agreement
with the one deduced by Moutou et al. (2009) from relationships between stellar
radius, luminosity, temperature, gravity and mass, namely
![]() .
.
The radius ratio
![]() and the timing of the transit that we found
significantly differ from the values derived from ground-based observation;
this is discussed below.
and the timing of the transit that we found
significantly differ from the values derived from ground-based observation;
this is discussed below.
6.3 Planetary radius
The radius ratio we found from the transit observed with Spitzer is
![]() .
By comparison, Winn et al. (2009a)
measured
.
By comparison, Winn et al. (2009a)
measured
![]() ;
Pont et al. (2009)
found the same radius ratio as Winn et al. (2009a), but with an
uncertainty three time larger, mainly due to the lack of ingress observation.
The radius ratio measured in the infrared from space is thus
;
Pont et al. (2009)
found the same radius ratio as Winn et al. (2009a), but with an
uncertainty three time larger, mainly due to the lack of ingress observation.
The radius ratio measured in the infrared from space is thus ![]() 3% smaller
than the one measured in the optical from ground. This is a
3% smaller
than the one measured in the optical from ground. This is a ![]() difference
according the error bar reported by Winn et al. (2009a). The two horizontal
dotted lines in the lower panel of Fig. 3 show the absorption depths
expected with the two values; the infrared radius ratio clearly is smaller than the optical one.
difference
according the error bar reported by Winn et al. (2009a). The two horizontal
dotted lines in the lower panel of Fig. 3 show the absorption depths
expected with the two values; the infrared radius ratio clearly is smaller than the optical one.
The uncertainties in the background measurement (Sect. 2.2)
are too small to account for such a radius difference.
A variation of the stellar brightness due to spots could explain time-variations
in the measured radius ratio (Désert et al. 2010). The upper limit of the
brightness variations of the non-active star HD 80606 (Sect. 4)
is however too small to explain a ![]() 3% radius-ratio variation.
The planetary thermal emission could produce an underestimation of
the measured radius ratio (Kipping & Tinetti 2010). The emission
level measured by Laughlin et al. (2009) at 8
3% radius-ratio variation.
The planetary thermal emission could produce an underestimation of
the measured radius ratio (Kipping & Tinetti 2010). The emission
level measured by Laughlin et al. (2009) at 8 ![]() m near the
periastron is higher than the planetary emission expected at 4.5
m near the
periastron is higher than the planetary emission expected at 4.5 ![]() m
at the transit; even with this overestimated planetary flux, the effect would be negligible
according the error bars on the radius ratio we measure at 4.5
m
at the transit; even with this overestimated planetary flux, the effect would be negligible
according the error bars on the radius ratio we measure at 4.5 ![]() m.
m.
The question of possible
interpretation in terms of differential atmospheric absorption could be raised.
The planet apparent radius as a function of the wavelength has been shown
to follow the equation
![]() (Lecavelier des Etangs et al. 2008a,b),
where
(Lecavelier des Etangs et al. 2008a,b),
where ![]() is the wavelength,
is the wavelength, ![]() is the cross section of the mean
atmospheric absorber,
is the cross section of the mean
atmospheric absorber,
![]() is the atmospheric scale height,
k is the Boltzmann constant, T is the temperature,
is the atmospheric scale height,
k is the Boltzmann constant, T is the temperature,
![]() is the molecular mass, and g is the planet gravity
which is about 100 m s-2. If the variation of the radius is due
to the variation of the absorption by haze in the atmosphere as for
the HD 189733b (Pont et al. 2008), even assuming
Rayleigh scattering which produces the steepest variation of absorption
as a function of wavelength, a temperature of about 5000 K is
required to interpret the present measurements, which is
much higher than actually measured (Laughlin et al. 2009).
Indeed, because of the large planetary mass
the scale height is only 60 km at a typical temperature
of 1000 K. The difference of the measured
radius is about 40 times this scale height and is therefore unlikely
due to atmospheric differential absorption.
is the molecular mass, and g is the planet gravity
which is about 100 m s-2. If the variation of the radius is due
to the variation of the absorption by haze in the atmosphere as for
the HD 189733b (Pont et al. 2008), even assuming
Rayleigh scattering which produces the steepest variation of absorption
as a function of wavelength, a temperature of about 5000 K is
required to interpret the present measurements, which is
much higher than actually measured (Laughlin et al. 2009).
Indeed, because of the large planetary mass
the scale height is only 60 km at a typical temperature
of 1000 K. The difference of the measured
radius is about 40 times this scale height and is therefore unlikely
due to atmospheric differential absorption.
We found no astrophysical interpretations able to explain the radius difference
between optical and infrared wavelengths. It is more likely that the error bars
are slightly underestimated, maybe in the ground-based composite light curve.
We note that since we obtain a larger stellar radius than Winn et al. (2009a),
we obtain a similar planetary radius despite the different radius ratio:
![]() .
.
6.4 Transit timing
The mid-times of the transit and the eclipse given in Table 1
are those that are measured. This means that the transit mid-time ![]() we report is in significant advance by about 2.5 min in comparison to that predicted
from the epoch T0 we report for the periastron of the planet
(see Sect. 5.1.2). Indeed, this latest time is in the referential frame of
the radial velocities, which are those of the star.
Similarly, the epoch
we report is in significant advance by about 2.5 min in comparison to that predicted
from the epoch T0 we report for the periastron of the planet
(see Sect. 5.1.2). Indeed, this latest time is in the referential frame of
the radial velocities, which are those of the star.
Similarly, the epoch ![]() of the eclipse reported in Table 1
is delayed by about 15 s compared with the ephemeris computed
from T0.
of the eclipse reported in Table 1
is delayed by about 15 s compared with the ephemeris computed
from T0.
The mid-time of the transit we obtain is accurate at the level of 1.5 min, whereas the accuracy is 6 min for the epoch of the periastron. Laughlin et al. (2009) obtained a 4-min accuracy for the mid-time of the eclipse. These accuracies are high, especially when they are compared with the long duration of the transit and the long orbital period. Using radial velocities alone, even if they span a time as long as 9.5 years, the error bars on the eclipse and periastron timing are three times larger. For the transit timing, the radial velocities cannot predict it at better than two to three hours. Transit and eclipse detections allow here more accurate timings.
This high-accuracy offers an opportunity to look for possible transit timing
variations (TTVs). According to the mid-transit time and the period we found,
we obtain for the 2009 February and June transits a mid-time that is ![]() 23 min
earlier than the
23 min
earlier than the ![]() time measured by Winn et al. (2009a) from these events.
Their accuracy on this timing was
time measured by Winn et al. (2009a) from these events.
Their accuracy on this timing was ![]() min,
so the disagreement is at the level of 3
min,
so the disagreement is at the level of 3![]() .
If it is not caused by underestimated systematic uncertainties,
this difference in the transit timing could in principle be due to
additional bodies in the system, like satellites of the transiting planet or
additional planetary-mass bodies in the system
(see e.g., Holman & Murray 2005;
Agol et al. 2005; Nesvorny & Beaugé 2010).
.
If it is not caused by underestimated systematic uncertainties,
this difference in the transit timing could in principle be due to
additional bodies in the system, like satellites of the transiting planet or
additional planetary-mass bodies in the system
(see e.g., Holman & Murray 2005;
Agol et al. 2005; Nesvorny & Beaugé 2010).
We explored a small region of the parameter space of a hypothetical additional
planet in search for a few examples that could explain a ![]() 20-min difference
between two nearby transits. To do this, we performed a series of 3-body
simulations by integrating the equations of motion using the Burlisch-Stoer
algorithm implemented in the Mercury6 package (Chambers 1999).
20-min difference
between two nearby transits. To do this, we performed a series of 3-body
simulations by integrating the equations of motion using the Burlisch-Stoer
algorithm implemented in the Mercury6 package (Chambers 1999).
Planets in resonant orbits could explain such TTV even with masses small
enough to prohibit their detection with the available radial velocities.
For example, a 15-Earth-mass
planet in a circular 4:1-resonant orbit
produces the adequate timing anomalies, with many pairs of transits
exhibiting a ![]() 20-min discrepancy. The simulated timing variations
exhibit an amplitude of 80 min in this case. A 0.17-Jupiter-mass planet
at the 6:1 resonance produces similar results, although the overall amplitude
is reduced to
20-min discrepancy. The simulated timing variations
exhibit an amplitude of 80 min in this case. A 0.17-Jupiter-mass planet
at the 6:1 resonance produces similar results, although the overall amplitude
is reduced to ![]() 40 min. Both cases would imply radial velocity
variations with semi-amplitudes
40 min. Both cases would imply radial velocity
variations with semi-amplitudes
![]() and 4 m s-1, respectively,
so we cannot exclude those two cases: the first one would be undetectable
in the available radial velocity dataset, whereas the second one would be at
the limit of detection.
More massive planets on non-resonant orbits could be excluded. For example,
a planet located in a circular orbit at 3 AU and having a mass of 1.7 Jupiter
masses would imply a small number of pairs of nearby transits exhibit a
variation of the order of 20 min. It would imply radial velocity
variations of
and 4 m s-1, respectively,
so we cannot exclude those two cases: the first one would be undetectable
in the available radial velocity dataset, whereas the second one would be at
the limit of detection.
More massive planets on non-resonant orbits could be excluded. For example,
a planet located in a circular orbit at 3 AU and having a mass of 1.7 Jupiter
masses would imply a small number of pairs of nearby transits exhibit a
variation of the order of 20 min. It would imply radial velocity
variations of ![]() m s-1 which is detectable with the available
radial velocities.
In all these cases, the short-term
variations (in timescales of the order of 2000 days) exhibited by the orbital
parameters of the transiting planet remain below the level of precision
reached from our combined fit (Sect. 5.1).
However, the variations in timescales on the order of 105-6 days are substantially
larger in all cases. In particular, some 4:1-resonant cases could be unstable
after a few thousands of years.
m s-1 which is detectable with the available
radial velocities.
In all these cases, the short-term
variations (in timescales of the order of 2000 days) exhibited by the orbital
parameters of the transiting planet remain below the level of precision
reached from our combined fit (Sect. 5.1).
However, the variations in timescales on the order of 105-6 days are substantially
larger in all cases. In particular, some 4:1-resonant cases could be unstable
after a few thousands of years.
We also explored the possibility that the observed discrepancy was
produced by a satellite of the transiting planet. In the more favorable
case of a satellite orbiting the planet at the Hill's radius, we found
that its mass must be around 3/100 that of HD 80606b
for it to be the cause of a ![]() 20-min delay in the transit occurrence,
which corresponds to 40 Earth masses.
20-min delay in the transit occurrence,
which corresponds to 40 Earth masses.
6.5 Spin-orbit misalignment
We confirm the spin-orbit misalignment in the HD 80606 system and reduce
the uncertainty in its measurement:
![]() .
This allows
scenarios with aligned spin-orbit to be rejected with a high level of confidence.
This misalignment would imply an asymmetry in the Rossiter-McLaughlin
anomaly as the star is not a perfect sphere but is slightly elongated at the
equator due to its rotation. However, the accuracy of the data is not high enough to
allow such a tiny effect to be detected.
.
This allows
scenarios with aligned spin-orbit to be rejected with a high level of confidence.
This misalignment would imply an asymmetry in the Rossiter-McLaughlin
anomaly as the star is not a perfect sphere but is slightly elongated at the
equator due to its rotation. However, the accuracy of the data is not high enough to
allow such a tiny effect to be detected.
The ![]() angle measures the sky-projected angle between the planetary orbital
axis and the stellar rotation axis. Its actual value remains unknown, as the
inclination I* of the stellar rotation axis is undetermined. In cases where
angle measures the sky-projected angle between the planetary orbital
axis and the stellar rotation axis. Its actual value remains unknown, as the
inclination I* of the stellar rotation axis is undetermined. In cases where
![]() is measured, it is reasonable to assume
is measured, it is reasonable to assume
![]() and an actual spin-orbit alignment. For cases like HD 80606, where
and an actual spin-orbit alignment. For cases like HD 80606, where ![]() is
significantly different from 0, there is certainly no reason to assume the
stellar rotation axis is parallel to the sky plan.
is
significantly different from 0, there is certainly no reason to assume the
stellar rotation axis is parallel to the sky plan.
The projected stellar rotational velocity we get from the Rossiter-McLaughlin
fit is
![]() km s-1. According to our measured
radius for HD 80606,
km s-1. According to our measured
radius for HD 80606,
![]() ,
and to the relation
from Bouchy et al. (2005), this
,
and to the relation
from Bouchy et al. (2005), this
![]() translates into a stellar rotation
period
translates into a stellar rotation
period
![]() days. So the stellar rotation
period apparently is shorter than 40 days. This is shorter than
the limit
days. So the stellar rotation
period apparently is shorter than 40 days. This is shorter than
the limit
![]() days we get in Sect. 3.2
from the low activity of HD 80606. This estimation based on the activity is not
accurate especially for long rotation periods, though. These two values suggest
a rotation period in the range of 40-50 days, so an I*-angle near
days we get in Sect. 3.2
from the low activity of HD 80606. This estimation based on the activity is not
accurate especially for long rotation periods, though. These two values suggest
a rotation period in the range of 40-50 days, so an I*-angle near
![]() .
The value
.
The value
![]() that we measure is thus
probably close to the value of the misalignment angle without projection effect.
This means that the actual angle between the spin-axis of HD 80606 and the
normal to the planetary orbital plane is about
that we measure is thus
probably close to the value of the misalignment angle without projection effect.
This means that the actual angle between the spin-axis of HD 80606 and the
normal to the planetary orbital plane is about
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{14327f9.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg157.png)
|
Figure 9:
Sky-projected |
| Open with DEXTER | |
The first case of a planetary system with a stellar spin misaligned
with the normal of the planetary orbit was discovered by Hébrard et
al. (2008)
in the XO-3 system. This result was hereafter confirmed by Winn
et al. (2009b), who however found a lower ![]() -value.
The HD 80606-system was the second one reported to
have a spin-orbit misalignement by Moutou et al. (2009).
This result was subsequently confirmed and refined successively by
Pont et al. (2009), Gillon (2009), Winn et al. (2009a)
and finally by the present study.
Other planetary systems with significantly misaligned spin-orbit have been
reported since then:
WASP-14 (Johnson et al. 2009),
WASP-17 (Anderson et al. 2010),
HAT-P-7 (Winn et al. 2009c; Narita et al. 2009a), and
CoRoT-1 (Pont et al. 2010).
There are thus now six known misaligned systems.
Two other systems may be misaligned, but the large uncertainties in the
reported
-value.
The HD 80606-system was the second one reported to
have a spin-orbit misalignement by Moutou et al. (2009).
This result was subsequently confirmed and refined successively by
Pont et al. (2009), Gillon (2009), Winn et al. (2009a)
and finally by the present study.
Other planetary systems with significantly misaligned spin-orbit have been
reported since then:
WASP-14 (Johnson et al. 2009),
WASP-17 (Anderson et al. 2010),
HAT-P-7 (Winn et al. 2009c; Narita et al. 2009a), and
CoRoT-1 (Pont et al. 2010).
There are thus now six known misaligned systems.
Two other systems may be misaligned, but the large uncertainties in the
reported ![]() -values prohibit definitive conclusion:
TrES-1 (Narita et al. 2007) and
CoRoT-3 (Triaud et al. 2009).
The recent case of Kepler-8 (Jenkins et al. 2010) is presented
as moderately misaligned, but this requires confirmation (see Sect. 5.2).
On the other hand, twelwe systems are apparently aligned, namely
HD 209458 (Queloz et al. 2000; Wittenmyer et al. 2005),
HD 189733 (Winn et al. 2006; Triaud et al. 2009; Collier Cameron et al. 2010),
HD 149026 (Wolf et al. 2007; Winn & Johnson, in prep.),
HD 17156 (Cochran et al. 2008; Barbieri et al. 2009; Narita et al. 2009b),
HAT-P-1 (Johnson 2008),
HAT-P-2 (Winn et al. 2007; Loeillet et al. 2008),
HAT-P-13 (Winn et al. 2010),
WASP-3 (Simpson et al. 2010; Tripathi et al. 2010),
WASP-6 (Gillon et al. 2009),
TrES-2 (Winn et al. 2008),
TrES-4 (Narita et al. 2010), and
CoRoT-2 (Bouchy et al. 2008).
-values prohibit definitive conclusion:
TrES-1 (Narita et al. 2007) and
CoRoT-3 (Triaud et al. 2009).
The recent case of Kepler-8 (Jenkins et al. 2010) is presented
as moderately misaligned, but this requires confirmation (see Sect. 5.2).
On the other hand, twelwe systems are apparently aligned, namely
HD 209458 (Queloz et al. 2000; Wittenmyer et al. 2005),
HD 189733 (Winn et al. 2006; Triaud et al. 2009; Collier Cameron et al. 2010),
HD 149026 (Wolf et al. 2007; Winn & Johnson, in prep.),
HD 17156 (Cochran et al. 2008; Barbieri et al. 2009; Narita et al. 2009b),
HAT-P-1 (Johnson 2008),
HAT-P-2 (Winn et al. 2007; Loeillet et al. 2008),
HAT-P-13 (Winn et al. 2010),
WASP-3 (Simpson et al. 2010; Tripathi et al. 2010),
WASP-6 (Gillon et al. 2009),
TrES-2 (Winn et al. 2008),
TrES-4 (Narita et al. 2010), and
CoRoT-2 (Bouchy et al. 2008).
Fabrycky & Winn (2009) have shown that the whole sample of the
measured ![]() -angles could be well reproduced with a bimodal distribution
by assuming that a fraction of the orbits have random orientations relative to the stars
and the remaining ones are perfectly aligned. The systems of misaligned orbits
would be those which experienced gravitational interactions between planets
and/or stars, like as Kozai migration.
-angles could be well reproduced with a bimodal distribution
by assuming that a fraction of the orbits have random orientations relative to the stars
and the remaining ones are perfectly aligned. The systems of misaligned orbits
would be those which experienced gravitational interactions between planets
and/or stars, like as Kozai migration.
In Fig. 9 we show the measured ![]() -angles as a function
of the planetary masses for the 21 systems with published measurements reported above.
This plot suggests a scenario with three distinct populations.
Indeed, for the planets with masses similar to that of Jupiter, most of the spins are
aligned with the orbits; this is expected for planets that formed in a protoplanetary disk far
from the star and that slowly migrated closer-in at a later time.
A small fraction of these Jupiter-mass
planets however exhibits large
-angles as a function
of the planetary masses for the 21 systems with published measurements reported above.
This plot suggests a scenario with three distinct populations.
Indeed, for the planets with masses similar to that of Jupiter, most of the spins are
aligned with the orbits; this is expected for planets that formed in a protoplanetary disk far
from the star and that slowly migrated closer-in at a later time.
A small fraction of these Jupiter-mass
planets however exhibits large ![]() -angles; this could be the signature of the
second population in the scenario by Fabrycky & Winn (2009), those
which experienced gravitational interactions and that apparently are less frequent.
These planets also seem to be those than can have extreme
-angles; this could be the signature of the
second population in the scenario by Fabrycky & Winn (2009), those
which experienced gravitational interactions and that apparently are less frequent.
These planets also seem to be those than can have extreme ![]() -values.
-values.
A third population could be formed by the large-mass planets. Indeed, most of them
exhibit a misaligned spin-orbit (see also Johnson et al. 2009),
maybe all of them![]() .
This is at first surprising as one can expect the most
massive planets are the ones for which exciting the inclination is more difficult.
If indeed such misalignments are frequent for the high-mass-planet
population, this suggests a different evolution scenario for them.
Maybe the more massive planets could not really slowly migrate because
of the interactions with the disk. In that case, only more severe interactions with
another planet or a star could be the cause of migration for massive planets, such
interactions also affecting the inclination of the orbit.
We also note that the
.
This is at first surprising as one can expect the most
massive planets are the ones for which exciting the inclination is more difficult.
If indeed such misalignments are frequent for the high-mass-planet
population, this suggests a different evolution scenario for them.
Maybe the more massive planets could not really slowly migrate because
of the interactions with the disk. In that case, only more severe interactions with
another planet or a star could be the cause of migration for massive planets, such
interactions also affecting the inclination of the orbit.
We also note that the ![]() -angles seem lower for the massive planets
than those of the misaligned planets with lower masses; this also suggests
a different scenario for the processes able to modify the inclination of low-
and large-mass planets.
-angles seem lower for the massive planets
than those of the misaligned planets with lower masses; this also suggests
a different scenario for the processes able to modify the inclination of low-
and large-mass planets.
Rossiter-McLaughlin observations of other systems with transiting massive planets should be performed to confirm whether or not they are preferentially tilted.
7 Conclusion
We presented an observation of the 12-hour-long transit of the highly eccentric,
111.4-day-period exoplanet HD 80606b performed in 2010 January.
The transit light curve we present is among the first carried with the
post-cryogenic Spitzer. Its shows systematic effects stronger than those seen
in the Cold-Spitzer, but the accuracy remains clearly better than ground-based observations.
Together with the SOPHIE measurements acquired at the same epoch, this is
one of the first observational campaigns performed simultaneously in radial
velocities and space-based high-accuracy photometry.
With previously available datasets, this allows the parameters of this system
to be significantly refined thanks to combined fits.
There is a possible detection of a variation in the transit timing, which has
to be confirmed by additional observations of HD 80606b transits from ground or space.
A dark spot was also possibly detected on the surface of this inactive star.
The spin-orbit misalignment is clearly confirmed and the ![]() angle is accurately
measured. Like most of the massive planets for which this angle is measured, the orbit
of HD 80606b is misaligned with the equatorial plan of its host star.
This suggests a separate evolution scenario for massive planets compared with
Jupiter-mass planets.
angle is accurately
measured. Like most of the massive planets for which this angle is measured, the orbit
of HD 80606b is misaligned with the equatorial plan of its host star.
This suggests a separate evolution scenario for massive planets compared with
Jupiter-mass planets.
We thank the Haute-Provence Observatory staff that allowed SOPHIE observations despite the ongoing break of the 193-cm telescope, and in particular Fabien Fillion, François Moreau, Jacky Taupenas, Jean-Pierre Troncin and Stéphane Favard. We are grateful to C. Adami, D. Russeil and M. Dennefeld for their flexibility in the OHP 120-cm photometry observations, M. Gillon and J. N. Winn for useful discussions, and the referee G. Laughlin. We thank the Spitzer director for having awarded us discretionary time, and the Spitzer staff and in particular Nancy Silbermann for their assistance in the preparation of the observation. We acknowledge support of the ``Programme National de Planétologie'' (PNP) of CNRS/INSU, the Swiss National Science Foundation, and the French National Research Agency (ANR-08-JCJC-0102-01 and ANR-NT05-4-44463). D.E. is supported by CNES. A.E. is supported by a fellowship for advanced researchers from the Swiss National Science Foundation. N.C.S. acknowledges the support of the European Research Council/European Community under the FP7 through a Starting Grant, and the Fundação para a Ciência e a Tecnologia (FCT), Portugal, for a Ciência 2007 contract funded by FCT/MCTES (Portugal) and POPH/FSE (EC), and in the form of grants reference PTDC/CTE-AST/66643/2006 and PTDC/CTE-AST/098528/2008.
References
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, D. R., Hellier, C., Gillon, M., et al. 2010, ApJ, 709, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1994, A&AS, 119, 373 [Google Scholar]
- Barbieri, M., Alonso, R., Desidera, S., et al. 2009, A&A, 503, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Moutou, C., Vidal-Madjar, A., et al. 2009, A&A, 495, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Bouchy, F., Chazelas, B., et al. 2010a, New technologies for probing the diversity of brown dwarfs and exoplanets, EPJ Web of Conferences, in press [arXiv:1001.0794] [Google Scholar]
- Boisse, I., Eggenberger, A., Santos, N. C., et al. 2010b, A&A, accepted [Google Scholar]
- Bouchy, F., Pont, F., Melo, C., et al. 2005, A&A, 431, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Queloz, D., Deleuil, M., et al. 2008, A&A, 482, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Charbonneau, D., Alle, L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Cochran, W. D., Redfield, S., Endl, M., & Cochran, A. L. 2008, ApJ, 683, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Bruce, V. A., Miller, G. R. M., Triaud, A. H. M. J., & Queloz, D. 2010, MNRAS, 403, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Deeg, H. J., Moutou, C., Erikson, A., et al. 2010, Nature, 464, 384 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deming, D., Seager, S., Richardson, L. J., & Harrington, J. 2005, Nature, 434, 740 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Désert, J.-M., Lecavelier des Etangs, A., Hébrard, G., et al. 2009, ApJ, 699, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Sing, D. K., Vidal-Madjar, A., et al. 2010, ApJ, submitted [Google Scholar]
- Ehrenreich, D., Hébrard, G., Lecavelier des Etangs, A., et al. 2007, ApJ, 668, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., & Winn, J. N. 2009, ApJ, 696, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandes, J., & Santos, N. C. 2004, A&A, 427, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossey, S. J., Waldmann, I. P., & Kipping, D. M. 2009, MNRAS, 396, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Melendo, E., & McCullough, P. R. 2009, ApJ, 698, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M. 2009, MNRAS, submitted [arXiv:0906.4904] [Google Scholar]
- Gillon, M., Demory, B.-O., Barman, T., et al. 2007, A&A, 471, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Anderson, D. R., Triaud, A. H. M. J., et al. 2009, A&A, 501, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hébrard, G., Lemoine, M., Vidal-Madjar, A., et al. 2002, ApJ, 140, 103 [Google Scholar]
- Hébrard, G., Bouchy, F., Pont, F., et al. 2008, A&A, 481, 52 [Google Scholar]
- Hébrard, G., Udry, S., Lo Curto, G., et al. 2010a, A&A, 512, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hébrard, G., Bonfils, X., Ségransan, D., et al. 2010b, A&A, 513, 69 [Google Scholar]
- Hidas, M. G., Tsapras, Y., Street, R. A., et al. 2010, MNRAS, accepted[arXiv:1002.1052] [Google Scholar]
- Hirano, T., Suto, Y., Taruya, A., et al. 2010, ApJ, 709, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jenkins, J. M., Borucki, W., J., Koch, D. G., et al. 2010, ApJ, submitted[arXiv:1001.0416] [Google Scholar]
- Johnson, J. A., Winn, J. N., Narita, N., et al. 2008, ApJ, 686, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Winn, J. N., Albrecht, S., et al. 2009, PASP, 121, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M., & Tinetti, G. 2010, MNRAS, accepted [arXiv:0912.1133] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Laughlin, G., Deming, D., Langton, J., et al. 2009, Nature, 457, 562 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lecavelier des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008a, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Vidal-Madjar, A., Désert, J.-M., & Sing, D. 2008b, A&A, 485, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loeillet, B., Shporer, A., Bouchy, F., et al. 2008, A&A, 481, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Morales-Calderón, M., Stauffer, J. R., Kirkpatrick, J. D., et al. 2006, ApJ, 653, 1454 [NASA ADS] [CrossRef] [Google Scholar]
- Moutou, C., Pont, F., Bouchy, F., & Mayor, M. 2004, A&A, 424, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Hébrard, G., Bouchy, F., et al. 2009, A&A, 498, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naef, D., Latham, D. W., Mayor, M., et al. 2001, A&A, 375, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narita, N., Enya, K., Sato, B., et al. 2007, PASJ, 59, 763 [NASA ADS] [Google Scholar]
- Narita, N., Sato, B., Hirano, T., & Tamura, M. 2009a, PASJ, 61, L35 [NASA ADS] [Google Scholar]
- Narita, N., Hirano, T., Sato, B., et al. 2009b, PASJ, 61, 99 [Google Scholar]
- Narita, N., Sato, B., Hirano, T. et al. 2010, PASJ, 62, 653 [NASA ADS] [Google Scholar]
- Nesvorny, D., & Beaugé, C. 2010, ApJ, 709, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Ohta, Y., Taruya, A, & Suto, Y. 2005, ApJ, 622, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- O'Toole, S. J., Tinney, C. G., Jones, H. R. A., et al. 2009, MNRAS, 392, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perruchot, S., Kohler, D., Bouchy, F., et al., 2008, in Ground-based and Airborn Instrumentation for Astronomy II, ed. I. S., McLean, & M. M., Casali, Proc. SPIE, 7014, 70140J [Google Scholar]
- Pont, F., Gilliland, R. L., Moutou, C., et al. 2007, A&A, 476, 1347 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Pont, F., Knutson, H., Gilliland, R. L., Moutou, C., & Charbonneau, D. 2008, MNRAS, 385, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Hébrard, G., Irwin, J. M., et al. 2009, A&A, 509, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pont, F., Endl, M., Cochran, W. D., et al. 2010, MNRAS, 402, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Eggenberger, A., Mayor, M., et al. 2000, A&A, 359, L13 [NASA ADS] [Google Scholar]
- Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rabus, M., Alonso, R., Belmonte, J. A., et al. 2009, A&A, 494, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reach, W. T., Surace, J. A., Glaccum, W. J., et al. 2006, Infrared Array Camera Data Handbook, Version 3.0 [Google Scholar]
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 741 [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
- Scoupeet al. 2006, LPQ, 1931, 2 [Google Scholar]
- Sing, D. K. 2010, A&A, 510, 21 [Google Scholar]
- Simpson, E. K., Pollacco, D., Hébrard, G., et al. 2010, MNRAS, 405, 1867 [NASA ADS] [Google Scholar]
- Triaud, A. H. M. J., Queloz, D., Bouchy, F., et al. 2009, A&A, 506, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tripathi, A., Winn, J. N., Johnson, J. A., et al. 2010, ApJ, 715, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Fischer, D. A., 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Winn, J. N. 2010, [arXiv:1001.2010] [Google Scholar]
- Winn, J. N., Noyes, R. W., Holman, M. J., et al. 2005, ApJ, 631, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Marcy, G. W., et al. 2006, ApJ, 653, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Peek, K. M. G., et al. 2007, ApJ, 665, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Narita, N., et al. 2008, ApJ, 682, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Howard, A. W., Johnson, J. A., et al. 2009a, ApJ, 703, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Fabrycky, D., et al. 2009b, ApJ, 700, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Albrecht, S., et al. 2009c, ApJ, 703, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Howard, A. W., et al. 2010, ApJ, 718, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Welsh, W. F., Orosz, J. A., et al. 2005, ApJ, 632, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Endl, M., Cochran, W. D., Levison, H. F., & Henry, G. W. 2009, ApJS, 182, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, A. S., Laughlin, G., Henry, G. W., et al. 2007, ApJ, 667, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Murray, N. 2003, ApJ, 589, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... HD 80606b
![[*]](/icons/foot_motif.png)
- Based on observations collected with the SOPHIE spectrograph on the 1.93-m telescope at the Observatoire de Haute-Provence (CNRS), France, and with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Radial velocity and photometry tables are available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/516/A95
- ... known cases
![[*]](/icons/foot_motif.png)
- See also the 95-day-period transiting exoplanet CoRoT-9b announced after the submission of the present paper (Deeg et al. 2010).
- ...
Library
![[*]](/icons/foot_motif.png)
- http://idlastro.gsfc.nasa.gov/homepage.html
- ... them
![[*]](/icons/foot_motif.png)
- The only exception, HATP-P-2, could actually be also misaligned as the inclination of the stellar rotation axis is unknown.
All Tables
Table 1: Parameters for the HD 80606 system.
All Figures
| |
Figure 1: Schematic view of the HD 80606 system. The red dots show the positions of the planet each 24 h. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14327f2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg28.png)
|
Figure 2: Spitzer photometry of HD 80606. From top to bottom, the three panels show the raw photometry, the photometry after correction of the pixel-phase and ramp effects, and the residuals respectively. The black points are the measurements (binned per 5 frames) and the red solid lines are the fits. The vertical dotted lines show the mid-transit, the vertical dot-dashed lines show the first and fourth contacts, and the vertical dot-dot-dashed lines show the second and third contacts. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14327f3.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg32.png)
|
Figure 3:
Radial velocities and photometry of HD 80606 as a function of the orbital phase or
the time after periastron.
Upper panel: radial velocities as measured with
ELODIE (red open squares, Moutou et al. 2009),
HRS (purple open circles, Wittenmyer et al. 2009),
HIRES (Winn et al. 2009a)
pre- and post-upgrade (green open upward and downward triangles,
respectively) and around the 2009 June transit (green filled downward triangles), and
SOPHIE during the 2009 February and 2010 January transits (blue open and filled
diamonds, respectively).
Middle panel: same as above, but enlarged around the transit phase.
Lower panel: Spitzer photometry during the 2010 January transit. The
Spitzer data are binned
per 250, i.e. one point each 100 s.
The two horizontal dotted-lines show the absorption depth expected with the
value
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14327f4.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg45.png)
|
Figure 4:
Plot of the orbital velocity of the planet and orbit direction during the
transit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{old/14327f5a.ps}\par\includegraphics[width=8.8cm,clip]{old/14327f5b.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg68.png)
|
Figure 5:
Distributions of the parameters obtained for the
15 000 fits performed with the prayer bead and bootstrap (Sect. 5.1.4).
As an example, four parameters are plotted here: a/R* vs.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=9cm,clip]{14327f6.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg124.png)
|
Figure 6: Root mean square (RMS) of binned residuals of the Spitzer transit light curve as a function of the bin size n. The solid red line is proportional to n-1/2, as expected if only photon noise is considered. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14327f7.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg125.png)
|
Figure 7:
Radial velocities of HD 80606b around transits and their Rossiter-McLaughlin fit.
The upper panel shows the SOPHIE observations around the 2009 February 14 transit (Moutou
et al. 2009), the middle panel shows the HIRES observations around the
2009 June 5 transit (Winn et al. 2009a), and the lower panel shows the SOPHIE
observations around the 2010 January 13-14 transit (Sect. 3).
On each of these three panels the data are plotted together with the 1- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{14327f8.ps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg130.png)
|
Figure 8:
Confidence interval contours for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{14327f9.ps}
\end{figure}](/articles/aa/full_html/2010/08/aa14327-10/Timg157.png)
|
Figure 9:
Sky-projected |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


