| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014094 | |
| Published online | 30 June 2010 | |
A&A 516, A68 (2010)
Circumstellar molecular composition of the oxygen-rich AGB star IK Tauri
I. Observations and LTE chemical abundance analysis
H. Kim1,2 - F. Wyrowski1 - K. M. Menten1 - L. Decin3,4
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121
Bonn, Germany
2 - Max-Planck-Institut für Gravitationsphysik, Callinstr. 38, 30167
Hannover, Germany
3 - Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001
Leuven, Belgium
4 - Sterrenkundig Instituut Anton Pannekoek, University of Amsterdam,
PO Box 9429, 1090 CE Amsterdam, The Netherlands
Received 18 January 2010 / Accepted 8 April 2010
Abstract
Context. Molecular lines in the (sub)millimeter
wavelength range can provide important information about the physical
and chemical conditions in the circumstellar envelopes around
asymptotic giant branch stars.
Aims. The aim of this paper is to study the
molecular composition in the circumstellar envelope around the
oxygen-rich star IK Tau.
Methods. We observed IK Tau in several
(sub)millimeter bands using the APEX telescope during three observing
periods. To determine the spatial distribution of the
![]() emission,
mapping observations were performed. To constrain the
physical conditions in the circumstellar envelope, multiple rotational
CO emission lines were modeled using a nonlocal thermodynamic
equilibrium radiative transfer code. The rotational temperatures and
the abundances of the other molecules were obtained assuming local
thermodynamic equilibrium.
emission,
mapping observations were performed. To constrain the
physical conditions in the circumstellar envelope, multiple rotational
CO emission lines were modeled using a nonlocal thermodynamic
equilibrium radiative transfer code. The rotational temperatures and
the abundances of the other molecules were obtained assuming local
thermodynamic equilibrium.
Results. An oxygen-rich asymptotic giant branch star
has been surveyed in the submillimeter wavelength range. Thirty four
transitions of twelve molecular species, including maser lines, were
detected. The kinetic temperature of the envelope was determined, and
the molecular abundance fractions of the molecules were estimated. The
deduced molecular abundances were compared with observations and
modeling from the literature and agree within a factor of 10, except
for SO2, which is found to be almost a factor
100 stronger than predicted by chemical models.
Conclusions. From this study, we found that IK Tau
is a good laboratory for studying the conditions in circumstellar
envelopes around oxygen-rich stars with (sub)millimeter-wavelength
molecular lines. We could also expect from this study that the
molecules in the circumstellar envelope can be explained more
faithfully by non-LTE analysis with lower and higher transition lines
than by simple LTE analysis with only lower transition lines. In
particular, the observed CO line profiles could be well reproduced by a
simple expanding envelope model with a power-law structure.
Key words: line: profiles - methods: observational - telescopes - stars: mass-loss - stars: abundances - submillimeter: stars
1 Introduction
Stars with initial masses lower than ![]() 8
8
![]() evolve to a pulsationally
unstable red
giant star on the asymptotic giant branch (AGB). At this stage, mass
loss from the evolved central star produces an expanding
envelope. Further on, carbon, C, is fused in the core and then oxygen,
O (Yamamura
et al. 1996; Fukasaku et al. 1994).
evolve to a pulsationally
unstable red
giant star on the asymptotic giant branch (AGB). At this stage, mass
loss from the evolved central star produces an expanding
envelope. Further on, carbon, C, is fused in the core and then oxygen,
O (Yamamura
et al. 1996; Fukasaku et al. 1994).
AGB stars are characterized by low surface temperatures,
![]() K,
high
luminosities up to several
K,
high
luminosities up to several
![]() ,
and a very large geometric size up to several AU (Habing 1996). In general, these
highly
evolved stars are surrounded by envelopes with expansion velocities
between 5
,
and a very large geometric size up to several AU (Habing 1996). In general, these
highly
evolved stars are surrounded by envelopes with expansion velocities
between 5
![]() and 40
and 40
![]() .
They have high mass-loss
rates between
.
They have high mass-loss
rates between ![]() and
and ![]() .
Their atmospheres provide favorable thermodynamic conditions
for the formation of simple molecules, owing to the low temperatures
and,
simultaneously, high densities.
Because of pulsation, molecules may reach a distance at which the
temperature is
lower than the condensation temperature and at which the density is
still high
enough for dust grains to form. Radiation pressure drives the dust away
from
the star. Molecules surviving dust formation are accelerated by
dust-grain collisions (Goldreich
& Scoville 1976).
.
Their atmospheres provide favorable thermodynamic conditions
for the formation of simple molecules, owing to the low temperatures
and,
simultaneously, high densities.
Because of pulsation, molecules may reach a distance at which the
temperature is
lower than the condensation temperature and at which the density is
still high
enough for dust grains to form. Radiation pressure drives the dust away
from
the star. Molecules surviving dust formation are accelerated by
dust-grain collisions (Goldreich
& Scoville 1976).
The chemistry of the atmospheres and, farther out, of the
circumstellar envelopes (CSEs) around AGB
stars is dependent on the chemical class. They are classified either as
M stars (C/O abundance ratio <1), S stars (C/O ![]() 1), or C
stars (C/O >1). The optical and infrared spectra of AGB stars
show
absorption from the stellar atmosphere. M-type stellar spectra are
dominated by lines of oxygen-bearing molecules, e.g., the metal oxides
SiO and
TiO, and by
1), or C
stars (C/O >1). The optical and infrared spectra of AGB stars
show
absorption from the stellar atmosphere. M-type stellar spectra are
dominated by lines of oxygen-bearing molecules, e.g., the metal oxides
SiO and
TiO, and by ![]() .
In C-star atmospheres, carbon-bearing molecules
like, a.o., CH, C2,
.
In C-star atmospheres, carbon-bearing molecules
like, a.o., CH, C2,
![]() ,
and HCN are detected at optical and infrared wavelengths, and in the
microwave regime (e.g. Gautschy-Loidl
et al. 2004).
While the atmospheric abundance fractions are
nowadays quite well understood in terms of initial chemical
composition, which may be altered by nucleosynthetic products that are
brought to the surface by dredge-ups,
the main processes determining the circumstellar
chemical abundance stratification of many molecules are still largely
not understood. In the stellar photosphere, the high gas density
ensures thermal equilibrium (TE). Pulsation-driven shocks in the inner
wind region suppress TE. This region of strong shock activity is also
the locus of grain formation, resulting in the depletion of few
molecules such as SiO and SiS. Other molecules, such as CO and CS, are
thought to be unreactive in the dust-forming region (Duari et al. 1999). At
larger radii, the so-called outer envelope is penetrated by ultraviolet
interstellar photons and cosmic rays resulting in a chemistry governed
by photochemical and ion-molecule reactions. This picture of the
chemical processes altering the abundance stratification is generally
accepted, but many details on chemical reactions rates, molecular
left-overs after the dust formation, shock strengths inducing a fast
chemistry zone, etc., are not yet known.
,
and HCN are detected at optical and infrared wavelengths, and in the
microwave regime (e.g. Gautschy-Loidl
et al. 2004).
While the atmospheric abundance fractions are
nowadays quite well understood in terms of initial chemical
composition, which may be altered by nucleosynthetic products that are
brought to the surface by dredge-ups,
the main processes determining the circumstellar
chemical abundance stratification of many molecules are still largely
not understood. In the stellar photosphere, the high gas density
ensures thermal equilibrium (TE). Pulsation-driven shocks in the inner
wind region suppress TE. This region of strong shock activity is also
the locus of grain formation, resulting in the depletion of few
molecules such as SiO and SiS. Other molecules, such as CO and CS, are
thought to be unreactive in the dust-forming region (Duari et al. 1999). At
larger radii, the so-called outer envelope is penetrated by ultraviolet
interstellar photons and cosmic rays resulting in a chemistry governed
by photochemical and ion-molecule reactions. This picture of the
chemical processes altering the abundance stratification is generally
accepted, but many details on chemical reactions rates, molecular
left-overs after the dust formation, shock strengths inducing a fast
chemistry zone, etc., are not yet known.
Spectroscopical studies of molecular lines in the (sub)milli-
meter range are very useful tools for estimating the physical and
chemical conditions in CSEs. Due to its proximity, the carbon-rich AGB
star IRC+10216 has attracted a lot of attention, resulting in
the detection of more than 60 different chemical compounds in
its CSE (e.g. Cernicharo
et al. 2000; Ridgway et al.
1976). Until now, detailed studies of oxygen-rich envelopes
have been rare. Recently, Ziurys
et al. (2004) have focused on the chemical analysis
of the oxygen-rich peculiar red supergiant VY CMa.
VY CMa is, however, not a prototype of an evolved oxygen-rich star. A
complex geometry is deduced from Hubble Space Telescope images (Smith et al. 2001) with
a luminosity higher than ![]() and a mass-loss rate of
and a mass-loss rate of ![]()
![]() /yr
(Sopka
et al. 1985; Bowers et al. 1983).
VY CMa is a spectacular object, which can explode as a
supernova at any time because of its extreme evolutionary state.
Interpreting the molecular emission profiles of VY CMa is
therefore a very complex task, subject to many uncertainties. To
enlarge our insight into the chemical structure in the envelopes of
oxygen-rich low and intermediate-mass stars, we therefore have started
a submillimeter survey of the oxygen-rich AGB star
IK Tau, which is thought to be (roughly) spherically
symmetric (Lane
et al. 1987; Marvel 2005). We thereby hope
to advance understanding of the final stages of stellar evolution of
the majority of stars in galaxies like our Milky Way and their
resulting impact on the interstellar medium and the cosmic cycle.
/yr
(Sopka
et al. 1985; Bowers et al. 1983).
VY CMa is a spectacular object, which can explode as a
supernova at any time because of its extreme evolutionary state.
Interpreting the molecular emission profiles of VY CMa is
therefore a very complex task, subject to many uncertainties. To
enlarge our insight into the chemical structure in the envelopes of
oxygen-rich low and intermediate-mass stars, we therefore have started
a submillimeter survey of the oxygen-rich AGB star
IK Tau, which is thought to be (roughly) spherically
symmetric (Lane
et al. 1987; Marvel 2005). We thereby hope
to advance understanding of the final stages of stellar evolution of
the majority of stars in galaxies like our Milky Way and their
resulting impact on the interstellar medium and the cosmic cycle.
Mira variable IK Tau, also known as NML Tau, is located at
![]()
![]() 8,
8,
![]() .
It was found to be an
extremely cool star with large infrared (J-K)
excess (Alcolea et al. 1999)
consistent with a 2000 K blackbody. IK Tau shows regular
optical variations
with an amplitude of
.
It was found to be an
extremely cool star with large infrared (J-K)
excess (Alcolea et al. 1999)
consistent with a 2000 K blackbody. IK Tau shows regular
optical variations
with an amplitude of ![]() 4.5 mag.
It is an O-rich star of spectral type ranging from M8.1 to M11.2
(Wing & Lockwood 1973).
Its distance was derived by Olofsson
et al. (1998) to be 250 pc
assuming a stellar temperature of 2000 K. The pulsation period
is
4.5 mag.
It is an O-rich star of spectral type ranging from M8.1 to M11.2
(Wing & Lockwood 1973).
Its distance was derived by Olofsson
et al. (1998) to be 250 pc
assuming a stellar temperature of 2000 K. The pulsation period
is ![]() 470 days (Hale et al. 1997). The
systemic velocity of the star is 33.7
470 days (Hale et al. 1997). The
systemic velocity of the star is 33.7
![]() .
Mass-loss rate
estimates range from
.
Mass-loss rate
estimates range from
![]() (from
the CO(J=1-0) line; Olofsson
et al. 1998) to
(from
the CO(J=1-0) line; Olofsson
et al. 1998) to
![]() (from an
analysis of multiple SiO lines; González Delgado
et al. 2003).
(from an
analysis of multiple SiO lines; González Delgado
et al. 2003).
In the circumstellar envelope of IK Tau maser emission from OH
(Bowers et al. 1989),
![]() (Lane et al. 1987),
and SiO
(Boboltz & Diamond 2005),
and thermal emission
of SiO, CO, SiS, SO,
(Lane et al. 1987),
and SiO
(Boboltz & Diamond 2005),
and thermal emission
of SiO, CO, SiS, SO, ![]() ,
and HCN have previously been found
(Lindqvist
et al. 1988; Bujarrabal et al. 1994;
Omont
et al. 1993). Obviously, IK Tau is a prime candidate
for circumstellar chemistry studies.
,
and HCN have previously been found
(Lindqvist
et al. 1988; Bujarrabal et al. 1994;
Omont
et al. 1993). Obviously, IK Tau is a prime candidate
for circumstellar chemistry studies.
2 Observations
Table 1: Overview of the molecular line transitions observed with APEX.
The observations were performed with the
APEX![]() 12 m telescope in Chile (Güsten
et al. 2006) located at the 5100 m high site on
Llano de Chajnantor.
The data were obtained during observing periods in 2005 November and
2006 April
and August. The receivers used were the facility APEX-2A (Risacher et al. 2006)
and the MPIfR FLASH receivers (Heyminck
et al. 2006). Typical system noise
temperatures were about 200 K-1000 K at 290 GHz and
350 GHz, and 1000 K at 460
GHz, and 5000 K at 810 GHz. The spectrometers for the
observations
were fast fourier transform spectrometers (FFTS) with 1 GHz bandwidth,
and the
channel width for the 290-350 GHz observations was
approximately 122.07
kHz (8192 channels), and for the 460 GHz and 810 GHz
observations 488.28 kHz
(2048 channels). For the observations, a position-switching mode was
used with
the reference position typically 180
12 m telescope in Chile (Güsten
et al. 2006) located at the 5100 m high site on
Llano de Chajnantor.
The data were obtained during observing periods in 2005 November and
2006 April
and August. The receivers used were the facility APEX-2A (Risacher et al. 2006)
and the MPIfR FLASH receivers (Heyminck
et al. 2006). Typical system noise
temperatures were about 200 K-1000 K at 290 GHz and
350 GHz, and 1000 K at 460
GHz, and 5000 K at 810 GHz. The spectrometers for the
observations
were fast fourier transform spectrometers (FFTS) with 1 GHz bandwidth,
and the
channel width for the 290-350 GHz observations was
approximately 122.07
kHz (8192 channels), and for the 460 GHz and 810 GHz
observations 488.28 kHz
(2048 channels). For the observations, a position-switching mode was
used with
the reference position typically 180
![]() off-source. The antenna
was focused on the available planets. IK Tau itself was strong
enough to serve
as a line pointing source, so small cross scans in the 12CO(3-2)
line monitored
the pointing during the observations. The telescope beam sizes (HPBW)
at
frequencies of the observed molecular lines are shown in Table 1. The antenna
beam efficiencies are given in Table 2 of Güsten et al. (2006).
off-source. The antenna
was focused on the available planets. IK Tau itself was strong
enough to serve
as a line pointing source, so small cross scans in the 12CO(3-2)
line monitored
the pointing during the observations. The telescope beam sizes (HPBW)
at
frequencies of the observed molecular lines are shown in Table 1. The antenna
beam efficiencies are given in Table 2 of Güsten et al. (2006).
To map the circumstellar envelope in the 12CO(3-2)
line, 30 positions distributed on a 5![]() 6
grid in right ascension and declination were observed. The grid spacing
was
9
6
grid in right ascension and declination were observed. The grid spacing
was
9
![]() (half the FWHM beam size at
345 GHz). A raster mapping
procedure was used along the parallel grid lines with an integration
time of 15 s.
(half the FWHM beam size at
345 GHz). A raster mapping
procedure was used along the parallel grid lines with an integration
time of 15 s.
Table 2: Beam efficiencies for the different receivers.
The spectra were reduced using the CLASS
program of the IRAM GILDAS![]() .
To calculate the
main-beam brightness temperatures of the lines,
.
To calculate the
main-beam brightness temperatures of the lines,
![]() ,
the following
relation was used:
,
the following
relation was used:
Here
3 Observational results
Thirty-four transitions from 12 molecular species including maser lines were detected with the APEX telescope toward IK Tau. The detected molecular lines are listed in Table 1 and their spectra are displayed in Figs. 1 to 5.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{00014fg1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg42.png)
|
Figure 1:
Observed |
| Open with DEXTER | |
Figures 6
and 7
show the ![]() maser
lines and SiO maser lines observed toward IK Tau, respectively; the
maser line parameters are given in Table 3. Maser emission
from
maser
lines and SiO maser lines observed toward IK Tau, respectively; the
maser line parameters are given in Table 3. Maser emission
from ![]() at 321 GHz and 325 GHz was detected, as it was in the
J=7-6 and J=8-7 rotational
transitions within the v=1 and v=3
vibrationally excited states of
at 321 GHz and 325 GHz was detected, as it was in the
J=7-6 and J=8-7 rotational
transitions within the v=1 and v=3
vibrationally excited states of
![]() ,
,
![]() ,
and
,
and ![]() .
.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{00014fg2.eps}
\vspace*{-2mm} \end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg43.png)
|
Figure 2:
Observed HCN, |
| Open with DEXTER | |
3.1 Line parameters
Table 3: Line parameters for the detected maser lines.
To get the mean brightness temperature estimates, the spectra
were
corrected by the beam-filling factors assuming a CO source size of
17
![]() (Bujarrabal
& Alcolea
1991),
an HCN source size of
3.85
(Bujarrabal
& Alcolea
1991),
an HCN source size of
3.85
![]() (Marvel
2005)
and source sizes for the
other molecules of 2.2
(Marvel
2005)
and source sizes for the
other molecules of 2.2
![]() (Lucas
et al. 1992). The CO size may be uncertain, probably
underestimated, since the signal-to-noise (S/N) ratios of the profiles
obtained by Bujarrabal
& Alcolea (1991) are much lower than those of the CO
profiles presented in this paper.
(Lucas
et al. 1992). The CO size may be uncertain, probably
underestimated, since the signal-to-noise (S/N) ratios of the profiles
obtained by Bujarrabal
& Alcolea (1991) are much lower than those of the CO
profiles presented in this paper.
The beam-filling factor is given by
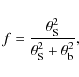
|
(2) |
where
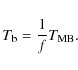
|
(3) |
Line parameters were derived with CLASS (see more details on http://www.iram.fr/IRAMFR/GILDAS) from fitting the spectral lines with expanding shell fits, from which the expansion velocity of the envelope is obtained. The observed maser line and thermal emission line parameters are given in Tables 3 and 4, including the envelope expansion velocity
When the S/N is high enough to warrant a
consideration of the shape of the line profiles, they appear to be
characteristic of circumstellar envelopes (for more detail
see Zuckerman 1987):
the ![]() lines have the parabolic
shape of optically thick lines, and the
lines have the parabolic
shape of optically thick lines, and the
![]() (3-2)
line
has the
double-horn shape of spatially resolved optically thin lines (see
Fig. 1).
Lines
from the three SiO isotopologues and SiS lines have a Gaussian shape
(see Fig. 4),
indicating that they are partially formed in the wind acceleration
regime where the stellar winds has not yet reached its full terminal
velocity (Bujarrabal &
Alcolea 1991). Some of the
(3-2)
line
has the
double-horn shape of spatially resolved optically thin lines (see
Fig. 1).
Lines
from the three SiO isotopologues and SiS lines have a Gaussian shape
(see Fig. 4),
indicating that they are partially formed in the wind acceleration
regime where the stellar winds has not yet reached its full terminal
velocity (Bujarrabal &
Alcolea 1991). Some of the
![]() lines seem
to show the square shape characteristic of unresolved
optically thin
lines and some of them have the parabolic shape of optically thick
lines
(see Fig. 5).
The CS and SO lines seem to have the square shape of unresolved
optically
thin lines for low excitation transitions and the parabolic shape of
optically thick lines for high excitation transitions
(see Fig. 3).
HCN shows a
global parabolic shape with a weak double-peak profile on the top
(see Fig. 2).
For the CN molecule, fits to the spectra were done that take the
hyperfine structure of the molecule into account. Although the S/N of
the individual
components is low, the observations do not agree with the
optical thin ratio of different HFS components and hint at hyperfine
anomalies, as already reported by Bachiller
et al. (1997).
lines seem
to show the square shape characteristic of unresolved
optically thin
lines and some of them have the parabolic shape of optically thick
lines
(see Fig. 5).
The CS and SO lines seem to have the square shape of unresolved
optically
thin lines for low excitation transitions and the parabolic shape of
optically thick lines for high excitation transitions
(see Fig. 3).
HCN shows a
global parabolic shape with a weak double-peak profile on the top
(see Fig. 2).
For the CN molecule, fits to the spectra were done that take the
hyperfine structure of the molecule into account. Although the S/N of
the individual
components is low, the observations do not agree with the
optical thin ratio of different HFS components and hint at hyperfine
anomalies, as already reported by Bachiller
et al. (1997).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{00014fg3.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg50.png)
|
Figure 3: Observed CN, SO, and CS line profiles (solid lines) and the expanding shell fit (dotted lines). |
| Open with DEXTER | |
Table 4: Line parameters for each (nonmasering) transition.
3.2 CO maps
The spectra resulting from mapping the
![]() transition
in a region of 45
transition
in a region of 45
![]()
![]() 54
54
![]() around IK Tau
are shown in Fig. 8.
These spectra provide us with a tool for deriving
the source size as a function of radial velocity (see
Fig. 9).
The envelope of IK Tau roughly appears spherically
symmetric in
around IK Tau
are shown in Fig. 8.
These spectra provide us with a tool for deriving
the source size as a function of radial velocity (see
Fig. 9).
The envelope of IK Tau roughly appears spherically
symmetric in ![]() with a deconvolved extent at a half-peak integrated intensity of 20
with a deconvolved extent at a half-peak integrated intensity of 20
![]() .
The physical diameter of
the emission region is thus
.
The physical diameter of
the emission region is thus
![]() cm
where assuming a source
distance of 250 pc.
cm
where assuming a source
distance of 250 pc.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{00014fg4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg55.png)
|
Figure 4: Observed SiS and SiO line profiles (solid lines) and the expanding shell fit (dotted lines). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{00014fg5.eps} \vspace*{1mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg56.png)
|
Figure 5:
Observed |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{00014fg6.eps} \vspace*{0.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg57.png)
|
Figure 6:
321 GHz and 325 GHz |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{00014fg7.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg58.png)
|
Figure 7:
|
| Open with DEXTER | |
4 Modeling results
4.1 Physical structure of the envelope
The CO lines are among the best tools for estimating the global properties of circumstellar envelopes, since the abundance of CO is quite constant across the envelope, except for photo-dissociation effects at the outer edge (Mamon et al. 1988). The spatial distribution of CO was found from our mapping observation to be spherically symmetric (see Sect. 3.2). A detailed multiline non-LTE (non-local thermodynamic equilibrium) study of CO can therefore be used to determine the physical properties of the envelope.
The one-dimensional version of the Monte Carlo code RATRAN (Hogerheijde & van der Tak 2000) was used to simulate the CO lines' emission. The basic idea of the Monte Carlo method is to split the emergent radiative energies into photon packages, which perform a random walk through the model volume. This allows the separation of local and external contributions of the radiation field and makes it possible to calculate the radiative transfer and excitation of molecular lines. The Monte Carlo method for molecular line transfer has been described by Bernes (1979) for a spherically symmetric cloud with a uniform density. The code is formulated from the viewpoint of cells rather than photons. It shows accurate and fast performance even for high opacities (for more details see Hogerheijde & van der Tak 2000). The circumstellar envelope is assumed to be spherically symmetric, to be produced by a constant mass-loss rate, and to expand at a constant velocity. In the Monte Carlo simulation, typically 103 model photons are followed throughout the envelope until they escape. The region is divided into discrete grid shells, each with constant properties (density, temperature, molecular abundance, turbulent line width, etc.).
For the case of a steady-state, spherically symmetric outflow,
the gas
density as a function of radial distance from the center of the AGB
star is given by
where
The kinetic temperature is assumed to vary as
where T0 is the temperature at
The best-fit model is found by minimizing the total ![]() using
the
using
the ![]() statistic defined as
statistic defined as
where
where d.f. is the degree of freedom being N-p, with p the number of adjustable parameters. Figure 10 shows the
The best-fit model parameters are listed in Table 5.
The results of the model fits are shown in Fig. 11. In
Fig. 12
theoretical model predictions for the
![]() lines are shown with different
inner
radii, different T0, and
different outer radii.
Predictions for
lines are shown with different
inner
radii, different T0, and
different outer radii.
Predictions for
![]() with different T0
are
presented in Fig. 13.
Predictions for intensities at the observed offset positions were done
from the
best-fit model and are consistent with the size determined from the
observed
CO maps.
with different T0
are
presented in Fig. 13.
Predictions for intensities at the observed offset positions were done
from the
best-fit model and are consistent with the size determined from the
observed
CO maps.
Table 5: Parameters for the best-fit model to the observed 12CO and 13CO line profiles.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{00014fg8.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg77.png)
|
Figure 8:
Map of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{00014fg9.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg79.png)
|
Figure 9:
Contour maps of the |
| Open with DEXTER | |
As shown in Fig. 11,
the overall line profiles are fit very well
for the higher J transitions (
![]() ,
,
![]() ,
,
![]() ).
However, the model intensities of the IRAM
).
However, the model intensities of the IRAM
![]() and
and
![]() transitions
are somewhat higher than the observational data taken from
the literature, but the shapes fit satisfactorily. The predictions for
the
transitions
are somewhat higher than the observational data taken from
the literature, but the shapes fit satisfactorily. The predictions for
the ![]() line are still within the absolute uncertainty of the line, but this is
not the case for the
line are still within the absolute uncertainty of the line, but this is
not the case for the ![]() line. An obvious reason for this mismatch could be a problem with the
outer radius value. However, our sensitivity analysis (see
Fig. 12
and see discussion in next paragraphs) shows that, while lowering the
outer radius value indeed the total integrated intensity decreases, the
line shape is not reproduced well anymore. Since the relative
uncertainty (i.e., the line shape) is much lower than the absolute
intensity (i.e., the integrated intensity), we put more weight on the
reproduction of the line shapes. Moreover, we note that this is not the
first time that an incompatability of the IRAM fluxes with other
observed data is reported (e.g. Decin
et al. 2008).
The
line. An obvious reason for this mismatch could be a problem with the
outer radius value. However, our sensitivity analysis (see
Fig. 12
and see discussion in next paragraphs) shows that, while lowering the
outer radius value indeed the total integrated intensity decreases, the
line shape is not reproduced well anymore. Since the relative
uncertainty (i.e., the line shape) is much lower than the absolute
intensity (i.e., the integrated intensity), we put more weight on the
reproduction of the line shapes. Moreover, we note that this is not the
first time that an incompatability of the IRAM fluxes with other
observed data is reported (e.g. Decin
et al. 2008).
The ![]() line clearly shows a double-horn profile
and the best-fit results in a somewhat different T0
and a
different outer radius than for the 12CO data.
Nevertheless, the
best-fit value for T0
derived from
line clearly shows a double-horn profile
and the best-fit results in a somewhat different T0
and a
different outer radius than for the 12CO data.
Nevertheless, the
best-fit value for T0
derived from ![]() still gives a
reasonable fit to the
still gives a
reasonable fit to the ![]() line (Fig. 13).
As
shown in Fig. 13,
the intensities of the profiles do not
change so much with T0, but
the lines show a flat shape on top for
the lower temperatures (30 K and 40 K), and a double-horn shape at
higher temperatures.
line (Fig. 13).
As
shown in Fig. 13,
the intensities of the profiles do not
change so much with T0, but
the lines show a flat shape on top for
the lower temperatures (30 K and 40 K), and a double-horn shape at
higher temperatures.
As shown in Fig. 12,
the line shapes and intensities for all
transitions are not influenced much by the inner radius variations
since the ![]() emission dominanting the
spectra arises from regions farther out in the envelope. The outer
radius variations mainly affect the
emission dominanting the
spectra arises from regions farther out in the envelope. The outer
radius variations mainly affect the
![]() line,
which is formed farther out in the envelope than the other
line,
which is formed farther out in the envelope than the other
![]() transitions.
transitions.
4.2 Chemical abundance structure
As explained in the introduction, the density distribution of each
molecule is different, depending on the chemical processes taking
place:
in the envelope. The fractional abundance of a
species A is
usually specified as
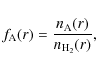
|
(8) |
where
A first-order assessment of the molecular abundance fractions
can be obtained by assuming that the envelope structure is in local
thermodynamic equilibrium. Assuming a spherically symmetric envelope,
the fractional abundance for an optically thin rotational line (
![]() )
of a linear rotor is given by Olofsson
et al. (1991):
)
of a linear rotor is given by Olofsson
et al. (1991):
where
![\begin{figure}
\par\includegraphics[width=7cm,clip]{00014fg10.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg98.png)
|
Figure 10:
Reduced |
| Open with DEXTER | |
The ![]() abundance with respect to
abundance with respect to ![]() is estimated using the equation given by Morris
et al. (1987):
is estimated using the equation given by Morris
et al. (1987):
where
A mass-loss rate of
![]()
![]() (see
Sect. 4.1,
and Teyssier et al. 2006)
was adopted to calculate the abundances. Since the outer radius of the
molecular emitting region can be quite uncertain for molecules for
which no observational maps exist, two different outer radii will be
used for these molecules (``case A'' and ``case B'').
For SiO, the value for the outer radius was taken to be
(see
Sect. 4.1,
and Teyssier et al. 2006)
was adopted to calculate the abundances. Since the outer radius of the
molecular emitting region can be quite uncertain for molecules for
which no observational maps exist, two different outer radii will be
used for these molecules (``case A'' and ``case B'').
For SiO, the value for the outer radius was taken to be
![]() cm
(case A) and
cm
(case A) and
![]() cm (case B), and for the other
molecules
cm (case B), and for the other
molecules
![]() cm (case A) and
cm (case A) and
![]() cm
(case B) was
assumed (Bujarrabal
et al. 1994). For all lines from this work, we
adopted expansion velocities from Table 4. For lines
taken from the literature (see Table 7),
an expanding velocity of 18
cm
(case B) was
assumed (Bujarrabal
et al. 1994). For all lines from this work, we
adopted expansion velocities from Table 4. For lines
taken from the literature (see Table 7),
an expanding velocity of 18
![]() is
used that is consistent with our non-LTE CO modeling of the
envelope.
For the
excitation temperatures,
is
used that is consistent with our non-LTE CO modeling of the
envelope.
For the
excitation temperatures, ![]() ,
rotational temperatures
as computed from Boltzmann diagrams are taken (see Table 6). Values for
the upper energy level and line strength (
,
rotational temperatures
as computed from Boltzmann diagrams are taken (see Table 6). Values for
the upper energy level and line strength (![]() )
can be found in Table 4.
)
can be found in Table 4.
4.2.1 Results
Using the method outlined above, the fractional abundances of all
molecules (except CO) were determined (see Table 7).
The most uncertain parameters used to derive the fractional abundances
are ![]() ,
D, and
,
D, and ![]() (the outer
radius). Here,
(the outer
radius). Here, ![]() is obtained from the rotational diagram
analysis, D is taken from the literature, and the
outer radius of
is obtained from the rotational diagram
analysis, D is taken from the literature, and the
outer radius of
![]() has been
adopted differently for each individual molecule. We
also note that our analysis assumes optically thin emission, which is
not always the case for the studied line profiles. The line opacity
is expected to be greater for higher J rotational
transitions, so
that lower J rotational transitions are expected to
better probe the
fractional abundance.
has been
adopted differently for each individual molecule. We
also note that our analysis assumes optically thin emission, which is
not always the case for the studied line profiles. The line opacity
is expected to be greater for higher J rotational
transitions, so
that lower J rotational transitions are expected to
better probe the
fractional abundance.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{00014fg11.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg111.png)
|
Figure 11:
Best-fit model spectra for the different CO transitions to the
available set of data at offset (0
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.2cm,angle=270,clip]{00014fg12.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg112.png)
|
Figure 12:
Model fits with different input parameters to the set of data at offset
(0
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.2cm,angle=270,clip]{00014fg13.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg113.png)
|
Figure 13:
Model fits of the |
| Open with DEXTER | |
Table 6: Rotational temperature and beam-averaged column density.
Table 7: Derived molecular fractional abundance for each transition.
5 Discussion
Table 8: Comparison of the derived molecular fractional abundances with other published results.
![\begin{figure}
\par\includegraphics[width=18.3cm,clip]{00014fg14.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg119.png)
|
Figure 14: Comparison of the molecular fractional abundances derived in this work (case A and case B-study) and values found in the literature (Lindqvist et al. 1988; Duari et al. 1999; Bujarrabal et al. 1994; Willacy & Millar 1997; Omont et al. 1993). The errors are estimated from the abundance variations for the different transitions (see Table 8). Panel a) gives a comparison to other observational results, panel b) to chemical model predictions. |
| Open with DEXTER | |
Table 8 and
Fig. 14
compare the average abundance of each molecule to values found in the
literature. Compared to observational results (Lindqvist et al. 1988;
Bujarrabal
et al. 1994; Omont et al. 1993),
our deduced fractional abundances agree within a factor of 3.5 for the
smaller outer radius (case A), and for the larger outer radius (case B)
within a factor of 10.
Compared to the predicted abundances from theoretical chemical models
by Willacy & Millar (1997)
and Duari et al. (1999),
we found that the predictions are comparable to our deduced values
(using the smaller outer radius, case A) within a factor of ![]() 3 for
3 for ![]() and
and ![]() .
Our deduced value for the SO, SiO, CN, and SiS fractional abundances
agree with the results of Willacy
& Millar (1997), but the predicted values by Duari et al. (1999) are
much lower. The
.
Our deduced value for the SO, SiO, CN, and SiS fractional abundances
agree with the results of Willacy
& Millar (1997), but the predicted values by Duari et al. (1999) are
much lower. The ![]() abundance from this work
is almost two orders of magnitude higher than the value predicted by Willacy & Millar (1997).
abundance from this work
is almost two orders of magnitude higher than the value predicted by Willacy & Millar (1997).
As noted above, the SiS abundance in the chemical models of Duari et al. (1999) is much lower than the observed value. The chemical models by Duari et al. (1999) focus on the inner envelope (within few stellar radii), while Willacy & Millar (1997) studied the chemical processes partaking in the outer envelope. The agreement between our deduced value for the fractional abundance of SiS and the predictions by Willacy & Millar (1997) suggests that SiS is formed in the outer envelope.
The deduced SO abundance is a factor ![]() 10 higher than the inner wind predictions by Duari et al. (1999),
but they agree with the outer wind predictions by Willacy & Millar (1997).
Willacy & Millar (1997)
assumed no SO injection, but only in-situ formation. CN is clearly
produced in the outer envelope, as a photo-dissociation product of HCN.
10 higher than the inner wind predictions by Duari et al. (1999),
but they agree with the outer wind predictions by Willacy & Millar (1997).
Willacy & Millar (1997)
assumed no SO injection, but only in-situ formation. CN is clearly
produced in the outer envelope, as a photo-dissociation product of HCN.
The abundance of ![]() found by Willacy & Millar
(1997) is
much lower than the observed ones. A value of
found by Willacy & Millar
(1997) is
much lower than the observed ones. A value of
![]() (case
A) means that SO2 contains 80% of the
solar sulfur value.
Willacy & Millar (1997)
suggest that SO2 may be formed in a different
part of the envelope compared to the other sulfur-bearing molecules,
for example, in shocks in bipolar outflow or in the inner envelope. An
indication for the typical behavior of
(case
A) means that SO2 contains 80% of the
solar sulfur value.
Willacy & Millar (1997)
suggest that SO2 may be formed in a different
part of the envelope compared to the other sulfur-bearing molecules,
for example, in shocks in bipolar outflow or in the inner envelope. An
indication for the typical behavior of
![]() also comes
from the line profiles; e.g., the
also comes
from the line profiles; e.g., the
![]() (14-14) line
is clearly narrower and
shifted to the red.
(14-14) line
is clearly narrower and
shifted to the red.
The SiO abundance derived in this study is close to the
abundance predicted
by the theoretical chemical models.
Cherchneff (2006)
investigated the nonequilibrium chemistry of the inner
winds of AGB stars and derived an almost constant, high SiO abundance
(about
![]() before the condensation of
dust). Duari
et al. (1999) and Willacy
& Millar (1997) derived
before the condensation of
dust). Duari
et al. (1999) and Willacy
& Millar (1997) derived
![]() and
and
![]() for
the inner and outer winds, respectively. Furthermore, González Delgado
et al. (2003) performed an extensive radiative
transfer analysis of circumstellar SiO emission from a large sample of
M-type AGB stars, where they adopted the assumption that the gas-phase
SiO abundance stays high close to the star, and farther out the SiO
molecular abundance fraction decreases due to absorption onto dust
grains. Their results show that the derived abundances are always
below the abundances expected from stellar atmosphere equilibrium
chemistry. For a mass-loss rate of
for
the inner and outer winds, respectively. Furthermore, González Delgado
et al. (2003) performed an extensive radiative
transfer analysis of circumstellar SiO emission from a large sample of
M-type AGB stars, where they adopted the assumption that the gas-phase
SiO abundance stays high close to the star, and farther out the SiO
molecular abundance fraction decreases due to absorption onto dust
grains. Their results show that the derived abundances are always
below the abundances expected from stellar atmosphere equilibrium
chemistry. For a mass-loss rate of
![]() /yr,
the equilibrium chemistry abundance of SiO is
/yr,
the equilibrium chemistry abundance of SiO is ![]() 3.5
3.5
![]() (Cherchneff
2006). Taking the scenario of depletion due to dust
formation into account, the higher excitation SiO(8-7) would probe a
higher SiO abundance. As seen in Table 7, the SiO(8-7)
indeed probes a
higher fractional abundance, although not significantly higher than
the other lines.
(Cherchneff
2006). Taking the scenario of depletion due to dust
formation into account, the higher excitation SiO(8-7) would probe a
higher SiO abundance. As seen in Table 7, the SiO(8-7)
indeed probes a
higher fractional abundance, although not significantly higher than
the other lines.
6 Conclusions
In this work, we present for the (sub)millimeter survey
for an oxygen-rich evolved AGB star, IK Tau, in order to study the
chemical composition in the envelope around the central target. An
extensive non-LTE radiative transfer analysis of circumstellar CO
was performed using a model with a power-law structure in temperature
and density and a constant expansion. The observed line profiles of
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() are fit very well
by our model, yielding a mass-loss rate of
are fit very well
by our model, yielding a mass-loss rate of
![]() /yr.
The line shapes and intensities for all
/yr.
The line shapes and intensities for all
![]() transitions are not influenced
much by variations
in the inner radius, which is understandable since the bulk of the
transitions are not influenced
much by variations
in the inner radius, which is understandable since the bulk of the
![]() emission is produced in the
outer envelope. The
intensities for the higher excitation CO lines depend strongly on the
assumed temperature but not on the value of the outer radius.
emission is produced in the
outer envelope. The
intensities for the higher excitation CO lines depend strongly on the
assumed temperature but not on the value of the outer radius.
For 7 other molecules (SiO, SiS, HCN, CS, CN, SO, and SO2) a fractional abundance study based on the assumption of LTE is performed. A full non-LTE analysis of all molecules is beyond the scope of this observational paper, but will be presented in a next paper (Decin et al. 2010). This study shows that IK Tau is a good laboratory to study the conditions in circumstellar envelopes around oxygen-rich stars with submillimeter-wavelength molecular lines. The improved abundance estimates of this study will allow refinements of the chemical models in the future.
Molecular line modeling predicts the abundance of each
molecule
as a function of radial distance from the star, although some ambiguity
about an inner or outer wind formation process often exists.
To get a clear picture of the different chemistry processes partaking
in the different parts in the envelope,
mapping observations for molecules other than CO should
be performed. Since most of the submillimeter emission from molecules
less abundant than CO probably arises from the inner part
of the envelope at 2-4
![]() ,
meaningful observations require interferometers such as the future
Atacama Large Millimeter Array (ALMA).
,
meaningful observations require interferometers such as the future
Atacama Large Millimeter Array (ALMA).
This publication is based on data acquired with the Atacama Pathfinder Experiment (APEX). APEX is a collaboration between the Max-Planck-Institut für Radioastronomie, the ESO, and the Onsala Space Observatory. We are grateful to the APEX staff for their assistance with the observations. L.D. acknowledges support from the Fund of Scientific Research, Flanders, Belgium.
References
- Alcolea, J., Pardo, J., & Bujarrabal, V. 1999, ApJ, 139, 461 [Google Scholar]
- Bachiller, R., Fuente, A., Bujarrabal, V., et al. 1997, A&A, 319, 235 [NASA ADS] [Google Scholar]
- Bernes, C. 1979, A&A, 73, 67 [NASA ADS] [Google Scholar]
- Boboltz, D., & Diamond, P. 2005, A&A, 625, 978 [Google Scholar]
- Bowers, P. F., Johnston, K. J., & Spencer, J. H. 1983, ApJ, 274, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Bowers, P. E., Johnston, K. J., & de Vegt, C. 1989, ApJ, 340, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Bujarrabal, V., & Alcolea, J. 1991, ApJ, 251, 536 [Google Scholar]
- Bujarrabal, V., Fuente, A., & Omont, A. 1994, ApJ, 285, 247 [Google Scholar]
- Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cherchneff, I. 2006, A&A, 456, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Blomme, L., Reyniers, M., et al. 2008, A&A, 484, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., De Beck, E., Brünken, S., et al. 2010, A&A, 516, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duari, D., Cherchneff, I., & Willacy, K. 1999, ApJ, 341, L47 [Google Scholar]
- Fukasaku, S., Hirahara, Y., Masuda, A., et al. 1994, ApJ, 437, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Gautschy-Loidl, R., Höfner, S., Jørgensen, U., & Hron, J. 2004, A&A, 422, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Scoville, N. 1976, ApJ, 205, 144 [Google Scholar]
- González Delgado, D., Olofsson, H., Kerschbaum, F., et al. 2003, A&A, 411, 123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güsten, R., Nyman, L., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. 1996, A&ARv, 7, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, D. D. S., Bester, M., Danchi, W. C., et al. 1997, ApJ, 490, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Heyminck, S., Kasemann, C., Güsten, R., et al. 2006, A&A, 454, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hogerheijde, M., & van der Tak, F. 2000, ApJ, 362, 697 [Google Scholar]
- Lane, A., Johnston, K., Bowers, P., et al. 1987, ApJ, 323, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Lindqvist, M., Nyman, L.-A., Olofsson, H., & Winnberg, A. 1988, ApJ, 205, L15 [Google Scholar]
- Lucas, R., Bujarrabal, V., Guilloteau, S., et al. 1992, ApJ, 262, 491 [Google Scholar]
- Mamon, G. A., Glassgold, A. E., & Huggins, P. J. 1988, ApJ, 328, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Marvel, K. 2005, AJ, 130, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M., Guilloteau, S., Lucas, R., & Omont, A. 1987, ApJ, 321, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, H., Lindqvist, M., Nyman, L.-A., et al. 1991, ApJ, 245, 611 [Google Scholar]
- Olofsson, H., Lindqvist, M., Nyman, L., & Winnberg, A. 1998, A&A, 329, 1059 [NASA ADS] [Google Scholar]
- Omont, A., Lucas, R., Morris, M., & Guilloteau, S. 1993, ApJ, 267, 490 [Google Scholar]
- Ridgway, S. T., Hall, D. N. B., Wojslaw, R. S., Kleinmann, S. G., & Weinberger, D. A. 1976, Nature, 264, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Risacher, C., Vassilev, V., Monje, R., et al. 2006, A&A, 454, L17R [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, N., Humphreys, R., Davidson, K., et al. 2001, AJ, 121, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Sopka, R. J., Hildebrand, R., Jaffe, D. T., et al. 1985, ApJ, 294, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, D., Hernandez, R., Bujarrabal, V., et al. 2006, A&A, 450, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willacy, K., & Millar, T. 1997, A&A, 324, 237 [NASA ADS] [Google Scholar]
- Wing, R., & Lockwood, G. 1973, ApJ, 184, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamura, I., Onaka, T., Kamijo, F., et al. 1996, ApJ., 465, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L., Milam, S., Apponi, A., & Woolf, N. 2004, Nature, 447, 1094 [Google Scholar]
- Zuckerman, B. 1987, IAUS, 120, 345 [Google Scholar]
Footnotes
- ...
APEX
![[*]](/icons/foot_motif.png)
- This publication is based on data acquired with the Atacama Pathfinder Experiment (APEX). APEX is a collaboration between the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory.
- ... GILDAS
![[*]](/icons/foot_motif.png)
- GILDAS is a collection of software oriented toward (sub-) millimeter radio astronomical applications developed by IRAM (see more details on http://www.iram.fr/IRAMFR/GILDAS).
All Tables
Table 1: Overview of the molecular line transitions observed with APEX.
Table 2: Beam efficiencies for the different receivers.
Table 3: Line parameters for the detected maser lines.
Table 4: Line parameters for each (nonmasering) transition.
Table 5: Parameters for the best-fit model to the observed 12CO and 13CO line profiles.
Table 6: Rotational temperature and beam-averaged column density.
Table 7: Derived molecular fractional abundance for each transition.
Table 8: Comparison of the derived molecular fractional abundances with other published results.
All Figures
![\begin{figure}
\par\includegraphics[width=5cm,clip]{00014fg1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg42.png)
|
Figure 1:
Observed |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{00014fg2.eps}
\vspace*{-2mm} \end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg43.png)
|
Figure 2:
Observed HCN, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{00014fg3.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg50.png)
|
Figure 3: Observed CN, SO, and CS line profiles (solid lines) and the expanding shell fit (dotted lines). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{00014fg4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg55.png)
|
Figure 4: Observed SiS and SiO line profiles (solid lines) and the expanding shell fit (dotted lines). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{00014fg5.eps} \vspace*{1mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg56.png)
|
Figure 5:
Observed |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{00014fg6.eps} \vspace*{0.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg57.png)
|
Figure 6:
321 GHz and 325 GHz |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{00014fg7.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg58.png)
|
Figure 7:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{00014fg8.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg77.png)
|
Figure 8:
Map of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{00014fg9.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg79.png)
|
Figure 9:
Contour maps of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{00014fg10.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg98.png)
|
Figure 10:
Reduced |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{00014fg11.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg111.png)
|
Figure 11:
Best-fit model spectra for the different CO transitions to the
available set of data at offset (0
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.2cm,angle=270,clip]{00014fg12.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg112.png)
|
Figure 12:
Model fits with different input parameters to the set of data at offset
(0
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.2cm,angle=270,clip]{00014fg13.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg113.png)
|
Figure 13:
Model fits of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18.3cm,clip]{00014fg14.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14094-10/Timg119.png)
|
Figure 14: Comparison of the molecular fractional abundances derived in this work (case A and case B-study) and values found in the literature (Lindqvist et al. 1988; Duari et al. 1999; Bujarrabal et al. 1994; Willacy & Millar 1997; Omont et al. 1993). The errors are estimated from the abundance variations for the different transitions (see Table 8). Panel a) gives a comparison to other observational results, panel b) to chemical model predictions. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



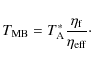
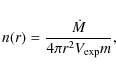
![\begin{displaymath}
T=T_{0}\left[\frac{10^{16}}{r({\rm cm})}\right]^{\alpha}+T_{{\rm bg}}~,
\end{displaymath}](/articles/aa/full_html/2010/08/aa14094-10/img62.png)
![\begin{displaymath}
\chi^2=\sum_{i=1}^{N}{\frac{[I_{{\rm mod}}-I_{{\rm obs}}]^2}{\sigma^2}},
\end{displaymath}](/articles/aa/full_html/2010/08/aa14094-10/img64.png)
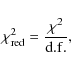
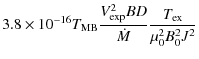
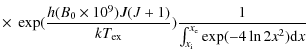
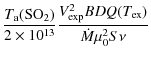
![$\displaystyle \times~ \frac{1}{\exp[-1.44E_{{\rm u}}/T_{{\rm ex}}]}\frac{1}{\int^{x_{\rm e}}_{x_{\rm i}}\exp(-4\ln{2}x^{2}){\rm d}x}$](/articles/aa/full_html/2010/08/aa14094-10/img101.png)