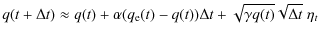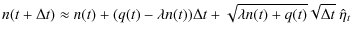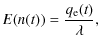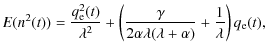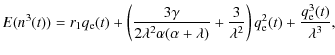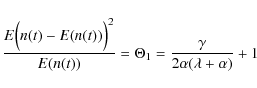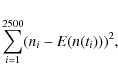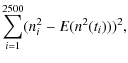EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 516 (June-July 2010) A&A, 516 (2010) A114 Full HTML
Free Access
Issue
A&A
Volume 516, June-July 2010
Article Number A114
Number of page(s) 5
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913978
Published online 22 July 2010
A&A 516, A114 (2010)

Derivation of stochastic differential equations for sunspot activity

E. J. Allen - C. Huff

Department of Mathematics and Statistics, Texas Tech University, Lubbock, TX 79409-1042, USA

Received 28 December 2009 / Accepted 12 April 2010

Abstract
Aims. A system of stochastic differential equations (SDEs) is derived for sunspot activity.
Methods. The SDE derivation relies on basic assumptions about a cyclic but randomly varying source of sunspots and on an average lifetime for sunspots. The SDE model parameters are fit to sunspot data for three different 11-year sunspot cycles. Results of calculations for the SDE system are compared with the data for each of the three sunspot cycles.
Results. Certain characteristics are shared by both the SDE model and the data. In particular, the second and third moments about the mean divided by the mean are similar for the SDE system and for the data and appear to be approximately constant over the cycle.

Key words: Sun: activity - sunspots

1 Introduction

There has been much interest in developing mathematical models to describe sunspot activity as exemplified by the investigations of Charbonneau (2005), Haviland (1996), Orfila et al. (2002), Sello (2003), or Spiegel & Wolf (1987). It is now generally accepted that magnetic cycles in the Sun are generated by a solar dynamo produced through nonlinear interactions between solar plasmas and magnetic fields as reviewed by Choudhuri (2000). It appears that the average or large-scale features of the solar cycle can be explained by solar dynamo models (Cameron & Schüssler 2007; Charbonneau 2005; Choudhuri 2000; Dikpati et al. 2006, 2007; or Passos 2008). However, as pointed out, for example by Passos (2008), the variation in the amplitude and period in the 11-year cycle is still difficult to understand. Also, as indicated by Letellier et al. (2006) or Usoskin (2008), it still appears that uncertainty exists about whether the irregularities in the sunspot cycle can be best described by using deterministic or stochastic models, that is, whether the observations favor an explanation in terms of chaotic dynamics or stochastic dynamics. The chaotic behavior of the cycle has been studied with some success, for example, by Jevtic et al. (2001), Letellier et al. (2006), or Orfila et al. (2002). Chaotic processes involve deterministic (predictable) dynamical systems that are sensitive to initial conditions and can appear to be random. In principle, the solar dynamo is deterministic, hence, predictable. In practice, however, the variables in this hydromagnetic process may be inaccurately known so random models may be useful.

In the present investigation, simple, basic assumptions are made that involve the presence of a cyclic but randomly varying solar source of sunspots along with an average lifetime of sunspots. Using these basic assumptions, a system of two stochastic differential equations (SDEs) is derived for the dynamics of the sunspot source and for the number of sunspots.

The parameters in the SDE model are estimated by a least-squares method using sunspot data for three different 11-year cycles. The derived model is compared with the sunspot data for the three 11-year cycles. It is observed that certain characteristics are shared by both the SDE model and the data. In particular, the second and third moments about the mean divided by the mean are similar for the SDE model and the data and appear to be approximately constant over the sunspot cycle. The results indicate that the dynamics of a simple stochastic model, derived from a few basic assumptions, have certain features in common with the complex dynamics of sunspot activity.

2 Sunspot data

The data used in this research were obtained from the United States National Geophysical Data Center, NGDC, which provides long-term scientific data stewardship for the nation's geophysical data. Daily sunspot data were obtained from NGDC for the three 11-year cycles from 1943 to 1953, 1954 to 1964, and 1965 to 1975. The three solar cycles were chosen somewhat arbitrarily in the present investigation. However, the cycles were selected to be three successive cycles occurring within the last century with somewhat different levels of sunspot activity.

There are few sunspots at the beginning and end of each 11-year sunspot cycle with a corresponding increase in noise in the sunspot data. To reduce the influence of this noisy data in estimating model parameters for each 11-year cycle, only 2500 days of data (approximately 7 years of data), with the maximum activity of the cycle located at the center of the 2500 days, are used to fit the model parameters for each cycle.

In Fig. 1, the daily sunspot data is displayed for 2500 days about the maximum activity for each of the three 11-year cycles.

\begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg1a.e... ...eps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg1c.eps}\end{figure} Figure 1:

From left to right, 1943-1953, 1954-1964, and 1965-1975 sunspot data with least squares curves.

Open with DEXTER
The least squares curves in the figures were estimated for each cycle by fitting a cosine curve, $a_{1}(a_2 + \cos (a_{3}t+a_{4}))$, to the data. A cosine fit to the number of sunspots was chosen based on the curve fit discussed by Haviland (1996). For example, the cycle 1965-1975 of Fig. 1 gave the curve $45.16(1.4776 + \cos (0.00174t+3.448))$where t is in days. For this cycle, the maximum occurred at approximately day 1630. Analogous procedures were applied to the other two sunspot cycles to avoid noisy data. For 1965-1975 the maximum occurred near day 1700, and for 1943-1953 the maximum occurred near day 2050. In the remainder of this investigation, the data for each sunspot cycle is restricted to the 2500 days about the maximum sunspot activity and the model parameters are estimated based on these 2500 days.

Table 1:   Probabilities for the changes in the sunspot source for small $\Delta t$.

3 SDE model derivation

In this section, a derivation is presented of an SDE system that models the number of sunspots with time. There are two basic assumptions made in this derivation. It is hypothesized that there exists a cyclic but randomly varying source of sunspots and, second, it is assumed that sunspots exponentially decay, i.e., sunspots have an average lifetime inversely proportional to their decay rate. To derive the SDE model, it is useful to define a few variables:

q(t):
randomly varying source of sunspots;
n(t):
the number of sunspots at time t;
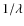$1/\lambda$:
average lifetime of a sunspot in days;
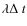$\lambda \Delta~ t$:
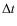the probability that a sunspot decays in time $\Delta t$;
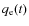$q_{\rm e}(t)$:
the mean or equilibrium sunspot source.
The sunspot source, q(t), mathematically models, in a simple way, the rate of formation of sunspots arising from the complex physical processes occurring within in the Sun. That is, the rate of formation of sunspots due to strong magnetic fields generated within the Sun is included in the sunspot source q(t). In addition, in the present investigation, the average lifetime, $1/\lambda$, of a sunspot is taken as 14 days (see, for example, Kopecký 1960 and Taylor 1992). The equilibrium or mean sunspot source is assumed to have a cosine shape, i.e., $q_{\rm e}(t) = r( a + \cos (bt+c))= E (q(t))$. In this expression, $2 \pi/b$ is the solar cycle period in days, values of c and a are determined from the shape of the cycle, and the value of r is determined from the level of sunspot activity.

To develop the SDE model for sunspot activity, the possible changes in the sunspot source and in the number of sunspots are determined for a small interval of time $\Delta t$. (See, for example, Allen 2007, Allen et al. 2008; or Allen 2003, for a description of a procedure to derive accurate SDE models.) In Table 1, the changes and probabilities in the sunspot source and in the number of sunspots are listed for a small time interval. This table defines a discrete stochastic model for the sunspot source and for the number of sunspots. The forms of the probability terms are selected so that the sunspot source does not wander randomly away from the equilibrium sunspot source $q_{\rm e}(t)$. In particular, the probability terms $\alpha(q_{\rm e}(t)-q(t))/2$ result in a drift of the sunspot source, q(t), toward the equilibrium source $q_{\rm e}(t)$, i.e., $\alpha(q_{\rm e}(t)-q(t))/2$ represents the tendency for the sunspot source to approach $q_{\rm e}(t)$. The $\gamma q(t)/2$ term represents a purely random component in sunspot source changes. For example, if $\gamma =0$, the source strength q(t) adjusts to $q_{\rm e}(t)$ at a rate determined by the magnitude of $\alpha$. Lower values of $\alpha$ and higher values of $\gamma$ imply increased randomness in sunspot activity. For the number of sunspots, the parameter $\lambda$ represents the rate of decay of the sunspots.

An Itô SDE system for sunspot activity is developed directly from Tables 1 and 2 and has the form:

    $\displaystyle {\rm d}q(t)= \alpha(q_{\rm e}(t)-q(t)) ~ {\rm d}t + \sqrt{\gamma q(t)} \; {\rm d} (1)
    $\displaystyle {\rm d}n(t) = (-\lambda n(t) + q(t)) ~ {\rm d}t + \sqrt{\lambda  

where W1(t) and W2(t) are independent Wiener processes and $q_{\rm e}(t) = r(a + \cos(bt+c))$ is the equilibrium or average sunspot source. A Wiener process, W(t), is almost surely continuous and, for 0 < t1 < t2 <t3, W(t2)-W(t1) is normally distributed with mean 0 and variance t2 -t1 and is independent of W(t3)-W(t2). (See, for example, Gard 1987; or Kloeden & Platen 1992.) Notice that the SDE for the sunspot source is a form of Ornstein-Uhlenbeck stochastic process, i.e., a mean-reverting process. To see that (1) is an accurate model, the Euler-Maruyama approximation (Gard 1987; Kloeden & Platen 1992; or Kloeden et al. 1994) to Eq. (1) gives for small $\Delta t$:
    $\displaystyle q(t + \Delta t) \approx q(t) + \alpha(q_{\rm e}(t)-q(t)) \Delta t + (2)
    $\displaystyle n(t + \Delta t) \approx n(t) + (q(t) - \lambda n(t)) \Delta t + \sqrt{\lambda  

where $\eta_t$ and $\hat \eta_t$ are independent normally distributed numbers with zero mean and unit variance. Approximation (2) has the same mean changes and mean square changes to order $(\Delta t)^2$ as the discrete model defined by Tables 1 and 2 indicating an accurate SDE model as explained, for example, by Allen (2007) and Huff (2009). Indeed, to order $(\Delta t)^2$, both (2) and Tables 1 and 2 give $E(\Delta q) = \alpha (q_{\rm e}(t) - q(t))\Delta t$, $E((\Delta q)^2) = \gamma q(t)\Delta t$, $E(\Delta n) = (q(t)-\lambda n(t))\Delta t$, and $E((\Delta n)^2) = (q(t)+\lambda n(t))\Delta t$.

Table 2:   Probabilities for the changes in the number of sunspots for small $\Delta t$.

For data analysis and comparison purposes, it is useful to determine mean values of certain quantities for SDE model (1). To find these mean quantities, Itô's formula (Gard 1987; or Kloeden & Platen 1992) is applied to Eq. (1). The following ordinary differential equations are then obtained for expectations of several different powers of q and n where, e.g., E(q2(t)) =E(q2) is the expectation of q2(t):

\begin{eqnarray*}&& \frac{{\rm d}E(q(t))}{{\rm d}t} = \alpha(q_{\rm e}(t)-E(q(t)...


These differential equations are solved assuming that $\alpha$ is much greater than b, as is found to be the case for the sunspot data for which $\alpha/b > 30$. The assumption that $\alpha$ is much greater than b implies that random fluctuations in the source return to the equilibrium source curve, $q_{\rm e}(t)$, at a faster rate than the frequency of the sunspot cycle. Solving these equations under this assumption yields the following equilibrium values for the first, second, and third moments for the number of sunspots:
    $\displaystyle E(n(t)) = \frac{q_{\rm e}(t)}{\lambda},$ (3)
    $\displaystyle E(n^2(t)) = \frac{q_{\rm e}^2(t)}{\lambda^2} +  
    $\displaystyle E(n^3(t)) =  

where $\displaystyle{r_1 = \frac{\gamma^2}{\lambda \alpha^2(\alpha+2\lambda)(\alpha+\lambda)} + \frac{3 \gamma}{2 \alpha \lambda (\alpha+\lambda)} + \frac{1}{\lambda}}.$

Using (3), second and third moments about the mean divided by the mean are calculated as:

\begin{displaymath}\frac{E\Big(n(t) -E(n(t))\Big)^2}{E(n(t))} = \Theta_1 = (4)

and

\begin{displaymath}\frac{E\Big(n(t)-E(n(t))\Big)^3}{E(n(t))}= 1+\frac{\gamma}{\a... ...\frac{\gamma}{\alpha(\alpha+2\lambda)}+\frac{3}{2}\right)\cdot \end{displaymath} (5)

Equations (4) and (5) indicate that these ratios are constant independent of time t during the cycle for the SDE model, assuming that $\alpha$ is much greater than b. That is, Eqs. (4) and (5) imply that the variance and the third moment about the mean are both proportional to the mean number of sunspots throughout the cycle. As shown later, the sunspot data also appears to share this characteristic. Thus, the simple stochastic SDE model is consistent in this manner with the data. Furthermore, it can also be shown that the fourth moment about the mean divided by the mean is not constant with respect to time in the cycle for either the SDE model or for the data.

4 Estimation of model parameters

By considering Eq. (1), the parameters r, a, b, c, $\alpha$, $\gamma$, and $\lambda$ need to be estimated to define the SDE model. The parameter $\lambda$ is taken as 1/14days-1 as stated in the previous section. As $ E(n(t)) = q_{\rm e}(t)/ \lambda = r(a+ \cos (bt+c))/\lambda$, the values of r, a, b, c are estimated by fitting a cosine curve to the number of sunspots for each cycle for 2500 days around the peak sunspot activity. Using a least squares procedure, the estimated values for r, a, b, c for each of the three sunspot cycles are given in Table 3, and since t is in days, then b has units of 1/day. For these parameter values, the equilibrium sunspot source, $q_{\rm e}(t)$, satisfies $q_{\rm e}(t) \ge 3$ for most values of time tbetween 0 and 2500.

Table 3:   Estimated values of r, a, b, c for $E(n(t))= (r(a + \cos (bt+c))/\lambda$.

To estimate the parameters $\alpha$ and $\gamma$, it is assumed that $\gamma$ is equal to $ k \alpha$ where k is a constant which is the same for all sunspot cycles. By considering SDE (1) for the sunspot source, i.e., ${\rm d}q(t)= \alpha( q_{\rm e}(t) -q(t)) ~ {\rm d}t + \sqrt{\gamma q(t)} \; {\rm d} W_{1}(t)$, then if $q_{\rm e}(t) \ge 3$, values of $\gamma \le 6 \alpha$ ensure that the sunspot source, q(t), is nonnegative with probability unity as inferred from Allen (2007). In addition, if $\gamma \le 2 \alpha$, test simulations with the SDE model (1), with estimated values of $\alpha$, do not produce good comparisons with the sunspot data. To satisfy these constraints on $\gamma$, i.e., $2 \alpha \le \gamma \le 6 \alpha$, $\gamma$ is set equal to $4 \alpha$ in the present investigation. (This is not a strong assumption as the results of the SDE model are relatively insensitive to values of $\gamma / \alpha$ between 2 and 6.) Also, assuming a fixed ratio of $\gamma / \alpha$, expression (4) for $\Theta_1$ indicates greater variability in the sunspot activity with smaller estimated values of $\alpha$ and $\gamma$.

To estimate $\alpha$, assuming a fixed ratio of $\gamma / \alpha$, the value of $\Theta_1$ in Eq. (4) is estimated using a least squares procedure for each sunspot cycle. Specifically, a least squares procedure is first used to estimate the parameters r,a,b, and c by minimizing for each cycle

\begin{displaymath}\sum^{2500}_{i=1}(n_{i}- E(n(t_i)))^2, \end{displaymath} (6)

where ni is the ith data value for the number of sunspots and $E(n(t_i))=q_{\rm e}(t_i)/ \lambda$. Next, a least squares procedure is used to find $\Theta_1$, and hence $\alpha$, by minimizing the expression
$\displaystyle \sum^{2500}_{i=1}(n^2_{i}- E(n^2(t_i)))^2,$ (7)

where, by (3), $E(n^2(t_i))= (E(n(t_i)))^2 + \Theta_1 E(n(t_i))$. Minimiz- ing (7) for $\Theta_1$ gives

\begin{displaymath}\frac{\sum^{2500}_{i=1}(n_{i}^2f_{i}-f_{i}^3)}{\sum^{2500}_{i... ...ta_1 = \left(\frac{\gamma}{2\alpha(\lambda+\alpha)} + 1\right) \end{displaymath} (8)

where $f_i= q_{\rm e}(t_i)/\lambda$. Finally, as $\gamma = 4 \alpha$, then $\Theta_{1} = 2/ (\alpha+\lambda)+1$ can be solved for $\alpha$ for each sunspot cycle. Estimated values for $\alpha$and $\gamma$ are given in Table 3 for each sunspot cycle.

The lower values of $\alpha$ and $\gamma$ for the 1943-1953 cycle indicate that the sunspot activity for that cycle experienced a greater level of variability than the other two cycles. Indeed, the estimated values for $\Theta_1$ for the three successive cycles are 16.76, 12.13, and 12.10, respectively, indicating that the 1943-1953 cycle experienced greater variability in the sunspot activity than the other two cycles. Estimated values of a, b, and c are approximately the same for all three cycles indicating a similar shape in the sunspot levels throughout the cycles. The value of r changes for each cycle and is related to the occurrence of different levels of sunspot activity for each cycle.

5 Comparisons between SDE model and data

In this section, comparisons between the SDE model and the data are described. In particular, similarities between the data and the SDE model are discussed such as the behavior of the second and third moments about the mean divided by the mean.

The data for the three sunspot cycles are compared in Figs. 1-4. The sunspot data along with least squares curves are given in Fig. 1. In Fig. 1, the pronounced maximum activity near day 1250 is clearly seen. In Figs. 2-4, the sunspot data for each cycle is analyzed for fifty 50-day intervals for each 2500-day interval. In Fig. 2, the mean number of sunspots is plotted for each of the fifty 50-day periods. Ratios of second and third moments about the mean divided by the mean are obtained for each 50-day period and are plotted in Figs. 3 and 4. From these figures, no pronounced maximum occurs in the ratios of second and third moments about the mean divided by the mean. Indeed, although variations are present throughout the 2500 days, these ratios appear to be roughly constant for each sunspot cycle.

\begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg2a.e... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg2c.eps} \end{figure} Figure 2:

Average number of sunspots for 1943-1953, 1954-1964, and 1965-1975 cycles for fifty 50-day periods.

Open with DEXTER
\begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg3a.e... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg3c.eps} \end{figure} Figure 3:

Ratio of second moment about the mean to the mean for fifty 50-day periods for the three successive sunspot cycles.

Open with DEXTER
\begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg4a.e... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg4c.eps} \end{figure} Figure 4:

Ratio of third moment about the mean to the mean for fifty 50-day periods for the three successive sunspot cycles.

Open with DEXTER

Next, the SDE model is studied. First, SDE system (1), with the estimated parameter values of Table 3, are simulated for 2000 sample paths using the Euler-Maruyama method. Two sample paths and the mean path are given in Fig. 5 for each sunspot cycle. It is clear that the simulations are similar to the sunspot data of Fig. 1. As derived in Eqs. (4) and (5), the SDE system has the feature that the ratios of second and third moments about the mean divided by the mean are constant, independent of time, throughout the sunspot cycle. Calculated ratios of second and third moments about the mean to the mean for 2000 sample paths of the SDE system are given in Figs. 6 and 7 where it is clearly illustrated that the calculated ratios are constant and independent of time in the three sunspot cycles. The ratios in these figures are averaged over 2000 sample paths and, thus, have relatively little variability over the 2500 days.

\begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg5a.e... ...eps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg5c.eps}\end{figure} Figure 5:

Two calculated sample paths and average path for the SDE model for each cycle.

Open with DEXTER
\begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg6a.e... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg6c.eps} \end{figure} Figure 6:

Average calculated ratio of second moment about the mean to the mean for 2000 sample paths of the SDE model for each cycle.

Open with DEXTER
\begin{figure} \par\includegraphics[height=1.60in,width=1.154in,clip]{13978fg7a.... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg7c.eps} \end{figure} Figure 7:

Average calculated ratio of third moment about the mean to the mean for 2000 samples paths of the SDE model for each cycle.

Open with DEXTER
For each of the three sunspot cycles, ratios of second and third moments about the mean to the mean were calculated for the sunspot data over the 2500 days. A comparison of the ratios obtained from the data and from the SDE model are given in Table 4.

Table 4:   Ratios of second and third moments about the mean divided by the mean, R2 and R3, for the data and for the SDE model using 2000 sample paths.

The ratios of the second and third moments about the mean to the mean for the SDE model and for the data are similar. The values for the 1954-1964 sunspot cycle differ by about 30%. However, for sunspot cycles 1943-1953 and 1954-1964, the ratios of second moment about the mean to the mean are quite close and differ by less than 10%.

6 Summary and conclusions

A simple SDE model for sunspot activity is derived. In this derivation, basic assumptions are made about a sunspot source and lifetime of sunspots. The primary assumption in the derivation is that the source of sunspots randomly varies about a periodic mean sunspot source. A second assumption is that sunspots decay with an average lifetime of 14 days. (In a more detailed SDE derivation, the lifetime of sunspot groups may be treated separately from the lifetime of individual sunspots.) It is shown for the SDE system that the second and third moments about the mean divided by the mean are constant, independent of time in the cycle.

The parameters of the SDE system are estimated for three successive sunspot cycles. Only 2500 days of highest sunspot activity for each cycle is used to avoid noisy data.

The SDE model is compared with the data for three sunspot cycles. An unexpected and interesting result is that certain similarities are shared by the SDE model and by the data. In particular, it appears that the variance and the third moment about the mean are both approximately proportional to the mean number of sunspots throughout the cycle for both the SDE model and the sunspot data.

Acknowledgements
The authors are grateful to the anonymous reviewer and to the editor, Hardi Peter, for their helpful comments.



References

  1. Allen, E. J. 2007, Modeling With Itô Stochastic Differential Equations (Dordrecht: Springer) [Google Scholar]
  2. Allen, E. J., Allen, L. J. S., Arciniega, A., & Greenwood, P. E. 2008, Stoch Anal Appl, 26, 274 [Google Scholar]
  3. Allen, L. J. S. 2003, An Introduction to Stochastic Processes with Applications to Biology (Upper Saddle River, New Jersey: Pearson Education Inc.) [Google Scholar]
  4. Cameron, R., & Schüssler, M. 2007, ApJ, 659, 801 [NASA ADS] [CrossRef] [Google Scholar]
  5. Charbonneau, P. 2005, Living Rev. Solar Phys., 2, http://solarphysics.livingreviews.org/Articles/ [Google Scholar]
  6. Choudhuri, A. R. 2000, J. Astrophys. Astron, 21, 373 [NASA ADS] [Google Scholar]
  7. Dikpati, M., de Toma, G., & Gilman, P. A. 2006, Geophys. Res. Lett., 33, L05102 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dikpati, M., Gilman, P. A., de Toma, G., & Ghosh, S. S. 2007, Sol. Phys., 245, 1 [NASA ADS] [CrossRef] [Google Scholar]
  9. Gard, T. C. 1987, Introduction to Stochastic Differential Equations (New York: Marcel Decker) [Google Scholar]
  10. Haviland, R. P. 1996, IEEE Antennas and Propagation Magazine, 37, 38 [NASA ADS] [CrossRef] [Google Scholar]
  11. Huff, C. 2009, Thesis in Mathematics and Statistics, Texas Tech University [Google Scholar]
  12. Jevtic, N., Schweitzer, J. S., & Cellucci, C. J. 2001, A&A, 379, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Kloeden, P. E., & Platen, E. 1992, Numerical Solution of Stochastic Differential Equations (New York: Springer-Verlag) [Google Scholar]
  14. Kloeden, P. E., Platen, E., & Schurz, H. 1994, Numerical Solution of SDE Through Computer Experiments (Berlin: Springer) [Google Scholar]
  15. Kopecký, M. 1960, BAC, 11, 110 [NASA ADS] [Google Scholar]
  16. Letellier, C., Aguirre, L. A., Maquet, J., & Gilmore, R. 2006, A&A, 449, 379 [Google Scholar]
  17. NGDC, National Geophysical Data Center, Boulder, Colorado, http://www.ngdc.noaa.gov/stp/SOLAR/ftpsunspotnumber.html [Google Scholar]
  18. Orfila, A., Ballester, J. L., Oliver, R., Alvarez, A., & Tintore, J. 2002, A&A, 386, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Passos, D., & Lopes, I. 2008, ApJ, 686, 1420 [NASA ADS] [CrossRef] [Google Scholar]
  20. Sello, S. 2003, A&A, 410, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Spiegel, E. A., & Wolf, A. N. 1987, Annals of the New York Academy of Sciences, 497, 55 [NASA ADS] [CrossRef] [Google Scholar]
  22. Taylor, P. O. 1992, Observing the Sun (New York: Cambridge University Press) [Google Scholar]
  23. Usoskin, I. G. 2008, Living Rev. Solar Phys., 5, http://solarphysics.livingreviews.org/Articles/ [Google Scholar]

All Tables

Table 1:   Probabilities for the changes in the sunspot source for small $\Delta t$.

Table 2:   Probabilities for the changes in the number of sunspots for small $\Delta t$.

Table 3:   Estimated values of r, a, b, c for $E(n(t))= (r(a + \cos (bt+c))/\lambda$.

Table 4:   Ratios of second and third moments about the mean divided by the mean, R2 and R3, for the data and for the SDE model using 2000 sample paths.

All Figures

  \begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg1a.e... ...eps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg1c.eps}\end{figure} Figure 1:

From left to right, 1943-1953, 1954-1964, and 1965-1975 sunspot data with least squares curves.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg2a.e... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg2c.eps} \end{figure} Figure 2:

Average number of sunspots for 1943-1953, 1954-1964, and 1965-1975 cycles for fifty 50-day periods.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg3a.e... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg3c.eps} \end{figure} Figure 3:

Ratio of second moment about the mean to the mean for fifty 50-day periods for the three successive sunspot cycles.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg4a.e... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg4c.eps} \end{figure} Figure 4:

Ratio of third moment about the mean to the mean for fifty 50-day periods for the three successive sunspot cycles.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg5a.e... ...eps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg5c.eps}\end{figure} Figure 5:

Two calculated sample paths and average path for the SDE model for each cycle.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=1.60in,width=1.14in,clip]{13978fg6a.e... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg6c.eps} \end{figure} Figure 6:

Average calculated ratio of second moment about the mean to the mean for 2000 sample paths of the SDE model for each cycle.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=1.60in,width=1.154in,clip]{13978fg7a.... ...ps}\includegraphics[height=1.60in,width=1.14in,clip]{13978fg7c.eps} \end{figure} Figure 7:

Average calculated ratio of third moment about the mean to the mean for 2000 samples paths of the SDE model for each cycle.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.