| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913904 | |
| Published online | 22 June 2010 | |
Numerical and semi-analytic core mass distributions in supersonic isothermal turbulence
W. Schmidt1,2 - S. A. W. Kern2,3 - C. Federrath3,4 - R. S. Klessen4
1 - Institut für Astrophysik, Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
2 - Lehrstuhl für Astronomie, Institut für Theoretische Physik und
Astrophysik, Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
3 -
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
4 - Zentrum für Astronomie, Institut für Theoretische Astrophysik,
Universität Heidelberg, Albert-Ueberle-Str. 2, 69120 Heidelberg,
Germany
Received 18 December 2009 / Accepted 19 February 2010
Abstract
Context. Supersonic turbulence in the interstellar medium
plays an important role in the formation of stars. The origin of this
observed turbulence and its impact on the stellar initial mass function
(IMF) still remain open questions.
Aims. We investigate the influence of the turbulence forcing on
the mass distributions of gravitationally unstable cores in simulations
of isothermal supersonic turbulence.
Methods. Data from two sets of non-selfgravitating hydrodynamic
FLASH3 simulations with external stochastic forcing are analysed, each
with static grid resolutions of 2563, 5123 and 10243
grid points. The first set applies solenoidal (divergence-free)
forcing, while the second set uses purely compressive (curl-free)
forcing to excite turbulent motions. From the resulting density field,
we compute the mass distribution of gravitationally unstable cores by
means of a clump-finding algorithm. Using the time-averaged probability
density functions of the mass density, semi-analytic mass distributions
are calculated from analytical theories. We apply stability criteria
that are based on the Bonnor-Ebert mass resulting from the thermal
pressure and from the sum of thermal and turbulent pressure.
Results. Although there are uncertainties in applying of the
clump-finding algorithm, we find systematic differences in the mass
distributions obtained from solenoidal and compressive forcing.
Compressive forcing produces a shallower slope in the high-mass
power-law regime compared to solenoidal forcing. The mass distributions
also depend on the Jeans length resulting from the choice of the mass
in the computational box, which is freely scalable for
non-selfgravitating isothermal turbulence. If the Jeans length
corresponding to the density peaks is less than the grid cell size, the
distributions obtained by clump-finding show a strong resolution
dependence. Provided that all cores are numerically resolved and most
cores are small compared to the length scale of the forcing, the
normalised core mass distributions are close to the semi-analytic
models.
Conclusions. The driving mechanism of turbulence has a potential
impact on the shape of the core mass function. Especially for the
high-mass tails, the Hennebelle-Chabrier theory implies that the
additional support due to turbulent pressure is important.
Key words: hydrodynamics - ISM: clouds - ISM: kinematics and dynamics - methods: numerical - stars: formation - turbulence
1 Introduction
The observed supersonic turbulence in the interstellar medium (ISM)
plays an important role in the process of star formation (e.g., Scalo & Elmegreen 2004; Elmegreen & Scalo 2004; McKee & Ostriker 2007; Mac Low & Klessen 2004; Ballesteros-Paredes et al. 2007).
The origin of this turbulence and the characteristics of different
turbulence-driving mechanisms are still a matter of debate. Owing to
the ability to counterbalance gravity globally and to provoke
gravitational collapse locally, turbulence is expected to have a strong
impact on the shape of the stellar initial mass function (IMF). The
high-mass end (
![]() )
is typically observed to exhibit a power law of the form
)
is typically observed to exhibit a power law of the form
![]() (e.g., Lada & Lada 2003; Kroupa 2001; Salpeter 1955; Chabrier 2003), where
(e.g., Lada & Lada 2003; Kroupa 2001; Salpeter 1955; Chabrier 2003), where
![]() is the number of stars in the linear mass interval
is the number of stars in the linear mass interval ![]() with Salpeter (1955) power-law index
with Salpeter (1955) power-law index
![]() .
Observations of dense cores embedded in star-forming regions of
turbulent giant molecular clouds show a similar but slightly shallower
power-law distribution of mass with an exponent
.
Observations of dense cores embedded in star-forming regions of
turbulent giant molecular clouds show a similar but slightly shallower
power-law distribution of mass with an exponent ![]() in the range of 1.5-2.5 (Motte et al. 1998; Elmegreen & Falgarone 1996).
The origin of the IMF and the Salpeter power law for the high-mass tail
are still under debate, but there is a possible connection between the
core mass function (CMF) and the IMF Motte et al. 1998; Johnstone & Bally 2006; Nutter & Ward-Thompson 2007; Johnstone et al. 2001; Williams et al. 2000; Testi & Sargent 1998; Johnstone et al. 2000; Alves et al. 2007; see however, the critical discussion by Clark et al. 2007. Padoan & Nordlund (2002)
propose a theoretical explanation for the CMF/IMF based on scaling
properties of turbulence and the Jeans criterion for gravitational
instability. Combining the formalism of
Press & Schechter (1974) for
cosmological structure formation with the notion of a turbulent Jeans
mass, a new analytic theory of the IMF was formulated by Hennebelle & Chabrier (2008).
in the range of 1.5-2.5 (Motte et al. 1998; Elmegreen & Falgarone 1996).
The origin of the IMF and the Salpeter power law for the high-mass tail
are still under debate, but there is a possible connection between the
core mass function (CMF) and the IMF Motte et al. 1998; Johnstone & Bally 2006; Nutter & Ward-Thompson 2007; Johnstone et al. 2001; Williams et al. 2000; Testi & Sargent 1998; Johnstone et al. 2000; Alves et al. 2007; see however, the critical discussion by Clark et al. 2007. Padoan & Nordlund (2002)
propose a theoretical explanation for the CMF/IMF based on scaling
properties of turbulence and the Jeans criterion for gravitational
instability. Combining the formalism of
Press & Schechter (1974) for
cosmological structure formation with the notion of a turbulent Jeans
mass, a new analytic theory of the IMF was formulated by Hennebelle & Chabrier (2008).
Numerical simulations of turbulent molecular clouds reported in the literature (for instance, Federrath et al. 2010b; Banerjee et al. 2009; Hennebelle et al. 2008; Schmidt et al. 2009; Kritsuk et al. 2007) inject the turbulent energy via different methods, but apart from an early study by Klessen (2001), there has been no systematic analysis of how different driving schemes affect the CMF. Possible physical mechanisms for maintaining ISM turbulence range from stellar feedback (supernovae, outflows, ionizing radiation) to large-scale dynamical instabilities in the Galaxy (Elmegreen & Scalo 2004; Norman & Ferrara 1996; Mac Low & Klessen 2004), in this work we investigate the influence of the compressibility of the turbulence forcing on the mass spectra of gravitationally unstable cores.
We apply a clump-finding algorithm to the density fields from recent
simulations of supersonic isothermal gas, using the FLASH3 code to
solve the equations of hydrodynamics on static grids with resolutions
of 2563, 5123 and 10243 grid points and periodic boundary conditions (Federrath et al. 2010b,2009,2008b). The turbulent energy is continuously injected by a specific force f on length scales corresponding to wavenumbers 1<k<3, where k is normalised by ![]() for a box of size X. Each component of this force is modelled by an Ornstein-Uhlenbeck process (Federrath et al. 2010b; Eswaran & Pope 1988; Schmidt et al. 2006,2009). We define the integral scale L by the mean wavelength of the forcing, i.e., L=X/2. The relative importance of solenoidal and compressive modes of the stochastic forcing is set by the parameter
for a box of size X. Each component of this force is modelled by an Ornstein-Uhlenbeck process (Federrath et al. 2010b; Eswaran & Pope 1988; Schmidt et al. 2006,2009). We define the integral scale L by the mean wavelength of the forcing, i.e., L=X/2. The relative importance of solenoidal and compressive modes of the stochastic forcing is set by the parameter
![]() .
The simulations represent two extreme cases: Purely solenoidal forcing (
.
The simulations represent two extreme cases: Purely solenoidal forcing (
![]() ,
,
![]() ), on the one hand, and purely compressive forcing (
), on the one hand, and purely compressive forcing (
![]() ,
,
![]() ), on the other, driven to an RMS Mach number of
), on the other, driven to an RMS Mach number of
![]() .
Turbulence becomes statistically stationary for
.
Turbulence becomes statistically stationary for
![]() ,
where
,
where
![]() is the dynamical timescale. In order to take the intermittent nature of
the density field into account, we analyse each of the 81 density
snapshots available in the time interval
is the dynamical timescale. In order to take the intermittent nature of
the density field into account, we analyse each of the 81 density
snapshots available in the time interval
![]() to compute time-averaged core statistics. For a detailed description of the simulation setup and numerical techniques, see Federrath et al. (2010b).
Recent results of isothermal turbulence simulations indicate a strong
dependence of the density field statistics on the compressibility of
the stochastic forcing (Federrath et al. 2010b; Schmidt et al. 2009; Federrath et al. 2009,2008b).
This effect makes it is a reasonable assumption that the resulting core
mass distributions should show different properties for different
turbulence driving mechanisms. Furthermore, the datasets enable us to
study in which way the effective resolution of the simulation affects
the resulting mass distributions.
to compute time-averaged core statistics. For a detailed description of the simulation setup and numerical techniques, see Federrath et al. (2010b).
Recent results of isothermal turbulence simulations indicate a strong
dependence of the density field statistics on the compressibility of
the stochastic forcing (Federrath et al. 2010b; Schmidt et al. 2009; Federrath et al. 2009,2008b).
This effect makes it is a reasonable assumption that the resulting core
mass distributions should show different properties for different
turbulence driving mechanisms. Furthermore, the datasets enable us to
study in which way the effective resolution of the simulation affects
the resulting mass distributions.
This article is structured as follows. In the next section, we review the analytical theories for the CMF by Padoan & Nordlund (2002) and Hennebelle & Chabrier (2008). For the sake of clarity, we express the main results of these theories in a consistent notation. In Sect. 3, we discuss the parameters determining the global mass scale, which plays a key role in computations of the core mass functions. The clump-finding algorithm is briefly described in Sect. 4, and the resulting mass distributions are presented. Particular emphasis is put on the question of numerical convergence. The distributions obtained by clump-finding are compared to semi-analytic computations of the CMF in Sect. 5, and the results are summarised and discussed in Sect. 6.
2 Analytical theories for the core mass function
In this work, we follow Hennebelle & Chabrier (2008) by writing
![]() ,
where N(M) is the cumulative number of cores with masses below M. The function
,
where N(M) is the cumulative number of cores with masses below M. The function
![]() is also called the mass spectrum. Because of the wide range of
different masses, it is useful to define the CMF by the number of cores
per logarithmic mass interval. To that end, we define
two dimensionless mass variables:
is also called the mass spectrum. Because of the wide range of
different masses, it is useful to define the CMF by the number of cores
per logarithmic mass interval. To that end, we define
two dimensionless mass variables:
-
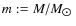 is the mass relative to the solar mass.
is the mass relative to the solar mass.
-
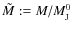 is the mass relative to the thermal Jeans mass
at the mean density
is the mass relative to the thermal Jeans mass
at the mean density
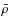 .
.
Integration of over M yields the total number of cores,
2.1 Padoan-Nordlund theory
Padoan & Nordlund (2002) based
their analytical approach on the following assumptions.
The core size is comparable to the thickness of isothermal postshock
gas, the turbulent velocity fluctuations follow a power law, and the
minimal mass that is unstable against gravitational collapse is given
by the thermal Jeans mass. They show that the number of cores per mass
interval is given by an expression of the form
where the parameter x depends on the scaling properties of turbulence. Integration of the probability density function
Equation (3) can be written in terms of the probability density function
![]() of the logarithmic density fluctuation
of the logarithmic density fluctuation
![]() .
Since the Jeans stability criterion implies
.
Since the Jeans stability criterion implies
![]() ,
we have
,
we have
![]() ,
and it follows that
,
and it follows that
The upper bound on the core mass corresponds to a lower bound on the density fluctuation. The distribution (4) is invariant under a change in the global scales. Obviously, this cannot be the physical CMF if
![\begin{displaymath}{\rm pdf}(\delta)=
\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\left[-\frac{(\delta-\bar{\delta})^{2}}{2\sigma^{2} }\right]\cdot
\end{displaymath}](/articles/aa/full_html/2010/08/aa13904-09/img52.png)
|
(5) |
where
Originally, the power-law exponent x was obtained from the
jump conditions for shocks in magnetohydrodynamic turbulence, and it
was shown that the resulting slope of the high-mass tail is close to
the Salpeter slope
![]() (see Padoan & Nordlund 2002). Padoan et al. (2007), hereafter referred to as PN07, also determined x for isothermal hydrodynamic (HD) turbulence:
(see Padoan & Nordlund 2002). Padoan et al. (2007), hereafter referred to as PN07, also determined x for isothermal hydrodynamic (HD) turbulence:
where
2.2 Hennebelle-Chabrier theory
The theory of Hennebelle & Chabrier (2008) provides a general framework for mass distributions
of cores on the basis of the Press-Schechter statistical formalism. In contrast to the
theory by Padoan & Nordlund (2002), there is an inherent notion of a core scale R
that is connected to its mass. Assuming a log-normal distribution of
the gas density, analytic formulae for the mass distribution
![]() can be derived. In the simplest case, M
is given by the thermal Jeans mass for a given density. While the
Padoan-Nordlund theory only uses thermal support, the
Hennebelle-Chabrier theory considers a combination of thermal and
turbulent support. On the one hand, turbulence is promoting star
formation through the broadening of the density PDF, while on the
other, it also quenches star formation through the scale-dependent
support of the cores.
can be derived. In the simplest case, M
is given by the thermal Jeans mass for a given density. While the
Padoan-Nordlund theory only uses thermal support, the
Hennebelle-Chabrier theory considers a combination of thermal and
turbulent support. On the one hand, turbulence is promoting star
formation through the broadening of the density PDF, while on the
other, it also quenches star formation through the scale-dependent
support of the cores.
By applying an approximation that excludes the largest cores,
it is possible to generalise their approach to arbitrary PDFs of the
mass density. For cores on a length scale R comparable to the integral scale L, the mass distribution depends on the derivative of
![]() with respect to R,
which in turn depends on the slope of the
spectrum of the density fluctuations. It would be worthwhile
investigating the influence of
the spectral properties of the density field on the CMF. Because of the
difficulties in the numerical determination of the derivative of the
with respect to R,
which in turn depends on the slope of the
spectrum of the density fluctuations. It would be worthwhile
investigating the influence of
the spectral properties of the density field on the CMF. Because of the
difficulties in the numerical determination of the derivative of the ![]() -PDF, however, we restrict our investigation to
length scales
-PDF, however, we restrict our investigation to
length scales ![]() ,
for which the general form of the mass spectrum (Eq. (33) in Hennebelle & Chabrier 2008) simplifies to
,
for which the general form of the mass spectrum (Eq. (33) in Hennebelle & Chabrier 2008) simplifies to
For a comparison with the Padoan-Nordlund theory, the case of purely thermal support is treated as follows. The core mass
The dimensionless scale parameter is defined by
This expression for the CMF is fully determined by the lower bound of the integral in Eq. (4), and, generally, the high-mass tail does not obey a power law.
If turbulence pressure contributes to the support against gravitational
collapse, an implicit relation between the gravitationally unstable
mass and the density fluctuation results:
The intensity of turbulence is specified by the Mach number
where
where
3 Clump-finding and scaling
For the calculation of the mass distributions we applied the
implementation of the clump-finding algorithm by PN07. As a first step
the algorithm divides the three-dimensional density field into k discrete density levels ![]() based upon the settings of the input parameters
based upon the settings of the input parameters
![]() and
and
![]() with
with
![]() .
The former parameter defines the minimum density level in units of the average density
.
The former parameter defines the minimum density level in units of the average density
![]() ,
while the latter defines the spacing between two adjacent levels. In
the next step each density level is scanned for regions of connected
cells with density values higher than the current density level. A
connected region
is counted as an object (a core) if its mass exceeds the local
Bonnor-Ebert mass (Ebert 1955; Bonnor 1956). The ratio of the Bonnor-Ebert mass to the solar mass is given by
,
while the latter defines the spacing between two adjacent levels. In
the next step each density level is scanned for regions of connected
cells with density values higher than the current density level. A
connected region
is counted as an object (a core) if its mass exceeds the local
Bonnor-Ebert mass (Ebert 1955; Bonnor 1956). The ratio of the Bonnor-Ebert mass to the solar mass is given by
where the gravitational constant
For this analysis, it is crucial to consider the degrees of freedom in the scaling of
isothermal, non-self-gravitating turbulence. For a given temperature T and box size L,
the hydrodynamical scales of the system are fixed, and the forcing magnitude determines
the RMS Mach number
![]() of
turbulence in the statistically stationary state. If self-gravity is
not included, the flow properties are invariant with respect to the
choice
of the mean mass density
of
turbulence in the statistically stationary state. If self-gravity is
not included, the flow properties are invariant with respect to the
choice
of the mean mass density
![]() .
This is palpable if the compressible
Euler equations are written in terms of the logarithmic density
.
This is palpable if the compressible
Euler equations are written in terms of the logarithmic density
![]() (see, for instance, Federrath et al. 2010b). Therefore, the mass scale is arbitrary.
(see, for instance, Federrath et al. 2010b). Therefore, the mass scale is arbitrary.
On the other hand, if gravitationally unstable cores are identified via postprocessing, then the value of
![]() (13) resulting from the chosen values of n and T fixes the mass scale. In this paper, we characterise the mass scale by the total number
(13) resulting from the chosen values of n and T fixes the mass scale. In this paper, we characterise the mass scale by the total number
![]() of Bonnor-Ebert masses with respect to the mean density contained in the simulation box:
of Bonnor-Ebert masses with respect to the mean density contained in the simulation box:
where
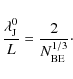
|
(15) |
The Hennebelle-Chabrier theory accounts for the dependence of the core statistics on the parameter
where
The turbulent velocity dispersion
The physical scales that were chosen by PN07 are
![]() ,
,
![]() and
and
![]() .
In this case,
.
In this case,
![]() and
and
![]() .
For the simulations with the highest
resolution, we have
.
For the simulations with the highest
resolution, we have
![]() ,
where
,
where ![]() is the
size of the grid cells. As we see in the next section, this introduces
a serious resolution issue, because many cores only extend over a few
cells for this parameter set. Another difficulty is that the above
parameters are atypical for observed molecular cloud properties.
According to the Larson (1981) relation,
is the
size of the grid cells. As we see in the next section, this introduces
a serious resolution issue, because many cores only extend over a few
cells for this parameter set. Another difficulty is that the above
parameters are atypical for observed molecular cloud properties.
According to the Larson (1981) relation,
![]() (see also Heyer et al. 2009; Falgarone et al. 1992). This suggests that the assumed forcing scale
(see also Heyer et al. 2009; Falgarone et al. 1992). This suggests that the assumed forcing scale
![]() is too large for molecular clouds of mean number density
is too large for molecular clouds of mean number density
![]() .
To analyse the impact of the physical scales, we computed the core mass distributions for
.
To analyse the impact of the physical scales, we computed the core mass distributions for
![]() again without changing the temperature and the mean number density. For
these parameters, the number density is consistent with the Larson
relation within a factor of two, which is reasonable given the
scattering of observed molecular cloud properties (Falgarone et al. 1992). In this case,
again without changing the temperature and the mean number density. For
these parameters, the number density is consistent with the Larson
relation within a factor of two, which is reasonable given the
scattering of observed molecular cloud properties (Falgarone et al. 1992). In this case,
![]() ,
and
,
and
![]() .
We also note, however, that the validity of Larson-type relations for the mass density was questioned by Ballesteros-Paredes & Mac Low (2002).
.
We also note, however, that the validity of Larson-type relations for the mass density was questioned by Ballesteros-Paredes & Mac Low (2002).
4 Core statistics
We begin with a detailed analysis of the mass distributions obtained for
purely thermal support and the PN07 mass scale corresponding to
![]() .
In particular, the tuning of the
clump-finding algorithm and influence of numerical resolution are
considered in Sects. 4.1 and 4.2. Finally, the mass distributions for fewer
Bonner-Ebert masses in the box,
.
In particular, the tuning of the
clump-finding algorithm and influence of numerical resolution are
considered in Sects. 4.1 and 4.2. Finally, the mass distributions for fewer
Bonner-Ebert masses in the box,
![]() ,
as
well as the influence of turbulent pressure are discussed in Sect. 4.3.
,
as
well as the influence of turbulent pressure are discussed in Sect. 4.3.
![\begin{figure}
\par\subfigure[Solenoidal forcing.]{\includegraphics[width=9cm,cl...
...{\includegraphics[width=9cm,clip]{13904fg1b.eps} }
\vspace*{2.8mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg114.png)
|
Figure 1:
The core mass distributions for the 5123 solenoidal a) and compressive b) simulations as a function of the clump-finding algorithm parameter f
(increasing from top curve to bottom curve) which sets the relative
spacing between two adjacent density levels. Error bars contain the 1 |
| Open with DEXTER | |
Table 1: Time-averaged properties of the mass distributions for solenoidal and compressive forcing calculated with the physical scalings applied in PN07.
4.1 Tuning of the clump-finding algorithm
As described in Sect. 3 the clump-finding routine needs two
technical input parameters: the relative spacing f between two adjacent density levels and the minimum
density level
![]() above which the datacube is divided into
discrete levels. The influence of these parameters has already been described in
PN07. For the minimum density level, we choose the mean density
above which the datacube is divided into
discrete levels. The influence of these parameters has already been described in
PN07. For the minimum density level, we choose the mean density ![]() of
the simulation box, since we observe no significant differences in the
resulting core mass distributions for values of
of
the simulation box, since we observe no significant differences in the
resulting core mass distributions for values of
![]() ,
which
is also found in PN07. The influence of the level spacing f on the
resulting mass distributions is shown in Fig. 1.
The slope of the high-mass range and the total number of cores is very
sensitive to the chosen spacing of the density levels. For higher f-values
the algorithm detects less but more massive cores. For decreasing
spacing between density levels and therefore finer ``scanning'' of the
datacube, the massive cores are split into many more lower mass cores,
and this leads to a steepening of the high-mass tail
of the core mass distributions. For f=1.04, 1.08, and 1.16, this effect
lies within the temporal fluctuations of the mass distributions as indicated
by the error bars in Fig. 1.
PN07 also conclude that the mass distributions are basically converged for
,
which
is also found in PN07. The influence of the level spacing f on the
resulting mass distributions is shown in Fig. 1.
The slope of the high-mass range and the total number of cores is very
sensitive to the chosen spacing of the density levels. For higher f-values
the algorithm detects less but more massive cores. For decreasing
spacing between density levels and therefore finer ``scanning'' of the
datacube, the massive cores are split into many more lower mass cores,
and this leads to a steepening of the high-mass tail
of the core mass distributions. For f=1.04, 1.08, and 1.16, this effect
lies within the temporal fluctuations of the mass distributions as indicated
by the error bars in Fig. 1.
PN07 also conclude that the mass distributions are basically converged for
![]() .
For the calculations in the present study, we chose a value of f=1.04.
Nevertheless, our numerical mass distributions should be compared to
the observed IMF/CMF with caution, especially, in the high-mass range.
The parameter dependency of core mass distributions is a common
problem for all clump-finding methods in the
literature. Smith et al. (2008)
apply different clump-finding methods to data
of SPH simulations of molecular clouds with the result that the
definition of an individual core and its mass depend strongly on the
method
and the parameter settings (see also Klessen & Burkert 2000; Klessen 2001). In the observers' community, the clump-finding routines CLUMPFIND
(Williams et al. 1994) and GAUSSCLUMPS (Stutzki & Guesten 1990) are commonly
used to decompose position-position-velocity information of molecular clouds
into individual cores. These techniques suffer from the same
parameter dependency, as shown by Schneider & Brooks (2004) and
more recently by Pineda et al. (2009).
.
For the calculations in the present study, we chose a value of f=1.04.
Nevertheless, our numerical mass distributions should be compared to
the observed IMF/CMF with caution, especially, in the high-mass range.
The parameter dependency of core mass distributions is a common
problem for all clump-finding methods in the
literature. Smith et al. (2008)
apply different clump-finding methods to data
of SPH simulations of molecular clouds with the result that the
definition of an individual core and its mass depend strongly on the
method
and the parameter settings (see also Klessen & Burkert 2000; Klessen 2001). In the observers' community, the clump-finding routines CLUMPFIND
(Williams et al. 1994) and GAUSSCLUMPS (Stutzki & Guesten 1990) are commonly
used to decompose position-position-velocity information of molecular clouds
into individual cores. These techniques suffer from the same
parameter dependency, as shown by Schneider & Brooks (2004) and
more recently by Pineda et al. (2009).
![\begin{figure}
\par\subfigure[Solenoidal forcing, $N_{{\rm BE}}=1.2\times10^{5}$...
...]{\includegraphics[width=9cm,clip]{13904fg2d.eps} }
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg177.png)
|
Figure 2:
Core mass distributions for solenoidal (left) and compressive forcing (right) at numerical resolutions of 2563 (dashed), 5123 (dot-dashed), and 10243 (solid), normalised to the total number of cores,
|
| Open with DEXTER | |
4.2 Numerical resolution study for purely thermal support
Figure 2 indicates that the mass distributions are very sensitively to the grid resolution of the simulation. For
![]() ,
the high-mass tails steepen systematically with increasing grid
resolution for both solenoidal and compressive forcing, showing no sign
of convergence in the sense of an asymptotic limit, even for the
highest resolution of 10243 grid points. The mass distributions for
,
the high-mass tails steepen systematically with increasing grid
resolution for both solenoidal and compressive forcing, showing no sign
of convergence in the sense of an asymptotic limit, even for the
highest resolution of 10243 grid points. The mass distributions for
![]() appear
to be better converged, at least in the case of solenoidal forcing. The
statistical properties of the core mass distributions are summarised in
Table 1. The mean mass
appear
to be better converged, at least in the case of solenoidal forcing. The
statistical properties of the core mass distributions are summarised in
Table 1. The mean mass
![]() shifts to lower values with increasing resolution, approaching a time-averaged value of
shifts to lower values with increasing resolution, approaching a time-averaged value of
![]() for the 10243 runs, while the width
for the 10243 runs, while the width
![]() of the distributions decreases. This is caused by the fragmentation of
the cores found in the low resolution simulations into smaller and
denser cores in the high resolution simulations which also satisfy the
condition for gravitational instability. The sum of all core masses,
of the distributions decreases. This is caused by the fragmentation of
the cores found in the low resolution simulations into smaller and
denser cores in the high resolution simulations which also satisfy the
condition for gravitational instability. The sum of all core masses,
![]() ,
is a few percent of the total box mass
,
is a few percent of the total box mass
![]() .
.
An important property of the mass distributions is the slope x of the high-mass wings of
![]() ,
which is related to the exponent
,
which is related to the exponent ![]() of the linear distribution via
of the linear distribution via
![]() .
Assuming that there is a power-law range, we applied error-weighted least squares fits to the high-mass power-law regime (2563:
.
Assuming that there is a power-law range, we applied error-weighted least squares fits to the high-mass power-law regime (2563:
![]() ,
5123:
,
5123:
![]() ,
10243:
,
10243:
![]() )
in Fig. 2. The power-law exponents obtained by this method are referred to as
)
in Fig. 2. The power-law exponents obtained by this method are referred to as
![]() .
For the highest resolution, we find
.
For the highest resolution, we find
![]() for solenoidal forcing and a shallower slope of
for solenoidal forcing and a shallower slope of
![]() for compressive forcing. The mass distributions of the solenoidal runs
tend to show a higher degree of convergence. The differences in the
slopes between the three solenoidal simulations decrease with
increasing resolution. The slope
for compressive forcing. The mass distributions of the solenoidal runs
tend to show a higher degree of convergence. The differences in the
slopes between the three solenoidal simulations decrease with
increasing resolution. The slope
![]() obtained from the 5123 simulation is steeper by a value of 1.0 than the 2563 while the values of
obtained from the 5123 simulation is steeper by a value of 1.0 than the 2563 while the values of
![]() for the resolutions of 5123 and 10243
are nearly identical in the solenoidal case. In contrast, the slopes of
the mass distributions obtained from the pure compressive forcing
increase by a value of 0.6 (
for the resolutions of 5123 and 10243
are nearly identical in the solenoidal case. In contrast, the slopes of
the mass distributions obtained from the pure compressive forcing
increase by a value of 0.6 (
![]() )
and by a value of 0.5 (
)
and by a value of 0.5 (
![]() ), indicating slower convergence than in the solenoidal forcing case.
), indicating slower convergence than in the solenoidal forcing case.
We also used the method of maximum likelihood estimation (MLE) (for details see Appendix A) inspired by the work of Clauset et al. (2007) to determine the slope
![]() of the core mass distributions and to check that the distribution really follows a power law.
This method avoids biases that can result from least-square fits (e.g., Bauke 2007)
and provides an estimate of the mass value
of the core mass distributions and to check that the distribution really follows a power law.
This method avoids biases that can result from least-square fits (e.g., Bauke 2007)
and provides an estimate of the mass value
![]() above which the power-law assumption is made. Furthermore, the probability p that the power-law assumption holds can be calculated. Following Clauset et al. (2007), we rule out power laws if
above which the power-law assumption is made. Furthermore, the probability p that the power-law assumption holds can be calculated. Following Clauset et al. (2007), we rule out power laws if
![]() .
The results of the MLE method applied to the data of our core masses are summarised in Table 1. For the highest resolution, we find a power-law slope of
.
The results of the MLE method applied to the data of our core masses are summarised in Table 1. For the highest resolution, we find a power-law slope of
![]() for
for
![]() in the case of compressive forcing
and
in the case of compressive forcing
and
![]() for
for
![]() in the solenoidal forcing case. The errors are the 1
in the solenoidal forcing case. The errors are the 1![]() temporal
fluctuations of these values. The slopes are consistent with the values
obtained via least squares fits. At numerical resolutions of 2563 and 5123, the time-averaged p-values
are less than 0.1 for both solenoidal and compressive forcing. Thus,
they are not consistent with power laws. However, at a numerical
resolution of 10243, we find
temporal
fluctuations of these values. The slopes are consistent with the values
obtained via least squares fits. At numerical resolutions of 2563 and 5123, the time-averaged p-values
are less than 0.1 for both solenoidal and compressive forcing. Thus,
they are not consistent with power laws. However, at a numerical
resolution of 10243, we find
![]() for solenoidal and
for solenoidal and
![]() for compressive forcing. The standard deviations of these p-values are
very large, such that instantaneous CMFs can either be consistent with
power laws or do not exhibit power-law behaviour at the high-mass end
of the distribution. We emphasise that it is absolutely necessary to
compute time-averaged quantities in order to obtain statistically
meaningful results.
The p-value can only rule out the power law hypothesis, while other distributions could be a better fit even for
for compressive forcing. The standard deviations of these p-values are
very large, such that instantaneous CMFs can either be consistent with
power laws or do not exhibit power-law behaviour at the high-mass end
of the distribution. We emphasise that it is absolutely necessary to
compute time-averaged quantities in order to obtain statistically
meaningful results.
The p-value can only rule out the power law hypothesis, while other distributions could be a better fit even for ![]() .
The possible inconsistency of the high-mass CMFs with a power law-model was also discussed by Ballesteros-Paredes et al. (2006).
.
The possible inconsistency of the high-mass CMFs with a power law-model was also discussed by Ballesteros-Paredes et al. (2006).
Table 2:
Least-square estimates of the power-law exponent
![]() obtained from the 10243 simulations for different values of
obtained from the 10243 simulations for different values of
![]() with/without turbulent
pressure included in the core stability criterion.
with/without turbulent
pressure included in the core stability criterion.
![\begin{figure}
\subfigure[Solenoidal forcing, $N_{{\rm BE}}=1.2\times10^{5}$ , t...
...t.]{\includegraphics[width=9cm,clip]{13904fg3b.eps} }
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg209.png)
|
Figure 3:
PDF of core size r defined in Eq. (18) for solenoidal a) and compressive b) forcing for a numerical resolution of 2563 (dashed), 5123 (dot-dashed), and 10243 (solid) and PN07 scaling. Error bars indicate 1 |
| Open with DEXTER | |
For
![]() ,
the scatter around the tails of the mass distributions is too large for
the MLE method to be applicable. Therefore, we only list the power-law
exponents
,
the scatter around the tails of the mass distributions is too large for
the MLE method to be applicable. Therefore, we only list the power-law
exponents
![]() of the high-mass tails of the CMFs in Table 2.
Although it is quite inaccurate, especially because of the low number
statistics, this method can be used to describe the general trend of
the CMFs. For the solenoidal simulation with turbulent support and
of the high-mass tails of the CMFs in Table 2.
Although it is quite inaccurate, especially because of the low number
statistics, this method can be used to describe the general trend of
the CMFs. For the solenoidal simulation with turbulent support and
![]() ,
we do not give a value for the power-law exponent because the error bars are simply too large.
Decreasing the total number of Bonner-Ebert masses in the box from
,
we do not give a value for the power-law exponent because the error bars are simply too large.
Decreasing the total number of Bonner-Ebert masses in the box from
![]() from
from
![]() to 103 leaves the fitted value of
to 103 leaves the fitted value of
![]() relatively unchanged (taking the large error bars into account). The
effect of adding turbulent support on the slope of the CMF is discussed
in Sect. 4.3.
relatively unchanged (taking the large error bars into account). The
effect of adding turbulent support on the slope of the CMF is discussed
in Sect. 4.3.
To further investigate the effects of numerical resolution on the core properties, we looked at the size r of the cores. We defined the approximate size of a core as
where
Table 3: Time-averaged properties of the core size PDFs for solenoidal and compressive forcing.
For a certain variance,
![]() ,
of the density fluctuations, we expect that cores of size
,
of the density fluctuations, we expect that cores of size
![]() are most frequent, because the Jeans length changes with the inverse square root of the mass density. From the values of
are most frequent, because the Jeans length changes with the inverse square root of the mass density. From the values of ![]() for solenoidal and compressive forcing (see Federrath et al. 2010b, Table 1), it follows that
for solenoidal and compressive forcing (see Federrath et al. 2010b, Table 1), it follows that
![]() .
This agrees with the relative peak positions of the distributions for N=1024 in Fig. 3. Moreover, the mean size
.
This agrees with the relative peak positions of the distributions for N=1024 in Fig. 3. Moreover, the mean size
![]() of the cores for solenoidal forcing is about the same factor more than
of the cores for solenoidal forcing is about the same factor more than
![]() for compressive forcing, as one can see from the values listed in Table 3.
for compressive forcing, as one can see from the values listed in Table 3.
The minimal core size is roughly given by the peak densities
![]() in the turbulent gas. The definition of the Jeans length implies
in the turbulent gas. The definition of the Jeans length implies
![]() .
Since
.
Since
![]() is roughly
is roughly
![]() for solenoidal forcing and
for solenoidal forcing and
![]() for compressive forcing (Federrath et al. 2009), it follows that
for compressive forcing (Federrath et al. 2009), it follows that
![]() and
and
![]() ,
respectively, for the highest resolution. Consequently,
the smallest cores are marginally resolved in the 10243
simulation with solenoidal forcing, while they are definitely below the
resolution limit for compressively driven turbulence. As an indicator,
we calculated the fractions
,
respectively, for the highest resolution. Consequently,
the smallest cores are marginally resolved in the 10243
simulation with solenoidal forcing, while they are definitely below the
resolution limit for compressively driven turbulence. As an indicator,
we calculated the fractions
![]() of cores with
of cores with ![]() (see Table 3). Indeed, significant fractions
(see Table 3). Indeed, significant fractions
![]() were obtained for all resolutions in the case of compressive forcing. In the solenoidal simulations, on the other hand,
were obtained for all resolutions in the case of compressive forcing. In the solenoidal simulations, on the other hand,
![]() drops from
drops from ![]() (2563) to
(2563) to ![]() in the 10243 simulation. These trends are also visible in Fig. 3.
in the 10243 simulation. These trends are also visible in Fig. 3.
Setting
![]() ,
the estimate of the minimal core size
from the peak density yields
,
the estimate of the minimal core size
from the peak density yields
![]() for solenoidal forcing and
for solenoidal forcing and
![]() for compressive forcing. In the solenodial case,
for compressive forcing. In the solenodial case,
![]() drops to zero for the
highest resolution. Compared to the PN07 setting, the cores are in general larger
(see Table 3 and the top panels of Fig. 4).
Accordingly, the resolution dependence of the mass distributions is
less pronounced, particularly in the case of solenoidal forcing.
However, comparing the mass distributions without normalisation
in Figs. 5a and 5c, one can see that the total number of cores decreases by two orders of magnitude if the mass scale is chosen such that
drops to zero for the
highest resolution. Compared to the PN07 setting, the cores are in general larger
(see Table 3 and the top panels of Fig. 4).
Accordingly, the resolution dependence of the mass distributions is
less pronounced, particularly in the case of solenoidal forcing.
However, comparing the mass distributions without normalisation
in Figs. 5a and 5c, one can see that the total number of cores decreases by two orders of magnitude if the mass scale is chosen such that
![]() .
As in the case
.
As in the case
![]() ,
we find that the mean core size for solenoidal forcing is roughly twice as large as for compressive forcing.
,
we find that the mean core size for solenoidal forcing is roughly twice as large as for compressive forcing.
![\begin{figure}
\par\subfigure[Solenoidal forcing, $N_{{\rm BE}}=10^{3}$ , therma...
...{\includegraphics[width=8.9cm,clip]{13904fg4d.eps} }
\vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg303.png)
|
Figure 4:
PDFs of core size distribution as in Fig. 3 but for
|
| Open with DEXTER | |
4.3 Influence of the turbulent pressure
As explained in Sect. 3, we used the effective speed of sound according to Eq. (17) in the definition of the Bonnor-Ebert mass, Eq. (13), to compute the mass distributions of cores with thermal and turbulent support. For brevity, we use the term turbulent support, for which it is understood that the instability criterion is based on the sum of thermal and turbulent pressure.
![\begin{figure}
\par\subfigure[$N_{{\rm BE}}=1.2\times10^{5}$ , thermal support.]...
...bulent support.]{\includegraphics[width=9cm,clip]{13904fg5d.eps} }\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg304.png)
|
Figure 5:
CMFs of compressive (solid) and solenoidal (dot-dashed) forcing for different values of
|
| Open with DEXTER | |
Figures 5b and 5d compare the CMFs for
![]() and
and
![]() with turbulent support for the highest grid resolution of 10243. While turbulent support has no significant impact on the CMF for
with turbulent support for the highest grid resolution of 10243. While turbulent support has no significant impact on the CMF for
![]() ,
it clearly changes the CMF for
,
it clearly changes the CMF for
![]() .
For solenoidal forcing, turbulent support leads to a large shift in the
peak in the CMF, corresponding to the pronounced change of the core
size distribution. As one can see in Fig. 5d,
however, the temporal fluctuations are larger than the time average.
This is a consequence of how few cores there are. In the compressive
case with turbulent support, the peak of the CMF is relatively robust,
but we observe a flattening of the high-mass tail
from
.
For solenoidal forcing, turbulent support leads to a large shift in the
peak in the CMF, corresponding to the pronounced change of the core
size distribution. As one can see in Fig. 5d,
however, the temporal fluctuations are larger than the time average.
This is a consequence of how few cores there are. In the compressive
case with turbulent support, the peak of the CMF is relatively robust,
but we observe a flattening of the high-mass tail
from
![]() for the CMF without turbulent support to
for the CMF without turbulent support to
![]() (see Table 2), which is close to the Salpeter value of 1.35.
(see Table 2), which is close to the Salpeter value of 1.35.
Table 3 gives
a summary of the basic properties of the core size distribution for all
possible combinations of grid resolution, turbulent/thermal support,
and
![]() .
If turbulent support is included,
.
If turbulent support is included,
![]() becomes negligible both for solenoidal and for
compressive forcing if N=1024. The core size PDFs are plotted in Fig. 4.
The large error bars are the result of
to find large cores increases substantially for solenoidal forcing,
while the PDF for compressive forcing
does not change appreciably. In the case of solenoidal forcing, the
greatest effect on the core size is observed for the highest resolution
of 10243
grid cells. Thus, the support of cores against gravitational collpase
is greatly enhanced by the turbulent pressure on length scales that are
sufficiently large compared to the grid scale. In Sect. 5.2, we show that the turbulent pressure exceeds the thermal pressure on length scales above
becomes negligible both for solenoidal and for
compressive forcing if N=1024. The core size PDFs are plotted in Fig. 4.
The large error bars are the result of
to find large cores increases substantially for solenoidal forcing,
while the PDF for compressive forcing
does not change appreciably. In the case of solenoidal forcing, the
greatest effect on the core size is observed for the highest resolution
of 10243
grid cells. Thus, the support of cores against gravitational collpase
is greatly enhanced by the turbulent pressure on length scales that are
sufficiently large compared to the grid scale. In Sect. 5.2, we show that the turbulent pressure exceeds the thermal pressure on length scales above ![]() ,
i.e., outside the range of length scales that are subject to significant numerical dissipation.
,
i.e., outside the range of length scales that are subject to significant numerical dissipation.
5 Comparison to theoretical models
In this section, the core mass distributions computed with the
clump-finding algorithm are compared to theoretical predictions of Padoan & Nordlund (2002) as well as Hennebelle & Chabrier (2008).
The influence of the width of the density PDF resulting from different forcing was investigated by
Hennebelle & Chabrier (2009).
Because Federrath et al. (2010b,2008b) showed that the density PDFs are not exactly log-normal, we evaluated Eqs. (4), (9), and (12) for the numerical PDFs calculated from the simulation data. The PDFs
for the three numerical resolutions are plotted in Federrath et al. (2010b, Figs. 4 and 6).
The resulting
CMFs are thus semi-analytic. This is particularly important for the
case of compressively driven turbulence, for which the core mass
distributions calculated from log-normal fits to the PDFs of the mass
density deviate substantially from the semi-analytic distributions
based on the numerical PDFs (see also Schmidt et al. 2009).
For the comparison with the data from our clump-finding analysis, we normalise the distributions
with the total number of cores
![]() ,
which is calculated from Eq. (2).
Allowing for an arbitrary geometry factor
,
which is calculated from Eq. (2).
Allowing for an arbitrary geometry factor
![]() in the definition of the thermal Jeans mass (see Hennebelle & Chabrier 2008), we set
in the definition of the thermal Jeans mass (see Hennebelle & Chabrier 2008), we set
![]() and identify
and identify
![]() with the Bonnor-Ebert mass
with the Bonnor-Ebert mass
![]() (see
Eq. (13)).
With this, we have a criterion for gravitational instability on the
basis of the thermal pressure that is consistent with the clump-finding
algorithm.
(see
Eq. (13)).
With this, we have a criterion for gravitational instability on the
basis of the thermal pressure that is consistent with the clump-finding
algorithm.
5.1 Purely thermal support
Substitution of the time-averaged PDFs obtained from 10243 simulations (Federrath et al. 2010b,2008b) into Eqs. (4) and (9), yields the semi-analytic CMFs plotted in the top panels (a,b) of Fig. 6. These distributions are independent of the parameter
![]() because of the normalisation by the total number of cores,
because of the normalisation by the total number of cores,
![]() .
As one can see, both the Padoan-Nordlund and the Hennebelle-Chabrier
theory imply that the peak of the CMF is shifted towards lower masses
for compressively driven turbulence. This is a direct consequence of
the shape of the density PDFs.
Since compressive forcing produces higher density peaks, there is a
higher fraction of low Jeans masses compared to solenoidal forcing.
This results in the formation of smaller cores, as noted in Sect. 4.2).
As a consequence, the high-mass tail of the CMF (9) is significantly less stiff in the compressive case (the asymptote for
.
As one can see, both the Padoan-Nordlund and the Hennebelle-Chabrier
theory imply that the peak of the CMF is shifted towards lower masses
for compressively driven turbulence. This is a direct consequence of
the shape of the density PDFs.
Since compressive forcing produces higher density peaks, there is a
higher fraction of low Jeans masses compared to solenoidal forcing.
This results in the formation of smaller cores, as noted in Sect. 4.2).
As a consequence, the high-mass tail of the CMF (9) is significantly less stiff in the compressive case (the asymptote for
![]() is mainly given by the factor
is mainly given by the factor
![]() .
The slope of the CMF (4), on the other hand, is determined by the factor
.
The slope of the CMF (4), on the other hand, is determined by the factor
![]() ,
where x is defined by Eq. (6), in the limit of high masses.
The turbulence energy spectra computed from the simulation data yield the power-law exponents
,
where x is defined by Eq. (6), in the limit of high masses.
The turbulence energy spectra computed from the simulation data yield the power-law exponents
![]() for solenoidal forcing and
for solenoidal forcing and
![]() for compressive forcing (Federrath et al. 2010b). Thus, the slopes of the high-mass tails predicted by the Padoan-Nordlund theory are
for compressive forcing (Federrath et al. 2010b). Thus, the slopes of the high-mass tails predicted by the Padoan-Nordlund theory are
![]() for solenoidal forcing and
for solenoidal forcing and
![]() for compressive forcing.
for compressive forcing.
![\begin{figure}
\par\subfigure[Thermal support, $\lambda_{{\rm J}}^{0}/L=0.04$ , ...
...BE}}=10^{3}$ .]{\includegraphics[width=9cm,clip]{13904fg6d.eps} }
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg317.png)
|
Figure 6: Comparison of the semi-analytic mass distribution following from the Hennebelle-Chabrier (HC) theory and the Padoan-Nordlund (PN) theory with the corresponding distributions obtained via clump-finding (large dots) for two different choices of global mass scale. The thin dotted lines are the tangents to the mass distributions with the Salpeter slope x=1.35. For an explanation of turbulent support, see Sects. 2.2 and 3. |
| Open with DEXTER | |
![\begin{figure}
\par\subfigure[$\lambda_{{\rm J}}^{0}/L=0.04$ , $N_{{\rm BE}}=2\t...
...]{\includegraphics[width=9cm,clip]{13904fg7b.eps} }
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg320.png)
|
Figure 7:
Normalised gravitationally unstable mass as a function of the
logarithmic density fluctuation for purely thermal support (thick
dashed lines) and with additional turbulent support (solid lines), as
defined by Eqs. (8) and (10). For solenoidal forcing (see Table 4), the mass corresponding to the scale for which thermal pressure equals turbulent pressure (
|
| Open with DEXTER | |
Figure 6 shows also the results from the clump-finding analysis. Let us first consider the case
![]() (
(
![]() ).
For compressively driven turbulence, the clump-finding data match the
theoretical predictions very poorly. As discussed in Sect. 4.2,
the size of the smallest cores is less than the grid resolution in this
case. Since the numerically unresolved cores are missing in the core
statistics, the distribution is biased towards higher masses in
comparison to the semi-analytic distributions.
For solenoidal forcing, on the other hand, the smallest cores are at
least marginally resolved (see Table 4),
and the low-mass wing, as well as the peak position following from the
clump-finding analysis, is reasonably close to the theoretical
predictions. While the distribution obtained by clump-finding roughly
agrees with the CMF following from the Padoan-Nordlund theory also for
).
For compressively driven turbulence, the clump-finding data match the
theoretical predictions very poorly. As discussed in Sect. 4.2,
the size of the smallest cores is less than the grid resolution in this
case. Since the numerically unresolved cores are missing in the core
statistics, the distribution is biased towards higher masses in
comparison to the semi-analytic distributions.
For solenoidal forcing, on the other hand, the smallest cores are at
least marginally resolved (see Table 4),
and the low-mass wing, as well as the peak position following from the
clump-finding analysis, is reasonably close to the theoretical
predictions. While the distribution obtained by clump-finding roughly
agrees with the CMF following from the Padoan-Nordlund theory also for
![]() ,
the slope of
,
the slope of
![]() (see Table 2) is significantly steeper than the theoretical value 2.3. In Sect. 5.2,
it is shown that this discrepancy can be resolved by including
turbulent pressure. Remarkably, the mass distributions from the
clump-finding analysis are matched quite well by distributions of the
form (9) for
(see Table 2) is significantly steeper than the theoretical value 2.3. In Sect. 5.2,
it is shown that this discrepancy can be resolved by including
turbulent pressure. Remarkably, the mass distributions from the
clump-finding analysis are matched quite well by distributions of the
form (9) for
![]() (
(
![]() ). There are small deviations in the high-mass tails, which are, however, well within the error bars (see Fig. 5). In comparison to the distribution (4)
predicted by the Padoan-Nordlund theory, large discrepancies become
apparent. Since the cores are resolved enough both for solenoidal and
for compressive forcing for
). There are small deviations in the high-mass tails, which are, however, well within the error bars (see Fig. 5). In comparison to the distribution (4)
predicted by the Padoan-Nordlund theory, large discrepancies become
apparent. Since the cores are resolved enough both for solenoidal and
for compressive forcing for
![]() (see Table 4), the most likely explanation is that
(see Table 4), the most likely explanation is that
![]() is too small and, consequently, the high-mass cores are not within the
asymptotic regime to which the Padoan-Nordlund theory applies.
is too small and, consequently, the high-mass cores are not within the
asymptotic regime to which the Padoan-Nordlund theory applies.
Table 4: Dependence of various parameters on the mass scale and the forcing.
5.2 Turbulent support
Since Padoan & Nordlund (2002)
consider only the thermal Jeans mass, we concentrate on the
Hennebelle-Chabrier theory for the case that includes both thermal and
turbulent support.
Eliminating ![]() from Eqs. (10) by means of numerical root finding yields the mass-density relations plotted in Fig. 7. For comparison, also the relation (8) for purely thermal support is shown. One can see that low-density cores of size R greater than
from Eqs. (10) by means of numerical root finding yields the mass-density relations plotted in Fig. 7. For comparison, also the relation (8) for purely thermal support is shown. One can see that low-density cores of size R greater than
![]() can maintain a much higher mass against gravitational collapse if
turbulent pressure is included in the Jeans criterion. The high-density
asymptote, on the other hand, coincides with the thermally supported
branch, because cores of high enough density are associated with small
length scales R, for which the turbulent velocity dispersion becomes negligible compared to the speed of sound, i.e.,
can maintain a much higher mass against gravitational collapse if
turbulent pressure is included in the Jeans criterion. The high-density
asymptote, on the other hand, coincides with the thermally supported
branch, because cores of high enough density are associated with small
length scales R, for which the turbulent velocity dispersion becomes negligible compared to the speed of sound, i.e.,
![]() .
This implies
.
This implies
![]() .
For the length scale
.
For the length scale
![]() ,
we have
,
we have
![]() ,
i.e., the turbulent pressure of the gas equals its thermal pressure.
Substituting the values of the RMS Mach numbers and the scaling
exponents from Federrath et al. (2010b), the values of
,
i.e., the turbulent pressure of the gas equals its thermal pressure.
Substituting the values of the RMS Mach numbers and the scaling
exponents from Federrath et al. (2010b), the values of
![]() listed in Table 4 are obtained. It follows that
listed in Table 4 are obtained. It follows that
![]() and 0.082L for solenoidal and compressive forcing, respectively. These scales are close to the sonic length scales
and 0.082L for solenoidal and compressive forcing, respectively. These scales are close to the sonic length scales
![]() and 0.074L, which Federrath et al. (2010b) determined from the turbulence energy spectra. The corresponding dimensionless masses,
and 0.074L, which Federrath et al. (2010b) determined from the turbulence energy spectra. The corresponding dimensionless masses,
![]() ,
are also listed in Table 4
,
are also listed in Table 4![]() .
.
An important limitation of calculations based on the approximation (7) is that R has to be small compared to the box size 2L, i.e.,
![]() .
The mass parameters
.
The mass parameters
![]() corresponding to
corresponding to
![]() are indicated in Fig. 7. The values of
are indicated in Fig. 7. The values of
![]() are listed in Table 4 for all parameter sets. As one can see, we have the constraints
are listed in Table 4 for all parameter sets. As one can see, we have the constraints
![]() and
and
![]() for
for
![]() and 0.04, respectively. Since these limits are much higher than the
peak positions of the mass distributions, there is a sufficient margin
to study the high-mass wings.
and 0.04, respectively. Since these limits are much higher than the
peak positions of the mass distributions, there is a sufficient margin
to study the high-mass wings.
The PDF data for the density fluctuation ![]() yield the mass distributions plotted in the bottom panels (c,d) of Fig. 6.
Comparing the mass distributions with and without turbulent support,
the high-mass tails are flatter in the former. As expected, the
difference is more pronounced for
yield the mass distributions plotted in the bottom panels (c,d) of Fig. 6.
Comparing the mass distributions with and without turbulent support,
the high-mass tails are flatter in the former. As expected, the
difference is more pronounced for
![]() ,
because of the higher contribution of turbulent pressure for large core masses
(see Fig. 7). Remarkably, the tail of the mass distribution for compressively driven turbulence that is plotted in Fig. 6d is much less stiff than what PN07 report for hydrodynamic turbulence and is in very good agreement
with the Salpeter power law.
The peak positions, on the other hand, are nearly unaffected, because the turbulent pressure on the
length scales corresponding to the peaks of the mass distributions is low compared to the thermal pressure.
,
because of the higher contribution of turbulent pressure for large core masses
(see Fig. 7). Remarkably, the tail of the mass distribution for compressively driven turbulence that is plotted in Fig. 6d is much less stiff than what PN07 report for hydrodynamic turbulence and is in very good agreement
with the Salpeter power law.
The peak positions, on the other hand, are nearly unaffected, because the turbulent pressure on the
length scales corresponding to the peaks of the mass distributions is low compared to the thermal pressure.
Regarding the mass distributions obtained by clump-finding with turbulent support (bottom panels of Fig. 6), similar trends to the distributions with purely thermal support can be seen.
For
![]() (
(
![]() ),
the clump-finding distribution is shifted towards higher masses for
compressively driven turbulence because the smallest cores cannot be
resolved (see Sect. 5.1). The discrepancy
is much less in the case of solenoidal forcing, for which the overall shape of the semi-analytic
and clump-finding distributions agree quite closely. However, the slopes of the tails following from the
clump-finding data are steeper in both cases. Consequently, it appears that the clump-finding algorithm
underestimates the turbulent support of high-mass cores, provided that the theoretical description
of the CMF is correct.
),
the clump-finding distribution is shifted towards higher masses for
compressively driven turbulence because the smallest cores cannot be
resolved (see Sect. 5.1). The discrepancy
is much less in the case of solenoidal forcing, for which the overall shape of the semi-analytic
and clump-finding distributions agree quite closely. However, the slopes of the tails following from the
clump-finding data are steeper in both cases. Consequently, it appears that the clump-finding algorithm
underestimates the turbulent support of high-mass cores, provided that the theoretical description
of the CMF is correct.
In the case
![]() (
(
![]() ),
the mass distributions agree for compressive forcing (except for a
small shift), whereas the mass distribution obtained by clump-finding
is markedly different from the semi-analytic model for solenoidal
forcing. The analysis in Sect 4.2
showed that the cores tend to be smaller for compressively driven
turbulence. In accordance with the clump-finding results, the
Hennebelle-Chabrier theory implies a significant flattening of the
high-mass wing in this case, and the slope is found to be close to the
Salpeter value. For solenoidal forcing, however, a significant number
of cores have sizes that are of the same order of magnitude as the
integral scale L (see Table 3 and Fig. 4).
This entails a violation of the basic assumption that was made in the derivation of Eq. (12).
Apart from that, it is important to realize that both the clump-finding
algorithm and the semi-analytic approach rely on the notions of the
Bonnor-Ebert or Jeans mass and turbulence pressure. Since it is based
on the collapse of a spherical cloud, the former is highly idealised
and does not apply to the fully non-linear regime, while turbulence
pressure is an ensemble-average property of isotropic turbulence. One
mechanism that might account for the massive cores is merging; indeed,
since the gas is less compressed, the cores are more extended and
should merge more easily than in the compressible forcing case. Also
they should live longer, as it takes more time for them to be
assembled, and it is likely that these cores are destroyed by violent
passing shocks.
),
the mass distributions agree for compressive forcing (except for a
small shift), whereas the mass distribution obtained by clump-finding
is markedly different from the semi-analytic model for solenoidal
forcing. The analysis in Sect 4.2
showed that the cores tend to be smaller for compressively driven
turbulence. In accordance with the clump-finding results, the
Hennebelle-Chabrier theory implies a significant flattening of the
high-mass wing in this case, and the slope is found to be close to the
Salpeter value. For solenoidal forcing, however, a significant number
of cores have sizes that are of the same order of magnitude as the
integral scale L (see Table 3 and Fig. 4).
This entails a violation of the basic assumption that was made in the derivation of Eq. (12).
Apart from that, it is important to realize that both the clump-finding
algorithm and the semi-analytic approach rely on the notions of the
Bonnor-Ebert or Jeans mass and turbulence pressure. Since it is based
on the collapse of a spherical cloud, the former is highly idealised
and does not apply to the fully non-linear regime, while turbulence
pressure is an ensemble-average property of isotropic turbulence. One
mechanism that might account for the massive cores is merging; indeed,
since the gas is less compressed, the cores are more extended and
should merge more easily than in the compressible forcing case. Also
they should live longer, as it takes more time for them to be
assembled, and it is likely that these cores are destroyed by violent
passing shocks.
6 Conclusions
After omputing the distributions of gravitationally unstable cores by means of a clump-finding algorithm as well as semi-analytic methods for hydrodynamic simulations of forced supersonic turbulence, we have found significant differences resulting from the turbulence forcing, the choice of the global mass scale, and the effects of turbulent support. For a comparison with theoretical predictions, the numerical probability density functions of the mass density fluctuations were used to evaluate the formulae for the mass distribution. Our analysis completes a comprehensive study of the influence of forcing on the density and velocity statistics of isothermal supersonic turbulence (Schmidt et al. 2008; Federrath et al. 2010b,2009,2008b). In the following, we summarise the main results:
- 1.
- For hydrodynamic simulations without explicit treatment of
self-gravity, the CMF depends on the choice of the global mass scale,
which determines the number of Bonnor-Ebert masses,
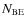 ,
with respect to the mean density in the computational domain. For clump-finding, one has to observe two constraints:
,
with respect to the mean density in the computational domain. For clump-finding, one has to observe two constraints:
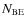 must be large enough to allow for many cores, but if
must be large enough to allow for many cores, but if
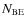 is chosen too large, a significant fraction of cores will be
numerically unresolved and the resulting CMF will be shifted towards
higher masses. In our analysis, these constraints are satisfied for two
cases: solenoidal forcing with
is chosen too large, a significant fraction of cores will be
numerically unresolved and the resulting CMF will be shifted towards
higher masses. In our analysis, these constraints are satisfied for two
cases: solenoidal forcing with
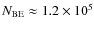 and compressive forcing with
and compressive forcing with
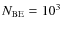 .
The lower value of
.
The lower value of
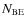 is consistent with Larson-type relations.
is consistent with Larson-type relations.
- 2.
- Comparing the results for solenoidal and compressive forcing, the most noticeable trends are that the CMF for compressively driven turbulence displays more low-mass cores, while the high-mass tails are flatter, particularly if turbulent support is significant. These trends are implied by Eqs. (8) and (10) for the stronger density contrast produced by compressive forcing (also see Fig. 7). We also found that the CMF peaks at lower mass in the case of compressive forcing. These results follow both from the clump-finding analysis and the semi-analytic computation of the mass distributions.
- 3.
- Because of the considerable scatter of core masses and
possible biases of the clump-finding algorithm, it is difficult to
ascertain power laws for the mass distributions. Nevertheless, we
attempted to determine power-law exponents for the high-mass tails from
least-square fits and by means of MLE. The results agree within the
statistical uncertainties for both methods. However, the results for
purely thermal support are at odds with the theory of Padoan & Nordlund (2002), which asymptotically applies to
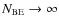 and predicts power-law tails for the CMF. In particular, the difference
between the exponents following from the clump-finding analysis is more
pronounced than the theoretical prediction.
and predicts power-law tails for the CMF. In particular, the difference
between the exponents following from the clump-finding analysis is more
pronounced than the theoretical prediction.
- 4.
- The mass distributions for cores with purely thermal support agree well with the theory of Hennebelle & Chabrier (2008) for
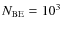 ,
although the tails are less stiff towards high masses than what is expected on the basis of the semi-analytic models.
There are large discrepancies for
,
although the tails are less stiff towards high masses than what is expected on the basis of the semi-analytic models.
There are large discrepancies for
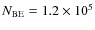 ,
but the disagreement might be spurious because of the strong dependence
of the high-mass wings on the numerical resolution. Apparently, the
mass distributions for high values of
,
but the disagreement might be spurious because of the strong dependence
of the high-mass wings on the numerical resolution. Apparently, the
mass distributions for high values of
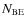 are in closer agreement with Padoan & Nordlund (2002)
if purely thermal support is assumed. However, it should be noted that
the mass-density pdfs will be strongly affected by self-gravity in this
case.
are in closer agreement with Padoan & Nordlund (2002)
if purely thermal support is assumed. However, it should be noted that
the mass-density pdfs will be strongly affected by self-gravity in this
case. - 5.
- For
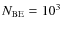 ,
turbulent pressure is important for a wider range of core masses than for
,
turbulent pressure is important for a wider range of core masses than for
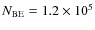 .
For this reason, the CMFs change substantially if turbulent support is
included. The effect is particularly strong for
turbulence that is driven by solenoidal forcing, because the mass and
the size of virtually all cores is increased by turbulent support.
However, the mass distribution obtained by clump-finding cannot be
reproduced theoretically, because the basic assumption
that the size of the cores is much smaller than the integral scale is
clearly not fulfilled in this case. Moreover, a stability criterion
that is based on the notions of Jeans mass and turbulent pressure might
fail if the cores become too large. On the other hand, we find very
good agreement between the clump-finding analysis and the
Hennebelle-Chabrier for compressively driven turbulence with
.
For this reason, the CMFs change substantially if turbulent support is
included. The effect is particularly strong for
turbulence that is driven by solenoidal forcing, because the mass and
the size of virtually all cores is increased by turbulent support.
However, the mass distribution obtained by clump-finding cannot be
reproduced theoretically, because the basic assumption
that the size of the cores is much smaller than the integral scale is
clearly not fulfilled in this case. Moreover, a stability criterion
that is based on the notions of Jeans mass and turbulent pressure might
fail if the cores become too large. On the other hand, we find very
good agreement between the clump-finding analysis and the
Hennebelle-Chabrier for compressively driven turbulence with
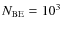 .
Compared to purely thermal support, the high-mass tail is considerably flatter in this
case.
.
Compared to purely thermal support, the high-mass tail is considerably flatter in this
case.
Even so, we have been able to shed more light on the gravitational fragmentation of turbulent gas. The influence of the forcing is irrefutable for a range of length scales that certainly extends beyond the energy-containing range. An open question is which regime in the interstellar medium is suitably modelled by a particular mode of forcing. If compressive excitation of turbulence occurs on length scales that tend to be larger than the size of molecular clouds, then the core statistics on much smaller scales, i.e., inside the cores of the clouds, still might be universal. Federrath et al. (2010b), however, suggests that different forcing mechanisms can produce genuine differences in molecular clouds, which affect the properties of turbulence even on the length scales of molecular cloud cores. This calls for further advances from both observational and the theoretical directions.
Another important result is the influence of turbulent pressure on the gas fragmentation. This is not new at all from the theoretical point of view. But we have been able to demonstrate numerically that turbulent support entails a flattening of the CMF towards high masses. In one extreme case, the slope of the high-mass tail was found to be close to the Salpeter slope. In this respect, the effect of turbulent pressure on gravitational fragmentation is analogous to the effect of magnetic pressure in magnetohydrodynamical turbulence. This can be understood on the basis of the dispersion relation resulting from a linear stability analysis, which shows that the magnetic pressure, as well as the turbulent pressure, contributes to the effective pressure of the gas. We do not suggest that the observed CMF might be explicable in terms of hydrodynamical turbulence alone, because it is known that magnetic fields play an important role in the interstellar medium. However, our results show that turbulent pressure might significantly contribute to the slope of the high-mass tail of the CMF. Apart from that, this effect is important in numerical simulations, where unresolved turbulent velocity fluctuations are close to the speed of sound or higher. In this case, the corresponding turbulent pressure can be computed with a subgrid-scale model (Schmidt 2009).
To achieve further progress with the theoretical explanation of the
CMF, it is paramount to account for processes that modify the PDFs of
the mass density. One such process is the thermal instability induced
by radiative cooling in the interstellar medium. It has already been
noticed by Passot & Vázquez-Semadeni (1998)
that polytropic equations of state, which are simple models for
cooling, lead to power-law tails in the density PDFs. This is confirmed
by
Li et al. (2003) for three-dimensional turbulence-in-a-box simulations and by Audit & Hennebelle (2009) for three-dimensional simulations of colliding flows with a polytropic exponent
![]() ,
although a power law was not obtained for thermally bistable turbulence. Seifried et al. (2010),
on the other hand, find power-law tails for thermally bistable
turbulence produced by compressive forcing, using the cooling function
of Audit & Hennebelle (2005). The effects of a polytropic equation of state on the CMF have been analysed by Hennebelle & Chabrier (2009).
,
although a power law was not obtained for thermally bistable turbulence. Seifried et al. (2010),
on the other hand, find power-law tails for thermally bistable
turbulence produced by compressive forcing, using the cooling function
of Audit & Hennebelle (2005). The effects of a polytropic equation of state on the CMF have been analysed by Hennebelle & Chabrier (2009).
Another process that gives rise to density PDFs with power-law tails is the accretion and contraction of gas in self-gravitating turbulence (e.g. Klessen et al. 2000; Federrath et al. 2008a). Moreover, dense structures can merge because of their mutual gravitational attraction. Consequently, the statistical characteristics will evolve with time (Klessen 2000), and the corresponding core mass distribution can differ significantly from the non-selfgravitating case (Klessen 2001), depending on the relative strength of selfgravity and the evolutionary stage of the star-forming cloud. Indeed, power-law, high-density tails are observed in high-resolution extinction maps of nearby molecular clouds (Kainulainen et al. 2009).
In numerical simulations of self-gravitating turbulence, the mass
distribution of gravitationally collapsing objects can be determined
directly. However, the sink particles that are usually applied to
numerically capture the collapsing gas (Padoan & Nordlund 2009; Federrath et al. 2010a; Bate et al. 1995; Jappsen et al. 2005; Krumholz et al. 2004)
do not directly correspond to the cores we have considered here. While
sink particles are dynamic objects that accrete gas and thus can
acquire different masses, they are obviously not associated with a
variable length scale, as is the case for cores![]() .
Theoretically, the relation between length scale and mass becomes
apparent in the Hennebelle-Chabrier theory, but also the clump-finding
algorithm identifies regions of variable size as cores. For this
reason, relating the mass distributions of sink particles and cores is
not trivial. Nevertheless, the approach via sink particles has the
considerable advantage that concepts such as the Bonner-Ebert mass,
which is rather arbitrary in the highly non-linear regime, are not
required. In either case, including self-gravity in turbulence
simulations is indispensable to improve our understanding of
gravoturbulent fragmentation.
.
Theoretically, the relation between length scale and mass becomes
apparent in the Hennebelle-Chabrier theory, but also the clump-finding
algorithm identifies regions of variable size as cores. For this
reason, relating the mass distributions of sink particles and cores is
not trivial. Nevertheless, the approach via sink particles has the
considerable advantage that concepts such as the Bonner-Ebert mass,
which is rather arbitrary in the highly non-linear regime, are not
required. In either case, including self-gravity in turbulence
simulations is indispensable to improve our understanding of
gravoturbulent fragmentation.
We thank Paolo Padoan (UCSD) for making his clump-finding algorithm available for this work and for critical comments. We are grateful to Patrick Hennebelle (ENS Paris) for numerous discussions and plenty of advice. Thanks also to Jens C. Niemeyer (IAG) for his support. The simulations and data analysis used resources from HLRBII project h0972 at the Leibniz Supercomputer Centre in Garching, Germany. CF is grateful for financial support from the International Max Planck Research School for Astronomy and Cosmic Physics (IMPRS-A) and the Heidelberg Graduate School of Fundamental Physics (HGSFP), which is funded by the Excellence Initiative of the Deutsche Forschungsgemeinschaft (DFG) GSC 129/1. R.S.K. acknowledges financial resources provided by the Deutsche Forschungsgemeinschaft under grants no. KL 1358/1, KL 1358/4, KL 1359/5. R.S.K. furthermore is grateful for subsidies from a Frontier grant of Heidelberg University sponsored by the German Excellence Initiative and for support from the Landesstiftung Baden-Württemberg via their programme International Collaboration II, grant no. P-LS-SPII/18. R.S.K. also acknowledges financial support from the German Bundesministerium für Bildung und Forschung via the ASTRONET project STAR FORMAT (grant 05A09VHA).
Appendix A: Maximum likelihood estimation for power-law scaling parameters
Estimating the parameters ![]() and
and
![]() of a power-law distribution of the form
of a power-law distribution of the form
with a constant C and exponent
Clauset et al. (2007) use a maximum likelihood estimator
for the power-law exponent ![]() assuming that the dataset, consisting of n values xi with
assuming that the dataset, consisting of n values xi with
![]() is drawn from a continuous power-law distribution for
is drawn from a continuous power-law distribution for
![]() ,
and
,
and
![]() is the estimated value for
is the estimated value for ![]() of the underlying distribution (Eq. (A.1)). The value of the lower bound
of the underlying distribution (Eq. (A.1)). The value of the lower bound
![]() of the distribution is the crucial factor in this calculation. If the estimated
of the distribution is the crucial factor in this calculation. If the estimated
![]() is too small (
is too small (
![]() ), we fit a power-law to non-power-law data and the parameter estimation will be biased. Too high values (
), we fit a power-law to non-power-law data and the parameter estimation will be biased. Too high values (
![]() )
will throw out a certain amount of legitimate, power-law-distributed data points. A reasonable value for
)
will throw out a certain amount of legitimate, power-law-distributed data points. A reasonable value for
![]() minimises the Kolmogorov-Smirnov (KS) statistics defined by
minimises the Kolmogorov-Smirnov (KS) statistics defined by
where S(x) is the cumulative distribution function (CDF) of the observed data points and P(x) the CDF of the fitted power-law model. The optimal value for
![]() gives the minimum difference between the data and the fitted model, which is just the minimised KS-statistics D of Eq. (A.3).
gives the minimum difference between the data and the fitted model, which is just the minimised KS-statistics D of Eq. (A.3).
To check that the observed dataset is likely to be drawn from a power-law distribution, we calculate a p-value
using a semi-parametric bootstrap approach. Therefore, we create 2500
synthetic datasets per snapshot, which follow a real power law with the
estimated parameters
![]() and
and
![]() of the observed core mass values. For
of the observed core mass values. For
![]() ,
the synthetic distributions follow the same non-power law behaviour as the observed dataset.
For each of the synthetic distributions, we again estimate the parameters
,
the synthetic distributions follow the same non-power law behaviour as the observed dataset.
For each of the synthetic distributions, we again estimate the parameters ![]() and
and
![]() and compute the KS-statistics.
The p-value
is the fraction of the KS-statistics of the synthetic datasets whose
value is higher than the KS-statistics of the observed dataset. This
means that p is the probability of getting a goodness of fit,
e.g. the KS-statistics, for a real power-law distributed synthetic
dataset that is at least as bad as the goodness of fit of our observed
dataset.
For
and compute the KS-statistics.
The p-value
is the fraction of the KS-statistics of the synthetic datasets whose
value is higher than the KS-statistics of the observed dataset. This
means that p is the probability of getting a goodness of fit,
e.g. the KS-statistics, for a real power-law distributed synthetic
dataset that is at least as bad as the goodness of fit of our observed
dataset.
For
![]() the power-law assumption has to be ruled out. A p-value higher than 0.1 does not necessarily mean that the underlying distribution follows a power law. The p-value can only rule out the hypothesis of a power-law distribution.
the power-law assumption has to be ruled out. A p-value higher than 0.1 does not necessarily mean that the underlying distribution follows a power law. The p-value can only rule out the hypothesis of a power-law distribution.
References
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audit, E., & Hennebelle, P. 2005, A&A, 433, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audit, E., & Hennebelle, P. 2010, A&A, 511, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J., Gazol, A., Kim, J., et al. 2006, ApJ, 637, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Klessen, R. S., Mac Low, M.-M., & Vazquez-Semadeni, E. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 63 [Google Scholar]
- Ballesteros-Paredes, J., & Mac Low, M. 2002, ApJ, 570, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, R., Vázquez-Semadeni, E., Hennebelle, P., & Klessen, R. S. 2009, MNRAS, 398, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Bauke, H. 2007, EPJ B, 58, 167 [NASA ADS] [Google Scholar]
- Bonazzola, S., Heyvaerts, J., Falgarone, E., Perault, M., & Puget, J. L. 1987, A&A, 172, 293 [NASA ADS] [Google Scholar]
- Bonnor, W. B. 1956, MNRAS, 116, 351 [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, P. C., Klessen, R. S., & Bonnell, I. A. 2007, MNRAS, 379, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Clauset, A., Rohilla Shalizi, C., & Newman, M. E. J. 2009, SIAM Review, 51, 661 [Google Scholar]
- Ebert, R. 1955, Zeitschrift fur Astrophysik, 37, 217 [Google Scholar]
- Elmegreen, B. G., & Falgarone, E. 1996, ApJ, 471, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Eswaran, V., & Pope, S. B. 1988, Computers and Fluids, 16, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Puget, J., & Perault, M. 1992, A&A, 257, 715 [NASA ADS] [Google Scholar]
- Federrath, C., Banerjee, R., Clark, P. C., & Klessen, R. S. 2010a, ApJ, 713, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & Mac Low, M.-M. 2010b, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Federrath, C., Glover, S. C. O., Klessen, R. S., & Schmidt, W. 2008a, Physica Scripta T, 132, 014025 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2008b, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2009, ApJ, 692, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Banerjee, R., Vázquez-Semadeni, E., Klessen, R. S., & Audit, E. 2008, A&A, 486, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2008, ApJ, 684, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2009, ApJ, 702, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Jappsen, A., Klessen, R. S., Larson, R. B., Li, Y., & Mac Low, M. 2005, A&A, 435, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, D., & Bally, J. 2006, ApJ, 653, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Fich, M., Mitchell, G. F., & Moriarty-Schieven, G. 2001, ApJ, 559, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Wilson, C. D., Moriarty-Schieven, G., et al. 2000, ApJ, 545, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S. 2001, ApJ, 556, 837 [Google Scholar]
- Klessen, R. S., & Burkert, A. 2000, ApJS, 128, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., Heitsch, F., & Mac Low, M. 2000, ApJ, 535, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., Padoan, P., & Wagner, R. 2007, ApJ, 665, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Klein, R. I. 2004, ApJ, 611, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Klessen, R. S., & Mac Low, M. 2003, ApJ, 592, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Modern Phys., 76, 125 [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Newman, M. 2005, Contemporary Physics, 46, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Norman, C. A., & Ferrara, A. 1996, ApJ, 467, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Nutter, D., & Ward-Thompson, D. 2007, MNRAS, 374, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., & Nordlund, Å. 2002, ApJ, 576, 870 [Google Scholar]
- Padoan, P., & Nordlund, A. 2009, ApJ, submitted, e-print [arXiv:0907.0248] [Google Scholar]
- Padoan, P., Nordlund, Å., Kritsuk, A. G., Norman, M. L., & Li, P. S. 2007, ApJ, 661, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Passot, T., & Vázquez-Semadeni, E. 1998, Phys. Rev. E, 58, 4501 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. E., Rosolowsky, E. W., & Goodman, A. A. 2009, ApJ, 699, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Scalo, J., & Elmegreen, B. G. 2004, ARA&A, 42, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, W. 2009, e-print [arXiv:0910.0183], to appear in Proceedings of ASTRONUM 2009, 4th International Conference on Numerical Modeling of Space Plasma Flows in Chamonix [Google Scholar]
- Schmidt, W., Federrath, C., Hupp, M., Kern, S., & Niemeyer, J. C. 2009, A&A, 494, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, W., Federrath, C., & Klessen, R. 2008, Phys. Rev. Lett., 101, 194505 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schmidt, W., Hillebrandt, W., & Niemeyer, J. C. 2006, Computers and Fluids, 35, 353 [Google Scholar]
- Schneider, N., & Brooks, K. 2004, PASA, 21, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Schmidt, W., & Niemeyer, J. C. 2010, A&A, submitted [Google Scholar]
- Smith, R. J., Clark, P. C., & Bonnell, I. A. 2008, MNRAS, 391, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., & Guesten, R. 1990, ApJ, 356, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., & Sargent, A. I. 1998, ApJ, 508, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., Blitz, L., & McKee, C. F. 2000, Protostars and Planets IV, 97 [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... follows
![[*]](/icons/foot_motif.png)
- In this article,
 denotes the natural logarithm.
denotes the natural logarithm.
- ...
![[*]](/icons/foot_motif.png)
- These values implicitly depend on the integral scale L, which is set to half the box size (see Sect. 1). More accurately, L can be determined from the velocity structure functions (Kritsuk 2010, private communication). Indeed, this would entail a somewhat closer match between the semi-analytic core mass distributions and the clump-finding data. Since the trends remain unaltered, however, we keep the simple definition of L in this article.
- ... cores
![[*]](/icons/foot_motif.png)
- There is a fixed accretion radius extending over a few grid cells, which can be interpreted as the length scale associated with sink particles.
All Tables
Table 1: Time-averaged properties of the mass distributions for solenoidal and compressive forcing calculated with the physical scalings applied in PN07.
Table 2:
Least-square estimates of the power-law exponent
![]() obtained from the 10243 simulations for different values of
obtained from the 10243 simulations for different values of
![]() with/without turbulent
pressure included in the core stability criterion.
with/without turbulent
pressure included in the core stability criterion.
Table 3: Time-averaged properties of the core size PDFs for solenoidal and compressive forcing.
Table 4: Dependence of various parameters on the mass scale and the forcing.
All Figures
![\begin{figure}
\par\subfigure[Solenoidal forcing.]{\includegraphics[width=9cm,cl...
...{\includegraphics[width=9cm,clip]{13904fg1b.eps} }
\vspace*{2.8mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg114.png)
|
Figure 1:
The core mass distributions for the 5123
solenoidal a) and compressive b)
simulations as a function of the clump-finding algorithm parameter f
(increasing from top curve to bottom curve) which sets the relative
spacing between two adjacent density levels. Error bars contain the 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\subfigure[Solenoidal forcing, $N_{{\rm BE}}=1.2\times10^{5}$...
...]{\includegraphics[width=9cm,clip]{13904fg2d.eps} }
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg177.png)
|
Figure 2:
Core mass distributions for solenoidal (left) and
compressive forcing (right) at numerical resolutions
of 2563 (dashed), 5123
(dot-dashed), and 10243 (solid), normalised to
the total number of cores, |
| Open with DEXTER | |
In the text
![\begin{figure}
\subfigure[Solenoidal forcing, $N_{{\rm BE}}=1.2\times10^{5}$ , t...
...t.]{\includegraphics[width=9cm,clip]{13904fg3b.eps} }
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg209.png)
|
Figure 3:
PDF of core size r defined in Eq. (18) for
solenoidal a) and compressive b)
forcing for a numerical resolution of 2563
(dashed), 5123 (dot-dashed), and 10243
(solid) and PN07 scaling. Error bars indicate 1 |
| Open with DEXTER | |
In the text
![\begin{figure}
\par\subfigure[Solenoidal forcing, $N_{{\rm BE}}=10^{3}$ , therma...
...{\includegraphics[width=8.9cm,clip]{13904fg4d.eps} }
\vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg303.png)
|
Figure 4:
PDFs of core size distribution as in Fig. 3
but for |
| Open with DEXTER | |
In the text
![\begin{figure}
\par\subfigure[$N_{{\rm BE}}=1.2\times10^{5}$ , thermal support.]...
...bulent support.]{\includegraphics[width=9cm,clip]{13904fg5d.eps} }\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg304.png)
|
Figure 5:
CMFs of compressive (solid) and solenoidal (dot-dashed) forcing for
different values of |
| Open with DEXTER | |
In the text
![\begin{figure}
\par\subfigure[Thermal support, $\lambda_{{\rm J}}^{0}/L=0.04$ , ...
...BE}}=10^{3}$ .]{\includegraphics[width=9cm,clip]{13904fg6d.eps} }
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg317.png)
|
Figure 6: Comparison of the semi-analytic mass distribution following from the Hennebelle-Chabrier (HC) theory and the Padoan-Nordlund (PN) theory with the corresponding distributions obtained via clump-finding (large dots) for two different choices of global mass scale. The thin dotted lines are the tangents to the mass distributions with the Salpeter slope x=1.35. For an explanation of turbulent support, see Sects. 2.2 and 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\subfigure[$\lambda_{{\rm J}}^{0}/L=0.04$ , $N_{{\rm BE}}=2\t...
...]{\includegraphics[width=9cm,clip]{13904fg7b.eps} }
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/08/aa13904-09/Timg320.png)
|
Figure 7:
Normalised gravitationally unstable mass as a function of the
logarithmic density fluctuation for purely thermal support (thick
dashed lines) and with additional turbulent support (solid lines), as
defined by Eqs. (8)
and (10).
For solenoidal forcing (see Table 4),
the mass corresponding to the scale for which thermal pressure equals
turbulent pressure (
|
| Open with DEXTER | |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



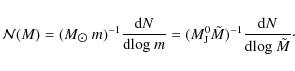
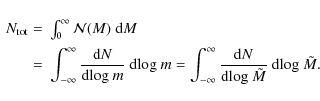
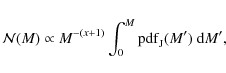
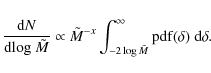
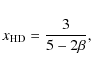
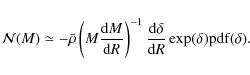
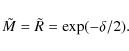
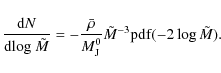
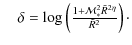
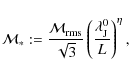
![\begin{displaymath}
\begin{array}{rl}
\displaystyle \frac{{\rm d}N}{{\rm d}{\rm ...
...\rm pdf}\left[\log(\tilde{M}/\tilde{R}^{3})\right],
\end{array}\end{displaymath}](/articles/aa/full_html/2010/08/aa13904-09/img78.png)
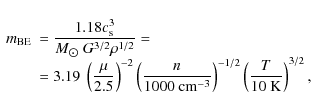
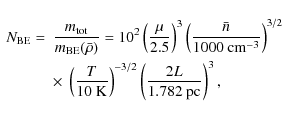
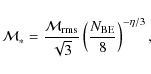
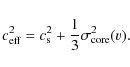
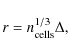
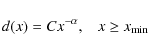
![\begin{displaymath}
\hat{\alpha}=1+n\left[\sum_{i=1}^{n}{\ln \frac{x_{i}}{x_{{\rm min}}}}\right]^{-1}
\end{displaymath}](/articles/aa/full_html/2010/08/aa13904-09/img344.png)