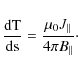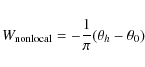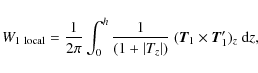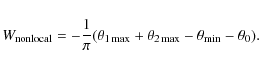| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913578 | |
| Published online | 24 June 2010 | |
The writhe of helical structures in the solar corona
T. Török1,2 - M. A. Berger2,3 - B. Kliem2,4,5
1 - LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
2 -
University College London, Mullard Space Science Laboratory, Holmbury St. Mary, Dorking, Surrey, RH5 6NT, UK
3 -
University of Exeter, SECAM, Exeter, EX4 4QE, UK
4 -
Universität Potsdam, Institut für Physik und Astronomie, 14482 Potsdam, Germany
5 -
Naval Research Laboratory, Space Science Division, Washington, DC 20375, USA
Received 1 November 2009 / Accepted 21 April 2010
Abstract
Context. Helicity is a fundamental property of magnetic
fields, conserved in ideal MHD. In flux rope geometry, it consists of
twist and writhe helicity. Despite the common occurrence of helical
structures in the solar atmosphere, little is known about how their
shape relates to the writhe, which fraction of helicity is contained in
writhe, and how much helicity is exchanged between twist and writhe
when they erupt.
Aims. Here we perform a quantitative investigation of these questions relevant for coronal flux ropes.
Methods. The decomposition of the writhe of a curve into local
and nonlocal components greatly facilitates its computation. We use it
to study the relation between writhe and projected S shape of helical
curves and to measure writhe and twist in numerical simulations of flux
rope instabilities. The results are discussed with regard to filament
eruptions and coronal mass ejections (CMEs).
Results. (1) We demonstrate that the relation between writhe and projected S shape is not
unique in principle, but that the ambiguity does not affect low-lying
structures, thus supporting the established empirical rule which
associates stable forward (reverse) S shaped structures low in the
corona with positive (negative) helicity. (2) Kink-unstable erupting
flux ropes are found to transform a far smaller fraction of their twist
helicity into writhe helicity than often assumed. (3) Confined flux
rope eruptions tend to show stronger writhe at low heights than
ejective eruptions (CMEs). This argues against suggestions that the
writhing facilitates the rise of the rope through the overlying field.
(4) Erupting filaments which are S shaped already before the eruption
and keep the sign of their axis writhe (which is expected if field of
one chirality dominates the source volume of the eruption), must
reverse their S shape in the course of the rise. Implications for the
occurrence of the helical kink instability in such events are
discussed. (5) The writhe of rising loops can easily be estimated from
the angle of rotation about the direction of ascent, once the apex
height exceeds the footpoint separation significantly.
Conclusions. Writhe can straightforwardly be computed for
numerical data and can often be estimated from observations. It is
useful in interpreting S shaped coronal structures and in constraining
models of eruptions.
Key words: magnetic fields - magnetohydrodynamics (MHD) - Sun: corona - Sun: filaments, prominences - Sun: coronal mass ejections (CMEs)
1 Introduction
Observations of the solar corona display a variety of structures that appear S shaped when viewed in projection on the disk, as for example filaments with curved ends, soft X-ray sigmoids, and magnetic loops that connect different active regions. The presence of an S shape is regarded to be evidence for current-carrying twisted or sheared magnetic fields which possess magnetic helicity. The link to helicity is underlined by the fact that the orientation of the S shows a hemispheric preference, as other indicators of magnetic chirality (the helicity sign) do (e.g., Rust & Kumar 1996; Zirker et al. 1997). Coronal currents store the energy required to power eruptions (Forbes 2000). Indeed, it has been shown that active regions exhibiting a sigmoidal morphology are more likely to erupt than non-sigmoidal ones (Canfield et al. 1999).
Twisted or sheared coronal fields carrying nearly force-free volume currents, especially magnetic flux ropes, are central in models of filaments and prominences (e.g., Bobra et al. 2008; Aulanier & Démoulin 1998), of sigmoids (e.g., Titov & Démoulin 1999; Low & Berger 2003; Rust & Kumar 1996; Kliem et al. 2004; Gibson et al. 2004), and of eruptions (e.g., Antiochos et al. 1999; Forbes & Isenberg 1991; Török & Kliem 2005; Fan & Gibson 2003; Amari et al. 2000; Yeates & Mackay 2009). The amount of twist or shear in them can be quantified by the magnetic helicity. For a magnetic flux rope, the helicity is proportional to the sum of its twist and writhe. The twist measures how much the field lines wind about the magnetic axis of the rope, whereas the writhe quantifies the helical deformation of the axis itself.
The orientation of the S in helical structures on the Sun is highly
correlated with the prevailing sign of magnetic helicity in their source volume.
For example, Rust & Martin (1994) found a one-to-one correlation between
the chirality of sunspot whirls and the orientation (sinistral
vs. dextral) of the axial field of filaments that spiral into their
periphery. Here, an apparent, or true, clockwise (counterclockwise)
rotation of the sunspot, associated with positive (negative) helicity of
its field, corresponds to forward (reverse) S shape of the filament end.
Pevtsov et al. (1997) found that forward (reverse) S-shaped sigmoids in active regions
were formed in predominantly positive
(negative) helicity regions for ![]() 90% of the cases investigated.
In the remaining cases the helicity sign of the host active region was
ambiguous, which is consistent with the possibility of a universal relation
between the orientation of the S in such structures and their chirality. In a study
of rotating erupting filaments, Green et al. (2007) found a one-to-one relationship between
the sign of dominant helicity, the orientation of associated sigmoids,
and the orientation of the rising filament's developing S shape
(but see Muglach et al. 2009, for
occasional exceptions in the latter association).
90% of the cases investigated.
In the remaining cases the helicity sign of the host active region was
ambiguous, which is consistent with the possibility of a universal relation
between the orientation of the S in such structures and their chirality. In a study
of rotating erupting filaments, Green et al. (2007) found a one-to-one relationship between
the sign of dominant helicity, the orientation of associated sigmoids,
and the orientation of the rising filament's developing S shape
(but see Muglach et al. 2009, for
occasional exceptions in the latter association).
In addition to stable structures, erupting filaments and prominences can also exhibit helical deformations. These eruptions are seen as rising loops in the corona, which in most cases become the core of a coronal mass ejection (CME), or else fall back in a confined eruption. Their change of shape can be described as a writhing of the filament axis out of the plane defined by the filament's foot points and apex, or equivalently, as a rotational motion of the filament axis in the upper part of the loop about the direction of ascent. The total writhe varies widely from event to event, and is often acquired to a large part already in the low and middle corona. Some very clear cases of such writhing have been described by Ji et al. (2003), Romano et al. (2003), Williams et al. (2005), and Zhou et al. (2006). These events include a wide range of dynamical behaviour, from a confined eruption to the fastest CME so far recorded. The writhing in the course of eruptions has attracted interest for three main reasons.
First, it indicates that the erupting field has the magnetic structure of a freely moving flux rope, line tied only at its ends, at the onset of the helical deformation (e.g., Green et al. 2007; Rust 2003).
Second, the observed deformations correspond exactly to the evolution of the helical kink instability of the current channel in the core of a flux rope (hereafter KI) and have, therefore, been taken as strong indication of this instability's occurrence (Williams et al. 2005; Török & Kliem 2005; Sakurai 1976; Gilbert et al. 2007; Rust & LaBonte 2005; Romano et al. 2003; Zhou et al. 2006). The KI transforms some of the twist of the field lines about the magnetic axis of the rope into writhe of the axis. In doing so, it lowers the magnetic energy by reducing the tension in the twisted field. Since this is an ideal MHD instability and the corona is a nearly perfectly conducting medium, the conversion of twist into writhe is constrained by the approximate conservation of the magnetic helicity contained in the rope (Berger 1984). It has been suggested that the writhing of the flux rope's upper part into the direction of the overlying field is energetically favourable for its passage through the overlying field to become a CME (Fan 2005; Sturrock et al. 2001). Thus, the deformations yield hints on the physical processes of CME initiation.
Third, the writhing is the major factor in determining the final magnetic orientation
of the CME (apart from influences during the interplanetary propagation), which,
in turn, is one of the critical parameters that control the strength of the
interaction if the CME hits the terrestrial magnetosphere - its
geoeffectiveness. The final orientation can differ largely from the erupting
structure's initial orientation: rotations as large as ![]() have been
reported (albeit the estimated angles are very approximate, see Yurchyshyn 2008; Démoulin 2008, and references therein).
have been
reported (albeit the estimated angles are very approximate, see Yurchyshyn 2008; Démoulin 2008, and references therein).
Despite the common occurrence of both stable and dynamic helical structures on the Sun, measurements of the axis writhe of such structures have not yet been undertaken. So far, only estimates based on qualitative considerations have been reported (e.g., Vrsnak et al. 1993; Rust 2003). This is mainly due to the fact that the observations have been limited to a 2D projection of intrinsically 3D structures onto the plane of the sky. With the advent of the STEREO mission, true 3D reconstructions of coronal structures are possible, as long as the angular separation between the twin satellites or between one of them and the Earth stays within certain intervals. Even for numerical simulations which provide the 3D magnetic field of evolving unstable flux ropes, the temporal evolution of twist and writhe has only extremely rarely been quantified (Linton et al. 1998). This is mainly due to the fact that the calculation of these quantities based on their general definitions is a relatively complicated task. The computation of the writhe is greatly facilitated by its decomposition into local and nonlocal components in Berger & Prior (2006). Here we make use of these expressions.
| Figure 1: A closed flux tube as seen from three different angles. The number of apparent crossings one sees depends on the viewing angle. Crossings can be called left-handed (negative) or right-handed (positive), depending on the relative orientations of the upper and lower field lines. The diagrams shown in d) give the two possible cases (up to rotation). The tube shown has an average crossing number, or writhe, of W = 0.566. Most viewing angles display a positive crossing, as in b). However, some angles do not show any crossings, as in a), and there is a small set of angles which display a negative crossing, as in c). (The latter picture of the tube is obtained by viewing it from the top.) |
|
| Open with DEXTER | |
Our aim in this paper is to describe and discuss possible applications of writhe measurements for both stable and erupting objects in the solar corona. To this end, we first review, in Sect. 2, the concepts of twist and writhe and the decomposition of the latter. We study the dependence of writhe on the geometrical properties of helical curves, paying particular attention to their height above a plane and to the presence of dips. The relationship between shape, writhe, and helicity of S-shaped flux ropes is then discussed (Sect. 3). In Sect. 4 we measure the conversion of twist into writhe in several numerical simulations of unstable magnetic flux ropes and discuss the implications of the results for erupting filaments and CMEs. We also point out that estimates of the writhe of erupting filaments can easily be obtained from their apex rotation as soon as the apex height significantly exceeds the footpoint separation. Section 5 summarizes the findings.
2 Twist and writhe
2.1 Definitions
Calugareanu (1959) introduced a quantity called writhe to measure how much a closed curve coils and supercoils. This quantity is extensively used in DNA research to describe the physical configuration of the DNA molecule (Maggioni & Ricca 2008) (in addition to the basic double helix structure, the molecule must be highly coiled in order to fit into a microscopic cell). There are several equivalent definitions of writhe for closed curves (e.g. Berger & Prior 2006; Aldinger et al. 1995). Perhaps the simplest definition to understand without getting lost in mathematical details involves counting crossings in pictures of a curve (see, for example, Fig. 1). If we draw a two-dimensional projection of the curve, it crosses itself a certain number of times. Highly coiled or tangled curves will show many crossings, while a non-intersecting curve confined to a plane will show no crossings at all (unless seen exactly edge-on). Crossings can be labelled positive or negative depending on the orientation of the sections of the curve above and below the crossing, as shown in the figure. Thus if an arrow pointing along the direction of the lower curve rotates clockwise to match the direction of the upper curve, then the sign is positive. Note that the sign of a crossing stays the same if we reverse the direction of the curve, because both segments above and below a crossing change direction.
Given a curve and a viewing angle, we can count the number of positive crossings N+ and subtract the number of negative crossings N-. The result is an integer - however, this integer depends on which viewing angle we are using. The writhe averages N+ - N- over all viewing angles.
As a consequence the writhe of a circular coil depends not only on how many coils there are, but on whether the coils are fat or thin, i.e. on the ratio between its height and width (Fig. 2). For thin coils, only special viewing angles (from near the axis) will see crossings. But for fat coils most viewing angles display crossings.
![\begin{figure}
\par\includegraphics[width=7cm]{13578fg2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg27.png)
|
Figure 2: The writhe of a coil depends on its aspect ratio (height/width) as well as how many turns it has. Both coils shown have 3 turns, but the fat coil in a) has a writhe W = 2.68, while the thin coil in b) has a writhe W = 0.46. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg3.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg29.png)
|
Figure 3:
A loop with one maximum, seen from the side a) and the top b). The nonlocal writhe is proportional to the difference in angle between the
tangent vector at the top, and the line connecting the footpoints. This angle
is
|
| Open with DEXTER | |
While the writhe is a property of a single curve, the definition of
twist involves two curves, which can be viewed as the edges of a ribbon.
Calugareanu (1959) derived a remarkable formula for the structure of a
ribbon. Consider two closely aligned curves, like the two sides of a ribbon or
the two strands of a DNA molecule. Assume that the ribbon or molecule closes upon
itself, so that the two curves do not have endpoints. These two curves link each
other by some (integer) amount L; they also twist about each other by some
(usually non-integer) amount T. Let the writhe W be the writhe of one of the
two curves (alternatively a central curve between the two). Then linking number
equals twist plus writhe,
| L=T+W. | (1) |
For our purposes we need two modifications. First, we are concerned with magnetic flux tubes rather than ribbons. Also, our tubes are not closed: they have ends (footpoints) on a boundary plane or planes. For these two reasons, we use modified expressions for writhe as given in Berger & Prior (2006). For a magnetic field, we can replace linking number L with magnetic helicity H, which averages the linking of all pairs of field lines. For a straight flux tube of flux F, the helicity is H=TF2. (By definition, if field lines twist around the axis by an angle of
The writhe for a curve with endpoints (e.g. the axis of an arbitrary shaped flux tube) is defined by the magnetic Calugareanu formula (Berger & Field 1984; Moffatt & Ricca 1992)
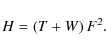
|
(3) |
A current-free tube has zero twist, by Eq. (2). Thus we can define the writhe of a curve also as the helicity (divided by F2) of a thin current-free flux tube which follows the curve.
![\begin{figure}
\par\includegraphics[width=13cm]{13578fg4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg35.png)
|
Figure 4:
The writhe for a family of dipped curves with height function
given by a cubic spline (Eqs. (11)-(14)). All curves
have |
| Open with DEXTER | |
2.2 Local and nonlocal writhe
Berger & Prior (2006) give expressions for the writhe of curves stretching between
two parallel planes, as well as loops with both endpoints on a bottom plane.
The method consists of separating the curve into pieces at maxima and minima
in height z. Let us suppose, for simplicity, that there is just one maximum,
at height z=h. We first ask how much the two pieces, or legs, rotate about
each other while rising from the bottom to the top (see Fig. 3).
Let ![]() be the orientation of the tangent vector at the top of the loop
with respect to the x axis. Also suppose that the line from the positive
endpoint in the bottom plane (z=0) to the negative endpoint has an orientation
be the orientation of the tangent vector at the top of the loop
with respect to the x axis. Also suppose that the line from the positive
endpoint in the bottom plane (z=0) to the negative endpoint has an orientation
![]() .
Then the two legs of the curve rotate about each other by
.
Then the two legs of the curve rotate about each other by
![]() .
The quantity
.
The quantity
contributes to the total writhe. It is called the nonlocal writhe, because for most of their lengths, the two legs are far away from each other. Similar formulae can be derived for loops with more than one maximum (Berger & Prior 2006).
In addition, each leg on its own may contribute to the total writhe. An individual
leg may have a helical shape, for example. The individual contributions will be
called local writhe. Thus for a loop with legs 1 and 2, we have the
decomposition
Let
with a similar expression for W2 (see Berger & Prior 2006).
If only the S shaped projection of the loop onto the bottom plane is available, as it is often the case in solar observations, we can still infer the sign of the local writhe. If the loop bends in a clockwise (counterclockwise) manner from the apex to either footpoint, the local writhe is positive (negative).
2.3 Height dependence of writhe
To illustrate how the writhe behaves, we consider a family of basic
loop shapes. Place the endpoints of the loops at
(x,y,z)=(-1/2,0,0)
and
(x,y,z)=(1/2,0,0). Thus the horizontal distance between the
endpoints is one; equivalently, all lengths will be scaled to this
distance. Let the axis of the loop be a curve
(x(s), y(s), z(s))
for
![]() .
We choose the horizontal coordinate functions
separately from the height function. A family of S shapes can be
generated using the form
.
We choose the horizontal coordinate functions
separately from the height function. A family of S shapes can be
generated using the form
The number
We also need a height function z(s). Figure 3a,b employs
a parabolic shape
where h is the maximum height, and
For curves of this form, local and nonlocal writhe give contributions of
opposite sign. We can ask what the writhe will be as a function of height
h and maximum rotation ![]() (see Fig. 3c).
For tall curves, the nonlocal writhe dominates, while for short curves
the local writhe dominates. Thus, for a given
(see Fig. 3c).
For tall curves, the nonlocal writhe dominates, while for short curves
the local writhe dominates. Thus, for a given ![]() ,
the sign of
writhe depends on the height of the curve. For the family of curves shown
in Fig. 3, the writhe vanishes for all curves with
,
the sign of
writhe depends on the height of the curve. For the family of curves shown
in Fig. 3, the writhe vanishes for all curves with
![]() .
Hence the writhe can be zero, even if the curve exhibits
an S shape when seen from above.
.
Hence the writhe can be zero, even if the curve exhibits
an S shape when seen from above.
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg5.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg52.png)
|
Figure 5:
Heights of the maxima of dipped curves at which the writhe changes sign, for different dip strengths |
| Open with DEXTER | |
Changing the height function seems to make little difference, as long as
the height function has only one maximum.
For example, for
![]() we find almost identical values for the writhe; the crossover height where
writhe vanishes goes down to near
we find almost identical values for the writhe; the crossover height where
writhe vanishes goes down to near
![]() .
A quadratic function
z(s) = h(1 - (2s-1)4) gives similar results, with crossovers
.
A quadratic function
z(s) = h(1 - (2s-1)4) gives similar results, with crossovers
![]() .
.
The writhe graphs do change if the curve has more than one maximum. Consider
a loop with a dip at its central part. We keep the same horizontal coordinate
functions as defined in Eqs. (7)-(9),
but change the height function to a cubic spline. The spline is defined by
the conditions
| z(0) | = | z(1) = 0; | (11) |
| z(0.5-w/2) | = | z(0.5+w/2) = h; | (12) |
| z'(0.5-w/2) | = | z'(0.5) = z'(0.5+w/2) = 0; | (13) |
| z(0.5) | = | (14) |
in addition, second derivatives match at the extrema. The parameter
For these curves, there are two maxima and one minimum. Let the tangent
vector orientations at the maxima be
![]() and
and
![]() ,
with orientation at the minimum
,
with orientation at the minimum
![]() .
Then we replace
Eq. (4) with
.
Then we replace
Eq. (4) with
For such curves, the writhe often has the same sign for all heights h (see the bottom two curves in Fig. 4c). Note that forward (reverse) S shape then gives positive (negative) writhe, for all heights. For some dip shapes (e.g., the top two curves in Fig. 4c) there is still a change in sign of writhe, but at different (and usually larger) heights than in the curves without a dip. For example, Fig. 4d shows the particular case w=0.4 for four different values of rotation angle
Figure 5 shows that the range of w which
yields a sign change of writhe decreases with increasing dip strength
![]() .
For w>0.45, the writhe does not change sign for all
.
For w>0.45, the writhe does not change sign for all
![]() .
Hence, in order for a sign change of writhe at a certain
height to occur, the dip must be relatively small, both in width and depth.
.
Hence, in order for a sign change of writhe at a certain
height to occur, the dip must be relatively small, both in width and depth.
3 Sign of writhe and helicity for S-shaped coronal flux ropes
The height dependence of writhe for loop-shaped curves obtained in Sect. 2 has implications for the relation between S shape, sign of axis writhe, and chirality of coronal flux ropes, which we discuss in the following two sections.
Since a projected S shape of a curve rooted at both ends in the photosphere is an immediate signature of the writhing of the curve out of a plane, one is tempted to expect a unique relationship between the orientation of the S and the sign of the curve's total writhe. However, as shown in Berger & Prior (2006) and in Sect. 2.3, this relationship is not unique. The ambiguity can affect the relationship between the orientation of S-shaped flux ropes and their chirality, since the total axis writhe contributes to the helicity. This leads to the question why the solar observations indicate such a strong association between S shape and chirality.
![\begin{figure}
\par\includegraphics[width=18cm]{13578fg6.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg62.png)
|
Figure 6: a, b) Two kink-unstable flux ropes, displayed by isosurfaces of current density (from Török et al. 2004). Both simulations start from the same configuration with left-handed twist (i.e. negative helicity) and zero axis writhe, but with oppositely directed initial perturbations. The top panels show a top view and the bottom panels show a side view. The rope in a) kinks downward and develops a reverse S shape when seen from above. The rope in b) kinks upward and develops a forward S shape when seen from above. c) Top view on the magnetic axis of the downward kinking rope, shown at the same time as in a). d) Same as c) for the upward kinking rope. Contour plots of the vertical magnetic field in the bottom plane are included in c) and d). White (black) contours show Bz>0 (Bz<0). |
| Open with DEXTER | |
Let us recast the two striking properties
of curves with an S-shaped projection, which are apparent from the results
in Sect. 2.3. First, for curves without a dip, the sign
of the total writhe will flip if the apex height h is changed in a certain
range while the S orientation is kept (Fig. 3c).
Equivalently, if the sign of the total writhe is kept, the orientation of
the S will flip (see Figs. 6 and 11 below). The
flip occurs for h of order 0.4 the footpoint distance, which is relevant
for solar filaments. Second, the occurrence or disappearance of a dip (of
rather moderate depth [Fig. 4]) in a curve of sufficient height
(
![]() )
can flip the sign of the total writhe if the S
orientation is kept (compare Figs. 3 and 4).
)
can flip the sign of the total writhe if the S
orientation is kept (compare Figs. 3 and 4).
These results demonstrate that care is needed when deriving the sign of the
writhe from the observed orientation of S-shaped structures on the solar
disk. It must be ensured that the height of the object is estimated
correctly, and the possibility that the object's axis has a dip must be
taken into account if
![]() .
.
First consider filaments. The height of stable filaments falls below the limit
![]() in most cases. The presence or absence of a dip is then
irrelevant for the relationship between the S orientation
and the sign of the total writhe. For erupting filaments, on the other hand,
it is often possible to follow their evolution into the height range
in most cases. The presence or absence of a dip is then
irrelevant for the relationship between the S orientation
and the sign of the total writhe. For erupting filaments, on the other hand,
it is often possible to follow their evolution into the height range
![]() ,
especially in EUV observations. If filaments rise to such and
greater heights, they hardly ever display a dip in their top part
(see Sects. 4.3 and 4.4). Thus, in practice,
S shape and writhe can be unambiguously related to each other if a distinction
is made between low-lying (stable) and high-arching (erupting) filaments
and intermediate cases are excluded.
,
especially in EUV observations. If filaments rise to such and
greater heights, they hardly ever display a dip in their top part
(see Sects. 4.3 and 4.4). Thus, in practice,
S shape and writhe can be unambiguously related to each other if a distinction
is made between low-lying (stable) and high-arching (erupting) filaments
and intermediate cases are excluded.
The observed correlation between the magnetic orientation (sinistral vs. dextral) of stable active-region filaments and the orientation of their curved ends in the vicinity of sunspots with whirls (Rust & Martin 1994; Zirker et al. 1997) then implies that such filaments possess positive (negative) writhe if the orientation of their axial field is sinistral (dextral). Thus, the sign of writhe is identical to the chirality of the sunspot field near the end of the filament. This corroborates the expectation that such filaments are threaded by field emanating from the sunspot, which suggests that the chirality of their field is right (left) handed for the sinistral (dextral) orientation of the axial field. Also, it allows for the possibility that writhe helicity contains a considerable fraction of the helicity of the field that threads such filaments.
The above relationships also have an interesting implication for
erupting filaments which start from
low heights (
![]() ), possess writhe (S shape) already before
they rise and keep the sign of writhe during their evolution.
These filaments must reverse their S orientation in the course of the rise.
We will consider this in Sect. 4.3.
), possess writhe (S shape) already before
they rise and keep the sign of writhe during their evolution.
These filaments must reverse their S orientation in the course of the rise.
We will consider this in Sect. 4.3.
The relation between S shape and chirality is likely to be simpler for sigmoids. These sources are supposed to lie in separatrix surfaces or quasi-separatrix layers of the field underneath flux ropes (Titov & Démoulin 1999), especially if they form a continuous S (Green & Kliem 2009; Gibson et al. 2004). Consequently, they outline low-lying helical field lines at the periphery of a flux rope, not the axis of a rope. The writhe of these field lines has the same sign as their twist (i.e., as the twist helicity of the rope), and it has a unique relationship to the S orientation.
4 Writhe of erupting flux ropes and filaments
In this section, we measure the writhe of the magnetic axis of a flux rope in the course of ideal MHD instabilities in numerical simulations, and we discuss the implications of the results for filament eruptions and CMEs. In flux rope geometry, the spine of a filament follows the magnetic axis of the rope closely (e.g., Bobra et al. 2008; Aulanier & Démoulin 1998). All simulations presented below integrate the ideal MHD equations and use the analytical coronal flux rope model by Titov & Démoulin (1999) as initial condition. The model consists of a line-tied, arched, and twisted magnetic flux tube embedded in an arcade-like potential field (see Titov & Démoulin 1999, for details). The eruptions of the flux rope are driven either by the helical kink instability (KI) alone, or by the combined action of the KI and the torus instability (Bateman 1978; Kliem & Török 2006, hereafter TI). Numerical diffusion permits magnetic reconnection to occur where current layers steepen in response to the development of these ideal MHD instabilities. In all simulations, we measure the writhe of the rope's magnetic axis using Eqs. (4)-(6) and (15).
4.1 Kink-unstable magnetic flux ropes
Both types of curves discussed in Sect. 2.3, with
and without a dip at the apex, are realised in the 3D MHD simulations
of kink-unstable flux ropes by Török et al. (2004). Figure 6 shows
snapshots of the current channel in the core of the flux rope
in the course of the instability for two of these simulations.
Both simulations start from the same flux rope configuration with a
left-handed average twist angle of
![]() and vanishing
writhe of the axis (whose projection on the bottom plane is a straight
line). In the following we will use the twist angle in
quantitative statements.
Its end-to-end value is calculated as an average over the cross-section
of the current channel in the core of the flux rope (Török et al. 2004).
and vanishing
writhe of the axis (whose projection on the bottom plane is a straight
line). In the following we will use the twist angle in
quantitative statements.
Its end-to-end value is calculated as an average over the cross-section
of the current channel in the core of the flux rope (Török et al. 2004).
The downward kinking rope shown in Fig. 6a has a dip in
its middle part and displays a reverse S shape when seen from above.
Using the parameters defined in Sect. 2.3, its axis can
be described by h=0.26, w=0.57, ![]() ,
and
,
and
![]() .
The rope axis runs relatively flat, has a strong dip, and the two maxima
are relatively far away from each other. From our considerations in
Sect. 2.3, we therefore expect the writhe to be
negative. The negative sign of the writhe follows also, of course, from
the conservation of magnetic helicity in the course of the instability.
The axis writhe is W=-0.26, with
.
The rope axis runs relatively flat, has a strong dip, and the two maxima
are relatively far away from each other. From our considerations in
Sect. 2.3, we therefore expect the writhe to be
negative. The negative sign of the writhe follows also, of course, from
the conservation of magnetic helicity in the course of the instability.
The axis writhe is W=-0.26, with
![]() ,
,
![]() (the latter being made up of contributions -0.23 at the minimum and
-0.13 at each maximum).
(the latter being made up of contributions -0.23 at the minimum and
-0.13 at each maximum).
The axis of the upward kinking rope develops a forward S shape when seen
from above (Fig. 6b). It has only one maximum, at h=0.53.
This height is larger than the crossover height for curves with one
maximum (Sect. 2.3), hence we expect the writhe to
be negative. Again, this follows from helicity conservation. We find
W=-0.30, with
![]() and
and
![]() (
(
![]() ).
Note that
).
Note that
![]() and
and
![]() have the same sign, which is never
the case for the family of S-shaped curves with one maximum discussed in
Sect. 2.3.
This discrepancy is due to the fact that the flux rope axis in the simulation
is not perfectly S-shaped when seen from above (Fig. 6c, d).
Rather, close to the footpoints, the axis bends in the direction opposite
to the overall orientation of the S, contributing negative local writhe.
This additional bending is an indication
for the occurrence of KI eigenmodes with axial wavenumbers k>1
(see, e.g., Linton et al. 1998), which seems plausible given the relatively
large twist used in the simulations. As a consequence, the local writhe
changes sign as one follows the axis from the apex to either footpoint,
which is not the case for the perfectly S-shaped curves discussed in
Sect. 2.3.
have the same sign, which is never
the case for the family of S-shaped curves with one maximum discussed in
Sect. 2.3.
This discrepancy is due to the fact that the flux rope axis in the simulation
is not perfectly S-shaped when seen from above (Fig. 6c, d).
Rather, close to the footpoints, the axis bends in the direction opposite
to the overall orientation of the S, contributing negative local writhe.
This additional bending is an indication
for the occurrence of KI eigenmodes with axial wavenumbers k>1
(see, e.g., Linton et al. 1998), which seems plausible given the relatively
large twist used in the simulations. As a consequence, the local writhe
changes sign as one follows the axis from the apex to either footpoint,
which is not the case for the perfectly S-shaped curves discussed in
Sect. 2.3.
Note that the writhe of the two kinked ropes is very similar. Thus, the two simulations illustrate that flux ropes of equal writhe can have opposite orientations of their projected S-shape, depending on the apex height.
Let us now consider the amount of twist that is converted into writhe in
the course of the KI for the cases shown in Fig. 6. Since
the KI is an ideal MHD instability, both the axial flux and the helicity
of the flux rope must be conserved, i.e., twist must be converted into an
equal amount of writhe of the same sign. However, we must take care when
using the axis writhe to estimate the twist converted within the entire rope, since flux
surfaces far away from the axis might bend in a different way than
the axis (for example if the flux rope expands significantly). In the
simulations shown in Fig. 6, this is not the case, so we can
estimate the twist converted within the entire rope (not just in the vicinity
of its axis) from the axis writhe. The writhe W=-0.26 (W=-0.30)
for the downward (upward) kinking rope corresponds to a converted twist of
![]() (
(
![]() ). In order to check the reliability of
this estimate, we independently measure the flux rope twist for the upward
kinking case at the stage of the evolution shown in Fig. 6b,
using Eqs. (12), (13) in Berger & Prior (2006). We find that the converted twist
measured that way and the value estimated from the axis writhe differ by
less than 1%, as long as we exclude flux surfaces very close to the
rope surface, where the twist is strongly nonuniform (see Fig. 2 in Török et al. 2004). This shows that the
twist converted in the course of the KI can be reliably estimated from the
axis writhe if the inhomogeneity of the radial twist profile and its
changes remain modest. It also shows that the helicity is conserved to a
high degree of accuracy in the simulation.
). In order to check the reliability of
this estimate, we independently measure the flux rope twist for the upward
kinking case at the stage of the evolution shown in Fig. 6b,
using Eqs. (12), (13) in Berger & Prior (2006). We find that the converted twist
measured that way and the value estimated from the axis writhe differ by
less than 1%, as long as we exclude flux surfaces very close to the
rope surface, where the twist is strongly nonuniform (see Fig. 2 in Török et al. 2004). This shows that the
twist converted in the course of the KI can be reliably estimated from the
axis writhe if the inhomogeneity of the radial twist profile and its
changes remain modest. It also shows that the helicity is conserved to a
high degree of accuracy in the simulation.
Interestingly, the amount of converted twist of ![]()
![]() at
the stage of the instabilities shown in Fig. 6 is smaller (only
at
the stage of the instabilities shown in Fig. 6 is smaller (only
![]() 10
10![]() of the initial twist) than one might intuitively expect
from the relatively strong deformation of the flux ropes. It is often
assumed that the KI converts a twist of
of the initial twist) than one might intuitively expect
from the relatively strong deformation of the flux ropes. It is often
assumed that the KI converts a twist of ![]() ,
which probably arises from the fact that helically deformed structures on
the Sun typically exhibit one helical turn, and are therefore often believed
to have a writhe of
,
which probably arises from the fact that helically deformed structures on
the Sun typically exhibit one helical turn, and are therefore often believed
to have a writhe of ![]() (e.g. Rust 2003; see also Sect. 4.2). However,
as Fig. 2 shows, the number of helical turns of a curve or flux
rope can be very different from its writhe, so that estimations of writhe
(and of twist converted in the course of the KI) cannot be made from the
observed number of turns alone. In the following subsection, we will investigate
the conversion of twist into writhe in the course of flux rope
instabilities in more detail.
(e.g. Rust 2003; see also Sect. 4.2). However,
as Fig. 2 shows, the number of helical turns of a curve or flux
rope can be very different from its writhe, so that estimations of writhe
(and of twist converted in the course of the KI) cannot be made from the
observed number of turns alone. In the following subsection, we will investigate
the conversion of twist into writhe in the course of flux rope
instabilities in more detail.
| Figure 7:
Confined filament eruption on 2002 May 27 observed by TRACE in the
195 Å band, and magnetic field lines outlining the core of the kink-unstable flux rope
in the confined eruption simulation by Török & Kliem (2005). The flux
rope axis in the simulation has a writhe of W=0.67 at the state shown
(
|
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg8.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg83.png)
|
Figure 8:
a) Filament eruption on 2003 February 18 observed by the EUV
Imaging Telescope (EIT) onboard the Solar and Heliospheric Observatory
in the 195 Å band at 02:12 UT.
b) The same filament as in a), observed as CME core by HAO's
Mauna Loa Solar Observatory Mk4 white-light coronagraph at 02:34 UT.
The filament as seen by EIT does not show indications for the occurrence
of a significant rotation about its rise direction, whereas the CME
core does (note the crossings of its legs).
c) Two snapshots of the CME simulation in
Török & Kliem (2005) at the same viewing angle but
different spatial scale, taken at
|
| Open with DEXTER | |
| Figure 9:
a) Absolute values of total writhe (dashed) and nonlocal writhe
(solid) as a function of time for the confined (blue) and ejective (red)
flux rope eruption simulations in Török & Kliem (2005).
b) Absolute values of flux rope axis apex rotation in degrees
for the two simulations, as a function of axis apex height normalized to
its initial value. Note that the rotation is proportional to the nonlocal
writhe (a nonlocal writhe of |
|
| Open with DEXTER | |
4.2 Writhe in confined and ejective eruptions
Török & Kliem (2005) presented two simulations of erupting kink-unstable flux
ropes with identical initial average flux rope twist,
![]() ,
and nearly identical geometrical rope parameters, but
different ambient potential fields. In the first simulation (hereafter
TK1; Fig. 7), the potential field decays only slowly with
height above the initial flux rope position. The rope ascends driven by
the KI (similar to the case shown in Fig. 6b), but its rise
terminates at an apex height of
,
and nearly identical geometrical rope parameters, but
different ambient potential fields. In the first simulation (hereafter
TK1; Fig. 7), the potential field decays only slowly with
height above the initial flux rope position. The rope ascends driven by
the KI (similar to the case shown in Fig. 6b), but its rise
terminates at an apex height of ![]() 3.5 times the initial height
h0, in very good quantitative agreement with a confined filament eruption
observed on 2002 May 27 (see Ji et al. 2003).
3.5 times the initial height
h0, in very good quantitative agreement with a confined filament eruption
observed on 2002 May 27 (see Ji et al. 2003).
In the second simulation (hereafter TK2; Fig. 8), the potential field decreases much faster with height. As a result, the TI sets in once the KI has lifted the rope to a height where the potential field drops off sufficiently steeply. The rope is then additionally accelerated by the TI and eventually ejected. The flux rope rise characteristics could be scaled to closely match the acceleration profile of a CME on 2001 May 15 (see Maricic et al. 2004).
Here we measure the evolution of the writhe of the flux rope axis in these
simulations. As in the simulations described in Sect. 4.1,
the writhe vanishes initially. Figure 9 shows the evolution of
W, of
![]() ,
and of the apex rotation. The rotation is proportional
to
,
and of the apex rotation. The rotation is proportional
to
![]() ,
since the axis has only one maximum at all times. The
writhe first grows exponentially, followed by a transition to a saturation phase.
The second strong increase in TK1 at
,
since the axis has only one maximum at all times. The
writhe first grows exponentially, followed by a transition to a saturation phase.
The second strong increase in TK1 at
![]() is caused by an
additional deformation of the flux rope axis due to the onset of magnetic
reconnection with the overlying field around this time (see Török & Kliem 2005).
is caused by an
additional deformation of the flux rope axis due to the onset of magnetic
reconnection with the overlying field around this time (see Török & Kliem 2005).
![]() reaches
reaches ![]() 0.5 in TK2, corresponding to a rotation of
0.5 in TK2, corresponding to a rotation of
![]()
![]() .
A very similar value is found for the rope in TK1 before
it starts to reconnect with the overlying field.
As expected from Sect. 2.3, the nonlocal
writhe clearly dominates the local writhe once the flux rope has sufficiently
risen. In both simulations, the rope develops a clear S shape when viewed in
projection on the bottom plane.
.
A very similar value is found for the rope in TK1 before
it starts to reconnect with the overlying field.
As expected from Sect. 2.3, the nonlocal
writhe clearly dominates the local writhe once the flux rope has sufficiently
risen. In both simulations, the rope develops a clear S shape when viewed in
projection on the bottom plane.
The temporal evolution of the writhe is very similar in TK1 and TK2, since the growth rate of the KI, largely set by the initial twist, is nearly the same (Fig. 9a). The evolution as a function of height, however, is quite different (Fig. 9b). The additional acceleration of the rope by the TI spreads the rotation of the apex over a larger height range (compare also Figs. 1 and 4 in Török & Kliem 2005). The TI, which is a form of the lateral kink instability, primarily expands the unstable flux loop, while the KI primarily produces a helical shape.
Given the nearly identical choice of the initial flux rope parameters in the two simulations, one can conclude from Fig. 9b that a stronger field immediately above the initial rope does not only resist the evolution into a CME more efficiently, but also produces a more pronounced writhing at low heights. This association is opposite to the suggestion in Sturrock et al. (2001) and Fan (2005) that the writhing facilitates the rupture of an unstable flux rope through the overlying field (which is of course strongest at low heights), and it underlines the importance of magnetic reconnection below the rope in permitting the erupting flux rope to pass through the overlying field (e.g., Vrsnak 2008; Lin & Forbes 2000).
Since the writhing in CMEs tends to be distributed over a large height range
(Fig. 9b), much of it may escape detection.
Typically, the writhing is apparent from the apex rotation of an
associated erupting filament or prominence observed in H![]() or in the
EUV, and this is usually limited to the low and middle corona. Therefore,
a significant rotation (and the KI) may occur in a larger fraction of CMEs
than usually thought.
or in the
EUV, and this is usually limited to the low and middle corona. Therefore,
a significant rotation (and the KI) may occur in a larger fraction of CMEs
than usually thought.
An illustrative example, the filament eruption and CME on 2003 February 18
(Fan 2005; Rust & LaBonte 2005), is shown in Fig. 8. The EIT data do not
yield indications of a significant rotation, but the Mk4 coronagraph reveals
that the legs of the CME core cross to form an ``inverse ![]() '' shape
when the core reaches a height of
'' shape
when the core reaches a height of
![]()
![]() above the solar surface. Such a shape develops due to
writhing and is commonly regarded to be evidence of the KI
(e.g., Gilbert et al. 2007).
above the solar surface. Such a shape develops due to
writhing and is commonly regarded to be evidence of the KI
(e.g., Gilbert et al. 2007).
We note that the inverse ![]() shape has been associated for the two
events shown in Figs. 7 and 8 with a writhe
of +1 and -1, respectively (Rust & LaBonte 2005; Rust 2003). However, the values
obtained from the simulations indicate that the writhe of such structures
is rather some number between 0 and 1. This appears plausible if one
recalls that the writhe can be expressed as average crossing number (see
Sect. 2.1 and Fig. 1). Consider, for example,
the filament shown in Fig. 7: from the particular viewing
angle of the observation we see one (positive) crossing of the axis.
Other viewing angles will display either one crossing or
no crossing, so that the average crossing number, i.e. the writhe,
must be less than unity.
shape has been associated for the two
events shown in Figs. 7 and 8 with a writhe
of +1 and -1, respectively (Rust & LaBonte 2005; Rust 2003). However, the values
obtained from the simulations indicate that the writhe of such structures
is rather some number between 0 and 1. This appears plausible if one
recalls that the writhe can be expressed as average crossing number (see
Sect. 2.1 and Fig. 1). Consider, for example,
the filament shown in Fig. 7: from the particular viewing
angle of the observation we see one (positive) crossing of the axis.
Other viewing angles will display either one crossing or
no crossing, so that the average crossing number, i.e. the writhe,
must be less than unity.
4.3 Changing S shape
The simulations presented in Sects. 4.1 and 4.2
all start from a flux rope which is straight in projection on the bottom plane.
Filaments, however, often exhibit an S shape already in their equilibrium
state. In general, the spine of such filaments is a curve of nonvanishing writhe.
In considering their eruption, we assume that the magnetic field has formed
a flux rope topology before or in the early stages of the eruption.
If the filament erupts from a low height (
![]() ), keeping the
sign of writhe (which is expected if one chirality dominates the field in the
source volume), then, according to Sects. 2 and 3,
a change of the S orientation must occur.
), keeping the
sign of writhe (which is expected if one chirality dominates the field in the
source volume), then, according to Sects. 2 and 3,
a change of the S orientation must occur.
Figure 10a, b shows a filament eruption in which an initial strong reverse-S shaped bending is completely straightened out. A change to a forward S may have followed, suggested by the rapid rotation of the filament. However, the eruption occurred about 700 arcsec from disc center, so that the expected transition to a forward S could not be witnessed. Figure 10c-e shows an erupting filament that formed an incomplete S. As expected, it changed its J shape from reverse to forward while rising. See Romano et al. (2005), Rust & LaBonte (2005), and Green et al. (2007) for descriptions and discussions of the apex rotation and the magnetic environment in these events.
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg10.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg91.png)
|
Figure 10: Top row: filament eruption on 2001 June 15 observed by TRACE in 195 Å. a) At 09:57 UT, just before the eruption. The filament exhibits a clear inverse S shape in its upper part. b) At 10:06, during the eruption. The shape of the filament has straightened out. Flare ribbons have formed. Bottom row c-e) filament eruption on 2000 June 6 observed by TRACE in 171 Å at 13:29:27, 13:31:34, and 13:32:20 UT, respectively. The filament (outlined by yellow dots) changes its orientation from a reverse J to a forward J. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg11.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg92.png)
|
Figure 11:
Perspective and top view on magnetic field lines outlining the flux rope core in the simulation described in Sect. 4.3.
a) After the initial relaxation (time reset to t=0).
The two maxima of the flux rope axis have a height of
0.17 of the footpoint separation and
|
| Open with DEXTER | |
Observationally, it is difficult to confirm the dynamic transition from one
complete S shape to the other (e.g., Green et al. 2007). In order to demonstrate
the transition, we perform a
simulation similar to the ones described in Sect. 4.2, but now
starting from an initially S-shaped flux rope. To this end, we construct a stable
numerical equilibrium of a modified version of the Titov & Démoulin (T&D)
model, which contains such a rope. The rope has left-handed average twist of
![]()
![]() ,
similar to the initial twist in the simulations described
above. Note that the helical shape of the constructed flux rope permits a
larger twist in stable equilibrium than the original, toroidal T&D rope of
identical aspect ratio in rather similar ambient field.
We trigger the eruption of the flux rope by imposing slow, quasi-static
converging flows towards the polarity inversion line in the bottom boundary.
The construction of the modified equilibrium and the details of the simulation
will be described in a separate publication. Here we are merely interested in
the evolution of writhe and S shape of the erupting flux rope.
,
similar to the initial twist in the simulations described
above. Note that the helical shape of the constructed flux rope permits a
larger twist in stable equilibrium than the original, toroidal T&D rope of
identical aspect ratio in rather similar ambient field.
We trigger the eruption of the flux rope by imposing slow, quasi-static
converging flows towards the polarity inversion line in the bottom boundary.
The construction of the modified equilibrium and the details of the simulation
will be described in a separate publication. Here we are merely interested in
the evolution of writhe and S shape of the erupting flux rope.
Initially, the flux rope has a dip in its middle part and displays a clear
reverse S shape when seen from above (Fig. 11a). Using the
parameters discussed in Sect. 2.3, its axis can be
characterised by
![]() ,
h=0.17,
,
h=0.17, ![]() ,
and w=0.43.
Inspecting Fig. 4, we expect an axis writhe of about -0.2for these values. Measuring the axis writhe, we find W=-0.07.
As in the above simulations, the writhe is smaller than expected from the
curves discussed in Sect. 2.3, since also here the axis
bends opposite to the overall S close to the flux rope footpoints. However,
only the sign of the writhe is important for the present discussion.
,
and w=0.43.
Inspecting Fig. 4, we expect an axis writhe of about -0.2for these values. Measuring the axis writhe, we find W=-0.07.
As in the above simulations, the writhe is smaller than expected from the
curves discussed in Sect. 2.3, since also here the axis
bends opposite to the overall S close to the flux rope footpoints. However,
only the sign of the writhe is important for the present discussion.
As the converging flows are applied, the flux rope first rises slowly
in response to the progressive weakening of the tension of the overlying
potential field. After
![]() it accelerates rapidly,
most likely due to the onset of the KI or TI (we refrain here from a
detailed investigation of the acceleration mechanism). As the rope rises,
its shape first straigthens out, similar to the filament eruptions shown
in Fig. 10, and the axis writhe goes to zero. At the state
shown in Fig. 11b (
it accelerates rapidly,
most likely due to the onset of the KI or TI (we refrain here from a
detailed investigation of the acceleration mechanism). As the rope rises,
its shape first straigthens out, similar to the filament eruptions shown
in Fig. 10, and the axis writhe goes to zero. At the state
shown in Fig. 11b (
![]() ), the axis has developed
a single maximum (i.e., the dip has disappeared), its height is 0.27, and
its writhe is W=0.01. Subsequently, the rope rapidly develops a forward
S shape, and the writhe becomes negative again. At the state shown in
Fig. 11c (
), the axis has developed
a single maximum (i.e., the dip has disappeared), its height is 0.27, and
its writhe is W=0.01. Subsequently, the rope rapidly develops a forward
S shape, and the writhe becomes negative again. At the state shown in
Fig. 11c (
![]() ), one finds h=0.69 and W=-0.15.
Except for the short period when the writhe is close to zero (as is expected
since the axis becomes almost straight in projection in the reversal), it stays
always negative during the rise of the rope. Therefore, a transition from a
reverse to a forward S shape must occur.
), one finds h=0.69 and W=-0.15.
Except for the short period when the writhe is close to zero (as is expected
since the axis becomes almost straight in projection in the reversal), it stays
always negative during the rise of the rope. Therefore, a transition from a
reverse to a forward S shape must occur.
| Figure 12:
Snapshots of two simulations of kink-unstable flux ropes with an initial average twist of
|
|
| Open with DEXTER | |
A qualitatively similar transition occurred in the simulation of a kink-unstable erupting flux rope by Fan (2005, see her Fig. 6a, b), although the flux rope equilibrium, the external potential field, and the driving in the photospheric boundary all differed from our simulation. Note that Fan displays only field lines below the magnetic axis of the flux rope, but these extend up to the vicinity of the axis, so that the actual rope axis must behave in the same manner. Also note that the straightening of the S occurs in the slow-rise phase for both simulations. These results have interesting consequences for the occurrence of the KI in filament eruptions.
First, it is important to note that both systems are constructed such that only one sign of helicity is present at the onset of the rise. Thus, the initial reduction of the writhe (from a negative value to nearly zero) cannot be driven by a conversion of flux rope twist into writhe under conservation of helicity, since the twist has the same sign as the initial writhe. In other words, if an equilibrium flux rope possesses writhe (i.e., an S shape), its initial slow rise, which must reduce the S shape to a nearly straight rope, cannot be caused by a helical kink instability, since this instability transforms twist into writhe. A different process is required, which actually transforms writhe into twist. The details of this process will likely require further study, but it is obvious that the converging flows in the simulation of Fig. 11 and the continuing emergence of a twisted flux rope through the bottom boundary in Fan (2005) were the drivers in the two simulations.
Second, the ability of the S-shaped flux rope to remain in stable equilibrium for a higher twist than a straight flux rope could accommodate, and the writhe conversion into twist in the slow-rise phase, both support the occurrence of the KI after the flux rope has become straight. The two simulations demonstrate a scenario that enables the KI in a system which is driven significantly beyond the threshold of the instability by the straightening in the slow-rise phase, permitting a significant growth rate.
4.4 Writhe estimate for rotating eruptive filaments
The dominance of the nonlocal writhe over the local writhe for tall curves discussed in Sect. 2.3 provides the possibility of estimating the writhe of rotating filaments that erupt near Sun center even if no 3D observations are available. When the filament has reached a sufficient height, the writhe can be approximated by the nonlocal writhe (see Fig. 9a). The latter can easily be obtained from Eq. (4) by inserting the observed rotation angle (Fig. 3b). For this estimate, one has to verify that the erupting filament does not possess a dip in its upper part in the relevant height range.
Limb observations of erupting filaments and prominences do not indicate the presence of such a dip. We can ask under which circumstances a central dip in an erupting flux rope might occur. In the simulation described in Sect. 4.3, the flux rope has a dip prior to eruption. As the rope rises, the dip disappears early in the evolution, long before the rope reaches a height where the nonlocal writhe dominates the local writhe (Fig. 11b). A dip in the central part of a flux rope will naturally develop if the rope is kink-unstable and is perturbed such that its apex moves downward, as in the simulation shown in Fig. 6a. However, in this simulation the rope does not erupt, rather its central part is continuously moving downward while the remaining parts of the rope do not ascend significantly.
It is well known that a kink-unstable flux rope can develop more than one
helical turn if it is sufficiently twisted (e.g. Linton et al. 1998). For a
flux rope with two turns, a dip might form between the two helical turns.
To check this, we perform a simulation similar to the ones described in
Sects. 4.1 and 4.2, but now we consider a very
large initial flux rope twist of
![]() (Fig. 12a).
As expected, the rope undergoes a strong helical deformation.
However, no dip forms in its central part.
Rather, two dips develop along the legs of the rope, while its central
part ascends (Fig. 12b). For such a configuration, care
must be taken when estimating the writhe from the apex rotation, since the
axis rotation at the other extrema contributes to the nonlocal writhe as
well. However, such a strong writhing is only very rarely observed
(see, e.g., Romano et al. 2003, for a filament
eruption that corresponds quite well to the simulation in
Fig. 12b).
(Fig. 12a).
As expected, the rope undergoes a strong helical deformation.
However, no dip forms in its central part.
Rather, two dips develop along the legs of the rope, while its central
part ascends (Fig. 12b). For such a configuration, care
must be taken when estimating the writhe from the apex rotation, since the
axis rotation at the other extrema contributes to the nonlocal writhe as
well. However, such a strong writhing is only very rarely observed
(see, e.g., Romano et al. 2003, for a filament
eruption that corresponds quite well to the simulation in
Fig. 12b).
When the simulation is repeated with a small, downward directed initial velocity perturbation, a remarkably different shape is obtained. Now the rope develops a large dip in its central part. As in the simulation shown in Fig. 6a, the central section moves downward. However, in contrast to that simulation, the remaining parts of the rope now rise significantly (Fig. 12c). Still, they do not succeed in pulling the central part upward, that part rather keeps moving downward until it hits the bottom plane - a situation never observed on the Sun.
One can construct a rising flux rope with dipped apex by making it simultaneously strongly unstable with respect to the KI and TI. While such a situation can be realized in laboratory and corresponding numerical simulations of filament eruptions (Bellan & Hansen 1998; Arnold et al. 2008), it appears very special and, hence, unlikely to occur under solar conditions.
We conclude that the writhe of erupting filaments can be reliably estimated from the apex rotation in the relevant height range where the nonlocal writhe dominates, unless the filament develops a very particular shape with multiple maxima or minima.
5 Summary
The availability of 3D observations provided by the STEREO spacecraft, combined with recently developed analytical expressions, facilitates obtaining the writhe of helical structures in the solar corona. In order to explore the relevance of this quantity for coronal phenomena, we investigated how it relates to the projected shape of helical curves and measured its evolution in numerical simulations of ideal MHD flux rope instabilities. Our results and their implications for stable and eruptive coronal objects can be summarized as follows.
(1) The relation between writhe and projected S shape of a curve with both end points in a plane is not unique. It depends on the height of the curve and on the presence or absence of dips. Therefore, in principle, care must be taken when associating a sign of writhe to an observed S shape on the Sun. However, we demonstrated that this ambiguity does not affect low-lying filaments, as long as their height remains below about 0.4 their footpoint distance, or soft X-ray sigmoids. This supports the established empirical rule which associates stable forward (reverse) S shaped structures low in the corona with positive (negative) helicity.
(2) Kink-unstable erupting flux ropes transform a far smaller fraction of their twist helicity into writhe helicity than often assumed. The writhe and the number of turns of a helical object differ in general. In particular, a simple leg crossing of a rising filament in sky projection can not be taken as evidence that the writhe of the filament is close to unity.
(3) Confined flux rope eruptions tend to show stronger writhe at low heights than ejective eruptions (CMEs), which acquire writhe over a larger height range. This argues against suggestions that the writhing facilitates the rise of unstable flux ropes through the overlying field, and it implies that a significant rotation may occur in a larger fraction of CMEs than suggested by the apex rotation of associated erupting filaments low in the corona.
(4) Erupting filaments which are S shaped already before the eruption and keep the sign of their axis writhe (which is expected if field of one chirality dominates the source volume of the eruption), must reverse their S shape in the course of the rise. In flux rope geometry, the initial straightening up to the reversal represents a conversion of writhe into twist, which cannot be caused by the helical kink instability. However, the writhe conversion can be a mechanism that triggers the instability after the straightening.
(5) The writhe of rising loops of simple shape (which do not have secondary maxima or minima) can be estimated from the angle of rotation about the direction of ascent, once the apex height exceeds the footpoint separation significantly. This provides a convenient means to estimate the writhe of erupting filaments which rise towards the observer, even if no 3D observations are available.
We emphasize that for flux tubes where the twist varies significantly with radius, the interplay between twist, writhe, and helicity becomes more difficult (Longcope & Malanushenko 2008). Usually an average of the twist over the cross section of a flux tube is of interest, while the writhe is a property of a single field line, in this context the reference field line of the twist.
This work shows that writhe is a useful quantity in interpreting S shaped coronal structures and in constraining eruption models. It can straightforwardly be computed for numerical data and can often be estimated from observations. It has a range of further applications in solar physics, for example, the study of the dynamo (Asgari-Targhi & Berger 2009), of flux ropes rising through the convection zone (e.g., Linton et al. 1998), and of magnetic loops connecting different active regions, including transequatorial loops (e.g., Chen et al. 2007).
AcknowledgementsWe thank the referee for his/her useful suggestions and L. van Driel-Gesztelyi and P. Démoulin for many helpful discussions. T.T. and B.K. acknowledge an invitation to the University of New Hampshire and helpful discussions with T. G. Forbes. This work was supported by an STFC Rolling Grant, the DFG, and NASA grants NNH06AD58I and NNX08AG44G. Financial support by the European Comission through the SOLAIRE network (MTRM-CT-2006-035484) is gratefully acknowledged. The research leading to these results has received funding from the European Commission's Seventh Framework Programme (FP7/2007-2013) under the grant agreement No. 218816 (SOTERIA project, www.soteria-space.eu).
References
- Aldinger, J., Klapper, I., & Tabor, M. 1995, J. Knot Theory Ram., 4, 343 [CrossRef] [Google Scholar]
- Amari, T., Luciani, J. F., Mikic, Z., & Linker, J. 2000, ApJ, 529, L49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Antiochos, S. K., DeVore, C. R., & Klimchuk, J. A. 1999, ApJ, 510, 485 [Google Scholar]
- Arnold, L., Dreher, J., Grauer, R., Soltwisch, H., & Stein, H. 2008, Phys. Plasmas, 15, 042106 [NASA ADS] [CrossRef] [Google Scholar]
- Asgari-Targhi, M., & Berger, M. 2009, Geophys. Astrophys. Fluid Dynamics, 103, 69 [Google Scholar]
- Aulanier, G., & Démoulin, P. 1998, A&A, 329, 1125 [NASA ADS] [Google Scholar]
- Bateman, G. 1978, MHD instabilities (Cambridge, Mass.: MIT Press) [Google Scholar]
- Bellan, P. M., & Hansen, J. F. 1998, Phys. Plasmas, 5, 1991 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, M. A. 1984, Geophys. Astrophys. Fluid Dynamics, 30, 79 [Google Scholar]
- Berger, M. A., & Field, G. B. 1984, J. Fluid Mech., 147, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, M. A., & Prior, C. 2006, J. Phys. A: Math. Gen., 39, 8321 [Google Scholar]
- Bobra, M. G., van Ballegooijen, A. A., & DeLuca, E. E. 2008, ApJ, 672, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Calugareanu. 1959, Czechoslovak Math. J., 11, 588-625 [Google Scholar]
- Canfield, R. C., Hudson, H. S., & McKenzie, D. E. 1999, Geophys. Res. Lett., 26, 627 [Google Scholar]
- Chen, J., Bao, S., & Zhang, H. 2007, Sol. Phys., 242, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P. 2008, Annales Geophysicae, 26, 3113 [CrossRef] [Google Scholar]
- Fan, Y. 2005, ApJ, 630, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y., & Gibson, S. E. 2003, ApJ, 589, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, T. G. 2000, J. Geophys. Res., 105, 23153 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, T. G., & Isenberg, P. A. 1991, ApJ, 373, 294 [Google Scholar]
- Gibson, S. E., Fan, Y., Mandrini, C., Fisher, G., & Demoulin, P. 2004, ApJ, 617, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, H. R., Alexander, D., & Liu, R. 2007, Sol. Phys., 245, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Green, L. M., & Kliem, B. 2009, ApJ, 700, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Green, L. M., Kliem, B., Török, T., van Driel-Gesztelyi, L., & Attrill, G. D. R. 2007, Sol. Phys., 246, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, H., Wang, H., Schmahl, E. J., Moon, Y.-J., & Jiang, Y. 2003, ApJ, 595, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Kliem, B., & Török, T. 2006, , 96, 255002 [Google Scholar]
- Kliem, B., Titov, V. S., & Török, T. 2004, A&A, 413, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, J., & Forbes, T. G. 2000, J. Geophys. Res., 105, 2375 [NASA ADS] [CrossRef] [Google Scholar]
- Linton, M. G., Dahlburg, R. B., Fisher, G. H., & Longcope, D. W. 1998, ApJ, 507, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., & Malanushenko, A. 2008, ApJ, 674, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C., & Berger, M. A. 2003, ApJ, 589, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Maggioni, F., & Ricca, R. L. 2008, Comput. Math. Appl. Amsterdam, 55, 1044 [Google Scholar]
- Maricic, D., Vrsnak, B., Stanger, A. L., & Veronig, A. 2004, Sol. Phys., 225, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Moffatt, H. K., & Ricca, R. L. 1992, Proc. Roy. Soc. A, 439, 411 [Google Scholar]
- Muglach, K., Wang, Y., & Kliem, B. 2009, ApJ, 703, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Pevtsov, A. A., Canfield, R. C., & McClymont, A. N. 1997, ApJ, 481, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Contarino, L., & Zuccarello, F. 2003, Sol. Phys., 214, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Contarino, L., & Zuccarello, F. 2005, A&A, 433, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rust, D. M. 2003, Adv. Space Res., 32, 1895 [NASA ADS] [CrossRef] [Google Scholar]
- Rust, D. M., & Kumar, A. 1996, ApJ, 464, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Rust, D. M., & LaBonte, B. J. 2005, ApJ, 622, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Rust, D. M., & Martin, S. F. 1994, in Solar Active Region Evolution: Comparing Models with Observations, ed. K. S. Balasubramaniam, & G. W. Simon, ASP Conf. Ser., 68, 337 [Google Scholar]
- Sakurai, T. 1976, PASJ, 28, 177 [NASA ADS] [Google Scholar]
- Sturrock, P. A., Weber, M., Wheatland, M. S., & Wolfson, R. 2001, ApJ, 548, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Titov, V. S., & Démoulin, P. 1999, A&A, 351, 707 [NASA ADS] [Google Scholar]
- Török, T., & Kliem, B. 2005, ApJ, 630, L97 [Google Scholar]
- Török, T., Kliem, B., & Titov, V. S. 2004, A&A, 413, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vrsnak, B. 2008, Annales Geophysicae, 26, 3089 [Google Scholar]
- Vrsnak, B., Ruzdjak, V., Rompolt, B., Rosa, D., & Zlobec, P. 1993, Sol. Phys., 146, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D. R., Török, T., Démoulin, P., van Driel-Gesztelyi, L., & Kliem, B. 2005, ApJ, 628, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Yeates, A. R., & Mackay, D. H. 2009, ApJ, 699, 1024 [Google Scholar]
- Yurchyshyn, V. 2008, ApJ, 675, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, G. P., Wang, J. X., Zhang, J., et al. 2006, ApJ, 651, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Zirker, J. B., Martin, S. F., Harvey, K., & Gaizauskas, V. 1997, Sol. Phys., 175, 27 [Google Scholar]
All Figures
| |
Figure 1: A closed flux tube as seen from three different angles. The number of apparent crossings one sees depends on the viewing angle. Crossings can be called left-handed (negative) or right-handed (positive), depending on the relative orientations of the upper and lower field lines. The diagrams shown in d) give the two possible cases (up to rotation). The tube shown has an average crossing number, or writhe, of W = 0.566. Most viewing angles display a positive crossing, as in b). However, some angles do not show any crossings, as in a), and there is a small set of angles which display a negative crossing, as in c). (The latter picture of the tube is obtained by viewing it from the top.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm]{13578fg2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg27.png)
|
Figure 2: The writhe of a coil depends on its aspect ratio (height/width) as well as how many turns it has. Both coils shown have 3 turns, but the fat coil in a) has a writhe W = 2.68, while the thin coil in b) has a writhe W = 0.46. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg3.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg29.png)
|
Figure 3:
A loop with one maximum, seen from the side a) and the top b). The nonlocal writhe is proportional to the difference in angle between the
tangent vector at the top, and the line connecting the footpoints. This angle
is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm]{13578fg4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg35.png)
|
Figure 4:
The writhe for a family of dipped curves with height function
given by a cubic spline (Eqs. (11)-(14)). All curves
have |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg5.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg52.png)
|
Figure 5:
Heights of the maxima of dipped curves at which the writhe changes sign, for different dip strengths |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{13578fg6.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg62.png)
|
Figure 6: a, b) Two kink-unstable flux ropes, displayed by isosurfaces of current density (from Török et al. 2004). Both simulations start from the same configuration with left-handed twist (i.e. negative helicity) and zero axis writhe, but with oppositely directed initial perturbations. The top panels show a top view and the bottom panels show a side view. The rope in a) kinks downward and develops a reverse S shape when seen from above. The rope in b) kinks upward and develops a forward S shape when seen from above. c) Top view on the magnetic axis of the downward kinking rope, shown at the same time as in a). d) Same as c) for the upward kinking rope. Contour plots of the vertical magnetic field in the bottom plane are included in c) and d). White (black) contours show Bz>0 (Bz<0). |
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
Confined filament eruption on 2002 May 27 observed by TRACE in the
195 Å band, and magnetic field lines outlining the core of the kink-unstable flux rope
in the confined eruption simulation by Török & Kliem (2005). The flux
rope axis in the simulation has a writhe of W=0.67 at the state shown
(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg8.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg83.png)
|
Figure 8:
a) Filament eruption on 2003 February 18 observed by the EUV
Imaging Telescope (EIT) onboard the Solar and Heliospheric Observatory
in the 195 Å band at 02:12 UT.
b) The same filament as in a), observed as CME core by HAO's
Mauna Loa Solar Observatory Mk4 white-light coronagraph at 02:34 UT.
The filament as seen by EIT does not show indications for the occurrence
of a significant rotation about its rise direction, whereas the CME
core does (note the crossings of its legs).
c) Two snapshots of the CME simulation in
Török & Kliem (2005) at the same viewing angle but
different spatial scale, taken at
|
| Open with DEXTER | |
| In the text | |
| |
Figure 9:
a) Absolute values of total writhe (dashed) and nonlocal writhe
(solid) as a function of time for the confined (blue) and ejective (red)
flux rope eruption simulations in Török & Kliem (2005).
b) Absolute values of flux rope axis apex rotation in degrees
for the two simulations, as a function of axis apex height normalized to
its initial value. Note that the rotation is proportional to the nonlocal
writhe (a nonlocal writhe of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg10.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg91.png)
|
Figure 10: Top row: filament eruption on 2001 June 15 observed by TRACE in 195 Å. a) At 09:57 UT, just before the eruption. The filament exhibits a clear inverse S shape in its upper part. b) At 10:06, during the eruption. The shape of the filament has straightened out. Flare ribbons have formed. Bottom row c-e) filament eruption on 2000 June 6 observed by TRACE in 171 Å at 13:29:27, 13:31:34, and 13:32:20 UT, respectively. The filament (outlined by yellow dots) changes its orientation from a reverse J to a forward J. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{13578fg11.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa13578-09/Timg92.png)
|
Figure 11:
Perspective and top view on magnetic field lines outlining the flux rope core in the simulation described in Sect. 4.3.
a) After the initial relaxation (time reset to t=0).
The two maxima of the flux rope axis have a height of
0.17 of the footpoint separation and
|
| Open with DEXTER | |
| In the text | |
| |
Figure 12:
Snapshots of two simulations of kink-unstable flux ropes with an initial average twist of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.