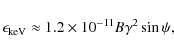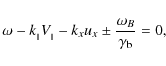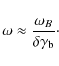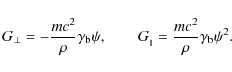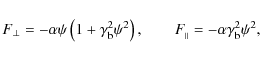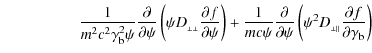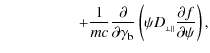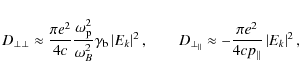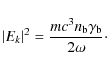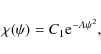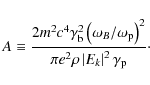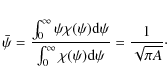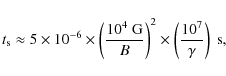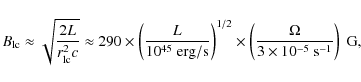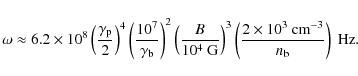EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 516 (June-July 2010) A&A, 516 (2010) A12 Full HTML
Free Access
Issue
A&A
Volume 516, June-July 2010
Article Number A12
Number of page(s) 4
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/200913515
Published online 17 June 2010
A&A 516, A12 (2010)

Quasi-linear diffusion driving the synchrotron emission in active galactic nuclei

Z. Osmanov - G. Machabeli

Center for Theoretical Astrophysics, ITP, Ilia State University, Kazbegi str. 2a, Tbilisi 0160, Georgia

Received 20 October 2009 / Accepted 3 March 2010

Abstract
Aims. We study the role of the quasi-linear diffusion (QLD) in producing X-ray emission by means of ultra-relativistic electrons in AGN magnetospheric flows.
Methods. We examined two regions: (a) an area close to the black hole and (b) the outer magnetosphere. The synchrotron emission has been studied for ultra-relativistic electrons and was shown that the QLD generates the soft and hard X-rays, close to the black hole and on the light cylinder scales respectively.
Results. By considering the cyclotron instability, we show that despite the short synchrotron cooling timescales, the cyclotron modes excite transverse and longitudinal-transversal waves. On the other hand, it is demonstrated that the synchrotron reaction force and a force responsible for the conservation of the adiabatic invariant tend to decrease the pitch angles, whereas the diffusion, that pushes back on electrons by means of the aforementioned waves, tends to increase the pitch angles. By examining the quasi-stationary state, we investigate a regime in which these two processes are balanced and a non-vanishing value of pitch angles is created.

Key words: galaxies: active - instabilities - magnetohydrodynamics (MHD) - radiation mechanisms: non-thermal

1 Introduction

One of the major problems related to active galactic nuclei is the origin of the nonthermal high energy radiation. According to standard approaches, the most commonly encountered radiation mechanisms at a level sufficient for application to AGN is the synchrotron mechanism and the inverse Compton scattering (Blandford et al. 1990). Because of strong synchrotron losses, relativistic electrons in general, quickly lose their perpendicular energy, and on a synchrotron cooling timescale ${\sim} 10^{-6}{-}10^{-3}$ s, the particles transit to their ground Landau state. In this case, the electrons may be described approximately as moving one-dimensionally along the field lines and the synchrotron radiation to have been absorbed. This is why the broadband emission spectrum of AGN consists of two components: the high-energy (from X-rays to $\gamma$-rays) component is formed by the inverse Compton scattering and not by the synchrotron mechanism, which is supposed to be involved only in the low-energy (from radio to optical/UV) band. However, under certain conditions, due to the QLD of cyclotron waves, the pitch angles might increase, leading to the efficient production of synchrotron radiation.

The QLD was applied to pulsars in a series of papers (Machabeli & Usov 1979; Lominadze et al. 1979 ; Malov & Machabeli 2001). Malov & Machabeli (2001) studied optical synchrotron emission of radio pulsars. In the outer parts of pulsar magnetospheres, these authors demonstrated that because of the cyclotron instability, the transverse momenta of relativistic particles is non-zero, giving rise to the pitch angle distribution, which in turn, via the QLD, leads to the synchrotron emission. Applying the kinetic approach to a particular pulsar, RX J1856.5-3754, Chkheidze & Machabeli (2007) showed that waves excited by the cyclotron mechanism, in terms of the creation of the pitch angles, come into the radio domain. The QLD interesting because the recent detection of very high energy (VHE) pulsed emission form the Crab pulsar (Albert et al. 2008). The MAGIC Cherenkov telescope discovered the pulsed emission above 25 GeV between 2007 October and 2008 February. It has been shown that the corresponding VHE signal peaks at the same phase as the signal in the optical spectrum (Albert et al. 2008). In turn this indicates that the polar cap models must be excluded from the possible scenario of the radiation. On the other hand, analysis of the MAGIC data implies that the location of the aforementioned VHE and optical radiation must be the same. According to the quasi-linear diffusion, on length scales typical of the light cylinder (a hypothetical zone, where the linear velocity of rigid rotation equals exactly the speed of light), the cyclotron instability occurs in the optical band, leading to an increase in the pitch angles via the QLD. This mechanism automatically explains the coincidence of phases in the optical and VHE bands (Machabeli & Osmanov 2009 ).

AGN magnetospheres are supported by strong magnetic fields and therefore, the QLD might also be of great importance to these particular objects. As aforementioned, for ultra-relativistic electrons the synchrotron losses are so efficient that the synchrotron mechanism takes place only for relatively low energy particles and highly relativistic electrons are involved in radiation via the inverse Compton scattering. This is not true for the QLD, because as for the pulsar magnetospheres, AGN magnetospheric particles will undergo the QLD, preventing the rapid damping of pitch angles, giving rise to the emission process.

In the present paper, we study the role of the QLD in producing the X-rays via the synchrotron mechanism in AGN magnetospheres. The paper is organized as follows. In Sect. 2, we consider the kinetic approach to the quasi-linear diffusion, in Sect. 3 we present our results and in Sect. 4 we summarize them.

2 Main consideration

When relativistic particles move in the magnetic field, they emit electromagnetic waves corresponding to the photon energies (Rybicki & Lightman 1979)

\begin{displaymath}% \epsilon_{{\rm keV}}\approx 1.2\times 10^{-11}B\gamma^2\sin\psi, \end{displaymath} (1)

where by B we denote the magnetic induction, $\gamma$ is the Lorentz factor of particles, and $\psi$ denotes the pitch angle. Equation (1) represents the photon energy in the maximum emission intensity. As we already mentioned in the introduction, the timescale is very short for the transit to the ground Landau state that provides quasi-one-dimensional motion of electrons along the field lines without radiation. As investigated in a series of papers (Machabeli & Usov 1979; Malov & Machabeli 2001), the cyclotron instability of the electron-positron plasma under certain conditions, may however ``create'' pitch angles, which activate the subsequent synchrotron process.

We consider the plasma to consist of two components: (a) the electron-positron plasma component with the Lorentz factor, $\gamma_{\rm p}$ and (b) highly relativistic electrons, the so-called beam component with the Lorentz factor, $\gamma_{\rm b}$ $(\gamma_{\rm b}\gg\gamma_{\rm p})$. According to the the QLD model, the consequent transverse modes generate frequencies (Kazbegi et al. 1992)

\begin{displaymath}% \omega_{\rm t} \approx kc\left(1-\delta\right), \end{displaymath} (2)

where

\begin{displaymath}% \delta = \frac{\omega_{\rm p}^2}{4\omega_B^2\gamma_{\rm p}^3}\cdot \end{displaymath} (3)

We denote by k the modulus of the wave vector, where c is the speed of light, $\omega_{\rm p} \equiv \sqrt{4\pi n_{\rm p}e^2/m}$ is the plasma frequency, $\omega_B\equiv eB/mc$ is the cyclotron frequency, e and m are the electron charge and the rest mass, respectively, and $n_{\rm p}$ is the plasma density.

Kazbegi et al. (1992) demonstrated that the aforementioned waves are excited if the cyclotron resonance condition

\begin{displaymath}% \omega - k_{_{\Vert}}V_{_{\Vert}}-k_xu_x\pm\frac{\omega_B}{\gamma_{\rm b}} = 0, \end{displaymath} (4)

is satisfied, where $u_x\equiv cV_{_{_{\Vert}}}\gamma_{\rm b}/\rho\omega_B$ denotes the drift velocity of particles, $k_{_{\Vert}}$ is the wave vector's longitudinal (parallel to the background magnetic field) component, kx is the wave vector's component along the drift, $V_{_{\Vert}}$ is the component of velocity along the magnetic field lines, and $\rho$ is field line's curvature radius. By taking into account the resonance condition, from Eq. (2), one can obtain an expression for the excited cyclotron frequency

\begin{displaymath}% \omega\approx \frac{\omega_B}{\delta\gamma_{\rm b}}\cdot \end{displaymath} (5)

In deriving Eq. (5), we have taken into account the condition $\lambda>n_{\rm p}^{-1/3}$, which means that in exciting waves all resonance particles participate (collective phenomena), therefore the range of spectral frequencies is wide. In general, the cyclotron mode excites if the distribution function, f, is almost one dimensional and depends on the longitudinal momentum. On the other hand, the magnetic field in AGN magnetospheres is strong enough to maintain the frozen-in condition, which in turn means that the particles follow field lines and thus, f behaves according to p||.

When particles move in a nonuniform magnetic field, they undergo a force $\vec{G}$ that is responsible for the conservation of the adiabatic invariant, $I = 3cp_{\perp}^2/2eB$ (Landau & Lifshitz 1971). The corresponding components of this force are given by

\begin{displaymath}% G_{\perp} = -\frac{mc^2}{\rho}\gamma_{\rm b}\psi, \qquad G_{_{\Vert}} = \frac{mc^2}{\rho}\gamma_{\rm b}\psi^2. \end{displaymath} (6)

In the synchrotron regime, we should detect the radiative force (Landau & Lifshitz 1971):

\begin{displaymath}% F_{\perp} = -\alpha\psi\left(1 + \gamma_{\rm b}^2\psi^2\right), \qquad F_{_{\Vert}} = -\alpha\gamma_{\rm b}^2\psi^2, \end{displaymath} (7)

where $\alpha = 2e^2\omega_B^2/(3c^2)$.

These forces $(\vec{F}, \vec{G})$ tend to decrease the pitch angle of the particle. On the other hand, the feedback of low frequency waves excited by particles be means of the cyclotron resonance, leads to the quasi-linear diffusion of particles. In turn, the QLD, attempts to widen the range of the pitch angles opposing both $\vec{F}$ and $\vec{G}$. The dynamical process saturates when the effects of the above-mentioned forces are balanced by the diffusion. There are, in general two different mechanisms of radiation: (I) the resonance cyclotron emission and (II) the synchrotron process, the first of which, as we have already mentioned, is a collective phenomenon $(\lambda>n_{\rm p}^{-1/3})$, whereas the second is a single particle process $(\lambda<n_{\rm p}^{-1/3})$ that does not require superposition.

We consider the case $\vert G_{\perp}\vert\gg \vert F_{\perp}\vert$ and $\vert G_{_\parallel}\vert\ll \vert F_{_\parallel}\vert$. By assuming a quasi-stationary scenario $(\partial/\partial t = 0)$, the corresponding kinetic equation can be given by (Malov & Machabeli 2001)

                                        $\displaystyle \frac{1}{mc\gamma_{\rm b}\psi}\frac{\partial}{\partial\psi} \left... ..._{\rm b}}\left(F_{_\parallel} f\right) + \upsilon\frac{\partial f}{\partial r}=$  
    $\displaystyle \qquad\qquad\quad\frac{1}{m^2c^2\gamma_{\rm b}^2\psi}\frac{\parti... ...ft(\psi^2 D_{_{\perp\parallel}}\frac{\partial f}{\partial\gamma_{\rm b}}\right)$  
    $\displaystyle \qquad\qquad\quad+\frac{1}{mc}\frac{\partial}{\partial\gamma_{\rm b}} \left(\psi D_{_{\perp\parallel}}\frac{\partial f}{\partial\psi}\right),$ (8)

where $f = f(\psi,p{_{_\parallel}})$ is the distribution function of particles, $p_{_\parallel}$ is the longitudinal momentum,

\begin{displaymath}% D_{\perp\perp}\approx \frac{\pi e^2}{4c}\frac{\omega_{\rm p... ...rox -\frac{\pi e^2}{4cp_\parallel}\left\vert E_k\right\vert^2, \end{displaymath} (9)

are the diffusion coefficients, $n_{\rm b}$ is the density of the beam component, and |Ek|2 is the energy density per unit wavelength. The corresponding energy density can be estimated to be |Ek|2k. We assume that half of the plasma energy density, $mc^2n_{\rm b}\gamma_{\rm b}/2$ is converted into the waves, such that |Ek|2 is given by

\begin{displaymath}% \left\vert E_k\right\vert^2 = \frac{mc^3n_{\rm b}\gamma_{\rm b}} {2\omega}\cdot \end{displaymath} (10)

By expressing the distribution function as $\chi(\psi)f(p_{_\parallel})$, one can solve Eq. (9) for $\chi$

\begin{displaymath}% \chi(\psi) = C_1{\rm e}^{-A\psi^2}, \end{displaymath} (11)

where

\begin{displaymath}% A\equiv \frac{2m^2c^4\gamma_{\rm b}^2\left(\omega_B/\omega_... ...2} {\pi e^2\rho\left\vert E_k\right\vert^2\gamma_{\rm p}}\cdot \end{displaymath} (12)

The corresponding mean value of the pitch angle can be estimated as to be

\begin{displaymath}% \bar{\psi} = \frac{\int_{0}^{\infty}\psi\chi(\psi){\rm d}\p... ...}^{\infty}\chi(\psi){\rm d}\psi} = \frac{1}{\sqrt{\pi A}}\cdot \end{displaymath} (13)

Therefore, as we see, the QLD maintains the pitch angles and prevents them from damping, which in turn maintains the properties of the synchrotron process.

3 Discussion

Most AGN exhibit VHE emission, which in turn indicates that the AGN magnetosphere is contained of ultra-relativistic electrons. In this context, the origin of acceleration of particles is very important. Proposed mechanisms such as Fermi-type acceleration (Catanese & Weeks 1999), centrifugal acceleration (Machabeli & Rogava 1994; Osmanov et al. 2007; Rieger & Aharonian 2008), and acceleration due to the black hole dynamo mechanism (Levinson 2000) can effectively provide Lorentz factors of the order of ${\sim} 10^{5-9}$.

For an isotropic distribution of relativistic electrons (Blandford et al. 1990) in very strong magnetic fields, particles emit in the synchrotron regime with the power, $P\approx 2e^4B^2\beta_{\perp}^2\gamma^2/(3m^2c^3)$, therefore by assuming $\beta_{\perp}\sim 1$, the synchrotron cooling timescale, $t_{\rm s}\equiv\gamma mc^2/P$ can be estimated to be

\begin{displaymath}% t_{\rm s}\approx 5\times 10^{-6}\times\left(\frac{10^4~{\rm G}}{B}\right)^2\times\left(\frac{10^7}{\gamma}\right)~{\rm s}, \end{displaymath} (14)

where we have taken into account that the energy is uniformly distributed between the beam and the plasma components, $n_{\rm b}\gamma_{\rm b}\approx n_{\rm p}\gamma_{\rm p}$, and the magnetic field is normalized to the typical value of the magnetic induction close to the supermassive black hole (Thorne et al. 1988). As is clear from this expression, the synchrotron timescale for ultra-relativistic electrons in the very vicinity of the black hole is so short ( ${\sim} 10^{-5}$ s) that these particles very rapidly lose their perpendicular kinetic energy and transit to the ground Landau state. One can obtain a similar result for outer magnetospheric lengthscales, thus for the light cylinder area, when the magnetic field is determined by the bolometric luminosity, L of AGN to be the equipartition field

\begin{displaymath}% B_{\rm {lc}}\approx \sqrt{\frac{2L}{r_{\rm {lc}}^2c}}\appro... ...t(\frac{\Omega}{3\times 10^{-5}~ {\rm s}^{-1}}\right)~{\rm G}, \end{displaymath} (15)

where $r_{\rm {lc}} = c/\Omega$ is the light cylinder radius and $\Omega$ the angular velocity of rotation. If we consider a typical value of the bolometric luminosity, ${\sim} 10^{45}$ erg/s, then one can see from Eq. (15) that the magnetic induction equals approximately 290 G, which, combined with Eq. (14), leads to the cooling timescale, $5.6\times 10^{-4}$ s.

All quantities vary because of the cyclotron instability, which causes to the QLD. By using Eqs. (3-5), we can estimate the frequency of the cyclotron mode to be

\begin{displaymath}% \omega\approx 6.2\times 10^8\left(\frac{\gamma_{\rm p}}{2}\... ...(\frac{2\times 10^3~{\rm cm}^{-3}}{n_{\rm b}}\right)~{\rm Hz}. \end{displaymath} (16)

We consider a nearby zone of the AGN with mass $M_{\rm BH} = 10^9~M_{\odot}$ ($M_{\odot}$ is the solar mass) and typical magnetospheric parameters $n_{\rm b} = 2000~{\rm cm}^{-3}$, B = 104 G and $\gamma _{\rm p} = 2$. Then, examining the ultra-relativistic beam component electrons with Lorentz factors $\gamma_{\rm b}\in\{3;4\}\times 10^7$ and assuming that the curvature radius $\rho$ of field lines is of the order of the gravitational radius, $R_{\rm g}\equiv 2GM_{\rm BH}/c^2$, one can see from Eq. (13) that the created pitch angle is of the order of 10-9 rad, which indicates the synchrotron emission in the X-ray domain [see Eq. (1)]. In Fig. 1, we show the synchrotron emission energy versus the excited cyclotron frequency. As is clear from the figure, the cyclotron instability appears in the radio band leading to the X-ray emission. One can see that the radio emission is generated by the collective phenomena. We consider the radio frequency 5 MeV, corresponding to the wavelength, $\lambda$, of the order of 6000 cm. On the other hand, the average distance between particles, $d=n_{\rm p}^{-1/3}$ is of the order of $2\times 10^{-4}$ cm, which is shorter by many orders of magnitude than $\lambda$. This in turn, indicates that emission in the radio band is provided by the collective phenomena. In contrast to this, the VHE radiation generated in the X-ray domain (see Fig. 1) is a single particle mechanism. The importance of the quasi-linear diffusion is twofold: (a) it generates the synchrotron radiation in strong magnetic fields for ultra-relativistic particles, which would be impossible without the QLD and (b) it simultaneously excites emission in two different domains. In this context, it is easy to check whether the emission is driven by the QLD by verifying that (I) the radiation is linearly polarized and (II) both signals have equal phases. In (Machabeli & Osmanov 2009 ), we performed the same theoretical analysis of the observed VHE (>25 GeV) pulsed emission of the Crab pulsar (Albert et al. 2008).

\begin{figure} \par\includegraphics[width=9cm,clip]{aa13515-09-fig1.eps} \end{figure} Figure 1:

The synchrotron emission energy versus the cyclotron frequency. The set of parameters is $M_{\rm BH} = 10^8~M_{\odot}$, $n_{\rm b} = 2000~{\rm cm}^{-3}$, B = 104 G, $\gamma _{\rm p} = 2$, $\gamma _{\rm b}\in \{4\times 10^7;10^9\}$, and $\rho = R_{\rm g}$. As we see from the plot, the low frequency cyclotron mechanism arises in the radio band, inducing the QLD and subsequently creating relatively high pitch angles, which in turn lead to the X-ray emission.

Open with DEXTER

Unlike the previous case, we show in Fig. 2 the same behavior for the outer magnetospheric (light cylinder) lengthscales. The set of parameters is $M_{\rm BH} = 10^9~M_{\odot}$, $n_{\rm b} = 2000~{\rm cm}^{-3}$, L = 1045 erg/s, $\Omega = 3\times 10^{-5}~{\rm s}^{-1}$, $\gamma_{\rm p} = 3$, $\gamma_{\rm b}\in\{3;4\}\times 10^7$ and $\rho = r_{\rm {lc}}$. As shown in Fig. 2, the radio frequency close to the light cylinder zone, in the kHz domain excites the hard X-ray emission by means of the QLD. From Eqs. (6, 7), one can straightforwardly check the validity of our assumptions, $\vert G_{\perp}\vert\gg \vert F_{\perp}\vert$ and $\vert G_{_\parallel}\vert\ll \vert F_{_\parallel}\vert$, confirming our approach. It is also interesting to investigate the QLD for different values of the luminosity. We examine the luminosity interval from 1045 erg/s to the Eddington limit, which for the given black hole mass, $10^9~M_{\odot}$, equals 1047 erg/s. In Fig. 3, we show the strong X-ray energy versus the AGN luminosity. The set of parameters is $M_{\rm BH} = 10^9~M_{\odot}$, $n_{\rm b} = 2000~{\rm cm}^{-3}$, L = 1045-47 erg/s, $\Omega = 3\times 10^{-5}~{\rm s}^{-1}$, $\gamma_{\rm p} = 3$, $\gamma_{\rm b} = 3\times 10^7$ and $\rho = r_{\rm {lc}}$. As is evident from the figure, the emission energy is a continuously decreasing function of the luminosity. Indeed, by combining Eqs. (1, 12, 13, 15), we see that the synchrotron emission energy behaves as L-3/4.

\begin{figure} \par\includegraphics[width=9cm,clip]{aa13515-09-fig2.eps}\vspace*{1.5mm} \end{figure} Figure 2:

The synchrotron emission energy versus the cyclotron frequency. The set of parameters is $n_{\rm b} = 2000~{\rm cm}^{-3}$, L = 1045 erg/s, $\Omega = 3\times 10^{-5}~{\rm s}^{-1}$, $\gamma _{\rm p} = 2$, $\gamma _{\rm b}\in \{4;5\}\times 10^6$ and $\rho = r_{\rm {lc}}$. As is clear, the low frequency cyclotron mechanism arises in the radio band, inducing via the QLD, the X-ray emission.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{aa13515-09-fig3.eps} \end{figure} Figure 3:

The synchrotron emission energy versus the AGN luminosity. The set of parameters is $n_{\rm b} = 2000~{\rm cm}^{-3}$, L = 1045-47 erg/s, $\Omega = 3\times 10^{-5}~{\rm s}^{-1}$, $\gamma _{\rm p} = 2$, $\gamma _{\rm b} = 5\times 10^6$ and $\rho = r_{\rm {lc}}$.

Open with DEXTER

Therefore, as our investigation shows, the QLD is a working mechanism in AGN magnetospheric flows and drives the synchrotron process.

4 Summary

The main aspects of the present work can be summarized as follows:

1.
We studied the quasi-linear interaction of proper modes of AGN magnetospheric plasmas with the resonant plasma particles. For this purpose, the synchrotron reaction force has been taken into account. The role of the QLD was studied in the context of producing the soft and hard X-ray emission from AGN.
2.
It has been shown that the synchrotron cooling timescales for ultra-relativistic electrons are very small, and particles rapidly transit to the ground Landau state, that in turn, prevents the subsequent radiation. We found that, under certain conditions the cyclotron instability develops, leading to the creation of pitch angles, and the subsequent synchrotron process.
3.
We have considered two extreme regions of magnetospheres: (a) relatively close to the black hole and (b) the light cylinder zone. As our model shows, the cyclotron instability, under certain conditions, generates the radio frequency in the range (0.06-35) MHz and creates the soft X-ray emission, (0.13-100) keV, via the QLD. For the light cylinder area, radio spectra occurs in the range (38-59) kHz, which produces the hard X-ray emission in the domain (1.8-2.9) keV. We have emphasized that from an observational evidence one can directly verify the validity of the QLD by determining (I) the polarization and (II) phases of signals in radio and X-ray domains respectively.
4.
The quasi-linear diffusion has also been studied versus the AGN luminosity. It was shown that for more luminous AGN, the corresponding photon energy of the hard X-ray emission, generated by the synchrotron mechanism is lower.

Acknowledgements
The research was supported by the Georgian National Science Foundation grant GNSF/ST07/4-193.

References

  1. Abert J., Alia, E., Anderhub, H., et al. 2008, ApJ, 674, 1037 [NASA ADS] [CrossRef] [Google Scholar]
  2. Blandford R. D., Netzer H., & Woltjer L. 1990, Active Galactic Nuclei (Springer-Verlag) [Google Scholar]
  3. Catanese M., & Weeks T. C. 1999, PASP, 111, 1193 [NASA ADS] [CrossRef] [Google Scholar]
  4. Chkheidze N. 2009, A&A, 500, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Chkheidze N., & Lomiashvili G. 2008, New. Ar., 13, 12 [Google Scholar]
  6. Chkheidze N., & Machabeli G. 2007, A&A, 471, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Kazbegi A. Z., Machabeli G. Z., & Melikidze G. I. 1992, MNRAS, 253, 377 [Google Scholar]
  8. Landau L. D., & Lifshitz E. M. 1971, Classical Theory of Fields (London: Pergamon) [Google Scholar]
  9. Levinson Amir 2000, Phys. Rev. L, 85, 912 [NASA ADS] [CrossRef] [Google Scholar]
  10. Lominadze J. G., Machabeli G. Z., & Mikhailovsky A. B. 1979, J. Phys. Colloq., 40, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Machabeli G., & Osmanov Z. 2009, ApJL, 700, 114 [Google Scholar]
  12. Machabeli G. Z., & Rogava A. D. 1994, Phys. Rev. A, 50, 98 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  13. Machabeli G. Z., & Usov V. V. 1979, AZhh Pis'ma, 5, 238 [Google Scholar]
  14. Malov I. F., & Machabeli G. Z. 2001, ApJ, 554, 587 [NASA ADS] [CrossRef] [Google Scholar]
  15. Osmanov Z., Rogava A. S., & Bodo G. 2007, A&A, 470, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Rieger F. M., & Aharonian F. A. 2008, A&A, 479, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Rybicki G. B., & Lightman A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley) [Google Scholar]
  18. Thorne K. S., Price R. H., & Macdonald D. A. 1988, Black Holes: The Membrane Paradigm (New Haven: Yale University Press) [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{aa13515-09-fig1.eps} \end{figure} Figure 1:

The synchrotron emission energy versus the cyclotron frequency. The set of parameters is $M_{\rm BH} = 10^8~M_{\odot}$, $n_{\rm b} = 2000~{\rm cm}^{-3}$, B = 104 G, $\gamma _{\rm p} = 2$, $\gamma _{\rm b}\in \{4\times 10^7;10^9\}$, and $\rho = R_{\rm g}$. As we see from the plot, the low frequency cyclotron mechanism arises in the radio band, inducing the QLD and subsequently creating relatively high pitch angles, which in turn lead to the X-ray emission.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{aa13515-09-fig2.eps}\vspace*{1.5mm} \end{figure} Figure 2:

The synchrotron emission energy versus the cyclotron frequency. The set of parameters is $n_{\rm b} = 2000~{\rm cm}^{-3}$, L = 1045 erg/s, $\Omega = 3\times 10^{-5}~{\rm s}^{-1}$, $\gamma _{\rm p} = 2$, $\gamma _{\rm b}\in \{4;5\}\times 10^6$ and $\rho = r_{\rm {lc}}$. As is clear, the low frequency cyclotron mechanism arises in the radio band, inducing via the QLD, the X-ray emission.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{aa13515-09-fig3.eps} \end{figure} Figure 3:

The synchrotron emission energy versus the AGN luminosity. The set of parameters is $n_{\rm b} = 2000~{\rm cm}^{-3}$, L = 1045-47 erg/s, $\Omega = 3\times 10^{-5}~{\rm s}^{-1}$, $\gamma _{\rm p} = 2$, $\gamma _{\rm b} = 5\times 10^6$ and $\rho = r_{\rm {lc}}$.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.