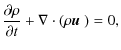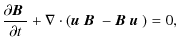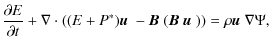EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 516 (June-July 2010) A&A, 516 (2010) A26 Full HTML
Free Access
Issue
A&A
Volume 516, June-July 2010
Article Number A26
Number of page(s) 10
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/200912443
Published online 22 June 2010
A&A 516, A26 (2010)

High-order Godunov schemes for global 3D MHD simulations of accretion disks

I. Testing the linear growth of the magneto-rotational instability

M. Flock1 - N. Dzyurkevich1 - H. Klahr1 - A. Mignone2

1 - Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
2 - Dipartimento di Fisica Generale, Universitá degli Studi di Torino, via Pietro Giuria 1, 10125 Torino, Italy

Received 7 May 2009 / Accepted 16 April 2010

Abstract
We assess the suitability of various numerical MHD algorithms for astrophysical accretion disk simulations with the PLUTO code. The well-studied linear growth of the magneto-rotational instability is used as the benchmark test for a comparison between the implementations within PLUTO and against the ZeusMP code. The results demonstrate the importance of using an upwind reconstruction of the electro-motive force (EMF) in the context of a constrained transport scheme, which is consistent with plane-parallel, grid-aligned flows. In contrast, constructing the EMF from the simple average of the Godunov fluxes leads to a numerical instability and the unphysical growth of the magnetic energy. We compare the results from 3D global calculations using different MHD methods against the analytical solution for the linear growth of the MRI, and discuss the effect of numerical dissipation. The comparison identifies a robust and accurate code configuration that is vital for realistic modeling of accretion disk processes.

Key words: accretion, accretion disks - magnetohydrodynamics (MHD) - methods: numerical

1 Introduction

It is widely accepted that the magneto-rotational instability (MRI) can be responsible for turbulence in proto-planetary disks, enabling the accretion of the disk material onto the star. The turbulence interacts with the gas-phase chemistry, grain growth and settling, and thermal evolution, which makes the understanding of planet formation a challenge. In particular, the effectiveness of MRI-driven turbulence depends on the ionization degree of the gas (Wardle 1999; Jin 1996; Blaes & Balbus 1994; Gammie 1996; Ilgner & Nelson 2006; Turner et al. 2007; Fleming et al. 2000; Sano et al. 2000). The collisional ionization rate depends on the temperature, which at sufficiently high accretion rates is governed by the dissipation of magnetic fields in the turbulence. Accurately capturing the magnetic energy loss during diffusion and reconnection as heat requires an energy-conserving numerical scheme.

Many classical studies of the magneto-rotational instability (MRI) were conducted with the ideal MHD approach and the local shearing box approximation (Hawley et al. 1995; Sano et al. 2004; Matsumoto & Tajima 1995; Brandenburg et al. 1995; Stone et al. 1996; Hawley et al. 1996), partly reviewed in Balbus & Hawley (1998). However, recent developments have shown that critical questions about turbulence in accretion disks can only be addressed in global simulations (Lyra et al. 2008; Davis et al. 2010; Fromang & Papaloizou 2007; Fromang & Nelson 2009,2006). The majority of the existing codes which can handle global disk simulations are based on Zeus-like finite difference schemes (Hawley 2000; Fromang & Nelson 2009,2006). Thus, it would be beneficial to tackle the open questions with an independent method. A number of investigators have recognized the importance of using conservative Godunov-type upwind schemes rather than non-conservative finite difference algorithms (Fromang et al. 2006; Stone & Gardiner 2005; Mignone et al. 2007), especially for jets and space weather simulations (Groth et al. 2000).

So far, no global calculation has treated temperature changes in the disk. Some first results in this direction apply the flux-limited radiation diffusion approach in shearing-box calculations (Flaig et al. 2009; Turner 2004; Hirose et al. 2006; Turner et al. 2002). The latter use a conservative, cell-centered finite volume scheme. A major challenge here is to accurately and effectively monitor and control the evolution of the divergence of the magnetic field, which should stay at ${\rm div}(\mbox{\boldmath$B$ })=0$.

Two main approaches for evolving the magnetic field have been established over the years. The first is the ``constrained transport'' (CT) method (Evans & Hawley 1988; Stone & Norman 1992; Hawley & Stone 1995; Devore 1991; Brecht et al. 1981). By discretizing the magnetic and electric vector fields on a staggered mesh, this scheme achieves the important property of maintaining ${\rm div}(\mbox{\boldmath$B$ })=0$ to machine accuracy. Several issues arise in choosing how to adapt the CT method to the cell-centered discretization used in the Godunov MHD schemes. Constrained transport Godunov schemes introduced by Dai & Woodward (1998), Ryu et al. (1998), Balsara & Spicer (1999), Komissarov (1999) and Tóth (2000) include both staggered and cell-centered magnetic fields. The difficulty is that the staggered field is not well suited for upwind Godunov schemes. For a staggered field, the one-dimensional solutions of the Riemann problem for density, momentum and the energy equation have no direct extension to the upwind fluxes in the induction equation (Balsara & Spicer 1999). Londrillo & Del Zanna (2000) and Londrillo & del Zanna (2004) enhanced the CT method to make it consistent with the one-dimensional solver for plane parallel, grid-aligned flows. Based on the Harten-Lax-van Leer (HLL) and Roe Riemann solver fluxes, they proposed a new way to reconstruct the electric fields now called ``upwind CT''. In Londrillo & del Zanna (2004) they followed a similar approach by using the Hamilton-Jacobi equations to derive the method as proposed in Kurganov et al. (2001). Further improvements of the CT approach were introduced in the ATHENA code Gardiner & Stone (2005) and the RAMSES code (Fromang et al. 2006), both based on the work of Londrillo & del Zanna (2004).

The second class of MHD methods exclusively uses the cell center discretization. Here there is no additional staggered grid and ${\rm div}(\mbox{\boldmath$B$ })$ is not automatically forced to vanish. Solution attempts for this problem were presented by Powell (1994), Powell et al. (1999) or Dedner et al. (2002). The so called ``eight waves'' method uses the modified MHD equations with specific source terms and allows magnetic monopoles to appear as an additional $8{\rm {th}}$ mode in the classical seven-mode Riemann fan. A further development is the hyperbolic cleaning method of Dedner et al. (2002). Here the conservative form of the MHD system is preserved by introducing a time-dependent wave equation which dampens the monopoles. Whether these technique sufficiently removes ${\rm div}(\mbox{\boldmath$B$ })$ strongly depends on the problem and for MHD turbulence this was never actually shown.

The PLUTO code is a conservative multi-dimensional and multi-geometry code that can be applied to relativistic or non-relativistic MHD or pure HD flows. The ability to switch between several different numerical modules in PLUTO allows us to test and compare a range of different methods, such as cell-centered and CT, and choose those giving the best convergence and stability properties, defining a consistent algorithm. For example, the code offers the possibility of using the Riemann solvers of Roe, Harten-Lax-van Leer Discontinuities (HLLD), Harten-Lax-van Leer Contact (HLLC), HLL and Lax-Friedrichs (Rusanov) types. The PLUTO code has successfully reproduced a series of standard MHD tests, including the rotating shock-tube, the fast rotor and the blast wave solution (Mignone et al. 2007). The methods are reviewed in Balsara (2004) and Mignone & Bodo (2008).

In this paper we investigate the behavior of various MHD algorithms in 3D global accretion disk calculations using cylindrical coordinates. The results from the PLUTO Godunov code are compared with those from ZeusMP, which represents a certain class of widespread finite difference codes. ZeusMP (Stone & Norman 1992; Hayes et al. 2006) uses a classical staggered discretization of the magnetic and electric vector fields (MoC-CT). We use the ZeusMP version 1b, which has already been applied successfully to 3D global MHD accretion disk calculations (Fromang & Nelson 2006; Dzyurkevich et al. 2010). We set up identical models in the two codes, and examine the performance of the different numerical schemes by comparing the growth of the MRI with the expectations from linear analysis. At the same time, unphysical results are easily discovered by comparison with linear analysis. In Sect. 2 we describe the differences between the numerical schemes of ZEUS and PLUTO. Sect. 3 presents the disk model and the measurement methods. In Sect. 4 we show the results of the inter-code comparison. The convergence properties of the finally identified best suited algorithm are investigated in Sect. 5. Conclusions and an outlook are given in Sect. 6.

2 Numerics

2.1 MHD equations

The equations of ideal magnetohydrodynamics written in conservative form as implemented in Godunov schemes are

$\displaystyle \frac{\partial\rho}{\partial t} + \nabla \cdot (\rho \mbox{\boldmath$u$ }) = 0,$   (1)


$\displaystyle \frac{\partial \rho\mbox{\boldmath$u$ } }{\partial t} + \nabla \c... ...} -\mbox{\boldmath$B$ }\mbox{\boldmath$B$ })= - \nabla P^{*} +\rho \nabla \Psi,$   (2)


$\displaystyle \frac{\partial \mbox{\boldmath$B$ }}{\partial t} + \nabla\cdot( \... ...oldmath$u$ }\mbox{\boldmath$B$ } - \mbox{\boldmath$B$ }\mbox{\boldmath$u$ })=0,$   (3)

and
$\displaystyle \frac{\partial E }{\partial t} + \nabla \cdot (( E+ P^{*})\mbox{\... ...ox{\boldmath$B$ }\mbox{\boldmath$u$ }))= \rho \mbox{\boldmath$u$ } \nabla \Psi,$   (4)

where $\rho$ is the gas density, $\rho \mbox{\boldmath$u$ }$ is the momentum density, $\mbox{\boldmath$B$ }$ is the magnetic field, and E is the total energy density. The total pressure is a sum of the magnetic and gas pressure, $P^{*}=P+( \mbox{\boldmath$B$ }\cdot \mbox{\boldmath$B$ })/2$. Total energy density is connected to internal energy $\epsilon$ as $E=\epsilon + \rho u^2/2 + B^2/2$. The gravitational potential is set to $\Psi \propto 1/R$ to set the azimuthal Keplerian shear flow of the gas.

2.1.1 ZEUS

The momentum equation is solved by ZeusMP in a non-conservative way,

$\displaystyle \rho \frac{{\rm d} \mbox{\boldmath$u$ } }{{\rm d} t}= - \nabla P ... ...\frac{1}{4\pi}[\nabla\times{}\mbox{\boldmath$B$ }]\times{}\mbox{\boldmath$B$ }.$   (5)

Density and pressure are stored at the cell center, but as the vector components of velocity and magnetic fields are stored at the grid interfaces, fluxes can be calculated directly in ZEUS. The scheme is second order in space and first order in time in regions between shocks. Although there are no shocks in our runs, we are aware of the anti-diffusive behavior of ZEUS for shocks as it was pointed out in Falle (2002) when using ZEUS without artificial viscosity.

In Sect. 5, we therefore present a test-run with ZEUS including the usual amount of artificial viscosity as it is used in global simulations.

2.1.2 PLUTO

Contrary to Zeus-type finite difference schemes, a Godunov type scheme follows a conservative ansatz. In general all quantities are stored at the cell center. Only for the CT MHD method there is an additional staggered magnetic field. The second order Runge-Kutta (RK) iterator is employed with a CFL about 0.25. Prior to flux calculation, variables are reconstructed at the grid interface, which implies interpolation with a limited slope. The resulting two different states at the interfaces allow us to solve the Riemann problem, which is the main feature of a Godunov code. We tested the different MHD Riemann solvers of Roe (Cargo & Gallice 1997), HLLD (Miyoshi & Kusano 2005), HLL and Lax-Friedrichs Rusanov in our inter-code comparison. The difference is the number of wave characteristics that are used by each solver. Harten-Lax-van Leer and Lax-Friedrichs solver use the fast magneto-sonic wave characteristic as maximal signal velocity. Harten-Lax-van Leer Discontinuities solver additionally includes the Alfvén wave characteristic and the contact discontinuity. The Roe solver follows all seven MHD waves, including the slow magneto-sonic characteristic. We note that compared to the HLLD and Roe solver, the ZEUS code is four to six times faster. This factor appears because of the two predictor and corrector steps in the Runge-Kutta time integration and the calculation of the different fluxes in the Riemann solver.

\begin{figure} \par\includegraphics[width=9cm,clip]{12443fg1.ps} \end{figure} Figure 1:

Analytical growth rate plotted for different qr (solid to dash-doted lines). Triangles present the measured MRI growth rates from our simulation with initial axisymmetric white noise disturbance from model $\rm {HLLD}_{LIN}$ $128\times 64 \times 64$with n=4. The values are measured for each radii and averaged. Results are similar to those in Hawley & Balbus (1991), Fig. 8.

Open with DEXTER

2.2 Constrained transport EMF reconstruction in PLUTO

In the CT approach, the staggered components of B are evolved as surface averaged quantities and are updated using Stokes' theorem. This requires constructing a line-averaged electric field along the face edges using some sort of reconstruction or averaging technique from the face centers, where different EMF components are usually available as face-centered upwind Godunov fluxes. As was already mentioned, it is difficult to represent the solenoidality of magnetic fields correctly in Godunov schemes. For the constrained transport we will concentrate on three different EMF reconstruction methods. The first method, here called ACT, describes the arithmetic average of the face-centered EMF's obtained by the upwind fluxes in the induction equation (Balsara & Spicer 1999) presented in Fig. 1,

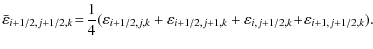
$\displaystyle %   (6)

This CT algorithm does not reproduce the correct solution for plane-parallel, grid-aligned flows (Gardiner & Stone 2005). In this case, considering the i-direction, one obtains $\varepsilon_{z,i,j+1/2} =\varepsilon_{z,i+1,j+1/2} $ and $\varepsilon_{z,i+1/2,j} =\varepsilon_{z,i,j}$. Then we get from the ACT Eq. (6)
$\displaystyle \bar{\varepsilon}_{i+1/2,j+1/2,k}=\frac{1}{4}(\varepsilon_{i,j,k}+\varepsilon_{i,j+1,k})+\frac{1}{2}\varepsilon_{i,j+1/2,k},$   (7)

in contrast to the correct solution, which is simply $\varepsilon_{i+1/2,j+1/2,k} =\varepsilon_{z,i,j+1/2}$. The reason is the lack of a directional bias in the formula. Therefore Balsara & Spicer (1999) apply weighting coefficients to grant the directional bias. Gardiner & Stone (2005) effectively double the amount of dissipation in their approach. They present a modified formula, which includes cell-center electric fields to recover the proper directional biasing, here called UCT,

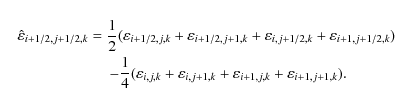
\begin{eqnarray*}&&\hat{\varepsilon}_{i+1/2,j+1/2,k}= \frac{1}{2}(\varepsilon_{i... ...epsilon_{i,j+1,k}+\varepsilon_{i+1,j,k}+\varepsilon_{i+1,j+1,k}).\end{eqnarray*}


$\varepsilon_{i,j,k}$ are the finite volume electric fields calculated from the cell center values. This ``upwind'' property of the algorithm is only strictly valid in the special limit of plane-parallel flow and it is not ``upwind'' in the general multidimensional sense. Based on this, Gardiner & Stone (2005) developed a new CT method, here called $\rm UCT_{\rm CONTACT}$,

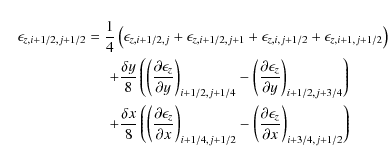
\begin{eqnarray*}&&\epsilon_{z,i+1/2,j+1/2}=\frac{1}{4}\left(\epsilon_{z,i+1/2,j... ...c{\partial \epsilon_{z}}{\partial x}\right)_{i+3/4,j+1/2}\right) \end{eqnarray*}


with

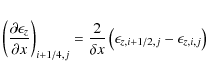
\begin{eqnarray*}\left(\frac{\partial \epsilon_{z}}{\partial x}\right)_{i+1/4,j}... ...{2}{\delta x}\left(\epsilon_{z,i+1/2,j} - \epsilon_{z,i,j}\right)\end{eqnarray*}


and

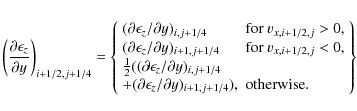
\begin{eqnarray*}\left(\frac{\partial \epsilon_{z}}{\partial y}\right)_{i+1/2,j+... ...ial y)_{i+1,j+1/4} ), & \rm {otherwise}.\\ \end{array} \right\} \end{eqnarray*}


Both methods, $\rm UCT$ and $\rm UCT_{\rm CONTACT}$, show exactly the same evolution in our test problems, because our Keplerian disk setup presents precisely the case of a plane-parallel, grid-aligned flow, where both methods should give the same result.

Table 1:   Initial parameter of global setup.

Table 2:   MRI growth rates measured for models with 4 and 8 MRI modes (n=4,8).

3 Linear MRI in a global disk

The analytical description of the the linear stage of MRI has been given by Balbus & Hawley (1991). Local shearing box simulations have confirmed the analytical expectation of the linear MRI growth (Hawley et al. 1995; Brandenburg et al. 1995). Global simulations and also the nonlinear evolution of the MRI was presented in Hawley & Balbus (1991). Our simplified setup here is representative for a global proto-planetary disk and made for a modest radial domain.

3.1 Global setup

We use cylindrical coordinates in our models with the notation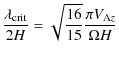 $(R,\phi, Z)$. The equations are solved using uniform grids. The domain extends $60^{\circ}$ in the azimuthal direction, ${Z}=\pm0.5~R_0$ and from 1 to 4 R0 in the radial direction. R0 is a free parameter for this dimensionless problem. Initial density $\rho$ and pressure P are constant in the entire disk patch with $\rho=1.0$, $P=c_{\rm s}^{2}\rho/\gamma$, $c_{\rm s}=0.1 u_{\phi,0}$ and $\gamma = 5/3$. The gas is set up initially with the Keplerian speed, $u_{\phi,0}^2=\frac{R_0}{R}$. A uniform vertical magnetic field is placed at radii between 2 and 3 units, reducing effects of the radial boundary. The resolution for the standard case is $[R,\phi,Z]=[128,64,64]$. For both codes (ZEUS and PLUTO) we use identical random generated velocity perturbations ( $10^{-4}u_{\rm Kep}$) for initial radial and vertical velocities. Boundary conditions are periodic for all variables in the vertical and azimuthal direction, and zero gradient for the radial one[*]. We calculate the critical wavelength over disk thickness according to Eq. (2.3) in Hawley & Balbus (1991)
$\displaystyle \frac{\lambda_{\rm crit}}{2H} = \sqrt{\frac{16}{15} } \frac{\pi V_{{\rm A}z}}{\Omega H}$   (8)

with the angular frequency $\Omega = R^{-1.5} $ and the Alfvén velocity $V_{{\rm A}z}=B_z/\sqrt{4 \pi \rho}$. We choose the uniform vertical magnetic field strength to obtain the fastest-growing wavelength fitting in the domain height at R=2, Bz=B0/n with B0=0.055 and n=1,2,..., 8. The critical wavelength and the growth rate can be directly measured from our simulations and then compared with the analytical prediction. The parameters of our setup are also listed in Table 1.

3.2 Physical limits of the MRI growth rate

Before using the ideal growth rate as a comparison value, the processes limiting the growth rate in the linear MRI for a real physical system have to be considered. When the magneto-rotational instability sets in, the magnetic fields are amplified with $B=B_{0}\exp({\gamma_{\rm MRI} t})$ until they reach saturation. As mentioned in Hawley & Balbus (1991), the absolute limit of the growth rate for ideal MHD is given for the zero radial wave vectors qr = 0 with the normalized wave vector qz,

$\displaystyle q_z=k_z\sqrt{16/15}\nu_{\rm A}/\Omega,$   (9)

with the Alfvén speed $\nu_{\rm A}=B/\sqrt{4\pi\rho}$. Then the critical mode qz=0.97 grows with $\gamma = 0.75 \Omega $, (see Fig. 1). As in Balbus & Hawley (1991b) we do not a priori know the radial MRI wavenumber in our simulations, therefor the maximum possible growth rate is reduced compared to the absolute limit. In Fig. 1 we plot the growth rate for different radial modes. In addition we also tested a fully axis-symmetric initial random velocity fields. The magnetic field evolution in our 3D setup is nearly axis-symmetric for both initial velocity field. The standard simulation shows a n=1 mode in the azimuthal direction with differences of under five percent compared to the fully axis-symmetric run. Therefore all simulations are comparable with the 2D setup presented in Hawley & Balbus (1991) and we obtain MRI growth rates which are comparable with Hawley & Balbus (1991, Fig. 8).

The additional effects reducing the MRI growth rate are viscous and resistive dissipation (Pessah & Chan 2008).

For the MRI, the numerical dissipation is the reason why we need some minimal amount of grid cells. Hawley et al. (1995) claim to need at least five grid cells per fastest growing mode for ZEUS to correctly resolve the MRI mode. For the inter-code comparison we used the setup described in Sect. 3.1 with a vertical magnetic field for n=4 and n=8. Then the total resolution of 64 gives 16 grid cells per fastest growing mode, which is enough even for very diffuse solvers. For a better differentiation between the code configurations we include also a weaker vertical magnetic field with n=8, because then only 8 cells per mode are available. Besides resolution and the kind of Riemann solver the order in the reconstruction step also has an impact on the dissipation.

3.3 Measurement method

In Fig. 2 we present the exponential growth of the fastest MRI mode for Br. The slope directly gives us the MRI growth rate. The black lines show the growth for each radial location. Time is given in local orbits. Most radial slices plotted in Fig. 2 show a growth rate close to the analytical limit (see dashed line in Fig. 2). The inner annuli (R=2, red line in Fig. 2) reach non-linear amplitudes first (Fig. 2), producing disturbances that propagate outward and affect the development of the slower-growing linear modes in annuli farther away from the star (R=3, blue line in Fig. 2). As a result the annuli near R=3 grow faster than indicated by the linear analysis and only annuli at R=2 show the predicted behavior. In the following sections the growth rate is calculated as the time average between 1 and 1.5 local orbits.

\begin{figure} \hspace{0.6cm}% \par\includegraphics[width=9cm,clip]{12443fg2a.ps}\vspace*{2.5mm} \includegraphics[width=9cm,clip]{12443fg2b.ps} \end{figure} Figure 2:

Maximal amplitude growth of the critical MRI mode plotted for the 42 radial slices between radii R=2 (red line) and R=3 (blue line) for local and inner orbits. The setup is constructed to excite the mode with $\lambda _{\rm crit}=H$ (n=1). For the radii near R=2, the MRI growth rate reaches the value of $\gamma = 0.75 \Omega $. At the outer edge of the radial domain, the growth rate becomes higher than $ 0.75 \Omega $ (blue line). The MRI modes there are affected by the inner part, where MRI already breaks into nonlinear evolution after eight inner orbits.

Open with DEXTER

4 Inter-code comparison

The models and results of the growth rate for the inter-code comparison are summarized in Table 2. Here the growth rate values $\gamma_{\rm MRI}$ are averaged over radius and time, as described in Sect. 3.3. Growth rates higher than the mean analytical value or its fluctuations are marked in red. The statistical error is estimated from the radial fluctuation in the growth rate (Figs. 4, 6 and 9).

4.1 Magnetic-energy evolution

\begin{figure} \hspace{0.6cm} \par\includegraphics[width=9cm,clip]{12443fg3a.ps}\vspace*{2.5mm} \includegraphics[width=9cm,clip]{12443fg3b.ps} \end{figure} Figure 3:

Radial magnetic energy integrated for the total domain for n=4 ( top) and n=8 ( bottom) with upwind CT (solid line), Powell 8-wave (dashed line) and arithmetic CT (dotted line). The values are normalized over the initial orbital kinetic energy. After the initial disturbance, the growth of critical mode dominates and there is a linear MRI region visible between two and eight inner orbits. For HLLD and Roe, the arithmetic CT shows a growth stronger then MRI until five inner orbits, caused by a numerical instability. Harten-Lax-van Leer and TVDLF have a much lower growth because both methods are viscous and do not resolve the critical mode for the adopted resolution.

Open with DEXTER

The growth of the magnetic field due to the excitation of the critical mode dominates at two inner orbits and the linear growth regime occurs. Figure 3 shows the radial magnetic-energy evolution $E_r \propto B^2_r$ for the n=4 and n=8 mode runs (see Table 2). In the n=8 mode setup we can clearly distinguish three different families of evolution. The first family consists of Roe and HLLD solver in combination with ACT (red colors in Table 2). If the slope is steeper, the analytical prediction is indicating a numerical problem. Second is the Lax-Friedrichs and HLL Riemann solver. They always show the slowest growth in energy, independent of the chosen MHD method. The third family consists of the HLLD and Roe solvers with upwind CT and the 8-wave method. Their results are the most similar to ZEUS. Below, we will compare the families in detail.

4.2 The arithmetic CT plus HLLD and Roe

For the ACT in combination with HLLD & Roe solvers the growth of the magnetic energy overshoots the analytical expectation for MRI growth (Table 2, Figs. 3, 4). A numerical instability dominates, which shows up in the fastest-growing mode that has a vertical wavelength shorter than predicted from linear analysis of MRI. In Fig. 5 we plotted the growth rate for each radial slice, calculated from 1 to 1.5 local orbits. Roe and HLLD show the same unphysical high radial variations in growth rate, which locally exceeds the analytical limit. The instability generates a ``checkerboard'' pattern in physical space for all variables (see example for $B_{\phi}$ in Fig. 5). Numerical instabilities rooted in the treatment of the Alfvén wave were already predicted by Miyoshi & Kusano (2008). They write that it is commonly known that highly accurate Riemann solvers for the Euler equations sometimes encounter multi-dimensional numerical instabilities at high mach numbers such as the ``carbuncle'' instability that may be related to the resolution of the contact wave (Robinet et al. 2000).

The reason for the ``checkerboard'' instability is based on the inconsistent EMF reconstruction of ACT for a plane-parallel flow as it is described in Sect. 2.2. The Roe and HLLD solvers include the Alfvén characteristics accurately and evolve the disturbances independently of the resolution (see Fig. 7a). The HLL and TVDLF solver do not include the Alfvén characteristics. For moderate resolutions they present correct results in combination with ACT because the ``checkerboard'' instability is suppressed by numerical dissipation. However, at higher resolutions the numerical instability occurs here as well (see Fig. 7b). For HLL and TVDLF it depends on the dissipation to resolve the numerical instability related to the Alfvén wave. For the Roe and HLLD solver the instability is present for basically any resolution.

\begin{figure} \hspace{0.6cm}% \par\includegraphics[width=9cm,clip]{12443fg4a.ps}\vspace*{2.5mm} \includegraphics[width=9cm,clip]{12443fg4b.ps} \end{figure} Figure 4:

Local growth rate for n=4 ( top) and n=8 ( bottom) with arithmetic CT. For HLLD and Roe the local growth rate exceeds the analytical limit and shows unphysical spatial variations. The problem does not affect the HLL and TVDLF solver at moderate resolution. Harten-Lax-van Leer (green) and TVDLF show exact the same results.

Open with DEXTER

\begin{figure} \hspace{0.6cm}% \par\includegraphics[width=9cm,clip]{12443fg5a.ps... ...g5b.ps}\vspace*{3mm} \includegraphics[width=9cm,clip]{12443fg5c.ps} \end{figure} Figure 5:

Contour plot of the azimuthal magnetic field for arithmetic CT (top), UCT ( middle) and ZEUS (bottom). For the arithmetic CT, the ``checkerboard'' instability dominates. For UCT and ZEUS the n=4 is most prominent. A change from blue to red indicates a change of sign in the magnetic field. This snap-shot of the magnetic field is taken after eight inner orbits.

Open with DEXTER

4.3 Upwind CT and 8-wave

With the upwind CT EMF reconstruction described in Sect. 2.2, there is no more ``checkerboard'' pattern visible. Figure 5 presents a contour plot of the azimuthal magnetic field after eight inner orbits. The HLLD solver with upwind CT and ZEUS shows four evolving modes. Figure 6 shows the small difference of local growth rates between ``8-waves'' (8W) and upwind CT (UCT & $UCT_{\rm CONTACT}$). One sees that the choice of the Riemann solver has a stronger effect on the growth rate than the MHD method. Thus, the solution in family ``3'' appears to be the proper choice for MRI simulations.

\begin{figure} \hspace{0.6cm} \par\includegraphics[width=9cm,clip]{12443fg6a.ps}\\ \vspace*{3mm} \includegraphics[width=9cm,clip]{12443fg6b.ps} \end{figure} Figure 6:

Local growth rate for n=4 (top) and n=8 (bottom) with upwind CT (solid line), $\rm {UCT}_{\rm {contact}}$ (dashed line) and Powell's Eight Wave (dotted line). The high-resolution MHD Riemann solver HLLD and Roe show the same MRI evolution, producing the same growth rate as ZEUS. The HLL solver and TVDLF are more diffusive.

Open with DEXTER

4.4 The resolution of the most unstable mode

\begin{figure} \hspace{0.6cm}% \par\includegraphics[width=9cm,clip]{12443fg7a.ps}\\ \vspace*{3mm} \includegraphics[width=9cm,clip]{12443fg7b.ps} \end{figure} Figure 7:

Top: contour plot of radial magnetic field for n=8 mode low resolution run. Even with a resolution of $16 \times 8 \times 8$ the HLLD solver can resolve the checkerboard pattern for ACT. Bottom: high resolution run for n=8 mode and the HLL solver with ACT. The checkerboard pattern becomes visible (red box).

Open with DEXTER

In the case of four MRI modes and 64 grid cells in the vertical direction, the resolution in the Z direction is sufficient for all Riemann solvers to resolve the critical mode, e.g. $16/\lambda$. The HLLD solver, Roe and ZEUS show the highest growth rate followed by TVDLF and HLL. The models for n=8 are summarized in Table 2 and Fig. 6. The resolution of eight grid cells per critical mode is not sufficient to resolve the MRI mode. Here, growth rates are significantly reduced for HLL and TVDLF solvers because they can only resolve the slower growing 4 mode for the used resolution. ZEUS and the MHD Riemann solver Roe and HLLD resolve seven modes. The additional Alfvén characteristics included in the HLLD solver lead effectively to lower numerical dissipation. Figure 8 shows a contour plot of the radial magnetic field after seven inner orbits for the HLLD solver, ZEUS and the HLL solver. The ZEUS code shows an MRI pattern very close to those of HLLD and Roe.

With the two different setups (n=4 & n=8) we can conclude that the HLL and TVDLF Riemann solver need at least 16 grid cells per mode to resolve the fastest growing MRI mode correctly. The HLLD and Roe solver can resolve the mode starting with 10 grid cells per mode.

\begin{figure} \par\includegraphics[width=9cm,clip]{12443fg8a.ps}\vspace*{2.8mm}... ...8mm} \includegraphics[width=9cm,clip]{12443fg8c.ps}\vspace*{-3.5mm} \end{figure} Figure 8:

Contour plot of the radial magnetic field in code units for the HLLD solver ( top), ZEUS ( middle) and HLL solver ( bottom). After seven inner orbits the inner radial part breaks into a nonlinear regime.

Open with DEXTER

4.5 The role of the reconstruction method for primitive variables

The reconstruction of the states at the interface is the main source of dissipation in Godunov schemes (see Sect. 2). In this subsection we test the third order piece-wise parabolic method (PPM) by Collela (1984) and compare the results with the piece-wise linear reconstruction method (PLM) used in the previous sections.

\begin{figure} \par\includegraphics[width=9cm,clip]{12443fg9a.ps}\vspace*{3mm} \includegraphics[width=9cm,clip]{12443fg9b.ps} \end{figure} Figure 9:

Growth rate of MRI for PPM (dashed line) and PLM (solid line). For the Lax-Friedrichs solver the PPM interpolation leads to growth rates closer to the analytic solution, which is due to lower numerical dissipation. Differences between HLLD and Roe solvers are less prominent.

Open with DEXTER
Figure 9 shows the difference in local MRI growth rate for simulations made for PLM and PPM with UCT. The results of MHD Riemann solver HLLD and Roe are not strongly affected by the choice of reconstruction order, though there is a slightly higher growth rate visible when PPM is used, indicating lower dissipation. In contrast, the more dissipative solvers HLL and TVDLF show a increasing growth rate. With the change to the PPM method both solvers improve significantly in their reproduction of linear MRI. With PPM, the HLL and TVDLF are able to resolve the critical mode with 10 grid cells per MRI mode against 16 grid cells per mode with PLM.

Nevertheless, using an order of spatial reconstruction beyond the order of time integration can lead to anti-diffusive behavior. This can artificially generate or amplify magnetic fields, as shown in Falle (2002). Therefore one should avoid to compensate the dissipation of the method with high order reconstruction and choose instead a high-order Riemann solver as HLLD or Roe.

Table 3:   Growth rates for the resolution tests with initial 4 mode (4M) and white noise perturbations (WN).

5 High-resolution comparison

The models in our convergence test are summarized in Table 3. We adopt the n=4 model with 2 different initial perturbations, white noise and a n=4 perturbation in velocity.

5.1 The role of initial perturbation

Usually the global 3D simulation of a disk starts with white-noise velocity perturbation. This initial configuration is least presumptive in the evolution. All three components of the velocity are perturbed, and a large range of MRI modes is excited. Due to the excitation of several radial modes, the growth rate of the MRI is below the analytical value $\gamma_{\rm MRI}=0.75\Omega_{0}$ as presented in Fig. 1. Nevertheless, such a test allows us to compare the codes in the most complete global setup, not precluding specific unstable modes. Another approach is to exclusively perturb the radial velocity with only one chosen mode, for example $v_{R}(z)=v_{0}\sin{4z/H} $ where H is the vertical size of the box. In combination with an initial magnetic field of Bz=0.05513/4, a pure clean n=4 mode will be exited. Such a perturbation is highly artificial, yet the purpose is to approach the analytical value for a linear MRI growth of $\gamma_{\rm MRI}=0.75\Omega_{0}$. As our tests are performed in the global framework, there is still the effect of radial change in orbital frequency, leading to local variation in the growth rate. Therefore we choose for our analysis one annulus close to R=2, where the growth rate seems to be least affected (see Fig. 2).

5.1.1 White noise perturbation

In the runs $\rm {ZEUS_{WN}}$, $\rm PLUTO_{WN}$, $\rm PLUTO_{WN-PPM}$ we used axis-symmetric white noise for the radial and vertical velocity perturbations. Table 3 summarizes the maximum growth rate for both initial perturbations. For $\rm PLUTO_{WN}$, $\rm PLUTO_{WN-PPM}$ and $\rm {ZEUS_{WN}}$, the linear MRI tops at a growth rate around 0.7 for higher resolutions. Only for the lowest resolution we can clearly see a lower growth rate, which stresses our earlier conclusion that 8 grid cells per critical mode are not sufficient. For this resolution the HLLD with the PPM reconstruction has the most similar behavior to ZEUS. In this set of tests, the reason for not reaching the analytical value of $\gamma_{\rm MRI}$ is a physical one. The limit of the growth rate is set by the various occurring radial modes which are excited in case of the white noise perturbation (see Fig. 1). With increasing resolution, smaller and smaller radial modes are resolved and no convergence can be achieved, because the setup changes. The details of the behavior of both codes for the low resolution and the white noise setup are available in Fig. 11.

\begin{figure} \par\includegraphics[width=9cm,clip]{12443fg10a.ps}\vspace*{2.5mm} \includegraphics[width=9cm,clip]{12443fg10b.ps}\vspace*{-2mm} \end{figure} Figure 10:

Convergence for the white noise ( top) and single 4 mode perturbation setup ( bottom). For the single 4 mode perturbation the growth rates exhibit a quick convergence to the analytical limit $\gamma _{\rm MRI} = 0.75$.

Open with DEXTER

5.1.2 Initial 4 mode perturbation

Only with this artificial setup can we assure that we have initial perturbations independent on resolution, which is necessary for convergence studies. In the runs $\rm PLUTO_{4M}$ and $\rm {ZEUS_{4M}}$ we avoid the excitation of MRI waves $k_{R} \neq 0$ by choosing $v_{R}(z)=v_{0}\sin{4z/H} $ for initial disturbance without any radial dependence. In Fig. 10 we plot the growth-rate evolution for a specific radial point near $R \geq 2$, which presents the region of the smoothest linear growth regime compared to the outer annulus at R=3 (Fig. 2). Table 3 summarizes the maximum growth rate measured in Fig. 10. Both the codes $\rm PLUTO_{4M}$ and $\rm {ZEUS_{4M}}$ converge on the analytical limit of $\gamma _{\rm MRI} = 0.75$. It is interesting to note that for the ultimately lowest resolution the growth rates from $\rm PLUTO_{4M}$ in combination with the second order piece-wise linear reconstruction method (PLM) is lower then the $\rm {ZEUS_{4M}}$ value. The reason for this is buried inside the PLM method, which causes a higher dissipation compared to PPM (Fig. 11 dash-dotted line). Additionally, we did not use artificial viscosity in ZEUS, which one would usually switch on in a global simulation and which reduces the growth rate (Fig. 11 dashed line). The dashed red line in Fig. 10 shows the growth rate for PLUTO with the third order convex-eno reconstruction (Del Zanna & Bucciantini 2002). The growth rate is closer to $\gamma_{\rm MRI}$ for the doubled resolution (green lines).

The highest resolution run is almost the limit on even the fastest computers; it was calculated on the Blue Gene/P taking nearly 50 000 CPU h for 11 inner orbits. In contrast, global simulations on viscous times-scales need 10 000 orbits.

\begin{figure} \par\includegraphics[width=9cm,clip]{12443fg11.ps} \end{figure} Figure 11:

Four mode perturbation setup for different reconstruction methods. For the lowest resolution, the base dissipation of the scheme becomes important for the growth rate value. The convex eno reaches the growth rate value as for the $128\times 64 \times 64$ run. It seems that 8 grid cells per critical mode is enough here.

Open with DEXTER

6 Conclusions

We have identified a robust and accurate Godunov scheme for 3D MHD simulations in curvilinear coordinate systems through demonstrating convergence and stability for the well studied linear growth phase of the MRI. Crucially, the scheme uses a constrained transport reconstruction of the EMF's which is consistent with the plane-parallel, grid-aligned flow, which is found in Keplerian flows in curvilinear coordinates. By contrast, a four-point arithmetic average CT method leads to the growth of a ``checkerboard'' numerical instability. The HLLD and Roe Riemann solvers present this instability independent of resolution. Both solvers treat the Alfvén characteristics in the Riemann fan. The numerical instability is obviously connected to the Alfvén wave (Miyoshi & Kusano 2008). Harten-Lax-van Leer and Lax-Friedrichs do not resolve the instability for moderate resolutions. The results of our inter-code comparison and convergence tests stress the importance of properly treating the Alfvén characteristics in Riemann solvers for flows driven by the MRI. Alongside loop advection (Gardiner & Stone 2008), the linear evolution of the MRI is a key test problem. We measured the linear MRI growth rates in both the finite difference code Zeus and the Godunov code PLUTO with several different Riemann solvers. More than eight grid cells per wavelength are needed to correctly evolve the MRI mode in both codes. The numerical dissipation is greater with the Lax-Friedrichs and HLL solvers than with the finite difference scheme of ZEUS, owing to the reconstruction of the interface states in the former. The HLLD and Roe Riemann solvers achieve a lower dissipation by including additional MHD characteristics. During the linear growth, the HLLD and Roe solvers show results similar to the finite difference scheme ZEUS for the same order of accuracy and resolution. In addition, the HLLD solver yields an evolution very similar to that obtained with the Roe solver, despite the neglect of the slow magneto-sonic characteristic. A consistent upwind EMF reconstruction in combination with the HLLD Riemann solver gives a consistent, conservative and efficient scheme for our future 3D global MHD calculations of accretion disks. In a follow-up work we will perform and study the non-linear MRI evolution including resistive MHD.

Acknowledgements
We thank Udo Ziegler for very useful discussions about the upwind constrained transport. We also thank Neal Turner, Ralf Kissmann, Thomas Henning and Matthias Griessinger for comments on the manuscript. H. Klahr, N. Dzyurkevich and M. Flock have been supported in part by the Deutsche Forschungsgemeinschaft DFG through grant DFG Forschergruppe 759 The Formation of Planets: The Critical First Growth Phase. Parallel computations have been performed on the PIA cluster of the Max-Planck Institute for Astronomy Heidelberg located at the computing center of the Max-Planck Society in Garching.


References

  1. Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
  2. Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
  3. Balsara, D. S. 2004, ApJS, 151, 149 [NASA ADS] [CrossRef] [Google Scholar]
  4. Balsara, D. S., & Spicer, D. S. 1999, J. Comput. Phys., 149, 270 [Google Scholar]
  5. Blaes, O. M., & Balbus, S. A. 1994, ApJ, 421, 163 [NASA ADS] [CrossRef] [Google Scholar]
  6. Brandenburg, A., Nordlund, A., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brecht, S. H., Lyon, J., Fedder, J. A., & Hain, K. 1981, Geophys. Res. Lett., 8, 397 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cargo, P., & Gallice, G. 1997, J. Comput. Phys., 136, 446 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dai, W., & Woodward, P. R. 1998, ApJ, 494, 317 [NASA ADS] [CrossRef] [Google Scholar]
  10. Davis, S. W., Stone, J. M., & Pessah, M. E. 2010, ApJ, 713, 52 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dedner, A., Kemm, F., Kröner, D., et al. 2002, J. Comput. Phys., 175, 645 [Google Scholar]
  12. Del Zanna L., & Bucciantini N. 2002, A&A, 390, 1177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Devore, C. R. 1991, J. Comput. Phys., 92, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  14. Dzyurkevich, N., Flock, M., Turner, N. J., Klahr, H., & Henning, Th. 2010, A&A, 515, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [Google Scholar]
  16. Falle, S. A. E. G. 2002, ApJ, 577, L123 [NASA ADS] [CrossRef] [Google Scholar]
  17. Flaig, M., Kissmann, R., & Kley, W. 2009, MNRAS, 282 [Google Scholar]
  18. Fleming, T. P., Stone, J. M., & Hawley, J. F. 2000, ApJ, 530, 464 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fromang, S., & Nelson, R. P. 2006, A&A, 457, 343 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  20. Fromang, S., & Nelson, R. P. 2009, A&A, 496, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Fromang, S., & Papaloizou, J. 2007, A&A, 476, 1113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gardiner, T. A., & Stone, J. M. 2005, J. Comput. Phys., 205, 509 [Google Scholar]
  25. Gardiner, T. A., & Stone, J. M. 2008, J. Comput. Phys., 227, 4123 [NASA ADS] [CrossRef] [Google Scholar]
  26. Groth C. P. T., De Zeeuw D. L., Gombosi T. I., & Powell K. G. 2000, J. Geophys. Res., 105, 25053 [Google Scholar]
  27. Hawley, J. F. 2000, ApJ, 528, 462 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hawley, J. F., & Balbus, S. A. 1991, ApJ, 376, 223 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hawley, J. F., & Stone, J. M. 1995, Comp. Phys. Comm., 89, 127 [Google Scholar]
  30. Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 464, 690 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hayes, J. C., Norman, M. L., Fiedler, R. A., et al. 2006, ApJS, 165, 188 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hirose S., Krolik J. H., & Stone J. M. 2006, ApJ, 640, 901 [NASA ADS] [CrossRef] [Google Scholar]
  34. Ilgner, M., & Nelson, R. P. 2006, A&A, 445, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Jin, L. 1996, ApJ, 457, 798 [NASA ADS] [CrossRef] [Google Scholar]
  36. Komissarov, S. S. 1999, MNRAS, 303, 343 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kurganov, A., Noelle, S., & Petrova, G. 2001, J. Sci. Comput., 23, 707 [Google Scholar]
  38. Londrillo, P., & Del Zanna, L. 2000, ApJ, 530, 508 [NASA ADS] [CrossRef] [Google Scholar]
  39. Londrillo, P., & del Zanna, L. 2004, J. Comput. Phys., 195, 17 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2008, A&A, 479, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Matsumoto, R., & Tajima, T. 1995, ApJ, 445, 767 [NASA ADS] [CrossRef] [Google Scholar]
  42. Mignone, A., & Bodo, G. 2008, in Lecture Notes in Physics, ed. S. Massaglia, G. Bodo, A. Mignone, & P. Rossi (Berlin: Springer Verlag), 754, 71 [Google Scholar]
  43. Mignone, A., Bodo, G., & Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
  44. Miyoshi, T., & Kusano, K. 2005, J. Comput. Phys., 208, 315 [NASA ADS] [CrossRef] [Google Scholar]
  45. Miyoshi, T., & Kusano, K. 2008, in Numerical Modeling of Space Plasma Flows, ed. N. V. Pogorelov, E. Audit, G. P. Zank, ASP Conf. Ser., 385, 279 [Google Scholar]
  46. Pessah, M. E., & Chan, C.k. 2008, ApJ, 684, 498 [NASA ADS] [CrossRef] [Google Scholar]
  47. Powell, K. G. 1994, Approximate Riemann solver for magnetohydrodynamics (that works in more than one dimension), Tech. Rep. [Google Scholar]
  48. Powell, K. G., Roe, P. L., Linde, T. J., Gombosi, T. I., & de Zeeuw, D. L. 1999, J. Comput. Phys., 154, 284 [NASA ADS] [CrossRef] [Google Scholar]
  49. Robinet J., Gressier J., Casalis G., & Moschetta J. 2000, J. Fluid Mech., 417, 237 [NASA ADS] [CrossRef] [Google Scholar]
  50. Ryu, D., Miniati, F., Jones, T. W., & Frank, A. 1998, ApJ, 509, 244 [NASA ADS] [CrossRef] [Google Scholar]
  51. Sano, T., Miyama, S. M., Umebayashi, T., & Nakano, T. 2000, ApJ, 543, 486 [NASA ADS] [CrossRef] [Google Scholar]
  52. Sano, T., Inutsuka, S.I., Turner, N. J., & Stone, J. M. 2004, ApJ, 605, 321 [NASA ADS] [CrossRef] [Google Scholar]
  53. Stone, J. M., & Gardiner, T. A. 2005, in Magnetic Fields in the Universe: From Laboratory and Stars to Primordial Structures, ed. E. M. de Gouveia dal Pino, G. Lugones, & A. Lazarian, AIP Conf. Ser., 784, 16 [Google Scholar]
  54. Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
  55. Stone, J. M., Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 463, 656 [NASA ADS] [CrossRef] [Google Scholar]
  56. Tóth, G. 2000, J. Comput. Phys., 161, 605 [Google Scholar]
  57. Turner, N. J. 2004, ApJ, 605, L45 [NASA ADS] [CrossRef] [Google Scholar]
  58. Turner, N. J., Stone, J. M., & Sano, T. 2002, ApJ, 566, 148 [NASA ADS] [CrossRef] [Google Scholar]
  59. Turner, N. J., Sano, T., & Dziourkevitch, N. 2007, ApJ, 659, 729 [NASA ADS] [CrossRef] [Google Scholar]
  60. Wardle, M. 1999, MNRAS, 307, 849 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... one[*]
The zero gradient boundary condition is similar to the often applied ``outflow'' boundary condition, but allows also inflow velocities. Due to the buffer zones from 1 to 2 R0 and 3 to 4 R0 we have no interaction with the radial boundary in our inner domain.

All Tables

Table 1:   Initial parameter of global setup.

Table 2:   MRI growth rates measured for models with 4 and 8 MRI modes (n=4,8).

Table 3:   Growth rates for the resolution tests with initial 4 mode (4M) and white noise perturbations (WN).

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{12443fg1.ps} \end{figure} Figure 1:

Analytical growth rate plotted for different qr (solid to dash-doted lines). Triangles present the measured MRI growth rates from our simulation with initial axisymmetric white noise disturbance from model $\rm {HLLD}_{LIN}$ $128\times 64 \times 64$with n=4. The values are measured for each radii and averaged. Results are similar to those in Hawley & Balbus (1991), Fig. 8.

Open with DEXTER
In the text

  \begin{figure} \hspace{0.6cm}% \par\includegraphics[width=9cm,clip]{12443fg2a.ps}\vspace*{2.5mm} \includegraphics[width=9cm,clip]{12443fg2b.ps} \end{figure} Figure 2:

Maximal amplitude growth of the critical MRI mode plotted for the 42 radial slices between radii R=2 (red line) and R=3 (blue line) for local and inner orbits. The setup is constructed to excite the mode with $\lambda _{\rm crit}=H$ (n=1). For the radii near R=2, the MRI growth rate reaches the value of $\gamma = 0.75 \Omega $. At the outer edge of the radial domain, the growth rate becomes higher than $ 0.75 \Omega $ (blue line). The MRI modes there are affected by the inner part, where MRI already breaks into nonlinear evolution after eight inner orbits.

Open with DEXTER
In the text

  \begin{figure} \hspace{0.6cm} \par\includegraphics[width=9cm,clip]{12443fg3a.ps}\vspace*{2.5mm} \includegraphics[width=9cm,clip]{12443fg3b.ps} \end{figure} Figure 3:

Radial magnetic energy integrated for the total domain for n=4 ( top) and n=8 ( bottom) with upwind CT (solid line), Powell 8-wave (dashed line) and arithmetic CT (dotted line). The values are normalized over the initial orbital kinetic energy. After the initial disturbance, the growth of critical mode dominates and there is a linear MRI region visible between two and eight inner orbits. For HLLD and Roe, the arithmetic CT shows a growth stronger then MRI until five inner orbits, caused by a numerical instability. Harten-Lax-van Leer and TVDLF have a much lower growth because both methods are viscous and do not resolve the critical mode for the adopted resolution.

Open with DEXTER
In the text

  \begin{figure} \hspace{0.6cm}% \par\includegraphics[width=9cm,clip]{12443fg4a.ps}\vspace*{2.5mm} \includegraphics[width=9cm,clip]{12443fg4b.ps} \end{figure} Figure 4:

Local growth rate for n=4 ( top) and n=8 ( bottom) with arithmetic CT. For HLLD and Roe the local growth rate exceeds the analytical limit and shows unphysical spatial variations. The problem does not affect the HLL and TVDLF solver at moderate resolution. Harten-Lax-van Leer (green) and TVDLF show exact the same results.

Open with DEXTER
In the text

  \begin{figure} \hspace{0.6cm}% \par\includegraphics[width=9cm,clip]{12443fg5a.ps... ...g5b.ps}\vspace*{3mm} \includegraphics[width=9cm,clip]{12443fg5c.ps} \end{figure} Figure 5:

Contour plot of the azimuthal magnetic field for arithmetic CT (top), UCT ( middle) and ZEUS (bottom). For the arithmetic CT, the ``checkerboard'' instability dominates. For UCT and ZEUS the n=4 is most prominent. A change from blue to red indicates a change of sign in the magnetic field. This snap-shot of the magnetic field is taken after eight inner orbits.

Open with DEXTER
In the text

  \begin{figure} \hspace{0.6cm} \par\includegraphics[width=9cm,clip]{12443fg6a.ps}\\ \vspace*{3mm} \includegraphics[width=9cm,clip]{12443fg6b.ps} \end{figure} Figure 6:

Local growth rate for n=4 (top) and n=8 (bottom) with upwind CT (solid line), $\rm {UCT}_{\rm {contact}}$ (dashed line) and Powell's Eight Wave (dotted line). The high-resolution MHD Riemann solver HLLD and Roe show the same MRI evolution, producing the same growth rate as ZEUS. The HLL solver and TVDLF are more diffusive.

Open with DEXTER
In the text

  \begin{figure} \hspace{0.6cm}% \par\includegraphics[width=9cm,clip]{12443fg7a.ps}\\ \vspace*{3mm} \includegraphics[width=9cm,clip]{12443fg7b.ps} \end{figure} Figure 7:

Top: contour plot of radial magnetic field for n=8 mode low resolution run. Even with a resolution of $16 \times 8 \times 8$ the HLLD solver can resolve the checkerboard pattern for ACT. Bottom: high resolution run for n=8 mode and the HLL solver with ACT. The checkerboard pattern becomes visible (red box).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{12443fg8a.ps}\vspace*{2.8mm}... ...8mm} \includegraphics[width=9cm,clip]{12443fg8c.ps}\vspace*{-3.5mm} \end{figure} Figure 8:

Contour plot of the radial magnetic field in code units for the HLLD solver ( top), ZEUS ( middle) and HLL solver ( bottom). After seven inner orbits the inner radial part breaks into a nonlinear regime.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{12443fg9a.ps}\vspace*{3mm} \includegraphics[width=9cm,clip]{12443fg9b.ps} \end{figure} Figure 9:

Growth rate of MRI for PPM (dashed line) and PLM (solid line). For the Lax-Friedrichs solver the PPM interpolation leads to growth rates closer to the analytic solution, which is due to lower numerical dissipation. Differences between HLLD and Roe solvers are less prominent.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{12443fg10a.ps}\vspace*{2.5mm} \includegraphics[width=9cm,clip]{12443fg10b.ps}\vspace*{-2mm} \end{figure} Figure 10:

Convergence for the white noise ( top) and single 4 mode perturbation setup ( bottom). For the single 4 mode perturbation the growth rates exhibit a quick convergence to the analytical limit $\gamma _{\rm MRI} = 0.75$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{12443fg11.ps} \end{figure} Figure 11:

Four mode perturbation setup for different reconstruction methods. For the lowest resolution, the base dissipation of the scheme becomes important for the growth rate value. The convex eno reaches the growth rate value as for the $128\times 64 \times 64$ run. It seems that 8 grid cells per critical mode is enough here.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.