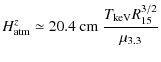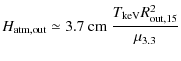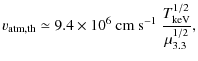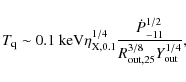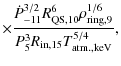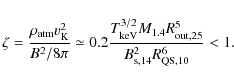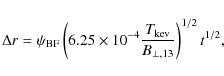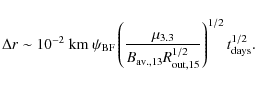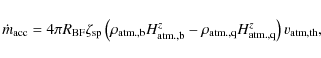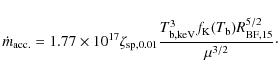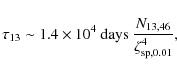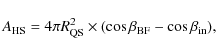| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200811114 | |
| Published online | 20 July 2010 | |
Quark-nova remnants
IV. Application to radio emitting anomalous X-ray pulsars transients
R. Ouyed - D. Leahy - B. Niebergal
Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Canada
Received 9 October 2008 / Accepted 12 April 2010
Abstract
XTE J1810-197 and 1E 1547.0-5408 are two transient anomalous X-rays pulsars (AXPs) exhibiting
radio emission with unusual properties. In addition, their spin down rates
during outburst show opposite trends, which so far has no explanation.
Here, we extend our quark-nova model for AXPs to include transient AXPs, in which the outbursts
are caused by transient accretion events from a Keplerian (iron-rich) degenerate ring.
For a ring with
inner and outer radii of 23.5 km and 26.5 km, respectively, our model
gives a good fit to the
observed X-ray outburst from XTE J1810-197 and the behavior
of temperature, luminosity, and area of the two X-ray blackbodies with time.
The two blackbodies in our model are related to
a heat front (i.e. Bohm diffusion front) propagating along the ring's surface
and an accretion hot spot on the quark star surface.
Radio pulsations in our model are caused by dissipation
at the light cylinder of magnetic bubbles, produced near the ring during the
X-ray outburst.
The delay between X-ray peak
emission and radio emission in our model is related to the propagation time
of these bubbles to the light cylinder and scale with the
period as
![]() where
where
![]() defines the radial dependence of matter density in the magnetosphere
(
defines the radial dependence of matter density in the magnetosphere
(
![]() ); for an equatorial wind,
); for an equatorial wind,
![]() ,
we predict a
,
we predict a
![]() 1 year and
1 year and ![]() 1 month delay for XTE J1810-197 and 1E 1547.0-5408,
respectively. The observed flat spectrum, erratic pulse profile,
and the pulse duration are all explained in our model as a result of X-point reconnection
events induced by
the dissipation of the bubbles at the light cylinder. The spin down
rate of the central quark star can either increase or decrease depending
on how the radial drift velocity of the magnetic islands changes with distance
from the central star. We suggest an evolutionary connection between
transient AXPs and typical AXPs in our model.
1 month delay for XTE J1810-197 and 1E 1547.0-5408,
respectively. The observed flat spectrum, erratic pulse profile,
and the pulse duration are all explained in our model as a result of X-point reconnection
events induced by
the dissipation of the bubbles at the light cylinder. The spin down
rate of the central quark star can either increase or decrease depending
on how the radial drift velocity of the magnetic islands changes with distance
from the central star. We suggest an evolutionary connection between
transient AXPs and typical AXPs in our model.
Key words: stars: evolution - accretion, accretion disks - magnetic fields - pulsars: general
1 Introduction
Anomalous X-ray pulsars (AXPs) are magnetars with rotation period
of 2-12 s and inferred surface magnetic field strength
![]() G (e.g.
Woods & Thompson 2006; Kaspi 2007). In this work we focus
on 2 AXPs, XTE J1810-197 and 1E 1547.0-5408, which are the only magnetars known
to emit in the radio (Camilo et al. 2006). Both are demonstrably
transient radio sources, having not been detected in previous
surveys of adequate sensitivity.
XTE J1810-197 is a transient AXP
G (e.g.
Woods & Thompson 2006; Kaspi 2007). In this work we focus
on 2 AXPs, XTE J1810-197 and 1E 1547.0-5408, which are the only magnetars known
to emit in the radio (Camilo et al. 2006). Both are demonstrably
transient radio sources, having not been detected in previous
surveys of adequate sensitivity.
XTE J1810-197 is a transient AXP![]() first detected when
its X-ray flux increased
first detected when
its X-ray flux increased ![]() 100-fold compared to a quiescent
level it maintained for at least 24 years (Ibrahim et al. 2004).
Discovered with the Einstein X-ray satellite in 1980,
1E 1547.0-5408 was eventually identified as a magnetar candidate
(Gelfand & Gaensler 2007) with spectral characteristics of an AXP.
In this paper we look at these sources
in the Quark-Nova context (hereafter QN; Ouyed et al. 2002) building
on three previous papers where we explore its application
to Soft Gamma-ray Repeaters (SGRs) (Ouyed et al. 2007a; OLNI),
to AXPs (Ouyed et al. 2007b; OLNII),
and to Rotating Radio Transients (RRATs) (Ouyed et al. 2009; OLNIII),
and superluminous supernovae (Leahy & Ouyed 2008). But first, we briefly describe
their observed X-ray and radio properties, during quiescence and bursting phases.
100-fold compared to a quiescent
level it maintained for at least 24 years (Ibrahim et al. 2004).
Discovered with the Einstein X-ray satellite in 1980,
1E 1547.0-5408 was eventually identified as a magnetar candidate
(Gelfand & Gaensler 2007) with spectral characteristics of an AXP.
In this paper we look at these sources
in the Quark-Nova context (hereafter QN; Ouyed et al. 2002) building
on three previous papers where we explore its application
to Soft Gamma-ray Repeaters (SGRs) (Ouyed et al. 2007a; OLNI),
to AXPs (Ouyed et al. 2007b; OLNII),
and to Rotating Radio Transients (RRATs) (Ouyed et al. 2009; OLNIII),
and superluminous supernovae (Leahy & Ouyed 2008). But first, we briefly describe
their observed X-ray and radio properties, during quiescence and bursting phases.
1.1 The X-ray emission
In the pre-burst era, XTE J1810-197's ROSAT spectrum showed a single blackbody (BB)
with temperature T = 0.18 keV, an emitting area of
![]() ,
and a luminosity of
,
and a luminosity of
![]() .
During its bursting phase, XTE J1810-197 showed a hot blackbody (
.
During its bursting phase, XTE J1810-197 showed a hot blackbody (
![]() keV)
with an exponential decay in X-ray luminosity of
keV)
with an exponential decay in X-ray luminosity of ![]() 280 days,
as well as a warm blackbody (
280 days,
as well as a warm blackbody (![]() keV) decaying at a rate of
keV) decaying at a rate of ![]() 870 days
(Gotthelf & Halpern 2007).
For the case of 1E 1547.0-5408, after its radio detection (Camilo et al. 2007a),
an X-ray outburst was confirmed
(Halpern et al. 2008) with a record high luminosity of
870 days
(Gotthelf & Halpern 2007).
For the case of 1E 1547.0-5408, after its radio detection (Camilo et al. 2007a),
an X-ray outburst was confirmed
(Halpern et al. 2008) with a record high luminosity of
![]() erg s-1 and with a total outburst energy
of
erg s-1 and with a total outburst energy
of
![]() erg.
erg.
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{11114fg1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa11114-08/Timg19.png)
|
Figure 1: Illustrated here are the stages involved in the transition from a neutron star (NS) (inclined rotator) to a quark star (QS) (aligned rotator) in the Quark-Nova scenario. The collapse of the quark core induces an explosive NS-to-QS transition ejecting iron-rich degenerate crust material. The QS enters a superconductive phase confining the interior field to vortices, forcing the exterior field to align with the rotation axis (see Ouyed et al. 2004, for more details; and Ouyed et al. 2006, for the related simulations). The iron-rich degenerate ejecta evolves into a Keplerian ring (at about 15-30 km from the star) surrounded, but not penetrated, by the dipole field (a co-rotating ejecta is also possible depending on the NS period; see OLNI). |
| Open with DEXTER | |
1.2 The radio emission
For XTE J1810-197, the radio emission began within 1 yr of its only known X-ray outburst (Camilo et al. 2006, and references therein). At its observed peak more than 3 yr after the X-ray outburst, the radio flux density was more than 50 times the pre-burst upper limit. The X-ray flux has since returned to its quiescent level nearly 4 yrs after the burst. 1E 1547.0-5408, although not as well sampled as XTE J1810-197, exhibits similar variations in flux density and was reported with a factor of 16 times the pre-burst upper limit (Camilo et al. 2007a).
Trends in radio emission between the 2 sources can be summarized as follows:
- both are very highly linearly polarized showing
a flat spectrum over a wide range of frequencies.
Their striking spectra (i.e. spectral index >-0.5) clearly distinguishable
from ordinary radio pulsars (with a spectral index
 -1.6; Camilo et al. 2007a,b);
-1.6; Camilo et al. 2007a,b);
- at their peak, both magnetars are very luminous in radio with
luminosity at 1.4 GHz
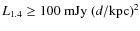 ,
which is larger than the
,
which is larger than the
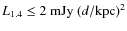 of most any ordinary young pulsar (e.g.
Camilo et al. 2006). For XTE J1810-197, its assumed isotropic radio luminosity
up to 42 GHz is about
of most any ordinary young pulsar (e.g.
Camilo et al. 2006). For XTE J1810-197, its assumed isotropic radio luminosity
up to 42 GHz is about
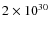 erg s-1 (Camilo et al. 2006);
erg s-1 (Camilo et al. 2006);
- both have variable pulse profiles (exhibiting sudden changes in radio pulse shape) and radio flux densities. The flux changes at all frequencies. At a given frequency there is no stable average pulse profile. Different pulse components change in relative intensity and new components sometimes appear. Sub-pulses with typical width approximately <10 ms are observed (Camilo et al. 2007a,b);
- for XTE J1810-197, the torque was decreasing, at a time when the star was returning to quiescence years after the large outburst. As the torque decreased, so did the radio flux (Camilo et al. 2007b);
- in 1E 1547.0-5408, in contrast, the torque has been increasing, at a time when the X-ray flux has been gradually decreasing (Camilo et al. 2007a).
2 Basic components of the model
The Quark-Nova is an explosive transition from a neutron star (NS) to quark star (QS) (Ouyed et al. 2002; Keränen & Ouyed 2003). The result is a partial ejection of the NS crust (Keränen et al. 2005) that leads to two possible types of debris surrounding the compact remnant (i.e. the QS) depending on the QS's birth period. In OLNI, we showed that if the QS is born slowly rotating, then the debris formed from the QN ejecta will be in co-rotation, which we argue is responsible for SGRs. In OLNII, we showed that for QS born with millisecond periods, the debris evolves into a Keplerian ring with applications to AXPs. Furthermore, RRATs are the result of late evolution of the Keplerian ring in our model (OLNIII). The interested reader is referred to these papers for more details. Below we give an overview of the salient features of the model in the case of a Keplerian ring before we apply our model to transient AXPs.
2.1 The quark star: magnetically aligned rotator
The QN compact remnant is a quark star in the Color-Flavor-Locked (CFL) phase, which due to it's rigorously electric neutrality (Rajagopal & Wilczek 2001) possesses no crust. Owing to the superconductivity of the CFL state, the star's interior contains a lattice of vortices that confine the magnetic field (Ouyed et al. 2004). This interior configuration consequently forces the exterior field to align with the rotation axis (Ouyed et al. 2006; Niebergal et al. 2006); this is illustrated in Fig. 1.
![\begin{figure}
\includegraphics[width=12.2cm,clip]{11114fg2a.eps}\vspace*{1.5mm}
\par\includegraphics[width=11.7cm,clip]{11114fg2b.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa11114-08/Timg24.png)
|
Figure 2:
The upper panel illustrates the ring structure during outburst.
Fiducial values of the ring inner radius (15 km) and outer radius
(25 km) are shown; the ring's vertical scale height is a few
kilometers (see Sect. 2.2; the figure is not to scale). The ring
is surrounded, but not penetrated, by the dipole field. The Bohm Front
- ``bump'' made of non-degenerate Keplerian material - propagates
outward at a speed
|
| Open with DEXTER | |
2.2 The Keplerian ring
Here we are concerned with compact remnants born with millisecond periods.
As shown in OLNII, the quark star is surrounded by Keplerian
debris we refer to as a ring.
This Keplerian ring is described in detail in Sect. 2.1 and Appendix A
in OLNII. Briefly, it is a high density (
![]() g cm-3) ring
rich in iron-group degenerate material (the ejected
NS crust material) in Keplerian
rotation around the QS.
The ring is highly
conducting, cool, and not threaded by
the magnetic field. It is
a (possibly amorphous) crystalline solid (like the outer crust of a neutron
star). The ring expands vertically and radially
in time to a structure depicted in Fig. 2 with the
ring inner radius at
g cm-3) ring
rich in iron-group degenerate material (the ejected
NS crust material) in Keplerian
rotation around the QS.
The ring is highly
conducting, cool, and not threaded by
the magnetic field. It is
a (possibly amorphous) crystalline solid (like the outer crust of a neutron
star). The ring expands vertically and radially
in time to a structure depicted in Fig. 2 with the
ring inner radius at
![]() km, and an outer radius at
km, and an outer radius at
![]() km (for these fiducial values the
total area of the ring is
km (for these fiducial values the
total area of the ring is
![]() km2).
km2).
The ring thickness in the z-direction can be shown to be
![]() where
where
![]() is the ring's density in units of 109 g m cm-3.
In reality, on finer scales than depicted in Fig. 2, the ring is subject to tidal fracture and is made up
of many cylinders we refer to as ``walls''. The width
of each cylinder is set by Keplerian shear resulting in meter size
pieces.
The mass and width of a wall are given in OLNII and are
is the ring's density in units of 109 g m cm-3.
In reality, on finer scales than depicted in Fig. 2, the ring is subject to tidal fracture and is made up
of many cylinders we refer to as ``walls''. The width
of each cylinder is set by Keplerian shear resulting in meter size
pieces.
The mass and width of a wall are given in OLNII and are
![]() and
and
![]() ,
respectively.
,
respectively.
The magnetic field penetrates a conductor of thickness ![]() on timescale
on timescale
![]() where
where ![]() is the conductivity (e.g. Sect. 4.1 in OLNII).
The QS dipole field will penetrate the ring via its innermost wall.
The wall is penetrated radially because
is the conductivity (e.g. Sect. 4.1 in OLNII).
The QS dipole field will penetrate the ring via its innermost wall.
The wall is penetrated radially because
![]() .
This occurs on timescales of
a few hundred years (see Eq. (17) in OLNII). As the QS magnetic field penetrates
the innermost wall, magnetic torques (due to induced
.
This occurs on timescales of
a few hundred years (see Eq. (17) in OLNII). As the QS magnetic field penetrates
the innermost wall, magnetic torques (due to induced ![]() )
slow down the wall, so it can accrete (see Sect. 4).
)
slow down the wall, so it can accrete (see Sect. 4).
2.3 The ring atmosphere
The ring's density decreases with height above the equatorial
plane. At any given temperature the ring's density below
which the ring's matter becomes non-degenerate is found
by equating the ring temperature to its Fermi temperature; this
defines the ring's vertical atmosphere.
The atmosphere is characterized by its base density, scale height in the z-direction
(vertical to the orbital plane), scale height in the radial direction (i.e.
on the outer ring edge,
![]() ;
see Appendix B in OLNII), and
thermal speed,
;
see Appendix B in OLNII), and
thermal speed,
where
![]() is the atmosphere temperature in keV,
is the atmosphere temperature in keV,
![]() is the
radial position in units of 15 km, and
is the
radial position in units of 15 km, and
![]() is the mean molecular
weight in units of 3.3 which represents a partially-ionized iron-rich atmosphere
(see Sect. 3.2 in OLNII). The ring atmosphere's scale height in the
z-direction is to be differentiated from that of the
ring itself
is the mean molecular
weight in units of 3.3 which represents a partially-ionized iron-rich atmosphere
(see Sect. 3.2 in OLNII). The ring atmosphere's scale height in the
z-direction is to be differentiated from that of the
ring itself
![]() which
is of the order of a few kilometers.
which
is of the order of a few kilometers.
The ring's atmosphere is penetrated by the magnetic field on timescales of
![]() .
This can be derived from
.
This can be derived from
![]() (as defined Sect. 2.2) using
(as defined Sect. 2.2) using
![]() and
and
![]() where
where
![]() is the atmosphere's sound speed.
The ring's temperature is in units
of 0.1 keV representative of its equilibrium temperature during the quiescent phase;
see Eq. (16) in OLNII.
Since
is the atmosphere's sound speed.
The ring's temperature is in units
of 0.1 keV representative of its equilibrium temperature during the quiescent phase;
see Eq. (16) in OLNII.
Since
![]() ,
the atmosphere is forced to co-rotate with the field inhibiting
accretion onto the star during the quiescent phase.
On timescales of a hundred years, outbursts are triggered by wall accretion.
These move degenerate ring material into the atmosphere (see Sect. 4 below) faster than the magnetic field
lines penetrate vertically into the
degenerate ring. The ring's penetration timescale is of the order of tens of millions of years because
of the
,
the atmosphere is forced to co-rotate with the field inhibiting
accretion onto the star during the quiescent phase.
On timescales of a hundred years, outbursts are triggered by wall accretion.
These move degenerate ring material into the atmosphere (see Sect. 4 below) faster than the magnetic field
lines penetrate vertically into the
degenerate ring. The ring's penetration timescale is of the order of tens of millions of years because
of the
![]() dependence, so that the ring is not penetrated from above.
dependence, so that the ring is not penetrated from above.
In our model, as we describe in more detail in Sect. 6.1
in this paper, transient AXPs do not accrete during their
quiescent phase while normal AXPs do accrete continuously from the ring's outer edge,
where
![]() .
For now we concern ourselves with transient AXPs whose quiescent
phase is dominated by emission from vortex expulsion as described next.
.
For now we concern ourselves with transient AXPs whose quiescent
phase is dominated by emission from vortex expulsion as described next.
3 The quiescent phase in our model
There are two critical radii in our model during the quiescent
phase, the inner radius
![]() ,
and the
outer ring radius
,
and the
outer ring radius
![]() .
In most cases these radii will be expressed in units of 15 km or 25 km thus
assigned a subscript 15 or 25. The other 2 parameters
related to the geometry of the ring are the ring's solid
angle divided by
.
In most cases these radii will be expressed in units of 15 km or 25 km thus
assigned a subscript 15 or 25. The other 2 parameters
related to the geometry of the ring are the ring's solid
angle divided by ![]() at
at
![]() and
and
![]() namely,
namely,
![]() and
and
![]() .
General relativistic (GR) effects are included
in the factors
.
General relativistic (GR) effects are included
in the factors
![]() ,
,
![]() ,
,
![]() while
while
![]() with
with
![]() being the star's Schwarszhild radius. Unless otherwise specified, quantities
such as luminosity, temperature, and area are local values. Values
at infinity are obtained by using the relevant GR factors.
Finally, the ring area which includes top, bottom and inner surfaces
is
being the star's Schwarszhild radius. Unless otherwise specified, quantities
such as luminosity, temperature, and area are local values. Values
at infinity are obtained by using the relevant GR factors.
Finally, the ring area which includes top, bottom and inner surfaces
is
![]() where
where
![]() .
.
3.1 The 2 blackbodies in quiescence
As discussed in OLNI and OLNII, during the quiescent phase we have 2 blackbodies,
one from the emission due to magnetic reconnection following
vortex expulsion (the emission occurs just outside the star's surface).
The resulting luminosity is (see Sect. 5 in OLNI)
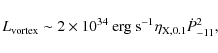
|
(2) |
with a corresponding temperature,
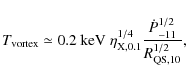
|
(3) |
where the period derivative is in units of 10-11 s s-1, the star's radius in units of 10 km, and
The second BB results from reprocessing by the ring of the first BB's X-ray emission,
![]() .
The ring-atmosphere system's temperature during quiescence is then,
since
.
The ring-atmosphere system's temperature during quiescence is then,
since
![]() ,
,
where the subscript ``q'' stands for quiescent in contrast to the values during the bursting phase denoted by subscript ``b''. These two blackbodies are generic emission components to reprocess the emission from the central object, irrespective of its ultimate origin. As such, they should also be expected in normal AXPs/SGRs, where the continuous emission is dominated by the constant accretion from the ring edge rather than by vortex annihilation. Since
The resulting temperature ratio in our model, using a fiducial
value
![]() ,
is
,
is
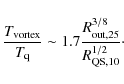
|
(5) |
Interestingly a similar correlation between the hot and cool BB for AXPs and SGRs has been observed (Nakagawa et al. 2009, see their Fig. 4), with
4 Bursting phase in our model
4.1 Consequences of wall penetration and accretion
The ring remains quiescent until magnetic penetration of the inner edge of the ring (wall). The magnetic field penetration and subsequent accretion events are very sporadic - they last for hours and occur roughly once every hundred years (see Sect. 4 in OLNII). The consequences of wall accretion are as follows:
- Change in ring's mean molecular weight:
the energy released by the wall accretion is sufficient to dissociate
a significant mass of iron nuclei in the ring into light nuclei (nuclei
with
 ). The state of the ring depends on the Coulomb parameter which gives a solidification
temperature of
). The state of the ring depends on the Coulomb parameter which gives a solidification
temperature of
 keV (see Sect. 3.2 in Ouyed & Leahy 2009).
The ring mean density (Eq. (A.8) in OLNII)
is
keV (see Sect. 3.2 in Ouyed & Leahy 2009).
The ring mean density (Eq. (A.8) in OLNII)
is
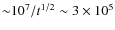 g cm-3, with age t in yrs.
This gives
g cm-3, with age t in yrs.
This gives
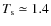 keV. However
during the wall accretion event, the ring temperature rises to
keV. However
during the wall accretion event, the ring temperature rises to  4-5 keV
(see Eq. (C.2)
in OLNII). This completely melts the ring, which allows light
elements to rise buoyantly. Then the ring re-solidifies on a few hour
timescale (Eq. (22) of OLNII). This creates a two layer system as
depicted in Fig. 2.
This process reduces the
molecular weight of the atmosphere from
4-5 keV
(see Eq. (C.2)
in OLNII). This completely melts the ring, which allows light
elements to rise buoyantly. Then the ring re-solidifies on a few hour
timescale (Eq. (22) of OLNII). This creates a two layer system as
depicted in Fig. 2.
This process reduces the
molecular weight of the atmosphere from
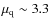 to
to
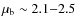 (we adopt an average
(we adopt an average
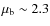 ).
).
As estimated in Sect. 4.4 in OLNII, for a typical wall mass
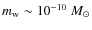 ,
the number of dissociations
following irradiation from wall
accretion is
,
the number of dissociations
following irradiation from wall
accretion is
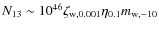 where
where
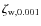 is the dissociation efficiency
in units of 0.001, and
is the dissociation efficiency
in units of 0.001, and
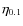 is the
wall accretion efficiency in units of 0.1.
The depth of the
is the
wall accretion efficiency in units of 0.1.
The depth of the 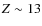 layer can be estimated to be
layer can be estimated to be
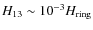 ;
that is, of the order of a few meters.
Subsequent depletion of the
;
that is, of the order of a few meters.
Subsequent depletion of the 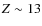 nuclei by accretion leads
to a return to an iron-rich atmosphere (i.e.
nuclei by accretion leads
to a return to an iron-rich atmosphere (i.e.
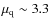 )
as shown
in OLNII (see also Appendix B.2 in this paper).
)
as shown
in OLNII (see also Appendix B.2 in this paper).
- The Bohm front (BF):
the sudden reheating
of the inner ring region triggers heat propagation outward
along the ring's atmosphere. Heat propagation normal to the magnetic
field can occur by either classical or Bohm diffusion.
The classical diffusion coefficient is
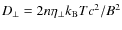 where
where
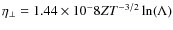 is the transverse Spitzer resistivity with
is the transverse Spitzer resistivity with
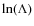 the Coulomb logarithm
(e.g. Eq. (5.71) in Chen 1984, for S. I. units).
The Bohm diffusion coefficient is given by
the Coulomb logarithm
(e.g. Eq. (5.71) in Chen 1984, for S. I. units).
The Bohm diffusion coefficient is given by
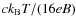 (see Eq. (5.111) in Chen 1984, for S. I. units).
The ratio of classical to Bohm coefficients for B=1013 G, T=0.2 keV and density
of 10 g cm-3 is of the order of 10-8 implying
that Bohm diffusion dominates over classical diffusion for magnetic
field strength and temperatures involved here.
Thus the heat diffuses outward
according to Bohm diffusion, introducing
a critical radius in our model (during the bursting phase),
(see Eq. (5.111) in Chen 1984, for S. I. units).
The ratio of classical to Bohm coefficients for B=1013 G, T=0.2 keV and density
of 10 g cm-3 is of the order of 10-8 implying
that Bohm diffusion dominates over classical diffusion for magnetic
field strength and temperatures involved here.
Thus the heat diffuses outward
according to Bohm diffusion, introducing
a critical radius in our model (during the bursting phase),
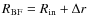 ,
where
,
where 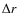 is the distance that the Bohm Front (BF) has travelled from
is the distance that the Bohm Front (BF) has travelled from
 (see
Appendix A for details).
(see
Appendix A for details).
- Atmosphere feeding:
the boundary between the non-degenerate atmosphere and degenerate
ring material, at the BF, moves downwards into higher density layers since
the BF heats up the interface to higher temperatures (recall that
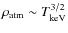 ;
see Eq. (1)).
Thus newly non-degenerate Keplerian ring material is
unveiled between the co-rotating atmosphere and the interface (Fig. 2).
We thus have two mechanisms that feed
the atmosphere with new non-degenerate
material. These two contributions are
seen when estimating the surface density
of the atmosphere
;
see Eq. (1)).
Thus newly non-degenerate Keplerian ring material is
unveiled between the co-rotating atmosphere and the interface (Fig. 2).
We thus have two mechanisms that feed
the atmosphere with new non-degenerate
material. These two contributions are
seen when estimating the surface density
of the atmosphere
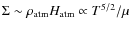 ;
the lower
;
the lower 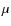 from the buoyancy and the higher T from the
heat front will increase the mass up by a factor of
from the buoyancy and the higher T from the
heat front will increase the mass up by a factor of  10.
10.
- Atmosphere ejection and accretion:
the huge shear between the co-rotating, magnetized atmosphere and the
underlying non-degenerate keplerian atmosphere leads to Kelvin-Helmholtz
instability that helps load the keplerian material onto
the magnetic field lines attached to the heat front
![[*]](/icons/foot_motif.png) . With simple
angular momentum arguments one can show that
any keplerian particle attached to a co-rotating field line
will slide along the field line moving radially outward.
The magnetic field acts as ramp for the plasma
particles to get rid of their excess angular momentum.
This is the slingshot effect in magneto-hydrodynamic (MHD) jets (discussed in Appendix B).
In the quiescent state there is a huge shear between the corotating
field lines (containing the non-degenerate atmosphere) and the Keplerian
degenerate ring material. However since the field lines do not
penetrate the degenerate ring no MHD ejection (and thus no accretion) is feasible.
. With simple
angular momentum arguments one can show that
any keplerian particle attached to a co-rotating field line
will slide along the field line moving radially outward.
The magnetic field acts as ramp for the plasma
particles to get rid of their excess angular momentum.
This is the slingshot effect in magneto-hydrodynamic (MHD) jets (discussed in Appendix B).
In the quiescent state there is a huge shear between the corotating
field lines (containing the non-degenerate atmosphere) and the Keplerian
degenerate ring material. However since the field lines do not
penetrate the degenerate ring no MHD ejection (and thus no accretion) is feasible.
In summary, the K-H instability would load mass onto the field line attached to the Bohm front and get ejected centrifugally along the field lines as explained in Appendix B (see also below). The wind is then channeled onto the star with an accretion rate,
 ,
given by Eq. (B.2) creating a hopt spot (HS) on the surface of the star.
,
given by Eq. (B.2) creating a hopt spot (HS) on the surface of the star.
![\begin{figure}
\par\includegraphics[width=14.5cm,height=4.7cm,clip]{11114fg3a.ep...
...m}
\includegraphics[width=14.5cm,height=4.7cm,clip]{11114fg3b.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa11114-08/Timg97.png)
|
Figure 3: Upper panels: model luminosity (L/1034), temperature and area (curves) from one side of the ring as observed at infinity compared to observations (dots) of the warm component of XTE J1810-197. The dotted line is the contribution inward of the BF, the dashed is from outward of the BF, and the solid is the combined contribution (see text). Lower panels: model luminosity (L/1034), temperature and area (curves) from one pole as observed at infinity compared to observations (dots) of the hot component of XTE J1810-197. In the right-most panel the dotted line traces the shrinkage of the HS as the BF moves outward, the dashed line shows the late contribution from accretion induced by heating of the back side of the ring, and the solid is the combined contribution. |
| Open with DEXTER | |
4.2 The 2 blackbodies during burst
Only magnetic field lines that are in the path of the heat front get loaded and accrete onto the star. The main consequence, as we show in details here, is that the HS on the star moves closer to the pole thus decreasing in area.
The temperature of the inner ring is obtained by equating heating from BF induced
accretion onto
the quark star
with blackbody cooling by the inner ring surface (
![]() );
);
![]() where
where
![]() is the accretion luminosity,
is the accretion luminosity, ![]() the accretion efficiency,
the accretion efficiency,
![]() ,
and the area created by the Bohm front is
,
and the area created by the Bohm front is
![]() .
Here
.
Here
![]() .
The resulting temperature is,
.
The resulting temperature is,
Here,
The accretion rate is then obtained by combining Eq. (B.2)
with equation above to get
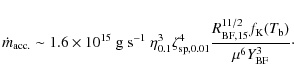
|
(7) |
The function
The natural connection between the
BF outward expansion and the resulting HS on the star is illustrated in Fig. 2.
The corresponding HS luminosity is
with a HS temperature
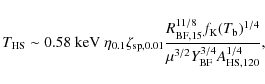
|
(9) |
where the HS area,
In summary, during the burst phase, the ring-atmosphere system consists of 2 BBs; the inner warmer part increasing in area at the Bohm diffusion rate and the outer cooler part decreasing in area. The hot BB in our model is provided by the HS which decreases in area as the BF propagates outwards.
4.3 Temperature ratio during burst
The temperature ratio in the bursting phase case is then:
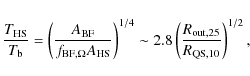
|
(10) |
where we approximated
4.4 Application to XTE J1810-197
The upper panels in Fig. 3 compares the time evolution of the ring's
luminosity, temperature and area in our model
to the observed warm BB in XTE J1810-197. In our
model the luminosity from the inner part of the ring is
![]() while the outer part gives
while the outer part gives
![]() with
with
![]() .
The total luminosity from the ring during burst is
.
The total luminosity from the ring during burst is
![]() while the corresponding effective area and temperature were derived by weighting
over luminosity,
while the corresponding effective area and temperature were derived by weighting
over luminosity,
![]() and
and
![]() .
.
The lower panels in Fig. 3 compare the time evolution of the HS's
luminosity, temperature and area in our model
to the observed hot BB in XTE J1810-197. In this case, only one component
comes into play, the accretion luminosity
![]() .
However, as the BF gets closer to
.
However, as the BF gets closer to
![]() the back side of the ring
is heated resulting in additional accretion by the same mechanism (i.e.
eating into Keplerian material in the radial direction this time) and additional area on the polar cap
defined by the field lines connecting the back side of the ring to the star (see
Fig. 2). The resulting area is
the back side of the ring
is heated resulting in additional accretion by the same mechanism (i.e.
eating into Keplerian material in the radial direction this time) and additional area on the polar cap
defined by the field lines connecting the back side of the ring to the star (see
Fig. 2). The resulting area is
![]() and temperature
and temperature
![]() .
.
The fits to XTE J1810-197 data were obtained for the following set of parameters:
| |
= | (11) | |
| = |
and by slightly adjusting the mass-load at the slow MHD point so that
Assuming that XTE J1810-197 has experienced a few bursting events,
using Eq. (A.7) in OLNII, the ring would have spread to no more than
![]() if the system's
temperature during quiescence remained on average
if the system's
temperature during quiescence remained on average ![]() 0.1 keV.
This is consistent with (
0.1 keV.
This is consistent with (
![]() )
found from fits to the XTE J1810-197 data thus providing a self-consistency check on our model.
This also confirms our overall findings in previous work (OLNI, OLNII and OLNIII)
that the ring should be a few kilometers in width after a few hundred years.
)
found from fits to the XTE J1810-197 data thus providing a self-consistency check on our model.
This also confirms our overall findings in previous work (OLNI, OLNII and OLNIII)
that the ring should be a few kilometers in width after a few hundred years.
4.5 Application to 1E 1547.0-5408
In its bursting phase, this
source was fitted with a ![]() keV hot BB with
keV hot BB with
![]() erg s-1 and a corresponding area decreasing from 180 km2 in June 2007
to 96 km2 in August 2007 (see Halpern et al. 2008).
During the quiescent phase,
erg s-1 and a corresponding area decreasing from 180 km2 in June 2007
to 96 km2 in August 2007 (see Halpern et al. 2008).
During the quiescent phase,
![]() erg s-1,
erg s-1,
![]() keV and
keV and
![]() km2 (see Table 1 in
Halpern et al. 2008).
km2 (see Table 1 in
Halpern et al. 2008).
This source has not been as well sampled as was XTE J1810-197.
Nevertheless, in our model, high BB temperatures during
the quiescent phase are suggestive of a more compact ring
which is closer to the star (see Eq. (4)).
In our model, such a small and compact ring could have been
a consequence of a smaller amount of crust material ejected during the
QN (see Eq. (2) in OLNII).
For example,
![]() km and
km and
![]() km,
which implies
km,
which implies
![]() ,
inserted in Eq. (4) gives
,
inserted in Eq. (4) gives
![]() keV;
we take
keV;
we take
![]() s s-1 for this source.
The ring's burst epoch temperature is then
s s-1 for this source.
The ring's burst epoch temperature is then ![]() 0.48 keV
with a corresponding peak luminosity from Eq. (8) of
0.48 keV
with a corresponding peak luminosity from Eq. (8) of
![]() erg s-1 for
erg s-1 for
![]() .
This is close to the
.
This is close to the
![]() erg s-1 measured in
June-July 2007 (the peak of the outburst was not observed and could have been
higher than this).
The initial area of the HS is given by Eq. (C.1)
and is estimated to be
erg s-1 measured in
June-July 2007 (the peak of the outburst was not observed and could have been
higher than this).
The initial area of the HS is given by Eq. (C.1)
and is estimated to be ![]() 80 km2 using
80 km2 using
![]() km and
km and
![]() km.
Finally, in the case of 1E 1547.0-5408 there seems to be hints
of an aligned rotator from its small X-ray pulsed fraction and its relatively broad
radio pulse. In our model, the QN compact remnant (the QS) is born as
an aligned rotator due to the vortex confinement of magnetic field (see Fig. 1).
km.
Finally, in the case of 1E 1547.0-5408 there seems to be hints
of an aligned rotator from its small X-ray pulsed fraction and its relatively broad
radio pulse. In our model, the QN compact remnant (the QS) is born as
an aligned rotator due to the vortex confinement of magnetic field (see Fig. 1).
5 The radio emission in our model
In this section we develop a scenario for radio emission. As discussed in Sect. 1.2, XTE J1810-197 and 1E 1547.0-5408 show unique characteristics in radio (including delay after X-ray outburst, a flat spectrum, and unusual spin-down behavior). In chronological order the sequence of events that leads to radio emission in our model is as follows:
- magnetic bubbles are generated at the ring during the X-ray outburst (see Sect. 5.1);
- the propagation time of these bubbles from the site of production (the ring) to the l.c. defines the delay between radio and X-ray outbursts (see Sect. 5.2);
- the unusual spin-down behavior is induced by torques on the magnetosphere from the co-rotating bubbles, during their outward propagation (see Sect. 5.5);
- relativistic collisionless reconnection at the l.c. destroys the bubbles;
- magnetic energy released by the bubbles is eventually radiated by particles accelerated by reconnection at the l.c., mostly at radio frequencies (Sect. 5.3). We suggest that the flat radio spectrum is naturally associated to this mechanism (see Sect. 5.4 below).
5.1 Magnetic reconnection and bubble generation
After penetration, the poloidal magnetic field (![]() )
lines
inside the wall (inner ring) are dragged by the Keplerian
shear generating a toroidal magnetic field,
)
lines
inside the wall (inner ring) are dragged by the Keplerian
shear generating a toroidal magnetic field, ![]() .
Continuous reconnection events during the winding
of the field lines lead to X-point generation and emergence of closed magnetic bubbles;
more concisely these magnetically confined plasma bubbles (plasmoids)
result from the Keplerian shear.
.
Continuous reconnection events during the winding
of the field lines lead to X-point generation and emergence of closed magnetic bubbles;
more concisely these magnetically confined plasma bubbles (plasmoids)
result from the Keplerian shear.
Generation of bubbles is a common feature of threaded disks as seen in many simulations (e.g. Romanova et al. 1998; Yelenina et al. 2006). These simulations show the magnetic bubbles to acquire enough speed to escape gravity and expand freely outward. Magnetic loops and bubbles are also common in the sun (referred to as plasmoids) and are also found to gain enough energy from the reconnection events to escape the system and expand freely (e.g. Wagner 1984; Tamano 1991).
One key difference between these cases and our model is the
fact that in our model, during quiescence, the degenerate ring is not
threaded by the magnetic field.
The bubbles form only during
the bursting phase once the magnetic field has penetrated
the inner ring and is sheared. The B field attached to
the broken inner pieces of the wall is wound up by the keplerian angular
velocity (![]() 6000 rad/s) of the piece vs. the corotation angular velocity
(
6000 rad/s) of the piece vs. the corotation angular velocity
(![]() 1 rad/s) of the footpoint of the fieldline on the
quark star. This rapid field line winding results in reconnection and magnetic
loop (bubble) formation. The B field penetration (and subsequent wall accretion with concurrent
bubble generation) events are very sporadic
and unique to our model - they
last for about an hour and occur once every century (see Sect. 4 in OLNII).
1 rad/s) of the footpoint of the fieldline on the
quark star. This rapid field line winding results in reconnection and magnetic
loop (bubble) formation. The B field penetration (and subsequent wall accretion with concurrent
bubble generation) events are very sporadic
and unique to our model - they
last for about an hour and occur once every century (see Sect. 4 in OLNII).
A rough estimate of the number of bubbles that can be generated is
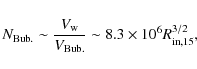
|
(12) |
where the total reconnection volume is
![\begin{figure}
\par\includegraphics[width=12cm,clip]{11114fg4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa11114-08/Timg158.png)
|
Figure 4: Keplerian shear during wall accretion leads to X-point reconnection which in turn causes the generation of closed magnetic loops, or ``bubbles'' (see Sect. 5.1 in text). In our model, these magnetic bubbles are responsible for the radio emission seen in some AXPs. The top panel illustrates the outward migration of a bubble through the surrounding magnetic field. The bubble's magnetic polarity in front as it moves outward is opposite to that of the surrounding dipole. This leads to reconnection and the motion of the bubble towards the light cylinder. The lower diagram shows the overall pattern of bubble migration (i.e. magnetic buoyancy) and expansion that leads to pile up near the light cylinder. The bubbles dissipate as they cross the light cylinder leading to the radio emission (see text for details). |
| Open with DEXTER | |
5.2 Delay between the X-ray and radio emission
Simulations of bubbles in threaded disks show that magnetic loops and bubbles propagate outward because of the
energy they gain from reconnection and because of
the dipolar B-field gradient from the central star, similar to the way
solar field disturbances propagate outward above the solar photosphere.
These bubbles propagate at the sound speed of non-dissipative magnetic field disturbances,
i.e. at the Alfvén speed.
Illustrated in Fig. 4 in this paper, is a rudimentary representation
of what is seen in these simulations; an
outward migration process through the dipole field involving
reconnection. This is a simple
and only qualitative model for bubble propagation, which is a
propagating geometric disturbance in the magnetic field/plasma. Bubble propagation
results in different field lines and different plasma making up the bubble as it
moves. As seen from Fig. 4, a magnetic field line in front of the
bubble is only temporarily part of the bubble, and leaves the bubble after
the bubble has propagated past it. The reconnection on
the front side of the bubble results in surface pressure similar to the
static ![]() ,
so the dynamics of reconnection during bubble migration are
important to how the bubble evolves (both its speed and change in volume) as
it migrates.
,
so the dynamics of reconnection during bubble migration are
important to how the bubble evolves (both its speed and change in volume) as
it migrates.
The Alfvén velocity depends on the
magnetic field geometry inside the light cylinder (which
we take to be nearly dipolar) and on the ambient density
which we take to scale as
![]() .
If there is a steady wind inside the magnetosphere, then if the wind is
spherically symmetric the density we expect would decline as r-2, or if it is equatorially confined the density would decline as r-1; that is
.
If there is a steady wind inside the magnetosphere, then if the wind is
spherically symmetric the density we expect would decline as r-2, or if it is equatorially confined the density would decline as r-1; that is
![]() .
Although the exact distribution is not at all
known (e.g. Michel 1969; Spitkovsky 2008;
see more discussion on this aspect of our model
in 6.5) we will adopt
.
Although the exact distribution is not at all
known (e.g. Michel 1969; Spitkovsky 2008;
see more discussion on this aspect of our model
in 6.5) we will adopt ![]() as we expect
the bubbles to remain along the equator since they are Keplerian at birth.
as we expect
the bubbles to remain along the equator since they are Keplerian at birth.
The bubbles move outwards at a rate given by
![]() where
where
![]() so that
so that
![]() is the radius beyond which the Alfvén speed becomes sub-relativistic; the star's magnetic field
is the radius beyond which the Alfvén speed becomes sub-relativistic; the star's magnetic field
![]() is in units of 1014 G.
is in units of 1014 G.
The time it takes the magnetic bubbles to reach the light cylinder (lc) at
![]() (at which
point they start dissipating) is found from
(at which
point they start dissipating) is found from
![]() ,
,
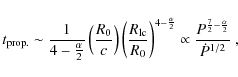
|
(13) |
where we made use of the definition of R0 and
where the period is given in units of 5 s; recall that
5.3 Duration and luminosity
The radio duration has two components in our model:
(i) the radiative lifetime
of the electrons,
![]() ;
(ii) the time difference between when the first bubble arrives and the
last bubble arrives at the l.c.,
;
(ii) the time difference between when the first bubble arrives and the
last bubble arrives at the l.c.,
![]() .
As we show at the end of this section,
propagation delays between bubbles is the dominant component.
Below we focus on case (ii).
.
As we show at the end of this section,
propagation delays between bubbles is the dominant component.
Below we focus on case (ii).
Since all bubbles are produced within a few hours (during the X-ray burst) and at the
same location, the radio duration is determined by variations in propagations times
of the bubbles to the l.c.
The magnetic reconnection events lead to variations in B which
translate to fluctuations in ![]() and thus propagation time (consequently arrival
time at the l.c.) resulting in
and thus propagation time (consequently arrival
time at the l.c.) resulting in
![]() where
where
![]() .
Or,
.
Or,
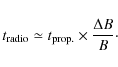
|
(15) |
For a homologous expansion during the outward propagation, a given bubble increases in size as
where
For XTE J1810-197, Camilo et al. (2007c) report radio emission
lasting at least 272 days with initial fading from 5 mJy to 2 mJy in the
first few weeks (see their Fig. 2). In our model,
![]() days gives
days gives
![]() .
Then using
.
Then using
![]() km (from the X-ray
fits in Sect. 4.4),
km (from the X-ray
fits in Sect. 4.4),
![]() erg s-1. This matches
the observed radio luminosity of
erg s-1. This matches
the observed radio luminosity of
![]() erg s-1 for
erg s-1 for
![]() which is suggestive of a high dissipation/reconnection efficiency of the bubbles at the l.c.
which is suggestive of a high dissipation/reconnection efficiency of the bubbles at the l.c.
For 1E 1547-5408, radio emission was observed (Camilo et al. 2008)
from June through August 2007 (![]() 90 days). It was not detected Jan. 22, 2009 within 18 h
of the first reports of renewed X-ray (SGR) bursting activity from it (Camilo et al. 2009).
In our model, this is suggestive of
90 days). It was not detected Jan. 22, 2009 within 18 h
of the first reports of renewed X-ray (SGR) bursting activity from it (Camilo et al. 2009).
In our model, this is suggestive of
![]() .
Then using
.
Then using
![]() km (from the X-ray
fits in Sect. 4.5),
km (from the X-ray
fits in Sect. 4.5),
![]() erg s-1. This matches
the observed radio luminosity of
erg s-1. This matches
the observed radio luminosity of
![]() erg s-1 for
erg s-1 for
![]() .
.
The fits above indicate an order of magnitude difference in efficiency,
![]() ,
between the two sources. However, a smaller
,
between the two sources. However, a smaller ![]() (i.e. a slower density decrease inside the l.c.)
for 1E 1547-5408 would lead to a longer propagation time and lower radio luminosity,
implying a higher reconnection efficiency. Alternatively, a more compact quark star
for 1E 1547-5408 would also imply a higher reconnection efficiency.
(i.e. a slower density decrease inside the l.c.)
for 1E 1547-5408 would lead to a longer propagation time and lower radio luminosity,
implying a higher reconnection efficiency. Alternatively, a more compact quark star
for 1E 1547-5408 would also imply a higher reconnection efficiency.
As a given bubble reaches the l.c. it is sheared and spread-out around
the equator of the l.c. The resulting bubble's magnetic field is
given by
![]() .
This yields
.
This yields
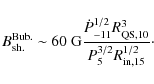
|
(17) |
After shearing, reconnection occurs accelerating electrons (see Sect. 5.4). The electrons emit synchrotron radiation with a critical frequency of
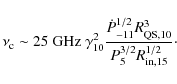
|
(18) |
For XTE J1810-159 the above gives
The above calculations neglect the radiative lifetime
of the electrons. However in cases where
the bubbles reach the l.c. simultaneously (i.e. with negligibly short time
delays), the radio duration will be dominated by the radiative cooling lifetime of the electrons,
![]() (Lang 1999).
For our estimated values of
(Lang 1999).
For our estimated values of ![]() and
and
![]() ,
the propagation delay is
much longer than the electron radiative lifetime. E.g. for 1E 1547-5408, the
radiative lifetime only becomes important, with
,
the propagation delay is
much longer than the electron radiative lifetime. E.g. for 1E 1547-5408, the
radiative lifetime only becomes important, with ![]() ,
for
,
for
![]() G,
which would also result in the critical synchrotron
G,
which would also result in the critical synchrotron
![]() below the observed radio
frequencies.
below the observed radio
frequencies.
5.4 The flat spectrum
As they cross the lc, the bubbles will
dissipate by braking up into smaller bubbles while driving
complex, non-linear reconnection events.
Particle in Cell simulations of X-point reconnection events in a pair plasma have shown that highly
variable radio emission, with an extremely flat spectrum (
If pair generation regions exist in the vicinity of the lc then, when combined with magnetic reconnection events from bubble dissipation, it would offer a natural explanation for the observed flat spectrum. This could also help account for the prevalence of emission at a particular rotation phase (see Fig. 2 in Camilo et al. 2006) which implies that the co-rotating bubbles must preferentially dissipate at a particular co-rotating longitude. It might also be the case that there exist a small non-uniformity at the light cylinder, caused by feedback from pairs produced by bubble dissipation mechanism itself.
5.5 Torques during radio emission
As each bubble expands toward the light cylinder it exerts a torque
![]() where
where
![]() is the moment of inertia of a bubble at a radius
r from the star; here
is the moment of inertia of a bubble at a radius
r from the star; here
![]() is the rate of change of the bubble mass.
For
is the rate of change of the bubble mass.
For
![]() ,
the total torque exerted,
,
the total torque exerted,
![]() ,
is then
,
is then
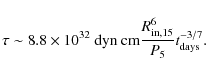
|
(19) |
The corresponding frequency derivative,
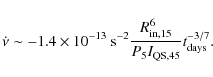
|
(20) |
This gives
In our model,
the torque decreases in time (as the X-ray decreases)
in accordance with what has been observed in the case of XTE J1810-197 (Camilo et al.
2007c). However, for 1E 1547.0-5408,
the torque increased in time as the X-ray flux decreased.
To explain the case of 1E 1547.0-5408 we recall that
the first term (
![]() )
in the torque equation gives a decreasing torque with radius
while the second one (
)
in the torque equation gives a decreasing torque with radius
while the second one (
![]() )
gives an increasing torque with radius.
Since the radius increases in time this is equivalent to the
torque changing accordingly in time. In order for the torque
to increase with time then
)
gives an increasing torque with radius.
Since the radius increases in time this is equivalent to the
torque changing accordingly in time. In order for the torque
to increase with time then
![]() which at a distance
half way to the l.c. implies
which at a distance
half way to the l.c. implies
![]() .
Thus a slight increase in the bubble's mass during propagation
can give an increasing torque with time.
.
Thus a slight increase in the bubble's mass during propagation
can give an increasing torque with time.
6 Discussion
6.1 Transient versus normal AXPs during quiescence in our model
The two sources studied here are termed transients in the sense that in
quiescence their measured temperatures are as low as those of
some ordinary young neutron stars. Only during their bursting phase
that their bolometric luminosity becomes comparable
to that of a typical AXP in quiescence (i.e. a bolometric
luminosity of
![]() ;
see Fig. 2 in OLNIII).
From approximate outburst time, the estimated initial bolometric luminosities
for the two transients are
;
see Fig. 2 in OLNIII).
From approximate outburst time, the estimated initial bolometric luminosities
for the two transients are
![]() .
.
In our model, to understand the difference between
transient and normal AXPs during quiescence, one
should note that the magnetic field would impose co-rotation of the ring's atmosphere (thus
no accretion onto the star)
as long as the magnetic energy density anywhere along
the ring's atmosphere exceeds the Keplerian energy density. The condition is
Thus during the evolution of the source as long as the condition above is satisfied there will be no accretion and the object's emission is dominated by vortex expulsion.
The star's magnetic field decays at a rate (see Sect. 3 in Niebergal et al. 2006)
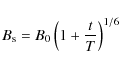
|
(22) |
where
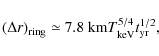
|
(23) |
where time is in years. The ring's radius at birth is given by Eq. (2) in OLNII and is
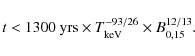
|
(24) |
To get Eq. (24) we start with condition (21) and
The magnetic field decay from vortex
expulsion implies that magnetic field lines deflate radially inwards![]() , so we expect that violation
of co-rotation to first occur at the ring's outer edge.
Also, at the outer edge of the disk, there is magnetic field of opposite
, so we expect that violation
of co-rotation to first occur at the ring's outer edge.
Also, at the outer edge of the disk, there is magnetic field of opposite ![]() being
produced when matter drags field lines. This is an unstable situation
since reconnection can occur between adjacent field lines of opposite
polarity leading to accretion along the reconnecting field lines.
Anywhere else on the surface of the disk, whenever
being
produced when matter drags field lines. This is an unstable situation
since reconnection can occur between adjacent field lines of opposite
polarity leading to accretion along the reconnecting field lines.
Anywhere else on the surface of the disk, whenever ![]() ,
the atmosphere winds up the field lines without reconnecting them until
the magnitude of the magnetic field is strong enough to re-inforce
corotation, i.e. the magnetic field stiffens, leading to a stable
balance.
,
the atmosphere winds up the field lines without reconnecting them until
the magnitude of the magnetic field is strong enough to re-inforce
corotation, i.e. the magnetic field stiffens, leading to a stable
balance.
In summary, a transient AXP quiescent phase is dominated by X-ray
emission from vortex expulsion only (
![]() erg s-1) with the source continuing to evolve along the vortex band (see Fig. 2 in OLNIII).
On the other hand, a typical AXP (older ring-bearing source) quiescent phase
is dominated by emission from the
HS induced by accretion from the outer edge of the ring with
erg s-1) with the source continuing to evolve along the vortex band (see Fig. 2 in OLNIII).
On the other hand, a typical AXP (older ring-bearing source) quiescent phase
is dominated by emission from the
HS induced by accretion from the outer edge of the ring with
![]() given by Eq. (8).
These will evolve horizontally (at constant
given by Eq. (8).
These will evolve horizontally (at constant
![]() erg s-1) as discussed
in OLNII (see Fig. 2 in OLNIII).
erg s-1) as discussed
in OLNII (see Fig. 2 in OLNIII).
It is only during the bursting phase that transient and regular AXPs would look the same since they both experience the BF effect and the related accretion and feedback process. In the transient case, as the BF dies out when reaching the outer edge, the system becomes dominated again by vortex expulsion while regular AXPs resume their accretion dominated (from the outer edge) quiescent phase.
6.2 Birthrate
In our model, a QS-ring system experiences an X-ray/radio outburst every few hundred years.
Since we have observed 2 in a few years, located at distances
of 3 to 9 kpc away (meaning we see about 30% of them), it is
suggestive of a rate of 1 per year for the whole galaxy. This implies
a total population of
![]() in the galaxy. Since the
ring will be consumed on a timescale of
in the galaxy. Since the
ring will be consumed on a timescale of
![]() years (see
Eq. (5) in OLNIII) this gives a birthrate of (1 per 1000 years) to (1 per 100 years).
Within uncertainties, the birth rate
of transient AXPs derived above is consistent with the expected
birthrate of AXPs (
years (see
Eq. (5) in OLNIII) this gives a birthrate of (1 per 1000 years) to (1 per 100 years).
Within uncertainties, the birth rate
of transient AXPs derived above is consistent with the expected
birthrate of AXPs (
![]() ;
Gill & Heyl 2007; Leahy & Ouyed 2009).
As we argued in the previous section, in our model transient AXPs
evolve into typical AXPs thus sharing the same birthrate.
;
Gill & Heyl 2007; Leahy & Ouyed 2009).
As we argued in the previous section, in our model transient AXPs
evolve into typical AXPs thus sharing the same birthrate.
6.3 Model features and predictions
The general predictions, starting with the X-ray emission, in our model are:
- The 2 blackbodies:
overall, during burst and quiescence, the cool BB (from Keplerian ring; or from the co-rotating
shell as in OLNI) arises from reprocessing
radiation of the hot BB from the star (either vortex annihilation or accretion HS).
We suggest, the relations in Fig. 6 in Nakagawa et al. (2009) can be explained
in the context of reprocessing during both quiescence and burst.
Table 1,
summarizes the different emission components for different objects in
different states in our model. Compared to SGRs (see OLNI) and
transient AXPs, typical AXPs acquire an additional BB from the HS
during quiecence. Only during bursting do transient AXPs acquire a HS.
As for SGRs in our model, we recall (see OLNI) they are born with a
co-rotating shell (i.e. non-Keplerian degenerate ring; see OLNI).
Future work will consider hard X-ray emission from non-thermal
processes related to magnetic reconnection following vortex expulsion
and to accretion onto the QS.
Table 1: Thermal components in our model.
- During X-ray burst: since the accreted material in our model consists mostly of dissociated
iron (
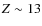 ), we predict some sort of signatures either
during channeling along the field line or on impact on the HS - maybe absorption lines or proton
cyclotron lines (
), we predict some sort of signatures either
during channeling along the field line or on impact on the HS - maybe absorption lines or proton
cyclotron lines (
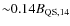 keV) from any of element in the Ne-to-S group (e.g. Ne, Al, Si).
These signatures should be common for both transient and typical AXPs
in our model.
keV) from any of element in the Ne-to-S group (e.g. Ne, Al, Si).
These signatures should be common for both transient and typical AXPs
in our model.
- During X-ray quiescence: when edge accretion occurs the
signatures (e.g. absorption lines or proton
cyclotron lines) should be from the Z=26 rather than the
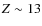 nuclei.
nuclei.
- X-ray variability: during both the quiescent and bursting phases, X-rays from the ring+atmosphere system should be unpulsed and may carry the Keplerian sgnature via millisecond variability.
- Radio delay: as can be seen from Eq. (14), the shorter the period
of the star the smaller the delay,
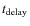 ,
between the X-ray burst and the
radio emission. Interestingly, the 2 radio emitting AXPs so far are observed
are those with the smallest period.
,
between the X-ray burst and the
radio emission. Interestingly, the 2 radio emitting AXPs so far are observed
are those with the smallest period.
- Radio flux: furthermore, as can be seen from Eq. (16), as P gets larger the radio following X-ray burst gets very faint making it more difficult to detect. Combined with long
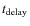 for large P, we argue these to be the reasons why radio
is not observed following X-ray bursts in AXPs with higher (
for large P, we argue these to be the reasons why radio
is not observed following X-ray bursts in AXPs with higher ( 10 s) period.
10 s) period.
- XMM warm BB: the XMM warm BB
for XTE J1810-197 (ring+atmosphere system in our model) will evolve
back to one single BB (ROSAT BB) with temperature
 .
.
- XMM hard BB: the XMM hard BB (the accretion HS in our model) will disappear following burst (i.e. once the Bohm front reaches
 ). However,
we expect edge effects to appear (e.g. flattening or even jump in the hot BB area; see last panel in Fig. 3) just before accretion shuts off.
). However,
we expect edge effects to appear (e.g. flattening or even jump in the hot BB area; see last panel in Fig. 3) just before accretion shuts off.
6.4 Further implications
There exist two aspects of our model that might
provide some answers to fundamental issues in pulsar
magnetospheres![]() .
First, the source in the quark-nova model is born as an aligned rotator
and secondly is the fact that here the degenerate ring,
by Keplerian shear, is a natural source of plasma (carried
by the bubbles to the l.c.) for the magnetosphere.
Also, pairs are naturally supplied to the magnetosphere
by vortex annihilation.
This is left as an avenue for future investigation.
.
First, the source in the quark-nova model is born as an aligned rotator
and secondly is the fact that here the degenerate ring,
by Keplerian shear, is a natural source of plasma (carried
by the bubbles to the l.c.) for the magnetosphere.
Also, pairs are naturally supplied to the magnetosphere
by vortex annihilation.
This is left as an avenue for future investigation.
6.5 Model Limitations
Our model suffers from a few caveats :
- (i)
- the interaction between the BF and the magnetic field in the atmosphere is rudimentary at this stage. Understanding the exact mechanism of feeding material from degenerate ring into the atmosphere and onto the field lines within the Bohm front is essential as this process is behind the feedback process between the ring and the HS on the star. This is a complex problem/system that would require detailed MHD simulations before we can confirm this aspect of our model;
- (ii)
- while the bubble generation mechanism we propose is common
in systems involving dipole files threaded by a disk
on one end and a star on the other, the outward propagation of the
bubbles within the l.c. depends crucially on conditions
within the magnetosphere. In particular, the value
 was chosen solely on the assumption that the bubbles will propagate in
an equatorial wind (given the Keplerian nature of the bubbles at birth)
within the magnetosphere. For highly magnetized, aligned rotators, the
physics of the magnetosphere within the l.c. is yet to be understood
and the problem solved. Furthermore, the bubble dissipation mechanism
as they reach the l.c. remains to be demonstrated. The detailed
structure of the thin shear layer at the light cylinder is not well
studied and would require numerical simulations. For now our
explanation is based on the assumption that the thin transition shear
layer at the l.c. slowly destroys the bubble by shearing off the part
that touched the light cylinder.
was chosen solely on the assumption that the bubbles will propagate in
an equatorial wind (given the Keplerian nature of the bubbles at birth)
within the magnetosphere. For highly magnetized, aligned rotators, the
physics of the magnetosphere within the l.c. is yet to be understood
and the problem solved. Furthermore, the bubble dissipation mechanism
as they reach the l.c. remains to be demonstrated. The detailed
structure of the thin shear layer at the light cylinder is not well
studied and would require numerical simulations. For now our
explanation is based on the assumption that the thin transition shear
layer at the l.c. slowly destroys the bubble by shearing off the part
that touched the light cylinder.
7 Conclusion
There are two fundamental components in our model for
AXPs and transient AXPs namely, the QS and the Keplerian ring.
In quiescence, vortex annihilation on the QS gives rise to thermal
and non-thermal X-ray emission. The ring reprocesses the emission
to give a second cooler BB emission component. Outburst
is triggered by accretion of a small inner part of the ring (i.e. the wall).
The two main consequences are production of light (![]() )
nuclei and triggering MHD accretion onto the QS (yielding the HS).
The interplay between the Bohm diffusion (i.e.
)
nuclei and triggering MHD accretion onto the QS (yielding the HS).
The interplay between the Bohm diffusion (i.e.
![]() term) and depletion of light nuclei
(i.e.
term) and depletion of light nuclei
(i.e. ![]() )
gives rise to a rich behavior, necessary
in order to account for the observed behavior of XTE J1810-197.
Finally, one can ask if such a small Keplerian degenerate iron-rich ring could
form around a neutron star. Ring formation
when the neutron star is born
appears implausible since a proto-neutron star is large
compared to the ring size. After formation, there is no obvious
mechanism to eject degenerate material unless a violent change
of state, like a QN occurs.
)
gives rise to a rich behavior, necessary
in order to account for the observed behavior of XTE J1810-197.
Finally, one can ask if such a small Keplerian degenerate iron-rich ring could
form around a neutron star. Ring formation
when the neutron star is born
appears implausible since a proto-neutron star is large
compared to the ring size. After formation, there is no obvious
mechanism to eject degenerate material unless a violent change
of state, like a QN occurs.
This research is supported by grants from the Natural Science and Engineering Research Council of Canada (NSERC). We thank the referee for comments that helped improve this paper.
Appendix A: The Bohm diffusion front
The hot front propagates from the inner parts of the ring at a Bohm diffusion rate given
by
where
The ring geometry allows us to write
![]() where to a first approximation
where to a first approximation
![]() and
and
![]() where
where
![]() ;
here
;
here
![]() and
and
![]() are the star's magnetic field and radius, respectively. The temperature cancels out from Eq. (A.1) since
are the star's magnetic field and radius, respectively. The temperature cancels out from Eq. (A.1) since
![]() so that,
so that,
Appendix B: Centrifugal ejection and channeled accretion
As the system (ring+atmosphere) is heated,
the boundary between the non-degenerate atmosphere and the degenerate
![]() layer moves downwards into higher density layers (see Eq. (1)).
Thus Keplerian ring material is fed into the atmosphere
and is ejected as a magnetohydrodynamic (MHD) wind as outlined below (see also
lower panel in Fig. 2).
layer moves downwards into higher density layers (see Eq. (1)).
Thus Keplerian ring material is fed into the atmosphere
and is ejected as a magnetohydrodynamic (MHD) wind as outlined below (see also
lower panel in Fig. 2).
At keV temperatures the gas is sufficiently ionized
everywhere in the atmosphere that ideal MHD can be used.
Since the Lorentz force only has components perpendicular to the field,
the gas is free to move along the co-rotating field line under the influence
of other forces.
Under these conditions, it
has been shown that the wind can be launched centrifugally if the
field direction is inclined at an angle less than
![]() to the radial
direction (Blandford & Payne 1982).
Using conservation of specific angular momentum (
to the radial
direction (Blandford & Payne 1982).
Using conservation of specific angular momentum (
![]() ),
a non-degenerate Keplerian particle (i.e.
),
a non-degenerate Keplerian particle (i.e.
![]() )
loaded at a
footpoint r0 will be flung out to larger radii; the so-called ``bead-on-wire'' analogy.
These conditions are easily met in our model so that
the newly unveiled Keplerian material (following heating of the
degenerate ring) finds itself threaded by the
highly inclined magnetic field and is flung out centrifugally.
The wind is then channeled towards the star's surface by the
strong dipole.
)
loaded at a
footpoint r0 will be flung out to larger radii; the so-called ``bead-on-wire'' analogy.
These conditions are easily met in our model so that
the newly unveiled Keplerian material (following heating of the
degenerate ring) finds itself threaded by the
highly inclined magnetic field and is flung out centrifugally.
The wind is then channeled towards the star's surface by the
strong dipole.
The mass flux,
![]() ,
is regulated by conditions (i.e. density) at the slow mode critical point:
,
is regulated by conditions (i.e. density) at the slow mode critical point:
where
The accretion rate,
![]() ,
can be recast to
,
can be recast to
The factor
B.1 Accretion shut-off
The accretion relies upon new Keplerian material being fed from the
degenerate ring to the atmosphere in the BF region, and ends once
the magnetic field has re-inforced co-rotation of the atmosphere.
This defines the inner edge of the BF as illustrated in the lower
panel of Fig. 2.
The penetration timescale
can be estimated from Eq. (16)
in OLNII to be
![]() where the depth of the non-degenerate Keplerian layer
where the depth of the non-degenerate Keplerian layer
![]() is in units
of centimeters.
The size (i.e. radial width) of the BF front is found from
is in units
of centimeters.
The size (i.e. radial width) of the BF front is found from
![]() cm which is of the same order as the
depth of the
cm which is of the same order as the
depth of the ![]() layer.
layer.
B.2 Depletion timescale of the Z  13 nuclei
13 nuclei
We recall that following wall accretion and subsequent
irradiation of the ring, up to 1046 of iron nuclei are dissociated forming
the ![]() layer.
Subsequent depletion of the
layer.
Subsequent depletion of the ![]() nuclei by accretion leads
to a return to an iron-rich atmosphere (i.e.
nuclei by accretion leads
to a return to an iron-rich atmosphere (i.e.
![]() )
as shown
in OLNII:
)
as shown
in OLNII:
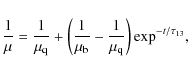
|
(B.3) |
where
where N13, 46 is the total number of dissociated iron nuclei in units of 1046.
We have already estimated the size of the BF region
above which we found to be of the same order as the depth
of the ![]() layer
which implies that our scenario self-consistently leads to the accretion
of most of the
layer
which implies that our scenario self-consistently leads to the accretion
of most of the ![]() material during burst (i.e. during the time it takes
the BF to comb the ring's surface). In other words, the
depletion timescale can also be estimated from Eq. (A.2) by taking
material during burst (i.e. during the time it takes
the BF to comb the ring's surface). In other words, the
depletion timescale can also be estimated from Eq. (A.2) by taking
![]() and
and
![]() to get
to get
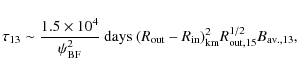
|
(B.5) |
where
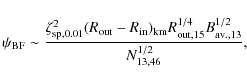
|
(B.6) |
which fine tunes the speed of the BF in our model (i.e. Eq. (A.2)).
Appendix C: Ring-Pole interaction: the hot spot
As illustrated in Fig. 2, there is a direct link between the BF
moving outward along the ring surface (increasing its area)
while decreasing the area of the HS on the surface of the star.
It is straightforward to show that the total HS area (both poles) is
where the angle
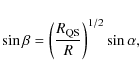
|
(C.2) |
where

|
(C.3) |
is the angle from the polar axis to the footpoint, at radial distance R, of the field line where the Keplerian material is loaded;
References
- Alexeff, I., & Rader, M. 1991, A simple derivation of classical and Bohm diffusion based on magneto-hydro-dynamics, in Proc. Conf. Rec. IEEE Int. Conf. Plasma Sci., Williamsburg, VA, Jun. 35, 199 [Google Scholar]
- Belyaev, V. 2001, Anomalous diffusion and photon-field fusion, 5th workshop on fast ignition of fusion targets, Funchak, 18022 June, 18 [Google Scholar]
- Bernardini, F., Israel, G. L., Dall'Osso, S., et al. 2009, A&A, 498, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Ransom, S. M., Halpern, J. P., et al. 2006, Nature, 442, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Camilo, F., Ransom, S. M., Halpern, J. P., & Reynolds, J. 2007a, ApJ, 666, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Cognard, I., Ransom, S. M., et al. 2007b, ApJ, 663, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Ransom, S. M., Peñalver, J., et al. 2007c, ApJ, 669, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Reynolds, J., Johnston, S., Halpern, J. P., & Ransom, S. M. 2008, ApJ, 679, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Halpern, J. P., & Ransom, S. M. 2009, The Astronomer's Telegram, 1907, 1 [NASA ADS] [Google Scholar]
- Chen, F. F. 1984, Introduction to Plasma Physics and Controlled Fusion (Springer) [Google Scholar]
- Gelfand, J. D., & Gaensler, B. M. 2007, ApJ, 667, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, R., & Heyl, J. 2007, MNRAS, 381, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Gotthelf, E. V., & Halpern, J. P. 2005, ApJ, 632, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Gotthelf, E. V., & Halpern, J. P. 2007, Ap&SS, 308, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Halpern, J. P., & Gotthelf, E. V. 2005, ApJ, 618, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Halpern, J. P., Gotthelf, E. V., Reynolds, J., Ransom, S. M., & Camilo, F. 2008, ApJ, 676, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Ibrahim, A. I., Markwardt, C. B., Swank, J. H., et al. ApJ, 2004, 609, L21 [Google Scholar]
- Jaroschek, C. H., Lesch, H., & Treumann, R. A. 2004, ApJ, 605, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M. 2007, Ap&SS, 308, 1 [Google Scholar]
- Keränen, P., & Ouyed, R. 2003, A&A, 407, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keränen, P., Ouyed, R., & Jaikumar, P. 2005, ApJ, 618, 485 [Google Scholar]
- Lang, K. R. 1999, Astrophysical formulae, ed K. R. Lang (New York: Springer), Astronomy and Astrophysics Library, ISSN0941-7834 [Google Scholar]
- Leahy, D., & Ouyed, R. 2009, Adv. Astron., 2009, 1 [CrossRef] [Google Scholar]
- Leahy, D., & Ouyed, R. 2008, MNRAS, 387, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C., & Dessler, A. J. 1981, ApJ, 251, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C. 1991, Theory of neutron star magnetospheres (Chicago, IL: University of Chicago Press) [Google Scholar]
- Nakagawa, Y. E., Yoshida, A., Yamaoka, K., & Shibazaki, N. 2009, PASJ, 61, 109 [NASA ADS] [Google Scholar]
- Niebergal, B., Ouyed, R., & Leahy, D. 2006, ApJ, 646, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Ouyed, R., & Leahy, D. 2009, ApJ, 696, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Ouyed, R., Pudritz, R. E., & Stone, J. M. 1997, Nature, 385, 409 [Google Scholar]
- Ouyed, R., Dey, J., & Dey, M. 2002, A&A, 390, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouyed, R., Clarke, D. A., & Pudritz, R. E. 2003, ApJ, 582, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Ouyed, R., Elgarøy, Ø., Dahle, H., & Keränen, P. 2004, A&A, 420, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouyed, R., Niebergal, B., Dobler, W., & Leahy, D. 2006, ApJ, 653, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Ouyed, R., Leahy, D., & Niebergal, B. 2007a, A&A, 473, 357 (OLNI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouyed, R., Leahy, D., & Niebergal, B. 2007b, A&A, 475, 63 (OLNII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouyed, R., Leahy, D., Niebergal, B., & Yue, Y. 2009, MNRAS, 396, 1058 (OLNIII) [NASA ADS] [CrossRef] [Google Scholar]
- Perna, R., & Gotthelf, E. V. 2008, ApJ, 681, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Rajagopal, K., & Wilczek, F. 2001, Phys. Rev. Lett., 86, 3492 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., Chechetkin, V. M., Lovelace, R. V. E., et al. 1998, ApJ, 500, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Spitkovsky, A. 2008, 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, 983, 20 [Google Scholar]
- Tamano, T. 1991, Sol. Phys., 134, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, W. J. 1984, Ann. Rev. Astr. Ap., 22, 267 [Google Scholar]
- Woods, P. M., & Thompson, C. 2006, Compact stellar X-ray sources, 547 [CrossRef] [Google Scholar]
- Yelenina, T. G., Ustyyugova, G. V., & Koldoba, A. V. 2006, A&A, 458, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... AXP
![[*]](/icons/foot_motif.png)
- In the sense that in quiescence their surface temperature are as low as those of some ordinary young neutron stars.
- ... front
![[*]](/icons/foot_motif.png)
- During quiescence the shear is between the solid degenerate Keplerian ring and the co-rotating atmosphere thus not prone to the instability. In contrast, during burst the shear is between one fluid (the new Keplerian atmosphere) and another fluid (the pre-existing co-rotating atmosphere).
- ... inwards
![[*]](/icons/foot_motif.png)
- Inside the star, the field lines expand outwards following the vortices.
- ...
magnetospheres
![[*]](/icons/foot_motif.png)
- A disk model for X-ray emission from pulsars was considered by Michel & Dessler (1981). However, their disk is fundamentally different from our ring in that, where they hypothesize electron degenerate material (left over from a supernova), in our model the material is completely relativistic-degenerate (from a Quark-Nova). This difference has many consequences, the most notable are a more efficient accretion mechanism (conversion energy from the hadron to quark transition as well as gravitational energy is released), and a slower (viscous) spreading rate for the ring.
- ... non-degeneracy
![[*]](/icons/foot_motif.png)
- We recall that in the degenerate Keplerian disk, lower viscosity and conservation of angular momentum imply mass flows in the ring is along lines of constant angular momentum which is nearly vertical (i.e. z-direction; see Appendix A in OLNII). Thus as the non-degenerate Keplerian material is ``sucked up'' in the wind, more material is supplied almost vertically from the underlying Keplerian material.
All Tables
Table 1: Thermal components in our model.
All Figures
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{11114fg1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa11114-08/Timg19.png)
|
Figure 1: Illustrated here are the stages involved in the transition from a neutron star (NS) (inclined rotator) to a quark star (QS) (aligned rotator) in the Quark-Nova scenario. The collapse of the quark core induces an explosive NS-to-QS transition ejecting iron-rich degenerate crust material. The QS enters a superconductive phase confining the interior field to vortices, forcing the exterior field to align with the rotation axis (see Ouyed et al. 2004, for more details; and Ouyed et al. 2006, for the related simulations). The iron-rich degenerate ejecta evolves into a Keplerian ring (at about 15-30 km from the star) surrounded, but not penetrated, by the dipole field (a co-rotating ejecta is also possible depending on the NS period; see OLNI). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=12.2cm,clip]{11114fg2a.eps}\vspace*{1.5mm}
\par\includegraphics[width=11.7cm,clip]{11114fg2b.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa11114-08/Timg24.png)
|
Figure 2:
The upper panel illustrates the ring structure during outburst.
Fiducial values of the ring inner radius (15 km) and outer radius
(25 km) are shown; the ring's vertical scale height is a few
kilometers (see Sect. 2.2; the figure is not to scale). The ring
is surrounded, but not penetrated, by the dipole field. The Bohm Front
- ``bump'' made of non-degenerate Keplerian material - propagates
outward at a speed
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.5cm,height=4.7cm,clip]{11114fg3a.ep...
...m}
\includegraphics[width=14.5cm,height=4.7cm,clip]{11114fg3b.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa11114-08/Timg97.png)
|
Figure 3: Upper panels: model luminosity (L/1034), temperature and area (curves) from one side of the ring as observed at infinity compared to observations (dots) of the warm component of XTE J1810-197. The dotted line is the contribution inward of the BF, the dashed is from outward of the BF, and the solid is the combined contribution (see text). Lower panels: model luminosity (L/1034), temperature and area (curves) from one pole as observed at infinity compared to observations (dots) of the hot component of XTE J1810-197. In the right-most panel the dotted line traces the shrinkage of the HS as the BF moves outward, the dashed line shows the late contribution from accretion induced by heating of the back side of the ring, and the solid is the combined contribution. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{11114fg4.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa11114-08/Timg158.png)
|
Figure 4: Keplerian shear during wall accretion leads to X-point reconnection which in turn causes the generation of closed magnetic loops, or ``bubbles'' (see Sect. 5.1 in text). In our model, these magnetic bubbles are responsible for the radio emission seen in some AXPs. The top panel illustrates the outward migration of a bubble through the surrounding magnetic field. The bubble's magnetic polarity in front as it moves outward is opposite to that of the surrounding dipole. This leads to reconnection and the motion of the bubble towards the light cylinder. The lower diagram shows the overall pattern of bubble migration (i.e. magnetic buoyancy) and expansion that leads to pile up near the light cylinder. The bubbles dissipate as they cross the light cylinder leading to the radio emission (see text for details). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.