EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 515 (June 2010) A&A, 515 (2010) A88 Full HTML
Free Access
Issue
A&A
Volume 515, June 2010
Article Number A88
Number of page(s) 6
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913976
Published online 11 June 2010
A&A 515, A88 (2010)

The helium star donor channel for the progenitors of type Ia supernovae with different metallicities

B. Wang1,2,3 - Z. Han1,2

1 - National Astronomical Observatories/Yunnan Observatory, the Chinese Academy of Sciences, Kunming 650011, PR China
2 - Key Laboratory for the Structure and Evolution of Celestial Objects, the Chinese Academy of Sciences, Kunming 650011, PR China
3 - Graduate University of the Chinese Academy of Sciences, Beijing 100049, PR China

Received 28 December 2009 / Accepted 18 March 2010

Abstract
Context. The nature of type Ia supernovae (SNe Ia) is still unclear. Metallicities may have an important effect on their properties.
Aims. In this paper, we study the He star donor channel towards SNe Ia comprehensively and systematically at various metallicities.
Methods. Employing Eggleton's stellar evolution code with the optically thick wind assumption, we calculated about 10 000 WD + He star systems and obtained SN Ia production regions of the He star donor channel with metallicities Z=0.03, 0.02, 0.004 and 0.0001. According to a detailed binary population synthesis approach, we also obtained SN Ia birthrates at various metallicities.
Results. Our study shows that both the initial mass of the He donor star and the initial orbital period for SNe Ia increase with metallicity, while the minimum initial mass of the carbon-oxygen white dwarfs producing SNe Ia decreases with metallicity. For a constant star-formation galaxy, SN Ia birthrates increase with metallicity. If a single starburst is assumed, SNe Ia occur systemically earlier and the peak value of the birthrate is larger for a high Z, and the He star donor channel with different metallicities can produce the young SNe Ia with delay times $\sim$45-220 Myr.

Key words: binaries: close - supernovae: general - white dwarfs - stars: evolution

1 Introduction

Type Ia supernova (SN Ia) explosions are among the most energetic events observed in the Universe. They appear to be good cosmological distance indicators and have been applied successfully in determining cosmological parameters (e.g., $\Omega_{\rm M}$ and $\Omega_{\Lambda}$; Riess et al. 1998; Perlmutter et al. 1999). The Phillips relation (a linear relation between the absolute magnitude of SNe Ia and the magnitude difference from maximum to 15 d after B maximum light) is adopted when SNe Ia are used as distance indicators (Phillips 1993), which is based on the SN Ia sample of the low red-shift Universe (z<0.05) and assumed to be valid at high red-shift. This assumption is precarious since there is still no agreement on the nature of their progenitors (Hillebrandt & Niemeyer 2000; Podsiadlowski et al. 2008; Wang et al. 2008a; Gilfanov & Bogdán 2010; Mennekens et al. 2010). If the properties of SNe Ia evolve with red-shift, the results for cosmology might be different. Since metallicity may represent red-shift to some extent, it will be a good method to study the properties of SNe Ia at various red-shift by finding the correlation between their properties and metallicity. In addition, some numerical and synthetical results show that metallicity may have an effect on the final amount of nickel-56, and thus the maximum luminosity of SNe Ia (Timmes et al. 2003; Podsiadlowski et al. 2006; Podsiadlowski 2010). There is also some other evidence of the correlation between the properties of SNe Ia and metallicity from observations (e.g., Branch & Bergh 1993; Hamuy et al. 1996; Wang et al. 1997; Cappellaro et al. 1997; Shanks et al. 2002).

It is generally believed that SNe Ia are thermonuclear explosions of carbon-oxygen white dwarfs (CO WDs) in binaries (Nomoto et al. 1997; Livio 2000). Over the past few decades, two families of SN Ia progenitor models have been proposed, i.e., the double-degenerate (DD) and single-degenerate (SD) models. It is suggested that the DD model, which involves the merger of two CO WDs (Iben & Tutukov 1984; Webbink 1984; Han 1998), likely leads to an accretion-induced collapse rather than to an SN Ia (Nomoto & Iben 1985; Timmes et al. 1994). For the SD model, the companion could be a main-sequence (MS) star or a slightly evolved star (WD + MS channel), or a red-giant star (WD + RG channel) (e.g., Hachisu et al. 1996, 1999a,b; Li & van den Heuvel 1997; Yungelson & Livio 1998; Langer et al. 2000; Fedorova et al. 2004; Han & Podsiadlowski 2004, 2006; Chen & Li 2007; Lü et al. 2009; Meng & Yang 2010; Wang et al. 2010a,b; Wang & Han 2010a). Note that some recent observations have indirectly implied that at least some SNe Ia can be produced by a variety of different progenitor systems (e.g., Hansen 2003; Ruiz-Lapuente et al. 2004; Patat et al. 2007; Voss & Nelemans 2008; Wang et al. 2008b; Justham et al. 2009).

Yoon & Langer (2003) followed the evolution of a CO WD + He star system with a $1.0~M_{\odot}$ CO WD and a $1.6~M_{\odot}$ He star in a 0.124 d orbit. In this binary, the WD accretes He from the He star and grows in mass to the Chandrasekhar (Ch) mass. Recently, Wang et al. (2009a) studied the He star donor channel of SNe Ia, in which a CO WD accretes material from an He MS star or a slightly evolved He subgiant to increase its mass to the Ch mass. The study shows the parameter space for the progenitors of SNe Ia with Z=0.02. By using a detailed binary population synthesis (BPS) approach, Wang et al. (2009b) found that the Galactic SN Ia birthrate from this channel is $\sim$ $0.3\times 10^{-3}\ {\rm yr}^{-1}$ and that this channel can produce the SNe Ia with short delay times ($\sim$45-140 Myr) from the star formation to SN explosion (see also Wang & Han 2010b). Considering that not all SNe Ia are found in the solar metallicity environment (Z=0.02), we will pay attention to the correlation between the properties of SNe Ia and metallicities in this paper.

The purpose of this paper is to study the He star donor channel towards SNe Ia comprehensively and systematically at various metallicities, and then to determine the parameter space for SNe Ia, which can be used in BPS studies. In Sect. 2, we describe the numerical code for the binary evolution calculations and the grid of the binary models. The binary evolutionary results are shown in Sect. 3. We describe the BPS method in Sect. 4 and present the BPS results in Sect. 5. Finally, a discussion is given in Sect. 6.

2 Binary evolution calculations

In WD + He star systems, the He star fills its Roche lobe at He MS or He subgiant stage, and then the mass transfer begins. The He star transfers some of its material onto the surface of the WD, which increases the mass of the WD as a consequence. We assume that, if the WD grows to 1.378 $M_{\odot }$, it explodes as an SN Ia.

2.1 Stellar evolution code

We use Eggleton's stellar evolution code (Eggleton 1971, 1972, 1973) to calculate the evolution of the WD + He star systems. The code has been updated with the latest input physics over the past four decades (Han et al. 1994; Pols et al. 1995, 1998). Roche lobe overflow (RLOF) is treated within the code described by Han et al. (2000). We set the ratio of mixing length to local pressure scale height, $\alpha=l/H_{\rm p}$, to be 2.0. The opacity tables are compiled by Chen & Tout (2007) from Iglesias & Rogers (1996) and Alexander & Ferguson (1994). Four metallicities are adopted in this study (i.e., Z=0.03, 0.02, 0.004 and 0.0001). Orbital angular momentum loss due to gravitational wave radiation (GWR) is also included.

2.2 WD mass growth

Instead of solving stellar structure equations of a WD, we use an optically thick wind model (Kato & Hachisu 1994; Hachisu et al. 1996) and adopt the prescription of Kato & Hachisu (2004, KH04) for the mass accumulation efficiency of He-shell flashes onto the WD. If the mass transfer rate, $\vert\dot M_2\vert$, is above a critical rate, $\dot M_{\rm cr}$, we assume that He burns steadily on the surface of the WD and that the He-rich material is converted into C and O at a rate $\dot M_{\rm cr}$. The unprocessed matter is lost from the system, presumably in the form of the optically thick wind at a mass loss rate $\dot M_{\rm wind}=\vert\dot M_2\vert - \dot M_{\rm cr}$. Based on the opacity from Iglesias & Rogers (1996), the optically thick wind is sensitive to Fe abundance, and it is likely that the wind does not work when Z is lower than a certain value 0.002 (Kobayashi et al. 1998). Thus, there should be an obvious low-metallicity threshold for SNe Ia in comparison with SN II. However, this metallicity threshold has not been found (Prieto et al. 2008). Considering the uncertainties in the opacities, we assume that the optically thick wind is still valid for a low metallicity Z=0.0001(see also Meng et al. 2009).

The critical mass transfer rate is

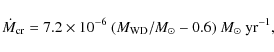
\begin{displaymath}\dot M_{\rm cr}=7.2\times 10^{-6}~(M_{\rm WD}/M_{\odot}-0.6)~M_{\odot}~\rm yr^{-1}, \end{displaymath} (1)

based on WD models computed with constant mass accretion rates (Nomoto 1982). Similar to the work of Wang et al. (2009a), following assumptions are adopted when $\vert\dot M_2\vert$ is smaller than $\dot M_{\rm cr}$. (1) If $\vert\dot M_2\vert$ is less than $\dot M_{\rm cr}$ but higher than the minimum accretion rate of stable He-shell burning, $\dot M_{\rm st}$ (KH04), it is assumed that the He-shell burning is stable and that there is no mass loss. (2) If $\vert\dot M_2\vert$ is less than $\dot M_{\rm st}$ but higher than the minimum accretion rate of weak He-shell flashes, $\dot M_{\rm low}=4.0\times10^{-8}~M_{\odot}~\rm yr^{-1}$ (Woosley et al. 1986), He-shell flashes occur and a part of the envelope mass is assumed to be blown off from the surface of the WD. The mass growth rate of WDs in this case is linearly interpolated from a grid computed by KH04, where a wide range of WD masses and accretion rates was calculated in the He-shell flashes. (3) If $\vert\dot M_2\vert$ is lower than $\dot M_{\rm low}$, the He-shell flashes will be so strong that no mass can be accumulated onto the WD.

We define the mass growth rate of the CO WD, $\dot{M}_{\rm CO}$, as

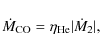
\begin{displaymath}\dot{M}_{\rm CO}=\eta _{\rm He}\vert\dot{M}_{\rm 2}\vert, \end{displaymath} (2)

where $\eta _{\rm He}$ is the mass accumulation efficiency for He-shell burning. According to the assumptions above, the values of $\eta _{\rm He}$ are:

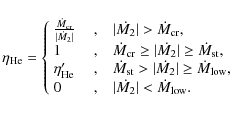
\begin{displaymath}\eta_{\rm He}= \left\{ \begin{array}{l@{\quad,\quad}l} \dot M... ...dot{M_2}\vert< \dot{M}_{\rm low}.\strut\\ \end{array} \right. \end{displaymath} (3)

2.3 Grid calculations

We incorporate the prescriptions above into Eggleton's stellar evolution code and follow the evolutions of the WD + He star systems. The mass lost from these systems is assumed to take away specific orbital angular momentum of the accreting WD. We calculated about 10 000 WD + He star systems, and obtained a large, dense model grid with four different metallicities. The initial mass of the He donor stars, $M_{\rm 2}^{\rm i}$, ranges from $0.8~M_{\odot}$ to $3.3~M_{\odot}$; the initial mass of the CO WDs, $M_{\rm WD}^{\rm i}$, is from $0.86~M_{\odot}$ to $1.20~M_{\odot}$; the initial orbital period of the binary systems, $P^{\rm i}$, changes from the minimum value, at which an He zero-age MS (ZAMS) star would fill its Roche lobe, to $\sim$400 d, where the He star fills its Roche lobe at the end of the Hertzsprung gap.

3 Binary evolution results

3.1 An example of binary evolution calculations

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13976fg1a.ps}\includegraphics[angle=270,width=8cm,clip]{13976fg1b.ps} \end{figure} Figure 1:

A representative case of binary evolution calculations with Z=0.004, in which the binary system is in the weak He-shell flash phase at the moment of the SN explosion. In panel a), the solid, dashed and dash-dotted curves show $\dot M_2$, $\dot{M}_{\rm CO}$ and $M_{\rm WD}$ varying with time, respectively. In panel b), the evolutionary track of the He donor star is shown as a solid curve and the evolution of the orbital period is shown as a dash-dotted curve. Dotted vertical lines in both panels and asterisks in panel b) indicate the position where the WD is expected to explode as an SN Ia. The initial binary parameters and the parameters at the moment of SN explosion are also given in these two panels.

Open with DEXTER

In Fig. 1, we present an example of binary evolution calculations with Z=0.004. Panel (a) shows the $\dot M_2$, $\dot{M}_{\rm CO}$and $M_{\rm WD}$ varying with time, while panel (b) is the evolutionary track of the He donor star in the Hertzsprung-Russell diagram, where the evolution of the orbital period is also shown. The binary is ( $M_2^{\rm i}$, $M_{\rm WD}^{\rm i}$, $\log (P^{\rm i}/{\rm day})$) = (1.35, 0.9, -1.20), where $M_2^{\rm i}$, $M_{\rm WD}^{\rm i}$ and $P^{\rm i}$ are the initial mass of the He star and of the CO WD in solar masses, and the initial orbital period in days, respectively. The He star fills its Roche lobe after the exhaustion of central He. The mass transfer rate $\vert\dot{M}_{\rm 2}\vert$ exceeds $\dot M_{\rm cr}$ soon after the onset of RLOF, resulting in a wind phase, where a part of the transferred mass is blown off in the form of the optically thick wind, and the left is accumulated onto the surface of the WD. After about $4\times10^{4}$ yr, $\vert\dot{M}_{\rm 2}\vert$ drops below $\dot M_{\rm cr}$ but still higher than $\dot M_{\rm st}$. Therefore, the optically thick wind stops and the He-shell burning is stable. With the continuous decreasing of $\vert\dot{M}_{\rm 2}\vert$, the binary system enters into a weak He-shell flash phase about $8\times10^{4}$ yr later. The WD always grows in mass until it explodes as an SN Ia in the weak He-shell flash phase. At this moment, the binary parameters are $M^{\rm SN}_2=0.8223~M_{\odot}$ and $\log (P^{\rm SN}/{\rm day})=-1.2080$.

3.2 Initial parameters for SN Ia progenitors

\begin{figure} \par\includegraphics[width=6.cm,angle=270,clip]{13976fg2.ps} \end{figure} Figure 2:

Parameter regions producing SNe Ia with different metallicities in the initial orbital period-secondary mass ( $\log P^{\rm i}$, $M^{\rm i}_2$) plane of the CO WD + He star system for initial WD mass of 1.2 $M_{\odot }$.

Open with DEXTER

Figures 2 and 3 show the initial contours for producing SNe Ia with different metallicities, from which we can see the strong influence of metallicity on the contours. With the increase of Z, the contours are shifted to higher periods and larger masses, indicating that the progenitor systems have longer periods and more massive companions for a higher Z. This is due to the correlation between the stellar structure and metallicity. (1) High metallicity leads to larger radii of He ZAMS stars, so the left boundaries of the regions will be shifted to longer period. (2) Stars with high metallicity evolve in a way similar to those with low metallicity but less mass (Umeda et al. 1999; Chen & Tout 2007), resulting that, for the WD binary systems with particular orbital periods, the companion mass increases with metallicity. Note that, there are some dent at the upper left boundary lines in Figs. 2 and 3. This is constrained mainly by a high mass transfer rate because of orbit decay induced by GWR and a large mass-ratio, leading to much of the mass being lost from the systems in the form of the optically thick wind.

\begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13976fg3ab.ps}\includegraphics[angle=270,width=8cm,clip]{13976fg3c.ps} \end{figure} Figure 3:

Similar to Fig.2, but for initial WD masses of 0.9, 1.0 and 1.1 $~M_{\odot}$.

Open with DEXTER

We also find that the minimum initial mass of the CO WDs producing SNe Ia decreases with metallicity (e.g., for Z=0.0001, 0.004, 0.02 and 0.03, the minimum initial WD masses are 0.88, 0.87, 0.865 and 0.86 $~M_{\odot}$, respectively). For a high Z, the companions in the WD binary systems producing SNe Ia are more massive, so more material from the companions will be transferred onto the surface of the WDs. Thus, the WDs do not need to be massive enough for the production of SNe Ia, resulting in a low minimum initial WD mass. These contours with various metallicities can be expediently used in BPS studies. The data points and the interpolation FORTRAN code for these contours can be supplied on request by contacting BW.

4 Binary population synthesis

In order to investigate SN Ia birthrates and delay times for the He star donor channel at various metallicities, we performed a series of Monte Carlo simulations in the BPS study. In each simulation, by using the Hurley's rapid binary evolution code (Hurley et al. 2000, 2002), we followed the evolution of $4\times10^{\rm 7}$ sample binaries from the star formation to the formation of the WD + He star systems according to three evolutionary channels (i.e., the He star channel, the EAGB channel, and the TPAGB channel; for details see Wang et al. 2009b). We assumed that, if the initial parameters of a CO WD + He star system at the onset of the RLOF are located in the SN Ia production regions with a specific metallicity, an SN Ia is produced.

4.1 Common envelope in binary evolution

In the He star donor channel, the progenitor of an SN Ia is a close WD + He star system, which has most likely emerged from the common envelope (CE) evolution of a binary involving a giant star. The CE ejection is still an open problem. Similar to the work of Wang et al. (2009b), we also use the standard energy equations (Webbink 1984) to calculate the output of the CE phase. For this prescription of the CE ejection, there are two highly uncertain parameters, i.e., $\alpha_{\rm ce}$ and $\lambda$, where $\alpha_{\rm ce}$ is the CE ejection efficiency, and $\lambda$ is a structure parameter that depends on the evolutionary stage of the donor. As in previous studies, we combine $\alpha_{\rm ce}$ and $\lambda$ into one free parameter $\alpha_{\rm ce}\lambda$, and set it to be 1.5 which is our standard model for the formation of the WD + He systems (Hurley et al. 2002).

4.2 Basic parameters for Monte Carlo simulations

In the BPS study, the Monte Carlo simulation requires as input the initial mass function (IMF) of the primary, the mass-ratio distribution, the distribution of initial orbital separations, the eccentricity distribution of binary orbit, and the star formation rate (SFR) (e.g., Han et al. 1995a, 2002, 2003; Wang & Han 2009, 2010c).

(1)
The IMF of Miller & Scalo (1979) is adopted. The primordial primary is generated according to the formula of Eggleton et al. (1989).

(2)
The initial mass-ratio distribution of the binaries, q', is quite uncertain for binary evolution. For simplicity, we take a constant mass-ratio distribution (Mazeh et al. 1992; Goldberg & Mazeh 1994),

\begin{displaymath}n(q')=1, \hspace{2.cm} 0<q'\leq1, \end{displaymath} (4)

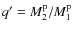where $q'=M_{\rm 2}^{\rm p}/M_{\rm 1}^{\rm p}$.

(3)
We assume that all stars are members of binaries and that the distribution of separations is constant in 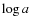$\log a$ for wide binaries, where a is separation and falls off smoothly at small separation

\begin{displaymath}a\cdot n(a)=\left\{ \begin{array}{lc} \alpha_{\rm sep}(a/a_... ...alpha_{\rm sep}, & a_{\rm0}<a<a_{\rm 1},\\ \end{array}\right. \end{displaymath} (5)

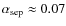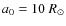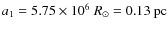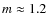where $\alpha_{\rm sep}\approx0.07$, $a_{\rm0}=10~R_{\odot}$, $a_{\rm 1}=5.75\times 10^{\rm 6}~R_{\odot}=0.13~{\rm pc}$ and $m\approx1.2$. This distribution implies that the numbers of wide binaries per logarithmic interval are equal, and that about 50% of stellar systems have orbital periods less than 100 yr (Han et al. 1995b).

(4)
A circular orbit is assumed for all binaries. The orbits of semidetached binaries are generally circularized by the tidal force on a timescale which is much smaller than the nuclear timescale.

(5)
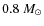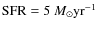We simply assume a constant SFR over the past 15 Gyr, or, alternatively, a delta function, i.e., a single starburst. In the case of the constant SFR, we calibrate the SFR by assuming that one binary with a primary more massive than $0.8~M_{\odot}$ is formed annually (see Iben & Tutukov 1984; Han et al. 1995b; Hurley et al. 2002). From this calibration, we can get ${\rm SFR}=5~M_{\rm \odot}{\rm yr}^{-1}$ (e.g., Willems & Kolb 2004). 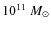For the case of the single starburst, we assume a burst producing $10^{11}~M_{\odot}$ in stars. In fact, a galaxy have a complicated star formation history. We only choose these two extremes for simplicity. A constant SFR is similar to the situation of spiral galaxies (Yungelson & Livio 1998; Han & Podsiadlowski 2004), while a delta function to that of elliptical galaxies or globular clusters.

5 The results of binary population synthesis

\begin{figure} \par\includegraphics[width=5.5cm,angle=270,clip]{13976fg4.ps} \end{figure} Figure 4:

The evolution of SN Ia birthrates for a constant SFR ( $5~M_{\odot}$ yr-1) with different metallicities.

Open with DEXTER

We performed four sets of simulations with different metallicities to systematically investigate SN Ia birthrates for the He star donor channel. In Fig. 4, we show SN Ia birthrates for the He star donor channel with different metallicities by adopting ${\rm SFR}=5~M_{\rm \odot}{\rm yr}^{-1}$. In this figure, we see that SN Ia birthrates increase with metallicity. This is due to the fact that the parameter space for SNe Ia increases with metallicity. The simulations give SN Ia birthrates of $\sim$0.06-0.43 $\times 10^{-3}\ {\rm yr}^{-1}$, which is lower than the value of observations (3- $4\times 10^{-3}\ {\rm yr}^{-1}$ in the Galaxy; van den Bergh & Tammann 1991; Cappellaro & Turatto 1997). This implies that the He star donor channel is only a subclass of SN Ia production, and there are some other channels or mechanisms also contributing to SNe Ia (e.g., WD + MS channel, WD + RG channel and double-degenerate channel). As mentioned by Wang et al. (2010), the WD + MS channel can give a Galactic birthrate of $\sim$ $1.8\times 10^{-3}\ {\rm yr}^{-1}$, and is considered to be an important channel to produce SNe Ia.

\begin{figure} \par\includegraphics[width=5.5cm,angle=270,clip]{13976fg5.ps} \end{figure} Figure 5:

The evolution of SN Ia birthrates for a single starburst of $10^{\rm 11}~M_{\odot}$ with different metallicities.

Open with DEXTER

Figure 5 displays the evolution of SN Ia birthrates for a single starburst of $10^{11}~M_{\odot}$ with different metallicities. In the figure SN Ia explosions occur between $\sim$45 Myr and $\sim$220 Myr after the starburst, which may explain the young SNe Ia implied by recent observations (Mannucci et al. 2006; Aubourg et al. 2008). We see that the peak value of the birthrate is larger for a high Z. This is because the parameter range of the initial WD masses is larger for a high metallicity. We also see that a high metallicity leads to a systematically earlier explosion time of the SNe Ia, owing to the effects of metallicity on the maximum initial mass of the companion for an SN Ia and on the stellar evolution. As shown in Figs. 2 and 3, $M_{\rm 2}^{\rm i}$ increases with metallicity. Generally, a massive star evolves more quickly than a low-mass one. Thus, the explosion time is earlier with a high Z. Although the high Z also slows down the evolution of a star, its influence is much less than that of stellar mass based on detailed calculations of stellar evolution (Umeda et al. 1999; Chen & Tout 2007).

The simulation in this paper was made with $\alpha_{\rm ce}\lambda =1.5$. If we adopt a lower value for $\alpha_{\rm ce}\lambda$, e.g., 0.5, SNe Ia occur systematically earlier for a specific metallicity. This is because a low value of $\alpha_{\rm ce}\lambda$ tends to have larger He star masses on average (see Fig. 5 of Wang et al. 2009b), which will evolve more quickly and hence produce an SN Ia at an earlier time.

6 Discussion

In our binary calculations, we have not considered the influence of rotation on the He-accreting WDs. Yoon et al. (2004) showed that, if rotation is taken into account, He burning is much less violent than that without rotating. This may significantly increase the He-accretion efficiency. Also, the maximum stable mass of a rotating WD may be above the Ch mass, i.e., the super-Ch mass WD explosions (Uenishi et al. 2003; Yoon & Langer 2005; Chen & Li 2009).

In addition, it is suggested that about 10% of WDs have magnetic fields higher than 1 MG (Liebert et al. 2003, 2005). The mean mass of these magnetic WDs is 0.93 $M_{\odot }$, compared with the mean mass (0.56 $M_{\odot }$) of all WDs (e.g., Parthasarathy et al. 2007). Therefore, the magnetic WDs are more likely to reach the Ch mass by accreting the He-rich material. Also, the magnetic field may affect some properties of the WD + He star systems (e.g., the mass transfer rate, the critical accretion rate, the thermonuclear reaction rate, etc), resulting in a different SN Ia birthrate.

In our BPS studies, we assume that all stars are in binaries and about 50% of stellar systems have orbital periods less than 100 yr. The binary fractions may depend on metallicity, environment, spectral type, etc. If we adopt 40% of stellar systems have orbital periods below 100 yr by adjusting the parameter $a_{\rm 1}$ in equation (6), SN Ia birthrate from this channel will decrease by 20%. We note that the SN Ia birthrate from this channel is low in comparison with observations, especially in the low metallicity environment. The smaller contribution of this channel to total SNe Ia does not change the statistics of birthrates, delay time distribution, etc. However, the He star donor channel should not be ignored when studying the progenitors of SNe Ia, because this channel is considered as a main contributor to the young population of SNe Ia (e.g., Wang & Han 2010b; Meng & Yang 2010). Moreover, SNe Ia from this channel can neatly avoid H lines. We also note that recent studies on He accretion to CO WDs reveal that double-detonation of sub-Chandrasekhar mass WDs produces an SN Ia that is much brighter than normal SNe Ia (e.g., Fink et al. 2010). If this type of explosion contributes to SNe Ia, the birthrate from the He donor star channel will increase to $\sim$ $10^{-3}\ {\rm yr}^{-1}$ (e.g., Yungelson 2005; Ruiter et al. 2009).

The companions in the He star donor channel would survive after SN explosion and potentially be identifiable. Wang & Han (2009) found that the surviving companions have a high spatial velocity (>400 km s-1), which could be an alternative origin for hypervelocity stars (HVSs), which are stars with a velocity so great that they are able to escape the gravitational pull of the Galaxy. Because SN Ia birthrates from the He star donor channel increase with metallicity, HVSs from the SN explosion scenario are more likely discovered in the high metallicity environment.

Currently, some observations support the existence of WD + He star systems (e.g., KPD 1930+2752, V445 Pup, and HD 49798 with its WD companion), which are candidates of SN Ia progenitors. (1) Maxted et al. (2000) suggested that KPD 1930+2752 is likely to eventually result in a merger and produce an SN Ia (see also Geier et al. 2007). However, the DD model is not supported theoretically. Meanwhile, KPD 1930+2752 may also produce an SN Ia via the SD model, but the parameters of the binary system are not located in the contours of the He donor star channel for producing SNe Ia, i.e., KPD 1930+2752 will not produce an SN Ia via the SD model. (2) V445 Pup is an He nova (Ashok & Banerjee 2003; Kato & Hachisu 2003). Kato et al. (2008) presented a free-free emission dominated light curve model of V445 Pup, based on the optically thick wind theory (Kato & Hachisu 1994; Hachisu et al. 1996). The light curve fitting in their study shows that the mass of the WD is more than $1.35~M_{\odot}$, and half of the accreted matter remains on the WD, leading to the mass increase of the WD. Thus, Kato et al. (2008) suggested that V445 Pup is a strong candidate of SN Ia progenitors (see also Woudt et al. 2009). However, we still do not know the orbital period of the binary system and the mass of the He donor star so far. This needs further observations of V445 Pup after the dense dust shell disappears. (3) HD 49798 is a H depleted subdwarf O6 star and also a single-component spectroscopic binary with an orbital period of 1.548 d (Thackeray 1970; Stickland & Lloyd 1994), which contains a X-ray pulsating companion (RX J0648.0-4418; Israel et al. 1995). The X-ray pulsating companion is suggested to be a massive WD (Bisscheroux et al. 1997). Based on the pulse time delays and the binary system's inclination, constrained by the duration of the X-ray eclipse, Mereghetti et al. (2009) recently derived the masses of the two components. The corresponding masses are 1.50 $\pm$ 0.05 $~M_{\odot}$ for HD 49798 and 1.28 $\pm$ 0.05 $~M_{\odot}$ for the WD. According to our binary evolution model, we found the massive WD can increase its mass to the Ch mass in future evolution. Thus, HD 49798 with its WD companion is a likely candidate of SN Ia progenitors.

The He star donor channel with different metallicities can produce the young SNe Ia with delay times $\sim$45-220 Myr. The young population of SNe Ia may have an effect on models of galactic chemical evolution, since they would return large amounts of iron to the interstellar medium earlier than previously thought. Especially, the high metallicity environments are much earlier to return iron to the interstellar medium, as SNe Ia from the He star donor channel occur systemically earlier for a high Z. In future investigations, we will explore the detailed influence of the young SNe Ia with different metallicity environments on the chemical evolution of stellar populations.

Acknowledgements
We thank the anonymous referee for his/her valuable comments that helped us to improve the paper. This work is supported by the National Natural Science Foundation of China (Grant No. 10821061), the National Basic Research Program of China (Grant No. 2007CB815406), and the Chinese Academy of Sciences (Grant No. KJCX2-YW-T24).

References

  1. Aubourg, E., Tojeiro, R., Jimenez, R., et al. 2008, A&A, 492, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
  3. Ashok, N. M., & Banerjee, D. P. K. 2003, A&A, 409, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bisscheroux, B. C., Pols, O. R., Kahabka, P., Belloni, T., & van den Heuvel, E. P. J. 1997, A&A, 317, 815 [NASA ADS] [Google Scholar]
  5. Branch, D., & Bergh, S. V. 1993, AJ, 105, 2231 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cappellaro, E., & Turatto, M. 1997, in Proc. NATO Advanced Study Institute 486, Thermonuclear Supernovae, ed. P. Ruiz-Lapuente, R. Cannal, & J. Isern (Dordrecht: Kluwer), 77 [Google Scholar]
  7. Cappellaro, E., Turatto, M., Tsvetkov, D. Y., et al. 1997, A&A, 322, 431 [NASA ADS] [Google Scholar]
  8. Chen, W.-C., & Li, X.-D. 2007, ApJ, 658, L51 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chen, W.-C., & Li, X.-D. 2009, ApJ, 702, 686 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chen, X., & Tout, C. A. 2007, Chin. J. Astron. Astrophys., 7, 245 [NASA ADS] [CrossRef] [Google Scholar]
  11. Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
  12. Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
  13. Eggleton, P. P. 1973, MNRAS, 163, 279 [NASA ADS] [CrossRef] [Google Scholar]
  14. Eggleton, P. P., Tout, C. A., & Fitechett, M. J. 1989, ApJ, 347, 998 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fedorova, A. V., Tutukov, A. V., & Yungelson, L. R. 2004, Astron. Lett., 30, 73 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fink, M., Röpke, F. K., Hillebrandt, W., et al. 2010, A&A, 514, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Geier, S., Nesslinger, S., Heber, U., et al. 2007, A&A, 464, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Gilfanov, M., & Bogdán, Á. 2010, Nat, 463, 924 [Google Scholar]
  19. Goldberg, D., & Mazeh, T. 1994, A&A, 282, 801 [NASA ADS] [Google Scholar]
  20. Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hachisu, I., Kato, M., Nomoto, K., & Umeda, H. 1999a, ApJ, 519, 314 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hachisu, I., Kato, M., & Nomoto, K. 1999b, ApJ, 522, 487 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hamuy, M., Phillips, M. M., Schommer, R. A., et al. 1996, AJ, 112, 2391 [NASA ADS] [CrossRef] [Google Scholar]
  24. Han, Z. 1998, MNRAS, 296, 1019 [NASA ADS] [CrossRef] [Google Scholar]
  25. Han, Z., & Podsiadlowski, Ph. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
  26. Han, Z., & Podsiadlowski, Ph. 2006, MNRAS, 368, 1095 [NASA ADS] [CrossRef] [Google Scholar]
  27. Han, Z., Eggleton, P. P., Podsiadlowski, Ph., & Tout, C. A. 1995a, MNRAS, 277, 1443 [NASA ADS] [CrossRef] [Google Scholar]
  28. Han, Z., Podsiadlowski, Ph., & Eggleton, P. P. 1995b, MNRAS, 272, 800 [NASA ADS] [Google Scholar]
  29. Han, Z., Podsiadlowski, Ph., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
  30. Han, Z., Podsiadlowski, Ph., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
  31. Han, Z., Podsiadlowski, Ph., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
  32. Han, Z., Tout, C. A., & Eggleton, P. P. 2000, MNRAS, 319, 215 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hansen, B. M. S. 2003, ApJ, 582, 915 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
  37. Iben, I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
  38. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  39. Israel, G. L., Stella, L., Angelini, L., White, N. E., & Giommi, P. 1995, IAU Circ, 6277 [Google Scholar]
  40. Justham, S., Wolf, C., Podsiadlowski, Ph., & Han, Z. 2009, A&A, 493, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Kato, M., & Hachisu, I. 1994, ApJ, 437, 802 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kato, M., & Hachisu, I. 2003, ApJ, 598, L107 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 (KH04) [NASA ADS] [CrossRef] [Google Scholar]
  44. Kato, M., Hachisu, I., Kiyota, S., & Saio, H. 2008, ApJ, 684, 1366 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kobayashi, C., Tsujimoto, T., Nomoto, K., et al. 1998, ApJ, 503, L155 [NASA ADS] [CrossRef] [Google Scholar]
  46. Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
  47. Li, X.-D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] [Google Scholar]
  48. Liebert, J., Bergeron, P., & Holberg, J. B. 2003, AJ, 125, 348 [NASA ADS] [CrossRef] [Google Scholar]
  49. Liebert, J., Bergeron, P., & Holberg, J. B. 2005, ApJS, 156, 47 [NASA ADS] [CrossRef] [Google Scholar]
  50. Livio, M. 2000, The Progenitors of Type Ia Supernovae, ed. J. C. Niemeyer, & J. W. Truran. (Cambridge Univ. Press), 33 [Google Scholar]
  51. Lü, G., Zhu, C., Wang, Z., & Wang, N. 2009, MNRAS, 396, 1086 [NASA ADS] [CrossRef] [Google Scholar]
  52. Mannucci, F., Della Valle, M., & Panagia, N. 2006, MNRAS, 370, 773 [NASA ADS] [CrossRef] [Google Scholar]
  53. Maxted, P. F. L., Marsh, T. R., & North, R. C. 2000, MNRAS, 317, L41 [NASA ADS] [CrossRef] [Google Scholar]
  54. Mazeh, T., Goldberg, D., Duquennoy, A., & Mayor, M. 1992, ApJ, 401, 265 [NASA ADS] [CrossRef] [Google Scholar]
  55. Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 2103 [NASA ADS] [CrossRef] [Google Scholar]
  56. Meng, X., & Yang, W. 2010, ApJ, 710, 1310 [NASA ADS] [CrossRef] [Google Scholar]
  57. Mennekens, N., Vanbeveren, D., De Greve, J. P., & De Donder, E. 2010, A&A, 515, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Mereghetti, S., Tiengo, A., Esposito, P., et al. 2009, Sci, 325, 1222 [Google Scholar]
  59. Miller, G. E., & Scalo, J. M. 1979, ApJS, 41, 513 [NASA ADS] [CrossRef] [Google Scholar]
  60. Nomoto, K. 1982, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
  61. Nomoto, K., & Iben, I. 1985, ApJ, 297, 531 [NASA ADS] [CrossRef] [Google Scholar]
  62. Nomoto, K., Iwamoto, K., & Kishimoto, N. 1997, Sci, 276, 1378 [Google Scholar]
  63. Parthasarathy, M., Branch, D., Jeffery, D. J., & Baron, E. 2007, New Astron. Rev., 51, 524 [NASA ADS] [CrossRef] [Google Scholar]
  64. Patat, F., Chandra, P., Chevalier, R., et al. 2007, Sci, 317, 924 [NASA ADS] [CrossRef] [Google Scholar]
  65. Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
  66. Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
  67. Podsiadlowski, Ph. 2010, Astron. Nachr., 331, 218 [NASA ADS] [CrossRef] [Google Scholar]
  68. Podsiadlowski, Ph., Mazzali, P., Lesaffre, P., Wolf, C., & Förster, F. 2006 [arXiv:astro-ph/0608324], unpublished [Google Scholar]
  69. Podsiadlowski, Ph., Mazzali, P., Lesaffre, P., Han, Z., & Förster, F. 2008, New Astron. Rev., 52, 381 [NASA ADS] [CrossRef] [Google Scholar]
  70. Pols, O. R., Schröder, K. P., Hurly, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
  71. Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
  72. Pols, O. R., Tout, C. A., Schröder, K. P., Eggleton, P. P., & Manners, J. 1997, MNRAS, 289, 869 [NASA ADS] [CrossRef] [Google Scholar]
  73. Prieto, J. L., Stanek, K. Z., & Beacom, J. F. 2008, ApJ, 673, 999 [NASA ADS] [CrossRef] [Google Scholar]
  74. Riess, A., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  75. Ruiz-Lapuente, P., Comeron, F., Méndez, J., et al. Nat, 431, 1069 [Google Scholar]
  76. Ruiter, A. J., Belczynski, K., & Fryer, C. L. 2009, ApJ, 699, 2026 [NASA ADS] [CrossRef] [Google Scholar]
  77. Shanks, T., Allen, P. D., Hoyle F., et al. 2002, ASPC, 283, 274 [NASA ADS] [Google Scholar]
  78. Stickland, D. J., & Lloyd, C. 1994, Obs, 114, 41 [Google Scholar]
  79. Thackeray, A. D. 1970, MNRAS, 150, 215 [NASA ADS] [CrossRef] [Google Scholar]
  80. Timmes, F. X., Woosley, S. E., & Taam, R. E. 1994, ApJ, 420, 348 [NASA ADS] [CrossRef] [Google Scholar]
  81. Timmes, F. X., Brown, E. F., & Truran, J. W. 2003, ApJ, 590, L83 [NASA ADS] [CrossRef] [Google Scholar]
  82. Uenishi, T., Nomoto, K., & Hachisu, I. 2003, ApJ, 595, 1094 [NASA ADS] [CrossRef] [Google Scholar]
  83. Umeda, H., Nomoto, K., Yamaoka, H., & Wanajo, S. 1999, ApJ, 513, 861 [NASA ADS] [CrossRef] [Google Scholar]
  84. van den Bergh, S., & Tammann, G. A. 1991, ARA&A, 29, 363 [NASA ADS] [CrossRef] [Google Scholar]
  85. Voss, R., & Nelemans, G. 2008, Nat, 451, 802 [Google Scholar]
  86. Wang, B., & Han, Z. 2009, A&A, 508, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Wang, B., & Han, Z. 2010a, Res. Astron. Astrophys., 10, 235 [Google Scholar]
  88. Wang, B., & Han, Z. 2010b, Ap&SS, in press [arXiv:0911.4998] [Google Scholar]
  89. Wang, B., & Han, Z. 2010c, MNRAS, 404, L84 [NASA ADS] [Google Scholar]
  90. Wang, L., Höflich, P., & Wheeler, J. C. 1997, ApJ, 483, L29 [NASA ADS] [CrossRef] [Google Scholar]
  91. Wang, B., Meng, X., Wang, X.-F., & Han, Z. 2008a, Chin. J. Astro. Astrophys., 8, 71 [CrossRef] [Google Scholar]
  92. Wang, X.-F., Li, W.-D., Filippenko, A. V., et al. 2008b, ApJ, 675, 626 [NASA ADS] [CrossRef] [Google Scholar]
  93. Wang, B., Meng, X., Chen, X., & Han, Z. 2009a, MNRAS, 395, 847 [NASA ADS] [CrossRef] [Google Scholar]
  94. Wang, B., Chen, X., Meng, X., & Han, Z. 2009b, ApJ, 701, 1540 [NASA ADS] [CrossRef] [Google Scholar]
  95. Wang, B., Li, X.-D., & Han, Z. 2010a, MNRAS, 401, 2729 [NASA ADS] [CrossRef] [Google Scholar]
  96. Wang, B., Liu, Z., Han, Y., et al. 2010b, Sci. China Ser. G, 53, 586 [CrossRef] [Google Scholar]
  97. Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
  98. Willems, B., & Kolb, U. 2004, A&A, 419, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Woudt, P. A., Steeghs, D., Karovska, M., et al. 2009, ApJ, 706, 738 [NASA ADS] [CrossRef] [Google Scholar]
  100. Woosley, S. E., Taam, R. E., & Weaver, T. A. 1986, ApJ, 301, 601 [NASA ADS] [CrossRef] [Google Scholar]
  101. Yoon, S.-C., & Langer, N. 2003, A&A, 412, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Yoon, S.-C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Yoon, S.-C., Langer, N., & Scheithauer, S. 2004, A&A, 425, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Yungelson, L. 2005, in White Dwarfs: Cosmological and Galactic Probes, ed. E. M. Sion, S. Vennes, & H. L. Shipman (Dordrecht: Springer), Astrophysics and Space Science Library, 332, 163 [Google Scholar]
  105. Yungelson, L., & Livio, M. 1998, ApJ, 497, 168 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13976fg1a.ps}\includegraphics[angle=270,width=8cm,clip]{13976fg1b.ps} \end{figure} Figure 1:

A representative case of binary evolution calculations with Z=0.004, in which the binary system is in the weak He-shell flash phase at the moment of the SN explosion. In panel a), the solid, dashed and dash-dotted curves show $\dot M_2$, $\dot{M}_{\rm CO}$ and $M_{\rm WD}$ varying with time, respectively. In panel b), the evolutionary track of the He donor star is shown as a solid curve and the evolution of the orbital period is shown as a dash-dotted curve. Dotted vertical lines in both panels and asterisks in panel b) indicate the position where the WD is expected to explode as an SN Ia. The initial binary parameters and the parameters at the moment of SN explosion are also given in these two panels.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.cm,angle=270,clip]{13976fg2.ps} \end{figure} Figure 2:

Parameter regions producing SNe Ia with different metallicities in the initial orbital period-secondary mass ( $\log P^{\rm i}$, $M^{\rm i}_2$) plane of the CO WD + He star system for initial WD mass of 1.2 $M_{\odot }$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8cm,clip]{13976fg3ab.ps}\includegraphics[angle=270,width=8cm,clip]{13976fg3c.ps} \end{figure} Figure 3:

Similar to Fig.2, but for initial WD masses of 0.9, 1.0 and 1.1 $~M_{\odot}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=5.5cm,angle=270,clip]{13976fg4.ps} \end{figure} Figure 4:

The evolution of SN Ia birthrates for a constant SFR ( $5~M_{\odot}$ yr-1) with different metallicities.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=5.5cm,angle=270,clip]{13976fg5.ps} \end{figure} Figure 5:

The evolution of SN Ia birthrates for a single starburst of $10^{\rm 11}~M_{\odot}$ with different metallicities.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.