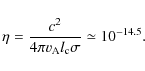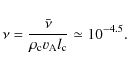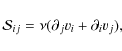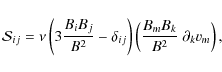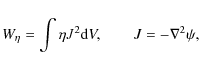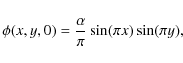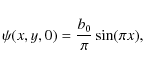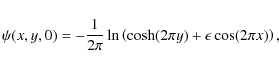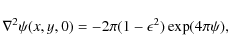EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 515 (June 2010) A&A, 515 (2010) A96 Full HTML
Free Access
Issue
A&A
Volume 515, June 2010
Article Number A96
Number of page(s) 6
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913829
Published online 15 June 2010
A&A 515, A96 (2010)

Anisotropic viscous dissipation in transient reconnecting plasmas

I. J. D. Craig

Department of Mathematics, University of Waikato, P. B. 3105, Hamilton, New Zealand

Received 9 December 2009 / Accepted 8 March 2010

Abstract
Aims. We examine the global energy losses associated with reconnecting coronal plasmas.
Methods. Using planar magnetic reconnection simulations we compute resistive and bulk viscous losses in transient coronal plasmas. Resistive scalings are computed for the case of incompressible reconnection powered by large scale vortical flows. These results are contrasted with an example of magnetic merging driven by the coalescence instability.
Results. We demonstrate that the large scale advective flows, required to sustain resistive current sheets, may be associated with viscous losses approaching flare-like rates of 1029 erg s-1. More generally, bulk viscous dissipation appears likely to dominate resistive dissipation for a wide variety of magnetic merging models. We emphasize that these results have potentially important implications for understanding the flare energy budget.

Key words: magnetohydrodynamics (MHD) - Sun: flares - magnetic fields

1 Introduction

Magnetic reconnection is recognized as a key process in the evolution of coronal plasmas. Since reconnection is the only mechanism that can alter the magnetic field topology, it is thought crucial in a variety of applications, for instance, in the explosive release of the solar flare and in the theory of magnetic coronal heating (Priest & Forbes 2000). A recurring difficulty however, is the slow rate of the magnetic energy release due to the weak coronal resistivity. Unless this rate is enhanced in some manner, say by the inclusion of Hall effects (Knoll & Chacon 2006), or by the adoption of a turbulent resistivity (Litvinenko & Craig 2000), reconnection models are unlikely to meet the explosive energy release requirements of the solar flare.

Motivated largely by the energy release problem, there has been a concerted theoretical effort to incorporate extra physical ingredients into magnetic merging models. One promising approach is the adoption of a generalized Ohms law to account for non-collisional effects (Birn et al. 2001). It has been claimed for instance that Hall effects can speed up the reconnection rate independently of the size of the system (Cassak et al. 2006), a claim contested on the basis of kinematic reconnection simulations (Daughton et al. 2006) and X-point collapse merging (Craig & Litvinenko 2008). More recently, studies of 3D stochastic merging have suggested a ``fast'' regime in which the reconnection rate is effectively independent of the plasma resistivity (Kowal et al. 2009).

A further possibility is to account for the effects of viscosity in the magnetic merging model. Observational support for the presence viscous effects can be inferred from studies of impulsive hard X-ray bursts (McKenzie & Hudson 1999; Asai et al. 2004) which indicate that reconnective outflows may be considerably slower than the Alfvénic exhausts predicted by typical merging solutions. More theoretically, as emphasised by Hollweg (1985, 1986), since the dimensionless viscosity coefficient easily exceeds the normalized resistivity - an inverse Lundquist number of order $\eta \simeq 10^{-14} $ - viscous processes are likely to be important in a wide variety of coronal processes. Yet although the classical shear viscosity is routinely employed in reconnection simulations, it often assumes a passive role, that of simply stabilizing numerical computations. In reality, shear viscous effects are likely to be strongly suppressed in magnetically stratified plasmas such as the solar corona: a more accurate treatment requires an anisotropic bulk viscosity (Hollweg 1986).

The purpose of the present study is to assess the role of viscous damping on transient magnetic reconnection solutions. This work extends recent analytic studies that focus on steady incompressible reconnection within ``open'' two and three dimensional geometries (Litvinenko 2005; Craig & Litvinenko 2009). By ``open'' we mean that energy dissipated within the reconnection region is continually replenished by energy fluxes through inflow boundary surfaces. In this type of flow-driven merging, bulk viscous losses are found to scale independently of the merging rate which is controlled essentially by the plasma resistivity. What is not clear is whether this property extends to more general physical situations or whether it appears as an artifact of the restricted analytic treatment.

In the present study we consider transient, incompressible reconnection within a ``closed'' magnetic geometry. The problem is formulated in Sect. 2 where we discuss appropriate forms for the bulk viscous tensor. Our central results, presented in Sect. 3, are obtained in a doubly periodic, planar configuration, and describe reconnection driven by large scale advective motions. These simulations are similar to those performed previously (e.g. Heerikhuisen et al. 2000) but differ by the inclusion an anisotropic bulk viscosity. To complement this analysis, Sect. 4 presents an example of ``magnetically driven'' visco-resistive reconnection: in this case the merging develops self-consistently from a loss of magnetic equilibrium. In Sect. 5 we summarize our findings.

2 The visco-resistive system

2.1 Governing MHD equations

The equations to be resolved are the MHD momentum and induction equations for the magnetic and velocity fields. These are scaled with respect to typical solar coronal values for field strength $ B_{\rm c} = 10^2~{\rm G} $, size scale $ l_{\rm c} = 10^{9.5}~{\rm cm} $ and number density $ n_{\rm c} = 10^{9}~ {\rm cm}^{-3} $. Times are measured in units of $ l_{\rm c}/ v_{\rm A} $ where $ v_{\rm A} \simeq 10^9~{\rm cm}\; {\rm s}^{-1} $ is the Alfvén speed. The global energy loss rate has the units $ E_{\rm c} = v_{\rm A} ~ {l_{\rm c}}^2 {B_{\rm c}}^2 /(8 \pi) \simeq 4 \times 10^{30} ~ {\rm erg} ~{ \rm s}^{-1} $.

We are interested in the evolution of the $\vec{B}$ and $\vec{v} $fields in the presence of small viscous and resistive damping coefficients. Since we consider planar, incompressible plasmas, the constraint equations $ \nabla \cdot \vec{B} = \nabla \cdot \vec{v} = 0 $can be satisfied by adopting the flux function and stream function representations

\begin{displaymath}{\vec B} = \nabla \psi(x,y,t) \times \hat{\vec z}, ~ \quad {\vec v} = \nabla \phi(x,y,t) \times \hat{\vec z}. \end{displaymath} (1)

Introducing the Poisson bracket notation typified by

\begin{displaymath}[\psi, \phi]= \partial_x \psi \partial_y \phi - \partial_y \psi \partial_x \phi, \end{displaymath} (2)

the momentum and induction equations take the dimensionless forms

\begin{displaymath}\partial_t (\nabla^2 \phi) + [\nabla^2 \phi, \phi] = [\nabla^2\psi, \psi] + G, \end{displaymath} (3)

\begin{displaymath}\partial_t \psi + [\psi, \phi] = \eta \nabla^2 \psi. \end{displaymath} (4)

Here $\eta$ is the dimensionless resistivity and viscous effects are represented by the term

\begin{displaymath}G = - (\nabla \times \nabla \cdot {\cal S}) \cdot \hat{\vec{z}}, \end{displaymath} (5)

where $ {\cal S} $ an appropriate viscous tensor (see below). Note that (3) is the curled form of the momentum equation and that the stream function $ \phi $ has to be recovered from the Poisson equation for the computed vorticity $ (-\nabla^2 \phi) $.

2.2 Resistive and viscous dissipation

Energy losses from the source volume are controlled by two small parameters, the dimensionless resistivity $\eta$ and the dimensionless plasma viscosity $ \nu $. For a collisional plasma of temperature T = 106 K with conductivity $\sigma \sim T^{3/2} $ (Spitzer 1962), $\eta$ is an inverse Lundquist number of magnitude

\begin{displaymath}\eta = \frac {c^2} {4\pi v_{\rm A} l_{\rm c} \sigma} \simeq 10^{-14.5}. \end{displaymath} (6)

This number is considerably smaller than the Reynolds number associated with the viscous losses. For a plasma of mass density $ \rho_{\rm c} $ in which the viscosity scales as $ {\bar \nu} \sim T^{5/2} $ (Spitzer 1962), we find the following value for the dimensionless viscosity coefficient:

\begin{displaymath}\nu = \frac {\bar {\nu}} {\rho_{\rm c} v_{\rm A} l_{\rm c}} \simeq 10^{-4.5}. \end{displaymath} (7)

Since $ \nu \gg \eta $ it is natural to expect viscous dissipation to dominate resistive losses in most coronal applications. This dominance is likely to be maintained for turbulent resistivities since enhancements of order 106 are the most that can be expected (Litvinenko & Craig 2000). Also, because of the strong temperature dependencies involved, viscous effects may be even more prominent in flare plasmas where temperatures routinely exceed several million degrees. We must remember, however, that only resistive dissipation can liberate energy tied up in the topology of the magnetic field. A further complication is that viscous effects become highly anisotropic in strongly magnetized plasmas (Braginskii 1965; Hollweg 1986). Isotropy breaks down when the proton mean free path exceeds the gyro radius: specifically $\omega_{\rm p} \tau_{\rm p} \gg 1$, where $\omega_{\rm p} = e B / (m_{\rm p} c)$ is the proton cyclotron frequency and $\tau_{\rm p} \simeq 0.75 ~ T^{3/2}/n$ is the mean time (in seconds) between momentum-changing collisions. The fact that $\omega_{\rm p} \tau_{\rm p} \simeq 10^6 \gg 1$ for the parameters adopted above suggests that an anisotropic viscosity should be used in almost all coronal applications.

We conclude that the classical tensor $ {\cal S} $ for the shear viscosity namely,

\begin{displaymath}{\cal S}_{ij} = \nu (\partial_j v_i + \partial_i v_j), \end{displaymath} (8)

is generally inappropriate for magnetic coronal plasmas. More suitable is the strong field, bulk viscosity tensor (Braginskii 1965):

\begin{displaymath}{\cal S}_{ij} = \nu \left( 3 \frac {B_i B_j} {B^2} - \delta_{... ...ght) \left( \frac {B_m B_k} {B^2} ~ \partial_k {v_m} \right), \end{displaymath} (9)

where summation over repeated suffixes is assumed. Note that a necessary condition for bulk viscous dissipation is that velocity gradients along the field lines be non-vanishing.

One minor complication is that the Braginskii tensor (9) cannot by extrapolated down to arbitrarily weak fields, for instance, those associated with magnetic nulls. In practice therefore we adopt the so called ``Liley form'' for the viscous tensor (Hosking & Marinoff 1973). This form, although not critical for the present applications, recovers expression (9) in strong field regions but also includes the weak field (shear viscosity) limit (8) that may apply sufficiently close to a magnetic null.

2.3 Global energy losses

In what follows we model reconnection within a closed, periodic geometry ( $ -1 \le x,y \le 1$). Of central interest is a comparison of the Ohmic dissipation rate

\begin{displaymath}W_\eta = \int \eta J^2 {\rm d}V, \quad \quad J = - \nabla^2 \psi, \end{displaymath} (10)

where $ \vec{J} = \nabla \times \vec{B} $ is dimensionless current density, with the global viscous losses (Hollweg 1986; Craig & Litvinenko 2009)

\begin{displaymath}W_\nu = \int {\cal S}_{i j} ~ \partial_i v_j ~ {\rm d}V. \end{displaymath} (11)

Since it is not feasible to model the system for collisional resistivities approaching $\eta \simeq 10^{-14} $, we adopt the strategy of obtaining resistive scalings by fixing the dimensionless viscosity at some representative value while systematically reducing the resistivity to levels $\eta \ll \nu $. We argue that, although it is unphysical for $W_{\eta }$ to increase as $ \eta \to 0$, the viscous losses, which act primarily by damping the velocity field, should be far less sensitive to this reduction. The implication is that if bulk viscous losses can be shown to dominate Ohmic losses for computationally accessible resistivities, then this dominance should be maintained as $\eta$ approaches physically realistic levels.

3 Flow driven reconnection

3.1 The model

In this section we employ a doubly periodic code to model transient reconnection (e.g. Watson et al. 2007). An initial velocity field of the form

\begin{displaymath}\phi(x,y,0) = \frac {\alpha} {\pi} \sin(\pi x) \sin(\pi y), \end{displaymath} (12)

where $ \alpha $ specifies the strength of flow, is used to power the merging. The initial flux function, namely

\begin{displaymath}\psi(x,y,0) = \frac {b_0} {\pi} \sin(\pi x), \end{displaymath} (13)

defines straight field lines, antiparallel about x = 0. These field lines rapidly distort as they are driven together by the flow ( $ \alpha < 0$). The resulting accumulation of field lines close to null leads to enhanced current densities and the onset of ``flux pile-up'' reconnection.

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig1.eps} \end{figure} Figure 1:

Time plot of the global Ohmic losses and bulk viscous dissipation. The Ohmic losses reflect the build up and localization of the current sheet. The peak current density in the sheet J0 (divided by one hundred for plotting purposes) is also shown. The plot is based on the parameters $ \alpha = -1, \eta = 10^{-3}, \nu = 4 \times 10^{-3} $ and b0 = 0.14.

Open with DEXTER

We shall not emphasize the phenomenology of the reconnection (see Heerikhuisen et al. 2000; or Watson et al. 2007) beyond noting that transient merging solutions produced by strong cellular flows, and analysed quantitatively at the time of maximum sheet development, are known to provide an excellent ``snapshot'' of formally exact, analytic merging solutions (Craig & Henton 1995). Figure 1 shows the build up of the current layer and the evolution of global losses up to the time of maximum current density for the parameters $ \alpha = -1, \eta = 10^{-3}, \nu = 4 \times 10^{-3} $ and b0 = 0.14. In this case, the resistivity is large enough for the Ohmic dissipation rate to increase to a level that exceeds the bulk viscous losses. What is not so clear is whether this dominance can be maintained as the resistivity is systematically reduced.

Figure 2 shows field line contours at the end of the build up phase ( $ t \simeq 1.2 $) while Fig. 3 shows the corresponding current density surface. Evidently a well defined, quasi one-dimensional current layer has developed over the origin. Note that identical reconnection sites are periodically reproduced at each corner of the computational mesh.

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig2.eps} \end{figure} Figure 2:

Field line plot taken at the time of maximum current density, $ t \simeq 1.2 $. Parameters are those of Fig. 1, namely $ \alpha = -1, \ \beta = 0, \eta = 10^{-3}, \nu = 4 \times 10^{-3} $ and b0 = 0.14.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig3.eps} \end{figure} Figure 3:

Surface plot of the current density at the time of peak current ( $ t \simeq 1.2)$. A well defined, symmetric current sheet overlies the origin. Magnetic field lines are shown in Fig. 2. Parameters are those of Fig. 2.

Open with DEXTER

A surface plot of the vorticity of the flow is shown in Fig. 4. Regions of strong vorticity correspond quite closely to regions of high current density. Were the shear viscosity not suppressed by the magnetic field, we would expect strong viscous damping in these regions. The surface plot of bulk viscous dissipation shown in Fig. 5 indicates that significant damping can occur even when the vorticity is weak. Therefore, the identification of regions of strong viscous damping with regions of strong Ohmic heating is weakened in the case of bulk viscous losses.

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig4.eps} \end{figure} Figure 4:

Surface plot of the vorticity at $ t \simeq 1.2 $. Comparison with Figs. 2 and 3 shows that vorticity is well correlated with regions of high current density. Parameters are those of Fig. 2.

Open with DEXTER

\begin{figure} \includegraphics[width=9cm,clip]{13829fig5.eps} \end{figure} Figure 5:

Surface plot of the volumetric bulk viscous dissipation $( {\cal S}_{i j} ~ \partial_i v_j) $ at the time of peak current $ t \simeq 1.2 $. Comparison with Fig. 4 shows that significant viscous dissipation is not limited to regions of strong vorticity. Parameters are those of Fig. 2.

Open with DEXTER

3.2 Resistive scalings

We now return to the problem of deducing resistive scalings for the Ohmic and viscous losses. Note that it is not sufficient to simply reduce $\eta$ while maintaining the intensity b0 of the advected field. This is because, if the flux pile-up field is allowed to build up too strongly, magnetic back pressures develop that stall the flow and arrest the development of the current layer. The merging rate is then compromised by the break down of the large scale vortical flows that drive the reconnection. To maintain near-optimum Ohmic dissipation rates, b0 should be adjusted to ensure that the current sheet pressure at full development is comparable to the dynamic pressure of the driving flow. Analytic arguments suggest that taking $b_0 \sim \sqrt \eta $ should provide a practical guide for ensuring that the peak magnetic field reflects the strength of the flow. With the peak field normalized to the flow amplitude in this manner, the current density builds up as $ \eta ^ {-1/2} $ (consistent with traditional Sweet-Parker merging). It follows that adequate resolution of the current layer requires grid sizes that scale as $ \sqrt \eta $, corresponding to several hundred mesh points for the lower resistivities $ \eta \simeq 10^{-4} $.

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig6.eps} \end{figure} Figure 6:

Scaling with resistivity of the bulk viscous losses and the peak Ohmic dissipation rate. The dashed reference line indicates an $ \eta ^{0.55} $ scaling. The fact that the Ohmic rate scales declines slightly faster than the analytic $ \eta ^{1/2} $ expectation is probably due to the decay of the global flow field.

Open with DEXTER

Figure 6 shows resistive scalings obtained over the range $10^{-4} \le \eta \le 10^{-2}$ for the parameters $ \nu = 0.004, \alpha = -1 $ with $b_0 \sim \sqrt \eta $. The systematic decline of the Ohmic losses with reductions in $\eta$ contrasts with the very weak dependency of the bulk viscous losses. The fact that the Ohmic rate declines slightly faster than the analytic $ \eta ^{1/2} $ expectation is probably due to the decay of the global flow field. But although the peak reconnecting field is always of order unity (commensurate with the flow amplitude), we see that viscous damping starts to dominate the Ohmic losses for $ \eta < 10^{-3.5} $. As expected this dominance is found to increase with further reductions in resistivity.

3.3 Summary

The present results suggest that viscous energy release could easily dominate resistive losses in typical coronal plasmas. For the flow driven reconnection model considered here, the viscous damping rate is insensitive to plasma resistivity.

To estimate the global viscous losses we can multiply the dimensionless rate $ W_\nu \simeq 0.1 $ from Fig. 6 by the dimensional factor $ E_{\rm c} \simeq 4 \times 10^{30} ~ {\rm erg} {~ \rm s}^{-1} $, based on the typical coronal parameters of Sect. 2.1. This suggests that flare-like damping rates exceeding 1029 erg s -1 could be achievable in practice. The assumption of stronger driving flows $ \vert\alpha\vert > 1 $ could increase this rate still further.

Finally we should mention that the present results are unlikely to depend critically on the orientation of the initial disturbance field. This follows from the fact that axial field components, unlike the planar field (13), are not amplified by the flow as they are swept towards the reconnection region.

4 Merging driven by the coalescence instability

4.1 Introduction

One limitation of the previous reconnection model is the a priori assumption of a large scale vortical flow to drive the merging. It is not clear for instance how these results apply to magnetic merging driven say, by an initial magnetic imbalance or MHD instability. With this in mind we now consider an example of bulk viscous damping based on reconnection driven by the coalescence instability. Our aim is to illustrate how fluid motions, developing as part of the reconnection process, can lead to strong bulk viscous damping.

4.2 The coalescence simulation

The coalescence instability provides a self consistent, two-dimensional model for magnetic reconnection within a closed semi-periodic geometry (e.g Prichett & Wu 1979; Rickard & Craig 1993). The initial configuration comprises a periodic chain of magnetic islands. These slowly merge together in pairs, forming well-defined current sheets at which reconnection occurs.

The initial magnetic field is derived from the flux function

\begin{displaymath}\psi(x,y, 0) = - \frac {1} {2 \pi} \ln \left(\cosh(2 \pi y) + \epsilon \cos(2 \pi x) \right), \end{displaymath} (14)

under the assumption of perfectly conducting walls at $y = \pm 1$. The parameter $ \epsilon $ sets the size of the magnetic islands and controls the flux to be reconnected through the assemblage of neutral points. Note that since the initial configuration comprises finite currents it is subject to static Ohmic decay. Specifically,

\begin{displaymath}\nabla^2 \psi(x, y, 0) = -2 \pi (1 - \epsilon^2) \exp(4 \pi \psi), \end{displaymath} (15)

defines the initial current density magnitude. However, provided the resistivity is not too large (say $\eta \le 10^{-2})$, the islands eventually squeeze together in pairs - ``like currents attract'' - generating significant mass flows and the potential for strong bulk viscous damping.

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig7.eps} \end{figure} Figure 7:

The flux function $ \psi $ at the time ( $t \simeq 6.8$ of maximum current density for the parameters $ \eta = 5 \times 10^{-4}, \nu = 4 \times 10^{-3}, \epsilon = 0.8 $. The field is weakest in the regions of strong dynamic pressure overlying the magnetic island.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig8.eps} \end{figure} Figure 8:

The stream function $ \phi $ at the time of maximum current for the parameters of Fig. 7. The strong velocity field gradients in the region overlying the magnetic island are linked to the strong exhaust of the current layer.

Open with DEXTER

Figures 7 and 8 show the stream and flux functions at the time of peak current density for the parameters $ \eta = 5 \times 10^{-4}, \nu = 4 \times 10^{-3}, \epsilon = 0.8 $. Although the bulk of the total energy remains in the magnetic field - and it is the magnetic pressure in the outer field that ultimately drives the merging - the dynamic pressure of the flow develops to a level where it is comparable to the magnetic pressure, especially in those regions of strong velocity gradient close to the reconnection sites. The flow pattern is clearly dominated by two distinct, clockwise rotating, cellular flows; one is centered on the magnetic island, the other extends further into the outer magnetic field.

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig9.eps} \end{figure} Figure 9:

Development of the Ohmic ($W_{\eta }$) and bulk viscous losses ($W_{\nu })$ against time for the parameters of Figs. 7 and 8. The plots show base ten logarithms of the global dissipation rates as well as the current density magnitude J0 (divided by 103 for plotting purposes). Note that the viscous losses are entirely negligible during the initial coalescence phase $ t \le 5 $.

Open with DEXTER

The resistivity in the present example has been chosen so that the peak Ohmic and viscous dissipation rates remain comparable. More specifically, Fig. 9 shows that the bulk viscous dissipation, although entirely negligible for the first four or five Alfvén times, is just starting to dominate the global losses by the time that the peak current density is achieved. The viscous build up accords with the dimensional estimate $W_{\nu} \sim \nu {v_m}^2 $ where vm is the peak speed of the flow.

\begin{figure} \par\includegraphics[width=9cm,clip]{13829fig10.eps} \end{figure} Figure 10:

Ohmic ($W_{\eta }$) and bulk viscous losses ($W_{\nu })$ against $ \log_{10} (\eta) $ for the parameters $ \nu = 4 \times 10^{-3}, \epsilon = 0.8 $. Although the Ohmic losses are only weakly dependent on resistivity, there is a systematic increase in viscous dissipation as the resistivity is reduced.

Open with DEXTER

Figure 10 presents a sequence of exploratory runs that show the effect of varying the resistivity $ \eta < \nu $while keeping all other parameters fixed in the simulation ( $ \nu = 0.004, ~ \epsilon = 0.8 $). The dissipation rates are again evaluated at the time of peak current density, but, unlike the results of Fig. 6, no attempt has been made to obtain ``saturated'' scalings by restricting the strength of the field washed into the reconnection region. The fact that the Ohmic losses are maintained against reductions in resistivity suggests that these results apply to a pre-saturation regime in which ``fast'' reconnection is achieved by the continual build-up of the field at the onset of the current layer. Evidently the strengthening viscous losses at the smaller resistivities are due to the increasing flow amplitude and alignment to the magnetic field. The implication, physically, is that the global viscous losses are likely to be significant even in the ``fast'' reconnection regime prior to saturation.

4.3 Summary

Although coalescence merging reinforces the notion that bulk viscous losses are likely to be important in flare plasmas, there are several phenomena that have no counterpart in the flow powered reconnection model of Sect. 3. For instance, a key element in the coalescence development is an initial transfer of magnetic energy into the velocity field of the plasma. The present example shows that strong field-aligned flows eventually develop in regions overlying the magnetic islands - and it these regions that are closely associated with the rapid rise in the global viscous losses.

In view of the sharp gradients present in the velocity field (see Fig. 8), it is perhaps worth speculating on the emergence of a small visco-resistive length scale for the merging. Of interest is the fact that a hybrid length scale $ (\eta \nu)^{1/4} $ has been identified in several visco-resistive studies (Park et al. 1984; Hassam & Lambert 1996). These involve the shear viscosity, but the more recent X-point collapse study of Craig (2008) suggests a similar scale may apply to bulk viscous damping. It should be stressed therefore that the present simulations provide little evidence for a visco-resistive scale that controls the dissipation. More critical, at least for the viscous losses, is the development of the global flow.

5 Discussion and conclusions

We have considered transient, incompressible reconnection within a closed magnetic geometry. Our results suggest that bulk viscous losses are likely to be important, if not dominant, in magnetic coronal plasmas. Detailed simulations, based on planar reconnection powered by large scale vortical flows, show that viscous damping rates may be insensitive to the very small coronal plasma resistivity. For plausible active region parameters (see Sect. 2.1), bulk viscous losses can approach flare-like levels of 1029 erg s-1. These results both extend and reinforce previous studies demonstrating the importance of bulk viscous damping in magnetic coronal plasmas (Litvinenko 2005; Craig 2008; Craig & Litvinenko 2009).

We have also made a preliminary study of the global losses in visco-resistive coalescence merging. The reconnecting current layer now emerges as the outgrowth of an initial magnetic imbalance - and the velocity field develops in sympathy with the burgeoning current sheet. The results of Sect. 4 show that bulk viscous losses associated with the global velocity field can eventually dominate the resistive losses of the current sheet. In contrast to the case of flow driven reconnection, sharp gradients are now present in the velocity field, but it is the emergence of strong global flows that appear most critical in determining the viscous losses.

In summary, the present reconnection simulations indicate that viscous effects could be important in a variety of magnetic merging applications. Although energy bound up in the magnetic field topology cannot be released by viscous effects, energy transferred into the velocity field, say by equipartition in the formative stages of current sheet development or by strong reconnective exhausts later on, can be very effectively damped. The implication, in practice, is that viscous effects are likely to account for a sizable fraction of the flare energy budget.

Acknowledgements
Comments by Yuri Litvinenko and Sean Oughton have been much appreciated.

References

  1. Akai, A., Yoshimoto, T., Shimojo, M., & Shibata, K. 2004, ApJ, 605, L77 [NASA ADS] [CrossRef] [Google Scholar]
  2. Birn, J., Drake, J. F., Shay, M. A., et al. 2001, J. Geophys. Res., 106, 3715 [Google Scholar]
  3. Braginskii, S. I. 1965, Rev. Plasma Phys., 1, 205 [NASA ADS] [Google Scholar]
  4. Cassak, P. A., Drake, J. F., & Shay, M. A. 2006, ApJ, 644, L145 [NASA ADS] [CrossRef] [Google Scholar]
  5. Craig, I. J. D. 2008, A&A, 487, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Craig, I. J. D., & Henton, S. M. 1995, ApJ, 450, 280 [NASA ADS] [CrossRef] [Google Scholar]
  7. Craig, I. J. D., & Litvinenko, Y. E. 2008, A&A, 484, 847 [Google Scholar]
  8. Craig, I. J. D., & Litvinenko, Y. E. 2009, A&A, 501, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Daughton, W., Scudder, J., & Karimabad, H. 2006, Phys. Plasmas, 13, 072101 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hassam, A. B., & Lambert, R. P. 1996, ApJ, 472, 832 [NASA ADS] [CrossRef] [Google Scholar]
  11. Heerikhuisen, J. Watson, P. G., & Craig, I. J. D. 2000, Geophys. & Astrophys. Fluid Dynamics, 93, 115 [Google Scholar]
  12. Hollweg, J. V. 1985, J. Geophys. Res., 90, 7620 [NASA ADS] [CrossRef] [Google Scholar]
  13. Hollweg, J. V. 1986, ApJ, 306, 730 [NASA ADS] [CrossRef] [Google Scholar]
  14. Hosking, R. J., & Marinoff, G. M. 1973, Plasma Phys., 15, 327 [NASA ADS] [CrossRef] [Google Scholar]
  15. Knoll, D. A., & Chacon, L. 2006, Phys. Rev. Lett., 96, 135001 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  16. Otmianowska Kowal, G., Lazarian, A., Vishniac, E. T., & Otmianowska-Mazur, K. 2009, ApJ, 700, 63 [NASA ADS] [CrossRef] [Google Scholar]
  17. Litvinenko, Y. E. 2005, Sol. Phys., 229, 203 [NASA ADS] [CrossRef] [Google Scholar]
  18. Litvinenko, Y. E., & Craig, I. J. D. 2000, ApJ, 544, 1101 [NASA ADS] [CrossRef] [Google Scholar]
  19. McKenzie, D. E., & Hudson, H. S. 1999, ApJ, 519, L93 [NASA ADS] [CrossRef] [Google Scholar]
  20. Park, W., Monticello, D. A., & White, R. B. 1984, Phys. Fluids, 27, 137 [NASA ADS] [CrossRef] [Google Scholar]
  21. Priest, E. R., & Forbes, T. 2000, Magnetic reconnection: MHD theory and applications (Cambridge Univ. Press) [Google Scholar]
  22. Pritchett, P. L., & Wu, C. C. 1979, Phys. Fluids, 22, 2140 [NASA ADS] [CrossRef] [Google Scholar]
  23. Rickard, G. J., & Craig, I. J. D. 1993, Phys. Fluids, B5, 956 [NASA ADS] [Google Scholar]
  24. Spitzer, L. 1962, Physics of fully ionized gases (John Wiley & Sons) [Google Scholar]
  25. Watson, P. G., Oughton, S., & Craig, I. J. D. 2007, Phys. Plasmas, 14, 2301 [CrossRef] [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig1.eps} \end{figure} Figure 1:

Time plot of the global Ohmic losses and bulk viscous dissipation. The Ohmic losses reflect the build up and localization of the current sheet. The peak current density in the sheet J0 (divided by one hundred for plotting purposes) is also shown. The plot is based on the parameters $ \alpha = -1, \eta = 10^{-3}, \nu = 4 \times 10^{-3} $ and b0 = 0.14.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig2.eps} \end{figure} Figure 2:

Field line plot taken at the time of maximum current density, $ t \simeq 1.2 $. Parameters are those of Fig. 1, namely $ \alpha = -1, \ \beta = 0, \eta = 10^{-3}, \nu = 4 \times 10^{-3} $ and b0 = 0.14.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig3.eps} \end{figure} Figure 3:

Surface plot of the current density at the time of peak current ( $ t \simeq 1.2)$. A well defined, symmetric current sheet overlies the origin. Magnetic field lines are shown in Fig. 2. Parameters are those of Fig. 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig4.eps} \end{figure} Figure 4:

Surface plot of the vorticity at $ t \simeq 1.2 $. Comparison with Figs. 2 and 3 shows that vorticity is well correlated with regions of high current density. Parameters are those of Fig. 2.

Open with DEXTER
In the text

  \begin{figure} \includegraphics[width=9cm,clip]{13829fig5.eps} \end{figure} Figure 5:

Surface plot of the volumetric bulk viscous dissipation $( {\cal S}_{i j} ~ \partial_i v_j) $ at the time of peak current $ t \simeq 1.2 $. Comparison with Fig. 4 shows that significant viscous dissipation is not limited to regions of strong vorticity. Parameters are those of Fig. 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig6.eps} \end{figure} Figure 6:

Scaling with resistivity of the bulk viscous losses and the peak Ohmic dissipation rate. The dashed reference line indicates an $ \eta ^{0.55} $ scaling. The fact that the Ohmic rate scales declines slightly faster than the analytic $ \eta ^{1/2} $ expectation is probably due to the decay of the global flow field.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig7.eps} \end{figure} Figure 7:

The flux function $ \psi $ at the time ( $t \simeq 6.8$ of maximum current density for the parameters $ \eta = 5 \times 10^{-4}, \nu = 4 \times 10^{-3}, \epsilon = 0.8 $. The field is weakest in the regions of strong dynamic pressure overlying the magnetic island.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig8.eps} \end{figure} Figure 8:

The stream function $ \phi $ at the time of maximum current for the parameters of Fig. 7. The strong velocity field gradients in the region overlying the magnetic island are linked to the strong exhaust of the current layer.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig9.eps} \end{figure} Figure 9:

Development of the Ohmic ($W_{\eta }$) and bulk viscous losses ($W_{\nu })$ against time for the parameters of Figs. 7 and 8. The plots show base ten logarithms of the global dissipation rates as well as the current density magnitude J0 (divided by 103 for plotting purposes). Note that the viscous losses are entirely negligible during the initial coalescence phase $ t \le 5 $.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13829fig10.eps} \end{figure} Figure 10:

Ohmic ($W_{\eta }$) and bulk viscous losses ($W_{\nu })$ against $ \log_{10} (\eta) $ for the parameters $ \nu = 4 \times 10^{-3}, \epsilon = 0.8 $. Although the Ohmic losses are only weakly dependent on resistivity, there is a systematic increase in viscous dissipation as the resistivity is reduced.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.