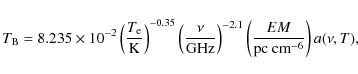| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913793 | |
| Published online | 09 June 2010 | |
A Sino-German
 6 cm polarization survey of the Galactic plane
6 cm polarization survey of the Galactic plane
II. The region from 129 to 230
to 230 longitude
longitude
X. Y. Gao1,2 - W. Reich2 - J. L. Han1 - X. H. Sun1 - R. Wielebinski2 - W. B. Shi1,3 - L. Xiao1 - P. Reich2 - E. Fürst2 - M. Z. Chen4 - J. Ma4
1 - National Astronomical Observatories, CAS, Jia-20 Datun Road, Chaoyang District, Beijing 100012, PR China
2 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
3 - School of Space Science and Physics, Shandong University at Weihai, 180 Cultural West Road, Shandong 264209, PR China
4 - Urumqi Observatory, National Astronomical Observatories, CAS, 40-5 South Beijing Road, Urumqi 830011, PR China
Received 2 December 2009 / Accepted 23 March 2010
Abstract
Context. Linearly polarized Galactic synchrotron emission
provides valuable information about the properties of the Galactic
magnetic field and the interstellar magneto-ionic medium, when Faraday
rotation along the line of sight is properly taken into account.
Aims. We aim to survey the Galactic plane at ![]() 6 cm
including linear polarization. At such a short wavelength Faraday
rotation effects are in general small and the Galactic magnetic field
properties can be probed to larger distances than at long wavelengths.
6 cm
including linear polarization. At such a short wavelength Faraday
rotation effects are in general small and the Galactic magnetic field
properties can be probed to larger distances than at long wavelengths.
Methods. The Urumqi 25-m telescope is used for a sensitive ![]() 6 cm
survey in total and polarized intensities. WMAP K-band (22.8 GHz)
polarization data are used to restore the absolute zero-level of the
Urumqi U and Q maps by extrapolation.
6 cm
survey in total and polarized intensities. WMAP K-band (22.8 GHz)
polarization data are used to restore the absolute zero-level of the
Urumqi U and Q maps by extrapolation.
Results. Total intensity and polarization maps are presented for a Galactic plane region of
![]() and
and
![]() in the anti-centre with an angular resolution of
in the anti-centre with an angular resolution of
![]() and an average sensitivity of 0.6 mK and 0.4 mK
and an average sensitivity of 0.6 mK and 0.4 mK ![]() in total and polarized intensity, respectively. We briefly discuss the
properties of some extended Faraday Screens detected in the
in total and polarized intensity, respectively. We briefly discuss the
properties of some extended Faraday Screens detected in the ![]() 6 cm polarization maps.
6 cm polarization maps.
Conclusions. The Sino-German ![]() 6 cm
polarization survey provides new information about the properties of
the magnetic ISM. The survey also adds valuable information for
discrete Galactic objects and is in particular suited to detect
extended Faraday Screens with large rotation measures hosting strong
regular magnetic fields.
6 cm
polarization survey provides new information about the properties of
the magnetic ISM. The survey also adds valuable information for
discrete Galactic objects and is in particular suited to detect
extended Faraday Screens with large rotation measures hosting strong
regular magnetic fields.
Key words: polarization - surveys - Galaxy: disk - ISM: magnetic fields - radio continuum: general - methods: observational
1 Introduction
Surveys of the Galactic plane at several frequencies are required to disentangle the individual star formation complexes, or thermal H II regions, non-thermal supernova remnants (SNRs) and extragalactic sources. The diffuse emission associated with the Galactic disk is produced by relativistic electrons spiraling in magnetic fields and by thin ionized thermal gas. Both the diffuse non-thermal emission and the SNRs have significant linear polarization. Mapping of the Galactic plane at several radio frequencies including linear polarization offers a method to separate these non-thermal components as well as allowing a delineation of the Galactic magnetic field.
The Galactic plane has been surveyed from 22 MHz up to 10 GHz, albeit usually without polarization measurements.
Sensitive Galactic polarization plane surveys began in the 1980s. A 2.7 GHz survey using the Effelsberg 100-m telescope by Junkes et al. (1987) showed a
section of the Galactic plane with
![]() angular resolution. Further Northern sky Galactic plane surveys at 2.7 GHz
(Fürst et al. 1990; Duncan et al. 1999; Reich et al. 1990) were complemented by 2.4 GHz Southern Galactic plane surveys using the Parkes 64-m telescope
(Duncan et al. 1995,1997). To achieve angular resolution of arc minutes at lower frequencies synthesis radio telescopes had
to be used for surveys: e.g. the Westerbork Synthesis Radio Telescope at 350 MHz (Wieringa et al. 1993; Haverkorn et al. 2003b,a),
the Dominion Radio Astrophysical Observatory synthesis telescope at 408 MHz and 1.4 GHz (Canadian Galactic Plane
Survey, CGPS) (Taylor et al. 2003), and the Australian Telescope Compact Array at 1.4 GHz (Southern Galactic Plane Survey, SGPS) (Gaensler et al. 2001; Haverkorn et al. 2006). Most of the mentioned surveys only cover a
narrow strip along the Galactic plane. To overcome this deficiency the Galactic plane was mapped at 1.4 GHz with
the Effelsberg 100-m telescope for
angular resolution. Further Northern sky Galactic plane surveys at 2.7 GHz
(Fürst et al. 1990; Duncan et al. 1999; Reich et al. 1990) were complemented by 2.4 GHz Southern Galactic plane surveys using the Parkes 64-m telescope
(Duncan et al. 1995,1997). To achieve angular resolution of arc minutes at lower frequencies synthesis radio telescopes had
to be used for surveys: e.g. the Westerbork Synthesis Radio Telescope at 350 MHz (Wieringa et al. 1993; Haverkorn et al. 2003b,a),
the Dominion Radio Astrophysical Observatory synthesis telescope at 408 MHz and 1.4 GHz (Canadian Galactic Plane
Survey, CGPS) (Taylor et al. 2003), and the Australian Telescope Compact Array at 1.4 GHz (Southern Galactic Plane Survey, SGPS) (Gaensler et al. 2001; Haverkorn et al. 2006). Most of the mentioned surveys only cover a
narrow strip along the Galactic plane. To overcome this deficiency the Galactic plane was mapped at 1.4 GHz with
the Effelsberg 100-m telescope for
![]() .
First maps from this survey were shown by Uyaniker et al. (1999) and by
Reich et al. (2004). To study the nature of
sources and the properties of the magnetic field, polarization surveys
at higher radio frequencies are needed.
Valuable information about diffuse polarized Galactic emission was
provided by WMAP at 22.8 GHz and higher frequencies (Hinshaw et al. 2009), although the angular resolution of
.
First maps from this survey were shown by Uyaniker et al. (1999) and by
Reich et al. (2004). To study the nature of
sources and the properties of the magnetic field, polarization surveys
at higher radio frequencies are needed.
Valuable information about diffuse polarized Galactic emission was
provided by WMAP at 22.8 GHz and higher frequencies (Hinshaw et al. 2009), although the angular resolution of
![]() at 22.8 GHz is in general too coarse to resolve the complex Galactic structures in the Galactic plane.
at 22.8 GHz is in general too coarse to resolve the complex Galactic structures in the Galactic plane.
The Sino-German ![]() 6 cm survey, covering a 10
6 cm survey, covering a 10
![]() wide strip of the Galactic plane, has been carried out
since 2004 using the 25-m radio telescope of the Urumqi Observatory, National Astronomical Observatories, CAS.
This survey fills the existing gap in frequency
coverage by providing maps of the Galactic plane from
wide strip of the Galactic plane, has been carried out
since 2004 using the 25-m radio telescope of the Urumqi Observatory, National Astronomical Observatories, CAS.
This survey fills the existing gap in frequency
coverage by providing maps of the Galactic plane from
![]() and
and
![]() with an angular resolution of
with an angular resolution of
![]() .
The survey maps and a list of compact sources will be released after completion of the
.
The survey maps and a list of compact sources will be released after completion of the
![]() 6 cm survey project expected for the end of 2010.
The first results have already been presented by Sun et al. (2007) (hereafter called Paper I), including details of the survey concept, the observing and
calibration methods and the reduction process. In Paper I, covering the longitude range from
6 cm survey project expected for the end of 2010.
The first results have already been presented by Sun et al. (2007) (hereafter called Paper I), including details of the survey concept, the observing and
calibration methods and the reduction process. In Paper I, covering the longitude range from
![]() to
to
![]() ,
we illustrated the scientific potential provided by the
,
we illustrated the scientific potential provided by the ![]() 6 cm survey by delineating new faint
H II
regions, studied spectra of SNRs, discovered Faraday Screens as well as
traced the magnetic fields in this section of the Galactic plane. Most
remarkable discoveries are two extended Faraday Screens located at the
Perseus arm. One of them is caused by a previously unknown faint H II region. Both Faraday Screens host strong regular magnetic fields with rotation measures (RM) of the order
of 200 rad m-2. They are not visible at low frequencies because such high RMs cause a
polarization angle rotation by more than
6 cm survey by delineating new faint
H II
regions, studied spectra of SNRs, discovered Faraday Screens as well as
traced the magnetic fields in this section of the Galactic plane. Most
remarkable discoveries are two extended Faraday Screens located at the
Perseus arm. One of them is caused by a previously unknown faint H II region. Both Faraday Screens host strong regular magnetic fields with rotation measures (RM) of the order
of 200 rad m-2. They are not visible at low frequencies because such high RMs cause a
polarization angle rotation by more than
![]() ,
or they are beyond the polarization horizon. This proves the value of a sensitive
,
or they are beyond the polarization horizon. This proves the value of a sensitive ![]() 6 cm
polarization survey to detect them in the magnetized interstellar
medium. The commonly adopted picture of the Galactic magnetic field in
the thin disk to consist of a regular component following
basically the spiral arms of the Galaxy together with a turbulent
magnetic field component of about similar strength might be modified in
case numerous extended Faraday Screens with a uniform regular magnetic
field exist. The origin of such magnetic bubbles acting as Faraday
Screens is not clear so far.
6 cm
polarization survey to detect them in the magnetized interstellar
medium. The commonly adopted picture of the Galactic magnetic field in
the thin disk to consist of a regular component following
basically the spiral arms of the Galaxy together with a turbulent
magnetic field component of about similar strength might be modified in
case numerous extended Faraday Screens with a uniform regular magnetic
field exist. The origin of such magnetic bubbles acting as Faraday
Screens is not clear so far.
Here we present the second section of the ![]() 6 cm survey for the outer Galaxy covering the region
6 cm survey for the outer Galaxy covering the region
![]() .
In Sect. 2 observation and data processing details for this survey area are discussed. In Sect. 3 we present
the total power and polarization maps (Sect. 3.1), followed by a brief discussion on the survey's potential to study
and detect SNRs (Sect. 3.2) and H II
regions (Sect. 3.3), while in Sect. 3.4 we focus on newly
detected and prominent Faraday Screens in the interstellar medium.
Results are summarized in Sect. 4.
.
In Sect. 2 observation and data processing details for this survey area are discussed. In Sect. 3 we present
the total power and polarization maps (Sect. 3.1), followed by a brief discussion on the survey's potential to study
and detect SNRs (Sect. 3.2) and H II
regions (Sect. 3.3), while in Sect. 3.4 we focus on newly
detected and prominent Faraday Screens in the interstellar medium.
Results are summarized in Sect. 4.
2 Observations and data reduction
2.1 Observation set-up
The Sino-German ![]() 6 cm polarization survey of the Galactic plane was carried out with the 25-m Urumqi telescope.
The
6 cm polarization survey of the Galactic plane was carried out with the 25-m Urumqi telescope.
The ![]() 6 cm
system is a copy of an Effelsberg single-channel receiver and has a
system temperature of about 22 K when pointing to the zenith at
clear sky. The half-power beam
width (HPBW) of the telescope was
6 cm
system is a copy of an Effelsberg single-channel receiver and has a
system temperature of about 22 K when pointing to the zenith at
clear sky. The half-power beam
width (HPBW) of the telescope was
![]() .
Survey observations were exclusively made during clear sky at night
time. In ``broad band mode'' the centre frequency was 4800 MHz
with a bandwidth of 600 MHz, while in ``narrow band mode'' the
centre frequency was 4963 MHz with a bandwidth of 295 MHz.
``Narrow band mode'' was used to avoid contamination by the
geostationary Indian INSAT-satellites located at four positions in
southern and western directions, which emit strong signals below
frequencies of about 4810 MHz. Thus all observations close to the
satellite positions were made in ``narrow band mode'',
while the ``broad band mode'' was used for all other directions.
The survey region was limited at
.
Survey observations were exclusively made during clear sky at night
time. In ``broad band mode'' the centre frequency was 4800 MHz
with a bandwidth of 600 MHz, while in ``narrow band mode'' the
centre frequency was 4963 MHz with a bandwidth of 295 MHz.
``Narrow band mode'' was used to avoid contamination by the
geostationary Indian INSAT-satellites located at four positions in
southern and western directions, which emit strong signals below
frequencies of about 4810 MHz. Thus all observations close to the
satellite positions were made in ``narrow band mode'',
while the ``broad band mode'' was used for all other directions.
The survey region was limited at
![]() ,
because regions with larger
,
because regions with larger ![]() have to be observed at very low elevations, so that the increased
ground radiation can not be subtracted with sufficient accuracy.
Measurements of the ground radiation properties of the Urumqi 25-m
telescope at
have to be observed at very low elevations, so that the increased
ground radiation can not be subtracted with sufficient accuracy.
Measurements of the ground radiation properties of the Urumqi 25-m
telescope at ![]() 6 cm were already reported by Wang et al. (2007).
The main observational survey parameters are listed in Table 1.
6 cm were already reported by Wang et al. (2007).
The main observational survey parameters are listed in Table 1.
Survey maps were observed in two orthogonal directions: along ![]() and b. The combined survey consists of a large number of individual
8
and b. The combined survey consists of a large number of individual
8
![]() or
or
![]() maps observed in
maps observed in ![]() direction and of
direction and of
![]() or
or
![]() maps observed along b.
Total intensity, Stokes I, and the linearly polarized components, Stokes U and Q,
were measured simultaneously.
3C286 and 3C295 served as the main polarized and un-polarized
calibration sources, while 3C48 and 3C138 served as secondary
polarized calibrators. Calibration sources were always observed before
starting a survey map in the same observation mode.
maps observed along b.
Total intensity, Stokes I, and the linearly polarized components, Stokes U and Q,
were measured simultaneously.
3C286 and 3C295 served as the main polarized and un-polarized
calibration sources, while 3C48 and 3C138 served as secondary
polarized calibrators. Calibration sources were always observed before
starting a survey map in the same observation mode.
We increased the original scanning speed of the observations from
![]() /min to
/min to
![]() /min
after tests performed in 2006. The reason was to minimize the influence
of system instabilities and also the contamination by changing ground
radiation and low-level RFI. To achieve the same S/N ratio we thus
mapped the same region more often. The sensitivity is not unique
throughout the entire survey section, since the coverages of
/min
after tests performed in 2006. The reason was to minimize the influence
of system instabilities and also the contamination by changing ground
radiation and low-level RFI. To achieve the same S/N ratio we thus
mapped the same region more often. The sensitivity is not unique
throughout the entire survey section, since the coverages of ![]() and b
maps differ. The effective integration time of each map pixel is at
least 2.6 s for total intensity and 1.9 s for polarization,
where the integration time of map pixel observed in ``narrow band
mode'' were divided by a factor of 2 to be comparable with that of
``broad band mode''.
The effective integration time of each sub-region in Stokes I, U and Q for 600 MHz bandwidth is shown in Fig. 1.
and b
maps differ. The effective integration time of each map pixel is at
least 2.6 s for total intensity and 1.9 s for polarization,
where the integration time of map pixel observed in ``narrow band
mode'' were divided by a factor of 2 to be comparable with that of
``broad band mode''.
The effective integration time of each sub-region in Stokes I, U and Q for 600 MHz bandwidth is shown in Fig. 1.
Table 1: Observational parameters.
2.2 Data reduction
Data reduction was done following the standard procedures, which were
already described in Paper I. Subsequently the following steps are
applied: for total intensity I maps, a baseline was
appropriately fitted for each sub-scan, which implies that large-scale
diffuse emission exceeding the length of the sub-scans of
![]() or
or
![]() is not preserved. In addition,
spiky pixels were removed, distorted sub-scan sections or entire
sub-scans were set to dummy values or, for smooth regions, replaced by
interpolation of the two neighboring sub-scans. The baselines of the
Stokes U and Q maps were
usually not fitted in order to preserve extended polarized emission,
unless strong ground radiation at low elevations clearly contaminates
the data. Baseline distortion effects along scanning direction were
suppressed by the ``unsharp masking'' method (Sofue & Reich 1979). Spiky pixels and bad sub-scans were corrected in the same way as the I
maps.
We noted that afterwards many maps show residual distortions visible as
inclined stripes, which seem to be caused by RFI-sources of unknown
origin.
They were well removed by rotating the map that the stripes align to
rows or columns of the map to apply the ``unsharp masking'' procedure
and then rotating the map back.
is not preserved. In addition,
spiky pixels were removed, distorted sub-scan sections or entire
sub-scans were set to dummy values or, for smooth regions, replaced by
interpolation of the two neighboring sub-scans. The baselines of the
Stokes U and Q maps were
usually not fitted in order to preserve extended polarized emission,
unless strong ground radiation at low elevations clearly contaminates
the data. Baseline distortion effects along scanning direction were
suppressed by the ``unsharp masking'' method (Sofue & Reich 1979). Spiky pixels and bad sub-scans were corrected in the same way as the I
maps.
We noted that afterwards many maps show residual distortions visible as
inclined stripes, which seem to be caused by RFI-sources of unknown
origin.
They were well removed by rotating the map that the stripes align to
rows or columns of the map to apply the ``unsharp masking'' procedure
and then rotating the map back.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{13793fig1.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg48.png)
|
Figure 1: Distribution of effective integration time in sec for the survey sub-areas shown for Stokes I, U and Q from top to bottom. |
| Open with DEXTER | |
Total intensity and polarization calibration was based on 3C286 (see Table 1).
Instrumental polarization from strong sources was removed by the
``REBEAM'' procedure of the NOD2 package as described in Paper I.
This method reduces the ringlike instrumental response in polarized
intensity PI by about 50%,
which leaves some residual instrumental response of the order of 1%. Our sensitivity limit on average (3 ![]() rms) is 1.2 mK
rms) is 1.2 mK ![]() (or 7.3 mJy/beam). Only strong sources exceeding about 0.7 Jy
will show weak polarization response of instrumental origin, which
will, however, in most cases confuse with diffuse Galactic emission.
(or 7.3 mJy/beam). Only strong sources exceeding about 0.7 Jy
will show weak polarization response of instrumental origin, which
will, however, in most cases confuse with diffuse Galactic emission.
Compact sources of the NVSS catalogue (Condon et al. 1998) were used to check the position accuracy. Finally, all individually edited maps were combined by applying the ``PLAIT''-algorithm (Emerson & Gräve 1988), where the Fourier transforms of the maps were added and the final map is obtained by an inverse Fourier transform. ``PLAIT'', in addition, is able to suppress remaining low-level scanning effects still visible in a few individual maps.
2.3 Absolute zero-level restoration for Stokes U and Q
We have observed scans of up to 10
![]() in length aiming to recover extended structures as large as possible.
All maps have a relative zero-level by arbitrarily setting the edge values of each scan to zero. Total intensity maps
(Stokes I) always miss a positive
temperature offset, while the offsets for Stokes U and Q maps may be positive or negative. Polarized intensity, PI,
of unknown intensity originating from Faraday rotated diffuse emission
in the interstellar medium may exist everywhere and is not related to
total intensity. Thus the true zero-level of the observed U and Q
maps remains unknown. Therefore PI and the polarization angle, PA, as calculated from U and Q, need to be corrected as well.
We note that relative polarization zero-level setting may be done in different ways, e.g. setting the mean value of U and Q of each scan to
zero (Junkes et al. 1987). After we combined maps observed along
in length aiming to recover extended structures as large as possible.
All maps have a relative zero-level by arbitrarily setting the edge values of each scan to zero. Total intensity maps
(Stokes I) always miss a positive
temperature offset, while the offsets for Stokes U and Q maps may be positive or negative. Polarized intensity, PI,
of unknown intensity originating from Faraday rotated diffuse emission
in the interstellar medium may exist everywhere and is not related to
total intensity. Thus the true zero-level of the observed U and Q
maps remains unknown. Therefore PI and the polarization angle, PA, as calculated from U and Q, need to be corrected as well.
We note that relative polarization zero-level setting may be done in different ways, e.g. setting the mean value of U and Q of each scan to
zero (Junkes et al. 1987). After we combined maps observed along ![]() direction with maps along b direction, the edge areas of the final combined maps differ from zero.
direction with maps along b direction, the edge areas of the final combined maps differ from zero.
Since polarized components are vectors, a missing large-scale component may lead to a misinterpretation of the
observed data (Reich 2006).
This is in particular important for polarized emission resulting from
Faraday rotation, which clearly dominates the Galactic polarization
maps at ![]() 6 cm. In Paper I, Sun et al. (2007) already presented a solution for this problem by adopting the three-year K-band (22.8 GHz) polarization data from WMAP (Page et al. 2007), which have a correct zero-level. Missing large-scale U and Q emission at
6 cm. In Paper I, Sun et al. (2007) already presented a solution for this problem by adopting the three-year K-band (22.8 GHz) polarization data from WMAP (Page et al. 2007), which have a correct zero-level. Missing large-scale U and Q emission at ![]() 6 cm is restored by scaling the K-band data by
a factor of
(4.8/22.8)-2.8, according to a temperature spectral index of
6 cm is restored by scaling the K-band data by
a factor of
(4.8/22.8)-2.8, according to a temperature spectral index of
![]() .
This procedure also assumes that the RM of the diffuse emission is not significant.
.
This procedure also assumes that the RM of the diffuse emission is not significant.
For this second much larger section of the ![]() 6 cm polarization survey we slightly modified the method applied in Paper I
by taking meanwhile available additional information into account. We now use the five-year release of the WMAP observations
(Hinshaw et al. 2009). We calculated the spectral index distribution between the polarized emission at 1.4 GHz (Wolleben et al. 2006) and
the K-band data for the entire survey section, smoothed to a common angular resolution of 2
6 cm polarization survey we slightly modified the method applied in Paper I
by taking meanwhile available additional information into account. We now use the five-year release of the WMAP observations
(Hinshaw et al. 2009). We calculated the spectral index distribution between the polarized emission at 1.4 GHz (Wolleben et al. 2006) and
the K-band data for the entire survey section, smoothed to a common angular resolution of 2
![]() .
We obtained a mean
spectral index of
.
We obtained a mean
spectral index of
![]() .
We note that this spectral index is largely biased by the dominating
polarized emission from the bright Fan-region, which is Faraday thin at 1.4 GHz. This, however, is likely not the
case for the Galactic plane emission at 1.4 GHz from large distances. Current estimates of the synchrotron total
intensity spectrum quote very similar spectral values between 1.4 GHz and 23.8 GHz (see Dickinson et al. (2009)
for a recent discussion), which we expect to be valid for the
extrapolation of Faraday thin diffuse large-scale polarized emission
from 22.8 GHz to 4.8 GHz as well.
.
We note that this spectral index is largely biased by the dominating
polarized emission from the bright Fan-region, which is Faraday thin at 1.4 GHz. This, however, is likely not the
case for the Galactic plane emission at 1.4 GHz from large distances. Current estimates of the synchrotron total
intensity spectrum quote very similar spectral values between 1.4 GHz and 23.8 GHz (see Dickinson et al. (2009)
for a recent discussion), which we expect to be valid for the
extrapolation of Faraday thin diffuse large-scale polarized emission
from 22.8 GHz to 4.8 GHz as well.
We compared the WMAP K-band (22.8 GHz) and Ka-band (33 GHz) polarization data (Hinshaw et al. 2009) at 2
![]() angular
resolution for common extended polarization structures in the present
survey area. Clearly, the vast majority of patchy, weak polarization
features in the two WMAP maps were not correlated and thus do not
show patches of polarized emission. This in turn means that an
extrapolation of the polarized K-band emission towards
angular
resolution for common extended polarization structures in the present
survey area. Clearly, the vast majority of patchy, weak polarization
features in the two WMAP maps were not correlated and thus do not
show patches of polarized emission. This in turn means that an
extrapolation of the polarized K-band emission towards ![]() 6 cm becomes questionable as it might introduce spurious features specific to the K-band map.
Large-scale polarization gradients,
however, are common in the K-band and Ka-band maps. We therefore decided to convolve the
6 cm becomes questionable as it might introduce spurious features specific to the K-band map.
Large-scale polarization gradients,
however, are common in the K-band and Ka-band maps. We therefore decided to convolve the ![]() 6 cm U and Q survey maps and
the corresponding K-band maps to 2
6 cm U and Q survey maps and
the corresponding K-band maps to 2
![]() angular resolution after having removed a few strong and compact polarized sources. The
convolved maps were split into sections, scaled by a factor of
(4.8/22.8)-2.9 and the difference values in their corner areas
were determined. These difference values were used to define correction hyper planes in U and Q for each
angular resolution after having removed a few strong and compact polarized sources. The
convolved maps were split into sections, scaled by a factor of
(4.8/22.8)-2.9 and the difference values in their corner areas
were determined. These difference values were used to define correction hyper planes in U and Q for each ![]() 6 cm
survey section and were applied to the data at their original resolution. In Table 2 we list the U and Q
intensities of the Urumqi
observations and the corresponding scaled K-map values together with
the resulting correction values. The maximum error introduced by
assuming a constant spectral index of
6 cm
survey section and were applied to the data at their original resolution. In Table 2 we list the U and Q
intensities of the Urumqi
observations and the corresponding scaled K-map values together with
the resulting correction values. The maximum error introduced by
assuming a constant spectral index of
![]() will occur at
will occur at
![]() and is estimated to be about
and is estimated to be about ![]() 1.5 mK
1.5 mK ![]() in case the assumed spectral index varies by
in case the assumed spectral index varies by
![]() .
.
A significant RM will change the extrapolated corrections for U and Q, while PI remains unchanged. Numerous RMs from
extragalactic sources in the Galactic plane are available (Brown et al. 2007). On average high RM-values are observed in the surveyed area with
a clear gradient along ![]() ,
but also a significant scatter of RM is noted. However, it is known that the RM of diffuse polarized Galactic emission
in this area is small (Spoelstra 1984; Haverkorn et al. 2003b). We used the recent 3D-model of Galactic emissivities by Sun et al. (2008), which is in agreement
with observed RMs, to model the polarized emission distribution at 4.8 GHz and 22.8 GHz. The distribution of RM was obtained from the
PA maps at both frequencies. The RM map shows small values in general, as expected, and a nearly linear increase of RM from
,
but also a significant scatter of RM is noted. However, it is known that the RM of diffuse polarized Galactic emission
in this area is small (Spoelstra 1984; Haverkorn et al. 2003b). We used the recent 3D-model of Galactic emissivities by Sun et al. (2008), which is in agreement
with observed RMs, to model the polarized emission distribution at 4.8 GHz and 22.8 GHz. The distribution of RM was obtained from the
PA maps at both frequencies. The RM map shows small values in general, as expected, and a nearly linear increase of RM from
![]() to
230
to
230
![]() .
For
.
For
![]() ,
,
![]() and
and
![]() the simulations predict RM values of -18, -35 and -25 rad m-2.
For
the simulations predict RM values of -18, -35 and -25 rad m-2.
For
![]() the RM values are +31, +66 and +38 rad m-2, respectively. The simulations by Sun et al. (2008)
did not take into account the excessive polarized emission from the
so-called ``Fan''-region, a discrete very extended and highly polarized
structure, which clearly dominates the large-scale polarized emission
for
the RM values are +31, +66 and +38 rad m-2, respectively. The simulations by Sun et al. (2008)
did not take into account the excessive polarized emission from the
so-called ``Fan''-region, a discrete very extended and highly polarized
structure, which clearly dominates the large-scale polarized emission
for ![]() lower than about
lower than about
![]() .
The ``Fan''-region is known to have RMs very close to zero at low angular resolution (Spoelstra 1984). Thus no RM based correction for the low
.
The ``Fan''-region is known to have RMs very close to zero at low angular resolution (Spoelstra 1984). Thus no RM based correction for the low ![]() end of the observed area is necessary. The maximum RM of 66 rad m-2 at
end of the observed area is necessary. The maximum RM of 66 rad m-2 at
![]() means a PA change between 4.8 GHz and 22.8 GHz of 14
means a PA change between 4.8 GHz and 22.8 GHz of 14
![]() .
Such an angle difference
should be taken into account. However, the zero-level corrections for U and Q in this area (see Table 2) are below the
3
.
Such an angle difference
should be taken into account. However, the zero-level corrections for U and Q in this area (see Table 2) are below the
3 ![]() rms-noise in U and Q of the observations, so that we neglect the RM effect on the U and Q corrections.
rms-noise in U and Q of the observations, so that we neglect the RM effect on the U and Q corrections.
Table 2:
Hyper plane corrections in mK ![]() .
.
The effect of the zero-level restoration process is illustrated in Fig. 2 by comparing the distributions of PI and
PA before and after the large-scale correction. Both distributions are clearly changed. In particular, PA changed from an almost
uniform distribution between
![]() and
and
![]() into a distribution with a clear maximum for PA near 0
into a distribution with a clear maximum for PA near 0
![]() for the restored data, reflecting the fact that significant large-scale corrections are
required for Stokes Q, while U remains almost unchanged. This means that on large scales the magnetic field is orientated along
for the restored data, reflecting the fact that significant large-scale corrections are
required for Stokes Q, while U remains almost unchanged. This means that on large scales the magnetic field is orientated along ![]() (
(
![]() )
)![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm]{13793fig2a.ps}\par\includegraphics[angle=-90,width=7.88cm]{13793fig2b.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg63.png)
|
Figure 2: Pixel distribution for PI ( top) and PA ( bottom) before and after restoring missing large-scale structures extrapolated from WMAP K-band. Details are discussed in Sect. 2.3. |
| Open with DEXTER | |
3 Analysis of the survey region
Large-scale emission seen in the present ![]() 6 cm survey section originates from the local arm, the Perseus arm and probably an
outer arm (Hou et al. 2009). Also emission contributed from the inter-arm regions is possible. A large number of extended and compact sources are
also visible in the surveyed area. The total intensity I maps very well resemble the emission structures visible in surveys at longer wavelengths
with similar angular resolution, e.g. the Effelsberg surveys at
6 cm survey section originates from the local arm, the Perseus arm and probably an
outer arm (Hou et al. 2009). Also emission contributed from the inter-arm regions is possible. A large number of extended and compact sources are
also visible in the surveyed area. The total intensity I maps very well resemble the emission structures visible in surveys at longer wavelengths
with similar angular resolution, e.g. the Effelsberg surveys at ![]() 21 cm (Reich et al. 1997; Kallas & Reich 1980) and at
21 cm (Reich et al. 1997; Kallas & Reich 1980) and at ![]() 11 cm (Fürst et al. 1990).
The
11 cm (Fürst et al. 1990).
The ![]() 6 cm polarization data, however, show rather different structures compared to partly available Effelsberg
6 cm polarization data, however, show rather different structures compared to partly available Effelsberg ![]() 21 cm
survey data (Reich et al. 2004; Uyaniker et al. 1999) and are therefore of particular interest, so that we focus on them in the following.
21 cm
survey data (Reich et al. 2004; Uyaniker et al. 1999) and are therefore of particular interest, so that we focus on them in the following.
Compact or slightly resolved sources of the entire ![]() 6 cm Urumqi survey will be listed in a separate paper after completion
of the survey. Several prominent sources like the Cygnus Loop (Sun et al. 2006), OA184 (Foster et al. 2006), the SNRs G156.2+5.7 (Xu et al. 2007),
S147 (Xiao et al. 2008), HB3 (Shi et al. 2008b), and G65.2+5.7 (Xiao et al. 2009) were already studied in detail based on observations made with the
Urumqi
6 cm Urumqi survey will be listed in a separate paper after completion
of the survey. Several prominent sources like the Cygnus Loop (Sun et al. 2006), OA184 (Foster et al. 2006), the SNRs G156.2+5.7 (Xu et al. 2007),
S147 (Xiao et al. 2008), HB3 (Shi et al. 2008b), and G65.2+5.7 (Xiao et al. 2009) were already studied in detail based on observations made with the
Urumqi ![]() 6 cm system, which prove the high quality of the data.
Data of three newly identified H II regions from the present survey region were published by Shi et al. (2008a). We will present a discussion of other SNRs, H II-regions and prominent extended emission complexes in subsequent papers.
6 cm system, which prove the high quality of the data.
Data of three newly identified H II regions from the present survey region were published by Shi et al. (2008a). We will present a discussion of other SNRs, H II-regions and prominent extended emission complexes in subsequent papers.
3.1 The survey maps
We show the maps of the outer Galactic plane in four parts (Part 1 to Part 4) in Figs. 3 to 6. The maps have an overlap in ![]() of 1
of 1
![]() .
We show Stokes I, U and Q maps as observed with the Urumqi 25-m telescope.
In addition, we show maps of PI, which were calculated from the U and Q maps but with the large-scale hyper plane corrections as
discussed in Sect. 2.3. When calculating PI the correction for the positive noise offset:
.
We show Stokes I, U and Q maps as observed with the Urumqi 25-m telescope.
In addition, we show maps of PI, which were calculated from the U and Q maps but with the large-scale hyper plane corrections as
discussed in Sect. 2.3. When calculating PI the correction for the positive noise offset:
![]() (Wardle & Kronberg 1974)
was applied, where
(Wardle & Kronberg 1974)
was applied, where
![]() (see Table 1) is the averaged rms-noise for the U and Q maps for a specific survey area.
Polarization bars in B-field direction are overlaid on the PI
image. The bars indicate the magnetic field direction in case of small
Faraday rotation.
The sensitivity throughout the surveyed region varies slightly due to
different integration time for different parts as outlined in
Sect. 2.1 and Fig. 1. In addition
smaller
(see Table 1) is the averaged rms-noise for the U and Q maps for a specific survey area.
Polarization bars in B-field direction are overlaid on the PI
image. The bars indicate the magnetic field direction in case of small
Faraday rotation.
The sensitivity throughout the surveyed region varies slightly due to
different integration time for different parts as outlined in
Sect. 2.1 and Fig. 1. In addition
smaller ![]() sections have in general a higher sensitivity than areas with larger
sections have in general a higher sensitivity than areas with larger ![]() ,
because they benefit from both the ``broad band mode''
and less contamination by ground radiation.
,
because they benefit from both the ``broad band mode''
and less contamination by ground radiation.
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm]{13793-09-Copie/13793f...
...ncludegraphics[angle=-90, width=15cm]{13793-09-Copie/13793fig3d.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg66.png)
|
Figure 3:
Urumqi |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm]{13793fig4a.ps}\par\in...
...fig4c.ps}\par\includegraphics[angle=-90, width=15cm]{13793fig4d.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg67.png)
|
Figure 4:
Sequence and contours as in Fig. 3 for Part 2. Vectors are shown for PI exceeding 2.5 mK |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm]{13793fig5a.ps}\par\in...
...fig5c.ps}\par\includegraphics[angle=-90, width=15cm]{13793fig5d.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg68.png)
|
Figure 5:
Sequence and contours as in Fig. 3 for Part 3. Vectors are shown for PI exceeding 1.5 mK |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm]{13793fig6a.ps}\par\in...
...fig6c.ps}\par\includegraphics[angle=-90, width=15cm]{13793fig6d.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg69.png)
|
Figure 6:
Sequence and contours as in Fig. 3 for Part 4. Vectors are shown for PI exceeding 0.9 mK |
| Open with DEXTER | |
The survey maps and the compact source list will be made publicly available after completion of the
entire project via the MPIfR survey-sampler![]() , the webpage at the National Astronomical Observatories, CAS
, the webpage at the National Astronomical Observatories, CAS![]() and possibly other
data centres.
and possibly other
data centres.
3.2 Supernova Remnants (SNRs)
SNRs play an important role for many processes in the interstellar
medium, such as energy input, chemical enrichment of heavy elements,
cosmic ray production, and thus influence the evolution of galaxies.
Most Galactic SNRs are well studied at low radio frequencies, while
information about their fainter high-frequency emission is limited. The
polarization properties of many SNRs are not well studied at all.
Sensitive observations of large SNRs are quite time consuming for large
single-dish telescopes at high frequencies because of their small
beam-size and the low intensity of SNRs. Observations with
interferometers have even higher angular resolution but suffer from
missing large-scale components. Our ![]() 6 cm survey complements high-frequency total power and polarization data for numerous large diameter SNRs.
6 cm survey complements high-frequency total power and polarization data for numerous large diameter SNRs.
Eleven known SNRs according to the most recent SNR catalogue![]() (Green 2009) are all visible in the present survey region. Several individual studies of SNRs
based on the Urumqi
(Green 2009) are all visible in the present survey region. Several individual studies of SNRs
based on the Urumqi ![]() 6 cm survey were already published as mentioned above, more are in preparation.
The sources HB3, OA184, S147 and the small
bottom part of G156.2+5.7 are included in the present survey section. For the first time polarized emission at
6 cm survey were already published as mentioned above, more are in preparation.
The sources HB3, OA184, S147 and the small
bottom part of G156.2+5.7 are included in the present survey section. For the first time polarized emission at ![]() 6 cm
is seen for the SNRs HB9 (G160.9+2.6), VRO42.05.01 (G166.0+4.3),
the Monoceros Nebula (G205.5+0.9), and PKS0646+06 (G206.9+2.3).
6 cm
is seen for the SNRs HB9 (G160.9+2.6), VRO42.05.01 (G166.0+4.3),
the Monoceros Nebula (G205.5+0.9), and PKS0646+06 (G206.9+2.3).
So far we have not unambiguously detected any new SNRs. The surface brightness limit for a
SNR with a thick shell according to a 3![]() detection limit is about
detection limit is about
![]() ]
for a temperature spectral index of
]
for a temperature spectral index of
![]() .
This is lower than that of G156.2+5.7 (Reich et al. 1992), which has the lowest surface
brightness in the SNR catalogues.
.
This is lower than that of G156.2+5.7 (Reich et al. 1992), which has the lowest surface
brightness in the SNR catalogues.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm]{13793fig7a.ps}\par\incl...
...93fig7b.ps}\par\includegraphics[angle=-90,width=8cm]{13793fig7c.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg72.png)
|
Figure 7:
Upper plot shows the PI map of W5 in grey scale, overlaid by contours of I. The contour lines run from the local 3 |
| Open with DEXTER | |
As an example to show the potential of the Urumqi ![]() 6 cm survey for SNR research, we
discuss the SNR candidate G151.2+2.85, which
was proposed by Kerton et al. (2007) based on a steep temperature spectrum (
6 cm survey for SNR research, we
discuss the SNR candidate G151.2+2.85, which
was proposed by Kerton et al. (2007) based on a steep temperature spectrum (
![]() )
of the filamentary structures designated CGPSE 172 and 168 (see their Fig. 5), which are clearly visible at 408 MHz and 1420 MHz in the CGPS (Taylor et al. 2003).
These two filamentary structures are aligned and about 1
)
of the filamentary structures designated CGPSE 172 and 168 (see their Fig. 5), which are clearly visible at 408 MHz and 1420 MHz in the CGPS (Taylor et al. 2003).
These two filamentary structures are aligned and about 1
![]() long in total. Both filaments are seen in the
long in total. Both filaments are seen in the
![]() 6 cm survey and the Effelsberg survey at
6 cm survey and the Effelsberg survey at ![]() 11 cm (Fürst et al. 1990) and
11 cm (Fürst et al. 1990) and ![]() 21 cm (Reich et al. 1997). From a TT-plot of
21 cm (Reich et al. 1997). From a TT-plot of ![]() 6 cm versus
6 cm versus
![]() 21 cm data we obtained temperature spectral indices of
21 cm data we obtained temperature spectral indices of
![]() and
and
![]() for CGPSE 172 and 168,
respectively, larger than those of Kerton et al. (2007). These results clearly confirm the non-thermal nature of these filaments
and support the suggestion by Kerton et al. (2007) that the filaments are part of a SNR shell. However, like Kerton et al. (2007)
we can not give the entire size and integrated flux density of the SNR
shell, because outside the filaments any SNR related emission is too
faint, so that it confuses with unrelated Galactic emission. Additional
observations, in particular outside of the radio range, are required to
trace this object.
for CGPSE 172 and 168,
respectively, larger than those of Kerton et al. (2007). These results clearly confirm the non-thermal nature of these filaments
and support the suggestion by Kerton et al. (2007) that the filaments are part of a SNR shell. However, like Kerton et al. (2007)
we can not give the entire size and integrated flux density of the SNR
shell, because outside the filaments any SNR related emission is too
faint, so that it confuses with unrelated Galactic emission. Additional
observations, in particular outside of the radio range, are required to
trace this object.
3.3 H II regions
Despite of numerous H II region catalogues, in particular that compiled by Paladini et al. (2003), there
are many more H II regions to be detected and their physical parameters to be determined. In this survey region many large H II regions have been detected.
At ![]() 6 cm the non-thermal to thermal emission
ratio is lower than that at longer wavelengths, so that the detection or isolation of H II
regions from diffuse Galactic non-thermal emission including survey
data at longer wavelengths in the analysis can be done more easily. We
have carefully analyzed the maps and searched for sources with flat
spectra and strong infrared emission and found several compact and
extended H II regions,
previously not catalogued. We also noted that many H II
regions have not well defined parameters, which we are able to improve
based on the new radio data. The results of this analysis will be
presented in a forthcoming paper.
6 cm the non-thermal to thermal emission
ratio is lower than that at longer wavelengths, so that the detection or isolation of H II
regions from diffuse Galactic non-thermal emission including survey
data at longer wavelengths in the analysis can be done more easily. We
have carefully analyzed the maps and searched for sources with flat
spectra and strong infrared emission and found several compact and
extended H II regions,
previously not catalogued. We also noted that many H II
regions have not well defined parameters, which we are able to improve
based on the new radio data. The results of this analysis will be
presented in a forthcoming paper.
3.4 Prominent Faraday Screens
Faraday Screens are magnetized interstellar objects, which do not
emit synchrotron emission themselves, but contain a regular magnetic
field and thermal electrons causing Faraday rotation. Depending on
their physical parameters, Faraday Screens depolarize and rotate
polarized background emission, which is observed together with the
polarized foreground emission. The observed polarized emission
surrounding a Faraday Screen may be either higher or lower than that
seen in the Faraday Screen direction, depending on its RM and on the properties of the foreground and background components. Faraday Screens become visible as coherent structures in
PI and/or PA maps compared to the diffuse polarized Galactic emission. A proper analysis of Faraday Screens requires the inclusion
of polarized structures on all scales. Faraday Screens were already discussed and analyzed in various earlier papers e.g. Wolleben & Reich (2004), Reich (2006), - Paper I.
Of particular interest are Faraday Screens detected in the ![]() 6 cm polarization survey maps, since they have larger RMs than those at
6 cm polarization survey maps, since they have larger RMs than those at ![]() 11 cm or
11 cm or ![]() 21 cm,
which might indicate regular magnetic fields with significant strength depending on their thermal electron densities and sizes.
If PA is rotated by 180
21 cm,
which might indicate regular magnetic fields with significant strength depending on their thermal electron densities and sizes.
If PA is rotated by 180
![]() by a Faraday Screen the background remains unchanged except for beam depolarization. This corresponds to a RM exceeding about 70 rad m-2 at
by a Faraday Screen the background remains unchanged except for beam depolarization. This corresponds to a RM exceeding about 70 rad m-2 at ![]() 21 cm or 260 rad m-2 at
21 cm or 260 rad m-2 at ![]() 11 cm, but about 800 rad m-2 at
11 cm, but about 800 rad m-2 at ![]() 6 cm.
The visibility of Faraday Screens in total intensity just depends on
their thermal electron density. Thus we do not distinguish between H II regions and Faraday Screens with no counterpart in total intensity or H
6 cm.
The visibility of Faraday Screens in total intensity just depends on
their thermal electron density. Thus we do not distinguish between H II regions and Faraday Screens with no counterpart in total intensity or H![]() in the following.
in the following.
3.4.1 Modeling Faraday Screens
A simple model to derive the physical parameters of a Faraday Screen
was already introduced in Paper I. The model uses two observed
components, marked as ``![]() '' and ``
'' and ``![]() '', where ``
'', where ``![]() '' is for the position where the line of sight passes the Faraday Screen. Through fitting the Faraday Screen parameters
by the observed data, the RM and the depolarization properties of a Faraday Screen can be derived.
The polarized background emission,
'' is for the position where the line of sight passes the Faraday Screen. Through fitting the Faraday Screen parameters
by the observed data, the RM and the depolarization properties of a Faraday Screen can be derived.
The polarized background emission,
![]() ,
is the component
originating at larger distances than the Faraday Screen, and the polarized foreground emission,
,
is the component
originating at larger distances than the Faraday Screen, and the polarized foreground emission,
![]() ,
originates in front of the Faraday Screen. The observed ``
,
originates in front of the Faraday Screen. The observed ``![]() ''
component is simply the combined polarized background and foreground emission, while the ``
''
component is simply the combined polarized background and foreground emission, while the ``![]() '' component is the polarized foreground emission
plus the modulated polarized background emission by the Faraday Screen. We assume both components are smooth and have the same PAfor the ``
'' component is the polarized foreground emission
plus the modulated polarized background emission by the Faraday Screen. We assume both components are smooth and have the same PAfor the ``![]() '' and ``
'' and ``![]() '' components. The equations below describe the model, details can be found in Paper I.
'' components. The equations below describe the model, details can be found in Paper I.
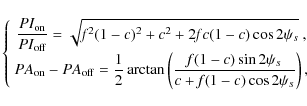
|
(1) |
here
Note that the model assumes that the PAs of the background and foreground emission are in general the same, because the dominating large-scale magnetic
field is oriented along the Galactic plane. A model which takes into account different PAs for foreground and background emission was presented
by Wolleben & Reich (2004), which, however, at least needs observations at two wavelengths. The equations above show the dependence of the observed
![]() and
and
![]() ,
the
,
the
![]() and the
and the
![]() from the modeled foreground
from the modeled foreground
![]() and
background
and
background
![]() emission components and the Faraday rotation angle
emission components and the Faraday rotation angle
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793fig8.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg90.png)
|
Figure 8:
Averaged observed values for the low-latitude W5 blob with centre coordinate (
|
| Open with DEXTER | |
Here,
![]() [rad m-2] = 0.81
[rad m-2] = 0.81 ![]() [cm
[cm
![]() G] l[pc], with
G] l[pc], with ![]() being the thermal electron density,
being the thermal electron density,
![]() the field strength of the line-of-sight component of the regular magnetic field and l
the line-of-sight length of the Faraday Screen. The size of the source
is usually assumed to be that seen in projection. In case the Faraday
Screen has measurable thermal emission,
the field strength of the line-of-sight component of the regular magnetic field and l
the line-of-sight length of the Faraday Screen. The size of the source
is usually assumed to be that seen in projection. In case the Faraday
Screen has measurable thermal emission, ![]() can be calculated from the emission measure (EM),
which is defined as
can be calculated from the emission measure (EM),
which is defined as
![]() .
For an optically thin H II region, the observed brightness temperature
.
For an optically thin H II region, the observed brightness temperature ![]() depends on EM,
depends on EM,
where the correction a(
![\begin{displaymath}EM = 2.75\ T_{4}^{0.9}I_{\rm H\alpha}\exp\ [2.44E(B-V)].
\end{displaymath}](/articles/aa/full_html/2010/07/aa13793-09/img97.png)
|
(3) |
Precise reddening measurements are difficult to obtain.
Prominent extended Faraday Screens seen in this survey section were
selected for discussion in the following in order of their ![]() .
.
3.4.2 W5 (
 )
and the ``lens'' Faraday Screen
)
and the ``lens'' Faraday Screen
W3/W4/W5 are prominent H II regions forming a chain together with the SNR HB3 in the Perseus arm about 2 kpc away. Gray et al. (1999) used the DRAO Synthesis Telescope and obtained 1
![]() resolution radio images of both total intensity and polarized emission
of this field at 1.4 GHz. We limit our discussion to W5 in the
following. At
resolution radio images of both total intensity and polarized emission
of this field at 1.4 GHz. We limit our discussion to W5 in the
following. At ![]() 6 cm PI in this area (Fig. 7) appears to be depolarized by a different amount and the distribution is mottled for our
6 cm PI in this area (Fig. 7) appears to be depolarized by a different amount and the distribution is mottled for our
![]() beam, although we see less fine structures when compared to the 1.4 GHz map of Gray et al. (1999).
beam, although we see less fine structures when compared to the 1.4 GHz map of Gray et al. (1999).
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793fig9.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg99.png)
|
Figure 9:
PA distribution in B-field direction for the ``drumstick'' area. I contours start at 1.5 mK |
| Open with DEXTER | |
Heiles (2000) compiled a catalogue of polarized stars and lists nine of them in the vicinity of W5. We calculated a mean
![]() up to the largest distance of 3.6 kpc, where PA runs counter-clockwise with the Galactic plane as reference. The alignment of PA around 0
up to the largest distance of 3.6 kpc, where PA runs counter-clockwise with the Galactic plane as reference. The alignment of PA around 0
![]() means that the magnetic field is orientated along the Galactic plane
for all distances and thus confirms the assumption of our Faraday
Screen-model. The
means that the magnetic field is orientated along the Galactic plane
for all distances and thus confirms the assumption of our Faraday
Screen-model. The ![]() 6 cm PAs in the W5 area, however, vary (Fig. 7) and mottled depolarization is also visible, which is explained by Faraday rotation of different amount.
6 cm PAs in the W5 area, however, vary (Fig. 7) and mottled depolarization is also visible, which is explained by Faraday rotation of different amount.
Westerhout (1958) listed some physical parameters of W5 such as EM = 4000 pc cm-6 and
![]() .
From the
.
From the ![]() 6 cm brightness temperature of W5 West of about 380 mK
6 cm brightness temperature of W5 West of about 380 mK ![]() ,
we calculated
a comparable EM value of 2900 pc cm-6 according to Eq. (2). In addition the H
,
we calculated
a comparable EM value of 2900 pc cm-6 according to Eq. (2). In addition the H![]() intensity of W5 can be extracted
from the H
intensity of W5 can be extracted
from the H![]() full sky map (Finkbeiner 2003) to be about 300 Rayleigh. A reddening measurement of the exciting star
full sky map (Finkbeiner 2003) to be about 300 Rayleigh. A reddening measurement of the exciting star
![]() ,
also named Hilt 360 (Hiltner 1956), gives an E(B-V) factor of 0.63. Following Eq. (3), EM can be estimated
to be 3140 pc cm-6, slightly above the radio-based result.
,
also named Hilt 360 (Hiltner 1956), gives an E(B-V) factor of 0.63. Following Eq. (3), EM can be estimated
to be 3140 pc cm-6, slightly above the radio-based result.
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig10.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg104.png)
|
Figure 10:
Average values in northern direction for the H II region LBN 676. Offsets are relative to the centre
coordinate (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig11.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg106.png)
|
Figure 11:
Average values starting from the coordinate (
|
| Open with DEXTER | |
If we take
![]() G as assumed by Gray et al. (1998) as the strength of the line-of-sight component of the regular
magnetic field within W5, the expected
G as assumed by Gray et al. (1998) as the strength of the line-of-sight component of the regular
magnetic field within W5, the expected
![]() value is about 970 rad m-2 for a size of 40 pc and for
value is about 970 rad m-2 for a size of 40 pc and for ![]() about
10 cm-3 (Westerhout 1958). This predicts about 217
about
10 cm-3 (Westerhout 1958). This predicts about 217
![]() for
for ![]() at
at ![]() 6 cm.
6 cm.
W5 is a large object, where the foreground polarization fraction c may vary across the source.
For
c = 0.7, 0.8, and 0.9, and assuming
![]() and
and ![]() to be uniform, we calculate
to be uniform, we calculate
![]() and
and
![]() for the Faraday Screen. As an example, we model
for the Faraday Screen. As an example, we model
![]() for the fairly uniform W5 East area for an average brightness temperature of about 270 mK
for the fairly uniform W5 East area for an average brightness temperature of about 270 mK ![]() and a size of
and a size of
![]() corresponding to 24 pc for 2 kpc distance. With c = 0.79 we calculate
corresponding to 24 pc for 2 kpc distance. With c = 0.79 we calculate
![]() rad m-2, which is
much smaller than the value estimated for W5 above. This indicates that
rad m-2, which is
much smaller than the value estimated for W5 above. This indicates that
![]() is about 1.5
is about 1.5 ![]() G and
G and ![]() about 9.2 cm-3 within W5 East.
about 9.2 cm-3 within W5 East.
Two remarkable polarization features are clearly visible at the edges of W5 in the ![]() 6 cm polarization map
(Fig. 7) at
6 cm polarization map
(Fig. 7) at
![]() and at
and at
![]() ,
which resemble Faraday Screens detected at the edges of molecular clouds by Wolleben & Reich (2004).
We apply the model fit to the eastern blob.
The problem is that we can not definitely decide from single-wavelength data whether
,
which resemble Faraday Screens detected at the edges of molecular clouds by Wolleben & Reich (2004).
We apply the model fit to the eastern blob.
The problem is that we can not definitely decide from single-wavelength data whether
![]() is
positive or negative, since the absolute values are very similar. We either obtain
is
positive or negative, since the absolute values are very similar. We either obtain
![]() rad m-2for c = 0.30 and
rad m-2for c = 0.30 and
![]() or
or
![]() rad m-2 for c = 0.60 and
rad m-2 for c = 0.60 and
![]() .
We show the averaged observed values and the fitted RMs in Fig. 8. If the blob is a Perseus arm object like W5, a positive
.
We show the averaged observed values and the fitted RMs in Fig. 8. If the blob is a Perseus arm object like W5, a positive
![]() is preferred, because of the larger c value. Brown et al. (2003b) examined the RM values of extragalactic sources and pulsars in the direction of
is preferred, because of the larger c value. Brown et al. (2003b) examined the RM values of extragalactic sources and pulsars in the direction of
![]() within the Galactic plane and found that most values are negative. However, Mitra et al. (2003) showed a schematic model (their Fig. 5) that the curvature of the magnetic field lines near H II regions may result in a reverse RM sign. Assuming 2 kpc distance the first three pixels give an average
within the Galactic plane and found that most values are negative. However, Mitra et al. (2003) showed a schematic model (their Fig. 5) that the curvature of the magnetic field lines near H II regions may result in a reverse RM sign. Assuming 2 kpc distance the first three pixels give an average ![]() of about 4.7 cm-3 assuming a blob-size of 10.5 pc, and
of about 4.7 cm-3 assuming a blob-size of 10.5 pc, and
![]() is about 8.8
is about 8.8 ![]() G.
These parameters clearly differ from the average values obtained
for W5. Of course, we could not entirely rule out a projection
effect, so that these blobs are seen at the periphery of W5 by
chance.
G.
These parameters clearly differ from the average values obtained
for W5. Of course, we could not entirely rule out a projection
effect, so that these blobs are seen at the periphery of W5 by
chance.
Table 3: Physical parameters for three LBNe.
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig12.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg123.png)
|
Figure 12:
Half ring average values from centre coordinate (
|
| Open with DEXTER | |
Wolleben & Reich (2004) discovered line-of-sight magnetic field components exceeding 20 ![]() G at the surface of the local
Taurus molecular clouds, which is morphologically quite similar to the W5 polarization blobs seen at
G at the surface of the local
Taurus molecular clouds, which is morphologically quite similar to the W5 polarization blobs seen at ![]() 6 cm.
Note that the uncertainty of the line-of-sight size of the Faraday Screen plays an important role in determining
6 cm.
Note that the uncertainty of the line-of-sight size of the Faraday Screen plays an important role in determining
![]() and
and ![]() .
A tube-like shaped Faraday Screen would reduce the values of
.
A tube-like shaped Faraday Screen would reduce the values of
![]() and
and ![]() .
To precisely constrain such high RM values, observations at even shorter wavelengths than
.
To precisely constrain such high RM values, observations at even shorter wavelengths than ![]() 6 cm
are needed, which are, however, difficult to do.
6 cm
are needed, which are, however, difficult to do.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig13.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg124.png)
|
Figure 13:
PI of the Faraday Screen G146.4-3.0 in grey scale. I contours are overlaid running from 3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig14.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg125.png)
|
Figure 14: Ring averaged data and modeled RMs for Faraday Screen G146.4-3.0 shown in Fig. 13. |
| Open with DEXTER | |
An elliptical polarized ``lens'' structure was reported by Gray et al. (1998) seen towards the central part of W5 at 1.4 GHz.
This elliptical structure was also observed by Uyaniker (2004) at the same frequency using the Effelsberg 100-m telescope.
Our ![]() 6 cm polarization data (Fig. 7), however, does not show such kind of regular Faraday Screen feature.
Gray et al. (1998) quote a
6 cm polarization data (Fig. 7), however, does not show such kind of regular Faraday Screen feature.
Gray et al. (1998) quote a ![]() of 110 rad m-2, which should have an effect at
of 110 rad m-2, which should have an effect at ![]() 6 cm. However, the new 1.4 GHz polarization survey by Landecker et al. (2010),
which includes large-scale polarization information, reduces the RM attributed to the ``lens'' by about a factor of 10, which makes the ``lens'' almost invisible at
6 cm. However, the new 1.4 GHz polarization survey by Landecker et al. (2010),
which includes large-scale polarization information, reduces the RM attributed to the ``lens'' by about a factor of 10, which makes the ``lens'' almost invisible at ![]() 6 cm.
6 cm.
3.4.3 The ``Drumstick'' at

Several H II regions are located around
![]() within a
within a
![]() field (Fig. 9).
Unfortunately, no information of the H II regions was given in the catalogue of Paladini et al. (2003). Three faint optically
visible H II regions of the Lynds catalogue are: the semi-ring shaped LBN 676 (
field (Fig. 9).
Unfortunately, no information of the H II regions was given in the catalogue of Paladini et al. (2003). Three faint optically
visible H II regions of the Lynds catalogue are: the semi-ring shaped LBN 676 (
![]() )
with a
size of
)
with a
size of
![]() ,
LBN 677 (SH 2-202) (
,
LBN 677 (SH 2-202) (
![]() ,
size of
,
size of
![]() ), and the bar-like shaped LBN 679
(
), and the bar-like shaped LBN 679
(
![]() ,
size of
,
size of
![]() ). For morphology reasons we name the three H II regions the ``Drumstick''
in the following.
). For morphology reasons we name the three H II regions the ``Drumstick''
in the following.
LBN 676 and LBN 679 are supposed to be at the same distance in the Perseus arm. They were already investigated in some detail by Green (1989) using DRAO Synthesis Telescope data at 408 MHz and discussed together with infrared and H I maps. Green (1989) found that the elongated H II region LBN 679 coincides with a large H I spur located in the Perseus arm and pointed out that it is a thermal rather than a non-thermal feature as suggested by Kallas (1983).
Karr & Martin (2003) studied all three H II regions with 1
![]() resolution using CGPS data at 1.4 GHz (Taylor et al. 2003). The thermal character of LBN 679 was again confirmed and in addition they derived a thermal spectrum with
resolution using CGPS data at 1.4 GHz (Taylor et al. 2003). The thermal character of LBN 679 was again confirmed and in addition they derived a thermal spectrum with
![]() for LBN 676, thus excluding
a possible SNR identification considered by Green (1989) for this shell structure. The
for LBN 676, thus excluding
a possible SNR identification considered by Green (1989) for this shell structure. The ![]() 6 cm data agree with
the thermal properties of all objects through a check of their temperature spectral indices via TT-plots using Effelsberg
6 cm data agree with
the thermal properties of all objects through a check of their temperature spectral indices via TT-plots using Effelsberg ![]() 21 cm data for comparison.
21 cm data for comparison.
All three LBNe appear to be depolarized at ![]() 6 cm when large-scale polarized emission is added. Estimates of the magnetic field strength from modeled
6 cm when large-scale polarized emission is added. Estimates of the magnetic field strength from modeled
![]() require the thermal radio continuum brightness temperature to find their EM. For a known distance the source size and
require the thermal radio continuum brightness temperature to find their EM. For a known distance the source size and ![]() need to be calculated in addition. Green (1989)
assumed that LBN 676 and LBN 679 are both at a distance of
3 kpc in the Perseus arm. However, the Perseus arm distance was
revised by Xu et al. (2006) to be about 2 kpc by triangulation of W3OH, which is just about 7
need to be calculated in addition. Green (1989)
assumed that LBN 676 and LBN 679 are both at a distance of
3 kpc in the Perseus arm. However, the Perseus arm distance was
revised by Xu et al. (2006) to be about 2 kpc by triangulation of W3OH, which is just about 7
![]() apart in Galactic longitude. In the following we adopt this distance.
apart in Galactic longitude. In the following we adopt this distance.
It turns out that a ring average of the PA/PI differences for
LBN 676 is difficult to perform because of confusion with
LBN 677 emission. Thus we just take the data from the upper part.
The model fit gives the best result (Fig. 10) for the first five pixels as
![]() rad m-2. Foreground polarized
emission comprises about 79% while
rad m-2. Foreground polarized
emission comprises about 79% while
![]() .
Likely most of the polarized emission originates in the local arm. The
total intensity attributed to LBN 676 is about 50 mK
.
Likely most of the polarized emission originates in the local arm. The
total intensity attributed to LBN 676 is about 50 mK ![]() at
at ![]() 6 cm. An apparent diameter of
6 cm. An apparent diameter of
![]() equals to a path length of 28 pc for 2 kpc distance. We obtain
equals to a path length of 28 pc for 2 kpc distance. We obtain ![]() as about 3.3 cm-3 and
as about 3.3 cm-3 and
![]()
![]() G.
G.
In the southern part of the 2
![]() long filamentary LBN 679, we find large PA changes and also in its outskirts beyond.
There is an inclined elongated PA structure, about 1
long filamentary LBN 679, we find large PA changes and also in its outskirts beyond.
There is an inclined elongated PA structure, about 1
![]() long, running from northeast to southwest. Model fitting (Fig. 11) is done for a 35
long, running from northeast to southwest. Model fitting (Fig. 11) is done for a 35
![]() wide cone in south-western direction of the rim. Best fit for the first ten pixels gives
wide cone in south-western direction of the rim. Best fit for the first ten pixels gives
![]() rad m-2, a foreground polarization fraction of about 60% for
rad m-2, a foreground polarization fraction of about 60% for
![]() .
From the
.
From the ![]() 6 cm brightness temperature
of about 40 mK
6 cm brightness temperature
of about 40 mK ![]() and assuming a line-of-sight length of the source of 35 pc, we calculated
and assuming a line-of-sight length of the source of 35 pc, we calculated
![]() G and
G and
![]() cm-3.
To the lower left direction of LBN 679, another PA structure is located at about
cm-3.
To the lower left direction of LBN 679, another PA structure is located at about
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig15.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg143.png)
|
Figure 15:
Dependence of the central
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig16.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg144.png)
|
Figure 16:
U map at |
| Open with DEXTER | |
Karr & Martin (2003) found that the northern
part of LBN 677 is associated with the exciting star HD 19820
at 1 kpc distance. 0.8 kpc distance
were quoted for associated CO-emission (Blitz et al. 1982),
which we adopt in the following discussion. A circular average is
difficult to apply to the large area of LBN 677 due to significant
variations and the non-symmetric distribution of PA. Different signs of PA in different areas indicate changing properties throughout the entire region.
We select the western part of LBN 677, where PA changes smoothly for modeling. Based on the central five pixels average, the best fit (Fig. 12) gives a
![]() value of
value of
![]() rad m-2. 69% of the total polarized emission originates in the foreground. The depolarization factor is
rad m-2. 69% of the total polarized emission originates in the foreground. The depolarization factor is
![]() .
The 2
.
The 2
![]() diameter source gives a depth of 28 pc assuming a spherical shape. With the
diameter source gives a depth of 28 pc assuming a spherical shape. With the ![]() 6 cm brightness temperature of about 20 mK
6 cm brightness temperature of about 20 mK ![]() we calculate EM = 137 pc cm-6.
we calculate EM = 137 pc cm-6.
![]() then is
then is ![]() G and
G and ![]() about 2.2 cm-3.
The reddening measurement of the exciting star HD 19820 (
about 2.2 cm-3.
The reddening measurement of the exciting star HD 19820 (
![]() )
is about 0.82 (Hiltner 1956). The H
)
is about 0.82 (Hiltner 1956). The H![]() intensity is about
14 Rayleigh (Finkbeiner 2003) after subtracting a background level of 11 Rayleigh. We obtain EM as 233 pc cm-6 by Eq. (3).
Then
intensity is about
14 Rayleigh (Finkbeiner 2003) after subtracting a background level of 11 Rayleigh. We obtain EM as 233 pc cm-6 by Eq. (3).
Then
![]() reduces to
reduces to ![]() G and
G and ![]() increases to 2.9 cm-3. The physical parameters from both methods are similar. The best fit of
increases to 2.9 cm-3. The physical parameters from both methods are similar. The best fit of
![]() for LBN 676 and LBN 679 is around 70%. We found almost the
same value also for LBN 677, which is unexpected in view of their
different distances. If the polarized emissivity in this direction is
fairly constant, this may indicate that LBN 677 is also at about
2 kpc distance.
For this distance
for LBN 676 and LBN 679 is around 70%. We found almost the
same value also for LBN 677, which is unexpected in view of their
different distances. If the polarized emissivity in this direction is
fairly constant, this may indicate that LBN 677 is also at about
2 kpc distance.
For this distance
![]() will change to
will change to ![]() G and
G and ![]() to 1.4 cm-3.
to 1.4 cm-3.
We summarize the derived parameters for the three LBNe in Table 3. We note that our modeled
![]() are rather similar to those found for
H II regions with a similar low electron density, e.g. S264 (Heiles et al. 1981) and G124.9+0.1 (Paper I).
are rather similar to those found for
H II regions with a similar low electron density, e.g. S264 (Heiles et al. 1981) and G124.9+0.1 (Paper I).
Besides the three LBN objects there are more ![]() 6 cm Faraday Screen structures in the field of Fig. 9. Some were listed below,
which we, however, will not analyze in detail in this paper. A large area with very uniform PAs, which deviate about 22
6 cm Faraday Screen structures in the field of Fig. 9. Some were listed below,
which we, however, will not analyze in detail in this paper. A large area with very uniform PAs, which deviate about 22
![]() from the Galactic plane direction, can be identified in southwestern
direction of the ``drumstick''. This Faraday Screen is centered at
around
from the Galactic plane direction, can be identified in southwestern
direction of the ``drumstick''. This Faraday Screen is centered at
around
![]() .
There is no counterpart in the I map (see Fig. 9), thus the thermal electron density must be very low. Polarization observations at other wavelengths are needed to analyze
this feature in some detail. Also the small objects at
.
There is no counterpart in the I map (see Fig. 9), thus the thermal electron density must be very low. Polarization observations at other wavelengths are needed to analyze
this feature in some detail. Also the small objects at
![]() and at
and at
![]() were found to be thermal (Gao et al., in prep.) and act as Faraday Screens. They also can be clearly identified in the PA map (Fig. 9).
were found to be thermal (Gao et al., in prep.) and act as Faraday Screens. They also can be clearly identified in the PA map (Fig. 9).
3.4.4 G146.4-3.0
G146.4-3.0 is a large Faraday Screen with a diameter of approximately
![]() ,
centered at
,
centered at
![]() .
This structure shows highly polarized emission in the original PI map at
.
This structure shows highly polarized emission in the original PI map at ![]() 6 cm and becomes depolarized after large-scale polarized emission is added. No counterpart can be found in the I map (see Fig. 13). The H
6 cm and becomes depolarized after large-scale polarized emission is added. No counterpart can be found in the I map (see Fig. 13). The H![]() intensity in this region is in general low and does not show any excess related to this Faraday Screen.
intensity in this region is in general low and does not show any excess related to this Faraday Screen.
A Faraday Screen model fit (Fig. 14) results in an average
![]() for the central area of 1
for the central area of 1
![]() diameter of -
diameter of -![]() 20 rad m-2.
26% of total PI in this area originates in front of the Faraday Screen for
20 rad m-2.
26% of total PI in this area originates in front of the Faraday Screen for
![]() .
The RM value is
not exceptionally high, but the scatter across the Faraday Screen is large enough to make the object invisible in the
.
The RM value is
not exceptionally high, but the scatter across the Faraday Screen is large enough to make the object invisible in the ![]() 21 cm polarization
survey by Landecker et al. (2010),
although their survey only covers the northern area of the Faraday Screen.
21 cm polarization
survey by Landecker et al. (2010),
although their survey only covers the northern area of the Faraday Screen.
The distance to this prominent Faraday Screen in the ![]() 6 cm survey is not clear. To derive
6 cm survey is not clear. To derive ![]() by its
free-free EM we used the 3
by its
free-free EM we used the 3![]() level of the
level of the ![]() 6 cm I map, means about 1.5 mK
6 cm I map, means about 1.5 mK ![]() ,
as a brightness temperature upper limit.
The fitted central
,
as a brightness temperature upper limit.
The fitted central
![]() and
and ![]() are estimated and shown in Fig. 15 as a function of distance.
Note that
are estimated and shown in Fig. 15 as a function of distance.
Note that ![]() is always an upper limit, while
is always an upper limit, while
![]() has to be taken as minimum.
has to be taken as minimum.
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig17.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg158.png)
|
Figure 17:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichi...
...e=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig18b.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg159.png)
|
Figure 18: Upper plot shows I, PA and PI averaged in the vertical rectangle region marked in Fig. 17, where data are averaged in columns. The vertical dashed lines mark the boundary of the highly polarized emission region. The lower plot shows the results when averaging in the horizontal rectangle in Fig. 17. |
| Open with DEXTER | |
The foreground polarized emission of about 26% is small compared to the fraction of about 70%
obtained for the LBNe in the Perseus arm (see Sect. 3.4.3). Thus the distance to G146.4-3.0 should be small.
Assuming the polarized emissivity along the line of sight to be the same as to the Perseus LBNe of about 3.4 mK kpc-1,
we estimate the distance to Faraday Screen G146.4-3.0 as about
690 pc, which implies a diameter of the Faraday Screen of about
40 pc. Then
![]() for its central area is about
for its central area is about ![]() G and
G and ![]() is about 0.5 cm-3.
However, the local emissivity is known to be two to three times larger than the average emissivity at 2 kpc distance (Fleishman & Tokarev 1995).
This will reduce the distance and the size of the Faraday Screen accordingly. For a distance of 280 pc, its size reduces
to about 16 pc,
is about 0.5 cm-3.
However, the local emissivity is known to be two to three times larger than the average emissivity at 2 kpc distance (Fleishman & Tokarev 1995).
This will reduce the distance and the size of the Faraday Screen accordingly. For a distance of 280 pc, its size reduces
to about 16 pc, ![]() increases to about 0.8 cm-3 and
increases to about 0.8 cm-3 and
![]() to
to ![]() G.
G.
Taylor et al. (2009) re-analyzed the NVSS (Condon et al. 1998) polarization data. RMs for 37 543 polarized radio sources were
derived. We examine our Faraday Screen model result by checking the RMs in the area of Fig. 13.
Two sources are located within the area of the Faraday Screen. The RMs of the two sources
![]() and
and
![]() are
are
![]() rad m-2 and
rad m-2 and
![]() rad m-2, respectively.
For another source at
rad m-2, respectively.
For another source at
![]() Brown et al. (2003a) reported a RM value of
Brown et al. (2003a) reported a RM value of ![]() 15 rad m-2 from the CGPS, which
is the most excessive RM value. Outside the Faraday Screen area Taylor et al. (2009) list RMs for 15 sources with an average
15 rad m-2 from the CGPS, which
is the most excessive RM value. Outside the Faraday Screen area Taylor et al. (2009) list RMs for 15 sources with an average
![]() rad m-2. Despite significant scatter the three sources show excessive negative RMs, which seem to be attributed to G146.4-3.0.
rad m-2. Despite significant scatter the three sources show excessive negative RMs, which seem to be attributed to G146.4-3.0.
3.4.5 Large magnetic bubbles at

Two coinciding magnetic bubbles of different sizes were identified in the area ![]() around
around
![]() by Kothes & Landecker (2004) from polarization observations with about 1
by Kothes & Landecker (2004) from polarization observations with about 1
![]() resolution at
resolution at ![]() 21 cm with the DRAO synthesis telescope. These bubbles
were also seen in the Effelsberg 1.4 GHz polarization data (Reich et al. 2004) at 9
21 cm with the DRAO synthesis telescope. These bubbles
were also seen in the Effelsberg 1.4 GHz polarization data (Reich et al. 2004) at 9
![]() resolution. The smaller bubble extends from
resolution. The smaller bubble extends from
![]() to
to
![]() and
and
![]() to 2
to 2
![]() in b, while the larger one has about the same projected centre but is approximately 9
in b, while the larger one has about the same projected centre but is approximately 9
![]() in size. At
in size. At ![]() 6 cm the two bubbles become very faint. The
6 cm the two bubbles become very faint. The ![]() 21 cm map (Kothes & Landecker 2004) was limited to
21 cm map (Kothes & Landecker 2004) was limited to
![]() ,
while the
,
while the ![]() 6 cm map shows the larger bubble to extend approximately to
6 cm map shows the larger bubble to extend approximately to
![]() (Figs. 4 and 16).
(Figs. 4 and 16).
The bubbles are faint but visible in the ![]() 6 cm Stokes U map
(Fig. 16). They are marginally traced in the Stokes Q map, regardless of including large-scale polarized emission or not.
At
6 cm Stokes U map
(Fig. 16). They are marginally traced in the Stokes Q map, regardless of including large-scale polarized emission or not.
At ![]() 6 cm the bubbles can not be identified as discrete objects in PI exceeding just a few times the rms-noise value of about 0.4 mK
6 cm the bubbles can not be identified as discrete objects in PI exceeding just a few times the rms-noise value of about 0.4 mK ![]() ,
although
some individual patches or filaments with stronger emission in this
large area may be attributed to them. The faintness of the bubbles
indicates that either their RM is not as high as that of the more pronounced
,
although
some individual patches or filaments with stronger emission in this
large area may be attributed to them. The faintness of the bubbles
indicates that either their RM is not as high as that of the more pronounced ![]() 6 cm Faraday Screens described in this paper, or that
the polarized background emission
is very faint in respect to the foreground, e.g. in terms of our Faraday Screen model c is close to 1.
6 cm Faraday Screens described in this paper, or that
the polarized background emission
is very faint in respect to the foreground, e.g. in terms of our Faraday Screen model c is close to 1.
In their preliminary model Kothes & Landecker (2004) discussed the large bubble as a Faraday Screen with a rather low electron density in agreement with the low H![]() emission in its direction. Rather important is the association of an H I bubble identified in the CGPS data with a velocity of about -20 km s-1
surrounding the outer larger magnetic bubble, which makes it a Perseus arm object at 1.5 kpc to 2 kpc distance.
This results in a very large object of about 240 pc to 310 pc in diameter. Our
emission in its direction. Rather important is the association of an H I bubble identified in the CGPS data with a velocity of about -20 km s-1
surrounding the outer larger magnetic bubble, which makes it a Perseus arm object at 1.5 kpc to 2 kpc distance.
This results in a very large object of about 240 pc to 310 pc in diameter. Our ![]() 6 cm data will not improve the physical parameters of the bubbles.
6 cm data will not improve the physical parameters of the bubbles.
3.4.6 The
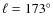 H II complex
H II complex
The survey region around
![]() is very rich in structures (Fig. 17). Nine H II regions from the
Sharpless catalogue are located within this very extended ``bow-tie'' shaped complex with the most prominent and extended H II region, SH 2-236, located in the southeast. There are four H II
regions, SH 2-231, SH 2-232, SH 2-233 and SH 2-235 located in
the north, among which, SH 2-235 is the strongest. The so-called
``Spider Nebula'' and the ``Fly Nebula'', SH 2-234 and SH 2-237,
are seen in the middle of the complex, while SH 2-229 is located
in the south-west. The central diffuse emission is attributed to
SH 2-230. All these H II regions are infrared-bright sources. Besides the Sharpless H II regions
additional ridge-shaped structures are seen in the
is very rich in structures (Fig. 17). Nine H II regions from the
Sharpless catalogue are located within this very extended ``bow-tie'' shaped complex with the most prominent and extended H II region, SH 2-236, located in the southeast. There are four H II
regions, SH 2-231, SH 2-232, SH 2-233 and SH 2-235 located in
the north, among which, SH 2-235 is the strongest. The so-called
``Spider Nebula'' and the ``Fly Nebula'', SH 2-234 and SH 2-237,
are seen in the middle of the complex, while SH 2-229 is located
in the south-west. The central diffuse emission is attributed to
SH 2-230. All these H II regions are infrared-bright sources. Besides the Sharpless H II regions
additional ridge-shaped structures are seen in the ![]() 6 cm I map, for example at
6 cm I map, for example at
![]() and
and
![]() .
Thermal characteristics of these filamentary structures are confirmed
by applying the TT-plot method to derive spectral information between
the
.
Thermal characteristics of these filamentary structures are confirmed
by applying the TT-plot method to derive spectral information between
the ![]() 6 cm and the corresponding Effelsberg
6 cm and the corresponding Effelsberg ![]() 21 cm
survey map.
21 cm
survey map.
Excessive polarized emission extending for about
![]() is seen in the southern part of the complex, distinct from SH 2-229 and SH 2-236 (Fig. 17). PI is about 3 mK
is seen in the southern part of the complex, distinct from SH 2-229 and SH 2-236 (Fig. 17). PI is about 3 mK ![]() higher compared to its surroundings (Fig. 18).
The distances to the two Sharpless regions are 510 pc for SH 2-229 and 3.2 kpc for SH 2-236 (Blitz et al. 1982).
No morphological resemblance exists between the polarized patch and
total intensity emission, while it seems that the western part of the
polarized structure is overlapped with a
southern extension from SH 2-229 (see Fig. 17). This patch coincides with thermal absorption structures visible in the
low-frequency maps at 10 MHz by Caswell (1976) and at 22 MHz by Roger et al. (1999) as shown in Fig. 19. Thus we expect thermal emission to act as a Faraday Screen.
However, we can not apply our simple Faraday Screen model, because the polarized ``
higher compared to its surroundings (Fig. 18).
The distances to the two Sharpless regions are 510 pc for SH 2-229 and 3.2 kpc for SH 2-236 (Blitz et al. 1982).
No morphological resemblance exists between the polarized patch and
total intensity emission, while it seems that the western part of the
polarized structure is overlapped with a
southern extension from SH 2-229 (see Fig. 17). This patch coincides with thermal absorption structures visible in the
low-frequency maps at 10 MHz by Caswell (1976) and at 22 MHz by Roger et al. (1999) as shown in Fig. 19. Thus we expect thermal emission to act as a Faraday Screen.
However, we can not apply our simple Faraday Screen model, because the polarized ``![]() '' emission exceeds the ``
'' emission exceeds the ``![]() '' emission, which requires that the background and the foreground PAs are different. According to the starlight polarization catalogue by Heiles (2000), large PA variations are observed in this direction. High-angular resolution Galactic emission simulations as described by Sun & Reich (2009) were used to simulate the
'' emission, which requires that the background and the foreground PAs are different. According to the starlight polarization catalogue by Heiles (2000), large PA variations are observed in this direction. High-angular resolution Galactic emission simulations as described by Sun & Reich (2009) were used to simulate the ![]() 6 cm PA, PI and I as a function of distance (Fig. 20). A significant change of PA is seen for distances below 300 pc, which is needed to explain a PI excess by Faraday rotation. This indicates that the Faraday Screen is nearer than 300 pc.
6 cm PA, PI and I as a function of distance (Fig. 20). A significant change of PA is seen for distances below 300 pc, which is needed to explain a PI excess by Faraday rotation. This indicates that the Faraday Screen is nearer than 300 pc.
Low-frequency absorption is more pronounced by local features with strong background emission than by more distant
objects having the same physical properties. The clear absorption at 10 MHz and 22 MHz of G172.3-2.9 (see Fig. 19)
further supports a local origin. The recent 1.4 GHz polarization survey by Landecker et al. (2010)
with 1
![]() angular resolution does not show a corresponding PI structure, however, the PA distribution is rather smooth in this area.
Observations at other wavelengths are needed to constrain the properties of this outstanding Faraday Screen in our
angular resolution does not show a corresponding PI structure, however, the PA distribution is rather smooth in this area.
Observations at other wavelengths are needed to constrain the properties of this outstanding Faraday Screen in our ![]() 6 cm map.
6 cm map.
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig19.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg179.png)
|
Figure 19:
22 MHz I map in grey scale of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793fig20.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg182.png)
|
Figure 20:
Simulated and accumulated |
| Open with DEXTER | |
4 Summary
In Paper II, we present the second section covering the outer Galaxy for the area
![]() ,
,
![]() of the Sino-German
of the Sino-German ![]() 6 cm polarization survey
of the Galactic plane at an angular resolution of
6 cm polarization survey
of the Galactic plane at an angular resolution of
![]() .
It is the ground-based polarization survey at the highest frequency for
the Galactic anti-centre region. The observed polarization data have
been restored to an absolute level by adding extrapolated large-scale
components from the WMAP K-band polarization maps (Hinshaw et al. 2009).
.
It is the ground-based polarization survey at the highest frequency for
the Galactic anti-centre region. The observed polarization data have
been restored to an absolute level by adding extrapolated large-scale
components from the WMAP K-band polarization maps (Hinshaw et al. 2009).
Numerous newly detected Faraday Screens indicate the presence of large
magnetic bubbles in the ISM hosting regular magnetic fields of a few ![]() G.
A simple model fit to selected Faraday Screens, which also includes H II regions, was used to estimate their physical parameters. Our main results are:
G.
A simple model fit to selected Faraday Screens, which also includes H II regions, was used to estimate their physical parameters. Our main results are:
- 1.
- We note that the remarkable polarized ``lens'' Faraday Screen in front of W5 detected by Gray et al. (1998) at
 21 cm becomes invisible at
21 cm becomes invisible at  6 cm, while previously unknown polarized structures were detected at
6 cm, while previously unknown polarized structures were detected at  6 cm at the boundaries of W5.
6 cm at the boundaries of W5.
- 2.
- The Faraday Screen model fits for LBN 676, LBN 677 and LBN 679 indicate that besides the established Perseus arm objects LBN 676 and LBN 679 also LBN 677 is located in the Perseus arm rather than at 0.8 kpc distance, because its polarized foreground level is as that of the other two objects. The parameters of the three LBNe are listed in Table 3. For LBN 676 the model fit indicates a magnetic field direction opposite to those of the other two LBNe. A similar case was noted by Mitra et al. (2003) for a few Perseus arm H II regions based on pulsar RMs shining through them.
- 3.
- The newly discovered extended Faraday Screen G146.4-3.0 is likely quite local.
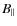 is estimated to be about
is estimated to be about 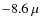 G
if located at 690 pc, which is most likely an upper limit. The
field strength within G146.4-3.0 will increase in case its distance is
smaller.
G
if located at 690 pc, which is most likely an upper limit. The
field strength within G146.4-3.0 will increase in case its distance is
smaller. - 4.
- The two huge polarized bubbles located at
 as revealed by Kothes & Landecker (2004)
at
as revealed by Kothes & Landecker (2004)
at  21 cm become very faint at
21 cm become very faint at  6 cm.
6 cm.
- 5.
- An extended blob showing excessive polarized emission is detected in the lower area of the ``bow-tie'' shaped H II region complex around
 .
Absorption at lower radio frequencies coincides with the PI
excess. We find evidence that this is a local Faraday Screen with a likely distance smaller than 300 pc.
.
Absorption at lower radio frequencies coincides with the PI
excess. We find evidence that this is a local Faraday Screen with a likely distance smaller than 300 pc.
The selected Faraday Screens from the ![]() 6 cm polarization survey demonstrate the existence of numerous high-RM features in the interstellar medium. These structures cover a significant fraction of
the surveyed area. RM studies based on pulsars or extragalactic sources aiming to derive the parameters of the
large-scale Galactic magnetic field need to take the RM-contribution from Faraday Screens into account. The formation
of strong regular magnetic fields in thermal low-density regions exceeding the interstellar value needs to be
investigated. We note that most of the
Faraday Screens visible at
6 cm polarization survey demonstrate the existence of numerous high-RM features in the interstellar medium. These structures cover a significant fraction of
the surveyed area. RM studies based on pulsars or extragalactic sources aiming to derive the parameters of the
large-scale Galactic magnetic field need to take the RM-contribution from Faraday Screens into account. The formation
of strong regular magnetic fields in thermal low-density regions exceeding the interstellar value needs to be
investigated. We note that most of the
Faraday Screens visible at ![]() 6 cm are not seen at longer wavelengths, where their RM causes polarization
angle rotations exceeding
6 cm are not seen at longer wavelengths, where their RM causes polarization
angle rotations exceeding
![]() .
Missing depolarization implies that small-scale fluctuations across the beam
may not be significant.
.
Missing depolarization implies that small-scale fluctuations across the beam
may not be significant.
We thank the staff of the Urumqi Observatory of NAOC on the Nanshan mountain for the assistance during the observations and its director, Prof. Nina Wang for granting observing time. Particularly, we like to thank Mr. Otmar Lochner for constructing and installing the6 cm receiving system at the Urumqi telescope and Dr. Peter Müller for the installation and adaptation of Effelsberg data reduction software at the Urumqi observatory. The Chinese survey team is supported by the National Natural Science foundation of China (10773016,10833003,10821061) and the National Key Basic Research Science Foundation of China (2007CB815403). X. Y. Gao thanks the joint doctoral training plan between CAS and MPG and financial support from CAS and MPIfR for making his stay possible at MPIfR Bonn.
References
- Blitz, L., Fich, M., & Stark, A. A. 1982, ApJS, 49, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Haverkorn, M., Gaensler, B. M., et al. 2007, ApJ, 663, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Taylor, A. R., & Jackel, B. J. 2003a, ApJS, 145, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Taylor, A. R., Wielebinski, R., et al. 2003b, ApJ, 592, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Caswell, J. L. 1976, MNRAS, 177, 601 [NASA ADS] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Eriksen, H. K., Banday, A. J., et al. 2009, ApJ, 705, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, A. R., Haynes, R. F., Jones, K. L., et al. 1997, MNRAS, 291, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, A. R., Reich, P., Reich, W., et al. 1999, A&A, 350, 447 [NASA ADS] [Google Scholar]
- Duncan, A. R., Stewart, R. T., Haynes, R. F., et al. 1995, MNRAS, 277, 36 [NASA ADS] [Google Scholar]
- Emerson, D. T., & Gräve, R. 1988, A&A, 190, 353 [NASA ADS] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Fleishman, G. D., & Tokarev, Y. V. 1995, A&A, 293, 565 [NASA ADS] [Google Scholar]
- Foster, T., Kothes, R., Sun, X. H., Reich, W., & Han, J. L. 2006, A&A, 454, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fürst, E., Reich, W., Reich, P., et al. 1990, A&AS, 85, 691 [NASA ADS] [Google Scholar]
- Gaensler, B. M., Dickey, J. M., McClure-Griffiths, N. M., et al. 2001, ApJ, 549, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, A. D., Landecker, T. L., Dewdney, P. E., et al. 1998, Nature, 393, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, A. D., Landecker, T. L., Dewdney, P. E., et al. 1999, ApJ, 514, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 1989, AJ, 98, 2210 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2009, Bull. Astron. Soc. India, 37, 45 [Google Scholar]
- Haffner, L. M., Reynolds, R. J., & Tufte, S. L. 1998, ApJ, 501, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Haverkorn, M., Gaensler, B. M., McClure-Griffiths, N. M., Dickey, J. M., & Green, A. J. 2006, ApJS, 167, 230 [CrossRef] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2003a, A&A, 403, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2003b, A&A, 404, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C. 2000, AJ, 119, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., Chu, Y., & Troland, T. H. 1981, ApJ, 247, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Hiltner, W. A. 1956, ApJS, 2, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Weiland, J. L., Hill, R. S., et al. 2009, ApJS, 180, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, L. G., Han, J. L., & Shi, W. B. 2009, A&A, 499, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Junkes, N., Fürst, E., & Reich, W. 1987, A&AS, 69, 451 [NASA ADS] [Google Scholar]
- Kallas, E. 1983, Ph.D. Thesis, Bonn University, Germany [Google Scholar]
- Kallas, E., & Reich, W. 1980, A&AS, 42, 227 [NASA ADS] [Google Scholar]
- Karr, J. L., & Martin, P. G. 2003, ApJ, 595, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Kerton, C. R., Murphy, J., & Patterson, J. 2007, MNRAS, 379, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Kothes, R., & Landecker, T. 2004, in The Magnetized Interstellar Medium, ed. B. Uyaniker, W. Reich, & R. Wielebinski (Copernicus GmbH), 33 [Google Scholar]
- Landecker, T. L., Reich, W., Reid, R. I., et al. 2010, A&A, in press [Google Scholar]
- Mitra, D., Wielebinski, R., Kramer, M., et al. 2003, A&A, 398, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Page, L., Hinshaw, G., Komatsu, E., et al. 2007, ApJS, 170, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Paladini, R., Burigana, C., Davies, R. D., et al. 2003, A&A, 397, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reich, W. 2006, in Cosmic Polarization, ed. R. Fabbri (Research signpost), 91 [Google Scholar]
- Reich, W., Fürst, E., & Arnal, E. M. 1992, A&A, 256, 214 [NASA ADS] [Google Scholar]
- Reich, W., Fürst, E., Reich, P., et al. 1990, A&AS, 85, 633 [Google Scholar]
- Reich, W., Fürst, E., Reich, P., et al. 2004, in The Magnetized Interstellar Medium, ed. B. Uyaniker, W. Reich, & R. Wielebinski (Copernicus GmbH), 45 [Google Scholar]
- Reich, P., Reich, W., & Fürst, E. 1997, A&AS, 126, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roger, R. S., Costain, C. H., Landecker, T. L., et al. 1999, A&AS, 137, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shi, W., Sun, X., Han, J., Gao, X., & Xiao, L. 2008a, ChJAA, 8, 575 [Google Scholar]
- Shi, W. B., Han, J. L., Gao, X. Y., et al. 2008b, A&A, 487, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofue, Y., & Reich, W. 1979, A&AS, 38, 251 [NASA ADS] [Google Scholar]
- Spoelstra, T. A. T. 1984, A&A, 135, 238 [NASA ADS] [Google Scholar]
- Sun, X. H., & Reich, W. 2009, A&A, 507, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, X. H., Han, J. L., Reich, W., et al. 2007, A&A, 463, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, X. H., Reich, W., Han, J. L., Reich, P., & Wielebinski, R. 2006, A&A, 447, 937 (Paper I) [Google Scholar]
- Sun, X. H., Reich, W., Waelkens, A., et al. 2008, A&A, 477, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, A. R., Gibson, S. J., Peracaula, M., et al. 2003, AJ, 125, 3145 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Stil, J. M., & Sunstrum, C. 2009, ApJ, 702, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Uyaniker, B. 2004, in The Magnetized Interstellar Medium, ed. B. Uyaniker, W. Reich, & R. Wielebinski (Copernicus GmbH), 71 [Google Scholar]
- Uyaniker, B., Fürst, E., Reich, W., Reich, P., & Wielebinski, R. 1999, A&AS, 138, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, C., Han, J. L., Sun, X. H., et al. 2007, Astronomical Research and Technology. Publications of National Astronomical Observatories of China, 4, 181 [Google Scholar]
- Wardle, J. F. C., & Kronberg, P. P. 1974, ApJ, 194, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Westerhout, G. 1958, Bull. Astron. Inst. Netherlands, 14, 215 [NASA ADS] [Google Scholar]
- Wieringa, M. H., de Bruyn, A. G., Jansen, D., Brouw, W. N., & Katgert, P. 1993, A&A, 268, 215 [NASA ADS] [Google Scholar]
- Wolleben, M., & Reich, W. 2004, A&A, 427, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolleben, M., Landecker, T. L., Reich, W., et al. 2006, A&A, 448, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xiao, L., Fürst, E., Reich, W., et al. 2008, A&A, 482, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xiao, L., Reich, W., Fürst, E., et al. 2009, A&A, 503, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, J. W., Han, J. L., Sun, X. H., et al. 2007, A&A, 470, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, Y., Reid, M. J., Zheng, X. W., et al. 2006, Science, 311, 54 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Footnotes
- ...
 )
)![[*]](/icons/foot_motif.png)
- PA is defined as the angle between E-vector and the Galactic north, which is equivalent to the angle between the B-vector and the Galactic plane. PA runs counter-clockwise.
- ... survey-sampler
![[*]](/icons/foot_motif.png)
- http://www.mpifr-bonn.mpg.de/survey.html
- ... CAS
![[*]](/icons/foot_motif.png)
- http://www.nao.cas.cn/zmtt/6cm/
- ... catalogue
![[*]](/icons/foot_motif.png)
- http://www.mrao.cam.ac.uk/surveys/snrs/
All Tables
Table 1: Observational parameters.
Table 2:
Hyper plane corrections in mK ![]() .
.
Table 3: Physical parameters for three LBNe.
All Figures
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{13793fig1.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg48.png)
|
Figure 1: Distribution of effective integration time in sec for the survey sub-areas shown for Stokes I, U and Q from top to bottom. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm]{13793fig2a.ps}\par\includegraphics[angle=-90,width=7.88cm]{13793fig2b.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg63.png)
|
Figure 2: Pixel distribution for PI ( top) and PA ( bottom) before and after restoring missing large-scale structures extrapolated from WMAP K-band. Details are discussed in Sect. 2.3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm]{13793-09-Copie/13793f...
...ncludegraphics[angle=-90, width=15cm]{13793-09-Copie/13793fig3d.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg66.png)
|
Figure 3:
Urumqi |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm]{13793fig4a.ps}\par\in...
...fig4c.ps}\par\includegraphics[angle=-90, width=15cm]{13793fig4d.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg67.png)
|
Figure 4:
Sequence and contours as in Fig. 3 for Part 2. Vectors are shown for PI exceeding 2.5 mK |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm]{13793fig5a.ps}\par\in...
...fig5c.ps}\par\includegraphics[angle=-90, width=15cm]{13793fig5d.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg68.png)
|
Figure 5:
Sequence and contours as in Fig. 3 for Part 3. Vectors are shown for PI exceeding 1.5 mK |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=15cm]{13793fig6a.ps}\par\in...
...fig6c.ps}\par\includegraphics[angle=-90, width=15cm]{13793fig6d.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg69.png)
|
Figure 6:
Sequence and contours as in Fig. 3 for Part 4. Vectors are shown for PI exceeding 0.9 mK |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm]{13793fig7a.ps}\par\incl...
...93fig7b.ps}\par\includegraphics[angle=-90,width=8cm]{13793fig7c.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg72.png)
|
Figure 7:
Upper plot shows the PI map of W5 in grey scale, overlaid by contours of I. The contour lines run from the local 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793fig8.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg90.png)
|
Figure 8:
Averaged observed values for the low-latitude W5 blob with centre coordinate (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793fig9.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg99.png)
|
Figure 9:
PA distribution in B-field direction for the ``drumstick'' area. I contours start at 1.5 mK |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig10.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg104.png)
|
Figure 10:
Average values in northern direction for the H II region LBN 676. Offsets are relative to the centre
coordinate (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig11.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg106.png)
|
Figure 11:
Average values starting from the coordinate (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig12.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg123.png)
|
Figure 12:
Half ring average values from centre coordinate (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig13.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg124.png)
|
Figure 13:
PI of the Faraday Screen G146.4-3.0 in grey scale. I contours are overlaid running from 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig14.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg125.png)
|
Figure 14: Ring averaged data and modeled RMs for Faraday Screen G146.4-3.0 shown in Fig. 13. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig15.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg143.png)
|
Figure 15:
Dependence of the central
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig16.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg144.png)
|
Figure 16:
U map at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig17.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg158.png)
|
Figure 17:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichi...
...e=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig18b.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg159.png)
|
Figure 18: Upper plot shows I, PA and PI averaged in the vertical rectangle region marked in Fig. 17, where data are averaged in columns. The vertical dashed lines mark the boundary of the highly polarized emission region. The lower plot shows the results when averaging in the horizontal rectangle in Fig. 17. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793-nouveaux-fichiers-auteurs/13793fig19.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg179.png)
|
Figure 19:
22 MHz I map in grey scale of the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90, width=8.5cm]{13793fig20.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13793-09/Timg182.png)
|
Figure 20:
Simulated and accumulated |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.