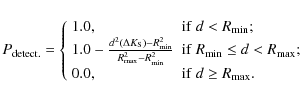| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200913688 | |
| Published online | 03 June 2010 | |
A MAD view of Trumpler 14![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
H. Sana1,2 - Y. Momany1,3 - M. Gieles1 - G. Carraro1 - Y. Beletsky1 - V. D. Ivanov1 - G. De Silva4 - G. James4
1 - European Southern Observatory, Alonso de Cordova 3107, Vitacura,
Santiago 19, Chile
2 - Sterrenkundig Instituut Anton Pannekoek, Universiteit van
Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
3 - INAF, Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio
5, 35122 Padova, Italy
4 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching bei München, Germany
Received 17 November 2009 / Accepted 1 March 2010
Abstract
We present adaptive optics (AO) near-infrared observations of the core
of the Tr 14 cluster in the Carina region obtained with the
ESO multi-conjugate AO demonstrator, MAD. Our campaign yields
AO-corrected observations with an image quality of about 0.2
![]() across the 2
across the 2![]() field of view, which is the widest AO mosaic ever obtained. We detected
almost 2000 sources spanning a dynamic range of
10 mag. The pre-main sequence (PMS) locus in the
colour-magnitude diagram is well reproduced by Palla & Stahler
isochrones with an age of 3 to
field of view, which is the widest AO mosaic ever obtained. We detected
almost 2000 sources spanning a dynamic range of
10 mag. The pre-main sequence (PMS) locus in the
colour-magnitude diagram is well reproduced by Palla & Stahler
isochrones with an age of 3 to ![]() yr,
confirming the very young age of the cluster. We derive a very high
(deprojected) central density
yr,
confirming the very young age of the cluster. We derive a very high
(deprojected) central density ![]() pc-3
and estimate the total mass of the cluster to be about
pc-3
and estimate the total mass of the cluster to be about ![]()
![]()
![]() ,
although contamination of the field of view might have a significant
impact on the derived mass. We show that the pairing process is largely
dominated by chance alignment so that physical pairs are difficult to
disentangle from spurious ones based on our single epoch observation.
Yet, we identify 150 likely bound pairs, 30% of these with a separation
smaller than 0.5
,
although contamination of the field of view might have a significant
impact on the derived mass. We show that the pairing process is largely
dominated by chance alignment so that physical pairs are difficult to
disentangle from spurious ones based on our single epoch observation.
Yet, we identify 150 likely bound pairs, 30% of these with a separation
smaller than 0.5
![]() (
(![]() 1300 AU).
We further show that at the 2
1300 AU).
We further show that at the 2![]() level massive stars have more companions than lower-mass stars and that
those companions are respectively brighter on average, thus more
massive. Finally, we find some hints of mass segregation for stars
heavier than about 10
level massive stars have more companions than lower-mass stars and that
those companions are respectively brighter on average, thus more
massive. Finally, we find some hints of mass segregation for stars
heavier than about 10 ![]() .
If confirmed, the observed degree of mass segregation could be
explained by dynamical evolution, despite the young age of the cluster.
.
If confirmed, the observed degree of mass segregation could be
explained by dynamical evolution, despite the young age of the cluster.
Key words: instrumentation: adaptive optics - stars: early-type - stars: pre-main sequence - binaries: visual - open clusters and associations: individual: Tr 14
1 Introduction
Massive stars do not form in isolation. They are born and, for most of them, are living in OB associations and young clusters (Maíz-Apellániz et al. 2004). Indeed, most of the field cases are runaway objects that can be traced back to their natal cluster/association (de Wit et al. 2005). Even the best cases of field massive stars are now questioned in favour of an ejection scenario (Gvaramadze & Bomans 2008).
One of the most striking and important properties of high-mass stars is their high degree of multiplicity. Yet accurate observational constraints of the multiplicity properties and of the underlying parameter distributions are still lacking. These quantities are however critical as they trace the final products of high-mass star formation and early dynamical evolution. In nearby open clusters, the minimal spectroscopic binary (SB) fraction is in the range of 40% to 60% (Sana et al. 2009,2008; Sana et al. in prep.), which is similar to the 57% SB fraction observed for the galactic O-star population as a whole (Mason et al. 2009).
While spectroscopy is suitable to detect the short- and
intermediate-period binaries (P<10 yr),
adaptive optics (AO) observations can tackle the problem from the other
side of the separation range (see e.g. discussion in Sana & Le Bouquin 2009).
As an example, Turner et al.
(2008) obtained
a minimal fraction of massive stars with companions of 37%
within an angular separation of 0.2 to 6
![]() .
However, their survey is limited to objects
with declination
.
However, their survey is limited to objects
with declination ![]()
![]() .
It is thus missing some of the
most interesting star formation regions of the Galaxy, like the Carina
nebula
region.
.
It is thus missing some of the
most interesting star formation regions of the Galaxy, like the Carina
nebula
region.
In this context, we undertook a multi-band NIR AO campaign on
the main Carina region clusters with the Multi-Conjugate Adaptive
Optics (MCAO) Demonstrator (MAD, Marchetti
et al. 2007). Beside deep NIR photometry of the
individual clusters, our survey was designed to provide us with
high-resolution imaging of the close environment of a sample of
60 O/WR massive stars in the Carina region. Unfortunately, the
bad weather at the end of the second MAD demonstration run in
January 2008 prevented the completion of the project. Valuable
H and ![]() photometry of the sole
Tr 14 cluster could be obtained. The 2
photometry of the sole
Tr 14 cluster could be obtained. The 2![]() field of view (fov) still provides us with high-quality information of
the surrounding of
field of view (fov) still provides us with high-quality information of
the surrounding of ![]() 30
early-type stars with masses above 10
30
early-type stars with masses above 10 ![]() .
It also
constitutes the most extended AO mosaic ever acquired.
.
It also
constitutes the most extended AO mosaic ever acquired.
Table 1: Field centering (F.C.) for on-object (Tr 14) and on-sky observations and coordinates of the natural guide stars (NGSs).
Located inside Carina at a distance of 1.5-3.0 kpc,
Tr 14 is an ideal target to search for multiplicity around
massive stars
because it contains more than 10 O-type stars and several hundreds of
B-type
stars (Vazquez et al. 1996).
Large differences in the distance to Trumpler 14 arise from adopting
different extinction laws and evolutionary tracks (Carraro
et al. 2004).
Differences in distance can partially account for diverse estimates
of mass and structural parameters.
Its mass was first estimated to be 2000 ![]() (Vazquez et al. 1996).
However, the photometry used by these authors barely reached
the turn-on point of the pre-main sequence (PMS), while they
extrapolated the mass
assuming a Salpeter initial mass function (IMF).
More recently, Ascenso et al.
(2007) used much deeper IR photometry, which
revealed the very rich PMS population and provided a more
robust mass estimate
of 9000
(Vazquez et al. 1996).
However, the photometry used by these authors barely reached
the turn-on point of the pre-main sequence (PMS), while they
extrapolated the mass
assuming a Salpeter initial mass function (IMF).
More recently, Ascenso et al.
(2007) used much deeper IR photometry, which
revealed the very rich PMS population and provided a more
robust mass estimate
of 9000 ![]() .
Vazquez et al. (1996)
reported a core radius of 4.2 pc, while Ascenso
et al. (2007)
revised it to 1.14 pc, and detected for the first
time a core-halo structure, which is typical of these young clusters
(e.g., Baume et al. 2004).
Tr 14 is indeed very young, not yet relaxed and has been
forming stars in the last 4 Myr (Vazquez
et al. 1996).
.
Vazquez et al. (1996)
reported a core radius of 4.2 pc, while Ascenso
et al. (2007)
revised it to 1.14 pc, and detected for the first
time a core-halo structure, which is typical of these young clusters
(e.g., Baume et al. 2004).
Tr 14 is indeed very young, not yet relaxed and has been
forming stars in the last 4 Myr (Vazquez
et al. 1996).
The layout of the paper is as follows. Sections 2 and 3 describe the observations, data reduction and photometric analysis. Section 4 presents the NIR properties of Tr 14 and discusses the cluster structure. Section 5 analyses the pairing properties in Tr 14. Section 6 describes an artificial star experiment designed to quantify the detection biases in the vicinity of the bright stars. It also presents two simple models that generalise the results of the artificial star experiment. As such, it provides support to the results of this paper. Finally, Sect. 7 investigates the cluster mass segregation status and Sect. 8 summarizes our results.
2 Observations and data reduction
The MAD instrument is an adaptive optics facility aiming at correcting
for the atmospheric turbulence over a wide field-of-view, and as such
constitutes a pathfinder experiment for MCAO techniques. Briefly,
MAD relies on three natural guide stars (NGSs)
to improve the image quality (IQ) over a 2![]() -diameter fov. Optimal
correction is reached within the triangle formed by the three
NGSs although some decent correction is still attained outside, mostly
depending on the observing conditions and on the coherence time of
the atmospheric turbulence.
-diameter fov. Optimal
correction is reached within the triangle formed by the three
NGSs although some decent correction is still attained outside, mostly
depending on the observing conditions and on the coherence time of
the atmospheric turbulence.
The CAMCAO IR camera images a ![]() region
in the MAD fov and is mounted on a scanning table, so that the full 2
region
in the MAD fov and is mounted on a scanning table, so that the full 2![]() -diameter fov
can be covered with a 4- or 5-point dither pattern.
The detector used is an Hawaii 2k
-diameter fov
can be covered with a 4- or 5-point dither pattern.
The detector used is an Hawaii 2k![]() 2k, yielding an effective
pixel size on sky of 0.028
2k, yielding an effective
pixel size on sky of 0.028
![]() .
.
Because of the constraints imposed by the geometry and the
magnitudes of
the NGSs as well as by the brightness limit of the detector (typically
![]() ), the Carina clusters turned
out to be ideal targets for our
purposes. Combined with the large collecting area of an 8-m class
telescope, MAD was offering a unique opportunity to collect the missing
high-spatial resolution observations to characterize a statistically
significant set of massive
stars.
), the Carina clusters turned
out to be ideal targets for our
purposes. Combined with the large collecting area of an 8-m class
telescope, MAD was offering a unique opportunity to collect the missing
high-spatial resolution observations to characterize a statistically
significant set of massive
stars.
On the night of January 10, 2008 during the second Science
Demonstration (SD) run, the MAD team acquired H and
![]() band
observations
of Tr 14. Because of the mentioned
constraints on the choice of the NGSs, the MAD pointing was offset
from the cluster centre by about 0.4
band
observations
of Tr 14. Because of the mentioned
constraints on the choice of the NGSs, the MAD pointing was offset
from the cluster centre by about 0.4![]() to the W-SW and a 4-point dither pattern was used to cover the (almost)
full 2
to the W-SW and a 4-point dither pattern was used to cover the (almost)
full 2![]() diameter
fov (Fig. 1).
We obtained 28 images for a total exposure time of 28 min on
the central field of the cluster (DP#1) and
eight 30 s images in the three remaining DPs. The
size of the jitter box was
10
diameter
fov (Fig. 1).
We obtained 28 images for a total exposure time of 28 min on
the central field of the cluster (DP#1) and
eight 30 s images in the three remaining DPs. The
size of the jitter box was
10
![]() .
We further followed a standard object-sky-object strategy. The jitter
and dither pattern for the on- and off-target observations
were identical, although the sky observations were obtained without AO
correction. The sky field, located about 5
.
We further followed a standard object-sky-object strategy. The jitter
and dither pattern for the on- and off-target observations
were identical, although the sky observations were obtained without AO
correction. The sky field, located about 5![]() SW from the cluster
centre, is
one of the few IR-source depleted regions of the neighbourhood.
The journal of the on- and off-target observations is summarized in
Table 2.
For each dither position (Col. 1), Cols. 2
and 3 list the coordinates of the four-point dither pattern.
The detector integration time (DIT) and
the number of repetitions at each jitter position (NDIT) are given in
Cols. 4 and 5.
Finally, Cols. 6 and 7 respectively indicate the
number of images and the total integration time spent on each dither
position.
SW from the cluster
centre, is
one of the few IR-source depleted regions of the neighbourhood.
The journal of the on- and off-target observations is summarized in
Table 2.
For each dither position (Col. 1), Cols. 2
and 3 list the coordinates of the four-point dither pattern.
The detector integration time (DIT) and
the number of repetitions at each jitter position (NDIT) are given in
Cols. 4 and 5.
Finally, Cols. 6 and 7 respectively indicate the
number of images and the total integration time spent on each dither
position.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{13688fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg39.png)
|
Figure 1:
2MASS K band image of Tr 14. The cross and
the large circle indicate the centre and the size of the 2 |
| Open with DEXTER | |
Table 2: Log of the MAD observations of Tr 14.
The data were reduced with the IRAF package. All science and sky frames were dark-subtracted and flatfielded with the calibrations obtained by the SD-team in January 2008. A master-sky was created for each dither position (DP) by taking the median of the corresponding sky images. The few visible sources in the sky images were manually masked out before computing the median sky. This master-sky was subtracted from the individual science images. While the point spread function (PSF) photometry (see Sect. 3) was performed on the individual images, we also combined the images into a 2Ambient conditions during our observations were as follows.
The R band seeing was
varying between 0.9
![]() and 1.8
and 1.8
![]() ,
corresponding to a
,
corresponding to a ![]() band
seeing between 0.7
band
seeing between 0.7
![]() and 1.5
and 1.5
![]() .
The coherence time was in
the range of 2 to 3 ms. Even though the ambient conditions
were clearly
below average for the Paranal site, the MCAO still provided a decent
improvement with an full-width half maximum (FWHM)
of the PSF of 0.2
.
The coherence time was in
the range of 2 to 3 ms. Even though the ambient conditions
were clearly
below average for the Paranal site, the MCAO still provided a decent
improvement with an full-width half maximum (FWHM)
of the PSF of 0.2
![]() over most of the 2
over most of the 2![]() fov.
The corresponding Strehl ratio was estimated in the range of 5-10%
(Fig. 2).
Figure 3
displays a false colour montage of our data on Tr 14, while
Fig. 4
presents a close-up view on a
fov.
The corresponding Strehl ratio was estimated in the range of 5-10%
(Fig. 2).
Figure 3
displays a false colour montage of our data on Tr 14, while
Fig. 4
presents a close-up view on a ![]()
![]() region, with the aim to emphasize the shape and smoothness of the PSF,
even on the co-added images.
region, with the aim to emphasize the shape and smoothness of the PSF,
even on the co-added images.
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=-90,clip]{13688fg2a.eps} \includegraphics[width=8.5cm,angle=-90,clip]{13688fg2b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg46.png)
|
Figure 2: Averaged FWHM and Strehl ratio maps as computed over the MAD field of view (yellow circle). The three red crosses show the locations of the NGSs. North is to the top and East to the right. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{13688fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg47.png)
|
Figure 3:
False colour image of the 2 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg48.png)
|
Figure 4:
Close-up view of the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg49.png)
|
Figure 5:
Comparison of the H ( upper panel)
and |
| Open with DEXTER | |
3 PSF photometry
Stellar photometry was obtained with the PSF fitting technique using the well-tested DAOPHOT/ALLSTAR/ALLFRAME (Stetson 1994,1987) packages. The advantage of using ALLFRAME is that it employs PSF photometry on the individual images, thereby it accounts better for the varying near infrared sky and seeing conditions. The latter have indeed a significant impact on the quality of the AO correction and thus of the actual IQ of the data. The PSF of each individual image was generated with a PENNY function that had a quadratic dependence on position in the frame, using a selected list of well isolated stars.
The calibration of the instrumental H and ![]() MAD data was done by direct comparison with the
MAD data was done by direct comparison with the ![]() calibrated SOFI catalogue of Ascenso
et al. (2007). Of particular importance is the
absence of (i) any colour term between the two photometric systems over
a six-magnitude range (Fig. 5), and (ii)
spatial systematics between the 4-single MAD pointings and the mean
zero-point difference with respect to the SOFI data. Open squares in
Fig. 5
highlight the stars used to estimate the mean offset between the two
systems, which were selected by applying a 3
calibrated SOFI catalogue of Ascenso
et al. (2007). Of particular importance is the
absence of (i) any colour term between the two photometric systems over
a six-magnitude range (Fig. 5), and (ii)
spatial systematics between the 4-single MAD pointings and the mean
zero-point difference with respect to the SOFI data. Open squares in
Fig. 5
highlight the stars used to estimate the mean offset between the two
systems, which were selected by applying a 3![]() clipping around the mean zero-point difference. We obtained
clipping around the mean zero-point difference. We obtained
|
|
= | (1) | |
| = | (2) |
Taking into account that some objects might be variable and that some others were likely not resolved by SOFI, we conclude that there is an almost perfect agreement between the two sets of measurements. We therefore continue without applying any correction to our photometry. After manually cleaning the handful of double entries, our photometric catalogue contains 1955 stars, most of them brighter than
4 A MAD view of Tr 14
4.1 Colour-magnitude diagram
Because we only have H and ![]() band observations, our data alone cannot altogether constrain the
reddening, the distance and the age of the stellar population. Below,
we adopt the results of Carraro
et al. (2004):
band observations, our data alone cannot altogether constrain the
reddening, the distance and the age of the stellar population. Below,
we adopt the results of Carraro
et al. (2004): ![]() kpc,
kpc,
![]() and
and ![]() .
Figure 7
presents the colour magnitude diagram (CMD) of Tr 14 for
dither positions DP #1 and 4, and for the full fov (DP#1-4) and
compares it with the main sequence (MS) and PMS locations
given the adopted cluster distance and reddening. Figure 7 further provides
an overview of the light-to-mass conversion scale used in the rest of
this paper.
.
Figure 7
presents the colour magnitude diagram (CMD) of Tr 14 for
dither positions DP #1 and 4, and for the full fov (DP#1-4) and
compares it with the main sequence (MS) and PMS locations
given the adopted cluster distance and reddening. Figure 7 further provides
an overview of the light-to-mass conversion scale used in the rest of
this paper.
While most of the stars brighter than ![]() agree well with the MS of Lejeune
& Schaerer (2001), the vast majority of the fainter
stars (
agree well with the MS of Lejeune
& Schaerer (2001), the vast majority of the fainter
stars (
![]() )
are still in the PMS stage. A comparison with the
PMS isochrones of Palla
& Stahler (1993) suggests a contraction age younger
than 1 Myr, and possibly as young as 0.3-0.5 Myr. At
this age, the transition between the PMS and the
MS occurs for stars with masses in the range of 4
)
are still in the PMS stage. A comparison with the
PMS isochrones of Palla
& Stahler (1993) suggests a contraction age younger
than 1 Myr, and possibly as young as 0.3-0.5 Myr. At
this age, the transition between the PMS and the
MS occurs for stars with masses in the range of 4 ![]() to 8
to 8 ![]() .
Although the PMS isochrones are still affected by
uncertainties in the colour transformation, our data clearly suggest
that the core of Tr 14 has undergone a very recent starburst
event, during which most of the low- and intermediate-mass stars in
Tr 14 have been formed.
.
Although the PMS isochrones are still affected by
uncertainties in the colour transformation, our data clearly suggest
that the core of Tr 14 has undergone a very recent starburst
event, during which most of the low- and intermediate-mass stars in
Tr 14 have been formed.
Table 3: Photometric catalogue of the sources detected in Tr 14.
Using a larger distance and/or a larger reddening (e.g., Ascenso et al. 2007) would result in even younger ages, which is the reason why we conservatively decided to adopt the former Carraro et al. results.Without control field observations, we cannot quantitatively
estimate the contamination of the CMD by field stars. Yet, the CMD from
DP#4 shows the least structure and provides some qualitative estimate
of the maximum contamination suffered by the central part of the
cluster. It indicates that the dispersion around the ![]() yr
isochrone is mostly real. Comparing them with PMS isochrones
of different ages, we estimated the duration of the starburst to be a
couple of 105 yr at most.
yr
isochrone is mostly real. Comparing them with PMS isochrones
of different ages, we estimated the duration of the starburst to be a
couple of 105 yr at most.
4.2 Foreground/background contamination
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13688fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg69.png)
|
Figure 6:
H and |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13688fg7.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg71.png)
|
Figure 7:
Left: Tr 14 CMD for DP #1.
Middle: CMD for DP #4. Right: complete
Tr 14 CMD (DP#1 to 4). The dashed lines show the
MS from Lejeune &
Schaerer (2001) and from Palla
& Stahler (1993) for stars with masses M>6 |
| Open with DEXTER | |
Both relations are obtained as an approximate to the
Figure 9 displays the spatial distribution of the rejected blue and red stars. The faint reddest stars agree well with a random spread in the field. The faint bluest ones are mostly located in the North and East edges and suggest larger color uncertainties in that zone. The surface density of the brighter red stars however shows a clear enhancement that correlates with the central part of the cluster. This suggests that the corresponding stars are rather highly reddened objects associated with Tr 14. We acknowledge that we might thus have rejected some members of Tr 14. Preserving the homogeneity of the reddening properties of the bright star sample is however more important and we argue that the resulting few extra rejections will not affect the statistical companionship properties discussed in Sect. 5.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13688fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg78.png)
|
Figure 8: Tr 14 CMD. The plain lines delimit the adopted locus of cluster members (see text) while the stars show the objects not considered in Sect. 5. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg9.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg79.png)
|
Figure 9:
Distribution of the reddest and bluest stars in Tr14. The dot and the
open circles show the location of the faint (
|
| Open with DEXTER | |
4.3 Cluster structure
Adopting the cluster centre as defined by Ascenso
et al. (2007), we computed the radial profile of the
star surface density (Fig. 10). Ascenso et al. (2007)
proposed a core-halo structure with a respective approximate radius of 1![]() and 5
and 5![]() .
Although our data set covers a limited area, there is no indication of
a transition between the two regimes. We can thus consider that our fov
is strictly dominated by the core of the cluster. The cluster
parameters derived below thus only apply to the core of the core-halo
structure.
.
Although our data set covers a limited area, there is no indication of
a transition between the two regimes. We can thus consider that our fov
is strictly dominated by the core of the cluster. The cluster
parameters derived below thus only apply to the core of the core-halo
structure.
To better quantify the surface density variations, we fitted Elson et al. (1987, hereafter EFF87)
profiles, better suited for young open clusters than King profiles, to
all three populations. Following EFF87, we adopt the notation
where
Table 4: Best-fit EFF87 parameters for different populations in Tr 14.
Integrating the surface number density profile to infinity and assuming an average stellar mass of 0.64![\begin{figure}
\par\includegraphics[width=7cm,clip]{13688fg10a.eps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{13688fg10b.eps}\vspace{2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg96.png)
|
Figure 10:
Tr 14 surface number density distributions for the full
cluster population (circles) and for the PMS (triangles) and
MS (diamonds) populations. Upper and lower panels
show the density profiles obtained, respectively, before and after
applying the colour criteria of Fig. 8. In both
cases only stars with magnitude |
| Open with DEXTER | |
As a first attempt to search for differences between the low- and
high-mass star properties, we also computed the density profiles of two
sub-populations in Tr 14: the MS stars (
![]() mag) and the
PMS stars (
mag) and the
PMS stars (
![]() mag). From
Fig. 10
(upper panel), the PMS stars occupy a larger core but display
a steeper decrease than the MS population. Because the
population of the cluster is dominated by low mass stars, there is
little difference between the number density profile of the
PMS stars and that of the whole cluster. The more massive
MS stars (
mag). From
Fig. 10
(upper panel), the PMS stars occupy a larger core but display
a steeper decrease than the MS population. Because the
population of the cluster is dominated by low mass stars, there is
little difference between the number density profile of the
PMS stars and that of the whole cluster. The more massive
MS stars (
![]() mag) however seem to
be slightly more concentrated towards the cluster centre (see also
discussion in Sect. 7).
As mentioned earlier, the PMS profile seems to display a
steeper slope, but Table 4
reveals that this difference is not very significant (only at the
mag) however seem to
be slightly more concentrated towards the cluster centre (see also
discussion in Sect. 7).
As mentioned earlier, the PMS profile seems to display a
steeper slope, but Table 4
reveals that this difference is not very significant (only at the ![]() level).
level).
As a second step, we also re-computed the density profiles
after applying the colour and magnitude criteria defined in the
previous section (Sect. 4.2), thus
focussing on the most probable members. The cluster core radius is
found to be larger and the profiles display a significantly steeper
decrease with radius (Fig. 10, lower panel).
The central surface density is also reduced by a factor 2.6 and the
deprojected central number density by a factor 4.7
(Table 4).
Following these adjustments, the asymptotic mass of the core is reduced
to ![]()
![]() .
Because of the sharper slope of the profile, one now finds 75% of the
total mass in the inner parsec. Interestingly, the more massive stars
show no core-structure, and their density profile is well represented
by a simple power-law. This is somewhat comparable to what Campbell et al. (2010)
found for the massive stars in R136.
.
Because of the sharper slope of the profile, one now finds 75% of the
total mass in the inner parsec. Interestingly, the more massive stars
show no core-structure, and their density profile is well represented
by a simple power-law. This is somewhat comparable to what Campbell et al. (2010)
found for the massive stars in R136.
5 Companion analysis
5.1 General properties
With about 1500 likely members in a 2![]() -diameter fov, the mean surface
density is 477 src/arcmin2, or
0.133 src/arcsec2. The closest pair
detected in our PSF photometry is separated by 0.24
-diameter fov, the mean surface
density is 477 src/arcmin2, or
0.133 src/arcsec2. The closest pair
detected in our PSF photometry is separated by 0.24
![]() and half the sources have a neighbour at no morethan 1.25
and half the sources have a neighbour at no morethan 1.25
![]() (Fig. 11).
Figure 12
illustrates empirically the maximum reachable flux contrast between two
close sources as a function of their separation. The magnitude
difference
(Fig. 11).
Figure 12
illustrates empirically the maximum reachable flux contrast between two
close sources as a function of their separation. The magnitude
difference![]()
![]() roughly scales as the cubic root of the separation:
roughly scales as the cubic root of the separation:
Flux contrasts of
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg105.png)
|
Figure 11:
Cumulative distribution of the distance to the closest
neighbour (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg106.png)
|
Figure 12:
Magnitude difference |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg13.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg108.png)
|
Figure 13:
Probability that a pair is physically bound |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg14.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg109.png)
|
Figure 14:
Same as Fig. 12
where the population of likely bound systems has been over-plotted with
red (
|
| Open with DEXTER | |
5.2 Chance alignment
Because of the high source surface density, the number of pairs quickly
increases with separation. To quantify the chance that an observed pair
results from spurious alignment, we followed the approach of Duchêne et al. (2001). We
define ![]() as the complementary probability to the one that a given pair
as the complementary probability to the one that a given pair ![]() ),
with a separation d, occurs by chance:
),
with a separation d, occurs by chance:
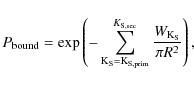
|
(7) |
where R is the field radius, taken as 60
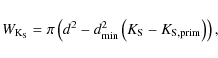
|
(8) |
where
As expected, Fig. 13 shows that the likelihood of finding physically bound pairs,
Table 5
lists the 150 pairs separated by 5
![]() or less and with
or less and with ![]() .
The first column indicates the primary and secondary IDs from
Table 3.
Columns 2, 3 and Cols. 4, 5 list
the H and
.
The first column indicates the primary and secondary IDs from
Table 3.
Columns 2, 3 and Cols. 4, 5 list
the H and ![]() magnitudes of the primary and secondary components, respectively. The
separation of the pair is given in Col. 6. The two closest
pairs detected have a separation of 0.24
magnitudes of the primary and secondary components, respectively. The
separation of the pair is given in Col. 6. The two closest
pairs detected have a separation of 0.24
![]() and 0.25
and 0.25
![]() (only 600 AU at the Tr 14 distance) and
(only 600 AU at the Tr 14 distance) and ![]() mag
(Fig. 15).
The closest probable companion to a massive star is a
mag
(Fig. 15).
The closest probable companion to a massive star is a ![]() mag
star at 0.4
mag
star at 0.4
![]() from the B1 V star Tr14-19 (pair ID #1530-1536 in
Table 5).
Of the 31 stars brighter than
from the B1 V star Tr14-19 (pair ID #1530-1536 in
Table 5).
Of the 31 stars brighter than ![]() mag,
only six have high probability companions in the range of 0.4
mag,
only six have high probability companions in the range of 0.4
![]() to 2.5
to 2.5
![]() ,
i.e. 19%. Because of the observational biases discussed and of the
filtering criteria applied, the statistical distribution of the
selected pairs is not representative of the underlying distribution and
will not be discussed further.
,
i.e. 19%. Because of the observational biases discussed and of the
filtering criteria applied, the statistical distribution of the
selected pairs is not representative of the underlying distribution and
will not be discussed further.
Table 5:
List of likely bound visual pairs (
![]() ).
).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13688fg15.eps} \vspace{-3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg122.png)
|
Figure 15:
Close-up view in the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg16.eps} \vspace{-2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg123.png)
|
Figure 16:
Left: average number of companions per star
for a given maximum companion magnitude. Right:
cumulative distribution functions (CDF) of the companion brightness.
The central stars are taken in four ranges as indicated in the upper
left-hand legend. Only pairs with separations in the range of 0.5
|
| Open with DEXTER | |
5.3 Companion frequency
To search for variations in the companionship properties of different
sub-populations, we first computed the average number of companions per
star, considering various magnitude ranges both for the central star
and for the companions (Fig. 16, left panel).
We applied the same colour and magnitude selections defined in
Sect. 4.2.
We further adopted an exclusion radius of 5
![]() between each central star so that each companion is only assigned to
one primary, preserving the independence of the different samples. In
this particular case and to allow direct comparison between the
different samples, we did not require that
between each central star so that each companion is only assigned to
one primary, preserving the independence of the different samples. In
this particular case and to allow direct comparison between the
different samples, we did not require that ![]() .
For the central stars, we consider four ranges of magnitudes:
.
For the central stars, we consider four ranges of magnitudes:
- 1.
- the massive stars:
 ,
corresponding to M>10
,
corresponding to M>10 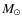 MS stars);
MS stars);
- 2.
- the intermediate-mass stars:
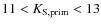 ,
corresponding to 10>M>4
,
corresponding to 10>M>4 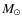 stars;
stars;
- 3.
- the solar-mass PMS stars:
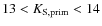 ,
corresponding to 2.5>M>0.5
,
corresponding to 2.5>M>0.5 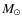 PMS stars;
PMS stars;
- 4.
- the low-mass PMS stars:
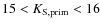 ,
corresponding to 0.2>M>0.1
,
corresponding to 0.2>M>0.1 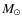 PMS stars;
PMS stars;
Under those assumptions, we found that massive
MS stars have on average ![]() companions, while solar-mass PMS stars have
companions, while solar-mass PMS stars have ![]() companions. The number of companions of intermediate-mass stars and of
low-mass PMS stars are not significantly different from one
another. Most of the difference is however found for
companions. The number of companions of intermediate-mass stars and of
low-mass PMS stars are not significantly different from one
another. Most of the difference is however found for ![]() :
:
![]() companions
for MS stars against
companions
for MS stars against ![]() for lower mass stars. The difference is thus significant at the 2.5
for lower mass stars. The difference is thus significant at the 2.5![]() .
This corresponds to a rejection of the null hypothesis that massive and
lower-mass stars have the same number of companions with a significance
level better than 0.01. Because this is seen against the
observational biases (see Sect. 6.2.2),
this result is likely to be even more significant.
.
This corresponds to a rejection of the null hypothesis that massive and
lower-mass stars have the same number of companions with a significance
level better than 0.01. Because this is seen against the
observational biases (see Sect. 6.2.2),
this result is likely to be even more significant.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg17.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg135.png)
|
Figure 17:
Average number of companions per star as a function of the companion
brightness. The central stars are taken in four ranges as indicated in
the upper left-hand legend. A moving average with a 2 mag bin
has been used and the considered separation range is 0.5
|
| Open with DEXTER | |
5.4 Magnitude distribution
We computed the distributions of the companion magnitudes for the
various stellar populations considered above using a 2-mag wide moving
average along the companion magnitude axis (Fig. ![]() ). Most of the differences between the
distribution functions of the massive stars and of the lower-mass stars
result from the range
). Most of the differences between the
distribution functions of the massive stars and of the lower-mass stars
result from the range ![]() .
The more massive stars display thus about twice as many solar-mass
companions as the lower mass stars. The situation is reverse for
fainter, low-mass PMS companions, where the lower-mass stars
tend to have more companions. The latter effect can however result from
the difficulty to detect extremely faint stars in the wings of the
brightest stars. To allow for quantitative statistical testing, we also
built the cumulative distribution functions (CDF) of the companion
brightness (Fig. 16,
right panel). Using a two-sided Kolmogorov-Smirnov (KS) test, one can
reject at the 2
.
The more massive stars display thus about twice as many solar-mass
companions as the lower mass stars. The situation is reverse for
fainter, low-mass PMS companions, where the lower-mass stars
tend to have more companions. The latter effect can however result from
the difficulty to detect extremely faint stars in the wings of the
brightest stars. To allow for quantitative statistical testing, we also
built the cumulative distribution functions (CDF) of the companion
brightness (Fig. 16,
right panel). Using a two-sided Kolmogorov-Smirnov (KS) test, one can
reject at the 2![]() level the null hypothesis that the high-mass and the solar-mass stars
share the same companion CDF.
level the null hypothesis that the high-mass and the solar-mass stars
share the same companion CDF.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg18.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg137.png)
|
Figure 18: Upper panel: growth curve for the companions of massive stars. The plain line indicates the expected distribution for a uniform distribution of the companions in the field of view. Lower panel: same as upper panel for the companions of solar-mass stars. |
| Open with DEXTER | |
5.5 Companion spatial distribution
To investigate the spatial distribution of the companions, we built the
growth curves of the number of companions as a function of the
separation. For the curves to be more robust against low number
statistics, we concentrated on the total growth curve of a given
stellar population rather than on the growth curve of individual
targets. We further limited the companions to masses above 0.1 ![]() ,
which roughly corresponds to a magnitude limit of
,
which roughly corresponds to a magnitude limit of ![]() mag
and, as in the previous paragraph, we restrained our comparison to the
0.5-2.5
mag
and, as in the previous paragraph, we restrained our comparison to the
0.5-2.5
![]() separation regime.
separation regime.
Figure 18 compares the companion growth curves around high-mass and around solar-mass stars with the theoretical distribution expected from random association with an underlying uniform distribution across the field. On the one hand, massive stars seem to have their companions statistically further away than expected from a uniform repartition. On the other hand, the growth curve of solar-mass PMS stars follows the expected trend from random association. Yet in both cases a KS test does not allow us to reject the null hypothesis that both realisations are compatible with the uniform distribution in the considered separation range. Similarly, a two-sided KS test does not allow us to claim that both growth curves are different from one another.
5.6 Summary
To summarize the results of this section, the closest pair of detected
stars in our data is separated by 0.24
![]() (
(![]() 600 AU),
in good agreement with the IQ of Sect. 2.
Equation (6)
gives an empirical estimate of the maximum contrast achieved as a
function of the separation (Sect. 5.1). The
pairing properties are well described by chance alignment except for
the closest pairs (d<0.5
600 AU),
in good agreement with the IQ of Sect. 2.
Equation (6)
gives an empirical estimate of the maximum contrast achieved as a
function of the separation (Sect. 5.1). The
pairing properties are well described by chance alignment except for
the closest pairs (d<0.5
![]() )
and for the pairs with similar magnitude components (Fig. 14), yet we
identified 150 likely bound pairs (Sect. 5.2).
Massive stars further tend to have more companions than lower-mass
stars (Sect. 5.3).
Those companions are brighter on average, thus more massive
(Sect. 5.4).
The spatial distribution of the companions of massive stars is however
not significantly different from those of PMS star companions
(Sect. 5.5).
The significance of those results is better than 2
)
and for the pairs with similar magnitude components (Fig. 14), yet we
identified 150 likely bound pairs (Sect. 5.2).
Massive stars further tend to have more companions than lower-mass
stars (Sect. 5.3).
Those companions are brighter on average, thus more massive
(Sect. 5.4).
The spatial distribution of the companions of massive stars is however
not significantly different from those of PMS star companions
(Sect. 5.5).
The significance of those results is better than 2![]() but no better than 3
but no better than 3![]() ,
and remains thus limited. The situation is however reminiscent of the
case of NGC 6611 where Duchêne
et al. (2001) found that massive stars are more
likely to have bound companions compared to solar-mass stars. For
Tr 14, the fov is definitely more crowded and probably more
heavily contaminated, which seriously complicates both the
companionship analysis and the interpretation of the results.
,
and remains thus limited. The situation is however reminiscent of the
case of NGC 6611 where Duchêne
et al. (2001) found that massive stars are more
likely to have bound companions compared to solar-mass stars. For
Tr 14, the fov is definitely more crowded and probably more
heavily contaminated, which seriously complicates both the
companionship analysis and the interpretation of the results.
6 Observational biases
This section first describes an artificial star experiment designed to quantify the detection biases in the vicinity of the bright stars. It also presents two simple models that generalise the results of the artificial star experiment and provide an estimate of the impact of various observational biases on the results of this paper.
6.1 Artificial star experiment
Most of the difference in the companion properties of massive and
lower-mass stars are found for companions in the range ![]() .
In this section, we describe and analyse the results of an artificial
star experiment that aims at better understanding the limitation of our
data in that range, justifying some of the choices made
in the previous section. The PSF of the brightest sources indeed show
strong and extended wings,
which decrease the detection likelihood in the neighbourhood of a
bright star. As a by-product, the results of this experiment also
provide an
independent estimate of the photometric errors and of the completeness
of
our catalogue for the tested parameter range, but this is not our main
purpose.
.
In this section, we describe and analyse the results of an artificial
star experiment that aims at better understanding the limitation of our
data in that range, justifying some of the choices made
in the previous section. The PSF of the brightest sources indeed show
strong and extended wings,
which decrease the detection likelihood in the neighbourhood of a
bright star. As a by-product, the results of this experiment also
provide an
independent estimate of the photometric errors and of the completeness
of
our catalogue for the tested parameter range, but this is not our main
purpose.
The artificial star experiment follows a procedure similar to
that presented in
Momany
et al. (2008,2002). In particular, stars with
known H and ![]() magnitudes were simulated into
the individual H and
magnitudes were simulated into
the individual H and ![]() images using the PSF of each image and taking into account the
quadratic dependence of the PSF with the position in each frame. The
entire reduction procedure was then repeated
and the artificial stars were reduced as described in Sect. 2.
images using the PSF of each image and taking into account the
quadratic dependence of the PSF with the position in each frame. The
entire reduction procedure was then repeated
and the artificial stars were reduced as described in Sect. 2.
To the first order, stars brighter than ![]() in Tr 14 have masses of 10
in Tr 14 have masses of 10 ![]() or more
(see e.g. Fig. 7).
As in Sect. 5,
we adopted this limit for our massive star sample. We thus selected 14
bright stars with
or more
(see e.g. Fig. 7).
As in Sect. 5,
we adopted this limit for our massive star sample. We thus selected 14
bright stars with ![]() .
Around each of them we simulated 50 companions with
.
Around each of them we simulated 50 companions with ![]() and
and ![]() ,
spread in a 5
,
spread in a 5
![]() radius. The colour of the artificial stars were chosen to reproduce the
colour of typical PMS stars in Tr 14, which are
the dominant type of sources in that magnitude range.
radius. The colour of the artificial stars were chosen to reproduce the
colour of typical PMS stars in Tr 14, which are
the dominant type of sources in that magnitude range.
Seven hundred artificial stars were thus simulated in the H
and ![]() images.
To optimise the computation time of this complicated procedure, all the
artificial stars were added simultaneously. While this led to some
heavier crowding than in the original field, this will be
taken into account in the analysis. This further allows us to study the
detection biases using artificially controlled pairs.
images.
To optimise the computation time of this complicated procedure, all the
artificial stars were added simultaneously. While this led to some
heavier crowding than in the original field, this will be
taken into account in the analysis. This further allows us to study the
detection biases using artificially controlled pairs.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg19.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg143.png)
|
Figure 19:
Cumulative distribution functions (CDFs) of the distance from each
artificial star to (i) the closest artificial star (plain curve), (ii)
the closest source in field (dashed line), (iii) the closest bright
star with |
| Open with DEXTER | |
6.1.1 Separation distribution
Figure 19 shows the cumulative distribution of the separations of the artificial stars with respect to one another, with respect to the closest source in the field and with respect to the closest bright source in the field. It shows that we are able to investigate various ranges of separation, from the crowding of the artificial stars among themselves to the effect of field density. We firstfocus on the closest detections. The main results of the artificial star experiment in this respect are:
- 1.
- the closest recovered pair of artificial stars is separated
by
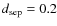
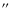 ,
in good agreement with the IQ derived earlier,
,
in good agreement with the IQ derived earlier,
- 2.
- the recovery fraction of artificial pairs for which both
components are further away
than 0.6
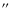 from any source in the image is better than 0.99 for
from any source in the image is better than 0.99 for 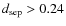
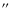 ,
,
- 3.
- excluding all pairs of artificial stars with
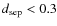
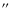 ,
the closest separation between a recovered artificial stars and a star
at least as bright is 0.23
,
the closest separation between a recovered artificial stars and a star
at least as bright is 0.23
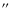 ,
,
- 4.
- similarly, the closest separation between a recovered
artificial star and a massive star (
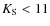 )
is 0.38
)
is 0.38
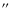 ,
in perfect agreement with what we found in our data (Sect. 5.2),
,
in perfect agreement with what we found in our data (Sect. 5.2),
- 5.
- all in all, there is a good agreement between the results of the artificial star experiment and the maximum reachable contrast as a function of the separation described empirically by Eq. (6).
6.1.2 Recovery fraction
To estimate the recovery fraction of solar-mass PMS stars in
the wings of the brighter massive stars, we first exclude all the close
artificial pairs from our analysis. We also exclude all the artificial
stars that fall closer than 0.3
![]() from any source fainter than
from any source fainter than ![]() in our data. With this we eliminate the uncertainties due
to (i) crowding among the artificial stars and (ii)
confusion between the artificial stars and the numerous field sources
in our data. Almost 500 artificial stars are left, providing a
decent coverage of the parameter space.
in our data. With this we eliminate the uncertainties due
to (i) crowding among the artificial stars and (ii)
confusion between the artificial stars and the numerous field sources
in our data. Almost 500 artificial stars are left, providing a
decent coverage of the parameter space.
Figure 21
shows the recovery fraction as a function of the separation to the
closest bright star. As mentioned earlier, the first detection occurs
for a separation of 0.38
![]() .
For
.
For ![]()
![]() ,
all the artificial stars are recovered. Between 0.38
,
all the artificial stars are recovered. Between 0.38
![]() and 0.53
and 0.53
![]() ,
the recovery fraction is approximately 0.4 and remains constant over
the interval.
,
the recovery fraction is approximately 0.4 and remains constant over
the interval.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg20.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg149.png)
|
Figure 20:
Lower panel: comparison between the input and
output magnitudes for the artificial star experiment as a function of
the separation the to closest bright star in the fov (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13688fg21.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg150.png)
|
Figure 21:
Artificial star recovery fraction as a function of the distance d
to a bright neighbour (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13688fg22.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg151.png)
|
Figure 22: Detection probability as a function of the stellar magnitude resulting from the effect of the crowding in the Tr 14 fov. |
| Open with DEXTER | |
6.1.3 Photometric uncertainties
The comparison between the artificial star input (
![]() )
and recovered (
)
and recovered (
![]() )
magnitudes provides us with a more realistic estimate of the
photometric errors (Fig. 20). It reveals
that the accuracy of both the retrieved magnitudes and of the colour
term is significantly affected within
)
magnitudes provides us with a more realistic estimate of the
photometric errors (Fig. 20). It reveals
that the accuracy of both the retrieved magnitudes and of the colour
term is significantly affected within ![]() 1
1
![]() from a bright star, the fainter companion being up to 0.1 mag
too red. It also reveals a slight systematic shift in the retrieved
colour and magnitudes, even at larger distance. Rejecting the few
significantly deviant points resulting from the crowding, we obtained
for the artificial stars more distant than 1.5
from a bright star, the fainter companion being up to 0.1 mag
too red. It also reveals a slight systematic shift in the retrieved
colour and magnitudes, even at larger distance. Rejecting the few
significantly deviant points resulting from the crowding, we obtained
for the artificial stars more distant than 1.5
![]() from the closest bright star
from the closest bright star
| = | (10) | ||
| = | (11) | ||
| = | (12) |
Those are slightly larger deviations that the formal errors of the PSF photometry (Fig. 6). The systematic increase of the
6.2 Analytical models
6.2.1 Impact of crowding
Given the very steep transition in the detection probability once the separation to a brighter source increases, and because the artificial star experiment generally agrees with the empirical detection limit given by Eq. (9), one can develop a very simple model to estimate the impact of the crowding in the field. It relies on the following hypotheses:
- 1.
- a brighter star is always detected if falling on top of or very close to a fainter one,
- 2.
- non-detection is the consequence of shadowing by brighter stars in the fov,
- 3.
- the spatial distribution of the stars in the field is random.
where
6.2.2 Companion detection threshold
In Sects. 5.3
to 5.5,
we focused our analysis to the 0.5-2.5
![]() separations. In this section, we develop again a simple model to better
quantify the impact of the observational biases in that range. As
above, we use Eq. (9)
to define the region where a star outshines close fainter neighbours
given the magnitude contrast of the pair. In particular, the detection
probability of a neighbour of magnitude
separations. In this section, we develop again a simple model to better
quantify the impact of the observational biases in that range. As
above, we use Eq. (9)
to define the region where a star outshines close fainter neighbours
given the magnitude contrast of the pair. In particular, the detection
probability of a neighbour of magnitude ![]() in the vicinity of a
in the vicinity of a ![]() central star can be modelled as the ratio between the area where one of
the components does not outshine the other and the total area
considered. For an annulus region
central star can be modelled as the ratio between the area where one of
the components does not outshine the other and the total area
considered. For an annulus region ![]() around the central star, the detection probability can thus be written
as
around the central star, the detection probability can thus be written
as
Figure 23 compares the detection probability in the 0.5-2.5
Our results show that the detection of the companions to
intermediate-mass stars (
![]() )
and to solar-mass PMS stars (
)
and to solar-mass PMS stars (
![]() )
stars is mostly unaffected. As expected, the lower mass PMS (
)
stars is mostly unaffected. As expected, the lower mass PMS (
![]() )
are less likely to be found close to a bright stars. However, taking
into account the number of bright stars in the field, one can prove
this to be completely negligible. The largest biases are affecting the
companions of bright stars.
)
are less likely to be found close to a bright stars. However, taking
into account the number of bright stars in the field, one can prove
this to be completely negligible. The largest biases are affecting the
companions of bright stars. ![]() is passing below 0.9 at
is passing below 0.9 at
![]() and below 0.5 at
and below 0.5 at
![]() .
One can further show that up to one companion per star is likely lost
at
.
One can further show that up to one companion per star is likely lost
at ![]() in Fig. 16.
in Fig. 16.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg23.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg172.png)
|
Figure 23:
Detection probability model for pairs with separation in the range of
0.5
|
| Open with DEXTER | |
7 Mass segregation
As introduced in Sect. 4.3,
the more massive MS stars seem more concentrated towards the
cluster centre than the lower mass PMS stars. The best-fit
EFF87 profiles (Table 4)
confirm that this difference is indeed significant at the 4![]() level. This could be interpreted as a hint for mass segregation,
although Ascenso et al. (2009)
warned against hasty conclusions because numerous observational biases
are actually favouring the detection of mass segregation, even in
non-segregated clusters.
level. This could be interpreted as a hint for mass segregation,
although Ascenso et al. (2009)
warned against hasty conclusions because numerous observational biases
are actually favouring the detection of mass segregation, even in
non-segregated clusters.
Allison et al.
(2009) recently introduced an alternative method to
investigate mass segregation, which is insensitive to biases like the
exact location of the cluster centre, and less sensitive (although
quantification is still lacking) to the incompleteness effects. Their
method compared the minimum spanning tree (MST), the shortest open path
connecting all points of a sample, of the massive stars to the
equivalent path of low mass stars (see Allison
et al. for a full description of the algorithm). The
mass segregation ratio (
![]() ), i.e. the ratio between the
average random path length and that of the massive stars, allows them
to quantify the deviation between the massive star sample and the
reference sample. Following their approach, Fig. 24 displays the
evolution of
), i.e. the ratio between the
average random path length and that of the massive stars, allows them
to quantify the deviation between the massive star sample and the
reference sample. Following their approach, Fig. 24 displays the
evolution of ![]() with the adopted magnitude limit (
with the adopted magnitude limit (
![]() )
for the massive star sample. The reference distribution consists of
stars with
)
for the massive star sample. The reference distribution consists of
stars with ![]() and was drawn 500 times from our catalogue, with each sample
containing the same number of stars as found in the bright sample. The
dispersion obtained gives us the error bars on
and was drawn 500 times from our catalogue, with each sample
containing the same number of stars as found in the bright sample. The
dispersion obtained gives us the error bars on ![]() as displayed in Fig. 24.
In the above procedure, we deliberately remained far from the limiting
magnitude of our catalogue to minimize the completion biases. The
method is in principle still affected by crowding and by the shadowing
in the vicinity of bright stars. We showed in Sect. 6.1.2
however that the former effect had a very limited impact down to
as displayed in Fig. 24.
In the above procedure, we deliberately remained far from the limiting
magnitude of our catalogue to minimize the completion biases. The
method is in principle still affected by crowding and by the shadowing
in the vicinity of bright stars. We showed in Sect. 6.1.2
however that the former effect had a very limited impact down to ![]() at least. The effect of the shadowing in the vicinity of bright stars
is more difficult to estimate, although one can expect that the
absolute number of
at least. The effect of the shadowing in the vicinity of bright stars
is more difficult to estimate, although one can expect that the
absolute number of ![]() stars lost is proportionally very small compared to the number of stars
in that interval. This results from the low number of bright stars and
from the limited radius at which they can outshine a fainter neighbour.
stars lost is proportionally very small compared to the number of stars
in that interval. This results from the low number of bright stars and
from the limited radius at which they can outshine a fainter neighbour.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg24.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg175.png)
|
Figure 24:
Evolution of |
| Open with DEXTER | |
Because the sensitivity of the MST to the completeness of a sample is not fully understood (Allison et al. 2009), we cannot draw firm conclusions. We note however that two independent methods, profile fitting and MST analysis, both point towards mass segregation, as can be expected for the most massive stars in such a cluster.
Obviously our observations only allow us to investigate the
current mass segregation status of the cluster and we cannot
distinguish whether this segregation, if confirmed, is primordial or is
the product of early dynamical evolution. Given the expected cluster
mass and size and its stellar contents as obtained in Sect. 4.3 after colour
selection, we estimated the typical dynamical friction time-scale ![]() of 10
of 10 ![]() and 20
and 20 ![]() stars (corresponding to resp.
stars (corresponding to resp. ![]() mag
and 9.5 mag in our data). Following Spitzer
& Hart (1971) and Portegies Zwart
& McMillan (2002), we obtained
mag
and 9.5 mag in our data). Following Spitzer
& Hart (1971) and Portegies Zwart
& McMillan (2002), we obtained ![]() yr
and
yr
and ![]() yr respectively.
Considering the estimated age of the cluster, 3-5
yr respectively.
Considering the estimated age of the cluster, 3-5
![]() yr, the dynamical
friction time-scales agree with the results of Fig. 24, where mass
segregation begins to appear somewhere between 10
yr, the dynamical
friction time-scales agree with the results of Fig. 24, where mass
segregation begins to appear somewhere between 10 ![]() and
20
and
20 ![]() .
As a consequence, if mass segregation is confirmed, it does not need to
be primordial but can probably be explained by dynamical evolution.
.
As a consequence, if mass segregation is confirmed, it does not need to
be primordial but can probably be explained by dynamical evolution.
8 Summary and conclusions
Using the ESO MCAO demonstrator MAD, we have acquired deep H
and ![]() photometry of a 2
photometry of a 2![]() region around the central part of Tr 14. The
average IQ of our campaign is about 0.2
region around the central part of Tr 14. The
average IQ of our campaign is about 0.2
![]() and the dynamic range is about 10 mag. The image presented in
Fig. 1
is by far the largest AO-corrected mosaic ever acquired.
and the dynamic range is about 10 mag. The image presented in
Fig. 1
is by far the largest AO-corrected mosaic ever acquired.
Using PSF photometry, we investigated the sensitivity of faint companions detected in the vicinity of bright sources. We derived several empirical relations that can be used as input for instrumental simulations, to estimate the performance of AO techniques versus seeing-limited techniques or, as done later in this paper, to build first-order analytical models of the impact of some observational biases. In particular, the contrast vs. separation limit has been validated over a 5 mag range by an artificial star experiment.
Despite a probably significant contamination by field stars,
the Tr 14 CMD shows a very clear PMS population. Its
location in the CMD can be reproduced by PMS isochrones with
contraction ages of 3 to ![]() yr.
Interestingly, Tr 14 cannot be significantly further away than
the distance obtained by Carraro
et al. (2004) i.e., 2.5 kpc, as this would
result in an even earlier contraction age. We derive the surface
density profile of the cluster core and of different subpopulations.
For stars brighter than
yr.
Interestingly, Tr 14 cannot be significantly further away than
the distance obtained by Carraro
et al. (2004) i.e., 2.5 kpc, as this would
result in an even earlier contraction age. We derive the surface
density profile of the cluster core and of different subpopulations.
For stars brighter than ![]() mag, the surface density profiles are well reproduced by EFF87 profiles
over our full fov, and we provide quantitative constraints on the
spatial extent of the cluster and on its stellar contents. Adopting the
core-halo description suggested by Ascenso
et al. (2007), we report that the transition between
the core and the halo is not covered by our data, implying that the
core is strictly dominating the density profile in a radius of
0.9 pc at least. Using colour criteria to select the most
likely cluster members, the density profiles of the more massive
MS stars are best described by a power-law (or, equivalently,
by an EFF87 profile with a very small core radius).
mag, the surface density profiles are well reproduced by EFF87 profiles
over our full fov, and we provide quantitative constraints on the
spatial extent of the cluster and on its stellar contents. Adopting the
core-halo description suggested by Ascenso
et al. (2007), we report that the transition between
the core and the halo is not covered by our data, implying that the
core is strictly dominating the density profile in a radius of
0.9 pc at least. Using colour criteria to select the most
likely cluster members, the density profiles of the more massive
MS stars are best described by a power-law (or, equivalently,
by an EFF87 profile with a very small core radius).
We also investigated the companionship properties in
Tr 14. We showed that the number of companions and the pair
association process is on average well reproduced by chance alignment
from a uniform population randomly distributed across the field. Only
stars with a brightness ratio close to unity or with a separation of
less less than 0.5
![]() cannot be explained by spuriousalignment and are thus true binary
candidates. This does not imply that large light-ratio and/or wider
pairs do not exist, but rather that they cannot be individually
disentangled with statistical arguments. Still, 19% of our massive star
sample have a high probability physical companion.
cannot be explained by spuriousalignment and are thus true binary
candidates. This does not imply that large light-ratio and/or wider
pairs do not exist, but rather that they cannot be individually
disentangled with statistical arguments. Still, 19% of our massive star
sample have a high probability physical companion.
Focusing on the 0.5
![]() -2.5
-2.5
![]() separation range, where the observational biases are unable to
invalidate our results, we compared the companion distributions of
massive stars with those of lower mass stars. In Tr 14, the
high-mass stars (M>10
separation range, where the observational biases are unable to
invalidate our results, we compared the companion distributions of
massive stars with those of lower mass stars. In Tr 14, the
high-mass stars (M>10 ![]() )
tend to have more solar-mass companions than lower-mass comparison
samples. Those companions are brighter on average, thus more massive.
Finally, no difference could be found in the spatial distribution of
the companions of low and high-mass stars.
)
tend to have more solar-mass companions than lower-mass comparison
samples. Those companions are brighter on average, thus more massive.
Finally, no difference could be found in the spatial distribution of
the companions of low and high-mass stars.
Lastly, we employed the MST technique of Allison et al. (2009)
to investigate possible mass segregation in Tr 14. Again we
found marginally significant results (at the 1.5![]() level), suggesting
some degree of mass segregation for the more massive stars of the
cluster (M>10
level), suggesting
some degree of mass segregation for the more massive stars of the
cluster (M>10 ![]() ). Although the sensitivity of
the method to incompleteness is still not fully quantified, we note
that early dynamical evolution can reproduce the observed hints of mass
segregation in Tr 14, despite the cluster's young age.
). Although the sensitivity of
the method to incompleteness is still not fully quantified, we note
that early dynamical evolution can reproduce the observed hints of mass
segregation in Tr 14, despite the cluster's young age.
The authors are greatly indebted to Paola Amico and to the MAD SD team for their excellent support during the preparation and execution of the observations. We also express our thanks to the referee for his help, which clarified the manuscript, and to Dr. Joana Ascenso for useful discussions.
References
- Allison, R. J., Goodwin, S. P., Parker, R. J., et al. 2009, MNRAS, 395, 1449 [Google Scholar]
- Ascenso, J., Alves, J., Vicente, S., & Lago, M. T. V. T. 2007, A&A, 476, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ascenso, J., Alves, J., & Lago, M. T. V. T. 2009, A&A, 495, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baume, G., Vázquez, R. A., & Carraro, G. 2004, MNRAS, 355, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, M. A., Evans, C. J., Mackey, A. D., et al. 2010, MNRAS, 405, 421 [NASA ADS] [Google Scholar]
- Carraro, G., Romaniello, M., Ventura, P., & Patat, F. 2004, A&A, 418, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Wit, W. J., Testi, L., Palla, F., & Zinnecker, H. 2005, A&A, 437, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G., Simon, T., Eislöffel, J., & Bouvier, J. 2001, A&A, 379, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elson, R. A. W., Fall, S. M., & Freeman, K. C. 1987, ApJ, 323, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., & Bomans, D. J. 2008, A&A, 490, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lejeune, T., & Schaerer, D. 2001, A&A, 366, 538 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz-Apellániz, J., Walborn, N. R., Galué, H. Á., & Wei, L. H. 2004, ApJS, 151, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Marchetti, E., Brast, R., Delabre, B., et al. 2007, The Messenger, 129, 8 [NASA ADS] [Google Scholar]
- Mason, B. D., Hartkopf, W. I., Gies, D. R., Henry, T. J., & Helsel, J. W. 2009, AJ, 137, 3358 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Momany, Y., Held, E. V., Saviane, I., & Rizzi, L. 2002, A&A, 384, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Momany, Y., Ortolani, S., Bonatto, C., Bica, E., & Barbuy, B. 2008, MNRAS, 391, 1650 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1993, ApJ, 418, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., & McMillan, S. L. W. 2002, ApJ, 576, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., & Le Bouquin, J.-B. 2009, in The interferometric view of hot stars, ed. T. Rivinius, & M. Curé, Rev. Mex. Conf. Ser., 38, 27 [Google Scholar]
- Sana, H., Gosset, E., Nazé, Y., Rauw, G., & Linder, N. 2008, MNRAS, 386, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Gosset, E., & Evans, C. J. 2009, MNRAS, 400, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. J., & Hart, M. H. 1971, ApJ, 164, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1994, PASP, 106, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. H., ten Brummelaar, T. A., Roberts, L. C., et al. 2008, AJ, 136, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Vazquez, R. A., Baume, G., Feinstein, A., & Prado, P. 1996, A&AS, 116, 75 [NASA ADS] [Google Scholar]
Footnotes
- ... 14
![[*]](/icons/foot_motif.png)
- Based on observations obtained with the MCAO Demonstrator (MAD) at the VLT Melipal Nasmyth focus (ESO public data release).
- ...
![[*]](/icons/foot_motif.png)
- Full Tables 3 and 5 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/515/A26
- ... value
![[*]](/icons/foot_motif.png)
- This value is often referred to as the core radius. Because
Tr 14 displayed a core-halo structure,
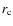 should be understood as the core radius of the core itself.
should be understood as the core radius of the core itself.
- ... difference
![[*]](/icons/foot_motif.png)
- Below, the brightest star of a pair is adopted as the
primary. We adopt the convention
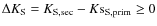 ,
where
,
where 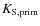 and
and 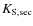 are the primary and secondary magnitudes respectively.
are the primary and secondary magnitudes respectively.
All Tables
Table 1: Field centering (F.C.) for on-object (Tr 14) and on-sky observations and coordinates of the natural guide stars (NGSs).
Table 2: Log of the MAD observations of Tr 14.
Table 3: Photometric catalogue of the sources detected in Tr 14.
Table 4: Best-fit EFF87 parameters for different populations in Tr 14.
Table 5:
List of likely bound visual pairs (
![]() ).
).
All Figures
![\begin{figure}
\par\includegraphics[width=6cm,clip]{13688fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg39.png)
|
Figure 1:
2MASS K band image of Tr 14. The cross and
the large circle indicate the centre and the size of the 2 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,angle=-90,clip]{13688fg2a.eps} \includegraphics[width=8.5cm,angle=-90,clip]{13688fg2b.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg46.png)
|
Figure 2: Averaged FWHM and Strehl ratio maps as computed over the MAD field of view (yellow circle). The three red crosses show the locations of the NGSs. North is to the top and East to the right. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{13688fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg47.png)
|
Figure 3:
False colour image of the 2 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg48.png)
|
Figure 4:
Close-up view of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg49.png)
|
Figure 5:
Comparison of the H ( upper panel)
and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13688fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg69.png)
|
Figure 6:
H and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13688fg7.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg71.png)
|
Figure 7:
Left: Tr 14 CMD for DP #1.
Middle: CMD for DP #4. Right: complete
Tr 14 CMD (DP#1 to 4). The dashed lines show the
MS from Lejeune &
Schaerer (2001) and from Palla
& Stahler (1993) for stars with masses M>6 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13688fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg78.png)
|
Figure 8: Tr 14 CMD. The plain lines delimit the adopted locus of cluster members (see text) while the stars show the objects not considered in Sect. 5. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg9.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg79.png)
|
Figure 9:
Distribution of the reddest and bluest stars in Tr14. The dot and the
open circles show the location of the faint (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13688fg10a.eps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{13688fg10b.eps}\vspace{2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg96.png)
|
Figure 10:
Tr 14 surface number density distributions for the full
cluster population (circles) and for the PMS (triangles) and
MS (diamonds) populations. Upper and lower panels
show the density profiles obtained, respectively, before and after
applying the colour criteria of Fig. 8. In both
cases only stars with magnitude |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg105.png)
|
Figure 11:
Cumulative distribution of the distance to the closest
neighbour (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg106.png)
|
Figure 12:
Magnitude difference |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg13.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg108.png)
|
Figure 13:
Probability that a pair is physically bound |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg14.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg109.png)
|
Figure 14:
Same as Fig. 12
where the population of likely bound systems has been over-plotted with
red (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13688fg15.eps} \vspace{-3mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg122.png)
|
Figure 15:
Close-up view in the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg16.eps} \vspace{-2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg123.png)
|
Figure 16:
Left: average number of companions per star
for a given maximum companion magnitude. Right:
cumulative distribution functions (CDF) of the companion brightness.
The central stars are taken in four ranges as indicated in the upper
left-hand legend. Only pairs with separations in the range of 0.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg17.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg135.png)
|
Figure 17:
Average number of companions per star as a function of the companion
brightness. The central stars are taken in four ranges as indicated in
the upper left-hand legend. A moving average with a 2 mag bin
has been used and the considered separation range is 0.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg18.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg137.png)
|
Figure 18: Upper panel: growth curve for the companions of massive stars. The plain line indicates the expected distribution for a uniform distribution of the companions in the field of view. Lower panel: same as upper panel for the companions of solar-mass stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg19.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg143.png)
|
Figure 19:
Cumulative distribution functions (CDFs) of the distance from each
artificial star to (i) the closest artificial star (plain curve), (ii)
the closest source in field (dashed line), (iii) the closest bright
star with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg20.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg149.png)
|
Figure 20:
Lower panel: comparison between the input and
output magnitudes for the artificial star experiment as a function of
the separation the to closest bright star in the fov (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13688fg21.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg150.png)
|
Figure 21:
Artificial star recovery fraction as a function of the distance d
to a bright neighbour (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13688fg22.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg151.png)
|
Figure 22: Detection probability as a function of the stellar magnitude resulting from the effect of the crowding in the Tr 14 fov. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg23.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg172.png)
|
Figure 23:
Detection probability model for pairs with separation in the range of
0.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13688fg24.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13688-09/Timg175.png)
|
Figure 24:
Evolution of |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.