| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 26 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913510 | |
| Published online | 08 June 2010 | |
Initial phases of massive star formation in high infrared extinction clouds![[*]](/icons/foot_motif.png) ,
,![[**]](/icons/foot_motif.png)
I. Physical parameters
K. L. J. Rygl![]() -
F. Wyrowski - F. Schuller - K. M. Menten
-
F. Wyrowski - F. Schuller - K. M. Menten
Max-Planck-Institut für Radioastronomie (MPIfR), Auf dem Hügel 69, 53121 Bonn, Germany
Received 20 October 2009 / Accepted 15 March 2010
Abstract
Aims. The earliest phases of massive star formation are
found in cold and dense infrared dark clouds (IRDCs). Since the
detection method of IRDCs is very sensitive to the local properties of
the background emission, we present here an alternative method to
search for high column density in the Galactic plane by using infrared
extinction maps. Using this method we find clouds between 1
and 5 kpc, of which many were missed by previous
surveys. By studying the physical conditions of a subsample of
these clouds, we aim at a better understanding of the initial
conditions of massive star formation.
Methods. We have made extinction maps of the Galactic plane based on the 3.6-4.5 ![]() m color excess between the two shortest wavelength Spitzer IRAC bands, reaching to visual extinctions of
m color excess between the two shortest wavelength Spitzer IRAC bands, reaching to visual extinctions of ![]() 100 mag and column densities of 9
100 mag and column densities of 9 ![]()
![]() .
From this we compiled a new sample of cold and compact high extinction
clouds. We used the MAMBO array at the IRAM 30 m telescope to
study the morphology, masses and densities of the clouds and the dense
clumps within them. The latter were followed up by pointed ammonia
observations with the 100 m Effelsberg telescope,
to determine rotational temperatures and kinematic distances.
.
From this we compiled a new sample of cold and compact high extinction
clouds. We used the MAMBO array at the IRAM 30 m telescope to
study the morphology, masses and densities of the clouds and the dense
clumps within them. The latter were followed up by pointed ammonia
observations with the 100 m Effelsberg telescope,
to determine rotational temperatures and kinematic distances.
Results. Extinction maps of the Galactic plane trace large scale
structures such as the spiral arms. The extinction method probes lower
column densities,
![]()
![]()
![]() ,
than the 1.2 mm continuum, which reaches up to
,
than the 1.2 mm continuum, which reaches up to
![]()
![]()
![]() but is less sensitive to large scale structures. The 1.2 mm
emission maps reveal that the high extinction clouds contain extended
cold dust emission, from filamentary structures to still diffuse
clouds. Most of the clouds are dark in 24
but is less sensitive to large scale structures. The 1.2 mm
emission maps reveal that the high extinction clouds contain extended
cold dust emission, from filamentary structures to still diffuse
clouds. Most of the clouds are dark in 24 ![]() m,
but several show already signs of star formation via maser emission or
bright infrared sources, suggesting that the high extinction clouds
contain a variety of evolutionary stages. The observations suggest an
evolutionary scheme from dark, cold and diffuse clouds, to clouds
with a stronger 1.2 mm peak and to finally clouds with many strong
1.2 mm peaks, which are also warmer, more turbulent and already
have some star formation signposts.
m,
but several show already signs of star formation via maser emission or
bright infrared sources, suggesting that the high extinction clouds
contain a variety of evolutionary stages. The observations suggest an
evolutionary scheme from dark, cold and diffuse clouds, to clouds
with a stronger 1.2 mm peak and to finally clouds with many strong
1.2 mm peaks, which are also warmer, more turbulent and already
have some star formation signposts.
Key words: dust, extinction - ISM: clouds - ISM: structure - stars: formation - radio lines: ISM - submillimeter: ISM
1 Introduction
Massive stars play a fundamental role in the evolution of galaxies through their strong UV radiation, stellar winds and supernovae explosions, which contribute to the chemical enrichment of the interstellar medium. Massive stars are rare, hence usually found at large distances. They form very rapidly while still deeply embedded in their natal molecular clouds. These characteristics impose several observational obstacles, like the necessity of high resolution and sensitivity in an un-absorbed frequency range, to study their formation.
Currently, the earliest stage of massive star formation is
thought to take place in the very dense clumps found in infrared dark
clouds (IRDCs). The properties of IRDCs are shown by Carey et al. (1998) to be dense (
![]() )
and cool (T <
)
and cool (T <
![]() )
aggregations of gas and dust in the Galaxy. They contain clumps with typical masses of
)
aggregations of gas and dust in the Galaxy. They contain clumps with typical masses of
![]() (Rathborne et al. 2006; Simon et al. 2006b; Pillai et al. 2006). From IRDC clumps to the next stage, the high-mass protostellar objects (HMPOs, Beuther et al. 2002; Sridharan et al. 2002), the temperatures increase (
(Rathborne et al. 2006; Simon et al. 2006b; Pillai et al. 2006). From IRDC clumps to the next stage, the high-mass protostellar objects (HMPOs, Beuther et al. 2002; Sridharan et al. 2002), the temperatures increase (
![]() ), the line widths increase, densities and masses rise (Motte et al. 2007). HMPOs are usually found prior to the formation of ultra compact H II (UCH II) regions, before the newly formed star begins to ionize its surrounding medium.
), the line widths increase, densities and masses rise (Motte et al. 2007). HMPOs are usually found prior to the formation of ultra compact H II (UCH II) regions, before the newly formed star begins to ionize its surrounding medium.
Motte et al. (2007) demonstrated the difficulty of finding massive objects in an early evolutionary phase: in their survey of 3 deg2
in Cygnus X, they found little evidence for dense clumps without
any trace of star formation, however dense clumps with already ongoing
star formation were found to be abundantly present. Based on these
results, the statistical life time of the high-mass protostars and
prestellar cores was estimated ![]()
![]() 104 yr (Motte et al. 2007), which is much shorter than what is found in nearby low-mass star-forming regions:
104 yr (Motte et al. 2007), which is much shorter than what is found in nearby low-mass star-forming regions: ![]() 3
3 ![]() 105 yr (Kirk et al. 2005).
It is these very early stages, which provide important clues to
construct a theoretical model of massive star formation, since the
initial fragmentation of the gas and dust in a clump will be different
in the case of monolithical collapse (Krumholz et al. 2009) compared to the
competitive accretion model (Clark et al. 2008; Bonnell et al. 2001).
105 yr (Kirk et al. 2005).
It is these very early stages, which provide important clues to
construct a theoretical model of massive star formation, since the
initial fragmentation of the gas and dust in a clump will be different
in the case of monolithical collapse (Krumholz et al. 2009) compared to the
competitive accretion model (Clark et al. 2008; Bonnell et al. 2001).
Massive stars generally form in clusters (Lada & Lada 2003), of which the precursors are massive clumps or the so-called precluster forming clumps, hereafter just clumps, of a ![]() 1 pc size. For many massive star-forming regions, we do not yet have the capacity to resolve the clumps into
prestellar cores and study the fragmentation (Beuther et al. 2007; Zhang et al. 2009; Rathborne et al. 2007,2008; Swift 2009).
In this paper, we report on the physical parameters of the clumps,
such as their morphology, density and temperature. Based on this,
we hypothesize on an evolutionary sequence of cluster formation.
1 pc size. For many massive star-forming regions, we do not yet have the capacity to resolve the clumps into
prestellar cores and study the fragmentation (Beuther et al. 2007; Zhang et al. 2009; Rathborne et al. 2007,2008; Swift 2009).
In this paper, we report on the physical parameters of the clumps,
such as their morphology, density and temperature. Based on this,
we hypothesize on an evolutionary sequence of cluster formation.
Our understanding of the clumps increased considerably with the
discovery of IRDCs. IRDCs are detected by a local absence of infrared
(IR) emission against the diffuse mid IR emission of the
Galactic plane (Perault et al. 1996; Egan et al. 1998) and are observed numerously throughout the Milky Way (Simon et al. 2006b). At the typical low temperatures of IRDCs (![]() K),
the dust emission peaks in the far-infrared and is optically thin
at mm/submm wavelengths. For a majority of IRDCs the mm dust
emission coincides with the morphology of the IR absorption (Rathborne et al. 2006; Pillai et al. 2006). Many clumps in IRDCs show signs of star formation via infrared emission at 24
K),
the dust emission peaks in the far-infrared and is optically thin
at mm/submm wavelengths. For a majority of IRDCs the mm dust
emission coincides with the morphology of the IR absorption (Rathborne et al. 2006; Pillai et al. 2006). Many clumps in IRDCs show signs of star formation via infrared emission at 24 ![]() m, or SiO emission from shocks driven by outflows (Motte et al. 2007; Beuther & Sridharan 2007; Chambers et al. 2009).
Observations tell that clumps in IRDCs span a very wide range of
masses, indicating that not all will form clusters with massive stars (Rathborne et al. 2006; Pillai et al. 2006).
m, or SiO emission from shocks driven by outflows (Motte et al. 2007; Beuther & Sridharan 2007; Chambers et al. 2009).
Observations tell that clumps in IRDCs span a very wide range of
masses, indicating that not all will form clusters with massive stars (Rathborne et al. 2006; Pillai et al. 2006).
The detection method of IRDCs is very sensitive to the local properties
of the background emission.
Also, not all massive dust condensations will be infrared dark if
there is enough foreground emission. Hence, to find the high mass
end of molecular clouds in an unbiased fashion, new, complementary
approaches are needed. We have developed such a new method, well known
from studies of low mass star-forming regions, to target more
efficiently the most massive clouds: Lada et al. (1994)
pioneered the method of measuring high amounts of extinction through
stellar color excess in the infrared. Applied to the 2 ![]() m data of the 2MASS survey, they covered the range up to 40 mag in visual extinction,
m data of the 2MASS survey, they covered the range up to 40 mag in visual extinction, ![]() .
However, this is not sufficient to probe the dense birthplaces of massive stars. Here the results of the Spitzer space telescope GLIMPSE survey (Benjamin et al. 2003) came to help: by applying the extinction curve of Indebetouw et al. (2005) we have extended the color excess method to reach up to peaks in
.
However, this is not sufficient to probe the dense birthplaces of massive stars. Here the results of the Spitzer space telescope GLIMPSE survey (Benjamin et al. 2003) came to help: by applying the extinction curve of Indebetouw et al. (2005) we have extended the color excess method to reach up to peaks in ![]() of
of ![]() 100 mag (or column densities
100 mag (or column densities
![]() of 9
of 9 ![]() 1022 cm-2),
thus entering the realm where massive star formation becomes possible.
The extinction method, however, is limited by the number of
available background stars, and will therefore detect mainly nearby
clouds (discussed in Sect. 2.1).
In the meanwhile, complementary, unbiased dust continuum surveys
were carried out: the ATLASGAL survey of the complete inner
Galactic plane at 870
1022 cm-2),
thus entering the realm where massive star formation becomes possible.
The extinction method, however, is limited by the number of
available background stars, and will therefore detect mainly nearby
clouds (discussed in Sect. 2.1).
In the meanwhile, complementary, unbiased dust continuum surveys
were carried out: the ATLASGAL survey of the complete inner
Galactic plane at 870 ![]() m by Schuller et al. (2009) and the 1.1 mm BOLOCAM survey (Rosolowsky et al. 2010) of the Galactic plane accessible from the northern hemisphere.
m by Schuller et al. (2009) and the 1.1 mm BOLOCAM survey (Rosolowsky et al. 2010) of the Galactic plane accessible from the northern hemisphere.
We selected the more compact and high extinction (mean
![]() or
or
![]()
![]() 1022 cm-2) sources from large scale extinction maps of the inner Galactic plane (
1022 cm-2) sources from large scale extinction maps of the inner Galactic plane (
![]() ,
,
![]() ). These high extinction clouds (HECs) were studied in the millimeter dust continuum and the rotational transitions of ammonia (
). These high extinction clouds (HECs) were studied in the millimeter dust continuum and the rotational transitions of ammonia (
![]() ).
).
![]() has proven to be a reliable tracer of dense gas in dark clouds: not only does the
has proven to be a reliable tracer of dense gas in dark clouds: not only does the
![]() emission
match the submillimeter dust emission peaks (Pillai et al. 2006), but also do observations show
that, unlike other molecules,
emission
match the submillimeter dust emission peaks (Pillai et al. 2006), but also do observations show
that, unlike other molecules,
![]() does not deplete from the gas phase for typical IRDC densities - Pagani et al. (2005) observed that
does not deplete from the gas phase for typical IRDC densities - Pagani et al. (2005) observed that
![]() depletes at densities of
depletes at densities of
![]() in agreement with the prediction of Bergin & Langer (1997). Moreover, throughout the evolutionary stages of massive star formation,
in agreement with the prediction of Bergin & Langer (1997). Moreover, throughout the evolutionary stages of massive star formation,
![]() shows an increasing trend in averaged line widths and temperatures from less to more evolved sources (Pillai et al. 2006), which indicates that the
shows an increasing trend in averaged line widths and temperatures from less to more evolved sources (Pillai et al. 2006), which indicates that the
![]() molecule is also a tracer of evolutionary phase.
molecule is also a tracer of evolutionary phase.
This study presents an overview from the high extinction complexes on Galactic size-scales, covering several tens of parsecs, to the clumps found in the 1.2 mm continuum of 0.1-0.7 pc in size. The connection between the largest and smallest scale is important for a comprehensive view of cluster formation in giant molecular clouds. In Sect. 2, we present the method of extinction mapping. Observations and data reduction are described in Sect. 3, and the results follow in Sect. 4. The analysis and discussion of the physical parameters are given in Sect. 5, and are compared to previous studies and theoretical predictions in Sect. 6.
2 High extinction clouds
2.1 Method: extinction mapping
The overall distribution of dust in a cloud can be traced by the extinction of background starlight at visual and near-infrared wavelengths as it passes through a cloud (Lada et al. 1994). Since extinction decreases with wavelength, observations at longer wavelengths probe deeper into the cloud and trace denser regions. Additionally the number of detectable background stars increases at these wavelengths. With the advance of infrared cameras it became possible to detect several hundreds of background stars through a cloud, allowing to convert the infrared images covering them in extinction maps of useful resolution.
The GLIMPSE survey employed the Infrared Array Cameras (Fazio et al. 2004) onboard the Spitzer Space telescope, operating at 3.6, 4.5, 5.8 and 8.0 ![]() m. We used the data provided by the GLIMPSE I survey (release April 2005), which covered longitudes of
m. We used the data provided by the GLIMPSE I survey (release April 2005), which covered longitudes of
![]() ,
,
![]() with
with
![]() .
The calibration of the data is described in Reach et al. (2005). The inner 20
.
The calibration of the data is described in Reach et al. (2005). The inner 20![]() of the Galactic Plane, except for the innermost
of the Galactic Plane, except for the innermost
![]() ,
was taken from the GLIMPSE II survey (2007).
,
was taken from the GLIMPSE II survey (2007).
To construct the extinction maps we used the averaged (3.6-4.5 ![]() m) color excess, because the
extinction law determination for these wavelengths is the most accurate of all the Spitzer bands.
The averaged color excess,
m) color excess, because the
extinction law determination for these wavelengths is the most accurate of all the Spitzer bands.
The averaged color excess,
![]() ,
was calculated from the color excess in a large scale field (a box of size
,
was calculated from the color excess in a large scale field (a box of size
![]()
![]()
![]() ):
):
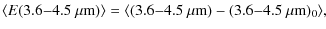
|
(1) |
where the background stars are taken to be common-type K giants. Measurements of
The color excess map can be contaminated by embedded stars in the cloud itself or by foreground stars. The latter will increase in number as the cloud is located at a farther distance. Since the foreground stars will not be reddened, they decrease the average color excess of the field. For example, if the number of foreground stars equals the number of background stars the color excess will be halved. It also means that for far away clouds the color excess will be underestimated. Rathborne et al. (2006) and Chambers et al. (2009) find signs of active massive star formation in one of our clouds. Such young red objects will contribute to the measured color excess, which will lead to an overestimation of the derived extinction. However, the selection of clouds associated with very early phases of star formation will not be affected.
In general, the limits of extinction mapping are set by the number of available background stars; their number has to be sufficient for a statistically meaningful color excess determination. Thus, the reach of the extinction method will change with Galactic latitude, because at higher latitudes the number of stars decreases. In the Galactic plane, there will be ``horizon'' to which one can measure a sufficient color excess, however this horizon will be far from uniform; it depends for every direction on the number of K giants in front and behind the clouds, which will differ when crossing a spiral arm or moving in toward the Galactic center.
Recently, Chapman et al. (2009)
studied the changes in the mid-infrared extinction law within a large
region with high resolution. They find that while in regions with a
K-band extinction of
![]() mag the extinction law is well fitted by an extinction factor of
mag the extinction law is well fitted by an extinction factor of
![]() (Weingartner & Draine 2001), the regions with
(Weingartner & Draine 2001), the regions with
![]() mag are more consistent with the Weingartner & Draine (2001) model of
mag are more consistent with the Weingartner & Draine (2001) model of
![]() ,
which uses larger maximum dust grain sizes. The high extinction clouds are by definition very dense regions for which
,
which uses larger maximum dust grain sizes. The high extinction clouds are by definition very dense regions for which
![]() mag. This means that the visual extinctions and column densities reached by the extinction mapping are a factor
mag. This means that the visual extinctions and column densities reached by the extinction mapping are a factor ![]() 1.8 higher than estimated from Eq. (2), where we used
1.8 higher than estimated from Eq. (2), where we used
![]() .
The near and mid-infrared extinction law is of great interest, and
recently many publications appeared on the mid-infrared (Flaherty et al. 2007; Zasowski et al. 2009; Nishiyama et al. 2009) and the near-infrared (Moore et al. 2005; Stead & Hoare 2009; Froebrich & del Burgo 2006) extinction law. Within the range of 3.6 and 4.5
.
The near and mid-infrared extinction law is of great interest, and
recently many publications appeared on the mid-infrared (Flaherty et al. 2007; Zasowski et al. 2009; Nishiyama et al. 2009) and the near-infrared (Moore et al. 2005; Stead & Hoare 2009; Froebrich & del Burgo 2006) extinction law. Within the range of 3.6 and 4.5 ![]() m, the range we used for our extinction maps, there is a reasonable agreement between the results of Indebetouw et al. (2005) and most recent studies.
m, the range we used for our extinction maps, there is a reasonable agreement between the results of Indebetouw et al. (2005) and most recent studies.
2.2 Catalog of high extinction clouds
We made extinction maps for the complete inner part of the Galaxy with a resolution of 108
![]() ,
plotted in Fig. 1.
The mid-infrared extinction is changing with longitude and latitude,
because it is sensitive to large-scale structures. Figure 2
shows histograms of the average color excess in longitude and latitude.
Most of the peaks in the color excess can be associated to Galactic
spiral arms. The large-scale structure of the extinction was excluded
by selecting only compact high extinction regions with an color excess
above 0.25 mag (equivalent to a hydrogen column density of 2
,
plotted in Fig. 1.
The mid-infrared extinction is changing with longitude and latitude,
because it is sensitive to large-scale structures. Figure 2
shows histograms of the average color excess in longitude and latitude.
Most of the peaks in the color excess can be associated to Galactic
spiral arms. The large-scale structure of the extinction was excluded
by selecting only compact high extinction regions with an color excess
above 0.25 mag (equivalent to a hydrogen column density of 2 ![]() 1022 cm-2). In a second step, smaller extinction maps with a higher resolution (
1022 cm-2). In a second step, smaller extinction maps with a higher resolution (
![]() )
were computed to obtain more accurate positions of the highest
extinction peaks. These peaks were selected by eye. Regions with known
sources, such as H II regions
and HMPOs, were discarded, leaving a sample of unknown and possibly
cold and massive clouds. In this paper we studied 25 high
extinction clouds (HECs) in the first Galactic quadrant. These were the
clouds, visible from the northern hemisphere, with the highest
extinction peaks which were not associated with H II regions from the Becker et al. (1994)
survey and which had no available mm/submm maps from the
literature. A complete catalog of all the high extinction clouds
is given in Table 10, where for each cloud the center position in J2000 coordinates is listed with its corresponding peak color excess.
)
were computed to obtain more accurate positions of the highest
extinction peaks. These peaks were selected by eye. Regions with known
sources, such as H II regions
and HMPOs, were discarded, leaving a sample of unknown and possibly
cold and massive clouds. In this paper we studied 25 high
extinction clouds (HECs) in the first Galactic quadrant. These were the
clouds, visible from the northern hemisphere, with the highest
extinction peaks which were not associated with H II regions from the Becker et al. (1994)
survey and which had no available mm/submm maps from the
literature. A complete catalog of all the high extinction clouds
is given in Table 10, where for each cloud the center position in J2000 coordinates is listed with its corresponding peak color excess.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{13510fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg51.png)
|
Figure 1:
The color excess
|
| Open with DEXTER | |
3 Observations and data reduction
3.1 Millimeter bolometer observations and calibration
The 1.2 mm dust continuum of the selected extinction peaks was
imaged with the 117-element Max-Planck Millimeter BOlometer array
(MAMBO-2) installed at the IRAM 30 m telescope. The observations
were performed in four sessions between 2006 October and
2007 March. The MAMBO passband has an equivalent width of
approximately 80 GHz centered on an effective frequency of
240 GHz (
![]() mm). The full width at half maximum (FWHM) beam size at this frequency is
mm). The full width at half maximum (FWHM) beam size at this frequency is
![]() .
The maps were taken in the dual-beam on-the-fly mapping mode, where the
telescope was scanning row by row in azimuth at a constant speed, while
the secondary beam was wobbling in azimuth with a throw of 92
.
The maps were taken in the dual-beam on-the-fly mapping mode, where the
telescope was scanning row by row in azimuth at a constant speed, while
the secondary beam was wobbling in azimuth with a throw of 92
![]() .
The map sizes were 6
.
The map sizes were 6![]()
![]() 6
6![]() ,
resulting in
,
resulting in ![]() 10
10![]()
![]() 10
10![]() images with a reduced sensitivity at the edges. Each scan was separated by 8
images with a reduced sensitivity at the edges. Each scan was separated by 8
![]() in elevation. We used a scanning velocity of 8
in elevation. We used a scanning velocity of 8
![]()
![]() with a wobbler rate of 2 Hz. The observation time per map was
with a wobbler rate of 2 Hz. The observation time per map was ![]() min. In total 25 high extinction clouds listed in Table 2 were observed, the respective center positions used for the observations are given in Table 10.
min. In total 25 high extinction clouds listed in Table 2 were observed, the respective center positions used for the observations are given in Table 10.
Table 2: Properties of the high extinction clouds.
The project was observed in the bolometer pool as a backup project
resulting in strongly varying weather conditions from one session to
another. The zenith atmospheric opacity, ![]() ,
was monitored by sky dips, performed every
,
was monitored by sky dips, performed every ![]() 1.5 h, and varied between 0.1 and 0.5. The calibration was performed every
1.5 h, and varied between 0.1 and 0.5. The calibration was performed every ![]() 3 h mainly on H II regions G34.3+0.2 and G10.2-0.4, and was found to be accurate within
3 h mainly on H II regions G34.3+0.2 and G10.2-0.4, and was found to be accurate within ![]() 10%.
Pointing checks were made roughly every half hour to hour, before and
usually also after each map. Bolometer observations are dominated by
the sky noise, the variation of the brightness of the sky, which
usually exceeds the intensity of astronomical
sources. The sky noise was reduced by subtracting the correlated noise
between the bolometers in the array. The average rms noise signal
in the individual maps was better than
10%.
Pointing checks were made roughly every half hour to hour, before and
usually also after each map. Bolometer observations are dominated by
the sky noise, the variation of the brightness of the sky, which
usually exceeds the intensity of astronomical
sources. The sky noise was reduced by subtracting the correlated noise
between the bolometers in the array. The average rms noise signal
in the individual maps was better than ![]()
![]() after reduction of the sky noise. The data were reduced using the MOPSI software package developed by R. Zylka.
after reduction of the sky noise. The data were reduced using the MOPSI software package developed by R. Zylka.
3.2 Ammonia observations
For each cloud, we selected by eye the mm emission peaks for follow-up
with pointed ammonia observations. All mm emission peaks above two
times the mean emission of the cloud, that is the rms emission in
the cloud where we omit the bright mm peaks, were observed. When
no clear emission peak was present, such as in a very diffuse
cloud, the center of the diffuse emission was targeted. Even in cases
where the mm emission was below ![]() ,
where
,
where ![]() is the noise in the bolometer map (
is the noise in the bolometer map (
![]() Jy beam-1),
we choose a few positions to observe the ammonia lines to search for a
cloud so cold and diffuse that is was missed by the bolometer.
For clouds that had several continuum emission peaks separated by
more than 20
Jy beam-1),
we choose a few positions to observe the ammonia lines to search for a
cloud so cold and diffuse that is was missed by the bolometer.
For clouds that had several continuum emission peaks separated by
more than 20
![]() from
each other, more than one position was observed, denoted by MM1,
MM2 etc. Several high exinction clouds had very weak or no
mm emission - in this case the name extension, which was
MM1, MM2 for the mm sources, was changed to 1 or 2,
e.g., G034.34-00.90 1.
from
each other, more than one position was observed, denoted by MM1,
MM2 etc. Several high exinction clouds had very weak or no
mm emission - in this case the name extension, which was
MM1, MM2 for the mm sources, was changed to 1 or 2,
e.g., G034.34-00.90 1.
The ammonia observations were performed with the MPIfR
100 m Effelsberg Telescope. We observed 54 positions, given
in Tables 3 and 4, between 2007 April and 2008 December. The Effelsberg beam is
![]() FWHM at the ammonia inversion line frequencies of
FWHM at the ammonia inversion line frequencies of ![]() 23.7 GHz.
The 2007 observations used the 8192 channel AK90 auto
correlator backend. The correlator was configured into eight spectral
windows with 20 MHz bandwidth and 1024 channels each, where
every window could be set to a different frequency. This provided the
opportunity to simultaneously observe the (J,K) =
(1, 1), (2, 2) and (3, 3) inversion lines of ammonia in
both polarizations. The spectral resolution with this setup was
0.25 km s-1. The 2008 observations used the
Fast Fourier Transform Spectrometer (FFTS) with a 500 MHz
bandwidth and 8192 channels. This bandwidth is sufficient to
simultaneously observe the three ammonia inversion lines with a
spectral resolution of 0.7 km s-1. All the observations were performed in frequency switching mode with
a throw of 7.5 MHz.
23.7 GHz.
The 2007 observations used the 8192 channel AK90 auto
correlator backend. The correlator was configured into eight spectral
windows with 20 MHz bandwidth and 1024 channels each, where
every window could be set to a different frequency. This provided the
opportunity to simultaneously observe the (J,K) =
(1, 1), (2, 2) and (3, 3) inversion lines of ammonia in
both polarizations. The spectral resolution with this setup was
0.25 km s-1. The 2008 observations used the
Fast Fourier Transform Spectrometer (FFTS) with a 500 MHz
bandwidth and 8192 channels. This bandwidth is sufficient to
simultaneously observe the three ammonia inversion lines with a
spectral resolution of 0.7 km s-1. All the observations were performed in frequency switching mode with
a throw of 7.5 MHz.
Table 3: Positions (J2000) and fluxes of the clumps from the 1.2 mm continuum data.
Table 4: Positions (J2000) and determined properties toward the positions without clumps.
3.2.1 Data calibration
During the observations, pointings on a nearby compact continuum source
were performed every hour for determining pointing corrections. For the
flux calibration, we observed a well-known flux calibrator,
NGC 7027 or 3C 286, in every run. The post-observational
calibration to obtain the main beam brightness temperature,
![]() ,
consisted of the opacity correction, elevation
correction, and flux calibration:
,
consisted of the opacity correction, elevation
correction, and flux calibration:
where A is a scaling factor,
The opacity, ![]() ,
was calculated by fitting a linear function to the system temperature against airmass (
,
was calculated by fitting a linear function to the system temperature against airmass (
![]() )
and taking the slope of the fit. We found a
)
and taking the slope of the fit. We found a ![]() of 0.031 for good weather. When it was not possible to retrieve the
of 0.031 for good weather. When it was not possible to retrieve the ![]() by this method the average
by this method the average ![]() of 0.054 at 23 GHz was assumed (the averaged water vapor radiometer value for 2007).
of 0.054 at 23 GHz was assumed (the averaged water vapor radiometer value for 2007).
For all parabolic dish telescopes the gain decreases at very low
and very high elevations. We corrected for this by dividing by ![]() taken from the Effelsberg website
taken from the Effelsberg website![]() (see Eq. (3)), which is given by
(see Eq. (3)), which is given by
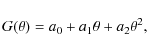
|
(4) |
where a0=0.88196, a1=6.6278
The calibrated spectra were baseline subtracted, and the ammonia lines were fitted by a Gaussian. Only the
![]() (1, 1)
line, for which the hyperfine structure was clearly detectable
given the signal to noise ratios, was fitted by special routine
``method nh3(1, 1)'' of the GILDAS/CLASS software. This
method calculates the optical depth from the hyperfine structure and
returns optical depth corrected line widths. The observed ammonia
parameters, such as the velocity in the local standard of rest
(LSR),
(1, 1)
line, for which the hyperfine structure was clearly detectable
given the signal to noise ratios, was fitted by special routine
``method nh3(1, 1)'' of the GILDAS/CLASS software. This
method calculates the optical depth from the hyperfine structure and
returns optical depth corrected line widths. The observed ammonia
parameters, such as the velocity in the local standard of rest
(LSR),
![]() ,
main beam temperatures,
,
main beam temperatures,
![]() ,
line widths,
,
line widths, ![]() ,
and the main group optical depth,
,
and the main group optical depth,
![]() are listed in Table 5.
are listed in Table 5.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.75cm,clip]{13510fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg86.png)
|
Figure 2:
Mean color excess along Galactic longitude (upper diagram, bins of 3 |
| Open with DEXTER | |
3.3 Water maser observations
Several positions with a peak in the 1.2 mm emission above twice
the mean cloud emission, indicating that they are possibly harboring
evolved clumps, were searched for water maser emission using the
100 m Effelsberg telescope on 5 and 24 of
February 2008. In total 24 positions in common with
![]() were observed (marked in Table 3).
We performed on-off observations using the FFTS backend with a
bandwidth of 20 MHz centered on 22.235 GHz. This setup
afforded a high spectral resolution of 0.04 km s-1, while allowing the water maser to have line widths of up to 100 km s-1. The bandwidth was 270 km s-1 and was centered on the
were observed (marked in Table 3).
We performed on-off observations using the FFTS backend with a
bandwidth of 20 MHz centered on 22.235 GHz. This setup
afforded a high spectral resolution of 0.04 km s-1, while allowing the water maser to have line widths of up to 100 km s-1. The bandwidth was 270 km s-1 and was centered on the
![]()
![]() of the observed clump. We applied the same data reduction as described above in Sect. 3.2.1 for the
ammonia observations. Table 6 lists the
of the observed clump. We applied the same data reduction as described above in Sect. 3.2.1 for the
ammonia observations. Table 6 lists the
![]() and peak intensity of the water maser detections. In case of multiple maser components we give the
and peak intensity of the water maser detections. In case of multiple maser components we give the
![]() range.
range.
4 Results
4.1 Kinematic distances
Accurate distance determination within the Galaxy is generally
difficult. Nevertheless, the kinematic distance is commonly used
as a distance measure. It is based on a model of Galactic
rotation, the ``rotation curve'' characterized by the distance
between the Sun and the Galactic Center, R0, and the rotation velocity at the Suns orbit, ![]() .
Toward the inner part of the Galactic plane, kinematic distances are
ambiguous: for a given Galactic longitude and
LSR velocity, it cannot a priori be determined if the
object is at the ``near'' or ``far'' kinematic distance.
All extinction clouds should be at the near kinematic distance
since at large distances the number of background stars decreases and
the percentage of foreground stars increases making it difficult to
measure any color excess. We calculated the kinematic distances for all
clumps with
.
Toward the inner part of the Galactic plane, kinematic distances are
ambiguous: for a given Galactic longitude and
LSR velocity, it cannot a priori be determined if the
object is at the ``near'' or ``far'' kinematic distance.
All extinction clouds should be at the near kinematic distance
since at large distances the number of background stars decreases and
the percentage of foreground stars increases making it difficult to
measure any color excess. We calculated the kinematic distances for all
clumps with
![]() detections, using a program of Todd Hunter, which applies the Galactic rotation model of
Fich et al. (1989) assuming a flat rotation curve,
detections, using a program of Todd Hunter, which applies the Galactic rotation model of
Fich et al. (1989) assuming a flat rotation curve,
![]() ,
and R0=8.5 kpc. The resulting kinematic distances are given in Tables 4 and 7.
,
and R0=8.5 kpc. The resulting kinematic distances are given in Tables 4 and 7.
4.2 Galactic scale extinction
The low resolution extinction maps show large extinction structures across the whole inner Galactic disk from 60![]() to -60
to -60![]() longitude (Fig. 1). In longitude, the 3
longitude (Fig. 1). In longitude, the 3![]() averaged distribution (Fig. 2,
top panel) shows signs of Galactic structure, meaning that peaks in the
distribution can be related to known spiral arms. The column density
appears higher in the fourth quadrant,
averaged distribution (Fig. 2,
top panel) shows signs of Galactic structure, meaning that peaks in the
distribution can be related to known spiral arms. The column density
appears higher in the fourth quadrant,
![]() ,
than in the first,
,
than in the first,
![]() .
Additionally, there seems to be a quasi symmetrical distribution around the Galactic Center around longitudes of
.
Additionally, there seems to be a quasi symmetrical distribution around the Galactic Center around longitudes of ![]() 15
15![]() ,
-10
,
-10![]() and
and ![]() 35
35![]() ,
-30
,
-30![]() .
In latitude (Fig. 2, lower panel), we found a peak towards
.
In latitude (Fig. 2, lower panel), we found a peak towards
![]() ,
which is also seen for the compact submillimeter
sources found in the ATLASGAL survey (Schuller et al. 2009).
The shift of the peak out of the midplane indicates that the Sun is
located above the midplane. Similar results have been found by the
studies using young open clusters and OB stars (see e.g. Joshi 2007). The FWHM of our distribution is
,
which is also seen for the compact submillimeter
sources found in the ATLASGAL survey (Schuller et al. 2009).
The shift of the peak out of the midplane indicates that the Sun is
located above the midplane. Similar results have been found by the
studies using young open clusters and OB stars (see e.g. Joshi 2007). The FWHM of our distribution is ![]() 1
1![]() ,
while in ATLASGAL this is more narrow,
,
while in ATLASGAL this is more narrow, ![]()
![]() .
If one assumes that the Galactic disk has a constant scale height,
then objects closer to the Sun should have a wider latitude
distribution then ones at larger distances. It therefore appears
that the high extinction clouds are on average closer to the Sun than
the ATLASGAL sources.
.
If one assumes that the Galactic disk has a constant scale height,
then objects closer to the Sun should have a wider latitude
distribution then ones at larger distances. It therefore appears
that the high extinction clouds are on average closer to the Sun than
the ATLASGAL sources.
With the kinematic distances we can place our sample of clouds within a face-on view of the Galactic plane (Fig. 3). They inhabit similar regions as IRDCs (see the IRDCs distribution by Jackson et al. 2008). The extinction method misses nearby (
![]() )
and most of the far away (
)
and most of the far away (
![]() )
clouds. The insensitivity to the latter stems from the increasing
number of foreground stars at larger distances (see Sect. 2.1). Between distances of one and four kilo parsec the high extinction clouds agree with the IRDCs regions.
)
clouds. The insensitivity to the latter stems from the increasing
number of foreground stars at larger distances (see Sect. 2.1). Between distances of one and four kilo parsec the high extinction clouds agree with the IRDCs regions.
![\begin{figure}
\par\includegraphics[angle=-90,width=5cm,clip]{13510fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg95.png)
|
Figure 3:
A face-on view of the Galactic plane. The Galactic center is located at (0, 0). The Galacitic longitudes of 12 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{13510fg4a.eps}\p...
...eps}\par\includegraphics[angle=-90,width=8.2cm,clip]{13510fg4c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg96.png)
|
Figure 4:
Examples of extinction maps (red dashed contour, starting at |
| Open with DEXTER | |
4.3 Extinction clouds
Millimeter continuum emission was detected in 88% of the bolometer maps. It usually followed well the 54
![]() resolution extinction maps (Fig. 4). Two examples of weak millimeter emission or non-detections are G034.03-00.33 and G034.34-00.90 (Fig. 5). Figure 5 shows the 24
resolution extinction maps (Fig. 4). Two examples of weak millimeter emission or non-detections are G034.03-00.33 and G034.34-00.90 (Fig. 5). Figure 5 shows the 24 ![]() m maps from the Multiband Imaging Photometer for Spitzer (MIPS) overlaid with the mm emission. While the high extinction clouds match well with 24
m maps from the Multiband Imaging Photometer for Spitzer (MIPS) overlaid with the mm emission. While the high extinction clouds match well with 24 ![]() m dark features, the 1.2 mm peaks often contain weak compact 24
m dark features, the 1.2 mm peaks often contain weak compact 24 ![]() m emission. The bolometer maps were sensitive to structures from
m emission. The bolometer maps were sensitive to structures from
![]() (FWHM) to
(FWHM) to ![]() 90
90
![]() ;
large-scale structures are not faithfully represented due to the sky
noise subtraction and chopping. We smoothed the maps, by convolving
with a 20
;
large-scale structures are not faithfully represented due to the sky
noise subtraction and chopping. We smoothed the maps, by convolving
with a 20
![]() Gaussian beam, to study the extended cloud structure and increase the signal-to-noise toward weak and diffuse sources.
Gaussian beam, to study the extended cloud structure and increase the signal-to-noise toward weak and diffuse sources.
We find single clouds and clusters of clouds, for example G014.63-00.57 in Fig. 5.
Based on the kinematic distance the clouds were identified as belonging
together in one large cloud, or being physically separated clouds if
the difference in distance was larger than 10%. The latter clouds
were marked as A, B etc. and were treated as distinct clouds
throughout the paper. For the total integrated flux of the cloud
(Table 2), we defined a cloud edge at a threshold of ![]() (of the smoothed map) and integrated all the emission within this
region using the Gildas Software package GREG. The corresponding radius
of the cloud,
(of the smoothed map) and integrated all the emission within this
region using the Gildas Software package GREG. The corresponding radius
of the cloud,
![]() with A the surface of the cloud, is given in arcseconds and parsecs (using the kinematic distance) in Table 2.
The average cloud radius was 0.7 pc. Certain clouds have spherical
shapes, for example G013.28-00.34, however, most are filamentary,
as can be seen in G024.94-00.15 or G016.93+00.24. Cloud sizes are
very diverse depending on the geometry; there are elongated
structures up to several parsecs in length. The number of clumps per
cloud varies from five (in G018.26-00.24, Fig. 5) to one or none in very diffuse clouds (G034.85+00.43, Fig. 5). We used the SIMBAD database to investigate if our clouds contain signs of star formation, such as maser emission, H II regions, and IRAS sources.
with A the surface of the cloud, is given in arcseconds and parsecs (using the kinematic distance) in Table 2.
The average cloud radius was 0.7 pc. Certain clouds have spherical
shapes, for example G013.28-00.34, however, most are filamentary,
as can be seen in G024.94-00.15 or G016.93+00.24. Cloud sizes are
very diverse depending on the geometry; there are elongated
structures up to several parsecs in length. The number of clumps per
cloud varies from five (in G018.26-00.24, Fig. 5) to one or none in very diffuse clouds (G034.85+00.43, Fig. 5). We used the SIMBAD database to investigate if our clouds contain signs of star formation, such as maser emission, H II regions, and IRAS sources.
![\begin{figure}
\par {\hspace*{4mm}\includegraphics[width=6.8cm, angle=-90]{13510...
...{10mm}}
\par\includegraphics[width=6.8cm, angle=-90]{13510fg5e.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg99.png)
|
Figure 5:
Spitzer/MIPS 24
|
| Open with DEXTER | |
![\begin{figure}
\par {\hspace*{4cm}\includegraphics[width=7cm, angle=-90]{13510fg...
...includegraphics[width=7cm, angle=-90]{13510fg5i.eps}\hspace*{4cm}}\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg100.png)
|
Figure 5: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm, angle=-90]{13510fg5j.eps}\include...
...dth=7cm, angle=-90]{13510fg5n.eps}\hspace*{3.8cm}}\vspace*{1.6mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg101.png)
|
Figure 5: continued. |
| Open with DEXTER | |
![\begin{figure}
\par {\hspace*{1cm}\includegraphics[width=7cm, angle=-90]{13510fg...
...cludegraphics[width=7cm, angle=-90]{13510fg5s.eps}\hspace*{3.8cm}}\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg102.png)
|
Figure 5: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm, angle=-90]{13510fg5t.eps}\inclu...
...udegraphics[width=6.8cm, angle=-90]{13510fg5y.eps}\hspace*{4.9cm}}\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg103.png)
|
Figure 5: continued. |
| Open with DEXTER | |
4.4 Clumps in high extinction clouds
To study the clumps we used the unsmoothed maps, as the extended
structure surrounding the clump complicates the definition of source
edge and confuses Gaussian fitting routines. We removed the extended
emission from the map by applying a median filter with a box size of 63
![]() (6
(6 ![]() beamsize)
using the MIRIAD task ``immedian''. After median removal,
the source-find algorithm of MIRIAD, ``sfind'', was run on these
images delivering 2D Gaussian fits, the peak flux, and the
integrated fluxes of the clumps. The median removal should strip the
low density mass reservoir which surrounds the denser part of
the clump.
beamsize)
using the MIRIAD task ``immedian''. After median removal,
the source-find algorithm of MIRIAD, ``sfind'', was run on these
images delivering 2D Gaussian fits, the peak flux, and the
integrated fluxes of the clumps. The median removal should strip the
low density mass reservoir which surrounds the denser part of
the clump.
First, we selected the peaks in the mm emission by eye, and then we took the parameters for the FWHM
size, the integrated flux and peak flux of the clump from ``sfind''.
The observed parameters of the clumps are presented in Table 3. The clumps have sizes (geometrical mean of the major and minor axis of the clump) of 10-30
![]() or
0.11-0.72 pc, peaking around 0.25 pc (Fig. 6). Most of the clumps are resolved with the
or
0.11-0.72 pc, peaking around 0.25 pc (Fig. 6). Most of the clumps are resolved with the
![]() beam of the 30 m telescope. The (physical) clump size follows a linear trend with distance (Fig. 7,
right panel). At far distances we observe only larger, hence
brighter clumps, which is expected for our sensitivity limited
selection. The angular sizes, however, are more equally distributed
(see Table 3).
For several clouds with very weak mm emission the selected
position was not the mm emission peak, but the emission center.
In such clouds ``sfind'' did not find any clumps; these positions
without clumps are listed in Table 4.
beam of the 30 m telescope. The (physical) clump size follows a linear trend with distance (Fig. 7,
right panel). At far distances we observe only larger, hence
brighter clumps, which is expected for our sensitivity limited
selection. The angular sizes, however, are more equally distributed
(see Table 3).
For several clouds with very weak mm emission the selected
position was not the mm emission peak, but the emission center.
In such clouds ``sfind'' did not find any clumps; these positions
without clumps are listed in Table 4.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg104.png)
|
Figure 6: Number distribution of 1.2 mm clumps with size determined from Gaussian fits and converted to physical units using the near kinematic distance. |
| Open with DEXTER | |
Ammonia emission was detected toward 94% of the observed positions. Figure 8
shows the spectra of the
![]() (1, 1),
(1, 1),
![]() (2, 2) and
(2, 2) and
![]() (3, 3)
transitions toward two compact clumps representing typical values for
an early stage where the clump is cold (14 K, G016.93+00.24 MM1)
and a more evolved stage, where the temperature has increased
(19 K, G017.19+00.81 MM2). In the early stage the
(3, 3)
transitions toward two compact clumps representing typical values for
an early stage where the clump is cold (14 K, G016.93+00.24 MM1)
and a more evolved stage, where the temperature has increased
(19 K, G017.19+00.81 MM2). In the early stage the
![]() (3, 3) line
is not detected, while for the warmer clump it is clearly present. The
results of the ammonia observations are summarized in Table 5. The main beam brightness temperatures of the
(3, 3) line
is not detected, while for the warmer clump it is clearly present. The
results of the ammonia observations are summarized in Table 5. The main beam brightness temperatures of the
![]() (1, 1) lines are, after baseline removal, between 0.5 and 4.0 K. The baseline rms is
(1, 1) lines are, after baseline removal, between 0.5 and 4.0 K. The baseline rms is ![]() 0.2 K, but several spectra are more noisy. The line widths from the main component of the
0.2 K, but several spectra are more noisy. The line widths from the main component of the
![]() (1, 1) range between 0.7 and 2.8 km s-1, yielding an average of 1.4 km s-1 (Fig. 9). These line widths are far above a thermal linewidth, which would be around 0.23 km s-1 for temperatures of
(1, 1) range between 0.7 and 2.8 km s-1, yielding an average of 1.4 km s-1 (Fig. 9). These line widths are far above a thermal linewidth, which would be around 0.23 km s-1 for temperatures of ![]() 18 K. For most of the sources, the
18 K. For most of the sources, the
![]() (1, 1) and
(1, 1) and
![]() (2, 2) lines are both detected, while the
(2, 2) lines are both detected, while the
![]() (3, 3) line is often very weak or not present. The
(3, 3) line is often very weak or not present. The
![]() (2, 2) and
(2, 2) and
![]() (3, 3) lines are on average both wider than the main
(3, 3) lines are on average both wider than the main
![]() (1, 1) line.
This implies that these lines do not trace exactly the same volume of
gas, meaning that the beam filling factor is not identical.
(1, 1) line.
This implies that these lines do not trace exactly the same volume of
gas, meaning that the beam filling factor is not identical.
Table 6: Detected water masers.
5 Analysis
5.1 Extinction masses
Since the color excess, or extinction, is a direct measure of the
amount of column density in a region, we could derive extinction
masses. One magnitude of ![]() is related to a hydrogen column density,
is related to a hydrogen column density,
![]() ,
according to Bohlin et al. (1978) and Frerking et al. (1982) by
,
according to Bohlin et al. (1978) and Frerking et al. (1982) by
Multiplying by the mass of a hydrogen atom,
![\begin{displaymath}%
M_{{\rm ext}} = 3.7\times10^{26}~\mu m_{\rm H} \langle E(3....
...m m}) \rangle \left( \frac{A}{{\rm pc^2}}\right)~[{M_\odot}].
\end{displaymath}](/articles/aa/full_html/2010/07/aa13510-09/img108.png)
|
(6) |
The extinction mass is independent of temperature, but it still depends on the distance via the cloud surface A. We derive extinction masses for the clouds from
5.2 Column densities and visual extinction
As mm emission from cool clouds is usually optically thin, the column density and the mass of a
cloud are well sampled by the observed flux density. The beam averaged column density is given by Motte et al. (2007):
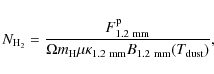
|
(7) |
where
We found clumps with column densities of the order of
![]() (Table 7). We derived corresponding peak visual extinction values by applying Eq. (5). The peak fluxes, column densities and peak visual extinction of Table 7 correspond to the positions listed in Table 3. The clumps have peaks in
(Table 7). We derived corresponding peak visual extinction values by applying Eq. (5). The peak fluxes, column densities and peak visual extinction of Table 7 correspond to the positions listed in Table 3. The clumps have peaks in ![]() from 31 to 280 mag, with an average value of 75 mag.
These values are much higher than the mean visual extinction reached by
the extinction method for this selected sample, which is
between 16 and 47 mag. This is expected because the peak
values are larger than the mean and with the limited resolution of 54
from 31 to 280 mag, with an average value of 75 mag.
These values are much higher than the mean visual extinction reached by
the extinction method for this selected sample, which is
between 16 and 47 mag. This is expected because the peak
values are larger than the mean and with the limited resolution of 54
![]() higher
extinction peaks (as found for example in IRDCs) are missed.
Additionally, also the temperature might play a role, since the
derivation of the
higher
extinction peaks (as found for example in IRDCs) are missed.
Additionally, also the temperature might play a role, since the
derivation of the ![]() from the mm emission depends on temperature while the extinction method does not.
from the mm emission depends on temperature while the extinction method does not.
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{13510fg7.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg122.png)
|
Figure 7: Distance as a function of clump mass ( left) and size ( right). In the left panel, the clump mass based on Gaussian fitting is marked by squares, and the clump mass within 0.25 pc around the center of a clump is indicated by crosses. There is a linear correlation with distance for the mass and the size. The most massive clumps are at large distances, whereas almost no low-mass clumps are found at distances larger than 4 kpc, which can be expected for a sensitivity limited selection of clouds. |
| Open with DEXTER | |
5.3 Masses from 1.2 mm emission
The clump mass can be derived from the 1.2 mm emission by (Motte et al. 2007; Hildebrand 1983):
where
The majority of the clumps have masses between 12 and 700 ![]() and are located at distances
between 2 and 5 kpc (see the squares in the left panel of Fig. 7 and Table 7). We find no low-mass clumps (
and are located at distances
between 2 and 5 kpc (see the squares in the left panel of Fig. 7 and Table 7). We find no low-mass clumps (
![]() )
further than 4 kpc, which is an bias of our extinction method (discussed in Sect. 6.4). Almost all high mass clumps (
)
further than 4 kpc, which is an bias of our extinction method (discussed in Sect. 6.4). Almost all high mass clumps (
![]() )
are located at distances larger than 4 kpc.
)
are located at distances larger than 4 kpc.
A second method was used as a comparison for the clump masses to
check if the source finding algorithm was biased to a source size (and
hence clump mass). Based on the (near) kinematical distances, we
defined circles of 0.25 pc diameter for each source. Then, we
derived the integrated
flux,
![]() ,
and the mass,
,
and the mass,
![]() ,
for the region within this circle (see Tables 3, 7 and 4). The crosses in the left panel of Fig. 7 show
,
for the region within this circle (see Tables 3, 7 and 4). The crosses in the left panel of Fig. 7 show
![]() as
a function of the distance. The clump masses within 0.25 pc show a
similar behavior as the clump masses determined by Gaussian fits.
On a larger scale, the cloud mass was derived from the
1.2 mm emission according to Eq. (8) using the integrated flux down to 3
as
a function of the distance. The clump masses within 0.25 pc show a
similar behavior as the clump masses determined by Gaussian fits.
On a larger scale, the cloud mass was derived from the
1.2 mm emission according to Eq. (8) using the integrated flux down to 3![]() .
The cloud diameters are of order
.
The cloud diameters are of order ![]() 90
90
![]() ,
so after resampling the extinction map, it was possible to
compare the cloud masses derived by extinction with the masses from the
1.2 mm emission. We find the extinction masses to be larger by a
factor
,
so after resampling the extinction map, it was possible to
compare the cloud masses derived by extinction with the masses from the
1.2 mm emission. We find the extinction masses to be larger by a
factor ![]() than the masses derived from the dust continuum maps (see Fig. 10).
This is expected, since the bolometer filters out large-scale
structures by the sky noise subtraction and chopping. The cloud masses
derived from the 1.2 mm emission and the extinction are listed in
Table 2.
than the masses derived from the dust continuum maps (see Fig. 10).
This is expected, since the bolometer filters out large-scale
structures by the sky noise subtraction and chopping. The cloud masses
derived from the 1.2 mm emission and the extinction are listed in
Table 2.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg8a.eps}\par...
...ludegraphics[angle=-90,width=8cm,clip]{13510fg8b.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg135.png)
|
Figure 8:
The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg9.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg136.png)
|
Figure 9:
Number distribution of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg10.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg137.png)
|
Figure 10: The cloud masses estimated from the color excess versus the masses estimated from the 1.2 mm continuum maps. The red dashed line is a help line indicating the trend in which both mass estimates are equal. |
| Open with DEXTER | |
Finally, we estimated the volume-averaged gas density of the clumps,
![]() ,
following Motte et al. (2007):
,
following Motte et al. (2007):
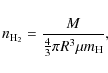
|
(9) |
where M is the clump mass, R the clump radius given by the geometrical mean of the semi major and semi minor axis from the Gaussian fit. The average gas density is
5.4 Virial masses
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg142.png)
|
Figure 11: Virial clump masses versus the 1.2 mm continuum clump masses. The red dashed line indicates the trend where the virial parameter is unity. |
| Open with DEXTER | |
The thermal line widths are usually one order of magnitude smaller than the observed
![]() line widths, which indicates that the observed line widths are
dominated by turbulence, hence contain information of the average
kinetic energy within a clump.
line widths, which indicates that the observed line widths are
dominated by turbulence, hence contain information of the average
kinetic energy within a clump.
Given an optically thin line width and a clump radius, the virial mass,
![]() ,
can be calculated (MacLaren et al. 1988). Here
,
can be calculated (MacLaren et al. 1988). Here ![]() is the three dimensional root-mean-square velocity, R the clump radius and k1 a density distribution constant. For a constant density distribution k1 = 5/3. After the conversion of
is the three dimensional root-mean-square velocity, R the clump radius and k1 a density distribution constant. For a constant density distribution k1 = 5/3. After the conversion of ![]() to the observable
FWHM line width
to the observable
FWHM line width ![]() ,
,
![]() (Rohlfs & Wilson 2004), the virial mass can be written as:
(Rohlfs & Wilson 2004), the virial mass can be written as:
The resultant virial masses,
5.5 Temperatures
The ammonia molecule, described thoroughly by Ho & Townes (1983), is often used as a molecular cloud thermometer (Danby et al. 1988). Its energy levels are parameterized by the J and K quantum
numbers, measuring, respectively, the magnitude of the total
angular momentum and its component along the symmetry axis. Each set of
rotational transitions is arranged into so-called K-ladders, levels of fixed K-value. From the symmetry of the electric dipole moment of the molecule, all dipole transitions with nonzero ![]() are forbidden, meaning that the K-ladders are independent of each other. The lowest transitions of each K-ladder are metastable, and can be excited via collisions. Additionally,
are forbidden, meaning that the K-ladders are independent of each other. The lowest transitions of each K-ladder are metastable, and can be excited via collisions. Additionally,
![]() also undergoes vibrational motion from the tunneling of the nitrogen
atom through the hydrogen plane, which splits the rotational energy
levels into inversion doublets.
also undergoes vibrational motion from the tunneling of the nitrogen
atom through the hydrogen plane, which splits the rotational energy
levels into inversion doublets.
The inversion transitions are further split into five
quadrupole hyperfine lines, which allow the calculation of the optical
depth (see the hyperfine lines in the
![]() (1, 1) transition in Fig. 8).
Typical values of the optical depth were between 1 and 3,
showing that ammonia is optically thick in most cases. With the optical
depth known, the rotational temperature follows from the ratio of the
peak intensities of
(1, 1) transition in Fig. 8).
Typical values of the optical depth were between 1 and 3,
showing that ammonia is optically thick in most cases. With the optical
depth known, the rotational temperature follows from the ratio of the
peak intensities of
![]() (1, 1) and
(1, 1) and
![]() (2, 2) lines after Mangum et al. (1992):
(2, 2) lines after Mangum et al. (1992):
![\begin{displaymath}%
T_{{\rm rot}} \!=\! -41.5 \left[ \ln \left[ -\frac{0.283 \D...
...}}(1 - {\rm e}^{-\tau})\right]\right] \right]^{-1}~[{\rm K}],
\end{displaymath}](/articles/aa/full_html/2010/07/aa13510-09/img151.png)
|
(11) |
where
The line width ratio in this equation is debatable. Observations show that the
![]() (1, 1) and
(1, 1) and
![]() (2, 2) line
widths are dominated by turbulence. If one assumes that both
transitions arise from the same region, they experience the same
turbulence, and the line widths are equal,
(2, 2) line
widths are dominated by turbulence. If one assumes that both
transitions arise from the same region, they experience the same
turbulence, and the line widths are equal,
![]() .
In this case, the linewidth ratio drops out of the equation, which becomes the equation from Ho & Townes (1983). We observed slightly larger
.
In this case, the linewidth ratio drops out of the equation, which becomes the equation from Ho & Townes (1983). We observed slightly larger
![]() (2, 2) line widths for
several clumps, probably since this transition has a higher energy and is therefore more
sensitive to warmer and more turbulent regions. The
(2, 2) line widths for
several clumps, probably since this transition has a higher energy and is therefore more
sensitive to warmer and more turbulent regions. The
![]() (2, 2) line
widths are therefore more sensitive to the peak temperature, determined
by the turbulent outliers. We considered it reasonable to use
(2, 2) line
widths are therefore more sensitive to the peak temperature, determined
by the turbulent outliers. We considered it reasonable to use
![]() =
=
![]() ,
since it would give an ``average'' of the
,
since it would give an ``average'' of the
![]() (2, 2) turbulence,
and hence an ``average'' rotational temperature of that region. The two
methods yield very similar results; the Ho & Townes (1983) temperatures were slightly lower (
(2, 2) turbulence,
and hence an ``average'' rotational temperature of that region. The two
methods yield very similar results; the Ho & Townes (1983) temperatures were slightly lower (
![]() K) than when using the formula of Mangum et al. (1992).
K) than when using the formula of Mangum et al. (1992).
The clumps are on average cold ![]() 16 K.
The temperatures range from 10 to 25 K. For such
low temperatures, the kinetic temperature is well approximated
by
16 K.
The temperatures range from 10 to 25 K. For such
low temperatures, the kinetic temperature is well approximated
by
![]() (Danby et al. 1988; Walmsley & Ungerechts 1983).
(Danby et al. 1988; Walmsley & Ungerechts 1983).
We derived column densities of the
![]() (1, 1) line (after Mangum et al. 1992):
(1, 1) line (after Mangum et al. 1992):
![\begin{displaymath}%
N_{(1,1)} = 6.60 \times 10^{14} \Delta v_{11} \tau \frac{T_{{\rm rot}}}{\nu_{11}}~[{\rm cm}^{-2.}].
\end{displaymath}](/articles/aa/full_html/2010/07/aa13510-09/img156.png)
|
(12) |
From this we estimated the total ammonia column density (following Li et al. 2003):
| |
= | 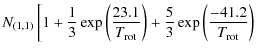
|
|
![$\displaystyle \left. + ~ \frac{14}{3}\exp\left(\frac{-99.4}{T_{{\rm rot}}}\right)\right]~[{\rm cm}^{-2}].$](/articles/aa/full_html/2010/07/aa13510-09/img159.png)
|
(13) |
The averaged ammonia column density for the clumps is 3.1
Table 7:
Properties of the clumps derived from
![]() and the 1.2 mm continuum.
and the 1.2 mm continuum.
6 Discussion
6.1 High extinction structures
Thanks to the high resolution Spitzer IRAC data, the
extinction method allows to follow the mass distribution from Galactic
size-scales down to single clouds. High extinction traces Galactic
structure (see the Galactic distribution of the color excess in
Fig. 2), similar to the CO survey of the Galactic plane (Dame et al. 1987) and the dust continuum surveys, ATLASGAL at 850
![]() (Schuller et al. 2009) and BOLOCAM at 1.1 mm (Rosolowsky et al. 2010).
In addition, the distribution of 6.7 GHz Class II
methanol masers traces high-mass star-forming regions and, thus,
Galactic structure (Pestalozzi et al. 2005). All these surveys, except for the methanol masers, peak toward the Galactic Center. The extinction maps miss the inner 1
(Schuller et al. 2009) and BOLOCAM at 1.1 mm (Rosolowsky et al. 2010).
In addition, the distribution of 6.7 GHz Class II
methanol masers traces high-mass star-forming regions and, thus,
Galactic structure (Pestalozzi et al. 2005). All these surveys, except for the methanol masers, peak toward the Galactic Center. The extinction maps miss the inner 1![]() around the Galactic Center, since the Spitzer
IRAC data were not publicly available for this region at the time.
However, a rising trend toward the Galactic Center was observed.
The extinction distribution indicates that the column densities are
higher towards the fourth quadrant,
around the Galactic Center, since the Spitzer
IRAC data were not publicly available for this region at the time.
However, a rising trend toward the Galactic Center was observed.
The extinction distribution indicates that the column densities are
higher towards the fourth quadrant,
![]() .
We find no evidence for this from the CO distribution, nor from the methanol masers. Only the ATLASGAL survey (Schuller et al. 2009) hints at a similar distribution, but needs to be extended in longitude range for giving conclusive evidence.
.
We find no evidence for this from the CO distribution, nor from the methanol masers. Only the ATLASGAL survey (Schuller et al. 2009) hints at a similar distribution, but needs to be extended in longitude range for giving conclusive evidence.
The next eye-catching features in the extinction distribution were two bumps, peaking roughly around longitudes of
![]() and
and
![]() (see Fig. 2), which were confirmed by the methanol maser distribution (Pestalozzi et al. 2005). We identified several spiral arms by comparing our results to the Galactic models of Vallée (2008). In Fig. 2
each spiral arm traced by a maximum in the extinction distribution is
marked. We can trace the tangential point of the Sagittarius-Carina arm
at
(see Fig. 2), which were confirmed by the methanol maser distribution (Pestalozzi et al. 2005). We identified several spiral arms by comparing our results to the Galactic models of Vallée (2008). In Fig. 2
each spiral arm traced by a maximum in the extinction distribution is
marked. We can trace the tangential point of the Sagittarius-Carina arm
at
![]() ,
the tangential points of the Scutum-Crux arm at
,
the tangential points of the Scutum-Crux arm at
![]() and
and
![]() ,
the beginning of the Norma-Cygnus arm on the near end of the Galactic bar
,
the beginning of the Norma-Cygnus arm on the near end of the Galactic bar
![]() ,
the beginning of the Sagittarius-Carina arm at the far end of
the Galactic bar
,
the beginning of the Sagittarius-Carina arm at the far end of
the Galactic bar
![]() ,
the beginning of the Perseus arm
,
the beginning of the Perseus arm
![]() ,
and the tangential point of the Norma-Cygnus arm at
,
and the tangential point of the Norma-Cygnus arm at
![]() .
Several of these features are also seen in the ATLASGAL survey, and to
a lesser extent in the CO distribution. Hence, the total
extinction distribution seems to agree with results of previous
studies, and tracks large scale mass structures.
.
Several of these features are also seen in the ATLASGAL survey, and to
a lesser extent in the CO distribution. Hence, the total
extinction distribution seems to agree with results of previous
studies, and tracks large scale mass structures.
The combination of submillimeter dust continuum emission and
extinction maps extends the size scales down to clump sizes of
fractions of parsecs. In Table 8
the mean masses, radii, and volume densities for different size-scales
of complexes, clouds and clumps are compared. Complexes are the low
density (
![]() or
or
![]()
![]()
![]() )
regions surrounding the cloud. In general, the masses and
sizes decrease towards the smaller scales, while the volume density
increases as expected. The cloud masses derived from the extinction are
higher than from the mm emission, as discussed in Sect. 5.3.
The complexes and the clouds are confined by the pressure of the
surroudning medium rather than by gravity. This is based on their
virial masses, where we used for the line width estimate the 13CO data from the Galactic Ring Survey (GRS) (Jackson et al. 2006). The 13CO line is a probe of the low density material and with the GRS resolution of 47
)
regions surrounding the cloud. In general, the masses and
sizes decrease towards the smaller scales, while the volume density
increases as expected. The cloud masses derived from the extinction are
higher than from the mm emission, as discussed in Sect. 5.3.
The complexes and the clouds are confined by the pressure of the
surroudning medium rather than by gravity. This is based on their
virial masses, where we used for the line width estimate the 13CO data from the Galactic Ring Survey (GRS) (Jackson et al. 2006). The 13CO line is a probe of the low density material and with the GRS resolution of 47
![]() the line width is represenative for a cloud-scale average. Most of the
clumps inside the clouds are, however, bound objects for which
the line width is represenative for a cloud-scale average. Most of the
clumps inside the clouds are, however, bound objects for which
![]() .
.
Table 8: Mean properties of high extinction complexes, clouds and clumps.
6.2 Evolutionary sequence
Our observations suggest different classes of clouds and in the
following we discuss their possible relation to different evolutionary
stages. Clouds, which either have no clumps or clumps of which the peak
in the mm emission is less than twice the mean emission in the cloud,
were defined as diffuse clouds - this definition is based on the
cloud morphology and therefore different from the ``classical diffuse
clouds'' defined by
![]() mag (Snow & McCall 2006).
Clouds which contain clumps with a higher contrast, above twice the
mean cloud emission, were considered to be peaked clouds. If the
peak flux was above thrice the mean emission and there were two or more
clumps the cloud was classified as a multiply peaked cloud. The ratio
of the clump peak emission to the mean emission of the cloud is given
in Table 2 together with
the classification. The mean physical properties such as temperature,
masses, column densities and line widths are put together in Table 9 for the three classes.
mag (Snow & McCall 2006).
Clouds which contain clumps with a higher contrast, above twice the
mean cloud emission, were considered to be peaked clouds. If the
peak flux was above thrice the mean emission and there were two or more
clumps the cloud was classified as a multiply peaked cloud. The ratio
of the clump peak emission to the mean emission of the cloud is given
in Table 2 together with
the classification. The mean physical properties such as temperature,
masses, column densities and line widths are put together in Table 9 for the three classes.
Diffuse clouds are the most likely candidates to form,
or harbor, starless clumps, which are expected to be cold, more
extended and more massive. The clump, or cloud, consists of low column
density material and contains no massive compact object. Indeed, for
very diffuse clouds, the source find algorithm yielded few clumps. On
the smoothed maps, the algorithm returned values which were close to
cloud size-scales without much substructure. This supports the idea
that these diffuse clouds represent the earliest stage in which few
condensations have formed and gravitational collapse has not yet
started. More evidence for the young nature of diffuse clouds was found
in the 24 ![]() m MIPS data: generally the (smoothed) dust emission followed the 24
m MIPS data: generally the (smoothed) dust emission followed the 24 ![]() m-dark regions and only a few 24
m-dark regions and only a few 24 ![]() m sources of
m sources of ![]() 100
100
![]() ,
located within 20
,
located within 20
![]() of mm peak, were found toward the clouds. In two cases 24
of mm peak, were found toward the clouds. In two cases 24 ![]() m source
m source
![]() were found the edge of the cloud, at
were found the edge of the cloud, at ![]() 1
1![]() from the mm peak.
Examples are G012.73-00.58, G013.28-00.34, and G034.85+00.43 (see Fig. 5).
from the mm peak.
Examples are G012.73-00.58, G013.28-00.34, and G034.85+00.43 (see Fig. 5).
Table 9: Mean physical properties of the clumps and star formation indicators in diffuse, peaked and multiply peaked clouds.
As the first clumps become more compact and their mm peak flux rises above twice the mean emission of cloud, in the peaked cloud
stage, the clump is accreting material from a lower density reservoir
or envelope surrounding it, and consequently the temperature and
turbulence rise. Since star formation is a process which is dynamic and
includes feedback and
triggering, already in this early stage a cloud can contain more than
one clump, though possibly the other peaks barely stick out above the
mean mm emission of the cloud. The peaked clouds are generally
dark at 24 ![]() m, except for a bright 24
m, except for a bright 24 ![]() m source located within
20
m source located within
20
![]() of the mm peak (see G013.91-00.51, G016.93+00.24, and G053.81-00.00 in Fig. 5). The peak flux of the 24
of the mm peak (see G013.91-00.51, G016.93+00.24, and G053.81-00.00 in Fig. 5). The peak flux of the 24 ![]() m sources is on average
m sources is on average
![]() ,
which is higher than what was found for the diffuse clouds.
,
which is higher than what was found for the diffuse clouds.
After more accretion from the reservoir, the clump will have a much
higher mm peak flux compared to the initial stage, reaching at least
trice the mean emission of the cloud. The clump mass will have
decreased toward the more evolved stage, since not all of the mass
reservoir will not be accreted
onto the clump, as the star formation efficiency is apparently
less then 100%. The column density, temperature and turbulence
will increase even further than in the peaked cloud stage. While in the
peaked stage, there were few clouds which had multiple clumps, in the
more evolved stage one expects to find more clouds with multiple
clumps. Most of these clumps should be well above the mean emission of
the cloud. In these multiply peaked clouds,
the clumps will be in different cloud stages of evolution depending on
the initial conditions of the clump. Also not all clumps will form
high-mass stars, so they will have different properties. And
indeed, several clumps in the multiply peaked clouds show bright,
![]() ,
24
,
24 ![]() m emission, indicating a protostar, within 10
m emission, indicating a protostar, within 10
![]() or less of the mm peak, while other clumps are infrared dark. Such
clouds with clumps in various phases are not completely infrared dark,
since the dust is locally heated from the already hot HMPO or UCH II region. Examples for multiply peaked clumps
are shown in Fig. 5: G014.63-00.57, with the very bright component MM1 and the cloud
G018.26-00.24 with five clumps.
or less of the mm peak, while other clumps are infrared dark. Such
clouds with clumps in various phases are not completely infrared dark,
since the dust is locally heated from the already hot HMPO or UCH II region. Examples for multiply peaked clumps
are shown in Fig. 5: G014.63-00.57, with the very bright component MM1 and the cloud
G018.26-00.24 with five clumps.
Additionally, one can check the evolutionary stage by searching for
signs of star formation such as water masers, Class II methanol
masers, and shocks. Table 9
also contains entries for such star formation tracers. Water masers are
thought to be caused by outflows during (low and high-mass) star
formation (Menten 1996). The Class II
methanol masers are uniquely associated with high-mass star formation,
and are usually found prior or coexistent with an H II region (Pestalozzi et al. 2007; Ellingsen 2006; Menten 1991).
While the water masers are found towards both the peaked and the
multiply peaked clouds, the methanol masers are only found toward the
latter class. Another indication for star formation comes from gas
excited by shocks, such as H2(v = 0-0), S(9, 10, 11) or CO(v = 1-0) gas. The IRAC 4.5 ![]() m
band contains both these transitions, and can therefore be used to
search for ongoing star formation. The close association of the
extended 4.5
m
band contains both these transitions, and can therefore be used to
search for ongoing star formation. The close association of the
extended 4.5 ![]() m objects with Class II methanol masers, found by Cyganowski et al. (2008), suggests that they might trace ongoing massive star formation. We find two multiple peaked clouds in our sample that contain such an extended 4.5
m objects with Class II methanol masers, found by Cyganowski et al. (2008), suggests that they might trace ongoing massive star formation. We find two multiple peaked clouds in our sample that contain such an extended 4.5 ![]() m source, of which one also contains Class II methanol masers.
m source, of which one also contains Class II methanol masers.
The peaked and multiply peaked clouds show active star formation, while
the diffuse clouds do not. Possibly, these clouds might not form stars
or will not have column densities high enough to form massive stars.
However, some, for example G013.28-00.34, seem to be forming clumps
which might evolve into active star-forming clumps. Table 9
shows that the clump temperatures are very similar, especially in the
case of peaked and the multiply peaked clouds; the diffuse clouds stand
out with their temperature of 13.5 ![]() 1.5 K against the average temperature of all clouds 16
1.5 K against the average temperature of all clouds 16 ![]() 1.8 K.
As star formation produces stars in a large range of masses,
so cluster-forming regions or clumps within one cloud are expected
to have different column densities and temperatures. Given the range of
column densities for the clumps 3-30
1.8 K.
As star formation produces stars in a large range of masses,
so cluster-forming regions or clumps within one cloud are expected
to have different column densities and temperatures. Given the range of
column densities for the clumps 3-30 ![]()
![]() not all clumps might evolve into clusters with massive stars,
even if mass accretion is still continued from the low density
material surrounding the clump.
not all clumps might evolve into clusters with massive stars,
even if mass accretion is still continued from the low density
material surrounding the clump.
6.3 Comments on individual sources
We performed a systematic search using the SIMBAD Astronomical Database of our cloud to find signs of star formation such as maser emission, H II regions and IRAS sources. We discuss here several diffuse, peaked and multiply peaked high extinction clouds, which are representative examples of typical clouds in our sample. Additionally, several unique and interesting clouds are mentioned.
6.3.1 G013.28-00.34
The cloud G013.28-00.34, with its one centrally located clump MM1, is a
good example of a cloud in a very early phase of protocluster
formation. This clump has a low column density 3 ![]()
![]() and contains less than 5% of the total cloud mass. Likely, this
clump did not yet start to collapse, since from the virial mass we know
that the clump is confined by gas pressure. Additionally,
the clump contains no 24
and contains less than 5% of the total cloud mass. Likely, this
clump did not yet start to collapse, since from the virial mass we know
that the clump is confined by gas pressure. Additionally,
the clump contains no 24 ![]() m emission, which is a further evidence for stage prior to star formation. The moderate
m emission, which is a further evidence for stage prior to star formation. The moderate
![]() line widths of
line widths of
![]() indicate a source of turbulence or large scale motions, however, without an
indicate a source of turbulence or large scale motions, however, without an
![]() map of the cloud it is impossible to isolate the source for the turbulence.
map of the cloud it is impossible to isolate the source for the turbulence.
6.3.2 G013.91-00.51
In the cloud G013.91-00.51 the 1.2 mm emission follows an infrared
dark patch. The one clump in this cloud which is three times above the
mean emission is located nearby two infrared
emission peaks and can be possibly triggered by the star formation in
these infrared bright sites. The clump is very massive, 145 ![]() ,
and cold. The virial mass is 50
,
and cold. The virial mass is 50 ![]() suggesting a collapse.
suggesting a collapse.
6.3.3 G014.63-00.57
Cloud G014.63-00.57 is nested around two bright infrared sources. The
1.2 mm peak fluxes are high,
especially for clumps nearby the infrared sources. The brightest
clump, MM1, contains a compact bright infrared source,
IRAS 18164-1631, with a flux density at 25 ![]() m
m
![]() Jy (Helou & Walker 1988) and has wide
Jy (Helou & Walker 1988) and has wide
![]() line widths of
line widths of
![]() indicating large turbulence. Additionally, water masers were detected towards this clump (Jaffe et al. 1981) and Cyganowski et al. (2008) showed that there is extended 4.5
indicating large turbulence. Additionally, water masers were detected towards this clump (Jaffe et al. 1981) and Cyganowski et al. (2008) showed that there is extended 4.5 ![]() m
emission - a further indication for outflows. All evidence
points to a state of ongoing star formation for the MM1 clump. The
other clumps of G014.63-00.57 are still infrared dark. The MM1 and
MM2 clumps have the theoretically required column density for
massive star formation (see Sect. 6.6).
m
emission - a further indication for outflows. All evidence
points to a state of ongoing star formation for the MM1 clump. The
other clumps of G014.63-00.57 are still infrared dark. The MM1 and
MM2 clumps have the theoretically required column density for
massive star formation (see Sect. 6.6).
6.3.4 G016.93+00.24
In G016.93+00.24 the 1.2 mm emission follows the infrared dark
filament. In the west end of the filament, the 1.2 mm
peak MM1, is a few arc seconds offset from a infrared
bright emission peak. The
![]() line widths are relatively narrow,
line widths are relatively narrow,
![]() ,
and the temperature is low, 14 K, which suggests that the clump is in a very early phase with little turbulence.
,
and the temperature is low, 14 K, which suggests that the clump is in a very early phase with little turbulence.
6.3.5 G017.19+00.81
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg190.png)
|
Figure 12:
A Spitzer GLIMPSE 8.0 |
| Open with DEXTER | |
The multiple peaked cloud G017.19+00.81 harbors several clumps, which are all at a kinematic distance of 2.3 ![]() 0.2 kpc, arranged in an infrared dark arc (Figs. 5 and 12). Such a morphology might point to triggered star formation. The location of this cloud, on the edge of the bright H II region
M16, the Eagle nebula, suggests that we are observing new massive
star-forming clumps in an early stage of evolution, whose creation
might be linked to the already ongoing star formation in this region.
G017.19+00.81 differs from the classical triggered star formation
scenario described by Zavagno et al. (2005). First, the absence of an H II region in the center of the arc; no radio emission was detected either in the 20 cm MAGPIS survey (Helfand et al. 2006), the 21 cm VLA survey (Condon et al. 1998), or in the 6 cm Parkes survey (Haynes et al. 1979) - the object was not covered by the 5 cm VLA survey (Becker et al. 1994). Second, an arc triggered by an H II region is expected to be infrared
bright, whereas G017.19+00.81's arc is partially infrared dark.
0.2 kpc, arranged in an infrared dark arc (Figs. 5 and 12). Such a morphology might point to triggered star formation. The location of this cloud, on the edge of the bright H II region
M16, the Eagle nebula, suggests that we are observing new massive
star-forming clumps in an early stage of evolution, whose creation
might be linked to the already ongoing star formation in this region.
G017.19+00.81 differs from the classical triggered star formation
scenario described by Zavagno et al. (2005). First, the absence of an H II region in the center of the arc; no radio emission was detected either in the 20 cm MAGPIS survey (Helfand et al. 2006), the 21 cm VLA survey (Condon et al. 1998), or in the 6 cm Parkes survey (Haynes et al. 1979) - the object was not covered by the 5 cm VLA survey (Becker et al. 1994). Second, an arc triggered by an H II region is expected to be infrared
bright, whereas G017.19+00.81's arc is partially infrared dark.
The clumps in the cloud have similar temperatures and sizes. The upper
two left clumps, MM2 and MM3, represent most of the mass in this cloud,
whereas the southern MM4, shows the largest amount of turbulence.
Toward the MM2 clump we detected water masers, within a beam
of 40
![]() .
It is coincident with a bright 24
.
It is coincident with a bright 24 ![]() m
source indicating a protostar. MM2 seems to be an evolved clump,
where star formation is just beginning. Additionally, the column
density of this clump theoretically allows high-mass star formation.
The MM4 clump is located nearby an H II region, which might explain the wide line width of
m
source indicating a protostar. MM2 seems to be an evolved clump,
where star formation is just beginning. Additionally, the column
density of this clump theoretically allows high-mass star formation.
The MM4 clump is located nearby an H II region, which might explain the wide line width of
![]() and high degree of turbulence. Nearby (1
and high degree of turbulence. Nearby (1![]() )
there is an infrared-bright source, IRAS 18164-1340, which is only detected at long mid-infrared wavelengths of 100
)
there is an infrared-bright source, IRAS 18164-1340, which is only detected at long mid-infrared wavelengths of 100 ![]() m (
m (
![]() Jy, Helou & Walker 1988)
We performed a more detailed study of this region; a molecular
line survey with IRAM 30 m and an interferometer study with the
SMA (Rygl et al., in preparation).
Jy, Helou & Walker 1988)
We performed a more detailed study of this region; a molecular
line survey with IRAM 30 m and an interferometer study with the
SMA (Rygl et al., in preparation).
6.3.6 G018.26-00.24
G018.26-00.24 is a cloud with five 1.2 mm peaks located northward of an infrared bright region with several H II regions
and water maser detections. There are several infrared sources present
in the cloud, however, the most mm emission peaks are
infrared dark. MM3 is an exception, here the infrared peak is just
a few arc seconds from the mm peak. MM1 has the largest
separation from
the infrared bright region. This clump has the highest column density
and the narrowest line width of the five clumps in this cloud. The
overall cloud shape suggests that the gas and dust was collected by a
driving force south-west of the cloud, possibly the infrared bright
source at (
![]() ,
,
![]() , J2000).
, J2000).
6.3.7 G022.06+00.21
G022.06+00.21 contains one clump with a bright mm peak, MM1, and
second clump with a weaker peak, MM2. MM1 is coincident with
IRAS 18278-0936 (
![]() Jy, Helou & Walker 1988), has 6.7 GHz methanol masers (Szymczak et al. 2000), extended 4.5
Jy, Helou & Walker 1988), has 6.7 GHz methanol masers (Szymczak et al. 2000), extended 4.5 ![]() m
emission (Cyganowski et al. 2008),
and has a sufficient column density for high-mass star formation.
Additionally, we detected water masers towards MM1, within a beam
of 40
m
emission (Cyganowski et al. 2008),
and has a sufficient column density for high-mass star formation.
Additionally, we detected water masers towards MM1, within a beam
of 40
![]() .
MM1 is a relatively warm clump,
.
MM1 is a relatively warm clump,
![]() ,
with ongoing star formation suggested by the masers and outflow
tracers. MM2 is more quiescent and coincident with a weak infrared
source.
,
with ongoing star formation suggested by the masers and outflow
tracers. MM2 is more quiescent and coincident with a weak infrared
source.
6.3.8 G024.37-00.15
G024.37-00.15 contains two clumps, one infrared bright, MM1, and one infrared dark, MM2. MM1 coincides with the bright IRAS source 18337-0743 (6.3.9 G024.61-00.33
In G024.61-00.33, the strongest mm emission peak, MM1, is coincident with IRAS 18346-0734 (
![]() Jy, Helou & Walker 1988) and nearby, separated by
Jy, Helou & Walker 1988) and nearby, separated by
![]() ,
Szymczak et al. (2000) detected 6.7 GHz methanol masers. The second clump, MM2, is infrared dark.
,
Szymczak et al. (2000) detected 6.7 GHz methanol masers. The second clump, MM2, is infrared dark.
6.3.10 G024.94-00.15
The mm emission follows closely the infrared dark filament in cloud
G024.94-00.15. The clumps, MM1 and MM2, are located near weak infrared
sources. We found water maser emission toward MM1, within a beam
of 40
![]() ,
indicating early phases of star formation.
,
indicating early phases of star formation.
6.3.11 G030.90+00.00 A, B, C, and D
G030.90+00.00 consists of several high extinction clouds at very different distances (Fig. 5). It is located at the tangential point of the Scutum-Crux spiral arm (
![]() km s-1), where it overlaps with the Sagittarius-Carina (
km s-1), where it overlaps with the Sagittarius-Carina (
![]() and
and ![]() km s-1) (Vallée 2008). The Scutum-Crux arm connects at this longitude of 30
km s-1) (Vallée 2008). The Scutum-Crux arm connects at this longitude of 30![]() with the Galactic bar, a region with highly shocked gas and explosive star formation (Garzon et al. 1997),
featuring additionally the mini-starburst region W 43. We
found one clump, MM2, which, considering the kinematic distance at
7.2 kpc, is located on the end of the bar.
with the Galactic bar, a region with highly shocked gas and explosive star formation (Garzon et al. 1997),
featuring additionally the mini-starburst region W 43. We
found one clump, MM2, which, considering the kinematic distance at
7.2 kpc, is located on the end of the bar.
6.3.12 G034.77-00.81
G034.77-00.81 is a cloud with very diffuse 1.2 mm emission
located in a infrared dark part of the sky. By smoothing with
a 20
![]() Gaussian the extended emission became more evident. We detected weak
Gaussian the extended emission became more evident. We detected weak
![]() (1, 1) emission
toward the center of the extended emission. The ammonia emission
indicates that there is a dense region in this cloud, however,
it has too low column density or is too extended to be detected by
MAMBO-2. Such clouds as G034.77-00.81 could be the most early stages of
within our sample.
(1, 1) emission
toward the center of the extended emission. The ammonia emission
indicates that there is a dense region in this cloud, however,
it has too low column density or is too extended to be detected by
MAMBO-2. Such clouds as G034.77-00.81 could be the most early stages of
within our sample.
6.3.13 G035.49-00.30 A and B
Cloud G035.49-00.30 A contains one clump, MM1, coincident with a
bright infrared source. In the nearby G035.49-00.30 B we found
five clumps located in an elongated infrared dark cloud with several
weak infrared sources. We detected water maser emission towards MM1 and
MM3, within a beam of 40
![]() .
MM1 is the most evolved clump, with ongoing star formation.
MM3 should be in a earlier stage of star formation, since the peak
of the mm emission is infrared dark.
.
MM1 is the most evolved clump, with ongoing star formation.
MM3 should be in a earlier stage of star formation, since the peak
of the mm emission is infrared dark.
6.4 Comparison with infrared dark clouds
Recent studies have shown that IRDCs generally have a filamentary shape and a high column density of ![]() 1023 cm-2 (Rathborne et al. 2006; Carey et al. 2000,1998).
IRDCs, which are very compact or have large aspect ratios, might not be
detected in the extinction maps because of the limited resolution. The
extincion method is more sensitive to the more extended and therefore
on average lower column density material than generally found in IRDCs.
However, the follow-up study of the 1.2 mm emission maps with
MAMBO is sensitive enough to reach the typical IRDC column densities,
allowing a comparison between the properties of the high extinction
clouds and the IRDCs.
1023 cm-2 (Rathborne et al. 2006; Carey et al. 2000,1998).
IRDCs, which are very compact or have large aspect ratios, might not be
detected in the extinction maps because of the limited resolution. The
extincion method is more sensitive to the more extended and therefore
on average lower column density material than generally found in IRDCs.
However, the follow-up study of the 1.2 mm emission maps with
MAMBO is sensitive enough to reach the typical IRDC column densities,
allowing a comparison between the properties of the high extinction
clouds and the IRDCs.
We find that almost 70% of the high extinction clouds have also IRDC characteristics using the Catalog of IRDC candidates from Simon et al. (2006a) and the Spitzer IRDC catalog of Peretto & Fuller (2009). This overlap caused that we incidentally studied the same source as Rathborne et al. (2006), namely G035.49-00.30 (listed as MSXDC G035.39-00.33 in the paper by Rathborne et al. 2006), allowing a direct comparison. Given the size of our bolometer map, we identified the same clumps within this cloud. Taking into account different analysis methods, we find similar fluxes and masses as Rathborne et al. (2006).
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg13.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg204.png)
|
Figure 13:
The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg14.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg205.png)
|
Figure 14:
The
|
| Open with DEXTER | |
In general, the temperature and the level of turbulence (line withs) of
the clumps in high extinction clouds was similar to values found for
IRDCs (Pillai et al. 2006). Figures 13 and 14 show that the turbulence tends to increase with ammonia column density and temperature, which is similar for IRDCs (Pillai et al. 2006).
The masses and volume averaged densities of the clumps in our sample
are similar to the averaged values for clumps in IRDCs (referred to
as ``cores'' in Rathborne et al. 2006).
However, at large distances the high extinction method is biased toward
more massive clumps. Comparing with the IRDCs sample of Rathborne et al. (2006) our sample is missing low-mass clumps (
![]() )
at large distances (d>4 kpc), see the left panel of Fig. 7. However, our goal, to search for high-mass molecular clouds, is not affected.
)
at large distances (d>4 kpc), see the left panel of Fig. 7. However, our goal, to search for high-mass molecular clouds, is not affected.
Although, the majority of the high extinction clouds is infrared dark,
there are a number of infrared bright sources. Especially amongst the
multiply peaked clouds, we find several cases of already ongoing star
formation via detections of H II regions, water and Class II methanol masers, and extended 4.5 ![]() m
emission. Since we did not require the high extinction clouds to be
infrared dark, the method is also sensitive to the evolved stages
of star formation. In addition, the color excess selection is
sensitive to embedded young stars with a color excess of
their own.
m
emission. Since we did not require the high extinction clouds to be
infrared dark, the method is also sensitive to the evolved stages
of star formation. In addition, the color excess selection is
sensitive to embedded young stars with a color excess of
their own.
6.5 Comparison with more evolved objects
Later stages of massive star formation are the HMPOs and the UCH II regions.
Since these objects are usually still embedded in their natal cloud,
they emit most strongly in the millimeter to infrared. Additionally,
UCH II regions emit free-free emission, which is
detectable at radio frequencies. Most red and bright IRAS sources are
such embedded stages of evolved star (or cluster) formation (Wood & Churchwell 1989). Ammonia observations of HMPOs and UCH II regions show that they are usually warm (![]() K, Churchwell et al. 1990; Sridharan et al. 2002) and very turbulent (line widths of 2-3 km s-1). Water and Class II methanol masers are observed towards these regions (Walsh et al. 1998), indicating outflows and infrared radiation, respectively.
K, Churchwell et al. 1990; Sridharan et al. 2002) and very turbulent (line widths of 2-3 km s-1). Water and Class II methanol masers are observed towards these regions (Walsh et al. 1998), indicating outflows and infrared radiation, respectively.
The high extinction clumps have lower temperatures and narrower line widths. Many of the more evolved clumps in high extinction clouds have their peak of mm emission nearby bright infrared sources. In several cases the two emission peaks even coincide. For three such cases, G014.63-00.57 MM1, G017.19+00.81 MM2, and G022.06+00.21 MM1, we find slightly higher rotational temperatures, respectively 18, 19 and 25 K, and detections of water masers reminiscent of outflows in the early phase of star formation.
The clump masses in the high extinction clouds are almost one order magnitude lower than the masses of HMPOs (Beuther et al. 2002).
Likely, by removing the median emission before performing the
source extraction, the low column density mass reservoir of the clump
is subtracted resulting in less massive clumps than in the HMPO
studies. Also the HMPOs are on average larger with an average FWHM of 0.5 pc, than the sizes of our clumps (![]() 0.3 pc).
0.3 pc).
In most of our clumps the ammonia column densities were of an order of magnitude higher than those for HMPOs. As a clump forms protostellar objects, the temperature and line widths increase, while the clump will start losing its envelope, which will decrease the ammonia column density on clump size-scales. Similar behavior of temperature, line width and ammonia column density is also observed for IRDCs (Pillai et al. 2006).
6.6 Comparison with theoretical models
There are two competing models to explain the formation of massive stars, core accretion (Krumholz et al. 2009; McKee & Tan 2003; Krumholz et al. 2005) and competitive accretion (Bonnell & Bate 2002; Klessen et al. 1998; Bonnell & Bate 2006; Bonnell et al. 2001). They differ primarily in how the mass is collected which will ultimately make the massive star. In the first model, core accretion, a massive star forms in a massive core, hence the mass reservoir of the core determines the mass of the star. In the second theory, a clump of gas will fragment into many low-mass objects containing masses around the thermal Jeans mass. The accretion will continue in this N-body system, where the overall system potential funnels gas down to the center of the potential, to be accreted by the massive stars forming there. A powerful way to distinguish between these scenarios are better determinations of the massive cores within the clumps. For the core accretion model these cores should be distributed similar to a stellar mass function. The degree of mass segregation of the cores in a clump and the limit of fragmentation will test the competitive accretion model. Such massive core studies require a resolution much higher than this study; they have to resolve the clumps into cores. Several studies on fragmentation were recently carried out using the Plateau du Bure or the SMA interferometers (Beuther et al. 2007; Zhang et al. 2009; Rathborne et al. 2007,2008; Swift 2009). They show that the 1.2 mm clumps fragment into smaller cores, but cannot tell at what level the fragmentation halts. With the advent of ALMA, the limit of fragmentation will finally come within observational reach.
Simulations of core accretion models by Krumholz & McKee (2008) put forward a minium column density of 1 g cm-2 for massive star formation. For reference, this corresponds to 4750
![]() or
or
![]()
![]()
![]() .
This limit would imply that only one clump from the high extinction clouds can form massive stars, namely G014.63-00.57 MM1.
We note here that Krumholz & McKee (2008) use a
.
This limit would imply that only one clump from the high extinction clouds can form massive stars, namely G014.63-00.57 MM1.
We note here that Krumholz & McKee (2008) use a
![]() ,
while we used
,
while we used
![]() .
To compare this limit with our measured column densities we would
have to scale our results by a factor 2.5, and in this case four
clumps would theoretically be able to form massive stars. Of these
four clumps only one, G014.63-00.57 MM2, is infrared dark. The other
three clumps are infrared bright, indicating that they already
commenced forming stars. It suggests that the theoretical column
density limit is too high for the very initial stages of star cluster
forming clumps.
.
To compare this limit with our measured column densities we would
have to scale our results by a factor 2.5, and in this case four
clumps would theoretically be able to form massive stars. Of these
four clumps only one, G014.63-00.57 MM2, is infrared dark. The other
three clumps are infrared bright, indicating that they already
commenced forming stars. It suggests that the theoretical column
density limit is too high for the very initial stages of star cluster
forming clumps.
7 Summary
We made infrared extinction maps of the first and fourth Galactic quadrant, compiling a catalog of compact high extinction features. We studied 25 high extinction clouds in detail, using IRAM 30 m bolometer observations and pointed ammonia observations with the Effelsberg Telescope. The main results of the paper can be summarized as:
- 1.
- Using the average color excess of the Spitzer 3.6-4.5
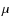 m
IRAC bands, we are able to trace high density structures across
the Galactic plane. The extinction selected clouds are found on
distances between 1 and 7 kpc. Most of them are concentrated
in the range of 1-4 kpc, and trace the same regions of the
Galactic plane as IRDCs.
m
IRAC bands, we are able to trace high density structures across
the Galactic plane. The extinction selected clouds are found on
distances between 1 and 7 kpc. Most of them are concentrated
in the range of 1-4 kpc, and trace the same regions of the
Galactic plane as IRDCs.
- 2.
- The extinction method is more sensitive to large scale lower
column density clouds than the bolometer observations of 1.2 mm
emission, which resulted in a few non detections of clouds in the mm
emission despite a mean visual extinction of
 30 mag
from the extinction map. In general, there is a good correlation
between the cloud masses derived from the extinction maps and from the
1.2 mm emission.
30 mag
from the extinction map. In general, there is a good correlation
between the cloud masses derived from the extinction maps and from the
1.2 mm emission.
- 3.
- From the 1.2 mm emission, we have found clumps with column densities of 3-30
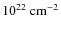 and masses of
and masses of
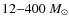 .
Evidently, not all clumps found by high extinction will be able to form
massive stars. It is expected for cluster-forming regions to
produce low and high-mass stars, thus to have a wide range in masses.
.
Evidently, not all clumps found by high extinction will be able to form
massive stars. It is expected for cluster-forming regions to
produce low and high-mass stars, thus to have a wide range in masses.
- 4.
- High extinction clouds contain a wide range of evolutionary
stages. 70% of the high extinction clouds are associated with
infrared dark clouds, however several clouds show more evolved stages
of ongoing (massive) star formation. Three different classes of clouds
are proposed:
- Diffuse clouds have no signs of masers, H II regions or extended 4.5
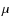 m
objects, which are general signposts of star formation. The 1.2 mm
emission shows no mm peaks above twice the mean emission of the cloud.
These clouds are cold (
m
objects, which are general signposts of star formation. The 1.2 mm
emission shows no mm peaks above twice the mean emission of the cloud.
These clouds are cold (
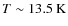 )
and line widths far above the thermal value mark the importance of
turbulence. The observations suggest that the diffuse clouds are in an
early phase, where the accretion of gas and dust into clumps might be
on the verge of beginning or might never reach the necessary column
density to form stars.
)
and line widths far above the thermal value mark the importance of
turbulence. The observations suggest that the diffuse clouds are in an
early phase, where the accretion of gas and dust into clumps might be
on the verge of beginning or might never reach the necessary column
density to form stars. - When the clumps manage to accrete more matter so that the mm emission exceeds twice the mean cloud emission they enter the next (peaked) stage. During the peaked stage already some clouds show more than one clump, which indicates that star formation can start in different regions in the same cloud at different times.
- Multiply peaked clouds show many signs of ongoing star formation, such as detections of masers, H II regions or extended 4.5
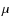 m
objects. Several clumps are infrared bright and show generally slightly
higher temperatures and turbulence than diffuse or peaked clouds.
Clumps within a cloud are not necessary in the same state, and will
likely not all form massive stars. We find four clumps that satisfy the
theoretical column density requirement for high-mass star formation.
m
objects. Several clumps are infrared bright and show generally slightly
higher temperatures and turbulence than diffuse or peaked clouds.
Clumps within a cloud are not necessary in the same state, and will
likely not all form massive stars. We find four clumps that satisfy the
theoretical column density requirement for high-mass star formation.
- Diffuse clouds have no signs of masers, H II regions or extended 4.5
We thank the anonymous referee, whose comments and suggestions resulted in a much improved paper. We also thank Malcolm Walmsley for the helpful discussion. This work is based on observations with the 100 m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg and the IRAM 30 m telescope at Pico Veleta. We are grateful to the staff of both observatories for their support. We thank Marion Wienen and Lies Verheyen for their help with the Effelsberg observations. This research has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration and the SIMBAD database, operated at CDS, Strasbourg, France. This publication makes use of molecular line data from the Boston University-FCRAO Galactic Ring Survey (GRS). The GRS is a joint project of Boston University and Five College Radio Astronomy Observatory, funded by the National Science Foundation under grants AST-9800334, AST-0098562, and AST-0100793. K.L.J.R. was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne.
References
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99
- Becker, R. H., White, R. L., Helfand, D. J., & Zoonematkermani, S. 1994, ApJS, 91, 347
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953
- Bergin, E. A., & Langer, W. D. 1997, ApJ, 486, 316
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140
- Beuther, H., & Sridharan, T. K. 2007, ApJ, 668, 348
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002, ApJ, 566, 945
- Beuther, H., Leurini, S., Schilke, P., et al. 2007, A&A, 466, 1065
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132
- Bonnell, I. A., & Bate, M. R. 2002, MNRAS, 336, 659
- Bonnell, I. A., & Bate, M. R. 2006, MNRAS, 370, 488
- Bonnell, I. A., Bate, M. R., Clarke, C. J., & Pringle, J. E. 2001, MNRAS, 323, 785
- Carey, S. J., Clark, F. O., Egan, M. P., et al. 1998, ApJ, 508, 721
- Carey, S. J., Feldman, P. A., Redman, R. O., et al. 2000, ApJ, 543, L157
- Chambers, E. T., Jackson, J. M., Rathborne, J. M., & Simon, R. 2009, ApJS, 181, 360
- Chapman, N. L., Mundy, L. G., Lai, S.-P., & Evans, N. J. 2009, ApJ, 690, 496
- Churchwell, E., Walmsley, C. M., & Cesaroni, R. 1990, A&AS, 83, 119
- Clark, P. C., Klessen, R. S., Bonnell, I. A., & Smith, R. J. 2008, in Massive Star Formation: Observations Confront Theory, ed. H. Beuther, H. Linz, & T. Henning, ASP Conf. Ser., 387, 208
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693
- Cyganowski, C. J., Whitney, B. A., Holden, E., et al. 2008, AJ, 136, 2391
- Dame, T. M., Ungerechts, H., Cohen, R. S., et al. 1987, ApJ, 322, 706
- Danby, G., Flower, D. R., Valiron, P., Schilke, P., & Walmsley, C. M. 1988, MNRAS, 235, 229
- Egan, M. P., Shipman, R. F., Price, S. D., et al. 1998, ApJ, 494, L199
- Ellingsen, S. P. 2006, ApJ, 638, 241
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10
- Fich, M., Blitz, L., & Stark, A. A. 1989, ApJ, 342, 272
- Flaherty, K. M., Pipher, J. L., Megeath, S. T., et al. 2007, ApJ, 663, 1069
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590
- Froebrich, D., & del Burgo, C. 2006, MNRAS, 369, 1901
- Garzon, F., Lopez-Corredoira, M., Hammersley, P., et al. 1997, ApJ, 491, L31
- Haynes, R. F., Caswell, J. L., & Simons, L. W. J. 1979, Aust. J. Phys. Astrophys. Suppl., 48, 1
- Helfand, D. J., Becker, R. H., White, R. L., Fallon, A., & Tuttle, S. 2006, AJ, 131, 2525
- Helou, G., & Walker, D. W. 1988, Infrared astronomical satellite (IRAS) catalogs and atlases, The small scale structure catalog, 7
- Hildebrand, R. H. 1983, QJRAS, 24, 267
- Hill, T., Thompson, M. A., Burton, M. G., et al. 2006, MNRAS, 368, 1223
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931
- Jackson, J. M., Finn, S. C., Rathborne, J. M., Chambers, E. T., & Simon, R. 2008, ApJ, 680, 349
- Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJS, 163, 145
- Jaffe, D. T., Guesten, R., & Downes, D. 1981, ApJ, 250, 621
- Joshi, Y. C. 2007, MNRAS, 378, 768
- Kirk, J. M., Ward-Thompson, D., & André, P. 2005, MNRAS, 360, 1506
- Klessen, R. S., Burkert, A., & Bate, M. R. 1998, ApJ, 501, L205
- Krumholz, M. R., & McKee, C. F. 2008, Nature, 451, 1082
- Krumholz, M. R., McKee, C. F., & Klein, R. I. 2005, Nature, 438, 332
- Krumholz, M. R., Klein, R. I., McKee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009, Science, 323, 754
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57
- Lada, C. J., Lada, E. A., Clemens, D. P., & Bally, J. 1994, ApJ, 429, 694
- Li, D., Goldsmith, P. F., & Menten, K. 2003, ApJ, 587, 262
- MacLaren, I., Richardson, K. M., & Wolfendale, A. W. 1988, ApJ, 333, 821
- Mangum, J. G., Wootten, A., & Mundy, L. G. 1992, ApJ, 388, 467
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850
- Menten, K. M. 1991, ApJ, 380, L75
- Menten, K. M. 1996, in Molecules in Astrophysics: Probes & Processes, ed. E. F. van Dishoeck, IAU Symp., 178, 163
- Moore, T. J. T., Lumsden, S. L., Ridge, N. A., & Puxley, P. J. 2005, MNRAS, 359, 589
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943
- Ott, M., Witzel, A., Quirrenbach, A., et al. 1994, A&A, 284, 331
- Pagani, L., Pardo, J., Apponi, A. J., Bacmann, A., & Cabrit, S. 2005, A&A, 429, 181
- Perault, M., Omont, A., Simon, G., et al. 1996, A&A, 315, L165
- Peretto, N., & Fuller, G. A. 2009, A&A, 505, 405
- Pestalozzi, M. R., Chrysostomou, A., Collett, J. L., et al. 2007, A&A, 463, 1009
- Pestalozzi, M. R., Minier, V., & Booth, R. S. 2005, A&A, 432, 737
- Pillai, T., Wyrowski, F., Carey, S. J., & Menten, K. M. 2006, A&A, 450, 569
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389
- Rathborne, J. M., Simon, R., & Jackson, J. M. 2007, ApJ, 662, 1082
- Rathborne, J. M., Jackson, J. M., Zhang, Q., & Simon, R. 2008, ApJ, 689, 1141
- Reach, W. T., Megeath, S. T., Cohen, M., et al. 2005, PASP, 117, 978
- Rohlfs, K., & Wilson, T. L. 2004, Tools of radio astronomy, ed. K. Rohlfs, & T. L. Wilson
- Rosolowsky, E., Dunham, M. K., Ginsburg, A., et al. 2010, ApJS, 188, 123
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415
- Simon, R., Jackson, J. M., Rathborne, J. M., & Chambers, E. T. 2006a, ApJ, 639, 227
- Simon, R., Rathborne, J. M., Shah, R. Y., Jackson, J. M., & Chambers, E. T. 2006b, ApJ, 653, 1325
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367
- Sridharan, T. K., Beuther, H., Schilke, P., Menten, K. M., & Wyrowski, F. 2002, ApJ, 566, 931
- Stead, J. J., & Hoare, M. G. 2009, MNRAS, 400, 731
- Swift, J. J. 2009, ApJ, 705, 1456
- Szymczak, M., Hrynek, G., & Kus, A. J. 2000, A&AS, 143, 269
- Vallée, J. P. 2008, AJ, 135, 1301
- Walmsley, C. M., & Ungerechts, H. 1983, A&A, 122, 164
- Walsh, A. J., Burton, M. G., Hyland, A. R., & Robinson, G. 1998, MNRAS, 301, 640
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296
- Wood, D. O. S., & Churchwell, E. 1989, ApJ, 340, 265
- Zasowski, G., Majewski, S. R., Indebetouw, R., et al. 2009, ApJ, 707, 510
- Zavagno, A., Deharveng, L., Brand, J., et al. 2005, in Massive Star Birth: A Crossroads of Astrophysics, ed. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 346
- Zhang, Q., Wang, Y., Pillai, T., & Rathborne, J. 2009, ApJ, 696, 268
Online Material
Table 1:
Catalog of high extinction clouds (HECs) with the peak color excess,
![]()
Table 5: Observed ammonia parameters with uncertainties (in parenthesis) from hyperfine and Gaussian fits with CLASS.
Footnotes
- ... clouds
![[*]](/icons/foot_motif.png)
- Tables 1 and 5 are only available in electronic form at http://www.aanda.org
- ...
![[**]](/icons/foot_motif.png)
- Table 1 and fits images associated with the extinction maps of Fig. 1 and the 1.2 mm continuum maps appearing in Fig. 5 can be queried from the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/515/A42
- ... Rygl
![[***]](/icons/foot_motif.png)
- Member of the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne.
- ... website
![[*]](/icons/foot_motif.png)
- http://www.mpifr-bonn.mpg.de/div/effelsberg/calibration/1.3cmsf.html
All Tables
Table 2: Properties of the high extinction clouds.
Table 3: Positions (J2000) and fluxes of the clumps from the 1.2 mm continuum data.
Table 4: Positions (J2000) and determined properties toward the positions without clumps.
Table 6: Detected water masers.
Table 7:
Properties of the clumps derived from
![]() and the 1.2 mm continuum.
and the 1.2 mm continuum.
Table 8: Mean properties of high extinction complexes, clouds and clumps.
Table 9: Mean physical properties of the clumps and star formation indicators in diffuse, peaked and multiply peaked clouds.
Table 1:
Catalog of high extinction clouds (HECs) with the peak color excess,
![]()
Table 5: Observed ammonia parameters with uncertainties (in parenthesis) from hyperfine and Gaussian fits with CLASS.
All Figures
![\begin{figure}
\par\includegraphics[width=15cm,clip]{13510fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg51.png)
|
Figure 1:
The color excess
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.75cm,clip]{13510fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg86.png)
|
Figure 2:
Mean color excess along Galactic longitude (upper diagram, bins of 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=5cm,clip]{13510fg3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg95.png)
|
Figure 3:
A face-on view of the Galactic plane. The Galactic center is located at (0, 0). The Galacitic longitudes of 12 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{13510fg4a.eps}\p...
...eps}\par\includegraphics[angle=-90,width=8.2cm,clip]{13510fg4c.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg96.png)
|
Figure 4:
Examples of extinction maps (red dashed contour, starting at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{4mm}\includegraphics[width=6.8cm, angle=-90]{13510...
...{10mm}}
\par\includegraphics[width=6.8cm, angle=-90]{13510fg5e.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg99.png)
|
Figure 5:
Spitzer/MIPS 24
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{4cm}\includegraphics[width=7cm, angle=-90]{13510fg...
...includegraphics[width=7cm, angle=-90]{13510fg5i.eps}\hspace*{4cm}}\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg100.png)
|
Figure 5: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm, angle=-90]{13510fg5j.eps}\include...
...dth=7cm, angle=-90]{13510fg5n.eps}\hspace*{3.8cm}}\vspace*{1.6mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg101.png)
|
Figure 5: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{1cm}\includegraphics[width=7cm, angle=-90]{13510fg...
...cludegraphics[width=7cm, angle=-90]{13510fg5s.eps}\hspace*{3.8cm}}\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg102.png)
|
Figure 5: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm, angle=-90]{13510fg5t.eps}\inclu...
...udegraphics[width=6.8cm, angle=-90]{13510fg5y.eps}\hspace*{4.9cm}}\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg103.png)
|
Figure 5: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg104.png)
|
Figure 6: Number distribution of 1.2 mm clumps with size determined from Gaussian fits and converted to physical units using the near kinematic distance. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{13510fg7.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg122.png)
|
Figure 7: Distance as a function of clump mass ( left) and size ( right). In the left panel, the clump mass based on Gaussian fitting is marked by squares, and the clump mass within 0.25 pc around the center of a clump is indicated by crosses. There is a linear correlation with distance for the mass and the size. The most massive clumps are at large distances, whereas almost no low-mass clumps are found at distances larger than 4 kpc, which can be expected for a sensitivity limited selection of clouds. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg8a.eps}\par...
...ludegraphics[angle=-90,width=8cm,clip]{13510fg8b.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg135.png)
|
Figure 8:
The
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg9.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg136.png)
|
Figure 9:
Number distribution of the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg10.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg137.png)
|
Figure 10: The cloud masses estimated from the color excess versus the masses estimated from the 1.2 mm continuum maps. The red dashed line is a help line indicating the trend in which both mass estimates are equal. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg142.png)
|
Figure 11: Virial clump masses versus the 1.2 mm continuum clump masses. The red dashed line indicates the trend where the virial parameter is unity. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg190.png)
|
Figure 12:
A Spitzer GLIMPSE 8.0 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg13.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg204.png)
|
Figure 13:
The
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{13510fg14.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13510-09/Timg205.png)
|
Figure 14:
The
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



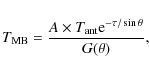
![\begin{displaymath}%
A_{\rm V} = \frac{ N_{{\rm H_2}}}{0.94 \times 10^{21}}~[{\rm mag}].
\end{displaymath}](/articles/aa/full_html/2010/07/aa13510-09/img105.png)
![\begin{displaymath}%
M_{{\rm vir}} = 210 \times \left(\frac{\Delta v}{{\rm km~s^{-1}}}\right)^2 \left(\frac{R}{{\rm pc}}\right)~[M_\odot].
\end{displaymath}](/articles/aa/full_html/2010/07/aa13510-09/img145.png)