| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913494 | |
| Published online | 31 May 2010 | |
Rotation-disk connection for very low
mass and substellar objects in the Orion Nebula Cluster![[*]](/icons/foot_motif.png)
M. V. Rodríguez-Ledesma1,2,3 - R. Mundt1 - J. Eislöffel4
1 - Max-Planck-Institut für Astronomie (MPIA), Königstuhl 17, 69117
Heidelberg, Germany
2 - International Max Planck Research School for Astronomy &
Cosmic Physics at the University of Heidelberg, Germany
3 - Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
4 - Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778
Tautenburg, Germany
Received 17 October 2009 / Accepted 13 January 2010
Abstract
Aims. Angular momentum (J) loss requires magnetic
interaction between the forming star and both the circumstellar disk
and the magnetically driven outflows. In order to test these
predictions many authors have investigated a rotation-disk connection
in pre-main sequence objects with masses larger than about 0.4 ![]() .
For brown dwarfs (BDs) this connection was not investigated as yet
because there are very few samples available. We aim to extend this
investigation well down into the substellar regime for our large sample
of
.
For brown dwarfs (BDs) this connection was not investigated as yet
because there are very few samples available. We aim to extend this
investigation well down into the substellar regime for our large sample
of ![]() 80 BDs
in the Orion Nebula Cluster, for which we have recently measured
rotational periods.
80 BDs
in the Orion Nebula Cluster, for which we have recently measured
rotational periods.
Methods. In order to investigate a rotation-disk
correlation, we derived near-infrared (NIR) excesses for a sample of
732 periodic variables in the Orion Nebula Cluster with masses ranging
between ![]() 1.5-0.02
1.5-0.02 ![]() and whose IJHK colors are available. Circumstellar
NIR excesses were derived from the
and whose IJHK colors are available. Circumstellar
NIR excesses were derived from the ![]() index. We performed our analysis in three mass bins
(>0.4
index. We performed our analysis in three mass bins
(>0.4 ![]() ,
0.4-0.075
,
0.4-0.075 ![]() ,
and <0.075
,
and <0.075 ![]() ).
).
Results. We found a rotation-disk correlation in the
high and intermediate mass regime, in which objects with NIR excess
tend to rotate slower than objects without NIR excess. Interestingly,
we found no correlation in the substellar regime. A tight correlation
between the peak-to-peak (ptp) amplitude of the rotational modulation
and the NIR excess was found however for all objects with available ptp
values (<0.4 ![]() ). We discuss possible
scenarios which may explain the lack of rotation-disk connection in the
substellar mass regime. One possible reason could be the strong
dependence of the mass accretion rate
). We discuss possible
scenarios which may explain the lack of rotation-disk connection in the
substellar mass regime. One possible reason could be the strong
dependence of the mass accretion rate ![]() on stellar mass in the investigated mass range (
on stellar mass in the investigated mass range (
![]() ), which is
expected to result in a corresponding mass dependence of
), which is
expected to result in a corresponding mass dependence of ![]() .
.
Key words: stars: low-mass - starts: pre-main sequence - stars: rotation - techniques: photometric - brown dwarfs - accretion, accretion disks
1 Introduction
At present observations and theory together give a comprehensive
picture of star formation. Nevertheless, how young pre-main sequence
(PMS) objects effectively lose angular momentum is still not fully
understood. PMS stars increase their mass by accreting material from
the circumstellar disk. At this stage, accretion and ongoing
contraction would contribute to a net spinning up of the PMS star,
which is expecting to rotate at nearly breakup velocity (e.g. Vogel
& Kuhi 1981).
Yet, numerous observations reveal that these objects rotate much
slower, with typical rotational velocities of ![]() 10% the breakup velocity (e.g.
Herbst et al. 2007
and references therein). It is clear that considerable amounts of
angular momentum are somehow removed from the star/disk system during
the accretion phase.
10% the breakup velocity (e.g.
Herbst et al. 2007
and references therein). It is clear that considerable amounts of
angular momentum are somehow removed from the star/disk system during
the accretion phase.
Various theories, all of them requiring ongoing mass accretion from the disk to the star in combination with magnetically driven outflows, are usually proposed to explain this enormous removal of angular momentum and the large spread of rotational velocities observed (e.g. Hillenbrand 1997; Herbst et al. 2002, hereafter H2002; Lamm et al. 2004, 2005; Scholz & Eislöffel 2004, 2005; Rodriguez-Ledesma et al. 2009a, hereafter Paper I). The proposed theories rely on a disk-locking mechanism (e.g. Camenzind 1990; Königl 1991), X-winds (e.g. Shu et al. 1994; Ferreira et al. 2006), disk winds or massive stellar winds working in conjunction with magnetospheric accretion (e.g. Matt & Pudritz 2005b) to account for the angular momentum loss. Irrespective of the specific model, there is a general consensus that circumstellar accretion disks are somehow responsible for the removal of angular momentum, and therefore accreting stars should on average rotate slower than non-accreting ones.
There is wide observational evidence that most low mass pre-main sequence stars and even substellar objects have circumstellar disks (e.g. Hillenbrand et al. 1998; Muench et al. 2001; Mohanty et al. 2004; Rebull et al. 2006; etc). Accretion features have also been observed in substellar objects (e.g. Mohanty et al. 2004).
For more than 15 years, several authors investigated possible
correlations between rotation rates and the presence of circumstellar
accretion disks (e.g. Edwards et al. 1993; Rebull 2001; H2002;
Lamm et al. 2005;
Rebull et al. 2006;
Cieza & Baliber 2007).
While many of them found a rotation-disk correlation for solar and low
mass stars (e.g. H2002; Lamm et al. 2005; Rebull
et al. 2006;
Cieza & Baliber 2007;
Biazzo 2009),
others did not (e.g. Rebull 2001;
Makidon 2004;
Nguyen et al. 2009).
As stated by Cieza & Baliber (2007), intrinsic
dependence of rotation on mass and age, which were not taken into
account in many of the previous works, were probably one of the reasons
for the discrepant results. An additional reason is probably the use of
different and sometimes ambiguous accretion indicators. Most of the
above mentioned studies are using near-infrared (NIR) excess as a
circumstellar disk indicator. While NIR excess probes the presence of
circumstellar dust, it does not probe ongoing accretion. However, a
remarkable correlation between mass accretion indicators such as H![]() emission line widths and NIR excess has been reported in the literature
(e.g. Sicilia-Aguilar et al. 2005, 2006) and
therefore using NIR excess as a mass accretion indicator is a
reasonable approach.
emission line widths and NIR excess has been reported in the literature
(e.g. Sicilia-Aguilar et al. 2005, 2006) and
therefore using NIR excess as a mass accretion indicator is a
reasonable approach.
Muench et al. (2001)
found that about 50% of their brown dwarf candidates in the Trapezium
region show near-infrared (NIR) excesses indicative of a circumstellar
disk. Lada (2000)
found that ![]() 50%
of objects in the Trapezium cluster have a JHK
excess, while their observations at
50%
of objects in the Trapezium cluster have a JHK
excess, while their observations at ![]() 3
3 ![]() m revealed a
much higher disk fraction of about 85%. Since longer wavelengths
provide a better disk indication than observations at NIR wavelengths,
the use of Spitzer data (IRAC bands: 3.6
m revealed a
much higher disk fraction of about 85%. Since longer wavelengths
provide a better disk indication than observations at NIR wavelengths,
the use of Spitzer data (IRAC bands: 3.6 ![]() m,
4.5
m,
4.5 ![]() m,
5.8
m,
5.8 ![]() m,
and 8
m,
and 8 ![]() m)
seems to be the solution towards an unambiguous disk indicator.
However, the evaluation of the IRAC data of the ONC encounters two
serious problems, namely a very strong nebular background and high
stellar densities. These two problems obviously get stronger with
decreasing distance to the cluster center. As stated by Rebull
et al. (2006),
due to the strong nebular background and source confussion, even
relatively bright periodic variables close to the Trapezium are missing
IRAC detections. Megeath et al. (2005) estimated
that about 700 stars may be missing IRAC detection in the inner
m)
seems to be the solution towards an unambiguous disk indicator.
However, the evaluation of the IRAC data of the ONC encounters two
serious problems, namely a very strong nebular background and high
stellar densities. These two problems obviously get stronger with
decreasing distance to the cluster center. As stated by Rebull
et al. (2006),
due to the strong nebular background and source confussion, even
relatively bright periodic variables close to the Trapezium are missing
IRAC detections. Megeath et al. (2005) estimated
that about 700 stars may be missing IRAC detection in the inner ![]() arcmin2
center of the ONC. Only objects in the ONC with spectral types earlier
than M2 (i.e.
arcmin2
center of the ONC. Only objects in the ONC with spectral types earlier
than M2 (i.e. ![]() if Baraffe et al. (1998)
models are used) were analyzed and searched for the presence of a disk
and a rotational-disk connection by means of IRAC data (Rebull
et al. 2006;
Cieza & Baliber 2007).
Since our sample of periodic variables is three magnitudes deeper than
previous studies and contains many objects in the inner most part of
the ONC, we have to rely on NIR data to identify the circumstellar
disks in our sample. Although NIR observations are less efficient in
detecting disks than observations at longer wavelengths, the relatively
high disk fraction of
if Baraffe et al. (1998)
models are used) were analyzed and searched for the presence of a disk
and a rotational-disk connection by means of IRAC data (Rebull
et al. 2006;
Cieza & Baliber 2007).
Since our sample of periodic variables is three magnitudes deeper than
previous studies and contains many objects in the inner most part of
the ONC, we have to rely on NIR data to identify the circumstellar
disks in our sample. Although NIR observations are less efficient in
detecting disks than observations at longer wavelengths, the relatively
high disk fraction of ![]() 50%
found by Lada (2000),
Muench et al. (2001)
among large samples of low mass stars and brown dwarfs by means of JHK
excesses provides valid support that NIR excess is a suitable disk
indicator for low mass and substellar objects.
50%
found by Lada (2000),
Muench et al. (2001)
among large samples of low mass stars and brown dwarfs by means of JHK
excesses provides valid support that NIR excess is a suitable disk
indicator for low mass and substellar objects.
A considerable number of studies, which have explored the connection between the presence of disks and rotation in low and very low mass stars, are summarized in Herbst et al. (2007) and Bouvier (2007). The major aim of this study is to constrain for the first time a possible rotation-disk connection in the substellar mass regime, and compare these results with higher mass objects. This study would not have been possible without the rotational period measurements of 124 BD candidates in Paper I.
In Paper I we confirmed the strong period dependence
on stellar mass found for higher mass stars by H2002 and extended it
into the brown dwarf regime down to ![]() 20
20
![]() .
We found that substellar objects tend to rotate faster than their
stellar counterparts. In order to constrain a possible rotation-disk
connection, in particular for the so far very poorly investigated very
low mass and substellar regime, we analyze here a sample of 732
periodic variables from Paper I and Herbst et al. (2002) which have
available JHK colors to be used as disk indicators.
In Sect. 2 we give details of the used NIR data sets.
Section 3 describes how we estimated the masses in our sample.
Section 4 defines the procedure to account for objects with
and without NIR excess. We present our results on the correlations
between rotational periods and peak-to-peak amplitudes with NIR excess
in Sects. 5 and 6 and briefly address the disk fraction found
in Sect. 7. In Sect. 8, we discuss in detail possible
scenarios which can result in a lack of correlation between NIR and
rotation and summarize our results in Sect. 9.
.
We found that substellar objects tend to rotate faster than their
stellar counterparts. In order to constrain a possible rotation-disk
connection, in particular for the so far very poorly investigated very
low mass and substellar regime, we analyze here a sample of 732
periodic variables from Paper I and Herbst et al. (2002) which have
available JHK colors to be used as disk indicators.
In Sect. 2 we give details of the used NIR data sets.
Section 3 describes how we estimated the masses in our sample.
Section 4 defines the procedure to account for objects with
and without NIR excess. We present our results on the correlations
between rotational periods and peak-to-peak amplitudes with NIR excess
in Sects. 5 and 6 and briefly address the disk fraction found
in Sect. 7. In Sect. 8, we discuss in detail possible
scenarios which can result in a lack of correlation between NIR and
rotation and summarize our results in Sect. 9.
![\begin{figure}
\par\includegraphics[width=8.25cm,height=7.8cm]{13494fg1-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg21.png)
|
Figure 1:
Spatial distribution of all 732 periodic variables with near-infrared
counterpart. Black squares are 113 objects with VLT JHK
measurements, red crosses are the 210 periodic variables with UKIDSS
JHK measurements and blue open circles are the 409 periodic
variables with 2MASS measurements. The circle centered on |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,height=13cm]{13494fg2.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg22.png)
|
Figure 2: Histograms showing the magnitude distribution of the periodic variables in I, J, H, and K. The three different NIR data sets finally used in this paper are shown separately. The I band data from Paper I are shown for comparison purposes. |
| Open with DEXTER | |
2 Optical and near-infrared data
The I band data were obtained with the wide field
imager (WFI) at the MPG/ESO 2.2-m telescope on La Silla, Chile (see
Paper I for details). We used the combined (i.e.
Paper I and H2002) I band data,
which include 746 periodic variables with masses ranging from about
1.5 ![]() (H2002) down into the BD regime. We combined these optical data with JHK
data from three different sources: UKIDSS
(H2002) down into the BD regime. We combined these optical data with JHK
data from three different sources: UKIDSS![]() ,
VLT (MacCaughrean et al. in prep.), and 2MASS. Ideally we
would have used only UKIDSS since it provides much deeper and much more
accurate JHK data than 2MASS, but unfortunately
only less than 50% of our ONC WFI field (
,
VLT (MacCaughrean et al. in prep.), and 2MASS. Ideally we
would have used only UKIDSS since it provides much deeper and much more
accurate JHK data than 2MASS, but unfortunately
only less than 50% of our ONC WFI field (
![]() arcmin2,
center approximately at the position of
arcmin2,
center approximately at the position of ![]() Ori) is covered in all three bands by the UKIDSS survey. In particular
the innermost part of the ONC is not covered (for details see
Fig. 1).
We therefore used for a fraction of the inner ONC region deep VLT-ISAAC
data (MacCaughrean et al., in prep.) covering approximately
the central
Ori) is covered in all three bands by the UKIDSS survey. In particular
the innermost part of the ONC is not covered (for details see
Fig. 1).
We therefore used for a fraction of the inner ONC region deep VLT-ISAAC
data (MacCaughrean et al., in prep.) covering approximately
the central ![]() arcmin2.
For those regions in our WFI field which were neither covered by UKIDSS
nor by the VLT data we used 2MASS data. The cross-identification
between the periodic variables and these near-infrared catalogues was
done by looking for positional matches within a 2
arcmin2.
For those regions in our WFI field which were neither covered by UKIDSS
nor by the VLT data we used 2MASS data. The cross-identification
between the periodic variables and these near-infrared catalogues was
done by looking for positional matches within a 2
![]() search radius. Finally 732 out of the 746 known periodic variables from
Paper I have an infrared counterpart for which data in J,
H, and K are available.
search radius. Finally 732 out of the 746 known periodic variables from
Paper I have an infrared counterpart for which data in J,
H, and K are available.
Many objects have JHK data in more than one of the used catalogues. Due to their higher accuracy we gave higher priority to the UKIDSS and VLT data than to the 2MASS data (see Sect. 2.2 for details).
The basis of the VLT catalogue are VLT-ISAAC images. This catalogue is supplemented and calibrated with data from a sizeable number of other surveys which have been transformed to the 2MASS system resulting in a homogeneous catalogue. To allow a proper comparison, we transformed the UKIDSS magnitudes into the 2MASS system using the relations described in Hewett et al. (2006). The magnitude distribution of the periodic variables in I and JHK are shown in Fig. 2 with separate distributions for the three infrared data sets used in this paper. As summarized in Table 1, we finally used 210, 113, and 409 JHK measurements from UKIDSS, VLT and 2MASS, respectively. Most objects in the innermost part of the ONC, for which 2MASS data had to be used, are bright objects from H2002, 95% of which have J magnitudes brighter than 14 mag.
2.1 Photometric errors of I-K, J-H and H-K colors
As we will outline in Sect. 4, our IR excess determinations are based on I-K, J-H, and H-K colors. Therefore we have to briefly discuss the accuracy of these color determinations.
There are basically two sources of errors: photometric errors of the individual I, J, H, and K measurements and errors resulting from variability of the periodic variables in combination with the non-simultaneous data acquisition in the used bands.
Non-simultaneous data acquisition occurred for all I-K
colors. As outlined in Paper I (see there Fig. 14),
the peak-to-peak (ptp) amplitudes in the I band for
periodic variables of 0.075-0.4 ![]() have a median value of about 0.06 mag, and for 85% of them the
ptp values were below 0.2 mag. Since we will rarely observe
the periodic variables in minimum in one band and in maximum in the
other band, I-K colors are
expected to have median errors due to variability of at most
0.06 mag. For the J-H
and H-K colors, it is irrelevant
in the 2MASS data, which are practically taken simultaneously. This
means that only for the UKIDSS and VLT-ISAAC data one has to
investigate the relevance of this effect. Since the ptp amplitudes are
expected to be significantly lower in the NIR than in the I
band, the J-H and H-K
colors calculated from the UKIDSS and VLT data are expected to have
median errors due to variability of
have a median value of about 0.06 mag, and for 85% of them the
ptp values were below 0.2 mag. Since we will rarely observe
the periodic variables in minimum in one band and in maximum in the
other band, I-K colors are
expected to have median errors due to variability of at most
0.06 mag. For the J-H
and H-K colors, it is irrelevant
in the 2MASS data, which are practically taken simultaneously. This
means that only for the UKIDSS and VLT-ISAAC data one has to
investigate the relevance of this effect. Since the ptp amplitudes are
expected to be significantly lower in the NIR than in the I
band, the J-H and H-K
colors calculated from the UKIDSS and VLT data are expected to have
median errors due to variability of ![]() 0.05 mag.
0.05 mag.
The expected mean photometric errors depend on the
survey/catalogue used. I band photometry from
Paper I has typical photometric errors for a I=14,
I=18 and I=20 of ![]() 0.001 mag,
0.001 mag,
![]() 0.01 mag,
and
0.01 mag,
and ![]() 0.03 mag,
respectively.
0.03 mag,
respectively.
The UKIDSS data are very deep and accurate with typical
photometric errors for a J=14 , H=13.5
and/or K=13 mag object of ![]() 0.002 mag
and typical errors of
0.002 mag
and typical errors of ![]() 0.01 mag
for 2 mag fainter objects. As stated above, observations in
the three bands are not taken simultaneously. Nevertheless, as already
discussed, we do not expect variability to cause errors in extent of
0.05 mag.
0.01 mag
for 2 mag fainter objects. As stated above, observations in
the three bands are not taken simultaneously. Nevertheless, as already
discussed, we do not expect variability to cause errors in extent of
0.05 mag.
The 2MASS data have photometric errors which are on average one order of magnitude higher than those from UKIDSS for the same magnitude. As already stated above, objects for which 2MASS data had to be used are those located in regions of our WFI field that are not covered by neither UKIDSS nor VLT (see Fig. 1).
The VLT catalogue reaches 5![]() point source limiting magnitudes at approximately 22, 21, and 20 for J,
H, and K, respectively. This is
about 2 mag fainter than UKIDSS, and typical photometric
errors are therefore expected to be
point source limiting magnitudes at approximately 22, 21, and 20 for J,
H, and K, respectively. This is
about 2 mag fainter than UKIDSS, and typical photometric
errors are therefore expected to be ![]() 5 times smaller than those of
UKIDSS for the same magnitude. As already mentioned the VLT data were
not taken simultaneously. However, each data point is the average of
several observations separated over timescales of hours to years, and
consequently ``variability errors'' will be smoothed out to some
degree.
5 times smaller than those of
UKIDSS for the same magnitude. As already mentioned the VLT data were
not taken simultaneously. However, each data point is the average of
several observations separated over timescales of hours to years, and
consequently ``variability errors'' will be smoothed out to some
degree.
We expect uncertainties in the I-K
color determination dominated by the non-simultaneous data acquisition
of ![]() 10%.
From the typical photometric errors we expect uncertainties in the J-H
and H-K colors calculation of
about 1% for the VLT data and for the 2MASS data between 3% and 10% for
a K=12 mag and K=14 mag
objects respectively. The colors derived from UKIDSS data are affected
by both photometric and variability errors. The J-H
and H-K color errors are
expected to be clearly smaller than 5% and 7% for a K=13
and 15 mag object, respectively. This means that in principle
we are able to detect excesses from the intrinsic J-H
and H-K colors which are larger
than about 1-5% for objects with masses of
10%.
From the typical photometric errors we expect uncertainties in the J-H
and H-K colors calculation of
about 1% for the VLT data and for the 2MASS data between 3% and 10% for
a K=12 mag and K=14 mag
objects respectively. The colors derived from UKIDSS data are affected
by both photometric and variability errors. The J-H
and H-K color errors are
expected to be clearly smaller than 5% and 7% for a K=13
and 15 mag object, respectively. This means that in principle
we are able to detect excesses from the intrinsic J-H
and H-K colors which are larger
than about 1-5% for objects with masses of ![]() 0.1
0.1
![]() and 7-10% for the less massive objects in our sample. A rough estimate
of the amount of NIR excess under typical
stellar + disk system parameters (e.g. Meyer
et al. 1997;
Hillenbrand et al. 1998)
results in H and K band
excesses which are expected to be of about 20%. Although the amount of
NIR excess is highly dependent on the different
stellar + disk parameters, the estimated errors in
the colors should not significantly affect our disk detectability.
and 7-10% for the less massive objects in our sample. A rough estimate
of the amount of NIR excess under typical
stellar + disk system parameters (e.g. Meyer
et al. 1997;
Hillenbrand et al. 1998)
results in H and K band
excesses which are expected to be of about 20%. Although the amount of
NIR excess is highly dependent on the different
stellar + disk parameters, the estimated errors in
the colors should not significantly affect our disk detectability.
Table 1: Number of periodic variables from Paper I with a near-infrared counterpart.
3 Mass estimates: Color-magnitude diagrams
To estimate masses from evolutionary models we need to know individual extinction values, which requires the knowledge of the spectral type. Since the spectral types of most of our periodic variables are unknown, individual extinction values cannot be determined. For the sake of simplicity we assumed in Paper I a uniform extinction value of Av=1.4 mag for all stars in the field, and we estimated masses based on the I band values. Although we still lack information on spectral types and therefore individual extinction values of our sample, we can make use of the near-infrared colors to perform additional/independent mass estimates, which are probably more accurate than the estimates based on the I band alone, due to the smaller extinction in the near-infrared bands and the smaller variability in this wavelength range.
We used the J vs. I-J
color-magnitude diagram for the mass estimates. In principle, H
and K bands would be even less affected by
extinction than the J band, but in these bands
infrared excess due to stellar disks can pretend a much higher stellar
flux than is actually present. We investigated the median extinction
values for the inside and outside ![]() in the literature (see Fig. 1 and
Paper I). First, we computed the median values of the
extinction provided by Hillenbrand (1997)
in both spatial regions, which resulted in Av=1.3 mag
and Av=0.7 mag
for the inner and outer regions, respectively. Second, we checked
extinction maps by Chaisson & Dopita (1977). The
latter reveals that there is no strong increase in the extinction
towards the inner regions, with median extinction values of about 1 and
1.5 in the innermost parts of the ONC and below 1 in the outer regions.
On the basis of these studies we assumed an average Av
of 1.4 mag for objects located inside
in the literature (see Fig. 1 and
Paper I). First, we computed the median values of the
extinction provided by Hillenbrand (1997)
in both spatial regions, which resulted in Av=1.3 mag
and Av=0.7 mag
for the inner and outer regions, respectively. Second, we checked
extinction maps by Chaisson & Dopita (1977). The
latter reveals that there is no strong increase in the extinction
towards the inner regions, with median extinction values of about 1 and
1.5 in the innermost parts of the ONC and below 1 in the outer regions.
On the basis of these studies we assumed an average Av
of 1.4 mag for objects located inside ![]() and 0.7 for objects outside
and 0.7 for objects outside ![]() .
We used the assumed extinction values together with a 1 Myr
isochrone by Baraffe et al. (1998)
.
We used the assumed extinction values together with a 1 Myr
isochrone by Baraffe et al. (1998)![]() to select objects with
masses higher than 0.4
to select objects with
masses higher than 0.4 ![]() (i.e.
(i.e. ![]() M2
or earlier), between 0.075-0.4
M2
or earlier), between 0.075-0.4 ![]() (i.e.
(i.e. ![]() M2
to M6), and <0.075
M2
to M6), and <0.075
![]() (i.e. later than
(i.e. later than ![]() M6).
We further constrained our sample by removing a)
objects to the left (i.e. bluer) of the 5 Myr isochrone from Baraffe
et al. (1998),
which are presumably background objects or in some cases young stars
with strong scattered light emission from a circumstellar envelope or a
nearly edge-on disk, and b) those objects located
in the top right-hand part of the J vs. I-J
color-magnitude diagram, which are presumably foreground objects with J
and I-J colors that cannot be
explained by any, even highly extincted, 1 Myr old star at the
distance of the ONC. Finally, our sample is reduced to 638 periodic
variables (Table 2).
M6).
We further constrained our sample by removing a)
objects to the left (i.e. bluer) of the 5 Myr isochrone from Baraffe
et al. (1998),
which are presumably background objects or in some cases young stars
with strong scattered light emission from a circumstellar envelope or a
nearly edge-on disk, and b) those objects located
in the top right-hand part of the J vs. I-J
color-magnitude diagram, which are presumably foreground objects with J
and I-J colors that cannot be
explained by any, even highly extincted, 1 Myr old star at the
distance of the ONC. Finally, our sample is reduced to 638 periodic
variables (Table 2).
For 81 periodic variables, 64 outside and 17 inside ![]() ,
we derived masses of <0.075
,
we derived masses of <0.075
![]() .
This number is smaller than the 124 BD candidates found in
Paper I from I band data alone, resulting
from the lower extinction in the near-infrared bands with the possible
combination of higher variability in the I band.
The determination of individual extinction values and spectral type
will be necessary to unambiguously determine the masses of the sample.
.
This number is smaller than the 124 BD candidates found in
Paper I from I band data alone, resulting
from the lower extinction in the near-infrared bands with the possible
combination of higher variability in the I band.
The determination of individual extinction values and spectral type
will be necessary to unambiguously determine the masses of the sample.
Table 2: Sample of the NIR catalogue of periodic variables in Paper I.
4 NIR excess determination
4.1 NIR excess from (I-K) colors
We used an index based on (I-K)
colors in which I-band fluxes are thought to be
dominated by photospheric emission, while K-band
fluxes can have an additional strong component from the circumstellar
disk (Hillenbrand et al. 1998).
This approach has the advantage of a longer wavelength base, which
should in principle result in more pronounced excess than other
commonly used indices (e.g. ![]() (H-K)).
Unfortunately, a NIR excess derived from I-K
colors requires the knowledge of individual extinction values and
spectral types, both unknown for most of our objects. As stated above,
we assumed average Av
values of 1.4 mag and 0.7 mag for objects inside and
outside
(H-K)).
Unfortunately, a NIR excess derived from I-K
colors requires the knowledge of individual extinction values and
spectral types, both unknown for most of our objects. As stated above,
we assumed average Av
values of 1.4 mag and 0.7 mag for objects inside and
outside ![]() ,
following the methodology stated in the previous section. We are aware
that near the ONC center many objects may be more highly extincted than
the average, resulting in a sample of objects pretending to have disks,
which is actually contaminated by highly extincted objects. On the
other hand, in the outer regions a certain fraction of objects have
lower extinction than the median value considered here and therefore we
may underestimate the fraction of objects showing indications of a
circumstellar disk in this region. Since we do not have information on
individual spectral types, we need to make an assumption on the
intrinsic photospheric color (I-K)0.
We used the observed I-J colors
corrected by the assumed average Av
values, and use the Baraffe et al. (1998) color
information for 1 Myr old objects to derive individual
intrinsic (I-K)0
colors for our sample.
,
following the methodology stated in the previous section. We are aware
that near the ONC center many objects may be more highly extincted than
the average, resulting in a sample of objects pretending to have disks,
which is actually contaminated by highly extincted objects. On the
other hand, in the outer regions a certain fraction of objects have
lower extinction than the median value considered here and therefore we
may underestimate the fraction of objects showing indications of a
circumstellar disk in this region. Since we do not have information on
individual spectral types, we need to make an assumption on the
intrinsic photospheric color (I-K)0.
We used the observed I-J colors
corrected by the assumed average Av
values, and use the Baraffe et al. (1998) color
information for 1 Myr old objects to derive individual
intrinsic (I-K)0
colors for our sample.
We then used the definition by Hillenbrand et al. (1998) to account for
the amount of near-infrared excess from the I-K
color:
| (1) |
where (I-K)0 are the intrinsic colors.
We considered ![]() mag
(Hillenbrand et al. 1998)
as a lower limit in order to be regarded as a result from a
circumstellar disk. We found that about 28% of the whole sample show a
NIR excess according to the
mag
(Hillenbrand et al. 1998)
as a lower limit in order to be regarded as a result from a
circumstellar disk. We found that about 28% of the whole sample show a
NIR excess according to the ![]() index. We denoted these objects as
index. We denoted these objects as ![]() + in
Table 3.
Although several assumptions were made to calculate the
+ in
Table 3.
Although several assumptions were made to calculate the ![]() index, the values derived here will allow for the first time the
comparison of the rotation-disk behavior between the higher mass
objects and the very low mass and even substellar objects.
index, the values derived here will allow for the first time the
comparison of the rotation-disk behavior between the higher mass
objects and the very low mass and even substellar objects.
4.2 Extinction-free indices
For comparison purposes we also calculated extinction-free indices. The
(unknown) extinction of the individual objects and the IR excess from a
circumstellar disk cannot be easily disentangled in color-color
diagrams. As a second disk-indicator, we use an
``extinction-free'' ![]() index Q as defined by Damiani et al. (2007). In a J-H
versus H-K diagram, there is a
permitted strip of colors on which dwarfs should be located and which
depends on the spectral type and the optical extinction. Since our
sample includes objects in a broad mass range (i.e. from about
1.5
index Q as defined by Damiani et al. (2007). In a J-H
versus H-K diagram, there is a
permitted strip of colors on which dwarfs should be located and which
depends on the spectral type and the optical extinction. Since our
sample includes objects in a broad mass range (i.e. from about
1.5 ![]() to
to ![]() 20
20
![]() ), we defined three limiting
values of the index
), we defined three limiting
values of the index ![]() according to the three different mass regimes considered here. The
extinction-free index provides a measurement of the deviation from
these permitted strips. We then used the NIR index
according to the three different mass regimes considered here. The
extinction-free index provides a measurement of the deviation from
these permitted strips. We then used the NIR index ![]() defined as follows
defined as follows
| QJHHK = (J-H)-(H-K)(E(J-H)/E(H-K)), | (2) |
in which the ratio of the color-extinctions E(J-H) / E(H-K) is based on the extinction law of Rieke & Lebofsky (1985).
We note that the calculated ![]() values provide a conservative limit on the presence of an IR excess and
therefore the presence of a disk. One should keep in mind that many
objects in the permitted strip presumably show red J-H
and/or H-K colors due to a
combination of extinction and near-infrared
emission from a circumstellar disk (see Meyer et al. 1997). For many
objects located at larger distances from the central Trapezium cluster,
where the average extinction is expected to be relatively small, NIR
colors redder than those of dwarf stars are more likely to be due to a
circumstellar disk, and are missed by the
values provide a conservative limit on the presence of an IR excess and
therefore the presence of a disk. One should keep in mind that many
objects in the permitted strip presumably show red J-H
and/or H-K colors due to a
combination of extinction and near-infrared
emission from a circumstellar disk (see Meyer et al. 1997). For many
objects located at larger distances from the central Trapezium cluster,
where the average extinction is expected to be relatively small, NIR
colors redder than those of dwarf stars are more likely to be due to a
circumstellar disk, and are missed by the ![]() .
This conservative disk indicator explains the
.
This conservative disk indicator explains the ![]() 20% disk fraction found, a
value significantly smaller than the one derived from the
20% disk fraction found, a
value significantly smaller than the one derived from the ![]() index. Although the
index. Although the ![]() index misses a large fraction of disks, we will mention the results
obtained from it for comparison purposes.
index misses a large fraction of disks, we will mention the results
obtained from it for comparison purposes.
![\begin{figure}
\par\includegraphics[width=8cm, height=6.73cm]{13494fg3.eps}\\
\...
...egraphics[width=8cm, height=6.73cm]{13494fg5.eps}\\\vspace*{-4mm}\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg40.png)
|
Figure 3:
Rotational period as a function of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm, height=16cm]{13494fg6.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg41.png)
|
Figure 4: Period distribution for objects with and without disks in the three mass bins investigated here (see text for details). Solid lines show the period distribution of objects without disks, while dotted lines represent the distribution for disk holders. Median rotational periods are shown as vertical lines. |
| Open with DEXTER | |
5 Correlation between infrared excess and rotational periods
Below we investigate whether there is a correlation between the period distribution of the periodic variables measured in Paper I and the infrared excess. As described in the introduction such a correlation was found in some studies for the higher mass periodic variables (e.g. H2002; Rebull et al. 2006; Cieza & Baliber 2007). Here we mainly want to find out whether there is a rotation-disk connection in the very low and substellar mass regime, and compare these results with higher mass objects.
Figure 3
shows the rotational period as a function of the ![]() index for objects in the whole WFI field. Since mass effects may bias
any existing correlation between rotation and disks we perform all
following analysis for the periodic variables in the already defined
three mass bins. In the highest and intermediate mass regime,
Fig. 3
shows that fast rotators (i.e.
index for objects in the whole WFI field. Since mass effects may bias
any existing correlation between rotation and disks we perform all
following analysis for the periodic variables in the already defined
three mass bins. In the highest and intermediate mass regime,
Fig. 3
shows that fast rotators (i.e. ![]() days)
are mostly objects without NIR excess, while there is a significant
fraction of slow rotators without indications of a disk, in addition to
the slow rotators with NIR excesses detected. In the substellar regime
no trend is clear from Fig. 3.
The horizontal lines in each diagram indicate the median rotational
periods for objects with and without IR excess (see Table 3).
In order to give statistical significance to the found trends we
performed a two-sample K-S test, which shows differences in the period
distribution of objects with and without disks in the highest mass bin
at >2
days)
are mostly objects without NIR excess, while there is a significant
fraction of slow rotators without indications of a disk, in addition to
the slow rotators with NIR excesses detected. In the substellar regime
no trend is clear from Fig. 3.
The horizontal lines in each diagram indicate the median rotational
periods for objects with and without IR excess (see Table 3).
In order to give statistical significance to the found trends we
performed a two-sample K-S test, which shows differences in the period
distribution of objects with and without disks in the highest mass bin
at >2 ![]() level (P=0.02, n1=27,
n2=85), in the intermediate
mass bin at
level (P=0.02, n1=27,
n2=85), in the intermediate
mass bin at ![]() 3
3 ![]() level (P=10-6, n1=121,
n2=324), while the period
distribution of disks and non-disks holders in the substellar mass bin
are statistically identical (P=0.95, n1=33,
n2=48).
level (P=10-6, n1=121,
n2=324), while the period
distribution of disks and non-disks holders in the substellar mass bin
are statistically identical (P=0.95, n1=33,
n2=48).
The period distribution of the periodic variables with and
without disks in the three mass bins are easier to visualise in
Fig. 4,
where the red dotted histograms represent the period distributions of
periodic variables with disks and the solid histograms are the
corresponding period distributions for objects without disks.
Figure 4
shows that the distribution of objects with and without disks in the
lowest mass bins look very similar. In the high and intermediate mass
bins objects with disks rotate on average ![]() 1.4-1.8 times slower than
objects without disks. In the substellar regime no such difference in
the median rotational periods of objects with and without disks was
found.
1.4-1.8 times slower than
objects without disks. In the substellar regime no such difference in
the median rotational periods of objects with and without disks was
found.
The same trend is found when the ![]() index is used as diagnosis of a circumstellar disk.
index is used as diagnosis of a circumstellar disk.
In addition to mass effects, age effects may bias the
resulting correlations, since older objects tend to rotate faster and
the disk-fraction among an older population should also be smaller. We
suggested a possible age spread in the ONC in Paper I, with
younger objects being located inside ![]() .
Therefore it would in principle be interesting to do the analysis shown
in Fig. 4
for inside and outside
.
Therefore it would in principle be interesting to do the analysis shown
in Fig. 4
for inside and outside ![]() .
However, due to the reduced number of objects in the two spatial
regimes and, particularly in the substellar mass regime, no
statistically meaningful analysis could be obtained. We only show the
median values of the rotational period distributions in
Table 3, which may suggest differences between the two spatial
regions.
.
However, due to the reduced number of objects in the two spatial
regimes and, particularly in the substellar mass regime, no
statistically meaningful analysis could be obtained. We only show the
median values of the rotational period distributions in
Table 3, which may suggest differences between the two spatial
regions.
![\begin{figure}
\par\includegraphics[width=8.1cm, height=6.5cm]{13494fg7.eps}\\
\includegraphics[width=8.1cm, height=6.5cm]{13494fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg44.png)
|
Figure 5: The same as Fig. 3 but for the peak-to-peak (ptp) amplitude. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm, height=11.5cm]{13494fg9.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg45.png)
|
Figure 6: Same as Fig. 4 but for the peak-to-peak (ptp) amplitude distribution. Only the intermediate and substellar mass bin is shown since we have no information on the ptp amplitudes for most of the highest mass periodic variables from H2002. |
| Open with DEXTER | |
6 Correlation between infrared excess and peak-to-peak amplitudes
In the following we analyze whether there is a correlation between the
peak-to-peak (ptp) amplitude of the periodic variables and NIR excess,
i.e. the presence of a circumstellar disk. Since H2002 did not provide
ptp amplitudes, we use here only the periodic variables measured in
Paper I and not the combined sample as in previous sections
(for details in how the ptp amplitudes were determined see
Paper I). Due to the small number of objects with ![]() we only investigate the ptp-disk correlation in the 0.4-0.075
we only investigate the ptp-disk correlation in the 0.4-0.075 ![]() and <0.075
and <0.075![]() mass bins.
mass bins.
![\begin{figure}
\par\includegraphics[width=6cm, height=5.5cm]{13494fg10.eps}\incl...
...94fg11.eps}\includegraphics[width=6cm, height=5.5cm]{13494fg12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg47.png)
|
Figure 7: Disk fraction as a function of rotational period for the three mass regimes studied here. The disk fractions are calculated for rotational period bins of 2.5 days with error bars representing the statistical standard error. |
| Open with DEXTER | |
The same trend, median ptp values, and level of significance
were found when the ![]() index is used as diagnosis of a circumstellar disk, providing
additional support for the found correlation.
index is used as diagnosis of a circumstellar disk, providing
additional support for the found correlation.
Table 3:
Median values of rotational period for objects with (
![]() and without (
and without (
![]() IR excess.
IR excess.
Table 4:
Median values of ptp amplitudes for objects with (
![]() )
and without (
)
and without (
![]() IR excess.
IR excess.
In Paper I we found a correlation between the rotational period and the level of variability for periodic variables in the ONC and NGC2264. As stated in Paper I, this finding can probably be explained by differences in the spot coverage and/or differences in the magnetic field topologies. The strong rotation-disk and ptp-disk correlations found in the intermediate mass bin studied here may support this scenario. We found it rather interesting that the correlation between ptp amplitudes and NIR excess is strong in the substellar mass bin, while no rotation-disk correlation was found. This finding may indicate that even dipolar-like magnetic field topologies, which more likely produce large spot groups near the magnetic poles resulting in a high level periodic variability, may not be strong enough to allow effective disk coupling and braking in the substellar mass regime.
7 Disk frequency
The disk frequency among our sample of 638 periodic variables can be
estimated from the number of objects with a NIR excess. According to
the ![]() index
index ![]() %
of them have circumstellar disks. From the more conservative
%
of them have circumstellar disks. From the more conservative ![]() index, a lower disk frequency of about 20% was derived. It has to be
pointed out that both disk indicators are biased towards a small disk
fraction since many periodic variables are WTTSs. If all stars in the
ONC are considered the disk-frequency is substantially higher, namely
between 50% and 90% (Hillenbrand et al. 1998). These numbers
are consistent with the considerably larger fraction of irregular
variables (CTTSs) relative to periodic variables we found in
Paper I for the ONC (ratio of irregular to periodic variables
index, a lower disk frequency of about 20% was derived. It has to be
pointed out that both disk indicators are biased towards a small disk
fraction since many periodic variables are WTTSs. If all stars in the
ONC are considered the disk-frequency is substantially higher, namely
between 50% and 90% (Hillenbrand et al. 1998). These numbers
are consistent with the considerably larger fraction of irregular
variables (CTTSs) relative to periodic variables we found in
Paper I for the ONC (ratio of irregular to periodic variables ![]() 1.7). In
addition, as will be discussed in Sect. 8, the derived
disk fraction may also be smaller than expected since NIR excess is not
an optimum disk indicator.
1.7). In
addition, as will be discussed in Sect. 8, the derived
disk fraction may also be smaller than expected since NIR excess is not
an optimum disk indicator.
In order to investigate a possible dependence of the disk
fraction on the mass of the periodic variable, we derived the fraction
of objects with and without disks in the three mass bins investigated
here. We found that the disk frequency slightly increases from
24% ![]() 4%
to 27%
4%
to 27% ![]() 2%
for the highest to the intermediate mass bins, while the increase in
the disk fraction among the substellar objects is stronger
(41%
2%
for the highest to the intermediate mass bins, while the increase in
the disk fraction among the substellar objects is stronger
(41% ![]() 5%)
5%)![]() . Figure 7 shows the disk
fraction as a function of rotational period, in the three mass regimes
studied. In the high and intermediate mass bin, the disk fractions are
computed in bins of 2.5 days up to 7.5 days, while due to the
small number of slow rotators, the last bin includes all objects with a
rotational period larger than 7.5 days. In the substellar
regime, due to the much smaller sample numbers, only three bins are
used, i.e. P<2.5 days,
. Figure 7 shows the disk
fraction as a function of rotational period, in the three mass regimes
studied. In the high and intermediate mass bin, the disk fractions are
computed in bins of 2.5 days up to 7.5 days, while due to the
small number of slow rotators, the last bin includes all objects with a
rotational period larger than 7.5 days. In the substellar
regime, due to the much smaller sample numbers, only three bins are
used, i.e. P<2.5 days, ![]() days,
and
days,
and ![]() days.
From Fig. 7
is evident that there is a trend towards larger disk fractions for the
slower rotating stellar objects, while in the substellar mass regime no
such trend is indicated at all, despite the fact that the disk fraction
is rather high for all periods. Figure 7 fully supports
the finding of a correlation between period and NIR excess for objects
with masses >0.075
days.
From Fig. 7
is evident that there is a trend towards larger disk fractions for the
slower rotating stellar objects, while in the substellar mass regime no
such trend is indicated at all, despite the fact that the disk fraction
is rather high for all periods. Figure 7 fully supports
the finding of a correlation between period and NIR excess for objects
with masses >0.075![]() .
.
In each mass regime we found that the disk frequency is always
higher inside ![]() than in the presumably older region outside
than in the presumably older region outside ![]() .
.
8 Discussion
8.1 Higher mass objects
According to Sect. 3,
a correlation between rotational periods and the presence of
circumstellar disks was found in the higher mass regime at
>2 ![]() level. As outlined in the Introduction, in the past decade several
authors have investigated correlations between rotation rates and the
presence of circumstellar disks in the solar and subsolar mass regime
(i.e.
level. As outlined in the Introduction, in the past decade several
authors have investigated correlations between rotation rates and the
presence of circumstellar disks in the solar and subsolar mass regime
(i.e. ![]() ;
e.g. H2002; Makidon 2004;
Lamm et al. 2005;
Rebull et al. 2006;
Cieza & Baliber 2007;
Nguyen et al. 2009).
Some studies found evidence for such a connection and others did not.
Most of the discrepant results are probably related to the
inhomogeneous samples that have been used for comparison. Due to the
strong dependence of the rotational period with mass and age, proper
comparisons can only be done if the samples contain periodic variables
in the same mass regime and of similar ages. In the ONC, the mass
effect was taken into account in the work of Cieza & Baliber (2007). They use
IRAC excesses as disk indicators together with rotational periods from
the literature, and find for objects with masses of
;
e.g. H2002; Makidon 2004;
Lamm et al. 2005;
Rebull et al. 2006;
Cieza & Baliber 2007;
Nguyen et al. 2009).
Some studies found evidence for such a connection and others did not.
Most of the discrepant results are probably related to the
inhomogeneous samples that have been used for comparison. Due to the
strong dependence of the rotational period with mass and age, proper
comparisons can only be done if the samples contain periodic variables
in the same mass regime and of similar ages. In the ONC, the mass
effect was taken into account in the work of Cieza & Baliber (2007). They use
IRAC excesses as disk indicators together with rotational periods from
the literature, and find for objects with masses of ![]() 0.4
0.4 ![]() clear evidence of angular momentum regulation by circumstellar disks,
confirming the correlation already found by H2002.
clear evidence of angular momentum regulation by circumstellar disks,
confirming the correlation already found by H2002.
H2002 argued for a significant correlation between ![]() and rotational periods for objects with masses of
and rotational periods for objects with masses of ![]() 0.2
0.2 ![]() (with very few objects with
(with very few objects with ![]() )
in the ONC. They tested the significance of the mentioned correlation
by a non-parametric Spearman test, which resulted in less than a 10-10
(n=325) chance that the quantities are not
correlated. Since they did not provide the significance of the
mentioned correlation for different mass regimes, we reanalyzed their
data set and found that when dividing in a higher and a lower mass bin
(i.e.
)
in the ONC. They tested the significance of the mentioned correlation
by a non-parametric Spearman test, which resulted in less than a 10-10
(n=325) chance that the quantities are not
correlated. Since they did not provide the significance of the
mentioned correlation for different mass regimes, we reanalyzed their
data set and found that when dividing in a higher and a lower mass bin
(i.e. ![]() or
or ![]() with the D'Antona & Mazzitelli 1997 models used
in H2002), the level of significance of the NIR-rotation correlation
decreases substantially to
with the D'Antona & Mazzitelli 1997 models used
in H2002), the level of significance of the NIR-rotation correlation
decreases substantially to ![]() (n=157) for objects with
(n=157) for objects with ![]() and
and ![]() (n=168) for the lower mass objects in their sample.
The correlation is much stronger for the less massive objects in their
sample, which agrees with our results.
(n=168) for the lower mass objects in their sample.
The correlation is much stronger for the less massive objects in their
sample, which agrees with our results.
The same test performed for our estimated ![]() index resulted in a 10-9 (n=638),
10-2 (n=112), 10-8
(n=445), and
index resulted in a 10-9 (n=638),
10-2 (n=112), 10-8
(n=445), and ![]() (n=81) chance that NIR-excess from the
(n=81) chance that NIR-excess from the ![]() index and rotational periods are not correlated for the whole sample,
the higher, intermediate, and lower mass objects, respectively. These
results show a trend which is consistent with H2002, in the sense that
both higher mass objects and substellar objects tend to have a weaker
correlation than the intermediate mass objects in our sample.
index and rotational periods are not correlated for the whole sample,
the higher, intermediate, and lower mass objects, respectively. These
results show a trend which is consistent with H2002, in the sense that
both higher mass objects and substellar objects tend to have a weaker
correlation than the intermediate mass objects in our sample.
We emphasise that it is not at all the purpose of this paper
to investigate the degree of significance of a NIR excess-rotation
correlation for higher mass stars (>0.4 ![]() ), but
mostly to investigate the relative change of such a correlation with
mass. This relative change is less affected by the use of a non-ideal
disk indicator, because the same disk indicator is used in all
investigated mass regimes.
), but
mostly to investigate the relative change of such a correlation with
mass. This relative change is less affected by the use of a non-ideal
disk indicator, because the same disk indicator is used in all
investigated mass regimes.
8.2 Substellar mass objects
According to Figs. 3 and 4 there is no correlation between the NIR excess (i.e. the presence of a circumstellar disk) and the rotation rate in the substellar mass regime. The lack of this correlation can in principle be caused by the combination of the following effects:
- 1.
- NIR excesses are not sufficiently good accretion disk indicators;
- 2.
- there is a certain angular momentum loss in the BD mass
regime at the age of
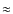 1 Myr,
but the following effects strongly weaken any correlation:
1 Myr,
but the following effects strongly weaken any correlation:
- -
- vast spread in rotational periods;
- -
- sample has a too large spread in mass and age;
- 3.
- angular momentum loss rates are indeed significantly lower in BDs than in higher mass objects.
8.2.1 Are NIR excesses good accretion disks indicators?
As outlined in the Introduction, theoretical models require ongoing
mass accretion from a circumstellar disk onto the star to account for
angular momentum losses. To test these theoretical predictions
observationally it is necessary to measure mass accretion rates. Some
of the more commonly used mass accretion indicators are the equivalent
width (EW) of H![]() or other suitable emission lines (e.g. Ca II triplet), continuum
veiling, and UV excess. Near-infrared excesses can only account for the
presence of dust in a circumstellar disk which does not imply that gas
is being accreted from this disk onto the star. This means it is
possible to detect a NIR excess from a purely irradiated circumstellar
disk even if the mass accretion rate is zero (see for example
Fig. 6 in Hillenbrand et al. 1998). Nevertheless,
an impressive correlation between NIR excess and mass accretion
indicators such as the H
or other suitable emission lines (e.g. Ca II triplet), continuum
veiling, and UV excess. Near-infrared excesses can only account for the
presence of dust in a circumstellar disk which does not imply that gas
is being accreted from this disk onto the star. This means it is
possible to detect a NIR excess from a purely irradiated circumstellar
disk even if the mass accretion rate is zero (see for example
Fig. 6 in Hillenbrand et al. 1998). Nevertheless,
an impressive correlation between NIR excess and mass accretion
indicators such as the H![]() emission line width has been found for many YSOs over a broad mass
range (e.g. Sicilia-Aguilar et al. 2005, 2006). This
strong correlation allows us to use NIR excess as a good accretion disk
indicator in this study, since a more direct accretion indicator (e.g. H
emission line width has been found for many YSOs over a broad mass
range (e.g. Sicilia-Aguilar et al. 2005, 2006). This
strong correlation allows us to use NIR excess as a good accretion disk
indicator in this study, since a more direct accretion indicator (e.g. H![]() emission line flux) is not available for our sample.
emission line flux) is not available for our sample.
Near-infrared excesses have been widely used as diagnostic of
a circumstellar disk and have succeeded in detecting large fraction of
very low mass stars and brown dwarfs with circumstellar disks (e.g.
Lada et al. 2000;
Muench et al. 2001).
Muench et al. (2001)
found that about 50% of their brown dwarf candidates in the Trapezium
region show NIR excesses suggestive of a circumstellar disk. This
fraction is similar to the one found by Lada et al. (2000) for very low
mass objects, which was increased to about 85% when L-band
(3.8 ![]() m)
observations were used. A similar increase in the disk fraction among
the brown dwarf population studied here would therefore be expected
from longer wavelength observations. In the last few years, IRAC
excesses were used in young clusters to unambiguously determine the
presence of a circumstellar disk (e.g. Megeath et al. 2005). The
problem with IRAC data arises in the inner region of the ONC, where the
nebular background and the stellar density is very high, and therefore
a considerable number of even bright objects are missing IRAC
detections (Megeath et al. 2005; Rebull
et al. 2006).
Up to now, only objects in the ONC with spectral types earlier than M2
can be precisely analyzed and searched for disk presence and a
rotational-disk connection by means of IRAC data (Rebull
et al. 2006;
Cieza & Baliber 2007).
We then have to rely on the less favourable NIR excesses as indicators
of disks around very low mass and substellar objects.
m)
observations were used. A similar increase in the disk fraction among
the brown dwarf population studied here would therefore be expected
from longer wavelength observations. In the last few years, IRAC
excesses were used in young clusters to unambiguously determine the
presence of a circumstellar disk (e.g. Megeath et al. 2005). The
problem with IRAC data arises in the inner region of the ONC, where the
nebular background and the stellar density is very high, and therefore
a considerable number of even bright objects are missing IRAC
detections (Megeath et al. 2005; Rebull
et al. 2006).
Up to now, only objects in the ONC with spectral types earlier than M2
can be precisely analyzed and searched for disk presence and a
rotational-disk connection by means of IRAC data (Rebull
et al. 2006;
Cieza & Baliber 2007).
We then have to rely on the less favourable NIR excesses as indicators
of disks around very low mass and substellar objects.
We like to remind the reader that the photometric method used for measuring periodic brightness modulations is more efficient among the WTTSs than for CTTSs, since irregular variations can add a strong noise to the periodic modulation, preventing the detection of the periodic signal. Due to this noise we are definitely missing periodic variables among the young highly active CTTSs, which are expected to have larger amounts of NIR excess (i.e. larger mass accretion rates) than the more common WTTSs in our sample of periodic variables. This bias is an additional factor which prevents us from finding a stronger correlation between rotational periods and the presence of a circumstellar disk.
In summary, we believe that the used NIR disk indicator is not a major cause for the lack of a disk-rotation correlation found in the substellar regime.
8.2.2 Correlation weakening/destroying effects
Below we discuss the effects that can weaken or even destroy a correlation between rotation and mass accretion, even in the case of an ``ideal'' mass accretion indicator.
- Large spread of rotational periods:
From Fig. 3 it is clear that the period distribution of the periodic variables in all three mass bins show a vast spread. If this spread can weaken or even destroy a correlation between rotation and NIR excess, it should in principle affect all three mass bins. To test whether there is a larger spread in rotational periods in the BD regime than in the intermediate mass regime, in which a highly significant correlation was found, we computed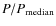 values and analyzed the median and standard deviation (
values and analyzed the median and standard deviation ( )
of these
)
of these 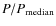 distributions. In addition, a log-normal
distribution was also fitted and both the geometric medians and the
multiplicative
distributions. In addition, a log-normal
distribution was also fitted and both the geometric medians and the
multiplicative  were compared. The
were compared. The  values provide the width of the distribution and therefore give
information on the spread of the values. We found that the distribution
of
values provide the width of the distribution and therefore give
information on the spread of the values. We found that the distribution
of  in the substellar mass regime is broader than the corresponding
distribution of the intermediate mass objects (i.e. the
in the substellar mass regime is broader than the corresponding
distribution of the intermediate mass objects (i.e. the  values are a factor
values are a factor 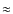 1.6
larger). In addition, even when the distribution is broader, the number
of outliers
1.6
larger). In addition, even when the distribution is broader, the number
of outliers![[*]](/icons/foot_motif.png) is higher in the BD mass
regime than in the intermediate mass regime, with 14% and 3% of
outliers in each region, respectively.
is higher in the BD mass
regime than in the intermediate mass regime, with 14% and 3% of
outliers in each region, respectively.
The larger spread in rotational periods among the BDs in our sample seems to be an important correlation decreasing factor in the BD regime.
- Mass and age effects:
As stated in Sect. 8.1, the correlation between rotational period and NIR excess can be biased by the strong dependence of rotation with mass and age.If a sample of periodic variables with a broad mass range is used in order to find a correlation with NIR excess the following effect may mimic a rotation-disk connection: higher mass objects rotate on average slower and show on average larger NIR excesses than lower mass objects, the latter due to the higher contrast between the photosphere and the inner disk emission (e.g. Littlefair et al. 2005).
An age spread may also mimic an intrinsic correlation between rotational periods and disks.
The intermediate mass regime has a mass range of about
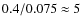 .
However, the mass range in the BD regime is most likely much smaller
since we have only very few objects below 0.025
.
However, the mass range in the BD regime is most likely much smaller
since we have only very few objects below 0.025 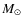 ,
i.e. the mass range is there about 3 (0.075/0.025). Due to the smaller
mass range in the BD regime it cannot be excluded that this effect
contributes to the lack of a correlation between disks and rotation
rates. To test this hypothesis, we divided the intermediate mass regime
in two mass bins, namely objects with
0.4<M< 0.17
,
i.e. the mass range is there about 3 (0.075/0.025). Due to the smaller
mass range in the BD regime it cannot be excluded that this effect
contributes to the lack of a correlation between disks and rotation
rates. To test this hypothesis, we divided the intermediate mass regime
in two mass bins, namely objects with
0.4<M< 0.17 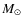 (intermediate-high) and
(intermediate-high) and 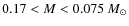 (intermediate-low), and analyzed the new period distributions of
objects with and without NIR excess. The KS test resulted in a 99% and
92% probability that the period distributions of objects with and
without NIR excess belong to different populations in the
intermediate-high and intermediate-low mass bins, respectively. The
mass ranges in both these newly defined mass bins are about 2.3 and
therefore smaller than the mass range in the substellar regime;
nevertheless, rotation-disk correlations are found to be more
significant than in the substellar mass regime. The statistical
significance of the mentioned correlation decreases toward lower
masses, which most probably indicates that mass effects are not
relevant within the mass intervals studied here.
(intermediate-low), and analyzed the new period distributions of
objects with and without NIR excess. The KS test resulted in a 99% and
92% probability that the period distributions of objects with and
without NIR excess belong to different populations in the
intermediate-high and intermediate-low mass bins, respectively. The
mass ranges in both these newly defined mass bins are about 2.3 and
therefore smaller than the mass range in the substellar regime;
nevertheless, rotation-disk correlations are found to be more
significant than in the substellar mass regime. The statistical
significance of the mentioned correlation decreases toward lower
masses, which most probably indicates that mass effects are not
relevant within the mass intervals studied here.
8.2.3 Are angular momentum loss rates smaller in BDs than in higher mass objects?
We discuss here possible physical processes which can account for smaller angular momentum loss rates in the substellar mass regime compared to higher mass objects.
- Low ionization:
All hydro-magnetically driven angular momentum loss mechanisms require a sufficiently high ionization of the disk and/or wind involved in the angular momentum transport from the star and/or disk to this circumstellar matter. Without a sufficient ionization the magnetic field would only poorly couple to the circumstellar matter, and therefore mass accretion rates and angular momentum transport would be correspondingly smaller. Since the X-ray and UV fluxes of BDs relative to their bolometric fluxes (i.e.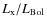 )
are certainly much lower than for higher mass stars, it is quite
conceivable that these effects reduce the angular momentum braking in
the BD regime. This low ionization/magnetic coupling consideration can
presumably explain the strong decrease of
)
are certainly much lower than for higher mass stars, it is quite
conceivable that these effects reduce the angular momentum braking in
the BD regime. This low ionization/magnetic coupling consideration can
presumably explain the strong decrease of 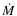 with decreasing
with decreasing 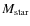 discussed in the next section.
discussed in the next section.
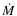 versus
versus
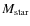 relation :
relation :
Observations over a broad mass range from intermediate mass stars down to brown dwarfs reveal a very strong dependence of the mass accretion rate on stellar mass with the global trend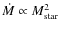 (Hartmann et al. 2006).
An even stronger dependence,
(Hartmann et al. 2006).
An even stronger dependence, 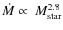 has been reported in the subsolar mass regime down to the substellar
limit by Fang et al. (2009). This dependence explains the very
small mass accretion rates of
has been reported in the subsolar mass regime down to the substellar
limit by Fang et al. (2009). This dependence explains the very
small mass accretion rates of 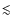 10-10
10-10 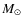 measured in very low mass and substellar objects (e.g. Muzerolle
et al. 2005). Obviously this non linear relation between mass
accretion and stellar mass indicates that the relative braking
measured in very low mass and substellar objects (e.g. Muzerolle
et al. 2005). Obviously this non linear relation between mass
accretion and stellar mass indicates that the relative braking 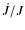 is strongly mass dependent, with a substantially smaller braking in the
lower mass objects.
is strongly mass dependent, with a substantially smaller braking in the
lower mass objects.
In addition, Hartmann et al. (2006) have shown that
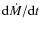 is probably also highly mass dependent in the sense that it strongly
increases with decreasing mass; i.e.
is probably also highly mass dependent in the sense that it strongly
increases with decreasing mass; i.e. 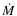 decreases much faster with evolutionary age in BDs than in solar mass
stars.
decreases much faster with evolutionary age in BDs than in solar mass
stars.
- Relevant time scales for disk-locking:
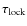 and
and 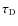 :
:
If one assumes that the disk locking scenario explains the rotational data one can consider two extreme cases: case 1; all objects are locked to their disks at their birth, and the amount of angular momentum loss strongly depends on how long this locking is effective (i.e. how long
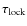 )
is, and case 2; they are not locked to their disks at early
stages and it takes a certain time
)
is, and case 2; they are not locked to their disks at early
stages and it takes a certain time 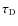 until they are locked.
until they are locked. In the first case, the above discussed
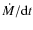 versus mass consideration do indeed argue that
versus mass consideration do indeed argue that 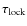 in BDs is much shorter than in solar-mass stars, since in the former
case
in BDs is much shorter than in solar-mass stars, since in the former
case  will decrease much more rapidly. Therefore BDs are expected to be
braked for a shorter time than higher mass objects, after which they
spin up conserving angular momentum or losing angular momentum in a
moderate way.
will decrease much more rapidly. Therefore BDs are expected to be
braked for a shorter time than higher mass objects, after which they
spin up conserving angular momentum or losing angular momentum in a
moderate way.
Concerning case 2, Hartmann (2002) argued that disk-locking is not instantaneous but a certain time
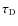 is needed before disk-locking is achieved. Equation (3) (which is
Eq. (8) in Hartmann 2002)
shows that this time is proportional to the mass, the angular velocity,
and to the inverse of the accretion rate:
is needed before disk-locking is achieved. Equation (3) (which is
Eq. (8) in Hartmann 2002)
shows that this time is proportional to the mass, the angular velocity,
and to the inverse of the accretion rate:
in which M0.5 and are the mass and mass accretion rates in units of 0.5
are the mass and mass accretion rates in units of 0.5  and 10-8
and 10-8  yr-1,
respectively and f is the angular velocity in units
of the breakup velocity.
yr-1,
respectively and f is the angular velocity in units
of the breakup velocity.
Typical values of these quantities for a 0.5
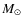 star are
star are 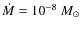 yr-1
and f=0.1 (see Herbst et al. 2001), which result
in a
yr-1
and f=0.1 (see Herbst et al. 2001), which result
in a 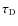
 0.5 Myr.
Since
0.5 Myr.
Since 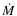 in BDs is highly time dependent
in BDs is highly time dependent 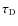 will strongly depend on the evolutionary phase. If one assumes an
optically observable
will strongly depend on the evolutionary phase. If one assumes an
optically observable  1 Myr
old BD, a typical
1 Myr
old BD, a typical 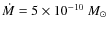 yr-1
is expected. In this case
yr-1
is expected. In this case 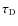 is about 10 Myr (for
is about 10 Myr (for 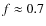 which is larger in BDs because they rotate close to break up velocity).
This all means that disk coupling in BDs can only be achieved within in
a reasonable time scale in very early evolutionary phases, when
which is larger in BDs because they rotate close to break up velocity).
This all means that disk coupling in BDs can only be achieved within in
a reasonable time scale in very early evolutionary phases, when 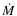 was presumably two to three orders of magnitude higher.
was presumably two to three orders of magnitude higher.
8.2.4 Concluding remarks
There is strong observational evidence that the mass accretion rateBefore reliable conclusions can be drawn, independent disk indicators (e.g. IR excess at longer wavelengths) should be correlated with rotation and, if possible, future substellar samples should include objects at slightly different ages.
9 Summary
We correlated rotational periods and peak-to-peak (ptp) amplitudes with NIR excess in a large sample of VLM stars and BDs in the ONC. Our results are summarized in the following:
- 1.
- We analyzed 638 periodic variables in the ONC from Paper I and H2002 with IJHK measurements.
- 2.
- We estimated masses from the J versus I-J color-magnitude diagram and found 81 objects with masses in the substellar mass regime.
- 3.
- We calculated the amount of NIR excess from a circumstellar
disk by means of the
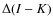 index and, for comparison purposes, we also computed an extinction-free
index QJHHK.
index and, for comparison purposes, we also computed an extinction-free
index QJHHK.
- 4.
- We performed all our analysis in three mass bins, namely
objects with masses >0.4
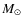 ,
0.4-0.075
,
0.4-0.075 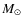 ,
and < 0.075
,
and < 0.075 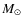 .
Our results show the existence of a highly significant rotation-disk
correlation for the intermediate mass objects, in which objects with
NIR excess tend to rotate slower than objects without NIR excess. In
the highest mass bin there is a correlation at >2
.
Our results show the existence of a highly significant rotation-disk
correlation for the intermediate mass objects, in which objects with
NIR excess tend to rotate slower than objects without NIR excess. In
the highest mass bin there is a correlation at >2  level. Interestingly, and most important for this study, we found no
correlation in the substellar regime.
level. Interestingly, and most important for this study, we found no
correlation in the substellar regime.
- 5.
- We found a highly significant correlation between the ptp
amplitudes and the NIR excess in the two mass bins (0.4-0.075
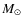 ,
and <0.075
,
and <0.075 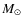 )
with available ptp values, in which objects with circumstellar disks
show on average a factor two to three larger ptp amplitudes than those
without indications of a disk.
)
with available ptp values, in which objects with circumstellar disks
show on average a factor two to three larger ptp amplitudes than those
without indications of a disk. - 6.
- We estimated a disk frequency between 20% and 28% among the 638 periodic variables in the ONC. This fraction is smaller than the one estimated for all objects in the ONC by Hillenbrand et al. (1998), which is expected because (a) the photometric method used to derived rotational periods is more effective among the WTTSs than for the CTTSs, with the former group having a much smaller disk frequency, (b) NIR excesses miss a certain fraction of objects with circumstellar disks.
- 7.
- The three mass regimes studied show different rotation-disk
behaviors which may be attributed to the different physical properties
of objects in each mass bin.
The first division line (0.4
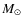 )
coincides with the onset of full convection. It may be possible that
the different behavior between high and intermediate mass objects in
our sample are related to the different ways magnetic fields are
produced, resulting in different topologies, spots coverages and/or
magnetic field strengths.
)
coincides with the onset of full convection. It may be possible that
the different behavior between high and intermediate mass objects in
our sample are related to the different ways magnetic fields are
produced, resulting in different topologies, spots coverages and/or
magnetic field strengths. The second boundary is the substellar limit. The strong dependence of mass accretion rate on mass seems to be crucial to understand why the lower mass objects in our sample suffer smaller angular momentum losses than those with larger masses. Our observations suggest that at an age of about 1 Myr disk-braking does not influence the rotational rate of most substellar objects.
In order to exclude possible observational biases by the method used here, future studies should consider IR excess at longer wavelengths or a direct mass accretion indicator.
The authors thank Mark MacCaughrean for providing the VLT-ISAAC NIR data used for 113 objects. We especially thank the anonymous referee for her/his valuable comments on the original version of this manuscript.
M.V.R.L. acknowledges support of the International Max Planck Reseach School for Astronomy and Cosmic Physics of the University of Heidelberg.
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work is based in part on data obtained as part of the UKIRT Infrared Deep Sky Survey.
References
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Biazzo, K., Melo, C. H. F., Pasquini, L., et al. 2009, A&A, 508, 1301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P. 1995, ARA&A, 33, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J. 2007, IAUS, 243, 231B [Google Scholar]
- Camenzind, M. 1990, RvMA, 3, 234 [Google Scholar]
- Carpenter, J. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Casali, M., Adamson, A., Alves de Oliveira, C., et al. 2007, A&A, 467, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaisson, E. J., & Dopita, M. A. 1977, A&A, 56, 385 [NASA ADS] [Google Scholar]
- Cieza, L., & Baliber, N. 2007, ApJ, 671, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Damiani, F., Prisinzano, L., Micela, G., & Sciortino, S. 2006, A&A, 459, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Antona, F., & Mazzitelli, I. 1997, in Cool stars in clusters and associations, ed. R. Pallavicini, & G. Micela, Mem. Soc. Astron. It., 68 [Google Scholar]
- Edwards, S., Strom, S. E., Hartigan, P., et al. 1993, AJ, 106, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1978, ApJ, 223, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, M., van Boekel, R., Wang, W., et al. 2009, A&A, 504, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L. 2002, ApJ, 578, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., D'Alessio, P., Calvet, N., & Muzerolle, J. 2006, ApJ, 648, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L., & Mundt R. 2001, ApJ, 554, L197 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L. Mundt R., Meisenheimer, K., & Wackermann, R. 2002, ApJ, 396, 513 [Google Scholar]
- Herbst, W., Eislöffel, J., Mundt R., & Scholz, A., 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 297 [Google Scholar]
- Hewett, P. C., Warren, S. J., Leggett, S. K., & Hodgkin, S. T. 2006, MNRAS, 367, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L., Strom, S., Calvet, N., et al. 1998, AJ, 116, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J., Reid, I., Liebert, J., et al. 2000, AJ, 120, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Königl, A. 1991, ApJ, 370, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Muench, A. A., Haisch, K. E. Jr., et al. 2000, AJ, 120.3162 [NASA ADS] [CrossRef] [Google Scholar]
- Lamm, M., Bailer-Jones, C. A. L., Mundt, R., Herbst, W., & Scholz, A. 2004, A&A, 417, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamm, M., Bailer-Jones, C. A. L., Mundt R., & Herbst, W. 2005, A&A, 430, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Littlefair, S. P., Naylor, T., Burningham, B., & Jeffries, R. D. 2005, MNRAS, 358, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Makidon, R. B., Rebull, L. M., Strom, S. E., Adams, M. T., & Patten, B. M. 2004, AJ, 127, 2228 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2005, ApJ, 632, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Flaherty, K. M., Hora, J., et al. 2005, IAU Symp. Proc., 227, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, M. R., Calvet, N., & Hillenbrand, L. A. 1997, AJ, 114, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Jayawardhana, R., & Basri, G. 2004 ApJ, 626, 498 [Google Scholar]
- Muench, A. A., Alves, J., Lada, C. J., & Lada, E. A. 2001, ApJ, 558, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, D. C., Jayawardhana, R., van Kerkwijk, M., et al. 2009, ApJ, 695, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M. 2001, AJ, 121, 1676 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Megeath, T., Hora, J., & Hartmann, L. 2006, ApJ 646, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Ledesma, M. V., Mundt R., & Eislöffel, J. 2009, A&A, 502, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scholz, A., & Eislöffel, J. 2004, A&A, 419, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scholz, A., & Eislöffel, J. 2005, A&A, 429, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sicilia-Aguilar, A., Hartmann, L. W., Szentgyorgyi, A. H., et al. 2005, AJ, 129, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Sicilia-Aguilar, A., Hartmann, L. W., Frsz, G., et al. 2006, AJ, 132, 2135 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Vogel, S. N., & Kuhi, L. V. 1981, ApJ, 245, 960 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... Cluster
![[*]](/icons/foot_motif.png)
- Full Table 2 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/515/A13
- ... UKIDSS
![[*]](/icons/foot_motif.png)
- The UKIDSS project as defined in Lawrence et al. (2007) uses the UKIRT Wide Field Camera (WFCAM; Casali et al. 2007).
- ...1998)
![[*]](/icons/foot_motif.png)
- As in Paper I, we use models by Baraffe et al. (1998) for our mass estimations. To allow a proper comparison with previous studies, each time a mass value is given here it is transfered into the mass scale of the mentioned model. Mass values estimated from other models are given explicitly only if needed.
- ...
``extinction-free''
![[*]](/icons/foot_motif.png)
- To compute those indices, an extinction law has to be assumed and therefore they are not completely independent of extinction. In all cases we assumed the Rieke & Lebofsky (1985) extinction law with R=3.1.
- ...%)
![[*]](/icons/foot_motif.png)
- Disk fraction uncertainties correspond to the statistical standard error [(diskfraction*(1 - diskfraction)/ N)]1/2.
- ... outliers
![[*]](/icons/foot_motif.png)
- Number of objects with values outside the following range:
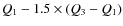 and
and 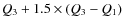 ,
where Q1 and Q3
are the first and third quartiles. For our sample, all outliers have
values higher than the upper limit, i.e. longer periods.
,
where Q1 and Q3
are the first and third quartiles. For our sample, all outliers have
values higher than the upper limit, i.e. longer periods.
All Tables
Table 1: Number of periodic variables from Paper I with a near-infrared counterpart.
Table 2: Sample of the NIR catalogue of periodic variables in Paper I.
Table 3:
Median values of rotational period for objects with (
![]() and without (
and without (
![]() IR excess.
IR excess.
Table 4:
Median values of ptp amplitudes for objects with (
![]() )
and without (
)
and without (
![]() IR excess.
IR excess.
All Figures
![\begin{figure}
\par\includegraphics[width=8.25cm,height=7.8cm]{13494fg1-NEW.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg21.png)
|
Figure 1:
Spatial distribution of all 732 periodic variables with near-infrared
counterpart. Black squares are 113 objects with VLT JHK
measurements, red crosses are the 210 periodic variables with UKIDSS
JHK measurements and blue open circles are the 409 periodic
variables with 2MASS measurements. The circle centered on |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,height=13cm]{13494fg2.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg22.png)
|
Figure 2: Histograms showing the magnitude distribution of the periodic variables in I, J, H, and K. The three different NIR data sets finally used in this paper are shown separately. The I band data from Paper I are shown for comparison purposes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=6.73cm]{13494fg3.eps}\\
\...
...egraphics[width=8cm, height=6.73cm]{13494fg5.eps}\\\vspace*{-4mm}\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg40.png)
|
Figure 3:
Rotational period as a function of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm, height=16cm]{13494fg6.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg41.png)
|
Figure 4: Period distribution for objects with and without disks in the three mass bins investigated here (see text for details). Solid lines show the period distribution of objects without disks, while dotted lines represent the distribution for disk holders. Median rotational periods are shown as vertical lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.1cm, height=6.5cm]{13494fg7.eps}\\
\includegraphics[width=8.1cm, height=6.5cm]{13494fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg44.png)
|
Figure 5: The same as Fig. 3 but for the peak-to-peak (ptp) amplitude. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm, height=11.5cm]{13494fg9.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg45.png)
|
Figure 6: Same as Fig. 4 but for the peak-to-peak (ptp) amplitude distribution. Only the intermediate and substellar mass bin is shown since we have no information on the ptp amplitudes for most of the highest mass periodic variables from H2002. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm, height=5.5cm]{13494fg10.eps}\incl...
...94fg11.eps}\includegraphics[width=6cm, height=5.5cm]{13494fg12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13494-09/Timg47.png)
|
Figure 7: Disk fraction as a function of rotational period for the three mass regimes studied here. The disk fractions are calculated for rotational period bins of 2.5 days with error bars representing the statistical standard error. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



