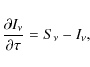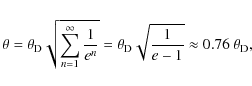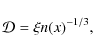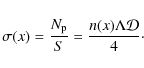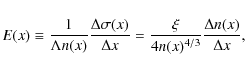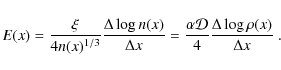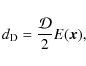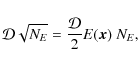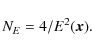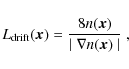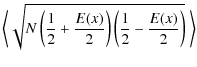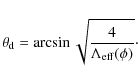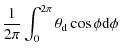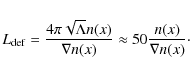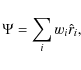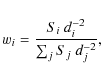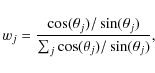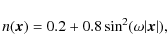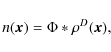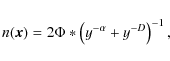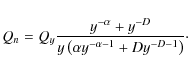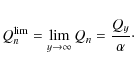| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 18 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/200913439 | |
| Published online | 11 June 2010 | |
Mathematical properties of the SimpleX algorithm
C. J. H. Kruip - J.-P. Paardekooper - B. J. F. Clauwens - V. Icke
Leiden Observatory, Leiden University, Postbus 9513, 2300RA Leiden, The Netherlands
Received 9 October 2009 / Accepted 11 February 2010
Abstract
Context. In the SimpleX radiative transfer
algorithm, photons are transported on an unstructured Delaunay
triangulation. This approach is non-standard, requiring a thorough
analysis of possible systematic effects.
Aims. We verify whether the SimpleX radiative transfer
algorithm conforms to mathematical expectations and develop both an
error analysis and improvements to earlier versions of the code.
Methods. We use numerical simulations and classical statistics to obtain quantitative descriptions of the systematics of the SimpleX algorithm.
Results. We present a quantitative description of the error properties of SimpleX,
numerical validation of the method and verification of the analytical
results. Furthermore we describe improvements in accuracy and speed of
the method.
Conclusions. It is possible to transport particles such as photons in a physically correct manner with the SimpleX
algorithm. This requires the use of weighting schemes or the
modification of the point process underlying the transport grid. We
explore and apply several possibilities.
Key words: radiative transfer - methods: analytical - methods: numerical
1 Introduction
A major challenge in computational astrophysics is to correctly account for radiative transfer in realistic macroscopic simulations. Whether one considers the formation of single stars or the evolution of merging galaxies, incorporation of radiative transfer is the next essential step of physical realism needed for a deeper understanding of the underlying mechanisms.
With the advent of the computer as an important catalyst, a myriad of efforts to solve the equations of radiative transport within a numerical framework have been developed. The resulting algorithms cover a wide range of applications where generally a method is tailored to a specific problem. In most cases, specialisation means either the choice of a specific physical scale (consider detailed models of stellar atmospheres or large-scale cosmological simulations) or emphasis on physical processes relevant to the problem at hand.
1.1 The SimpleX algorithm
The SimpleX algorithm for radiative transfer has been designed to be unaffected by these limitations. Owing to its modular structure, different physical processes can be included straightforwardly allowing different areas of application. More importantly, the method has no inherent reference to physical scale and thus can be applied to problems with typical length scales that lie many orders of magnitude apart. Because of its adaptive nature, many orders of magnitude in optical depth and spatial resolution can be resolved in the same simulation.
Conceived by Ritzerveld & Icke (2006) and implemented by Ritzerveld (2007), the SimpleX algorithm solves the general equations of particle transport by expressing them as a walk on a graph. The method can be thus considered to be a Markov Chain on a closed graph. Transported quantities travel from node to node on the graph, where each transition has a given probability.
This approach has several advantages that we now highlight. More specifically SimpleX
- does not increase its computational effort or memory use with the number of sources in a simulation and consequently treats for instance scattering by dust and diffuse recombination radiation without added computational effort;
- naturally adapts its resolution to capture the relevant physical scales, (expressed in photon mean free path lengths);
- works in parallel on distributed memory machines;
- is compatible with grid-based as well as point-based hydrodynamics codes (where the latter is the more natural combination due to the point-based nature of both SimpleX and SPH);
- is computationally cheap because of the local nature of the Delaunay grid
1.2 Error analysis
Covering many orders of magnitude in spatial resolution (and optical depth) is a considerable challenge for radiative transfer methods in general. Approximations often need to be employed to keep the problem tractable, which makes a robust error analysis difficult.
For the vast majority of numerical methods the errors are measured by comparing with a fiducial run of the code. This is usually a simulation wherein many more time steps and/or a higher spatial resolution are used than would normally be feasible. Convergence to a solution is usually observed and this solution is accepted as the correct one, at least within the limitations of the method.
For SimpleX we cannot perform a similar convergence test![]() .
For a spatial resolution that is significantly higher than the
resolution dictated by the local mean free path length of the photons,
several effects, described in Sect. 3 tend to make the radiation field more diffuse, decreasing instead of increasing accuracy. This property of SimpleX is not a weakness but instead inherent to the method using a physical grid wherein deviations from its natural resolution often cause a deterioration in the solution.
.
For a spatial resolution that is significantly higher than the
resolution dictated by the local mean free path length of the photons,
several effects, described in Sect. 3 tend to make the radiation field more diffuse, decreasing instead of increasing accuracy. This property of SimpleX is not a weakness but instead inherent to the method using a physical grid wherein deviations from its natural resolution often cause a deterioration in the solution.
Because of its mathematically transparent nature, the SimpleX algorithm has the great advantage that one can assess its error properties analytically. The resulting prescriptions are quite general and can be applied to different regions of parameter space, an advantage over the ``numerical converge approach'' usually applied in the error analysis of radiative transfer methods. The development of analytical descriptions and the discussion of their implications will be the main focus of this text.
1.3 Outline
Given the desirable properties of the SimpleX algorithm, we aim to assess whether the inaccuracies that inevitably arise in a numerical method can counterweigh SimpleX's virtues.
We will demonstrate that the use of high dynamic range Delaunay triangulations as the basis of radiative transfer introduces systematic errors that manifest themselves as four distinct effects: diffusive drift, diffusive clustering, ballistic deflection, and ballistic decollimation. We describe and quantify these effects and, subsequently, provide suitable solutions and strategies. We than demonstrate how the derived measures can be used to constrain the translation of a physical problem to a transport graph in such a way as to avoid or minimise errors. We finally discuss our results in a broader picture and outline related and future work, specifically an implementation of a dynamically updating grid in SimpleX.
Although developed in the context of SimpleX, many of our results are relevant for other transport algorithms that work on non-uniform grids (AMR grids or SPH particle sets).
2 Radiative transfer on unstructured grids
We describe the three means of transport that constitute the SimpleX algorithm. Starting from a general description of the equation of radiative transfer in inhomogeneous media, we delve into the specifics of SimpleX. This requires us to introduce the Delaunay triangulation, which lies at the heart of our method and plays a central role in this text.
2.1 General radiation transfer
The equation of radiative transfer for a medium whose properties can change both in space and time is given by
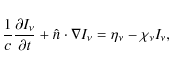
|
(1) |
where
If
![]() ,
in other words, if
,
in other words, if ![]() is not explicitly time dependent or the time and space discretisation is such that c can be considered infinite, this equation simplifies to
is not explicitly time dependent or the time and space discretisation is such that c can be considered infinite, this equation simplifies to
If we take the spatial derivative along the ray and divide by
where we define the source function
2.2 A natural scale
The fundamental idea behind the SimpleX algorithm is that there exist a natural scale for the description of radiative processes: the photon local mean free path
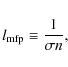
|
(4) |
where
Following this line of reasoning, the next step is to choose a
computational mesh that inherently carries this natural scale, in other
words, use an irregular grid whose resolution adapts locally to the
mean free path of the photons traveling over it![]() .
.
2.3 The grid
This computational mesh or transport graph is constructed by first defining a point process that represents the underlying (physical) problem and second by connecting these points according to a suitable prescription.
The point process is defined by prescribing the local point field density as a function of the scattering and absorption properties of the medium through which the particles propagate. The resulting points are connected by means of the unique Delaunay triangulation (Delone 1934). Thus, the points that carry the triangulation, which we refer to as nuclei in the remaining text, are connected as a graph, along whose connecting lines (called edges) the particles are required to travel.
This decision to construct a transport graph has several advantages: first, the connection with the physical processes is evident; second, the Delaunay triangulation (and the dual graph, the Voronoi tessellation (Voronoi 1908)) is unique and is in many respects the optimal unstructured partitioning of space (Schaap & Van de Weygaert 2000); third, the Voronoi-Delaunay structures carry all information required for the transport process, making the transport step itself very efficient.
We note that the use of Voronoi-Delaunay grids does not imply that the transfer of photons has to proceed along the edges of the Delaunay triangulation. Another approach would be to trace rays through either the Voronoi cells or Delaunay simplices. This ray-tracing could be done classically with long characteristics (Mihalas & Weibel Mihalas 1984) or using Monte Carlo methods (Abbott & Lucy 1985). In SimpleX, the photons travel from cell to cell interacting with the medium as they proceed. In this sense, the transport of radiation is treated as a local phenomenon and the global nature of the radiative transfer problem is dealt with by sufficient iterations of this local transport. The intimate relation between the structure of the grid and the transport of the photons is one of the reasons why the SimpleX algorithm is exceptionally efficient.
The construction of the grid itself is a task performed by dedicated software freely available on the web. Once the generating nuclei have been given, the Voronoi-Delaunay structure is unique. In creating the distribution of generating nuclei, we can manipulate the properties of our computational grid. The translation from a given density (opacity) field as either particles or cells to a Voronoi-Delaynay grid optimal for SimpleX is a fundamental part of the algorithm.
2.4 Voronoi-Delaunay structures
Because it plays a central role in this text, we now proceed with a concise introduction to the Voronoi-Delaunay grid.
We introduce a set of nuclei in a D-dimensional space together with a distance measure (in all of our applications, we use the isotropic ``Pythagoras'' measure). We partition this space by assigning every one of its points to its nearest nucleus. All the points in space assigned to a particular nucleus n form the Voronoi region of nucleus n (if D=2, the region is often called the Voronoi tile). By definition, the Voronoi region of n consists of all points of the given space that are at least as close to n (according to the distance measure of that space) as to any of the other nuclei. The set of all points that have more than one nearest nucleus constitute the Voronoi diagram of the set of nuclei (Vedel Jensen 1998; Okabe et al. 2000; Edelsbrunner 2006; O'Rourke 2001). For clarity, most of our explanatory illustrations will use D=2 (see Fig. 1 for an example in the plane), but our applications have D=3.
The set of all points that have exactly two nearest nuclei n1, n2 is the Voronoi wall between these nuclei. If D=2, this wall is a line; if D=3, it is a plane; and so on. In our astrophysical applications, D=3, in which case (pathological configurations excepted) triples of planar walls come together in lines, the points of which have three nearest nuclei; the lines, finally, join in quadruples at nodes, single points that have four nearest nuclei.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg35.png)
|
Figure 1: Voronoi tessellation of the plane (solid lines). Each cell contains all points that are closer to its nucleus (indicated by a dot) than to any other nucleus. The corresponding Delaunay triangulation is shown in dashed lines. Note: only visible nuclei are included in the triangulation. |
| Open with DEXTER | |
In our algorithm, no other connections between nuclei are allowed,
hence only adjacent Voronoi regions are connected. The expectation
value for the number of these Delaunay neighbours, ![]() ,
is 6 in 2D and 15.54
,
is 6 in 2D and 15.54![]() in 3D. Voronoi regions based on an
isotropic distance measure are convex; for a point process containing
N nuclei, the number of geometric entities (walls, edges, nodes,
etc.) is
in 3D. Voronoi regions based on an
isotropic distance measure are convex; for a point process containing
N nuclei, the number of geometric entities (walls, edges, nodes,
etc.) is
![]() .
.
For our application to transport theory, it is most important that the Delaunay triangulation has a minimax property, i.e. it is the triangulation with the largest smallest angle between adjacent triangle edges. Of all possible triangulations of a given point set, the Delaunay triangulation is the one that maximises the expectation value of the smallest angle of its triangles. In more colloquial terms, the Delaunay triangulation has the least ``sliver-like'' triangles, and the most ``fat'' triangles.
Another advantageous property of the Delaunay triangulation is that every edge pierces the wall between the Voronoi regions that it connects at right angles. This justifies the use of Eq. (3) where the spatial derivative is taken along the ray.
2.5 Three types of transport
In SimpleX, transport is always between neighbouring Voronoi cells
i.e., those connected by the Delaunay triangulation. On average, every
nucleus has 6 neighbours in 2D and 15.54![]() neighbours in 3D. When photons travel through a cell, the optical path length, l, is taken to be the average length of the Delaunay edges of that cell. If the number density of atoms in the cell is given by n the fraction of photons that are removed from the bundle,
neighbours in 3D. When photons travel through a cell, the optical path length, l, is taken to be the average length of the Delaunay edges of that cell. If the number density of atoms in the cell is given by n the fraction of photons that are removed from the bundle,
![]() ,
is given by
,
is given by
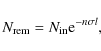
|
(5) |
where
In general, extinction can be subdivided into absorption and scattering. Radiation that is removed by absorption processes will in general change the both the temperature of the medium and its chemical state but need not be transported further at this point.
Photons that are removed from the bundle by scattering should
propagate to neighbouring cells, either isotropically or with a certain
directionality![]() . This can be accomplished using the diffuse transport method schematically depicted in the left panel of Fig. 2 and explained in more detail in Sect. 2.5.1.
The radiation that is not removed from the bundle, however, needs to
travel straight on along the original incoming direction. For optically
thick (
. This can be accomplished using the diffuse transport method schematically depicted in the left panel of Fig. 2 and explained in more detail in Sect. 2.5.1.
The radiation that is not removed from the bundle, however, needs to
travel straight on along the original incoming direction. For optically
thick (
![]() )
cells, we simulate this using ballistic transport (see the central panel of Fig. 2 and Sect. 2.5.2).
)
cells, we simulate this using ballistic transport (see the central panel of Fig. 2 and Sect. 2.5.2).
In regions of the grid where the cells are optically thin (
![]() ), ballistic transport becomes too diffusive and we need to resort to direction-conserving transport or DCT (see the right panel of Fig. 2 and Sect. 2.5.3).
), ballistic transport becomes too diffusive and we need to resort to direction-conserving transport or DCT (see the right panel of Fig. 2 and Sect. 2.5.3).
We now proceed by describing these transport methods in more detail and show how they are combined in a general simulation.
2.5.1 Diffuse transport
We begin with the description of conceptually the simplest form of transport implemented in SimpleX. At each computational cycle, which we refer to as sweep![]() in the remaining text, the content of each nucleus is distributed
equally among its neighbouring nuclei (see the left panel of Fig. 2.)
in the remaining text, the content of each nucleus is distributed
equally among its neighbouring nuclei (see the left panel of Fig. 2.)
| Figure 2: Three principal means of transport supported in SimpleX. Left panel: diffuse transport, photons from the incoming edge (not shown) are distributed outward along all edges (including the incoming edge). Central panel: ballistic transport, photons are transported along the D edges directed most forward with respect to the incoming direction. Right panel: direction-conserving transport, photons (indicated with the dotted arrows) are transported as in ballistic transport but their direction is stored indefinitely in a global set of solid angles. |
|
| Open with DEXTER | |
2.5.2 Ballistic transport
We now consider a group of photons that is transported along a Delaunay edge to a certain nucleus. We assume that the nucleus represents a finite optical depth. A fraction of the photons will be removed from the group by the interaction and another fraction will fly straight onward. Diffusive transport is not suited to describing this behaviour, so we introduce ballistic transport.
In the ballistic case, the incoming direction of the photons is used to
decide the outgoing direction (introducing a memory of one step into the past). In the generic Delaunay triangulation,
there is no outgoing edge parallel to the incoming one, so the
outgoing photons are distributed over the D most forward pointing
edges, where D is the dimension of the propagation space (see centre panel of Fig. 2.)
As such, we ascertain that for an isotropically radiating source the
complete ``sky'' is filled with radiation because the opening angle
associated with each edge on average corresponds to
![]() or
or
![]() in two and three dimensions respectively
in two and three dimensions respectively![]() .
.
Because of the random nature of the directions in the Delaunay grid, we
note that radiation will tend to lose track of its original direction
after several steps, a property that we call decollimation as it will steadily increase the opening angle of a beam of radiation as it travels along the grid (see Fig. 3).
This property renders ballistic transport appropriate for highly to
moderately optically thick cells only, where just a negligible amount
of radiation has to be transported more than a few steps. If we take
unity as a lower limit to the optical depth of a cell for which
ballistic transport is used, at every intersection a fraction of (1-1/e) of the photons becomes absorbed and the
cumulative average deflection (decollimation) ![]() becomes
becomes
where
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg47.png)
|
Figure 3: Example of decollimation in the plane for five ballistic steps. The arrow indicates the initial influx of photons. According to the ballistic transport mechanism, photons are transported along the D most forward edges with respect to the incoming direction. The colour coding is as follows: with every step the photons acquire a colour that is less red and more blue. As the angle between adjacent edges is large in 2D (60 degrees on average), the bundle loses track of its original direction in only a few ballistic steps. |
| Open with DEXTER | |
A visual extension of the statement given by Eq. (6) is shown in Fig. 4. From the figure, it is evident that the fraction of photons that is (ever) deflected more than 45![]() centred around the initial direction falls off sharply with the optical
depth of a cell. Only for optically thin (say 0.2) cells, the
fraction of photons whose deflection stay under 45
centred around the initial direction falls off sharply with the optical
depth of a cell. Only for optically thin (say 0.2) cells, the
fraction of photons whose deflection stay under 45![]() is lower than 0.5.
is lower than 0.5.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg48.png)
|
Figure 4:
Fractions of photons (contours) with deflection angle within 45 |
| Open with DEXTER | |
In realistic cosmological simulations, the effect of decollimation results in diffusion that softens shadows behind opaque objects (e.g., filaments and halos). The diffuse radiation field will penetrate into the opaque objects and ionise the high density gas inside. This results in ionisation of dense structures at too early times and the stalling of the ionisation front farther from the source. This clearly necessitates the introduction of a means of transporting photons in the optically thin regime.
2.5.3 Direction-conserving transport
If the cells are optically thin, the loss of directionality introduced by ballistic transport over many steps becomes prohibitively great and we switch to direction-conserving transport (DCT for short). Here the radiation is confined in solid angles corresponding to global directions in space: if a photon has been emitted in a certain direction associated with a solid angle, it will remember this direction while travelling along the grid. This effectively decouples the directionality of the radiation field from the directions present in the grid (see right panel of Fig. 2.)
For an example of the improvement of DCT over ballistic transport in a realistic case see Fig. 5. The contour for DCT shows a sharp ``shadow'' (in good agreement with the C2-ray result) where the dense filament is left neutral whereas ballistic transport results in a more diffuse, softer, shadow. Moreover, the ballistic ionisation front stalls with respect to the DCT result. This is another symptom of spurious diffusion: the positive radial component of the diffuse radiation is smaller than it should be resulting in more ionisations close to the source and less flux into the ionisation front.
We note, however, that the transport of photons still occurs along the
three most forward directed Delaunay edges of the grid, where
``forward'' is now with respect to the global directions of the solid
angles![]() . These edges may lead to nuclei that lie outside the solid angle associated with the direction of the photons.
. These edges may lead to nuclei that lie outside the solid angle associated with the direction of the photons.
In this sense, we now have two types of angular resolution in our
method. The first is related to the size of the solid angle in which
radiation is confined spatially, which is set by the number of Voronoi
neighbours of a typical nucleus (15.54![]() in 3D). We call this spatial resolution
and emphasize that it depends solely on the nature of the Delaunay
triangulation and as such is not adjustable. The second type of angular
resolution is set by the global division of the sky into arbitrarily
many directions (not necessarily constant along the grid) and we call
this the directional resolution.
For the tests presented here, we use 40 directions (a directional resolution of 40), implying a solid angle of
in 3D). We call this spatial resolution
and emphasize that it depends solely on the nature of the Delaunay
triangulation and as such is not adjustable. The second type of angular
resolution is set by the global division of the sky into arbitrarily
many directions (not necessarily constant along the grid) and we call
this the directional resolution.
For the tests presented here, we use 40 directions (a directional resolution of 40), implying a solid angle of ![]() sr for each unit vector.
sr for each unit vector.
A technical consequence of the approach sketched above is the need to divide space into equal portions of solid angle whose normal vectors are isotropic. There are many ways to divide the unit sphere into equal patches but the requirement of isotropy in general cannot be met exactly.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg50.png)
|
Figure 5:
Shadow behind a dense filament irradiated by ionising radiation
(indicated as a black dot). The hydrogen number density is plotted
logarithmically in greyscale and ranges between
|
| Open with DEXTER | |
For maximal flexibility in angular resolution, we construct sets of unit vectors that are distributed isotropically in angle using a simulated annealing scheme.
One major drawback of the introduction of global directions in the simulation is that they will give rise to artifacts much like those observed in hydrodynamical simulations on regular grids. This must in turn be counteracted by the randomisation of these global directions at appropriate time intervals, which makes DCT computationally relatively expensive.
2.6 Combined transport
The three means of transport described above in general are applied simultaneously. If the total optical depth
![]() for a given cell is caused by multiple extinction processes
for a given cell is caused by multiple extinction processes
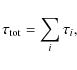
|
(7) |
the fraction, fi, of the incoming ray of photons that will be removed by process i is given by
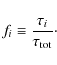
|
(8) |
Depending on the physical nature of this process, the photons are either removed from the bundle (to heat up the medium) or redistributed isotropically (or with some directionality) using diffuse transport. The remaining photons (those that are not removed from the ray) are transported with either ballistic or direction-conserving transport, depending on the total optical depth of the cell (ballistic if
3 Anisotropy and its consequences
Notwithstanding the ``ideal'' properties of the Delaunay triangulation, the probability density distribution of the angle between adjacent Delaunay edges is quite broad (Okabe et al. 2000; Icke & van de Weygaert 1987, Sect.5.5.4), so that, even though the average triangle is the ``fattest'' possible, many ``thin'' triangles will occur. This situation may be changed by iteratively adapting the underlying point process, in such a way that each nucleus comes to coincide with the centre-of-mass of its Voronoi region (see Lloyd 1982, for such an algorithm), resulting in so-called Centroidal Voronoi Tessellations (see e.g. Du et al. 1999). This procedure produces ``most spherical'' Voronoi regions (hexagons if D=2), but is in general far too costly for practical computations in which the triangulation must be re-computed frequently. Moreover, the shifting of the nuclei implies that the connection with the physical properties of the underlying medium is no longer entirely faithful. Another reason to refrain from the use of Centroidal Voronoi Tessellations is the introduction of regularity and hence symmetry in the grid. In two dimensions, for instance, the hexagonal Voronoi cells tend to align, introducing globally preferential directions in the transport of radiation. This will inevitably give rise to artifacts in the radiation field transported on such a grid.
Although the Voronoi-Delaunay construction is the optimal choice for the tessellation of a random (Poisson process) point set, it is not obvious that this is true when the point set is inhomogeneous or anisotropic. Inhomogeneity is, of course, the property we encounter in all practical cases. The probability distribution of the directions of Delaunay edges on a Poisson nucleus is isotropic, but this is no longer the case when the distribution of the nuclei is structured.
This inherent anisotropy of the graph introduces a bias that is the cause of some undesirable effects. It is these effects, and their treatment, that we consider here. We have tried in vain to find a mathematical treatment of related questions, such as: (1) is the Delaunay triangulation the one that maximises the isotropy of the edges emanating from a given nucleus? (2) can a process be found that adjusts the positions of the nuclei in such a way as to increase the isotropy of the edges? Concerning (1), we conjecture that the answer is yes, because (at least superficially) that would seem to follow from the minimax property of the angles between the edges. As to (2), we have looked for a procedure analogous to the ``centre-of-mass'' stratagem mentioned above, but have been unable to find one.
Thus, we must face the consequences of the anisotropy bias on inhomogeneous point processes. We note in passing that this bias will exist locally even in the case of a Poisson process for placing the nuclei, because, due to shot noise, every instance of a random point process is locally anisotropic, even if homogeneous and isotropic when averaged over multiple instances.
3.1 Error measure
For a homogeneous Poisson distribution of nuclei, the expectation
value for the number of Delaunay neighbours (and thus edges), ![]() ,
is 6
in two- and
,
is 6
in two- and
![]() in three-dimensional space. These Delaunay edges have no preferential
orientation and their statistical properties are well known (e.g. Okabe et al. 2000).
in three-dimensional space. These Delaunay edges have no preferential
orientation and their statistical properties are well known (e.g. Okabe et al. 2000).
We now consider an inhomogeneous distribution of nuclei.
Spatial gradients then appear in the density of nuclei,
![]() ,
and the Delaunay edges connecting these nuclei are no
longer distributed evenly over all possible orientations. For a given
nucleus, there will be, on average, more edges pointing towards
high-density regions than away from them.
,
and the Delaunay edges connecting these nuclei are no
longer distributed evenly over all possible orientations. For a given
nucleus, there will be, on average, more edges pointing towards
high-density regions than away from them.
This can be quantified as follows. Without loss of generality, we may assume a number density of nuclei that has a gradient in some fixed direction x provided that the characteristic length scale of the gradient is much larger than the mean distance between nuclei, a provision we assume to be fulfilled from now on.
We take a cross-section perpendicular to the direction of the gradient through the box at an arbitrary position x0. The resulting plane of surface S is pierced by Delaunay edges connecting nuclei on either side of the plane.
The number of edges piercing the plane can be estimated as follows.
The local density of edges is the product of the number density of nuclei
and ![]() .
An edge is able to pierce the plane when two requirements concerning its orientation are fulfilled:
.
An edge is able to pierce the plane when two requirements concerning its orientation are fulfilled:
- 1.
- its projected length must be larger than the distance between its originating nucleus and the plane.
- 2.
- it must point in the correct direction.
in three dimensions, where
where
The second requirement effectively excludes half (up to first order) of
the edges because they point away from the plane. This statement is
equivalent to noting that every piercing edge connects exactly two
nuclei at opposite sides of the plane. By including both factors, we
find that the number of piercing lines,
![]() ,
is given by
,
is given by
The surface density of lines piercing the slab,
The sought-after fractional excess, E(x), of parallel (with respect to the gradient) over anti-parallel Delaunay edges is thus given by differencing
where we used Eq. (9) to eliminate
In that case, Eq. (13) becomes
If
3.2 Effects on diffusive transport
In Sect. 2.5.1, we stated that for diffusive transport in a homogeneous distribution of nuclei, the radiation propagates spherically away from a source. On a graph corresponding to an inhomogeneous distribution of nuclei, however, this is not the case. The spreading of the transported quantity will no longer be spherical anymore for two reasons:
- 1.
- the Delaunay edges are shorter when the nuclei are spaced more closely.
- 2.
- the orientation of the Delaunay edges is no longer isotropic: more edges point towards the overdense regions.
3.2.1 Physical slow down
The first reason reduces the transport velocity and can be interpreted as a physical phenomenon. If we were to identify the length of a Delaunay edge with the local mean free path of the transported quantity (e.g. photons), the shorter edges would simply express that we have entered a region of increased optical depth where it takes a greater number of mean free path lengths to traverse a given physical distance. It has been shown (Ritzerveld & Icke 2006) that identifying the average Delaunay edge length with the local mean free path of the relevant processes is natural choice when constructing the triangulation and the observed behaviour is therefore both expected and physical.
3.2.2 Drift
The second reason, quantified by Eq. (13), is an artifact of the Delaunay triangulation itself and causes unphysical behaviour. When too many edges are pointing into the overdense regions, the transported particles are deflected into those regions and the direction of propagation tends to align with the gradient (see Fig. 6 for an example in the plane). We call this effect drift and now proceed to quantify its consequences for diffusive transport.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg78.png)
|
Figure 6: Schematic example of a nucleus and its edges subject to a gradient in the number density of nuclei in the positive x-direction. More edges point toward the overdense region (along the gradient). If every edge were to transport an equal number of photons to neighbouring nuclei, the anisotropy of outgoing edges would produce an unphysical net flow along the gradient indicated by the arrow, which is the vector sum of the edges scaled down by roughly a factor of three. |
| Open with DEXTER | |
A photon scattering at a nucleus has the following probabilities of
moving in the dense (subscript d) or underdense (subscript u)
direction:
The expectation value
in which
We consider a scattering experiment where a number of photons is
placed at one position of a triangulation with a density gradient. We
expect the photons to diffuse outward with an ever decreasing radial
velocity (the distance travelled, L, scales with the root of the
number of steps) and at the same time drift towards the dense region
with a constant velocity. There comes a time (or distance) at which
the drift is equal in magnitude to the diffusion radius. We define the
drift length,
![]() ,
as the scale on which the diffusion distance is equal to the distance travelled through drift. Roughly speaking,
diffusion dominates for
,
as the scale on which the diffusion distance is equal to the distance travelled through drift. Roughly speaking,
diffusion dominates for
![]() and drift dominates for
and drift dominates for
![]() .
Setting the diffusion distance equal to the distance travelled through drift,
.
Setting the diffusion distance equal to the distance travelled through drift,
we find that the number of steps at equality is given by
Using Eq. (9) and (13) gives an equality length of
independent of
For a given density distribution n(x), the length
![]() can
be evaluated everywhere
can
be evaluated everywhere![]() . This parameter can be interpreted as
follows. We define the minimum
. This parameter can be interpreted as
follows. We define the minimum
![]() for all
for all ![]() to be Ntimes the box side length, such that the drift can be at most 1/N of a
box side while the radiation scatters throughout the box. In any case,
we must ensure that
to be Ntimes the box side length, such that the drift can be at most 1/N of a
box side while the radiation scatters throughout the box. In any case,
we must ensure that
![]() is much longer than the box
side length.
is much longer than the box
side length.
Thus, even if the density contrast is
very small, it must not fluctuate too severely. We note that it does
not help to increase the number of nuclei, since both
![]() and
and
![]() in Eq. (20) scale with that
number.
Using more nuclei reduces the anisotropy per nucleus,
Eq. (13), but because the number of steps to be taken increases accordingly, the effect simply adds up to the same macroscopic
behaviour. Only the shape of
in Eq. (20) scale with that
number.
Using more nuclei reduces the anisotropy per nucleus,
Eq. (13), but because the number of steps to be taken increases accordingly, the effect simply adds up to the same macroscopic
behaviour. Only the shape of
![]() determines the magnitude of
determines the magnitude of
![]() .
.
To determine the resulting constraint on the grid, we consider the case in which
![]() does not
depend on position. Setting
does not
depend on position. Setting
![]() in
Eq. (20) defines an exponential density
distribution, where the anisotropy is smeared out
maximally over the domain. In this case, if we wish the drift to be
less than 1/8 of the box length, the density contrast must
be less than a factor
in
Eq. (20) defines an exponential density
distribution, where the anisotropy is smeared out
maximally over the domain. In this case, if we wish the drift to be
less than 1/8 of the box length, the density contrast must
be less than a factor
![]() implying that the restrictions put by our isotropy demands are rather stringent.
implying that the restrictions put by our isotropy demands are rather stringent.
3.2.3 Clustering
We have seen that the spurious drift for diffuse scattering places restrictions on the density contrasts that can be simulated by the plain implementation of SimpleX introduced in Sect. 3.2.2. We have assumed that the scale of the density fluctuations is comparable to the box size. This is not a restriction: if we are interested in a case where the density fluctuations are of a much smaller scale than the box size, we can just place an imaginary box around each density fluctuation and use all the quantitative results from above. In doing so, we see that for any given ``snapshot'' too many photons will be present in the local overdense regions, but if there are no overall density contrasts on large scales, there will be no significant macroscopic drift. The effect of the local drift on small scales can, however, still influence results on a large scale. Not only does the drift influence the average position of the photons, it also influences the standard deviation about this average. Isotropic scattering maximises the spreading of photons, but in an extreme case where for example at every nucleus 90% of the photons move in the same general direction, they will stick together for a longer period and therefore the size of a ``light cloud'' will grow more slowly. This is an effect that shows up if we have a highly fluctuating density field on small scales, a case in point being the simulation of the filaments of large-scale cosmic structures.
We consider a density distribution that is homogeneous in the
y- and z-direction but highly fluctuating in the x-direction. For the
probabilities to travel into the dense or underdense regions, we again
use Eq. (16) but with the difference that now d and u no
longer denote global directions. We describe the
transportation process by a binomial distribution. If there are no
large scale-density contrasts, the drift is zero on average, but
for the standard deviation we find
where N is the number of sweeps. For small values of E, this reduces to
This factor is always smaller than unity, indicating a reduction in the spreading of the photons. This effect can be significant for small-scale fluctuations with either a very high amplitude or a very short length. The effect slowly becomes smaller if the number of nuclei is increased. The value of E(x) comes close to unity or exceeds unity only if the characteristic density fluctuation length is smaller than a Delaunay length, which we had pointedly excluded.
3.3 Effects on ballistic transport
For ballistic transport, problems similar to those of diffusive transport arise but that the transport is locally anisotropic complicates the picture. We first describe some properties of this kind of transport on a homogeneous grid to appreciate deviations from the ``normal'' case later on.
We identify two distinct phenomena that photons travelling ballistically may experience: deflection and decollimation. Deflection is here understood as ``loss of direction'', where the direction is given by the vector sum of the three most forward pointing directions. Decollimation is defined to be the effect of the increase in opening angle of a beam of photons as they are transported ballistically. The first phenomenon depends on the evolution of the vector sum of the three most forward directions, whereas the second phenomenon is related to the angular separation between these directions individually. In the case of a homogenous distribution of nuclei, the net effect of deflection will vanish because there is no preferential direction in the grid.
3.3.1 Decollimation
As stated in Sect. 2.5.2,
the angular resolution, and therefore the minimal opening angle, is a
property of the Voronoi cell and is thus fixed for the chosen
triangulation. To exemplify this, we consider a typical Voronoi nucleus
in 3D, connected to ![]() neighbouring nuclei. The expectation value for the solid angle,
neighbouring nuclei. The expectation value for the solid angle, ![]() ,
subtended by each edge is thus
,
subtended by each edge is thus
In Fig. 7, the distribution of angles is given for a grid of 105 homogeneously placed nuclei in three dimensions. For the vector sum, the average departure from the incoming direction is about 15
For the distribution of the three separate most forward edges,
we find a standard deviation of about ![]() ,
which means that after
,
which means that after
![]() steps the photon has lost all memory of its original direction. We note
that the width of the vector sum of the weighted edges is smaller than
that of the most forward directed edge (indicated by ``1'' in the
figure) alone.
steps the photon has lost all memory of its original direction. We note
that the width of the vector sum of the weighted edges is smaller than
that of the most forward directed edge (indicated by ``1'' in the
figure) alone.
In general, the gradual loss of direction is not a major concern since most sources emit isotropically anyway, but the effect becomes important when many edges are traversed, because then the photons behave diffusively, producing an intensity profile that deviates from the correct r-(d-1)-form. Simulations in which the mean free path for scattering or absorption is much smaller than 5 edges are fine in this respect, because then the ballistic photons never enter this random walk regime (see also the discussion in Sect. 7).
![\begin{figure}
\includegraphics[width=9cm,clip]{13439f7.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg106.png)
|
Figure 7: Normalised distribution
of angles between the incoming direction and the vector sum of the
(three) most forward pointing edges (solid line) and the separate most
forward edges (dotted, dashed and dot-dashed lines) for a homogeneous
distribution of nuclei. The distribution of the most forward edges
added is shown as the long dot-dashed line with label ``Added'' and is
related to the decollimation effect. The standard deviation (
|
| Open with DEXTER | |
where
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg113.png)
|
Figure 8:
The projected step-size in the x-direction
as a function of sweeps together with a least squares fit for the
unweighted ballistic transport (solid line) and with ballistic weights
as described in Sect. 4.2 (dashed line). A region indicating unit standard deviation is shaded in grey around the markers. Error bars correspond to
|
| Open with DEXTER | |
3.3.2 Deflection
We are now ready to quantify the effect of the anisotropy of the triangulation on the ballistic transport of photons, which travel along the three edges closest (in angular sense) to the incoming direction. For the sake of simplicity, we estimate the deflection for radiation travelling along the most forward pointing edge and discuss the applicability to three edges afterwards.
We consider photons streaming perpendicular to the gradient direction (see Fig. 9
for the geometry of this situation.) The standard deviation in the
deflection of the outgoing edge with respect to the incoming direction
is typically 15![]() (see Fig. 7) for a homogeneous grid but in general depends on the local value for the gradient.
(see Fig. 7) for a homogeneous grid but in general depends on the local value for the gradient.
| Figure 9:
Geometry of radiation travelling perpendicular to the gradient direction. The deflection angle toward the underdense region,
|
|
| Open with DEXTER | |
where
For a homogeneous distribution of nuclei, this angle equals approximately
![\begin{displaymath}\theta_{{\rm d}} = (\Lambda [ 1 + E(x) \cos \phi ])^{-1/2},
\end{displaymath}](/articles/aa/full_html/2010/07/aa13439-09/img121.png)
|
(27) |
where we have used Eq. (25) to substitute for
![\begin{displaymath}\theta_{{\rm d}} \simeq \Lambda^{-1/2} \left[ 1 -\frac{ E(x) \cos \phi}{2} \right]\cdot
\end{displaymath}](/articles/aa/full_html/2010/07/aa13439-09/img122.png)
|
(28) |
To obtain the deflection per step over the grid, we average
The sign of
We note that this effective deflection angle is an upper limit to the
deflection encountered in a simulation because of the following. The
effect is maximal for radiation travelling perpendicular to the
direction of the gradient and this is the situation we have used as a
starting point for the above derivation of
![]() .
Secondly, that
.
Secondly, that
![]() increases the likelihood of selecting edges in the overdense region
effectively diminishing the deflection, an effect that we have
neglected in the derivation above. To include this effect, one would
have to know the distribution of outgoing edges as a function of angle
with the gradient, and assign a probability to the selection of an edge
accordingly. As we see in Sect. 5.3, the omission of this effect does not seem to be of much importance to our predictions.
increases the likelihood of selecting edges in the overdense region
effectively diminishing the deflection, an effect that we have
neglected in the derivation above. To include this effect, one would
have to know the distribution of outgoing edges as a function of angle
with the gradient, and assign a probability to the selection of an edge
accordingly. As we see in Sect. 5.3, the omission of this effect does not seem to be of much importance to our predictions.
Sending radiation along three edges rather than one decreases the effect of deflection. This is expected because the deflection of one edge is larger than that of the vector sum of three outgoing edges as we saw in the case of a homogeneous grid.
The growth of the deflection when traversing the grid can be found by dividing Eq. (30) by the typical step-size,
![]()
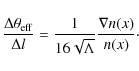
|
(31) |
As for the drift length of Eq. (20), we can define a deflection length,
![]() ,
at which the cumulative deflection is equal to say,
,
at which the cumulative deflection is equal to say, ![]() ,
,
Comparing with Eq. (20), we see that both the diffuse drift and the ballistic deflection place approximately the same restrictions on the box size, the only difference being a factor of 50 instead of 8. The interpretation again is simple. If
4 Weighting schemes
We describe several possible ways to correct for the unphysical effects described in Sect. 3.
4.1 Diffuse transport
A straightforward cure of the problems addressed in Sects. 3.2.2 and 3.2.3 (diffuse drift and clustering, respectively) is to assign weights wi to the edges emanating from a given nucleus in such a way that the anisotropy vanishes. This means that the fractions of the quantity transported to the neighbours are no longer equal to 1/N but directly proportional to the solid angle that the corresponding Voronoi face spans. We refer to Fig. 10 for an example in two dimensions, the three-dimensional case being analogous.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13439f10.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg134.png)
|
Figure 10: Solid angles for two edges in the case of the Voronoi weighting scheme (cell 3) and the icosahedron weighting scheme (cell 1). |
| Open with DEXTER | |
- 1.
- Voronoi weights: based on the natural properties of the triangulation. Its advantages are that it is automatically and ``naturally'' adapted to the physics of the transport problem. Its disadvantage is the statistical noise inherent to the procedure.
- 2.
- icosahedron weights: based on a division of the unit sphere using the icosahedron. Its advantages are that it is flexible (the procedure does not depend on type of triangulation) and that it is refinable. Its main disadvantage is that it is computationally expensive.
- 3.
- Distance weights: based on the distance to a neighbour squared. It main advantage is that is very fast. Unfortunately we have only empirical evidence of its correctness.
4.1.1 Centre of gravity weighting
In all three weighting methods, the sum of the weights equal unity, guaranteeing conservation
of photons. In addition, the vector sum
of the weighted Delaunay
edges emanating from a nucleus should be zero to conserve momentum of
the radiation field. We obtain this by adjusting the weights of the
(two) edges most parallel and anti-parallel to the ``centre of
gravity'', ![]() ,
of the nucleus defined by
,
of the nucleus defined by
such that in that direction the magnitude of
![\begin{figure}
\par\includegraphics[width=6cm,clip]{13439f11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg138.png)
|
Figure 11: Geometry of the COG weighting procedure. |
| Open with DEXTER | |
4.1.2 Voronoi weighting
The Voronoi weighting scheme uses the faces of the Voronoi cells to
calculate the wi for each nucleus by estimating the
solid angles subtended by the walls of the Voronoi regions, normalised
to unity. The weights are then
where Si denotes the surface of the Voronoi face perpendicular to the Delaunay edge connecting the current nucleus and its i-th neighbour, and di is the length of that edge (because the Voronoi face cuts the Delaunay edge in the middle, 0.5 di being the distance from the nucleus to the face). We note that Eq. (34) is an approximate expression neglecting projection effects for large angles. With some computational effort, this estimate could be refined. The solid angle subtended by a Voronoi face depends on the size of the cell but also on the precise position of the nuclei. Referring to Fig. 10, we see that cell ``3'' has a relatively small surface because its nucleus is close to that of neighbour ``4'' and its nucleus is a bit further from the central nucleus than that of neighbour ``4''. If that last statement were reversed, neighbour ``4'' would have the smaller surface and would thus get the smaller weight. This property may seem harmful at first but it is of stochastic nature, meaning that some noise will be introduced but no systematic error.
To demonstrate our method, we construct a Delaunay triangulation
of 105 nuclei in three-space with a linear gradient in
![]() along the horizontal direction which runs from 0.005 on the left to
0.995 on the right. As a measure of the anisotropy in orientations of
Delaunay edges, we take the angle between an edge and the
direction of the gradient and plot the number of edges in an angular
bin (see Fig. 12). Because we are interested in the
relative deviation from a horizontal line (which would correspond to the
isotropic situation), the results are given as a fraction of the
average,
along the horizontal direction which runs from 0.005 on the left to
0.995 on the right. As a measure of the anisotropy in orientations of
Delaunay edges, we take the angle between an edge and the
direction of the gradient and plot the number of edges in an angular
bin (see Fig. 12). Because we are interested in the
relative deviation from a horizontal line (which would correspond to the
isotropic situation), the results are given as a fraction of the
average, ![]() .
The data displayed in the topmost panel corresponds to the weighting
schemes described above, which can be thought of
as a basic correction plus a refinement thereof (the ``centre of
gravity'' correction). We show the effects on the angular distribution
of the edges as we apply these corrections cumulatively.
.
The data displayed in the topmost panel corresponds to the weighting
schemes described above, which can be thought of
as a basic correction plus a refinement thereof (the ``centre of
gravity'' correction). We show the effects on the angular distribution
of the edges as we apply these corrections cumulatively.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg140.png)
|
Figure 12:
Fraction of edges, |
| Open with DEXTER | |
The initial anisotropy apparent from the inclination of the line labeled ``unweighted'' is reduced significantly (to about half its original value) after applying the Voronoi weighting alone (dashed line). After application of the ``centre of gravity'' correction, the scatter around the isotropic value of unity is below 0.25%, except at the outer edges where the normalisation dramatically increases the errors.
Apart from the anisotropy caused by the gradient, the triangulation shows some noise of order 0.5% itself (the light grey areas around the uncorrected lines in the three panels having a width of one standard deviation). After all weighting has been applied, some noise remains (a unit-standard deviation area is shaded in dark grey). This noise is related to features of the triangulation itself. If the triangulation itself has more edges in a certain direction, this cannot be corrected with a local weighting scheme because it is a global property subject to chance. This noise can be reduced by either placing more points, or, equivalently, constructing several instances of the same triangulation and averaging over the results.
Because all the information needed for the Voronoi weighting scheme is
intrinsic to the tessellation and its triangulation, the associated
computational
overhead is potentially small. Unfortunately, in most tessellation
software, the areas of the Voronoi walls are not computed with the
other properties of the tessellation. Calculating these areas is
computationally costly because in three dimensions the walls are
generally irregular polygons with M vertices where ![]() .
.
4.1.3 icosahedron weighting
The second method is based on an ``independent'' division of the unit-sphere into M (approximately) equal parts. We take the M vectors (originating in the nucleus under consideration) that point to these parts and assign weights wi to the outgoing Delaunay edges as follows. We take a vector and calculate the N dot products with the Delaunay edges. The Delaunay edge that has the smallest dot product has a fraction 1/M added to its weight. In the icosahedron scheme, the weight is thus proportional to the solid angle a Delaunay line occupies considering the angular vicinity of its neighbouring edges (in 2D the solid angle is thus bound by the two bisectors shown as dotted lines in Fig. 10).
We chose the icosahedron as the basis of our weighting scheme. We use vectors to the middle of its 30 edges and its 12 vertices, yielding 42 reference vectors.
One significant advantage of the icosahedron method is that it is independent of the nature of the triangulation and is therefore very flexible. It becomes more accurate as the division of space is refined (M is increased) by taking other tessellations of the unit-sphere. The computational cost, however, scales linearly with M forcing us to trade off accuracy with speed. Unfortunately this ``independence'' also has a drawback: the reference vectors are oriented statically in space, introducing a systematic bias in those directions. To reduce this effect, one is forced to add some random noise to the procedure, for example by applying random rotations of the whole icosahedron, another computationally costly operation.
After the correction with icosahedron weights (see middle panel of Fig. 12, dashed line), the anisotropy decreases below the 0.5% level. This immediately shows the strength of this method over the more noisy Voronoi scheme (compare also the unit standard deviation regions in dark grey).
4.1.4 Distance weighting
Empirically we found that in 3D the square of the distance between nuclei is also a robust estimator of wi. This quantity is readily calculated and provides by far the most rapid solution to the problem at hand. After the initial correction (see bottom panel of Fig. 12, dashed line), the anisotropy of edges diminishes to values lower than 0.5% even slightly better than in the icosahedron scheme. The deviations from the ideal isotropic case after the COG correction are of the same order as in the Voronoi and the icosahedron case.
We could not find a valid explanation for the success of this method. Intuitively, one would think that the opening angle, ![]() ,
of a Voronoi wall with respect to its nucleus would scale as r-2 rather than r2. To find a mathematical reason for the proportionality between
,
of a Voronoi wall with respect to its nucleus would scale as r-2 rather than r2. To find a mathematical reason for the proportionality between ![]() and r2, one would have to delve more deeply into the field of computational geometry which is beyond the scope of this text.
and r2, one would have to delve more deeply into the field of computational geometry which is beyond the scope of this text.
4.2 Ballistic weighting
Assigning weights to the outgoing edges as described above removes the drift and clustering problems for diffusive transport described in Sect. 3.
The effects of anisotropy in the ballistic case are intrinsically more challenging to correct because it is not a priori clear how the anisotropy of all outgoing edges of a nucleus should be used to choose three weights for the outgoing edges. As described in Sects. 3.3.1 and 3.3.2, in the ballistic case we must distinguish between decollimation and deflection first one of which the dominates the overall ``loss of direction''. To diminish the decollimation of a beam, we can assign weights to the most forward pointing edges. If we make these weights somehow proportional to the inner product of the edge and the incoming direction, the most forward pointing edges transport most of the photons.
There are many possible ways to assign weights to the D most forward directed edges, which each optimise different aspects of the transportation process. If the exact direction is important, for instance, the weights should be chosen such that the vector sum of the resulting edges points straight ahead. On the other hand, minimising the decollimation will in general yield a different set of weights, those that maximise the length of the vector sum.
From this myriad of possibilities, we choose a very simple and computationally cheap approach. To edge j we assign the weight wj given by
where
Applying this weighting scheme to the point distribution used to produce Fig. 7 yields the distribution of edges shown in Fig. 13. As specified by Eq. (35), the ballistic weights have the desired effect of decreasing the width of the distributions of the edges used in ballistic transport.
In Fig. 8,
evolution of the step-size of ballistic transport in the weighted case
is shown with crosses. The decollimation angle per step is
substantially smaller than in the case without weighting (![]() compared to
compared to ![]() ).
This decrease in decollimation angle consequently relaxes the
requirement that the number of ballistic steps must remain below 5.
Including ballistic weights typically allows for up to 12 ballistic
steps before the original direction is lost.
).
This decrease in decollimation angle consequently relaxes the
requirement that the number of ballistic steps must remain below 5.
Including ballistic weights typically allows for up to 12 ballistic
steps before the original direction is lost.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f13.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg144.png)
|
Figure 13: Normalised distribution
of angles between the incoming direction and the vector sum of the
(three) most forward pointing edges (solid line) and the separate most
forward edges (dotted, dashed and dot-dashed lines) for a homogeneous
distribution of nuclei with ballistic weights. The distribution of the
most forward edges added is shown as the long dot-dashed line and
labeled ``Added''. The standard deviation (
|
| Open with DEXTER | |
Finally, there are cases where the anisotropy of edges emanating from a cell cannot be solved by any weighting scheme. If there is no edge in a given direction, the radiation cannot go there, regardless of the weight values. One should begin with a reasonably isotropic triangulation to apply a weighting scheme in a useful way. In the case of Delaunay triangulations in three-space, this is almost always the case.
4.3 DCT throughout the grid
A conceptually different solution to the problems described in Sect. 3 is to apply the direction-conserving transport from Sect. 2.5.3 throughout the simulation domain. As the angular direction of the radiation is effectively decoupled from the grid in this approach, all drift, clustering, decollimation, and deflection are solved for at once. The cone containing the nuclei that receive radiation will however still be dependent on the grid itself as already pointed out in Sect. 2.5.3.
5 Numerical examples
After considering the various systematic effects affecting the SimpleX algorithm, we now present some sample cases that demonstrate them. In general, all of the effects described above occur simultaneously, but for transparency we analyse them in isolation.
5.1 Effects on diffusive transport: drift
We now proceed by describing the numerical experiment designed to show
the effects of diffuse drift. The simulation domain of unity volume in three
dimensions is filled with
![]() nuclei subject to a gradient in the
point density of the form n(x)= x.
We choose this linear form because it locally approximates every other
type of gradient. The number of nuclei results in roughly 32 steps
across the box along the gradient direction and 38 in the directions
perpendicular to the gradient. These numbers allow for most of the
photons to travel through the box for more than 100 steps before being
captured in the absorbing boundaries.
nuclei subject to a gradient in the
point density of the form n(x)= x.
We choose this linear form because it locally approximates every other
type of gradient. The number of nuclei results in roughly 32 steps
across the box along the gradient direction and 38 in the directions
perpendicular to the gradient. These numbers allow for most of the
photons to travel through the box for more than 100 steps before being
captured in the absorbing boundaries.
At the site closest to the centre of the domain, a number of photons is placed. Neither the outcome nor the speed of our simulation depends on this number as we use floating point numbers to represent photons.
Photons are transported over this grid using diffusive transport without
absorption. With every sweep, the photon cloud is expected to grow in
size. In the case of a homogeneous point density, the photons will be
distributed normally, as must be expected for pure diffusion. The
gradient in the point density will distort the form of the
distribution function for two reasons. First, the mean free
path on the grid, ![]() ,
scales with the point density according to
Eq. (9) allowing photons to diffuse faster into the
underdense regions where the step sizes are larger. Second, the drift
phenomenon described in Sect. 3.2.2 will counteract this physical diffusion and move the
cloud into the overdense region.
,
scales with the point density according to
Eq. (9) allowing photons to diffuse faster into the
underdense regions where the step sizes are larger. Second, the drift
phenomenon described in Sect. 3.2.2 will counteract this physical diffusion and move the
cloud into the overdense region.
To separate these two effects, we performed a one-dimensional Monte
Carlo simulation of
![]() ``random walkers'' that take steps with a size given by the recipe of Eq. (9). The experiment
described above is emulated in one dimension but without the Delaunay grid as
an underlying structure. The random walkers are thus expected to
experience the physical diffusion into the underdense region only. The
unphysical drift is caused exclusively by the Delaunay grid and will not
be present in our results.
``random walkers'' that take steps with a size given by the recipe of Eq. (9). The experiment
described above is emulated in one dimension but without the Delaunay grid as
an underlying structure. The random walkers are thus expected to
experience the physical diffusion into the underdense region only. The
unphysical drift is caused exclusively by the Delaunay grid and will not
be present in our results.
In Fig. 14, the intensity-weighted position of the
photon cloud (along the direction of the gradient) versus the number
of sweeps in the simulation is shown for SimpleX and the Monte Carlo
experiments in the cases of both with and without weights![]() . We can see that
the behaviour conforms to our expectation. The weighting corrected SimpleX result coincides with the Monte Carlo as shown in the bottom panel.
. We can see that
the behaviour conforms to our expectation. The weighting corrected SimpleX result coincides with the Monte Carlo as shown in the bottom panel.
Furthermore, we took our drift description Eq. (13) and applied it to the Monte Carlo experiment thus introducing a drift toward the overdense region similar to that experienced by a photon in SimpleX. The effect counteracts the physical diffusion into the underdense region resulting in a positive slope for the position of the photon cloud as a function of sweeps (see top panel of Fig. 14.) This procedure thus provides a direct quantitative check of the correctness of Eq. (13).
The slopes of the Monte Carlo experiment agree to within a thousandth of a degree with the SimpleX results for both the uncorrected and weighted results. This implies that the weighting schemes discussed in Sect. 4 do not only correct the orientation of the edges in a statistical sense (as shown in Fig. 12) but also allow for correct transport over these edges. This may seem a trivial statement, but despite everything being fine in a global sense, local anomalies may prevail. The transport of photons, however, depends strongly on the local correctness of the weighting scheme and is thus a more stringent test. Furthermore, the recovery of the SimpleX results with the Monte Carlo experiments suggests that Eq. (13) describes the drift phenomenon accurately in a quantitative sense.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f14.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg147.png)
|
Figure 14: Intensity-weighted position of a photon cloud released in the centre of a simulation domain with a linear gradient in the number denisty of nuclei as a function of the number of sweeps. Results obtained with SimpleX are shown with filled symbols and results obtained by the Monte Carlo experiments are indicated with open symbols. We use triangles and squares in the corrected and uncorrected case, respectively. |
| Open with DEXTER | |
5.2 Effects on diffuse transport: clustering
As seen in Sect. 3.2.3
the expansion
of a photon cloud is stalled by small (relative to the
simulation domain) scale gradients in the grid. To illustrate this
effect performed the following experiment. The simulation domain is
again given
by the unit cube with a large number of photons at the centre. The
![]() nuclei are distributed according to the probability
distribution
nuclei are distributed according to the probability
distribution
where
We now prepare a similar simulation with a homogeneous
distribution of nuclei where the box-size measured in units of
![]() is the same. A comparison of the spread of the photon cloud in
the homogenous setup with that given by Eq. (36) provides a direct measure of the effect described by Eq. (22).
is the same. A comparison of the spread of the photon cloud in
the homogenous setup with that given by Eq. (36) provides a direct measure of the effect described by Eq. (22).
Application of a weighting scheme for diffusive transport described in Sect. 4
should remove the difference between the spread of the cloud in the two
cases described above. As a check, we also compare the results to the
analytical result given by Eq. (21) and the expected spread of the photon cloud in the homogenous case (which is simply
![]() )
.
)
.
In Fig. 15, the spread of the photon cloud in terms of the normalised standard deviation in the intensity-weighted positions is shown for the inhomogeneous point density given by Eq. (36) (solid lines) and the analytical prediction (dashed line). The data are obtained from twenty runs with different realisations of the grid.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f15.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg151.png)
|
Figure 15:
Normalised standard deviation of the intensity-weighted positions of a
photon cloud expanding in a distribution of nuclei with small-scale
gradients with and without weights (thick and thin solid lines,
respectively) and the analytical expectations according to Eq. (21) (dashed line). A dotted line at
|
| Open with DEXTER | |
As expected, the photon cloud expands (almost 6%) more slowly when no
weights are used in the case of small-scale gradients (thin solid
line). Application of the weighting scheme results in a cloud that
(after a slow start) conforms to the expected size (dotted line at
![]() ).
The analytical model predicts this behaviour to within 3% after
30 sweeps, and increasingly poorly for fewer sweeps (although the
deviation remains below 10%). The larger deviations for fewer sweeps
are caused by the cloud size (expressed in standard deviations) being
small and the results are divided by this small number. We note that
the unit standard deviation region for the weighted case is narrower in
the weighted case (light gray) than the unweighted case (dark gray).
This is expected because the weighting scheme corrects for local
anisotropies and thus reduces the noise in the diffusive transport.
).
The analytical model predicts this behaviour to within 3% after
30 sweeps, and increasingly poorly for fewer sweeps (although the
deviation remains below 10%). The larger deviations for fewer sweeps
are caused by the cloud size (expressed in standard deviations) being
small and the results are divided by this small number. We note that
the unit standard deviation region for the weighted case is narrower in
the weighted case (light gray) than the unweighted case (dark gray).
This is expected because the weighting scheme corrects for local
anisotropies and thus reduces the noise in the diffusive transport.
In the homogeneous case we have verified that applying a weighting scheme does not alter the expansion speed of a photon cloud significantly, as expected. We can thus conclude that, although clustering can impose a substantial effect on the expansion of diffuse radiation, our weighting scheme corrects for it appropriately.
5.3 Effects on ballistic transport: deflection
To study whether anisotropy has any effect on the direction of a beam
of photons, we considered a triangulation of a random point
distribution containing
![]() nuclei placed in a cube of
unit dimensions with a linear gradient along the x-direction.
In the centre, we included a spherical volume of
radius 0.05 and place a number of photons in each nucleus contained in
this volume. The photons were assigned a direction by sending them
along the edge whose direction is maximally perpendicular to the x-axis.
The simulation was executed with ballistic transport using both one and
three outgoing edges and in addition with the direction-conserving
implementation of SimpleX (as described in Sect. 2.5.3). Every run was repeated 10 times with different instances of the grid to suppress shot noise and obtain error estimates.
nuclei placed in a cube of
unit dimensions with a linear gradient along the x-direction.
In the centre, we included a spherical volume of
radius 0.05 and place a number of photons in each nucleus contained in
this volume. The photons were assigned a direction by sending them
along the edge whose direction is maximally perpendicular to the x-axis.
The simulation was executed with ballistic transport using both one and
three outgoing edges and in addition with the direction-conserving
implementation of SimpleX (as described in Sect. 2.5.3). Every run was repeated 10 times with different instances of the grid to suppress shot noise and obtain error estimates.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f16.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg153.png)
|
Figure 16:
Mean angular directionality of a photon cloud as a function of the
number of sweeps. In this simulation, a linear gradient in the density
of nuclei is present and the angle is measured relative to the
direction of the gradient, so smaller values of the angle point toward
the denser region. As expected, the direction-conserving implementation
of SimpleX (as described in Sect. 2.5.3,
indicated by filled squares) has no long-term loss of directionality,
although it shows some oscillatory behaviour that dampens with time.
Ballistic transport with one edge (open triangles) shows a deflection
towards larger angles for number of sweeps of order
|
| Open with DEXTER | |
When applying our ballistic transport method, the photons undergo small
angular deflections into the underdense region as predicted in
Sect. 3.3.2.
Using Eq. (30), the expected effective deflection for this setup is
![]() rad/sweep, which yields a cumulative result of approximately
rad/sweep, which yields a cumulative result of approximately
![]() rad after 50 sweeps. This estimate is consistent with the result
of the simulation with one forward edge denoted by the open triangles
in Fig. 16.
As expected, sending radiation along three edges decreases the
deflection and fluctuation of the angular direction in general because
radiation is distributed over many (3Ns) edges, which quickly reduces shot noise with time. When using the direction-conserving implementation of SimpleX (filled squares), the radiation does not suffer from ballistic deflection.
rad after 50 sweeps. This estimate is consistent with the result
of the simulation with one forward edge denoted by the open triangles
in Fig. 16.
As expected, sending radiation along three edges decreases the
deflection and fluctuation of the angular direction in general because
radiation is distributed over many (3Ns) edges, which quickly reduces shot noise with time. When using the direction-conserving implementation of SimpleX (filled squares), the radiation does not suffer from ballistic deflection.
6 Application
We illustrate how to apply the results of the above analysis to a more astro-physically relevant problem. We ask ourselves whether given a density (or opacity) distribution, how we can construct a Voronoi-Delaunay structure that keeps the described problems acceptably small while representing the physical problem as accurately as possible. This often means maximising the dynamic range with the prerequisite that low density regions have sufficiently high resolution.
6.1 Sampling function
The trade-off is thus between maximising dynamic range and
minimising the strong gradients this inevitably introduces. In other
words, we must investigate the effects that different sampling
functions have on the triangulation and its transport properties. These
functions translate the physical medium (expressed as an opacity or
density map)
to a point distribution ![]() whose points form the nuclei of
the triangulation. As mentioned in Sect. 3.2.2, the
average Delaunay edge length can be associated with the mean free path
of the photons in a very natural way. This is achieved when
whose points form the nuclei of
the triangulation. As mentioned in Sect. 3.2.2, the
average Delaunay edge length can be associated with the mean free path
of the photons in a very natural way. This is achieved when ![]() scales with the opacity (or density) to the D-th power
(Ritzerveld & Icke 2006, Eq. (14))
scales with the opacity (or density) to the D-th power
(Ritzerveld & Icke 2006, Eq. (14))
where
One drawback of using Eq. (37) is that the resulting point process, given a substantial density contrast, places many nuclei in dense regions and very few in underdense regions. For many applications, simulating the true mean free path may thus require a number of nuclei that is prohibitively high.
We therefore adopt a more flexible sampling function that behaves
differently for the extremal densities of the grid. According to this
function, the number density of nuclei that generate the Voronoi grid
is given by
where
According to Eq. (20) and (32),
the quantity that links the properties of the grid (density of nuclei
and gradients therein) to the systematic effects described in the
previous sections is
![]() .
We are now in the position to define, in a way analogous to Qn, the quantity
.
We are now in the position to define, in a way analogous to Qn, the quantity
![]() ,
which can be measured over the physical density (opacity) field. As the sampling function of Eq. (38) translates the physical field to the density of nuclei, the measured value of Qy and the upper limit of Qn (posed by the maximally acceptable value for either
,
which can be measured over the physical density (opacity) field. As the sampling function of Eq. (38) translates the physical field to the density of nuclei, the measured value of Qy and the upper limit of Qn (posed by the maximally acceptable value for either
![]() or
or
![]() )
constrain the sampling parameters
)
constrain the sampling parameters ![]() and
and ![]() .
.
6.2 Cosmological density field
We now apply this idea to a more realistic example and see what this all means in practice. A typical application wherein the strength of the SimpleX algorithm can be fully deployed is the epoch of reionisation (see Paardekooper et al. (2010) for an account of relevant test cases). Both the wide range of densities (four to five orders of magnitude) and the large number of sources (hundreds to thousands in realistic cosmological volumes) can be treated naturally by SimpleX due to the adaptive nature of the Delaunay grid and because the computational effort does not increase with increasing number of sources.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13439f17.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg165.png)
|
Figure 17: Cut through a cosmological density field ( left panel; colours indicate number density in logarithmic scale) sampled with 105 points using the sampling function of Eq. (37) ( middle panel) and Eq. (38) ( right panel) with the parameters obtained from analysis of the underlying density field. |
| Open with DEXTER | |
We now consider a typical (0.5/h Mpc comoving) cosmological volume (as used in test 4 of Iliev et al. (2006)) and construct a representative point set using constraints from analysis of the original data. In this specific case, the cosmological density field was presented as a regular grid of 1283 equal size cells.
6.3 Constraints
Given the regular grid, the quantity Qy can be determined for every pair of adjacent cells. The mean value of Qy obtained is thus 1.6.
This value implies that if we would use a linear translation between
the mass density of the original data and the number density of the
nuclei of the Delaunay grid, the equality length (see Eq. (20)) would become
![]() and the deflection length of Eq. (32) becomes
and the deflection length of Eq. (32) becomes
![]() .
This means that radiation can travel 13 box-lengths before diffuse
drift starts to dominate the transport of radiation, and 81 box-lengths
before ballistic deflection reaches a cumulative magnitude of
.
This means that radiation can travel 13 box-lengths before diffuse
drift starts to dominate the transport of radiation, and 81 box-lengths
before ballistic deflection reaches a cumulative magnitude of ![]() .
.
This linear sampling could be performed using
![]() in Eq. (14) or, equivalently,
in Eq. (14) or, equivalently,
![]() and
and
![]() in Eq. (38).
Linear sampling is hardly ever desirable in a cosmological setting,
however, as it tends to place the bulk of the nuclei in high density
regions resulting in oversampling (many nuclei per grid cell of the
original grid) of filaments and clumps and undersampling of voids.
in Eq. (38).
Linear sampling is hardly ever desirable in a cosmological setting,
however, as it tends to place the bulk of the nuclei in high density
regions resulting in oversampling (many nuclei per grid cell of the
original grid) of filaments and clumps and undersampling of voids.
We proceed by finding optimal values of our sample parameters, given the measured value of Qy and a chosen value for the maximum allowed equality length. An upper limit to the equality length, by means of Eq. (20), immediately implies a maximal Qn.
For example, if we set
![]() (and consequently
(and consequently
![]() ), we see that we need to choose
), we see that we need to choose ![]() and
and ![]() such that Qn=5. From Eq. (38), we can derive an expression that links the measured value of Qy to Qn and thus to the sample parameters, given by
such that Qn=5. From Eq. (38), we can derive an expression that links the measured value of Qy to Qn and thus to the sample parameters, given by
Solutions for Qn =Qy exist only for certain pairs of
If we were to choose
Solving Eq. (40) for
Qy =1.6, we find
![]() to be the maximal value. Taking the somewhat smaller value of 0.3, the corresponding value for
to be the maximal value. Taking the somewhat smaller value of 0.3, the corresponding value for ![]() is
is
![]() cm-3 which is significantly higher than the lowest densities in the cosmological field, which are about
cm-3 which is significantly higher than the lowest densities in the cosmological field, which are about
![]() .
.
6.4 The grid
In the right panel of Fig. 17, a cut at z=0.5
through the sampling defined by these parameters is shown. The middle
panel shows the point distribution one obtains when sampling with ![]() throughout the grid. This distribution does not accurately reproduce
the low-density regions, placing almost all points in the dense
filaments and their intersections. In contrast, the ``hybrid'' sampling
method provides sufficient resolution in both the low- and high-density
regions. For the
throughout the grid. This distribution does not accurately reproduce
the low-density regions, placing almost all points in the dense
filaments and their intersections. In contrast, the ``hybrid'' sampling
method provides sufficient resolution in both the low- and high-density
regions. For the ![]() sampling, the cell size in the filaments and dense clumps is many times
smaller than that of the original regular grid. No information is
carried, however, by this extra resolution, effectively wasting
computational resources. As an extra constraint (apart from
sampling, the cell size in the filaments and dense clumps is many times
smaller than that of the original regular grid. No information is
carried, however, by this extra resolution, effectively wasting
computational resources. As an extra constraint (apart from
![]() and
and
![]() ),
one could demand that the smallest Voronoi volume is equal to the
resolution of the original data. This could either be the highest AMR
resolution or, in the case of SPH, the minimal smoothing length.
),
one could demand that the smallest Voronoi volume is equal to the
resolution of the original data. This could either be the highest AMR
resolution or, in the case of SPH, the minimal smoothing length.
6.5 Speed considerations
Although we do not consider details here, the speed of SimpleX also depends on the form of the grid. Because in every sweep all nuclei are visited exactly once, the execution time of the method scales linearly with the number of nuclei. In turn, the number of sweeps needed to reach convergence roughly scales as the number of sweeps it takes to enable every point within the simulation domain to ``communicate'' its physical properties with every other location by an exchange of photons.
Now consider the point distribution in the middle panel of Fig. 17.
The resulting grid will have many short edges in the high density clump
in the east of the domain. For diffusive transport or ballistic
transport over many (more than roughly 5) edges, such a clump will
trap photons for many sweeps because their travelled distance after N sweeps is given by
![]() where
where
![]() is small. This is another reason not to use high sampling powers throughout the simulation domain.
is small. This is another reason not to use high sampling powers throughout the simulation domain.
7 Discussion
After identifying and correcting the various effects caused by anisotropy in the Delaunay grid, we discuss their implications in a broader context.
7.1 Prevention versus correction
It is impossible in general to define the perfect grid. As already
pointed out, a large dynamic range inevitably leads to gradients that,
in turn, produce the unphysical effects described in this text.
Although we have shown that these effects can be corrected by weighting
schemes, these corrections are not fail-safe if the gradients are too
strong. In particular, when the density of nuclei changes
appreciatively on length scales smaller than
![]() (or, more precise,
(or, more precise,
![]() ),
the lack of edges towards the underdense region may lead to extreme
decollimation as there are simply hardly any edges that point that way.
In this case, a weighting scheme is not feasible as there are no edges
to assign weights to in the underdense direction. We therefore need to
begin with a fairly well behaved grid in the first place.
),
the lack of edges towards the underdense region may lead to extreme
decollimation as there are simply hardly any edges that point that way.
In this case, a weighting scheme is not feasible as there are no edges
to assign weights to in the underdense direction. We therefore need to
begin with a fairly well behaved grid in the first place.
One could argue that if the grid is constructed such that the unphysical effects are below a predefined tolerance, the deployment of weighting schemes can be circumvented. On the other hand, this rather tight constraints on the grid and it might be preferable to retain a greater dynamic range (and thus structure) in the grid at the expense of the need for weighting.
An intermediate solution will often be the most viable option, where we retain the dynamic range of the data as much as possible while weighting schemes and DCT are employed at certain locations in the simulation domain only.
7.2 Number of steps versus
 and
and
In Sect. 3, we
determined the typical length scales on which the unphysical effects
become important in a relative sense. Being cautious, we defined these
length scales to many times the size of the simulation domain, although
this is not necessary in most real-life situations because radiation
typically travels only moderate distances along the grid. It might
therefore be more intuitive to think about the number of steps a photon
travels along the grid before being scattered or absorbed instead of
![]() and
and
![]() .
In the event of either absorption or scattering, the past of the photon
is essentially erased and it starts a new life, so decollimation,
deflection, and drift are basically ``reset'' to zero.
.
In the event of either absorption or scattering, the past of the photon
is essentially erased and it starts a new life, so decollimation,
deflection, and drift are basically ``reset'' to zero.
We can thus assess the possible harm of anisotropy in a simulation by
monitoring the fraction of Delaunay length and physical mean free path,
R, defined as
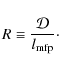
|
(41) |
First of all, R should not be much smaller than 1, because this would cause decollimation and in extreme cases even the simulation of straight light rays by a random walk (see also the discussion in Sect. 3.3.1).
In the limit of large R, however, a large portion of the photons will be absorbed after travelling along this edge. This is merely a resolution issue: the photons will never travel further than one Voronoi region away from the place where they ought to have been absorbed.
Using a sampling function of the form of Eq. (37) would result in R being a constant along the grid. If we use a more general sampling method, R is no longer a global constant. We can however still adjust the local optical depth for absorption with the local value of R. If we do so, the place where a photon finally becomes absorbed or leaves the simulation domain still has the right probability distribution, but the interpretation of intermediate photon densities in the simulation becomes less intuitive. The photon densities are not ``time'' densities but ``step'' densities, but now photons in regions with different densities will travel a different amount of mean free paths per sweep. If we are interested in the effect of the photons on the medium and in the directions of photons that leave the box, we are justified in sampling using any other power than 3, as long as we make local corrections to the optical depth that are proportional to R.
7.3 A dynamic grid
We have argued that the ratio of the local mean free path to the Delaunay edges should be chosen with care to ensure meaningful results. Because the local mean free path can change due to changes in the medium properties, the Delaunay edge length should adapt accordingly to keep R fixed.
The SimpleX code has been extended to handle dynamic media (Paardekooper et al. 2010), where nuclei can be added or deleted during the simulation. This allows the triangulation to adjust itself to the (changing) local properties of the medium.
We can set up strict conditions under which a nucleus is deleted (and its attributes divided between its neighbours). A possible condition could be to delete a nucleus whenever the local mean free path of the ionising photons exceeds the average length of its outgoing edges. In this way, we would keep deflection and decollimation acceptably small in the case of ballistic transport.
8 Future work
In this section we discuss several limitations of the current SimpleX method and indicate a possible route forward to overcome these limitation in future versions of the code.
8.1 Multiple frequencies
In the current incarnation of SimpleX, a grey approximation is used where the effect of a source spectrum is taken into account by the use of effective, intensity-weighted, cross-sections. Implementation of a full multi-frequency treatment is not trivial because it formally requires a separate grid for every new frequency bin. In practice, however, we have found that by transporting similar frequencies over the same grid, the computational demands will not become prohibitive. A version of SimpleX incorporating multiple frequencies is currently under development and we postpone a discussion of related issues to future articles.
8.2 Cosmological redshift
For cosmological simulations, the expansion of space will shift the frequency of the transported photons. In our one-frequency approach, this is nothing more than a gradual loss of ionizing energy for the photons. In future multi-frequency versions of the code, more care should be taken with this issue especially when line-transfer is included.
In principle, relativistic ``beaming'' could also play a non-negligible role in simulations of large cosmological volumes. Owing to expansion of the universe, an absorbing parcel of gas will have different relative velocities to sources at different distances. The resulting enhancement of the observed intensity (Eq. (4.9) in Rybicki & Lightman 1986) can be substantial. This beaming could in principle be modeled in SimpleX by adjusting the weighting factors for diffuse and ballistic transport appropriately, but we leave a detailed analysis to future work.
8.3 Strong scattering
Finally, in the case of strong scattering (if the cross-section for absorption is negligibly small compared to the cross-section for scattering) the SimpleX method only converges asymptotically to the correct answer. This is because transport occurs on a cell-to-cell basis and this can take a large number of sweeps to bring all scattering particles in the simulation domain into equilibrium. This problem is well known and has been overcome by classical radiative transfer methods by using so-called accelerated lambda iteration methods.
In the cosmological applications of SimpleX, strong scattering is not, however, a dominant process, and we do not pursue an implementation of accelerated Lambda iteration schemes in our method in the near future.
9 Summary
We now summarize the main insights and results from the above analysis.
- 1.
- The SimpleX algorithm is a relatively new and non-standard method, whose systematic effects should be thoroughly analyzed. This assessment has two important purposes: first, exploring the boundaries of its reliability and accuracy and, second, increasing its region of application by improvements.
- 2.
- The mathematically transparent nature of the SimpleX algorithm allows a rigorous and general assessment of its systematic effects to be performed. Although only some of the described effects (diffuse drift and ballistic decollimation) need to be considered in typical applications (see Paardekooper et al. 2010), we have investigated all four in detail for completeness.
- 3.
- The use of a random Delaunay triangulation in the radiative transfer method SimpleX introduces global errors when the point-density is inhomogeneous. We have identified and quantified four distinct effects: ``drift'' and ``clustering'' of photons in diffusive transport, and ``decollimation'' and ``deflection'' in ballistic transport.
- 4.
- We have shown that decollimation become troublesome only when the number of traversed edges becomes larger than roughly 5 steps. This implies that one either preclude this regime or, when this is undesirable or impossible, correct for the unphysical behaviour.
- 5.
- A weighting method for ballistic transport has been shown to decrease the effect of decollimation significantly by pushing the limit for correct transport from 5 to 12 steps.
- 6.
- We have shown how drift and clustering can be adequately corrected for by adopting a weighting scheme. Three weighting schemes for diffusive transport have been discussed and compared.
- 7.
- The use of a direction-conserving variant of the ballistic transport has been introduced as an alternative to the weighting procedure and to prevent loss of angular direction in optically thin regions. This approach also provides a means of correcting for deflection, drift, and clustering. The computational cost and need for additional randomisation of the solid angle directions ensures, however, that the employment of DCT is not generally favourable.
- 8.
- Finally, we have applied our analysis to an astrophysically relevant example. This elucidated the intimate relation between the construction of a computational grid and the possible need for weighting schemes.
Part of this work was supported by the German Deutsche Forschungsgemeinschaft, DFG project number Ts 17/2-1. CJHK would like to extend his gratitude to Rien van de Weijgaert, Jakob van Bethlehem, Sven de Man en Marcel Kruip for proofreading the manuscript and valuable discussion. We also thank the anonymous referee for useful comments on the manuscript.
References
- Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Delone, B. N. 1934, Bull. Acad. Sci. USSR: Classe Sci. Mat, 793, 7 [Google Scholar]
- Du, Q., Faber, V., & Gunzburger, M. 1999, SIAM Rev., 41, 637 [Google Scholar]
- Edelsbrunner, H. 2006, Geometry and topology for mesh generation, 1st edn. (Cambridge University Press) [Google Scholar]
- Icke, V., & van de Weygaert, R. 1987, A&A, 184, 16 [NASA ADS] [Google Scholar]
- Iliev, I. T., Ciardi, B., Alvarez, M. A., et al. 2006, MNRAS, 371, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Lloyd, S. P. 1982, IEEE Transactions on information theory, IT-28, No 2, 129 [Google Scholar]
- Mellema, G., Iliev, I. T., Alvarez, M. A., et al. 2006, New Astron., 11, 374 [Google Scholar]
- Mihalas, D., & Weibel Mihalas, B. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press) [Google Scholar]
- Okabe, A., Boots, B., Sugihara, K., Chiu, S. N., & Kendall, D. G. 2000, Spatial tessellations: concepts and applications of Voronoi diagrams, 2nd edn. (Wiley) [Google Scholar]
- O'Rourke, J. 2001, Computational Geometry in C, 2nd edn. (Cambridge University Press) [Google Scholar]
- Paardekooper, J.-P., Kruip, C. J. H., & Icke, V. 2010, A&A, 515, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ritzerveld, J., & Icke, V. 2006, Phys. Rev. E, 74, 026704 [NASA ADS] [CrossRef] [Google Scholar]
- Ritzerveld, N. G. H. 2007, PhD Thesis, Leiden Observatory, Leiden University [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics, ed. G. B. Rybicki, & A. P. Lightman [Google Scholar]
- Schaap, W. E., & Van de Weygaert, R. 2000, A&A, 363, L29 [NASA ADS] [Google Scholar]
- Vedel Jensen, E. B. 1998, Local Stereology, 1st edn. (World Scientific) [Google Scholar]
- Voronoi, G. 1908, J. Reine Angew. Math., 134, 198 [CrossRef] [Google Scholar]
Footnotes
- ... test
![[*]](/icons/foot_motif.png)
- This is possible, however, if the direction-conserving transport to be introduced in Sect. 2.5.3 is used. Alternatively, several instances of the same simulation with a different random seed for the grid construction can be averaged to obtain error estimates as well.
- ... it
![[*]](/icons/foot_motif.png)
- In our implementation, we use a single frequency bin and an effective cross-section such that the mean free path depends on the number density and the point-to-point distance only.
- ... directionality
![[*]](/icons/foot_motif.png)
- As we see in Sect. 4.1, anisotropic scattering processes can be simulated straightforwardly by assigning weights to the outgoing edges so that more radiation is transported in the appropriate directions.
- ...sweep
![[*]](/icons/foot_motif.png)
- Although in our current implementation each photon takes exactly one step per sweep, this need not in general be the case.
- ... respectively
![[*]](/icons/foot_motif.png)
- Another way to look at this is that, for an isotropically emitting source, the number of nuclei that receive radiation must scale as the square (cube) of the travelled distance for two (three) dimensions.
- ... angles
![[*]](/icons/foot_motif.png)
- DCT can thus be viewed as ballistic transport with complete memory of direction.
- ... random
![[*]](/icons/foot_motif.png)
- The orientation might be correlated with the direction of the gradient but we neglect this at the moment because it would only influence our results to second order.
- ... small
![[*]](/icons/foot_motif.png)
- We emphasize the discrete nature of this
derivative by noting that
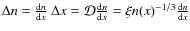 etc.
etc.
- ... everywhere
![[*]](/icons/foot_motif.png)
- It may surprise the reader that
values for
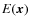 and
and 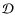 are taken to be local, while
the argument seems to involve a domain in which these values could
change. What happens is that we adopt the local
values for the whole domain in
Eq. (18).
are taken to be local, while
the argument seems to involve a domain in which these values could
change. What happens is that we adopt the local
values for the whole domain in
Eq. (18).
- ... weights
![[*]](/icons/foot_motif.png)
- We used icosahedron weights in this case but this choice does not influence the results.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg35.png)
|
Figure 1: Voronoi tessellation of the plane (solid lines). Each cell contains all points that are closer to its nucleus (indicated by a dot) than to any other nucleus. The corresponding Delaunay triangulation is shown in dashed lines. Note: only visible nuclei are included in the triangulation. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: Three principal means of transport supported in SimpleX. Left panel: diffuse transport, photons from the incoming edge (not shown) are distributed outward along all edges (including the incoming edge). Central panel: ballistic transport, photons are transported along the D edges directed most forward with respect to the incoming direction. Right panel: direction-conserving transport, photons (indicated with the dotted arrows) are transported as in ballistic transport but their direction is stored indefinitely in a global set of solid angles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg47.png)
|
Figure 3: Example of decollimation in the plane for five ballistic steps. The arrow indicates the initial influx of photons. According to the ballistic transport mechanism, photons are transported along the D most forward edges with respect to the incoming direction. The colour coding is as follows: with every step the photons acquire a colour that is less red and more blue. As the angle between adjacent edges is large in 2D (60 degrees on average), the bundle loses track of its original direction in only a few ballistic steps. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg48.png)
|
Figure 4:
Fractions of photons (contours) with deflection angle within 45 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg50.png)
|
Figure 5:
Shadow behind a dense filament irradiated by ionising radiation
(indicated as a black dot). The hydrogen number density is plotted
logarithmically in greyscale and ranges between
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg78.png)
|
Figure 6: Schematic example of a nucleus and its edges subject to a gradient in the number density of nuclei in the positive x-direction. More edges point toward the overdense region (along the gradient). If every edge were to transport an equal number of photons to neighbouring nuclei, the anisotropy of outgoing edges would produce an unphysical net flow along the gradient indicated by the arrow, which is the vector sum of the edges scaled down by roughly a factor of three. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=9cm,clip]{13439f7.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg106.png)
|
Figure 7: Normalised distribution
of angles between the incoming direction and the vector sum of the
(three) most forward pointing edges (solid line) and the separate most
forward edges (dotted, dashed and dot-dashed lines) for a homogeneous
distribution of nuclei. The distribution of the most forward edges
added is shown as the long dot-dashed line with label ``Added'' and is
related to the decollimation effect. The standard deviation (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg113.png)
|
Figure 8:
The projected step-size in the x-direction
as a function of sweeps together with a least squares fit for the
unweighted ballistic transport (solid line) and with ballistic weights
as described in Sect. 4.2 (dashed line). A region indicating unit standard deviation is shaded in grey around the markers. Error bars correspond to
|
| Open with DEXTER | |
| In the text | |
| |
Figure 9:
Geometry of radiation travelling perpendicular to the gradient direction. The deflection angle toward the underdense region,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13439f10.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg134.png)
|
Figure 10: Solid angles for two edges in the case of the Voronoi weighting scheme (cell 3) and the icosahedron weighting scheme (cell 1). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{13439f11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg138.png)
|
Figure 11: Geometry of the COG weighting procedure. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f12.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg140.png)
|
Figure 12:
Fraction of edges, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f13.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg144.png)
|
Figure 13: Normalised distribution
of angles between the incoming direction and the vector sum of the
(three) most forward pointing edges (solid line) and the separate most
forward edges (dotted, dashed and dot-dashed lines) for a homogeneous
distribution of nuclei with ballistic weights. The distribution of the
most forward edges added is shown as the long dot-dashed line and
labeled ``Added''. The standard deviation (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f14.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg147.png)
|
Figure 14: Intensity-weighted position of a photon cloud released in the centre of a simulation domain with a linear gradient in the number denisty of nuclei as a function of the number of sweeps. Results obtained with SimpleX are shown with filled symbols and results obtained by the Monte Carlo experiments are indicated with open symbols. We use triangles and squares in the corrected and uncorrected case, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f15.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg151.png)
|
Figure 15:
Normalised standard deviation of the intensity-weighted positions of a
photon cloud expanding in a distribution of nuclei with small-scale
gradients with and without weights (thick and thin solid lines,
respectively) and the analytical expectations according to Eq. (21) (dashed line). A dotted line at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13439f16.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg153.png)
|
Figure 16:
Mean angular directionality of a photon cloud as a function of the
number of sweeps. In this simulation, a linear gradient in the density
of nuclei is present and the angle is measured relative to the
direction of the gradient, so smaller values of the angle point toward
the denser region. As expected, the direction-conserving implementation
of SimpleX (as described in Sect. 2.5.3,
indicated by filled squares) has no long-term loss of directionality,
although it shows some oscillatory behaviour that dampens with time.
Ballistic transport with one edge (open triangles) shows a deflection
towards larger angles for number of sweeps of order
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{13439f17.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13439-09/Timg165.png)
|
Figure 17: Cut through a cosmological density field ( left panel; colours indicate number density in logarithmic scale) sampled with 105 points using the sampling function of Eq. (37) ( middle panel) and Eq. (38) ( right panel) with the parameters obtained from analysis of the underlying density field. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.