EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 515 (June 2010) A&A, 515 (2010) A5 Full HTML
Free Access
Issue
A&A
Volume 515, June 2010
Article Number A5
Number of page(s) 10
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200913317
Published online 28 May 2010
A&A 515, A5 (2010)

High resolution X-ray spectroscopy of SN 1987 A: monitoring with XMM-Newton

R. Sturm1 - F. Haberl1 - B. Aschenbach1 - G. Hasinger1,2

1 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
2 - Max-Planck-Institut für Plasmaphysik, Boltzmannstraße 2, 85748 Garching, Germany

Received 17 September 2009 / Accepted 1 February 2010

Abstract
Context. The ongoing propagation of the supernova blast wave of SN 1987 A through its inner circumstellar ring has caused a drastic increase in X-ray luminosity in the past few years, which has allowed detailed high resolution X-ray spectroscopy to be performed with the Reflection Grating Spectrometer.
Aims. We report the results of our XMM-Newton monitoring of SN 1987 A, which may be used to follow the detailed evolution of the arising supernova remnant.
Methods. The fluxes and broadening of the numerous emission lines measured in the dispersed spectra provide information about the evolution of the X-ray emitting plasma and its dynamics. These were analyzed in combination with the EPIC-pn spectra, which allow a precise determination of the higher temperature plasma. We modeled individual emission lines and fitted plasma emission models.
Results. For observations between 2003 and 2007 in particular, we detect significant evolution in the plasma parameters and a deceleration of the radial velocity in the lower temperature plasma regions. We detected (at 3$\sigma$-level) an iron K feature in the coadded EPIC-pn spectra.
Conclusions. By comparing with Chandra grating observations in 2004, we observe a clear temporal coherence of the spectral evolution and the sudden deceleration of the expansion velocity detectable in X-ray images $\sim$6100 days after the explosion.

Key words: ISM: supernova remnants - supernovae: general - supernovae: individual: SN 1987 A - X-rays: general - X-rays: stars - shock waves

1 Introduction

The circumstellar ring system around SN 1987 A was ejected by the progenitor star approximately 20 000 years before the supernova explosion. About 10 years after the explosion, the blast wave started to propagate through the inner ring, causing compression, heating, and ionization of its matter. At that time, bright unresolved regions, so-called hot spots, appeared all around the ring in HST images (Lawrence et al. 2000), and the rather linear increase in the soft X-ray band brightness, observed with ROSAT since 1992 (Beuermann et al. 1994; Hasinger et al. 1996), was followed by an exponential brightening, which was monitored with XMM-Newton, Chandra, Suzaku, and Swift. In the recent years, some flattening of the flux increase is seen (Sturm et al. 2009, and references therein for the individual fluxes).

The X-ray spectra are interpreted as thermal emission composed of a lower temperature component ($\sim$0.5 keV) and a higher temperature component ($\sim$2.5 keV). Deep Chandra grating observations have allowed the bulk gas velocity to be inferred from spectral line deformation. Surprisingly these values were lower than the velocities expected from the plasma temperatures. This suggests that reflected shocks are contributing, in additional to the ``normal'' forward shock (Zhekov et al. 2006; Dewey et al. 2008; Zhekov et al. 2009,2005). The expansion velocity derived from Chandra X-ray images is even higher. About 6100 days after the explosion, a sharp deceleration to 1600-2000 km s-1 was observed (Racusin et al. 2009).

Shocks transmitted into denser regions of the ring have slower shock wave velocities and therefore can be responsible for the low temperature component. This interpretation is supported by the morphology seen in optical and X-ray images (McCray 2007), as well as the similar evolution of the soft X-ray flux (0.5-2.0 keV) and the evolution of highly ionized optical emission lines from the hot spots (Gröningsson et al. 2006). This emission might be caused by even slower radiative shocks.

Renewed radio emission of SN 1987 A was detected in July 1990 (Turtle et al. 1990). A continuously rising flux and increasing source radius has been observed by the ATCA since then (Ng et al. 2008; Gaensler et al. 2007). The increase in the intensity of the radio light curve matches the evolution in the hard X-ray flux (2-10 keV) quite closely (Aschenbach 2007; Park et al. 2005), thus the synchrotron radio emission may originate in the hot thermal plasma between the forward and reverse shock and a fraction of the hard X-ray flux may also have a non-thermal origin. Broad H${\alpha}$ and Ly${\alpha}$ lines are indicative of reverse shocks (Heng et al. 2006; Michael et al. 2003).

This study reports the yearly XMM-Newton monitoring observations of SN 1987 A between January 2007 and January 2009, and one prior observation from May 2003, which enabled the detailed plasma evolution to be inferred. We measured light curves and the widths of individual emission lines and analyzed the spectral plasma evolution by fitting thermal plasma emission models.

Table 1:   XMM-Newton observations of SN 1987 A and data selection.

2 Observations and data reduction

Since January 2007, we have performed yearly monitoring of SN 1987 A using XMM-Newton (Jansen et al. 2001). Including an earlier observation from May 2003, four observations with an exposure each exceeding 100 ks were performed. A summary is listed in Table 1. Earlier observations and the May 2003 data were previously analyzed by Haberl et al. (2006), and Heng et al. (2008) evaluated the Jan. 2007 observation concentrating on the elemental abundances. In this study, we use consistent models to analyze two new observations in combination with the previous data, to obtain the evolution of the X-ray spectra as seen by the Reflection Grating Spectrometer (RGS, den Herder et al. 2001). To extend the X-ray band to 10 keV, we also included the EPIC-pn (Strüder et al. 2001) spectra in our analysis.

We used XMM-Newton SAS 8.0.0[*] to process the data. For the extraction of EPIC-pn spectra, single-pixel events in good time intervals (GTIs) with low background (threshold at 8 cts s-1 arcmin-2) were selected from the source region, centered on SN 1987 A, and a point source free background region, each with a radius of 30 $^{\prime\prime}$. The RGS spectra were obtained using rgsproc, and GTIs (RATE < 2.0) were used to select low background intervals. In the 2003 observation, the Honeycomb nebula is located on the dispersion axis. Using the intrinsic energy resolution of the RGS Focal Plane Camera CCDs, counts from the Honeycomb nebula are excluded. For the other three observations, the Honeycomb nebula lies at the cross-dispersion axis at the very rim of the CCDs. By comparing our background spectra with the RGS background model (created by rgsbkgmodel), we find no significant contribution from the Honeycomb nebula to the background spectra.

To obtain a detailed spectrum of $\sim$438 ks exposure, the RGS spectra of the four observations were added with rgscombine, which also calculates combined response files. To allow reliable application of the $\chi$-statistics, all spectra were binned to obtain at least 30 (RGS) or 20 (EPIC-pn) counts per bin. Owing to the high quality statistics of the RGS-spectra, a binning of 30 cts/bin does not influence most emission lines, which have far more than 30 cts in most bins. Thus this binning has no influence on the measured line parameters.

\begin{figure} \par\includegraphics[width=6.05cm,angle=-90,clip]{rgs-spec-0.ps}\... ...pace*{1.5mm} \includegraphics[width=6.3cm,angle=-90]{rgs-spec-3.ps} \end{figure} Figure 1:

The RGS1 (black) and RGS2 (red) spectra of SN 1987 A observations in 2003, 2007, 2008, and 2009.

Open with DEXTER

Table 2:   Identified lines in the RGS spectra.

3 Spectral analysis

Spectral fitting was performed using XSPEC (Arnaud 1996) version 12.5.0x. The errors are given for certain $\Delta \chi^2$ ranges. In general, $\Delta \chi ^2=2.71$ is associated with the 90% confidence range for one parameter of interest.

\begin{figure} \par\includegraphics[angle=-90,width=17.5cm,clip]{sumspec1a.ps}\p... ....ps}\par\includegraphics[angle=-90,width=17.5cm,clip]{sumspec2.ps} \end{figure} Figure 2:

Coadded RGS1 (black) and RGS2 (red) spectra from all 4 observations of SN 1987 A together with the best-fit empirical model (green) and the absorbed bremsstrahlung continuum (blue). The line labels mark the strongest lines expected from the two component vpshock model at the best-fit model energy of the line center.

Open with DEXTER

3.1 Identification of emission lines

Since the RGS spectra of SN 1987 A are dominated by emission lines (see Fig. 1), we first identified the individual lines using the coadded spectra. We constructed an empirical model and fitted it to the combined RGS1 and RGS2 spectra simultaneously.

As a quasi-continuum, we used a thermal bremsstrahlung model with absorption, which is formally a good approximation to the observed continuum, that also includes radiative recombination and two photon decays. This component also represents various weak emission lines, which are not resolved in the RGS spectra. A constant factor was allowed to vary between the two RGS spectra. We first fitted the strong lines with Gaussian profiles. The high statistical quality of the summed spectrum required the introduction of additional weak lines where we noticed residua. Our final model comprises 53 lines, which are listed in Table 2. Fitted to the coadded spectra, all lines have a normalization inconsistent with 0 for $\Delta \chi ^2=2.71$, except for the intercombination lines of helium-like N and Mg. For line complexes, the line energies were combined to a single value based on their relative ratios in ATOMDB 1.3.1[*], and the line widths were linked. For weak lines, it was not possible to fit individual line widths, thus we coupled them with the closest strong line. We obtain a best fit with $\chi^2/{\rm d.o.f.} = 1843/1465$. The summed RGS spectra are shown in Fig. 2 with the best-fit model and the bremsstrahlung quasi-continuum ( kT = 402-6+5 eV). The line labels mark the best-fit energy of the fitted Gaussian model and indicate the strongest emission line expected from plane-parallel shocked plasma emission codes (see below) at this energy. With these identifications, we obtain line shifts consistent with a systemic redshift of $349\pm24$ km s-1(see Fig. 3).

The high statistical quality of the coadded RGS spectra allowed us to investigate emission lines in unprecedented detail, e.g. the N VI helium-like triplet at $\sim$0.42 keV is clearly seen in the summed spectra (cf. Fig. 2). Other examples of emission line complexes are shown in Fig. 4. Next to the N VII Ly$_{\alpha }$ (at 0.50 keV) line, we found an additional line at slightly lower energy (see Fig. 4), most likely N VI He$_{\beta }$, which is the strongest line at this position in the plasma codes. But argon lines also contribute here, which may be the cause of the higher line shift. In previous analyses with lower statistics, this line likely was blended with the $\sim$10 times more luminous N VIII Ly$_{\alpha }$ line. The line shape at the energy of the O VIII Ly$_{\beta }$ (0.77 keV) line is inconsistent with a Gaussian profile, and the line width for a single Gaussian is significantly larger than found for the surrounding lines (2 eV versus 0.25 eV). Plasma models suggest that two iron line transitions contribute at slightly lower energies, which were included in our model. The shape of the Ne IX triplet ($\sim$0.91 keV) is also not reproducible using three Gaussians. Here Fe XIX (917.1 eV) may contribute to the flux, although this line is not expected to be strong on the basis of emission codes.

For strong lines in the summed spectra, we measured line widths that are inconsistent with zero within a confidence range of $\Delta \chi ^2=2.71$, which demonstrates that line broadening can be reliably detected with RGS. A trend of increasing width with rising energy is also seen. A fit of an energy-dependent line width $\sigma(E)= \sigma_0 (E/1~{\rm keV})^{\alpha}$ yields $\sigma_0=(1.35\pm0.36)$ eV and $\alpha=2.05_{-0.72}^{+0.66}$. The power law index agrees well with the Chandra LEGT 2007 results (Zhekov et al. 2009).

A clear evolution in emission line ratios is evident, for example by comparing the nearly absent Fe XVII lines at $\sim$0.72 keV in 2003 to the strong lines seen in the later observations (see Fig. 1). The Ne X Ly$_{\alpha }$ (1.02 keV) flux also increases relative to the Ne IX triplet ($\sim$0.91 keV). Therefore, in a second step, we fitted the empirical model to the spectra of the individual observations to follow the evolution of the individual emission lines in a consistent way. Only parameters that were expected to have a time dependence, i.e., the line fluxes and the parameters of the bremsstrahlung continuum, were allowed to vary. The absorption as well as the central energy and width of the Gaussians were fixed to the values obtained from the summed spectra. Here these values were determined more precisely than in the individual spectra. Using the RGS spectra with the highest quality statistics (i.e., the 2009 data), we compared line widths inferred when fixed in the individual fits with those for when the line widths were allowed to vary during the fitting. We found that 20 of 21 line widths are consistent. Our time-dependent analysis of the line widths is described in Sect. 3.2, in which we used plasma models and assumed a power-law dependence. The line fluxes for both fixed and variable widths are also consistent and we conclude that the fixed line widths do not influence the derived line fluxes.

The individual line fluxes are listed in Table 2, and light curves for prominent oxygen and neon lines are shown in Fig. 5. We note that the temperature of the quasi-bremsstrahlung continuum shows a trend of an increase ( $ \rm 254_{-40}^{+64}$, $\rm 413_{-21}^{+30}$, $\rm 436_{-19}^{+26}$, and $\rm 405_{-14}^{+17}$ eV for the 2003, 2007, 2008, and 2009 observation, respectively), but emphasize, that this component represents not only bremsstrahlung.

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{lineshift.ps} \end{figure} Figure 3:

Line shifts according to the empirical model. The horizontal line shows the best fit for a systemic redshift. Errors are for $\Delta \chi ^2=2.71$ confidence range.

Open with DEXTER

We also searched for a Fe K line complex between 6.4 and 6.7 keV in a summed EPIC-pn spectrum of the three observations between 2007 and 2009, where we have superior statistics in this energy band. To characterise the feature, we fitted a bremsstrahlung continuum ( $kT=(3.3\pm 0.5)$ keV, $EM=(1.3\pm0.3)\times 10^{58}$ cm-3) and one Gaussian in the 4.0-10.0 keV band.

The best-fit Gaussian central energy is ( $6.57~\pm ~0.08$) keV with a $\sigma$-width of 62.7-62.7+141 eV and the line flux is $7.3_{-4.2}^{+5.7} \times 10^{-7}$ photons cm-2 s-1. Heng et al. (2008) noted a possible detection in the 2007 data, but the individual EPIC-pn and the summed EPIC-MOS spectra do not have sufficient statistics for a detailed analysis. With increasing ionization, the centroid energy of the Fe K line complex is shifted from the 6.4 keV fluorescent line via various ionization stages to the He-like emission of Fe XXV at $\sim$6.7 keV. To account for this effect, we fitted an exposure-weighted sum of the plane-parallel shock model derived for the high temperature component in Sect. 3.2, but used NEI-model version 1.1, which also contains Fe-ions that are less ionized than He-like ions. We allowed a constant factor to account for the normalization and measured the flux of the iron K lines from the shocked plasma to be $4.9\times 10^{-7}$ photons cm-2 s-1. As can be seen in the right panel of Fig. 4, the resulting line shape does not explain the observed feature on the lower energy side. We investigated the possibility of an additional line with zero width (also shown in Fig. 4). The best-fit model values are $4.7\pm3.3 \times 10^{-7}$ photons cm-2 s-1 at a central energy of $\rm 6.48_{-0.12}^{+0.17}$ keV.

\begin{figure} \par\resizebox{18cm}{!}{\includegraphics[clip=,width=6.0cm,angle=... ...residua.ps} \includegraphics[clip=,width=6.0cm,angle=-90]{FeK3.ps}} \end{figure} Figure 4:

Examples for emission line complexes from the summed spectra: N VII Ly $_{\alpha }$, O VIII Ly$_{\beta }$, and the Ne IX triplet as seen by the RGS1 (black) and RGS2 (red). The empirical model and its components are also plotted. In the right panel, an indication of a Fe K feature is seen in the summed EPIC-pn spectrum of the newer three observations. A sum of the high temperature component plane-parallel shock models derived from the individual observations (black) is compared with a model containing an additional Gaussian (red). Horizontal axes: channel energy in keV; vertical axes: counts s-1 keV-1.

Open with DEXTER

\begin{figure} \par\resizebox{18cm}{!}{\includegraphics[clip=,width=6cm,angle=-9... ...ad \includegraphics[clip=,width=6cm,angle=-90]{lineratios-Ne.ps}} \end{figure} Figure 5:

The lower panels show the light curves of various emission lines with fluxes in 10-5 photons cm-2 s-1. The upper panels show the corresponding line ratios (not absorption corrected). The G-ratio is defined as the helium like line flux ratio of (f+i)/r. Overlapping data points are shifted by 10 days for clarity.

Open with DEXTER

3.2 Plasma evolution

To probe the physical parameters of the X-ray emitting plasma, we fitted plasma emission models. In neither XMM-Newton (e.g., Heng et al. 2008) nor Chandra (e.g., Zhekov et al. 2006) observations was the spectrum described well by just one emission component. Zhekov et al. derived a bimodal temperature distribution in differential emission measure, peaking at $\sim$0.5 keV and $\sim$2.5 keV. A non-thermal component might also contribute to the hard component (Park et al. 2005). We note that the emission lines in the XMM-Newton spectra can also be described by the sedov-model in XSPEC, which has a temperature distribution given by the Sedov self-similar solution for SNRs. Here a power law is necessary to fit the high energy tail (cf. Fig. 6).

The abundances of the sedov component are significantly higher than normally found in X-ray analyses, thus we doubt the physical correctness of this component, but the model demonstrates the possible contribution of a non-thermal component with a normalisation of up to $(1.44\pm0.03) \times 10^{-3}$ photons keV-1 cm-2 s-1 at 1 keV for a power law index $\Gamma=3.00\pm0.02$ (for the 2009 observation). Formally, the sedov+powerlaw model provides the closest fit to the data (e.g., for the 2009 observation: $\chi^{2}_{\rm red} = 1.35$ versus 1.48). However, we decided to use the approximation of a plane-parallel shock structure at two temperatures, as commonly adopted in the literature, since the sedov model is numerically slow and the RGS does not provide high resolved lines above 2.0 keV.

For a precise determination of the high temperature plasma component, we extended the energy band to 10 keV by fitting the RGS1, 2 and EPIC-pn spectra simultaneously, as it is successfully applied during calibration (Plucinsky et al. 2008).

A comparison of the empirical model fitted to the 2009 RGS data and to a dataset that also contains the EPIC-pn spectrum in the 0.2-2.0 keV energy range indicates again that 20 of 21 line widths were consistent. Because of the lower energy resolution of EPIC-pn the line widths are determined by the RGS spectra. We found inconsistent fluxes of the helium-like N VI and N VII Ly$_{\alpha }$ line between the EPIC-pn and RGS spectra. This is probably caused by calibration problems in the modeled redistribution of the EPIC-pn response at low energies. Thus we decided to limit the EPIC-pn band to 0.53-10 keV in this study. In future studies, the 0.2-0.53 keV EPIC-pn band with advanced calibration will provide additional information.

\begin{figure} \par\resizebox{17.5cm}{!}{\includegraphics[angle=-90]{rgs+pn-3-2vpshock.ps} \includegraphics[angle=-90]{rgs+pn-3-sedov+po.ps}} \end{figure} Figure 6:

The XMM-Newton RGS1 (black), RGS2 (red) and EPIC-pn (green) spectra of the 2009 observation. Plotted is also a model containing two plane-parallel shock components ( left panel) and a sedov+powerlaw model ( right panel).

Open with DEXTER

To infer the plasma evolution, we fitted a two-component plane-parallel shock model (vpshock, Borkowski et al. 2001) using NEI-version 2.0 and an ionization timescale range $0<\tau<\tau_{\rm u}$. In a similar way to Zhekov et al. (2009, and references therein), the chemical composition of the plasma component was assumed to be constant in time and all model abundances were fitted with the exception of He (set to 2.57), C (0.09), Ar (0.54), Ca (0.34), and Ni (0.62), which produce no significant features in our data. The photoelectric absorption by the Galactic interstellar medium was set to be $N_{\rm H}$ = 6  $\times~ 10^{20}$ cm-2, whereas the LMC column density with abundances set to be 0.5 for metals was a free parameter. The abundances of the absorption and emission components are given according to the abundance table of Wilms et al. (2000), which produced a slightly better fit ( $\chi^{2}_{\rm red} = 1.32$ vs. 1.38) than the abundances of Anders & Grevesse (1989). The main impact was on the absorption, which influences the continuum emission and line ratios. We found no impact on the main results of our study. A constant factor was allowed to vary to account for calibration differences between the individual instruments. We modified the shock model line widths to be described by the power law function mentioned above, thus our custom version of the vpshock model contains two more parameters ($\sigma _0$, ${\alpha}$).

We fitted the four XMM observations (12 spectra) simultaneously, resulting in a $\chi^2/{\rm d.o.f.}=5400/4084$. As best-fit model parameters, we obtained for the LMC absorption $N_{\rm H}$= $(2.23\pm0.02)\times 10^{21}$ cm-2, for the systemic velocity $v_{\rm 87A}=326_{-16}^{+13}$ km s-1, and for the instrument-dependent constants $c_{\rm RGS2}=1.03\pm0.01$ and $c_{\rm pn}=1.04\pm0.01$ (relative to $c_{\rm RGS1}=1$). For the time-dependent parameters, we refer to Table 3 and Fig. 7, and for the abundances see Table 4.

Table 3:   Results from the VPSHOCK+VPSHOCK model fits.

Table 4:   Abundances of SN 1987 A.

3.3 Integrated flux

To derive the detected flux in an analogous way to Haberl et al. (2006) and Heng et al. (2008), the vpshock+vpshock model was fitted separately to the most recent two EPIC-pn spectra. The inferred fluxes do not depend strongly on the individual model parameters. The fluxes for various sub-bands are given in Table 5.

Table 5:   EPIC-pn fluxes.

\begin{figure} \par\resizebox{17cm}{!}{\hspace*{2mm}\includegraphics[clip=,width... ...lip=,width=2.4cm,angle=-90]{vpshock-evolution-8.ps}} \vspace*{-2mm} \end{figure} Figure 7:

Time evolution of the plasma variables: horizontal axes are days after explosion. T1,2 is given in keV, EM1,2 in 1058 cm-3, $\tau _{1,2}$ in 1011 cm-3 s, and $\sigma _0$ in eV.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{linewidth-sumspec-new.ps} \vspace*{-2mm} \end{figure} Figure 8:

Squares denote the bulk gas velocity corresponding to the emission line broadening derived from the Gaussian model fitted to the coadded RGS spectra. Errors are for $\Delta \chi ^2=1$. The solid black line shows the best-fit power-law function to these data points. The other (red) lines show the best-fit power-law functions as derived with the modified vpshock model from the individual spectra. For clarity, the errors are not plotted. Note for the 2003 data in particular the errors are large (cf. Fig. 7 right panels). The horizontal blue lines indicate the post-shock gas velocities produced by strong adiabatic shocks that heat the plasma to a temperatures of kT= 0.5 and 2.5 keV after thermal equilibration.

Open with DEXTER

4 Discussion

We have monitored SN 1987 A with XMM-Newton and obtained RGS spectra of unprecedentedly high statistical quality. We have analyzed individual line shapes and fluxes with an empirical model and applied physical models to a combined set of RGS and EPIC-pn spectra.

The line shifts derived from the empirical model ( $349\pm24$ km s-1) and the plasma codes ($326\pm16$ km s-1) are consistent with each other. In terms of the RGS wavelength scale calibration, the line shifts are consistent with the systemic velocity derived from optical SN 1987 A observations ( $286.74\pm0.05$ km s-1, e.g., Gröningsson et al. 2008).

Line broadening is detected significantly in the RGS spectra. To obtain a conversion factor for the measured line widths and the bulk gas velocity, we convolved the emission spectrum of a cylindrically expanding ring at an inclination of 45$^\circ$and a temperature of kT = 0.5 keV in a bulk gas velocity range of $0 <v_{\rm bulk} < 1000$ km s-1 with the RGS response function and fitted a Gaussian to the resultant line profile. In this simulation, we obtained $v_{\rm bulk}=0.80 \times \Delta v$ (FWHM). For a similar analysis, we refer to Michael et al. (2002).

As seen in Fig. 8, $v_{\rm bulk}$ is most accurately described by the profiles of the two strongest lines N VII Ly$_{\alpha }$ and O VIII Ly$_{\alpha }$. The broadening of the former line is 518-150+130 km s-1 FWHM for a statistical confidence level with $\Delta \chi ^2=2.71$. Since the instrumental line broadening is somewhat higher, the uncertainty of the RGS line spread function (lsf) causes a similar error. A 10% uncertainty in the lsf ( $\Delta \lambda_{\rm lsf} \sim 0.07 ~\AA\ $ FWHM) infers an uncertainty range of 400-600 km s-1 FWHM. But recent studies indicate that the current lsf-model overestimates the instrumental line width (Jelle Kaastra, private communication). In our modeling of the RGS lines, the extent of the source ($\sim$ $1\hbox{$.\!\!^{\prime\prime}$ }5$) is negligible. For a thermally equilibrated plasma, as expected for the shock velocity range of the lower temperature component (Rakowski 2005), the thermal line broadening does not contribute significantly (e.g., 133 km s-1 FWHM for nitrogen at kT=0.5 keV). We also found no influence to be caused by the two unresolved Lyman transitions by modeling the line with two Gaussians, and other unresolved lines should not contribute significantly either.

The line width of the N VII Ly$_{\alpha }$ line indicates a bulk velocity of $(414\pm120)$ km s-1. In the case of gas shocked by a strong adiabatic shock wave and thermal equilibration, we found that $v_{\rm sh}= 4/3 v_{\rm bulk} = 552$ km s-1 and inferred a post shock temperature of $ kT= 3/16~\mu {\rm v}_{\rm sh}^2 =0.435_{-0.22}^{+0.25}$ keV. We assumed an adiabatic index of $\gamma = 5/3$ and an average molecular weight of $\mu = 0.73m_{\rm p}$ according to the abundances of the inner ring. As for the O VIII Ly$_{\alpha }$ line, we found that kT=0.75-0.36+0.22 keV. Thus these line widths are consistent with the temperatures derived from the plasma models.

The bulk gas velocities derived from these two lines are also consistent with the result of the Chandra LETG observation in 2007 ($\sim$360 km s-1, Zhekov et al. 2009). However the bulk gas velocities as a function of line energy that can be described globally by power laws, are in general higher for the RGS derived values than the values deduced from the Chandra spectra (e.g., by a factor of $\sim$2 at 1 keV). Some of this difference is caused by thermal broadening, which contributes to the XMM-Newton derived line widths, but not to the Chandra values, which are based on spatial spectral deformation (i.e., the bulk gas velocity is inferred from the difference in the line broadening between the two grating arms). But this effect would only become significant for plasma out of thermal equilibrium. The radial velocity distribution of the shocked plasma might also contribute differently to the line broadening seen in the RGS and dispersed Chandra spectra, but it cannot fully explain the large difference. We believe that most of the difference is caused by both the different modeling methods and calibration differences.

With our modified plasma emission code, we can also investigate the evolution of the line broadening and we can reduce the artificial broadening due to blended lines. The increase in ${\alpha}$ indicates that the velocity of regions with a lower temperature decreases relative to the regions with higher temperature. The RGS-derived line widths are determined most accurately in the 0.5-1.0 keV band, where we have the highest quality statistics and strong emission lines. Conspicuous is the sudden decrease of the line broadening for this energy band between 2003 and 2007, indicating a deceleration in the bulk velocity. Although the statistics of this observation are of low quality, a comparison with a line broadening based on the function derived from the empirical model shows that the individually derived energy dependence of the line broadening is reliable (f-test probability $1.4\times10^{-4}$). From 2007 to 2009, the XMM-Newton derived line widths had a rather constant line width, similar to those of the Chandra grating observations in 2004 and 2007. But from the HETG observation in 1999, Michael et al. (2002) report line widths corresponding to a post-shock plasma velocity of $\sim$2500 km s-1. Thus the line broadening must have decreased in-between the XMM-Newton observation (5918 SN days) and the Chandra LETG sequence ($\sim$6400 SN days) by $\sim$50% at 1 keV. We note that during this time interval a sudden deceleration of the expansion is seen in X-ray images around day 6100 (Racusin et al. 2009). We emphasize that the spectra in 2003 might be more complex than assumed by adopting two shock components, possibly containing a more complex mixture of radial velocity and temperature components.

The derived plasma parameters of the plasma emission model show a clear evolution between 2003 and 2007, and the emission measure ratio EM2/EM1 decreases. During this time, the soft flux increases dramatically. In later observations, the EM ratio remains quite constant with a tendency to increase.

We also observed the ongoing ionization of the plasma. This causes e.g., the increase in the [Ne X Ly$_{\alpha }$]/[Ne IX He r] flux ratio by $\sim$26% during the last two observations. The upper limit to the ionization timescale range $\tau_{\rm u}$ steadily increases for both plasma components. For the lower temperature plasma component, $\tau_{{\rm u,}1}$ indicates some upturn after the first observation, which could be caused by an increasing density. A fit of a linear function to the last three values of $\tau_{{\rm u,}1}$ (see Fig. 7) yields an ``average'' density of $n_1= (3.24~\pm~0.64)$  $\times~ 10^{3}$ cm-3. For the high temperature component, no evolution in density is observed and a similar fit yields $n_2= (4.8~\pm~1.4)$  $\times~ 10^{2}$ cm-3. The ratio of the emission measures of the low to high temperature components is roughly constant with a volume ratio of $\sim$7.5.

The densities derived from the unshocked gas in the optical are $6\times10^{3}$ cm $^{-3}<n<3\times10^{4}$ cm-3 for the ring and $\sim$102 cm-3 for the extended nebula (Lundqvist & Fransson 1996). A strong adiabatic shock wave increases these densities by a factor of four. Our values are indicative of less dense regions in the ring and suggest that the surrounding nebula is the origin of the X-rays. The vpshock model assumes a ionization time distribution that is linear in emission measure, which is clearly not true for SN 1987 A. A complex density distribution and the effects of radial expansion influence the derived densities. However, these values are not consistent with those inferred from the modeling of the light curve (Aschenbach 2007; Haberl et al. 2006), and should be interpreted with care.

The temperature of the soft plasma component shows a strong increase between the first two observations, and a slight increase in the later ones. From Chandra observations, a rising temperature of this component is derived (Park et al. 2006). Between 2004 and 2007, Zhekov et al. (2009) report a nearly constant temperature. With RGS we can see an ongoing small increase in the temperature of the soft component. However, a decrease caused by the deceleration of the shock wave and adiabatic expansion of the shocked plasma is expected, which is seen in the high temperature component. An increase is possible, if regions with slightly higher temperatures contribute more to the emission measure with time, e.g., because of the more rapidly rising volume of these regions. But the effects of incomplete thermal equilibration might contribute to a rising electron temperature, especially initially after the shock wave has reached denser protrusions of the ring.

The abundances derived from the two component plan-parallel shock model (cf. Table 4) are higher (on average by a factor of 1.8), than derived by Heng et al. (2008, VPSHOCK+VPSHOCK W00 model). Heng et al. used a similar model but fitted only the 2007 EPIC-pn spectum and derived different plasma parameters (e.g., temperatures), which influences the derived abundances. Compared to the Chandra grating results of Zhekov et al. (2009), our abundances are consistent within 20%, except nitrogen where our value is higher (by a factor of 1.7) but agrees more with the Lundqvist & Fransson (1996) value, and Mg and Fe, for which our values are $\sim$30% lower. We see that the individual modeling causes systematic differences, which are much larger than the statistical errors. We also note that the abundances derived from the plane-parallel shock model are lower than the abundances of the inner ring derived from Lundqvist & Fransson (1996), whereas the abundances of the sedov+powerlaw model are higher. Thus the lower abundances derived so far by X-ray analyse may be caused by the assumption of a two-component plan-parallel shock structure.

As shown in the right panel of Fig. 4, we see a clear indication of an Fe K feature. The black curve in Fig. 4 shows the emission for the shocked plasma of the inner ring, as expected from our two-component shock model, which describes the Fe L lines well. We surprisingly find that the feature implies an emission contribution at lower energy of less ionized, or even neutral, iron, as present in both the unshocked part of the ring and the supernova debris. In the case of a very young ( $\tau_{\rm u}\le3\times 10^{10}$) reverse shock in an iron-rich region, we would also expect emission from other elements in the RGS spectra. If the additional emission were caused by fluorescence (6.4 keV), this would need neutral iron. In this case, the iron could be excited by X-rays from the shocked ring, but this would imply a much higher column density in the unshocked region. Thus the emission might originate in the supernova debris, where a higher column density is possible and reprocessed radiation from nuclear decays might contribute.

5 Conclusions

The main conclusions of our present study are:

1.
With our monitoring, we have been able to follow the detailed evolution of the supernova remnant of SN 1987 A, detecting e.g., an upturn in ionization age and emission measure ratio between 2003 and 2007, which indicates that the blast wave was propagating into the inner ring.

2.
The decrease in line widths at lower energies in-between the first two observations indicate a deceleration of the lower temperature plasma, which correlates well with the decelerating ring expansion observed in the Chandra images.

3.
The electron temperature derived for the soft temperature component with plasma models is consistent with the line widths of the emission lines in the corresponding energy range. This is expected, if the emission is primarily caused by shocks transmitted into denser regions.

4.
The lower quality statistics of the data at higher energies do not justify these conclusions for the high temperature component, where the bulk velocity can be reduced by the contribution of reflected shocks that would also heat the plasma further. But the decrease in temperature with time and the higher line widths seen by XMM-Newton and Chandra rather suggest forward shocks in less denser regions represent the dominating process.

5.
The iron K feature is indicative of a thermal high energy component and little if any non-thermal contribution. The line shape also suggests the contribution (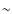$\sim$50%) of a cold iron line (2.3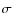$\sigma$ level), possibly emitted from the supernova debris.
Additional future monitoring will yield information about the arising SNR of SN 1987 A, and improved statistics of data for the brightening source will allow even more detailed analyses beyond the assumption of plane-parallel geometry. This might place stronger constraints on the origin of the X-ray emitting regions and their dynamics. The iron K emission may also provide information about the evolution of the debris.

References

  1. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
  2. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
  3. Aschenbach, B. 2007, in Supernova 1987A: 20 Years After: Supernovae and Gamma-Ray Bursters, ed. S. Immler, K. Weiler, & R. McCray, AIP Conf. Ser., 937, 33 [Google Scholar]
  4. Beuermann, K., Brandt, S., & Pietsch, W. 1994, A&A, 281, L45 [NASA ADS] [Google Scholar]
  5. Borkowski, K. J., Lyerly, W. J., & Reynolds, S. P. 2001, ApJ, 548, 820 [NASA ADS] [CrossRef] [Google Scholar]
  6. den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Dewey, D., Zhekov, S. A., McCray, R., & Canizares, C. R. 2008, ApJ, 676, L131 [NASA ADS] [CrossRef] [Google Scholar]
  8. Gaensler, B. M., Staveley-Smith, L., Manchester, R. N., et al. 2007, in Supernova 1987A: 20 Years After: Supernovae and Gamma-Ray Bursters, ed. S. Immler, K. Weiler, & R. McCray, AIP Conf. Ser., 937, 86 [Google Scholar]
  9. Gröningsson, P., Fransson, C., Lundqvist, P., et al. 2006, A&A, 456, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Gröningsson, P., Fransson, C., Leibundgut, B., et al. 2008, A&A, 492, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Haberl, F., Geppert, U., Aschenbach, B., & Hasinger, G. 2006, A&A, 460, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Hasinger, G., Aschenbach, B., & Truemper, J. 1996, A&A, 312, L9 [NASA ADS] [Google Scholar]
  13. Heng, K., McCray, R., Zhekov, S. A., et al. 2006, ApJ, 644, 959 [NASA ADS] [CrossRef] [Google Scholar]
  14. Heng, K., Haberl, F., Aschenbach, B., & Hasinger, G. 2008, ApJ, 676, 361 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hughes, J. P., Hayashi, I., & Koyama, K. 1998, ApJ, 505, 732 [NASA ADS] [CrossRef] [Google Scholar]
  16. Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Lawrence, S. S., Sugerman, B. E., Bouchet, P., et al. 2000, ApJ, 537, L123 [NASA ADS] [CrossRef] [Google Scholar]
  18. Lundqvist, P., & Fransson, C. 1996, ApJ, 464, 924 [NASA ADS] [CrossRef] [Google Scholar]
  19. McCray, R. 2007, in Supernova 1987A: 20 Years After: Supernovae and Gamma-Ray Bursters, ed. S. Immler, K. Weiler, & R. McCray, AIP Conf. Ser., 937, 3 [Google Scholar]
  20. Michael, E., Zhekov, S., McCray, R., et al. 2002, ApJ, 574, 166 [NASA ADS] [CrossRef] [Google Scholar]
  21. Michael, E., McCray, R., Chevalier, R., et al. 2003, ApJ, 593, 809 [NASA ADS] [CrossRef] [Google Scholar]
  22. Ng, C.-Y., Gaensler, B. M., Staveley-Smith, L., et al. 2008, ApJ, 684, 481 [NASA ADS] [CrossRef] [Google Scholar]
  23. Park, S., Zhekov, S. A., Burrows, D. N., et al. 2006, ApJ, 646, 1001 [NASA ADS] [CrossRef] [Google Scholar]
  24. Park, S., Zhekov, S. A., Burrows, D. N., & McCray, R. 2005, ApJ, 634, L73 [NASA ADS] [CrossRef] [Google Scholar]
  25. Plucinsky, P. P., Haberl, F., Dewey, D., et al. 2008, in SPIE Conf. Ser., 7011 [Google Scholar]
  26. Racusin, J. L., Park, S., Zhekov, S., et al. 2009, ApJ, 703, 1752 [NASA ADS] [CrossRef] [Google Scholar]
  27. Rakowski, C. E. 2005, Adv. Space Res., 35, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  28. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Sturm, R., Haberl, F., Hasinger, G., Kenzaki, K., & Itoh, M. 2009, PASJ, 61, 895 [NASA ADS] [Google Scholar]
  30. Turtle, A. J., Campbell-Wilson, D., Manchester, R. N., Staveley-Smith, L., & Kesteven, M. J. 1990, IAU Circ., 5086, 2 [NASA ADS] [Google Scholar]
  31. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
  32. Zhekov, S. A., McCray, R., Borkowski, K. J., Burrows, D. N., & Park, S. 2005, ApJ, 628, L127 [NASA ADS] [CrossRef] [Google Scholar]
  33. Zhekov, S. A., McCray, R., Borkowski, K. J., Burrows, D. N., & Park, S. 2006, ApJ, 645, 293 [NASA ADS] [CrossRef] [Google Scholar]
  34. Zhekov, S. A., McCray, R., Dewey, D., et al. 2009, ApJ, 692, 1190 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... 8.0.0[*]
Science Analysis Software (SAS), http://xmm.vilspa.esa.es/sas/
... 1.3.1[*]
http://cxc.harvard.edu/atomdb/

All Tables

Table 1:   XMM-Newton observations of SN 1987 A and data selection.

Table 2:   Identified lines in the RGS spectra.

Table 3:   Results from the VPSHOCK+VPSHOCK model fits.

Table 4:   Abundances of SN 1987 A.

Table 5:   EPIC-pn fluxes.

All Figures

  \begin{figure} \par\includegraphics[width=6.05cm,angle=-90,clip]{rgs-spec-0.ps}\... ...pace*{1.5mm} \includegraphics[width=6.3cm,angle=-90]{rgs-spec-3.ps} \end{figure} Figure 1:

The RGS1 (black) and RGS2 (red) spectra of SN 1987 A observations in 2003, 2007, 2008, and 2009.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=17.5cm,clip]{sumspec1a.ps}\p... ....ps}\par\includegraphics[angle=-90,width=17.5cm,clip]{sumspec2.ps} \end{figure} Figure 2:

Coadded RGS1 (black) and RGS2 (red) spectra from all 4 observations of SN 1987 A together with the best-fit empirical model (green) and the absorbed bremsstrahlung continuum (blue). The line labels mark the strongest lines expected from the two component vpshock model at the best-fit model energy of the line center.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{lineshift.ps} \end{figure} Figure 3:

Line shifts according to the empirical model. The horizontal line shows the best fit for a systemic redshift. Errors are for $\Delta \chi ^2=2.71$ confidence range.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{18cm}{!}{\includegraphics[clip=,width=6.0cm,angle=... ...residua.ps} \includegraphics[clip=,width=6.0cm,angle=-90]{FeK3.ps}} \end{figure} Figure 4:

Examples for emission line complexes from the summed spectra: N VII Ly $_{\alpha }$, O VIII Ly$_{\beta }$, and the Ne IX triplet as seen by the RGS1 (black) and RGS2 (red). The empirical model and its components are also plotted. In the right panel, an indication of a Fe K feature is seen in the summed EPIC-pn spectrum of the newer three observations. A sum of the high temperature component plane-parallel shock models derived from the individual observations (black) is compared with a model containing an additional Gaussian (red). Horizontal axes: channel energy in keV; vertical axes: counts s-1 keV-1.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{18cm}{!}{\includegraphics[clip=,width=6cm,angle=-9... ...ad \includegraphics[clip=,width=6cm,angle=-90]{lineratios-Ne.ps}} \end{figure} Figure 5:

The lower panels show the light curves of various emission lines with fluxes in 10-5 photons cm-2 s-1. The upper panels show the corresponding line ratios (not absorption corrected). The G-ratio is defined as the helium like line flux ratio of (f+i)/r. Overlapping data points are shifted by 10 days for clarity.

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{17.5cm}{!}{\includegraphics[angle=-90]{rgs+pn-3-2vpshock.ps} \includegraphics[angle=-90]{rgs+pn-3-sedov+po.ps}} \end{figure} Figure 6:

The XMM-Newton RGS1 (black), RGS2 (red) and EPIC-pn (green) spectra of the 2009 observation. Plotted is also a model containing two plane-parallel shock components ( left panel) and a sedov+powerlaw model ( right panel).

Open with DEXTER
In the text

  \begin{figure} \par\resizebox{17cm}{!}{\hspace*{2mm}\includegraphics[clip=,width... ...lip=,width=2.4cm,angle=-90]{vpshock-evolution-8.ps}} \vspace*{-2mm} \end{figure} Figure 7:

Time evolution of the plasma variables: horizontal axes are days after explosion. T1,2 is given in keV, EM1,2 in 1058 cm-3, $\tau _{1,2}$ in 1011 cm-3 s, and $\sigma _0$ in eV.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{linewidth-sumspec-new.ps} \vspace*{-2mm} \end{figure} Figure 8:

Squares denote the bulk gas velocity corresponding to the emission line broadening derived from the Gaussian model fitted to the coadded RGS spectra. Errors are for $\Delta \chi ^2=1$. The solid black line shows the best-fit power-law function to these data points. The other (red) lines show the best-fit power-law functions as derived with the modified vpshock model from the individual spectra. For clarity, the errors are not plotted. Note for the 2003 data in particular the errors are large (cf. Fig. 7 right panels). The horizontal blue lines indicate the post-shock gas velocities produced by strong adiabatic shocks that heat the plasma to a temperatures of kT= 0.5 and 2.5 keV after thermal equilibration.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.